Abstract
As biocatalysts, enzymes are characterized by their high catalytic efficiency and strong specificity but are relatively fragile by requiring narrow and specific reactive conditions for activity. Synthetic catalysts offer an opportunity for more chemical versatility operating over a wider range of conditions but currently do not reach the remarkable performance of natural enzymes. Here we consider some new design strategies based on the contributions of nonlocal electric fields and thermodynamic fluctuations to both improve the catalytic step and turnover for rate acceleration in arbitrary synthetic catalysts through bioinspired studies of natural enzymes. With a focus on the enzyme as a whole catalytic construct, we illustrate the translational impact of natural enzyme principles to synthetic enzymes, supramolecular capsules, and electrocatalytic surfaces.
Short abstract
Designed strategies based on electric fields and thermodynamic fluctuations are considered to improve the catalytic step and turnover in synthetic catalysts through bioinspired studies of natural enzymes.
Introduction
Natural enzymes are marvelous catalysts, operating with high efficiency and selectivity under moderate ambient conditions by performing tasks such as “cold combustion” in the biological cell. An enzyme profits from the chemical precision of the active site at which substrates bind, creating a segregated microenvironment that promotes and stabilizes transition-state formation and shielding the chemical reaction from interference from bulk solvent and/or undesired competing reactions.1 Rational synthetic catalyst design is met with a significant challenge to meet such high biocatalyst standards in performance, and yet, it has the potential to offer profound flexibility and applicability under alternative solvent or interfacial environments, over a wider range of temperature and pressure if desired, and the possibility of performing new types of catalytic chemistry.2
Traditionally, the prime design target for synthetic catalysts is of course both the lowering of the activation free energy and thus the optimization of kcat, as well as the binding affinity through optimization of intermolecular interactions. However, enzymes are much more than an active site utilizing local energetics within a physical protein carrier, but instead are well-integrated, exploiting the benefits of a greater protein scaffold through long-ranged electrostatic organization that also lowers the activation energy3 and harvesting productive dynamical fluctuations that complete the catalytic cycle.4 In this Outlook, we highlight recent promising investigations on design strategies for synthetic catalysts by a focused illumination on these expanded set of principles of natural enzymatic reactions.1,5−7 We consider diverse synthetic catalytic constructs such as supramolecular capsules that accelerate many organic reactions,8,9 fundamental surface science studies that connect to electrocatalysis of CO2 reduction reaction (CO2RR) on metals,10,11 and the improvement in catalysis of so-called de novo enzymes.12−16 In this Outlook, we illustrate how electric field optimization can be used to mitigate or lower reorganization costs for both synthetic enzymes and supramolecular capsules, as well as the remarkable ability of enzymes to utilize thermal fluctuations for activity that has given insight into theoretical approaches to analyzing heterogeneous catalysts for CO2RR.
Natural Enzymes and Electric Field Organization
One of the main strategies for optimizing synthetic catalysts is lowering the energy barrier via transition state stabilization,17,18 which is sensibly focused on the reactive-center energetics. However, the large integrative effect of long-ranged electrostatics from the environment can also play a significant role, such as the solvent environment and folded protein scaffold that can be a determinant for the stabilization of the transition state (TS) relative to the reactant state (RS), ultimately accelerating the chemical process.19,20 As such, natural enzymes minimize the reorganization energy, that is ,the cost of rearrangements of charge distributions and structural changes of the enzyme–substrate interaction along the reaction path with respect to the uncatalyzed reaction in water.3,21−23
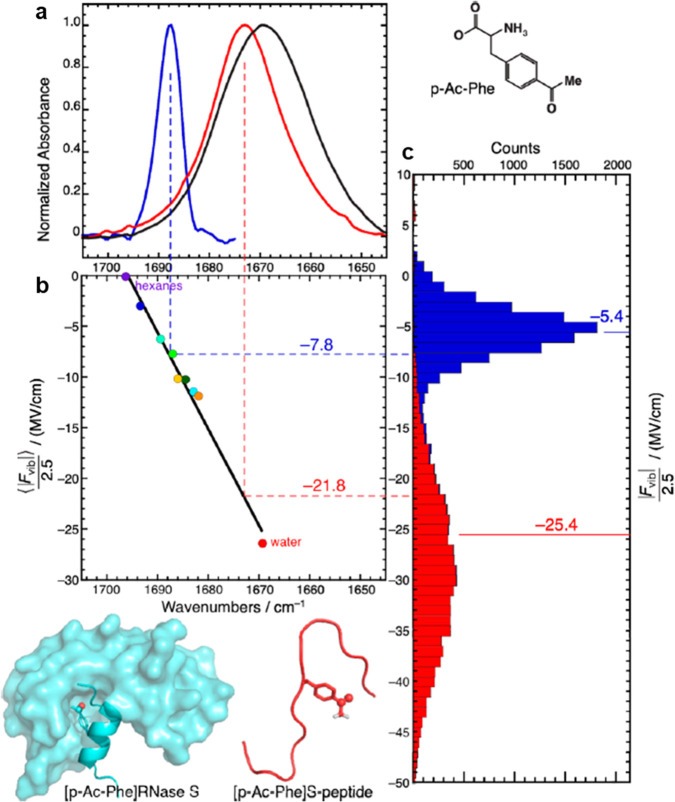
Electric fields are excellent probes of how the protein scaffold is organized to create electrostatic interactions that act on a substrate molecule in the active site. Significant experimental progress in characterizing electric fields within the active site of natural enzymes has been made by Boxer and co-workers using vibrational Stark spectroscopy of C=O vibrations, which we illustrate here for the solvarochromatic probe p-acetyl-l-phenylalanine (p-Ac-Phe) (Figure 1).24 By measuring the C=O vibrational shifts of the free form of p-Ac-Phe under systematic changes in applied electric fields (Figure 1b), this calibration step allows for an “inverted” vibrational Stark measurement to now use the frequency shifts to measure the electric fields when the probe is placed in two different protein constructs, RNase S and S-peptide (Figure 1a). Using molecular simulation to calculate electric fields at the C=O bond from the two different environments of the two proteins, good correlation with the experimental electric field estimate was found (Figure 1c).
Figure 1.
Relationship between C=O vibrational frequency and the corresponding electrostatic field calibrated by a solvatochromic model.24 (a) FTIR spectra of C=O in p-Ac-Phe (black), [p-Ac-Phe]RNase S (blue), and [p-Ac-Phe]S-peptide (red). (b) The calibration of the free p-Ac-Phe with different applied electric fields. Dotted blue and red lines present the experimental data of peak frequencies of the probe placed in the two protein constructs. (c) MD simulated results with the average values illustrated by solid lines that correlate well with the calibration measurement in (b). Permission is obtained from ref (24). Copyright (2013) American Chemical Society.
In enzyme catalysis, the scaffold outside the active site is an important player by creating an electrostatically preferable environment for the catalytic reaction occurring at the reaction center. The natural enzyme ketosteroid isomerase (KSI) serves as an ideal case study25 (Figure 2) to investigate how an electric field contributes to catalytic prowess for a reaction that is effectively diffusion controlled.20,26,27 The groups of Boxer and Markland and co-workers established a linear correlation between the activation free energy of the reaction ΔGelec† and electric fields acting on the KSI active site28 from a set of highly conserved residues (Asp-40 which is the catalytic base, Tyr-16, and Asp-103) that preserves a tightly coupled hydrogen-bonded network when bound to the 19-NT inhibitor (a transition state analogue). A direct connection between the strength of the hydrogen bonding network and the exerting electric field was also established.29
Figure 2.
Ketosteroid Isomerase (KSI). (a) KSI with inhibitor 19-NT in the active site (PDB: 5KP4); (b) active site and reaction mechanism that starts the two-step acid/base process; (c) Electric field projections by KSI residue onto carbonyl bond of 19-NT,4 using molecular dynamic simulations with a polarizable force field. The electric field is the sum of the direct field (from permanent electrostatics) and the induced filed (from the induced dipole term). ∼ 90% of the total electric field comes from the three main active site residues: Asp-40 (−15.85 MV/cm), Tyr-16 (−44.47 MV/cm), and Asp-103 (−37.75 MV/cm). Permission is obtained from ref (4). Copyright (2019) American Chemical Society.
In terms of modeling electrostatic effects in catalysis, Head-Gordon and co-workers and Hammes-Schiffer et al. have utilized a bond dipole (μ) and electric field (E) theoretical model,6,30 which projects the field onto the relevant chemical bonds that break and form along the reaction pathway:19,27
| 1 |
We note that electric field alignment with the transition state’s dipole orientation will accelerate the reaction, a strategy almost exclusively used by natural enzymes (i.e., as opposed to also exploiting reaction state destabilization).17,18,31,32 The bond dipole-field model was used to quantifies the electrostatic effects on free energy (ΔGelec†) using eq 1 for KSI, in which the electric field operator can be broken down by regions from the protein scaffold as well as aqueous solvent organization at the protein surface and from the bulk water.33 From this it has been shown that the electric fields outside the active site (i.e., from the scaffold and bulk solvent) completely support the reactive site transition state energetics, with electric fields well aligned with the carbonyl bond of 19-NT,4 consistent with an enzyme that has minimized its reorganization energy.22
Designed Enzymes
If natural enzymes utilize the whole protein scaffold for catalysis, then it follows that engineering in a new active site into an arbitrary scaffold will detrimentally affect the synthetic enzyme performance. This is illustrated in the de novo design of the Kemp elimination (KE) reaction,34 in which most design strategies have been concentrated on related TIM barrel scaffolds to create different catalytic motifs, such as KE07, KE15, KE59, KE70 and HG3.17.35−38 Mostly these initial rational designs yielded enzymes with marginal performance and thus most often subsequently relied on laboratory directed evolution (LDE),39 a protein engineering tool to steer synthetic enzymes toward enhanced catalytic performance through multiple iterative rounds of mutagenesis36,37,40,41
However, in essence the reorganization energy cost is largely insurmountable in these cases because the scaffold is incommensurate with the new active site chemistry, and the resulting electric field organizations can destabilize the transition state. Hence, the LDE process would have to recreate the entire protein scaffold through an enormous number of mutation rounds that refolded the protein to better support the new reaction center. Instead, time, patience and cost would dictate that we settle on using LDE for a more limited strategy by focusing on and near the active site and the resulting smaller sequence space of mutations to improve the enzyme.
It is undeniable that precise chemical positioning of the substrate in the active site pocket, rigidifying the catalytic residues in de novo proteins such as HG4,42 is central and important. It is also not contradictory with the role of electric fields in and near the active site and from the long-ranged parts of the scaffold. Indeed, both contributions are by definition intimately coupled for determining the reaction rates, as better chemical positioning should correlate with better electric field alignment.43,44 In fact we found that the chemical positioning (i.e., the optimization of the active site base that interacts directly with the substrate) overwhelmingly improved the electric field alignments relative to the original design after 7 rounds of LDE of the catalytic base in KE07-R7.27
Furthermore, Vaissier et al. showed that with these principles, we could instead use computational mutations in the active site that improved electric fields of KE15, a Kemp Eliminase de novo construct that had not undergone LDE. With just four computationally guided “rounds” of mutations R2–R5 starting from the original design R1 (Figure 3a), both chemical positioning and electric field alignment with the transition state can be improved, as experimentally confirmed with a kcat increase of a factor of 50×, which is equivalent to 5–6 rounds of LDE (Figure 3b).43 The chemical positioning of the ligand relative to the catalytic base is a requirement for optimal electric field alignment, as these two factors are coupled since the electric field operator acts as a unifier across all noncovalent effects of excluded volume and protein hydrogen bonding in the active site.
Figure 3.
Electrostatic free energy guided mutations of KE15 (R1) and all improved mutants predicted (R2-R5) from electrostatic calculations using eq 1. (a) Location of the four mutations of KE15 best variant. (b) Electrostatic free energy stabilization diagram of KE15 and all improved mutants predicted from eq 1 for both RS and TS. There is moderate ground state destabilization going from R1 to R2 and R4 to R5, but most of the free energy improvements reported come from transition state stabilization that directly improves the catalytic step.43 Permission is obtained from ref (43). Copyright (2018) American Chemical Society.
Supramolecular Capsule Catalysts
Supramolecular capsules are thermodynamically stable assemblies such as ucurbiturils,45 cyclodextrins,46,47 calixarenes,48,49 and self-assemblies that arise from appropriate stoichiometry of metal and ligands, M4L6 or M6L4.50,51 These synthetic constructs contain cavities that can encapsulate molecules52 and perform catalysis. Here we consider the M4L6 nanocages8,9,50,53,54 that have gained tremendous attention because of their excellent catalytic efficiencies, some with catalytic mechanisms that adhere closely to the Michaelis–Menten scheme55 used for natural metabolic enzymes.50,56−58 These catalytic species are thus thought to be biomimetic, creating an accommodating cavity which shields the reaction center from solvent with good chemical positioning of the substrate. The tetrahedral Ga4L612– cage synthesized by Raymond and co-workers via the metal coordination with naphthalene spacers can entrap an Au (III) complex that dramatically catalyzes a number of reactions as shown by Toste, but illustrated here with the alkyl–alkyl reductive elimination that exhibits a rate acceleration of 5.0 × 105 to 2.5 × 106, as illustrated in Figure 4a.8
Figure 4.
Ga4L612– supramolecular catalyst for reductive elimination from gold complexes.9 (a) Structure of Ga4L612– and the proposed reaction mechanism.8,9,58 (b) The gold complex, the reactive Au–C1 and Au–C2 bonds, and the complexed water molecule position in the transition state; the nanocage and greater water environment are not shown for clarity. (c) The activation free energy stabilization by region using eq 1 for the complexed water molecule, the nanocage, and the remaining water solvent obtained by ensemble-averaged MD calculations.61
In order to understand the encapsulation and reaction chemistry of these supramolecular assemblies, theoretical simulations have provided insight into the origin of their catalysis mechanisms.59−62 Ujaque and co-workers comprehensively investigated the acceleration in methanol solvent (as per the experiment) using high-level theoretical approaches62 in which they determined two local active site factors that reduce the free energy barrier: preference for the encapsulation of the dehalogenated form of the gold complex and variation in the microsolvation events in the nanocage.62
Recently we evaluated electric fields for the same alkyl–alkyl reductive elimination reaction for the Ga4L612- system in water solvent, projecting the electric field onto the bond dipoles Au–C1 and Au–C2 of the methylated gold substrate using eq 1 and yielding an activation energy that is stabilized by ∼5 kcal/mol relative to the uncatalyzed reaction in water. However, in order to understand how closely nanocapsules adhere to enzyme principles, we broke the electric field down into different regions to evaluate their contribution to the activation energy stabilization.60,61 We found that a single encapsulated water molecule (Figure 4b) and the nanocage itself stabilizes the transition state relative to the reactant state, thereby acting as a type of preorganized electrostatic environment when compared with the uncatalyzed reaction in water (Figure 4c). However, the water solvent outside the capsule is found to be highly detrimental (9.02 kcal mol–1) to transition state stabilization, which is only marginally better than the uncatalyzed reaction (10.58 kcal mol–1). In essence the nanocapsule is missing an extended scaffold that either keeps water at a greater distance and/or lacks surface chemistry that can better align solvent dipoles to be commensurate with the active site chemistry. Inspired by these findings, future work can focus on redesign of the ligand and/or metal chemistry, or careful additional chemical support of the nanocage itself, to reduce the reorganization cost of the near water environment to further achieve the reaction rate improvement in nanocapsules.
Conformational Fluctuations in Natural Enzymes
The role of conformational fluctuations and their relative importance to preorganization in biocatalysis has been the subject of a long-standing debate in enzyme chemistry.63,64 Hammes-Schiffer and Benkovic have previously developed a joint theoretical-experimental approach to investigate the relation between enzyme motion and catalytic activity65 for dihydrofolate reductase (DHFR).66,67 Their conclusion is that thermally averaged motions do impact the free energy barrier, contributing to the exponential of the rate expression from transition state theory, but dynamical effects arising from recrossings only effect a prefactor of the rate expression and ultimately are not a decisive factor in the catalysis outcome for DHFR.68 Much later, Boekelheide et al. largely reached the same conclusion for a minimal role for nonlocal vibrational dynamics in DHFR.69 The existence of multiple conformations in apo-enzymes that support binding of substrates are known,5 and recent advances in both experimental and theoretical methods have provided new insights into the role of conformational fluctuations in biocatalysis.70 For example, electron density analysis of high-resolution X-ray crystals detected rotamer changes via the catalytic residue in H-ras, supporting the existence of the conformational fluctuations for catalysis,71 and dynamic regions in both active sites and distal sites of enzymes can be identified by temperature jump X-ray scattering experiments.72 Schwartz and co-workers performed microsecond-scale all-atom molecular dynamic simulations on the reaction catalyzed by lactate dehydrogenase (LDH),73 revealing the conformational heterogeneity within the Michaelis complex of LDH and providing a detailed view of kinetic network to characterize the distribution of the conformations. Very recently, they found that the LDE re-engineering of the enzyme brought about density fluctuations throughout the enzyme reshaped the hydrogen bonding network.70 Hence, conformational motions and their effect on the catalytic step are likely important.
Furthermore, large conformational motions do often reset the enzyme, eliminating the product to complete a catalytic turnover event. While most natural enzymes undergo overt conformational transitions that explain the product release step, it has been a mystery of how an inherently rigid protein like KSI undergoes enzyme turnover. The total electric field involved in the catalytic step emanates from just three residues (Asp-40, Asp-103, and Tyr-16 as seen in Figure 2), giving rise to electric fields that correlate with strong hydrogen-bonding of Tyr-16 and Asp-103 to the NT-19 inhibitor (Figure 5a). However, the entire protein scaffold undergoes a concerted fluctuation on longer time scales—on the order of hundreds of nanoseconds to microseconds—that repacks the side chains of the KSI protein, thereby permitting Asp-103 to adopt a different rotomer state (Figure 5b). This decoupling of the Asp-103 from its binding mode used to stabilize the transition state gives rise to reduced electric fields that are no longer consistent with the catalytic step and in fact signals the release of the NT-19 product-like inhibitor from the active site. It is an astonishing thought that over evolutionary time even thermal fluctuations can be productively utilized for enzyme function, and it illustrates the subtle elegance of these amazing molecular catalysts.
Figure 5.
Electric fields for ketosteroid isomerase (KSI) for both the bound and unbound states between active site residues Tyr-16 and Asp-103 and the 19-NT inhibitor. (a) O–O distance between oxygen atoms in Tyr-16 and Asp-103 to carbonyl oxygen of 19-NT inhibitor in the bound state (the structure is illustrated in Figure 2). (b) The cross-correlation between the total electric field from KSI (black) and the electric fields from Tyr-16 (red) and Asp-103 (green) in the bound state as a function of time. (c) A statistical fluctuation gives rise to a broken hydrogen bond between Asp-103 and NT-19, that (d) reduces the correlation (and magnitude) of the electric field from Asp-103. With permission from ref (4). Copyright (2019) American Chemical Society.
The Importance of Thermal Fluctuations for Heterogeneous Catalysis
As we strive toward reducing greenhouse gas emissions through a closed cycle for carbon, a current success story is that binding CO on Cu produces viable reaction pathways to C1 and C2 products formed from the electrochemical CO2 reduction reaction (CO2RR). However, there has been a long-standing discrepancy between theory and experiment for CO binding on electrocatalytic metals that impedes our mechanistic understanding to push this success story further. While density functional theory (DFT) is the most tractable approach, it has been a challenge for DFT to accurately predict the bare metal surface properties and binding energetics and preferred adsorption sites for the CO intermediate on electrocatalytically relevant metals with weak (Ag, Au) to strong (Cu, Pt) binding surfaces for the CO2RR. At present almost all affordable GGA and meta-GGA DFT functionals tend to overbind CO, and also fail to predict the preferred atop metal site for chemisorption. In fact, at present, the preferred DFT functional of choice is RPBE, which tends to better minimize this overbinding problem, presumably by not accounting for attractive dispersion,74 although dispersion forces are a universal intermolecular interaction.
Inspired by enzymatic cases like KSI, thermal motion should also play a crucial role in influencing the reaction mechanism and determining the energetic stability of CO binding (and other reactants, intermediates, and products) in heterogeneous catalysis of CO2RR.75,76 Yet, for nearly all electrocatalysis DFT studies, all absorbate and surface properties are evaluated at 0 K, although all experiments produce observables at finite temperatures. While entropic corrections based on the harmonic approximations have been used to address this discrepancy, such corrections do not actually describe true thermal fluctuations, statistical averaging, and relaxation processes that may influence catalytic outcomes in electrocatalysis. In fact, Wang and Hu thoroughly investigated CO adsorption/desorption on Pt(111) using MD simulations to further understand CO adsorption on Pt(111),75 where they found the atop site is more preferable for the CO adsorption, in agreement with experimental observations. These findings indicate that proper accounting of statistical mechanics in addition to quantum mechanics is necessary for this important problem.
In our own work, we found that thermalization activates metal surface relaxation modes that allow for more systematic preference for low-coordinated metal surface sites for both the popular RPBE GGA and newer B97M-rV meta-GGA functionals for both Cu(111) and Pt(111). While it is true that RPBE now does much more poorly than B97M-rV for the weakly binding Au(111) and Ag(111) metals–for the reason that the former does not have a dispersion correction that would stabilize binding against kbT fluctuations—what is more interesting is that a good DFT functional gives us a first look at the CO binding motifs on the weak binding metal surfaces, which we find is a mixture of chemisorbed and physisorbed species (Figure 6).
Figure 6.

Representative configuration showing the mixture of chemisorbed and physisorbed CO molecules (circled in green) at the last 2.0 ps time point of the AIMD simulation for CO binding to Ag(111) for B97M-rV. The statistical data is collected after 500 fs’s pre-equilibration for the 2 ps trajectories.
This work better places theory as an equal partner to experimental electrocatalysis and heterogeneous catalysis in general, which has been stymied by an incorrect focus on the problems of electronic structure at 0 K. We note that a meta-GGA such as B97M-rV has been shown to yield excellent bulk water properties77,78 and that great strides have now been made such that theory is now capable of reliably modeling the liquid–solid interface.
Conclusions and Outlook
The idea of using biomimetic principles for improving synthetic analogues, in this case for catalysis, is not a new idea. However, while electrostatic preorganization ideas have been promulgated by Warshel and co-workers since the 1980s in regard to enzyme catalysis, these ideas are seeing a renaissance in applications to many other areas of chemical reactivity.79 Many exciting examples of electrostatic principles include the use of orienting electric fields to marshal the large collective effect of solvent on reactive chemistry,80 mechanistic understanding of CO activation in electrocatalytic CO2RR,81 and driving famous organic chemistry reactions such as Diels–Alder at surfaces.82 There seems to be no limit at present to reaching out further into broader categories of catalysts containing modifiable “pocket” frameworks, such as supramolecular assemblies, zeolites, and metal organic frameworks for which externally applied electric fields can be used to change or accelerate reaction outcome. What we are suggesting instead is that the catalytic construct itself can create and/or tune the orienting electric fields through modifications of intermolecular interactions, for example, through point mutations, functionalization of the chemical structure, and/or changing solvent polarity.19
The importance of thermal fluctuations is evident in a number of catalytic systems, for example, the ion fluctuations in the double layer at an electrocatalytic surface that can rearrange charge distributions and reactant concentration near the solid–liquid interface, thereby modulating the reaction rate.83 In the critical stage of a surface reaction, a thermal fluctuation brings the density of states (DOS) of the adsorbates to activated states, and the reaction is promoted because it bridges the Fermi level and is partially filled.84−86 However, we still consider exploiting statistical fluctuations and thermal motion as a design strategy is an area in its infancy for driving greater catalytic activity. This will likely be much more challenging to control and utilize, just as any entropic effect is by definition not easily harnessed. However, by considering the exquisite control of statistical fluctuations utilized by enzymes almost literally, it seems that there should be imaginative ways for conformational variation to be included in any reactive scaffold to drive through a catalytic cycle.
Acknowledgments
This work was supported under the CPIMS program by the Director, Office of Science, Office of Basic Energy Sciences, Chemical Sciences Division of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
The authors declare no competing financial interest.
References
- Wolfenden R.; Snider M. J. The Depth of Chemical Time and the Power of Enzymes as Catalysts. Acc. Chem. Res. 2001, 34 (12), 938. 10.1021/ar000058i. [DOI] [PubMed] [Google Scholar]
- Chokhawala H. A.; Roche C. M.; Kim T.-W.; Atreya M. E.; Vegesna N.; Dana C. M.; Blanch H. W.; Clark D. S. Mutagenesis of Trichoderma reesei endoglucanase I: impact of expression host on activity and stability at elevated temperatures. BMC Biotechnol. 2015, 15 (1), 11. 10.1186/s12896-015-0118-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel A. Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites. J. Biol. Chem. 1998, 273 (42), 27035. 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
- Welborn V. V.; Head-Gordon T. Fluctuations of Electric Fields in the Active Site of the Enzyme Ketosteroid Isomerase. J. Am. Chem. Soc. 2019, 141 (32), 12487. 10.1021/jacs.9b05323. [DOI] [PubMed] [Google Scholar]
- Benkovic S. J.; Hammes G. G.; Hammes-Schiffer S. Free-Energy Landscape of Enzyme Catalysis. Biochemistry 2008, 47 (11), 3317. 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
- Liu C. T.; Layfield J. P.; Stewart R. J.; French J. B.; Hanoian P.; Asbury J. B.; Hammes-Schiffer S.; Benkovic S. J. Probing the Electrostatics of Active Site Microenvironments along the Catalytic Cycle for Escherichia coli Dihydrofolate Reductase. J. Am. Chem. Soc. 2014, 136 (29), 10349. 10.1021/ja5038947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak W. S.; Siegel J. B. Computational enzyme design: Transitioning from catalytic proteins to enzymes. Curr. Opin. Struct. Biol. 2014, 27, 87. 10.1016/j.sbi.2014.05.010. [DOI] [PubMed] [Google Scholar]
- Kaphan D. M.; Levin M. D.; Bergman R. G.; Raymond K. N.; Toste F. D. A supramolecular microenvironment strategy for transition metal catalysis. Science 2015, 350 (6265), 1235. 10.1126/science.aad3087. [DOI] [PubMed] [Google Scholar]
- Levin M. D.; Kaphan D. M.; Hong C. M.; Bergman R. G.; Raymond K. N.; Toste F. D. Scope and Mechanism of Cooperativity at the Intersection of Organometallic and Supramolecular Catalysis. J. Am. Chem. Soc. 2016, 138 (30), 9682. 10.1021/jacs.6b05442. [DOI] [PubMed] [Google Scholar]
- Nitopi S.; Bertheussen E.; Scott S. B.; Liu X.; Engstfeld A. K.; Horch S.; Seger B.; Stephens I. E. L.; Chan K.; Hahn C.; et al. Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte. Chem. Rev. 2019, 119 (12), 7610. 10.1021/acs.chemrev.8b00705. [DOI] [PubMed] [Google Scholar]
- Fan L.; Xia C.; Yang F.; Wang J.; Wang H.; Lu Y. Strategies in catalysts and electrolyzer design for electrochemical CO2 reduction toward C2+ products. Sci. Adv. 2020, 6 (8), eaay3111. 10.1126/sciadv.aay3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel J. B.; Zanghellini A.; Lovick H. M.; Kiss G.; Lambert A. R.; St.Clair J. L.; Gallaher J. L.; Hilvert D.; Gelb M. H.; Stoddard B. L.; et al. Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction. Science 2010, 329 (5989), 309. 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong Z.; Luo Q.; Liu J. Artificial Enzymes Based on Supramolecular Scaffolds. Chem. Soc. Rev. 2012, 41 (23), 7890. 10.1039/c2cs35207a. [DOI] [PubMed] [Google Scholar]
- Korendovych I. V.; DeGrado W. F. Catalytic efficiency of designed catalytic proteins. Curr. Opin. Struct. Biol. 2014, 27, 113. 10.1016/j.sbi.2014.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly A. E.; Murphy G. S.; Digianantonio K. M.; Hecht M. H. A de novo enzyme catalyzes a life-sustaining reaction in Escherichia coli. Nat. Chem. Biol. 2018, 14 (3), 253. 10.1038/nchembio.2550. [DOI] [PubMed] [Google Scholar]
- Basanta B.; Bick M. J.; Bera A. K.; Norn C.; Chow C. M.; Carter L. P.; Goreshnik I.; Dimaio F.; Baker D. An enumerative algorithm for de novo design of proteins with diverse pocket structures. Proc. Natl. Acad. Sci. U. S. A. 2020, 117 (36), 22135. 10.1073/pnas.2005412117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frushicheva M. P.; Cao J.; Chu Z. T.; Warshel A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proc. Natl. Acad. Sci. U. S. A. 2010, 107 (39), 16869. 10.1073/pnas.1010381107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frushicheva M. P.; Cao J.; Warshel A. Challenges and Advances in Validating Enzyme Design Proposals: The Case of Kemp Eliminase Catalysis. Biochemistry 2011, 50 (18), 3849. 10.1021/bi200063a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welborn V. V.; Ruiz Pestana L.; Head-Gordon T. Computational optimization of electric fields for better catalysis design. Nature Catalysis 2018, 1 (9), 649. 10.1038/s41929-018-0109-2. [DOI] [Google Scholar]
- Fried S. D.; Boxer S. G. Electric Fields and Enzyme Catalysis. Annu. Rev. Biochem. 2017, 86 (1), 387. 10.1146/annurev-biochem-061516-044432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuxreiter M.; Mones L. The role of reorganization energy in rational enzyme design. Curr. Opin. Chem. Biol. 2014, 21, 34. 10.1016/j.cbpa.2014.03.011. [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C. L.; Sharma P. K.; Chu Z. T.; Warshel A. Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proc. Natl. Acad. Sci. U. S. A. 2010, 107 (9), 4075. 10.1073/pnas.0914579107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel A.; Sharma P. K.; Kato M.; Xiang Y.; Liu H.; Olsson M. H. M. Electrostatic Basis for Enzyme Catalysis. Chem. Rev. 2006, 106 (8), 3210. 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- Fried S. D.; Bagchi S.; Boxer S. G. Measuring Electrostatic Fields in Both Hydrogen-Bonding and Non-Hydrogen-Bonding Environments Using Carbonyl Vibrational Probes. J. Am. Chem. Soc. 2013, 135 (30), 11181. 10.1021/ja403917z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried S. D.; Bagchi S.; Boxer S. G. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 2014, 346 (6216), 1510. 10.1126/science.1259802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollack R. M. Enzymatic mechanisms for catalysis of enolization: ketosteroid isomerase. Bioorg. Chem. 2004, 32 (5), 341. 10.1016/j.bioorg.2004.06.005. [DOI] [PubMed] [Google Scholar]
- Bhowmick A.; Sharma S. C.; Head-Gordon T. The Importance of the Scaffold for de Novo Enzymes: A Case Study with Kemp Eliminase. J. Am. Chem. Soc. 2017, 139 (16), 5793. 10.1021/jacs.6b12265. [DOI] [PubMed] [Google Scholar]
- Wu Y.; Boxer S. G. A Critical Test of the Electrostatic Contribution to Catalysis with Noncanonical Amino Acids in Ketosteroid Isomerase. J. Am. Chem. Soc. 2016, 138 (36), 11890. 10.1021/jacs.6b06843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.; Fried S. D.; Markland T. E. Proton Network Flexibility Enables Robustness and Large Electric Fields in the Ketosteroid Isomerase Active Site. J. Phys. Chem. B 2017, 121 (42), 9807. 10.1021/acs.jpcb.7b06985. [DOI] [PubMed] [Google Scholar]
- Reppert M.; Tokmakoff A. Computational Amide I 2D IR Spectroscopy as a Probe of Protein Structure and Dynamics. Annu. Rev. Phys. Chem. 2016, 67 (1), 359. 10.1146/annurev-physchem-040215-112055. [DOI] [PubMed] [Google Scholar]
- Jindal G.; Ramachandran B.; Bora R. P.; Warshel A. Exploring the Development of Ground-State Destabilization and Transition-State Stabilization in Two Directed Evolution Paths of Kemp Eliminases. ACS Catal. 2017, 7 (5), 3301. 10.1021/acscatal.7b00171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaissier Welborn V.; Head-Gordon T. Computational Design of Synthetic Enzymes. Chem. Rev. 2019, 119, 6613. 10.1021/acs.chemrev.8b00399. [DOI] [PubMed] [Google Scholar]
- Fried S. D.; Boxer S. G. Measuring Electric Fields and Noncovalent Interactions Using the Vibrational Stark Effect. Acc. Chem. Res. 2015, 48 (4), 998. 10.1021/ar500464j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Röthlisberger D.; Khersonsky O.; Wollacott A. M.; Jiang L.; DeChancie J.; Betker J.; Gallaher J. L.; Althoff E. A.; Zanghellini A.; Dym O.; et al. Kemp elimination catalysts by computational enzyme design. Nature 2008, 453 (7192), 190. 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- Khersonsky O.; Röthlisberger D.; Dym O.; Albeck S.; Jackson C. J.; Baker D.; Tawfik D. S. Evolutionary Optimization of Computationally Designed Enzymes: Kemp Eliminases of the KE07 Series. J. Mol. Biol. 2010, 396 (4), 1025. 10.1016/j.jmb.2009.12.031. [DOI] [PubMed] [Google Scholar]
- Khersonsky O.; Röthlisberger D.; Wollacott A. M.; Murphy P.; Dym O.; Albeck S.; Kiss G.; Houk K. N.; Baker D.; Tawfik D. S. Optimization of the In-Silico-Designed Kemp Eliminase KE70 by Computational Design and Directed Evolution. J. Mol. Biol. 2011, 407 (3), 391. 10.1016/j.jmb.2011.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blomberg R.; Kries H.; Pinkas D. M.; Mittl P. R. E.; Grütter M. G.; Privett H. K.; Mayo S. L.; Hilvert D. Precision is essential for efficient catalysis in an evolved Kemp eliminase. Nature 2013, 503 (7476), 418. 10.1038/nature12623. [DOI] [PubMed] [Google Scholar]
- Khersonsky O.; Kiss G.; Röthlisberger D.; Dym O.; Albeck S.; Houk K. N.; Baker D.; Tawfik D. S. Bridging the Gaps in Design Methodologies by Evolutionary Optimization of the Stability and Proficiency of Designed Kemp Eliminase KE59. Proc. Natl. Acad. Sci. U. S. A. 2012, 109 (26), 10358. 10.1073/pnas.1121063109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold F. H. Design by directed evolution. Acc. Chem. Res. 1998, 31 (3), 125. 10.1021/ar960017f. [DOI] [Google Scholar]
- Giger L.; Caner S.; Obexer R.; Kast P.; Baker D.; Ban N.; Hilvert D. Evolution of a designed retro-aldolase leads to complete active site remodeling. Nat. Chem. Biol. 2013, 9 (8), 494. 10.1038/nchembio.1276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunzel H. A.; Kries H.; Marchetti L.; Zeymer C.; Mittl P. R. E.; Mulholland A. J.; Hilvert D. Emergence of a Negative Activation Heat Capacity during Evolution of a Designed Enzyme. J. Am. Chem. Soc. 2019, 141 (30), 11745. 10.1021/jacs.9b02731. [DOI] [PubMed] [Google Scholar]
- Broom A.; Rakotoharisoa R. V.; Thompson M. C.; Zarifi N.; Nguyen E.; Mukhametzhanov N.; Liu L.; Fraser J. S.; Chica R. A. Ensemble-based enzyme design can recapitulate the effects of laboratory directed evolution in silico. Nat. Commun. 2020, 11 (1), 4808. 10.1038/s41467-020-18619-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaissier V. V.; Sharma S. C.; Schaettle K.; Zhang T.; Head-Gordon T. Computational Optimization of Electric Fields for Improving Catalysis of a Designed Kemp Eliminase. ACS Catal. 2018, 8 (1), 219. 10.1021/acscatal.7b03151. [DOI] [Google Scholar]
- Hennefarth M. R.; Alexandrova A. N. Direct Look at the Electric Field in Ketosteroid Isomerase and Its Variants. ACS Catal. 2020, 10 (17), 9915. 10.1021/acscatal.0c02795. [DOI] [Google Scholar]
- Klöck C.; Dsouza R. N.; Nau W. M. Cucurbituril-Mediated Supramolecular Acid Catalysis. Org. Lett. 2009, 11 (12), 2595. 10.1021/ol900920p. [DOI] [PubMed] [Google Scholar]
- Szejtli J. Introduction and General Overview of Cyclodextrin Chemistry. Chem. Rev. 1998, 98 (5), 1743. 10.1021/cr970022c. [DOI] [PubMed] [Google Scholar]
- Schneider H.-J.; Hacket F.; Rüdiger V.; Ikeda H. NMR Studies of Cyclodextrins and Cyclodextrin Complexes. Chem. Rev. 1998, 98 (5), 1755. 10.1021/cr970019t. [DOI] [PubMed] [Google Scholar]
- Ikeda A.; Shinkai S. Novel Cavity Design Using Calix[n]arene Skeletons: Toward Molecular Recognition and Metal Binding. Chem. Rev. 1997, 97 (5), 1713. 10.1021/cr960385x. [DOI] [PubMed] [Google Scholar]
- Schühle D. T.; Peters J. A.; Schatz J. Metal binding calixarenes with potential biomimetic and biomedical applications. Coord. Chem. Rev. 2011, 255 (23), 2727. 10.1016/j.ccr.2011.04.005. [DOI] [Google Scholar]
- Brown C. J.; Toste F. D.; Bergman R. G.; Raymond K. N. Supramolecular Catalysis in Metal–Ligand Cluster Hosts. Chem. Rev. 2015, 115 (9), 3012. 10.1021/cr4001226. [DOI] [PubMed] [Google Scholar]
- Pappalardo A.; Puglisi R.; Trusso Sfrazzetto G. Catalysis inside Supramolecular Capsules: Recent Developments. Catalysts 2019, 9 (7), 630. 10.3390/catal9070630. [DOI] [Google Scholar]
- Koblenz T. S.; Wassenaar J.; Reek J. N. H. Reactivity within a confined self-assembled nanospace. Chem. Soc. Rev. 2008, 37 (2), 247. 10.1039/B614961H. [DOI] [PubMed] [Google Scholar]
- Yan K.; Fujita M. A speedy marriage in supramolecular catalysis. Science 2015, 350 (6265), 1165. 10.1126/science.aad7245. [DOI] [PubMed] [Google Scholar]
- Hart-Cooper W. M.; Sgarlata C.; Perrin C. L.; Toste F. D.; Bergman R. G.; Raymond K. N. Protein-like proton exchange in a synthetic host cavity. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (50), 15303. 10.1073/pnas.1515639112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelis L.; Menten M. M. L. The kinetics of invertin action. FEBS Lett. 2013, 587 (17), 2712. 10.1016/j.febslet.2013.07.015. [DOI] [PubMed] [Google Scholar]
- Wiester M. J.; Ulmann P. A.; Mirkin C. A. Enzyme Mimics Based Upon Supramolecular Coordination Chemistry. Angew. Chem., Int. Ed. 2011, 50 (1), 114. 10.1002/anie.201000380. [DOI] [PubMed] [Google Scholar]
- Cullen W.; Misuraca M. C.; Hunter C. A.; Williams N. H.; Ward M. D. Highly efficient catalysis of the Kemp elimination in the cavity of a cubic coordination cage. Nat. Chem. 2016, 8 (3), 231. 10.1038/nchem.2452. [DOI] [PubMed] [Google Scholar]
- Hong C. M.; Bergman R. G.; Raymond K. N.; Toste F. D. Self-Assembled Tetrahedral Hosts as Supramolecular Catalysts. Acc. Chem. Res. 2018, 51 (10), 2447. 10.1021/acs.accounts.8b00328. [DOI] [PubMed] [Google Scholar]
- Xu L.; Hua W.; Hua S.; Li J.; Li S. Mechanistic Insight on the Diels–Alder Reaction Catalyzed by a Self-Assembled Molecular Capsule. J. Org. Chem. 2013, 78 (8), 3577. 10.1021/jo4000509. [DOI] [PubMed] [Google Scholar]
- Vaissier Welborn V.; Head-Gordon T. Electrostatics Generated by a Supramolecular Capsule Stabilizes the Transition State for Carbon–Carbon Reductive Elimination from Gold(III) Complex. J. Phys. Chem. Lett. 2018, 9 (14), 3814. 10.1021/acs.jpclett.8b01710. [DOI] [PubMed] [Google Scholar]
- Welborn V. V.; Li W.-L.; Head-Gordon T. Interplay of water and a supramolecular capsule for catalysis of reductive elimination reaction from gold. Nat. Commun. 2020, 11 (1), 415. 10.1038/s41467-019-14251-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norjmaa G.; Maréchal J.-D.; Ujaque G. Microsolvation and Encapsulation Effects on Supramolecular Catalysis: C–C Reductive Elimination inside [Ga4L6]12– Metallocage. J. Am. Chem. Soc. 2019, 141 (33), 13114. 10.1021/jacs.9b04909. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Bora R. P. Perspective: Defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 2016, 144 (18), 180901. 10.1063/1.4947037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohen A. Role of Dynamics in Enzyme Catalysis: Substantial versus Semantic Controversies. Acc. Chem. Res. 2015, 48 (2), 466. 10.1021/ar500322s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanoian P.; Liu C. T.; Hammes-Schiffer S.; Benkovic S. Perspectives on Electrostatics and Conformational Motions in Enzyme Catalysis. Acc. Chem. Res. 2015, 48 (2), 482. 10.1021/ar500390e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agarwal P. K.; Billeter S. R.; Hammes-Schiffer S. Nuclear Quantum Effects and Enzyme Dynamics in Dihydrofolate Reductase Catalysis. J. Phys. Chem. B 2002, 106 (12), 3283. 10.1021/jp020190v. [DOI] [Google Scholar]
- Agarwal P. K.; Billeter S. R.; Rajagopalan P. T. R.; Benkovic S. J.; Hammes-Schiffer S. Network of coupled promoting motions in enzyme catalysis. Proc. Natl. Acad. Sci. U. S. A. 2002, 99 (5), 2794. 10.1073/pnas.052005999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammes-Schiffer S. Impact of Enzyme Motion on Activity. Biochemistry 2002, 41 (45), 13335. 10.1021/bi0267137. [DOI] [PubMed] [Google Scholar]
- Boekelheide N.; Salomón-Ferrer R.; Miller T. F. Dynamics and dissipation in enzyme catalysis. Proc. Natl. Acad. Sci. U. S. A. 2011, 108 (39), 16159. 10.1073/pnas.1106397108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer J. W.; Schwartz S. D. Directed Evolution’s Influence on Rapid Density Fluctuations Illustrates How Protein Dynamics Can Become Coupled to Chemistry. ACS Catal. 2020, 10 (15), 8476. 10.1021/acscatal.0c01618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawaya M. R.; Kraut J. Loop and Subdomain Movements in the Mechanism of Escherichia coli Dihydrofolate Reductase: Crystallographic Evidence. Biochemistry 1997, 36 (3), 586. 10.1021/bi962337c. [DOI] [PubMed] [Google Scholar]
- Thompson M. C.; Barad B. A.; Wolff A. M.; Sun Cho H.; Schotte F.; Schwarz D. M. C.; Anfinrud P.; Fraser J. S. Temperature-jump solution X-ray scattering reveals distinct motions in a dynamic enzyme. Nat. Chem. 2019, 11 (11), 1058. 10.1038/s41557-019-0329-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan X.; Schwartz S. D. Free Energy Surface of the Michaelis Complex of Lactate Dehydrogenase: A Network Analysis of Microsecond Simulations. J. Phys. Chem. B 2015, 119 (17), 5430. 10.1021/acs.jpcb.5b01840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer B.; Hansen L. B.; Nørskov J. K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59 (11), 7413. 10.1103/PhysRevB.59.7413. [DOI] [Google Scholar]
- Guo C.; Wang Z.; Wang D.; Wang H.-F.; Hu P. First-Principles Determination of CO Adsorption and Desorption on Pt(111) in the Free Energy Landscape. J. Phys. Chem. C 2018, 122 (37), 21478. 10.1021/acs.jpcc.8b06782. [DOI] [Google Scholar]
- Li W.-L.; Lininger C. N.; Welborn V. V.; Rossomme E.; Bell A. T.; Head-Gordon M.; Head-Gordon T.. The Critical Role of Thermal Fluctuations for Electrocatalytic Metal Surface Properties and CO Binding Trends. arXiv (Chemical Physics), June 6, 2020, arXiv:2006.03971. https://arxiv.org/abs/2006.03971. [Google Scholar]
- Pestana L. R.; Marsalek O.; Markland T. E.; Head-Gordon T. The Quest for Accurate Liquid Water Properties from First Principles. J. Phys. Chem. Lett. 2018, 9 (17), 5009. 10.1021/acs.jpclett.8b02400. [DOI] [PubMed] [Google Scholar]
- Pestana L. R.; Mardirossian N.; Head-Gordon M.; Head-Gordon T. Ab initio molecular dynamics simulations of liquid water using high quality meta-GGA functionals. Chemical Science 2017, 8 (5), 3554. 10.1039/C6SC04711D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaik S.; Danovich D.; Joy J.; Wang Z.; Stuyver T. Electric-Field Mediated Chemistry: Uncovering and Exploiting the Potential of (Oriented) Electric Fields to Exert Chemical Catalysis and Reaction Control. J. Am. Chem. Soc. 2020, 142 (29), 12551. 10.1021/jacs.0c05128. [DOI] [PubMed] [Google Scholar]
- Dutta Dubey K.; Stuyver T.; Kalita S.; Shaik S. Solvent Organization and Rate Regulation of a Menshutkin Reaction by Oriented External Electric Fields are Revealed by Combined MD and QM/MM Calculations. J. Am. Chem. Soc. 2020, 142 (22), 9955. 10.1021/jacs.9b13029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L. D.; Urushihara M.; Chan K.; Nørskov J. K. Electric Field Effects in Electrochemical CO2 Reduction. ACS Catal. 2016, 6 (10), 7133. 10.1021/acscatal.6b02299. [DOI] [Google Scholar]
- Aragonès A. C.; Haworth N. L.; Darwish N.; Ciampi S.; Bloomfield N. J.; Wallace G. G.; Diez-Perez I.; Coote M. L. Electrostatic catalysis of a Diels–Alder reaction. Nature 2016, 531, 88. 10.1038/nature16989. [DOI] [PubMed] [Google Scholar]
- Liu M.; Pang Y.; Zhang B.; De Luna P.; Voznyy O.; Xu J.; Zheng X.; Dinh C. T.; Fan F.; Cao C.; et al. Enhanced electrocatalytic CO2 reduction via field-induced reagent concentration. Nature 2016, 537 (7620), 382. 10.1038/nature19060. [DOI] [PubMed] [Google Scholar]
- Santos E.; Schmickler W. Fundamental aspects of electrocatalysis. Chem. Phys. 2007, 332 (1), 39. 10.1016/j.chemphys.2006.11.033. [DOI] [Google Scholar]
- Santos E.; Schmickler W. Electrocatalysis of Hydrogen Oxidation—Theoretical Foundations. Angew. Chem., Int. Ed. 2007, 46 (43), 8262. 10.1002/anie.200702338. [DOI] [PubMed] [Google Scholar]
- Forster R. J.; Loughman P.; Keyes T. E. Effect of Electrode Density of States on the Heterogeneous Electron-Transfer Dynamics of Osmium-Containing Monolayers. J. Am. Chem. Soc. 2000, 122 (48), 11948. 10.1021/ja002616u. [DOI] [Google Scholar]