Skip to main content
NCBI home page
ACS Central Science logoLink to ACS Central Science
. 2020 Dec 29;7(1):135–144. doi: 10.1021/acscentsci.0c01153

Monodisperse Long-Chain Sulfobetaine-Capped CsPbBr3 Nanocrystals and Their Superfluorescent Assemblies

Franziska Krieg †,‡, Peter C Sercel §,∥, Max Burian ⊥, Hordii Andrusiv †,‡, Maryna I Bodnarchuk †,‡, Thilo Stöferle #, Rainer F Mahrt #, Denys Naumenko ∇, Heinz Amenitsch ∇, Gabriele Rainò †,‡, Maksym V Kovalenko †,‡,*
PMCID: PMC7845019  PMID: 33532576

Abstract

graphic file with name oc0c01153_0006.jpg

Ligand-capped nanocrystals (NCs) of lead halide perovskites, foremost fully inorganic CsPbX3 NCs, are the latest generation of colloidal semiconductor quantum dots. They offer a set of compelling characteristics—large absorption cross section, as well as narrow, fast, and efficient photoluminescence with long exciton coherence times—rendering them attractive for applications in light-emitting devices and quantum optics. Monodisperse and shape-uniform, broadly size-tunable, scalable, and robust NC samples are paramount for unveiling their basic photophysics, as well as for putting them into use. Thus far, no synthesis method fulfilling all these requirements has been reported. For instance, long-chain zwitterionic ligands impart the most durable surface coating, but at the expense of reduced size uniformity of the as-synthesized colloid. In this work, we demonstrate that size-selective precipitation of CsPbBr3 NCs coated with a long-chain sulfobetaine ligand, namely, 3-(N,N-dimethyloctadecylammonio)-propanesulfonate, yields monodisperse and sizable fractions (>100 mg inorganic mass) with the mean NC size adjustable in the range between 3.5 and 16 nm and emission peak wavelength between 479 and 518 nm. We find that all NCs exhibit an oblate cuboidal shape with the aspect ratio of 1.2 × 1.2 × 1. We present a theoretical model (effective mass/k·p) that accounts for the anisotropic NC shape and describes the size dependence of the first and second excitonic transition in absorption spectra and explains room-temperature exciton lifetimes. We also show that uniform zwitterion-capped NCs readily form long-range ordered superlattices upon solvent evaporation. In comparison to more conventional ligand systems (oleic acid and oleylamine), supercrystals of zwitterion-capped NCs exhibit larger domain sizes and lower mosaicity. Both kinds of supercrystals exhibit superfluorescence at cryogenic temperatures—accelerated collective emission arising from the coherent coupling of the emitting dipoles.

Short abstract

We report scalable isolation of monodisperse ensembles of long-chain zwitterion-capped CsPbBr3 nanocrystals, their size-dependent optical characteristics, and superfluorescent, long-range ordered superlattice assemblies.

In the past five years, colloidal nanocrystals (NCs) of lead-halide perovskites (APbX3, A = methylammonium, formamidinium, or cesium, and X = Cl, Br, I),1−6 chiefly CsPbX3 NCs, have become a highly popular class of light emitters, considered for applications in LEDs,7−9 LCD displays,10,11 lasers,12−15 photodetectors,16,17 scintillators,18,19 solar cells20−22 and solar concentrators,23−28 and quantum light applications.29−35 Perovskite semiconductors are often praised for their defect tolerance,3,36−41 which manifests itself in NCs as a bright photoluminescence (PL) without the necessity for electronic surface passivation with epitaxial shells.3,42,43 The PL of perovskite NCs spans the entire visible spectral range (410–800 nm), with small emission line widths (<100 meV) and high PL quantum yields (QYs) of up to unity.

The backstage problems of perovskite NCs are mainly rooted in their much higher structural lability,36 as compared to earlier generations of colloidal quantum dots (metal chalcogenides and pnictides), owing to more ionic bonding and finite solubility in polar solvents, low internal lattice energy, and dynamic and loose ligand binding.45−47 At present, there exists no synthesis method that yields monodisperse perovskite NCs that are broadly tunable in their mean size and yet are sufficiently durable for diverse purposes. The latter range from the basic photophysics studies at single-particle and ensemble levels to self-assembly and integration into devices. A typical problem encountered is the loss of ligands and subsequent disintegration of NCs upon intense purification (especially NCs smaller than 6 nm),45−47 in the case of standard ligand systems comprising carboxylic acids and primary5 or secondary amines,48 such as oleic acid/oleylamine capping (OA/OLA). We note that the synthesis difficulties are the sole reason why small NCs (sub-8 nm) are not well-characterized across the entire APbX3 compositional space, except for CsPbBr3.49−51

We have recently shown that tight ligand binding and hence improved colloidal stability, which is retained also after multiple steps of isolation and purification, can be imparted using long-chain zwitterionic ligands such as synthetic sulfobetaines, phosphocholines, and γ-amino acids52 and natural lecithin.53 Importantly, the syntheses with zwitterionic ligands have gram-scale yields of NCs at conventional reaction scales (20–50 mL of the crude solution). Among these ligands, long-chain sulfobetaines, such as 3-(N,N-dimethyloctadecylammonio)-propanesulfonate (denote further as ASC18), allow for the widest tuning of the mean NC size (by the reaction temperature). The only apparent shortcoming of zwitterionic capping is a relatively broad initial size distribution in crude solutions of ca. 50%. This difficulty is commonplace for other ligands, too, and can be ascribed to very fast reaction kinetics with inefficient separation of nucleation and growth events.5,54 It is also likely that Ostwald ripening can occur in unpurified crude solutions even at room temperature and hence contributes to the broadening of the NC size distribution.55 In known reports on monodisperse perovskite NCs, they have been studied in the unpurified state or after extremely lossy isolation.5,48,56−60

In this work, we report on the simple and scalable size-fractioning of ASC18-capped NCs, yielding monodisperse (standard size deviation of ca. 9%) CsPbBr3 NC fractions, >100 mg from the initial 0.9 g scale batch. We then utilize these size-uniform NCs in order to first determine their shape (oblate cuboids) and then establish size dependencies of the first and second excitonic transitions in the optical absorption spectra and correlate it with an effective mass/k·p model. We then demonstrate that size-selected NCs are readily suited as building blocks for constructing long-range ordered nanocrystal superlattices, which exhibit superfluorescence at cryogenic temperatures.

In systems where monodispersity cannot be reached synthetically, size-selection procedures have been proven to be effective. Size-selective precipitation exploits size-dependent solubility of NCs, whereby a gradual increase in the amount of anti-solvents leads to the destabilization and precipitation of the largest NCs.61−63 In practice, stepwise addition of anti-solvent, followed by centrifugation steps, results in NC fractions of decreasing mean size with much narrower size dispersion. The key advantage of zwitterionic ligands is a much slower rate of ligand desorption in the solvent mixture containing large quantities of polar anti-solvent (such as acetone).52,53Figure 1 outlines a size-selection procedure that yielded monodisperse NCs with a mean size adjustable between 3.5 and 16 nm (mean edge length). Centrifuging of the crude solution yields a substantial amount of precipitate (p) only for reaction temperatures exceeding 150 °C. At 180 °C, the remaining NC quantity in the supernatant (s) became negligible. We also note that the first fractions (sf1 or pf1) can substantially deviate from the other fractions as they contain not only the largest NCs but also NCs that are less colloidally stable for other reasons such as agglomeration or surface damaging. The size-selected fractions were characterized by PL spectra, PL QYs, optical absorption, and transmission electron microscopy (TEM). The mass yield of each fraction was quantified from optical absorbance at 335 nm, following Maes et al.64

Figure 1.

Figure 1

Open in a new tab

(a) Scheme of size selection of CsPbBr3 NCs. (b, c) The normalized absorption and PL spectra of crude supernatant (s) and the resulting fractions of NCs synthesized at 150 °C (7.3–4.7.nm; see also Table S3 and Figure S3). (d) Zwitterionic sulfobetaine ligand (ASC18) used in the synthesis.

See further details in the Supporting Information, as well as Tables S1–S6 and Figures S1–S6 for all fractions within the 3.5–16 nm range (obtained from 6 different batches of NCs). Size-fractioning of one batch is exemplified by the respective PL and absorption spectra in Figure 1b,c. After isolation and purification, these NCs are stable for months. Generally, the energies of the PL peak and of the absorption onset (s-s transition) increase with decreasing the NC size. NCs with a PL peak below 515 nm exhibit a second excitonic transition (p-p transition), resolvable due to narrow size dispersion.

The PL and absorption spectra of two exemplary fractions corresponding to large (black/red lines) and small (black/blue lines) NCs are displayed in Figure 2a. The optical properties of NCs are dependent on NC size and shape. Shape analysis from TEM images (2D projections of a 3D object) can be misleading due to preferred orientation. We therefore reverted to small-angle X-ray scattering (SAXS) measurements, providing statistically significant 3D-structural information for monodisperse NCs in their colloidal state. The experimental patterns for the same two exemplary fractions are shown in Figure 2b along with their respective analytical model fit (black dashed line). The scattering patterns for a range of other NC samples are included in Figure S7. All patterns show form-factor scattering of non-interacting NCs, as evidenced by the characteristic q–0 slope in the low-q regime (q < 0.3 nm–1).65 Pattern refinement of the experimental data using an analytical model yields a detailed quantification of shape, size, and polydispersity (see model details in the Supporting Information and results in Table S7). We find an oblate cuboidal shape for all data sets with two sides of equal length and one side 20% shorter. The short NC side is termed c, while the long edges are termed a and b. The effects of preferred orientation in high-angle annular dark-field scanning transmission electron micrographs (HAADF-STEM) of NCs deposited onto a carbon-coated grid can explain the small discrepancies with regard to the mean NC edge length, d = (a + b + c)/3, derived from number distributions of SAXS. The large NCs in Figure 2c orient preferentially with their a-b facet orthogonal to the beam, and hence the mean edge length corresponds well to the long edge found in SAXS, while the small NCs in Figure 2d lie preferably on their small sides and hence agree more closely to the short edge determined from SAXS. Generally, the polydispersity decreases for higher fraction numbers within the same size selection series. Values between 1.3 and 0.4 nm (error bars in Figure 3c) are found corresponding to ca. 1–2 crystal-lattice unit cells only.

Figure 2.

Figure 2

Open in a new tab

(a) PL and absorption spectra for small (a = 4.5 nm, blue/black line, 1sf6) and large (a = 13 nm, red/black line, 5sf2) NCs isolated by size-selective precipitation; (b) their small-angle X-ray scattering traces fitted to an orthorhombic model revealing one NC dimension to be 20% shorter with respect to the other two. (c, d) Cryo-HAADF-STEM images of the NCs with edge length statistics and high resolution image. For small NCs, the lattice fringes could not be resolved even under cryo conditions.

Figure 3.

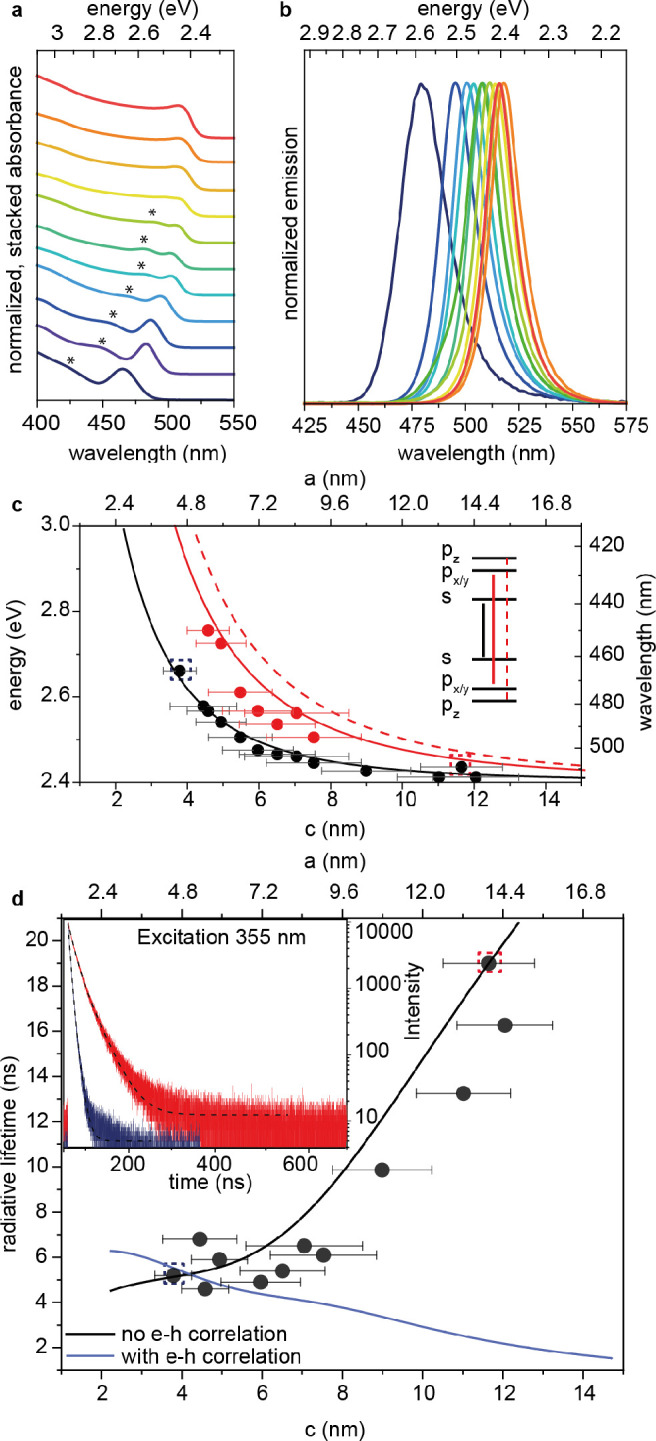
Figure 3

Open in a new tab

(a) Normalized absorbance spectra of size-selected CsPbBr3 NCs of different sizes. The p-p transition is marked with (∗). (b) Respective normalized PL spectra. In (c), the energy of the allowed optical transitions against the edge length is plotted. For the experimental values (black and red points), edge lengths were received from SAXS volume distributions, s-s and p-p transition energies from absorption spectra. The error bars indicate the absolute polydispersity and refer to the lower axis. The lines are the energies calculated using an effective mass/k·p model. Panel (d) shows the radiative lifetime as a function of the edge length. Exemplary traces are shown in the inset (red 5sf2 and blue 1sf6 remaining traces and fits; see Figure S9). The line indicates the theoretical expectation using a Boltzmann state mixing model, with (blue line) and without (black line) the inclusion of the electron-hole correlated motion.

The wide tuning range and regular shape allowed for delineating the size dependence of the excitonic transitions and comparing it with an effective mass/k·p model. Absorption and PL spectra for a selected set of fractions (Figure 3a,b; Figure S7) characterized by solution SAXS (Figure S8) were chosen for modeling. The two samples featured in Figure 2 are also included and plotted in the same respective colors. The absorption transitions were used in the model to take advantage of the availability of resolved p-p transitions and to avoid complications from potentially size-dependent PL Stokes shifts.50,66 Both the s-s and p-p transitions shift to higher energies in smaller NCs as expected from the quantum confinement effect (Figure 3c). This size dependence is well described by an intermediate confinement model (see detailed description in the Supporting Information, Figures S10–S16), which includes the effects of band non-parabolicity and the effect of correlated motion of the electron and hole in NCs whose sizes are larger than the exciton Bohr radius. As shown in ref (67), the effective mass of carriers in lead-halide perovskites is energy-dependent. This was accounted for by using a two-band Kane model. The model (lines) accurately describes both the first (s-s) as well as second (p-p) optically allowed excitonic transitions accounting for the effect of measured NC shape anisotropy. The energy of the s-states are very weakly dependent on the NC shape as is the energy of the s-s transition. Conversely, the splitting in the p-p transition is due to the anisotropic NC shape. The states along the more confined z direction are destabilized relative to the cubic model, while the states along the less confined x and y directions are stabilized (Figure 3c and Figures S11 and S12). Due to the identical edge length (a and b) in x and y directions, the px-px and py-py transitions remain degenerate. A comparison to a more extended data set is possible once the edge length is replaced by the effective edge length Leff, chosen as the edge length of a cube with the same kinetic energy for the lowest-energy exciton (see the Supporting Information for details). This renders the ordinate of the sizing curve shape-independent, and samples of different shapes can be compared (Figure S13). In this way, not only the NC size can be determined based on absorption data, from the shape-independent s-s transition, but also the NCs’ deviation from the cubic shape can be assessed based on the observed s-p splitting and its size dependence.

The discretization of energy levels strongly affects the carrier dynamics and the exciton radiative decay. In CsPbBr3 perovskite NCs, the room-temperature PL lifetime is strongly dependent on the NC size and increases significantly for NCs larger than 8 nm (Figure 3d, points). This trend is in contrast with expectations based on Fermi’s golden rule, which predicts that the radiative rate should scale linearly with the emission energy for an ideal two-level system with a size-independent transition matrix element. It is also in contrast to the expectation that the oscillator strength of the exciton should increase with the size of the NC owing to the phenomenon of giant oscillator strength (GOS) of bound excitons, generally observed in perovskites NCs at cryogenic temperatures.68,69 To account for this counterintuitive behavior, we consider the energy levels obtained from the sizing curve and their complex interplay mediated by temperature. Considering all possible transitions at the band edge, a Boltzmann state mixing model leads to a good agreement with the experimental data (Figure 3d and Figure S17), revealing that symmetry forbidden transitions (s-p) are responsible for the elongation of the radiative lifetime in larger NCs. This follows previous results obtained on CdSe and CdTe NCs, which demonstrated that the thermal population of various hole states with low transition probability (i.e., dark states) is responsible for the longer lifetime in larger NCs.70 Remarkably, the model which includes the GOS effect does not match the measured data at room temperature, while the model without the GOS effect does. We speculate that, at room temperature, PL emission (occurring in the ns time range) involves de-cohered states in which the electron-hole correlation, which gives rise to the accumulation of oscillator strength responsible for GOS, is broken up by phonon interactions. On the other hand, a good description of absorption, being a prompt process, requires the inclusion of the electron-hole correlation as indicated by the analysis in Figure S17. Further investigation of the mechanism of thermal disruption of the GOS effect, which governs PL emission at low temperature,68 is in progress. Overall, the theoretical model developed can predict the size-dependent optical properties of CsPbBr3 NCs. The insights gained on their optical properties (i.e., exciton level structure and oscillator strength) not only are relevant for fundamental research but also have direct implications on device design strategies. In fact, the rate of spontaneous emission determines the statistics of the output of a single photon source, the maximum light intensity of NC-based light emitting diodes, and the output of coherent sources such as lasers.

A high degree of size and shape uniformity is a prerequisite for using NCs as building blocks for novel metamaterials.71,72 Monodisperse CsPbBr3 NCs capped with a standard OA/OLA ligand shell undergo self-assembly into long-range ordered superlattices, upon either solvent evaporation58,60,73−75 or addition of an anti-solvent,76 wherein cuboid NCs pack into a primitive cubic lattice. An important difference with long-chain zwitterionic ligands is their higher short-range interparticle repulsion of entropic origin.53 Solution SAXS of the zwitterion-capped NCs indicates that the interaction potential is rather weakly attractive (Table S7). Generally, disorder-to-order transition at a late stage of drying of steric-stabilized NC colloids is assumed to be entropy-driven and is favored in systems with stronger short-range steric repulsion and minimal NC-NC attraction (hard-sphere model).71

We thus have set to test the propensity of monodisperse zwitterion-capped NCs (ca. 7.8 ± 0.9 nm in size) to self-organize into NC superlattices and compared the results with similar sizes of NCs capped with OA/OLA ligands (ca. 7.8 ± 0.8 nm, Figure S18). Figure 4a,e illustrates a typical outcome: in both cases, three-dimensional cubic-shaped supercrystals of several microns in size formed. The degree of order was assessed with grazing incidence small-angle X-ray scattering (GISAXS, Figure S19). We also note that supercrystals of OA/OLA-capped NCs have not thus far been characterized with GISAXS. Both samples show distinct scattering patterns with strong reflections from primitive tetragonal unit cells with slight out-of-plane compression (c direction of the superlattice), caused presumably by drying effects (see Figure S19 for indexed scattering images). Quantitatively, the lattice dimensions differ only slightly: a = b = 11.4 nm and c = 11.0 nm for OA/OLA-capped NCs, while a = b = 11.5 nm and c = 11.3 nm for zwitterion-capped NCs. There appears to be a significant difference in the long-range order. The scattering image from OA/OLA-capped NCs shows ring-like distortion of the reflections, linked to either mosaicity (orientation misalignment) or inhomogeneity in growth of different superlattices (Figure 4b). In the case of the zwitterion-capped NCs, no such mosaicity effects are evident (Figure 4f). The comparison of horizontal cuts at the specular reflection order (qV = 0.29 nm–1; see white boxes in Figure 4b,f) shown in Figure 4c,g for both kinds of superlattices shows significantly sharper scattering peaks from zwitterion-capped NCs, suggesting a higher degree of long-range order. We find a mean size of long-range ordered domains of 57 nm for the OA/OLA-case and 121 nm for zwitterion-capped NCs. This corresponds to domain volumes comprising 125 and 1000 NCs, respectively.

Figure 4.

Figure 4

Open in a new tab

Superlattices of OA/OLA-capped CsPbBr3 NCs (left) and zwitterion-capped CsPbBr3 NCs (right). (a, e) Fluorescence microscopy images of the obtained cuboid-shaped supercrystals (SEM image in Figure S21). (b) GISAXS patterns showing mosaicity (rings) in the OA/OLA-case and (f) sharp reflections indicating large domain sizes obtained with zwitterion-capped NCs. (c, g) The cross-sectional plots (see corresponding white lines in b, f) yield similar unit cell parameters but larger domain sizes for zwitterion-capped NCs. (d, h) Pictograms representing the crystallographic information found by GISAXS; the mosaicity (reported value is the average mosaicity) is mostly present within the a–b plane of the superlattices.

CsPbX3 NC superlattices have recently triggered interest due to the emergence of collective light-emission phenomena, namely, superfluorescence (SF).58,77 Specifically, at cryogenic temperatures—given the high oscillator strength of the transitions, low energetic disorder, and long exciton coherence time—these NCs undergo cooperative emission, which results in a red-shifted band with strongly accelerated radiative rates. Similarly, we find such superfluorescent emission also in supercystals of zwitterion-capped NCs (Figure 5). At 6 K, the PL spectrum is composed of two bands split by ca. 40 meV (Figure 5a), associated with the uncoupled (gray) and coupled (green) NC emission, respectively.58 Fluence-dependent experiments (inset of Figure 5a) evidence an almost linear dependence of the integrated PL intensity, which attests to the absence of competing, power-dependent nonradiative processes (e.g., the Auger process). Drastic shortening of the exciton radiative lifetime and the appearance of intensity oscillations with increasing excitation fluence (Figure 5b,c) are a signature of the occurrence of collective emission.78 The radiative lifetime, defined here as the 1/e decay time, is inversely proportional to the number of coherently coupled NCs, N, which increases with excitation fluence. A strong acceleration of the radiative lifetime down to 10 ps has been observed at high fluences (Figure 5d, upper plot). As a result, the height of the SF burst peak intensity increases superlinearly (Figure 5d, middle panel), exhibiting a power-law dependence with an exponent m = 1.3. Furthermore, a shortening of the SF build-up time, after which the photon burst is emitted, is observed (Figure 5d, bottom panel; Figure S22). This is a peculiar characteristic of SF emission, distinctly different from amplified spontaneous emission (ASE) which exhibits no build-up time (sub-ps time range, set by photon traveling time). Together with the absence of a clear threshold in the light-in/light-out curve (inset Figure 5a), the observed dynamics exclude stimulated emission processes as alternative explanation.

Figure 5.

Figure 5

Open in a new tab

(a) A 6 K PL spectrum from a supercrystal comprising zwitterion-capped NCs (8.2 × 8.2 × 6.7 nm NCs). The experimental data have been fitted to a sum of two Lorentzian functions, depicted in gray and green. The inset shows a log–log plot of both peak heights with power-law fits (solid lines), yielding exponents of m = 0.92 and m = 0.98 for the gray and green peaks, respectively. (b) Color-coded streak camera image obtained with an excitation fluence of 114 μJ/cm2. (c) Spectrally integrated time-resolved emission intensity traces for the several excitation fluences. The traces are shifted in time to account for a constant time offset (ca. 22 ps) present in the streak camera images. (d) Measured data (points) and the model curves of: (top) the decay time as a function of the excitation fluence, fitted according to the SF model;58 (middle) the SF burst peak height that increases superlinearly with excitation fluence, corresponding to a power-law dependence with an exponent m = 1.3; (bottom) the extracted build-up time decreases at high excitation fluence due to the increased interaction among the emitters, and can be well reproduced by the log(N)/N theoretical expected trend.58

Superfluorescent emission has been observed from several fractions of NCs of similar size, showing variation in the peak energy and energy splitting with respect to spontaneous emission (Figure S21). Notably, the energy of the coupled-NC band varies when comparing superlattices made of different NC fractions (Figure S21), in contrast to the hypothesis that the red-shifted emission band would emerge from merged bulk-like microcrystals.79 We systematically examined the emergence of the coupled NC emission band from different regions in the sample. The sample itself comprises not only large supercrystals commonly seen in the fluorescent microscopy images (Figure 4a,e) but also smaller supercrystals and continuous films of NCs (Figure S24b). Only the relatively small supercrystals exhibit a double peaked PL with accelerated radiative lifetime. On the contrary, superfluorescent emission from OLA/OA samples is readily found from the large supercrystals. This difference remains unexplained.

Conclusion

In conclusion, we have developed a size-selection methodology for obtaining sizable quantities of monodisperse 3.5 and 16 nm zwitterion-capped CsPbBr3 NCs. Solution SAXS measurements retrieved the same NC shape—an oblate cuboid with the aspect ratio of 1.2 × 1.2 × 1—for all size fractions. These NCs exhibit narrow PL line widths (17–25 nm) and high PL QYs (up to 90%). We have then extended the model of the size dependence of the excitonic transitions to noncubic shapes and found that not only the s-s but also higher energy p-p transitions could be fitted well within the theoretical description. We propose a sizing curve using an effective NC length. The longer PL lifetimes for NC sizes larger than 8 nm at room temperature are due to a thermal mixing with optically forbidden transitions. GOS effects—the dominant mechanism at low temperatures68—have to be excluded for the model to fit the experimental observation at room temperature. This can be explained by the breakup of the electron-hole correlation on a time scale long enough to be relevant for emission but not for absorption. We also showcase that monodisperse zwitterion-capped NCs readily form long-range ordered NC superlattices exhibiting superfluorescent emission at cryogenic temperatures.

Methods

The methods used are described in the Supporting Information. No unexpected or unusually high safety hazards were encountered.

Acknowledgments

The authors thank Dr. Frank Krumeich for acquisition of the cryo-HAADF-STEM and SEM images, Dr. Simon C. Böhme for measuring tr-PL traces, and Yuliia Berezovska for assistance with SAXS measurements. The authors are thankful for the access to NFFA and CERIC-ERIC, the Scientific Center for Optical and Electron Microscopy (ScopeM) at ETH Zurich and the Empa Electron Microscopy Center for use of their facilities.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.0c01153.

  • Synthesis protocols for the fabrication of NCs, protocol for size selection and self-assembly of superlattices, description of protocols and instrumentation used for data acquisition (optical, TEM, SEM, SAXS), fitting procedures for fitting of tr-PL and SAXS traces, detailed description of the models for quantum confinement in oblate cuboidal perovskite NCs and the size dependence of the tr-PL decay at room temperature, optical, TEM and SAXS characterization of NCs, indexed GI-SAXS diffraction patterns, fluence dependence of assembled NCs, characteristics of further superlattices as demonstration of reproducibility, characteristics of other spots on a film of superlattices (PDF)

This work was financially supported by the Swiss Innovation Agency (Innosuisse, No. 32908.1 IP-EE) and, in part, by the European Union through the Horizon 2020 research and innovation program (grant agreement No. 819740, project SCALE-HALO). The authors are thankful for the funding received from the EU-H2020 research and innovation program under grant agreement No 654360 supporting the Transnational Access Activity within the framework NFFA-Europe to the TUG’s ELETTRA SAXS beamline of CERIC-ERIC. Theoretical calculations of exciton level structure and radiative lifetime were supported as part of the Center for Hybrid Organic Inorganic Semiconductors for Energy (CHOISE), an Energy Frontier Research Center funded by the Office of Basic Energy Sciences, Office of Science, within the U.S. Department of Energy.

The authors declare no competing financial interest.

Supplementary Material

oc0c01153_si_001.pdf (3.9MB, pdf)

References

  1. Li Y.; Zhang X.; Huang H.; Kershaw S. V.; Rogach A. L. Advances in metal halide perovskite nanocrystals: Synthetic strategies, growth mechanisms, and optoelectronic applications. Mater. Today 2020, 32, 204–221. 10.1016/j.mattod.2019.06.007. [DOI] [Google Scholar]
  2. Shamsi J.; Urban A. S.; Imran M.; De Trizio L.; Manna L. Metal halide perovskite nanocrystals: Synthesis, post-synthesis modifications, and their optical properties. Chem. Rev. 2019, 119 (5), 3296–3348. 10.1021/acs.chemrev.8b00644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kovalenko M. V.; Protesescu L.; Bodnarchuk M. I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 2017, 358, 745–750. 10.1126/science.aam7093. [DOI] [PubMed] [Google Scholar]
  4. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Bertolotti F.; Masciocchi N.; Guagliardi A.; Kovalenko M. V. Monodisperse formamidinium lead bromide nanocrystals with bright and stable green photoluminescence. J. Am. Chem. Soc. 2016, 138 (43), 14202–14205. 10.1021/jacs.6b08900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of cesium lead halide perovskites (CsPbX3, X = Cl, Br, and I): Novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 2015, 15 (6), 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Swarnkar A.; Chulliyil R.; Ravi V. K.; Irfanullah M.; Chowdhury A.; Nag A. Colloidal CsPbBr3 perovskite nanocrystals: Luminescence beyond traditional quantum dots. Angew. Chem., Int. Ed. 2015, 54 (51), 15424–15428. 10.1002/anie.201508276. [DOI] [PubMed] [Google Scholar]
  7. Cao M.; Xu Y.; Li P.; Zhong Q.; Yang D.; Zhang Q. Recent advances and perspectives on light emitting diodes fabricated from halide metal perovskite nanocrystals. J. Mater. Chem. C 2019, 7 (46), 14412–14440. 10.1039/C9TC03978C. [DOI] [Google Scholar]
  8. Lu M.; Zhang Y.; Wang S.; Guo J.; Yu W. W.; Rogach A. L. Metal halide perovskite light-emitting devices: Promising technology for next-generation displays. Adv. Funct. Mater. 2019, 29 (30), 1902008. 10.1002/adfm.201902008. [DOI] [Google Scholar]
  9. Chiba T.; Kido J. Lead halide perovskite quantum dots for light emitting devices. J. Mater. Chem. C 2018, 6 (44), 11868–11877. 10.1039/C8TC03561J. [DOI] [Google Scholar]
  10. He Z.; Zhang C.; Dong Y.; Wu S.-T. Emerging perovskite nanocrystals-enhanced solid-state lighting and liquid-crystal displays. Crystals 2019, 9 (2), 59. 10.3390/cryst9020059. [DOI] [Google Scholar]
  11. Yoon H. C.; Lee H.; Kang H.; Oh J. H.; Do Y. R. Highly efficient wide-color-gamut QD-emissive LCDs using red and green perovskite core/shell QDs. J. Mater. Chem. C 2018, 6 (47), 13023–13033. 10.1039/C8TC04537B. [DOI] [Google Scholar]
  12. Schlaus A. P.; Spencer M. S.; Miyata K.; Liu F.; Wang X.; Datta I.; Lipson M.; Pan A.; Zhu X. Y. How lasing happens in CsPbBr3 perovskite nanowires. Nat. Commun. 2019, 10 (1), 265. 10.1038/s41467-018-07972-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Stylianakis M. M.; Maksudov T.; Panagiotopoulos A.; Kakavelakis G.; Petridis K. Inorganic and hybrid perovskite based laser devices: A review. Materials 2019, 12 (6), 859. 10.3390/ma12060859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Zhang Y.; Lim C.-K.; Dai Z.; Yu G.; Haus J. W.; Zhang H.; Prasad P. N. Photonics and optoelectronics using nano-structured hybrid perovskite media and their optical cavities. Phys. Rep. 2019, 795, 1–51. 10.1016/j.physrep.2019.01.005. [DOI] [Google Scholar]
  15. Yakunin S.; Protesescu L.; Krieg F.; Bodnarchuk M. I.; Nedelcu G.; Humer M.; De Luca G.; Fiebig M.; Heiss W.; Kovalenko M. V. Low-threshold amplified spontaneous emission and lasing from colloidal nanocrystals of caesium lead halide perovskites. Nat. Commun. 2015, 6, 8056. 10.1038/ncomms9056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Wang Y.; Song L.; Chen Y.; Huang W. Emerging new-generation photodetectors based on low-dimensional halide perovskites. ACS Photonics 2020, 7 (1), 10–28. 10.1021/acsphotonics.9b01233. [DOI] [Google Scholar]
  17. Bao C.; Yang J.; Bai S.; Xu W.; Yan Z.; Xu Q.; Liu J.; Zhang W.; Gao F. High performance and stable all-inorganic metal halide perovskite-based photodetectors for optical communication applications. Adv. Mater. 2018, 30 (38), 1803422. 10.1002/adma.201803422. [DOI] [PubMed] [Google Scholar]
  18. Maddalena F.; Tjahjana L.; Xie A.; Arramel; Zeng S.; Wang H.; Coquet P.; Drozdowski W.; Dujardin C.; Dang C.; Birowosuto M. Inorganic, organic, and perovskite halides with nanotechnology for high–light yield X- and γ-ray scintillators. Crystals 2019, 9 (2), 88. 10.3390/cryst9020088. [DOI] [Google Scholar]
  19. Chen Q.; Wu J.; Ou X.; Huang B.; Almutlaq J.; Zhumekenov A. A.; Guan X.; Han S.; Liang L.; Yi Z.; Li J.; Xie X.; Wang Y.; Li Y.; Fan D.; Teh D. B. L.; All A. H.; Mohammed O. F.; Bakr O. M.; Wu T.; Bettinelli M.; Yang H.; Huang W.; Liu X. All-inorganic perovskite nanocrystal scintillators. Nature 2018, 561 (7721), 88–93. 10.1038/s41586-018-0451-1. [DOI] [PubMed] [Google Scholar]
  20. Fu H. Colloidal metal halide perovskite nanocrystals: a promising juggernaut in photovoltaic applications. J. Mater. Chem. A 2019, 7 (24), 14357–14379. 10.1039/C8TA12509K. [DOI] [Google Scholar]
  21. Sanehira E. M.; Marshall A. R.; Christians J. A.; Harvey S. P.; Ciesielski P. N.; Wheeler L. M.; Schulz P.; Lin L. Y.; Beard M. C.; Luther J. M. Enhanced mobility CsPbI3 quantum dot arrays for record-efficiency, high-voltage photovoltaic cells. Sci. Adv. 2017, 3 (10), eaao4204. 10.1126/sciadv.aao4204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Swarnkar A.; Marshall A. R.; Sanehira E. M.; Chernomordik B. D.; Moore D. T.; Christians J. A.; Chakrabarti T.; Luther J. M. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite forhigh-efficiency photovoltaics. Science 2016, 354 (6308), 92–95. 10.1126/science.aag2700. [DOI] [PubMed] [Google Scholar]
  23. Bagherzadeh-Khajehmarjan E.; Nikniazi A.; Olyaeefar B.; Ahmadi-Kandjani S.; Nunzi J.-M. Bulk luminescent solar concentrators based on organic-inorganic CH3NH3PbBr3 perovskite fluorophores. Sol. Energy Mater. Sol. Cells 2019, 192, 44–51. 10.1016/j.solmat.2018.12.009. [DOI] [Google Scholar]
  24. Tong J.; Luo J.; Shi L.; Wu J.; Xu L.; Song J.; Wang P.; Li H.; Deng Z. Fabrication of highly emissive and highly stable perovskite nanocrystal-polymer slabs for luminescent solar concentrators. J. Mater. Chem. A 2019, 7 (9), 4872–4880. 10.1039/C8TA12149D. [DOI] [Google Scholar]
  25. Mendewala B.; Nikolaidou K.; Hoffman C.; Sarang S.; Lu J.; Ilan B.; Ghosh S. The potential of scalability in high efficiency hybrid perovskite thin film luminescent solar concentrators. Sol. Energy 2019, 183, 392–397. 10.1016/j.solener.2019.03.042. [DOI] [Google Scholar]
  26. Wang Z.; Lin Q.; Wenger B.; Christoforo M. G.; Lin Y.-H.; Klug M. T.; Johnston M. B.; Herz L. M.; Snaith H. J. High irradiance performance of metal halide perovskites for concentrator photovoltaics. Nat. Energy 2018, 3 (10), 855–861. 10.1038/s41560-018-0220-2. [DOI] [Google Scholar]
  27. Nikolaidou K.; Sarang S.; Hoffman C.; Mendewala B.; Ishihara H.; Lu J. Q.; Ilan B.; Tung V.; Ghosh S. Hybrid perovskite thin films as highly efficient luminescent solar concentrators. Adv. Opt. Mater. 2016, 4 (12), 2126–2132. 10.1002/adom.201600634. [DOI] [Google Scholar]
  28. Mirershadi S.; Ahmadi-Kandjani S. Efficient thin luminescent solar concentrator based on organometal halide perovskite. Dyes Pigm. 2015, 120, 15–21. 10.1016/j.dyepig.2015.03.035. [DOI] [Google Scholar]
  29. Tamarat P.; Bodnarchuk M. I.; Trebbia J. B.; Erni R.; Kovalenko M. V.; Even J.; Lounis B. The ground exciton state of formamidinium lead bromide perovskite nanocrystals is a singlet dark state. Nat. Mater. 2019, 18 (7), 717–724. 10.1038/s41563-019-0364-x. [DOI] [PubMed] [Google Scholar]
  30. Utzat H.; Sun W.; Kaplan A. E. K.; Krieg F.; Ginterseder M.; Spokoyny B.; Klein N. D.; Shulenberger K. E.; Perkinson C. F.; Kovalenko M. V.; Bawendi M. G. Coherent single-photonemission from colloidal lead halide perovskite quantum dots. Science 2019, 363, 1068–1072. 10.1126/science.aau7392. [DOI] [PubMed] [Google Scholar]
  31. Tong Y.; Fu M.; Bladt E.; Huang H.; Richter A. F.; Wang K.; Muller-Buschbaum P.; Bals S.; Tamarat P.; Lounis B.; Feldmann J.; Polavarapu L. Chemical cutting of perovskite nanowires into single-photon emissive low-aspect-ratio CsPbX3 (X = Cl, Br, I) nanorods. Angew. Chem., Int. Ed. 2018, 57 (49), 16094–16098. 10.1002/anie.201810110. [DOI] [PubMed] [Google Scholar]
  32. Li B.; Huang H.; Zhang G. F.; Yang C. G.; Guo W. L.; Chen R. Y.; Qin C. B.; Gao Y.; Biju V. P.; Rogach A. L.; Xiao L. T.; Jia S. T. Excitons and biexciton dynamics in single CsPbBr3 perovskite quantum dots. J. Phys. Chem. Lett. 2018, 9 (24), 6934–6940. 10.1021/acs.jpclett.8b03098. [DOI] [PubMed] [Google Scholar]
  33. Becker M. A.; Scarpelli L.; Nedelcu G.; Raino G.; Masia F.; Borri P.; Stoferle T.; Kovalenko M. V.; Langbein W.; Mahrt R. F. Long exciton dephasing time and coherent phonon coupling in CsPbBr2Cl perovskite nanocrystals. Nano Lett. 2018, 18 (12), 7546–7551. 10.1021/acs.nanolett.8b03027. [DOI] [PubMed] [Google Scholar]
  34. Fu M.; Tamarat P.; Huang H.; Even J.; Rogach A. L.; Lounis B. Neutral and charged exciton fine structure in single lead halide perovskite nanocrystals revealed by magneto-optical spectroscopy. Nano Lett. 2017, 17 (5), 2895–2901. 10.1021/acs.nanolett.7b00064. [DOI] [PubMed] [Google Scholar]
  35. Raino G.; Nedelcu G.; Protesescu L.; Bodnarchuk M. I.; Kovalenko M. V.; Mahrt R. F.; Stoferle T. Single cesium lead halide perovskite nanocrystals at low temperature: Fast single-photon emission, reduced blinking, and exciton fine structure. ACS Nano 2016, 10 (2), 2485–2490. 10.1021/acsnano.5b07328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Akkerman Q. A.; Rainò G.; Kovalenko M. V.; Manna L. Genesis, Challenges and Opportunities for Colloidal Lead Halide Perovskite Nanocrystals. Nat. Mater. 2018, 17 (5), 394–405. 10.1038/s41563-018-0018-4. [DOI] [PubMed] [Google Scholar]
  37. Wang F.; Bai S.; Tress W.; Hagfeldt A.; Gao F. Defects Engineering for High-Performance Perovskite Solar Cells. npj Flex. Electron. 2018, 2 (1), 22. 10.1038/s41528-018-0035-z. [DOI] [Google Scholar]
  38. Huang H.; Bodnarchuk M. I.; Kershaw S. V.; Kovalenko M. V.; Rogach A. L. Lead Halide Perovskite Nanocrystals in the Research Spotlight: Stability and Defect Tolerance. ACS Energy Lett. 2017, 2 (9), 2071–2083. 10.1021/acsenergylett.7b00547. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Li W.; Wang Z.; Deschler F.; Gao S.; Friend R. H.; Cheetham A. K. Chemically Diverse and Multifunctional Hybrid Organic–Inorganic Perovskites. Nat. Rev. Mater. 2017, 2 (3), 16099. 10.1038/natrevmats.2016.99. [DOI] [Google Scholar]
  40. Huang J.; Yuan Y.; Shao Y.; Yan Y. Understanding the Physical Properties of Hybrid Perovskites for Photovoltaic Applications. Nat. Rev. Mater. 2017, 2 (7), 17042. 10.1038/natrevmats.2017.42. [DOI] [Google Scholar]
  41. Ball J. M.; Petrozza A. Defects in Perovskite-Halides and their Effects in Solar Cells. Nat. Energy 2016, 1 (11), 16149. 10.1038/nenergy.2016.149. [DOI] [Google Scholar]
  42. Bodnarchuk M. I.; Boehme S. C.; Ten Brinck S.; Bernasconi C.; Shynkarenko Y.; Krieg F.; Widmer R.; Aeschlimann B.; Gunther D.; Kovalenko M. V.; Infante I. Rationalizing and controlling the surface structure and electronic passivation of cesium lead halide nanocrystals. ACS Energy Lett. 2019, 4 (1), 63–74. 10.1021/acsenergylett.8b01669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. ten Brinck S.; Infante I. Surface termination, morphology, and bright photoluminescence of cesium lead halide perovskite nanocrystals. ACS Energy Lett. 2016, 1 (6), 1266–1272. 10.1021/acsenergylett.6b00595. [DOI] [Google Scholar]
  44. Grisorio R.; Di Clemente M. E.; Fanizza E.; Allegretta I.; Altamura D.; Striccoli M.; Terzano R.; Giannini C.; Irimia-Vladu M.; Suranna G. P. Exploring the surface chemistry of cesium lead halide perovskite nanocrystals. Nanoscale 2019, 11 (3), 986–999. 10.1039/C8NR08011A. [DOI] [PubMed] [Google Scholar]
  45. Smock S. R.; Williams T. J.; Brutchey R. L. Quantifying the thermodynamics of ligand binding to CsPbBr3 quantum dots. Angew. Chem., Int. Ed. 2018, 57 (36), 11711–11715. 10.1002/anie.201806916. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. De Roo J.; Ibanez M.; Geiregat P.; Nedelcu G.; Walravens W.; Maes J.; Martins J. C.; Van Driessche I.; Kovalenko M. V.; Hens Z. Highly dynamic ligand binding and light absorption coefficient of cesium lead bromide perovskite nanocrystals. ACS Nano 2016, 10 (2), 2071–2081. 10.1021/acsnano.5b06295. [DOI] [PubMed] [Google Scholar]
  47. Imran M.; Ijaz P.; Baranov D.; Goldoni L.; Petralanda U.; Akkerman Q.; Abdelhady A. L.; Prato M.; Bianchini P.; Infante I.; Manna L. Shape-pure, nearly monodispersed CsPbBr3 nanocubes prepared using secondary aliphatic amines. Nano Lett. 2018, 18 (12), 7822–7831. 10.1021/acs.nanolett.8b03598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Li Y.; Luo X.; Ding T.; Lu X.; Wu K. Size- and halide-dependent auger recombination in lead halide perovskite nanocrystals. Angew. Chem., Int. Ed. 2020, 59, 14292. 10.1002/anie.202004668. [DOI] [PubMed] [Google Scholar]
  49. Brennan M. C.; Forde A.; Zhukovskyi M.; Baublis A. J.; Morozov Y. V.; Zhang S.; Zhang Z.; Kilin D. S.; Kuno M. K. Universal size-dependent stokes shifts in lead halide perovskite nanocrystals. J. Phys. Chem. Lett. 2020, 11 (13), 4937–4944. 10.1021/acs.jpclett.0c01407. [DOI] [PubMed] [Google Scholar]
  50. Rossi D.; Liu X.; Lee Y.; Khurana M.; Puthenpurayil J.; Kim K.; Akimov A.; Cheon J.; Son D. H.. Intense dark exciton emission from strongly quantum confined CsPbBr3 nanocrystals. arXiv:2002.08589 [physics.app-ph]. 2020. 10.1021/acs.nanolett.0c02714. [DOI] [PubMed] [Google Scholar]
  51. Krieg F.; Ochsenbein S. T.; Yakunin S.; ten Brinck S.; Aellen P.; Suess A.; Clerc B.; Guggisberg D.; Nazarenko O.; Shynkarenko Y.; Kumar S.; Shih C.-J.; Infante I.; Kovalenko M. V. Colloidal CsPbX3 (X = Cl, Br, I) nanocrystals 2.0: Zwitterionic capping ligands for improved durability and stability. ACS Energy Lett. 2018, 3 (3), 641–646. 10.1021/acsenergylett.8b00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Krieg F.; Ong Q. K.; Burian M.; Raino G.; Naumenko D.; Amenitsch H.; Suess A.; Grotevent M. J.; Krumeich F.; Bodnarchuk M. I.; Shorubalko I.; Stellacci F.; Kovalenko M. V. Stable ultraconcentrated and ultradilute colloids of CsPbX3 (X = Cl, Br) nanocrystals using natural lecithin as a capping ligand. J. Am. Chem. Soc. 2019, 141 (50), 19839–19849. 10.1021/jacs.9b09969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Lignos I.; Stavrakis S.; Nedelcu G.; Protesescu L.; deMello A. J.; Kovalenko M. V. Synthesis of cesium lead halide perovskite nanocrystals in a droplet-based microfluidic platform: Fast parametric space mapping. Nano Lett. 2016, 16 (3), 1869–1877. 10.1021/acs.nanolett.5b04981. [DOI] [PubMed] [Google Scholar]
  54. Koolyk M.; Amgar D.; Aharon S.; Etgar L. Kinetics of cesium lead halide perovskite nanoparticle growth; focusing and de-focusing of size distribution. Nanoscale 2016, 8 (12), 6403–6409. 10.1039/C5NR09127F. [DOI] [PubMed] [Google Scholar]
  55. Shynkarenko Y.; Bodnarchuk M. I.; Bernasconi C.; Berezovska Y.; Verteletskyi V.; Ochsenbein S. T.; Kovalenko M. V. Direct synthesis of quaternary alkylammonium-capped perovskite nanocrystals for efficient blue and green light-emitting diodes. ACS Energy Lett. 2019, 4 (11), 2703–2711. 10.1021/acsenergylett.9b01915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Dong Y.; Qiao T.; Kim D.; Parobek D.; Rossi D.; Son D. H. Precise control of quantum confinement in cesium lead halide perovskite quantum dots via thermodynamic equilibrium. Nano Lett. 2018, 18 (6), 3716–3722. 10.1021/acs.nanolett.8b00861. [DOI] [PubMed] [Google Scholar]
  57. Raino G.; Becker M. A.; Bodnarchuk M. I.; Mahrt R. F.; Kovalenko M. V.; Stoferle T. Superfluorescence from lead halide perovskite quantum dot superlattices. Nature 2018, 563 (7733), 671–675. 10.1038/s41586-018-0683-0. [DOI] [PubMed] [Google Scholar]
  58. Akkerman Q. A.; Park S.; Radicchi E.; Nunzi F.; Mosconi E.; De Angelis F.; Brescia R.; Rastogi P.; Prato M.; Manna L. Nearly monodisperse insulator Cs4PbX6 (X = Cl, Br, I) nanocrystals, their mixed halide compositions, and their transformation into CsPbX3 nanocrystals. Nano Lett. 2017, 17 (3), 1924–1930. 10.1021/acs.nanolett.6b05262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Kovalenko M. V.; Bodnarchuk M. I. Lead halide perovskite nanocrystals: From discovery to self-assembly and applications. Chimia 2017, 71 (7), 461–470. 10.2533/chimia.2017.461. [DOI] [PubMed] [Google Scholar]
  60. Poznyak S. K.; Osipovich N. P.; Shavel A.; Talapin D. V.; Gao M.; Eychmüller A.; Gaponik N. Size-dependent electrochemical behavior of thiol-capped CdTe nanocrystals in aqueous solution. J. Phys. Chem. B 2005, 109 (3), 1094–1100. 10.1021/jp0460801. [DOI] [PubMed] [Google Scholar]
  61. Guzelian A. A.; Katari J. E. B.; Kadavanich A. V.; Banin U.; Hamad K.; Juban E.; Alivisatos A. P.; Wolters R. H.; Arnold C. C.; Heath J. R. Synthesis of size-selected, surface-passivated InP nanocrystals. J. Phys. Chem. 1996, 100 (17), 7212–7219. 10.1021/jp953719f. [DOI] [Google Scholar]
  62. Murray C. B.; Norris D. J.; Bawendi M. G. Synthesis and characterization of nearly monodisperse CdE (E = sulfur, selenium, tellurium) semiconductor nanocrystallites. J. Am. Chem. Soc. 1993, 115 (19), 8706–8715. 10.1021/ja00072a025. [DOI] [Google Scholar]
  63. Maes J.; Balcaen L.; Drijvers E.; Zhao Q.; De Roo J.; Vantomme A.; Vanhaecke F.; Geiregat P.; Hens Z. Light absorption coefficient of CsPbBr3 perovskite nanocrystals. J. Phys. Chem. Lett. 2018, 9 (11), 3093–3097. 10.1021/acs.jpclett.8b01065. [DOI] [PubMed] [Google Scholar]
  64. Glatter O. Determination of particle-size distribution functions from small-angle scattering data by means of the indirect transformation method. J. Appl. Crystallogr. 1980, 13, 7–11. 10.1107/S0021889880011429. [DOI] [Google Scholar]
  65. Brennan M. C.; Herr J. E.; Nguyen-Beck T. S.; Zinna J.; Draguta S.; Rouvimov S.; Parkhill J.; Kuno M. origin of the size-dependent stokes shift in CsPbBr3 perovskite nanocrystals. J. Am. Chem. Soc. 2017, 139 (35), 12201–12208. 10.1021/jacs.7b05683. [DOI] [PubMed] [Google Scholar]
  66. Sercel P. C.; Lyons J. L.; Bernstein N.; Efros A. L. Quasicubic model for metal halide perovskite nanocrystals. J. Chem. Phys. 2019, 151 (23), 234106. 10.1063/1.5127528. [DOI] [PubMed] [Google Scholar]
  67. Becker M. A.; Vaxenburg R.; Nedelcu G.; Sercel P. C.; Shabaev A.; Mehl M. J.; Michopoulos J. G.; Lambrakos S. G.; Bernstein N.; Lyons J. L.; Stoferle T.; Mahrt R. F.; Kovalenko M. V.; Norris D. J.; Raino G.; Efros A. L. Bright triplet excitons in caesium lead halide perovskites. Nature 2018, 553 (7687), 189–193. 10.1038/nature25147. [DOI] [PubMed] [Google Scholar]
  68. Rahsba E. I.; Gurgenishvili G. E. Edge absorption theory in semiconductors. Sov. Phys. Solid State 1962, 4, 759–760. [Google Scholar]
  69. van Driel A. F.; Allan G.; Delerue C.; Lodahl P.; Vos W. L.; Vanmaekelbergh D. Frequency-dependent spontaneous emission rate from CdSe and CdTe nanocrystals: influence of dark states. Phys. Rev. Lett. 2005, 95 (23), 236804. 10.1103/PhysRevLett.95.236804. [DOI] [PubMed] [Google Scholar]
  70. Boles M. A.; Engel M.; Talapin D. V. Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 2016, 116 (18), 11220–11289. 10.1021/acs.chemrev.6b00196. [DOI] [PubMed] [Google Scholar]
  71. Murray C. B.; Kagan C. R.; Bawendi M. G. Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies. Annu. Rev. Mater. Sci. 2000, 30, 545–610. 10.1146/annurev.matsci.30.1.545. [DOI] [Google Scholar]
  72. Tong Y.; Yao E. P.; Manzi A.; Bladt E.; Wang K.; Doblinger M.; Bals S.; Muller-Buschbaum P.; Urban A. S.; Polavarapu L.; Feldmann J. Spontaneous self-assembly of perovskite nanocrystals into electronically coupled supercrystals: Toward filling the green gap. Adv. Mater. 2018, 30, 1801117. 10.1002/adma.201801117. [DOI] [PubMed] [Google Scholar]
  73. Nagaoka Y.; Hills-Kimball K.; Tan R.; Li R.; Wang Z.; Chen O. Nanocube superlattices of cesium lead bromide perovskites and pressure-induced phase transformations at atomic and mesoscale levels. Adv. Mater. 2017, 29 (18), 1606666. 10.1002/adma.201606666. [DOI] [PubMed] [Google Scholar]
  74. Toso S.; Baranov D.; Giannini C.; Marras S.; Manna L. Wide-angle X-ray diffraction evidence of structural coherence in CsPbBr3 nanocrystal superlattices. ACS Materials Lett. 2019, 1 (2), 272–276. 10.1021/acsmaterialslett.9b00217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. van der Burgt J. S.; Geuchies J. J.; van der Meer B.; Vanrompay H.; Zanaga D.; Zhang Y.; Albrecht W.; Petukhov A. V.; Filion L.; Bals S.; Swart I.; Vanmaekelbergh D. Cuboidal supraparticles self-assembled from cubic CsPbBr3 perovskite nanocrystals. J. Phys. Chem. C 2018, 122 (27), 15706–15712. 10.1021/acs.jpcc.8b02699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Zhou C.; Zhong Y.; Dong H.; Zheng W.; Tan J.; Jie Q.; Pan A.; Zhang L.; Xie W. Cooperative excitonic quantum ensemble in perovskite-assembly superlattice microcavities. Nat. Commun. 2020, 11 (1), 329. 10.1038/s41467-019-14078-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Cong K.; Zhang Q.; Wang Y.; Noe G. T.; Belyanin A.; Kono J. Dicke superradiance in solids. J. Opt. Soc. Am. B 2016, 33 (7), C80. 10.1364/JOSAB.33.000C80. [DOI] [Google Scholar]
  78. Baranov D.; Fieramosca A.; Yang R. X.; Polimeno L.; Lerario G.; Toso S.; Giansante C.; De Giorgi M.; Tan L. Z.; Sanvitto D.; Manna L.. Temporal evolution of self-assembled lead halide perovskite nanocrystal superlattices: Effects on photoluminescence and energy transfer. arXiv:2008.02853 [physics.app-ph]. 2020. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc0c01153_si_001.pdf (3.9MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES