Bayesian Joint Spike-and-Slab Graphical Lasso

Abstract

In this article, we propose a new class of priors for Bayesian inference with multiple Gaussian graphical models. We introduce Bayesian treatments of two popular procedures, the group graphical lasso and the fused graphical lasso, and extend them to a continuous spike-and-slab framework to allow self-adaptive shrinkage and model selection simultaneously. We develop an EM algorithm that performs fast and dynamic explorations of posterior modes. Our approach selects sparse models efficiently and automatically with substantially smaller bias than would be induced by alternative regularization procedures. The performance of the proposed methods are demonstrated through simulation and two real data examples.

1. Introduction

Bayesian formulations of graphical models have been widely adopted as a way to characterize conditional independence structure among complex high-dimensional data. These models are popular in scientific domains including genomics (Briollais et al., 2016; Peterson et al., 2013), public health (Dobra, 2014; Li et al., 2017b), and economics (Dobra et al., 2010). In practice, data often come from several distinct groups. For example, data may be collected under various conditions, at different locations and time periods, or correspond to distinct subpopulations. Assuming a single graphical model in such cases can lead to unreliable estimates of network structure, whereas the alternative, estimating different graphical models separately for each group, may not be feasible for high dimensional problems.

Several approaches have been proposed to learn graphical models jointly for multiple classes of data. Much of this work extends the penalized maximum likelihood approach to incorporate additional penalty terms that encourage the class-specific precision matrices to be similar (Guo et al., 2011; Danaher et al., 2014; Saegusa & Shojaie, 2016; Ma & Michailidis, 2016). In the Bayesian literature, Peterson et al. (2015) and Lin et al. (2017) utilize Markov Random Field priors to model a super-graph linking different graphical models. Tan et al. (2017) uses a logistic regression model to link the connectivity of nodes to covariates specific to each graph. These approaches only model the similarity of the underlying graphs, and thus are limited in their ability to borrow information when estimating the precision matrices. Borrowing strength is especially important when some classes have small sample sizes.

In this work, we introduce a new Bayesian formulation for estimating multiple related Gaussian graphical models by leveraging similarities in the underlying sparse precision matrices directly. We first present two shrinkage priors for multiple related precision matrices, as the Bayesian counterpart of joint graphical lasso estimators (Danaher et al., 2014). We then propose a doubly spike-and-slab mixture extension to these priors, which allows us to achieve simultaneous shrinkage and model selection, as well as handle missing observations. In Section 5 and 6, we extend from the recent literature on deterministic algorithms for Bayesian graphical models (Gan et al., 2018; Li & McCormick, 2019; Deshpande et al., 2019) and provide a fast Expectation-Maximization (EM) algorithm to quickly identify the posterior modes. We also propose a procedure to sequentially explore a series of posterior modes. We then demonstrate the substantial improvements in both model selection and parameter estimation over the original joint graphical lasso approach using both simulated data and two real datasets in Section 7. Finally, in Section 8 we discuss future directions for improvements.

2. Preliminaries

2.1. The joint graphical lasso

We first briefly introduce the notation used throughout this paper. We let G denote the number of classes in the data, and let Ω_g and Σ_g denote the precision and covariance matrix for the g-th class. We let ${\omega }_{jk}^{(g)}$ denote the (j, k)-th element in Ω_g and ${\omega }_{jk}=\{{\omega }_{jk}^{(g)}{\}}_{g=1,\dots ,G}$ denote the vector of all the (j, k)-th elements in {Ω}. Suppose we are given G datasets, X⁽¹⁾,…, X^(G), where X^(g) is a n_g × p matrix of independent centered observations from the distribution Normal(0, ${\Omega }_g^{-1}$). As maximum likelihood estimates of Ω_g can have high variance and are ill-defined when p > n_g, the joint penalized log likelihood for the G dataset is usually considered instead:

$$\ell (\{\Omega \})=\frac{1}{2}\sum _{g=1}^G{n}_g\log \text{det}{\Omega }_g-tr({\mathit{S}}_g{\Omega }_g)-pen(\{\Omega \}),$$ (1)

where S_g = (X^(g))^T X^(g). The penalty function encourages {Ω} to have zeros on the off-diagonal elements and be similar across groups. In particular, we consider two useful penalty functions studied in Danaher et al. (2014), the group graphical lasso (GGL), and the fused graphical lasso (FGL):

$$\begin{gathered} pen(\{\Omega \})=\frac{{\lambda }_0}{2}\sum _g\sum _j\mid {\omega }_{jj}^{(g)}\mid +{\lambda }_1\sum _g\sum _{j<k}\mid {\omega }_{jk}^{(g)}\mid \\ +{\lambda }_2\sum _{j<k}\widetilde{pen}({\omega }_{jk}), \end{gathered}$$ (2)

where $\widetilde{pen}({\omega }_{jk})=\Vert {\omega }_{jk}{\Vert }_2$ for GGL and ${\sum }_{g<g^{\prime }}\mid {\omega }_{jk}^{(g)}-{\omega }_{jk}^{(g^{\prime })}\mid$ for FGL. Both penalties encourage similarity across groups when λ₂ > 0, and reduce to separate graphical lasso problems when λ₂ = 0. The group graphical lasso encourages only similar patterns of zero elements across the G precision matrices, while the fused graphical lasso encourages a stronger form of similarity: the values of off-diagonal elements are also encouraged to be similar across the G precision matrices. In practice, λ₀ is typically set to 0 when the diagonal elements are not to be penalized.

2.2. Bayesian formulation of Gaussian graphical models

One of the most popular approaches for Bayesian inference with Gaussian graphical models is the G-Wishart prior (Lenkoski & Dobra, 2011; Mohammadi et al., 2015). The G-Wishart prior estimates the precision matrices with exact zeros in the off-diagonal elements and enjoys the conjugacy with the Gaussian likelihood. However, posterior inference under the G-Wishart prior can be computationally burdensome and has to rely on stochastic search algorithms over the large model space, consisting of all possible graphs. In recent years, several classes of shrinkage priors have been proposed for estimating large precision matrices, including the graphical lasso prior (Wang, 2012; Peterson et al., 2013), the continuous spike-and-slab prior (Wang, 2015; Li et al., 2017b), and the graphical horseshoe prior (Li et al., 2017a). This line of work draws direct connections between penalized likelihood schemes and, as their names suggest, the posterior modes in a Bayesian setting. Unlike the G-Wishart prior, these shrinkage priors do not take point mass at zero for the off-diagonal elements in the precision matrix, and thus usually lead to efficient block sampling algorithms with improved scalability. However, fully Bayesian procedures still need to rely on stochastic search to achieve model selection, making it less appealing for many problems.

To address this issue, deterministic algorithms have been proposed to perform fast posterior exploration and mode searching in Gaussian graphical models (Gan et al., 2018; Li & McCormick, 2019; Deshpande et al., 2019). Motivated by the EMVS (Ročková & George, 2014) and spike-and-slab lasso (Ročková & George, 2018) procedures in the linear regression literature, the idea is to use a two-component mixture distribution, i.e., spike-and-slab priors, to parameterize off-diagonal elements in the precision matrix, which allows simultaneous model selection and parameter estimation. We will utilize a similar strategy for model estimation in this paper.

3. Bayesian joint graphical lasso priors

We first provide a Bayesian interpretation of the group and fused graphical lasso estimators. From a probabilistic perspective, it is well understood that estimators that optimize a penalized likelihood can often be seen as the posterior mode estimator under some suitable prior distributions. The Bayesian counterpart to (2) can be constructed by placing the prior p({Ω}) ∝ exp(−pen({Ω})) on the precision matrices. Following directly from the Bayesian representation of lasso variants demonstrated in Kyung et al. (2010), we can rewrite p({Ω}) as products of scale mixtures of normal distributions on the off-diagonal elements. That is, for the GGL prior, we can let

$$\begin{gathered} p(\{\Omega \}\mid \tau ,\rho )=C_{\tau ,\rho }^{-1}\prod _{j<k}\text{Normal}({\omega }_{jk};0,({\Theta }_{jk}^{(G)}{)}^{-1}) \\ \prod _g\prod _j\text{Exp}({\omega }_{jj}^{(g)};\frac{{\lambda }_0}{2})1_{\{\Omega \}\in \{M^{+}\}}, \end{gathered}$$ (3)

$${\Theta }_{jk}^{(G)}=\text{diag}(\{\frac{1}{{\rho }_{jk}}+\frac{1}{{\tau }_{jkg}}{\}}_{g=1,\dots ,G}),$$ (4)

$$\begin{gathered} p(\tau ,\rho )\propto C_{\tau ,\rho }\prod _{j<k}(\text{exp}(-\frac{{\lambda }_1^2}{2}\sum _g{\tau }_{jkg}-\frac{{\lambda }_2^2}{2}{\rho }_{jk}){\rho }_{jk}^{-\frac{1}{2}}\phantom{)} \\ \phantom{(}\prod _g({\tau }_{jkg}(\frac{1}{{\tau }_{jkg}}+\frac{1}{{\rho }_{jk}}){)}^{-\frac{1}{2}}), \end{gathered}$$ (5)

where C_τ,ρ is a normalizing constant and M⁺ denotes the space of symmetric positive definite matrices. The normalizing constant is analytically intractable due to this constraint, but it cancels out in the marginal distribution of p({Ω}). Such cancellation has been studied by several authors (Wang, 2012; 2015; Liu et al., 2014). Similarly, the FGL prior can be defined as

$$\begin{gathered} p(\{\Omega \}\mid \tau ,\varphi )=C_{\tau ,\varphi }^{-1}\prod _{j<k}\text{Normal}({\omega }_{jk};0,({\Theta }_{jk}^{(F)}{)}^{-1}) \\ \prod _g\prod _j\text{Exp}({\omega }_{jj}^{(g)};\frac{{\lambda }_0}{2})1_{\{\Omega \}\in \{M^{+}\}}, \end{gathered}$$ (6)

$${\Theta }_{jk}^{(F)}=\{\begin{array}{cc}{\theta }_{gg}=\frac{1}{{\tau }_{jkg}}+{\sum }_{g\ne g^{\prime }}\frac{1}{{\varphi }_{jkg{g}^{\prime }}}\hfill & g=1,\dots ,G\hfill \\ {\theta }_{g{g}^{\prime }}=-\frac{1}{{\varphi }_{jkg{g}^{\prime }}}\hfill & g^{\prime }\ne g\hfill \end{array}\phantom{\}}$$ (7)

$$\begin{gathered} p(\tau ,\varphi )\propto C_{\tau ,\varphi }\prod _{j<k}(\mid {\Theta }_{jk}^{(F)}{\mid }^{-\frac{1}{2}}\text{exp}(-\frac{{\lambda }_1^2}{2}\sum _g{\tau }_{jkg}\phantom{)} \\ \phantom{(}-\frac{{\lambda }_2^2}{2}\sum _{g<g^{\prime }}{\varphi }_{jkg{g}^{\prime }})\prod _g{\tau }_{jkg}^{-\frac{1}{2}}\prod _{g<g^{\prime }}{\varphi }_{jkg{g}^{\prime }}^{-\frac{1}{2}}). \end{gathered}$$ (8)

It is also worth noting that both of the above priors are proper, and we leave the proof of the following proposition in the supplement.

Proposition 1. The priors defined in (3)-(5) and (6)-(8) are proper and the posterior mode of {Ω} is the solution of the group and fused graphical lasso problem with penalty terms defined in (2).

4. Bayesian joint spike-and-slab graphical lasso priors

The Bayesian formulation of the joint graphical lasso problems discussed in the previous section provide shrinkage effects at the level of both individual precision matrices and across different classes. However, two issues remain. First, shrinkage priors alone do not produce sparse models since the posterior draws are never exactly 0. Thus, additional thresholding is needed to obtain a sparse representation of the graph structure. Second, the fixed penalty term, λ₁ and λ₂ may be too restrictive, as the non-zero elements in {Ω} are penalized equally to elements close to zero (Li & McCormick, 2019). To reduce the bias from over-penalizing the large elements, different hyper-priors on λ₁ have been proposed to adaptively estimate the penalty term in Bayesian graphical lasso (Wang, 2012; Peterson et al., 2013).

Here we address both challenges simultaneously using the spike-and-slab approaches in Bayesian variable selection (George & McCulloch, 1993). In particular, we employ a set of latent indicators to construct a “selection” prior on both the group level and within-groups for the similarity penalties. We first let binary variables δ = {δ_jk}_j<k denote the existence of each edge in the graph, indexing the 2^p(p–1)/2 possible models at the group level, so that δ_jk = 1 indicates the (j, k)-th edge is selected for all precision matrices. We then let another set of binary variables ξ = [ξ_jk]_j<k denote the non-existence of ‘similarities’ among the elements in the same cell of different precision matrices, so that ξ_jk = 0 indicates the (j, k)-th element is expected to be similar. We use the term ‘similarity’ here as a broad term parameterized by λ₂, since the behavior of the similarity depends on the form of the penalization. Conditional on the two binary indicators, we replace the fixed penalty parameters λ₁ and λ₂ by a mixture of edge-wise penalties that take values from {λ₁/v₀, λ₁/v₁}, and {λ₂/v₀, λ₂/v₁} respectively, with fixed v₁ > v₀ > 0. That is, we introduce the following penalties conditional on δ and ξ, and we propose the doubly spike-and-slab extensions to GGL and FGL as

$$\begin{gathered} pen(\{\Omega \}\mid \delta ,\xi )=\frac{{\lambda }_0}{2}\sum _g\sum _j\mid {\omega }_{jj}^{(g)}\mid +{\lambda }_1\sum _g\sum _{j<k}\frac{\mid {\omega }_{jk}^{(g)}\mid }{v_{{\delta }_{jk}}} \\ {\lambda }_2\sum _{j<k}\frac{\widetilde{pen}({\omega }_{jk})}{v_{{\xi }_{jk}^{\ast }}}, \end{gathered}$$ (9)

where $\widetilde{pen}({\omega }_{jk})$ is defined as before and ${\xi }_{jk}^{\ast }={\xi }_{jk}{\delta }_{jk}$. The prior defined in (9) relate to the unconditional penalties by pen({Ω}) = pen({Ω}∣δ, ξ) – log(p(δ, ξ)), and we will refer to them as DSS-FGL and DSS-GGL.

In practice, we find it usually reasonable to enforce all elements from the spike distribution to also be similar, since the spike distribution is always chosen to have large penalization and leads to posterior modes at exactly 0. However, other types of element-wise dependence between δ_jk and ξ_jk are also possible with minor modifications. For example, we can also fix ξ_jk to be 1, so that the two penalty terms will always be proportional. We refer to this setting as spike-and-slab group and fused lasso (SS-GGL and SS-FGL) and discuss their behavior in the supplements.

The original GGL and FGL suffer from the same bias induced by the excessive shrinkage of lasso estimates. With the introduction of v₀ and v₁, we can adaptively estimate which ω_jk to penalize in a data-driven way. As we discuss in more detail in Section 6, this adaptive shrinkage property can indeed significantly reduce bias imposed on the lasso penalty. That is, by choosing the hyperparameters so that λ_i/v₀ ≫ λ_i/v₁, we impose only minimal shrinkage on values arising from the slab distribution. From now on, in order to avoid confusion from the overparameterization, we always fix v₁ = 1, and report results with the effective shrinkage parameters λ_i/v_j, i, j ∈ {1, 2}. At this point, it may still seem that we need introduced one more hyperparameter that needs to be tunned, but as we show in Section 6, model selection can be achieved automatically without cross-validation.

For a Bayesian setup, we employ standard priors on the binary indicators to allow the edges to further share information on the sparsity level. The full generative model for {Ω} is:

$$p(\{\Omega \}\mid \delta ,\xi ,\theta )=C_{\theta }^{-1}{C}_{\delta ,\xi }^{-1}\text{exp}(-pen(\{\Omega \}\mid \delta ,\xi ))1_{\{\Omega \}\in \{M^{+}\}},$$ (10)

$$\begin{gathered} p(\delta ,\xi \mid {\pi }_{\delta },{\pi }_{\xi })\propto C_{\delta ,\xi }\prod _{j<k}({\pi }_{\delta }^{{\delta }_{jk}}(1-{\pi }_{\delta }{)}^{1-{\delta }_{jk}}\phantom{)} \\ \phantom{(}{\pi }_{\xi }^{{\xi }_{jk}}(1-{\pi }_{\xi }{)}^{1-{\xi }_{jk}}). \end{gathered}$$ (11)

where θ denote (τ, ρ) for DSS-GGL, and (τ, ϕ) for DSS-FGL. C_δ,ξ is another intractable normalizing constant. We put standard Beta hyperpriors on the sparsity parameters so that π_δ ~ Beta(a₁, b₁) and π_ξ ~ Beta(a₂, b₂). Throughout this paper, we let a₁ = a₂ = 1 and b₁ = b₂ = p.

Additionally, the above prior can be easily reparameterized with scale mixture of normal prior distributions similar as before by modifying the precision matrix Θ into the following form, and they can be shown to be proper priors (the proofs can be found in the supplement):

$${\tilde{\Theta }}_{jk}^{(F)}=\{\begin{array}{cc}{\theta }_{gg}=\frac{v_{{\delta }_{jk}}}{{\tau }_{jkg}}+{\sum }_{g<g^{\prime }}\frac{v_{{\xi }_{jk}^{\ast }}}{{\varphi }_{jkg{g}^{\prime }}}\hfill & g=1,\dots ,G\hfill \\ {\theta }_{g{g}^{\prime }}=-\frac{v_{{\xi }_{jk}^{\ast }}}{{\varphi }_{jkg{g}^{\prime }}}\hfill & g^{\prime }\ne g\hfill \end{array}\phantom{\}}$$ (12)

$${\tilde{\Theta }}_{jk}^{(G)}=\text{diag}(\{\frac{v_{{\xi }_{jk}^{\ast }}}{{\rho }_{jk}}+\frac{v_{{\delta }_{jk}}}{{\tau }_{jkg}}{\}}_{g=1,\dots ,G}).$$ (13)

Proposition 2. The priors defined in (10)-(13) are proper, and the posterior mode of {Ω} is the solution to the corresponding spike-and-slab version of joint graphical lasso penalties.

Finally, it is straightforward to see that the proposed DSS-GGL and DSS-FGL penalties reduce to their non spike-and-slab counterparts when δ and ξ are fixed to be 1. Several other spike-and-slab formulations in the literature can be seen as the special case of this prior when G = 1 as well. For example, the spike-and-slab mixture of double exponential priors considered in Deshpande et al. (2019) is a special case with λ₂ = 0. The spike-and-slab Gaussian mixtures in Li & McCormick (2019) can also be considered as a special case where we further fix τ_jkg = ∞. This approach is also related to the work on sparse group selection in linear regression, as has been discussed in Xu et al. (2015) and (Zhang et al., 2014). As opposed to the point mass priors for the spike distribution commonly in the literature, our doubly spike-and-slab formulation of continuous mixtures allows the spike distribution to absorb small non-zero noises and facilitates fast dynamic explorations, as we will show in Section 6.

5. Model estimation

Given fixed λ₁, λ₂, and v₀, The representation of p({Ω}) with the scale mixture of normal distributions allows the posterior to be sampled using a block Gibbs algorithm, as described in the supplement. However, choosing the hyperparameters can usually be a nontrivial task. Instead, we focus on faster deterministic methods to detect posterior modes under different choices of hyperparameters (Ročková & George, 2014). We present an EM algorithm that maximizes the complete-data posterior distribution p({Ω}, δ, ξ, π_δ, π_ξ∣X) by treating the binary latent variables as “missing data.” Similar ideas have been explored in recent work for linear regression (Ročková & George, 2014; 2018) and single graphical model estimation (Deshpande et al., 2019; Li & McCormick, 2019). Our EM algorithm maximizes the objective function $E_{\delta ,\xi \mid \{\Omega {\}}^{(t)},{\pi }_{\delta }^{(t)},{\pi }_{\xi }^{(t)},\mathit{X}}(\log p(\{\Omega \},{\pi }_{\delta },{\pi }_{\xi }\mid \mathit{X}\mid \cdot )$ by iterating between the E-step and M-step until changes in {Ω} are within a small threshold.

In the E-step, we compute the conditional expectation terms in the objective function. It turns out that it suffices to find the conditional distribution of (δ_jk, ξ_jk). The corresponding cell probabilities are proportional the the following mixture densities:

$$\begin{gathered} p_{{\delta }_{jk},{\xi }_{jk}}^{\ast }(j,k)\propto \\ \{\begin{array}{cc}{\pi }_{\delta }(1-{\pi }_{\xi })\frac{{\lambda }_1{\lambda }_2}{v_0{v}_1}\psi (v_1,v_0)\hfill & {\delta }_{jk}=1,{\xi }_{jk}=0\hfill \\ {\pi }_{\delta }{\pi }_{\xi }\frac{{\lambda }_1{\lambda }_2}{v_1^2}\psi (v_1,v_1)\hfill & {\delta }_{jk}=1,{\xi }_{jk}=1\hfill \\ (1-{\pi }_{\delta })(1-{\pi }_{\xi })\frac{{\lambda }_1{\lambda }_2}{v_0^2}\psi (v_0,v_0)\hfill & {\delta }_{jk}=0,{\xi }_{jk}=0\hfill \end{array}\phantom{\}} \end{gathered}$$

where $\psi (a,b)=\text{exp}(-{\lambda }_1{\sum }_g\mid {\omega }_{jk}^{(g)}\mid ∕a-{\lambda }_2\widetilde{pen}({\omega }_{jk})∕b)$.

It is interesting to note that the three scenarios above represent three types of relationships among ω_jk: weak shrinkage but strong similarity, weak shrinkage and weak similarity, and strong shrinkage across classes. E_·∣·(δ_jk) and E_·∣· (ξ_jk) are then simply the marginal probabilities in this 2 by 2 table, i.e., $E_{\cdot \mid \cdot }({\delta }_{jk})=p_{1,0}^{\ast }(j,k)+p_{1,1}^{\ast }(j,k)$, and $E_{\cdot \mid \cdot }({\xi }_{jk})=E_{\cdot \mid \cdot }({\delta }_{jk}{\xi }_{jk})=p_{1,1}^{\ast }(j,k)$. The EM algorithm also handles missing cells in X naturally. Assuming missing at random, the expectation can also be taken over the space of missing variables, by additionally computing E_·∣·(tr(S_gΩ_g)) = tr(E_·∣·((X^(g))^TX^(g))Ω_g)), using the conditional Gaussian distribution of ${\mathit{x}}_{i,miss}^{(g)}\mid {\mathit{x}}_{i,obs}^{(g)}$. We relegate the derivations of the objective function to the supplement.

Given the expectations calculated in the E-step, one might proceed with conditional maximization steps using gradient ascent similar to the Gibbs sampler (Li & McCormick, 2019). Alternatively, since the maximization step is equivalent to solving the following joint graphical lasso problem:

$$\begin{gathered} \{\Omega \}={\text{argmax}}_{\{\Omega \}}\sum _g\frac{n_g}{2}\log \mid {\Omega }_g\mid -\frac{1}{2}\sum _{g}tr({\mathit{S}}_g{\Omega }_g) \\ -\frac{{\lambda }_0}{2}\sum _j\sum _g\mid {\omega }_{jj}^{(g)}\mid \\ -\sum _{j<k}{\lambda }_1(\frac{p_{0,0}^{\ast }(j,k)}{v_0}+\frac{1-p_{0,0}^{\ast }(j,k)}{v_1})\sum _g\mid {\omega }_{jk}^{(g)}\mid \\ -\sum _{j<k}{\lambda }_2(\frac{1-p_{1,1}^{\ast }(j,k)}{v_0}+\frac{p_{1,1}^{\ast }(j,k)}{v_1})\widetilde{pen}({\omega }_{jk}), \end{gathered}$$

meaning we can use the ADMM algorithm described in Danaher et al. (2014).

6. Dynamic posterior exploration

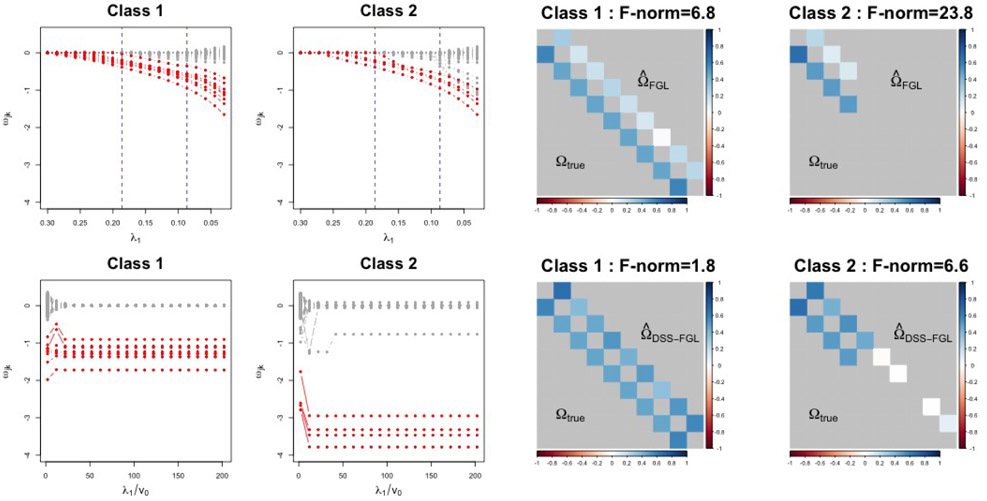
The algorithm proposed in the previous section requires a fixed set of hyperparameters, (λ₀, λ₁, λ₂, v₀). The posterior is relatively insensitive to the choice of λ₀ as long as it is not too large (Wang, 2015). Furthermore, unlike the original joint graphical lasso, where two tuning parameters need to be selected using cross-validation or model selection criterion, it turns out that we can leverage the self-adaptive property from the doubly spike-and-slab mixture setup to achieve automatic tuning using a path-following strategy (Ročková & George, 2018). Specifically, we consider a sequence of decreasing $v_0=\{v_0^1,\dots ,v_0^L\}$ and some small λ₁ and λ₂. We initiate {Ω}₀ so that Ω_g0 = (S_g/n_g + cI)⁻¹, and iterative estimate $\{\widehat{\Omega }{\}}_l$ with $v_0=v_0^l$. After fitting the l-th model, we use the estimated graph structure to warm start the (l + 1)-th model by initiating Ω_g to be ${\Omega }_{g0}\circ 1_{\widehat{\delta }>0}^l$, where $1_{\widehat{\delta }>0}^l$ denotes the group level graph structure at the l-th iteration. As v₀ decreases, the shrinkage imposed on the spike elements steadily increases and leads to sparser models. As noted in Ročková & George (2018), the solution path from such dynamic reinitialization procedure usually ‘stabilizes’ as v₀ becomes closer to 0 in linear regression. We found similar behavior in our spike-and-slab joint graphical lasso models too, as illustrated in Figure 1.

Figure 1.

The solution paths and estimated precision matrices of FGL (upper row) and DSS-FGL (lower row). The red nodes correspond to true edges and the gray nodes correspond to 0’s. The two vertical lines in the FGL solution path indicate the model that best matches the true sparsity (left) and the model with the lowest AIC (right). The block containing the edges is plotted for the estimated values (upper triangular) against the truth (lower triangular). The model that best matches the true graphs is plotted for FGL. The off-diagonal values are rescaled and negated to partial correlations, and 0’s are colored with light gray background for easier visual comparison. The bias of the estimated precision matrix as measured by the Frobenius norm, $\Vert {\widehat{\Omega }}_g-{\Omega }_g{\Vert }_F$, is also printed in the captions.

To demonstrate the dynamic posterior exploration in action, we simulated a small dataset from two classes, with n_g = 150 for g = 1, 2, and p = 100. The two underlying graphs differ by 5 edges: The first precision matrix contains a 10-node block with an AR(1) precision matrix where $({\Omega }^{-1}{)}_{jk}={\rho }_1^{\mid j-k\mid }$, and ρ₁ = 0.7; the second precision matrix in the second class contains a common 5-node AR(1) block with ρ₂ = 0.9. The rest of the nodes are all independent. We fit the fused graphical lasso with a sequence of λ₁, and fixed λ₂ = 0.1, which leads to the best performance in this experiment; and DSS-FGL with λ₁ = 1, and λ₂ = 1. Figure 1 shows the FGL and DSS-FGL solution path. Unlike the continuous shrinkage of FGL, the zero and non-zero elements under DSS-FGL tend to be separated into two stable clusters as the effective shrinkage λ₁/v₀ increases beyond a critical point. Danaher et al. (2014) noted that graph selection using AIC tends to favor large models. This example also confirms this observation as the likelihood evaluation for smaller models suffers from the overly aggressive shrinkage. In this example, AIC selects 27 edges in both classes, leading to 41 false positives. Assuming we know the true graphs, the best model in terms of edge selection along the FGL solution path contains one false negative edge as shown in Figure 1. However, without accurate prior knowledge of graph sparsity, correctly identifying this model is typically difficult, if not impossible. On the other hand, the stable model from the DSS-FGL solution path yields 4 false positive edges in the second graph, but with clear visual separation from the regularization plot: only one false positive edge stabilizing to a larger value away from 0. Thus in practice, the solution path also provides a visual tool to threshold the small values close to 0. Additionally, the bias of the final precision matrices compared to the truth is also much smaller than the best FGL solution.

We also find that the converged region is insensitive to the choice of λ₁ and λ₂ in all our experiments, as the model allows a flexible combination of shrinkage through the adaptive estimation of p*. The supplement includes an empirical assessment of sensitivity in the simulation experiments.

7. Numerical results

Simulation experiments

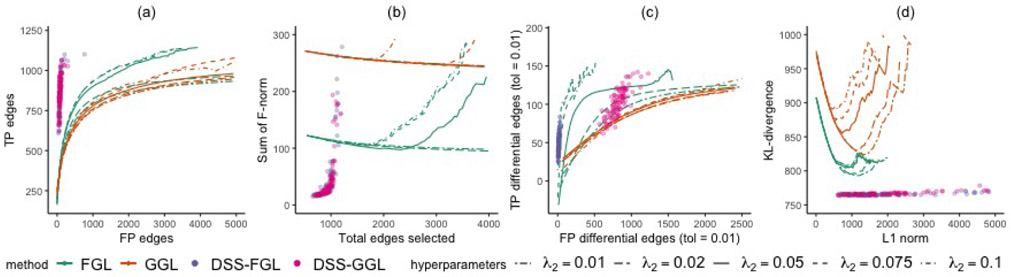
To assess the performance of the proposed models, we consider a three-class problem similar to the study carried out in Danaher et al. (2014). We first generate three networks with p = 500 features with 10 equal sized unconnected subnetworks following power law degree distributions. Exactly one and two subnetworks are removed from the second and third class. The details of the data generating process can be found in the supplement. The results comparing the proposed model and joint graphical lasso are shown in Figure 2. As discussed before, the DSS-FGL and DSS-GGL achieve model selection automatically. Thus we compare the selected models with the average curve of FGL and GGL under different tuning parameters. Figure 2(a) and (c) show that DSS-FGL and DSS-GGL usually achieves better structure learning performance for both identifying edges and differential edges. The differential edges are defined as the edges for the (g, g′) pair with $\mid {\omega }_{jk}^{(g)}-{\omega }_{jk}^{(g^{\prime })}\mid >0.01$. Figure 2(b) and (d) demonstrate the bias-diminishing property of the proposed models compared to the joint graphical lasso estimator at varying sparsity levels, measured by the number of edges in (b) and L₁ norm of the estimator in (d). On average, both the sum of bias as measured by the Frobenius norm, $\Vert {\widehat{\Omega }}_g-{\Omega }_g{\Vert }_F$, and the Kullback-Leibler (KL) divergence achieved by the proposed model is much smaller.

Figure 2.

Performance of FGL, GGL, DSS-FGL, and DSS-GGL over 100 replications. The dots represent the metrics for the 100 selected models under DSS-FGL and DSS-GGL, and the lines represent the average performance of FGL and GGL over 100 replications under different tuning parameters.

Symptom networks of verbal autopsy data

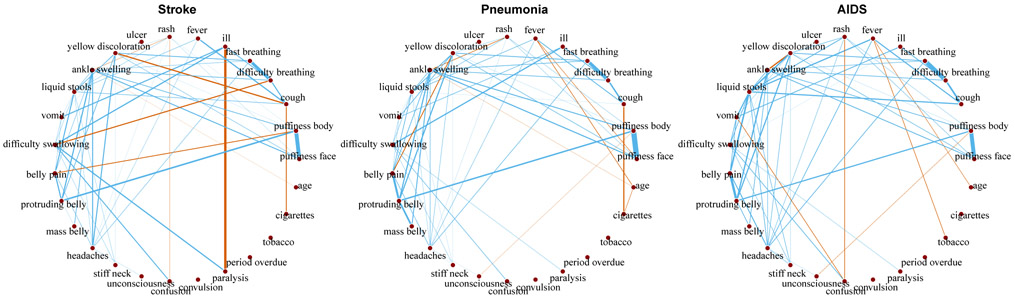
We applied the DSS-FGL and DSS-GGL to a gold-standard dataset of verbal autopsy (VA) surveys (Murray et al., 2011). VA surveys are widely adopted in countries without full-coverage civil registration and vital statistics systems to estimate cause of death. They are conducted by interviewing caregiver of a recently deceased person about the decedent’s health history. The standard procedure of preparing the collected data is to dichotomize all continuous variables into binary indicators and many algorithms have been proposed to automatically assign causes of death using the binary input (Byass et al., 2012; Serina et al., 2015; McCormick et al., 2016). However, more information may be gained by modeling the continuous variables directly (Li et al., 2017b). Here we focus on modeling the joint distribution of the continuous variables. The 27 continuous variables in this dataset contain representations of the duration of symptoms, such as response to the question ‘how many days did the fever last’, and age of the decedents. It is usually reasonable to assume the response to these questions are jointly distributed in similar ways conditional on each cause of death. We take the raw responses and transform raw duration x_ij by log(x_ij + 1). We then let $X_{ij}^{(g)}$ denote the j-th transformed variable for observation i due to the cause g. The full dataset contains death assigned to 34 causes. We applied DSS-FGL with λ₁ = λ₂ = 1 to the three largest determined causes of death in this data: Stroke (n = 630), Pneumonia (n = 540), and AIDS (n = 542) in Figure 3. The estimated graphs under other models are discussed in the supplement. Both DSS-FGL and DSS-GGL estimated similar graphs and discovered interesting differential symptom pairs, such as the strong conditional dependence between the duration of illness and paralysis in deaths due to stroke. Further incorporating the DSS-FGL and DSS-GGL formulation of multiple precision matrices into a classification framework would likely improve accuracy over existing methods (e.g. McCormick et al. (2016); Byass et al. (2012)) for automatic cause-of-death assignment.

Figure 3.

Estimated edges between the symptoms under the three causes using DSS-FGL. The width of the edges are proportional to the size of $\mid {\omega }_{jk}^{(g)}\mid$. Common edges across all groups are colored in blue, and the differential edges are colored in red.

Prediction of missing mortality rates

Beyond structure learning, the bias reduction in estimating {Ω} also makes the proposed method more appealing for prediction tasks involving sparse precision matrices. In this example, we illustrate the potential of using the proposed methods to impute missing mortality rates using a cross-validation study. We construct the data matrices $X_{ij}^{(g)}$ as the log transformed central mortality rate of age group j in year i for subpopulation g (e.g., male and female). Standard approaches in demography, such as the Lee-Carter model (Lee & Carter, 1992), typically use dimension reduction techniques to estimate mean effects due to age and time, and consider the residuals as independent measurement errors. However, residuals from such models are usually still highly correlated (Fosdick & Hoff, 2014). We consider estimating the residual structure with the 1 × 1 gender-specific mortality table up to age 100 in the US over the period of 1960 to 2010 using data obtained from the Human Mortality Database (HMD) (University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany)). For both the male and female mortality, we first randomly selected 25 years and remove 25 data points in each of those years. We then fit a Lee-Carter model to estimate the mean model and interpolate the missing rates. Next, we estimate the covariance matrices among the 101 age groups in both genders using FGL and DSS-FGL from the residuals.

The estimated residuals for the missing values can then be obtained by the E-step in our EM algorithm, or as the expectation from the conditional Gaussian distributions with covariance matrices estimated by FGL. The average mean squared errors (MSEs) for the prediction of missing log rates are summarized in Table 1. Imputation based on DSS-FGL precision matrix reduces the MSE by 27.8% compared to simple interpolation of the mean model (i.e., assuming i.i.d errors), compared to the 6.5% reduction from the FGL precision matrix with the same complexity. The estimated graphs are in the supplement.

Table 1.

Average and standard deviation of the mean squared errors from 50 cross-validation experiments. The FGL model is selected to have the same number of edges as the DSS-FGL.

	i.i.d	FGL	DSS-FGL
Average MSE	0.00372	0.00348	0.00268
SE of the MSEs	0.00030	0.00031	0.00028

8. Discussion

In this paper, we introduced a new class of priors for joint estimation of multiple graphical models. The proposed doubly spike-and-slab mixture priors, DSS-FGL and DSS-GGL, provide self-adaptive extensions to the joint graphical lasso penalties, and achieves simultaneous model selection and parameter estimation. Moreover, while taking advantage of the flexible class of penalty functions, the dynamic posterior exploration procedure allows the penalties to be adaptively estimated in a data-driven way, thus freeing practitioners from choosing multiple tuning parameters. This is especially useful in domains where sample sizes are too small to reliably perform cross-validation. Finally, additional procedures such as multiple random initializations and deterministic annealing may be further incorporated into the proposed algorithm to better expore the posterior surface. While not discussed in the main paper, we note that the posterior uncertainty may be estimated using the Gibbs sampler described in the supplement.

The proposed framework can be extended in a few directions. First, we have assumed all classes to be exchangeable, as reflected in the penalty functions for the between-class similarity. When the classes exhibit hierarchical structures or different strengths of similarities, the indicator ξ may be modeled as functions of the class membership as well. Markov Random Field priors discussed in Saegusa & Shojaie (2016) and Peterson et al. (2015) may also be used to model the between-class similarities. Second, we have considered the estimation of missing values in the data matrices. It is also straightforward to extend to data with missing class labels. In this way, the proposed methods can be extended to classification or discriminant analysis based on sparse precision matrices (Hao et al., 2016). Finally, the proposed model is estimated using an EM algorithm that is iteratively solving the joint graphical lasso problem. It may be interesting to construct coordinate ascent algorithms that optimize on the objective function directly, similar to that described in Ročková & George (2018) for linear regression.

The codes for the proposed algorithm are available at https://github.com/richardli/SSJGL.