Voltage-gated Na+ channels activate faster than K+ channels in excitable cells. Catacuzzeno et al. develop a model that shows how the dielectric properties of a divergent side chain produce this difference in speed.
Abstract
The generation of action potentials in excitable cells requires different activation kinetics of voltage-gated Na (NaV) and K (KV) channels. NaV channels activate much faster and allow the initial Na+ influx that generates the depolarizing phase and propagates the signal. Recent experimental results suggest that the molecular basis for this kinetic difference is an amino acid side chain located in the gating pore of the voltage sensor domain, which is a highly conserved isoleucine in KV channels but an equally highly conserved threonine in NaV channels. Mutagenesis suggests that the hydrophobicity of this side chain in Shaker KV channels regulates the energetic barrier that gating charges cross as they move through the gating pore and control the rate of channel opening. We use a multiscale modeling approach to test this hypothesis. We use high-resolution molecular dynamics to study the effect of the mutation on polarization charge within the gating pore. We then incorporate these results in a lower-resolution model of voltage gating to predict the effect of the mutation on the movement of gating charges. The predictions of our hierarchical model are fully consistent with the tested hypothesis, thus suggesting that the faster activation kinetics of NaV channels comes from a stronger dielectric polarization by threonine (NaV channel) produced as the first gating charge enters the gating pore compared with isoleucine (KV channel).
Introduction
The most important role of voltage-gated sodium (NaV) and potassium (KV) channels is to generate action potentials, all-or-none (i.e., binary) rapid and transient changes of the electric potential difference across the plasma membrane, that propagate signals long distances in the nervous system. This ability is essentially due to the different timing with which these two channels respond to a potential change (Fig. 1 A); NaV channels activate rapidly upon an initial depolarization of the membrane, allowing a Na current to enter the cell and induce a further membrane depolarization along the nerve during the first millisecond or so after the initial trigger. By contrast, KV channels remain essentially closed during this initial interval and open only later, causing the repolarization of the membrane to the resting condition (Bezanilla et al., 1970; Hodgkin and Huxley, 1952; Rojas et al., 1970).
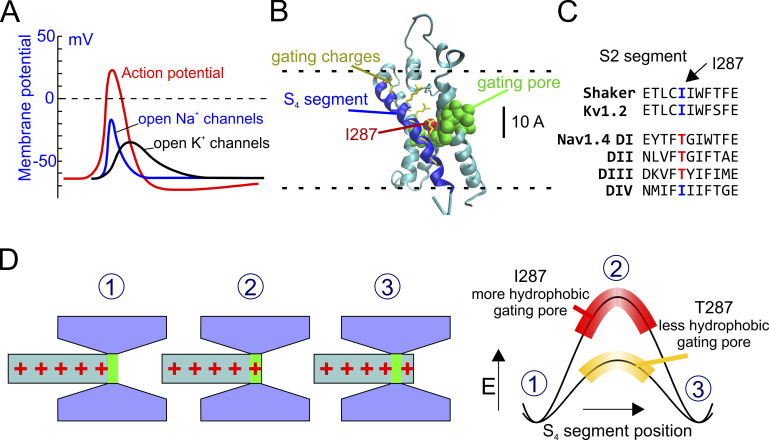
Figure 1.
A hypothesis for the kinetic differences between Kv and Nav channels. (A) Schematic plot showing the activity of NaV and KV channels during an action potential (red line). NaV channels open more rapidly than KV channels, creating the depolarizing phase of the action potential. (B) 3-D structure of the active state of the VSD of the Shaker channel (from Henrion et al., 2012). The S4 segment is in blue, and the S1–S3 segments are in cyan. The hydrophobic residues forming the gating pore (V236, I237, S240, I241, F244, C286, I287, F290, A319, and I320; Lacroix et al., 2014) are shown in van der Waals (VdW) representation (green). The residue 287 is colored in red. Gating charge side chains are shown in licorice representation and colored in yellow. (C) Portion of the S2 segments of several voltage sensors belonging to Shaker, KV, and fast NaV channels, showing the highly conserved isoleucine at position 287 in Shaker-like potassium channels and the threonine residue at the corresponding position in the fast NaV1.4 channel. (D) Schematic representation of the hypothesis tested in this paper. Left: The S4 voltage sensor is represented as a cylinder with the gating charges in red. The rest of the VSD is in gray and forms the gating pore and the intra- and extracellular vestibules. Right: Energetic profiles encountered by the first gating charge across the gating pore in the presence of two different hydrophobicity levels of the gating pore. When the gating charge enters the gating pore, there is an increase in the energy of the system due to the destabilizing (hydrophobic) environment within the gating pore. The more hydrophobic the gating pore, the higher the energy barrier and slower the activation rate.
The molecular and physical basis for the different kinetics of NaV and KV channels has long been sought. The recently determined crystal structure of the voltage sensor domain (VSD) of KV and NaV channels has allowed investigation of the structure-function relationship of the voltage sensor, its environment, and the forces controlling its movement. In both channels, the VSD is formed by the transmembrane segments 1–4 (S1–S4), with the S4 segment containing positively charged residues every third amino acid and forming the voltage sensor, the structure that senses the electric field applied across the membrane and moves upon depolarization (Long et al., 2007; Long et al., 2005; Pan et al., 2018; Payandeh et al., 2011).
The S4 segment is surrounded for most of its length by wide intracellular and extracellular vestibules, where water and ions can easily access and balance the gating charges (Fig. 1 B). The two vestibules are separated by a series of mostly nonpolar residues that form a region, the gating pore, thought to be hardly accessible to water (green and red residues in Fig. 1 B). Several mutagenesis experiments suggest that some of these residues are in direct contact with the moving gating charges and modulate the voltage-dependent properties of the channels (Lacroix et al., 2012, 2013, 2014; Lacroix and Bezanilla, 2011; Tao et al., 2010).
One of the residues of the gating pore that determine the slow kinetics of KV channels, compared with faster NaV channels, is isoleucine at position 287, located in the middle of the S2 segment (red in Fig. 1 B; notice that in this paper we will always use the residue numbering of the Shaker channel). This nonpolar, highly hydrophobic residue is found in many KV channels. It is conserved by evolution presumably because of its essential role. By contrast, in the S2 segment of the first three domains of fast NaV channels, at the corresponding position of isoleucine in KV channels, we consistently find the uncharged but much more hydrophilic residue threonine (Fig. 1 C; see also Fig. S1 for a more extended sequence alignment; Lacroix et al., 2013). This seems to be an example of divergent side-chain evolution, in which two related proteins (NaV and KV channels) have selected two different side chains as an adaptation to create different dielectric polarization and different activation kinetics, and thus to create a propagating action potential. Notably, when isoleucine at position 287 is mutated to threonine (or to other polar amino acids), the Shaker gating currents become much faster and similar to the activation rate of NaV channel gating currents (Lacroix et al., 2013, 2014). These results strongly suggest that the physical structure and the underlying mechanism controlling the activation rate of voltage-gated ion channels involve the hydrophobic strength (i.e., the polarizability) of the gating pore, especially of the residue at position 287. They suggest that a highly nonpolar, hydrophobic gating pore creates an energetically unfavorable condition, a high-energetic barrier (mostly a dielectric barrier) for the gating charges to move through upon depolarization, resulting in a slowing of the voltage sensor activation (Fig. 1 D). In this view, increasing the polarizability of this region by replacing a highly nonpolar side-chain residue with a more polar amino acid lowers the dielectric energy barrier, provides counter charge (in the wall of the gating pore) for the gating charges, and ultimately increases the activation rate of the voltage sensor.
Figure S1.
Conservation of the speed-control residue in the S2 segment in different types of fast and slowly activating NaV channels and slowly activating KV channels. The residues homologous to Shaker I287 are marked in red if hydrophobic (E and D) and in blue if hydrophilic (I, V, and M). The data clearly show that in the first three domains of all the reported fast-activating Na channels the position homologous to Shaker I287 is occupied by a threonine residue, confirming the functional importance of the hydrophilic threonine at this position. The IV domain of fast-activating NaV channels shows instead either an isoleucine or a valine at the corresponding position, in accordance with a functional role of this domain not primarily involved in the activation but in the slower inactivation process. As for the slowly activating bacterial Na channels, hydrophobic isoleucine or leucine is found, again in accordance with a direct correspondence between the hydrophilicity of this residue and the rate of voltage sensor activation. Finally, as in Shaker channels, also in KvAP and the 31 members of the first 9 families of human KV channels, the position homologous to Shaker I287 is occupied by a hydrophobic residue (isoleucine to valine, methionine in one case), thus strengthening the notion of a strict association between the slow voltage activation of KV channels and the presence of a hydrophobic residue at this position. This association is instead not respected in the last three families of KV channels (EAG or Kv10, ERG or Kv11, and ELK or Kv12), where a negatively charged residue at the position homologous to Shaker I287 is always found. Although we do not have a clear explanation for this finding, it is interesting to see that for these groups of KV channels, a different interdomain assembly, with a nonswapped topology between VSD and pore domain, has been found (Butler et al., 2020; Wang and MacKinnon, 2017; Whicher and MacKinnon, 2016). It is also interesting that MTSET accessibility data indicate that in human ERG KV channels the extracellular water crevice enters into the VSD well beyond the residue D460 (homologous to Shaker I287) and F463 (homologous to Shaker F290). Thus, the organization of the VSD in these channels appears markedly different as compared with the KV channels with a swapped-domain topology, of interest in our study.
We test this mechanistic hypothesis using a multiscale modeling approach (i.e., an approach that investigates the system at two different time and space scales) in a series of hierarchical computational methods whereby the calculated quantities from a computational simulation at an atomistic scale are used to define the parameters of the model at a coarser, macroscopic scale that satisfies conservations laws (Eisenberg, 2018). In the specific case studied here (voltage-dependent gating), the idea translates into using Brownian modeling to macroscopically describe the system and obtain gating currents and then using MD simulations to determine the needed free parameters present in the Brownian model. It is difficult to determine these parameters experimentally, but there is hope from the exciting work of the Boxer group (Fried et al., 2014; Fried and Boxer, 2017; Suydam et al., 2006). The multiscale approach appears feasible, because assessing free parameters through MD simulations is much less susceptible to artifact and is less computationally demanding than simulating the overall movement of the voltage sensor. It also has the advantage of using a Brownian model that automatically satisfies conservation laws of mass, current, and charge and Poisson’s equations. It is difficult to satisfy Poisson’s equations and conservation of current when using the periodic boundary conditions common in MD.
Materials and methods
MD simulations
The VSD used in the simulation was taken from the Shaker model of Henrion et al. (2012) in the activated state. For MD simulations, the protein was embedded on a membrane environment made of POPC, with dimensions of 80 × 80 Å, and solvated in two steps. The distance between the maximum and minimum z coordinates and the water box edges in the z axis was set to 15 Å. The system was first solvated below the membrane plane with a water box of dimensions 83.46 Å, 80.05 Å, and 16.19 Å (x, y, and z, respectively), where 9,462 TIP3 water molecules (Jorgensen et al., 1983) were placed. Then, the system was solvated above the membrane plane with a water box of dimensions 83.46 Å, 80.05 Å, and 20.02 Å (x, y, and z, respectively), where a total of 9,462 TIP3 water molecules were placed. After the addition of the water molecules, the system presented a total net charge of −2. The system was balanced, and a total of 27 Cl ions plus 29 Na ions were added to the system, making up a salt concentration of 0.15 mol/liter. The MD simulations in the present study were performed using the NAMD MD package (Phillips et al., 2005). The CHARMM36 force field (Best et al., 2012; MacKerell et al., 1998) was used in all MD simulations. A distance cutoff of 12.0 Å was applied to short-range, nonbonded interactions and a cutoff of 10.0 Å was used for the smothering functions. Long-range electrostatic interactions were treated using the particle-mesh Ewald (Darden et al., 1993) method. Before the MD simulations, all systems were submitted to an energy minimization protocol for 2,000 steps. After minimization, an annealing of 0.29 ns was performed, with a temperature ramp of 0.24 ns of simulation, where the temperature was raised from 60 K to 300 K. The pressure was maintained at 1 atm using a Nosé-Hoover Langevin piston (Feller et al., 1995; Martyna et al., 1994). The equations of motion were integrated using the r-RESPA (reversible reference system propagator algorithm) multiple time-step scheme (Phillips et al., 2005) to update the short-range interactions every one step and long-range electrostatics interactions every two steps. The time step of integration was chosen to be 2 fs for all simulations. During annealing, the motion of the backbone of the protein was restrained. After annealing, a 10-ns equilibration was performed while maintaining the restriction of the backbone motion, during which the temperature was maintained at 300 K using Langevin dynamics. The pressure was maintained at 1 atm using a Nosé-Hoover Langevin piston. A distance cutoff of 12.0 Å was applied to short-range, nonbonded interactions and a cutoff of 10.0 Å was used for the smoothing functions. Long-range electrostatic interactions were treated using the particle-mesh Ewald method. Finally, we performed unrestricted MD simulations by applying different values of the electric field in the z direction. These simulations were used to assess the running average of total dipole moment, which was used to estimate the dielectric constant as described in the Results section.
The Brownian model of voltage gating
A full description of the Brownian model of voltage gating can be found elsewhere (Catacuzzeno and Franciolini, 2019; Catacuzzeno et al., 2020). Briefly, in our model, the VSD was approximated by an hourglass structure consisting of a cylindrical gating pore with a length of 7 Å and a diameter of 10 Å flanked by internal and external water-accessible (WA) vestibules with a length of 3.15 nm each and a conical shape opening with a half angle of 15° into two hemispherical subdomains of bath solution, both having a radius of 1 µm. The S4 charge profile (ZS4) was built by considering the six positive charges, whose mean distance between the charged atoms was determined from a 3-D Shaker channel model, with each giving rise to a charge profile normally distributed with a standard deviation of 0.1 nm. The permanently charged profile (ZF), which in this case deserves the name “fixed” because it does not move, was similarly built by considering the vertical dimension of the Cα of all the charged residues on segments S1–S3 of the VSD.
Ions moved by electrodiffusion governed by the following flux conservation equation:
| (1) |
where is the concentration of ion j, t is the time, is the spatial gradient operator, and is the flux (mole per second per unit area) of ion j, given by the Nernst–Planck equation:
| (2) |
where and are the diffusion coefficient profile and the valence of ion j, respectively; F, R, and T have their usual meanings; and is the electrical voltage profile. Because ions move much faster in the bath than the voltage sensor moves in the gating, a quasi-equilibrium assumption was made for ion electrodiffusion by imposing
The S4 segment was assumed to move in one dimension as a Brownian particle, with dynamics governed by the following overdamped Langevin’s equation:
| (3) |
Here, represents the position of the voltage sensor (distance between the R2–R3 midpoint and the center of the gating pore), is the external force acting on the particle, and R(t) is a random force due to the collision of the fluid and the rest of the protein on the S4 segment, which has a probability distribution with zero mean and second moment given by where is the Boltzmann constant and is the delta function. The external force was assumed to have an electrical component, assessed from the electric voltage profile, and a spring component with force constant of 0.005 N/m to account for the force exerted by the channel permeation pore, which in this model has not been considered (Catacuzzeno and Franciolini, 2019). the friction coefficient of the S4 voltage sensor, was set to 2 × 10−6 kg/s based on the comparison between experimental and predicted macroscopic gating currents (note that in Catacuzzeno and Franciolini, 2019, this parameter was set to twice this value).
The dynamics of the S4 segment may also be described in terms of the time evolution of the probability density function profile, given by the following Fokker–Planck (FP) equation:
| (4) |
Here, represents the probability density function for the position of the S4 segment and is This partial differential equation was solved with elastic boundary conditions at in order to set the allowed movement of the particle to 3.6 nm. The elastic boundary condition was imposed by setting the particle flux equal to zero at the boundaries:
The electrical voltage profile V(x) was assessed from the net charge density profile using the following Poisson’s equation:
| (5) |
where 8.854 × 10−12 F × m−1 is the vacuum permittivity, is the position-dependent dielectric coefficient, is the electric potential, and is the position dependent surface. Programs were written in C and are available upon request. Figures were prepared using Origin v4.0 and CorelDraw v18.1.
Assessment of the energetic profile associated with the voltage sensor position
The energy profiles are assessed self-consistently by computing (and not assuming) electrostatics. More specifically, for each point of the reaction coordinate (i.e., for each position of the voltage sensor along its activation pathway), the corresponding associated energy was assessed by solving iteratively the flux conservative equation for the ionic distribution in the baths and vestibules and the Poisson's equation for the voltage profile until reaching a steady-state (or equilibrium, for equal bath ion concentrations) solution. Once steady state (or equilibrium) is reached, the resulting voltage profile is used to assess the electrostatic energy by integrating the charge on the voltage sensor multiplied by voltage over the entire space domain (cf. the mathematical relationship in the legends of Figs. 5 and 7; note that Fig. 7 reports the sole electrostatic energy, while Fig. 5 reports the total energy experienced by the voltage sensor, including the mechanical energy due to the attached spring). Obviously the calculation of the energy profile as a function of the voltage sensor position does not involve the solution of the Langevin (or the Fokker–Planck) equation, since in our model these equations are used to assess the movement of the voltage sensor (e.g., during the evolution of the gating currents), and because we choose the position of the voltage sensor while assessing the energetic profile, as it represents the independent variable of the plot. Thus, the electrostatic energy profile shown in Fig. 7 essentially comes from the solution of the Poisson–Nernst–Planck equations while varying the position of the voltage sensor. It is important to note that the reliable output of our calculations is the shape of the gating current and other associated variables. The potential profiles are computed to make our results more understandable and to relate to traditional views of channels. The variable nature of the potential profile is not included in this classical view or in our calculation of potential profiles. Much of the variable nature of the potential profile is included in our solution of the Langevin equations and gating currents.
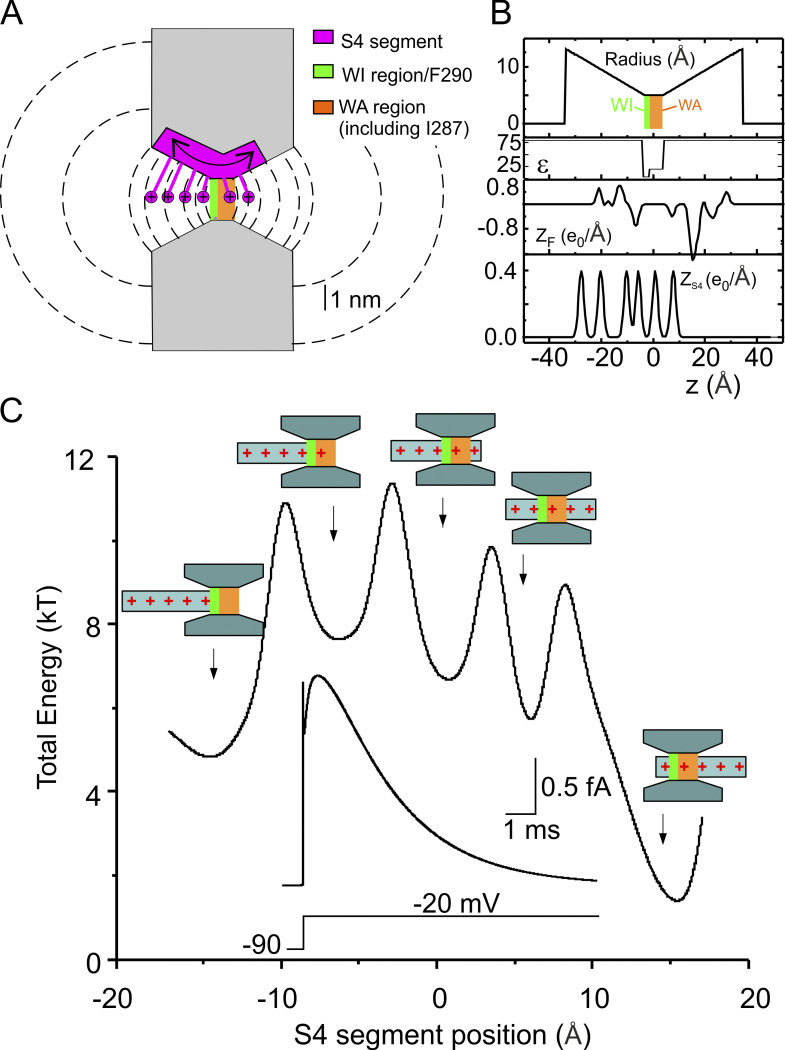
Figure 5.
The macroscopic model of voltage gating. (A) Schematic showing the geometry of the VSD assumed in our model. The S4 segment containing the gating charges was assumed to move perpendicular to the membrane through the gating pore (7 Å long) and the extracellular and intracellular vestibules (each 31.5 Å long, and opening with a half angle of 15°). Note that compared with the model presented in Catacuzzeno and Franciolini (2019), the gating pore is 5 Å longer to accommodate several hydrophobic residues, including residue I287. The vestibules are correspondingly shorter to give the same overall length. The dashed lines represent some of the surfaces delimiting the volume elements considered in our numerical simulations (see Catacuzzeno and Franciolini, 2019 for details). (B) Profile of the gating pore radius illustrating the 2-Å region, comprising F290 and assumed to be fully impermeant to water (WI, green bar), and the WA 5-Å region comprising I287 (WA, red bar), the effective dielectric constant (ε), the fixed charge density located in the S1–S3 region of the VSD (ZF), and the charge density on the S4 segment (ZS4), for the Shaker model structure. x = 0 was placed in the center of the gating pore. (C) Plot showing the total energy associated to the S4 segment, assessed as as a function of the S4 segment position. The electrostatic energy profile displays five clear energy wells associated with five different positions of the voltage sensor (represented in schematic form). Inset: Simulated macroscopic gating current evoked by a voltage pulse from −90 to −20 mV, using our Brownian model of the voltage sensor. Note that the energy used here does not include entropic effects or frictional losses.
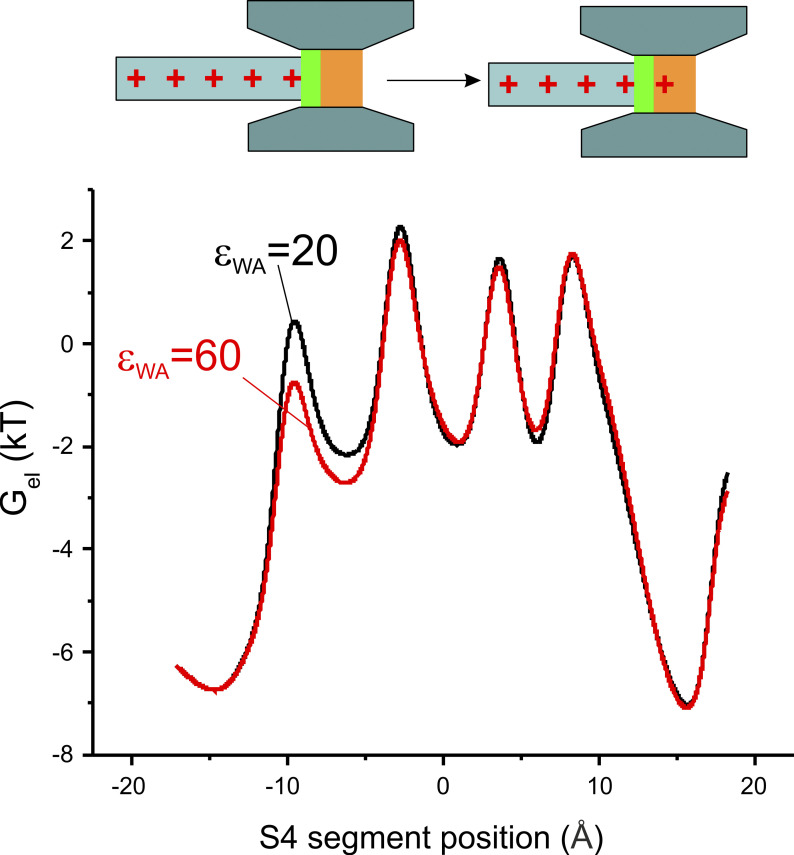
Figure 7.
Mechanisms at the base of the change in the kinetics of the gating current induced by the I287T mutation. Bottom: Plot showing the electrostatic energy associated with the S4 segment, assessed as as a function of the S4 segment position, for the two models of voltage-dependent gating differing by the dielectric constant in the WA region of the gating pore. Top: Schematic drawing showing that the change in the electrostatic energy exclusively at the first peak may be explained by the addition of the first gating charge to the WA region of the gating pore.
In our model, we assume ionic steady-state equilibrium (i.e., the overdamped system established mathematically by, for example, Eisenberg et al., 1995) that was derived rather than assumed using the overdamped high friction limit. This assumption was also used in Horng et al. (2019), justified by the fact that the voltage sensor moves much more slowly than the ionic re-equilibration in the baths and vestibules. Under this assumption, the energetic profile shown in Fig. 5 (i.e., total energy = electrostatic + mechanical) is exactly the energy encountered by the voltage sensor during its movement and the energy used to drive the voltage sensor movement through the Langevin (or Fokker–Planck) equation. Mathematically speaking, the spatial gradient of the same energy profile represents the force acting on the voltage sensor, Fex, present in Eq. 3 (the Langevin equation) and Eq. 4 (the Fokker–Planck equation).
Assessment of the macroscopic gating current
Once the energetic profile associated with the voltage sensor as a function of its position has been determined (see above), the dynamics (position versus time) of the voltage sensor may be found by solving the Fokker–Planck equation (Eq. 4, with Fex determined by the gradient of the energetic profile). The Fokker–Planck equation gives the time evolution of the probability of finding the voltage sensor in the different allowed positions, assumed that it behaves as a Brownian particle (i.e., its single-particle dynamics is described by the Langevin Eq. 3). Thus, at every successive time steps t and t + dt, we know exactly (from the numerical solution of the Fokker–Planck equation) how the probability density function describing the voltage sensor position changes (e.g., from f(x,t) to f(x,t + dt)). In response to this voltage sensor movement, the ion (cation and anion) distributions in the WA regions (baths and vestibules) will change (these distributions are assessed together with the energetic profile by solving the Poisson–Nernst–Planck equations, as described above), and as a consequence, the total net charge in these regions will change (from Q(t) to Q(t + dt)). From the principle of charge conservation, the net charge difference Q(t + dt) − Q(t) must necessarily come from the left (or right) electrode, and thus, the current at the electrode can be derived as (Q(t + dt) − Q(t))/dt. Of course, this current will be exactly the same when measured in the two WA regions (left and right, as we constantly verified). This method can also be used to assess the current in whatever position along the mono-dimensional coordinate by simply assessing the charge accumulated from the edge of the channel up to the position considered, as we did to demonstrate that the total current is conserved in space. Mathematically speaking, the gating current is determined using the following equation:
| (6) |
where
represents the net charge found in the left (or right) bath when the position of the S4 segment is xS4, and the integration covers the whole left (right) bath. We checked that the total current density was independent of location x at all times, even though the components of the current vary a great deal with x (Eisenberg, 2019 Preprint; Eisenberg, 2020 Preprint; Horng et al. 2019) and of course time t.
We emphasize that the main outputs of this paper are the actual calculations of charge movements, potential fields, effective dielectric constants, and most importantly the functional output of the system, the gating currents themselves. The potential profiles were used to provide a comforting link with the past in Figs. 7 and 8. They are most helpful in a human sense but are likely to be misleading when the more complex interactions described in the last paragraphs are important.
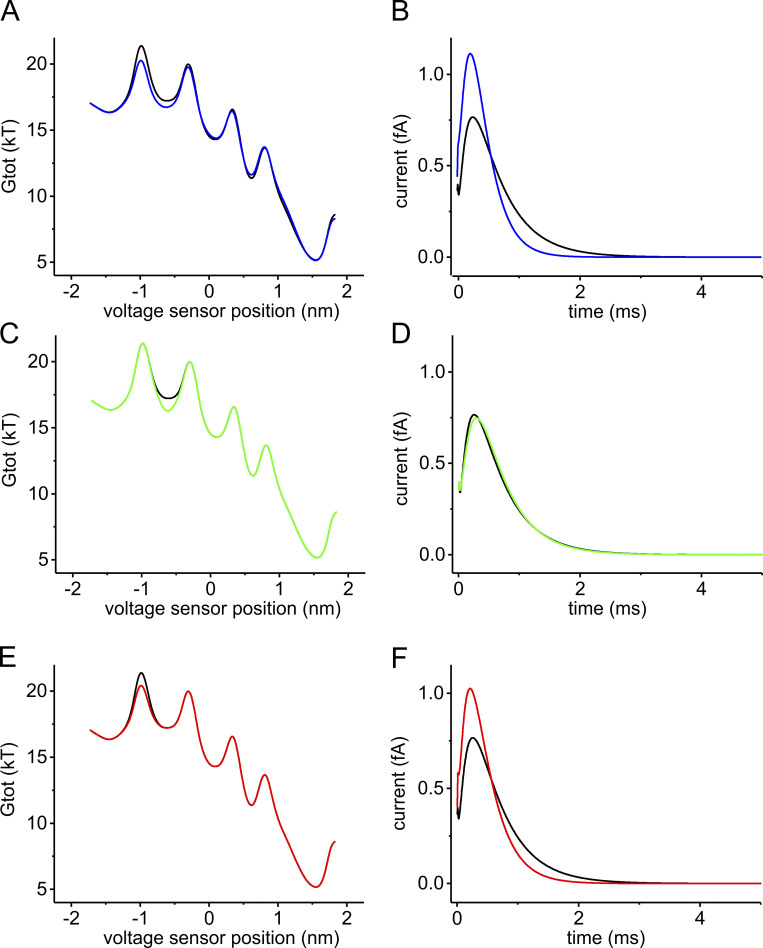
Figure 8.
Contribution of the changes in the energy peak and well to the kinetic change of gating currents. (A) Total energy profiles (Gtot) of the voltage sensor assessed at +30 mV of applied potential using our Brownian model, with a relative dielectric constant of the WA region of the gating pore set to either 20 (black) or 60 (blue), in order to predict the effect of the I287T mutation. (B) Macroscopic gating currents predicted for the energy profiles in A using the Fokker–Planck equation. The initial condition of the simulation is a probability density function placing all voltage sensors at the first well of the energy profile (xS4 = −1.425 nm). (C–F) Starting from the WT model, the energy profile was manually altered to selectively lower the second well (brown trace in C) or the first barrier (green trace in E). The effects of these changes on the time course of the macroscopic gating currents, predicted using the Fokker–Planck equation, are shown in D and F, respectively.
Online supplemental material
Fig. S1 shows conservation of the speed-control residue in the S2 segment in different types of fast and slowly activating NaV channels and slowly activating KV channels. Fig. S2 shows an extended sequence alignment for NaV and KV channel voltage sensors and additional information regarding the water accessibility of the VSD in the I287T Shaker channel.
Figure S2.
Water accessibility of the gating pore in WT and I287T mutant voltage sensor domain. (A) Left: 3-D structure of the Shaker VSD carrying the mutation I287T, obtained after 100 ns of a MD simulation in which water was allowed to equilibrate inside the intracellular and extracellular vestibules. The protein backbone is represented in cyan/transparent, the side chains of the gating pore residues are shown in licorice representation (green), and water molecules are shown in van der Waals representation (red). Right: Same as the structure shown to the left, but here, the water molecules from 20 consecutive frames of the simulation (one every 0.1 ns) are superimposed in order to define the WA region of the VSD. Note that only a very short region inside the gating pore is totally inaccessible to water. (B) Plot of the mean number of water molecules inside the gating pore region (defined as the water molecules residing inside a cylinder of 5 Å radius, extending from −1 Å to 6 Å with respect to the z component of the center of mass of the F290 aromatic ring) as a function of the simulation time. The black and red lines refer to the simulation performed with the WT structure (the same shown in Fig. 2) and with the mutant (I287T) structure, respectively.
Results
The microscopic scale description
MD simulations performed on available crystal structures can be used to predict the polarizability of a protein or part of it and thus its effective dielectric constant (Guest et al., 2011; King et al., 1991; Patargias et al., 2010; Simonson and Perahia, 1996; Smith et al., 1993; Voges and Karshikoff, 1998; Warshel et al., 2006), a parameter needed in the coarser-scale Brownian modeling of voltage gating because it determines the amount of polarization charge available to balance movements of permanent charges, like those of the gating particle. We thus used MD to assess whether the substitution of threonine (found in the NaV channel) in place of isoleucine (found in the KV channel) at position 287 can sensibly change the polarizability and consequently the dielectric constant, ε, of the gating pore and ultimately the movement and stability of the gating charges inside it.
Water accessibility estimates with MD
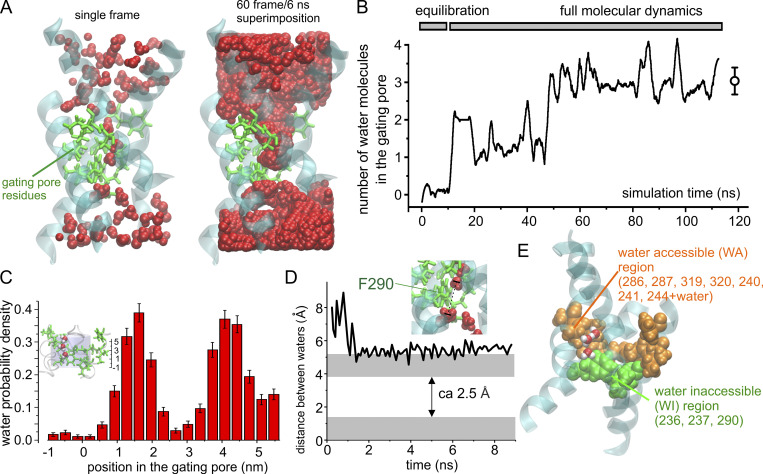
As a first step, we determined the water accessibility of the VSD in the voltage-gated Shaker K channel by performing an MD simulation using the activated state of the Shaker VSD model (Fig. 2). After inserting the protein in a phospholipid bilayer and water box and performing the minimization, annealing, and equilibration of the overall system, we ran a 100-ns MD simulation to look for water inside the vestibules and the gating pore. At the end of the simulation, we looked at the position of water molecules inside the VSD to determine whether water could also access the gating pore. The structure on the left of Fig. 2 A shows a frame at the end of the simulation, while the one on the right shows the WA space of the VSD obtained by the superposition of the water molecules from 60 consecutive frames (one every 0.1 ns). These pictures show that water readily enters both intracellular and extracellular vestibules. The pictures also identify two distinct regions inside the gating pore with different water accessibility. One region, in direct contact with the intracellular vestibule, is totally inaccessible to water, thus forming an effective water-inaccessible (WI) region. This region is very narrow (∼2–3 Å), as judged by the distance between the closest water molecules in the two vestibules (Fig. 2 D). It is located at the level of the gating pore in adjacency to residues F290 on S2 and V236 and I237 on S1 (Fig. 2 E). The second region, located between the WI region and the extracellular vestibule, including the other seven hydrophobic residues forming the gating pore (including residue I287; Fig. 2 E), is WA. As shown in Fig. 2 B, the equilibrated simulation shows three water molecules on average in this region (defined as a cylinder of 5 Å radius and extending from −1 Å to 6 Å with respect to the center of mass of the F290 aromatic ring; cf. inset to Fig. 2 C). These results show the gating pore has two regions with different accessibility to water, a WI region totally inaccessible to water and an adjacent WA region containing three water molecules most of the time. Due to the different water accessibility, we expect these two regions to have a quite different effective polarizability, with a relative effective dielectric constant close to 4 (the value typical for the interior of proteins) for the WI region but sensibly higher for the WA region, since here, water dipoles could significantly contribute to the stabilization of charges.
Figure 2.
Assessment of water accessibility of the gating pore in Shaker channels. (A) Left: 3-D structure of the Shaker VSD obtained after 100 ns of a MD simulation in which water was allowed to equilibrate inside the intracellular and extracellular vestibules. The protein backbone is represented in cyan/transparent, while the side chains of the gating pore residues are shown in licorice representation in green. Finally, water molecules are in van der Waals (VdW) representation in red. Right: Same as the structure shown to the left, but this time the water molecules from 60 consecutive frames of the simulation (one every 0.1 ns) are superimposed in order to define the WA region of the VSD. Note that only a very short region inside the gating pore is totally inaccessible to water. (B) Plot of the mean number of water molecules inside the gating pore region (defined as specified in C) as a function of the simulation time. (C) Plot of the mean number of water molecules in the gating pore. Error bars in B and C represent the SD. Water molecules were counted when residing inside a cylinder of 5 Å radius and 7 Å high, extending from −1 Å to 6 Å with respect to the z component of the center of mass of the F290 aromatic ring (see inset). (D) Plot of the distance between the centers of mass of the two closest intracellular and extracellular water molecules as a function of the simulation time. If the radius of a water molecule is 1.4 Å (gray regions), a WI region of 2.5 Å is estimated. (E) 3-D structure of the Shaker VSD obtained after 20-ns MD simulation in which water was allowed to equilibrate inside the intracellular and extracellular vestibules. The protein backbone is represented in cyan/transparent, while the side chains of the gating pore residues are shown in VdW representation in green for the three residues forming the region totally WI and orange for the remaining seven residues forming the remaining part of the gating pore, which is partially WA. Two water molecules inside the gating pore are also shown (red oxygens and white hydrogens).
Estimating the dielectric constant of WA and WI regions of the gating pore using MD simulations
The dielectric constant has two main components, one given by the polarization of the electronic clouds, and the other due to the reorientation of permanent dipoles along the applied electric field, Of these, can be measured experimentally (in bulk solutions) by impedance spectroscopy (Macdonald, 1992) or by the refractive index of the material (Gussoni et al., 1998), which depends strictly on the dielectric constant at the appropriate frequency. In addition, the of a protein region may simply be crudely estimated by summing up the individual polarizability levels of the various amino acids present that can be obtained experimentally (Voges and Karshikoff, 1998). There is regrettably no experimentally recognized method to assess inside a protein region, although it is known to depend on the reorientation of dipoles along the electric field. Indeed, the assignment of polarizability in an atomic scale system has serious ambiguities, as described in Purcell and Morin (2012). For a small spherical volume of material surrounded by an infinite and homogeneous medium, can be estimated by running extended MD simulations and analyzing the equilibrium fluctuation of the total dipole moment of the sample volume by applying the Kirkwood–Frohlich theory of dielectrics (Frohlich 1949; Simonson and Perahia, 1996). Unfortunately, the structure we are studying—the voltage sensor—is immersed in a highly inhomogeneous medium (water and protein residues) on which this approach becomes impractical. In this case, the dielectric constant in the small sample volume in the protein interior will also depend on the polarizability of the surrounding medium, whose value is neither known nor can be assumed to be homogeneous. The assumption of homogeneity is crucial because inhomogeneity creates dielectric boundary charges that can easily dominate the properties of a system (Nadler et al., 2004; Nadler et al., 2003). One can hardly imagine a more inhomogeneous environment than that of a gating pore embedded in a dielectric membrane immersed in an ionic solution.
We thus reasoned that under our conditions, the dielectric constant of the sample volume could be estimated from MD simulations run at variable applied electric fields. More specifically, using the basic definition of polarization (P) as the sum of the dipole moments (µ) per unit volume and its relation to the dielectric constant usually valid at moderately low electric fields, we can write:
where is the permittivity of vacuum, E is the applied electric field, and Vol is the sample volume. The total dipole moment of the sample can be determined using time averaging over the MD simulation (<M>z) while applying an electric field along the z direction (Ez). This allows us to calculate εpd as
| (7) |
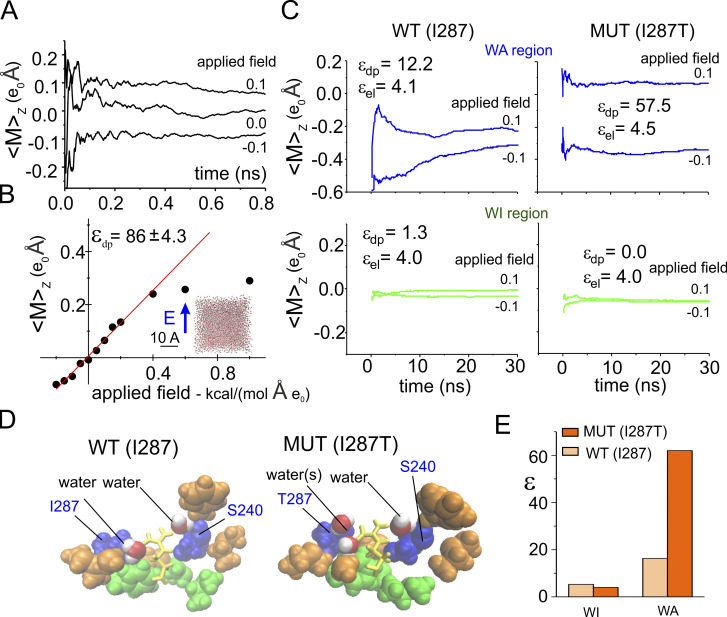
This method emerges naturally from consideration of the relation of charge and electric fields in proteins (Eisenberg, 1996b) and has been successfully applied to estimate the dielectric constant of a protein, as well as water confined inside the pore of a synthetic ion channel (Sansom et al., 1997; Xu et al., 1996). To validate this method for estimating we first applied it to water molecules in a cubic water box that is known to have a dielectric constant close to 82 for our TIP3P water model (Simonson, 1996). We ran several MD simulations under different electric fields, applied along the z direction, and measured each time the z component of the total dipole moment associated with one water molecule (chosen at random) inside the cubic box. The plot in Fig. 3 A reports a running average of the total dipole moment assessed for three different applied electric fields and shows that the value of the dipole moment varies with the applied fields. Fig. 3 B illustrates the relationship between the total dipole moment along the z direction and the applied electric field. As expected, this relationship is linear for moderate applied fields, while it saturates at higher values. From the slope of this relationship within the linear regimen, we obtained an effective dielectric constant of ∼86, a value quite close to what was expected, indicating that our method to estimate the dielectric constant works satisfactorily in this situation.
Figure 3.
Estimation of the dielectric constant in the gating pore. (A) Running average of the dipole moment assessed for a water molecule inside a 30 Å cubic water box during three MD simulations performed under different applied electric fields along the z direction. (B) Plot of the mean total dipole moment of a water molecule as a function of the applied electric field. Each symbol represents the total dipole moment estimated for a water molecule taken at random during the last nanosecond of a 4-ns-long simulations performed in presence of variable applied fields (indicated). Data obtained at applied electric fields of ±0.2 kcal/(mol·Å·eo) were fitted with a straight line, and the dielectric constant reported in the plot was estimated from Eq. 7. Note that 1 kcal/(mol·Å·eo) corresponds to ∼0.4 V/nm. For comparison, a constant electric field of 0.2 kcal/(mol·Å·eo) would correspond to an electric potential difference of ∼240 mV across a phospholipid bilayer. (C) Plots of the mean total dipole moment at two different applied electric fields for the WA region (top) and WI region (bottom) of the gating pore, assessed from MD simulations using the WT (I287; left) of the mutated (MUT; I287T; right) structure of the VSD. From these data, the εpd was estimated and reported in each plot. The εel, also reported in the plot, was estimated from the Clausius–Mosotti relationship where α is the polarizability and Vol is the volume of the region considered, estimated from the molar polarizability of the amino acidic residues reported in Table 1 of Voges and Karshikoff (1998). The plots show running averages performed over the last 30-ns simulation, taken from a simulation in which the indicated electric field was applied for 100 ns to let the molecules to reorient. (D) 3-D structures of the gating pore in the WT and mutated VSD. The gating pore residues are shown in van der Waals (VdW) representation in green or orange/blue depending on their location in the WA or WI region of the gating pore, respectively. Residues 287 and 240, located very close to the gating charge, are colored in blue. Also shown (in VdW representation [red/white]) are the water molecules inside the WA region, within 3 Å of the charge on R371. The gating charge, R371, is shown in licorice representation (yellow). (E) Plot of the dielectric constant in the WA and WI regions of the gating pore, estimated as shown in C. MUT, mutated.
We then applied this method to estimate the effective dielectric constant of the WI and WA regions of the gating pore, both in the WT and in the mutant structure in which isoleucine 287 (found in KV channels) had been replaced by threonine (mutant I287T) found in NaV channels. In the calculation of the dielectric constant of the WI region, we considered all three residues present in this region, namely residues F290, V236, and I237, since they all surround the gating charges while they move through this region of the gating pore (Fig. 3 D, green residues). As expected for a very hydrophobic, nonpolar region, the polarizability of the WI region was electronic in nature, with a value ∼4.0, irrespective of the residue present at position 287 (Fig. 3, C and E).
The situation is quite different for the WA region, where the gating pore widens, and not all residues are close to the moving gating charges. In the assessment of the effective dielectric constant, we thus considered only those residues adjacent to the gating charge (i.e., placed at a distance less than 3 Å), namely, residues I287 and S240, plus few water molecules (Fig. 3 D, blue residues and red/white water molecules). The dielectric constant estimated in this region was much higher than in the WI region, but, most relevantly, it was quite different in the two WA structures being considered (∼20 in the WT and ∼60 in the I287T mutant; Fig. 3, C and E). These results indicate that the nature of the residue at position 287 critically contributes to the polarizability of the WA region around the gating charge, and a mutation of hydrophobic isoleucine at this position introducing a more hydrophilic amino acid like threonine markedly increases the polarization charge in this region.
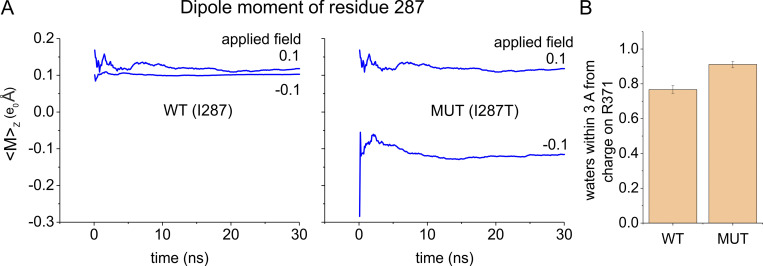
Two main reasons explain why the WA region has a higher polarizability in the mutant compared with WT. First, the threonine residue has a much higher permanent dipole because of its hydroxyl group, and thus stronger hydrophilic power than isoleucine. As a result, the dipole moment contributed by this one residue is much higher in the I287T mutant than in the WT structure (Fig. 4 A). Second, the region close to the gating charge R371 in the I287T mutant appears to have a slightly higher water content than in WT (Fig. 4 B), presumably because threonine stabilizes nearby water molecules with hydrogen bonds. However, the overall water content inside the gating pore was the same in WT and mutant structures (Fig. S2).
Figure 4.
Mechanism of the dielectric constant increase induced by the I287T mutation. (A) Running average of the dipole moment associated to the side chain of residue 287 assessed for the WT and the mutated (MUT) structure from the same simulations shown in Fig. 3 C. The mutant threonine is much more polarizable than WT isoleucine. (B) Mean number of water molecules found inside the WA region of the gating pore and within 3 Å of the charge of R371 in MD simulations performed using either the WT or the I287T mutated structure of the VSD (same simulations shown in A). Error bars represent the SD.
The macroscopic scale description
The macroscopic scale description of voltage gating is based on the Brownian model that we have recently developed and is a good predictor of the major signature features of experimental gating currents of Shaker channels (Catacuzzeno and Franciolini, 2019; Catacuzzeno et al., 2020; see Materials and methods). Other papers (Horng et al., 2019; Kim and Warshel, 2014; Peyser et al., 2014; Peyser and Nonner, 2012b, 2012a) give other views of the voltage sensor and resulting currents at different resolutions. Only Horng et al. (2019) and Catacuzzeno and Franciolini (2019) calculate gating currents comparable to those measured experimentally under a range of conditions, with Horng et al. (2019) having less atomic detail. Our model takes the relevant structural and electrostatic parameters directly from the 3-D structural model of the Shaker VSD (Fig. 5, A and B). The electrodiffusion of ions in the bath is described through a flux conservation equation that assumes a quasi-equilibrium, on the time scale of gating currents, and the motion of S4 segments is described by Brownian dynamics. The electric potential profile is modeled using the Poisson equation and includes all the charges present in the system, including the gating charges on the S4 segment and the fixed charges on segments S1–S3 of the VSD. Notably, the Poisson equation that is used in our model to assess the electric potential profile contains the relative dielectric constant, ε, as an undetermined parameter that we have estimated above for both the WT and mutant gating pores using MD simulations. It should clearly be understood that this form of coarse graining has the significant advantage that the coarser, lower-resolution treatment satisfies conservation laws of mass, charge, and current. Coarse graining procedures that do not explicitly introduce the Poisson equation and boundary conditions are unlikely to satisfy conservation laws of charge and current. Periodic boundary conditions in traditional MD make it difficult to satisfy Poisson’s equations and conservation of current in a spatially inhomogeneous, nonperiodic system like an ion channel protein or gating pore.
In our previous model, we assumed a 2-Å-long gating pore localized at the level of F290 that separated electrically the intracellular and extracellular solutions. The effective dielectric constant was set to 4 in this short region and to 80 elsewhere, including the adjacent region containing residue I287 (Catacuzzeno and Franciolini, 2019). The gating pore used in the present study has been changed to account for our MD results shown above. More specifically, the gating pore is now pictured as made of two distinct regions. One region has all the properties previously described, with 2 Å length comprising F290, and is fully impermeant to water (green bar in Fig. 5, A and B). The second region (5 Å long), comprising several hydrophobic residues, including I287, is accessible to water and has now been assigned a dielectric constant of 20, in accordance with the MD results (Fig. 5, A and B). As shown in Fig. 5 C, the updated model continues to predict the major features of experimental gating currents obtained in response to a depolarizing pulse. First, a very fast gating current component is present at the beginning of the depolarizing step, rising instantaneously and then falling very rapidly. Second, a later slower current component develops, starting with a plateau/rising phase and proceeding with a slow decay. Both these features have been observed in experiments (Bezanilla, 2000; Sigg et al., 2003). The plot in Fig. 5 C represents the total energy profile assessed for the various allowed positions of the voltage sensor. It can be seen that the model predicts five energy wells corresponding to the five different positions the S4 segment can assume in accordance with many studies showing that the voltage sensor moves in multiple steps during the activation process (Bezanilla et al., 1994; Henrion et al., 2012; McCormack et al., 1994; Schoppa et al., 1992; Tytgat and Hess, 1992; Zagotta et al., 1994). In our model, each step represents the passage of a different gating charge through the high-resistance and WI region of the gating pore (compare drawings in Fig. 5 C).
Testing the effects of a dielectric constant change on the gating current kinetics
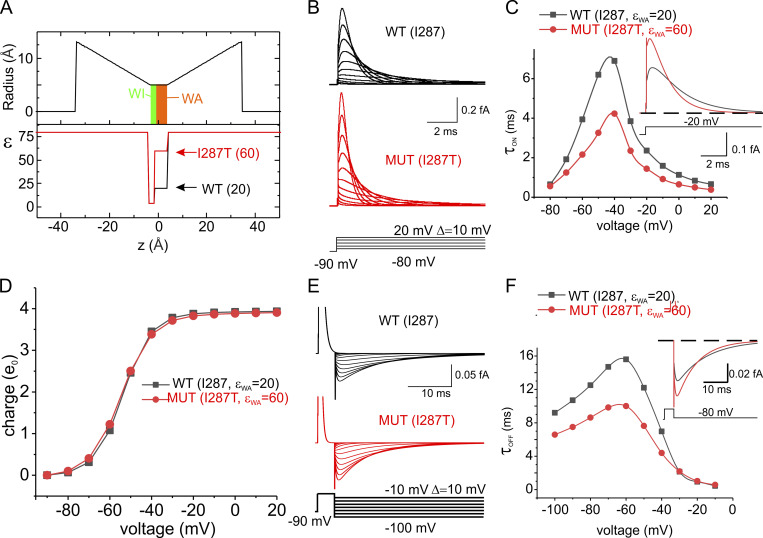
We verified that a different dielectric constant of the WA region can explain the different kinetics of the macroscopic gating current of WT and I287T mutant found experimentally (Lacroix et al., 2013). We used our macroscopic Brownian model of voltage gating to see whether changing the dielectric constant of the WA region from 20 to 60 reproduces the increased rate of gating current seen in mutagenesis experiments.
As shown in Fig. 6, B and C, there was a significant increase in the rate of change of the gating currents evoked by depolarizing pulses (ON gating currents), especially at intermediate levels of depolarization (Fig. 6 C), as observed experimentally. The model also predicted an increased rate of the OFF gating currents induced by repolarization after a short depolarizing pulse (Fig. 6, E and F). No change was observed in the charge versus voltage relationship (Fig. 6 D). Overall, these results are very similar to those observed experimentally with the mutation I287T, suggesting that a change in the dielectric constant within the gating pore is a major determinant of the functional effects induced by the mutation.
Figure 6.
Prediction of the effect of the I287T mutation on the kinetics of gating currents. (A) Profile of the gating pore radius and the effective dielectric constant along the VSD of the WT and the I287T mutated models of voltage gating. The two models only differ in the dielectric constant in the WA region of the gating pore. (B) Simulated gating currents obtained in response to depolarizing pulses from a holding potential of −90 mV for both the WT (black) and the mutated (red) models. (C) Plot of the decay time constant of the ON gating currents shown in B as a function of voltage. When the gating current decay was clearly biexponential, a mean of the two time constants weighted for the respective areas was reported. Inset: Superimposed ON gating currents obtained in response to a depolarization to −20 mV for the two models. (D) Plot of the mean charge versus the applied voltage, obtained by integrating the ON gating currents over 40-ms-long simulations at different applied voltages. No appreciable difference was observed in the two models. (E) Simulated gating currents obtained in response to repolarizing pulses after a short (4 ms) depolarizing step to 20 mV for the WT (black) and the mutated (red) models. (F) Plot of the decay time constant of the OFF gating currents shown in E as a function of voltage. Inset: Superimposed OFF gating currents obtained in response to a repolarization to −80 mV for the two models. MUT, mutated.
We then examined the effects of changing the polarizability of the WA region on the electrostatic energy profile and found that the mutation selectively lowers the first of the four peaks present in the profile (Fig. 7). This result appears quite reasonable, since the first energetic peak essentially represents the dielectric boundary energy commonly (but incorrectly) called the Born energy for the addition of one (gating) charge to the WA region of the gating pore (Nadler et al., 2004, 2003), and we expect this quantity to depend on the dielectric constant present there (compare inset to Fig. 7)1. The remaining energy peaks are instead essentially unmodified as the voltage sensor continues to move. This presumably occurs because the charge residing in the WA region is simply replaced by the next charge of the S4 segment, as the voltage sensor moves in response to an applied voltage, keeping the overall charge content in the WA region constant.
The energy profile presented in Fig. 7 shows that the I287T mutation, besides lowering the first energy barrier, also reduces (by approximately the same amount) the energy of the neighboring well, corresponding to the first gating charge sitting close to the WA region of the gating pore. If, intuitively, a reduction of an energy barrier leads to a faster activation time course while a reduction of a local minimum is instead associated with a slowing of the voltage sensor activation, then the overall effect of simultaneous lowering an energy barrier and nearby energy well is difficult to foresee and could result, in principle, in either speeding or slowing the voltage sensor movement, depending on which of the two effects will prevail.
Based on our modeling results, we conclude that the decrease of the first energy barrier is by far the most important effect of the I287T mutation. To verify this conclusion, we modeled the effect on gating currents kinetics of altering selectively either the first peak or the second well of the energetic profile by amounts comparable to those observed following the I287T mutation (Fig. 8). The results of these computations show that the effect of altering the energy barrier is much more pronounced than the effect of altering the neighboring local minimum and thus explain why the mutation results in a net increase in the gating current kinetics.
Discussion
Several conclusions may be drawn from the results of our multiscale analysis. First, using MD simulations, we have shown that the gating pore of the Shaker channel, defined in terms of the 10 residues proposed by Lacroix et al. (2014), does not have uniform accessibility to water. More specifically, we have found that the region totally inaccessible to water is actually very short, with a length of 2–2.5 Å, and includes the three most intracellular residues, namely F290 on the S2 segment and V236 and I237 on S1. The remaining part of the gating pore, covering a length of ∼5 Å, is by contrast accessible to water, with three water molecules often found in this region, as shown by our MD simulations. These results appear in agreement with previous MD simulations performed on the VSD of other voltage-gated ion channels. More specifically, an almost continuous arrangement of water molecules was found in the VSD of the KvAP channel (a bacterial KV channel from Aeropyrum pernix), with a very short interruption at the level of the R133–D62 salt bridge (Freites et al., 2006). A similar conclusion was reached in MD simulations of the Shaker homologue KV1.2, where a very short constriction, localized at the K5–D259 salt bridge and forming the so-called gating charge transfer center together with F233 (the homologue of F290 in Shaker), prevented communication between the upper and lower crevices (Delemotte et al., 2010; Tao et al., 2010). Finally, a short 2-Å WI region centered on a conserved phenylalanine was also found in the VSDs of the first three domains of NaV channels and thought to be functionally similar to the VSD of the KV channel (Gosselin-Badaroudine et al., 2012). The potential difference applied to the membrane will then drop mostly over the very short WI region, because this part of the gating pore is the only region with very high resistance to water and ions. The notion of a very narrow high-resistance region that focuses virtually the entire transmembrane voltage drop has already been suggested by several studies (Ahern and Horn, 2005; Asamoah et al., 2003; Islas and Sigworth, 2001). The focusing of the electric field is of course incompatible with the idea of “constant fields” that has been a mainstay of biophysics for more than 50 years and remains so in teaching materials to this day. Electric fields change shape as conditions change because of the fundamental properties of the electric field, as pointed out in the context of channels some years ago (Eisenberg, 1996a). F290 has been proposed to act as a gating charge transfer center (Tao et al., 2010), although its role has been later refined to stabilizing the activated VSD conformation (Lacroix et al., 2014; Lacroix and Bezanilla, 2011). In our view, this residue is important for creating the only very-high-resistance region inside the VSD, where most of the voltage drops. It is in the 2-Å-wide region that includes F290 that the moving gating charges experience the electrostatic force that stabilizes either the closed or open conformation, depending on the applied voltage.
A second result of this study is the quantitative demonstration that the polarizability (i.e., the hydrophobicity) of the residue at position 287 of Shaker channels can greatly modulate the field strength acting on the gating charge as it enters the gating pore. We showed this by estimating the dielectric constant of the region surrounding the gating charge, using MD simulations at variable applied electric fields, and assessing the change in the total dipole moment of the region. In contrast to the computational methods usually employed to assess the dielectric constant (Guest et al., 2011; King et al., 1991; Simonson and Perahia, 1996; Smith et al., 1993; Warshel et al., 2006), which are based on the Kirkwood–Frohlich theory of spatially uniform dielectrics (Frohlich, 1949; Simonson and Perahia, 1996), our method does not assume a homogeneous environment of known polarizability surrounding the sample volume of interest. For this reason, our approach can be applied also to restricted regions inside a protein containing a small number of side chains. This method has been already successfully applied to estimate the dielectric constant of a homogeneous liquid, as well as of water confined inside the pore of a synthetic ion channel (Kolafa and Viererblová, 2014; Riniker et al., 2011; Sansom et al., 1997; Xu et al., 1996; Yeh and Berkowitz, 1999). However, to the best of our knowledge, it has not been applied before to assess the local dielectric constant inside a (channel) protein.
We found that changing the residue at position 287 significantly changes the effective dielectric constant acting on the gating charge. More specifically, when the isoleucine found at this position in Shaker (as well as in other KV channels) is changed to threonine, the residue found at the corresponding position in NaV channels, the estimated dielectric constant appears to increase by as much as three times. The observed increase may have two components: (1) the much higher permanent dipole present on the threonine side chain (as compared with isoleucine, mostly because of the hydroxyl group there), which contributes directly to increase the polarizability, and (2) the possibility that threonine, as a polarizable dipole, attracts more waters inside the WA region of the gating pore, electrostatically and by establishing weak hydrogen bonds (Desiraju and Steiner, 1999). In summary, our data suggest that the WA region of the NaV channel has a higher effective dielectric constant, and this possibly allows the first gating charge to enter the gating pore more easily than in KV channels. The change in dielectric constant lowers the energetic barrier gating charge encounters in entering the gating pore.
We are aware that our model has limitations. One is related to the estimation of the local dielectric constant inside the gating pore, which we have obtained with classical MD. As there is no electronic polarization with MD, it might be possible that the resulting dipole moment responses are overestimated and so would be the dipolar component of the dielectric constant. The estimation of the dielectric constant could also be biased by our assumption of a linear relationship between the applied field and the total dipole moment, which we know to be valid in water for moderate fields. We do not know whether this assumption is valid in the complex dielectric environment of the voltage sensor. A second limitation relates to our MD simulations in two respects. They were run in a limited spatial environment using periodic boundary conditions and might have produced time-varying electric fields as the dimensions of the box changed. In addition, their limited time span (100 ns) might not be sufficient to cover wetting/dewetting transitions, which also have an impact on the estimation of the dielectric constant. Nonetheless, in spite of these limitations, we believe that our study provides an important testable hypothesis and opens new avenues for the field of voltage-dependent gating.
We also used our Brownian model (Catacuzzeno and Franciolini, 2019) to see if the predicted change in the effective dielectric constant found by MD explains the functional effect of the I287T mutation found in experiments (i.e., a noticeable increase in both the ON and OFF gating currents kinetics but only a small change in the charge–voltage relationship). The output of our Brownian model was quite similar to the experimental results, suggesting that the polarizability change caused by the I287T mutation is a major determinant for the effects observed on the macroscopic gating currents. More specifically, we found that the mutation caused a maximum decrease in the time constant of the ON gating currents of ∼57% of its WT value, not very far from the ∼48% found in experiments (Lacroix et al., 2013). Thus, the real effect of the I287T mutation on the gating current kinetics appears slightly higher than that predicted by our multiscale model. In this regard, it should be pointed out that mutagenesis experiments have shown that the size of the residue is also important (Lacroix et al., 2013, 2014). Considering the critical location of this residue (very close to the moving gating charges), it is not surprising that steric effects may also be involved, perhaps by changing the friction experienced by the moving voltage sensor and thus the rate of the gating currents.
We then looked at the mechanism linking the effective dielectric constant of the WA region to the rate of movement of the voltage sensor by analyzing the effects of the mutation on the energy profile encountered by the voltage sensor as it moves into the gating pore. We found that the reduction in the dielectric constant of the WA region produces a selective decrease in the first of the four energy peaks encountered by the voltage sensor, corresponding to the entry of the first gating charge (R1) into the gating pore. This result is not unexpected since this step involves the entry of a charge into the WA region, a process modulated by its polarizability. It is important to realize that what we show is a prediction of gating currents performed without using adjustable parameters, not a fitting routine where free parameters are adjusted to match the model output with the experimental data (Horng et al., 2019).
In this study, we have analyzed in detail the functional properties of Shaker channel gating, with isoleucine or threonine at location 287, since the type of residue present at this position (or equivalent position in NaV channels) is thought to create the kinetic differences between NaV and KV channels (Lacroix et al., 2013). The results obtained suggest that different activation kinetics of voltage-gated Na and K channels come from different dielectric forces exerted by threonine compared with isoleucine, as the first gating charge enters the WA region of the gating pore. It seems that evolution uses a single side chain to control the speed of the KV and NaV channels and ultimately allow the action potential to exist.
Other processes could contribute to the time course of Na and K channels, as pointed out by Francisco Bezanilla. First, residue 363 in S4 is a highly conserved threonine in domains I, II, and III of NaV channels, while it is a highly conserved isoleucine in KV channels. Mutation of this isoleucine to threonine makes the voltage sensor of KV channels move faster, as inferred from the time course of the gating currents (Lacroix et al., 2013). From the position of this residue relatively far from the gating charge R1, we suspect that its contribution to the polarizability would not be significant, suggesting that a different mechanism is likely responsible for this effect. Second, the presence of the β1 subunit of NaV channels also accelerates the voltage sensor by an unknown mechanism (Lacroix et al., 2013). Finally, the sensors in NaV channels exhibit positive cooperativity, which also accelerates the overall speed of channel activation (Chanda et al., 2004).
We point out that, within the limitations of our models, what we propose is both logically sufficient and logically necessary to account for the difference in speed and the structural movements of the voltage sensor. It is sufficient because we reproduce the properties of gating current under a realistic range of conditions. It is necessary because the movement of charges that we calculate must produce the currents we calculate given the universal and exact nature of the Maxwell equations that link charge and current. Of course, evolution is not logical. It often provides redundant mechanisms that are beyond the necessary and sufficient, that is to say, beyond the barely sufficient. These redundant mechanisms may provide properties not glimpsed in gating currents studied with step functions in the way they are usually measured. These mechanisms may make the gating system controllable and/or robust in conditions we have not explored. After all, most devices designed by engineers have multiple controls of the same output. It is not unreasonable to expect the same in devices designed by evolution, like the VSD.
A similar multiscale approach may also be used in the future to understand the physics of the functional effects of the many other mutations that have been performed on the VSD, thereby giving a deeper understanding of voltage-dependent gating.
Acknowledgments
Jeanne M. Nerbonne served as editor.
We are grateful to Prof. Bezanilla for teaching us the importance of his results in a discussion that motivated the models of this paper. We thank the referees for suggesting significant improvements to our calculations and presentation of results.
This work was supported by the University of Perugia (grant Ricerca di Base 2017).
The authors declare no competing financial interests.
Author contributions: L. Catacuzzeno conceived the modeling strategy and performed the theoretical simulations. L. Catacuzzeno, L. Sforna, F. Franciolini, and R.S. Eisenberg discussed the model results. L. Catacuzzeno, F. Franciolini, and R.S. Eisenberg wrote the paper. All authors approved the final version of the paper.
Footnotes
The Born energy was computed by Born in an infinite homogeneous domain without dielectric discontinuities. The system we study is about as far from homogeneous as one could imagine, and its biological functions are determined by the heterogeneous distribution of polarization and dielectric properties. The use of the phrase “Born energy” is seriously misleading in the opinion of at least one of the authors.
References
- Ahern, C.A., and Horn R.. 2005. Focused electric field across the voltage sensor of potassium channels. Neuron. 48:25–29. 10.1016/j.neuron.2005.08.020 [DOI] [PubMed] [Google Scholar]
- Asamoah, O.K., Wuskell J.P., Loew L.M., and Bezanilla F.. 2003. A fluorometric approach to local electric field measurements in a voltage-gated ion channel. Neuron. 37:85–97. 10.1016/S0896-6273(02)01126-1 [DOI] [PubMed] [Google Scholar]
- Best, R.B., Zhu X., Shim J., Lopes P.E.M., Mittal J., Feig M., and Mackerell A.D. Jr. 2012. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 8:3257–3273. 10.1021/ct300400x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla, F. 2000. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 80:555–592. 10.1152/physrev.2000.80.2.555 [DOI] [PubMed] [Google Scholar]
- Bezanilla, F., Rojas E., and Taylor R.E.. 1970. Sodium and potassium conductance changes during a membrane action potential. J. Physiol. 211:729–751. 10.1113/jphysiol.1970.sp009301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla, F., Perozo E., and Stefani E.. 1994. Gating of Shaker K+ channels: II. The components of gating currents and a model of channel activation. Biophys. J. 66:1011–1021. 10.1016/S0006-3495(94)80882-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler, A., Helliwell M.V., Zhang Y., Hancox J.C., and Dempsey C.E.. 2020. An Update on the Structure of hERG. Front. Pharmacol. 10:1572 10.3389/fphar.2019.01572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catacuzzeno, L., and Franciolini F.. 2019. Simulation of Gating Currents of the Shaker K Channel Using a Brownian Model of the Voltage Sensor. Biophys. J. 117:2005–2019. 10.1016/j.bpj.2019.09.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catacuzzeno, L., Sforna L., and Franciolini F.. 2020. Voltage-dependent gating in K channels: experimental results and quantitative models. Pflugers Arch. 472:27–47. 10.1007/s00424-019-02336-6 [DOI] [PubMed] [Google Scholar]
- Chanda, B., Asamoah O.K., and Bezanilla F.. 2004. Coupling interactions between voltage sensors of the sodium channel as revealed by site-specific measurements. J. Gen. Physiol. 123:217–230. 10.1085/jgp.200308971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darden, T., York D., and Pedersen L.. 1993. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 98:10089–10092. 10.1063/1.464397 [DOI] [Google Scholar]
- Delemotte, L., Treptow W., Klein M.L., and Tarek M.. 2010. Effect of sensor domain mutations on the properties of voltage-gated ion channels: molecular dynamics studies of the potassium channel Kv1.2. Biophys. J. 99:L72–L74. 10.1016/j.bpj.2010.08.069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desiraju, G.R., and Steiner T.. 1999. The Weak Hydrogen Bond: In Structural Chemistry and Biology. International Union of Crystallography, Chester, UK: p. 526 pp. [Google Scholar]
- Eisenberg, R.S. 1996a Atomic biology, electrostatics, and ionic channels; In New Developments and Theoretical Studies of Proteins. World Scientific, Philadelphia, PA. 269–357. [Google Scholar]
- Eisenberg, R.S. 1996b Computing the field in proteins and channels. J. Membr. Biol. 150:1–25. 10.1007/s002329900026 [DOI] [PubMed] [Google Scholar]
- Eisenberg, R.S. 2018. Asking Biological Questions of Physical Systems: The Device Approach to Emergent Properties. J. Mol. Liq. 270:212–217. 10.1016/j.molliq.2018.01.088 [DOI] [Google Scholar]
- Eisenberg, R.S. 2019. Kirchhoff’s law can be exact. arXiv. http://arxiv.org/abs/1905.13574. (Preprint posted July 17, 2019)
- Eisenberg, R.S. 2020. Electrodynamics correlates knock-on and knock-off: Current is spatially uniform in ion channels. arXiv. . (Preprint posted May 14, 2020).
- Eisenberg, R.S., Kłosek M.M., and Schuss Z.. 1995. Diffusion as a Chemical Reaction: Stochastic Trajectories between Fixed Concentrations. J. Chem. Phys. 102:1767–1780. 10.1063/1.468704 [DOI] [Google Scholar]
- Feller, S.E., Zhang Y., Pastor R.W., and Brooks B.R.. 1995. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 103:4613–4621. 10.1063/1.470648 [DOI] [Google Scholar]
- Freites, J.A., Tobias D.J., and White S.H.. 2006. A voltage-sensor water pore. Biophys. J. 91:L90–L92. 10.1529/biophysj.106.096065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried, S.D., and Boxer S.G.. 2017. Electric Fields and Enzyme Catalysis. Annu. Rev. Biochem. 86:387–415. 10.1146/annurev-biochem-061516-044432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried, S.D., Bagchi S., and Boxer S.G.. 2014. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science. 346:1510–1514. 10.1126/science.1259802 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frohlich, H. 1949. Theory of Dielectrics Dielectric Constant and Dielectric Loss. Clarendon Press, Oxford, UK. [Google Scholar]
- Gosselin-Badaroudine, P., Delemotte L., Moreau A., Klein M.L., and Chahine M.. 2012. Gating pore currents and the resting state of Nav1.4 voltage sensor domains. Proc. Natl. Acad. Sci. USA. 109:19250–19255. 10.1073/pnas.1217990109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guest, W.C., Cashman N.R., and Plotkin S.S.. 2011. A theory for the anisotropic and inhomogeneous dielectric properties of proteins. Phys. Chem. Chem. Phys. 13:6286–6295. 10.1039/c0cp02061c [DOI] [PubMed] [Google Scholar]
- Gussoni, M., Rui M., and Zerbi G.. 1998. Electronic and Relaxation Contribution to Linear Molecular Polarizability. An Analysis of the Experimental Values. J. Mol. Struct. 447:163–215. 10.1016/S0022-2860(97)00292-5 [DOI] [Google Scholar]
- Henrion, U., Renhorn J., Börjesson S.I., Nelson E.M., Schwaiger C.S., Bjelkmar P., Wallner B., Lindahl E., and Elinder F.. 2012. Tracking a complete voltage-sensor cycle with metal-ion bridges. Proc. Natl. Acad. Sci. USA. 109:8552–8557. 10.1073/pnas.1116938109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin, A.L., and Huxley A.F.. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horng, T.L., Eisenberg R.S., Liu C., and Bezanilla F.. 2019. Continuum Gating Current Models Computed with Consistent Interactions. Biophys. J. 116:270–282. 10.1016/j.bpj.2018.11.3140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Islas, L.D., and Sigworth F.J.. 2001. Electrostatics and the gating pore of Shaker potassium channels. J. Gen. Physiol. 117:69–89. 10.1085/jgp.117.1.69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen, W.L., Chandrasekhar J., Madura J.D., Impey R.W., and Klein M.L.. 1983. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 79:926–935. 10.1063/1.445869 [DOI] [Google Scholar]
- Kim, I., and Warshel A.. 2014. Coarse-grained simulations of the gating current in the voltage-activated Kv1.2 channel. Proc. Natl. Acad. Sci. USA. 111:2128–2133. 10.1073/pnas.1324014111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King, G., Lee F.S., and Warshel A.. 1991. Microscopic Simulations of Macroscopic Dielectric Constants of Solvated Proteins. J. Chem. Phys. 95:4366–4377. 10.1063/1.461760 [DOI] [Google Scholar]
- Kolafa, J., and Viererblová L.. 2014. Static Dielectric Constant from Simulations Revisited: Fluctuations or External Field? J. Chem. Theory Comput. 10:1468–1476. 10.1021/ct500025m [DOI] [PubMed] [Google Scholar]
- Lacroix, J.J., and Bezanilla F.. 2011. Control of a final gating charge transition by a hydrophobic residue in the S2 segment of a K+ channel voltage sensor. Proc. Natl. Acad. Sci. USA. 108:6444–6449. 10.1073/pnas.1103397108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix, J.J., Pless S.A., Maragliano L., Campos F.V., Galpin J.D., Ahern C.A., Roux B., and Bezanilla F.. 2012. Intermediate state trapping of a voltage sensor. J. Gen. Physiol. 140:635–652. 10.1085/jgp.201210827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix, J.J., Hyde H.C., Campos F.V., and Bezanilla F.. 2014. Moving gating charges through the gating pore in a Kv channel voltage sensor. Proc. Natl. Acad. Sci. USA. 111:E1950–E1959. 10.1073/pnas.1406161111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix, J.J., Campos F.V., Frezza L., and Bezanilla F.. 2013. Molecular bases for the asynchronous activation of sodium and potassium channels required for nerve impulse generation. Neuron. 79:651–657. 10.1016/j.neuron.2013.05.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, S.B., Campbell E.B., and Mackinnon R.. 2005. Voltage sensor of Kv1.2: structural basis of electromechanical coupling. Science. 309:903–908. 10.1126/science.1116270 [DOI] [PubMed] [Google Scholar]
- Long, S.B., Tao X., Campbell E.B., and MacKinnon R.. 2007. Atomic structure of a voltage-dependent K+ channel in a lipid membrane-like environment. Nature. 450:376–382. 10.1038/nature06265 [DOI] [PubMed] [Google Scholar]
- Macdonald, J.R. 1992. Impedance spectroscopy. Ann. Biomed. Eng. 20:289–305. 10.1007/BF02368532 [DOI] [PubMed] [Google Scholar]
- MacKerell, A.D., Bashford D., Bellott M., Dunbrack R.L., Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., et al. . 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- Martyna, G.J., Tobias D.J., and Klein M.L.. 1994. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 101:4177–4189. 10.1063/1.467468 [DOI] [Google Scholar]
- McCormack, K., Joiner W.J., and Heinemann S.H.. 1994. A characterization of the activating structural rearrangements in voltage-dependent Shaker K+ channels. Neuron. 12:301–315. 10.1016/0896-6273(94)90273-9 [DOI] [PubMed] [Google Scholar]
- Nadler, B., Hollerbach U., and Eisenberg R.S.. 2003. Dielectric boundary force and its crucial role in gramicidin. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 68:021905 10.1103/PhysRevE.68.021905 [DOI] [PubMed] [Google Scholar]
- Nadler, B., Schuss Z., Hollerbach U., and Eisenberg R.S.. 2004. Saturation of conductance in single ion channels: the blocking effect of the near reaction field. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70:051912 10.1103/PhysRevE.70.051912 [DOI] [PubMed] [Google Scholar]
- Pan, X., Li Z., Zhou Q., Shen H., Wu K., Huang X., Chen J., Zhang J., Zhu X., Lei J., et al. . 2018. Structure of the human voltage-gated sodium channel Nav1.4 in complex with β1. Science. 362:eaau2486 10.1126/science.aau2486 [DOI] [PubMed] [Google Scholar]
- Patargias, G.N., Harris S.A., and Harding J.H.. 2010. A demonstration of the inhomogeneity of the local dielectric response of proteins by molecular dynamics simulations. J. Chem. Phys. 132:235103 10.1063/1.3430628 [DOI] [PubMed] [Google Scholar]
- Payandeh, J., Scheuer T., Zheng N., and Catterall W.A.. 2011. The crystal structure of a voltage-gated sodium channel. Nature. 475:353–358. 10.1038/nature10238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyser, A., and Nonner W.. 2012a The sliding-helix voltage sensor: mesoscale views of a robust structure-function relationship. Eur. Biophys. J. 41:705–721. 10.1007/s00249-012-0847-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyser, A., and Nonner W.. 2012b Voltage sensing in ion channels: mesoscale simulations of biological devices. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 86:011910 10.1103/PhysRevE.86.011910 [DOI] [PubMed] [Google Scholar]
- Peyser, A., Gillespie D., Roth R., and Nonner W.. 2014. Domain and interdomain energetics underlying gating in Shaker-type Kv channels. Biophys. J. 107:1841–1852. 10.1016/j.bpj.2014.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kalé L., and Schulten K.. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell, E.M., and Morin D.J.. 2012. Electricity and Magnetism. Vol. 2 Third edition. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Riniker, S., Kunz A.P., and van Gunsteren W.F.. 2011. On the Calculation of the Dielectric Permittivity and Relaxation of Molecular Models in the Liquid Phase. J. Chem. Theory Comput. 7:1469–1475. 10.1021/ct100610v [DOI] [PubMed] [Google Scholar]
- Rojas, E., Bezanilla F., and Taylor R.E.. 1970. Demonstration of sodium and potassium conductance changes during a nerve action potential. Nature. 225:747–748. 10.1038/225747a0 [DOI] [PubMed] [Google Scholar]
- Sansom, M.S.P., Smith G.R., Adcock C., and Biggin P.C.. 1997. The dielectric properties of water within model transbilayer pores. Biophys. J. 73:2404–2415. 10.1016/S0006-3495(97)78269-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoppa, N.E., McCormack K., Tanouye M.A., and Sigworth F.J.. 1992. The size of gating charge in wild-type and mutant Shaker potassium channels. Science. 255:1712–1715. 10.1126/science.1553560 [DOI] [PubMed] [Google Scholar]
- Sigg, D., Bezanilla F., and Stefani E.. 2003. Fast gating in the Shaker K+ channel and the energy landscape of activation. Proc. Natl. Acad. Sci. USA. 100:7611–7615. 10.1073/pnas.1332409100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonson, T. 1996. Accurate Calculation of the Dielectric Constant of Water from Simulations of a Microscopic Droplet in Vacuum. Vol. 250. [Google Scholar]
- Simonson, T., and Perahia D.. 1996. Polar fluctuations in proteins: molecular-dynamic studies of cytochrome c in aqueous solution. Faraday Discuss. 103:71–90. 10.1039/fd9960300071 [DOI] [PubMed] [Google Scholar]
- Smith, P.E., Brunne R.M., Mark A.E., and Van Gunsteren W.F.. 1993. ‘Dielectric Properties of Trypsin Inhibitor and Lysozyme Calculated from Molecular Dynamics Simulations’. J. Phys. Chem. 97:2009–2014. 10.1021/j100111a046 [DOI] [Google Scholar]
- Suydam, I.T., Snow C.D., Pande V.S., and Boxer S.G.. 2006. Electric fields at the active site of an enzyme: direct comparison of experiment with theory. Science. 313:200–204. 10.1126/science.1127159 [DOI] [PubMed] [Google Scholar]
- Tao, X., Lee A., Limapichat W., Dougherty D.A., and MacKinnon R.. 2010. A gating charge transfer center in voltage sensors. Science. 328:67–73. 10.1126/science.1185954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tytgat, J., and Hess P.. 1992. Evidence for cooperative interactions in potassium channel gating. Nature. 359:420–423. 10.1038/359420a0 [DOI] [PubMed] [Google Scholar]
- Voges, D., and Karshikoff A.. 1998. A Model of a Local Dielectric Constant in Proteins. J. Chem. Phys. 108:2219–2227. 10.1063/1.475602 [DOI] [Google Scholar]
- Wang, W., and MacKinnon R.. 2017. Cryo-EM Structure of the Open Human Ether-à-go-go-Related K+ Channel hERG. Cell. 169:422–430.e10. 10.1016/j.cell.2017.03.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel, A., Sharma P.K., Kato M., and Parson W.W.. 2006. Modeling electrostatic effects in proteins. Biochim. Biophys. Acta. 1764:1647–1676. 10.1016/j.bbapap.2006.08.007 [DOI] [PubMed] [Google Scholar]
- Whicher, J.R., and MacKinnon R.. 2016. Structure of the voltage-gated K+ channel Eag1 reveals an alternative voltage sensing mechanism. Science. 353:664–669. 10.1126/science.aaf8070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, D., Phillips J.C., and Schulten K.. 1996. Protein Response to External Electric Fields: Relaxation, Hysteresis, and Echo. J. Phys. Chem. 100:12108–12121. 10.1021/jp960076a [DOI] [Google Scholar]
- Yeh, I.C., and Berkowitz M.L.. 1999. Dielectric Constant of Water at High Electric Fields: Molecular Dynamics Study. J. Chem. Phys. 110:7935–7942. 10.1063/1.478698 [DOI] [Google Scholar]
- Zagotta, W.N., Hoshi T., and Aldrich R.W.. 1994. Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J. Gen. Physiol. 103:321–362. 10.1085/jgp.103.2.321 [DOI] [PMC free article] [PubMed] [Google Scholar]