Disease-driven reduction in human mobility influences human-mosquito contacts and dengue transmission dynamics

Abstract

Heterogeneous exposure to mosquitoes determines an individual’s contribution to vector-borne pathogen transmission. Particularly for dengue virus (DENV), there is a major difficulty in quantifying human-vector contacts due to the unknown coupled effect of key heterogeneities. To test the hypothesis that the reduction of human out-of-home mobility due to dengue illness will significantly influence population-level dynamics and the structure of DENV transmission chains, we extended an existing modeling framework to include social structure, disease-driven mobility reductions, and heterogeneous transmissibility from different infectious groups. Compared to a baseline model, naïve to human pre-symptomatic infectiousness and disease-driven mobility changes, a model including both parameters predicted an increase of 37% in the probability of a DENV outbreak occurring; a model including mobility change alone predicted a 15.5% increase compared to the baseline model. At the individual level, models including mobility change led to a reduction of the importance of out-of-home onward transmission (R, the fraction of secondary cases predicted to be generated by an individual) by symptomatic individuals (up to -62%) at the expense of an increase in the relevance of their home (up to +40%). An individual’s positive contribution to R could be predicted by a GAM including a non-linear interaction between an individual’s biting suitability and the number of mosquitoes in their home (>10 mosquitoes and 0.6 individual attractiveness significantly increased R). We conclude that the complex fabric of social relationships and differential behavioral response to dengue illness cause the fraction of symptomatic DENV infections to concentrate transmission in specific locations, whereas asymptomatic carriers (including individuals in their pre-symptomatic period) move the virus throughout the landscape. Our findings point to the difficulty of focusing vector control interventions reactively on the home of symptomatic individuals, as this approach will fail to contain virus propagation by visitors to their house and asymptomatic carriers.

Author summary

Human mobility patterns can play an integral role in vector-borne disease dynamics by characterizing an individual’s potential contacts with disease-transmitting vectors. Dengue virus is transmitted by a sedentary vector, but human mobility allows individuals to have contact with mosquitoes at their home and other houses they frequent (their activity space). When accounting for the decreased mobility of symptomatic dengue cases in an agent-based simulation model, however, we found a severely diminished role of the activity space in onward transmission. Those who received the majority of their mosquito contacts outside their home experienced decreases in expected bites and onward transmission when mobility changes were accounted for. Onward transmission was driven by a synergistic relationship between the number of mosquitoes in an individual’s home and their biting suitability, where even those with the highest biting suitability would have limited contribution to transmission given a low number of household mosquitoes. Reactive vector control, which often targets symptomatic cases, could be effective for slowing onward transmission from these cases, but will fail to control virus transmission due to the disproportionate contribution of asymptomatic infections.

Introduction

The rate at which humans encounter vectors (mosquitoes, ticks, bugs) is a fundamental driver of vector-borne disease transmission dynamics [1,2]. Human-vector contacts can be influenced by a myriad of factors, including the vector’s host-seeking behavior [3,4], the host’s biting attractiveness to biting vectors [5–8], and the spatial distribution/density of both hosts and vectors [9–12]. Variations in some or all of these factors can lead to heterogeneous exposure, where certain individuals have higher contact rates with vectors than others [13–15]. The epidemiological consequence of such uneven distribution of human-vector contacts could be significant, particularly if it results in key encounters where a large number of vectors are infected [2]. Therefore, an individual’s contribution to transmission is influenced by not only how many vector bites are received, but also which vectors the bites are from and whom those vectors encounter next [16].

Given the central epidemiological role of mixing between hosts and vectors, there is a need for better quantification of its frequency and temporal variability, particularly because epidemiological outcomes depend on coupling among a variety of heterogeneities; i.e., human (behavior, immunity, etc.), vector (dispersal, longevity, etc.), and environmental [17]. Theoretical and simulation models have been used to assess the importance of such factors. One model focused on how heterogeneous exposure to vectors, poor mixing, and finite host numbers can determine the spatial scale of transmission [16]. Poor mixing can lead to infections being clustered in groups of closely connected individuals, as observed in the clustering of infections within social groups [18–20]. This association between human behavior and mixing is of particular relevance for dengue and other Aedes-borne viruses (dengue, chikungunya, Zika) [1,21–23], because house-to-house human movement, rather than mosquito mobility, is an underlying feature of spatial patterns of human incidence [18,20,24].

Dengue is an acute illness caused by any of four immunologically related viruses in the family Flaviviridae and transmitted by Aedes spp. mosquitoes (primarily Aedes aegypti). Prevalent in the tropics and subtropics, it is the most important mosquito-borne viral disease of humans worldwide [25]. Symptoms associated with dengue (acute fever, headache, musculoskeletal pain, and rash) only disrupt a person’s daily routine or result in treatment seeking in a small proportion of cases, whereas the other 70% of infected individuals experience either mild symptoms (inapparent) or no symptoms (asymptomatic) [26–28]. It has been recently shown that human mobility patterns change during the course of symptomatic (febrile) dengue infection. Specifically, symptomatic individuals visit fewer locations and stay at home more than when they were not infected [29–32]. Although disease-driven mobility changes have been shown to significantly influence the spread of directly transmitted pathogens, they have not yet been included in theoretical models of dengue virus (DENV) transmission [33,34]. For DENV, we hypothesize that the distribution of mosquitoes at an individual’s home and across the rest of the places they frequent (their activity space) will determine the impact of disease-driven mobility reductions on their mosquito contacts and onward transmission potential [17,21,32]. At a population level, we predict that human mobility changes could affect pathogen spread in a variety of ways depending upon which individuals in the population experience symptoms and change their mobility and potential exposure to Aedes aegypti mosquitoes.

For those DENV-infected individuals who experience symptoms, infectiousness tends to peak during the first few days after symptom onset when mobility is restricted and human-mosquito contacts are most likely occurring in the individual’s home [35–37]. There are, however, a few days before symptom onset when individuals have sufficient viremia levels to be infectious to mosquitoes, but have not yet changed their mobility [35,37]. A recent theoretical model of within-host viral dynamics estimated that 24% of an individual’s onward transmission results from mosquito bites during this pre-symptomatic phase [38]. We hypothesize that the pre-symptomatic period could have a significantly different contribution to onward transmission when accounting for mobility reductions, where individuals have normal mobility patterns during the pre-symptomatic period and decreased mobility during symptomatic infectiousness. To test our hypotheses, we examined the role of disease-driven mobility change in DENV transmission by theoretically exploring how day-to-day reductions in a symptomatic individual’s mobility and contacts with mosquitoes, combined with heterogeneous attractiveness to mosquitoes, may impact population-level DENV transmission dynamics.

Methods

Ethics statement

This manuscript is a theoretical modeling exercise and no field collected human or entomological data was included. The modeling was supported under human use protocol NAMRU-62014.0028 approved by the NAMRU-6 ethic committee and the Loreto Regional Health Department.

Model framework

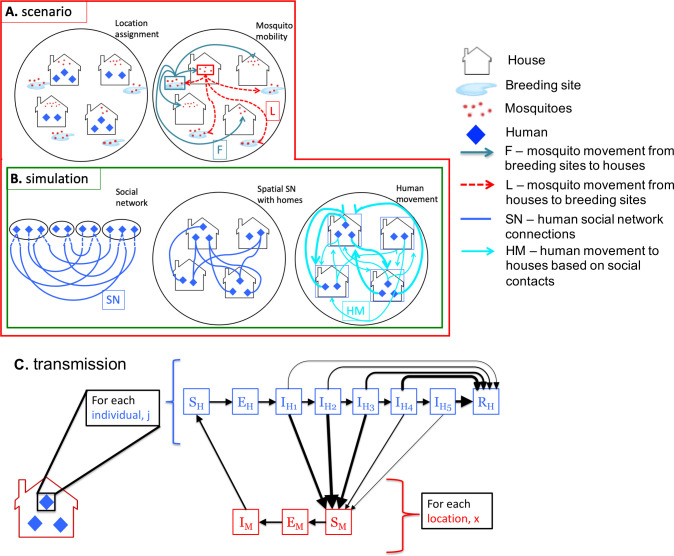
Our model builds on a previously published mathematical framework that describes where and when human-mosquito contacts occur based on fine-scale human and mosquito mobility [16]. In the original framework, parameters with set values were defined (S1 Table), then a set of houses, {f}, and larval development sites, {l}, were arranged on a disc. Each house was assigned a number of residents equal to 2 plus a Poisson random variable (λ = 3.5), creating a two-person minimum per household. In order to assign the numbers of mosquitoes/larvae at each house/larval site, mosquito movement and reproduction were simulated for a total of 200 time steps, with the first 100 acting as a burn-in period. Counts of mosquitoes and larvae at each location were averaged over the second 100 time steps, providing the ‘equilibrium’ values (Fig 1A). Poorly mixed mosquito movement was characterized by matrices L and F, giving the distance-based probabilities of an adult female mosquito moving from any house to any larval site, and vice versa (Fig 1A and S2 Table) [16].

Fig 1. Diagram with setup of model framework for each scenario and simulation run.

(A) For each scenario, this model includes houses and larval sites in which mosquitoes breed and move with specific daily probabilities. (B) For each of 200 simulation runs, a random social network (SN) is generated for humans, defining their contacts at home and at other houses and further determining the human movement matrix (HM). (C) Diagram of our stochastic compartmental transmission model in which mosquitoes at the household level were modeled as SEI (with M subscripts) and humans as an individual-based SEIR (with H subscripts). The I (infectious) stage for humans was divided into five sub-stages, each with their infectiousness value, shown here with weighted arrows. Individuals can either progress to the next (I_Hi) infectious sub-stage or move straight to the (R_H) recovered stage based on a probability function. The probability of moving to the recovered stage is shown with weighted arrows (thicker arrows indicate higher weights).

Rather than defining human mobility patterns based on distance (as in [16]), we generated a socially structured human mobility matrix for each of 200 simulation runs (Fig 1B). First, a random social network with household structure was constructed using the “configuration model” [39]. Each individual was assigned a number of “half-edges” (their degree) from a Poisson distribution with rate λ = 2.8, the mean number of residential locations visited in a data set described by Perkins et al. [32]. Based on human mobility data indicating that 14.7% of people do not regularly visit any houses (based on a 15 day monitoring period), a random sample of individuals predicted in the model to have a degree higher than 0 were reassigned a degree of 0 in order for the total modeled population to reach 15% of individuals with no half-edges and therefore no movement from their home [20]. Half-edges were then paired uniformly at random to form the edges of the social network, making sure there were no self-loops, multiple edges, or loops within houses (Fig 1B). This random network was represented as an |h|-by-|h| adjacency matrix SN, where |h| is the size of the set of hosts {h} (Table 1). A separate |h|-by-|f| presence/absence matrix, Homes, is constructed, where Homes[j,x] denotes whether or not the j^th host lives at the x^th residential site (Fig 1B and Table 1). Multiplying the SN and Homes matrices produced an |h|-by-|f| matrix, HM, denoting which residential sites an individual will visit based on their social network (note that this matrix was not presence/absence, as when the j^th host was socially connected to multiple individuals at the x^th residential site, HM[j,x] > 1) (Fig 1B and Table 1). This matrix was used to populate the human mobility matrix, H, which documented the proportion of time each host spent at each household (Table 1). Each host, j, spent 50% of their time at home (H[j, home] = 0.5) and divided the remaining 50% of their time into the houses visited in HM (When HM[j,x] > 1, as mentioned above, a proportionally larger amount of time was allocated at that residential location). For the 15% of individuals, j, who had no mobility outside their home H[j, home] = 1. As in the original model, each row of the H matrix described where a single host spent time and each column detailed all of the individuals spending time at a single household [16].

Table 1. Definitions of parameters mentioned in text.

Symbol	Type: Size	Definition
{f}	Vector: | f |	Number of houses
{l}	Vector: | l |	Number of larval sites
{h}	Vector: | h |	Number of hosts
ci	Vector: 5	Host-to-mosquito transmission efficiency for infectiousness stage Ii
L	Matrix: | f | x | l |	Probability of mosquito movement from house to larval site
F	Matrix: | l | x | f |	Probability of mosquito movement from larval site to house
SN	Matrix: | h | x | h |	Random presence/absence social network
Homes	Matrix: | h | x | f |	Presence/absence matrix denoting where each host lives
HM	Matrix: | h | x | f |	Houses each host will visit based on SN
H	Matrix: | h | x | f |	Proportion of time each host spends at each house, based on SN and HM
U	Matrix: | f | x | h |	Distribution of mosquito bites on each host at each house
Bnorm	Matrix: | h | x | f |	Expected number of mosquito bites on each host at each house pre-epidemic
Bi	Matrix: | h | x | f |	Expected number of mosquito bites on each host at each house for each infectiousness stage, i (I1 –I5)
V	Matrix: | h | x | h |	Expected secondary bites on each host arising from primary bites on all other hosts over one time step
Vi	Matrix: | h | x | h |	Expected secondary bites on each host arising from primary bites on all other hosts at each time step of infectiousness, i (I1 –I5), accounting for mobility change
Rnorm	Matrix: | h | x | h |	Expected probability of a host receiving 1+ secondary infectious bites arising from primary infection of any other host
Rmovement	Matrix: | h | x | h |	Expected probability of a host receiving 1+ secondary infectious bites arising from primary infection of any other host, accounting for mobility changes
Rx(home)	Matrix: | h | x | h |	Subset of Rx accounting for secondary cases that arise only from primary infectious bites at the primary host’s home (x = norm, movement)
Rx(other houses)	Matrix: | h | x | h |	Subset of Rx accounting for secondary cases that arise from primary infectious bites that occur anywhere but at the primary host’s home (x = norm, movement)

Following the original model, each individual was also assigned a biting suitability score (which accounts for biting attractiveness, avoidance behavior, and defensive behavior) using a random exponential draw with rate based on empirical biting data [40]. Based on the mobility matrix, H, and biting suitability scores, an |f|-by-|h| matrix U was created to describe the distribution of mosquito bites on all individuals at each house, where each row gave the distribution of bites on all hosts at a single household and each column depicted the bites distributed on a single individual across all households (Table 1).

A stochastic transmission model was layered on top of this framework, which included a household-level SEI (susceptible, exposed, infectious) model for mosquitoes and an individual-based SEIR (susceptible, exposed, infectious, recovered) model for hosts (Fig 1C and S1 Fig). Individuals transitioned through one exposed (E) stage, based on pathogen latency of DENV in terms of feeding-cycle-length time steps. Hosts also transitioned through a maximum of five infectious (I₁ –I₅) sub-stages, until a stochastic transition into the recovered (R) stage. Rather than use a single set value for human infectiousness (as seen in Perkins et al.), values were chosen for each of these sub-stages (I₁ –I₅) based on data giving the mean daily probability of infection for mosquitoes after feeding on individuals with primary infections [16,38] (Fig 1C). For each 3-day infection time point in our model, we averaged these mean infectiousness values (Table 2). The updated transmission model also defined the first time step in the human infectiousness stage (I₁) as the “pre-symptomatic period” and all subsequent infectious time steps (I₂ –I₅) as the “symptomatic” period, where the pre-symptomatic period contributed to 25% of infectiousness for individuals who progressed through all five infectiousness stage (I₁ –I₅) before recovery [38]. Simulation outbreaks were initiated by moving a single human into the first infectious (I) stage.

Table 2. Parameters that vary by infectiousness stage.

Stage of infectiousness	S	I1	I2	I3	I4	I5
Day of Symptoms	− − −	Pre-symptomatic	Days 1–3	Days 4–6	Days 7–9	Days 10–12
Infectiousness	− − −	0.4	0.7	0.4	0.1	0.01
Time at home (%)	50%	50%	100%	80%	70%	50%
Fraction of original houses being visited	1	1	0/3	1/3	2/3	1

Values calculated for individuals when susceptible, and at each sub-stage of infectiousness based on data from [31,38].

Model simulations had discrete time steps to capture the length of a mosquito gonotrophic cycle (~3 days). During each time step, hosts would allocate their time at houses based on H. The mosquitoes at each house would take blood meals from possible hosts (one blood meal per mosquito) based on U matrix probabilities and move to a larval site based on L probabilities. Eggs were laid based on a Poisson distribution with mean equal to number of adult females at the site multiplied by average egg batch size. Adult mosquitoes then moved to a house searching for their next blood meal based on F probabilities. During each time step, mosquito larvae also progressed through 4 developmental stages based on site-specific density dependence until emerging into adult mosquitoes. For both mosquitoes and humans, each time step also accounted for progression through incubation (E), infectiousness (I), and (for hosts) recovery (R). Virus transmission occurred from infectious hosts to susceptible mosquitoes and from infectious mosquitoes to susceptible hosts. At the end of each time point, host mobility was changed for those hosts who were symptomatically infectiousness.

Host Mobility Changes: Two different scenarios were considered to examine mobility changes: (1) no symptomatic movement change and (2) movement change throughout symptomatic infection. For scenario (1) no changes were made to the mobility matrix. For scenario (2), host mobility changes occurred at each 3-day time step of symptomatic infection based on recently published data on human mobility throughout symptomatic DENV infection [31] (Table 2 and S2 Fig). As data from Schaber et al. [31] were grouped as days 1–3, 4–6, and 7–9 after symptom onset, they corresponded to the I₂, I₃, and I₄ stages here. When individuals were in the first three days after symptom onset, they were significantly more likely to spend all of their time at home and visit no other residential places. Accordingly, when an individual transitioned into symptomatic infection in the simulation (I₂), their movement was completely stopped (HM[j,] = 0) and all time was spent at home (HM[j, home] = 1). During days 4–6 after symptom onset (sub-stage I₃), individuals spent an average of 76% of time at home and visited approximately 1/3 of normally frequented places. On days 7–9 after symptom onset (sub-stage I₄) time at home and fraction of places being visited averaged 69% and 2/3, respectively. Therefore, we set the time at home to be 80% (70%) for the I₃ (I₄) stage and had individuals visiting 1/3 (2/3) of their originally frequented houses (Table 2). The order in which houses were added back into an individual’s movements in stages I₃ and I₄ was determined by random sample where a house’s probability of being chosen was weighted by its original HM value. This made it more likely that individuals would resume visiting houses where they were socially connected to multiple residents. When individuals reached the I₅ stage (days 10–12 after symptom onset), movement patterns and time at home were reset to original values (Table 2). At the end of each time step, once these movement changes were updated for all symptomatic individuals in the HM matrix, the H and U matrices were recalculated as described above.

The effect of the pre-symptomatic period was accounted for by including two more scenarios of interest: (1b) no movement changes and no pre-symptomatic period and (2b) movement change throughout symptomatic infection and no pre-symptomatic period. For these scenarios the first stage of infectiousness (I₁), the pre-symptomatic period, was removed and individuals became symptomatic immediately after the incubation period (E), with infectiousness and movements corresponding to the I₂ –I₅ stages.

In order to simplify the model and the effects of mobility change, two simplifications were made: inapparent cases were left out and mobility was completely halted on the first three days of symptoms. Two further versions of scenario (2) were created to ascertain the robustness of the model to changes in these parameters. The impact of symptomatic mobility change in the presence of inapparent and asymptomatic infections was examined with scenario (2c), where only 30% of individuals (chosen from a random binomial draw) had symptomatic infection with mobility change. In scenario (2d), we assessed the sensitivity of model outputs to mobility changes the first three days of symptoms. Rather than having mobility completely stop after symptom onset, it was decreased to the same level as days 4–6, where 80% of time was spent at home and 1/3 of original houses were visited (S3 Table).

Model Outputs: Perkins et al. created multiple metrics to explore how mobile hosts and mosquitoes contribute to pathogen dispersal [16]. Of particular interest was the matrix R, which corresponded to the concept of effective reproductive number. This matrix gave the probability that a primary infection in one host will result in a secondary infection in some other host, where summing each row provided the number of expected secondary infections arising from a single individual. The B matrix was also utilized to measure the expected number of bites per time step on each host at each blood-feeding habitat (house). Each row of B provided the number of expected bites on a single individual at all households and each column gave the expected number of bites occurring on all individuals at a single household during one time step. At the population level, dynamics were examined using the simulation outputs of cumulative number of infections at each time step and number of infectious hosts at each time step. We utilized these original metrics and created versions that accounted for mobility change.

The B matrix could be used as a way to examine heterogeneity in human-mosquito contact rates, not only across hosts/locations, but also throughout an individual’s infectiousness period. This metric was derived to account for multiple sources of heterogeneous biting, namely spatial variation in biting intensity, hosts’ allocation of time at a location, and relative biting attractiveness of hosts at that location. Spatial variation in biting intensity was included as a numeric vector with the number of expected bites per feeding cycle at each house (based on average number of new adult females emerging at each larval site and their subsequent mobility to nearby houses). Multiplying this numeric vector by the distribution of bites across hosts at each site (U), which account for the latter two factors of heterogeneous biting, results in the B matrix. Because this metric was based on the U matrix, and therefore affected by the human mobility matrix (H), a list of B matrices was created to measure biting pre-epidemic (with normal movements) and during each time step of infectiousness. Within each simulation, B_norm was calculated for all individuals before infection spread began. During disease spread, B_i[j,] was recorded for each host, j, at each infectiousness sub-stage (I₁ –I₅), i. This set of matrices gave us the expected number of mosquito bites on each host at each house throughout infectiousness/mobility changes (Table 1).

The previously-derived version of the R matrix, referred to as R_norm, measured the probability of host k receiving one or more secondary infectious bites arising from primary infectious host, j (Table 1). This accounts for the primary infectious host transmitting the virus to a susceptible mosquito (the primary infectious bite) and that newly infectious mosquito then transmitting the virus to a susceptible host (the secondary infectious bite). The R metric was slightly adjusted to account for time-step-specific infectiousness where

$$R_{j,k}=1-e^{-bV\left(c_1+c_2+c_3+c_4+c_5\right)}$$

with c_i values representing an individual’s time-step-specific infectiousness values. The V matrix gave the number of expected secondary bites on each host arising from primary bites on all other hosts over one time step, where each column provides the number of expected secondary bites received by a single individual from primary bites on all other hosts during one time step and each row described the number of expected secondary bites on all hosts from primary bites on a single individual. To derive the V matrix, we considered an individual, k, who received an expected number of (primary) bites per feeding cycle at each house based on the B matrix. The mosquitoes from this house then went on to make an expected number of (secondary) bites at all possible houses based on mosquito mobility matrices. These secondary bites were distributed among hosts according to the U matrix. Because the U matrix affected the V matrix, host mobility change was accounted for by creating a set of matrices, V_i, for each sub-stage of infectiousness (I₁ –I₅) (Table 1). When host j was infectious in the simulation, their V_i[j,] values were recorded for each I sub-stage (I₁ –I₅). At the end of the simulation run a matrix referred to as R_movement was created, where

$$R_{movement}=1-e^{-b\left(V_1{c}_1+V_2{c}_2+V_3{c}_3+V_4{c}_4+V_5{c}_5\right)}.$$

In order to examine the importance of the location where the primary infectious bite occurs on host j, we also divided R_movement into two separate matrices, R_movement (home), and R_movement (other houses) (Table 1). This was done by calculating V_i(home) and V_i(other houses), which derived the number of expected secondary bites on each host arising from primary bites that occur at each time point of infectiousness, i, on all other hosts at their home and everywhere but their home, respectively. These V_i (home) and V_i (other houses) matrices were then used to derive R_movement (home) and R_movement (other houses), respectively. Similarly, R_norm was divided into R_norm (home) and R_norm (other houses) in order to compare the effect of where a primary infectious bite occurred when not accounting for mobility (Table 1).

A new metric that focused on the number of mosquitoes present in each individual’s home was also calculated. The number of mosquitoes in each individual’s home was recorded at the beginning of the simulation run (pre-epidemic) and at each time point of infectiousness for that individual. For each scenario a list was output with all of these metrics for each of 200 simulation runs.

Data analysis

Analysis of simulation outputs had three main objectives: determining the effects of disease-driven mobility changes on (1) population-level outbreak dynamics (e.g., total infections, timing of infection peak, length of epidemic), (2) individual-level onward transmission (i.e., the number of secondary infections arising from a single individual), and (3) individual-level human-mosquito contacts (i.e., the number of mosquito bites on a single host at each location during each stage of infectiousness).

For the first objective, determining the effects of mobility change on population-level disease dynamics, we compared four scenarios: no mobility change and no pre-symptomatic period (baseline); no mobility change and pre-symptomatic period; mobility change and no pre-symptomatic period; mobility change and pre-symptomatic period. The effect of mobility changes could be determined by comparing the “no mobility change” and “mobility change” scenarios. To determine the role of the pre-symptomatic period when mobility changes occur, we compared the difference in ‘mobility change, no pre-symptomatic’ and ‘mobility change, pre-symptomatic’ to the difference in ‘no mobility change, no pre-symptomatic’ and ‘no mobility change, pre-symptomatic’ in order to account for the effect of removing one period of infectiousness (the pre-symptomatic period).

The number of infectious hosts at each time step was used to calculate the maximum infection prevalence, the time to maximum prevalence, and the length of the epidemic (when the number of infectious hosts was 0 without increasing again). The cumulative number of infections at each time step was utilized to record the total percent of the population infected in an epidemic, as well the time point when the percent of cumulative infections reached 10% and 65% (representing the time the epidemic starts to take off and starts to slow down). For the remaining two objectives, we focused our analyses on the scenario where a pre-symptomatic period was present and mobility changes were occurring. In order to determine the effect of these mobility changes on onward transmission, the R_norm and R_movement matrices were utilized. Row sums of R_movement and R_norm gave the expected number of secondary infectious bites arising from all primary bites on an individual host either with or without accounting for movement changes. Similarly, row sums of R_movement(home), R_movement(other houses), R_norm(home), and R_norm(other houses) determined the expected secondary bites arising from an individual due to only primary bites at their home or only primary bites at other houses (with and without movement changes). The distributions of R_movement and R_norm values were compared and both absolute (R_{abs_change}) and relative change (R_{rel_change}) were calculated to examine how accounting for mobility affects an individual’s R-value, where

$$R_{abs\_change}=R_{movement}-R_{norm}$$

and

$$R_{rel\_change}=\frac{R_{movement}-R_{norm}}{R_{norm}}.$$

Possible predictor variables for onward transmission were examined using generalized additive models (GAMs) [41]. Best-fit models were determined for R_norm, R_movement, R_movement(home), R_{rel_change}, and R_{rel_change}(home). The variables considered as predictors were an individual’s biting suitability score (which accounts for biting attractiveness, avoidance behavior, and defensive behavior), the number of mosquitoes in their home, the number mosquitoes in their activity space pre-exposure (places they frequented), and the percent of expected mosquito bites that occur at their home pre-exposure (i.e., prior to being bitten by a virus-infected mosquito). Best-fit was determined with ΔAICc and the percent of deviance explained by each model.

For the third objective, we calculated the expected number of mosquito contacts for each individual pre-exposure and at each stage of infectiousness (I₁ –I₅). Expected counts were calculated as row sums of B_norm and each B_i matrix. For all individuals that experienced infection, the change in number of expected mosquito contacts was calculated for each infectiousness stage, as compared to pre-exposure. Percent change was also calculated to account for variation in healthy mosquito contact counts

$$\frac{B_i-B_{norm}}{B_{norm}}.$$

We examined the importance of these variations in healthy mosquito contacts for the entire population. Further, given the epidemiological significance of those with the top 20% of contacts [15], we also compared individuals with the top 20% of expected contacts pre-exposure to the rest of the population (bottom 80%). B matrices were also used to determine the percent of an individual’s mosquito contacts that occurred at their home. Generalized additive models (GAMs) were examined for change in expected mosquitoes contacts, both as a number and a percent. Predictors and methods for finding best-fit models are as mentioned above. All statistical analyses were performed in R 3.3.0 statistical computing software.

Results

Epidemic dynamics

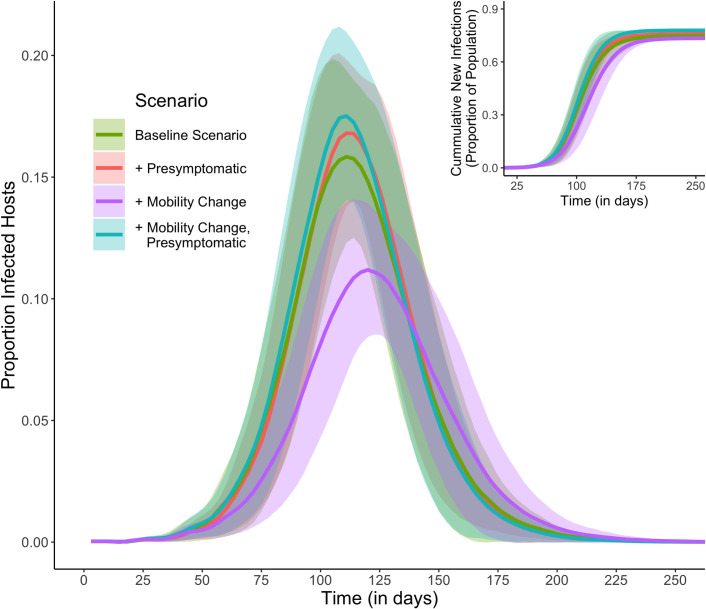
Compared to a baseline model, naïve to pre-symptomatic infectiousness and disease-driven mobility change, a model including both parameters predicted an increase of 37% in the probability of a DENV outbreak occurring (from 39.5% to 76.0%) (Table 3). Models only including disease-driven mobility change or pre-symptomatic infectiousness increased the probability of an outbreak by 14% and 15.5%, respectively, compared to the baseline model (Table 3). In the simulations where outbreaks did not occur, the infection only spread to a few people (<1% of the population) before virus transmission ceased. For simulations leading to epidemics, the inclusion of pre-symptomatic infectiousness had minimal effects on parameters such as time to peak infection, the length of the epidemic, or how many individuals were infected (Table 3). Adding symptomatic mobility reductions to the baseline scenario had little effect on when the epidemic peaked or how long it lasted; however, there was a 5.2% decrease in peak transmission (Table 3). This reduction was compensated by accounting for infectiousness in the pre-symptomatic period (Fig 2).

Table 3. Dengue virus predicted infection prevalence based on presence of pre-symptomatic period and/or disease-driven mobility reductions, presented as mean ± 2SEM.

Scenarios*	Percent of Simulations Where Outbreak Occurred†	Maximum Percent Infection Prevalence	Days Until Maximum Prevalence	Days Until Epidemic End
Baseline Scenario	39.5%	19.0 ± 0.2%	113.0 ± 2.9	253.2 ± 6.0
+ Pre-symptomatic	53.5%	19.6 ± 0.1%	112.9 ± 2.1	259.1 ± 4.9
+ Mobility Changes	55.0%	13.8 ± 0.1%	122.9 ± 2.7	265.4 ± 4.9
+ Mobility Changes, Pre-symptomatic	76.0%	20.3 ± 0.1%	111.1 ± 1.8	250.3 ± 4.0

*Infection prevalence data were analyzed from four scenarios: (1) a baseline scenario with no mobility changes and no pre-symptomatic period, and alternate models that included (2) no mobility change and pre-symptomatic period included, (3) mobility change and no pre-symptomatic period, and (4) mobility change and pre-symptomatic period included. For each scenario, the average time point was listed for when infection prevalence reached its maximum and reached 0% at the end of epidemic. The percent of the population infected during maximum infection prevalence was also listed, as well as the number of simulations where an outbreak occurred. Time steps values were converted to days (1 time step = 3 days).

† Given as a percent out of 200 possible simulations.

Fig 2. Predicted influence of disease-driven mobility reduction and pre-symptomatic transmission on DENV epidemic dynamics.

For each scenario and for each time step, (main) the average proportion of infected hosts is calculated and (inset) the average proportion of cumulative infections is calculated. Averages are calculated across all simulation runs where an outbreak occurred, with standard deviations included in the shaded ribbons. The baseline scenario is one with no mobility change and no pre-symptomatic period.

Onward transmission

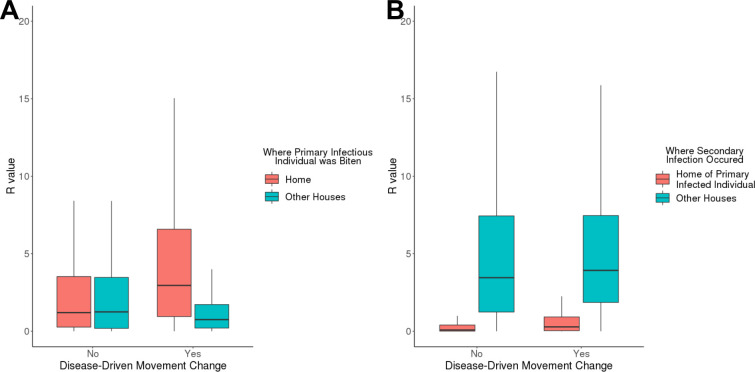
At the population level, the distributions of onward transmission (R) values increased slightly when disease-driven mobility reductions were added to a model without them (from an average ± SD of 5.4 ± 5.1 to 5.9 ± 4.8 infections) (Table 4 and S3 Fig). At the individual level, models including mobility change led to a reduction of the importance of out-of-home onward transmission by symptomatic individuals (reductions in R for primary and secondary bites of -62% and -17%, respectively) at the expense of an increase in the relevance of their home (increases in R for primary and secondary bites of 40% and 32%, respectively) (Table 4 and Fig 3). While the home environment played a key role in primary infections (Fig 3A), the majority of secondary infectious bites contributing to transmission occurred at other houses (Fig 3B).

Table 4. Average onward transmission (R) values with and without mobility change and change in R due to mobility change inclusion.

	Mean (sd) Onward Transmission		Mean (sd) Change in Individual Onward Transmission with Movement Changes
	Rnorm	Rmovement	Rabs_change	Rrel_change
1° bites at home	2.3 (2.7)	4.3 (4.2)	1.0 (1.1)	39.74% (22.67)
1° bites at other houses	2.2 (2.6)	1.1 (1.2)	-1.9 (1.9)	-62.28% (9.13)
2° bites at infectious individual’s home	0.3 (0.4)	0.6 (0.7)	0.1 (0.2)	31.86% (35.59)
2° bites elsewhere	5.0 (4.7)	5.2 (4.2)	-1.5 (3.2)	-17.1% (28.97)
Total	5.4 (5.1)	5.9 (4.8)	-1.1 (2.5)	-15.14% (29.94)

R_norm values were calculated using an individual’s healthy movement patterns, while R_movement values accounted for changes in mobility throughout infectiousness. Changes in R-values due to mobility inclusion were calculated for each individual as a raw number (R_{abs_change}) and as a percent of R_norm value (R_{rel_change}). Overall R-values were listed, as well as R-values based on only primary bites occurring at home or at other houses.

Fig 3. Expected onward transmission (R) values with and without mobility changes accounted for, separated by where primary bites occur and where secondary bites occur.

(A) gives onward transmission for primary bites occurring at home (red) and at other houses (blue) both without (left) and with (right) movement change included. [from left to right: R_norm(home), R_norm(other houses), R_movement(home), and R_movement(other houses)] (B) gives onward transmission for secondary bites at the home of the primary infected individual (red) and at other houses (blue).

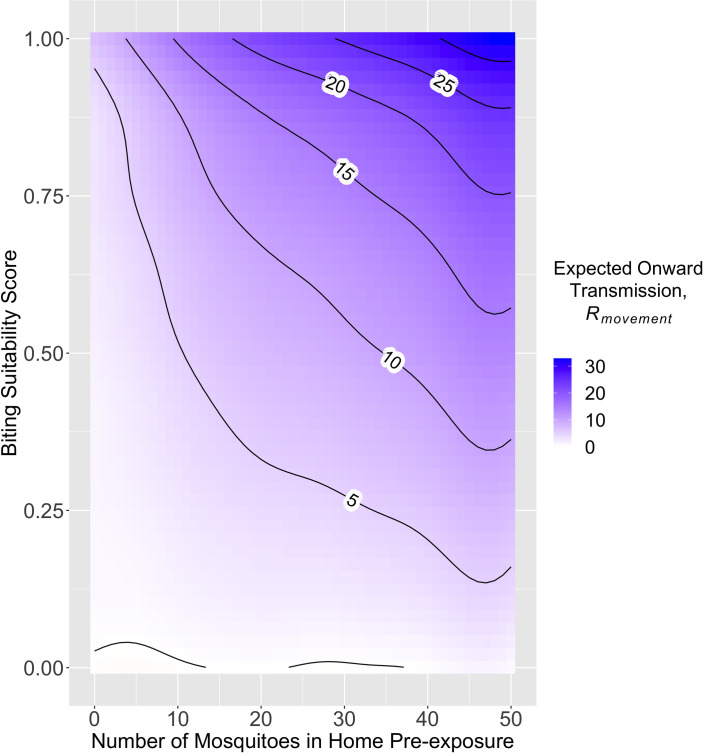
GAMs fitted to individual-level estimates of R_movement allowed understanding the mechanism by which mobility change influences onward transmission. In univariate GAMs, biting suitability score (which accounts for biting attractiveness, avoidance behavior, and defensive behavior) and number of mosquitoes at home pre-exposure explained 32.3% and 27.7% of deviance, respectively, whereas percent of bites expected at home pre-exposure only explained 9.3% of deviance (S5 Table). Increases in onward transmission were best explained by a GAM including an individual’s biting suitability and the number of mosquitoes in their home as well as their interaction (S5 Table and S4 Fig). Increasing biting suitability score from 0 to 1 only increased predicted R_movement by 5 new infections when there was a low mosquito count at home (e.g., 1–3 mosquitoes), compared to an increase of 30 new infections for those with high mosquito density (e.g., 40–50 mosquitoes) at home (Fig 4). In univariate GAMs for the two main parameters, including mobility change (R_movement) increased dramatically the % deviance explained compared to models excluding it (R_norm) (from 13.6% to 27.7% for number of mosquitoes at home and from 37.7% to 67.1% for biting suitability score) (S4 and S5 Tables). Including a variable for the total number of mosquitoes in all houses an individual visited pre-exposure (their activity space) did not increase the fit of GAMs (S4 Table).

Fig 4. Predicted contribution to onward DENV transmission (R_movement) based on a GAM with predictor variables number of mosquitoes in home pre-exposure, biting suitability score, and their interaction.

The predicted values of onward transmission based on biting suitability and number of mosquitoes at home pre-exposure, presented as a heatmap with contours.

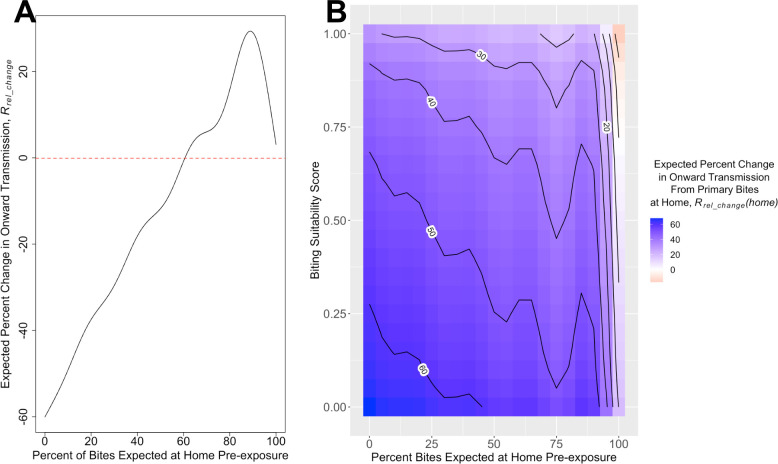
Disease-driven mobility changes can either increase or decrease an individual’s contribution to onward transmission. GAMs were fitted to the percent change in onward transmission arising from all mosquito bites (R_{rel_change}) and from only bites at home (R_{rel_change}(home)). For both metrics, the best-fit GAM included biting suitability, percent of bites at home, their non-linear interaction, and the number of mosquitoes at home (S6 Table). For R_{rel_change} there was only a 3.0% loss in deviance explained when instead using a univariate GAM with percent of bites expected to occur at home pre-exposure (from 83.6% to 80.6%) (S6 Table). When the percent of bites expected to occur at home pre-exposure was below 61%, there was a predicted decrease in onward transmission, whereas those with greater than 61% of bites expected at home pre-exposure saw increases in onward transmission when mobility was accounted for (Fig 5A). The notable exception to this monotonically increasing effect was the tempered increase in onward transmission for those who received their pre-exposure bites almost exclusively at home (Fig 5A). When examining the percent change in onward transmission only from primary bites at home (R_{rel_change}(home)), a majority of the deviance was explained in a model with percent bites expected at home pre-exposure and biting suitability score (S6 Table). The percent change in onward transmission from primary bites at home was predicted to be positive for all individuals, with the largest percent increase for individuals with low biting suitability scores and a small percent of bites expected to occur at home pre-exposure (Fig 5B).

Fig 5. Predictions for percent change in expected onward transmission when mobility is included ((R_{rel_change} and R_{rel_change}(home)) based on GAM models.

(A)The predicted percent change in onward transmission (R_{rel_change}) based on percent of bites expected at home pre-exposure. (B) The predicted percent change in onward transmission from primary bites at home R_{rel_change}(home)) based on biting suitability and percent of bites expected at home pre-exposure, presented as a heatmap with contours.

Human-mosquito contacts during illness

At the population level, the number of expected mosquito contacts was similarly distributed for each infectiousness sub-stage: before (I₁), during (I₂ –I₄), and after (I₅) mobility changes occurred (S7 Table and S5 Fig). When examining the change in an individual’s expected contacts at each infectiousness sub-stage during symptomatic mobility change, however, 57% of individuals had a decrease in expected contact and 38% had an increase (S6 and S7 Figs). During the first three days after symptom onset, the average change in expected contacts for individuals who received the top 20% and bottom 80% of expected mosquito contacts pre-exposure was a decrease of 13% and 17.5%, respectively (Table 5). Further, of those individuals who received the top 20% of expected mosquito contacts pre-exposure, 24% had a large enough decrease in mosquito contacts on the first three days after symptom onset to no longer be in the top 20% when symptomatic (S5 Fig).

Table 5. Average change in expected mosquito bites for each infectiousness sub-stage when symptomatic mobility changes are occurring (I₂ –I₄), separated based on expected bite values pre-exposure, provided as raw number and percent change relative to expected bites pre-exposure.

	Top 20% bites pre-exposure		Bottom 80% bites pre-exposure
	Mean (sd) change in expected bites	Mean (sd) percent change in expected bites	Mean (sd) change in expected bites	Mean (sd) percent change in expected bites
Days 1–3 after symptom Onset	-0.9 (3.8)	-13.0% (48.9)	-0.2 (0.7)	-17.5% (51.0)
Days 4–6 after symptom Onset	-0.3 (2.7)	-5.6% (37.1)	-0.1 (0.5)	-8.7% (38.1)
Days 7–9 after symptom Onset	-0.1 (1.6)	-1.6% (22.1)	-0.1 (0.3)	-4.9% (23.2)

The percent change in expected mosquito contacts from pre-exposure to the first three days after symptom onset was best explained by a GAM including biting suitability score, percent of bites expected at home pre-exposure, number of mosquitoes at home pre-exposure, and the interaction between biting suitability and percent bites at home, which explained 93.4% of deviance (S8 Table). The model with only a term for percent of bites expected at home pre-exposure, however, was able to explain 92.1% of the deviance (S8 Table). The effect of percent bites at home on percent change in expected mosquito contacts was very similar to the effect on percent change in onward transmission, where those with less than 55% of bites at home pre-exposure had a predicted decrease in mosquito contacts during the first three days of illness and those with greater than 55% were predicted to see an increase in mosquito contacts (S8 Fig). Individuals who received none of their bites at home pre-exposure were expected to have the largest percent decrease, whereas those who received around 90% of their bites at home pre-exposure had the largest percent increase (S8 Fig). If change in expected mosquito contacts was examined as a raw value rather than a percent change, all three variables and the interaction between number of mosquitoes at home and percent of bites at home were needed to provide an accurate prediction and explain a large amount of the deviance (S8 Table).

Sensitivity analyses

For the scenario where only 30% of cases experienced symptoms (and symptomatic mobility change), the expected values and relative changes for onward transmission and human-mosquito contacts had similar dynamics as in the case above where all individuals were symptomatic (S9–S15 Tables and S9–S13 Figs). In the scenario where symptomatic individuals did not completely halt mobility the first three days of symptoms, we saw similar albeit less intense dynamics as those above (S16–S22 Tables and S14–S18 Figs). This relaxing of mobility rules on the first days of symptoms did, however, curtail the importance of the household in onward transmission. When mobility was halted on days 1–3 there was a 40% increase in expected onward transmission from primary bites at home, as compared to a 30% increase with partial mobility on days 1–3 of symptoms (Tables 3 and S16 and S18 Fig). Similarly, the decrease in expected onward transmission from bites at other residential locations was 62% with no mobility on days 1–3 and 48% with partial mobility (Tables 3 and S16 and S18 Fig). Given this decreased role of the household in the case of partial mobility on the first three days of symptoms, the best-fit GAMs for predicting changes in onward transmission and changes in mosquito contacts could explain less deviance than their counterparts above (S17–S19 and S22 Tables). Regardless, we still saw the same predictor variables/reduced models with the largest contribution to explaining outcomes in the cases with partial and no mobility during days 1–3 after symptom onset (S17–S19 and S22 Tables).

Discussion

Transmission of DENV is highly focal and dependent on key human-Ae. aegypti encounters [23,42–44]. Fine-scale human mobility expands the spatial scale of transmission and causes contacts to occur throughout an individual’s activity space (the houses they routinely visit), generating variation in exposure to mosquitoes [18,20,21,30,45]. Indeed, in the absence of mobility changes our models found primary bites at home and in the activity space both significantly contributed to an individual’s onward transmission potential. When more realism was incorporated into DENV simulation models, through the coupling between illness and human mobility and the addition of pre-symptomatic infectiousness, significant changes in the number of expected mosquito bites for an individual, the locations the bites occurred, the number of secondary cases they were expected to cause, and the overall epidemic dynamics were detected compared to models not including such parameters. Effects were apparent both at the population level, where the consideration of human pre-symptomatic infectiousness and disease-driven mobility change increased the probability of a DENV outbreak by 37%, and at the individual level where onward transmission increased in the home environment at the expense of the activity space, primarily driven by houses with high mosquito density and inhabited by individuals with a high biting attractiveness score. Our findings were robust to assumptions of the amount of human mobility change and the presence of asymptomatic infections, providing a mechanistic understanding of the effect of human movement in disease dynamics.

Symptom-driven reductions in mobility determined an individual’s onward transmission potential due to the increased role of mosquito contacts in the home and the diminished role of mosquitoes in the rest of the activity space. This shift in where mosquito contacts occurred while individuals were infectious led to both increased and decreased contact rates, largely based on what percent of mosquito contacts were already expected to occur at home before mobility changed. While the majority (57%) of individuals saw a decrease, those with greater than 55% of mosquito contacts in their home pre-exposure saw increases in expected mosquito contacts when mobility changes were present. These individuals were subsequently predicted to have relative increases in onward transmission. Those with a low percent of mosquito bites at home pre-exposure were predicted to see a decrease in overall onward transmission; however, they saw a relative increase in transmission from primary bites at home due to the increased time spent at home while infectious, as did those with low biting attractiveness scores. These changes in expected bites, and subsequently onward transmission, may be particularly important for superspreaders, those with the top 20% of expected mosquito contacts who are often targeted for control measures given their significant contributions to onward transmission. However, we found that a quarter (24%) of the individuals with the top 20% of expected contacts pre-exposure had drastic enough decreases in expected bites that they were no longer in the top 20% during infectiousness. Accordingly, a portion of individuals who weren’t identified before symptomatic mobility change entered the top 20% during the peak of their infectiousness (days 1–3 after symptom onset). Our models identify the problem in only focusing on individuals with high expected contact rates pre-exposure and suggest that if control targets are selected this way some potential superspreaders will likely be overlooked and control measures may be less efficacious than expected.

At the individual level, biting suitability has previously been recognized as an important determinant in onward transmission potential [1,2]. In our model, biting suitability accounts for host biting attractiveness as well as avoidance and defensive behaviors, leading to a distribution in the number of effective bites each individual is expected to receive. Our analysis further identified the significance of a synergistic interaction between biting suitability and the density of mosquitoes in an individual’s home. Those with only a few mosquitoes in their home (<10) could go from lowest to highest biting suitability score and cause only a couple more secondary infections, whereas those with large numbers of mosquitoes in their home (>30) could cause many more secondary cases. Furthermore, individuals with low values in either biting suitability score or number of mosquitoes at home were predicted to have low onward transmission, partially due to the interaction effect of these two variables. A recent study characterizing absolute indoor Ae. Aegypti abundance found an average of 12.9 (range: 1–169) females per house, indicating that the ranges of simulated densities and expected findings are within values characterized in endemic areas [46]. While biting suitability has been proposed as an important driver of DENV transmission dynamics [5,47], our study emphasizes that its role in onward DENV transmission prevails even in the presence of other sources of heterogeneity, such as disease-driven mobility change or human social structure.

While an individual’s biting suitability may not change, the number of mosquitoes in their home can, which has significant implications for disease control. Reducing household mosquitoes is predicted to decrease onward transmission for all individuals, but it would be particularly effective for those with high biting suitability given the synergistic effect of the two factors on expected transmission. In the case of reactive vector control, reducing mosquitoes at the home of a symptomatic individual would be important given that the majority of onward transmission is expected to stem from primary bites occurring in their home; however, only spraying the homes of symptomatic cases would fail to control virus transmission due to the prevalence of asymptomatic infections. In comparison, proactive vector control (where residual vector control is deployed prior to the onset of seasonal transmission and with high coverage) would lower an individual’s risk of becoming infected (due to decreased expected human-mosquito contacts in their home) and if infection did occur, both symptomatic and inapparent cases would be predicted to have decreased expected onward transmission due to the effect of vector control [48,49]. Moreover, reducing the number of mosquitoes in an individual’s home pre-infection could also decrease the percent of bites expected at home (relative to the rest of the activity space), meaning symptomatic mobility changes could further decrease expected onward transmission. In the presence of social distancing due to COVID-19, it is therefore critical to reduce household-level mosquito bites to prevent DENV onward transmission in the home environment as predicted by our model.

One limitation of our study was the lack of an empirical social network to accurately parameterize our model framework. However, the configuration model generates a random graph with a given degree sequence that exhibits the “small world” property [50], allowing us to account for the inhomogeneous nature of social interactions while also allowing conclusions to be generalized to multiple locations. Further, by wiring a new random social network at the beginning of each simulation, it’s unlikely that outcomes will be caused by specific artifacts of the network structure. The model was also limited by its size, being representative of a neighborhood rather than an entire city (due to computational limitations). However, given that the most significant effects were seen at the individual level (rather than the population-level), increasing the number of houses in the framework would likely not have a dramatic impact. Further research should focus on possible refinements of the model, including the impact of multiple dengue serotypes (which have different rates of infection in humans and infectiousness to mosquitoes), or the effect of heterogeneous mobility and biting attractiveness on vaccination and vector control strategies.

There are numerous factors that can contribute an individual’s onward transmission potential. In order to better understand the complex dynamics of DENV transmission, we developed a framework that examines the contribution of multiple heterogeneous factors, both individually and in relation to each other. In particular, the association between mobility and symptom severity was empirically parameterized to better understand its role in disease dynamics and to validate a conceptual model of the role of coupled heterogeneities in disease dynamics [17,51]. Symptomatic mobility change can have a significant impact on the relationship between biting suitability, density of mosquitoes, and location where the majority of mosquito contacts are occurring, leading to a spectrum of changes in expected mosquito contacts and onward transmission potential. It is necessary to account for the interconnectedness of these factors in order to understand the relative contribution of symptomatic individuals to overall epidemic transmission dynamics and predict the efficacy of control measures.

Copyright statement

Author A.C.M. is a federal/contracted employee of the United States government. This work was prepared as part of her official duties. Title 17 U.S.C. §105 provides that ‘Copyright protection under this title is not available for any work of the United States Government.’ Title 17 U.S.C. §101 defines a U.S. Government work as a work prepared by a military service member or employee of the U.S. Government as part of that person’s official duties.

Supporting information

S1 Table. Simulation parameters with set values for all scenarios.

(PDF)

S2 Table. Simulation parameters set for each scenario.

(PDF)

S3 Table. Parameters that vary by infectiousness stage in the scenario with minor mobility the first three days after symptom onset.

Values calculated for individuals when susceptible, and at each sub-stage of infectiousness based on data from [31,38].

(PDF)

S4 Table. Comparison of GAMs for expected onward transmission without mobility change, R_norm.

Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S5 Table. Comparison of GAMs for expected onward transmission.

Models are compared for response variables R_movement and R_movement(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S6 Table. Comparison of GAMs for percent change in expected onward transmission when mobility is included.

Models are compared for response variables R_{rel_change} and R_{rel_change}(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S7 Table. Average expected mosquito bites per person per time step for each sub-stage of infectiousness after symptom onset (I₂ –I₅), separated based on expected bite values pre-exposure, presented as mean (SD).

(PDF)

S8 Table. Comparison of GAMs for change in expected mosquito contacts in the first three days after symptom onset when all time is spent at home (sub-stage I₂).

Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S9 Table. Average onward transmission (R) values with and without mobility change and change in R due to mobility change inclusion for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

R_norm values were calculated using an individual’s healthy movement patterns, while R_movement values accounted for changes in mobility throughout infectiousness. Changes in R-values due to mobility inclusion were calculated for each individual as a raw number and as a percent of R_norm value. Overall R-values were listed, as well as R-values based on only primary bites occurring at home or at other houses.

(PDF)

S10 Table. Comparison of GAMs for expected onward transmission without mobility change, R_norm, for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S11 Table. Comparison of GAMs for expected onward transmission for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

Models are compared for response variables R_movement and R_movement(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S12 Table. Comparison of GAMs for percent change in expected onward transmission when mobility is included for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

Models are compared for response variables R_{rel_change} and R_{rel_change}(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S13 Table. Average expected mosquito bites per person per time step for each sub-stage of infectiousness after symptom onset (I₂ –I₅) for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases, separated based on expected bite values pre-exposure, presented as mean (SD).

(PDF)

S14 Table. Average change in expected mosquito bites for each infectiousness sub-stage when symptomatic mobility change is occurring (I₂ –I₄), for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases, separated based on expected bite values pre-exposure.

Average changes are given both as raw numbers and percent change relative to number of expected bites pre-exposure.

(PDF)

S15 Table. Comparison of GAMs for change in expected mosquito contacts in the first three days after symptom onset when all time is spent at home (sub-stage I₂) for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

Models are compared for response variable as a raw number and a percentage. Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S16 Table. Average onward transmission (R) values with and without mobility change and change in R due to mobility change inclusion in the scenario with partial mobility on days 1–3 after symptom onset.

R_norm values were calculated using an individual’s healthy movement patterns, while R_movement values accounted for changes in mobility throughout infectiousness. Changes in R-values due to mobility inclusion were calculated for each individual as a raw number and as a percent of R_norm value. Overall R-values were listed, as well as R-values based on only primary bites occurring at home or at other houses.

(PDF)

S17 Table. Comparison of GAMs for expected onward transmission without mobility change, R_norm, in the scenario with partial mobility on days 1–3 after symptom onset.

Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S18 Table. Comparison of GAMs for expected onward transmission in the scenario with partial mobility on days 1–3 after symptom onset.

Models are compared for response variables R_movement and R_movement(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S19 Table. Comparison of GAMs for percent change in expected onward transmission when mobility is included in the scenario with partial mobility on days 1–3 after symptom onset.

Models are compared for response variables R_{rel_change} and R_{rel_change}(home). Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S20 Table. Average expected mosquito bites per person per time step for each sub-stage of infectiousness after symptom onset (I₂ –I₅) in the scenario with partial mobility on days 1–3 after symptom onset, separated based on expected bite values pre-exposure, presented as mean (SD).

(PDF)

S21 Table. Average change in expected mosquito bites for each infectiousness sub-stage when symptomatic mobility change is occurring (I₂ –I₄), in the scenario with partial mobility on days 1–3 after symptom onset, separated based on expected bite values pre-exposure.

Average changes are given both as raw numbers and percent change relative to number of expected bites pre-exposure.

(PDF)

S22 Table. Comparison of GAMs for change in expected mosquito contacts in the first three days after symptom onset when all time is spent at home (sub-stage I₂) in the scenario with partial mobility on days 1–3 after symptom onset.

Models are compared for response variable as a raw number and a percentage. Amount of deviance explained (%), degrees of freedom (DF), change in AICc compared to the best fit model (ΔAICc), and model weight are provided for each model. The best-fit model is highlighted in red.

(PDF)

S1 Fig. Equations for human and mosquito transmission models, as seen in [16].

(A) Stochastic, individual-based SEIR dynamics for hosts. ρ_fail is a failure distribution that defines the probability of recovering after i time steps. (B) Stochastic, household-level SEI dynamics for mosquitoes. Bernoulli, Binomial, and Multinomial functions generate random numbers from those distributions with the supplied parameters. See Tables 1 and S1 and S2 for parameter definitions.

(PDF)

S2 Fig. Mobility values during illness (in 3-day intervals), as seen in [31].

(A) Average number of locations visited per 3-day period. (B) Average proportion of time spent at home per 3-day period. Significant differences, denoted by letters, were detected using pairwise paired Wilcoxon Sign Rank tests with Bonferroni’s correction to account for a family-wise error-rate of 0.05. All significant differences had p-values < 0.05.

(PDF)

S3 Fig. Distribution of R_norm and R_movement values.

Outliers were removed.

(PDF)

S4 Fig. Factors influencing the contribution of an individual to onward DENV transmission.

Smooth functions for R_movement based on a GAM model containing number of mosquitoes in home pre-exposure, biting suitability score, and their interaction. The component smooths for each predictor variable are provided. For the 1-d smooths, the y-axis is the contribution of the predictor variable to the fitted response, centered around 0 (with 0 denoted by a red dashed line). For the 2-d smooth for the interaction term, a heatmap with overlaid contours is provided. The values of the contours represent the contribution of the interaction term to the fitted response. Positive values are in red and negative values are in blue.

(PDF)

S5 Fig. Distribution of expected mosquito contacts at each infectiousness sub-stage, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S6 Fig. Distribution of change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S7 Fig. Distribution of percent change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S8 Fig. Predictions for percent change in expected mosquito contacts based on GAM model containing percent of bites expected at home pre-exposure.

The predicted percent change in expected bites based on percent of bites expected at home pre-exposure. As there is only one predictor variable in this model, shifting the y-axis by the intercept value provides the smooth for the predictor variable.

(PDF)

S9 Fig. Distribution of R_norm and R_movement values for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

Outliers were removed.

(PDF)

S10 Fig. Expected onward transmission values with and without mobility changes accounted for, separated by where primary bites occur and where secondary bites occur, for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases.

(A) gives onward transmission for primary bites occurring at home (red) and at other houses (blue) both without (left) and with (right) movement change included. [from left to right: R_norm(home), R_norm(other houses), R_movement(home), and R_movement(other houses)] (B) gives onward transmission for secondary bites at the home of the primary infected individual (red) and at other houses (blue).

(PDF)

S11 Fig. Distribution of expected mosquito contacts at each infectiousness sub-stage, for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S12 Fig. Distribution of change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S13 Fig. Distribution of percent change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, for only symptomatic individuals in the scenario with 70% inapparent cases and 30% symptomatic cases, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S14 Fig. Distribution of R_norm and R_movement values in the scenario with partial mobility on days 1–3 after symptom onset.

Outliers were removed.

(PDF)

S15 Fig. Expected onward transmission values with and without mobility changes accounted for, separated by where primary bites occur and where secondary bites occur, in the scenario with partial mobility on days 1–3 after symptom onset.

(A) gives onward transmission for primary bites occurring at home (red) and at other houses (blue) both without (left) and with (right) movement change included. [from left to right: R_norm(home), R_norm(other houses), R_movement(home), and R_movement(other houses)] (B) gives onward transmission for secondary bites at the home of the primary infected individual (red) and at other houses (blue).

(PDF)

S16 Fig. Distribution of expected mosquito contacts at each infectiousness sub-stage in the scenario with partial mobility on days 1–3 after symptom onset, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S17 Fig. Distribution of change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, in the scenario with partial mobility on days 1–3 after symptom onset, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

S18 Fig. Distribution of percent change in expected mosquito contacts at each infectiousness sub-stage relative to pre-exposure values, in the scenario with partial mobility on days 1–3 after symptom onset, separated based on top 20/bottom 80% of expected bites pre-exposure.

(PDF)

Data Availability

Code for generating datasets and reproducing analyses in this study is available on Github (https://github.com/KathrynSchaber/Mobility-Model).

Funding Statement

This research was supported by funding from the US National Institutes of Health-National Institute of Allergy and Infectious Diseases (NIH-NIAID) award number P01AI098670 (to T.W.S.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.