Summary
Bisulfite DNA methylation sequencing (Methyl-Seq) becomes one of the most important technologies to study methylation level difference at a genome-wide scale. Due to the complexity and large scale of methyl-Seq data, power calculation and study design method have not been developed. Here, we propose a “MethylSeqDesign” framework for power calculation and study design of Methyl-Seq experiments by utilizing information from pilot data. Differential methylation analysis is based on a beta-binomial model. Power calculation is achieved using mixture model fitting of p-values from pilot data and a parametric bootstrap procedure. To circumvent the issue of existing tens of millions of methylation sites, we focus on the inference of pre-specified targeted regions. The performance of the method was evaluated with simulations. Two real examples are analyzed to illustrate our method. An R package “MethylSeqDesign” to implement this method is publicly available.
Keywords: Bisulfite sequencing, Methyl-Seq, Power calculation, Study design
1. Introduction
DNA methylation is a chemical modification of DNA nucleotides when a methyl-group (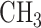 ) is attached at the 5th position of cytosine (5mC). It is one of the best characterized and the most studied epigenetic markers, which has shown to control gene expression in both normal cell development and abnormal biological process such as cancer. Particularly in gene promoter regions, hyper-methylation is shown closely related to silencing gene expressions. In mammals, such as human, DNA methylation happens almost exclusively at cytosine site that follows with guanine known as CpG site. There are tens of thousands of regions with a high frequency of CpG sites in the whole genome that are classified as CpG islands, which typically exist at or near the transcription starting sites of genes. DNA methylation process has been found to link to many important biological processes, such as genomic imprinting, X-chromosome inactivation, repression of repetitive elements, aging, and carcinogenesis (Li and others, 1993; Paulsen and Ferguson-Smith, 2001; Robertson, 2005). In cancer studies, aberrant DNA methylation changes are considered as one of the leading factors in developing tumors (Esteller, 2005; Baylin, 2005; Delpu and others, 2013; Licht, 2015).
) is attached at the 5th position of cytosine (5mC). It is one of the best characterized and the most studied epigenetic markers, which has shown to control gene expression in both normal cell development and abnormal biological process such as cancer. Particularly in gene promoter regions, hyper-methylation is shown closely related to silencing gene expressions. In mammals, such as human, DNA methylation happens almost exclusively at cytosine site that follows with guanine known as CpG site. There are tens of thousands of regions with a high frequency of CpG sites in the whole genome that are classified as CpG islands, which typically exist at or near the transcription starting sites of genes. DNA methylation process has been found to link to many important biological processes, such as genomic imprinting, X-chromosome inactivation, repression of repetitive elements, aging, and carcinogenesis (Li and others, 1993; Paulsen and Ferguson-Smith, 2001; Robertson, 2005). In cancer studies, aberrant DNA methylation changes are considered as one of the leading factors in developing tumors (Esteller, 2005; Baylin, 2005; Delpu and others, 2013; Licht, 2015).
Over the past couple decades, sodium bisulfite treatment has become widely used tool to study DNA methylation at the level of single nucleotide resolution. When DNA is treated with sodium bisulfite, the unmethylated cytosines are converted to uracil and amplified by polymerase chain reaction as thymine while methylated cytosines remain protected from this conversion (see Figure 1(A)). The outcome of this treatment leads to identifying methylated and unmethylated cytosines when the sequencing reads are mapped to reference genome using special mapping pipelines such as Bismark, which consider Thymine/Cytosine mismatch. Two major technologies have been developed to quantify the DNA methylation after bisulfite conversion. One is methylation microarray, which targets on pre-selected CpG sites in certain regions, mostly within CpG islands. The total number of targeted CpG sites is relatively small, for example, Illumina HumanMethylation27 and HumanMethylation450 Bead chips cover only about 27K and 480K CpG sites) compared to over 28 million CpG sites in human genome (Schumacher and others, 2006). Another recently developed technology is coupling bisulfite conversion with next generation sequencing (NGS) to quantitatively query the methylation status across the whole genome. Whole genome bisulfite sequencing (WGBS) can provide accurate and quantitative estimates of the proportion of methylated cells in a population at each of the tens of millions of CpG sites across genome. However, accurate estimates of methylation level requires large number of reads to cover CpG sites of interest. Because of unevenly distributed CpG sites across the genome, a large proportion of sequencing reads do not contain any CpG sites, which results in high cost of WGBS. To overcome this disadvantage, reduced representation bisulfite sequencing (RRBS) (Meissner and others, 2005) was introduced to target on CpG rich regions, relying on restriction enzyme that can ensure the capture of at least one CpG site per sequencing read. Using RRBS, methylation levels of a portion of genome regions can be accurately obtained at much lower cost compared to WGBS. Here, we use “Methyl-Seq” to refer to bisulfite sequencing technology including WGBS and RRBS. Due to the popularity of Methyl-Seq and the high sequencing cost with limited budget, sample size and power calculation methods become critical for design of such studies.
Fig. 1.
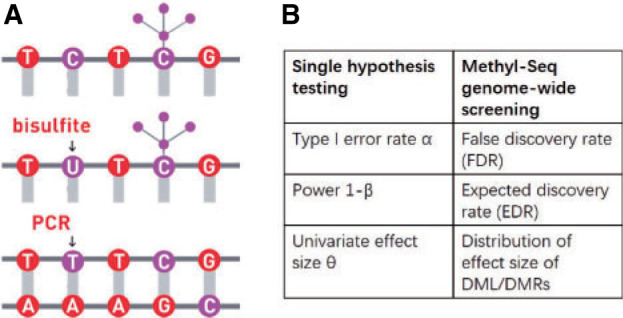
(A) An illustration of sodium bisulfite modification. (B) Comparison of three elements between single hypothesis testing and Methyl-Seq genome-wide screening.
Traditional power calculation methods seek the statistical power (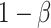 ;
; 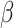 here is type II error) to detect the difference between groups by pre-specifying effect size (
here is type II error) to detect the difference between groups by pre-specifying effect size (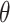 ), type I error rate (
), type I error rate (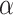 ), and sample size (
), and sample size (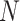 ). Alternatively, one can calculate the required sample size with pre-specified statistical power,
). Alternatively, one can calculate the required sample size with pre-specified statistical power, 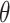 and
and 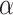 . The effect size
. The effect size 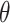 is the measure of group difference that is generally obtained from a pilot study or researchers’ belief. Usually, the type I error rate is set to be 5% and the desired statistical power is 70–80% for a study design. This classical framework is based on performing a single hypothesis testing. For high-throughput genome-wide experimental data, however, many hypotheses are tested simultaneously to compare the methylation difference at the thousands of regions or millions of CpG sites. Therefore, genome-wide power calculation should be based on appropriately controlled type I error rates. One widely used in Genomic study is false discovery rate (FDR; Benjamini and Hochberg, 1995) and in this article, we use FDR to control genome-wide type I error rate. In addition, Gadbury and others (2004) introduced a useful concept, called expected discovery rate (EDR), to replace test power
is the measure of group difference that is generally obtained from a pilot study or researchers’ belief. Usually, the type I error rate is set to be 5% and the desired statistical power is 70–80% for a study design. This classical framework is based on performing a single hypothesis testing. For high-throughput genome-wide experimental data, however, many hypotheses are tested simultaneously to compare the methylation difference at the thousands of regions or millions of CpG sites. Therefore, genome-wide power calculation should be based on appropriately controlled type I error rates. One widely used in Genomic study is false discovery rate (FDR; Benjamini and Hochberg, 1995) and in this article, we use FDR to control genome-wide type I error rate. In addition, Gadbury and others (2004) introduced a useful concept, called expected discovery rate (EDR), to replace test power 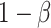 from single hypothesis to address genome-wide detection power. Since genome-wide screening considers the whole set of differentially methylated loci/regions (DML/DMRs), specifying a single effect size
from single hypothesis to address genome-wide detection power. Since genome-wide screening considers the whole set of differentially methylated loci/regions (DML/DMRs), specifying a single effect size 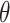 for power calculation is no longer valid. Alternatively, the distribution of effect sizes of DML/DMRs is needed, which could be estimated from pilot data. Figure 1(B) shows changes of the essential elements in genome-wide screening, compared to traditional single hypothesis testing.
for power calculation is no longer valid. Alternatively, the distribution of effect sizes of DML/DMRs is needed, which could be estimated from pilot data. Figure 1(B) shows changes of the essential elements in genome-wide screening, compared to traditional single hypothesis testing.
There are three unique characteristics inside Methyl-Seq data that should be considered in power and sample size calculation. First, it generates random binomial data for each sample at each CpG site. A model with discrete distributions is more suitable for Methyl-seq data and both sampling and biological variations should be considered. For this reason, the beta-binomial model (Dolzhenko and Smith, 2014; Feng and others, 2014; Park and others, 2014) has gained popularity over the binomial model. Second, for Methyl-Seq experiments, researchers have choices of different sequencing depth (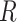 ) for the design. In other words, one can choose to process one sample per lane, which results in roughly 250 million reads in Illumina HiSeq 2500 platform or three samples per lane each with 83 million reads for the same sequencing cost. Therefore the power calculation problem may need to consider both
) for the design. In other words, one can choose to process one sample per lane, which results in roughly 250 million reads in Illumina HiSeq 2500 platform or three samples per lane each with 83 million reads for the same sequencing cost. Therefore the power calculation problem may need to consider both 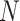 and
and 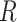 . Finally, there are about 28 million CpG sites in human genome. Based on the current technology, it is impossible to sequence most CpG sites with sufficient coverage even with ultra-deep sequencing depth. As a result, many CpG sites will have zero or almost zero reads in many subjects. We further discussed the coverage of single CpG sites and CpG region in the Section 1 of the supplementary material available at Biostatistics online. Therefore, it is not realistic to study the differences of methylation levels at all CpG sites. To circumvent this difficulty, we restrict to methylation regions by aggregating methylation data across multiple CpG sites within a particular region, such as promoter regions, for power calculation.
. Finally, there are about 28 million CpG sites in human genome. Based on the current technology, it is impossible to sequence most CpG sites with sufficient coverage even with ultra-deep sequencing depth. As a result, many CpG sites will have zero or almost zero reads in many subjects. We further discussed the coverage of single CpG sites and CpG region in the Section 1 of the supplementary material available at Biostatistics online. Therefore, it is not realistic to study the differences of methylation levels at all CpG sites. To circumvent this difficulty, we restrict to methylation regions by aggregating methylation data across multiple CpG sites within a particular region, such as promoter regions, for power calculation.
Many power calculation methods have been developed for RNA-Seq data, such as RNASeqPower (Hart and others, 2013), Scotty (Busby and others, 2013), and PROPER (Wu and others, 2015). For microarray methylation data, Tsai and Bell (2015) proposed method for study design and power calculation. To the best of our knowledge, for Methyl-seq data, no existing power calculation method has been developed so far in the literature. Here, we propose a statistical framework “MethylSeqDesign” for sample size and power calculation for studies with Methyl-seq data. The “MethylSeqDesign” R package is publicly available at https://github.com/liupeng2117/MethylSeqDesign.
The article is structured as follows. In Section 2, the statistical framework of MethylSeqDesign is proposed. In Section 3, we present comprehensive simulations and real data applications. Section 4 is real data application. Section 5 provides conclusion and discussion.
2. Genome-wide power calculation in Methyl-Seq
2.1. Notations and terminology
Consider 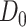 ={
={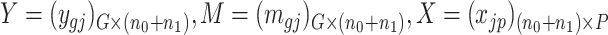 } (
} (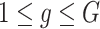 ,
, 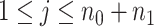 ) a pilot Methyl-Seq dataset, where
) a pilot Methyl-Seq dataset, where 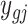 and
and 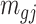 represent the methylated and total read counts for CpG region
represent the methylated and total read counts for CpG region 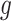 of subject
of subject 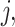 respectively. Let
respectively. Let 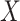 be a design matrix of dimension
be a design matrix of dimension 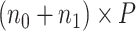 , which contains case/control group information and other continuous or discrete covariates.
, which contains case/control group information and other continuous or discrete covariates. 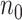 and
and 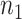 are the number of controls and cases in the pilot data. Denote
are the number of controls and cases in the pilot data. Denote 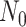 and
and 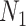 the target number of controls and cases for power calculation. Let
the target number of controls and cases for power calculation. Let 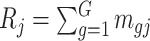 be the total number of reads observed in subject
be the total number of reads observed in subject 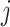 (a.k.a. library size). We consider genome-wide power calculations under genome-wide type I error control using FDR = E (number of claimed false positives/number of claimed positives). Following Gadbury and others (2004), we use expected discovery rate, EDR = E (number of claimed true positives/number of total true positives), as the genome-wide power. The methylation level is the proportion of methylated cells among all cells at a particular CpG site or region. Statistical power is impacted by both sample size and sequencing depth. Therefore, the statistical framework of MethylSeqDesign becomes to estimate the genome-wide power
(a.k.a. library size). We consider genome-wide power calculations under genome-wide type I error control using FDR = E (number of claimed false positives/number of claimed positives). Following Gadbury and others (2004), we use expected discovery rate, EDR = E (number of claimed true positives/number of total true positives), as the genome-wide power. The methylation level is the proportion of methylated cells among all cells at a particular CpG site or region. Statistical power is impacted by both sample size and sequencing depth. Therefore, the statistical framework of MethylSeqDesign becomes to estimate the genome-wide power 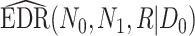 based on the pilot data (
based on the pilot data (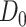 with
with 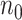 controls,
controls,  cases, and sequencing depth
cases, and sequencing depth 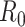 ) for designing a future experiment with
) for designing a future experiment with 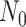 controls,
controls, 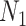 cases, sequencing depth
cases, sequencing depth 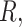 and under a prespecified FDR level (e.g. FDR = 5%).
and under a prespecified FDR level (e.g. FDR = 5%).
2.2. Three sequential steps for genome-wide Methyl-Seq power calculation
Park and Wu (2016) proposed the “DSS-general” method, a model-based method for detecting DML/DMRs based on beta-binomial model with arcsine link function. The estimation procedure is based on generalized least square (GLS) approach, which can significantly reduce the computation demands compared to other beta-binomial based methods (Dolzhenko and Smith, 2014; Feng and others, 2014). In addition, Park and Wu (2016) showed superior performance of their method in terms of DMR detection accuracy and type I error rate control. Therefore, in this article, we will adopt Park and Wu (2016)’ s approach for our power calculation tool.
Below we propose three sequential steps in MethylSeqDesign to estimate EDR. In Step I, p-values and effect size distribution of all methylated regions from pilot data are obtained using DSS-general. In Step II, a beta-uniform mixture (BUM) model is applied to characterize the genome-wide p-value distribution and to estimate the proportion of true DMRs. In Step III, a parametric bootstrapping method based on DMR posterior probability is used to simulate and transform the genome-wide p-value distribution towards the targeted sample size and sequencing depth. The detailed description of our method is as follows.
Step I. Differential methylation analysis on pilot data.
To account for both sampling and biological variation, denote by 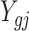 the methylated read count for gene
the methylated read count for gene 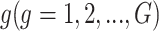 in sample
in sample 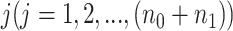 , let
, let 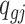 be the underlying methylation level for gene g and sample j,
be the underlying methylation level for gene g and sample j, 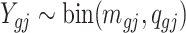 and
and 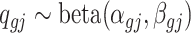 . Marginally,
. Marginally, 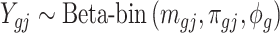 , where
, where 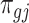 and
and 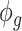 are the mean and dispersion parameter of beta distribution, such that
are the mean and dispersion parameter of beta distribution, such that 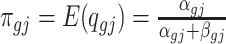 ,
, 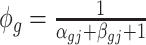 and we assume
and we assume 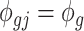 for all
for all 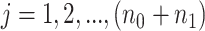 . Here, we account for covariate effect as,
. Here, we account for covariate effect as,
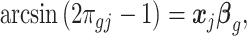 |
(2.1) |
where 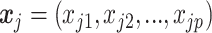 is
is 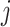 th subject’ s covariate, and
th subject’ s covariate, and 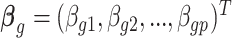 is a vector of
is a vector of 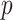 covariate coefficients for
covariate coefficients for  th CpG region.
th CpG region.
Denote 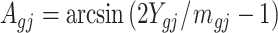 . As shown in Park and Wu (2016), the expectation of
. As shown in Park and Wu (2016), the expectation of 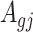 can be approximated as
can be approximated as 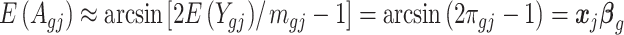 . Furthermore, the variance of
. Furthermore, the variance of 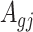 can also be also approximated as
can also be also approximated as 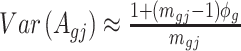 , which is approximately independent of the mean structure. Given dispersion parameter
, which is approximately independent of the mean structure. Given dispersion parameter 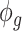 , the regression coefficients
, the regression coefficients 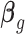 can be estimated using GLS method, i.e.
can be estimated using GLS method, i.e. 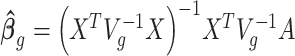 , where
, where 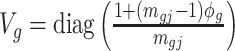 is the covariance matrix. The estimator of
is the covariance matrix. The estimator of 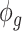 is given by
is given by 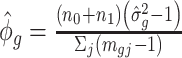 , where
, where 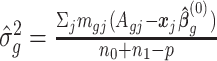 ,
, 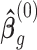 is the GLS estimator of
is the GLS estimator of 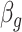 under
under 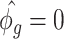 . The estimate of covariance structure is
. The estimate of covariance structure is 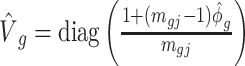 . Given
. Given 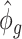 and
and 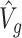 , the estimator of variance of
, the estimator of variance of  is
is 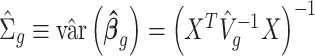 .
.
Hypothesis testing for 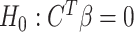 vs.
vs. 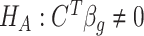 is based on Wald statistics
is based on Wald statistics
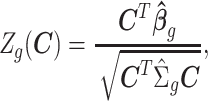 |
where 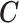 can be any linear combination of the covariate effects. The statistic approximately follows a standard normal distribution under null hypothesis.
can be any linear combination of the covariate effects. The statistic approximately follows a standard normal distribution under null hypothesis.
For simplicity, here we consider the study with two groups (case and control), i.e. 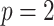 with intercept and case/control effect. Let
with intercept and case/control effect. Let 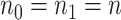 be the number of subjects in each group in pilot data, and
be the number of subjects in each group in pilot data, and 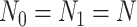 be the target number of subjects in each group. Here, we assume equal sample sizes for control and cases in pilot and target cohorts while the method can be easily generalized for
be the target number of subjects in each group. Here, we assume equal sample sizes for control and cases in pilot and target cohorts while the method can be easily generalized for 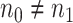 and
and 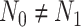 later (see the leukemia application in Section 4.2). Then the model becomes
later (see the leukemia application in Section 4.2). Then the model becomes 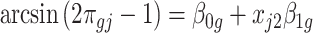 . In this case,
. In this case, 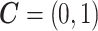 . Here the variance of
. Here the variance of 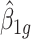 is
is
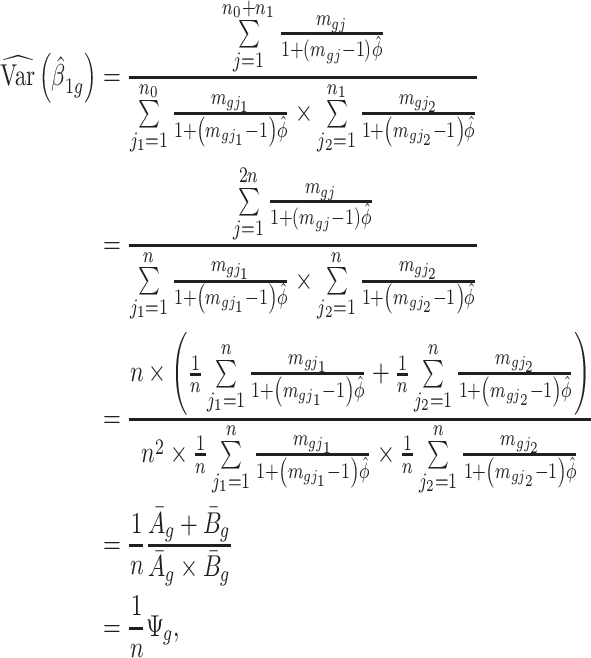 |
(2.2) |
where 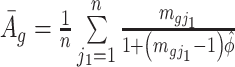 and
and 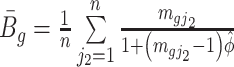 . The Wald test statistic becomes
. The Wald test statistic becomes
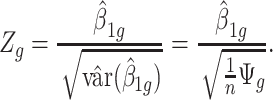 |
(2.3) |
where 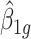 is the GLS estimator of
is the GLS estimator of 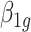 .
.
Remark 1: A common over-dispersion parameter (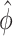 ) over all CpG regions is used which is the mean of all tag-wise dispersion parameters (
) over all CpG regions is used which is the mean of all tag-wise dispersion parameters (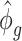 ) estimated from the procedure proposed by Park and Wu (2016). This is because when sample size is small, estimation of region-specific dispersion parameter is not precise, and region-specific power calculation is very challenging.
) estimated from the procedure proposed by Park and Wu (2016). This is because when sample size is small, estimation of region-specific dispersion parameter is not precise, and region-specific power calculation is very challenging.
Remark 2: One interesting finding is that the quantities 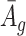 and
and  in (2.2) are in the mean form that depends on coverage and dispersion parameter given a region g. When
in (2.2) are in the mean form that depends on coverage and dispersion parameter given a region g. When 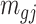 is small, it has negative correlation with
is small, it has negative correlation with 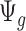 , while
, while 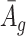 and
and 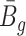 are roughly independent on
are roughly independent on 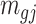 when
when 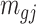 is large. If we assume the dispersion parameter stay constant,
is large. If we assume the dispersion parameter stay constant, 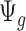 is mostly impacted by sequencing depth. In Section 2.1 of the supplementary material available at Biostatistics online, we further studied the property of the quantity
is mostly impacted by sequencing depth. In Section 2.1 of the supplementary material available at Biostatistics online, we further studied the property of the quantity 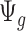 by simulation.
by simulation.
Step II. Mixture model fitting for p-value distribution.
A BUM model (Allison and others, 2002) has been proposed to fit the p-value distribution. To be specific, we use a beta distribution 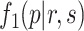 with shape parameter
with shape parameter 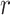 and
and 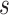
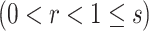 for p-values of DMRs and a uniform distribution
for p-values of DMRs and a uniform distribution 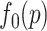 for p-values of non-DMRs. The mixture density of overall p-value distribution is
for p-values of non-DMRs. The mixture density of overall p-value distribution is 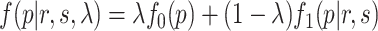 , where
, where 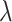 is the proportion of non-DMRs. The constraints for
is the proportion of non-DMRs. The constraints for 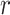 and
and 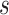 is used to have a proper shape for the p-value distribution of DMRs. A proper estimation of
is used to have a proper shape for the p-value distribution of DMRs. A proper estimation of 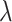 is essential in fitting a BUM model. We apply censored BUM (CBUM) proposed by Markitsis and Lai (2010) to reduce the impact of extremely small p-values, since our main purpose is to estimate the proportion of true DMRs for those with relatively larger p-values. The detailed comparisons of performance between BUM and CBUM methods are included in Section 2.2 of the supplementary material available at Biostatistics online. The shape parameters
is essential in fitting a BUM model. We apply censored BUM (CBUM) proposed by Markitsis and Lai (2010) to reduce the impact of extremely small p-values, since our main purpose is to estimate the proportion of true DMRs for those with relatively larger p-values. The detailed comparisons of performance between BUM and CBUM methods are included in Section 2.2 of the supplementary material available at Biostatistics online. The shape parameters 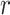 and
and 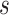 can then be estimated using maximum likelihood approach using
can then be estimated using maximum likelihood approach using 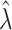 estimated from the CBUM method.
estimated from the CBUM method.
Step III. Parametric bootstrapping based on DMR posterior probability to estimate EDR.
Theoretically, the p-value distribution for non-DMRs with zero effect size follows a uniform distribution that does not change with the sample size. However, we expect that the p-values for those DMRs will be more significant as sample sizes increase. Equations (2.2) and (2.3) reveal a transformation of Z-statistics of DMRs from the pilot data with sample size 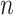 to the targeted sample size
to the targeted sample size 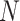 . When the effect size
. When the effect size 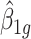 and the common over-dispersion parameter
and the common over-dispersion parameter 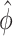 stay approximately unchanged, the Wald test statistics change by a factor of
stay approximately unchanged, the Wald test statistics change by a factor of 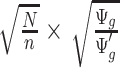 (see (2.2) and item (2) below;
(see (2.2) and item (2) below; 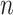 is the pilot sample size,
is the pilot sample size, 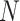 is the targeted sample size,
is the targeted sample size, 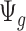 is the quantity under pilot sequencing depth
is the quantity under pilot sequencing depth 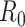 , and
, and 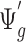 is the quantity under the targeted sequencing depth
is the quantity under the targeted sequencing depth 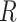 ). Throughout this article, we assume sequencing depth of pilot data
). Throughout this article, we assume sequencing depth of pilot data 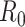 is deep enough and the targeted sequencing depth
is deep enough and the targeted sequencing depth 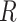 does not exceed
does not exceed 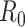 (i.e.
(i.e. 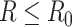 ). Since
). Since 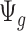 is a function depending on pre-estimated dispersion parameter
is a function depending on pre-estimated dispersion parameter 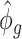 and count data
and count data 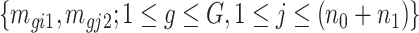 , it is readily calculated from pilot data. To estimate for
, it is readily calculated from pilot data. To estimate for 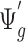 , we can randomly subsample from pilot data to achieve sequencing depth
, we can randomly subsample from pilot data to achieve sequencing depth 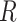 and derive
and derive 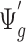 by definition based on subsampled counts
by definition based on subsampled counts 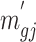 and
and 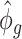 . The influence of sequencing depth on
. The influence of sequencing depth on 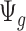 is further discussed in Section 2.1 of the supplementary material available at Biostatistics online. We found that when the median coverage level is above 160,
is further discussed in Section 2.1 of the supplementary material available at Biostatistics online. We found that when the median coverage level is above 160, 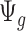 is roughly constant and the correction term for different sequencing depth is not necessary. Otherwise, the correction term
is roughly constant and the correction term for different sequencing depth is not necessary. Otherwise, the correction term 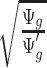 is needed.
is needed.
Let 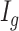 be the latent variable indicating region
be the latent variable indicating region 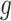 a DMR (
a DMR (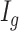 =1) or non-DMR (
=1) or non-DMR (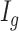 =0), and let
=0), and let 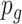 be the p-value of region
be the p-value of region 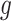 from the aforementioned Wald test in pilot data. The detailed parametric bootstrapping procedure is described as follows:
from the aforementioned Wald test in pilot data. The detailed parametric bootstrapping procedure is described as follows:
- (1) Calculate the posterior probability of the DMR indicator
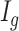 with posterior probability
with posterior probability
where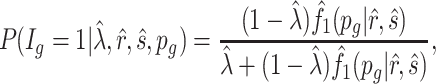
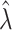 ,
, 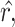 and
and 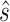 are estimated in Step II. In the
are estimated in Step II. In the 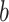 th parametric bootstrapping (
th parametric bootstrapping (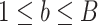 ), draw
), draw 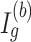 from
from 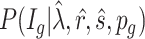 for
for 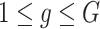 .
. - (2) Transform Z-statistics for DMRs using equation
where we assume that the effect size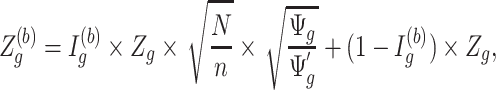
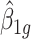 and the common over-dispersion parameter
and the common over-dispersion parameter 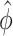 of a DMR in (2.2) and (2.3) are roughly fixed. Therefore, when
of a DMR in (2.2) and (2.3) are roughly fixed. Therefore, when 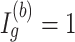 , region
, region 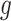 is a DMR in the
is a DMR in the 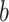 th parametric bootstrap and the Wald statistic is transformed to
th parametric bootstrap and the Wald statistic is transformed to 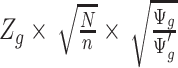 . When
. When 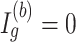 , the Wald statistic remains unchanged.
, the Wald statistic remains unchanged. (3) Compute p-value based on the 2-sided test:
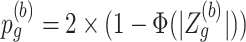 for a DMR region (
for a DMR region (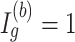 ), where
), where 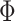 is a cumulative density function of a standard normal distribution. When
is a cumulative density function of a standard normal distribution. When 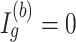 ,
, 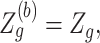 and
and 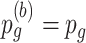 remain unchanged.
remain unchanged.-
(4) Control FDR at level
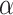 :
:(a) In the
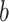 th simulation, calculate
th simulation, calculate 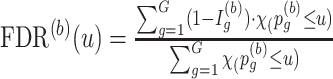 for a given p-value threshold
for a given p-value threshold 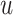 , where
, where 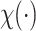 is an indicator function that takes value one when the statement is true and zero otherwise. Here, by definition, the denominator is the number of detected regions under p-value threshold
is an indicator function that takes value one when the statement is true and zero otherwise. Here, by definition, the denominator is the number of detected regions under p-value threshold 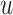 , and the numerator is the number of non-DMRs among those detected regions.
, and the numerator is the number of non-DMRs among those detected regions.(b) Let
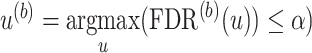 , where
, where 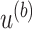 is the p-value threshold to keep FDR at
is the p-value threshold to keep FDR at 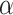 level for the
level for the 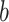 th simulation.
th simulation.
(5) Obtain the estimated EDR for the
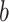 th simulation with
th simulation with 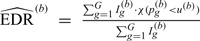 . Here, by definition, the denominator is the number of total DMRs and the numerator is the number of detected true DMRs.
. Here, by definition, the denominator is the number of total DMRs and the numerator is the number of detected true DMRs.(6) Repeat steps (1) to (5) for B times and the robust estimator of EDR from the B simulations is
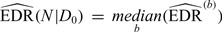 . The first and third quantile of bootstrapped EDRs can also be derived to account for the variability of EDR estimation.
. The first and third quantile of bootstrapped EDRs can also be derived to account for the variability of EDR estimation.
3. Simulation
3.1. Simulation scheme
We simulated data based on parameters estimated directly from the mouse pregnancy dataset (see details in Section 4.1 (Katz and others, 2015)). We empirically drew the total number of reads and baseline methylation level of control group from the data. Effect size (methylation level difference between two groups) was either fixed or randomly generated from 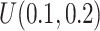 . In total, 10,000 regions were simulated, and we assigned 10% regions as DMRs. The common dispersion parameter was set to
. In total, 10,000 regions were simulated, and we assigned 10% regions as DMRs. The common dispersion parameter was set to 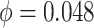 , which was the mean dispersion parameters estimated from the data.
, which was the mean dispersion parameters estimated from the data.
The steps to simulate pilot data with sample size 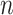 and sequencing depth
and sequencing depth 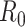 , and targeted data with sample size
, and targeted data with sample size 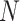 and sequencing depth
and sequencing depth  are shown below.
are shown below.
(1) Draw total read
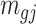 for region
for region  and sample
and sample 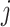 randomly from the mouse pregnancy data, and baseline methylation level
randomly from the mouse pregnancy data, and baseline methylation level 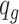 for each CpG region from the empirical distribution estimated from the mouse pregnancy data.
for each CpG region from the empirical distribution estimated from the mouse pregnancy data.(2) To simulate pilot data with sequencing depth
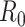 , we directly use the total reads drawn from step 1. When simulating the targeted data with sequencing depth
, we directly use the total reads drawn from step 1. When simulating the targeted data with sequencing depth 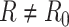 , we downsample the matrix of total reads based on the ratio of
, we downsample the matrix of total reads based on the ratio of 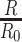 .
.(3) DM index: Generate random number
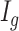 from
from 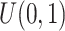 for each region. If
for each region. If 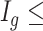 0.1 the
0.1 the 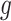 th region is DMR and
th region is DMR and 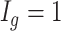 . Otherwise, it is non-DMR and
. Otherwise, it is non-DMR and 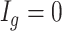 . This generates roughly 10% DMRs.
. This generates roughly 10% DMRs.(4) Effect size
 : Draw effect size from
: Draw effect size from 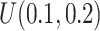 for each DMR. The effect size for non-DMRs is set to 0.
for each DMR. The effect size for non-DMRs is set to 0.(5) Generate the number of methylated reads: If the
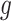 th region is non-DMR, then
th region is non-DMR, then 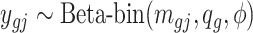 . If the
. If the 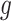 th region is DMR, then in control group
th region is DMR, then in control group 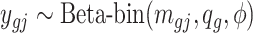 while in case group, the methylated counts
while in case group, the methylated counts 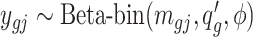 , where
, where 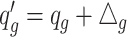 if
if 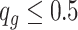 and
and  otherwise.
otherwise.(6) Follow above steps to simulate pilot data and the targeted data.
3.2. Performance comparison with other hypothesis testing methods
We compared the statistical power of our proposed test statistic (3) with other three methods: Beta value (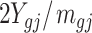 ) with t-test, M value (
) with t-test, M value (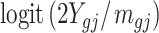 ) with t-test, and A value (
) with t-test, and A value (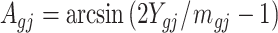 ) with t-test.
) with t-test.
To compare the performance, we conducted the analysis by stratifying the baseline methylation proportion in control group into three categories: low (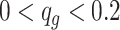 ), medium (
), medium (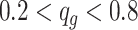 ), and high (
), and high (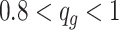 ). In each baseline group, we simulated 20 times independent analysis, in which pilot data had 10 subjects in each group (i.e.,
). In each baseline group, we simulated 20 times independent analysis, in which pilot data had 10 subjects in each group (i.e., 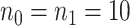 ), and 10 000 regions (10% are DMRs). As shown in Figure S3 of the supplementary material available at Biostatistics online, we compared the power based on how many true DMRs could be declared among different numbers of top declared DMRs. As a result, the result clearly shows better performance of using our arcsin transformation and Wald statistics compared to other approaches. Furthermore, we observe that the power of each method is stronger in either low or high baseline group and relatively weaker in medium baseline group, which is reasonable because the effect size is at methylation level scale and for binomial distribution, the same difference is easier to detect when methylation is close to boundary 0 or 1. Overall, the results justifies the need of using arcsine transformation and Wald test statistics for our power calculation framework.
), and 10 000 regions (10% are DMRs). As shown in Figure S3 of the supplementary material available at Biostatistics online, we compared the power based on how many true DMRs could be declared among different numbers of top declared DMRs. As a result, the result clearly shows better performance of using our arcsin transformation and Wald statistics compared to other approaches. Furthermore, we observe that the power of each method is stronger in either low or high baseline group and relatively weaker in medium baseline group, which is reasonable because the effect size is at methylation level scale and for binomial distribution, the same difference is easier to detect when methylation is close to boundary 0 or 1. Overall, the results justifies the need of using arcsine transformation and Wald test statistics for our power calculation framework.
3.3. Performance evaluation
We simulated 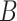 =10 pilot datasets (
=10 pilot datasets (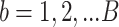 ) with pilot sample size
) with pilot sample size 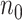 = 2, 4, 6, 8, 9, and 10 when
= 2, 4, 6, 8, 9, and 10 when 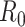 are 5 million reads. For each pilot dataset with (
are 5 million reads. For each pilot dataset with (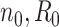 ), the projected power for targeted sample size
), the projected power for targeted sample size 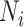 =2, 6, 10, 15, 25, 50 (
=2, 6, 10, 15, 25, 50 (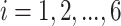 ) and
) and 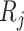 = 0.25, 0.5, 1, 2, 3, 4 million reads (
= 0.25, 0.5, 1, 2, 3, 4 million reads (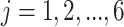 ) from a power calculation method is denoted by
) from a power calculation method is denoted by  . Since the underlying truth is known, the true EDR for each (
. Since the underlying truth is known, the true EDR for each (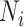 ,
, 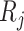 ) can be estimated as
) can be estimated as  is the actual EDR in the
is the actual EDR in the 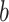 th simulation when sample size
th simulation when sample size 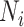 and
and 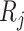 are simulated. We propose the following benchmarks based on root mean squared error (RMSE) to evaluate performance of different power calculation methods:
are simulated. We propose the following benchmarks based on root mean squared error (RMSE) to evaluate performance of different power calculation methods:
(1) Consider two-dimensional power calculation from (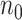 ,
, 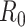 ) to (
) to (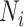 ,
, 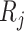 ) (
) (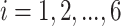 and
and 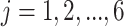 ). The RMSE of estimated EDR from power calculation is
). The RMSE of estimated EDR from power calculation is
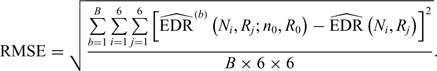 |
We first performed a stratified analysis based on different level of effect size, as we already know it will impact the EDR. 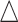 was set as 0.1, 0.14, and 0.18. In each setting, we generated the same number of regions to compare the performance (Figure 2 for
was set as 0.1, 0.14, and 0.18. In each setting, we generated the same number of regions to compare the performance (Figure 2 for 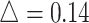 , Figures S4 and S5 of the supplementary material available at Biostatistics online for
, Figures S4 and S5 of the supplementary material available at Biostatistics online for  and 0.18). Table 1 shows the RMSEs and computing time of Figure 2, Figures S4 and S5 of the supplementary material available at Biostatistics online. As shown in Figure 2, similarly in Figures S4 and S5 of the supplementary material available at Biostatistics online, the estimated true EDR increases as the sequencing depth increases; however, the gain of EDR decreases as the sequencing depth increases. When the ratio of targeted sequencing depth to the pilot sequencing depth
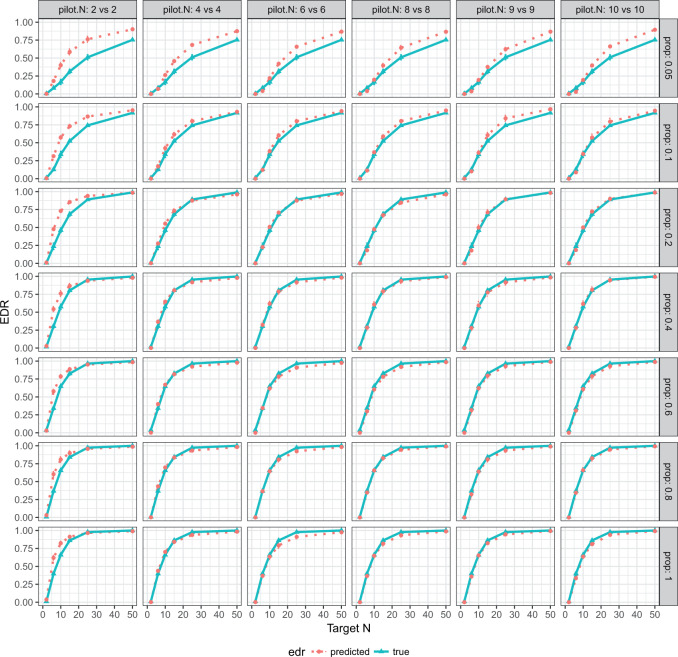
and 0.18). Table 1 shows the RMSEs and computing time of Figure 2, Figures S4 and S5 of the supplementary material available at Biostatistics online. As shown in Figure 2, similarly in Figures S4 and S5 of the supplementary material available at Biostatistics online, the estimated true EDR increases as the sequencing depth increases; however, the gain of EDR decreases as the sequencing depth increases. When the ratio of targeted sequencing depth to the pilot sequencing depth 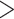 0.4 (i.e. prop
0.4 (i.e. prop 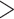 0.4), increasing sequencing depth has almost no effect on the true EDR. The observed trend of true EDR is consistent with the trend of predicted EDR as described in Section 2.1 of the supplementary material available at Biostatistics online. This consistency indicates that our method can estimate EDR prediction well when sequencing depth changes. We also observed that the predicted EDR curves from MethylSeqDesign are close to the true EDR curves, and the performance improves as the sample size of pilot data (
0.4), increasing sequencing depth has almost no effect on the true EDR. The observed trend of true EDR is consistent with the trend of predicted EDR as described in Section 2.1 of the supplementary material available at Biostatistics online. This consistency indicates that our method can estimate EDR prediction well when sequencing depth changes. We also observed that the predicted EDR curves from MethylSeqDesign are close to the true EDR curves, and the performance improves as the sample size of pilot data (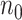 ) increased. The result of Table 1 shows affordable computing time (2–5 min using a regular laptop) for one run under this simulation setting. Secondly, to mimic real situation, we generated
) increased. The result of Table 1 shows affordable computing time (2–5 min using a regular laptop) for one run under this simulation setting. Secondly, to mimic real situation, we generated 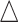 from
from 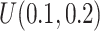 and compared the predicted versus true curves as shown in Figure S6 of the supplementary material available at Biostatistics online. We observed results similar to that in the case of fixed
and compared the predicted versus true curves as shown in Figure S6 of the supplementary material available at Biostatistics online. We observed results similar to that in the case of fixed 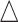 .
.
Fig. 2.
EDR prediction from MethylSeqDesign compared with true EDR under different pilot data sample sizes and sequencing depth. Effect size  is fixed at 0.14. The pilot data sample size per group varied from 2 to 10, and
is fixed at 0.14. The pilot data sample size per group varied from 2 to 10, and 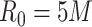 is fixed. The predicted EDRs by the pilot data are shown by the dotted curves. The targeted data sample size per group varied from 2 to 50, and the ratio of targed sample sequencing depth to that of pilot is
is fixed. The predicted EDRs by the pilot data are shown by the dotted curves. The targeted data sample size per group varied from 2 to 50, and the ratio of targed sample sequencing depth to that of pilot is 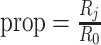 , which varied from 0.05 to 1. The estimated true EDRs by targeted data are in solid curves.
, which varied from 0.05 to 1. The estimated true EDRs by targeted data are in solid curves.
Table 1.
Performance evaluation in simulation study stratified by different effect sizes. Performance evaluation based on RMSE of 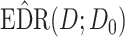 in simulation analysis. Results based on different pilot sample size (
in simulation analysis. Results based on different pilot sample size (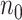 = 2, 4, 6, 8, 9, and 10) are shown in different rows. In the first three columns, stratified analysis is performed as
= 2, 4, 6, 8, 9, and 10) are shown in different rows. In the first three columns, stratified analysis is performed as 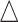 =0.1, 0.14, and 0.18. In the last column, “sOverall” refers to generating
=0.1, 0.14, and 0.18. In the last column, “sOverall” refers to generating 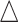 from
from 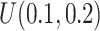
| RMSE (computing time in seconds) | ||||
|---|---|---|---|---|
Pilot 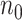
|
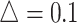
|
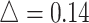
|

|
Overall |
| 2 | 0.27(332) | 0.12(176) | 0.04(171) | 0.10(198) |
| 4 | 0.16(190) | 0.04(175) | 0.04(172) | 0.03(179) |
| 6 | 0.08(150) | 0.02(164) | 0.02(144) | 0.01(148) |
| 8 | 0.05(153) | 0.02(149) | 0.01(154) | 0.02(144) |
| 9 | 0.03(153) | 0.02(151) | 0.02(158) | 0.01(150) |
| 10 | 0.02(116) | 0.01(121) | 0.03(118) | 0.01(120) |
3.4. Cost and benefit analysis and study design
In this subsection, we illustrated two scenarios where our method can guide Methyl-Seq study design. In scenario 1, a desired level of EDR was given, and we would like to find the optimal combination of N and R that achieves the desired EDR with the minimal budget. Whereas in scenario 2, a fixed budget limit was given, and we would like to find the optimal combination of N and R which spends within the budget and maximizes the EDR. We obtained the sequencing cost information from Sequencing and Microarray Facility core at MD Anderson for this example. Price per lane (P) is 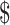 1500 dollars when the total number of reads per lane (D) is set at 250 M with alignment rate (A) of 50%. Library preparation cost per sample (X) including bisulfite conversion treatment is
1500 dollars when the total number of reads per lane (D) is set at 250 M with alignment rate (A) of 50%. Library preparation cost per sample (X) including bisulfite conversion treatment is 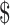 300. The total cost can be written as:
300. The total cost can be written as:
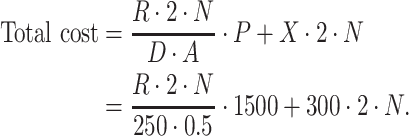 |
(3.4) |
Based on (3.4), we can calculate the cost for any combination of N and R. Given this extra information, the optimal combinations of N and R in both scenarios can be derived. In scenario 1, the optimal N and R combination corresponds to the design with the lowest cost among those with the desired level of EDR; in scenario 2, the optimal design is the one with the highest EDR with costs at most the given budget.
We simulated pilot data (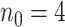 and
and 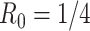 lane) based on the settings described in Section 3.1. The targeted sample size
lane) based on the settings described in Section 3.1. The targeted sample size 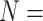 4 to 50 by a gap of 2, and targeted sequencing depth
4 to 50 by a gap of 2, and targeted sequencing depth 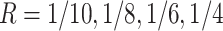 of one lane. The EDR for each
of one lane. The EDR for each 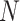 and
and 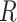 combination is estimated from pilot data and the corresponding cost for each design is calculated. The optimal design can be identified according to different constraints: (i) in scenario 1, we want to achieve at least 80% EDR; (ii) a limited budget
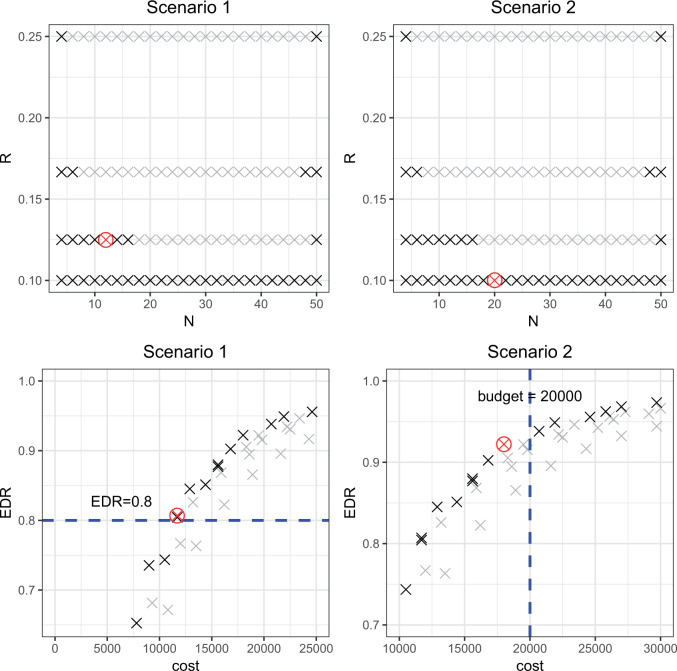
combination is estimated from pilot data and the corresponding cost for each design is calculated. The optimal design can be identified according to different constraints: (i) in scenario 1, we want to achieve at least 80% EDR; (ii) a limited budget 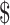 20 000 dollars is given in scenario 2. For any given design (i.e. combination of N and R), if there is no other design achieving higher EDR with lower cost than the current one, it is called an admissible design (in dark color), otherwise it is an inadmissible design (in light color). Figure 3 shows the resulting N–R and cost-EDR corresponding plots. The optimal design is highlighted and circled. In scenario 1, the optimal design to achieve at least 80% EDR is to perform
20 000 dollars is given in scenario 2. For any given design (i.e. combination of N and R), if there is no other design achieving higher EDR with lower cost than the current one, it is called an admissible design (in dark color), otherwise it is an inadmissible design (in light color). Figure 3 shows the resulting N–R and cost-EDR corresponding plots. The optimal design is highlighted and circled. In scenario 1, the optimal design to achieve at least 80% EDR is to perform 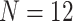 and
and 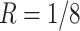 lane and the design will cost
lane and the design will cost 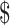 11 700 to achieve EDR = 0.807 (see the left two plots in Figure 3). In scenario 2, with maximal budget of
11 700 to achieve EDR = 0.807 (see the left two plots in Figure 3). In scenario 2, with maximal budget of 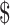 20 000, the optimal design is
20 000, the optimal design is 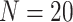 and
and 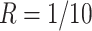 lane, which will cost
lane, which will cost 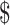 18 000 and achieve EDR = 0.922 (the two plots on the right of Figure 3).
18 000 and achieve EDR = 0.922 (the two plots on the right of Figure 3).
Fig. 3.
Illustration of study design optimization in two scenarios. The first row plots all N and R combinations. The optimal N and R combination is highlighted and circled, the admissible combinations are highlighted in dark and inadmissible ones are in light background. The second row plots the corresponding Budget and EDR relation for N and R combinations. The dashed line marked the targeted EDR in scenario 1 and budget limit in scenario 2.
4. Real data application
4.1. Breast cancer mouse data
In this subsection, we demonstrated the performance of MethylSeqDesign using the Katz’s data (Katz and others, 2015), which was used to investigate the protective risk effect of pregnancy toward breast cancer in a mouse model. The DNA methylation data were from the mammary gland tissue. The sample library was prepared using Agilent SureSelectXT Mouse Methyl-Seq Kit. The kit design covered 109 Mb of Ensemble regulatory features (promoters, promoter flanking regions, enhancers, etc.), CpG islands, known tissue-specific DMR, and open regulatory elements. The dataset was generated with mm9 mouse reference genome (Kent and others, 2002). Aligned reads outside of the targeted regions (provided by Agilent SureSelectXT Mouse Kit) were removed. Data preprocessing was performed by R package “MethyKit.” We only used samples from batch one, which harvested from mammary gland tissue immediately after involutions including five parous and five non-parous mice.
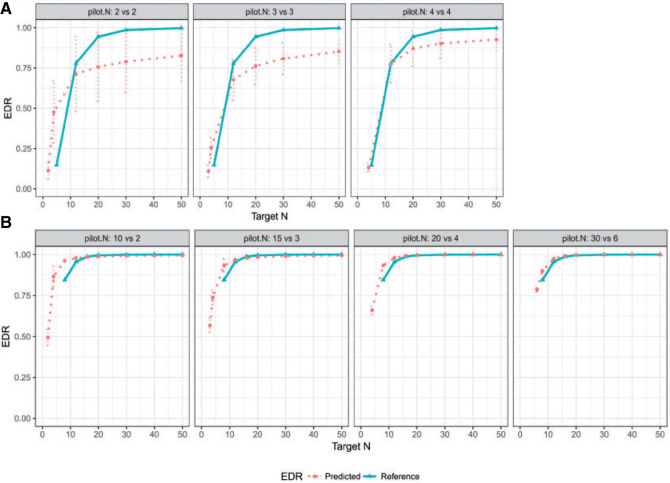
A total of 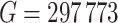 methylation regions of interest (ROI) are pre-defined from the Agilent SureSelectXT kit. We randomly subsampled 2 vs. 2, 3 vs. 3, and 4 vs. 4 samples from the full data as the pilot data, and used MethylSeqDesign to calculate the predicted EDR. We repeated this procedure for 10 times. The predicted EDR from the subsampled data was compared with the reference EDR calculated using the full data. As shown in Figure 4, although the underlying true EDR is unknown, as the sample size of subsampled data increases, the predicted EDR from subsampled data converges to the predicted EDR from the full 5 vs. 5 samples.
methylation regions of interest (ROI) are pre-defined from the Agilent SureSelectXT kit. We randomly subsampled 2 vs. 2, 3 vs. 3, and 4 vs. 4 samples from the full data as the pilot data, and used MethylSeqDesign to calculate the predicted EDR. We repeated this procedure for 10 times. The predicted EDR from the subsampled data was compared with the reference EDR calculated using the full data. As shown in Figure 4, although the underlying true EDR is unknown, as the sample size of subsampled data increases, the predicted EDR from subsampled data converges to the predicted EDR from the full 5 vs. 5 samples.
Fig. 4.
(A) Real data application using mouse pregnancy dataset. (B) Real data application using CLL dataset. The mean and 95% CI of the predicted EDR from subsampled data is shown in dotted curve, and the solid curve is the reference EDR from the full data. As sample size of subsampled data increases, the predicted EDR becomes closer to the reference.
4.2. Chronic lymphocytic leukemia data
Kushwaha and others (2016) studied hypomethylated and hypermethylated regions and how the methylation changes affect gene expression in the oncogenesis of chronic lymphocytic leukemia (CLL) (GEO accession number GSE66167). RRBS was performed for a genome-wide DNA methylation analysis in 43 tumors and 8 controls. We implemented MethylSeqDesign to the dataset using targeted regions defined as 250 bp tiling windows with at least 10 read counts.
Similar to the previous example, the true underlying EDR is unknown in real data. We instead showed the performance of our method by comparing the predicted EDR from smaller sample size to full sample size. Since the sample size in control and tumor groups were unbalanced (number of tumor samples is roughly 5 times more than that of controls), we kept this ratio and randomly subsampled 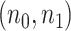 = (2,10), (4,20), and (6,30) from full dataset to treat as pilot data and repeated independent subsampling for 10 times for each
= (2,10), (4,20), and (6,30) from full dataset to treat as pilot data and repeated independent subsampling for 10 times for each 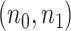 pair (see formulation for unbalanced design in Section 3 of the supplementary material available at Biostatistics online).
pair (see formulation for unbalanced design in Section 3 of the supplementary material available at Biostatistics online).
For full data 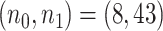 , we also derived predicted EDR and treated it as a reference to compare with predicted EDR from smaller pilot data (shown in Figure 4). Although no underlying truth was available for this application, predicted EDR from our method gave reasonably accurate results, where increased sample size in pilot data generated less variation in predicted EDR curves and converged to the result from large pilot data. In this example, power calculation using
, we also derived predicted EDR and treated it as a reference to compare with predicted EDR from smaller pilot data (shown in Figure 4). Although no underlying truth was available for this application, predicted EDR from our method gave reasonably accurate results, where increased sample size in pilot data generated less variation in predicted EDR curves and converged to the result from large pilot data. In this example, power calculation using 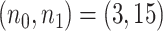 pilot data is roughly sufficient. The required larger sample size is reasonable due to unbalanced design and small sample size in
pilot data is roughly sufficient. The required larger sample size is reasonable due to unbalanced design and small sample size in 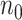 .
.
5. Discussion and conclusion
NGS-based bisulfite sequencing is an increasingly important high-throughput technology to measure genome-wide methylation patterns. An important goal of Methyl-Seq is to detect DMRs, such as promoter regions and transcription biding sites. During the study design stage, it is essential to accurately estimate study power based on appropriate method, particularly when pilot data exist. Given thousands of targeted methylation regions are considered simultaneously to detect differential methylation, it is imperative that the power calculation method is able to appropriately control genome-wide type I error rate, to evaluate genome-wide statistical power and to account for varying DMR effect sizes. To our knowledge, there is no existing method for this purpose. In this article, we proposed a MethylSeqDesign statistical framework to accommodate all three elements mentioned above with FDR, EDR, and estimating effect sizes from pilot data. This method uses a beta-binomial model to account for variations in the Methyl-Seq count data that is due to sampling variations and biological heterogeneities between subjects. We use FDR to control genome-wide type I error rate, and EDR as the genome-wide power. In addition, the use of Wald test statistic enables the transformation of statistics from pilot data to targeted sample size and sequencing depth, which allows two-way power calculation and saves computing time. Our method utilizes the pilot data to estimate the genome-wide distribution of methylation level difference between two groups (effect size) and the proportion of true DMRs, which can be efficiently avoid arbitrary guesses by researchers. Finally, with the specified cost function, we demonstrated how our method guides the selection of proper study designs in two scenarios.
The MethylSeqDesign framework needs a pilot dataset as input. It is crucial that the pilot data are technically similar to the targeted data as possible. If no pilot dataset is available in the local lab, existing datasets on the public domain with similar biological and technical setting (e.g. similar tissue, disease, and sequencing protocols) are the appropriate alternative. In general, a pilot data with larger sample size would yield a superior estimate of EDR. Although pilot sample size required for accurate power calculation depends on biological and experimental variability in each project, from our experience, 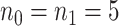 is usually sufficient for accurate power calculation. Our second real example shows that unbalanced
is usually sufficient for accurate power calculation. Our second real example shows that unbalanced 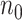 and
and 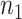 design requires larger pilot sample size.
design requires larger pilot sample size.
In this article, we restricted the power calculation framework to pre-defined targeted regions since only small proportion of CpG sites (5–20%) is available for differential methylation analysis. When the sequence depth is sufficiently deep, the effect on identifying DMRs is minimal, so does on power calculation. However, sequencing depth can still play important roles when sequencing depth is not deep enough. In this article, our method allows a two-dimensional power calculation by considering both sample size and sequencing depth.
In summary, we proposed a MethylSeqDesign framework to deal with the study design and power calculation issues for epigenetic studies of DNA methylation where the ROI are prespecified. As technology advances and sequencing cost decreases, the emergence of more large-scale Methyl-Seq studies will lead to increased demand for Methyl-Seq study design and power calculation. An R package “MethylSeqDesign” is publicly available at https://github.com/liupeng2117/ MethylSeqDesign and all code and data used in this article are available at https://github.com/liupeng2117/MethylSeqDesign_data_code.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
National Institutes of Health (NIH; R01CA190766).
References
- Allison, D. B., Gadbury, G. L., Heo, M., Fernandez, J. R., Lee, C.-K., Prolla T. A., Weindruch, R. (2002). A mixture model approach for the analysis of microarray gene expression data. Computational Statistics & Data Analysis 39, 1–20. [Google Scholar]
- Baylin, S. B. (2005). DNA methylation and gene silencing in cancer. Nature Reviews. Clinical Oncology 2, S4. [DOI] [PubMed] [Google Scholar]
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society B 57, 289–300. [Google Scholar]
- Busby, M. A., Stewart, C., Miller, C. A., Grzeda, K. R. and Marth, G. T. (2013). Scotty: a web tool for designing RNA-Seq experiments to measure differential gene expression. Bioinformatics 29, 656–657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delpu, Y., Cordelier, P., Cho, W. C. and Torrisani, J. (2013). DNA methylation and cancer diagnosis. International Journal of Molecular Sciences 14, 15029–15058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolzhenko, E. and Smith, A. D. (2014). Using beta-binomial regression for high-precision differential methylation analysis in multifactor whole-genome bisulfite sequencing experiments. BMC Bioinformatics 15(1), 215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esteller, M. (2005). Aberrant DNA methylation as a cancer-inducing mechanism. Annual Review of Pharmacology and Toxicology 45, 629–656. [DOI] [PubMed] [Google Scholar]
- Feng, H., Conneely, K. N. and Wu, H. (2014). A Bayesian hierarchical model to detect differentially methylated loci from single nucleotide resolution sequencing data. Nucleic Acids Research 42, e69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadbury, G. L., Page, G. P., Edwards, J., Kayo, T., Prolla, T. A., Weindruch, R., Permana, P. A., Mountz, J. D. and Allison, D. B. (2004). Power and sample size estimation in high dimensional biology. Statistical Methods in Medical Research 13, 325–338. [Google Scholar]
- Hart, S. N., Therneau, T. M., Zhang, Y., Poland, G. A. and Kocher, J.-P. (2013). Calculating sample size estimates for RNA sequencing data. Journal of Computational Biology 20, 970–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz, T. A., Liao, S. G., Palmieri, V. J., Dearth, R. K., Pathiraja, T. N., Huo, Z., Shaw, P., Small, S., Davidson, N. E., Peters, D. G., and others (2015). Targeted DNA methylation screen in the mouse mammary genome reveals a parity-induced hypermethylation of igf1r that persists long after parturition. Cancer Prevention Research 8, 1000–1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent, W. J., Sugnet, C. W., Furey, T. S., Roskin, K. M., Pringle, T. H., Zahler, A. M. and Haussler, D. (2002). The human genome browser at UCSC. Genome Research 12, 996–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kushwaha, G., Dozmorov, M., Wren, J. D., Qiu, J., Shi, H. and Xu, D. (2016). Hypomethylation coordinates antagonistically with hypermethylation in cancer development: a case study of leukemia. Human Genomics 10, 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, E., Beard, C. and Jaenisch, R. (1993). Role for DNA methylation in genomic imprinting. Nature 366, 362–365. [DOI] [PubMed] [Google Scholar]
- Licht, J. D. (2015). DNA methylation inhibitors in cancer therapy: the immunity dimension. Cell 162, 938–939. [DOI] [PubMed] [Google Scholar]
- Markitsis, A. and Lai, Y. (2010). A censored beta mixture model for the estimation of the proportion of non-differentially expressed genes. Bioinformatics 26, 640–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meissner, A., Gnirke, A., Bell, G. W., Ramsahoye, B., Lander, E. S. and Jaenisch, R. (2005). Reduced representation bisulfite sequencing for comparative high-resolution DNA methylation analysis. Nucleic Acids Research 33, 5868–5877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, Y., Figueroa, M. E., Rozek, L. S. and Sartor, M. A. (2014). MethylSig: a whole genome DNA methylation analysis pipeline. Bioinformatics 30, 2414–2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, Y. and Wu, H. (2016). Differential methylation analysis for BS-seq data under general experimental design. Bioinformatics 32, 1446–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulsen, M. and Ferguson-Smith, A. C. (2001). DNA methylation in genomic imprinting, development, and disease. The Journal of Pathology 195, 97–110. [DOI] [PubMed] [Google Scholar]
- Robertson, K. D. (2005). DNA methylation and human disease. Nature Reviews Genetics 6, 597–610. [DOI] [PubMed] [Google Scholar]
- Schumacher, A., Kapranov, P., Kaminsky, Z., Flanagan, J., Assadzadeh, A., Yau, P., Virtanen, C., Winegarden, N., Cheng, J., Gingeras, T.. and others (2006). Microarray-based DNA methylation profiling: technology and applications. Nucleic Acids Research 34, 528–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai, P.-C. and Bell, J. T. (2015). Power and sample size estimation for epigenome-wide association scans to detect differential DNA methylation. International Journal of Epidemiology 44, 1429–1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, H., Wang, C. and Wu, Z. (2015). PROPER: comprehensive power evaluation for differential expression using RNA-seq. Bioinformatics 31, 233–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.