Mechanism of C-type inactivation in the hERG potassium channel

C-type inactivation in hERG is associated with an asymmetrical constricted-like conformation of the selectivity filter.

Abstract

The fast C-type inactivation displayed by the voltage-activated potassium channel hERG plays a critical role in the repolarization of cardiac cells, and malfunction caused by nonspecific binding of drugs or naturally occurring missense mutations affecting inactivation can lead to pathologies. Because of its impact on human health, understanding the molecular mechanism of C-type inactivation in hERG represents an advance of paramount importance. Here, long–time scale molecular dynamics simulations, free energy landscape calculations, and electrophysiological experiments are combined to address the structural and functional impacts of several disease-associated mutations. Results suggest that C-type inactivation in hERG is associated with an asymmetrical constricted-like conformation of the selectivity filter, identifying F627 side-chain rotation and the hydrogen bond between Y616 and N629 as key determinants. Comparison of hERG with other K⁺ channels suggests that C-type inactivation depends on the degree of opening of the intracellular gate via the filter-gate allosteric coupling.

INTRODUCTION

The human ether-a-go-go-related gene K⁺ channel (hERG) is a voltage-activated channel known for its role in the repolarization of cardiac cells (1, 2). A hallmark of hERG channels is an extremely fast and atypical C-type inactivation (3–5), critical for their normal physiological function in repolarizing the cardiac action potential (6). From a pharmacological standpoint, the C-type inactivated state of hERG forms a promiscuous binding site for a large set of chemically diverse drugs (7). Nonspecific binding of drugs can lead to long QT syndrome (2, 8, 9), a disorder of ventricular repolarization associated with life-threatening arrhythmias. Knowledge of the inactivated state could help screening compounds for their impact on hERG activity, an indispensable step for drug development (7). While the first experimental atomic structure of the hERG channel from single-particle cryo–electron microscopy (cryo-EM) recently became available (10), it did not explain the structural basis of inactivation.

At the atomic level, our understanding of K⁺ channel C-type inactivation mainly relies on an important prototypical model, the pH-activated KcsA channel (K channel of streptomyces A). Strong evidence from x-ray crystallography (11–15), nuclear magnetic resonance spectroscopy (16, 17), and molecular dynamics (MD) simulations (18–21) indicates that the C-type inactivation of the KcsA K⁺ channel is associated with a structural constriction of the selectivity filter. The conductive-to-constricted transition of the selectivity filter is allosterically enhanced by the opening of the intracellular activation gate, which indirectly set the inactivation rate (19). However, the molecular mechanism of voltage-gated K⁺ channels (Kv) in general, and of the hERG channel, in particular, remains largely unknown. In view of the high similarity of the pore domain (PD) of K⁺ channels, and by analogy with the well-documented case of the KcsA channel, we hypothesize that the molecular mechanism of C-type inactivation process in the hERG channel is caused by some constricted-like conformation of the selectivity filter. We have tested this hypothesis by characterizing a number of mutations in and near the selectivity filter that interfere with C-type inactivation using MD simulations, free energy landscape calculations, and electrophysiological measurements.

RESULTS

Unbiased MD simulations were first carried out to provide an overview of the channel by starting from the recently determined cryo-EM structure [Protein Data Bank (PDB) ID: 5VA2], which displays an open activation gate with a canonical conductive filter (10). In three multi-microsecond trajectories, the selectivity filter consistently underwent a rapid (within 1 μs or less) spontaneous transition toward a constricted-like conformation (fig. S1). However, in contrast with the KcsA channel (19), the filter constriction in the hERG channel is asymmetrical (Fig. 1, A to C). An asymmetric conformation of the hERG channel was also observed in MD simulations recently (22), though some differences with respect to the conformation of F627 are noted. There are also recent reports that asymmetric constriction of the filter occurs for the C-type inactivation in the Kv_1.2 and K_2P channels (23, 24). Although the structural details are different between our study and previous reports, the asymmetric constriction is emerging as a common phenomenon for C-type inactivation among a number of potassium channels.

Fig. 1. Asymmetrical constricted conformation of the selectivity filter.

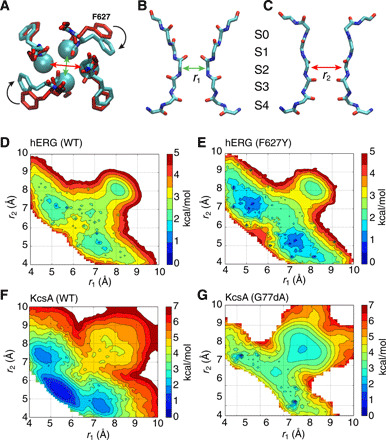
(A to C) The C2 model based on an average structure (cyan) symmetrized by swapping between two opposite subunits shown from the top view is overlaid with the cryo-EM structure (red) (A), two side views highlighting different pairs of subunits with ion-binding sites marked (B and C). (D to G) 2D-PMF of the hERG and KcsA channels reveals local free energy basins corresponding to a general asymmetrically constricted conformation. The horizontal and vertical reaction coordinates, respectively, represent the cross-subunit distance between the Cα atoms of glycine (G626 in hERG or G77 in KcsA) of diagonally opposed subunits A and C (r₁), and B and D (r₂). Results for WT KcsA (F) and KcsA^D-ala77 (G) from a similar PMF calculation were previously reported (18).

The correlation between the side-chain orientation of F627, a residue linked to hERG inactivation (10, 25), and the constriction of the selectivity filter is observed in all simulations. The F627 side chain seems to play a structural role similar to that of the inactivating water molecules in KcsA in stabilizing the inactivated structure. The binding of three inactivating water molecules to fill the space behind the constricted filter (fig. S2) is indispensable to stabilize the constricted conformation in KcsA (16, 18–20). In hERG, the F627 side-chain rotation of two diagonally opposed subunits partially fills the space behind the selectivity filter of the other two subunits, forming favorable van der Waals contacts with a “second layer” of residues to stabilize this asymmetric constriction (fig. S3). This stabilization is weaker than the effect of inactivating water molecules on KcsA (18, 20), consistent with the observation that the recovery rate from inactivation (repriming) is slower for KcsA than for hERG (4, 20).

To quantitatively assess the propensity of this constricted-like conformation of the selectivity filter of the hERG channel, we calculated the free energy landscape or potential of mean force (PMF) using MD simulations (fig. S4). The projected two-dimensional (2D) PMF along the G626 Cα-Cα cross-subunit distances A-C (r₁) and B-D (r₂) is shown in Fig. 1D. The 2D-PMF clearly displays two local free energy minima corresponding to a nonconductive asymmetrical conformation, which are slightly more stable than the conductive conformation. The local minimum along the diagonal corresponds to a symmetrical-like conductive conformation of the selectivity filter (both cross-subunit distances of ~8 Å), while the two off-diagonal slightly deeper minima correspond to the asymmetrical conformations (one cross-subunit distance around 5 Å and the other 7 Å). The 2D-PMF is consistent with the dynamical trajectories displayed in fig. S1, where the nonconductive asymmetrical constricted conformation of the filter first appears at about tens to hundreds of nanoseconds and then persists for several microseconds.

Similar asymmetrical conformations of the filter are also observed as local free energy minima for the F627Y mutant of hERG (Fig. 1E), as well as for the wild-type (WT) KcsA (Fig. 1F) and KcsA^D-ala77 synthetic channels (Fig. 1G) in our previous report (18, 20), which indicates that the existence of such asymmetric constriction is a general property of the selectivity filter among K⁺ channels. A model based on the KcsA channel shows that a symmetrically constricted state of hERG is energetically unstable because of the absence of favorable van der Waals contacts between the selectivity filter and the “YF” motif in the second layer (fig. S3).

To validate the MD calculations, we examined a number of key mutations known to have an impact on C-type inactivation in the hERG channel. The first mutant examined is F627Y, which is known to enhance C-type inactivation (10, 25). As shown in Fig. 2, the mutation favors the constricted filter. Compared to WT, the PMF local minimum in F627Y clearly shifts toward a constricted state (this is only slightly favored in WT). This behavior was confirmed by electrophysiological recordings showing that the C-type inactivation is faster and much more complete compared to WT (Fig. 2 and fig. S5). The 2D-PMF shows that the filter was constricted to a similar asymmetrical conformation as WT. However, the mutation introduces a new hydrogen bond between Y627 and S620 from the adjacent subunit (Fig. 2), which contributes to the stability of the constricted conformation and enhances the C-type inactivation.

Fig. 2. Impacts of multiple mutations in hERG channel.

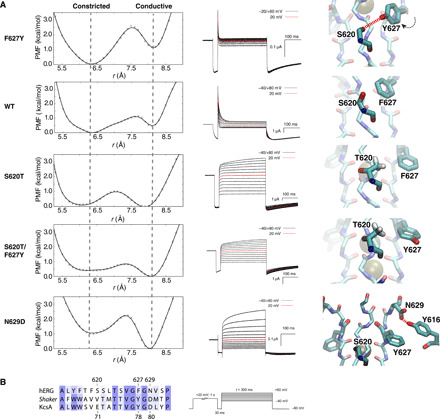
(A) Computational and experimental measurements for WT and mutants. Left: 1D-PMFs along the constriction coordinate r (via integration of the 2D PMF). Middle: Representative currents in electrophysiological recordings for mutants and WT (in 10-mV increments). Right: Side view of representative conformations. (B) Sequence alignment among hERG, Shaker, and KcsA channels for the residues in or close to the selectivity filter (left) and the triple-pulse protocol to measure the inactivation of hERG channel (right).

The second mutant examined is N629D, which is known to abolish C-type inactivation (26). According to the calculated free energy landscape shown in Fig. 2, the N629D filter prefers to adopt a conductive conformation—the local minimum in the PMF is switched to the conductive state. This is the opposite effect of F627Y. In Fig. 2, representative snapshots from the local free energy minima correspond to the canonical conductive filter conformations, all displaying stable hydrogen bonding between D629 and Y616. On the basis of this observation, we suggest that in the WT channel, the structural restraint from this tyrosine-asparagine hydrogen bond must be released to enable the constricted conformation of the selectivity filter. When this bond is replaced by the stronger tyrosine-aspartate hydrogen bond in all four subunits, it substantially increases the stability of the conductive conformation.

Furthermore, S620T, which decreases C-type inactivation (27), displays a PMF where the constricted state is less favorable than the conductive state (Fig. 2). In this case, the free energy basin of the S620T mutant is shifted toward the conductive state, consistent with the functional measurements showing that C-type inactivation of T620 is essentially abolished (Fig. 2). Our simulation provides a clear atomistic explanation for this notable phenotype. The side-chain rotation of F627 is blocked in S620T because of the steric effect of the methyl group of T620 from the neighboring subunit (Fig. 2). In addition, the hydroxyl group of T620 could form a hydrogen bond with the backbone amide group of F627 within the same subunit, forcing the methyl group of T620 to point toward the side chain of F627 from the adjacent subunit and then to block its rotation.

Considering that the mutations S620T and F627Y show opposite effects on C-type inactivation, and residues F627 and S620 are in contact when the filter is constricted, a double mutant S620T/F627Y was engineered to test the combined impact of these two residues. The calculated free energy landscape shows that the double mutant S620T/F627Y prefers to be conductive, its effect being similar as the single mutant S620T. The methyl group of T620 sterically blocks the side-chain rotation of Y627, preventing the side-chain rotation of Y627 that allows the formation of a hydrogen bond between Y627 and T620 (fig. S6). This explains why S620T is dominant while F627Y displays a silent phenotype in the double mutant. Functional measurements show that the double mutant S620T/F627Y abolishes inactivation like the single mutant S620T—as predicted by the computational analysis (Fig. 2). This provides strong evidence that the side-chain rotation of F627 is indeed critical for the constriction of the selectivity filter. The side-chain rotation of F627 is a key factor underlying the molecular basis of C-type inactivation in hERG.

The noninactivating double mutant G628C/S631C was also examined. This construct introduces a disulfide bond near the extracellular end of the selectivity filter (4). For this reason, the underlying mechanism preventing inactivation is expected to be different. As indicated by a multi-microsecond MD trajectory, this double mutant leads to a structural rearrangement with a K⁺ bound in the S3 site and a widening of S1 and S2 (see fig. S7 and movies S1 and S2), suggesting that the predominant state of the double mutant locked by the disulfide bond remains conductive but less selective. These substantial structural differences serve as a caveat to the interpretation of mutagenesis results affecting C-type inactivation.

A comparison of hERG with other K⁺ channels, the bacterial KcsA channel and the voltage-activated Shaker channel, sheds additional light on the factors that control the extent of C-type inactivation. It is known that KcsA (13, 28, 29) inactivates less than hERG (6) but more than Shaker (30). For the same degree of opening of the intracellular activation gate, the PMF calculations of Fig. 3 show that the filter of the hERG channel favors a constricted conformation, the filter in Shaker channel favors the conductive conformation, and the KcsA filter exhibits an intermediate behavior. Thus, the free energy landscapes indicate that the relative stability of the constricted filter conformation directly correlates with the propensity of C-type inactivation displayed by these three channels in functional experiments.

Fig. 3. Comparison of the free energy landscape for the hERG, KcsA, and Shaker channels.

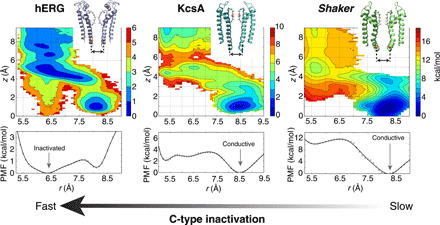
The opening of the intracellular gate was selected to be almost the same for all these channels (16 to 18 Å). In the 2D-PMFs, the horizontal reaction coordinate r describes the constriction of the selectivity filter (defined as the average cross-diagonal distance between the Cα atoms of the central glycine equivalent to G77 in KcsA). The vertical reaction coordinate z indicates the position of the external K⁺ ion along the pore relative to its center of the selectivity filter. The bottom panel shows the integrated 1D-PMFs along r. The PMF for WT KcsA from a similar calculation was reported previously (18). The PMF for Shaker was calculated using a model based on the x-ray structure (PDB ID: 2R9R) of the Kv_1.2/Kv_2.1 chimera channel (57).

DISCUSSION

Before discussing these results any further, it is important to acknowledge the limitations of the simulation approach. Despite their high numerical precision, they do not account for the inherent complexity of all the known and unknown factors affecting the kinetics of a real hERG channel in a biological membrane. Thus, it is prudent and advisable to limit our interpretation to the most salient qualitative trends displayed by the computations. From this perspective, the impact of most of the mutations examined here appears to be mediated by two major mechanisms. Most of the mutants either facilitate (F627Y) or block (S620T and S620T/F627Y) the side-chain rotation of F627 that allows the asymmetric constriction of the filter. Only the mutant N629D affects inactivation by tuning the strength of a hydrogen bond (Y616-D629) that enhances the stability of the conductive conformation. On the basis of these observations, we suggest that the constricted conformation in hERG is mainly controlled by two molecular determinants: the hydrogen bond between Y616 and N629 and the side-chain rotation of F627. The former stabilizes the conductive conformation, slowing down the C-type inactivation, while the latter triggers the asymmetric constriction of the selectivity filter, facilitating inactivation. This is consistent with the importance of hydrogen bonds noted in other studies (31–33). The conformational change associated with C-type inactivation is also coupled to the configuration of the K⁺ ions in the selectivity filter (Fig. 3). The constriction of the selectivity filter is accompanied by an outward shift of a K⁺ from the site S2 to the site S1. Analysis of the displacement charge associated with the conformational change indicates that a positive membrane potential favors the constricted filter in qualitative agreement with experiment (fig. S5).

The nearly complete inactivation of hERG is consistent with the modest changes seen in the calculations because small changes in relative free energy between the constricted and conductive conformations of the filter would be reflected by a very large population shift of these two states (Fig. 2). However, the corresponding activation free energy barriers are small, and the transition rates estimated from Kramers-Smoluchowski theory (34) are considerably larger than experimental values. This does not indicate that the MD simulations are fundamentally wrong, but rather that the experimentally observed kinetics is controlled by some slow molecular process other than the constriction of the filter. In a previous study of KcsA (19), it was observed that the kinetics underlying activation/inactivation gating reflect a rapid (within 1 μs or less) conductive-to-constricted transition of the selectivity filter that is allosterically controlled by the slow opening of the intracellular gate. It appears that this situation is also present in the hERG channel.

According to the present analysis, C-type inactivation in the hERG channel is associated with a structural transition of the conductive selectivity filter toward an asymmetric nonconductive constricted-like conformation. Although there are some important differences, the overall picture may be understood by leaning on our previous studies of C-type inactivation in the KcsA channel (18–21). While the analysis points to a number of commonalities in the mechanism underlying C-type inactivation in all K⁺ channels, the wide disparity in the phenotype of C-type inactivation in different K⁺ channels remains somewhat confounding. For example, hERG (6) inactivates more than the KcsA channel (13, 28, 29), but KcsA itself inactivates more than the voltage-activated Shaker channel (30). As demonstrated by the free energy landscape for these three different channels calculated for the same degree of opening of the intracellular activation gate (Fig. 3), the relative stability of the constricted filter conformation correlates with propensity of C-type inactivation displayed by these channels in functional experiments. Given similar degrees of opening at the activation gate (the intracellular inner helical bundle), PMF calculations show that the filter of the hERG channel favors a constricted conformation, whereas the filter in Shaker channel favors the conductive conformation. Under equivalent conditions, the KcsA filter displays an intermediate behavior. The free energy difference between the conductive and constricted conformations for three channels is consistent with the observation that inactivation of hERG is fast, KcsA is moderate, and Shaker is the slowest (and the least complete). Furthermore, the relative free energy between conductive and constricted states correlates well with the opening of the intracellular gate (fig. S8).

KcsA and hERG are both homotetramer but appear to differ crucially in terms of the constricted selectivity filter conformation: symmetrical for KcsA and asymmetrical for hERG. One noteworthy structural difference between KcsA and hERG in the surrounding of the selectivity filter is the “WW” motif in KcsA, which is highly conserved in many K⁺ channels but replaced by YF in the hERG channel. The two large tryptophans side chains located in a second layer of residues packing around the selectivity filter structurally serve as a scaffold, or a “cuff” (35), holding up the filter. In the hERG channel, the two tryptophans are replaced by two residues that are considerably less bulky (Y616 and F617), leaving unoccupied empty space around the selectivity filter. A hypothetical fourfold symmetric constricted model of hERG generated using the KcsA channel as a template reveals the presence of a strong repulsion among the four subunits in the selectivity filter and no favorable van der Waals contacts between the selectivity filter and the YF motif in the second layer (fig. S3), showing why the symmetrically constricted structure is energetically unstable. In contrast, an asymmetric conformation, with two diagonally opposed subunits slightly more constricted than in the fourfold constricted KcsA structure, provides favorable van der Waals contacts between the side chains of F627 and the YF motif from a pair of subunits that stabilize this conformation of the hERG filter (fig. S3).

Despite the strong propensity of the hERG channel to undergo kinetically invisible C-type inactivation as only little K⁺ current is shown immediately following membrane depolarization, the first atomic structure obtained by cryo-EM presents a canonical fourfold symmetric conductive selectivity filter. A comparison between the density extracted from the cryo-EM structure (PDB ID: 5VA2) and a computational map extracted from MD simulation clearly shows that the two structures are different (fig. S1, E to G). It is not clear what prevents hERG from undergoing C-type inactivation under cryo-EM conditions, while the same structure spontaneously and rapidly transits toward an asymmetric constricted-like conformation during MD simulations. However, a number of different factors (e.g., temperature and detergent) could have a critical impact on the conformational preference of the channel.

Previous studies indicated that there is a strong and mutual allosteric coupling between the intracellular gate and the selectivity filter among K⁺ channels (13, 36–39). The implication is that there is not only a significant impact of the intracellular gate opening on the conformational preference of the selectivity filter, but, conversely, that there is also an influence of the conformational stability of the selectivity filter on the behavior of the intracellular gate. In our PMF calculations for hERG in its open structure, there is indeed a modest but clear difference between WT and S620T or S620T/F627Y. The relatively higher stability of the conductive filter in S620T (or S620T/F627Y) could also change the degree of opening of the gate or slow down its opening; thus, the mutational effects could be magnified in the kinetics observed in experiments.

MATERIALS AND METHODS

MD simulation

Atomic models of the WT hERG were constructed on the basis of the cryo-EM structure (PDB ID: 5VA2) (10). Ten missing residues (residues 578 to 582 and 598 to 602) were added by using VMD psfgen plugin (40). For all MD simulations, the channel, comprising the PD (trajectories 1 and 2) or the PD plus the four voltage-sensing domains (PD + VSDs) (trajectory 3 shown in fig. S1A), was embedded in a bilayer of 3POPC:1POPG lipids and solvated in 150 mM KCl using the web service CHARMM-GUI (41, 42). Most residues were assigned their standard protonation state at pH 7. The total number of atoms in the MD systems is on the order of 60,000 (PD only) or 126,000 (PD + VSDs). The CHARMM force field PARAM36 for proteins (43–45), lipids (46), and ions (47) was used. Explicit water was described with the TIP3P model (48). All the simulations were performed under NPT (constant number of particle N, pressure P, and temperature T) conditions at 310 K and 1 atm, and periodic boundary conditions with electrostatic interactions were treated by the particle mesh Ewald method (49) and a real-space cutoff of 12 Å. The simulations used a time step of 2 fs, with bond distances involving hydrogen atoms fixed using the SHAKE algorithm (50). After minimization and equilibrations with harmonic positional restraints, the equilibrated systems were simulated at a microsecond time scale either using NAMD version 2.13 (51) or on the special purpose computer Anton (52). The conformational change of the selectivity filter was monitored by following the cross-subunit distance between the G626 Cα atoms of the two pairs of diagonally opposed subunits. In unbiased simulations, the asymmetric constriction of the filter is very similar in the PD-only system (trajectories 1 and 2 shown in fig. S1A) and the PD + VSD system (trajectory 3 in fig. S1A).

Free energy landscapes

Two-dimensional PMF calculations were performed using NAMD 2.12 (51), with respect to the two coordinates that were validated in our previous computational studies for the other K⁺ channel (KcsA) (18–20). One reaction coordinate r describes the width of the selectivity filter and is defined as the average cross-subunit distance between the Cα atoms of G626, whereas the other reaction coordinate z indicates the position of the external K⁺ ion along the z axis relative to the center of the selectivity filter. The region of interest in the (r, z) space was covered by a grid of equally spaced umbrella sampling (US) windows (fig. S4). To improve the statistical sampling, the US calculations were performed using Hamiltonian replica-exchange MD (US/H-REMD) (53, 54). Controlling the K⁺ ion position in the US/H-REMD calculations is necessary for computational efficiency because its movements through the binding sites S0-S1-S2 is tightly coupled with the constricted-to-conductive transition of the filter. The combination of distance (r) and position of K⁺ ion (z) has been proved as proper reaction coordinates to efficiently characterize the conformational free energy landscape of the selectivity filter (18–20). The system with PD only was used for all the 2D-PMF calculations.

For WT, some initial coordinates for the US windows were taken from the unbiased trajectories, and initial coordinates for the missing windows were obtained by driven MD simulations along the reaction coordinates to the space of the missing windows. Different from previous studies (20), there is no restraint on water molecules to access or leave the inactivating water binding site behind the selectivity filter, and all the 97 windows were extended to 100 ns. For mutants N629D, F627Y, S620T, and S620T/F629Y, the initial coordinates for the US windows were mutated on the basis of WT, and all windows were extended to 130 or 140 ns (only the last 100 ns was used for PMF calculation). The total aggregate simulation time for all US/H-REMD calculations is 62 μs. Exchange attempts were made every 500 steps (or 1 ps of simulation time), and neighboring windows were swapped if the Metropolis Monte Carlo exchange probability was satisfied. Windows were unbiased using the weighted histogram analysis method (55, 56), which only required that the US windows were generated according to Boltzmann statistics. Besides 2D-PMF for the (r, z) space, a different 2D-PMF was constructed for the two coordinates (r₁ and r₂) representing the cross-subunit distance between the Cα atoms of G626 of diagonally opposed subunits A and C as well as B and D, which were also symmetrized by swapping between two neighboring subunits—that is, A and B or C and D. The PMF for Shaker was generated using a similar computational protocol using a model based on the x-ray structure (PDB ID: 2R9R) of the Kv_1.2/Kv_2.1 chimera channel (57).

Displacement charge calculation

The membrane potential affects the relative free energy of two different conformations (a and b) of a membrane protein via changes in the average displacement charge

$$\langle \Delta Q_{\mathrm{d}}\rangle =\langle {\sum }_i{q}_i\frac{z_i}{L_z}\rangle (\mathrm{\text{a}})-\langle {\sum }_i{q}_i\frac{z_i}{L_z}\rangle (\mathrm{\text{b}})$$ (1)

where q_i are the partial charge, z_i are the unwrapped z coordinate of all the atoms, and L_z is the length of the simulation box along the z direction (58). The averages are taken over the conformations a and b corresponding to the constricted and conductive states, respectively. The average displacement charge of the WT hERG at the constricted state and the conductive state was calculated using Eq. 1 from 5-ns simulations; 400 snapshots at every 10 ps of the last 4-ns trajectory were used for the calculation. The starting configurations of the two states were extracted from the corresponding US window trajectories with harmonic restraints centered at r = 6.25 Å and z = 5.25 Å, and r = 8.25 Å and z = 1.25 Å, respectively. Harmonic restraints of 1 kcal/mol per square angstrom were applied to the two reaction coordinates (r, z) during these simulations as in the PMF calculations. The change in the displacement of charge going from the conductive and constricted conformations, 〈ΔQ_d〉, is about 0.7 unit charge. At +100 mV, this corresponds to a population shift of about 14 favoring the constricted state, in qualitative agreement with experiment (fig. S5).

Molecular biology and electrophysiological recordings

The complementary DNA of the full-length hERG channel was cloned into the pSP64 Poly(A) vector. Point mutations were generated using site-directed mutagenesis. All plasmids were linearized by restriction enzyme Eco RI. Complementary RNA was transcribed in vitro using the mMESSAGE mMACHINE SP6 Transcription Kit (Ambion, Invitrogen) and was last dissolved in ribonuclease-free water at a concentration of approximately 1 mg/ml. Each collagenase-defolliculated Xenopus laevis oocyte was injected with 50 nl of RNA. Injected oocytes were incubated for 1 to 2 days at 18°C in the standard oocytes solution containing the following components: 100 mM NaCl, 5 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 10 mM Hepes at pH 7.4, and gentamycin (50 μg/ml).

Ionic currents were recorded at room temperature on a cut-open oocyte voltage-clamp setup (59) with a CA-1 amplifier (Dagan Corporation, Minneapolis, MN). Current data were filtered at 10 kHZ with a low-pass four-pole Bessel filter within the amplifier. An in-house software (GPatch), provided by F. Bezanilla, was used to acquire and analyze data. The external solution contained 12 mM K–methanesulfonic acid (MES), 2 mM Ca-MES, 10 Hepes, and 108 mM N-methyl-d-glucamine–MES at pH 7.4; the internal solution contained 120 mM K-MES, 2 mM EGTA, and 10 mM Hepes at pH 7.4.

To study the inactivation of the WT and mutant channels, we used a triple-pulse protocol, as inactivation is much faster than activation in hERG (4). From a holding potential of −80 mV, a 1-s depolarizing pulse to +20 mV was applied to activate the channels followed by a short 30-ms hyperpolarizing pulse to −80 mV allowing the channels to recover rapidly from inactivation. Then, 300-ms test pulses ranging from −40 to +80 mV (−20 to +60 mV for the F627Y mutant due to its low expression level in oocytes) were applied to measure the reinactivation before major deactivation happened. Last, the voltage returned to the holding potential. The reinactivation currents of the WT and F627Y channels were fitted by a single exponential function to get the time constants τ of inactivation at different depolarizing potentials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/5/eabd6203/DC1

View/request a protocol for this paper from Bio-protocol.