Layer- and gate-tunable spin-orbit coupling in a high-mobility few-layer semiconductor

Rashba spin-orbit coupling in atomically thin InSe is varied layer by layer and by tuning out-of-plane electric field.

Abstract

Spin-orbit coupling (SOC) is a relativistic effect, where an electron moving in an electric field experiences an effective magnetic field in its rest frame. In crystals without inversion symmetry, it lifts the spin degeneracy and leads to many magnetic, spintronic, and topological phenomena and applications. In bulk materials, SOC strength is a constant. Here, we demonstrate SOC and intrinsic spin splitting in atomically thin InSe, which can be modified over a broad range. From quantum oscillations, we establish that the SOC parameter α is thickness dependent; it can be continuously modulated by an out-of-plane electric field, achieving intrinsic spin splitting tunable between 0 and 20 meV. Unexpectedly, α could be enhanced by an order of magnitude in some devices, suggesting that SOC can be further manipulated. Our work highlights the extraordinary tunability of SOC in 2D materials, which can be harnessed for in operando spintronic and topological devices and applications.

INTRODUCTION

In a crystal, the twofold degeneracy of spins is protected by the combined inversion symmetry in both space and time. In the well-known Zeeman effect, an external magnetic field breaks the time reversal symmetry (TRS) and splits the spin degeneracy by gμ_BB, where g is the gyromagnetic ratio and μ_B is Bohr magneton. Alternatively, spin degeneracy can be lifted by spin-orbit coupling (SOC) when spatial inversion symmetry is broken, even in the absence of a TRS-breaking magnetic field. In crystals lacking structural inversion symmetry, the SOC coupling is of the Rashba form, $H_{\mathrm{R}}=\raisebox{1ex}{$\mathrm{\alpha }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\hslash }$}\right.(\widehat{\mathit{z}} \mathit{\times } \mathit{p})\bullet \mathbf{\sigma }$, where α is the Rashba parameter, p is the momentum, and σ is the Pauli spin matrices (2, 3). As a result, the energy band of the crystal is spin-split; within each subband, the charges’ spin is locked to their direction of momentum (Fig. 1A). A large SOC can be used to manipulate spins and generate interesting phenomena (4–6), such as the spin Hall effect, spin-orbit torque, and topological phenomena including the quantum spin Hall effect and quantum anomalous Hall effect.

Fig. 1. Crystal structure, device schematics, and magnetotransport data.

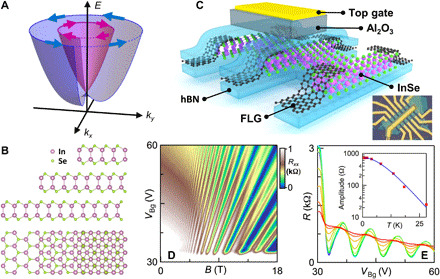
(A) Rashba SOC–induced spin splitting of bands. (B) Side and top views of the crystalline structure of γ-InSe. The middle and bottom layers are partially exposed for better visualization [images created using VESTA software (1)]. Inset: Optical image of a device. (C) Schematics of device structure. (D) Landau fan R_xx(V_Bg, B) of device D1 from B = 0 to 18 T. (E) SdH oscillations at B = 10 T for temperatures ranging from 0.6 to 28 K. Inset: Amplitude of the oscillations as a function of temperature. The line is a fit to the Lifshitz-Kosevich formula.

The advent of two-dimensional (2D) materials provides platforms with unprecedented opportunities for SOC tuning. For instance, sizable SOC can be “endowed” to graphene by proximitization with transition metal dichalcogenides (7–19), and intrinsic SOC in 2D semiconductors has been studied by weak-antilocalization measurements (20–22). Here, we exploit the atomically thin sheets of InSe to demonstrate the extraordinary tunability of SOC in 2D materials.

InSe is a layered semiconductor with thickness-dependent bandgaps that range from 1 to 3 eV. Its direct bandgap (except in monolayers), combined with extraordinarily high mobility (23, 24), makes it a very attractive electronic and optoelectronic material. The 2D unit cell of an InSe monolayer is composed of two vertically aligned In atoms, sandwiched between two planes of Se atoms. When projected onto a plane, an InSe monolayer forms a honeycomb lattice, where the metallic and chalcogen atoms occupy the two sublattices, respectively (Fig. 1B). Bulk crystals of InSe are found in several polytypes, including γ, β, ε, and δ phases (25). In this study, crystals are grown by the Bridgeman technique and are confirmed by a transmission electron microscope (TEM) to be predominantly γ phase with rhombohedral stacking, though stacking faults and nanotwins are rather common (see the Supplementary Materials). The γ phase belongs to the space group R3m and is noncentrosymmetric; this lack of inversion symmetry is a key ingredient that allows SOC-induced spin-split bands in the absence of an external magnetic field. Although SOC in InSe has been measured via weak-localization studies on relatively thick flakes (20, 22), the values obtained have relatively large error bars, while the single-gated devices do not allow independent tuning of the Rashba SOC.

Our devices consist of atomically thin InSe sheets with thicknesses ranging from four to 10 layers (Table 1) and sandwiched between hexagonal BN (hBN) layers, with few-layer graphene (FLG) contacts, a silicon back gate, and a metal top gate (Fig. 1C). By varying voltages applied to the top gate V_Tg and back gate V_Bg, we can independently control the charge density $n=\frac{1}{e}(C_{\text{Bg}}{V}_{\text{Bg}}+C_{\text{Tg}}{V}_{\text{Tg}})$ and out-of-plane electric field $E_{\perp }=\frac{C_{\text{Tg}}{V}_{\text{Tg}}-C_{\text{Bg}}{V}_{\text{Bg}}}{2{\mathrm{\epsilon }}_0}$. Here, C_Tg and C_Bg are capacitance per unit area between the gates and InSe, e is the electron charge, and ε₀ is the permittivity of vacuum. We note that the application of E_⊥ is particularly crucial for modulation of Rashba SOC strength, which, depending on the direction of application, can either further break the inversion symmetry or compensate for the built-in asymmetry of the lattice.

Table 1. Device parameters.

Device	Estimated thickness	α0 (10−11 eV m)	α′ (10−2 e nm2)
D1	Six-layer	3.5	3.0
D2	Four-layer	0.6	−1.2
D3	Seven-layer	0.2	−1.2
D3	Eight-layer	0.15	−1.15
D3	Nine-layer	0.08	−1.1
D4	Six-layer	0.3	1.1
D5	Four-layer	0.8	1.3

RESULTS AND DISCUSSION

Figure 1D presents the longitudinal resistance R_xx of device D1, which has a thickness of ~6 layers, as a function of back gate voltage and magnetic field B. A prominent Landau fan is observed. Shubnikov de Haas (SdH) oscillations start at B as low as 2.5 T, indicating a quantum mobility exceeding 4000 cm²/Vs, which is the highest value reported to date. At B > 12 T, quantized plateaus for filling factor ν < 10 are observed. To estimate the effective mass of the charge carriers, we extract the amplitude A of the SdH oscillations at B = 10 T at different temperatures (Fig. 1E). From the Lifshitz-Kosevich equation, A = CT/sinh(bT), where T is the temperature, $b=\frac{2{\mathrm{\pi }}^2{k}_{\mathrm{B}}T}{\mathrm{\hslash }{\mathrm{\omega }}_{\mathrm{c}}}$, ${\mathrm{\omega }}_{\mathrm{c}}=\frac{\text{eB}}{m^{*}{m}_0}$ is the cyclotron frequency, m* is the reduced effective mass, m₀ is the rest mass of electrons, k_B is the Boltzmann constant, ℏ is the reduced Planck constant, and C is a constant, we estimate that m* ~ 0.14, in excellent agreement with prior reports (23, 24). Similar measurements on 4-layer and 10-layer devices yield m* = 0.15 and 0.13, respectively. Thus, we will use m* = 0.14 throughout the rest of the manuscript.

The high device mobility enables manifestation of the hallmark of Rashba SOC—in 2D conductors with spin-split bands, the different concentrations of spin-up and spin-down electrons give rise to a characteristic beating pattern in the SdH oscillations. Figure 2A displays dR_xx/dB for device D2, which is estimated to be ~4 layers thick, as a function of n and B at a constant E_⊥ = −0.33 V/nm, where the nodes in the oscillations appear as a white band for B ~4 to 6 T. A line cut of dR_xx/dB(B) at n = 7 × 10¹² cm⁻² is shown in Fig. 2B, where the nodes are indicated by the arrows. The presence of two distinct frequencies is clearly reflected in the Fourier transform of the data (Fig. 2C), where we observe two distinct peaks in 1/B, and the separation between the two peaks is larger at higher charge density.

Fig. 2. Beating patterns in SdH oscillations from device D2 at T = 0.3 K.

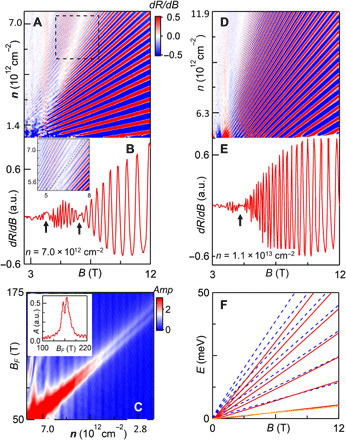
(A) dR_xx/dB(n, B) at E_⊥ = 0.33 V/nm. (B) Line trace of (A) at n = 7.0 × 10¹² cm⁻². Arrows indicate nodes of oscillations. Inset: Zoom-in plot of the dashed square in (A). Dashed line indicates the transition from minima to maxima. a.u., arbitrary units. (C) Fast Fourier transform of the data in (A), display two distinct frequencies. Inset: line trace of fast Fourier transform amplitude versus B_F at n = 2.8 × 10¹² cm⁻². (D) dR_xx/dB(n, B) at E_⊥ = 0. (E) Line trace of (D) at n = 1.1 × 10¹³ cm⁻². (F) LL energies calculated using Eq. 1 and α = 1.0 × 10⁻¹¹ eVm. The orange line denotes the zeroth LL, whereas the red solid and blue dashed lines represent spin-up and spin-down levels for N > 0.

Intriguingly, the parity of the oscillations changes after crossing the nodes—as shown in Fig. 2B inset, as B increases, the conductance minima at a fixed filling factor become maxima and vice versa. Since the degeneracy of the oscillations is two at these fields, such a change in parity indicates that only odd integer states are resolved for B below the nodes, and even integer states for B above the nodes.

The beating pattern, the beating frequency that scales linearly with charge density, and the alternating parities in the SdH oscillations are the hallmark signatures of large Rashba SOC in a 2D semiconductor, in which the quadratic band is spin-split by Δ_R = 2|αk_F| (here, k_F is the Fermi momentum). The different Fermi surface areas of spin-up and spin-down bands give rise to different oscillation frequencies, which interfere to generate the characteristic beating pattern. The Landau level (LL) spectrum is then given by (2, 3, 6)

$$E_N^{\pm }=\mathrm{\hslash }{\mathrm{\omega }}_{\mathrm{c}}[N\pm \frac{1}{2}\sqrt{{(1-\mathrm{gm}*/2)}^2+N\frac{{\mathrm{\Delta }}_R^2}{E_{\mathrm{F}}\mathrm{\hslash }{\mathrm{\omega }}_{\mathrm{c}}}}],E_0=\frac{1}{2}\mathrm{\hslash }{\mathrm{\omega }}_{\mathrm{c}}$$ (1)

Here, N is the LL index, E_F is the Fermi energy, and g is the effective g-factor. Figure 2F plots the LL spectrum for N = 0 to 10. Pronounced LL crossings occur between spin-split bands. Notably, the Rashba SOC strength can be extracted from the beating patterns

$$\mathrm{\alpha }\approx \frac{{\mathrm{\hslash }}^2}{m*m_0}\sqrt{\frac{\mathrm{\pi }}{2}}\frac{\mathrm{\Delta }n}{\sqrt{n}}$$ (2)

where Δn = (e/h)B_F,beat is the difference in densities between majority and minority spin carriers and B_F,beat is the beating frequency in SdH oscillations. Using Eq. 2, we estimate that α ~ 0.9 × 10⁻¹¹ eV m for the dataset shown in Fig. 2, A to C.

Since Rashba SOC is a consequence of broken inversion symmetry, we expect that an externally applied E_⊥ can either induce additional asymmetry or compensate for the inversion symmetry of the lattice, thus providing an experimental knob to tune the SOC strength in situ. This is borne out experimentally—a similar dataset of device D2 taken at E_⊥ = 0 (Fig. 2D) displays a substantially different beating pattern: Comparing with that at E_⊥ = −0.33 V/nm, the nodes shift to smaller B, indicating that the SOC strength is reduced.

To systematically examine the variation of SOC with E_⊥, we measure R_xx of device D2 as a function of n and E_⊥ at constant B = 6 T (Fig. 3A). As E_⊥ varies, the oscillations’ maxima clearly transition into minima and vice versa; the transition points move approximately linearly on the n-E_⊥ plane. In the SdH oscillations regime, the magnetoresistance of the device is related to the LL spectrum by (26)

$${\mathrm{\rho }}_{\mathrm{xx}}\sim B^2{\mathrm{\sigma }}_{\mathrm{xx}}\sim B^2\Sigma (N\pm \frac{1}{2})e^{-{(E_{\mathrm{F}}-E\frac{+}{N})}^2/{\mathrm{\Gamma }}^2}$$ (3)

where E_F is the Fermi energy and Γ is the LL broadening. We model the effect of the electric field by taking

$$\mathrm{\alpha }=\mid {\mathrm{\alpha }}_0+\mathrm{\alpha }\prime E_{\perp }\mid$$ (4)

where α is the “intrinsic” Rashba parameter, arising from the asymmetry of the intrinsic lattice and/or the confining potentials, including the different dielectric thicknesses for the gates; α^′ parametrizes the effectiveness of the electric field at tuning the SOC coupling, which can be positive or negative, depending on the field’s orientation relative to the built-in inversion asymmetry of the lattice. Combining Eqs. 1 and 3, and assuming Γ = 1 meV, m* = 0.14, we are able to satisfactorily reproduce the data by using α = 0.6 − 1.2 E_⊥, where α is in unit of 10⁻¹¹ eVm and E_⊥ in V/nm (Fig. 3B). Magnitude of these values agrees with those obtained from density functional theory (DFT) calculations (Fig. 4D) (27, 28). Together, these results underscore the highly tunable nature of the Rashba SOC in a 2D semiconductor, which, by applying an external E_⊥, can be enhanced, reduced, and even completely suppressed to zero.

Fig. 3. Magnetotransport data dR_xx/dn(n, E_⊥) at constant B.

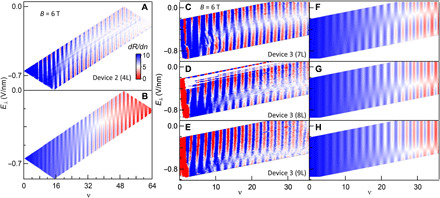
(A and B) Data and simulation for device D2. (C to E) Data for different regions of device D3 that are seven, eight, and nine layers thick, respectively. (F to H) Simulations for device D3.

Fig. 4. Magnetotransport data and anomalously large SOC parameter.

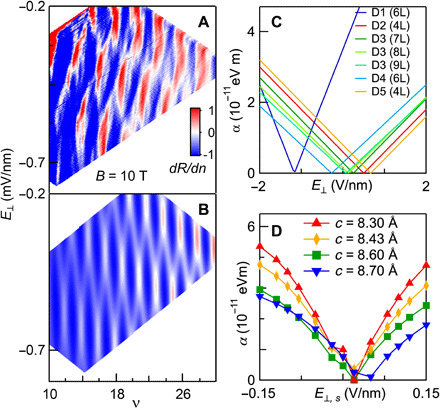
(A and B) dR_xx/dn(n, E_⊥) and simulations at constant B = 10 T for device D1. (C) Extracted Rashba parameter and its dependence on E_⊥ for different devices. (D) DFT calculations of Rashba parameter versus E_{⊥, s} for different c-axis lattice constants. Here, E_{⊥, s} is the out-of-plane electric field used in calculations, which, due to screening, is substantially reduced from the experimental values calculated from external gate voltages.

A unique opportunity afforded by the atomically thin 2D membranes is the exploration of SOC in a layer-by-layer fashion. To this end, we fabricate devices on a single piece of InSe flake with adjacent regions that differ by a single atomic layer in thickness (see Supplementary Materials). Figure 3 (C to E) presents data for such a device D3, which hosts regions that are estimated to be seven, eight, and nine layers, respectively. The overall features in the dR_xx/dn(n, E_⊥) plots at B = 6 T are qualitatively similar, with an important difference: As the thicknesses increase, the transition points shift to lower (more negative) E_⊥ values. These patterns can be satisfactorily captured by our simulations, yielding the intrinsic Rashba parameter α₀ = 0.2 × 10⁻¹¹, 0.15 × 10⁻¹¹, and 0.08 × 10⁻¹¹ eVm, respectively, for the regions that are seven, eight, and nine layers thick; α′, the effective tunability of the SOC, is extracted to be −1.2 × 10, −1.15 × 10, and −1.1 × 10 e nm², respectively. Thus, as the layer number increases, both the intrinsic SOC strength and its scaling with external E_⊥ are diminished (27). This trend is opposite to that predicted by theory calculations (28). Such discrepancy is not understood at this point and should stimulate further theoretical and experimental works to explore, for example, variations of hopping parameters with number of layers, variations of intra- and interlayer SOC with energy, and effects of electron interactions and screening. The strength and tunablility of the Rashba SOC of different devices are summarized in Fig. 4C.

Last, we observe that some devices appear to be markedly enhanced. Figure 4A presents dR_xx/dn(n, E_⊥) at B = 10 T for device D1. Notably, instead of a single transition point at a given n, several crossing points are visible. Such large number of transitions indicates much higher SOC—we are able to reproduce the patterns by taking α = 3.5 + 3.0 E_⊥ (Fig. 4B). Compared to values in the previous plots, αʹ increases by as much as an order of magnitude, while tunability αʹ is enhanced by a factor of 3. Such a large SOC strength is unexpected and unlikely to originate from variations such as thicknesses of flake or gate dielectrics. Instead, it suggests a fundamental mechanism at play. One possibility is variations in the interlayer spacing c, which, according to DFT calculations, is an extremely effective “knob” to tune the SOC parameter. For instance, increasing c by a mere 1.9% (from 8.43 to 8.6 Å) results in a reduction of α₀ by 57% (from 0.89 × 10⁻¹¹ to 0.57 × 10⁻¹¹ eVm) (Fig. 4D). The small variations in interlayer spacing may arise from stacking faults: Although the γ phase is the most dominant phase in our crystals, TEM studies reveal high densities of stacking faults that are generated by dislocation dissociation or by growth, including ones with wrongly stacked monolayers (see figs. S1 and S2). The large electrostatic pressure generated by the displacement fields, which exceeds 20 MPa in our devices, may further compress the interlayer spacing. Another possibility is the nonlinear scaling of α with E_⊥ in the presence of stacking faults or twin boundaries. Although further work is required to ascertain the mechanism, these data show that Rashba SOC can be tuned through a much larger range than previously thought possible.

In summary, we observe the hallmarks of large Rashba SOC in few-layer InSe field effect transistor devices, where the unprecedented mobility enables quantitative extraction of the Rashba parameter. The two-dimensionality of the devices enables the SOC strength to be modulated by the layer thickness and by an electric field that breaks or compensates for the inversion symmetry. The possibility of piezo-SOC tuning, which has not been observed to date, warrants further theoretical and experimental investigation. The extraordinary tunability of SOC in 2D materials, as demonstrated here, can be exploited for a variety of phenomenon and devices, such as spin Hall effect, spin-orbit torque, and spin helix with long spin coherence time, with in situ control.

MATERIALS AND METHODS

Single crystals of InSe were synthesized from 6N-pure indium and 6N-pure selenium pellets in a ratio In_0.52Se_0.48. The starting materials were sealed in a quartz ampule and then vacuumed to 10⁻³ torr. They were subsequently prereacted by gradually heating the ampule to 800°C and kept at this temperature for 96 hours. After the reaction, the ampule was then placed into a radio frequency (RF) furnace where the RF power was gradually increased to raise the temperature up to 800°C. The ampule was then pulled through the hottest zone at a rate of 2 mm/hour.

Bulk InSe crystals are characterized by atomic-resolution high-angle annular dark-field scanning transmission electron microscopy using a probe aberration–corrected JEOL JEM-ARM200cF at 200 kV. TEM samples were made by focused ion beam in a Helios G4 DualBeam.

InSe and hBN crystals are exfoliated on polydimethylsiloxane into atomically thin sheets, with InSe thicknesses ranging from 4 to 10 layers. FLG for contacts is exfoliated on Si chips covered with 300-nm SiO₂. Using the dry-transfer technique (29) at room temperature, we assemble hexagonal hBN/few-layer InSe/hBN heterostructures, with contacts that consist of few FLG sheets. First, we pick up the FLG contacts, followed by InSe and, last, the bottom hBN. The exfoliation and stack assembly processes are performed in a glove box to minimize degradation. We then etch the heterostructure into the Hall bar geometry in two steps, first using SF₆ gas for hBN and then Ar gas for InSe (pressure, 15 mtorr; power, 60 W; average etch time, 15 s and 5 min for SF₆ and Ar, correspondingly), and deposit a layer of aluminum oxide covering the channel, followed by Cr/Au for electrodes and the top gate. The electrodes formed 1D contact to FLG.

Transport measurements are performed using SR830 and SR860 lock-in amplifiers at an ac bias current of 50 nA. All measurements are performed at base temperature in ³He or pumped ⁴He cryostats.

We used ab initio DFT to investigate the thickness dependence of functional properties in atomically thin InSe. DFT calculations were performed using the Vienna Ab initio Simulation Package (30, 31) within the generalized gradient approximation with Perdew-Burke-Ernzerhof (32, 33) functional. A plane-wave cutoff of 350 eV and Γ point–centered 12 × 12 × 1 k mesh for integration in reciprocal space are used (34). While we keep in-plane periodic boundary conditions, a vacuum of 12 Å is added perpendicular to the plane to minimize interactions between the periodic images of the films. Grimme’s D2 (35) functional is used in all calculations to include the van der Waals interaction between the layers. When applying an external field on the slab, we turned on the dipole correction along the c axis to avoid interactions between the periodically repeated images. To determine the Rashba splitting for the bottom of the conduction band, fully relativistic SOC was included into the calculations in addition to the applied field. To accurately determine the position of the shifted conduction band minima, band energies were calculated for a large number of k points in the vicinity of the Γ point, and the Rashba parameter (α) is determined by $\mathrm{\alpha }=\frac{\mathrm{\Delta }E}{2\mathrm{\Delta }k}$.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/5/eabe2892/DC1