Abstract
Sex offers advantages even in primarily asexual species. Some ciliates appear to utilize such reproductive strategy with many mating types. However, the factors determining the composition of mating types in the unicellular ciliate Tetrahymena thermophila are poorly understood, and this is further complicated by non-Mendelian determination of mating type in the offspring. We therefore developed a novel population genetics model to predict how various factors influence the dynamics of mating type composition, including natural selection. The model predicted either the coexistence of all seven mating types or fixation of a single mating type in a population, depending on parameter combinations, irrespective of natural selection. To understand what factor(s) may be more influential and to test the validity of theoretical prediction, five replicate populations were maintained in laboratory such that several factors could be controlled or measured. Whole-genome sequencing was used to identify newly arising mutations and determine mating type composition. Strikingly, all populations were found to be driven by strong selection on newly arising beneficial mutations to fixation of their carrying mating types, and the trajectories of speed to fixation agreed well with our theoretical predictions. This study illustrates the evolutionary strategies that T. thermophila can utilize to optimize population fitness.
Keywords: ciliate, mating type dynamics, population genetics, experimental evolution, facultative sex, genetic hitchhiking
Introduction
The advantages of sex as a fundamental mechanism for improving the fitness of an organism are well established (Weismann 1889; Fisher 1930; Muller 1932; Hill and Robertson 1966; Otto and Lenormand 2002; McDonald et al. 2016). Although the advantages of sex were initially considered for obligate sexual organisms, both theory and empirical data have demonstrated that these advantages also apply to facultative sexual species that primarily reproduce asexually (Burt 2000; D’Souza and Michiels 2008; Becks and Agrawal 2012). In anisogamous organisms, sexual reproduction usually takes place between two different sexes, which are defined according to the size of their gametes. In contrast, the gametes of isogamous organisms are morphologically indistinguishable; however, they can still be categorized into genetically determined self-incompatible classes, called mating types (Billiard et al. 2011; Czuppon and Constable 2019). Most sexually reproducing unicellular eukaryotes such as ciliates and fungi are isogamous and engage in facultative sex, and some have more than two mating types (Phadke and Zufall 2009; Billiard et al. 2011; Lehtonen et al. 2016).
In obligate sexual organisms with only two sexes, the composition of sexes is dominated by frequency-dependent selection (Fisher 1930); in contrast, the dynamics of mating type composition in facultative sexual organisms can be complicated by many other factors. First, because facultative sex enables organisms to reproduce asexually, the rate of sex (i.e., the proportion of offspring produced by sexual reproduction each generation) appears to shift the dynamics of mating type composition (Constable and Kokko 2018; Ennos and Hu 2019). Second, in organisms with more than two sexes, the evolutionary consequences of sex composition in a population are predicted to depend greatly on detailed mating schemes that differ in the degree of rare sex advantage (Orias and Rohlf 1964; Iwasa and Sasaki 1987). Additionally, mechanisms that control sex determination (SD) in organisms with multiple mating types can further complicate mating type composition within a population (Paixao et al. 2011). The effects of single or combinations of a few factors (mating scheme, sex rate, SD) on mating type composition within a population have been studied, but it is unclear how such factors interact with each other and with natural selection. A single theoretical framework is unlikely to cover all organisms. Furthermore, studies into mating type composition in natural populations of facultative sexual organisms with more than two mating types show that mating type frequencies are often uneven and vary among populations (Doerder et al. 1995, 1996; Arslanyolu and Doerder 2000; Douglas et al. 2016), and the underlying driving factors have not yet been experimentally tested.
Ciliates are large group of unicellular eukaryotes that possess a diploid, silenced germline nucleus (micronucleus, or MIC) and a highly polyploid, actively transcribed somatic nucleus (macronucleus, or MAC) that determines the cell’s phenotype. Most ciliates are facultatively sexual: cells reproduce asexually by binary fission when food is abundant and conjugation, the sexual phase of the life cycle, which is independent of reproduction, is often induced between cells of different mating types under starvation (Orias et al. 2011). During conjugation, the MIC undergoes meiosis to generate gamete nuclei that fuse and divide mitotically to form the new MIC and new MAC, whereas the parental MAC is destroyed (supplementary fig. S1, Supplementary Material online). Furthermore, among ciliates, mating system features are highly divergent, particularly the number of mating types and the SD mechanism. For example, Paramecium spp. have 2–8 mating types and Tetrahymena spp. have 3–9, and their SD mechanisms differ widely, ranging from Mendelian systems to developmental nuclear differentiation, with either stochastic or maternal inheritance (Orias et al. 2017). These features provide a unique opportunity to study the dynamics of mating type composition in a multisex mating system.
The model ciliate, Tetrahymena thermophila, has seven self-incompatible mating types (I–VII) that are determined by alleles at a single locus (mat locus). Most eukaryotes have an SD mechanism that conforms to Mendelian laws (i.e., mating type is determined precisely by the genotype inherited from parents). In contrast, T. thermophila has a probabilistic SD mechanism: the allele at the MIC mat locus of an individual cell only determines the probability that a progeny cell will develop into one of the seven mating types. For example, a classic B-type mat allele specifies the following probabilities for the seven mating types: I, 0; II, 0.275; III, 0.192; IV, 0.278; V, 0.076; VI, 0.041; and VII, 0.138 (Nanney 1960). Tetrahymena thermophila has two types of mat alleles: A-type alleles that specify all mating types except for types IV and VII, and B-type alleles that specify all mating types except for type I (Nanney 1959). mat alleles can also determine the relative probability distributions of mating types (called SD patterns) (Paixao et al. 2011). Over 14 mat alleles with distinct SD patterns have been identified in natural populations of T. thermophila (Doerder et al. 1995, 1996; Arslanyolu and Doerder 2000). Moreover, for each mat allele the SD pattern can be affected by environmental conditions, including temperature and nutritional state during sexual reproduction (Nanney 1960; Orias and Baum 1983). A recent study revealed that the B-type mat allele in the MIC contains six incomplete mating type gene pairs that specify mating types II–VII (Cervantes et al. 2013). During MAC development, only a single gene pair, which is selected with a specific probability, is completely assembled at the MAC mat locus. This developmental process results in mature cells that express a single mating type in the MAC. This probabilistic SD mechanism (also called caryonidal inheritance) seems to be common in ciliates (Phadke and Zufall 2009).
A theoretical model previously showed that the probabilistic SD mechanism can cause uneven mating type frequencies to evolve in natural populations of T. thermophila (Paixao et al. 2011). However, this model assumed that in a sexual generation, any individual that does not reproduce sexually, does not reproduce at all, which is in obvious disagreement with its life cycle features. In addition, this model did not consider the impact of fitness differences between cells of different mating types during asexual reproduction. So far, no theory can predict mating type composition in a T. thermophila population based on the aforementioned factors, including mating scheme, sex rate, SD, and natural selection. We therefore applied a set of realistic assumptions to study the dynamics of mating type composition in T. thermophila. For this, we first developed a population genetics model with a flexible mating scheme in a large population of T. thermophila to make quantitative predictions about the evolution of population mating type composition. We then investigated the impact of different model parameters on the dynamics of mating type composition armed by combination of analytics and simulation. We next established five replicate experimental populations to determine whether mating type composition could be predicted by the model and to identify the factors that regulate the dynamics of mating type composition.
Materials and Methods
The Model
The model considered a large population of T. thermophila, in which asexual growth is interrupted at regular intervals by sexual reproduction (which we call sex:asex cycles). Sexual reproduction consists of two steps: cell pairing and generation of offspring.
Pairing Schemes
Sexual reproduction starts with cell pairing which is assumed to be random but synchronized, thus proceeding as multiple rounds. A further assumption is that at each round of pairing incompatible pairs (i.e., cells of the same mating type) separate and that all unsuccessfully paired cells participate in the next round of pairing. This process stops when a prespecified round of pairing is complete or when no further pairing is possible (i.e., all unpaired cells are of the same mating type; fig. 1). This process can be described mathematically, as follows. If is the frequency of mating type right before the sexual reproduction and is the relative frequency of mating type after the tth round of pairing, then . Since pairing is random, the probability of a cell of mating type not being paired at the tth round is and, therefore, the frequency of mating type among unpaired cells is:
| (1) |
where is the expected proportion of unpaired cells after the tth round of pairing. Thus, the overall proportion of unpaired cells after T rounds of pairing is:
| (2) |
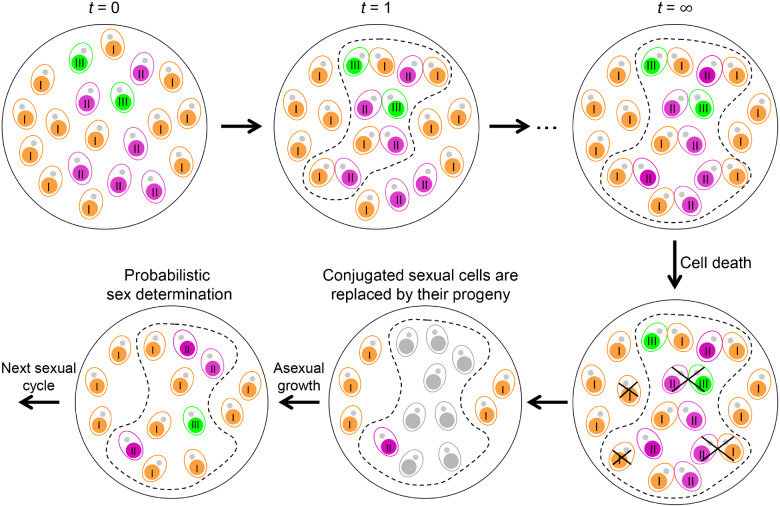
Fig. 1.
Diagram illustrating the mating scheme and dynamics of mating type composition within a population. Each T. thermophila cell contains a MIC (gray dot) and a MAC (colored). MAC colors represent different mating types (I, II, and III in this example). At t = 0, the population initiates a sexual reproduction cycle and all cells become sexually active. After the first round of pairing (t = 1), cells of different mating types pair together (denoted by the dash line). Note that cells of rare mating types tend to find compatible partners more quickly than cells of common mating types. Cells of the same mating type cannot pair and continue to another round of mate-finding until no suitable mates are available. At the end of mating (t=∞), all unpaired cells are of the same mating type, most likely the one with the largest initial frequency. Note that some paired cells may separate and may not find a partner in the current sexual cycle. Both conjugated cells and unpaired cells undergo viability selection and some will die due to developmental failure and/or starvation stress (used to induce sexual reproduction). Surviving conjugated cells are replaced by their sexual progeny. After sufficient rounds of asexual growth to reach sexual maturity, each sexual progeny cell will develop into a specific mating type, the probability of which is determined by the mat allele. A new sexual cycle is then induced.
When T is sufficiently large and the initial population size is practically infinite, the unpaired cells are necessarily all cells of the most frequent mating type (k) before the start of sexual reproduction. Although completion of the pairing process depends on the number and frequency of cells of the initial mating types, it typically requires only a handful of rounds (fig. 2). Moreover, the values of parameter T can reflect different mating schemes. For example, scenarios in which T = 1 and T=∞ are equivalent to the first and the third mating schemes, respectively, were previously explored by Iwasa and Sasaki (1987).
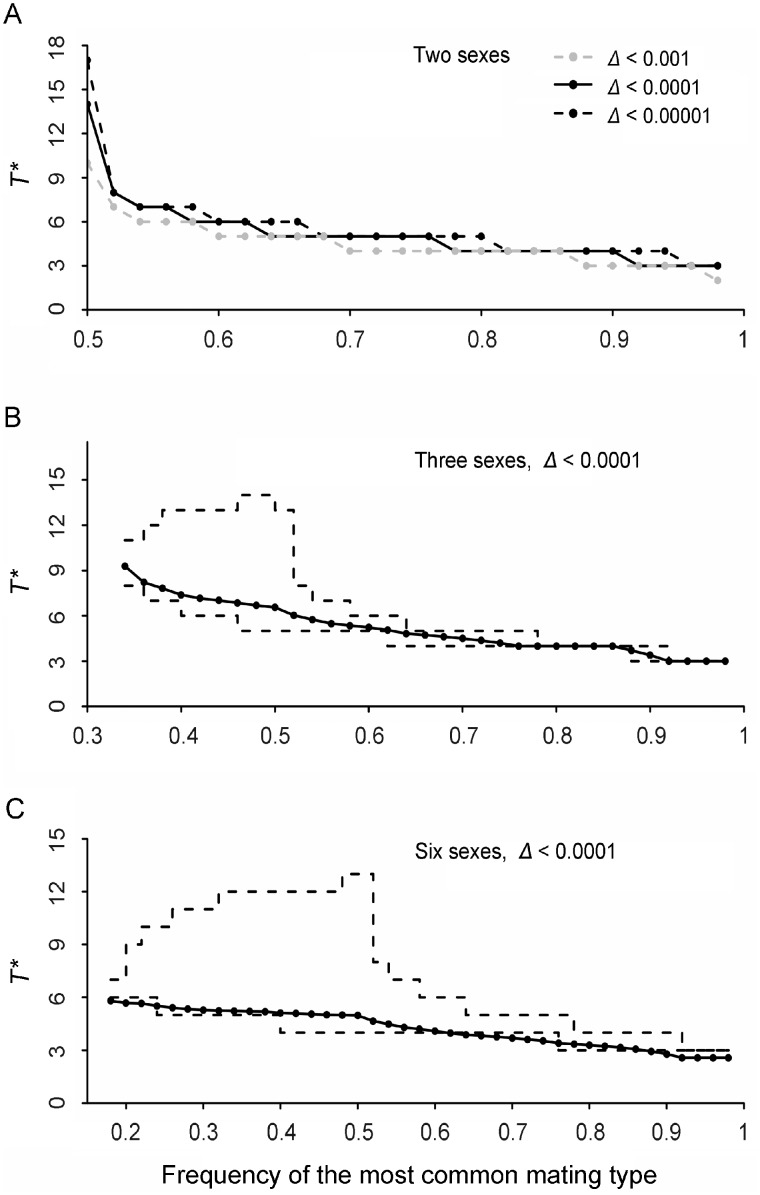
Fig. 2.
Relationships between the expected number T* of rounds to complete the pairing process and the initial number and frequencies of mating types in the population. T* depends on the criteria for judging the completion of the pairing process, which was defined as the amount of change (Δ) in after a round of pairing. (A) Graph showing two sexes with three different values of Δ = 0.001, 0.0001, and 0.00001. (B and C) Graphs showing three sexes with Δ = 0.0001 (B) and six sexes with Δ = 0.0001 (C). Solid lines represent the average number of rounds to complete pairing and dashed lines represent the maximum and minimum number of rounds. Frequencies of the less common sexes were set by generating random numbers from the uniform distribution (with a sum of one minus the frequency of the most common mating type). In general, the closer the frequency of the two most common sexes, the larger the value of T*.
Reproduction and Population Dynamics
At the end of the pairing process, not all properly paired cells may remain intact and even if they do, not all may succeed in generating offspring. Therefore, it was further assumed that each pair of properly paired cells had a probability β of separating (and, therefore, of not participating in sexual reproduction). Unpaired cells were assumed to have a probability of surviving the induction period of sexual reproduction (e.g., due to the harsh environment and poor nutrition). Furthermore, it was assumed that each intact mating pair (conjugated sexual cells) had a probability of producing offspring (e.g., due to possible developmental failure during sexual reproduction). Each sexual offspring had probability of developing into mating type .
Table 1 lists all the parameters included in the model. Since conjugated sexual cells undergo a series of complex cellular processes involving many potential failure points to produce progeny and as Tetrahymena does not form a resistant structure (such as a spore) during sexual production, it was expected that in general (Levitis et al. 2017). Therefore, is generally <1. Under the T-rounds pairing scheme, the proportion of mating type among the paired cells is:
| (3) |
Table 1.
Summary of Parameters in the Model
| Parameter | Description |
|---|---|
| N | Population size |
| n | Number of rounds of asexual cell division between sexual cycles |
| The frequency of mating type i right before the sexual cycle | |
| The relative frequency of mating type after the tth round of pairing | |
| T | The total number of rounds allowed for cell pairing |
| αT | Proportion of unpaired cells after the Tth round of pairing |
| β | Probability that two successfully paired cells will separate |
| Ratio of the probability that an intact pair produces sexual offspring () to the probability that unmated cells will survive the induction period for sexual reproduction () | |
| Probability that an offspring cell (from sexual reproduction) is of mating type i | |
| Selection coefficient for a mutant allele |
cells will not participate in sexual reproduction and the remaining cells commit to sexual reproduction. After sexual reproduction, the total number of cells is:
where
| (4) |
Thus, the proportion of unmated cells is:
| (5) |
and the number of cells of mating type is:
| (6) |
where the first term=number of unpaired cells×asexual survival probability, the second term=number of paired cells that have separated×asexual survival probability and the third term=number of conjugated sexual cells×sexual survival probability×the probability of expressing each of the mating types. If is the frequency of mating type after the sexual reproduction, then it follows that:
| (7) |
Since is assumed to be sufficiently large that random genetic drift is negligible, will be the frequency of mating type immediately before the next cycle of sexual reproduction in the absence of natural selection.
By setting , we can solve the equation for the equilibrium mating type frequencies, which leads to:
| (8) |
where for each quantity the subscript ∞ indicates its limiting value, that is, the value at equilibrium. Although it may at first appear that the equilibrium frequencies do not relate to β, this is not true since its impact is reflected through the limiting α value.
Next, we considered the impact of selection for advantageous mutations. Suppose a mutation emerges immediately after sexual reproduction in a MAC of mating type with a frequency of and a growth rate of per cell division. Then immediately before the next cycle of sexual reproduction, the proportion of cells of each mating type () is:
| (9) |
where if and = 0 under all other conditions. The frequency of cells containing the mutation immediately before sexual reproduction is:
| (10) |
As a mutant cell will remain so only if it does not participate in sexual reproduction, the sexual process acts to slow down the selection of mutations. Immediately after the next cycle of sexual reproduction, the mutant allele frequency becomes:
| (11) |
Substituting the value for in equation (11) by the value in equation (10) leads to:
which leads to the equilibrium solution for> 0
| (12) |
If (i.e., a single mating type is fixed), this will lead to fixation of the mutant allele; otherwise, internal equilibrium can be reached. In T. thermophila, a beneficial mutation would initially be present in one of the 45 copies of a MAC chromosome in a single individual. During asexual reproduction, the MAC would divide by amitosis, which would create copy number variation in the beneficial allele (Doerder 2014). Thus, some descendant cells would be expected to show selective benefits larger than 1+. However, this possibility was not considered in our model.
If an advantageous mutation (in terms of growth) occurred in a MIC, which is not expressed during growth, the growth advantage would be hidden until the mutation passed into a MAC during sexual reproduction. The difference here is that the growth advantage would be heritable, so after sexual reproduction the mutation would spread to all mating types and would eventually become fixed without the need to fix the mating type. The mathematic model was analyzed using Java SE 9 and the source code is available in Supplementary Material online.
The Experiment
Experimental Design
In order to 1) develop a better understanding of how various factors might affect the fate of a population and 2) test whether mating type composition dynamics agrees with our theoretical predictions, five replicate experimental populations (CS1–CS5) were established. Each population was initiated by induced mating between equal proportions of homogeneous ancestor cells of mating types IV and VI. The resulting population grew asexually for about 100 generations, with a large stable population achieved by daily serial transfer (about 4 × 104 cells per transfer and 5.3 asexual generations per day), and then underwent a round of starvation-induced sexual reproduction. This sex:asex cycle was repeated ten times. Immediately before the induction of sexual reproduction, a large sample of cells was extracted, a portion of which was stored in liquid nitrogen (Cassidy-Hanley 2012), with the remainder used for whole-genome sequencing to identify mutations and determine the mating type composition. Due to the high cost of the whole-genome sequencing, we chose to sequence only DNA samples from CS1–CS3 across all time points. Although samples from CS4 and CS5 were not sequenced, they provided useful information on which mating type eventually became fixed in these populations (i.e., the MACs of all cells expressing the same mating type). Essential features of experiments are described below and more details are provided in Supplementary Material online.
Ancestral Population
Tetrahymena thermophila strain SB210 was mated with the star strain B* VII through genomic exclusion crosses (Allen 1967). The crosses yielded homozygous progeny in both MAC and MIC genomes, but with different progeny cells exhibiting different mating types in the MAC due to probabilistic SD. When the progeny population matured, one cell of mating type IV and one cell of type VI (named Anc_IV and Anc_VI, respectively) were selected as the two ancestral cells. Asexual clonal populations of these cells were used to initiate each of the five replicate experimental populations. The two ancestral cells and their sexually and asexually reproducing progeny inherited the same B-type mat allele in the MIC from strain SB210.
Parameter Estimation in the Experimental Populations
To estimate parameters β and , the proportion of surviving cells (a) at the end of sexual reproduction and within which the proportion of asexual offspring (b) were required (when is known). For example, when , it follows from equations (4) and (5) that and Mating type composition of the evolving population at the end of the first sex:asex cycle (i.e., at generation 100) was used to estimate that is the vector of all values. As unmated Anc_IV and Anc_VI cells underwent serial transfer along with the sexual progeny, correction for the background mating type frequencies of unmated cells was necessary to obtain the true value (representing the mating type composition of sexual progeny). In addition, because natural selection during serial transfer also affects the estimation of , we calculated the daily growth rate (i.e., fitness) of the two ancestral populations at 1 week before mating and of the resulting evolving populations according to the formula, (Kishimoto et al. 2010). For each evolving population, the parameter was calculated as the ratio of the eventual growth rate to the mean growth rate for the two ancestral populations during the week of serial passage. The relative growth rate trajectory for each evolving population was analyzed by the SSlogis model in R 3.4.1 (http://www.r-project.org/; last accessed July 8, 2017).
Calculating the Ratio of Mating Pairs to Unmated Cells
During each sexual cycle, we calculated mating pair ratio at 9-h poststarvation when cell pairing had reached a plateau. For this, 100 µl cells were stained with 5 µl Lugol’s iodine (Chen et al. 2014) and mating pairs were counted under an optical microscope. The pair ratio was defined as the fraction of paired cells: 2 × number of pairs÷(2 × number of pairs+number of single cells). The ratio of unmated cells was calculated at the end of starvation (i.e., 48-h poststarvation). For this, 100 µl cells were fixed in 2% paraformaldehyde, stained with 50 ng/ml 4′,6-diamidino-2-phenylindole, and observed under fluorescence microscopy. Sexual progeny cells are characterized by having two MACs and one MIC (conjugation stage 7; supplementary fig. S1, Supplementary Material online), whereas unmated cells only contain one MAC and one MIC (vegetative stage V0). The unmated cell ratio is defined as: number of unmated cells÷(number of sexual progenies+number of unmated cells). Each ratio was calculated based on a random sample of 200 cells.
Determining the Population Mating Type Composition
The mating type composition in each sample was determined by mapping sequencing reads to the MIC genome (Hamilton et al. 2016). After removing the background of internally eliminated sequences (IESs) within the MIC mat locus, the sequencing depth of gene segments specific to each mating type was used to determine the proportion of each mating type.
Whole-Genome Sequencing, SNP Calling, and Annotation
DNA samples were taken from populations CS1, CS2, and CS3 every 100 asexual generations until generation 1,000. Sequencing libraries were constructed using a standard Illumina protocol, as previously described (Xiong et al. 2015). All libraries were sequenced to a depth of ∼30-fold coverage, except for libraries of the two ancestral samples that were sequenced to 250-fold coverage, using Illumina HiSeq 2000 or HiSeq 2500 instruments. A detailed SNP calling pipeline is given in Supplementary Material online. Briefly, we aligned reads sequenced after trimming off adapters to the T. thermophila MAC reference genome (Eisen et al. 2006). We then marked PCR duplicate reads, performed local realignment around potential indels, and recalibrated the base quality score (McKenna et al. 2010), and then ran VarScan for SNP calling (Koboldt et al. 2012). To reduce the risk of false positives, each mutation had to be supported by at least three forward and three reverse reads (Long et al. 2016). Time-course sequencing enabled us to further refine candidate mutations based on mutation frequency trajectories, as previously reported (Lang et al. 2013; McDonald et al. 2016). In particular, imprecise IES excision in the newly developing MAC during mating can lead to the formation of many SNPs or indels around the IES junction sites (Hamilton et al. 2016). Therefore, candidate mutations were required to be located at least 50 bp from the IES excision end point (Chen et al. 2019). Functional annotation of each mutation was carried out using SnpEff (Cingolani et al. 2012).
Identification and Functional Validation of Beneficial Mutations
We used two criteria to identify putative beneficial mutations. First, as beneficial mutations are more likely than neutral or deleterious mutations to spread within a population, we considered mutations that reached a frequency of at least 0.9 as candidate beneficial mutations. Second, as frequency of beneficial mutations should correlate with changes in the growth rate, we determined the Pearson correlation coefficient for changes in growth rate and the frequency of each identified mutation. Putative beneficial mutations were required to have a correlation coefficient of at least +0.8 (supplementary table S1, Supplementary Material online). Mutations that met both criteria were classified as beneficial. To validate whether a mutation confers a growth advantage, we introduced it into both ancestral cells (Supplementary Material online). We then mixed each mutant cell population with the two ancestral cell populations in equal proportions, respectively, and propagated the cells under the same conditions used in the evolution experiment. Sanger sequencing was performed every 2 days to determine whether one cell type had been completely replaced by another. The PCR primers used to amplify sequences covering the mutation site were: Mut-f4001, 5′-TAGATTAAGACACTTTAGAAAAAGC-3′; and Mut-r4898, 5′-TCATTGATTCATTAGATTATCTTTC-3′. Competition assays were carried out in duplicate.
Results
Impact of Model Parameters on the Equilibrium Mating Type Composition
As shown in the model, parameters influencing the equilibrium mating type composition of the population include the initial mating type frequencies, β, , T, , and . We therefore performed a numerical exploration of the impact of these parameters.
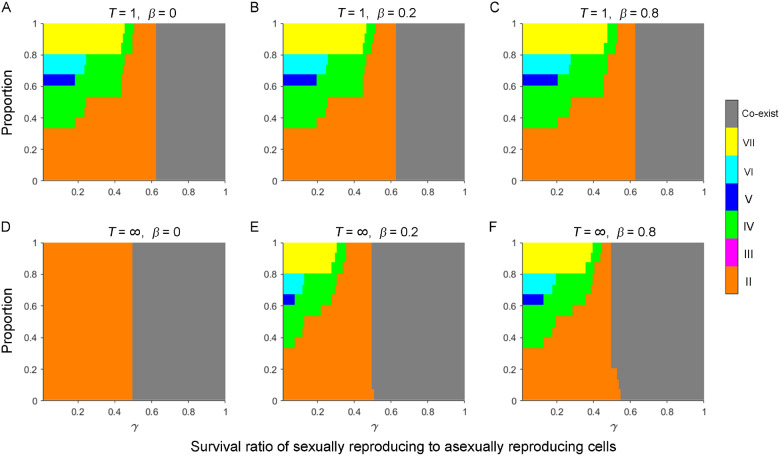
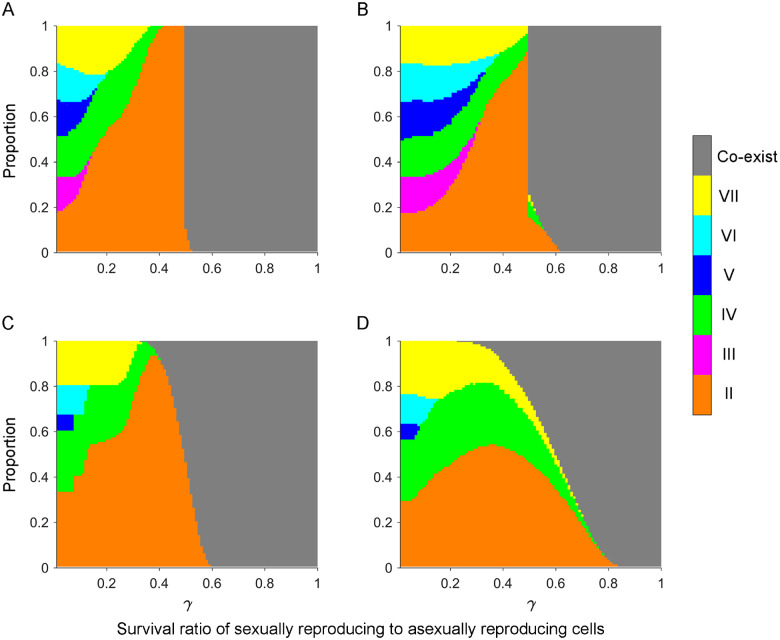
To simplify the illustration, we set as the estimated SD pattern (II, 0.302; III, 0.010; IV, 0.271; V, 0.047; VI, 0.118; and VII, 0.252) from our experimental populations. We started by considering the following scenario: the population starts with two randomly selected mating types of equal proportion (15 combinations), only one round of cell pairing is allowed (T = 1), and all cells that forms pairs will end up in the pool of conjugated sexual cells (). Assuming just two mating types is equivalent to a scenario in which two allopatric populations that have each fixed a different mating type come into secondary contact. As shown in figure 3A, mating type composition at equilibrium exhibits two patterns: 1) all six mating types coexist or 2) a single mating type is fixed. As the survival ratio of sexual cells to asexual cells () increases, more sexual progeny are produced and develop into different mating types so that all mating types eventually coexist in the population. However, when is smaller, a single mating type becomes fixed, and the proportions of cells with different mating types becoming fixed correlate positively with the mating type frequency distribution in . It seemed counterintuitive that the mating type with the largest is often selected because evolutionary models for the number of mating types often feature negative frequency-dependent selection (Iwasa and Sasaki 1987). However, by assuming that conjugated sexual cells experience higher mortality (), the model selected against those mating types more likely to end up in the pool of sexual cells. Since these are the rare mating types, our model actually generates positive frequency-dependent selection. This was demonstrated more clearly in figure 3D. When T=∞, only the most common mating types do not form pairs. Therefore, the mating type with the largest has the highest reproductive rate and becomes fixed with certainty when is not very large.
Fig. 3.
Patterns of mating type composition at equilibrium under different combinations of parameters. Populations initially contained equal proportions of any two mating types. The stacked bar charts depict differences in the proportion of parameter space for fixation of a specific mating type or for the coexistence of all six mating types in populations with different parameter values. (A–F) We varied the number of cell pairing rounds, T = 1 (A–C) and T=∞ (D–F); and the probability of paired cells separating, β = 0 (A and D), β = 0.2 (B and E), and β = 0.8 (C and F). Other parameters were population size, N = 106; number of asexual growth rounds, n = 100; and SD pattern, =0.302 (II), 0.010 (III), 0.271 (IV), 0.047 (V), 0.118 (VI), and 0.252 (VII). We assumed no fitness differences between cells of different mating types during asexual growth. Results show the average of 15 random combinations of two initial mating types.
We also found that increasing has a minimal effect on the patterns of mating type composition, except in the special case when = 0 and T=∞ (fig. 3D). However, a larger can increase the proportion of parameter space, leading to the fixation of mating types with smaller values. When > 0, cells that forms pairs have probability of separating and not engaging in sexual reproduction. Therefore, one of the initial two mating types is more likely to be most common after sexual reproduction and then to become fixed under certain parameter values owing to positive frequency-dependent selection, despite not having the largest value.
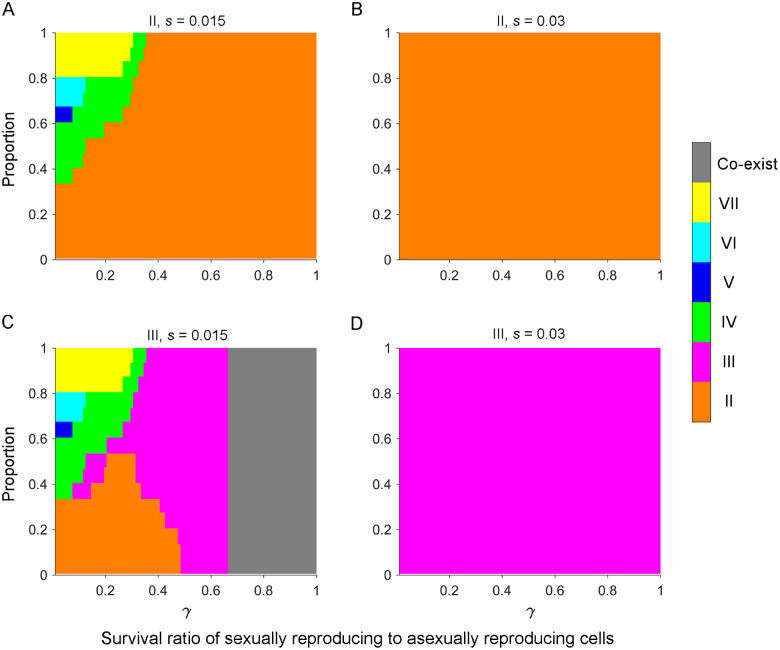
We further investigated how mutation of the MAC immediately after sexual reproduction affects the evolution of mating type composition. For simplicity, we considered two cases in which the mating type with the largest (fig. 4A and B) or smallest (fig. 4C and D) value obtains a beneficial mutation and assumed that the population starts with equal proportions of any two mating types and that T=∞ and (estimated from the experimental populations). The patterns of equilibrium mating type composition were strikingly different from figure 3E. The mating type that obtained a beneficial mutation had an increased parameter space to be fixed and did in fact become fixed when was larger than a certain threshold.
Fig. 4.
The action of natural selection on a beneficial mutation promotes fixation of a single mating type. Populations initially contained equal proportions of any two mating types. (A–D) Immediately after the first sexual cycle, mating type II (A and B) or III (C and D) obtained a beneficial mutation in the MAC, with a selection coefficient s of 0.015 (A and C) or 0.03 (B and D). Population size, N = 106. The initial mutation frequency was 1/N. Other parameters were number of asexual growth rounds, n = 100; number of cell pairing rounds, T=∞; probability of paired cells separating, ; and SD pattern, =0.302 (II), 0.010 (III), 0.271 (IV), 0.047 (V), 0.118 (VI), and 0.252 (VII). Results show the average of 15 random combinations of two initial mating types.
To summarize, by assuming , our model can generate positive frequency-dependent selection that is reinforced by smaller T or larger values. In the model, selection for beneficial mutations can increase the range of parameter values that lead to the fixation of a single mating type.
Impact of Environmental Changes on the Equilibrium Mating Type Composition
In the numerical exploration, parameter was fixed. However, changes in some environmental factors may lead to modifications of the values of and other parameters. For example, temperature and food availability during conjugation significantly affect the SD patterns (Nanney 1960; Orias and Baum 1983), and migration among populations can lead to immediate changes in the initial mating type frequencies. We therefore explored the impact of these changes on the equilibrium mating type composition.
For simplicity, we assumed that T=∞, , and the population with the above estimated contained equal proportions of two randomly selected mating types. By varying the initial mating type composition (fig. 5A and B) or the value (fig. 5C and D) to simulate the impact of environmental changes, we found that mating type composition patterns were changed dramatically and that fluctuations in had a greater impact on mating type fixation or coexistence in contrast to figure 3E.
Fig. 5.
Fluctuations in initial mating type frequency and SD pattern affect mating type composition. Populations initially contained equal proportions of any two mating. (A–D) Frequencies of the initial two mating types (A and B) or SD pattern (C and D) varied by 5% and 30%, respectively. Parameters were population size, N = 106; number of asexual growth rounds, n = 100; number of cell pairing rounds, T=∞; probability of paired cells separating, ; selection coefficient, ; and SD pattern, =0.302 (II), 0.010 (III), 0.271 (IV), 0.047 (V), 0.118 (VI), and 0.252 (VII). A total of 10,000 replicates were run for each random combination of two initial mating types.
Estimating Parameters , , and in Experimental Populations
At the end of the first cycle of sexual reproduction in the five replicate experimental populations, the number of individuals decreased to an average of 52%; of this population, 38% were the unmated cells of the two ancestral populations. As sufficient time (48 h) had been allowed for cell mating and the experimental populations had contained equal proportions of the two ancestral populations, T=∞ and . It was difficult to directly measure the survival probability of unmated ancestral cells (parameter ) because we could not determine whether the dead cells derived from unmated ancestral cells or from conjugated sexual cells in the mating population. Therefore, the was measured indirectly by starving each ancestral population for 48 h under the same conditions used for the mating population and then calculating the cell survival ratio (table 2). The average cell survival ratio was 1.0 for both of the ancestral populations, so . According to equations (4) and (5), parameters and . As there was no significant difference in growth rate between the two ancestral populations and the experimental population after mating (supplementary fig. S2, Supplementary Material online), it is reasonable to assume that the proportion of unmated ancestral cells did not change significantly and that the level of natural selection for a faster growing subpopulation during serial transfer in the first 100 generations was negligible. Thus, after correction by subtracting the background proportions of unmated ancestral cells (19% for each ancestral population) from population mating type frequencies at generation 100, the mean value of parameter with standard deviation in the three sequenced evolving populations, CS1–CS3, was: II, 0.302 ± 0.084; III, 0.010 ± 0.005; IV, 0.271 ± 0.012; V, 0.047 ± 0.018; VI, 0.118 ± 0.072; and VII, 0.252 ± 0.021.
Table 2.
Cell Survival Ratio in Ancestral and Sexual Populations after Starvation and Unmated Cell Ratio in Sexual Populations
| Survival Ratio |
Ratio of Unmated Ancestral Cells in Sexual Population | |||
|---|---|---|---|---|
| Replicate | Anc_IV | Anc_VI | Sexual Population | |
| 1 | 1.01 | 1.02 | 0.52 | 0.36 |
| 2 | 1.00 | 1.01 | 0.55 | 0.35 |
| 3 | 0.97 | 0.98 | 0.52 | 0.40 |
| 4 | 1.03 | 0.98 | 0.51 | 0.38 |
| 5 | 1.01 | 1.02 | 0.50 | 0.39 |
| Average | 1.00 | 1.00 | 0.52 | 0.38 |
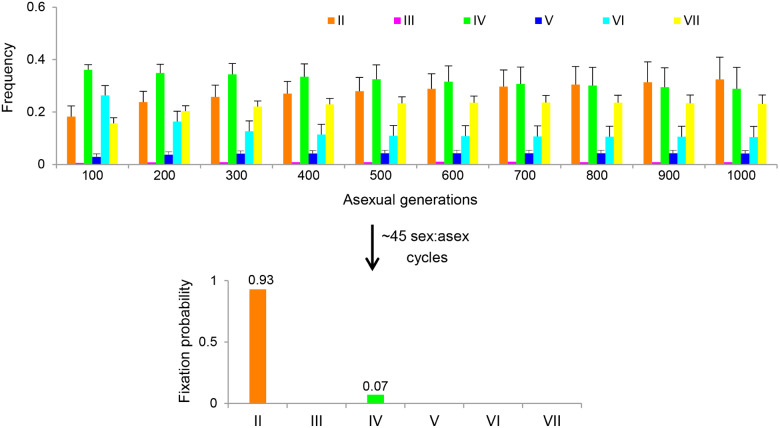
Using these estimated parameter values, we predicted the dynamics of mating type composition in experimental populations in the absence of natural selection during asexual cycles. Figure 6 shows that the frequency of mating type II tends to increase gradually, whereas frequencies of other types decrease during the ten sex:asex cycles. If sufficient sex:asex cycles were performed, mating type II would almost certainly become fixed in the population. Due to fluctuations in parameter , mating type IV also had a probability of about 7% of becoming fixed.
Fig. 6.
Predicted dynamics of mating type composition in experimental populations. Bar chart depicting the changes in mating type frequencies during the first ten sex:asex cycles. Error bars represent standard deviation. After about 45 cycles, mating type II and IV are predicted to be fixed with probabilities of 93% and 7%, respectively. To simulate fluctuations in parameter , we generated each value drawn from a normal distribution with mean and standard deviation that were estimated from the experimental populations and normalized it by the sum of all values in . A total of 10,000 replicates were run.
Estimating Selection Coefficient and Identifying Beneficial Mutations
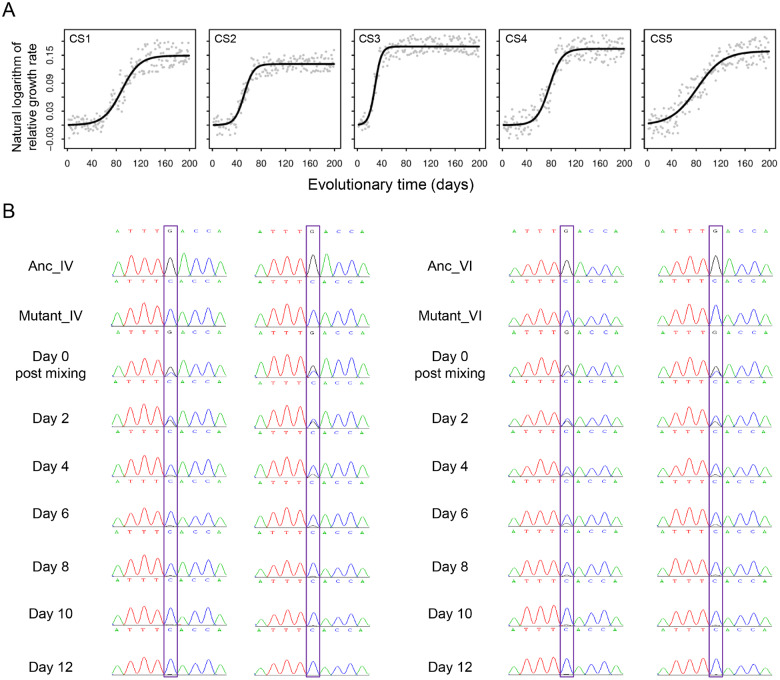
Regression analysis of the growth rate trajectories estimated the size of the selection coefficient (95% confidence interval) as: CS1, 0.117 ± 0.004; CS2, 0.102 ± 0.002; CS3, 0.136 ± 0.002; CS4, 0.130 ± 0.002; and CS5, 0.125 ± 0.002 (fig. 7A). To dissect the molecular basis for the increased growth rates, we performed whole-genome sequencing of the selected populations CS1–CS3. An average of 13.3 de novo mutations per population were detected and one candidate beneficial mutation was identified in each of the three sequenced populations. To verify the findings, we selected the candidate mutation in CS1, which results in a premature termination codon in a gene encoding a serine/threonine kinase (supplementary table S1, Supplementary Material online). Mutant cells were constructed by introducing this mutation into ancestor cells, mixed with corresponding ancestral cells, and propagated. Within 12 days, the ancestral cells had been completely replaced by the mutant cells (fig. 7B), providing clear evidence that the selected mutation confers a growth rate advantage.
Fig. 7.
Dynamics of population growth rate and functional validation of a candidate beneficial mutation. (A) Changes in the natural logarithm of daily relative growth rate (dots) in evolving populations were fitted with growth rate trajectories (lines). (B) In competition assays, mutant cells were mixed with an equal proportion of ancestral cells (left, Mutant_IV and Anc_IV; right, Mutant_VI and Anc_VI) and propagated for 12 days. Assays were performed in duplicate.
Natural Selection Is Responsible for Fixing a Single Mating Type in Each Population
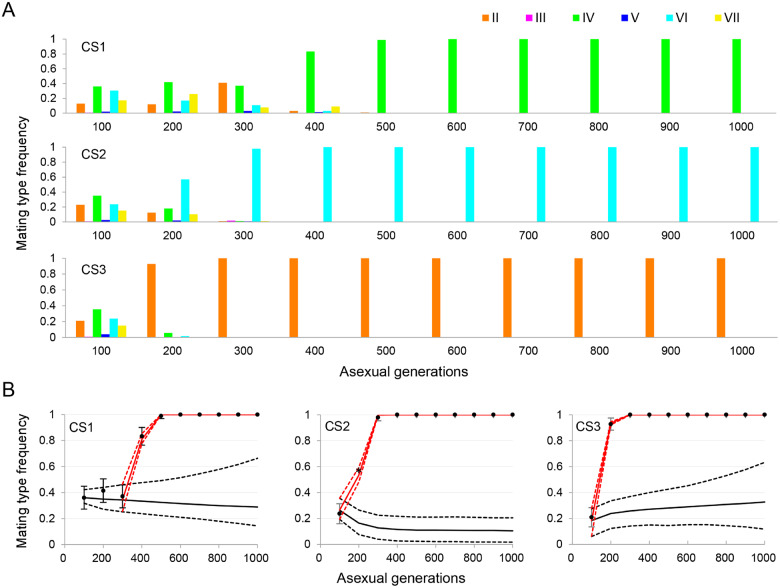
Mating type composition dynamics showed that at generation 100 populations CS1–CS3 each contained a mixture of cells with mating types II–VII. However, within each population a different single mating type quickly became dominant and then fixed (fig. 8A). Cytological observations also showed that after several sex:asex cycles mating eventually stopped in each population, indicating that the population evolved asexually from then onward (table 3). At generation 600, samples of cells from each population were mixed with cells of each of the six known mating types (II–VII) to determine the fixed mating type. Four different mating types had become fixed among the five replicate populations; this finding contradicts the theoretical analysis, which found that under the neutral model mating type II had a 93% chance of being fixed and mating type IV had a 7% chance of being fixed (fig. 6). Strikingly, mating type II became fixed in only one of the five populations.
Fig. 8.
Fixation of a single mating type in a population is caused by newly arising beneficial mutations. (A) Dynamics of mating type composition in populations CS1–CS3. Colored bars show the frequency of each mating type, as determined by sequencing. (B) Comparison of theoretical predictions and experimental observations of mating type fixation trajectories. Black dots show the observed frequency and error bars represent standard deviation. Solid lines show the predicted frequency trajectories with (red) and without (black) natural selection and dashed lines show the 99% confidence intervals. The frequency of mating type VI (and mating type composition) in population CS2 at generation 200 (marked with an asterisk) was estimated by setting the mating pair ratio as 0.81 (see table 3, CS2, cycle 3).
Table 3.
Cytological Determination of the Mating Pair Ratio in Each Sex:Asex Cycle
| Mating Pair Ratio |
|||||
|---|---|---|---|---|---|
| Sex:Asex Cycle | CS1 | CS2 | CS3 | CS4 | CS5 |
| 1 | 0.88 | 0.86 | 0.86 | —a | — |
| 2 | 0.83 | 0.80 | 0.82 | — | — |
| 3 | 0.87 | 0.81 | 0 | 0.80 | 0.86 |
| 4 | 0.73 | 0.03 | 0 | 0.87 | 0.56 |
| 5 | 0.32 | 0 | 0 | 0.43 | 0.06 |
| 6 | 0.01 | 0 | 0 | 0 | 0 |
| 7b | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 |
Data not observed.
Fixed mating types in population CS1–CS5 were IV, VI, II, IV, and VII, respectively.
The larger than expected number of fixed mating types among the five populations provided strong evidence for natural selection. Therefore, we further examined the speed of mating type fixation to see if this agreed with the theoretical prediction based on the estimated selection coefficients, as follows. For each population, by comparing the observed frequency trajectory of the fixed mating type with the model’s prediction without selection, we determined the point at which a significant discrepancy appeared and thus inferred when the beneficial mutation was most likely to arise. For this, we used the newly developed population genetics model incorporating computer simulation that allows consideration of temporal changes in the SD pattern and experimental details such as periodic cell transfer. The model had excellent agreement with experimental findings when the mutations were assumed to arise in the MAC during sexual reproduction after the point at which the discrepancy appeared, for example, the fourth round of mating at generation 300 for CS1 (fig. 8B). Due to a capacity issue, sequencing of population CS2 at generation 200 was delayed, resulting in an unreliable result. However, we used computer simulation based on the observed mating pair ratio at the third sex:asex cycle to estimate the maximum frequency of mating type VI at this point. This method was quite accurate. For example, based on pairing ratio of 0.32 for CS1 at generation 400, the frequency of mating type IV was estimated as 0.84, in good agreement with the frequency obtained from sequencing (0.83).
Analysis of populations CS1–CS3 suggested that the similar increase in fitness in populations CS4 and CS5 was probably also caused by newly arising beneficial mutations (fig. 7A) and the fixation of mating types (IV and VII, respectively) similarly occurred more quickly than predicted under the neutral model.
Discussion
In this study, we used a newly developed population genetics model to analyze the dynamics of population mating type composition in T. thermophila. This ciliate has a facultative sexual life cycle in which seven mating types are inherited through an unusual probabilistic SD mechanism. The theoretical model predicted the coexistence of all mating types or fixation of a single mating type, depending on the combination of parameters and the presence/absence of natural selection. However, when selection is strong enough, the model always predicted fixation of a mating type carrying a beneficial mutation.
When mating is induced by starvation in laboratory populations of Tetrahymena, a fraction of cells usually fail to conjugate even under optimal conditions (e.g., equal proportions of two mating types and sufficient time allowed for pairing) (Bruns et al. 1980). Our model therefore assumed that cells that remained unmated at the end of the pairing period consisted of 1) unpaired cells, caused by a limited chance of pairing (parameter αT) or a lack of compatible mating types when ; and 2) separation of compatible pairs (parameter β). In addition, the number of cells often decreases at the end of mating induction (table 2). Therefore, we assumed a probability of unmated cells surviving the starvation treatment and a probability of mated pairs producing viable sexual progeny. However, the ratio of to (parameter ) mainly determines the mating type composition pattern of the population (fig. 3). Previous evolutionary models for the number of mating types have often assumed that sex is obligate, and predicted that common mating types have lower reproductive success (Iwasa and Sasaki 1987). This assumption is equivalent to making infinitely large in our model. In this case, our model predicted that the distribution of mating types at equilibrium would be equal to SD pattern (eq. 8) and that this equilibrium would be reached after a single sexual cycle. However, by assuming that , our model actually generated positive frequency-dependent selection so that the mating type with the highest frequency or largest value would become fixed when was not very large. Most importantly, these parameters can be readily controlled or measured in experimental populations, making it possible to test the model’s validity as well as determining the predominant driving force for mating type composition in laboratory populations.
A striking feature of our experimental populations was the rapid fixation of a single mating type. As each population exhibited a substantial increase in growth rate compared with the ancestral population, the beneficial mutations were almost certainly responsible for mating type fixation. Since SD genes are not expressed in the MAC during asexual growth (Cervantes et al. 2013), fixation of a single mating type is likely due to so-called genetic hitchhiking of a beneficial mutation (Barton 2000). This result is consistent with a recent theoretical prediction that the number of mating types decreases with increasing fitness differences among mating types (Krumbeck et al. 2020). A previous theoretical study suggested that mating type switching (or probabilistic SD) might have evolved to increase the chance of finding a compatible sexual partner in the face of reduced diversity caused by genetic drift (Hadjivasiliou et al. 2016). However, our model and experimental results show that even in the presence of probabilistic SD, mating type diversity is still often lost in Tetrahymena.
All seven mating types of T. thermophila are generally present in adjacent natural habitats (Doerder et al. 1995). However, mating type composition was found to vary remarkably among different ponds, with local and seasonal variation in the same pond. Such situations were postulated to be caused by fluctuations in SD pattern through interactions between mat alleles of different strains and environmental factors (Arslanyolu and Doerder 2000). This hypothesis is consistent with our analysis, in that both the coexistence of all seven mating types and the fixation of a single mating type result from environmental changes that lead to the modification of key parameters (fig. 5). Interestingly, when examining local populations, often only a single mating type is found (Doerder et al. 1995), consistent with our analytical/simulation analysis that the overall probability is greater for fixation than for coexistence, particularly when natural selection is operating. This is advantageous for T. thermophila, since fixation of a single mating type that confers an advantage to the MAC enables the local population to grow faster, whereas the whole population retains all seven mating types through periodic sexual reproduction between local populations with different fixed mating types. In our experimental populations, mating types appeared to be fixed at random, reflecting the random generation of beneficial mutations with regard to mating type. About 25% of wild Tetrahymena isolates, including T. thermophila, are reported to have lost their germline MIC and are unable to form mating pairs (Doerder 2014). A possible cause may be that during extended periods of asexual growth, cells of a single mating type tend to accumulate changes that eventually lead to the loss of sexual capacity.
In conclusion, our theoretical model provides a powerful framework to analyze the dynamics of mating type composition in T. thermophila. Our experimental observations of mating type composition dynamics agreed well with the model’s predictions. Furthermore, the operation of natural selection on a newly arising beneficial mutation was the driving force in all five replicate populations. The ease of maintaining T. thermophila populations in the laboratory means that a deeper understanding of the relative importance of and interplay between various factors can be obtained in experimental populations in the future by altering environmental conditions and parameter values. The methodological framework we have developed could be applied in principle or with minor modifications to the study of other facultative sexual organisms with a multisex mating system, such as sister/related species of T. thermophila.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Supplementary Material
Acknowledgments
We would like to thank Eduardo Orias and Yong Zhang for helpful discussions during the course of the study. This work was supported by the National Natural Science Foundation of China (Grant Nos. 31525021, 31900316, 91631303 and 91631304) and the Wuhan Branch, Supercomputing Center, Chinese Academy of Science, China.
Data Availability
The raw DNA-seq data are deposited at the National Center for Biotechnology Information Sequence Read Archive database under accession number SRP080979.
Literature Cited
- Allen SL. 1967. Genomic exclusion: a rapid means for inducing homozygous diploid lines in Tetrahymena pyriformis, syngen 1. Science 155(3762):575–577. [DOI] [PubMed] [Google Scholar]
- Arslanyolu M, Doerder FP. 2000. Genetic and environmental factors affecting mating type frequency in natural isolates of Tetrahymena thermophila. J Eukaryot Microbiol. 47(4):412–418. [DOI] [PubMed] [Google Scholar]
- Barton NH. 2000. Genetic hitchhiking. Philos Trans R Soc Lond B. 355(1403):1553–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becks L, Agrawal AF. 2012. The evolution of sex is favoured during adaptation to new environments. PLoS Biol. 10(5):e1001317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billiard S, et al. 2011. Having sex, yes, but with whom? Inferences from fungi on the evolution of anisogamy and mating types. Biol Rev Camb Philos Soc. 86(2):421–442. [DOI] [PubMed] [Google Scholar]
- Bruns PJ, Møller KM, Leick V. 1980. Magnetic purification of mating Tetrahymena. Carlsberg Res Commun. 45(1):29–33. [Google Scholar]
- Burt A. 2000. Perspective: sex, recombination, and the efficacy of selection–was Weismann right? Evolution 54:337–351. [DOI] [PubMed] [Google Scholar]
- Cassidy-Hanley DM. 2012. Tetrahymena in the laboratory: strain resources, methods for culture, maintenance, and storage. Methods Cell Biol. 109:237–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cervantes MD, et al. 2013. Selecting one of several mating types through gene segment joining and deletion in Tetrahymena thermophila. PLoS Biol. 11(3):e1001518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K, Wang GY, Xiong J, Jiang CQ, Miao W. 2019. Exploration of genetic variations through single-cell whole-genome sequencing in the model ciliate Tetrahymena thermophila. J Eukaryot Microbiol. 66(6):954–965. [DOI] [PubMed] [Google Scholar]
- Chen X, Feng W, Yu Y. 2014. Comparisons among six strains of Tetrahymena by microcalorimetry. J Therm Anal Calorim. 115(3):2151–2158. [Google Scholar]
- Cingolani P, et al. 2012. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly 6(2):80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constable GWA, Kokko H. 2018. The rate of facultative sex governs the number of expected mating types in isogamous species. Nat Ecol Evol. 2(7):1168–1175. [DOI] [PubMed] [Google Scholar]
- Czuppon P, Constable GW. 2019. Invasion and extinction dynamics of mating types under facultative sexual reproduction. Genetics 213(2):567–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Souza T, Michiels N. 2008. Correlations between sex rate estimates and fitness across predominantly parthenogenetic flatworm populations. J Evol Biol. 21(1):276–286. [DOI] [PubMed] [Google Scholar]
- Doerder FP. 2014. Abandoning sex: multiple origins of asexuality in the ciliate Tetrahymena. BMC Evol Biol. 14(1):112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doerder FP, et al. 1996. Ecological genetics of Tetrahymena thermophila: mating types, i‐antigens, multiple alleles and epistasis. J Eukaryot Microbiol. 43(2):95–100. [Google Scholar]
- Doerder FP, Gates MA, Eberhardt FP, Arslanyolu M. 1995. High frequency of sex and equal frequencies of mating types in natural populations of the ciliate Tetrahymena thermophila. Proc Natl Acad Sci U S A. 92(19):8715–8718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas TE, Strassmann JE, Queller DC. 2016. Sex ratio and gamete size across eastern North America in Dictyostelium discoideum, a social amoeba with three sexes. J Evol Biol. 29(7):1298–1306. [DOI] [PubMed] [Google Scholar]
- Eisen JA, et al. 2006. Macronuclear genome sequence of the ciliate Tetrahymena thermophila, a model eukaryote. PLoS Biol. 4(9):e286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ennos RA, Hu XS. 2019. Estimating the number of sexual events per generation in a facultatively sexual haploid population. Heredity 122(6):729–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. 1930. The genetical theory of natural selection. Oxford: Clarendon Press. [Google Scholar]
- Hadjivasiliou Z, Pomiankowski A, Kuijper B. 2016. The evolution of mating type switching. Evolution 70(7):1569–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton EP, et al. 2016. Structure of the germline genome of Tetrahymena thermophila and relationship to the massively rearranged somatic genome. Elife 5:e19090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. 1966. The effect of linkage on limits to artificial selection. Genet Res. 8(3):269–294. [PubMed] [Google Scholar]
- Iwasa Y, Sasaki A. 1987. Evolution of the number of sexes. Evolution 41(1):49–65. [DOI] [PubMed] [Google Scholar]
- Kishimoto T, et al. 2010. Transition from positive to neutral in mutation fixation along with continuing rising fitness in thermal adaptive evolution. PLoS Genet. 6(10):e1001164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt DC, et al. 2012. VarScan 2: somatic mutation and copy number alteration discovery in cancer by exome sequencing. Genome Res. 22(3):568–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumbeck Y, Constable GWA, Rogers T. 2020. Fitness differences suppress the number of mating types in evolving isogamous species. R Soc Open Sci. 7(2):192126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang GI, et al. 2013. Pervasive genetic hitchhiking and clonal interference in forty evolving yeast populations. Nature 500(7464):571–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehtonen J, Kokko H, Parker GA. 2016. What do isogamous organisms teach us about sex and the two sexes? Philos Trans R Soc B. 371(1706):20150532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitis DA, Zimmerman K, Pringle A. 2017. Is meiosis a fundamental cause of inviability among sexual and asexual plants and animals? Proc R Soc B. 284(1860):20170939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long H, et al. 2016. Low base-substitution mutation rate in the germline genome of the ciliate Tetrahymena thermophila. Genome Biol Evol. 8(12):3629–3639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald MJ, Rice DP, Desai MM. 2016. Sex speeds adaptation by altering the dynamics of molecular evolution. Nature 531(7593):233–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenna A, et al. 2010. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 20(9):1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller HJ. 1932. Some genetic aspects of sex. Am Nat. 66(703):118–138. [Google Scholar]
- Nanney D. 1959. Genetic factors affecting mating type frequencies in variety 1 of Tetrahymena pyriformis. Genetics 44(6):1173–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanney D. 1960. Temperature effects on nuclear differentiation in variety 1 of Tetrahymena pyriformis. Physiol Zool. 33(2):146–151. [Google Scholar]
- Orias E, Baum MP. 1983. Mating type differentiation in Tetrahymena thermophila: strong influence of delayed refeeding of conjugating pairs. Dev Genet. 4(3):145–158. [Google Scholar]
- Orias E, Cervantes MD, Hamilton EP. 2011. Tetrahymena thermophila, a unicellular eukaryote with separate germline and somatic genomes. Res Microbiol. 162(6):578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orias E, Rohlf FJ. 1964. Population genetics of the mating type locus in Tetrahymena pyriformis, variety 8. Evolution 18(4):620–629. [Google Scholar]
- Orias E, Singh DP, Meyer E. 2017. Genetics and epigenetics of mating type determination in Paramecium and Tetrahymena. Annu Rev Microbiol. 71(1):133–156. [DOI] [PubMed] [Google Scholar]
- Otto SP, Lenormand T. 2002. Resolving the paradox of sex and recombination. Nat Rev Genet. 3(4):252–261. [DOI] [PubMed] [Google Scholar]
- Paixao T, Phadke SS, Azevedo RB, Zufall RA. 2011. Sex ratio evolution under probabilistic sex determination. Evolution 65(7):2050–2060. [DOI] [PubMed] [Google Scholar]
- Phadke SS, Zufall RA. 2009. Rapid diversification of mating systems in ciliates. Biol J Linn Soc. 98(1):187–197. [Google Scholar]
- Weismann A. 1889. The significance of sexual reproduction in the theory of natural selection. In: Poulton EB, Schönland S, Shipley AE, editors. Essays upon heredity and kindred biological problems. Oxford: Clarendon Press. p. 255–332. [Google Scholar]
- Xiong J, et al. 2015. Genome of the facultative scuticociliatosis pathogen Pseudocohnilembus persalinus provides insight into its virulence through horizontal gene transfer. Sci Rep. 5(1):15470. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The raw DNA-seq data are deposited at the National Center for Biotechnology Information Sequence Read Archive database under accession number SRP080979.