The broadband power shifts in entorhinal EEG are related to the firing of grid cells

Abstract

The relationship between the firing of the grid cell and mesoscopic neural oscillations is one of the key issues to understand the neural mechanism of grid cells. Previous studies have focused more on the correspondence between neuronal firing and phases of oscillations, such as phase precession. There are also some conclusions about the relationship between the activity of grid cells and the intensity of neural oscillations, such as the disappearance of grid pattern caused by the blocking of theta rhythm, but the correlation between the firing rates of grid cells and the narrowband power of neural oscillations or the broadband LFP power is still scarce. Through analyzing the records of spike times of grid cells and local entorhinal EEG obtained by Hafting et al., in the spatial navigation experiment, we find that grid cells are, to a large proportion, a kind of broadband-shift neurons, and the positive correlation between grid cell activity and power of low theta and gamma bands was observed. These results have well verified, promoted, and connected many scattered research conclusions, such as the broadband shift phenomenon of hippocampal neurons, the influence of low theta activity on the firing pattern of grid cells, and the positive correlation between single-cell activity and gamma-band activity. This work is of great significance for the study of the neural mechanism of grid cells at the micro and mesoscopic levels, and may also inspire the use of indicators such as broadband power as markers for grid cell activity.

Grid cell; Broadband shift; Theta oscillations;Gamma oscillations; LFP power.

1. Introduction

Since the discovery of grid cells [1], the unique grid pattern of regular triangular periodic repetitive firing fields has attracted the attention of many scientists [2, 3, 4, 5]. Grid cells, which are located in the entorhinal cortex and have important functional significance for spatial orientation [6, 7, 8], not only play the role of measuring scale in spatial navigation and are the basis for realizing path integration [9] but also been believed to play an important role in cognitive abstract space and are a special type of neurons for constructing cognitive maps [10, 11, 12]. One of the fundamental questions in the study of grid cells is to investigate the relationship between the firing of an individual grid cell and neural oscillations recorded in local field potentials (LFPs) which reflects the activity of neuron assemblies [13], that is, the correlation analysis between the neural activity of grid cells at microscopic and mesoscopic levels. There is much evidence for associations between microscopic neuronal firing rate and mesoscale oscillations across the cortex. Fries et al. found in 2001 that neuronal Spiking and Gamma frequencies are positively correlated [14]. Mukamel et al. also found in a 2005 study of preoperative human patients that neuronal firing in the auditory cortex was positively correlated with Gamma activity and negatively correlated with theta rhythm [15]. In 2008, Rasch et al. recorded the data of the visual cortex of monkeys and found that with the increase of firing rates of neurons, the power gamma band (40–90 Hz) increased, while that of 1–10 Hz decreased [16]. Besides, Siapas et al. also found a phase-locking relationship between spiking of the prefrontal neuron and the hippocampal theta rhythm in 2005 [17]. These studies show that there is a specific correlation between neuronal firing and narrowband oscillations reflected by the overall synchronous activities of neuron assemblies. Further, in 2009 Manning et al. found in their experiment that there is a considerable proportion of broadband-shift neurons in MTL, whose firing rates are positively correlated with broadband power [18]. For the study of specific neurons related to spatial navigation, Okeef et al. found a special correspondence by recording oscillatory signals of hippocampal LFP while recording the spiking of place cells of rats [19]. The phase of the theta oscillations corresponding to the moment of place cells spiking was advanced periodically when the rat moved toward the center of the place cell's firing field. This phenomenon is called phase precession [20]. In recent years, many pieces of research have been carried out on the relationship between the firing of grid cells and oscillations [21, 22, 23]. In 2008, Hafting et al. also observed phase precession of grid cells in the rat's entorhinal cortex similar to place cells [21]. In 2011, Brandon et al. and Koening et al. both independently found that suppressing the activity of theta oscillations causes the pattern of equilateral triangular periodic firing fields of grid cells to degenerate or even disappear [22, 23]. These efforts have undoubtedly strengthened the understanding of the relationship between grid cells and oscillatory activity [24]. However, most of these studies focus on the relationship between neuronal firing and the phase of narrowband oscillations [21, 25, 26, 27], the corresponding relationship between grid cell firing and the power of oscillations is lacking. The importance of the power of oscillations at specific frequencies should not be overlooked, as it is more likely to reflect functional differentiation of neurons firing simultaneously at different narrowband or overall broadband ranges.

Our work is based on the spatial navigation task of rats by Hafting et al [1, 21]. To study the relationship between neural firing and the power of oscillations, we used the action potential recording of 115 grid cells in layer 2–3 of the entorhinal cortex provided by them, as well as LFP recording of synchronous measurement. Consistent with previous research methods, we also investigated the LFP power measured synchronically with grid cell activity on both broadband and narrowband. We found that the phenomenon of the broadband shift was prevalent in grid cells. Grid cells with this property can also be classified as broadband shift neurons, which varied their firing with the overall height of the LFP power spectrum at all frequencies. Interestingly, we found a strong positive correlation between grid cell activity and both theta power and gamma power in narrowband oscillations, which did not occur in other frequency bands. It is suggested that in the study of grid cells and neural oscillations, not only phase coupling but also the power of broadband and specific narrowband oscillations should be considered.

2. Materials and methods

2.1. Experimental paradigm and data collection

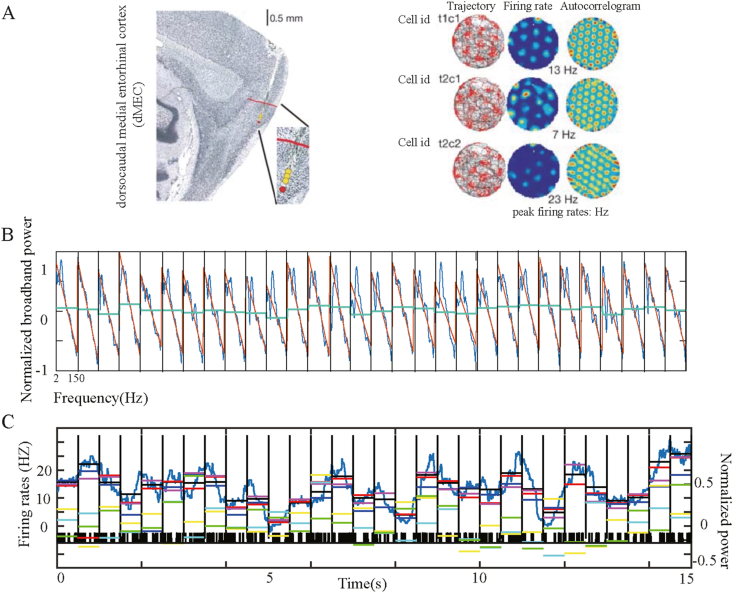
Experiment and data recordings were obtained from Hafting et al [1, 16]. Neuronal activity was recorded from 23 male Long-Evans rats (4–6 months old, 350–450 g). The animals were trained to collect chocolate chips that were thrown randomly into boxes, one at a time. Each trial lasted 10 min. Connect a rat to a recording device (Axona Ltd., Herts, U.K.) using ac-coupled Uni-Gain Operational amplifiers near the rat's head, and use a balancing cable so the rat can move freely in the available space. As shown in Figure 1A, red dots indicate recording locations. If the cells showed grid-like firing pattern (Figure 1A), the rats were moved to linear orbits for further recording. In a square cage, rats are trained to run back and forth in a straight line. The impetus for running comes from the chocolate chips at two turning points. Two linear tracks were further recorded, one 235 cm long and 10 cm wide, the other 320 cm long and 10 cm wide. The track is placed in the center of the open field (300 cm∗500 cm) and 50 cm above the ground. After the recorded neurons were identified as grid cells, the trial was conducted for 10–30 min, with at least 15 laps each time. A continuous record of the number of trials at each tetrode position ranging from 1 to 4. The cell samples included 115 mesenchymal cells from the second and third layers of the entorhinal cortex. The EEG signal sampling rate was 250 Hz and stored together with the spiking timestamp recorded by a single cell. Experiment recordings and data collection were obtained from the work of Hafting et al [1, 21]. Data is available from URL: https://www.ntnu.edu/kavli/research/grid-cell-data.4.2. Experimental ethics have been implemented in [1, 21], approved by the Norwegian Research Council's Centre.

Figure 1.

Recording positions in dorsal MEC, LFP power, and grid cell firing time series. A, The anatomical location of the grid cell of rats was recorded, as well as the grid pattern recorded in the spatial navigation experiment (figure quoted from Hafting et al., 2005) (left), The record position represented by red dots is displayed on the sagittal sections in layer 2 of the left dMEC (right), The Trajectory Maps (left), Rate Maps (middle), and spatial Autocorrelograms (right) of a typical grid cell recorded on the location of Figure A. Cell id refer to tetrode (t) and cell (c). B, Continuous 500 ms epochs were separated by vertical lines to observe the LFP power spectrum changes over time. In each epoch, the blue curve represents the overall LFP power spectrum, the orange line represents the linear fitting, and the green horizontal line represents the average broadband power. C, The variation of the grid cell's firing rates is compared with that of the power spectrum of each frequency band. The black ticks show the time when a single spike occurs, the dark blue curve indicates the smoothed firing rate of the grid cell, and the horizontal black lines show the average firing rate per epoch. The average power at each frequency band is represented by colored short horizontal lines with different proportional ordinates, with colors denoted as delta (yellow), low theta (blue), high theta (cyan), beta (green), gamma (purple), broadband (red).

2.2. EEG data processing

We convolute the spike sequence of each grid cell with a Gaussian kernel (half-width of 500 ms) to calculate the smoothed firing rate at each time point. In order to prevent the action potential waveform generated by the low-frequency component from polluting the LFP signal, interpolation replacement was performed for the data samples from 2 ms before to 8 ms after spike [38]. We used Morlet wavelets (wave number = 4) to measure the power of the LFP signal at 50 log-interval frequencies between 1 and 150 Hz. Since the oscillating power is chi-square distribution at a given frequency [39], we applied a logarithmic transformation to the power calculated by the wavelet to make its distribution closer to the normal distribution. To analyze the relationship between LFP spectral power and grid cell spiking activity, and to provide a reasonable balance between maximizing temporal resolution and minimizing the correlation between continuous measurements, we then divided each record into a 500 ms epoch. To eliminate the impact of non-biological noise on our analysis, we removed epochs with firing rates above the 99th percentile. We calculated the average power of LFP in the following frequency bands: delta (2–4 Hz), low theta (4–8 Hz), high theta (8–12 Hz), beta (12–30 Hz), and gamma (30–150 Hz). In addition to measuring the LFP power in the narrow band, we also used Manning's method to calculate the broadband power where the LFP voltage fluctuation occurred in a wide frequency range [18]. In this method, the wavelet power spectrum of each epoch is linearly fitted by the robust regression method [40]. The robust regression algorithm minimizes the influence of narrowband oscillations on the calculated broadband power. Narrowband oscillations appear as local peaks in the LFP power spectrum, while broadband power refers to the average height of the robust regression fitting line in each epoch (Figure 1C, red line).

2.3. Regression framework

Derived from Manning et al. 's methods, we used a series of least squares regressions to identify band shift neurons. For each neuron, we establish five regression equations (one equation for each frequency band and broadband) $R={\beta }_0+{\beta }_{B}B+{\beta }_{F}F$. In the regression equation, R is a vector containing the estimated firing rate of grid cell within each epoch, F is a vector containing the average power of one band in five narrowband frequencies within each epoch, and B is a vector containing the broadband power. Before calculating the average power of each electrode for each narrowband, we z-transformed the power of each frequency so that its mean value is 0 and SD is 1. This step ensures that the individual frequency contribution of each frequency band is equal, provided that the overall power spectrum remains in the shape of $1/f^a$.In this way, the regression model is used to calculate once in each frequency band, a total of five times, and the regression coefficient is calculated separately each time. If the ${\beta }_B$ coefficients on all five regressions are significantly different from 0 and all regressions have the same symbol, we call this grid cell a broadband shift neuron. This algorithm ensures that broadband power can explain the variation of grid cell firing rates more strongly than any narrowband power. Similarly, if the regression coefficient of narrowband power in the prediction model of firing rates is significantly different from 0, then the corresponding grid cells will be labeled as narrowband shift neurons in the corresponding frequency band. Here we can tell whether the shift is positive or negative by the sign of β. It should be noted that significant narrowband shift neurons may become not significant if the broadband is controlled.

2.4. Multiple comparison correction

To correct multiple comparisons among multiple frequency bands, the permutation test method was used for statistical analysis. The procedure of the permutation test is as follows: we used a bootstrap procedure to calculate a p threshold to use for each statistic. For each grid cell, the time series of firing rates are divided into two parts by randomly selected time points, and then the two parts are exchanged to reassemble a new vector of pseudo-random firing rates, which is then substituted into the regression equation to obtain a regression coefficient and p-value. This process was repeated 1000 times to obtain the distribution of the p-value at the random level and the p threshold at the significance level of 5%. Then the p-value obtained in the real situation was compared with the p threshold value to test whether the false positive rate of each grid cell was less than the significance level of 5%. At the level of all grid cells, we calculated the percentage of neurons with statistical significance and compared them with the percentage of research results of Manning et al [18]. Limited by the size of the sample size, we did not conduct statistical analysis at the subject level. All data processing and statistics were performed using MATLAB 2018b (Mathworks Inc, USA).

3. Results

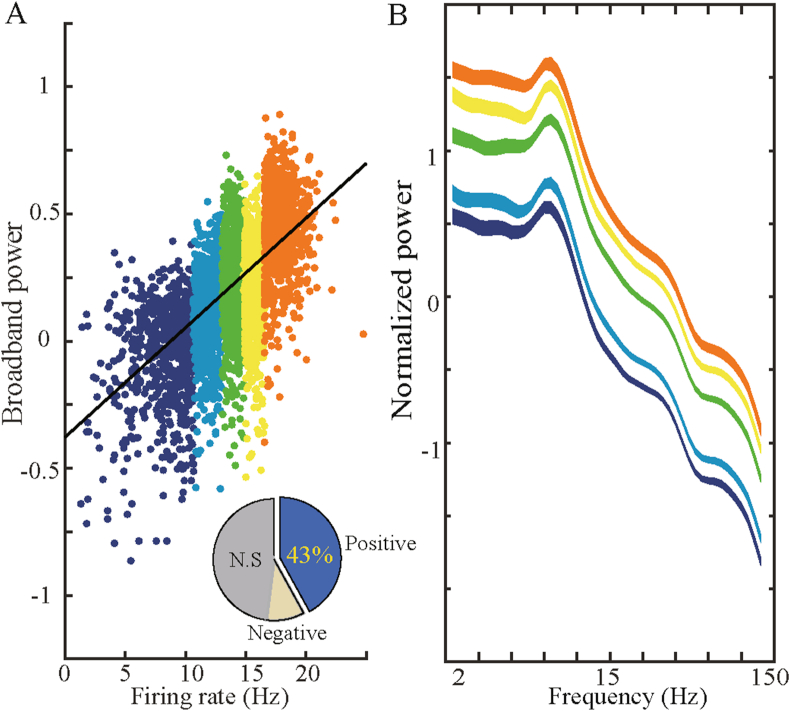
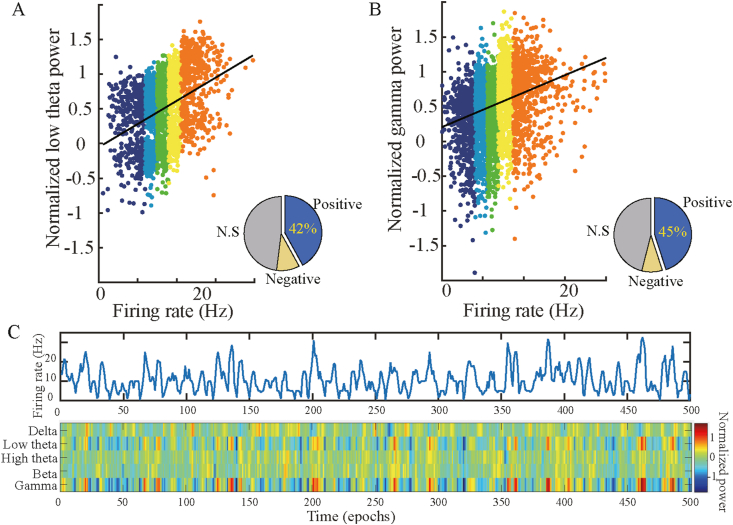
The spiking records of 115 grid cells in layer 2 and 3 of the medial entorhinal cortex (MEC) and the local entorhinal electroencephalogram (EEG) records of 23 male Long-Evans rats in the navigation experiment (available at https://www.ntnu.edu/kavli/research/grid-cell-data) were used in our work to analyze the synchronous activity between the firing rates of these grid cells and the power of oscillations in different narrowband and over broadband. In the analysis of broadband oscillations, we use Manning's method to calculate the broadband power (see Method) and measure the overall level of the LFP power spectrum without any influence of narrowband oscillations. Similar to what Manning et al. observed in hippocampal neurons before, we found the broadband-shift phenomenon of grid cells in MEC. In other words, firing rates of grid cells are positively correlated with broadband power. As depicted in Figure 1, a typical grid cell numbered T5C1 from #11 rats presents an obvious phenomenon of LFP broadband power shifts with the increase of spiking density. Figure 1A depicts 30 consecutive 500 ms epochs, within each epoch, a standardized LFP power spectrum was presented with a black line, a linear regression of broadband power with a brown line, and an average broadband power with a red horizontal line. Figure 1B shows the spiking density of grid cells represented by black tick marks, the curve of firing rates in blue, and horizontal short lines of various colors: the average broadband power (red), the average firing rate (black), and the average LFP power of five narrowband frequencies within each epoch. More specifically, delta (2–4 Hz) (yellow), low theta (4–8 Hz) (blue), high theta (8–12 Hz) (cyan), beta (12–30 Hz) (green), and gamma (30–150 Hz) (purple). The broadband power and the firing rates of grid cell recorded simultaneously are significantly positively correlated across epochs (Pearson's R = 0.85, p<${10}^{-10}$), reflecting the overall shift of the LFP power spectrum with the enhancement of grid cell firing. To determine whether this broadband shift mode was reliable throughout the recording process, we examined the average broadband LFP power and average firing rate recorded by the grid cell for each of 1,200 half-second epochs. Each color dot in Figure 2A represents a record of an epoch similar to that in Figure 1, which is 500 ms in length. The horizontal axis represents the firing rate of the grid cell, and the vertical axis represents the standardized broadband power. The scattered dots were marked with five different colors according to the firing rates of the grid cell, increasing from blue to red. It can be observed that colored dots cluster diagonally upward, meaning that firing rates and broadband power, respectively represented by horizontal and vertical coordinates, show significant positive correlations (Pearson's R = 0.7, P <${10}^{-10}$). This relationship is presented statistically at five levels of increasing firing rates, as shown in Figure 2B. Five LFP power spectrum curves with variance are represented by the same five colors as in Figure 2A. With the increasing of the level of firing rates, the whole LFP power spectrum curve shows an upward shift. Subsequently, similar work was done for the five narrowband LFP oscillations: delta (2–4 Hz), low theta (4–8 Hz), high theta (8–12 Hz), beta (12–30 Hz), and gamma (30–150 Hz). The observation of 30 consecutive epochs with a duration of 500 ms is shown in Figure 1B. Based on this method, the work of pattern discrimination is extended to the entire recording session. A significant positive correlation between narrowband power and firing rates (P <${10}^{10}$) was observed only in low theta and Gamma bands (Figure 3A-B). This can also be intuitively observed from the comparison of two-dimensional time-frequency graphs of power changes in each narrowband frequency and firing rates of grid cells (Figure 3C).

Figure 2.

Illustration of the positive shifts between the firing rate of the typical grid cell and broadband power. A, The average firing rate of the grid cell and broadband power in each 500 ms epoch in Figure 1D is shown in 2d space. A pair of data in each epoch is represented by a colored dot. The color of each dot represents the firing rate level of grid cells. Warm color represents epochs with high firing rates, and the cool color depicts the low firing rates epochs. The black line shows the linear fitting of the least-squares regression to the data. The proportion of all grid cells with significant positive shifts is shown in the figure at the bottom right (the positive proportion is 43% and N.S is not significant). B, The average LFP power spectrum at five levels of firing rates was presented by the same color scheme in A. The power spectrum curves show positive displacement with the increase of firing rate at all observed frequencies. The standard deviation of the data is expressed as the thickness of the curve.

Figure 3.

Relationship between narrowband power and grid cell's firing rate. A, Consistent with the color scheme in Figure 2, the data pairs of low theta power and grid cell's firing rate in the epoch of 500 ms in the records were represented by a scatter plot, and the black line was the linear fitting of all data points. Low theta power is significantly positively correlated with the firing rate (P < 0.001). The proportion of all grid cells with significant positive shifts is shown in the figure at the bottom right (the positive proportion is 42% and N.S is not significant). B, The scatter diagram of gamma power and firing rate in all epochs showed significant positive correlation (P < 0.001). The proportion of all grid cells with significant positive shifts is 45%. C, An illustration of time-frequency heat maps of power variations in the five narrowband on 500 epochs and firing rates curves of grid cells in corresponding time. Top: Curve of firing rates of grid cells; bottom: two-dimensional heat map depicts power changes of five narrowband over time. From top to bottom of the increasing frequency band is presented by five rows (delta, low theta, high theta, beta, gamma). The abscissa represents epochs increasing with time, and the color represents the normalized narrowband power in each epoch. Warm colors indicate high power values.

Then, we attempted to identify the larger range of relationship patterns between the large number of grid cell samples extracted from the data of Hafting et al. 's linear orbit experiment and the LFP record of the medial entorhinal cortex.

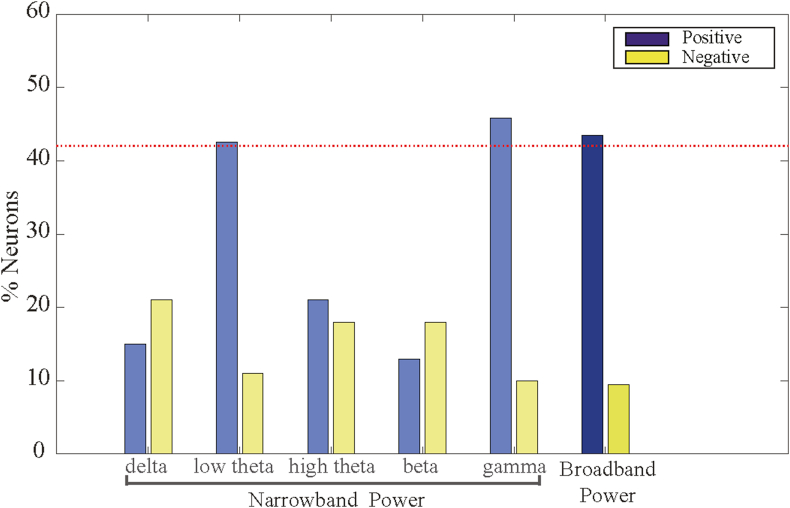
The grid cells in our study were recorded in layer 2 and 3 of the entorhinal cortex (Figure 1A), adjacent to the hippocampus in MTL. To further illustrate the robustness of the band shift phenomenon, we calculated the ratio of significant shifts in broadband and narrowband across all 115 grid cell neurons in the data set. As shown in Figure 4, we observed the broadband-shift pattern of grid cells and the band shift phenomena associated with low theta and gamma power. Of all recorded grid cells, 43% are broadband shift neurons and 45% are gamma-band shift neurons. Specifically, the proportion of low theta band shift neurons in grid cells was 42%, which is different from other neurons in MTL.

Figure 4.

The proportion of grid cells whose firing rate is significantly band shifts. The LFP component of the entorhinal cortex predicted the intensity of grid cell activity. The blue bars represent the percentage of grid cells showing positive band shifts. The yellow bars represent the percentage of grid cells with negative shifts. The columns on the left show the proportion of grid cells within each narrowband, namely delta (2–4 Hz), low theta (4–8 Hz), high theta (8–12 Hz), beta (12–30 Hz), and gamma (30–150 Hz). The right-most column shows the proportion of grid cells whose firing rate is related to broadband power.

This difference may be because the target neurons we selected for analysis are grid cells with specific equilateral triangular periodic firing fields rather than all neurons in the hippocampus. The grid pattern of grid cells has been shown in many studies to be significantly correlated with theta power [23, 28, 29], which is presumed to lead to the enhancement of the theta band shift phenomenon. The causality among them needs to be further studied. Unfortunately, both gamma and low theta bands have high levels of positive and negative correlation, which means that the narrowband shift pattern is not as stable and robust as that of broadband.

Our work shows that grid cell, an important specific neuron in the construction of the cognitive map, is a kind of broadband shift neuron. Moreover, the firing rates of grid cells was positively correlated with the power of low theta and gamma bands in narrowband LFP activity, but not significantly correlated with other bands such as delta, high theta, beta, etc. These conclusions further clarify the relationship between grid cell firing and LFP power described in the prior literature [22, 23] and provide insights for future studies on the intersection of grid cells at the microscopic and mesoscopic levels.

4. Discussion

We examined the relationship between the neuronal activity of the grid cell and the simultaneously measured LFP power. Although previous studies have shown that the firing of a single neuron is related to gamma power of narrowband oscillations [15, 16]and broadband LFP power [18], and some studies have shown that the firing of grid cells is closely related to the theta rhythm of LFP [22, 23, 28], there is no study on the relationship between the LFP power and the neuronal firing of the grid cell which is related to the construction of the cognitive map [7, 30, 31, 32]. In terms of the relationship between grid cell activity and narrowband LFP power, studies have shown that if the medial septal nucleus is inactivated to inhibit theta oscillations, the pattern of equilateral triangle periodic continuous firing fields of grid cell will gradually degenerate or disappear [22]. The study of Koenig et al. also confirmed the association between this grid pattern and theta rhythm [23]. However, there is no clear research on the correlation between firing rates of the grid cell and LFP power.

Our analysis showed that grid cells are indeed broadband-shift neurons, and their activity is positively correlated with the broadband LFP power. This consistent with the previous conclusion by Manning et al. that there is a broadband-shift phenomenon in neurons in the hippocampus [18]. In recent years, broadband effects have been widely observed in behavioral cognitive processes such as auditory stimuli [33], visual stimuli [34], and motor stimuli [35]. In particular, Broadband power is associated with some spatial and verbal memory processes, rather than within a specific narrowband range [36, 37]. Our work finds direct evidence for a correlation between the single-neuron activity of grid cells and the overall spectrum of LFP Power, demonstrating that grid cells are, to a large extent, a type of broadband-shift neurons.

At the same time, we also found a positive correlation between grid cell firing and gamma power, which verified the previous study on the consistency between single-neuron activity and gamma power. Furthermore, we also observed a similar positive synchronization of low theta power with grid cell activity intensity, which deepened our understanding of the relationship between grid cell firing and low theta oscillations: not only is the grid pattern associated with low theta rhythm but also the firing rates of the grid cell is associated with low theta power. It is important to note that these conclusions should be further examined after controlling for broadband power.

According to Manning's study on the percentage of positive broadband shift neurons in multiple brain regions, the proportion of positive broadband shift neurons in the medial temporal lobe (MTL) is significantly higher than that in the neocortex. In the subregions of MTL, the proportion of positive broadband shift neurons in the hippocampus (HPC) (42%) was higher than that in parahippocampal (PAR) and amygdala (AMAG). Manning et al. measured the proportion of band shift neurons in each frequency band. Only in the gamma band and over broadband, the proportion of neurons with positive shift characteristics is greater than 30%. Our conclusions are consistent with those of Manning et al.

However, the phenomenon of narrowband shift is not stable, and the obvious correlation is positive and negative interleaving. The factors that influence this stability will be further explored. The regression p-values were not corrected for multiple comparisons (for number of cells), so the estimates of the percentage of significant shift-cells are likely to be slightly high due to false positives. The results of our study are based on biological experiments on invasive single-cell records to discover the broadband- shift characteristic of grid cells. Broadband power may be used as a characteristic marker for grid cell firing. Moreover, with the power changes of the narrowband low theta and gamma oscillations, we can find more new research and discovery on the role of grid cells in complex cognitive activities and cognitive map construction at the mesoscopic level of neuron assemblies.

Declarations

Author contribution statement

Wenjing Wang: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.