Semi-automatic sigmoid colon segmentation in CT for radiation therapy treatment planning via an iterative 2.5-D deep learning approach

Abstract

Automatic sigmoid colon segmentation in CT for radiotherapy treatment planning is challenging due to complex organ shape, close distances to other organs, and large variations in size, shape, and filling status. The patient bowel is often not evacuated, and CT contrast enhancement is not used, which further increase problem difficulty. Deep learning (DL) has demonstrated its power in many segmentation problems. However, standard 2-D approaches cannot handle the sigmoid segmentation problem due to incomplete geometry information and 3-D approaches often encounters the challenge of a limited training data size. Motivated by human’s behavior that segments the sigmoid slice by slice while considering connectivity between adjacent slices, we proposed an iterative 2.5-D DL approach to solve this problem. We constructed a network that took an axial CT slice, the sigmoid mask in this slice, and an adjacent CT slice to segment as input and output the predicted mask on the adjacent slice. We also considered other organ masks as prior information. We trained the iterative network with 50 patient cases using five-fold cross validation. The trained network was repeatedly applied to generate masks slice by slice. The method achieved average Dice similarity coefficients of 0.82 0.06 and 0.88 0.02 in 10 test cases without and with using prior information.

1. Introduction

Organ segmentation is of critical importance for the treatment planning of radiation therapy. During the planning process, organs of interests are delineated to support the assessment of radiation doses to them, which is necessary to evaluate radiation toxicity and hence the quality of a treatment plan (Dolz et al., 2016; Gómez et al., 2017; Cefaro et al., 2013). This is especially important for those radiosensitive organs such as colon (Protection, 2007). Organ segmentation is conventionally performed manually by physicians or qualified staffs. This is a time-consuming process due to the complexity of segmenting a 3-D organ shape in a volumetric image by seeing only orthogonal 2-D planar images, as well as the large number of organs to be delineated for each patient case. It can take several hours to segment multiple organs of a patient (Pekar et al., 2004), depending on the institutional protocols and number of image slices (Mayadev et al., 2014). The task is also error prone, especially when it is performed under a time pressure (Campadelli et al., 2009). Errors such as inaccurate boundary delineation, missing slices, incorrect contours belonging to a different structure may occur (Hui et al., 2017), which affect the quality of treatment planning. Therefore, it is highly desired to automate the organ segmentation task for radiotherapy treatment planning to improve plan quality, patient safety, as well as workflow efficiency.

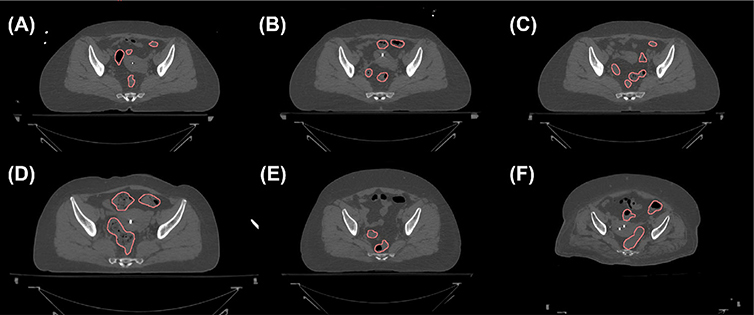
Automatic organ segmentation is a classical problem in medical imaging and extensive research efforts have led to a lot of successes for a variety of organs and clinical scenarios (Sharma and Aggarwal, 2010; Ghose et al., 2015; Meiburger et al., 2018). Nonetheless, one organ that remains challenging is sigmoid colon due to three main reasons. First, being a tube-like structure folded in the 3-D space, sigmoid colon naturally has a very complex 3-D shape. Second, there is a large variation of organ size, shape, and filling status among patients, even for the same patient at different time (see Fig. 1). Third, the sigmoid has a very similar image intensity in CT from other nearby organs, such as small bowel and uterus, making it hard to differentiate the sigmoid from other organs.

Fig. 1.

Axial CT slices containing the sigmoid colons (contours). Multiple disjointed regions can belong to the same sigmoid colon, as they are connected via the third dimension. (a)–(c) The same patients scanned at three different days separated by about one week. CT slices approximately at the same axial level are shown. (d)–(f) Three other patients.

Over the years, existing relevant studies mainly focused on CT colonography (Van Uitert et al., 2006; Franaszek et al., 2006; Gayathri Devi and Radhakrishnan, 2015; Lu and Zhao, 2013; Lu et al., 2012), which is in fact a different context from radiotherapy, as the bowel is typically evacuated in colonography and may contain contrast agents to distinguish it from surrounding structures. In these cases, thresholding has been proven to be a very effective method of segmentation, as the bowels are easily identified based on different HU values of air or contrast agents from the surrounding pelvic region. Lu and Zhao (2013) presented a method by first using a simple thresholding approach to obtain the organ region and then determining the centerline and filling gaps to improve the accuracy of the final result. Franaszek et al. (2006) segmented the colon wall based on an initial thresholding and using level set methods to obtain the wall boundary. Gayathri Devi and Radhakrishnan (2015) used thresholding to generate an initial colon segmentation and then applied machine learning methods to separate lung and fluids from the segmented colon wall. Zhang et al. (2012) developed a vasculature guided method to delineate the small bowel on contrast-enhanced CT angiography. Although these methods were able to generate satisfactory results, the success often relied on the intensity difference between colon and other nearby organs. Hence, these approaches may not be applicable to the context of radiation therapy treatment planning, where the patient bowel is often not purposely prepared, and CT contrast enhancement of bowel is usually not employed.

Lately, with the advancements in deep learning, deep neural networks (DNNs), especially convolutional neural networks (CNNs) (Litjens et al., 2017), have made great strides in medical image analysis (Shen et al., 2020), including image segmentation. Numerous DNNs have been trained to map an input image into the masks of interest. One remarkable example is U-Net that employs convolutional layers, down- and up-sampling layers, and skip connections to extract and analyze features at different spatial scales for effective image segmentations (Ronneberger et al., 2015). Without surprise, the success of DNN has also been extended to the organ segmentation context (Martin et al., 2010; Makni et al., 2009; Roth et al., 2017). The U-Net architecture has been used to segment a variety of structures (Kazemifar et al., 2018). For example, in Balagopal et al. (2018), the authors employed a 3-D U-Net and enhanced its performance by combining the network with ResNeXt blocks to simultaneously delineate the bladder, prostate, rectum, and femoral heads with superior results over other state-of-the-art methods. Many groups have reported novel DNN architectures to improve performance (Roth et al., 2017; Akkus et al., 2017; He et al., 2019). A recurrent neural network was also employed for general biomedical image segmentation, which refines the segmentation result over several time steps (Chakravarty and Sivaswamy, 2018).

Nonetheless, the simple application of a typical DNN-based segmentation approach that attempts to directly map an input image to the segmentation mask would encounter difficulties in the sigmoid segmentation problem. In fact, because of the tube-like structure folded in the 3-D space, multiple disjointed regions in a 2-D CT slice may belong to the same sigmoid, as they are connected via other slides. See Fig. 1 for examples. Hence, segmenting the sigmoid colon in a 2-D CT slice is an ill-defined problem due to incomplete geometry information. It is expected that methods working on 2-D images, including DNN-based ones, cannot solve the problem. On the other hand, a 3-D volumetric image has the complete geometry information and segmenting the organ in the 3-D space is feasible in principle. Yet apart from a high computational load, training a DNN requires a large amount of patient cases, as each patient case should be treated as an independent sample, which poses a practical challenge. The performance of the 2-D and 3-D DNN approaches will become more clear in Section 3.2.4.

Aiming at solving this challenging problem, in this paper, we propose a novel iterative 2.5-D deep-learning approach that segments this organ in a slice-by-slice fashion. The idea was motivated by the human’s behavior when solving this problem manually. When clinicians are tasked to delineate the sigmoid colon, they typically start from the top most level of the rectum, which is relatively easy to identify and is known to connect to the sigmoid. Then they outline the sigmoid by sequentially looping axial CT slices, while considering the connectivity between organ masks in adjacent slices. The major contributions of this work are three-fold.

1. Different from most of existing studies using DNNs for organ segmentation that directly establish a mapping between the input image and the output mask, we proposed an innovative idea to sequentially segment the organ slice by slice by using a CNN in an iterative fashion. This was designed to mimic the human’s behavior when segmenting the sigmoid colon.

2. We developed a CNN structure combining 2-D and 3-D filters and embedded it in an iterative scheme to realize the aforementioned idea. We further developed a training scheme with a long-term loss function to stabilize the CNN’s performance and avoid error propagation in the iterative inference process. The feasibility and advantages of the proposed approach were demonstrated in test patient cases.

3. To our knowledge, this was the first study tackling the sigmoid segmentation problem without special requirements on this organ, such as sigmoid colon evacuation or contrast agent enhancement.

The remaining sections are organized as following: Section 2 will present our proposed method, the training methodology and some implementation details. In Section 3, we will conduct extensive tests to evaluate the proposed method and demonstrate its effectiveness. After giving discussions in Section 4, we will conclude this work in Section 5.

2. Method

2.1. Overall idea

The overall idea was to build human’s actions in a deep-learning segmentation framework. In the manual segmentation process, a human typically starts with the top most level of rectum, for which the rectum mask is known (Fig. 2 A). S/he then loops over axial CT slides along the inferior to the superior direction to delineate the sigmoid slice by slice. When drawing a new mask in a certain slice, connectivity with the known mask in the previous slice is considered (Fig. 2 B). Since the sigmoid colon curves multiple times, a few sweeps along the inferior-to-superior and superior-to-inferior directions are needed to gradually segment the entire organ (Fig. 2 C–D). The goal of this study was to develop a CNN in lieu of a human in this process to generate the sigmoid colon mask.

Fig. 2.

Graphical illustration of the main idea. (A) The complete sigmoid colon (light blue) is connected to rectum (not shown). The yellow line indicates the superior-most mask of the rectum. (B) Starting at the rectum mask and moving towards the superior direction, only a portion of the sigmoid is segmented slice by slice (dark blue). (C) At the superior most slice, we iterate for the second time but towards the inferior direction to further segment a descending section of the sigmoid. (D) This process is repeated once more in the third sweep to fully segment the sigmoid colon. Directions of segmentation in sweeps are indicated by the red arrows. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Workflow and network structure

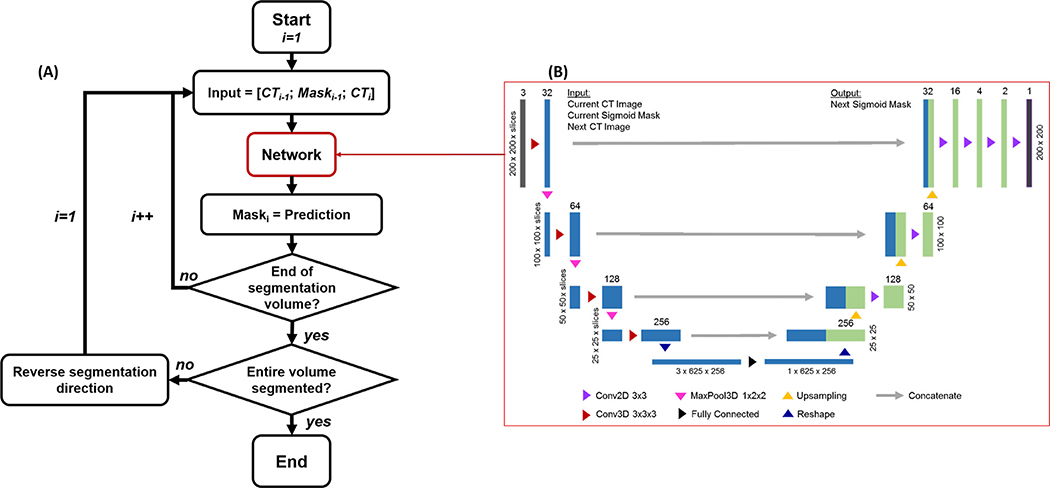
Because of the iterative nature of the idea, we would like to realize a workflow depicted in Fig. 3(A) with a network to realize a function

$$Y_i=f\left(Y_i\ast 1,x_{i-1},x_i\mid \theta \right)$$ (1)

where θ represents the network parameters, x_i−1 and Yi∗ 1 are the axial CT image and corresponding known binary sigmoid mask in the (i − 1)th slice, respectively. Y0∗ is the known rectum mask on the superior-most slice of the rectum. xi is the axial CT slice i that we would like to segment. Yi is the binary network output of the segmented region on this slice.

Fig. 3.

(A) Workflow employing the CNN in (B) for sigmoid segmentation slice by slice. (B) Detailed structure of the CNN. Layer height, width, and depth are marked on the sides of each layer. Number of channels at each layer is specified at the top.

Once this network function was developed, it was applied in the workflow in Fig. 3(A). The initial condition of this iterative process, i = 1, was chosen at the junction between rectum and sigmoid. We assumed that the rectum mask was known at the previous slice i = 0, which is typically true, as the rectum can be easily segmented manually or automatically. With the knowledge at the (i − 1)th slice, the network function was invoked to segment the sigmoid colon in the ith slice. The function was repeatedly invoked until we reached the top most axial slice of the CT volume. In this first sweep towards the superior direction, the first ascending section of the sigmoid colon was gradually generated. Note that the top most slice of the CT volume should be superior to the top of the first ascending section, as the sigmoid was fully contained in the volume. In this case, nothing was segmented, once the iteration went beyond the top of the ascending section. After reaching the top of the volume, we reversed the segmentation direction and entered into the second sweep towards the inferior direction. This generated the descending section of the sigmoid.

Again, the bottom slice should be lower than the lowest point of the descending section. The sweeps were repeated multiple times. In each sweep, we reversed the segmentation direction to capture one section of the organ. The segmentation process continued, until the predicted sigmoid volume did not change from one sweep to the next or until a predefined maximum number of sweeps was reached. In practice, we set the maximum number of sweeps to three, as this was found to be sufficient for all the cases studied in this paper.

The specific network structure to realize Eq. (1) is displayed in Fig. 3(B). We employed a network structure similar to U-Net. It had three input channels, each being a 2-D image. Along the descending arm of the network, the inputs were processed by 3-D convolutional layers prior to downsampling via 3-D max-pooling layers. 3-D convolutions were chosen along this arm, rather than 2-D ones, to allow the model to consider the relationship between the three input 2-D images. At the base of the network, the input was flattened and processed by a fully connected layer, reducing the data into one 2-D image. The result was then processed by 2-D convolutional layers along the ascending arm of the network. For each 2-D or 3-D convolutional layer, the output was processed by both a batch normalization layer (Ioffe and Szegedy, 2015 ) and a ReLU activation layer. At each level, a skip connection was used to bring information directly from the descending arm to the ascending arm by concatenating the feature images after the max-pooling layer on the descending arm with the image on the ascending side. The output of the final network was processed by a sigmoid-shape activation layer, followed by a thresholding operation to generate a 2-D binary mask. We would emphasize that although the network seemed to be similar in structure to the conventional U-Net (Ronneberger et al., 2015), it was different from the latter because of the mixed use of 3-D and 2-D operations in the descending and the ascending arms, respectively, to accommodate our problem. The network was further embedded in an iterative workflow. These features highlighted the novelty of our approach.

2.3. Training strategy

2.3.1. Loss function and its gradient

We used Dice similarity coefficient (DSC) D(Y, Y∗) = 2|Y ∩ Y∗|/(|Y| + |Y∗|) to judge the agreement between two mask regions (Milletari et al., 2016), where Y is the mask output by the network and Y∗ is the expected output. A straightforward optimization problem to train the network has the following form

$$\underset{\theta }{\min }\underset{t\in Tr}{\text{E}}[\left[\sum _{i}1-D[f\left(Y{\ast }_{i-1,t},x_{i-1,t},x_{i,t}\mid \theta \right),Y{\ast }_{i,t}]\right]],$$ (2)

where t is the index of patients and the expectation operation E[[·]] is taken over all the patient cases in the training data set Tr.

The optimization problem in Eq. (2) tried to enforce the agreement between the predicted mask on the slice i based on known reference mask on the slice i – 1. While this indeed followed the overall idea, after implementing this approach, we found the CNN model trained as such suffered from an instability problem. In fact, in the model inference stage, the predicted mask on a slice was based on the segmentation results on the previous slices. Hence, the error in predicted mask at one slice may propagate over slices and accumulate to a relatively large error after a few slices.

To mitigate this problem, the model training process had to be made aware of the iterative nature of model inference. Specifically, when predicting the mask on the slice i, the training process should not only consider information in the slice i − 1, but also the information in previous 1, 2, …, N slices. The optimization problem as such can be expressed as

$$\begin{gathered} \underset{\theta }{\min }L(\theta )=\underset{\theta }{\min }\underset{t\in Tr}{\text{E}}[[\sum _i\sum _{j=1}^{\max (N,i-1)}1 \\ -D[f(f\left(\dots f\left(Y{\ast }_{i-j-1,t},x_{i-j-1,t},x_{i-j,t}\mid \theta \right)\dots ,x_{i-2},x_{i-1,t}\mid \theta \right), \\ {x}_{i-1,t},x_{i,t}\mid \theta ),Y{\ast }_{i,t}]]. \end{gathered}$$ (3)

This modified long-term loss function explicitly ensured agreement between the expected output Yi∗,t with the actual output predicted based on the previous up to N slices. Note that for each of the first N slices, there were less than N slices proceeding to it. The upper limit of the second summation in Eq. (3) reflects this fact. In practice, we empirically chose N = 6 in our implementation, which was found to be computationally acceptable and was sufficient to mitigate the error propagation problem.

To solve the optimization problem in Eq. (3), we need to compute the gradient of the loss function L(θ). To simplify notation, denote

$$\begin{gathered} Y_{i,t}^j\equiv f\left(Y_{i-1,t}^j,x_{i-1,t},x_{i,t}\mid \theta \right) \\ =f\left(f\left(f\left(Y{\ast }_{i-j,t},x_{i-j-1,t},\mid \theta \right)\dots ,x_{i-2,t},x_{i-1,t}\mid \theta \right),x_{i-1,t},x_{i,t}\mid \theta \right), \end{gathered}$$ (4)

i.e. the predicted segmentation mask at the slice i based on the initial input at the slice i – j. After a straightforward derivation, the gradient of Eq. (3) can be expressed as

$$\begin{gathered} \frac{\partial L(\theta )}{\partial (\theta )}=-\underset{t\in Tr}{E}[[\sum _i\sum _{j=1}^{\max \{N,i-1\}}\frac{\partial D}{\partial Y_{i,t}^j}(\frac{\partial Y_{i,t}^j}{\partial \theta }+\frac{\partial Y_{i,t}^j}{\partial Y_{i-1,t}^j} \\ \left(\frac{\partial Y_{i-1,t}^j}{\partial \theta }+\dots \frac{\partial Y_{i-j+1,t}^j}{\partial Y_{i-j,t}^j}\left(\frac{\partial Y_{i-j,t}^j}{\partial \theta }\right)\right))\left]\right] \end{gathered}$$ (5)

2.3.2. Training data

One important issue to note is that the expected network output Y∗ does not necessarily equal to the ground truth sigmoid mask. In fact, when creating the mask for slice i while incorporating the known mask Y_i−1, one essentially considers connectivity between the predicted and the known masks. Hence, only part of the mask in the slice i that is connected to the known mask in the slice i − 1 should be considered in model training to represent this human’s consideration on connectivity, whereas the disconnected portion should be excluded. An example of this fact is shown in Fig. 4, where the prediction process is from the inferior side to the superior side. The zoomed-in region shows the expected predicted masks, which was generated based on the ground truth mask and was used for model training.

Fig. 4.

An example of modifying ground truth sigmoid mask to generate training data by only considering a partial mask connected to the mask in the previous slice. Arrow indicates the direction of iterative segmentation.

2.4. Incorporate prior organ information

In practice, there are a few other organs within the pelvic region, which are of relatively simple shapes and can often be easily segmented either manually or automatically using other segmentation algorithms. Examples include bladder, rectum, small bowel bag (the region encompassing all the bowel loops and interspaces), and uterus in the female case. It is expected that considering the organ information as prior knowledge would facilitate the sigmoid segmentation task. As such, we studied the performance of the model in three scenarios. (1) Without prior organ information. The sigmoid segmentation model was trained and applied without considering any other organ information. (2) With prior organ information in inference phase only. After the model was trained without considering any other organ information, in the inference stage, once a sigmoid mask was generated at one CT slice, we subtracted from the predicted mask the regions belonging to any known organ masks of the bladder, rectum, small bowel bag, and when applicable, the uterus. The modified mask was fed to the network as the input to segment the next slice. (3) With prior organ information in both training and inference phases. The step of subtracting known organ masks was included in both the training and the inference stages.

2.5. Competing methods

To demonstrate the advantages of our method, we compared its performance with those of the state-of-the-art deep learning based methods using 2-D and 3-D U-Nets. These U-Nets were created with an architecture similar to what we used (Fig. 3(B)) for a fair comparison. Specifically, for the 3-D U-Net, 3-D convolutions were used to connect subsequent layers in Fig. 3(B). Similarly, 2-D convolutions were used to create the 2-D U-Net. In addition, since the proposed method used 3-D convolutional layers in the left side to merge information among the three input channels, to investigate the effectiveness of this approach, we also studied another method that employed 2-D convolutional layers in the left side, with features from each channel extracted and processed independently before concatenation at the base of the network. Feather at each layer of the left side of the network were also transferred to the corresponding right side via skip connections and concatenated with the features there. Note that similar to the proposed method, this method also segmented sigmoid in an iterative way. We termed it as iterative method with 2-D convolutions to distinguish from the proposed iterative method with 3-D convolutions.

Number of trainable parameters per layer for each of the four models in this study are shown in Table 1. The number of parameters of the iterative method with 3-D convolutions was between that of the 2-D and 3-D methods, because the network used 3-D and 2-D convolutions in its left (layers 1–4) and right (layers 5–12) sides, respectively. The iterative method with 2-D convolutions had its number of parameters in the first four layers tripled, as compared to the 2-D method, because of the three input channels. There were more parameters in layers 5–9 than those in the 2-D method due to the concatenation of the features from the additional two input channels. The computational complexity of evaluating output of a network is approximately proportional to the number of parameters. However, the iterative nature of the iterative methods with 2-D or 3-D convolutions further increased their overall complexities to segment the whole volume.

Table 1.

Number of trainable parameters per layer in each model.

Layer	Iterative method with 3-D convolutions	Iterative method with 2-D convolutions	2-D method	3-D method
1	896	1152	384	896
2	55,488	55,872	18,624	55,488
3	221,568	222,336	74,112	221,568
4	885,504	887,040	295,680	885,504
5	295,296	885,120	295,296	885,120
6	442,752	1,032,576	442,752	1,327,488
7	147,648	295,104	147,648	442,550
8	36,960	73,824	36,960	110,688
9	9264	18,480	9264	13,872
10	588	588	588	1740
11	78	78	78	222
12	19	19	19	55
Total	2,096,061	3,472,189	1,321,405	3,945,191

We evaluated the network performances under the same three subcategories as explored above: without using prior organ information, with prior organ information in the inference phase, and with prior information considered in both training and inference phases. The 2-D, iterative with 2-D convolutions, and 3-D methods were trained and tested using the same patient cases as the proposed method to fairly compare their performances under the same practical constraints, e.g. availability of training data.

2.6. Implementations and validations

All CT volumes were collected from the database of cancer patients receiving radiation therapy in the Department of Radiation Oncology at UT Southwestern Medical Center. We used CT volumes from 50 patients to perform a five-fold cross-validation (CV) study. In each fold, 40 volumes were used to train the models, and the remaining 10 were used to evaluate the trained models. After the CV study, we used another 10 independent CT volumes to test models developed in the five CV folds. With the exception of one of the testing patient, all other patients were female patients treated using high-dose-rate brachytherapy (Gonzalez et al., 2020). A single male patient was included in the testing set to demonstrate that our model was applicable outside of the female training population. All the CT volumes retained the original image resolution of1. 1719 × 1. 1719 × 2 mm³, but were cropped along the x-y (patient 349anterior-posterior and left-right) dimensions to a size of 200 × 200 pixels from the original image size of 512 × 512 pixels for computational efficiency consideration. After cropping, CT image intensities were mapped from the original CT scale of [−1000, 2000] HU to [0, 1] by a linear scaling that maps [−100, 700] HU to [0, 1]. Any mapped value outside [0, 1] was cropped to this range. The sigmoid segmentation drawn by qualified physicians were exported from our radiotherapy treatment planning system via the DICOM-RT interface and were considered as ground truth. All prior organ information was generated by physicians manually during routine practice.

For the iterative method with 2-D and 3-D convolutions, the ground truth masks were used to create the expected model output masks according to the consideration described in Section 2.3.2. All data pre-processing steps were performed using MATLAB™. For the 2-D U-Net, each pair of an axial CT slice and the corresponding ground truth sigmoid mask in the slice was treated as a data sample. Hence, a large number (∼2000) of samples (40 CT volumes and on average 50 slices per volume for each CV fold) were available to train the model. As for the 3-D U-Net model, each pair of a CT volume and the 3-D mask was a data sample. The available training data became much less.

All the segmentation methods were implemented using Python with Tensorflow using one of 16 Nvidia Tesla K80 GPUs on a computer cluster. The network parameters were initialized with random numbers drawn from the standard normal distribution. The networks were trained via back-propagation using the built-in Adam optimizer in Tensorflow. The number of epochs for the case without prior organ information was 2000, and 1000 when prior information was used. A batch size of 10 was employed which was the maximum size given the memory constraints on our GPU. The learning rate was adjusted to gradually decay from 1 ×10⁻⁵ to ×10⁻⁷.

3. Results

3.1. Training and validation results

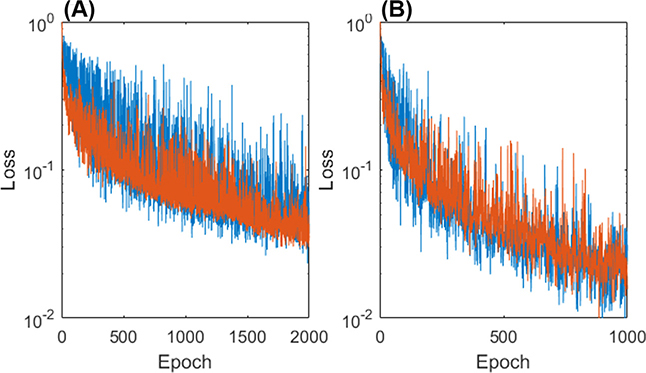
Fig. 5 plots the loss function in a logarithmic scale as a function of the number of epochs. Both loss functions with and without using prior organ information are shown. It can be seen that, although the training and validation loss function values fluctuated, they generally followed a decreasing trend as the number of epochs increased. The training and validation functions were close to each other, indicating no significant overfitting. The convergence was faster, when prior organ information was incorporated. The overall training time was approximately 30 hours without incorporating the prior. Incorporating the prior reduced the training time to approximately 15 hours due to faster convergency.

Fig. 5.

Network loss functions (A) without prior and (B) with prior information in training are shown with the training loss in blue and validation loss in orange.

We first report performance of our model in the 5-fold CV study. In each fold, we calculated the mean DSC of the trained model on the corresponding validation dataset in different scenarios. The model achieved DSC of 0.80 ± 0.03 without using prior, 0.84 ± 0.02 using prior in inference only, and 0.85 ± 0.03 using prior in both training and inference stages.

3.2. Testing results

3.2.1. A representative case

We first present a representative testing volume (not included in training) to demonstrate the performance of the proposed method in detail. It took three sweeps to fully segment this case and the segmentation results are presented in Fig. 6. The first sweep from the inferior to the superior direction started at the rectum-sigmoid junction with a known rectum contour drawn by the physician. The sweep gradually segmented the first section of the sigmoid. After the next two sweeps, from the superior to the inferior direction and then again from the inferior to the superior direction, respectively, two additional sections of the sigmoid were added to the segmentation masks, yielding the final segmentation result.

Fig. 6.

Compared to the ground truth (row 1), segmentation results after the first (column 1), second (column 2), and third (column 3) sweeps without prior information (row 2) and with prior information in the inference stage (row 3). Directions of segmentation in each sweep are shown by the red arrows. Surrounding organs are shown with the bladder (yellow), rectum (brown), small bowel (green) and uterus (pink). Segmentation results with prior information in both training and inference stages were similar to the results using prior in inference stage only, and hence are not shown. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

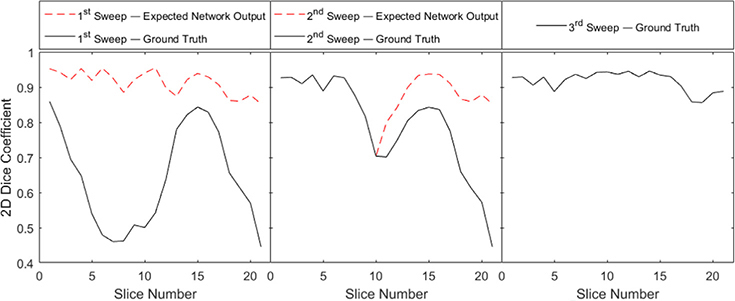
To look at the segmentation process quantitatively, we computed 2-D DSC between the network output mask and the expected network output for each slice, as well as with the final ground truth mask. The evolution of these DSCs for each slices during the three sweeps are shown in Fig. 7. Note that the expected network output and the ground truth mask are different in the first two sweeps but identical in the third sweep for the reasons explained in Section 2.3.2. In all the sweeps, the DSCs with respect to the expected network output were consistently high, indicating that the network were trained successfully to output the expected segmentation results. However, in the first and the second sweeps, the DSCs with respect to the ground truth was relatively low, which could be ascribed to the fact that each sweep added a partial section of the sigmoid to the segmented volume. Going from the first to the third sweeps, the DSCs with respect to the ground truth gradually increased.

Fig. 7.

2-D DSC after the three segmentation sweeps for the testing volume 1. DSCs were calculated for every slice with respect to both the expected network output and the ground truth.

3.2.2. All testing cases

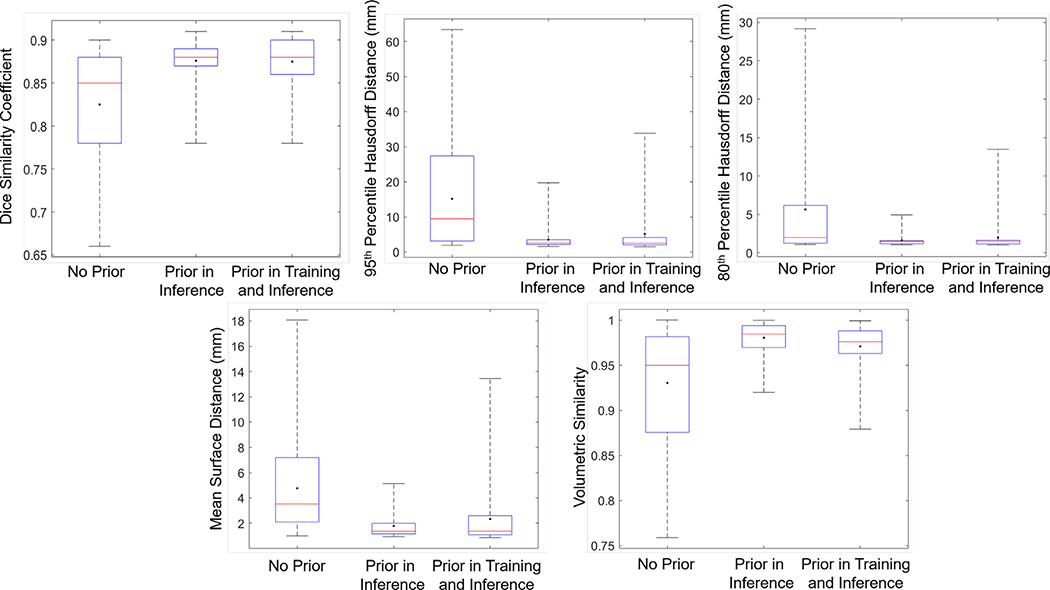
We tested all the trained models in the 5-fold CV study on testing 10 patient cases that were not included in the training process. Five metrics were used to comprehensively quantify performance. The first metric was DSC. We computed 2-D DSC between the segmentation result and the ground truth for each axial CT slice. We then computed the average over all slices for each case. Second and third, we computed both the 95th percentile and 80th percentile Hausdorff distance (HD95 and HD80) to quantify the agreement between the segmented and ground truth surfaces. We computed the HD80 to avoid the sensitivity issue with respect to outliers in HD95. Fourth, we calculated the mean surface distance (MSD) as an additional metric to quantify agreement between segmented and ground truth surfaces. Fifth, volume similarity (VS) was calculated to measure the similarity between the two volumes (Taha and Hanbury, 2015). The results are summarized in Fig. 8.

Fig. 8.

Box plots of testing results. DSC (top left), HD95 (top middle), HD80 (top right), MSD (bottom left), and VS (bottom right) for each scenario in the proposed method. Red horizontal line in each box is median value and dot indicates mean value. The box shows interquartile range. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

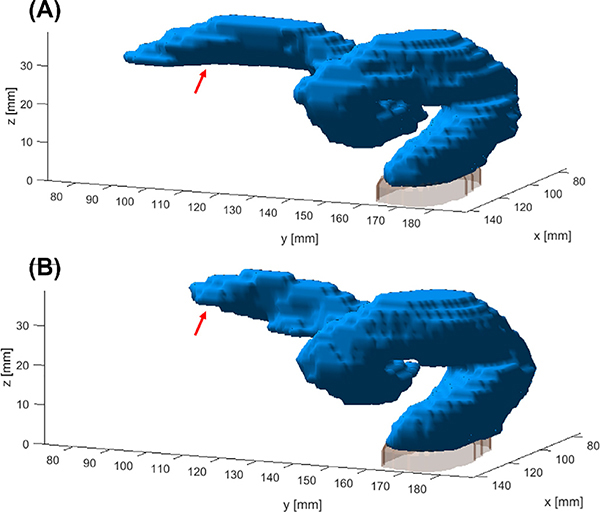
Without using the prior organ information, the proposed model was already able to segment the sigmoid colon with a DSC of 0.82 ± 0.06, HD95 of 15.16 ± 14.34 mm, HD80 of 5.64 ± 6.76 mm, MSD of 4.77 ± 3.68 mm, and VS of 0.93 ± 0.06. Further incorporating prior information in the inference stage boosted the DSC to 0.88 ± 0.02, HD95 of 3.50 ± 2.98 mm, HD80 to 1.62 ± 0.79 mm, MSD of 1.79 ± 0.99 mm, and VS to 0.98 ± 0.02. These values indicated satisfactory performance for such a challenging problem. Incorporating prior information in both training and inference did not further improve the performance, yielding similar DSC values of 0.87 ± 0.03, HD95 of 5.17 ± 6.73 mm, HD80 of 1.98 ± 2.03 mm, MSD of 2.34 ± 2.40 mm, and VS of 0.97 ± 0.02. We used a dataset of female cervical cancer patients to train our model, since this dataset was most readily accessible for us. We included one male patient case (Testing volume No. 5) in the testing dataset to validate the generalizability of the method. It was found that the network was able to segment the sigmoid colon in this case (Fig. 9) with a DSC of 0.85, HD95 of 3.29 mm, HD80 of 1.29 mm, MSD of 1.98 mm, and VS of 0.98 without using any organ prior information, showing the effectiveness of our method.

Fig. 9.

Ground truth for testing patient No. 5 (male anatomy) is shown in (A). Segmentation result is shown in (B). Regions with relatively large discrepancies are pointed out by the red arrows. Gray region in the inferior side is the top portion of the rectum. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2.3. Impact of prior organ information

As shown in Fig. 8, incorporating prior organ information boosted DSCs, HD95, HD80, MSD, and VS. This improvement can be noted by the representative case presented in Fig. 6. As indicated by the zoomed-in views, incorporating the prior information was able to remove some parts that were incorrectly segmented. In fact, one of the difficulties segmenting the sigmoid colon is to differentiate it from other nearby organs. It is common to see the sigmoid in contact with surrounding organs of similar CT values and there is no clear boundary between them in the CT images. Solving this problem in clinical practice requires a knowledgeable human to accurately differentiate the two structures. Similarly, in the proposed segmentation approach, incorporating the surrounding organ masks as prior information allows us to address this issue, as indicated by the improved metric values.

Compared with the scenario of incorporating prior information only in the inference phase, there was no further significant improvement in accuracy for the scenario with the prior in both the training and inference phases, as indicated by similar metric values. However, a major benefit using the prior information in the training stage was accelerating the training process to reach convergence faster, which was shown in Fig. 5.

3.2.4. Comparison with competing methods

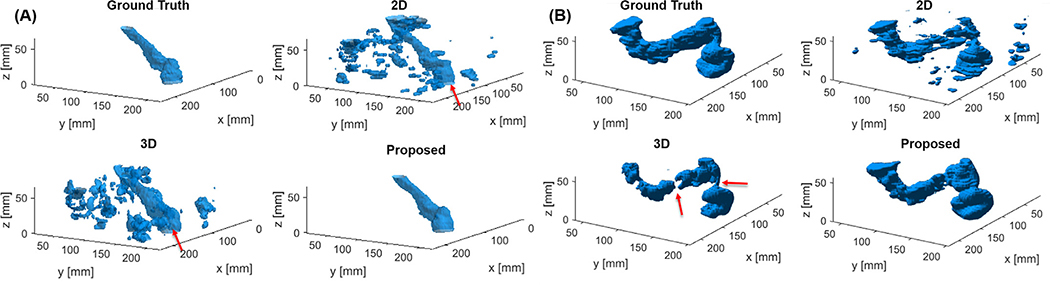
The proposed model substantially outperformed both the 2-D and 3-D U-net methods in all scenarios, as quantitatively shown in Table 2. In terms of DSC, the proposed method was able to improve this metric by 0.51 compared to the 2-D method and by 0.18 compared to the 3-D method, without the use of prior or with the use of prior in inference only. With the use of prior in training and inference, the DSC improvements was 0.41 and 0.14, respectively. Representative results from these three methods with prior organ information in the inference stage are presented in Fig. 10. There were two typical types of segmentation errors in the 2-D and 3-D U-net results. The first one was additional small structures (e.g. in Fig. 10(A)). Although the sigmoid structure can be still observed, as pointed out by the arrows, both networks segmented much more additional small regions surrounding the sigmoid and the use of prior information was not able to completely remove them. The second problem was a disconnected segmentation result (e.g. in Fig. 10(B)). The sigmoid was broken into several disjointed pieces.

Table 2.

Testing results for each scenario in different methods. Numbers in bold font indicate the best performance in each group. 2-D Iter means the iterative method using 2-D convolutions.

		DSC	HD95 (mm)	HD80 (mm)	MSD (mm)	VS
No Prior	Proposed	0.82 ± 0.01	15.16 ± 2.05	5.63 ± 0.94	4.77 ± 0.58	0.93 ± 0.01
	2-D Iter	0.69 ± 0.06	35.36 ± 11.44	22.77 ± 9.66	15.67 ± 6.18	0.84 ± 0.08
	2-D	0.31 ± 0.03	69.68 ± 4.15	47.67 ± 4.64	26.79 ± 2.95	0.65 ± 0.09
	3-D	0.64 ± 0.03	43.03±4.63	27.17 ± 3.58	18.05 ± 3.82	0.76 ± 0.05
Prior in Inference	Proposed	0.88 ± 0.01	3.50 ± 0.51	1.62 ± 0.07	1.79 ± 0.14	0.98 ± 0.01
	2-D Iter	0.70 ± 0.07	33.48 ± 12.70	22.39 ± 10.09	15.49 ± 6.69	0.84 ± 0.09
	2-D	0.37 ± 0.05	72.20 ± 6.54	45.89 ± 9.48	28.01 ± 6.23	0.59 ± 0.06
	3-D	0.70 ± 0.05	37.78 ± 2.51	22.52 ± 4.07	17.46 ± 5.93	0.78 ± 0.05
Prior in Training and Inference	Proposed	0.87 ± 0.01	5.17 ± 1.81	1.98 ± 0.31	2.34 ± 0.31	0.97 ± 0.01
	2-D Iter	0.75 ± 0.02	24.27 ± 4.62	14.56 ± 3.54	11.23 ± 3.48	0.92 ± 0.02
	2-D	0.46 ± 0.08	61.01 ± 4.77	33.07 ± 2.55	21.44 ± 1.93	0.64 ± 0.11
	3-D	0.73 ± 0.02	36.12 ± 2.36	18.75 ± 0.31	12.67 ± 0.43	0.79 ± 0.03

Fig. 10.

Segmentation results for testing patients (A) No. 6 and (B) No. 9 using the proposed, 2-D and 3-D U-net methods with prior organ information used in inference stage. Sigmoid colon is indicated by the red arrows in (A). Disjointed segmentation produced by the 3-D method is noted by the red arrows in (B). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The causes for the two problems were expected to be different for the 2-D and the 3-D approaches. Specifically, segmenting the sigmoid from a given 2-D axial CT slice is an ill-defined problem, as the sigmoid could exist as multiple disconnected sections in the slice. It requires additional information from other nearby slices to unambiguously determine the sigmoid mask. Hence, the performance of the 2-D network was relatively poor, as it cannot leverage the inter-slice information in the segmentation process. On the other hand, the 3-D approach is in principle able to employ the inter-slice geometry information. The unsatisfactory performance seen here was ascribed to the limited number of training samples. Comparing to the 2-D and the 3-D approach, the proposed method was able to avoid both problems because of the iterative nature that allowed us to build in inter-slice geometry information in the segmentation process.

As shown in Table 2, the iterative method with 2-D convolutions performed better than the 2-D and 3-D U-net methods under most scenarios and metrics, its performance was worse than the proposed method. Representative results from both iterative methods are presented in Fig. 11. While the iterative method with 2-D convolutions was able to predict the general shape of the sigmoid colon, there were some larger errors in the results as pointed out by the red arrow. We expect that the use of the 3-D convolutional layers allowed us to extract correlated information among the three input channels at multiple spatial scales, allowing the proposed method an advantage over solely using 2-D convolutions.

Fig. 11.

Segmentation results with prior in training and inference phase for testing patient No. 2 with ground truth contour (left), proposed method (middle), and iterative method with 2-D convolutions (right). Major error is noted by the red arrow. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

One drawback of the two iterative methods relative to the 2-D and 3-D U-Net approaches was longer model inference time. Once the models were trained, the average computation time to segment a CT volume via three sweeps was approximately 12 seconds. In contrast, the inference time was on average 0.5 seconds for the 2-D model for the entire volume. This was shorter than the computation time of 4 seconds per sweep over the entire volume in the iterative models because of less model parameters. The computation time for the 3-D U-Net model was on average 5 seconds. This was slightly longer than the time per sweep of the iterative models due to larger number of a network parameters, but still shorter than the total time of three sweeps.

4. Discussions

The proposed approach lied in between the 2-D and 3-D U-Net methods, hence we termed it as a 2.5-D approach. 2.5-D approaches have lately attracted a lot of attentions in different studies. By processing a few adjacent slices of images together, it can combine the computational advantage of the 2-D approach and the capability of addressing 3-D geometry constraints in the 3-D approach, while effectively generating more training samples out of a given number of 3-D volumes (Roth et al., 2015; Duan et al., 2019). Our method holds similar advantages, but it further employed an iterative approach to allow the propagation of segmentation mask from one slice to the next. We expect the simple 2.5-D approach that processes multiple axial slices together to segment the sigmoid in the middle slice would face the same challenge as in the 2-D approach, because a thin slab of axial CT slice would still not be sufficient to provide 3-D geometry information to determine the regions of sigmoid colon.

In essence, the key idea behind our method is to extend the segmentation information at one axial location to other axial locations and use it to guide the segmentation task. The proposed method explored the idea of extending the information by only one slice. It is possible to build other models to extend the information by more than one slice. For example, in each iteration step, the model could segment a number of slices simultaneously based on information in a number of previous slices. This would potentially lead to the advantages of more robust model training and rapid inference. But the validity may not hold, if the sigmoid masks in successive slices vary rapidly, and hence the known segmentation mask at one place may not be very helpful to guide the segmentation at other places. It would be an interesting study to investigate along this direction, which will be our future work.

There are a few limitations in our study, which require further discussions and future investigations. First, although the model was trained using a relatively small number of 50 patients via 5-fold CV, the number of the actual training data, i.e. successive pairs of CT slices and masks, was large. We expect that further expanding the size of the training dataset could help improving the model performance, but may not be significant. On the other hand, the model was tested in a relatively small number of 10 patients. More extensive tests on more patients are needed to further validate the observed performance. Second, since sigmoid segmentation is a challenging problem even for a human, we expect the accuracy of manual segmentation results highly depends on human factors such as physician’s experience, time available for the task, image quality, etc. Hence, there is a variation among results from different physicians. In our study, we used manual segmentation results generated by experienced physicians during routine practice as the ground truth. We expect the ground truth mask itself contained a certain level of uncertainty, which could impact the model training and testing. Third, we recognize that the pre-processing steps to acquire the expected model output (Section 2.3.2) is quite labor intensive. However, this is an essential step to generate data to train the model. Developing certain automation methods for this purpose would be helpful. Lastly, our method required an initialization of the rectum mask drawn at the rectum-sigmoid junction. In our study, the rectum mask used for initialization was manually drawn by the physician during treatment planning, making our method semi-automatic. Fully automating the workflow would require automatic segmentation of the rectum. We believe this to be possible due to the recent successes of employing deep learning-based methods for automatic segmentation of the rectum (Balagopal et al., 2018). Additionally, we had performed a robustness analysis on the proposed method with respect to the initial condition of the rectum mask. We dilated or contracted the rectum contour by 1 mm, and used the modified masks as the initial condition for our method. We found that this degree of deformation resulted in maximally 1% change in DSC of the segmented sigmoid volume among all cases. However, deformations of a larger degree may further impact segmentation results.

There are a few possible directions to further improve the method. First, in this work we only considered iterating through axial CT slices during the segmentation process. This choice was made, because a human segments the sigmoid primarily based on looping through axial CT slices. However, a human may occasionally uses coronal and sagittal views, or even oblique views to figure out the 3-D organ structure. It is expected that further extending the proposed method to enable iterations along the sagittal and coronal directions would enhance the accuracy of the results. Second, it may also be possible to improve result accuracy by building in organ shape prior in the model. Studies along these directions will be in our future work. Third, it was found that including the prior information of nearby organ masks during the training process was able to accelerate the convergence. Additional steps to accelerate training include better network initialization through the use of transfer learning. Our proposed network used a combination of 2-D and 3-D convolutions. Appropriately transferring weights from trained 2-D and 3-D models for segmentation problems may lead to shorter training times than random weight initialization.

5. Conclusion

In this paper, we proposed a novel iterative 2.5-D method to solve the sigmoid colon segmentation problem. The method was designed to target the clinical scenario of radiotherapy treatment planning, where no special preparation on sigmoid was included, such as bowel evacuation or the use of image contrast agent. This is a challenging problem due to its complex shape, close distance to other organs, and large inter- and intra-patient variations in organ size, shape, and filling status. Our method embedded a CNN in an iterative workflow to model the human’s behavior that segments this organ in a slice-by-slice fashion. We performed a 5-fold CV study and found that DSC was 0.80 without using prior information and 0.84 when incorporating prior organ information in the of inference stage. Further using the prior information in the training stage did not increase DSC, but accelerated the training process. Tested on 10 patient cases that were not included in the training stage, the method achieved an average DSC of 0.82. Incorporating prior information of other organ masks in the inference stage boosted the DSC to 0.88. Compared to methods using 2-D and 3-D U-Net structures, the proposed model achieved much higher segmentation accuracy using the same training data. To our knowledge, this is the first time that a deep-learning based method was applied to segment the sigmoid colon with a satisfactory level of accuracy.