Side effect of a 6 p.m curfew for preventing the spread of SARS-CoV-2: A modeling study from Toulouse, France

Abstract

The spread of SARS-CoV-2 and the resulting disease Covid-19 has killed over 2 million people as of January 22, 2021. We have designed a model and used it to quantify the effect of a 6 p.m curfew on the SARS-CoV-2 epidemic in Toulouse, France. The data show that this measure can lead to the opposite effect from that intended due to larger groups of people on the authorized hours.

Dear editor

The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) that emerged in Wuhan, China in December 2019 spreads mainly by sustained human-to-human transmission¹. This spread has been so rapid that the WHO declared the resulting disease a pandemic². After a first lockdown in March 2020, SARS-CoV-2 resumed its rampage in Europe, including France, at the end of the summer. We have used data from the measures to limit virus transmission, mask wearing, restricted access to public spaces and curfews, taken by several large cities to quantify their impact on virus proliferation³. The French authorities declared a new lockdown from October 29 to November 28, followed by a gradual release with a 8 p.m curfew from December 15, 2020. This curfew has shown its effectiveness in restricting the spread of the virus in France³. A recent study published in this journal assessed the impact of community-wide mask-wearing on the spread of SARS-CoV-2 in the Hong Kong population during the first phase of the epidemic, March 2020⁴. The efficacy of these public health measures has been widely questioned despite the fact that of they have all helped to restrict the spread of the virus^{3 , 5}. We have examined the impact of the 6 p.m. curfew imposed by the French government from January 16, 2021 on the resumed proliferation of the virus after the New Year celebrations using data for the city of Toulouse, France.

Our model is a discretized version of a susceptible infectious and recovered (SIR)-type model⁶. These compartmental models are well suited to studies of the spread of SARS-CoV-2 in different populations^{7 , 8}. Our model^{3 , 5 , 9} includes a diffusion/transmission coefficient $R_0$ that varies with the likelihood of contagion, and a reduction coefficient $\widehat{c}$ that accounts for the impact of public health measures on virus transmission in the French city of Toulouse. The model predicts how the SARS-CoV-2 virus would have evolved and projects the daily percentage of new positive cases. We estimated $\widehat{c}$ by correcting the values predicted by the model with observed data so that predictions and observations coincide over a given period. This model was then used to measure the influence of each individual public health measure on the dynamics of the SARS-CoV-2 infection. We focused on two periods: January 1–January 15, 2021, when an 8 p.m curfew was in force immediately after the New Year, and January 20–January 24, 2021, when the curfew was lowered to 6 p.m.

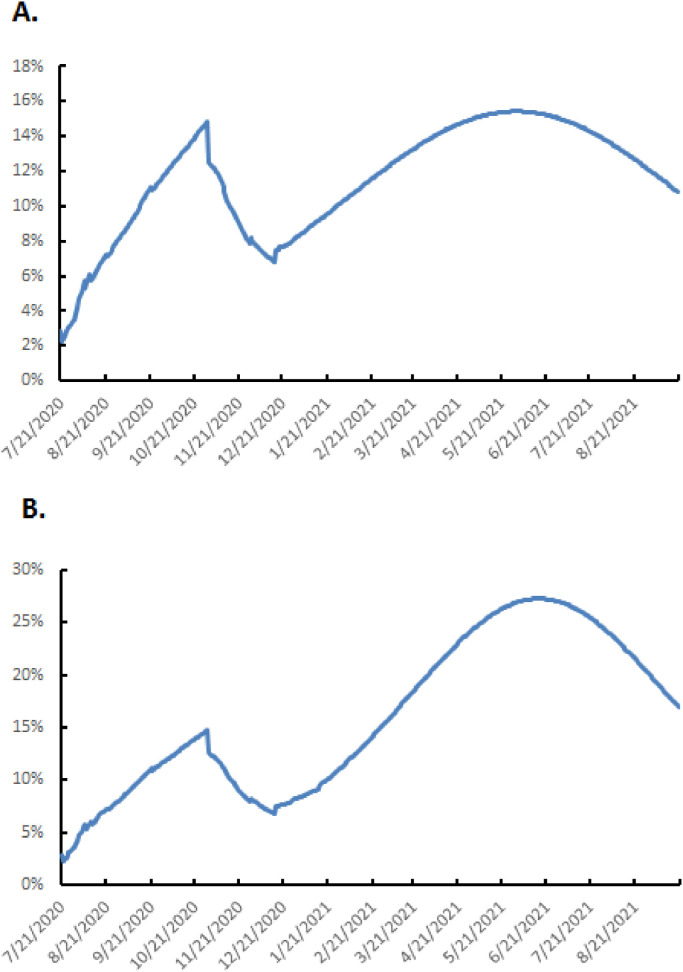
The January 1–January 15, 2021 period makes it possible to assess adherence to the curfew during the end-of-year holidays. The circulation of the virus among Toulouse inhabitants was reduced by 38% by the 8 pm curfew⁵. There should have been a 7–8% increase in positive RT-PCR tests between January 10 and 15 if the curfew had been strict adhered to. Instead, it was closer to 8.5–9%, which corresponds to less constraint of 37%. Using these data, the percentage of new positive cases per day would increase to 15.4% at the end of May 2021 and only then decrease to 10% of positive tests in early February 2021 (Fig. 1 A). The nation-wide 6 p.m curfew stating on January 16, 2021 provided the second data set for Toulouse (January 20–24, 2021). The real increase in positive PCR tests was above 10%, which was even greater than that predicted by the model after an 8 p.m curfew. The corresponding constraint was therefore 35% and the spread of virus would continue to increase, reaching 27.3% on June 15, 2021, before starting to decrease (Fig. 1B).

Fig. 1.

SARS-CoV-2 infections per day, July 21, 2020 - September 20, 2021 according to the protective measures adopted. A: closure of some public spaces, compulsory masks and 8 pm curfew from December 15, 2020. B: closure of some public spaces, compulsory masks and 6 pm curfew from January 15, 2021.

The 6 p.m curfew was intended to keep the circulation of SARS-CoV-2 under control after the Christmas/New Year period but it had exactly the opposite effect in the Toulouse urban area; it reduced the stress on virus spread by 2%. This could be because the more restrictive evening curfew results in larger groups of people in shops and supermarkets before they all hurried to get home.

This study shows that certain health measures can be ill-suited to local epidemiological situations and that their implementation must be accompanied by analysis of the local situation to avoid triggering an undesirable opposite effect.