Oxide superconductors—light on a continuing mystery

The discovery of a whole new class of cuprate superconductors (1) over 30 y ago resulted in euphoria, intense research efforts, and an expectation that in the course of the next few years, we would understand why these materials displayed superconductivity at an unanticipated high temperature. However, in spite of decades of theoretical and experimental efforts at an elevated intensity, there is still no widespread agreement on the mechanism responsible for this whole class of superconductors. The paper by Conradson et al. (2) describes some provocative work that should be taken seriously; this work is a culmination of earlier work by some of the same authors (3, 4) and triggered my own thoughts. The continuing discoveries after the first report of the cuprate superconductors have broadened the scope of discussions among scientists and engineers such that we no longer talk about limits of the superconducting critical temperatures (T_c’s) but how and where we can continue to push to higher temperatures and broader applications.

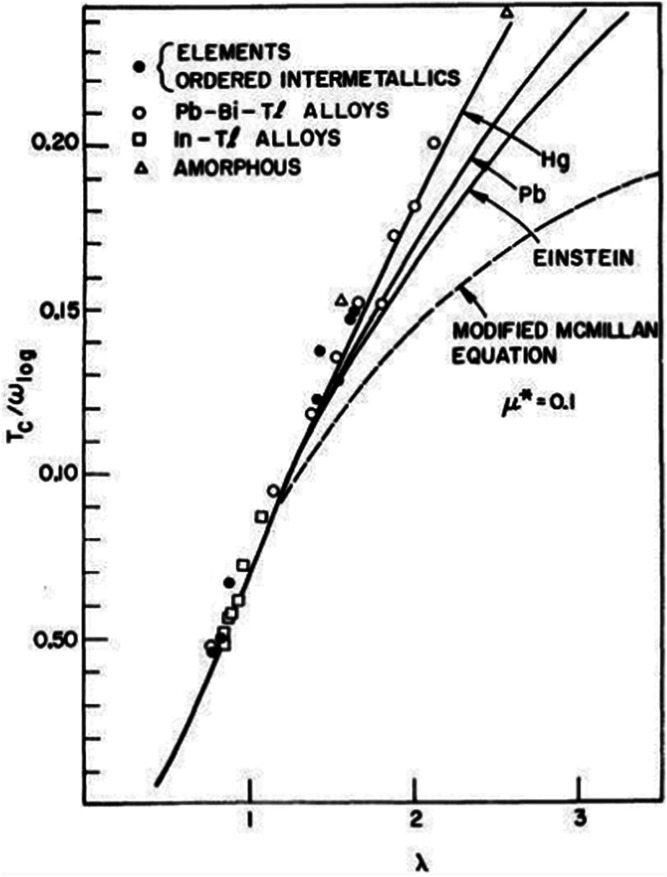
Following decades of work before these discoveries, the overwhelming opinion was that the mechanism responsible for the electron pairing resulting in superconductivity was the electron–phonon interaction (5). Theoretical and experimental studies concluded that the time-retarded electron–phonon interaction resulted in substantial screening of the coulomb repulsion and a resultant electron–electron attraction. With increasing interaction by synthesizing materials that we thought would enhance the electron–phonon coupling, we empirically concluded that the lattice became unstable, and a structural transformation resulted and reduced the electron–phonon interaction and hence, T_c. Theoretically, McMillan (6) solved the Eliashberg equations (7) and reported that with increasing the interaction measured by an electron–phonon interaction λ, the T_c reached a limit. Allen and Dynes (8) later showed that this theoretical limit was spurious and that inside the Eliashberg equations describing strong-coupled superconductors, there was no limit. This is illustrated in Fig. 1, where the exact solution of Eliashberg as a function of the coupling strength λ was not limited and higher-temperature superconductors were possible. Furthermore, λ could be a measure of coupling strength, not necessarily electron–phonon.

Fig. 1.

The calculated T_c/ωlog vs. coupling strength λ, where ωlog is a typical frequency. Conventional superconductors are plotted as data points. This curve illustrates that within the exact solution to Eliashberg theory, there is no limit to T_c. The modified McMillan curve reflects an approximation resulting in an incorrect maximum limit. Reprinted with permission from ref. 8. Copyright 1975 by the American Physical Society.

These circumstances guided our thinking, and so, it was the breakout discovery of the oxides that challenged our beliefs. It became clear that a broader way of thinking was necessary. A flood of theoretical models followed, which are far too numerous to list, but many of those attempted to describe the coupling in these materials to phonons or some other effective bosons (spin fluctuations, excitons). This paper by Conradson et al. (2) reminds us that we cannot think of any coupling mechanism in the weak coupling limit to understand the cuprate superconductors. While many investigations use diffraction techniques or variations of diffraction, other investigations employ EXAFS (extended X-ray absorption fine structure spectroscopy), which probes the near-neighbor statics and dynamics at the Cu K edge. This allows them to look at an internal quantum tunneling polaron locally in some copper oxide superconductors. Furthermore, these polarons are a component of a two-site distribution of the apical O in which the O can tunnel between these two configurations. This involves large atomic displacements sometimes greater than 1 Å.

Complementary to the EXAFS work described in the paper by Conradson et al. (2) is a series of structural diffraction measurements, which conclude that the several cuprates demonstrate static and dynamic charge density waves below certain temperatures and at specific q vectors. Phonons in a narrow range of q space near the charge density wave ordering vector exhibit extremely large superconductivity-induced line-shape renormalizations (9). Again, like the EXAFS measurements of reference (2), this implies sufficiently strong electron–lattice coupling that we can no longer think of these excitations as simply weakly coupled electrons or phonons. One could argue that these renormalizations stabilize the host lattice and result in coupling so strong that a polaron results. The energy scales associated with these hybrid excitations are on the order of ∼10 meV. Assuming this order of magnitude and referring back to Fig. 1 would imply a coupling strength λ of ∼5. This is a larger number than we have seen in conventional superconductors (data points in Fig. 1).

We have seen hints of the “renormalization” of lattice dynamics in more conventional superconductors but nothing on the scale of the static and dynamic effects seen in the cuprates. Axe and Shirane (10) studied phonon frequencies and line shapes in Nb₃Sn many years ago and found abrupt shifts in phonon lifetimes and structural line shapes at the T_c of the material. Again, these indications illustrate electron–phonon coupling modified at T_c, but these effects on the scale of the measurements in the cuprates are very small. Current research continues to find materials that display superconductivity at even higher temperatures. All we have to do is to find ways to stabilize these new materials. It is not an easy task.