Significance
Micrometer-sized uniform four-layer (ABCA) rhombohedral graphene is realized by introducing a small twist angle between two bilayers of Bernal graphene. By means of scanning tunneling spectroscopy we observe an extremely sharp van Hove singularity of 3–5-meV half-width and a correlated many-body gap of 9.5 meV at neutrality, thus making small twisted double-bilayer graphene a unique platform to realize electronic correlations in the absence of a moiré potential. Furthermore, ABCA graphene domain walls display tunable topological edge states, of great interest in Floquet engineering.
Keywords: scanning tunneling microscopy, scanning tunneling spectroscopy, graphene, electron correlations, topology
Abstract
Atomically thin van der Waals materials stacked with an interlayer twist have proven to be an excellent platform toward achieving gate-tunable correlated phenomena linked to the formation of flat electronic bands. In this work we demonstrate the formation of emergent correlated phases in multilayer rhombohedral graphene––a simple material that also exhibits a flat electronic band edge but without the need of having a moiré superlattice induced by twisted van der Waals layers. We show that two layers of bilayer graphene that are twisted by an arbitrary tiny angle host large (micrometer-scale) regions of uniform rhombohedral four-layer (ABCA) graphene that can be independently studied. Scanning tunneling spectroscopy reveals that ABCA graphene hosts an unprecedentedly sharp van Hove singularity of 3–5-meV half-width. We demonstrate that when this van Hove singularity straddles the Fermi level, a correlated many-body gap emerges with peak-to-peak value of 9.5 meV at charge neutrality. Mean-field theoretical calculations for model with short-ranged interactions indicate that two primary candidates for the appearance of this broken symmetry state are a charge-transfer excitonic insulator and a ferrimagnet. Finally, we show that ABCA graphene hosts surface topological helical edge states at natural interfaces with ABAB graphene which can be turned on and off with gate voltage, implying that small-angle twisted double-bilayer graphene is an ideal programmable topological quantum material.
Two-dimensional (2D) van der Waals heterostructures with an interlayer twist have provided a new avenue for observing emergent tunable many-body electron phenomena. Recent experimental realizations include twisted bilayer graphene (tBG) near the so-called “magic angle” of 1.1° (1–3), twisted double-bilayer graphene (tDBG) (4–6), ABC trilayer graphene on near-perfectly aligned hexagonal boron nitride (hBN) (ABC-tLG/hBN) (7, 8) and transition-metal dichalcogenide heterostructures (9–12) [with predictions on a variety of other systems (13, 14)]. All of these systems host an interplay of two phenomena––the presence of one or more van Hove singularities (which we colloquially refer to as “flat bands” henceforth) at low energy where the density of states is sharply peaked, and the existence of a moiré pattern that creates a unit cell that is about a hundred times larger than the carbon–carbon nearest-neighbor distance in graphene. The large number of electrons with quenched kinetic energy make the flat bands conducive to interaction-driven phases (15). The enlarged moiré unit cell is thought to reduce both the flat-band bandwidth and the interaction energy scales, and also introduces easily accessible integer fillings that create Mott-like insulating states (1–12), the relation of which to nearby superconductivity is debated. A natural question that arises from all of these works is whether the moiré pattern is a necessary condition for the observation of correlated many-body phases, or whether it is simply sufficient to further reduce the flat-band bandwidth and hence the kinetic energy in the heterostructure.
In this regard, multilayer rhombohedral (ABC) graphene offers a different perspective toward achieving a flat-band edge without the use of a moiré potential (16). Indeed, in a seminal work (17), it was theoretically shown that the low-energy band structure of multilayer rhombohedral graphene has a sharply peaked density of state (DOS), with the band structure (where N is the number of layers) at low energy in the nearest-neighbor hopping approximation. This implies a peak in the DOS at charge neutrality in this material for , with an appreciable fraction of the entire band within this peak (18). Indeed, this physics is already at play in ABC-tLG/hBN (7, 8), where some of the flatness of the bands comes from the intrinsic band structure of ABC graphene, which is then further flattened and isolated by the moiré pattern from the hBN alignment. A facile alternative to flatten the bandwidth without introducing a moiré potential is to simply increase the number of layers of the rhombohedral stacked graphene. Unfortunately, isolating rhombohedral stacked graphene of any thickness is extremely difficult as it is less energetically favorable than the multilayer counterpart, Bernal stacked graphene. Since the difference between rhombohedral and Bernal graphene is simply a lattice shift, and the interlayer van der Waals forces are weak, it is well known that rhombohedral graphene reverts to the Bernal form when samples are processed with heat, pressure, or while performing lithography (19). In this work, we show that twisting two sheets of tDBG by a tiny (<0.1°) angle is a simple and robust method to create large area (up to micrometer-scale) rhombohedral graphene of four-layer thickness (ABCA graphene). We present gate-tunable scanning tunneling microscopy and spectroscopy (STM/STS) measurements at 5.7 K on these regions. We show that correlated phases can be achieved without the need for a moiré pattern and that rhombohedral graphene has unique topological properties.
Results
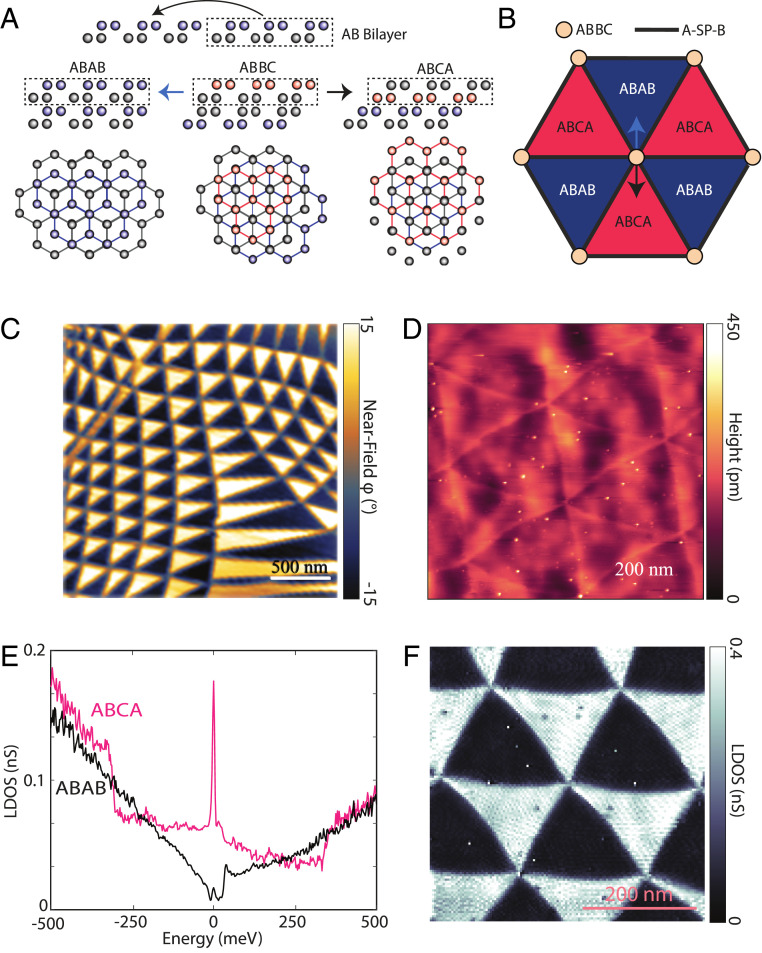
In the limit of small twist angles, it is well known that two twisted layers of graphene will prefer to form extended regions where the lattice is commensurate and Bernal stacked (called AB or BA stacking) (20), separated by sharp domain walls where the stacking order changes from AB to BA (21, 22). Where the domain walls intersect, the stacking order is locally AA, which is also where the low-energy electrons are localized (15). We begin by considering the atomic stacking nature of small-angle tDBG, as shown in Fig. 1 A and B. The easiest way to think of tDBG is to consider the middle two layers which form the same structure as tBG. The rest of the structure of tDBG can then be visualized by the fact that the two upper and two lower layers are both Bernal stacked. Using this visualization technique, it becomes clear that the equivalent of the AA stacking location in tBG is a ABBC stacking in tDBG. One can then displace the top bilayer by one atom in either direction to visualize the other commensurate stacking sites in a manner exactly analogous to tBG. The consequence of this as shown in Fig. 1A is the formation of ABAB (Bernal) and ABCA (rhombohedral) stacked four-layer graphene in the commensurate regions of the sample. Because it is energetically favorable for commensurate regions to maximize in area, small-angle tDBG has large, uniform extended regions of rhombohedral and Bernal graphene that push any effect of the tDBG moiré superlattice to the interfaces of the commensurate domains. At small angles, tDBG thus forms large, uniform rhombohedral domains that are decoupled from effects of the large-wavelength small-angle tDBG moiré. The final stacking arrangement that arises is then shown in Fig. 1B. The rhombohedral graphene is protected by the global symmetry enforced by the twist angle, making it stable and easy to produce. While in this work we show this case for small-angle tDBG, the atomic stacking arguments at hand will also extend to any angle including the magic angle of tDBG where the ABCA sites will likely play a role in electron localization along with the ABBC sites. These arguments also apply to monolayer–bilayer twisted trilayer graphene where the commensurate stackings become ABA and ABC [° tDBG is another interesting case where commensurate sites will be ABCB and BCBA].
Fig. 1.
Rhombohedral domains in small-angle tDBG. (A) Side view and top view of atomic-stacking considerations in a tDBG moiré pattern. Due to the enforced Bernal stacking of the top and bottom layer, the AA-site stacking equivalent in tDBG is ABBC. One can translate the bilayer–bilayer atomic alignment by one atom in either direction to visualize commensurate stackings around the ABBC site (as shown by arrows in B for a moiré unit-cell diagram). While the monolayer–monolayer case (which can be seen by the middle two layers) becomes AB/BA, when the top and bottom tDBG layers are considered the commensurate stacking sites become ABAB (Bernal) and ABCA (rhombohedral). (B) Cartoon moiré of small-angle tDBG with two example directions of atomic-stacking shift considered in A. (C) A nanoinfrared image of a large area of a small-angle tDBG sample. (D) An STM topographic image of small-angle tDBG (setpoints of 300 mV and 100 pA). (E) STS LDOS of ABCA and ABAB graphene domains in small-angle tDBG taken at the center of one of each domain (setpoints of 300 mV and 150 pA with a lock-in oscillation of 2.5 mV). (F) STS LDOS map at the energy of the ABCA flat-band edge (setpoints of 400 mV and 150 pA with a 2.5-mV oscillation).
We first use nanoinfrared imaging to visualize small-angle tDBG on a large scale. Fig. 1C shows a nanoinfrared image of a large-area region of small-angle tDBG. We see that there are two distinct sets of domains (bright and dark in the image) with quasihexagonal order. The average size of the domains in this sample is of order 200 nm on a side, though several larger domains of over a micrometer in size are seen, presumably due to local strain or pinning of particular stacking sites. We have observed such domain structures of hundreds of nanometers in width in every small-angle tDBG sample. The contrast between the two domains clearly shows that the two domains have distinct electronic responses, as we might expect for Bernal and rhombohedral graphene. Having seen the optical signatures of small-angle tDBG structure on a large length scale, we turn to STM/STS to study the atomic-scale spectroscopic properties. In Fig. 1D we show an STM topographic image of a homogeneous small-angle tDBG region with triangular domains that are about 220 nm per side. This can directly be contrasted with a small-angle tBG STM topography in SI Appendix, Fig. S1. In tBG, the STM topographic contrast is dominated by the AB/BA domain walls and the AA site centers, while the two commensurate AB and BA domains have identical contrast. In the case of tDBG, the contrast differs between the two sets of triangular domains, ABCA and ABAB.
We next turn to the electronic structure of the domains. In Fig. 1E we show STS local DOS (LDOS) on the ABCA and ABAB domains elucidating their starkly different electronic properties. While the ABAB domains show a gradually increasing density of states away from the Fermi level (consistent with measurements on multilayer graphite), the ABCA domains have an extremely sharp enhancement in the DOS near the Fermi level. In Fig. 1F we show an STS LDOS image at the energy of the LDOS peak. This image shows that the contrast between the ABCA and ABAB domains is uniformly observed in the low-energy electronic structure, and thus the peak in the LDOS in Fig. 1E is simply a property of the ABCA graphene itself and not due to confinement or impurity effects. Furthermore, the uniform spatial electronic structure proves that these ABCA domains have spatially maximized their commensurate area, pushing the unnatural atomic stackings of the spatially evolving tDBG moiré to the domain walls and decoupling the ABCA graphene from the effects of the superlattice potential. Thus, although we use a tDBG moiré to achieve the ABCA graphene regions, they are no longer affected by the much larger moiré, allowing the study of ABCA graphene without any superlattice potential affecting its low-energy electronic properties. From the topography and STS map in Fig. 1 D and F, it can also be seen that the ABAB Bernal domains are convex whereas the ABCA domains are concave. This domain shape can simply be understood as a competition between the desire on the part of the ABAB domains to maximize their area (being more energetically favorable) and the desire to minimize the length of the domain wall (similar to surface tension). This behavior is also different from tBG, where the two AB/BA domains are equivalent, leading to simple straight domain walls as seen in SI Appendix, Fig. S1 and previous works (22, 23).
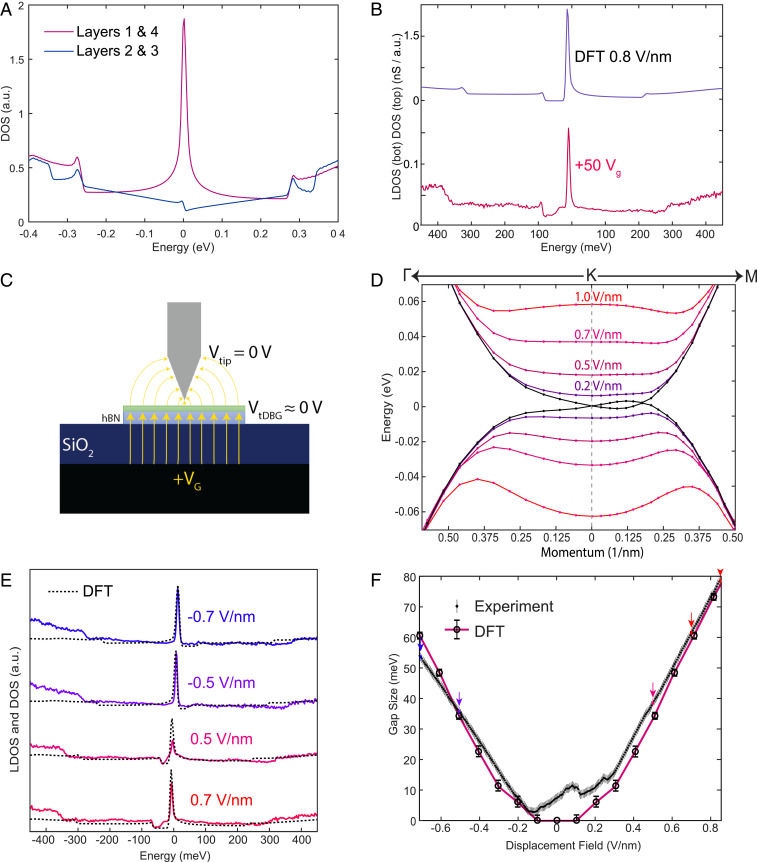
Having clearly identified the large regions of uniform ABCA graphene in our sample, we now focus on the low-energy gate-dependent spectroscopic structure. It is important to note that in STM measurements, the spectroscopic signals are dominated by the first conducting layer of the sample, and hence by the top layer of ABCA graphene. To begin, we compare the surface-measured experimental LDOS (Fig. 1E) to layer-dependent theoretical LDOS as calculated by density-functional theory (DFT) and shown in Fig. 2A. The low-energy density of states is concentrated on the outer layers (i.e., layers 1 and 4) and we find that when examined over a large energy range, the LDOS predicted by DFT for the top layer matches the observed spectroscopy in Fig. 1E strikingly well, including the high-energy bands appearing as steps in the spectrum.
Fig. 2.
Displacement-field-dependent LDOS in ABCA graphene. (A) Layer-dependent LDOS as calculated by self-consistent DFT. (B) STS LDOS curve at a gate voltage of 50 V and top-layer DFT-calculated DOS at 0.8 V/nm. (C) Cartoon of the STM/STS measurement geometry under an applied back-gate voltage. The sample is biased relative to the grounded tip. The back gate dopes the sample and inherently also induces a displacement field. (D) Displacement-field-dependent low-energy band structure of ABCA graphene as calculated by DFT. (E) A series of experimental STS LDOS (solid) and DFT top-layer LDOS (dotted) curves at various displacement-field magnitudes. (F) Extracted displacement-field gap sizes for 251 STS LDOS curves equally spaced between our displacement-field extremes. DFT-calculated displacement-field gap sizes are overlaid. STS measurements in B and E were at setpoints of 400 mV and 150 pA with a lock-in oscillation of 2.5 mV.
We now turn to the effect of a gate voltage on our measurements. In Fig. 2B we show a curve at our maximum positive gate voltage of 50 V (limited by gate leakage). We see that the shape of the measured spectrum has undergone significant changes. The low-energy peak and high-energy band edges are still present in the spectrum (although they have shifted due to doping), but in addition a clear gap has emerged below the Fermi level. To better understand the origin of this gap, in Fig. 2C we show a model for our geometry and basic electrostatics. In our measurement, the sample is biased relative to the tip, while the gate voltage is applied relative to the sample. The application of a back-gate voltage results in both electrostatic doping of the sample as a whole, as well as an electric field applied across the layers of the sample. In trilayer ABC layer graphene (24), it has indeed been shown that electric fields can cause a gap to form. To better understand this effect in four-layer ABCA graphene, we calculate the electric-field dependence of the band structure by means of self-consistent DFT in Fig. 2D. Upon application of a displacement field to the sample, a gap emerges in the ABCA graphene band structure as seen in Fig. 2B, which shows the DFT-calculated top-layer DOS on top. While the band structure of the top layer is electron–hole asymmetric in an applied displacement field, the bottom layer has a band structure that is approximately electron–hole mirror-symmetric with respect to the top layer. We also note that in the presence of a displacement field, the low-energy bands develop a topological character, with each of the valleys in the conduction and valence bands having a Chern number of 2, but with opposing signs (25, 26) (SI Appendix, Fig. S2).
For the STS curve at +50 VG in Fig. 2B, we estimate our displacement field to be 0.85 V/nm (we assume the tip to be one electrode of a parallel plate capacitor held at 0 V and account for intrinsic sample doping which displaces charge neutrality and the zero-field condition). The DFT prediction for the top-layer DOS with an electric field of 0.8 V/nm (solid black curve in Fig. 2B) matches the experimental spectrum well. We note that in the DFT calculation, the electric-field value is fixed at infinity, and the charge on the layers is allowed to redistribute itself self-consistently. We have measured the experimental LDOS for a range of gate voltages, a few of which are displayed in Fig. 2E. Overlaid on these curves are the DFT predictions at the corresponding electric-field values. As the field is increased, the displacement field gap grows in size. For electric fields pointing from the gate to the tip, the gap is located to the left (lower energy) of the main peak in the LDOS, while for fields pointing in the other direction the gap is located to the right (higher energy). In Fig. 2F we track the displacement-field-dependent gap size for 251 STS LDOS curves extending between our gate-voltage extremes of −75 and 50 V with DFT calculated gap size overlaid. For displacement-field magnitudes larger than about 0.3 V/nm, DFT and experiment are in excellent agreement. The curves shown in Fig. 2E are all in this category. While the match between experiment and DFT is excellent at high fields in Fig. 2F, for low fields the single-particle DFT fails to capture the experimental results. In particular, DFT predicts that for electric fields between −0.1 and 0.1 V/nm, the gap produced by the displacement field is negligible. This is a consequence of screening that reduces the field inside the ABCA graphene. The experimental data are in stark contrast to this prediction, always displaying a nonzero gap in this region that is of order 5–10 meV. The fact that the gap matches quantitatively at high positive and negative field negates any possibility of extraneous fields (for example from the tip) affecting this conclusion. We have also checked the effect of the hBN substrate with DFT calculations. Our results show that even though a band gap can be opened by hBN substrate in certain perfectly alignment at zero field, such gap will be closed when we apply certain displacement field (see more discussion in SI Appendix). This is also inconsistent with our experimental observation. We are thus forced to consider other explanations for the observed gap at charge neutrality in experiment.
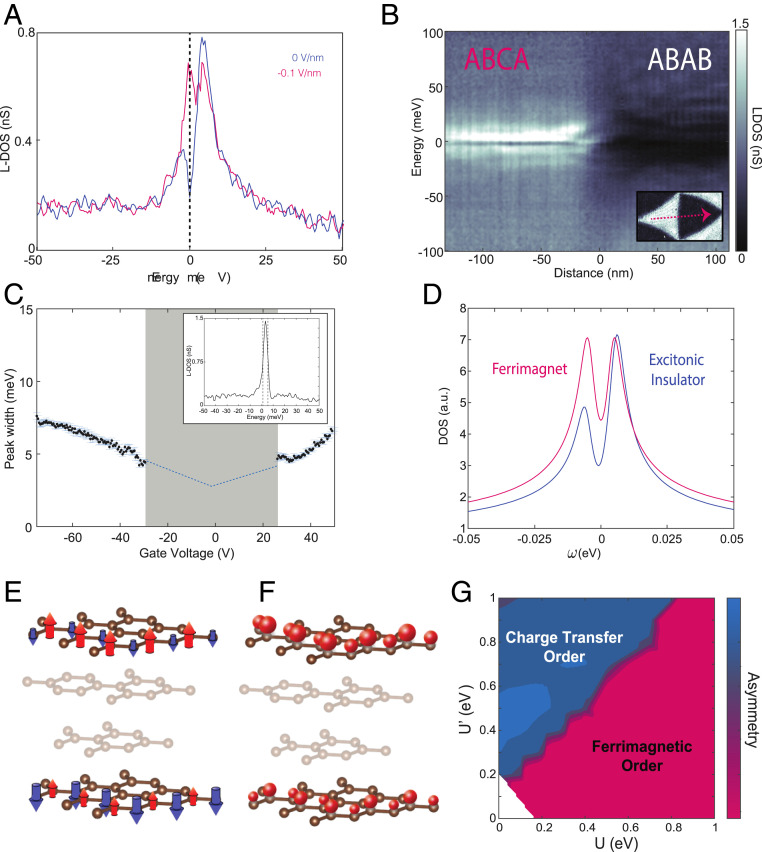
To highlight the gap at zero field, in Fig. 3A, we show two LDOS curves at small displacement-field values. The curve shown in blue is exactly at charge neutrality (and zero field) with a gap of 9.5 meV centered precisely at the Fermi level. The curve shown in magenta is the smallest gap observed at any value of gate voltage, 4.5 meV in magnitude, measured at a field of about −0.1 V/nm. This gap in the LDOS is consistent throughout the entire ABCA domain as can be seen in Fig. 3B where we plot the LDOS at a sequence of points across a whole ABCA and ABAB domain at charge neutrality. Given the clear disagreement with single-particle DFT calculations, this gap is a consequence of electron correlations. We note that we can rule out strain effects since strain values are minimum, as can be seen in Figs. 1 D and F and 4. Recently, in transport measurements, a large gap of 80 meV has been observed in four-layer ABCA graphene (27). The gap observed in our experiments is an order of magnitude smaller, and we see no evidence for the large transport gap in our microscopic measurements. Our measurements have been repeated on several samples showing ABCA domains, indicating the robustness of the gap values we measure. One question that arises is why ABCA graphene displays such a correlated gap, while ABC graphene has not displayed this phenomenon in previous spectroscopic measurements (28). To answer this question, we quantify the sharpness of the ABCA LDOS peak by extracting the half-width of the most prominent peak in the spectrum at each value of gate voltage. A plot of these widths as a function of gate voltage is shown in Fig. 3C. For a range of gate voltages near charge neutrality (gray region in Fig. 3C), the presence of the correlated gap in the peak makes it difficult to define a peak width cleanly. At larger gate voltages, we find that the peak width increases linearly with gate voltage, likely a quasiparticle lifetime effect. An extrapolation of the linear behavior to charge neutrality shows that without splitting, the peak would have a half-width of 3 meV when the sample is charge neutral. Previous measurements of ABC graphene have shown a peak width of 10–20 meV near charge neutrality (17) and about 50 meV on a conducting substrate (29). This sharpness of the peak in the DOS of ABCA graphene is far lower than trilayer ABC graphene (as expected in the low-energy approximation) or even the flat bands of magic-angle tBG (24, 30–32) which are about 10 meV in half-width (23). It is important to reiterate that at these small angles in tDBG, the commensurate ABCA regions are energetically maximized and have pushed any effects of the tDBG moiré to the domain walls, thus this finding is purely associated with ABCA graphene. ABCA graphene is thus a simple flat-band system, where no isolated flat bands emerge as the flatness comes from the band edge, where kinetic energy is sufficiently quenched such that a correlation-induced gap emerges without a relevant moiré periodicity.
Fig. 3.
Electronic correlations in ABCA graphene. (A) Two STS LDOS curves at small displacement fields (blue at neutrality and ∼0 V/nm and magenta at −0.1 V/nm) where in a single-particle picture there should be no gap. The van Hove singularity splits and shows a correlated gap of 9.5 and 4.5 meV, respectively. (B) STS LDOS linecut at charge neutrality across an ABCA and an ABAB domain. (C) ABCA van Hove singularity half-width as a function of gate voltage. The shaded region in gray is excluded as the van Hove singularity half-width cannot be cleanly extracted due to splitting. (Inset) An STS spectrum with the peak still far from the Fermi level, exhibiting a 4-meV half-width. STS measurements in A–C were taken at setpoints of 300 mV and 200 pA with a lock-in oscillation of 0.5 mV. (D) Tight-binding mean-field DOS for ferrimagnetic and charge-transfer excitonic insulator ordered states. (E and F) Visual representation of the two ordered states in ABCA graphene. The mostly irrelevant middle layers are shaded. Ferrimagnetic spin order (E) and charge-transfer insulating order (F) are shown by arrows pointing up or down as well as big or small spheres, respectively (shown on select sites only). (G) Asymmetry of peaks in mean-field tight-binding model as a function of U, intralayer, and U′, top–bottom layer interactions. The most likely ordered state in each region is labeled.
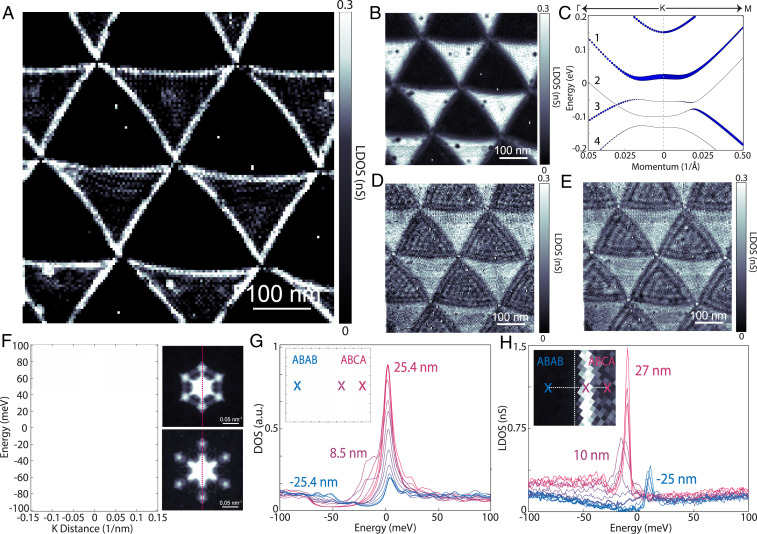
Fig. 4.
Gate-tunable topological edge states ABCA graphene. (A and B) STS LDOS map cuts at −20 meV (within the overlapping gap of ABAB and ABCA graphene) and −10 meV (at the flat-band edge peak). (C) Band structure of ABAB graphene at a displacement field of 0.8 V/nm as calculated by DFT with self-consistent charge screening. The size of the blue circles is proportional to the projection of the wavefunction on the top layer. (D and E) STS LDOS map cuts (from same map as A and B) at 37.5 and 22.5 meV. (F) Two-dimensional Fourier transform of D and E (Right) and a linecut through the primary electron scattering peaks (Left). (G) Tight-binding LDOS profiles at fixed spatial intervals crossing an ABAB–ABCA domain wall with their corresponding distances (with respect to the domain boundary) color coded and written for the beginning and end point as well as the dominant in-gap topological edge state. (H) STS LDOS profiles at fixed spatial intervals crossing the ABAB–ABCA domain wall at the represented and color-encoded distances (with respect to the domain wall as determined at higher energies) showing the dominant in gap topological edge state about 10 nm into the ABCA domain, consistent with tight binding in G. STS measurements in A, B, D, E, and H were taken at setpoints of 400 mV and 150 pA with lock-in oscillations of 2.5 mV (A, B, D, and E) and 1 mV (H).
Discussion
Our DFT result at zero displacement field is in consistent with previous calculations (33). In the previous work, Pamuk and coworkers showed that a magnetic gap can be opened in the ABCA multilayer graphene with the DFT calculations if one increases the electron–electron correlations by manually including certain portion of exact exchange in the DFT functionals. In order to understand the nature of the emergent insulating state, we theoretically investigate the ordered states that arise from adding correlation effects in this regime more systematically. To this end, we use a tight-binding model with a Hamiltonian of with the noninteracting part, and treat electron–electron interactions described by within a mean-field approximation (SI Appendix). Note that in doing so we treat both valley degrees of freedom. We first concentrate on short-range Hubbard-type interactions between the up and down spin electrons of the material within each layer by including where i runs over all lattice sites and is the density at site i. We treat the term in a self-consistent mean-field decoupling yielding the results shown by the magenta curve in Fig. 3D (SI Appendix, Fig. S3). The correlated (mean-field) state in this case is a ferrimagnetic state within the topmost layer which spontaneously breaks the spatial unitary group [SU(2)] invariance of the system and an antiferromagnetic ordering across the topmost and bottommost layer (opposite ferrimagnetic state in the bottommost layer) as shown in Fig. 3E. To have a more complete model, we now add longer-range interactions across topmost to bottommost layers on A and B sites, respectively. This is a valid choice of the next-order interactions as we know (from both tight binding and DFT) that the top and bottom layer dominate the low-energy physics. Toward this end and to keep the model as simple as possible, we add an additional contribution, to Hu and study the ordered states in the self-consistent mean-field approximation as we sweep U and U′, the intralayer interactions and the top–bottom layer interactions. When turning on U′, at values U′ ∼ U, the ferrimagnetic state discussed above (at U′ = 0) gives way to a charge-transfer (excitonic) insulating state which spontaneously breaks the inversion symmetry between bottom and top layer, spontaneously transferring charge across the A sites of the topmost and B sites of the bottommost layer as shown in Fig. 3F (SI Appendix, Figs. S4 and S5). Due to the spontaneous charge transfer, the local density of states at the A sites of the topmost layer becomes electron–hole asymmetric in contrast to the LDOS in a ferrimagnetically ordered state (also shown in Fig. 3E) that maintains electron–hole symmetry. We calculate a full phase diagram of the system as a function of U and U′, shown in Fig. 3G. The color scale on this plot displays the electron–hole asymmetry, which is seen to be generically large in the charge-transfer excitonic insulator state. Based upon this criterion alone, our experimental spectra at most gate voltages match the expectation for the charge-transfer excitonic insulator state. The only exception is the region around where the gap is a minimum, where it is observed to be more electron–hole symmetric. While the electron–hole asymmetry gives us some insight into the nature of the correlated gap, future measurements at high magnetic field can definitively answer whether the state involves magnetic order. We note explicitly that our simplified model leaves room for future investigations, trying to include the effects of correlations on a more quantitative level. Although our model shows results consistent with the experimental observations, other gap-opening mechanisms should be the subject of future studies. Two of such potential candidates (strain and substrate effects) have been ruled out above, leaving correlations as a plausible choice (note that the effects of the substrate might strengthen the charge-transfer mechanism over the ferromagnetic one.
We next look at the consequence of the topological character of ABCA graphene in an applied displacement field. In Fig. 4A, we show an STS LDOS image of several ABCA and ABAB domains at an electric field of 0.475 V/nm and −20 meV in energy. We clearly see the presence of edge states near ABCA–ABAB domain walls dominate the LDOS. Fig. 4B (at the flat-band edge peak, −10 meV) and D-E (above the flat-band edge) show more energy slices from the same LDOS map as Fig. 4A. In these images, there is no signature of the edge states, which only appear at particular energies and gate voltages. Toward understanding these edge states, we consider the nature of the ABAB domains in comparison to the ABCA domains. In Fig. 4C we show the DFT calculated flat-band structure of ABAB graphene under a displacement field (with the projection on the top layer shown by the size of the blue circles). The band structure is highly layer polarized. While the low-energy band labeled 1 dominates the top layer, band 2 has nearly zero weight. Under the application of a displacement field, a gap is observed on the top layer (between bands 1 and 3), although the ABAB graphene four-layer structure as a whole remains metallic. This is also confirmed by STS measurements in the ABAB regions under a displacement field, Fig. 4. We further confirm this band structure with quasiparticle interference mapping. Fig. 4 D and E show STS LDOS map cuts at two energies in the conduction band of ABAB graphene. The wavelike structure in the ABAB domains originates from backscattering from the ABCA domain walls. Shown in Fig. 4F are 2D Fourier transforms (right) of the LDOS maps in Fig. 4 D and E revealing the dominant hexagonal peaks from the scattering pattern. A line cut through the peaks (Fig. 4 F, Left) gives a direct visualization of the top-layer quasiparabolic band as well as a faint signature of the valence band (it dominates on the bottom layer), matching the theoretical band structure under field. Having confirmed the theoretically predicted band structure of ABAB graphene under a displacement field, we now consider its topological properties. As the domain boundary between ABCA and ABAB graphene varies smoothly across a scale of 5–10 nm, strong intervalley scattering is expected to be negligible. We can consider the valley Chern number as a good topology quantity across the domain-wall boundary. An analysis of band 1 yields a valley Chern number of 1, with opposing signs in the two valleys (SI Appendix, Fig. S2) in ABAB graphene. Thus, when considering the interface between ABCA and ABAB graphene seen in STM, both develop gaps in the presence of a displacement field with a difference in Chern number of 1 for each valley. This in turn implies that there are helical edge states of topological origin at the interface with one mode per valley [in contrast to the interface between AB and BA bilayer graphene where two modes per valley are expected (22, 34, 35)]. Although ABAB graphene remains metallic under displacement field, the system is strongly layer polarized. The topological edge states reside only in the top layer, while the other bulk states localized in other layers. Due to the layer polarization, scattering between the topological edge states in the top layer and other bulk states in ABAB graphene are significantly reduced although such scattering is not prevented by topology. The dominating edges in the LDOS map of Fig. 4A are a direct manifestation of these topological surface helical edge states.
For further insight into the observed interface properties of this topological edge state, we study a finite-size spatial region that includes a sharp boundary between ABCA and ABAB graphene at similar conditions as in experiment using tight binding (SI Appendix). In Fig. 4G we show the results of these calculations for the LDOS at a number of positions across the ABCA–ABAB interface. The calculations show that the topological edge mode is localized around 8 nm away from the interface inside the ABCA domain, characterized by an in-gap state within the overlapping displacement field gaps of ABCA and ABAB graphene. To compare to theory, we show the corresponding experimentally measured LDOS spectra across the interface in Fig. 4H. We see remarkable agreement between theory and experiment for the spatial LDOS dependence. Within the overlapping displacement-field gaps of the LDOS, an in-gap state is present which in experiment is located 10 nm away from the domain boundary (36) inside the ABCA region, in close accord with theory. Edge states are composed of linear combinations of the bulk states within each domain. Since the DOS of the ABCA domain is much higher than that of the ABAB domain, the contribution of the bulk states from the ABCA domain is much larger, so the resulting edge states localize more on the ABCA side. These measurements establish that the interface of ABCA–ABAB domains (which can be easily realized by small-angle tDBG) feature surface helical topological edge states which can be turned on and off with displacement field and gate voltage.
Our experiments show that small-angle tDBG moiré patterns are an easy platform to create large, stable, four-layer rhombohedral graphene domains. We commonly observe rhombohedral patches that are hundreds of nanometers to a micrometer in size, making them suitable for any technique including transport where electrodes can be directly placed on the rhombohedral regions. One can additionally explore stacking more bilayers at small angles toward even thicker rhombohedral graphene. Spectroscopy on ABCA graphene reveals a van Hove singularity of 3–5-meV half-width and a correlated gap at neutrality, making it a unique correlated van der Waals system where there is no need for a moiré superlattice to modify the low-energy electronic properties. Further exploration of ABCA graphene can provide answers to certain fundamental questions, for instance regarding the importance of moiré potentials and integer fillings in generating emergent phases such as superconductivity in neighboring regions of the phase diagram. The chiral nature of the tunable topological edge states in rhombohedral graphene also makes it of great interest to observe gyrotropic effects and toward Floquet engineering.
Materials and Methods
Experiment.
Our fabrication of tDBG samples follows the established “tearing” method, using polypropylene carbonate (PPC) as a polymer to sequentially pick up hBN, half of a piece of graphene followed by the second half with a twist angle. This structure is flipped over and placed on a Si/SiO2 chip. PPC polymer was removed by vacuum annealing at 250 °C. Afterward, direct contact is made to the tDBG via µ-soldering with Field’s metal (37), keeping temperatures below 80 °C during the entire process to minimize the chance of layers fully rotating back to Bernal stacking which happens on annealing the structures.
STM measurements are taken in a home-built 5.7 K system at ultrahigh vacuum. STM tips are prepared and calibrated for atomic sharpness and electronic integrity on freshly prepared Au (111) crystals. Samples were measured with multiple tips to ensure consistency of results.
The size of the experimental displacement field gap in Fig. 2F is defined as the distance from the van Hove singularity to the gap edge. We fitted a Gaussian function to the van Hove singularity in order to obtain its energy position. The gap edge is determined by the energy position at which the LDOS intensity reaches a plateau.
Nanoinfrared imaging in this work was performed using a commercial (Neaspec) scattering-type scanning near-field optical microscope. In this measurement, midinfrared light (continuous-wave CO2 gas laser at a wavelength of 10.6 µm) was focused on the apex of a metallic tip. The scattered light was collected by a cryogenic HgCdTe detector (Kolmar Technologies). The AFM tip was excited at a frequency of about 75 kHz, with a tapping amplitude of about 60 nm. The far-field contribution to the signal can be eliminated from the signal by locking to a high harmonic (here we used the third harmonic of the tapping). The phase of the backscattered signal was extracted using an interferometric detection method, the pseudoheterodyne scheme, by interfering at the detector the scattered light with a modulated reference arm.
Tight Binding and DFT.
The band structures and layer-projected LDOS of multilayer graphene with ABCA and ABAB stacking are calculated with first-principle calculations based on DFT as implemented in the Vienna Ab initio Simulation Package (38). The pseudopotentials are constructed with the projector augmented-wave method (39). The exchange-correlation functionals are treated at the local-density approximations (40) level. Plane-wave basis sets are employed with an energy cutoff of 600 eV. A dense k-point grid of 150 × 150 × 1 is adopted in the self-consistent calculations to ensure the convergence of the band structures and the LDOS. A vacuum region larger than 15 Å is added along the z direction to eliminate artificial interactions between slab images. Dipole corrections are included in all the calculations with displacement fields.
To simulate the STS measurement across the ABCA–ABAB domain walls, we calculate the LDOS at different locations across the domain walls with tight-binding model calculations. We model the domain walls with a flake of four-layer graphene with area larger than 200 nm × 200 nm in the real space. In the region with x < −1 nm, the stacking sequence is ABCA. In the region between x = −1 nm and x = 1 nm, the x coordinates of all lattice sites in the top two layers are linearly expanded such that the stackings become ABAB in the region with x > 1 nm. We model the system with the following tight-binding Hamiltonian (41): , where is the hopping parameter between pz orbitals at the two lattice sites and and it has the following form: where a = 1.412 Å is the in plane C–C bond length, c = 3.36 Å is the interlayer separation, n is the direction cosine of along the out of plane axis (z axis), is the intralayer (interlayer) hopping parameter, and is the intralayer (interlayer) decay constant. For the interlayer interaction, only the hopping between atoms in adjacent layers are considered. This tight-binding model has been shown to reproduce the low-energy structure of graphene calculated by local DFT calculations with the following value for the parameters: , , and (41). For the calculation of LDOS, we employ the Lanczos recursive method (42).
Supplementary Material
Acknowledgments
This work was supported by Programmable Quantum Materials, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences, under Award DE-SC0019443. STM equipment support was provided by the Air Force Office of Scientific Research via Grant FA9550-16-1-0601 and by the Office of Naval Research via Grant N00014-17-1-2967. C.R.-V. acknowledges funding from the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska Curie Grant Agreement 844271. L.X. and A.R. acknowledge funding from the European Research Council (ERC-2015-AdG694097), Cluster of Excellence Advanced Imaging of Matter EXC 2056 - 390715994 and RTG 2247 by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), SFB925 and Grupos Consolidados (IT1249-19). The Flatiron Institute is a division of the Simons Foundation. We acknowledge support from the Max Planck–New York City Center for Non-Equilibrium Quantum Phenomena. D.M.K. acknowledges funding from the DFG under Germany’s Excellence Strategy – Cluster of Excellence Matter and Light for Quantum Computing (ML4Q) EXC 2004/1 - 390534769 and within the Priority Program SPP 2244 “2DMP.” D.N.B. is Moore Investigator in Quantum Materials EPIQS #94553. D.H. was supported by a grant from the Simons Foundation (579913).
Footnotes
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2017366118/-/DCSupplemental.
Data Availability.
All study data are included in the article and/or SI Appendix.
References
- 1.Cao Y., et al. , Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018). [DOI] [PubMed] [Google Scholar]
- 2.Cao Y., et al. , Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018). [DOI] [PubMed] [Google Scholar]
- 3.Yankowitz M., et al. , Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019). [DOI] [PubMed] [Google Scholar]
- 4.Shen C., et al. , Correlated states in twisted double bilayer graphene. Nat. Phys. 16, 520–525 (2020). [Google Scholar]
- 5.Cao Y., et al. , Tunable correlated states and spin-polarized phases in twisted bilayer-bilayer graphene. Nature 583, 215–220 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Cao Y., et al. , Tunable correlated states and spin-polarized phases in twisted bilayer–Bilayer graphene. Nature 583, 215–220 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Chen G., et al. , Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019). [Google Scholar]
- 8.Chen G., et al. , Signatures of tunable superconductivity in a trilayer graphene moiré superlattice. Nature 572, 215–219 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Tang Y., et al. , Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Regan E. C., et al. , Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020). [DOI] [PubMed] [Google Scholar]
- 11.An L., et al. , Interaction effects and superconductivity s ignatures in twisted double-bilayer WSe2. arXiv:1907.03966 (9 July 2019). [DOI] [PubMed] [Google Scholar]
- 12.Wang L., et al. , Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020). [DOI] [PubMed] [Google Scholar]
- 13.Xian L., Kennes D. M., Tancogne-Dejean N., Altarelli M., Rubio A., Multiflat bands and strong correlations in twisted bilayer boron nitride: Doping-induced correlated insulator and superconductor. Nano Lett. 19, 4934–4940 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kennes D. M., Xian L., Claassen M., Rubio A., One-dimensional flat bands in twisted bilayer germanium selenide. Nat. Commun. 11, 1124 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bistritzer R., MacDonald A. H., Moire bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. U.S.A. 108, 12233–12237 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang F., Sahu B., Min H., Macdonald A. H., Band structure of ABC-stacked graphene trilayers. Phys. Rev. B 82, 035408 (2010). [Google Scholar]
- 17.Min H., Macdonald A. H., Electronic structure of multilayer graphene. Prog. Theor. Phys. 176, 227–252 (2008). [Google Scholar]
- 18.Yelgel C., Electronic structure of ABC-stacked multilayer graphene and trigonal Warping : A first principles calculation. J. Phys. Conf. Ser. 707, 012022 (2016). [Google Scholar]
- 19.Sugawara K., et al. , Selective fabrication of free-standing ABA and ABC trilayer graphene with/without Dirac-cone energy bands. NPG Asia Mater. 10, e466 (2018). [Google Scholar]
- 20.Yoo H., et al. , Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Wong D., et al. , Local spectroscopy of moiré-induced electronic structure in gate-tunable twisted bilayer graphene. Phys. Rev. B 92, 155409 (2015). [Google Scholar]
- 22.Huang S., et al. , Topologically protected helical states in minimally twisted bilayer graphene. Phys. Rev. Lett. 121, 037702 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Kerelsky A., et al. , Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019). [DOI] [PubMed] [Google Scholar]
- 24.Zou K., Zhang F., Clapp C., MacDonald A. H., Zhu J., Transport studies of dual-gated ABC and ABA trilayer graphene: Band gap opening and band structure tuning in very large perpendicular electric fields. Nano Lett. 13, 369–373 (2013). [DOI] [PubMed] [Google Scholar]
- 25.Zhang F., MacDonald A. H., Mele E. J., Valley Chern numbers and boundary modes in gapped bilayer graphene. Proc. Natl. Acad. Sci. U.S.A. 110, 10546–10551 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li J., Morpurgo A. F., Büttiker M., Martin I., Marginality of bulk-edge correspondence for single-valley Hamiltonians. Phys. Rev. B 82, 245404 (2010). [Google Scholar]
- 27.Myhro K., et al. , Large tunable intrinsic gap in rhombohedral- stacked tetralayer graphene at half filling. 2D Mater. 5, 4 (2018). [Google Scholar]
- 28.Yin L., Shi L., Li S., Zhang Y., Guo Z., He L., High-magnetic-field tunneling spectra of ABC -stacked trilayer graphene on graphite. Phys. Rev. Lett. 122, 146802 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Pierucci D., et al. , Atomic and electronic structure of trilayer graphene/SiC(0001): Evidence of strong dependence on stacking sequence and charge transfer. Sci. Rep. 6, 33487 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Choi Y., et al. , Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019). [Google Scholar]
- 31.Xie Y., et al. , Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019). [DOI] [PubMed] [Google Scholar]
- 32.Jiang Y., et al. , Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Pamuk B., Baima J., Mauri F., Calandra M., Magnetic gap opening in rhombohedral-stacked multilayer graphene from first principles. Phys. Rev. B 95, 075422 (2017). [Google Scholar]
- 34.Ju L., et al. , Topological valley transport at bilayer graphene domain walls. Nature 520, 650–655 (2015). [DOI] [PubMed] [Google Scholar]
- 35.Vaezi A., Liang Y., Ngai D. H., Yang L., Kim E., Topological edge states at a tilt boundary in gated multilayer graphene t ∝ y b = a x. Phys. Rev. X 3, 021018 (2013). [Google Scholar]
- 36.Halbertal D., et al. , Moiré metrology of energy landscapes in van der Waals heterostructures. Nat. Commun. 12, 242 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Girit Ç. Ö., Zettl A., Soldering to a single atomic layer. Appl. Phys. Lett. 91, 193512 (2007). [Google Scholar]
- 38.Kresse G., Hafner J., Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
- 39.Blöchl P. E., Projector augmented-wave method. Phys. Rev. B Condens. Matter 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- 40.Perdew J. P., Zunger A., Self-interaction correction to density-funcional approximations for many-electron systems. Phys. Rev. B Condens. Matter 23, 5048–5079 (1981). [Google Scholar]
- 41.Trambly de Laissardière G., Mayou D., Magaud L., Localization of Dirac electrons in rotated graphene bilayers. Nano Lett. 10, 804–808 (2010). [DOI] [PubMed] [Google Scholar]
- 42.Wang Z. F., Liu F., Chou M. Y., Fractal Landau-level spectra in twisted bilayer graphene. Nano Lett. 12, 3833–3838 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.