Abstract
Recent developments in the field of high efficiency perovskite solar cells are based on stabilization of the perovskite crystal structure of FAPbI3 while preserving its excellent optoelectronic properties. Compositional engineering of, for example, MA or Br mixed into FAPbI3 results in the desired effects, but detailed knowledge of local structural features, such as local (dis)order or cation interactions of formamidinium (FA) and methylammonium (MA), is still limited. This knowledge is, however, crucial for their further development. Here, we shed light on the microscopic distribution of MA and FA in mixed perovskites MA1–xFAxPbI3 and MA0.15FA0.85PbI2.55Br0.45 by combining high-resolution double-quantum 1H solid-state nuclear magnetic resonance (NMR) spectroscopy with state-of-the-art near-first-principles accuracy molecular dynamics (MD) simulations using machine-learning force-fields (MLFFs). We show that on a small local scale, partial MA and FA clustering takes place over the whole MA/FA compositional range. A reasonable driving force for the clustering might be an increase of the dynamical freedom of FA cations in FA-rich regions. While MA0.15FA0.85PbI2.55Br0.45 displays similar MA and FA ordering as the MA1–xFAxPbI3 systems, the average cation–cation interaction strength increased significantly in this double mixed material, indicating a restriction of the space accessible to the cations or their partial immobilization upon Br– incorporation. Our results shed light on the heterogeneities in cation composition of mixed halide perovskites, helping to exploit their full optoelectronic potential.
Introduction
Over the past decade, lead halide perovskites have attracted great interest due to their potential application in solar cells, with excellent power conversion efficiencies of currently up to 25.5%.1 Other efficient perovskite-based optoelectronic devices, such as light-emitting diodes and X-ray detectors, were demonstrated as well.2−6 A key aspect is the simplicity of tuning the composition of halide perovskites, which makes it possible to adapt their structural and optoelectronic properties, such as phase transitions, band gap energy, as well as charge-carrier lifetimes and mobilities,7−11 to achieve desired properties for the different applications. Halide perovskites typically have an APbX3 composition, in which Pb2+ forms corner-sharing PbX6 octahedra with X being a halide (X = Cl–, Br–, or I–).8,12,13 The dodecahedral A site is occupied by a monovalent cation, typically methylammonium (CH3NH3+, MA), formamidinium (CH3(NH2)2+, FA), or Cs+.12,14 The first efficient perovskite solar cells were realized using ternary halide perovskites, especially MAPbI3, before a further increase in efficiencies above 20% was achieved on the basis of mixed multinary halide perovskites,15,16 such as a “triple cation” perovskite of the form MAxFA0.95–xCs0.05Pb(I1–yBry)3.17 However, these highly alloyed perovskites show phase segregation especially under illumination,18,19 limiting their optoelectronic performance and long-term stability.20,21 In recent years, the highest perovskite solar cell efficiencies of >23% were achieved with perovskites that again have a less complex stoichiometry, e.g., double cation perovskites17 or even simple FAPbI3.22,23 The latter requires stabilization into its optoelectronically desired α-phase,24−26 which can be achieved by adding a second cation, e.g., MA.26−28 Upon incorporation of MA in FA-based perovskites, the Goldschmidt tolerance factor is better fulfilled,29 decreasing strain within the structure and thus improving charge transport properties.30,31
This recent progress has made it very clear how extremely sensitive the optoelectronic performance and stability of halide perovskites are with respect to their stoichiometry and compositional microstructure.9,32−37 Developing a fundamental understanding of structure–property relations is crucial to further advance perovskite-based optoelectronic devices. Even though the mixing behavior of A cations in the perovskite structure was the focus of various works in the past,26,38−43 a complete understanding of the microstructure of A cation mixtures is not yet established.
Nuclear magnetic resonance (NMR) spectroscopy provides an accurate probe of the local environment of different functional groups embedded in the crystal structure. NMR spectroscopy of perovskites has proven valuable to accurately probe the cation ratios of mixed compositions, halide order and disorder, halide or cation phase segregation, and cation dynamics.25,26,42,44 Organic A cation mixtures can be analyzed in terms of types, ratios, and dynamics by high-resolution 1H, 13C, and 14N NMR spectroscopy.26,42,45−49 Furthermore, 13C magic angle spinning (MAS) NMR offers a sensitive probe for the phase purity of single and mixed cation perovskites.482H and 14N NMR experiments are especially useful to study cation dynamics, which have been evaluated for the parent MA lead halide perovskite compounds45−47,49,50 and MA/FA and MA/guanidinum mixed systems.26,39 Often NMR spectroscopic studies are complemented with first-principles simulations to obtain even more detailed information about the investigated material structure.51−53 However, the description of disordered systems requires a large set of models and large supercells rendering it computationally expensive,54−56 which is aggravated if dynamics play an important role and need to be modeled in addition, such as in halide perovskites. Recent developments in machine-learning force-fields (MLFFs) opened up the possibility of achieving near first-principles accuracy molecular dynamics (MD) trajectories of thousands of atoms on a nanosecond time scale.57 This allows for capturing cation dynamics and gaining detailed information about the microstructure in perovskites by MD simulation approaches. These MLFF MDs are able to resolve the entropy-driven phase transitions in MAPbI3 and other related (inorganic) perovskites with great accuracy.57,58
In this work, we investigate the perovskite microstructure in detail, i.e., distribution and order/disorder of FA and MA in mixed halide perovskites of the form of MA1–xFAxPbI3 and MA0.15FA0.85PbI2.55Br0.45. High-resolution 1H MAS NMR spectroscopy based on double-quantum (DQ) coherences allows us to identify individual 1H–1H correlations55,59−61 of MA and FA cations in close proximity and to quantify the 1H dipolar interactions. Through a combination of the DQ NMR data with MLFF MD simulations of the disordered and highly dynamic MA1–xFAxPbI3 systems, we are able to identify and quantify the effects that influence the experimentally determined 1H–1H dipolar couplings. Here, we also find that the latter significantly increases upon Br– incorporation in the perovskite structure. The knowledge about the nature of the dipolar couplings enables us to quantitatively analyze the relative occurrence of contacts between different cations in the 2D 1H–1H DQSQ MAS NMR spectra. This analysis indicates the presence of local compositional fluctuations due to a partial clustering of MA and FA cations over the entire investigated compositional range.
Experimental and Computational Methods
Synthesis
We synthesized the powders employing a mechanochemical approach62 by ball-milling in a Fritsch “Pulverisette 5/4” planetary ball mill. The reactants (FAI, MAI, MABr, PbI2, and PbBr2 or already completely synthesized hybrid perovskites) were weighed to the desired stoichiometry (see Supporting Information for exact amounts) and transferred into an 80 mL stabilized ZrO2 milling jar, containing stabilized ZrO2 milling balls with 10 mm diameter. Then, 7–11 ml of cyclohexane was added as a milling agent. The powders were milled at 400 rpm for 5 min. Then milling was paused for 20 min to allow cooling of the jar. The procedure was repeated until the desired milling time was reached. The cyclohexane was evaporated by opening the finished milling jar and leaving it at room temperature in air for 15 min. Finally, we sieved the powder with a 90 μm sieve. The resulting powders were transferred into an inert atmosphere for storage. FAI, MAI, and MABr were synthesized as described in ref (62), while PbI2 (purity >99.8%) and PbBr2 (purity >98%) were purchased from Sigma-Aldrich.
X-ray Diffraction
For powder diffraction analysis, samples were prepared inside a glovebox by hermetically sealing the powder in a 0.5 mm soda lime glass capillary. The X-ray diffractograms were recorded in capillary mode on a Panalytical Empyrean diffractometer using Cu Kα radiation and a PIXcel3D 1 × 1 detector.
Solid-State NMR Spectroscopy
NMR spectra were recorded on Varian VNMRS systems operating at a magnetic field strength of 9.4 T (400 MHz) and 20.0 T (850 MHz). Probe heads used were a Varian 3.2 mm T3 HXY (400 MHz) and a Varian 1.6 mm T3 HXY (850 MHz) probe. The chemical shift was referenced using lead nitrate for 207Pb (−3494 ppm) and using adamantane for 1H (1.85 ppm) and 13C (38.5 ppm) as secondary references. All experiments were performed at room temperature and using boil-off nitrogen for performing MAS.
207Pb MAS NMR spectra were recorded at 5 kHz spinning speed with a recycle delay of 0.5 s.
Single-pulse excitation (SPE) 13C MAS NMR spectra were recorded at 12.5 kHz MAS rate, with a recycle delay of 75–90 s to ensure full relaxation (13C T1 ∼ 15s) and thus warrant quantitative results. SPINAL63 decoupling at an 1H decoupling strength of 50 kHz was employed during acquisition.
For 1H–13C CP-MAS spectra, rf field strengths were optimized using adamantane (ν (1H) ∼ 60 kHz and ν (13C) ∼ 72 kHz). CP contact times were optimized for each sample resulting in values of 15–50 ms. For such long pulses it is important to carefully obey the power limits of the hardware. Proton decoupling (SPINAL) was employed at a field strength of 50 kHz, the recycle delay was set to 50–70 s (1H T1 ∼ 10–14 s determined by 1H saturation recovery experiments), and an MAS frequency of 12.5 kHz was used.
High-resolution 1H MAS NMR experiments were performed at a magnetic field of 850 MHz and a MAS frequency of 35 kHz. For 1D 1H MAS NMR spectra the recycle delays (65–120 s) were optimized for each sample to reach full relaxation (1H T1 ∼ 13–24 s determined by 1H saturation recovery experiments). 2D 1H−1H DQSQ MAS NMR spectra and 1H DQ buildup curves were recorded using the BABA-xy1664 sequence (ν (1H) ∼ 140 kHz) at a MAS rate of 35 kHz. Zero-quantum (ZQ) reference measurements were used for a normalization of the 1H DQ buildup curves:60,64
| 1 |
Molecular Dynamics with Machine-Learning Force Fields
A smoothened machine-learned potential energy surface is modeled by the Gaussian approximation potential65 with two- and three-body descriptors and kernel function similar to the smooth overlap atomic positions (SOAP) method.66 The descriptors are defined within a cutoff sphere of 6 or 4 Å for the two or three body term, respectively. They are discretized on radial basis functions (NR = 6 or 7) and, for the three body term, multiplied with spherical harmonics (lmax = 4). The reference structures to train the MLFF are selected on-the-fly during first-principles molecular dynamics calculations under isothermal–isobaric conditions; see refs (57) and (67) for methodological details. This method is integrated in the Vienna ab initio simulation package (VASP) code68,69 and calculates the potential energy, forces on the atoms, and stress tensor for all the reference structures, which are, by construction, well spread over the available structural phase space. The state-of-the-art meta-gradient corrected functional SCAN70 is applied in the first-principles (FP) calculations, since it accurately describes the physical interactions in the material.71 The electronic minimization was performed within the projector augmented wave formalism72 with a plane wave basis (cutoff 350 eV), a 2 × 2 × 2 k-point grid, and Gaussian smearing (σ = 0.01 eV). For the training, three 2 × 2 × 2 unit cells of MA1–xFAxPbI3 (x = 0, 0.5, 1) each containing eight cations were used. Starting from scratch, we trained the MLFF on FAPbI3 (x = 1) for 100 ps at 400 K with time steps of 3 fs, resulting in 707 included reference structures. Hereafter, training was continued on MAPbI3 (x = 0) for the same time and at the same temperature. The total number of reference structures in the resulting MLFF was only raised to 836. Last, we trained in the same way on MA0.5FA0.5PbI3; this increased the number to a total of 960 structures. These structures supply the finished MLFF with 121, 1432, 201, 244, and 1213 local reference configurations for the Pb, I, C, N, and H atoms, respectively. This MLFF was then used (in production mode, i.e., no more training) for all MD simulations shown in this work.
For the MLFF isothermal and isobaric NPT-MD simulations 4 × 4 × 4 unit cells of MA1–xFAxPbI3 were constructed with x = 0, 1/8, 1/4, ..., 1, where Langevin thermo- and barostats were applied to control the conditions. To study the influence of the spatial distribution of the FA and MA cations, ordered (O) and randomly (R) packed cells were constructed. In the O case, the 4 × 4 × 4 cells are constructed by replicating 2 × 2 × 2 unit cells in which the cations are distributed to maximize the distance to neighboring cations of the same species. In the R cells, the cations are randomly placed. All 4 × 4 × 4 cells were run for 100 ps at 300 and 400 K under 1 bar standard pressure. We calculate the dipolar coupling coefficient between all H–H pairs and divide them in two groups, with the intra- and intermolecular H–H connecting vectors. Applying the ensemble averaging over time and space following the approach by Goc et al.73−75 (see Supporting Information for details) then gives the average dipolar coupling that can be compared to the value measured by NMR.
Results and Discussion
Characterization
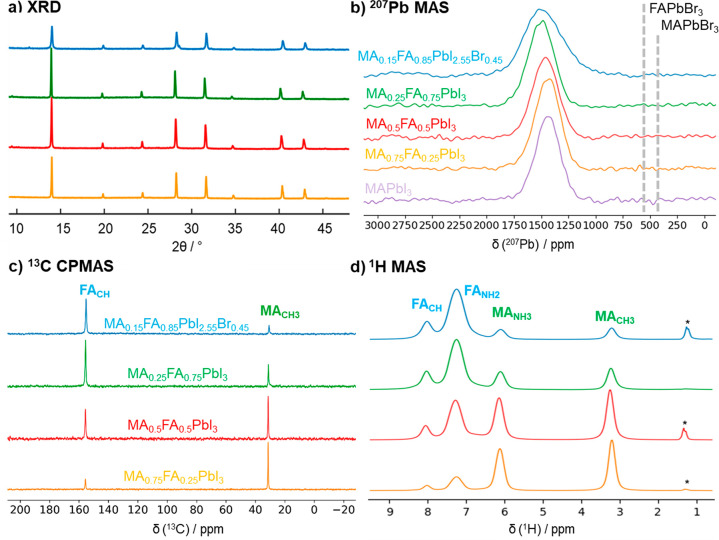
We prepared three mixed cation perovskites of the form MA1–xFAxPbI3 with x = 0.25, 0.50, 0.75 and a mixed cation and mixed halide composition MA0.15FA0.85PbI2.55Br0.45 (here referred to as double-mixed) by mechanochemical synthesis. The resulting powders were analyzed by powder X-ray diffraction, 207Pb MAS, as well as 13C MAS and high-resolution 1H MAS NMR spectroscopy to determine their crystal structure, exact FA/MA ratio, and possible impurities. The XRD patterns of all samples (Figure 1a) show reflections of a cubic lattice corroborating the stabilization of the cubic lattice upon mixing FA and MA cations.26−28 The corresponding lattice constants (Table S1) for MA1–xFAxPbI3 increase from 6.31 to 6.34 Å with increasing FA content, while the double-mix shows a smaller lattice constant of 6.30 Å due to incorporation of the smaller Br– ion, consistent with literature observations.34 All 207Pb MAS NMR spectra of the mixed samples and MAPbI3 (Figure 1b) show a single resonance, which gradually shifts with increasing FA content from 1430 ppm for MAPbI3 to 1490 ppm for α-FAPbI3.50,76,77 The 207Pb MAS NMR spectrum of the double-mixed sample MA0.15FA0.85PbI2.55Br0.45 (Figure 1b, blue) reveals a broadening of the 207Pb resonance in comparison to the other mixed cation perovskites. In general, multiple effects can play a role in the 207Pb line shape: T2 broadening due to very short spin–spin relaxation, scalar couplings between Pb–X species, or disorder around the lead atoms by halide mixing.49,76−79 Scalar couplings were found prominent for CsPbX3, while for MA- and FA-based perovskites only Pb–Cl species show features arising from the J-couplings but not for Pb–I or Pb–Br species at room temperature.78 Therefore, as the observed broadening is slightly asymmetric and the spin–spin relaxation (T2 relaxation) of pure MAPbI3 at room temperature is already very short (∼40 μs),49 we attribute the observed additional broadening for MA0.15FA0.85PbI2.55Br0.45 to I/Br mixing. This, in combination with the absence of any signal intensity in the chemical shift region for MAPbBr3 and FAPbBr3 (300–600 ppm),50,76,77,79 corroborates the incorporation of the Br– ions in the lattice.
Figure 1.
(a) XRD patterns, (b) 207Pb MAS NMR spectra, (c) 1H–13C CP-MAS NMR, and (d) 1H MAS NMR spectra of the three mixed MA1–xFAxPbI3 samples (x = 0.25, orange; x = 0.5, red; x = 0.75, green), as well as of the double-mixed sample MA0.15FA0.85PbI2.55Br0.45 (blue). (a) The XRD patterns of all samples show reflections of a cubic crystal lattice. The lattice constants are summarized in Table S1. (b) Additionally, a 207Pb MAS NMR spectrum of MAPbI3 (δiso = 1430 ppm) is depicted for comparison and dashed lines indicate chemical shifts for FAPbBr3 and MAPbBr3 from literature.50,76,77 The 207Pb isotropic chemical shift of α-FAPbI3 is reported to be 1495 ppm.77 (d) Asterisks in the 1H MAS NMR spectra indicate a small cyclohexane impurity, which is also observed in the 13C SPE MAS NMR spectra (Figure S2).
Characterization of the cations in terms of types and ratios, as well as the identification of impurities, is achieved by recording single-pulse 13C MAS (Figure S1) and 1H–13C cross-polarization (CP) MAS NMR spectra (Figure 1c), which show the typical resonances at 155.5 ppm for the CH-group of FA and at 31.3 ppm for the CH3-group of the MA cation. Additionally, the direct 13C single-pulse excitation (SPE) NMR spectra of MA0.15FA0.85PbI2.55Br0.45 and MA0.5FA0.5PbI3 (Figure S1) exhibit a sharp resonance at 27.5 ppm, which is absent in the CPMAS NMR spectra, suggesting that the heteronuclear dipolar coupling between 1H and 13C is averaged, indicative of a small, mobile impurity. The high-resolution 1H MAS NMR spectra of all samples (Figure 1d) show four distinct signals, which can readily be assigned to the 1H species of the MA and FA cations. The signals of the CH3-group and the NH3-group of the MA cation occur at chemical shifts of 3.3 and 6.2 ppm, respectively, while the NH2-groups and the CH-group of the FA cation are observed at 7.3 and 8.1 ppm. For MA0.15FA0.85PbI2.55Br0.45, MA0.5FA0.5PbI3, and MA0.75FA0.25PbI3 an additional sharp signal is observed at 1.4 ppm, which together with the 13C NMR signal at 27.5 ppm is assigned to residual cyclohexane, which was used as a milling agent in the mechanochemical synthesis of the powders. The cation ratios obtained from the 13C and 1H NMR spectra are in excellent agreement with the nominal ratios from the synthesis as summarized in Table S2.
Intermolecular Cation Interactions
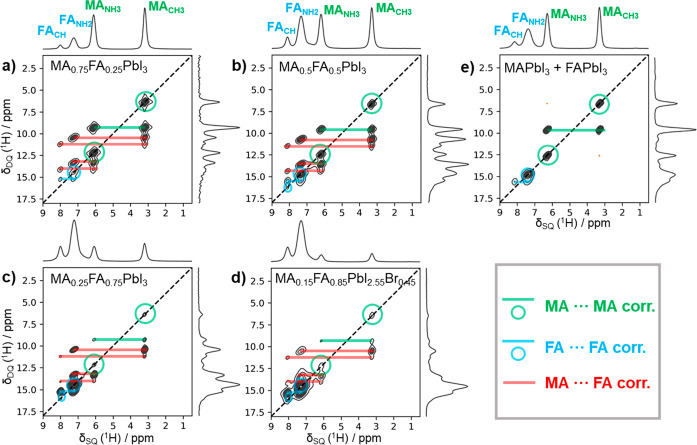
In order to probe the distribution and mixing behavior of MA and FA cations in the different mixed perovskite systems, we recorded two-dimensional (2D) 1H–1H DQSQ MAS NMR spectra. 1H–1H correlations of protons in close proximity with similar chemical environments result in signals along the diagonal (δDQ = 2δSQ) of the 2D spectra, while off-diagonal resonances stem from correlations between protons of differing chemical groups at the sum of the corresponding chemical shifts (δDQ = δSQ1 + δSQ2).
The experimental 2D 1H–1H DQSQ MAS NMR spectra of the four mixed samples are shown in Figure 2a–d. We observe correlations between the 1H resonances of MA cations (MA–MA; green; δDQ = 6.6, 9.5, and 12.4 ppm), between the 1H resonances of FA cations (FA–FA; blue; δDQ = 14.7, 15.5, and 16.2 ppm), and between the 1H resonances of MA and FA cations (MA–FA; red; δDQ = 10.7, 11.5, 13.6, and 14.4 ppm). The occurrence of MA–MA, FA–FA, and MA–FA correlations indicates the mixing of the cations for all compositions. In contrast, a 2D 1H–1H DQSQ MAS NMR spectrum for a physical mixture of α-FAPbI3 and MAPbI3 (Figure 2e) only shows DQ correlations between MA cations (green), as well as FA cations (blue), but no FA–MA correlations, as expected for a phase-separated system.
Figure 2.
2D 1H–1H DQSQ MAS NMR spectra of the mixed perovskite samples (a–d), as well as of a physical mixture of MAPbI3 and α-FAPbI3 (e) at an excitation time texc of 229 μs. Solid lines between resonances and circles on diagonal signals mark 1H–1H correlations between MA cations (green), FA cations (blue), and MA–FA cations (red). The existence of mixed MA–FA correlations demonstrates a successful mixing of MA and FA on the A site for all mixed perovskite compositions (a–d), while in the case of cation phase segregation the red correlations would diminish as in the case of a physical mixture MAPbI3 and α-FAPbI3 (e).
After qualitatively determining the 1H–1H correlations from the 2D 1H–1H DQSQ MAS NMR spectra, a quantification of the interaction strength between the coupled 1H species of the FA and MA cations provides further structural information. These can be accessed as the dipolar coupling is proportional to the number of contributing spins, as well as their relative alignment and distance (eq 4).55,60,80,81 Therefore, 1D 1H DQ buildup curves, which describe the buildup of DQ intensities of coupled spins as a function of excitation time, were recorded for all mixed perovskite samples, as well as the physical mixture of MAPbI3 and α-FAPbI3 (Figure S3). In the latter case, the DQ buildup curves are distinguishable for MA and FA signals (Figures 3a and S3). In contrast, for the mixed MA1–xFAxPbI3 and the double-mixed MA0.15FA0.85PbI2.55Br0.45, the individual DQ buildup curves for each 1H signal corresponding to MACH3, MANH3, FANH2, and FACH show a very similar behavior (Figure S3). Therefore, for each mixed composition, it is reasonable to average the individual DQ buildup curves resulting in the average DQ buildup curves shown in Figure 3b. All experimental DQ buildup curves exhibit the typical shape of a multispin system (Figure S3) with a distribution of dipolar interactions, which can be analyzed using either expensive modeling55 or a second moment approximation.60,64 Here, we used the so-called BABA-xy16 pulse sequence, which can be evaluated by the following approach to extract the average dipolar couplings:64
| 2 |
| 3 |
The average dipolar coupling D̅ in this approach is defined as60
| 4 |
Figure 3.
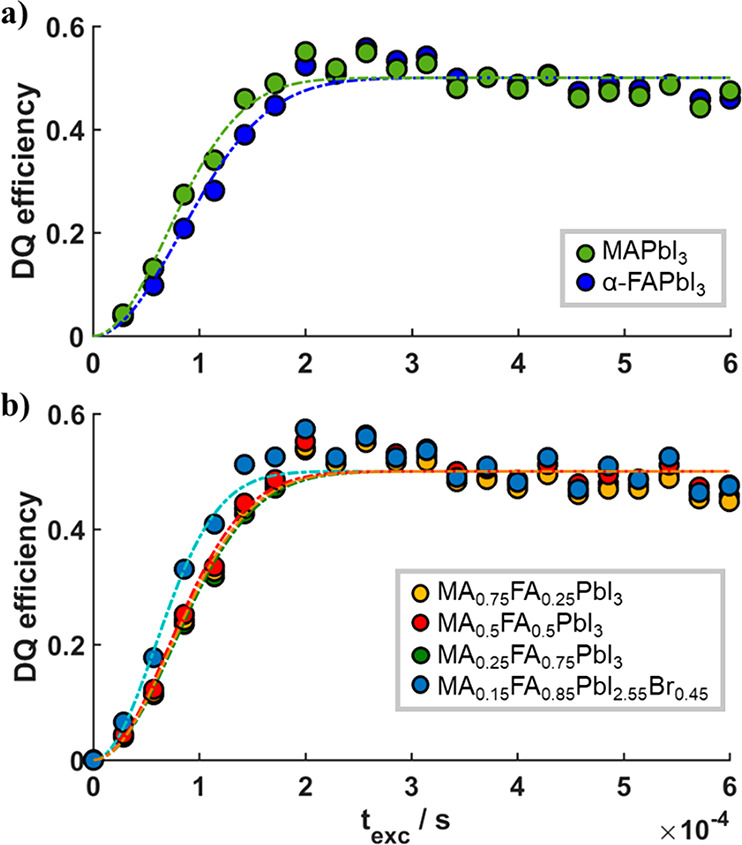
Average 1H DQ buildup curves (a) of MAPbI3 (green) and α-FAPbI3 (blue) and (b) of the mixed perovskite compositions MA1–xFAxPbI3(yellow, red, green), as well as MA0.15FA0.85PbI2.55Br0.45 (blue). The dashed lines are fits of the DQ buildup curves according to eq 2 to extract the average dipolar couplings, which are summarized in Figure 5 and Table S3.
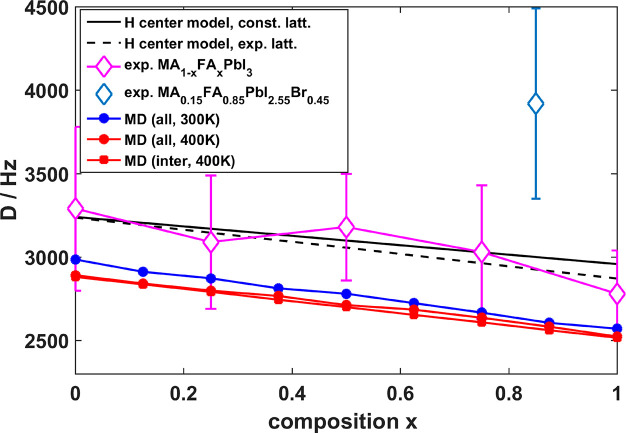
The extracted average dipolar couplings D̅ from the experimental data for the mixed compositions show a gradual increase with increasing MA content, from about 2800 Hz for pure α-FAPbI3 to ∼3300 Hz for MAPbI3 (Figure 5, pink, Table S3). In contrast, the double-mixed composition MA0.15FA0.85PbI2.55Br0.45 exhibits a significantly larger dipolar coupling of ∼3900 Hz (Figure 5, light blue, Table S3). It is expected that the fast reorientation of the MA and FA cations within their cage in the perovskite lattice26,43,47 will average the intramolecular dipolar interaction within the cations. Thus, the extracted dipolar couplings are connected to the number of FA and MA cations contributing, as FA has five and MA has six hydrogen atoms, and the average spatial intermolecular distances between neighboring cations. The decrease in D̅ with increasing FA content x could be related to a smaller number of contributing protons or to, on average, longer distances between hydrogens in nearest neighbor cations or a combination thereof.
Figure 5.
Average 1H dipolar couplings for MA1–xFAxPbI3 extracted from 1H DQ buildup curves (pink) and MD simulations at 300 K (blue) and 400 K (red, solid line). Additionally, solely intermolecular contributions to D̅ are shown for the MD run at 400 K (red, dashed lines) revealing minor differences to the full average dipolar coupling (red, solid line). Additionally, linear trends resulting from models, where all H atoms are placed in the center of the lattice A site neglecting dynamics, etc., are depicted in black. The solid line depicts the model with a fixed lattice constant over the whole compositional space resulting in a linear curve with a slope proportional to the hydrogen ratio of FA and MA (y = (√(5/6) – 1)D0 + D0, black solid). The dashed black line is the model using experimental lattice constants of MA1–xFAxPbI3, fitting the experimental data slightly better. This demonstrates that the linear dependence of D̅ on x is dominated by the number of contributing spins. Furthermore, the experimental average dipolar coupling of the double-mixed perovskite composition MA0.15FA0.85PbI2.55Br0.45 is depicted (light blue), revealing a significantly higher average dipolar coupling than the MA1–xFAxPbI3 compositions.
In order to understand the correlation between the dipolar coupling D̅ and the FA content x (Figure 5), we carry out state-of-the-art MLFF molecular dynamics simulations of MA1–xFAxPbI3 supercells containing a total of 64 MA and/or FA cations with long simulation times (100 ps). The MD trajectories are used to calculate the H–H pair distribution function g(r) (eq 5, Figure S4) that describes the likelihood to find H atoms at distances r:
| 5 |
Figure 4a depicts the pair distribution function for nearest neighbor coordinations (2–5 Å) for MAPbI3, MA0.5FA0.5PbI3, and α-FAPbI3 (see Figure S4 for full range). The distances resulting from intramolecular H–H pairs are between 1.5 and 4.5 Å depending on the molecular structure of the cations FA and MA (Figure S4). The onset of the intermolecular part of g(r) occurs at larger distances for MA cations (x = 0) than for FA cations (x = 1), and it gradually decreases with increasing x (Figure 4a), as expected considering the different MA and FA cation sizes.2 As observed above, an opposite trend is needed to explain the decrease of D̅ with increasing x considering only interatomic distances. Evidently, an interpretation of the dipolar couplings in terms of average intermolecular distances between the cations is insufficient.
Figure 4.
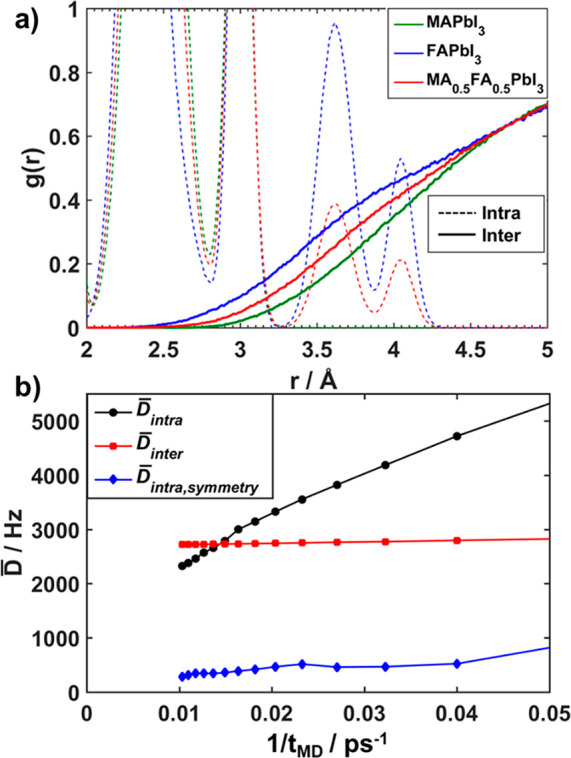
(a) Close-up of the pair distribution function between 2 and 5 Å for hydrogen atoms in MA1–xFAxPbI3 for x = 0, 0.5, and 1 obtained in the cubic phase at 400 K. The intra- and intermolecular contributions are depicted separately to demonstrate the onset of the intermolecular contributions. The full H–H pair distribution function of the simulation is depicted in the Supporting Information (Figure S4). (b) Intra- (black) and intermolecular (red) contributions to the average dipolar coupling as a function of simulation time for MA0.5FA0.5PbI3. Additionally, the intramolecular term averaged by applying symmetry of the intramolecular H–H vectors is shown in blue.
To clarify these apparently contradicting results, we calculate the average dipolar coupling (D̅) directly from the MD trajectories following the approach of Goc et al.73−75 (Supporting Information, section 5). This provides access to the intra- and intermolecular contribution to D̅ as a function of the inverse trajectory length (1/tMD). In Figure 4b the black and red lines show the intra- and intermolecular contribution in MA0.5FA0.5PbI3, respectively. The intramolecular contribution decays only slowly with time, whereas the intermolecular contribution quickly converges and thus appears nearly constant (see Figure 4b and Figure S5). About 100 ps (1/tMD = 0.01 ps–1) of simulation time is needed for the intramolecular contribution to be smaller than the intermolecular contribution. The intramolecular contribution is still noticeably decreasing after these 100 ps. In view of the nearly free rotation of the cations in the cubic perovskite lattice, on longer time scales (1/tMD → 0 ps–1) one would expect a (vanishly) small intramolecular dipolar coupling. This can be demonstrated if costly MD runs are carried out for which several orders of magnitude longer simulation times will be needed. As an alternative, it is possible to significantly reduce the computational effort by considering symmetry within the large supercell (see Supporting Information). Averaging over similar intramolecular H–H vectors results in three remaining inequivalent vectors for MA and six for FA. In this way we can improve the statistics for D̅intra without elongating the trajectory, which causes a drastic reduction of D̅intra (Figure 4b, blue, and Figure S5). These results demonstrate that the average dipolar coupling D̅ is very well approximated by solely considering intermolecular contributions, i.e., D̅intra = 0 on the NMR time scale.
In Figure 5 the calculated D̅ versus perovskite composition x is plotted as well as the experimental values obtained from the 1H DQ buildup curves. The values calculated for the MA1–xFAxPbI3 systems are in excellent agreement with the experiment. The small offset (∼300–400 Hz) of the calculated values is caused by the slightly larger lattice constant (∼0.08 Å) predicted by the MLFF (Figure S1). At 400 K simulation temperature the lattice constants are slightly larger (∼0.02 Å) than at 300 K due to thermal expansion (Figure S1), which results in a decrease of the calculated D̅ (Figure 5). In order to investigate the influence of the packing order on the calculated D̅ values, we also compared two types of homogeneous distributions of FA and MA cations, a random (R) and an ordered (O) packing. The O packing represents FA and MA cations in alternating positions resulting in solely nearest-neighbor MA–FA correlations for x = 0.5. Interestingly, we find that the packing order has no noticeable effect on the average dipolar interaction D̅ between the cations (Figure S6).
With these results it becomes clear that the linear dependence of D̅ on x stems from a change of the contributing average amount of hydrogen pairs in the mixed perovskites. As MA possesses six hydrogens, whereas FA has only five, the average dipolar coupling D̅ decreases with increasing FA content x (Figure 5, pink and black solid). Placing all H in the center of the A lattice site is also a good approximate model (Figure 5, black lines). In contrast, the ordering of MA/FA on the grid and the change of the (pseudo)cubic lattice constant have a much smaller effect. As the change of D̅ with x is dominated by the hydrogen content in mixed MA1–xFAxPbI3, we conclude that average intermolecular proton–proton distances in nearest neighbor coordination are rather similar throughout the investigated compositional range.
Figure 5 (light blue diamond) also shows the experimental average dipolar coupling of MA0.15FA0.85PbI2.55Br0.45. At about 3900 Hz it is significantly larger than for the binary MA/FA mixtures. Although the lattice contracts slightly upon Br– incorporation (Table S1), a shrinkage of the pseudocubic lattice constant of about 0.04 Å in comparison to MA0.25FA0.75PbI3 and α-FAPbI3 cannot account for an increase in D̅ of about 1000 Hz. The increase therefore indicates a restriction in cation mobility either by a significant reduction in reorientation frequency or by a restriction in spatial degrees of freedom, i.e., an anisotropic motion over specific orientations. Stronger interactions of the FA and MA cations with the inorganic sublattice, induced by the presence of more electronegative Br– ions (compared to I–), or the lattice contraction itself could cause this. Both these effects will raise the average dipolar couplings D̅ and might give rise to a non-negligible intramolecular contribution to D̅.
These findings fit in a recently proposed scenario of restricted MA cation dynamics upon mixing I– and Br– in the lattice. In this scenario specific hydrogen bonding situations for the MA cations result in a higher activation barrier for rotational jumps in certain directions and thus in their partial immobilization causing an anisotropic dynamical behavior.82 For FA cations, however, the hydrogen bonds to the inorganic sublattice are much weaker,26,83 initially resulting in faster reorientations in comparison to MA. Consequently, one would expect less influence of I/Br mixing on the FA dynamics, which was not resolved in our experiments. To fully understand the origin of the increase of D̅ and to characterize the possible dynamical restriction of cations due to interactions with the inorganic sublattice, further MLFF calculations on mixed cation and anion compositions are needed.
Microscopic Cation (Dis)order
The MLFF calculations corroborate that the intramolecular dipolar coupling of the cations is averaged through the rapid reorientation within the A site, and thus only intermolecular dipolar interactions are measured experimentally. Consequently, all 1H–1H correlations measured in the 2D 1H–1H DQSQ MAS NMR spectra (Figure 2) are due to a close proximity of protons on neighboring cations. As we established, the strength of the dipolar interaction only depends on the number of interacting spins and hardly on slight variations of the lattice parameters for the different compositions. Therefore, differences in DQ intensities in the 2D spectra of the different compounds are directly proportional to the number of intercation interactions, i.e., the relative amounts of MA and FA cations, taking the different numbers of protons for MA and FA into account. The quantitative analysis of the DQ signal intensities thus makes it possible to extract the relative occurrence of each of the intercation dipolar contacts MA–MA, MA–FA, and FA–FA (hereafter referred to as MA–MA, MA–FA, and FA–FA contacts). Their population provides a measure for the microscopic order/disorder of the cations within the perovskite lattice.
In the cubic perovskite lattice, each A site cation, MA or FA, is surrounded by six nearest-neighbor A cations. Different ordering of the cations within the cubic lattice, e.g., random mixing, alternating MA and FA ordering, or clustering of MA or FA cations, results in different probabilities for local nearest neighbor coordinations MA[MA6–nFAn] and FA[MA6–nFAn] (n = 1, 2, ..., 6). These are experimentally accessible as the sum of resulting MA–MA, FA–FA, and mixed MA–FA contacts. A random cation distribution can be described by a binomial distribution based on the relative occurrence of MA or FA in the lattice, providing the statistics of the total of MA–MA (Figure 2 and Figure 6, green), FA–FA (Figure 2 and Figure 6, blue), and MA–FA contacts (Figure 2 and Figure 6a, red).
Figure 6.
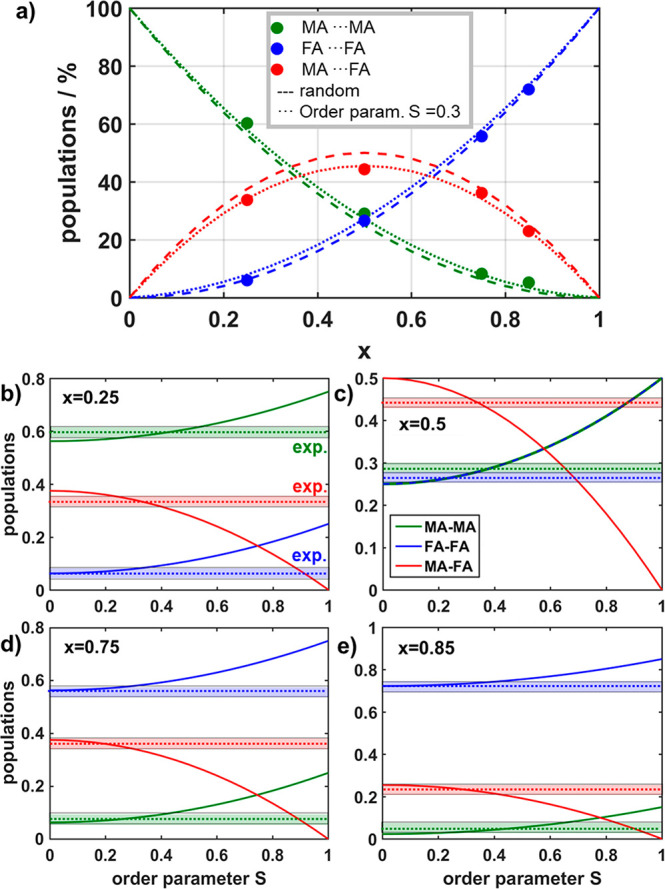
(a) Populations of cation–cation contacts, MA–MA (green), FA–FA (blue), and MA–FA (red), as a function of FA content x. The experimental data are indicated by dots, while the populations according to a random distribution of cations are shown by dashed lines. Dotted lines represent the populations of contacts for a cluster model with an order parameter S of 0.3. (b–e) Calculated populations of cation–cation contacts, MA–MA (green), FA–FA (blue), and MA–FA (red), as a function of order parameter S for the different compositions of the mixed MA1–xFAxPbI3 (b–d), as well as MA0.15FA0.85PbI2.55Br0.45 (e). The horizontal bars indicate the experimental accuracy for the observed populations (dashed lines) of cation–cation correlations in the 2D 1H–1H DQSQ MAS NMR spectra (Figure 2).
The comparison of the experimentally observed populations (Figure 6a, dots) with the populations resulting for a random distribution (Figure 6a, dashed lines) shows an overall good agreement, with small but systematic deviations especially for the mixed contact MA–FA (red). This indicates a weak tendency for clustering of MA and FA cations, leading to local fluctuations in composition, which can be quantified by introducing an order parameter S,84−86 in analogy to the analysis of XRD data.87 For a cluster model, an order parameter of S = 0 corresponds to a random distribution, whereas S = 1 characterizes a complete phase separation. The site occupancies rMA and rFA describing the clustering tendency of the cations and thus the local compositional changes can then be parametrized as
| 6 |
| 7 |
With that, the theoretical populations for the three cation–cation contacts are defined as
| 8 |
| 9 |
| 10 |
Parts b–e of Figure 6 depict the calculated populations for the three cation–cation contacts MA–MA (green), FA–FA (blue), and MA–FA (red) as a function of S for different mixed cation compositions MA1–xFAxPbI3 (x = 0.25 (b), x = 0.5 (c), x = 0.75 (d), x = 0.85 (e)). Additionally, the experimentally determined occurrence of each contact for each composition x is depicted as dashed lines, where the width of the bars accounts for the experimental error. The intersection of the observed occurrences with the calculated populations reveals that partial MA–MA and FA–FA clustering with an order parameter S between 0.2 and 0.4 takes place for compositions with x = 0.25 and x = 0.5. For compositions with higher FA contents (x = 0.75, 0.85, Figure 3d,e) the intersection covers a range between S = 0 and S = 0.3 for a composition x = 0.75 and covers a range between S = 0–0.4 for x = 0.85. At low and high values of x the changes in populations are less pronounced, preventing a precise assignment of S within the experimental accuracy. Interestingly, the experimentally determined populations show a similar trend over the entire compositional range.
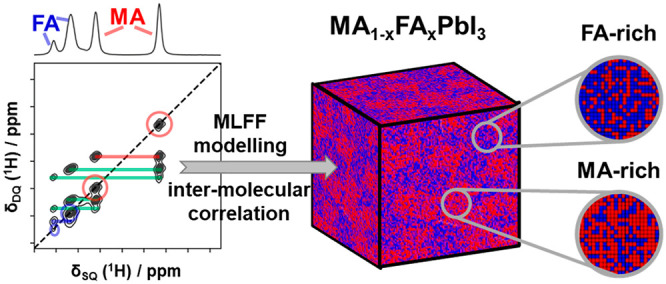
In order to visualize the effect of cation clustering with S = 0.3 in comparison to a random scenario, the distributions of FA (blue) and MA (red) cations for MA1–xFAxPbI3 compositions on a 2D grid are schematically depicted in Figure 7. The circles labeled rMA and rFA demonstrate the local compositional fluctuations resulting from MA and FA clustering, respectively, within the perovskite particles. The schematic representation illustrates that the nominal overall composition MA1–xFAxPbI3 is heterogeneous with MA and FA-rich regions, where the average compositional fluctuations can be described by rMA and rFA. An upper limit for the size of these clusters is deducted by analyzing the width of the X-ray reflections. Pronounced domains of local compositional fluctuations would lead to the measurement of a distribution of lattice constants and in turn to a broadening of XRD peaks. As no broadening is observed (Figure S7), the cluster domains must be smaller than of the order of 100 nm.
Figure 7.
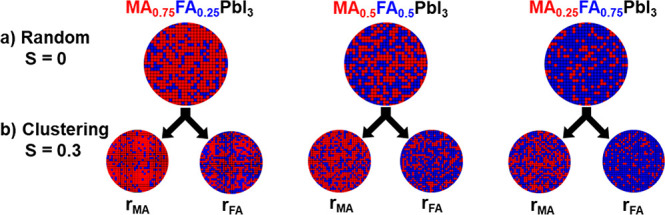
Schematic representation of MA (red)/FA (blue) distributions within MA1–xFAxPbI3 (x = 0.25, 0.50, 0.75) perovskites following random statistics (a) and MA or FA clustering (b) to a degree of S = 0.3 labeled rMA and rFA, respectively (according to eqs 6 and 7). As the experimental NMR data do not provide information about domain sizes of MA-rich and FA-rich regions, arbitrary sized circles were chosen to represent the statistics.
To be thermodynamically stable, the Gibbs free energy of the clustered structure must be lower than for the random mix (S = 0) structure. In general, the formation of domains results in strain at the domain walls, which is marginal in this particular case, as the pseudocubic lattice constants differ only 0.06 Å between the parent composition MAPbI3 and α-FAPbI3 and 0.03 Å for the mixed compositions x = 0.25 and x = 0.75. Furthermore, if the clusters are very small, i.e., in the range of several nearest neighbor shells, domain walls might not even form. If only gradual compositional changes occur, subtle distortions of the inorganic sublattice will be sufficient to compensate for the compositional fluctuations. In a clustered structure, there are less different ways to distribute the cations over the lattice of A sites, resulting in a lower entropy and thus higher free energy. However, the clustering might raise the entropy in case there is an impact on the cation dynamics. Recently it was discussed that the rotational motion of FA cations is confined upon mixing with MA+ or Cs+ cations because of a preferential orientation of the FA cations.41,43,88 As the local configuration of neighboring MA+ or Cs+ was important for the ordering of FA,43 local clustering of MA or FA cations may suppress this reduction of the degrees of motion, thus resulting in a higher dynamical freedom and lowering of the free energy compared to a random mixture.
Conclusion
We have combined NMR spectroscopy and MLFF MD simulations to study the dynamics and local (dis)order of FA and MA cations in the mixed hybrid perovskite systems MA1–xFAxPbI3 and MA0.15FA0.85PbI2.55Br0.45. On the basis of our results, we can sketch a plausible scenario for an ordering pattern of the cations in MA1–xFAxPbI3 mixed hybrid perovskites. The population analysis of the 1H–1H DQSQ MAS NMR spectra indicates that a microstructure (order parameter S ∼ 0.3) with MA-rich and FA-rich regions occurs. XRD analysis indicates that the average size of the domains is below ∼100 nm. Furthermore, the novel MLFF method has been shown to accurately predict the average dipolar coupling measured in the NMR experiment. Building on this excellent agreement, we can conclude (a) that the average dipolar coupling D̅ is dominated by intermolecular nearest neighbor cation interactions, (b) that it scales with the number of 1H spins on the neighboring cation, which explains its decrease with FA composition x, and (c) that it depends on average composition, i.e., we did not observe changes by short-range compositional fluctuations. While a similar MA and FA ordering was found for the double-mixed MA0.15FA0.85PbI2.55Br0.45 perovskite and the MA1–xFAxPbI3 systems, the average 1H−1H dipolar coupling was observed to be significantly higher in the double-mixed system. This indicates a restriction of the mobility of the organic cations resulting in an anisotropic motion upon incorporation of the smaller Br– ions, possibly induced through the slight lattice contraction. Both these effects will raise the average dipolar coupling D̅.
Heterogeneity in local cation compositions results in a local variation of perovskite lattice constants and in local variations of the electrostatic interaction between cations and inorganic sublattice.89,90 Both effects cause a distribution of band gap energies of mixed perovskites, as was concluded from the observed distribution of optical properties and ab initio calculations.89,90 As a consequence, the charge carriers will localize in energetically favorable domains limiting the overall charge transport. Furthermore, it was found that local compositional heterogeneities can cause the formation of clusters of deep traps.91 These trap clusters in turn appear to be the key factor limiting the optoelectronic properties,91 ion migration,92,93 and stability of mixed halide perovskites. On the basis of these considerations, it appears attractive to reduce the degree of mixing while ensuring a robust stabilization of the perovskite lattice. This indeed is in line with the most recent developments in the field of perovskite solar cells,17 where our results will help to better exploit the full potential of mixed halide perovskites and corresponding optoelectronic devices.
Acknowledgments
We thank NWO for the support of the “Solid-State NMR Facilities for Advanced Materials Science”, which is part of the uNMR-NL ROADMAP facility. The facilities technicians Gerrit Janssen, Hans Janssen, and Ruud Aspers are thanked for their support. H.G. thanks the “Deutsche Forschungsgemeinschaft (DFG)” for funding within Grant GR 5505/1-1. M.B. gratefully thanks Jonathan Lahnsteiner for stimulating discussions on mixed perovskite order. M.B. acknowledges funding by the Austrian Science Fund (FWF): Grant P30316-N27. Computations were partly performed on the Vienna Scientific Cluster VSC3. F.P. and N.L. thank the “Deutsche Forschungsgemeinschaft (DFG)” for funding (Project PA 3373/3-1).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.0c10042.
Exact precursor amounts for the syntheses; experimental and calculated average lattice constants of MA1–xFAxPbI3; 13C SPE MAS NMR spectra, individual 1H DQ buildup curves, exact MA/FA ratios and experimental dipolar couplings of MA1–xFAxPbI3 and MA0.15FA0.85PbI2.55Br0.45; full H–H pair distribution function extracted from MD simulations; further details on analyses of the MLFF MD simulations (PDF)
The authors declare no competing financial interest.
Special Issue
Published as part of The Journal of Physical Chemistry virtual special issue “Hellmut Eckert Festschrift”.
Supplementary Material
References
- NREL. Research Cell Record Efficiency Chart. https://www.nrel.gov/pv/cell-efficiency.html (accessed Sep 30, 2020).
- Jena A. K.; Kulkarni A.; Miyasaka T. Halide Perovskite Photovoltaics: Background, Status, and Future Prospects. Chem. Rev. 2019, 119, 3036–3103. 10.1021/acs.chemrev.8b00539. [DOI] [PubMed] [Google Scholar]
- Lin K.; Xing J.; Quan L. N.; de Arquer F. P. G.; Gong X.; Lu J.; Xie L.; Zhao W.; Zhang D.; Yan C.; et al. Perovskite Light-Emitting Diodes with External Quantum Efficiency Exceeding 20 per Cent. Nature 2018, 562, 245–248. 10.1038/s41586-018-0575-3. [DOI] [PubMed] [Google Scholar]
- Cho C.; Zhao B.; Tainter G. D.; Lee J.-Y.; Friend R. H.; Di D.; Deschler F.; Greenham N. C. The Role of Photon Recycling in Perovskite Light-Emitting Diodes. Nat. Commun. 2020, 11, 611. 10.1038/s41467-020-14401-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao L.; Yan Q. Recent Advances in Lead Halide Perovskites for Radiation Detectors. Sol. RRL 2020, 4, 1900210. 10.1002/solr.201900210. [DOI] [Google Scholar]
- Wei H.; Huang J. Halide Lead Perovskites for Ionizing Radiation Detection. Nat. Commun. 2019, 10, 1066. 10.1038/s41467-019-08981-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.; Yi H. T.; Wu X.; Haroldson R.; Gartstein Y. N.; Rodionov Y. I.; Tikhonov K. S.; Zakhidov A.; Zhu X. Y.; Podzorov V. Extended Carrier Lifetimes and Diffusion in Hybrid Perovskites Revealed by Hall Effect and Photoconductivity Measurements. Nat. Commun. 2016, 7, 12253. 10.1038/ncomms12253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh A. Principles of Chemical Bonding and Band Gap Engineering in Hybrid Organic-Inorganic Halide Perovskites. J. Phys. Chem. C 2015, 119, 5755–5760. 10.1021/jp512420b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon N. J.; Noh J. H.; Yang W. S.; Kim Y. C.; Ryu S.; Seo J.; Seok S. Il. Compositional Engineering of Perovskite Materials for High-Performance Solar Cells. Nature 2015, 517, 476–480. 10.1038/nature14133. [DOI] [PubMed] [Google Scholar]
- Petrus M. L.; Schlipf J.; Li C.; Gujar T. P.; Giesbrecht N.; Müller-Buschbaum P.; Thelakkat M.; Bein T.; Hüttner S.; Docampo P. Capturing the Sun: A Review of the Challenges and Perspectives of Perovskite Solar Cells. Adv. Energy Mater. 2017, 7, 1700264. 10.1002/aenm.201700264. [DOI] [Google Scholar]
- Panzer F.; Li C.; Meier T.; Köhler A.; Huettner S. Impact of Structural Dynamics on the Optical Properties of Methylammonium Lead Iodide Perovskites. Adv. Energy Mater. 2017, 7, 1700286. 10.1002/aenm.201700286. [DOI] [Google Scholar]
- Gao P.; Grätzel M.; Nazeeruddin M. K. Organohalide Lead Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 2448–2463. 10.1039/C4EE00942H. [DOI] [Google Scholar]
- Kazim S.; Nazeeruddin M. K.; Grätzel M.; Ahmad S. Perovskite as Light Harvester: A Game Changer in Photovoltaics. Angew. Chem., Int. Ed. 2014, 53, 2812–2824. 10.1002/anie.201308719. [DOI] [PubMed] [Google Scholar]
- Park N.; Grätzel M.; Miyasaka T.. Organic-Iorganic Halide Perovskite Photovoltaics: From Fundamentals to Devices Architectures; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Jeon N. J.; Na H.; Jung E. H.; Yang T.-Y.; Lee Y. G.; Kim G.; Shin H.-W.; Il Seok S.; Lee J.; Seo J. A Fluorene-Terminated Hole-Transporting Material for Highly Efficient and Stable Perovskite Solar Cells. Nat. Energy 2018, 3, 682–689. 10.1038/s41560-018-0200-6. [DOI] [Google Scholar]
- Yang W. S.; Park B.; Jung E. H.; Jeon N. J.; Kim Y. C.; Lee D. U.; Shin S. S.; Seo J.; Kim E. K.; Noh J. H.; et al. Iodide Management in Formamidinium-Lead-Halide-Based Perovskite Layers for Efficient Solar Cells. Science 2017, 356, 1376–1379. 10.1126/science.aan2301. [DOI] [PubMed] [Google Scholar]
- Lu H.; Krishna A.; Zakeeruddin S. M.; Grätzel M.; Hagfeldt A. Compositional and Interface Engineering of Organic-Inorganic Lead Halide Perovskite Solar Cells. iScience 2020, 23, 101359. 10.1016/j.isci.2020.101359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoke E. T.; Slotcavage D. J.; Dohner E. R.; Bowring A. R.; Karunadasa H. I.; McGehee M. D. Reversible Photo-Induced Trap Formation in Mixed-Halide Hybrid Perovskites for Photovoltaics. Chem. Sci. 2015, 6, 613–617. 10.1039/C4SC03141E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X.; Yan X.; Wang W.; Zhu X.; Li H.; Ma W.; Sheng C. Light Induced Metastable Modification of Optical Properties in CH3NH3PbI3-xBrx Perovskite Films: Two-Step Mechanism. Org. Electron. 2016, 34, 79–83. 10.1016/j.orgel.2016.04.020. [DOI] [Google Scholar]
- Knight A. J.; Herz L. M. Preventing Phase Segregation in Mixed-Halide Perovskites: A Perspective. Energy Environ. Sci. 2020, 13, 2024–2046. 10.1039/D0EE00788A. [DOI] [Google Scholar]
- Knight A. J.; Wright A. D.; Patel J. B.; McMeekin D. P.; Snaith H. J.; Johnston M. B.; Herz L. M. Electronic Traps and Phase Segregation in Lead Mixed-Halide Perovskite. ACS Energy Lett. 2019, 4, 75–84. 10.1021/acsenergylett.8b02002. [DOI] [Google Scholar]
- Jeong M.; Choi I. W.; Go E. M.; Cho Y.; Kim M.; Lee B.; Jeong S.; Jo Y.; Choi H. W.; Lee J.; et al. Stable Perovskite Solar Cells with Efficiency Exceeding 24.8% and 0.3-V Voltage Loss. Science 2020, 369, 1615–1620. 10.1126/science.abb7167. [DOI] [PubMed] [Google Scholar]
- Kim M.; Kim G.-H.; Lee T. K.; Choi I. W.; Choi H. W.; Jo Y.; Yoon Y. J.; Kim J. W.; Lee J.; Huh D.; et al. Methylammonium Chloride Induces Intermediate Phase Stabilization for Efficient Perovskite Solar Cells. Joule 2019, 3, 2179–2192. 10.1016/j.joule.2019.06.014. [DOI] [Google Scholar]
- Weller M. T.; Weber O. J.; Frost J. M.; Walsh A. Cubic Perovskite Structure of Black Formamidinium Lead Iodide, α-[HC(NH2)2]PbI3, at 298 K. J. Phys. Chem. Lett. 2015, 6, 3209–3212. 10.1021/acs.jpclett.5b01432. [DOI] [Google Scholar]
- Weber O. J.; Charles B.; Weller M. T. Phase Behaviour and Composition in the Formamidinium-Methylammonium Hybrid Lead Iodide Perovskite Solid Solution. J. Mater. Chem. A 2016, 4, 15375–15382. 10.1039/C6TA06607K. [DOI] [Google Scholar]
- Kubicki D. J.; Prochowicz D.; Hofstetter A.; Péchy P.; Zakeeruddin S. M.; Grätzel M.; Emsley L. Cation Dynamics in Mixed-Cation (MA)x(FA)1-xPbI3 Hybrid Perovskites from Solid-State NMR. J. Am. Chem. Soc. 2017, 139, 10055–10061. 10.1021/jacs.7b04930. [DOI] [PubMed] [Google Scholar]
- Pellet N.; Gao P.; Gregori G.; Yang T.-Y.; Nazeeruddin M. K.; Maier J.; Grätzel M. Mixed-Organic-Cation Perovskite Photovoltaics for Enhanced Solar-Light Harvesting. Angew. Chem., Int. Ed. 2014, 53, 3151–3157. 10.1002/anie.201309361. [DOI] [PubMed] [Google Scholar]
- Yi C.; Luo J.; Meloni S.; Boziki A.; Ashari-Astani N.; Grätzel C.; Zakeeruddin S. M.; Röthlisberger U.; Grätzel M. Entropic Stabilization of Mixed A-Cation ABX3 Metal Halide Perovskites for High Performance Perovskite Solar Cells. Energy Environ. Sci. 2016, 9, 656–662. 10.1039/C5EE03255E. [DOI] [Google Scholar]
- Goldschmidt V. M. Die Gesetze Der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. 10.1007/BF01507527. [DOI] [Google Scholar]
- Zhao J.; Deng Y.; Wei H.; Zheng X.; Yu Z.; Shao Y.; Shield J. E.; Huang J. Strained Hybrid Perovskite Thin Films and Their Impact on the Intrinsic Stability of Perovskite Solar Cells. Sci. Adv. 2017, 3, eaao5616 10.1126/sciadv.aao5616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu C.; Niu X.; Fu Y.; Li N.; Hu C.; Chen Y.; He X.; Na G.; Liu P.; Zai H.; et al. Strain Engineering in Perovskite Solar Cells and Its Impacts on Carrier Dynamics. Nat. Commun. 2019, 10, 815. 10.1038/s41467-019-08507-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motta C.; El-Mellouhi F.; Kais S.; Tabet N.; Alharbi F.; Sanvito S. Revealing the Role of Organic Cations in Hybrid Halide Perovskite CH3NH3PbI3. Nat. Commun. 2015, 6, 7026. 10.1038/ncomms8026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong J.; Yang M.; Ma X.; Schaller R. D.; Liu G.; Kong L.; Yang Y.; Beard M. C.; Lesslie M.; Dai Y.; et al. Electron-Rotor Interaction in Organic-Inorganic Lead Iodide Perovskites Discovered by Isotope Effects. J. Phys. Chem. Lett. 2016, 7, 2879–2887. 10.1021/acs.jpclett.6b01199. [DOI] [PubMed] [Google Scholar]
- Jesper Jacobsson T.; Correa-Baena J.-P. P.; Pazoki M.; Saliba M.; Schenk K.; Grätzel M.; Hagfeldt A. Exploration of the Compositional Space for Mixed Lead Halogen Perovskites for High Efficiency Solar Cells. Energy Environ. Sci. 2016, 9, 1706–1724. 10.1039/C6EE00030D. [DOI] [Google Scholar]
- Zheng X.; Wu C.; Jha S. K.; Li Z.; Zhu K.; Priya S. Improved Phase Stability of Formamidinium Lead Triiodide Perovskite by Strain Relaxation. ACS Energy Lett. 2016, 1, 1014–1020. 10.1021/acsenergylett.6b00457. [DOI] [Google Scholar]
- Xie L. Q.; Chen L.; Nan Z. A.; Lin H. X.; Wang T.; Zhan D. P.; Yan J. W.; Mao B. W.; Tian Z. Q. Understanding the Cubic Phase Stabilization and Crystallization Kinetics in Mixed Cations and Halides Perovskite Single Crystals. J. Am. Chem. Soc. 2017, 139, 3320–3323. 10.1021/jacs.6b12432. [DOI] [PubMed] [Google Scholar]
- Tennyson E. M.; Doherty T. A. S.; Stranks S. D. Heterogeneity at Multiple Length Scales in Halide Perovskite Semiconductors. Nat. Rev. Mater. 2019, 4, 573–587. 10.1038/s41578-019-0125-0. [DOI] [Google Scholar]
- Alanazi A. Q.; Kubicki D. J.; Prochowicz D.; Alharbi E. A.; Bouduban M. E. F.; Jahanbakhshi F.; Mladenović M.; Milić J. V.; Giordano F.; Ren D.; et al. Atomic-Level Microstructure of Efficient Formamidinium-Based Perovskite Solar Cells Stabilized by 5-Ammonium Valeric Acid Iodide Revealed by Multinuclear and Two-Dimensional Solid-State NMR. J. Am. Chem. Soc. 2019, 141, 17659–17669. 10.1021/jacs.9b07381. [DOI] [PubMed] [Google Scholar]
- Kubicki D. J.; Prochowicz D.; Hofstetter A.; Saski M.; Yadav P.; Bi D.; Pellet N.; Lewiński J.; Zakeeruddin S. M.; Grätzel M.; et al. Formation of Stable Mixed Guanidinium-Methylammonium Phases with Exceptionally Long Carrier Lifetimes for High-Efficiency Lead Iodide-Based Perovskite Photovoltaics. J. Am. Chem. Soc. 2018, 140, 3345–3351. 10.1021/jacs.7b12860. [DOI] [PubMed] [Google Scholar]
- Kubicki D. J.; Prochowicz D.; Hofstetter A.; Zakeeruddin S. M.; Gratzel M.; Emsley L. Phase Segregation in Cs-, Rb- and K-Doped Mixed-Cation (MA)x(FA)1-xPbI3 Hybrid Perovskites from Solid-State NMR. J. Am. Chem. Soc. 2017, 139, 14173–14180. 10.1021/jacs.7b07223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh D.; Smith A. R.; Walker A. B.; Islam M. S. Mixed A-Cation Perovskites for Solar Cells: Atomic-Scale Insights into Structural Distortion, Hydrogen Bonding, and Electronic Properties. Chem. Mater. 2018, 30, 5194–5204. 10.1021/acs.chemmater.8b01851. [DOI] [Google Scholar]
- Van Gompel W. T. M.; Herckens R.; Reekmans G.; Ruttens B.; D’Haen J.; Adriaensens P.; Lutsen L.; Vanderzande D. Degradation of the Formamidinium Cation and the Quantification of the Formamidinium-Methylammonium Ratio in Lead Iodide Hybrid Perovskites by Nuclear Magnetic Resonance Spectroscopy. J. Phys. Chem. C 2018, 122, 4117–4124. 10.1021/acs.jpcc.7b09805. [DOI] [Google Scholar]
- Fisicaro G.; La Magna A.; Alberti A.; Smecca E.; Mannino G.; Deretzis I. Local Order and Rotational Dynamics in Mixed A-Cation Lead Iodide Perovskites. J. Phys. Chem. Lett. 2020, 11, 1068–1074. 10.1021/acs.jpclett.9b03763. [DOI] [PubMed] [Google Scholar]
- Franssen W. M. J.; Kentgens A. P. M. Solid - State NMR of Hybrid Halide Perovskites. Solid State Nucl. Magn. Reson. 2019, 100, 36–44. 10.1016/j.ssnmr.2019.03.005. [DOI] [PubMed] [Google Scholar]
- Wasylishen R. E.; Knop O.; Macdonald J. B. Cation Rotation in Methylammonium Lead Halides. Solid State Commun. 1985, 56, 581–582. 10.1016/0038-1098(85)90959-7. [DOI] [Google Scholar]
- Knop O.; Wasylishen R. E.; White M. A.; Cameron T. S.; Van Oort M. J. M. Alkylammonium Lead Halides. Part 2. CH3NH3PbX3 (X = Cl, Br, I) Perovskites: Cuboctahedral Halide Cages with Isotropic Cation Reorientation. Can. J. Chem. 1990, 68, 412–422. 10.1139/v90-063. [DOI] [Google Scholar]
- Bernard G. M.; Wasylishen R. E.; Ratcliffe C. I.; Terskikh V.; Wu Q.; Buriak J. M.; Hauger T. Methylammonium Cation Dynamics in Methylammonium Lead Halide Perovskites: A Solid-State NMR Perspective. J. Phys. Chem. A 2018, 122, 1560–1573. 10.1021/acs.jpca.7b11558. [DOI] [PubMed] [Google Scholar]
- Franssen W. M. J.; Bruijnaers B. J.; Portengen V. H. L.; Kentgens A. P. M. Dimethylammonium Incorporation in Lead Acetate Based MAPbI3 Perovskite Solar Cells. ChemPhysChem 2018, 19, 3107–3115. 10.1002/cphc.201800732. [DOI] [PubMed] [Google Scholar]
- Franssen W. M. J.; Van Es S. G. D.; Dervişoǧlu R.; de Wijs G. A.; Kentgens A. P. M. Symmetry, Dynamics, and Defects in Methylammonium Lead Halide Perovskites. J. Phys. Chem. Lett. 2017, 8, 61–66. 10.1021/acs.jpclett.6b02542. [DOI] [PubMed] [Google Scholar]
- Roiland C.; Trippé-Allard G.; Jemli K.; Alonso B.; Ameline J.-C. C.; Gautier R.; Bataille T.; Le Pollès L.; Deleporte E.; Even J.; et al. Multinuclear NMR as a Tool for Studying Local Order and Dynamics in CH3NH3PbX3 (X = Cl, Br, I) Hybrid Perovskites. Phys. Chem. Chem. Phys. 2016, 18 (39), 27133–27142. 10.1039/C6CP02947G. [DOI] [PubMed] [Google Scholar]
- Martineau C.; Senker J.; Taulelle F. NMR Crystallography. Annu. Rep. NMR Spectrosc. 2014, 82, 1–57. 10.1016/B978-0-12-800184-4.00001-1. [DOI] [Google Scholar]
- Harris R. K.; Wasylishen R. E.; Duer M. J.. NMR-Crystallography; Wiley: Chichester, U.K., 2009. [Google Scholar]
- Charpentier T. The PAW/GIPAW Approach for Computing NMR Parameters: A New Dimension Added to NMR Study of Solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. 10.1016/j.ssnmr.2011.04.006. [DOI] [PubMed] [Google Scholar]
- Moran R. F.; Dawson D. M.; Ashbrook S. E. Exploiting NMR Spectroscopy for the Study of Disorder in Solids. Int. Rev. Phys. Chem. 2017, 36, 39–115. 10.1080/0144235X.2017.1256604. [DOI] [Google Scholar]
- Grüninger H.; Schmutzler A.; Siegel R.; Armstrong K.; Frost D. J.; Senker J. Quantitative Description of 1H SQ and DQ Coherences for the Hydroxyl Disorder within Hydrous Ringwoodite. Phys. Chem. Chem. Phys. 2018, 20, 15098–15105. 10.1039/C8CP00863A. [DOI] [PubMed] [Google Scholar]
- Moran R. F.; McKay D.; Pickard C. J.; Berry A. J.; Griffin J. M.; Ashbrook S. E. Hunting for Hydrogen: Random Structure Searching and Prediction of NMR Parameters of Hydrous Wadsleyite. Phys. Chem. Chem. Phys. 2016, 18, 10173–10181. 10.1039/C6CP01529H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jinnouchi R.; Lahnsteiner J.; Karsai F.; Kresse G.; Bokdam M. Phase Transitions of Hybrid Perovskites Simulated by Machine-Learning Force Fields Trained on the Fly with Bayesian Inference. Phys. Rev. Lett. 2019, 122, 225701. 10.1103/PhysRevLett.122.225701. [DOI] [PubMed] [Google Scholar]
- Lahnsteiner J.; Jinnouchi R.; Bokdam M. Long-Range Order Imposed by Short-Range Interactions in Methylammonium Lead Iodide: Comparing Point-Dipole Models to Machine-Learning Force Fields. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100, 094106. 10.1103/PhysRevB.100.094106. [DOI] [Google Scholar]
- Grüninger H.; Armstrong K.; Greim D.; Boffa-Ballaran T.; Frost D. J.; Senker J. Hidden Oceans? Unraveling the Structure of Hydrous Defects in the Earth’s Deep Interior. J. Am. Chem. Soc. 2017, 139 (30), 10499–10505. 10.1021/jacs.7b05432. [DOI] [PubMed] [Google Scholar]
- Saalwächter K. Robust NMR Approaches for the Determination of Homonuclear Dipole-Dipole Coupling Constants in Studies of Solid Materials and Biomolecules. ChemPhysChem 2013, 14, 3000–3014. 10.1002/cphc.201300254. [DOI] [PubMed] [Google Scholar]
- Brown S. P. Probing Proton-Proton Proximities in the Solid State. Prog. Nucl. Magn. Reson. Spectrosc. 2007, 50, 199–251. 10.1016/j.pnmrs.2006.10.002. [DOI] [Google Scholar]
- Leupold N.; Schötz K.; Cacovich S.; Bauer I.; Schultz M.; Daubinger M.; Kaiser L.; Rebai A.; Rousset J.; Köhler A.; et al. High Versatility and Stability of Mechanochemically Synthesized Halide Perovskite Powders for Optoelectronic Devices. ACS Appl. Mater. Interfaces 2019, 11, 30259–30268. 10.1021/acsami.9b09160. [DOI] [PubMed] [Google Scholar]
- Fung B. M.; Khitrin A. K.; Ermolaev K. An Improved Broadband Decoupling Sequence for Liquid Crystals and Solids. J. Magn. Reson. 2000, 142, 97–101. 10.1006/jmre.1999.1896. [DOI] [PubMed] [Google Scholar]
- Saalwächter K.; Lange F.; Matyjaszewski K.; Huang C.-F.; Graf R. BaBa-Xy16: Robust and Broadband Homonuclear DQ Recoupling for Applications in Rigid and Soft Solids up to the Highest MAS Frequencies. J. Magn. Reson. 2011, 212, 204–215. 10.1016/j.jmr.2011.07.001. [DOI] [PubMed] [Google Scholar]
- Bartók A. P.; Payne M. C.; Kondor R.; Csányi G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. 10.1103/PhysRevLett.104.136403. [DOI] [PubMed] [Google Scholar]
- Bartók A. P.; Kondor R.; Csányi G. On Representing Chemical Environments. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 184115. 10.1103/PhysRevB.87.184115. [DOI] [Google Scholar]
- Jinnouchi R.; Karsai F.; Kresse G. On-the-Fly Machine Learning Force Field Generation: Application to Melting Points. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100, 014105. 10.1103/PhysRevB.100.014105. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Sun J.; Ruzsinszky A.; Perdew J. P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
- Bokdam M.; Lahnsteiner J.; Ramberger B.; Schäfer T.; Kresse G. Assessing Density Functionals Using Many Body Theory for Hybrid Perovskites. Phys. Rev. Lett. 2017, 119, 145501. 10.1103/PhysRevLett.119.145501. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Goc R. Effective Spatial Averaging for NMR Second Moment Calculation. J. Magn. Reson. 1998, 132, 78–80. 10.1006/jmre.1998.1384. [DOI] [Google Scholar]
- Goc R. Calculation of the NMR Second Moment for Materials with Different Types of Internal Rotation. Solid State Nucl. Magn. Reson. 1998, 13, 55–61. 10.1016/S0926-2040(98)00082-4. [DOI] [PubMed] [Google Scholar]
- Goc R. Computer Calculation of the Van Vleck Second Moment for Materials with Internal Rotation of Spin Groups. Comput. Phys. Commun. 2004, 162, 102–112. 10.1016/j.cpc.2004.06.071. [DOI] [Google Scholar]
- Karmakar A.; Askar A. M.; Bernard G. M.; Terskikh V. V.; Ha M.; Patel S.; Shankar K.; Michaelis V. K. Mechanochemical Synthesis of Methylammonium Lead Mixed-Halide Perovskites: Unraveling the Solid-Solution Behavior Using Solid-State NMR. Chem. Mater. 2018, 30, 2309–2321. 10.1021/acs.chemmater.7b05209. [DOI] [Google Scholar]
- Askar A. M.; Wiltshire B. D.; Patel S.; Fleet J.; Shankar K.; Karmakar A.; Bernard G. M.; Ha M.; Michaelis V. K.; Terskikh V. V.; et al. Composition-Tunable Formamidinium Lead Mixed Halide Perovskites via Solvent-Free Mechanochemical Synthesis: Decoding the Pb Environments Using Solid-State NMR Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 2671–2677. 10.1021/acs.jpclett.8b01084. [DOI] [PubMed] [Google Scholar]
- Aebli M.; Piveteau L.; Nazarenko O.; Benin M. B.; Krieg F.; Verel R.; Kovalenko M. V. Lead-Halide Scalar Couplings in Pb NMR of APbX3 Perovskites (A = Cs, Methylammonium, Formamidinium ; X = Cl, Br, I). Sci. Rep. 2020, 10, 8229. 10.1038/s41598-020-65071-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosales B. A.; Men L.; Cady S. D.; Hanrahan M. P.; Rossini A. J.; Vela J. Persistent Dopants and Phase Segregation in Organolead Mixed-Halide Perovskites. Chem. Mater. 2016, 28, 6848–6859. 10.1021/acs.chemmater.6b01874. [DOI] [Google Scholar]
- Zorin V. E.; Brown S. P.; Hodgkinson P. Quantification of Homonuclear Dipolar Coupling Networks from Magic-Angle Spinning 1H NMR. Mol. Phys. 2006, 104, 293–304. 10.1080/00268970500351052. [DOI] [Google Scholar]
- Bradley J. P.; Tripon C.; Filip C.; Brown S. P. Determining Relative Proton-Proton Proximities from the Build-up of Two-Dimensional Correlation Peaks in 1H Double-Quantum MAS NMR: Insight from Multi-Spin Density-Matrix Simulations. Phys. Chem. Chem. Phys. 2009, 11, 6941–6952. 10.1039/b906400a. [DOI] [PubMed] [Google Scholar]
- Selig O.; Sadhanala A.; Müller C.; Lovrincic R.; Chen Z.; Rezus Y. L. A.; Frost J. M.; Jansen T. L. C.; Bakulin A. A. Organic Cation Rotation and Immobilization in Pure and Mixed Methylammonium Lead-Halide Perovskites. J. Am. Chem. Soc. 2017, 139, 4068–4074. 10.1021/jacs.6b12239. [DOI] [PubMed] [Google Scholar]
- Svane K. L.; Forse A. C.; Grey C. P.; Kieslich G.; Cheetham A. K.; Walsh A.; Butler K. T. How Strong Is the Hydrogen Bond in Hybrid Perovskites?. J. Phys. Chem. Lett. 2017, 8, 6154–6159. 10.1021/acs.jpclett.7b03106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knijn P. J.; van Bentum P. J. M.; van Eck E. R. H.; Fang C.; Grimminck D. L. A. G.; de Groot R. A.; Havenith R. W. A.; Marsman M.; Meerts W. L.; De Wijs G. A.; et al. A Solid-State NMR and DFT Study of Compositional Modulations in AlxGa1-xAs. Phys. Chem. Chem. Phys. 2010, 12, 11517–11535. 10.1039/c003624b. [DOI] [PubMed] [Google Scholar]
- Tycko R.; Dabbagh G.; Kurtz S. R.; Goral J. P. Quantitative Study of Atomic Ordering in Ga0.5In0.5P Thin Films by P31 Nuclear Magnetic Resonance. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 13452–13457. 10.1103/PhysRevB.45.13452. [DOI] [PubMed] [Google Scholar]
- Degen C.; Tomaselli M.; Meier B. H.; Voncken M. M. A. J.; Kentgens A. P. M. NMR Investigation of Atomic Ordering in AlxGa1-xAs Thin Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2004, 69, 1–4. 10.1103/PhysRevB.69.193303. [DOI] [Google Scholar]
- Cullity B. D.Elements of X-Ray Diffraction, 2nd ed.; Addison Wesley: Reading, MA, 1978. [Google Scholar]
- Mozur E. M.; Hope M. A.; Trowbridge J. C.; Halat D. M.; Daemen L. L.; Maughan A. E.; Prisk T. R.; Grey C. P.; Neilson J. R. Cesium Substitution Disrupts Concerted Cation Dynamics in Formamidinium Hybrid Perovskites. Chem. Mater. 2020, 32, 6266–6277. 10.1021/acs.chemmater.0c01862. [DOI] [Google Scholar]
- Chatterjee R.; Pavlovetc I. M.; Aleshire K.; Hartland G. V.; Kuno M. Subdiffraction Infrared Imaging of Mixed Cation Perovskites: Probing Local Cation Heterogeneities. ACS Energy Lett. 2018, 3, 469–475. 10.1021/acsenergylett.7b01306. [DOI] [Google Scholar]
- Maheshwari S.; Patwardhan S.; Schatz G. C.; Renaud N.; Grozema F. C. The Effect of the Magnitude and Direction of the Dipoles of Organic Cations on the Electronic Structure of Hybrid Halide Perovskites. Phys. Chem. Chem. Phys. 2019, 21, 16564–16572. 10.1039/C9CP02866H. [DOI] [PubMed] [Google Scholar]
- Doherty T. A. S.; Winchester A. J.; Macpherson S.; Johnstone D. N.; Pareek V.; Tennyson E. M.; Kosar S.; Kosasih F. U.; Anaya M.; Abdi-Jalebi M.; et al. Performance-Limiting Nanoscale Trap Clusters at Grain Junctions in Halide Perovskites. Nature 2020, 580, 360–366. 10.1038/s41586-020-2184-1. [DOI] [PubMed] [Google Scholar]
- Tong C.-J.; Geng W.; Prezhdo O. V.; Liu L.-M. Role of Methylammonium Orientation in Ion Diffusion and Current-Voltage Hysteresis in the CH3NH3PbI3 Perovskite. ACS Energy Lett. 2017, 2, 1997–2004. 10.1021/acsenergylett.7b00659. [DOI] [Google Scholar]
- Huang Y.; Li L.; Liu Z.; Jiao H.; He Y.; Wang X.; Zhu R.; Wang D.; Sun J.; Chen Q.; et al. The Intrinsic Properties of FA(1-x)MAxPbI3 Perovskite Single Crystals. J. Mater. Chem. A 2017, 5 (18), 8537–8544. 10.1039/C7TA01441D. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.