Polygenic Mendelian Randomization

Abstract

Many exposures considered in Mendelian randomization (MR) studies are polygenic in that they are influenced by thousands of genetic variants. By using many single-nucleotide polymorphisms (SNPs) as instrumental variables, more variation in the exposure is explained, increasing the precision of MR. Furthermore, methods can be designed that relax the assumptions of MR, especially concerning direct pleiotropic effects on the outcome. This article reviews the concepts and assumptions underlying the commonly used polygenic MR methods. Using a polygenic score as an instrument is equivalent to a weighted mean of individual SNP results, and the other fundamental averages, median and mode, may also be used to estimate causal effects. Outlier detection is useful for identifying pleiotropic SNPs to be excluded from analysis. Bayesian approaches are available to incorporate prior beliefs about pleiotropy. These methods each entail different assumptions, and together provide a set of sensitivity analyses to help triangulate evidence about causality.

Although the initial concept and early applications of Mendelian randomization (MR) used a single genetic variant with a known molecular function, most current applications use many genetic variants, which together influence a complex exposure. There are several reasons for this shift toward “polygenic” MR. First, in most cases, single genetic variants have small effects on the exposures of interest in MR studies. This can lead to weak instrument bias by which, if the genetic instrument explains little variation in the exposure, the MR estimate will be biased away from the true causal effect (Burgess and Thompson 2011). However, many exposures are substantially heritable, and polygenic in that they are influenced by thousands of genetic polymorphisms (Shi et al. 2016). Many variants used together as instruments can explain larger proportions of exposure variance, and possibly mitigate weak instrument bias. In addition, the precision of the estimated causal effect can be improved by combining information from many genetic instruments. Furthermore, when many instruments are available, methods can be designed with different assumptions to standard MR; this allows a range of sensitivity analyses to be performed in conjunction with the standard approach.

To fix concepts and notation, Figure 1 shows the standard directed acyclic graph (DAG) assumed by MR, in which a genetic instrument G, usually a single-nucleotide polymorphism (SNP), is associated with an exposure X, and an outcome Y only via its effect on X. Assuming the following linear models

$$X=\gamma G+{\text{β}}_{UX}U+{\epsilon }_X,$$

$$Y=\text{β}X+{\text{β}}_{UY}U+{\epsilon }_Y,$$

where ɛ_X is independent of G and U and ɛ_Y is independent of X and U, it is easy to see that the direct effect β of X on Y is just Γ/γ where Γ is the total effect of G on Y. It therefore natural to estimate β using sample estimates of γ and Γ obtained from regression models, $\widehat{\text{β}}=\hat{\mathrm{\Gamma }}/\hat{\gamma }$. However, this commonly used ratio estimator is biased by the sampling variation in $\hat{\gamma }$, with the bias greatest when this variance is high, which is the weak instrument bias.

Figure 1.

Standard directed acyclic graph (DAG) showing instrumental variable G for the association of exposure X with outcome Y in the presence of confounder U. The effect of interest is the causal effect β of X on Y.

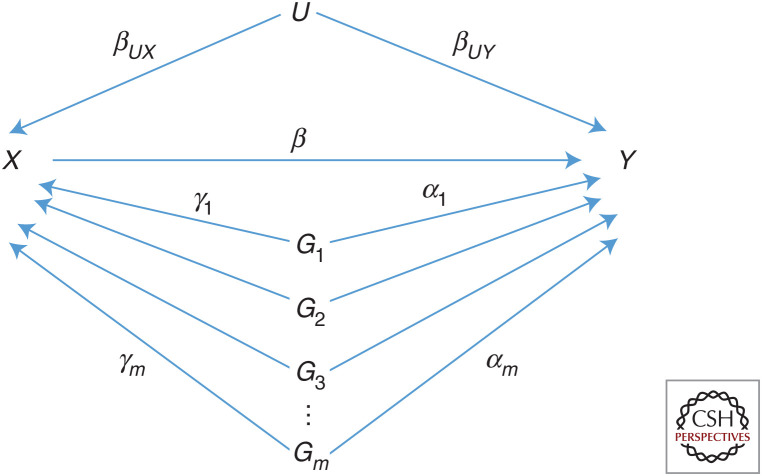
Figure 2 shows a DAG including several SNPs as instruments, allowing each SNP to have a direct pleiotropic effect on Y in addition to its indirect effect through X. These direct effects are denoted by α_j so that for each SNP j

$$Y={\alpha }_j{G}_j+\text{β}X+{\text{β}}_{UY}U+{\epsilon }_Y,$$

and the total effect of SNP j on Y is

$${\mathrm{\Gamma }}_j={\alpha }_j+\text{β}{\gamma }_j.$$

Figure 2.

Directed acyclic graph (DAG) showing m single-nucleotide polymorphisms (SNPs) G_j used as instrumental variables for the association of exposure X with outcome Y in the presence of confounder U. Each SNP has an effect γ_j on X and a direct pleiotropic effect α_j on Y. Under linear models for X and Y, the total effect of SNP j on Y is Γ_j = α_j + βγ_j.

(The presence of such direct effects is sometimes called “horizontal pleiotropy.” However, this usage has no geometric justification, and here, following conventions in mediation analysis, the term “direct pleiotropy” is used.)

The total effect of the confounders U on Y is β_UXβ + β_UY. Because U is unmeasured, it is sufficient to assume that it is scaled such that β_UY = 1. The parameters in the DAG are then β, β_UX, γ_j, and α_j, in total 2m + 2 parameters where m is the number of SNPs. Observational data provide associations between each SNP and X, between each SNP and Y, and between X and Y, in total 2m + 1 associations. To identify β then, at least one assumption must be made on the other parameters.

Observational analysis assumes that β_UX = 0, whereas single variant MR assumes that α₁ = 0. Polygenic MR methods make other assumptions to identify β. This article will review the concepts and assumptions underlying the commonly used polygenic MR methods, and point the reader toward more detailed literature on each approach.

POLYGENIC SCORE AND WEIGHTED MEAN

When many SNPs are available as instruments, two natural approaches to performing an MR analysis are available. The first is to combine the SNPs into a “polygenic score,” which is the weighted sum of genotypes over many SNPs,

$$S=\sum _{j=1}^m{\gamma }_j{G}_j,$$

where G_j is a numerical coding of the genotype of SNP j, typically the number of effect alleles carried. (Several other terms are in use, including allele score, gene score, and risk score, which may be regarded as equivalent for the present purposes.) The score S may now be used as a single instrumental variable in a standard MR analysis.

The second approach is to observe that each SNP provides its own MR ratio as Γ_j/γ_j and so these estimates may be combined by taking an average. Polygenic MR methods differ in how they take the average, making different assumptions in doing so.

The ratio estimate for the polygenic score S is

$$\frac{cov\left(S,Y\right)}{cov\left(S,X\right)}=\frac{\sum {\gamma }_{j}cov\left(G_j,Y\right)}{\sum {\gamma }_{j}cov\left(G_j,X\right)}$$

$$=\frac{\sum {\gamma }_j{\Gamma }_{j}var\left(G_j\right)}{\sum {\gamma }_j{\Gamma }_{j}var\left(G_j\right)}$$

$$=\sum _j\frac{{\gamma }_j^{2}var\left(G_j\right)}{{\sum }_k{\gamma }_k^{2}var\left(G_k\right)}\frac{{\mathrm{\Gamma }}_j}{{\gamma }_j}.$$

This is a weighted mean of the individual MR ratios, showing that the polygenic score approach is in fact equivalent to an average MR ratio approach (Burgess et al. 2016). This implies that weak instrument bias in individual SNPs is propagated into the polygenic score, which while explaining more variation in X also entails more degrees of freedom for error. The precise effect of weak instrument bias varies across the methods described below, and a generally applicable definition of polygenic instrument strength is lacking. However, Equation (2) also shows that the polygenic score approach can be applied in the two-sample MR design, by applying the equivalent MR ratio approach using summary statistics from separate studies of X and Y.

When Γ_j and γ_j are replaced by their sample estimates, Equation (2) is the weighted mean of the individual ratio estimates where the weights are approximately the inverse sampling variances of these estimates (Burgess et al. 2013). Explicitly, the inverse variance weighted (IVW) estimator of the causal effect is

$${\widehat{\text{β}}}_{IVW}=\frac{\sum {\hat{\gamma }}_j{\hat{\mathrm{\Gamma }}}_j{s}_j^{-2}}{\sum \hat{\gamma }{}_j^2{s}_j^{-2}},$$

where s_j is the standard error of ${\hat{\gamma }}_j$.

When all SNPs used as instruments are in linkage equilibrium, so that their genotypes are uncorrelated, the standard error is

$$se({\widehat{\text{β}}}_{IVW})={\left[\sum _j{\hat{\gamma }}_j^2{s}_j^{-2}\right]}^{--\frac{1}{2}}.$$

Recalling that Γ_j = α_j + βγ_j, the asymptotic expectation of the IVW estimator is

$$E({\widehat{\text{β}}}_{IVW})=\text{β}+\frac{\sum {\hat{\gamma }}_j{\alpha }_j{s}_j^{-2}}{\sum {\hat{\gamma }}_j^2{s}_j^{-2}}.$$

Therefore, the IVW estimator is only unbiased if the second term on the right-hand side is zero, a condition termed balanced pleiotropy, which is the identifying assumption for this estimator. A sufficient condition for balanced pleiotropy is that E(α_j) = 0 and that α_j and γ_j are independent, a condition termed “instrument strength independent of direct effect” (InSIDE). Clearly, balanced pleiotropy holds when all SNPs are valid instruments, α_j = 0.

Other genotype weightings may be used in a polygenic score and may be more efficient in some situations (Burgess and Thompson 2013; Burgess et al. 2016). When SNPs are in linkage disequilibrium (LD), the IVW estimator is generally unbiased but its standard error must be adjusted accordingly (Burgess et al. 2016; Zhu et al. 2018).

HETEROGENEITY AND OUTLIER DETECTION

SNPs can yield different ratios Γ_j/γ_j for a number of reasons including variation among the direct pleiotropic effects α_j, or if the actual causal effect β varies between SNPs. The latter might occur if different mechanisms that modify the exposure X, through different biological pathways, lead to different effects on the outcome Y. Both scenarios create heterogeneity in MR across SNPs.

The IVW estimator is identical to the fixed-effects meta-analysis of the ratio estimates, and the tools of meta-analysis are useful for reasoning about heterogeneity in MR (Bowden and Holmes 2019). The presence of heterogeneity may be formally tested by Cochran's Q statistic

$$Q=\sum _{j=1}^m{Q}_j=\sum _{j=1}^m\frac{{\hat{\gamma }}_j^2{s}_j^{-2}}{{\sum }_k{\hat{\gamma }}_k^2{s}_k^{-2}}{\left(\frac{{\hat{\mathrm{\Gamma }}}_j}{{\hat{\gamma }}_j}-{\widehat{\text{β}}}_{IVW}\right)}^2,$$

which under no heterogeneity is distributed as χ² with m − 1 degrees of freedom. When heterogeneity is present, a random-effects meta-analysis of the ratio estimates can reflect the additional variation (Bowden et al. 2017). In this context, the random-effects estimate is the expected MR ratio for an SNP randomly drawn from the same population as the SNPs actually analyzed. The expectation is over the distribution of pleiotropic effects α_j and of causal effects β resulting from possible modifications of X, but will only be unbiased under balanced pleiotropy. To simplify these considerations, a multiplicative random-effects model has been suggested that provides the same point estimate as the fixed-effects estimator ${\widehat{\text{β}}}_{IVW}$ but increases its standard error by a factor of $\sqrt{Q/m-1}$ (Bowden et al. 2017).

Overall heterogeneity may be driven by a few outlier SNPs that provide atypical ratio estimates, perhaps through specific pleiotropic effects. A sensible approach is to identify and discard those SNPs before performing polygenic MR on a more homogeneous subset. Each SNP contributes a term Q_j to Cochran's Q, and those with especially high contributions may be deemed outliers and discarded (Bowden et al. 2018b; Dai et al. 2018). In practice, there are some technical considerations, such as the fact that the estimate ${\widehat{\text{β}}}_{IVW}$ in Q may itself be biased by the outliers. The MR-PRESSO approach (Verbanck et al. 2018) evaluates each Q_j with a leave-one-out estimate of ${\widehat{\text{β}}}_{IVW}$, whereas the HEIDI-outlier method (Zhu et al. 2018) uses a quantile-based estimate of ${\widehat{\text{β}}}_{IVW}$. Robust regression approaches have also been developed that automatically downweight outliers (Rees et al. 2019). As an alternative to Q_j, Cook's distance can also be used to identify SNPs with especially strong contributions to ${\widehat{\text{β}}}_{IVW}$ (Corbin et al. 2016). In applying these approaches, it should be noted that the standard error of the MR estimator will usually decrease after outlier removal, increasing the possibility of type-1 error.

MR-EGGER REGRESSION

So far, the IVW estimator has been motivated as the ratio estimate from a polygenic score, the weighted mean of the individual SNP ratio estimates, and the meta-analysis of the individual ratio estimates. A fourth, very useful interpretation is as the slope of the linear regression of ${\hat{\mathrm{\Gamma }}}_j$ on ${\hat{\gamma }}_j$ weighted by $s_j^{-2}$, with the intercept set to zero (Fig. 3). If the intercept is now allowed to vary freely, then, from Equation (1), the intercept of the fitted regression is a weighted mean of the α_j and the slope is an estimate of β. The model now allows for unbalanced pleiotropy with, potentially, all SNPs having direct effects on Y (Fig. 4). The identifying assumption is that the residuals of the regression are independent of the predictor, and therefore that α_j is independent of γ_j, which is the InSIDE assumption previously discussed in relation to the IVW estimator.

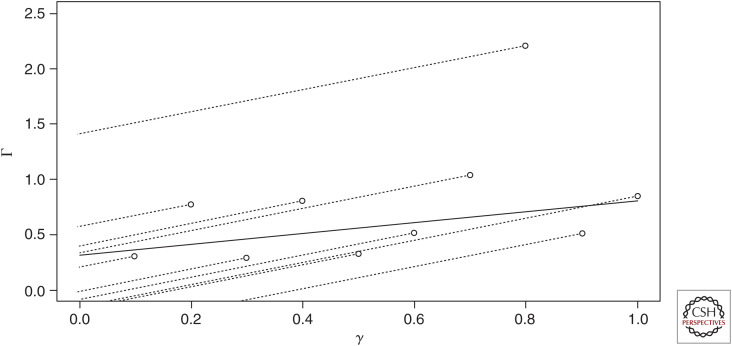
Figure 3.

Inverse variance weighted (IVW) estimator in the presence of heterogeneity. Ten single-nucleotide polymorphisms (SNPs) are simulated with true effects γ_j = 0.1, …1.0 on exposure X and true total effects Γ_j on outcome Y. Under the IVW model, each SNP yields a different ratio Γ_j/γ_j shown by the slopes of the dotted lines. The IVW estimate, shown by the slope of the solid line, is the mean of the ratios. Under homogeneity, all the dots would lie on the solid line. Heterogeneity creates uncertainty in the IVW estimate depending on the number of SNPs used as instruments.

Figure 4.

MR-Egger estimator. γ_j and Γ_j are the same as in Figure 3, but each single-nucleotide polymorphism (SNP) now has a direct pleiotropic effect α_j on Y such that Γ_j = α_j + 1 × γ_j for all j. The solid line shows the MR-Egger fit, which is close to the true common causal effect. This shows that the observed heterogeneity in Figure 3 could arise from variable pleiotropy with a common causal effect, or from no pleiotropy with variable causal effects, or indeed from variation in both pleiotropy and causal effects. Polygenic MR methods resolve these scenarios by making different assumptions about pleiotropy.

This approach is closely related to Egger regression, which is used to test for small-study bias in meta-analysis, and is known as “MR-Egger” (Bowden et al. 2015). Its appeal is that it allows all SNPs to have direct pleiotropic effects, a scenario that is probably common in complex traits (Pickrell et al. 2016; Verbanck et al. 2018). It provides a simple test for unbalanced pleiotropy, as the intercept is zero under balanced pleiotropy. A significantly nonzero intercept provides evidence of pleiotropic effects, implying that the IVW estimate is biased. The difficulty in practice is that the InSIDE assumption cannot be verified. Furthermore, estimating the intercept as a nuisance parameter leads to a substantially greater standard error on the slope, so that MR-Egger has reduced power to detect a causal effect compared with the IVW estimator.

MR-Egger regression would be consistent for β if γ_j were known exactly. However, in practice, only sample estimates are available, introducing measurement error into the predictor γ_j. This biases the slope β toward the null, so a correction for measurement error is required to obtain valid inference. Bowden et al. (2016b) proposed a diagnostic

$$I_{GX}^2=\frac{\left(Q_{GX}-\left(m-1\right)\right)}{Q_{GX}},$$

where Q_GX is Cochran's Q for the ${\hat{\gamma }}_j$, and for values close to 1 suggested using the SIMEX algorithm to correct to regression dilution in $\widehat{\text{β}}$.

Similar to the IVW estimator, heterogeneity may be present among the Γ_j after removing the intercept due to residual heterogeneity among the α_j, different causal effects associated with different genetic modifications of X, or some other reason. A modified heterogeneity statistic, Rücker's Q^′, can be used for MR-Egger

$$Q^{\mathrm{\prime }}=\sum _{j=1}^m{Q}_j^{\mathrm{\prime }}=\sum _{j=1}^m\frac{{\hat{\gamma }}_j^2{s}_j^{-2}}{{\sum }_k{\hat{\gamma }}_k^2{s}_k^{-2}}{\left(\frac{{\hat{\mathrm{\Gamma }}}_j}{{\hat{\gamma }}_j}-\frac{{\widehat{\text{β}}}_{0E}}{{\hat{\gamma }}_j}-{\widehat{\text{β}}}_{1E}\right)}^2,$$

where ${\widehat{\text{β}}}_{0E}$ and ${\widehat{\text{β}}}_{1E}$ are, respectively, the fitted intercept and slope from MR-Egger (Bowden et al. 2017). Under no heterogeneity, Q^′ is distributed as χ² with m − 2 degrees of freedom. When heterogeneity is present, a multiplicative random-effects model retains the same slope as MR-Egger but increases its standard error by a factor of $\sqrt{Q^{\mathrm{\prime }}/m-2}$.

A curious aspect of MR-Egger is that the intercept can be changed rather arbitrarily by changing the coding of the SNPs. If the effect allele is changed from (say) the minor to the major allele, then γ_j would change sign and Γ_j would change additively by 2γ_j. This would change the intercept of the fitted regression, so that changing the coding of particular combinations of SNPs could lead to an intercept near zero, suggesting balanced pleiotropy. Asymptotically the slope is unchanged, but in finite samples the slope can also vary with allele coding. A pragmatic solution is to fix the coding such that all effect alleles act to increase the exposure, so all ${\hat{\gamma }}_j$ are positive. The MR-Egger is then interpreted as a set of comparable interventions on X, but the resulting estimate of average pleiotropy in the intercept is no more than a mathematical construct.

An alternative formulation of MR-Egger is as the unweighted regression of ${\hat{\mathrm{\Gamma }}}_j{s}_j^{-1}$ on ${\hat{\gamma }}_j{s}_j^{-1}$ (Bowden et al. 2018c). Although the slope of this regression still estimates the causal effect, the intercept is different from standard MR-Egger and the InSIDE assumption changes subtly to independence of α_j and ${\gamma }_j{s}_j^{-1}$. This representation, termed “Radial MR-Egger,” has some advantages, including the ability to incorporate more accurate estimates of the IVWs, and a more intuitive graphical interpretation (Bowden et al. 2018c). Although it is ostensibly invariant to allele coding, there is an equivalent dichotomy in defining $s_j^{-1}$ as either the positive or negative square root of $s_j^{-2}$.

MEDIAN AND MODE ESTIMATORS

As the IVW and MR-Egger estimators take weighted means of the individual SNP ratio estimates, it is natural to consider the other fundamental averages. The median estimator (Bowden et al. 2016a) simply takes the median ratio ${\hat{\mathrm{\Gamma }}}_j/{\hat{\gamma }}_j$ over SNPs j. This has the advantage of improved robustness to outliers, which may be SNPs that violate the MR assumptions. Indeed, the median estimator is consistent for the causal effect if at least half the SNPs are valid instruments, because this guarantees that the median estimate comes from a valid instrument. This identifying assumption may seem strong, and it is very difficult to verify. Nevertheless, under that assumption, the median estimator is robust to arbitrary violations of the other MR assumptions in up to one-half of the SNPs, including violation of the InSIDE assumption.

As with the IVW, improved precision is possible by incorporating weights into the median estimator. Here, the idea is to rank the SNPs in order of their ratio estimates and sum the corresponding weights until reaching one-half of the total weight. The ratio estimate is then taken from the SNP whose weight brings the sum up to one-half of the total, or if this is not reached exactly, by interpolating between the SNPs whose weights bring the sum just below and above one-half of the total (Bowden et al. 2016a). Inverse-variance weights are recommended as for the IVW approach.

The mode estimator (Hartwig et al. 2017) takes the most common value of ${\hat{\mathrm{\Gamma }}}_j/{\hat{\gamma }}_j$ as the estimated causal effect. The identifying assumption is that the largest subgroup of SNPs having the same ratio estimate consists of valid instruments, and therefore have no pleiotropic effects α_j. This is equivalently termed the “zero modal pleiotropy assumption” (ZEMPA). Again, inverse-variance weights can be incorporated by weighting each SNP when estimating the mode of the ratio estimates. The ZEMPA assumption is then modified to assuming that the total weight of the valid instruments is greater than the total weight of any other subset of SNPs with a common ratio estimate.

Because individual SNP ratios are not estimated precisely, it is unlikely that any will share exactly the same ratio estimate and the mode cannot be identified exactly. One approach is to estimate the density function of the ratios using histogram-smoothing methods such as Gaussian kernel smoothing; the mode of the estimated density can then be easily identified (Hartwig et al. 2017). This approach requires a tuning parameter to control the degree of smoothing; although a default suggestion is available, it is prudent to consider a range of tuning parameters to assess the sensitivity of the mode estimate to this parameter.

A related method, called MRMix (Qi and Chatterjee 2019), achieves greater efficiency than the mode estimator under the same ZEMPA assumption, by imposing a stronger parametric model on SNP effects. Specifically, letting π₀ be the proportion of valid SNPs and σ² the variance of ${\hat{\alpha }}_j$ among all invalid SNPs, and assuming that all SNP effects are normally distributed with zero mean, then for a postulated causal effect β the maximum likelihood estimates of π₀ and σ² can be found. The estimated causal effect is then taken as the value of β that maximizes π₀. The ZEMPA assumption is then implied by construction. This approach has the additional advantage of not requiring a tuning parameter, while making realistic assumptions on the SNP effects.

Another modal approach considers all possible subsets of the SNPs at hand, and for each subset the IVW estimate is obtained together with a measure of heterogeneity (Burgess et al. 2018). A likelihood is constructed by weighting the sampling density of each IVW estimate, given a postulated causal effect, by its heterogeneity, with more homogeneous subsets given greater weight. The maximum likelihood estimator is consistent for the causal effect when the ZEMPA assumption holds, and again shows improved precision compared with the standard modal estimator.

BAYESIAN METHODS

A further approach to identifying the causal effect β in Figure 2 is through Bayesian inference including prior beliefs about model parameters. Equation (1) can be used to define a likelihood for β in terms of the estimated SNP effects ${\hat{\mathrm{\Gamma }}}_j$ and ${\hat{\gamma }}_j$. Informative priors can be placed on some or all of these parameters to improve precision in estimating the causal effect.

A relatively simple approach is to fit the MR-Egger model as a Bayesian linear regression with an informative prior on the intercept and a vague prior on the slope (Schmidt and Dudbridge 2018). This is motivated by observing that a noninformative prior on the intercept is conceptually equivalent to standard MR-Egger, but a prior concentrated entirely at zero recovers the IVW estimator. Although MR-Egger is robust to unbalanced pleiotropy, it has substantially less power than the IVW estimator to detect a causal effect. Because extremely unbalanced pleiotropy seems unlikely, a Gaussian prior on the intercept represents a compromise between MR-Egger and IVW that offers robustness to unbalanced pleiotropy while retaining power from the IVW estimator. A prior mean of zero reflects no prior belief in the direction of unbalanced pleiotropy. It is less clear how to specify the variance, but a range of values could be considered to identify the point at which qualitative conclusions change. This approach offers improved power over MR-Egger under unbalanced pleiotropy, but is much more sensitive to the InSIDE assumption.

Based on the same motivations, a more sophisticated approach (Thompson et al. 2017) assumes that one of three models holds. Model 1 assumes that all SNPs estimate the same causal effect, and there is no pleiotropy; this is the assumption of the standard IVW estimator. Model 2 allows for balanced pleiotropy as in the IVW with heterogeneity, and model 3 allows for unbalanced pleiotropy as in MR-Egger. Prior probabilities are specified for each model, along with possibly vague priors for the MR-Egger intercept and slope. After updating by the data, posterior probabilities are obtained for each model along with a posterior mean for the causal effect under each model. These posterior means can be weighted by the model probabilities to obtain a model-averaged estimate of the causal effect. This approach typically yields an estimate with some bias but reduces mean square error with respect to the true causal effect. Again, the InSIDE assumption is critical as it is required by all three models, and if it does not hold the data may favor the model that is most sensitive to the departure.

Although the above approaches specify a prior on the average pleiotropy, the other major focus of Bayesian MR is in specifying a prior for individual pleiotropic effects α_j. An appealing choice is a double exponential, or Laplace, prior, which has a discontinuous peak at zero and tends to yield posterior estimates of zero for a large number of parameters. It is equivalent to Lasso regression in the classical sense, which aims to minimize the objective function,

$$\sum _{j=1}^m{s}_j^{-2}{\left({\hat{\mathrm{\Gamma }}}_j-{\alpha }_j-\text{β}{\hat{\gamma }}_j\right)}^2+\lambda \sum _{j=1}^m|{\alpha }_j|,$$

over β and all α_j. Here, λ is a tuning parameter, related to the prior rate of a double exponential prior on α_j, which in practice controls the number of SNPs with posterior estimates of α_j at zero. The Lasso model is therefore appropriate when a substantial proportion of SNPs is believed to have no pleiotropy, and it automatically identifies such SNPs (Kang et al. 2016; Windmeijer et al. 2019). The tuning parameter λ has to be chosen, and a heuristic approach has been suggested in which it is set to the largest value under which the heterogeneity statistic Q is not statistically significant among the SNPs with no pleiotropy (Rees et al. 2019). Those SNPs can then be taken forward into the standard IVW estimator.

Fully Bayesian approaches simultaneously estimate the causal effect while identifying and adjusting for pleiotropic SNPs. In addition to the double exponential, other priors for the pleiotropic effects have been investigated. The horseshoe prior (Berzuini et al. 2018) is designed to shrink a proportion of the α_j to zero while leaving the remainder almost unchanged. Slab-and-spike priors (Li 2017; Bucur et al. 2019) are typically a mixture of two Gaussian components, one with small or zero variance, representing negligible pleiotropy, and one with larger variance, representing meaningful pleiotropy. Each of these prior structures has hyperparameters that can be estimated from the data.

In the Bayesian context, the InSIDE assumption is reflected in the prior distributions, namely, that α_j and γ_j have independent prior distributions (Berzuini et al. 2018). Violations of the InSIDE assumption would result in misleading posterior distributions, but an advantage of the Bayesian formulation is that, in principle, dependencies between α_j and γ_j could be encoded in the prior so as to achieve more robustness to InSIDE violations. The “CAUSE” model (Morrison et al. 2019) does this by allowing a proportion of SNPs to have direct pleiotropic effects mediated through U.

Bayesian MR generally improves the bias-variance tradeoff over regression-based methods, while making stronger assumptions about the models linking G, X, U, and Y. This stands in contrast to traditional priorities in causal inference, which value unbiased estimation with minimal assumptions about the data-generating mechanism (Vansteelandt and Joffe 2014). However, given that causal effects derived by MR may not correspond to the effects of modifying the exposure by other means (Burgess et al. 2012), some bias in their estimates may be acceptable in return for greater precision.

SELECTION OF SNPs FOR POLYGENIC MR

The choice of SNPs to include in polygenic MR is a key question when exposure may be influenced by thousands of SNPs. Two basic issues are how to deal with multiple SNPs in LD and how strongly associated should an SNP be with the exposure to qualify as a valid instrument.

Many SNPs in a genomic region are typically associated with the exposure owing to LD. Probably, only one or a few will be causal, but any SNPs in a region could be used as instrumental variables. A common practice is to select only the most significantly associated SNP in a region, and include many regions in the MR analysis in this way. Slightly more sophisticated are stepwise selection methods that identify SNPs with conditionally independent signals within a region. Although adequate for many complex exposures, these approaches are less satisfactory for molecular biomarkers that may be under the control of a small number of genomic regions (Swerdlow et al. 2016).

Many of the methods described so far have been developed assuming independent SNPs, but may be adapted to accommodate LD (Burgess et al. 2016; Zhu et al. 2018). This can be based on external reference panels for which LD has been estimated within dense panels of SNPs in multiple populations, leading to three-sample designs integrating data on SNP–exposure, SNP–SNP, and SNP–outcome associations from separate datasets. The MR-Egger formulation has been extended to allow for LD (Burgess and Thompson 2017; Barfield et al. 2018), and similar approaches could be taken into Bayesian models.

It is less straightforward to account for LD in median- and mode-based approaches. A useful general approach is to transform genotypes into their principal components, which are uncorrelated by construction. A limited number of these components could then be used as independent instruments using the standard methods (Burgess et al. 2017). An advantage of the principal components approach is that it is reasonably robust to algorithmic tuning issues, such as choosing how many components to include, in comparison with stepwise selection methods in which the choice of stopping criterion can have a marked influence on the final inference.

When including noncausal SNPs in LD with causal variants, there is greater potential for direct pleiotropic effects on the outcome. Functional data may be used to select SNPs with greater evidence of causality on the exposure, and colocalization methods used to assess evidence for the same variant affecting both exposure and outcome, implying lower probability of direct pleiotropy (Hemani et al. 2018).

The majority of polygenic MR studies to date have used SNPs that are individually associated with the exposure, typically having P < 5 × 10⁻⁸ in a discovery study followed by significant association in independent replication. As a result, the numbers of SNPs used have been in the order of tens, but together explain only a small fraction of exposure variation. One reason for this conservative approach is that it is more probable that each SNP is truly associated with the exposure and therefore meets the first assumption of MR. In contrast, an approach that includes a larger number of more weakly associated SNPs is more likely to include SNPs with pleiotropic effects on the outcome and possibly no true effect on the exposure, potentially violating all the assumptions of MR. Weak instrument bias would become more severe, and SNPs with effects on neither exposure nor outcome would have ratio estimates with undefined expectation, creating potentially unstable estimates in polygenic MR.

These arguments, while reasonable, were largely formed before the current generation of pleiotropy adjusted methods were developed (Evans et al. 2013). More recently, some investigators have advocated the inclusion of SNPs with much weaker evidence of association with the exposure—potentially, all the SNPs in the genome. When such SNPs severely violate the MR assumptions, they may present as outliers and be discarded or downweighted (Qi and Chatterjee 2019). A recent strand of work aims to model and account for weak instrument bias within the MR-Egger framework (Bowden et al. 2018a; Zhao et al. 2019). Thus, traditional problems associated with including possibly thousands of SNPs in a polygenic MR may be alleviated while explaining greater variation in the exposure. Furthermore the ZEMPA assumption may continue to be justifiable in a highly polygenic setting if the pleiotropic SNPs have heterogeneous direct effects on the outcome. Modal estimators could therefore become increasingly prominent in future MR studies.

DISCUSSION

There is now a wide choice of approaches available for researchers looking to conduct MR with many SNPs as instruments. Broadly speaking, IVW, MR-Egger, and regression-based approaches require the InSIDE assumption, median-based approaches require a majority validity assumption, and modal approaches require the ZEMPA assumption, but these assumptions have subtle variations between methods. A summary of the assumptions of the main methods discussed here is given in Table 1. The current consensus is that the IVW estimate can be reported as a primary result with several other methods additionally conducted as sensitivity analyses (Hemani et al. 2018). However, the ensemble of results should be interpreted with care. A traditional approach to sensitivity analysis involves modeling violations of assumptions to see how the conclusions would change. Here instead, we analyze the data under several models with different assumptions. If all the methods agree, then perhaps none of the assumptions are severely violated in any method. If some agree but others do not, which are the most credible? If one method gives a result at odds with all others, is it the only one whose assumptions are met, or is it the one whose assumptions are most severely violated? Informal synthesis of evidence from contrasting study designs, termed triangulation, is now advocated as a strategy to mitigate the hazards of untestable assumptions (Lawlor et al. 2016), but best practice within the MR setting remains a challenge and there is no one-size-fits-all solution.

Table 1.

Major assumptions of the main methods discussed in this article

Method	Assumptions
IVW fixed effects	All SNPs estimate the same causal effect	Balanced pleiotropy	InSIDE	NOME
IVW random effects		Balanced pleiotropy	InSIDE	NOME
MR-RAPS		Balanced pleiotropy	InSIDE
CAUSE		Balanced pleiotropy	Parametric model + priors
MR-Egger fixed effects	All SNPs estimate the same causal effect		InSIDE	NOME
MR-Egger fixed effects + SIMEX	All SNPs estimate the same causal effect		InSIDE
MR-Egger random effects			InSIDE	NOME
MR-Egger random effects + SIMEX			InSIDE
Bayesian model averaging			InSIDE	NOME
Median			At least 50% of SNPs are valid instruments	NOME
Mode			ZEMPA	NOME
MRMix			ZEMPA	NOME
Heterogeneity penalized			ZEMPA	NOME

(IVW) Inverse variance weighted, (SNPs) single-nucleotide polymorphisms, (InSIDE) instrument strength independent of direct pleiotropic effect, (NOME) no measurement error in the SNP-exposure effect, (MR-RAPS) Mendelian randomization-robust adjusted profile score, (ZEMPA) zero modal pleiotropy assumption, meaning that the mode of the direct pleiotropic effects is zero.

Despite considerable concerns in MR about direct pleiotropy, it is not a problem when the aim is to show a shared genetic basis between traits, as opposed to a causal effect of one trait on another. And in some studies presented as MR, a causal effect is arguably not relevant; in studying, for example, exposures such as height (Nüesch et al. 2016) or age at puberty (Minelli et al. 2018), one could never hope to intervene directly on such traits, but the interest is in showing that their genetic predisposition predicts clinical outcomes through a common mechanistic pathway (Schooling et al. 2013). Pleiotropy should be embraced in such cases, and a more relevant question may be to what extent is an observational association explained by shared genetics? Recent approaches to this problem have combined the causal and confounder effects in Figure 2 into a single nongenetic effect, allowing the total shared genetic effect to be identified (O'Connor and Price 2018; Pingault et al. 2019). These methods are not MR, but provide approaches to a related and sometimes more relevant question.

For addressing explicit questions of causality, however, the emergence of polygenic MR methods is a welcome development. This area is developing rapidly and many of the works cited here are, at the time of writing, still under peer review. Further advances can be expected as more is learned about the genetic relationships between complex phenotypes, and MR studies are conducted in a wider range of human populations.