Multivariable Mendelian Randomization and Mediation

Abstract

Mendelian randomization (MR) is the use of genetic variants associated with an exposure to estimate the causal effect of that exposure on an outcome. Mediation analysis is the method of decomposing the effects of an exposure on an outcome, which act directly, and those that act via mediating variables. These effects are decomposed through the use of multivariable analysis to estimate the causal effects between three types of variables: exposures, mediators, and an outcome. Multivariable MR (MVMR) is a recent extension to MR that uses genetic variants associated with multiple, potentially related exposures to estimate the effect of each exposure on a single outcome. MVMR allows for equivalent analysis to mediation within the MR framework and therefore can also be used to estimate mediation effects. This approach retains the benefits of using genetic instruments for causal inference, such as avoiding bias due to confounding, while allowing for estimation of the different effects required for mediation analysis. This review explains MVMR, what is estimated when one exposure is a mediator of another in an MVMR estimation, and how MR and MVMR can therefore be used to estimate mediated effects. This review then goes on to consider the advantages and limitations of using MR and MVMR to conduct mediation analysis.

Mendelian randomization (MR) is a form of instrumental variable (IV) analysis that uses genetic variants, normally single-nucleotide polymorphisms (SNPs), as instruments to obtain estimates of the causal effect of an exposure on an outcome that is, under certain assumptions, free from bias due to unobserved confounding, measurement error, and reverse causation (Davey Smith and Ebrahim 2003). This has recently been extended to estimate the independent direct effects of multiple, potentially related exposures through multivariable MR (MVMR) (Burgess and Thompson 2015; Sanderson et al. 2019). A key feature of MVMR is that it estimates the effect of each exposure included in the estimation on the outcome conditional on the other exposures included in the model, that is, the direct effect of each exposure.

Often in causal inference, we are interested in not only how much an exposure effects an outcome but also the mechanisms or pathways through which the exposure acts to affect that outcome. Mediation analysis is a field of analysis that attempts to unpick these effects and determine the causal pathways by which an exposure influences an outcome and their relative importance. Understanding the structure of this relationship is particularly important when the exposure is difficult or impossible to intervene on. Mediation analysis can identify which factors mediate the relationship between that exposure and the outcome enabling intervention on those mediators to mitigate the effects of the exposure. Mediation analysis can also identify where acting on an exposure will only have limited effectiveness in changing the outcome if the mediating factors do not also change in response to that intervention. An early use of MR to understand causal pathways was through “two-step epigenetic MR,” which applied MR to understand a causal pathway from an exposure on an outcome through DNA methylation (Relton and Davey Smith 2012). More recently, MVMR and network MR (Burgess et al. 2014) have been used to estimate mediation in MR studies (Carter et al. 2019b). Studies have looked at a range of different topics such as the effect of age of menarche on breast cancer risk and whether there is an indirect effect via body mass index (BMI) (Burgess et al. 2017), whether the effect of BMI on coronary heart disease is mediated by lipids and glycemic factors (Xu et al. 2017), the extent to which BMI, blood pressure, and smoking mediate the effects of education on cardiovascular disease outcomes (Carter et al. 2019a), whether DNA metalation mediates the effect of smoking on lung function (Jamieson et al. 2020), and whether pulmonary factors mediate the effect of height on coronary artery disease (Marouli et al. 2019).

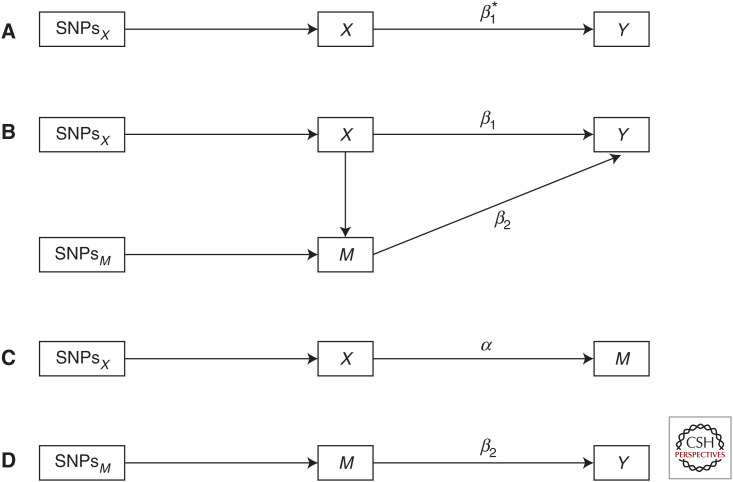
The causal effect of an exposure on an outcome of interest, including any effect through potential mediators, is the “total” effect of the exposure on the outcome. This effect can be decomposed into two parts. One part is the “direct” effect of the primary exposure on the outcome; this is the effect of the primary exposure that does not act through the mediators included in the model, represented by the arrow from X to Y labeled β₁ in Figure 1. The other part is the “indirect” effect, which is the effect of the primary exposure on the outcome that only operates through the mediators included in the model. In Figure 1, this is the edge from X to Y via M only; the size of this edge is αβ₂. The total effect of the exposure on the outcome is the sum of both of these effects, that is, total effect = direct effect + indirect effect. From these effects, the proportion of the total effect mediated can be calculated as the “indirect effect/total effect.”

Figure 1.

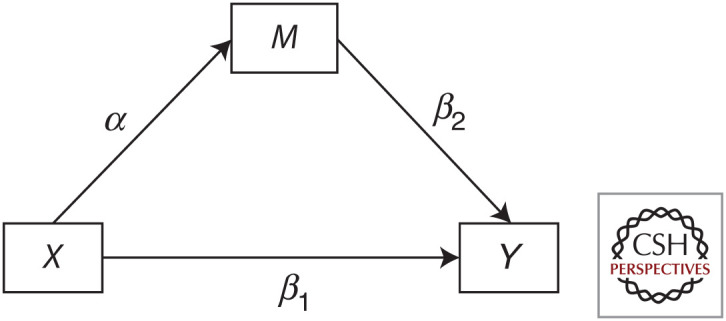
Illustration of the direct and indirect effects of X on Y. (X) exposure, (M) mediator, (Y) outcome.

Mediation analysis uses regression analysis to distinguish between the direct and indirect effects of the exposure on the outcome and calculate the proportion mediated (Baron and Kenny 1986; MacKinnon 2012; VanderWeele 2015, 2016). These traditional mediation methods have been extended to “counterfactual mediation analysis,” which uses a counterfactual framework to estimate mediation effects (MacKinnon 2012; VanderWeele 2013). Besides allowing the estimation of interaction effects, this form of mediation analysis also allows estimation of different effects such as the natural, controlled, and interventional direct and indirect effects (Naimi et al. 2014; VanderWeele et al. 2014). The natural direct and indirect effects are the effects estimated when the mediator is allowed to take its natural level given the exposure. These are estimated by traditional mediation analysis and by MVMR estimation; therefore, throughout the rest of this review, I use “direct effect” to mean the natural direct effect. Methods to estimate interaction effects using MR or MVMR are not currently well understood and, therefore, I do not discuss them here (Carter et al. 2019b).

There are a number of assumptions required for mediation analysis to give reliable estimates of the proportion of the total effect of the exposure on the outcome that is mediated (MacKinnon 2012). Important assumptions for mediation analysis to give unbiased estimates of the causal effects include that there are no unobserved confounders that cannot be accounted for in the estimation and no measurement error in the exposure or mediator. MR is an alternative method of estimation that can produce estimates of causal effects in the presence of unobserved confounding and measurement error in the exposure.

Using MR for mediation analysis does not change the objective of the mediation analysis to determine the proportion of the total effect of an exposure on an outcome that acts through a particular mediator or set of mediators. In this context, MR and MVMR use genetic variants to help researchers determine these causal pathways using a different set of assumptions to traditional mediation analysis. In the rest of this review, I describe MVMR and the assumptions underlying an MVMR estimation in detail. I explain how MR and MVMR can be used to unpick the total and direct effects of an exposure on an outcome in the presence of a mediator or group of mediators. I then go on to explain the benefits, limitations, and potential considerations required to obtain causal estimates for mediation from the use of MR and MVMR.

MULTIVARIABLE MR

MR can be conducted with either individual-level data or using summary data from genome-wide association studies (GWAS), which give the estimated effect of each SNP on each of the exposures and the outcome. For (univariable) MR to provide valid causal estimates of the effect of the exposure on the outcome, there are three assumptions that must be satisfied, the SNPs used as instruments must be:

1. IV1: associated with the exposure X (the “relevance” assumption);

2. IV2: independent of the outcome Y given the exposure X (the “exclusion restriction”); and

3. IV3: independent of all confounders of X and Y (the “exchangeability” assumption).

When these assumptions are satisfied, MR can test for a causal effect of an exposure on an outcome without bias from unobserved confounding. Under additional assumptions described in detail elsewhere (Didelez et al. 2010), MR will give an estimate of the size of the causal effect of the exposure on the outcome. MR methods, the assumptions required, and their implications are discussed in detail elsewhere (Lawlor et al. 2008; Burgess et al. 2013; Davey Smith and Hemani 2014).

MVMR is an extension of MR that allows for the causal effects of multiple exposures on an outcome to be estimated (Burgess and Thompson 2015; Sanderson et al. 2019). MVMR estimates the “direct” causal effects of each exposure included in the estimation on the outcome, conditional on the other exposures included in the model. It is, therefore, particularly useful where two or more potentially related exposures are of interest and the researcher wishes to understand whether both exposures exert a causal effect on the outcome or, as described later, where one exposure is potentially a mediator of another exposure. One example where MVMR has been used to estimate the direct effects of multiple related exposures is in estimating the effect of lipid traits on outcomes such as coronary heart disease (Richardson et al. 2019b), breast cancer (Johnson et al. 2019), and age-related macular degeneration (Burgess and Davey Smith 2017).

A simple MVMR model with two exposures is illustrated in Figure 2. The direct effects of X₁ and X₂ on the outcome Y are represented by β₁ and β₂, respectively.

Figure 2.

A simple multivariable Mendelian randomization (MVMR) model with two exposures. “SNPs” represents a group of single-nucleotide polymorphisms each associated with at least one of the exposures. The line between X₁ and X₂ is left bidirectional and dashed as no assumptions are made about this relationship in the estimation of β₁ and β₂. (X₁) exposure, (X₂) second exposure, (Y) outcome.

MVMR requires a set of SNPs, which are associated with the exposure variables but do not affect the outcome other than through these variables. In the same way as standard (univariable) MR, these SNPs are used to predict each of the exposure variables in the model and these predicted values are then used to estimate the effect of the exposures on the outcome in a multivariable regression analysis. With individual-level data, MVMR is implemented through two-stage least-squares (2SLS) regression of the model:

$$\begin{array}{c}Y={\text{β}}_0+{\text{β}}_1{X}_1+{\text{β}}_2{X}_2+v_y\end{array},$$

where Y is the outcome of interest, X₁ and X₂ are the exposures of interest, β₀, β₁, and β₂ are the intercept and effects of X₁ and X₂ on the outcome, respectively. ν_y is a random error term that is assumed to be normally distributed. This estimation includes all of the exposures in the MVMR model. Each of the exposures are predicted from the full set of SNPs in a first-stage regression:

$$\begin{array}{c}{X}_1={\pi }_{1}G+v_{x_1}\end{array},$$

$$\begin{array}{c}{X}_2={\pi }_{2}G+v_{x_2}\end{array},$$

where, in addition to the definitions for the previous equation, G is the set of SNPs used as instruments, π₁ is the effect of those SNPs on X₁, π₂ is the effect of those SNPs on X₂, and ${\nu }_{x_1}$ and ${\nu }_{x_2}$ are normally distributed random error terms. In the two sample summary data setting, Burgess and colleagues (Burgess and Thompson 2015; Burgess et al. 2015) show how MVMR can be implemented using GWAS summary data estimates of the association between SNP j (out of L) and the outcome, ${\hat{\mathrm{\Gamma }}}_j$; exposure X₁, ${\hat{\pi }}_{1j}$; and exposure X₂, ${\hat{\pi }}_{2j}$. This is performed by regressing the effect of each SNP on the outcome on the effect of each SNP on each exposure, that is, by fitting the model:

$${\hat{\mathrm{\Gamma }}}_j={\text{β}}_1{\hat{\pi }}_{1,\mathrm{j}}+{\text{β}}_2{\hat{\pi }}_{2,j}+{\in }_j.$$

Weighted by the inverse variance of ${\hat{\mathrm{\Gamma }}}_j$. ${\in }_j$ is a random error term for each SNP and all other terms are as defined above.

To conduct an MVMR analysis, it is necessary to have at least as many genetic instruments as there are exposures to be instrumented in the model; this is true regardless of whether single-sample or two-sample summary data are used. As with univariable MR, it is important that the IV assumptions are satisfied. In MVMR, these assumptions become:

1. MV-IV1: the exposures must be strongly predicted by the SNPs “given the other exposures included in the model”;

2. MV-IV2: the SNPs must be independent of the outcome Y given “all of” the exposures included in the model; and

3. MV- IV3: independent of all confounders of “any of the exposures” and the outcome Y.

MV-IV1

In any MR analysis, the set of genetic instruments G must be strong to avoid weak instrument bias (assumption IV1). In MVMR, it is necessary, but not sufficient, for the exposures to be strongly predicted by the set of SNPs; the exposures must also be strongly predicted by the SNPs conditional on the other exposures included in the estimation (Sanderson and Windmeijer 2016; Sanderson et al. 2019). For example, in a model with lipid traits high-density lipoprotein (HDL), low-density lipoprotein (LDL), and triglycerides included as exposures, the set of SNPs used as instruments must be able to strongly predict HDL once the association between the SNPs and LDL and triglycerides have been accounted for. If this assumption is not satisfied, then there will be multicollinearity between the predicted exposures and the MVMR estimates obtained will suffer from weak instrument bias (Cragg and Donald 1993; Sanderson and Windmeijer 2016).

MV-IV2/MV-IV3

MVMR analysis requires that the SNPs do not have an effect on the outcome other than through the set of exposures included in the model. However, SNPs that affect multiple phenotypes can be included in the estimation, as long as all of those phenotypes are included as exposures. These assumptions are therefore slightly less restrictive than for univariable MR. Pleiotropy, in which an SNP is associated with multiple phenotypes, can take two forms: vertical pleiotropy where the SNP is associated with one phenotype, which then affects another phenotype, and horizontal pleiotropy where the SNP is associated with two or more phenotypes independently. Horizontal pleiotropy is a violation of the third IV assumption if any phenotype associated with the SNP (other than the exposure of interest) is also associated with the outcome. MVMR can be used as a form of pleiotropy adjustment when SNPs have potential horizontal pleiotropic effects on a phenotype that influences the outcome as this phenotype can be included as an additional exposure in the analysis, accounting for the pleiotropic pathway. This is shown in the examples of MVMR using lipid traits as exposures given earlier; there is a high level of overlap between the SNPs associated with HDL, LDL, and triglycerides meaning that univariable MR analysis of any one of these exposures on an outcome will potentially be biased by pleiotropic effects through the other exposures. MVMR, however, avoids this bias by including all of these lipid traits in the same model. It is still necessary, however, to test for heterogeneity in the SNP outcome association as an indicator of potential pleiotropy in MVMR that has not been accounted for. This can be performed using a Sargan statistic (Sargan 1958) with individual-level data or an adjusted Cochran Q statistic with summary data (Sanderson et al. 2019). There are currently limited methods for sensitivity analysis/adjustment in MVMR if pleiotropy is thought to be present; however, one method of analysis that can be used to adjust for pleiotropy is multivariable MR-Egger (Rees et al. 2017), which allows for directional pleiotropy that is uncorrelated with the size of the SNP–exposure association.

What Is Estimated by Multivariable MR?

MR and MVMR target different causal effects of the exposure on the outcome. In general, MR estimates the “total” effect of the exposure on the outcome, whereas MVMR estimates the “direct” effect of each exposure on the outcome (Sanderson et al. 2019). Whether or not these are the same depends on the relationship between the exposures in the model, and between the other exposures and the outcome. Table 1 considers a model with two exposures, X₁, which is the primary exposure of interest, and X₂, which is an exposure of secondary interest. Three different relationships between the exposures are considered, where X₂ is a confounder of X₁ and the outcome, where X₂ is a collider of X₁ and the outcome, and where X₂ is a mediator of X₁ and the outcome. A collider is a variable that is independently affected by two other variables, in this case X₁ and the outcome Y. In a conventional (non-MR) analysis, conditioning on this variable by including it as an additional exposure in a regression of Y on X₁ will introduce bias in the estimated effect of X₁ on Y. This bias occurs because conditioning on the collider is equivalent to only observing the effect of X₁ on Y in a population of individuals who share the same value of X₂ and so can induce an association where none exists, or change the observed magnitude of the association (Hernán et al. 2004; Munafò et al. 2017). In each of the cases considered (confounder, collider, and mediator), Table 1 shows what is estimated by MR using the full set of SNPs for both exposures, for MR using only SNPs associated with X₁ and for MVMR.

Table 1.

Results for the effect of exposure X₁ on outcome Y^a

Relationship between X2 and X1	MR—including all SNPs	MR—including SNPs that only affect X1	MVMR
Confounder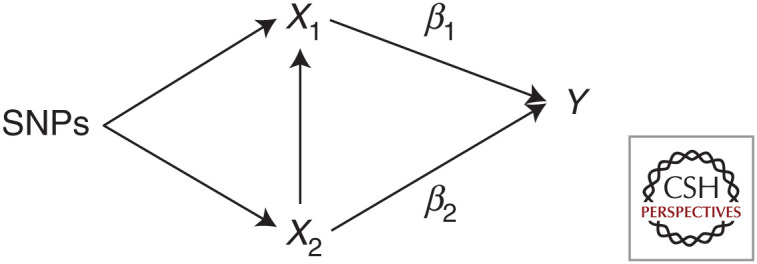	Biased—assumption IV2 is violated	Direct effect = total effect = β1	Direct effect = total effect = β1
Collider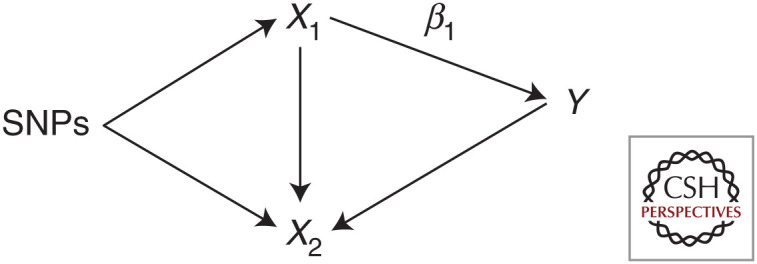	Direct/total effect = β1	Direct effect = total effect = β1	Direct effect = total effect = β1
Mediator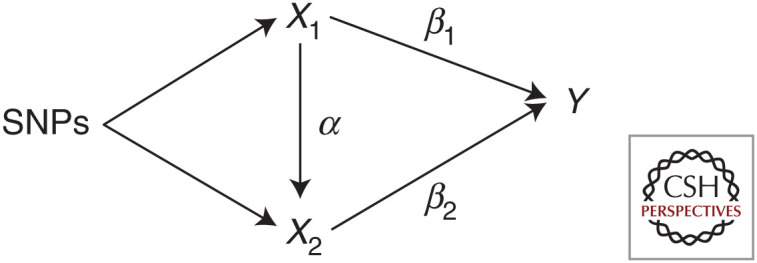	Biased—assumption IV2 is violated	Total effect = β1 + αβ2	Direct effect = β1

^aObtained from Mendelian randomization (MR) and multivariable MR (MVMR) under different relationships between exposures in a two-exposure model.

As this table shows, when X₂ is a confounder or collider of the relationship between X₁ and the outcome, both the univariable MR and MVMR estimate the same causal effect. However, MVMR has the advantage of not requiring that the SNPs only affect X₁ and so allowing estimation of the effect of X₁ on the outcome including SNPs that also have an effect on X₂. In the third scenario considered, X₂ is a mediator of the relationship between X₁ and the outcome, in this case univariable MR with all of the SNPs is biased but univariable MR using the appropriate set of SNPs (i.e., those that affect X₁ only) and MVMR estimate different causal effects. The univariable MR in this scenario estimates the total effect of X₁ on the outcome, including any effect that acts through X₂; however, MVMR estimates the effect of X₁ on the outcome holding X₂ constant and therefore gives an estimate of the effect of X₁ on the outcome that does not act through X₂, that is, the direct effect.

ESTIMATING MEDIATED EFFECTS USING MR AND MVMR

Table 1 shows that when a secondary exposure is a mediator of the exposure–outcome relationship, MR and MVMR estimate the total and direct effects of the exposure on the outcome, respectively. It is therefore possible to use MR and MVMR to estimate equivalent effects to traditional mediation analysis methods and so obtain estimates of the proportion of the effect of the exposure on the outcome that acts through a mediator or set of mediators.

Traditional mediation analysis uses two different methods to distinguish the direct and indirect effects and estimate the proportion mediated; the difference method and the product-of-coefficients method (Baron and Kenny 1986; MacKinnon 2012; VanderWeele 2016). Both methods rely on the estimation of a set of regressions from which the direct and indirect effects of the exposure on the outcome can be obtained by combining estimation results.

The “difference method” uses two regression models. First, the outcome is regressed on the primary exposure of interest and any confounders. The estimated parameter for the exposure from this regression gives the total effect of the exposure on the outcome. This model is then reestimated with the potential mediator included as an additional explanatory variable. The estimated parameter for the exposure from this second regression gives the direct effect of the exposure on the outcome that does not act through the mediator.

The “product of coefficients method” also uses two regression models to obtain the direct and indirect effects. First, the direct effect of the exposure and the mediator on the outcome are obtained through regression of the outcome on the exposure and mediator. The estimated parameter for the exposure from this regression gives the direct effect of the exposure on the outcome and the estimated parameter for the mediator gives the direct effect of the mediator on the outcome. The mediator is then regressed on the exposure to estimate the effect of the exposure on the mediator. Multiplying this result with the direct effect of the mediator on the outcome gives the indirect effect of the exposure on the outcome.

In each method described above, the proportion of the total effect that is mediated can be obtained by dividing the indirect effect of the exposure by the total effect. For the results obtained from these traditional mediation methods to be interpreted as causal estimates of the direct and indirect effects of the exposure on the outcome, two key assumptions are that there is no unmeasured confounding and no measurement error in the exposure or mediator. These are strong assumptions that are unlikely to be met in many scenarios. It is possible to apply MR and MVMR to obtain causal estimates of the total, direct, and indirect effects and so implement a mediation analysis without making these assumptions. However, these assumptions are replaced by the IV assumptions described earlier. Estimation of the size of the direct and indirect effects also only applies to continuous exposures and mediators as MR does not give accurate point estimates of the size of effect when the exposure is binary.

The Difference Method

Univariable MR estimates the total effect of the exposure on the outcome and MVMR estimates the direct effect of the exposure on the outcome conditional on the mediator. The difference between these estimates will then give the indirect effect of the exposure on the outcome that acts via the mediator (or mediators) included in the MVMR. This is equivalent to the difference method of mediation analysis described above.

The Product of Coefficients Method

An alternative method that uses MR to estimate these effects is network (or two-step) MR (Relton and Davey Smith 2012; Burgess et al. 2014). Network MR uses a series of univariable MR analyses to estimate the total effect of the exposure on the outcome, the effect of the exposure on the mediator, and the effect of the mediator on the outcome. However, the direct effect of the mediator on the outcome could also be estimated from MVMR estimation of the direct effects of the exposure and mediator on the outcome. The indirect effect of the exposure on the outcome can then be calculated by multiplying the effect of the exposure on the mediator and the effect of the mediator on the outcome. This is equivalent to the product of coefficients method of mediation analysis.

Network MR estimates the effect of an exposure on an outcome that acts via a single mediator variable at a time. Using MVMR, it is possible to determine the direct and indirect effects when there are multiple mediators included in the model as multiple exposures can be included in the MVMR estimation. It is not, however, possible to distinguish the effects of each of the mediators and so disentangle the contribution of each mediator to the indirect effect. This is because although MVMR estimates the direct effect of each exposure in the model, it does not say anything about the relationships between the exposure and the different mediators included. These two methods could, however, be combined to determine the total proportion of the effect of the primary exposure on the outcome that is mediated by the full set of potential mediators (through MVMR) and then the relative importance of each mediator (through a series of network MR analyses that looked at each mediator in turn) (Table 2; Fig. 3).

Table 2.

Estimation of total, direct, and indirect effects and proportion mediated using Mendelian randomization (MR) and multivariable MR (MVMR)

Effect	Estimation—difference method		Estimation—product of coefficients method (network/two-step MR)
Total effect	Univariable MR of exposure on outcome using single-nucleotide polymorphisms (SNPs) associated with exposure only (Fig. 3A)	${\text{β}}_1^{\ast }$	Univariable MR of exposure on outcome using SNPs associated with exposure only (Fig. 3A)	${\text{β}}_1^{\ast }$
Direct effect	Effect of exposure on outcome from MVMR including exposure and mediator as exposures (Fig. 3B)	β1	Total effect—indirect effect	${\text{β}}_1^{\ast }-\alpha {\text{β}}_2$
Indirect effect	Total effect—direct effect	${\text{β}}_1^{\ast }-{\text{β}}_1$	Effect of exposure on mediator from univariable MR (Fig. 3C) multiplied by effect of mediator on the outcome from univariable MR (Fig. 3D) or MVMR (Fig. 3B)	αβ2

Figure 3.

Illustration of the parameters estimated to obtain total, direct, and indirect effects and proportion mediated using Mendelian randomization (MR) and multivariable MR (MVMR). (X) exposure, (M) mediator, (Y) outcome, (SNPs_X) set of single-nucleotide polymorphisms associated with the exposure, (SNPs_M) set of SNPs associated with the mediator.

ADVANTAGES AND LIMITATIONS OF USING MENDELIAN RANDOMIZATION TO ESTIMATE MEDIATED EFFECTS

An important advantage of using MR and MVMR to estimate mediation effects is that if M is not a mediator of X and Y but is in fact a confounder (or even collider) of X and Y, the estimated direct effect will be equal to the estimated total effect and so the lack of mediation will be clear from the results obtained. This overcomes the limitation of traditional mediation analysis that the correct specification of the model through assignment of variables to mediators or confounders is essential to correctly identify the role of mediators. In mediation analysis, it is not possible to distinguish statistically between a model in which M is a mediator of X and Y and the equivalent model in which M is in fact a confounder of X and Y (MacKinnon et al. 2000). This is no longer the case for MR and MVMR, allowing for correct estimation even when a confounder is misspecified as a mediator.

Another key assumption of observational mediation analysis is the cross-world assumption. This assumption states that there must be no confounder of the mediation and outcome that is a descendent of the exposure (VanderWeele 2016). Violation of this assumption introduces bias in the observational mediation analyses as any variable violating this assumption is part of the total effect of the exposure on the outcome but should be adjusted for as a confounder of the mediator outcome association. Methods for mediation analysis are available that can adjust for variables that violate this assumption when they are observed (Vansteelandt and Daniel 2017). However, using MR and MVMR for meditation analyses, this assumption is no longer necessary and so reliable estimates can be obtained even when these variables are not observed. This is because it is no longer necessary to adjust for confounders and so the effect of the confounder that violates the cross-world assumption will be appropriately differentiated into the direct and indirect effects.

One advantage of MVMR is that it can be used to estimate direct effects even when SNPs are associated with multiple exposures, as long as all of those exposures are included in the model. However, when MR and MVMR are used to estimate direct and indirect effects, it is necessary to ensure that all SNPs used to estimate the total effect of the exposure on the outcome are only associated with the exposure, that is, they have no pleiotropic effects on the mediator. If this assumption is not satisfied then the estimated total effect of the exposure will be biased and consequently the estimate of the direct effect will also be biased. In the case in which the estimated direct effect differs from the estimated total effect, it is not possible to distinguish mediation from a pleiotropic effect of the SNPs for the exposure through the potential mediator. Therefore, it is important to be as confident as possible that the univariable MR estimates are not biased by a pleiotropic effect of the SNPs on the outcome. There are a number of sensitivity analyses that can be used to try to identify pleiotropic effects in the MR analysis (Chen et al. 2008; Davey Smith and Hemani 2014; Bowden et al. 2015, 2016, 2017; Hartwig et al. 2017; Spiller et al. 2018). However, pleiotropy is notoriously difficult to identify in MR analysis and this lack of distinction between mediation and pleiotropy driving a difference in results is an important weakness of MVMR when one exposure is a potential mediator of the other.

All of the description here focuses on the estimation of MVMR and mediation effects when the exposure, mediator, and outcome are continuous variables. When the outcome is binary and the effects are estimated on the odds ratio scale, it is no longer possible to reliably calculate direct and indirect effects caused by the noncollapsibility of odds ratios. The value of an odds ratio marginal on another variable may have a different value to the value of the odds ratio conditional on that variable, even when that variable is not associated with the exposure, that is, the value of an odds ratio is dependent on the distribution over which the odds ratio is evaluated (Greenland et al. 1999; VanderWeele and Vansteelandt 2010; Burgess 2017). In practice, this means that the total and direct effects estimated may differ because the direct effect is estimated conditional on the potential mediator, even if the potential mediator is not actually a mediator of the exposure outcome relationship. This problem cannot be avoided through the use of MR and is explored in more detail elsewhere (Carter et al. 2019b). When the exposure is binary, MR analyses can be used to test causal hypotheses; however, the effect estimates obtained are not reliable estimates of the size of the causal effect (Angrist et al. 1996; Palmer et al. 2011; Vansteelandt et al. 2011; Clarke and Windmeijer 2012). This applies to all MR analyses, including those for mediation analysis. Therefore, although the presence or lack of a mediation effect can be detected when the exposure or mediator is binary, caution should be exercised in interpreting the size of the direct and indirect effects from the results obtained.

A feature of MR analyses of all types is that they are primarily estimating lifetime effects of the exposure (or exposures) of interest on the outcome (Holmes et al. 2017; Labrecque and Swanson 2018). When interpreting the results from estimating the total and direct effects from an MR and MVMR analysis, it is therefore important to consider this. The effects obtained are the total and direct lifetime effects of the exposure on the outcome, which may differ from the effects at any time point if there is a bidirectional relationship or feedback loop between the exposure and the mediator that acts over time. If SNPs differ in their effects on an exposure over different time points, then it may be possible to distinguish the effects of exposure at each time point on an outcome using MVMR (Richardson et al. 2019a). However, it will not be possible to determine how much of the effect of an earlier time point is mediated by a later time point unless there are SNPs available as instruments, which only affect the earlier time point enabling unbiased univariable MR estimates to be obtained at the earlier time point on the outcome.

CONCLUSION

MVMR is a recently developed extension to MR that can be used to estimate the effect of multiple exposures on an outcome when the relationship between the exposures is unknown and/or the SNPs used as instruments are thought to have an effect on multiple exposures. When one exposure is a potential mediator of the effect of another on the outcome, MR and MVMR can be used to obtain an estimate of the total and direct effects of the exposure on the outcome even in the presence of unmeasured confounding. However, the assumption of no unmeasured confounding is replaced by a set of IV assumptions required for the estimates obtained to be consistent. Therefore, consideration of these assumptions and the weaknesses of using MR and MVMR to estimate mediated effects is required when estimating direct and indirect effects of an exposure on an outcome.