Abstract
High-throughput sequencing data sets are usually deposited in public repositories (e.g., the European Nucleotide Archive) to ensure reproducibility. As the amount of data has reached petabyte scale, repositories do not allow one to perform online sequence searches, yet, such a feature would be highly useful to investigators. Toward this goal, in the last few years several computational approaches have been introduced to index and query large collections of data sets. Here, we propose an accessible survey of these approaches, which are generally based on representing data sets as sets of k-mers. We review their properties, introduce a classification, and present their general intuition. We summarize their performance and highlight their current strengths and limitations.
Over the past decade, the cost of sequencing has decreased dramatically, making the generation of sequence data more accessible. This has led to increasingly ambitious sequencing projects. For example, the 1000 Genomes Project, which began in 2008 and was completed in 2012 (Clarke et al. 2012), led to the 100,000 Genomes Project, which began in 2014 and was completed in 2018 (Turnbull et al. 2018). There are dozens of other large-scale sequencing projects completed or underway, including GEUVADIS (Lappalainen et al. 2013), GenomeTrakr (Timme et al. 2018), and MetaSUB (The MetaSUB International Consortium 2016). An overwhelming amount of public data is now available at EBI's European Nucleotide Archive (ENA) (Cook et al. 2019) and NCBI's Sequence Read Archive (SRA) (Leinonen et al. 2011). The possibility of analyzing these collections of data sets, alone or in combination, creates vast opportunities for scientific discovery, exceeding the capabilities of traditional laboratory experiments. For this reason, there has been a substantial amount of work in developing methods to store and compress collections of high-throughput sequencing data sets in a manner that supports various queries.
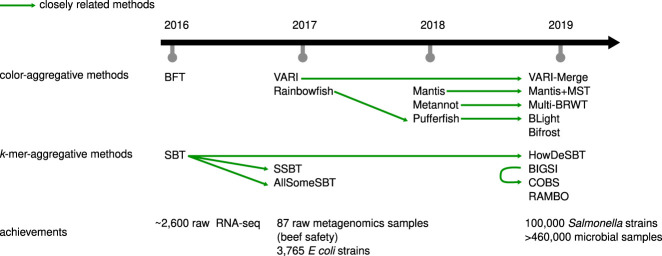
In this paper, we use the term “data set” to refer to a set of reads resulting from sequencing an individual sample (e.g., DNA-seq, or RNA-seq, or metagenome sequencing). Sequencing is routinely performed not only on a single sample but on a collection of samples, resulting in a collection of data sets. For instance, 100,000 human genomes were sequenced for the 100,000 Genomes Project and over 300,000 bacterial strains were sequenced for GenomeTrakr. One basic query that is fundamental to many different types of analyses of such collections of data sets can be formulated as follows: given a sequence, identify all data sets in which this sequence is found. For example, consider the problem of finding a RNA transcript within a collection of RNA-seq data sets. Similarly, we can ask to find which data sets contain a specific DNA sequence, such as a gene or a noncoding element, in a collection of bacterial strain genomes. In this paper, we present an overview of recent bioinformatics methods (Fig. 1) created to handle these types of queries.
Figure 1.
Timeline, main relationships, and application highlights for the methods covered in this survey.
Given the size of many collections and data sets, several different paradigms for storing them so that they can be efficiently queried have been developed many of which continue to be extended and explored. One paradigm is to store and index data sets as sets of k-length substrings, which are referred to as “k-mers.” We will refer to collections of data sets as “sets of k-mer sets.” The methods that use this paradigm build an index of all k-mer sets and support the basic query described above by splitting the query sequence into k-mers and determining their presence or absence in the index.
As we will discuss in this survey, this paradigm has proven to be useful in several ways. First, sets of k-mers are a more concise representation of the set of sequences of the samples, as they abstract some of the redundancy inherent in high sequencing coverage. Second, genetic variation and sequencing errors can be dealt with in a more efficient, albeit less accurate way than using sequence alignment. Instead of performing inexact pattern matching, as aligners do, k-mer-based methods can simply examine the fraction of matching k-mers within the query sequence. Since their initial development, k-mer-based analysis approaches have been widely adopted in the bioinformatics community due to their efficiency and ability to accurately summarize and compare large data sets. Hence, the methods we describe in this survey were imperative to a large number of biological analyses; from elucidating the evolutionary dynamics between substrains of Staphylococcus aureus (Young et al. 2012) to identification of recombination hotspots in bird species (Singhal et al. 2015) or enabling the search of over 400,000 viral and bacterial species (Bradley et al. 2019).
Even though k-mer-based methods have been popular, there do exist some trade-offs. More specifically, storing data using a k-mer index comes with some loss of information because it only gives information for each constituent k-mer of a sequence, rather than about the entire sequence. Hence, in most cases, a k-mer index does not provide exact answers for queries of longer sequences (e.g., whole transcript or entire gene) but instead provides a reasonable approximation.
Data structures for indexing a set of k-mers have been studied in depth (Chikhi et al. 2019). Here, we consider the problem of storing a set of k-mer sets. A naive approach would be to use such an index separately for each k-mer set in the collection. However, a key aspect is that sequencing experiments that are analyzed collectively typically share a large fraction of k-mers. Therefore, significant space savings can be achieved by the identification and clever storage of this redundant information. Here, we focus on the methods underlying the different building blocks of sets of k-mer sets structures. We review the different properties, the types of queries, and the computational performance that they offer. We highlight similarities of methods based on commonalities between building blocks where it is appropriate.
Biological applications
RNA-seq studies
Transcriptomics was one of the first areas of application of the reviewed methods. Solomon and Kingsford (2016) gathered more than 2500 samples of human RNA-seq, consisting of blood, brain, and breast tissue samples from SRA. This led to the possibility of identifying conditions which express isoforms by associating transcripts to tissues. Similar to tissue-specific associations, one can envision the numerous benefits of comparing patient cohorts in order to understand differences in pathologies or impact of medication. For instance, using RNA-seq for functional alterations profiling has become more frequent in cancer research (Byron et al. 2016). Thus, vast programs such as The Cancer Genome Atlas (TCGA) (Tomczak et al. 2015) provide RNA-seq data from a variety of cancer types. The authors of SeqOthello (Yu et al. 2018) showed how to investigate gene-fusion using a set of k-mer sets by first creating an index of all tumor samples from the TCGA. Then, they considered documented fusion events and their corresponding k-mer signatures and screened the index to detect these signatures. They confirmed some fusions and reported some novel ones. Fusion transcripts provide interesting targets for cancer immunotherapies because they are prone to exhibit tumor-specific markers.
One of the data structures covered in this survey, the colored de Bruijn graph, has also been used for rapid, alignment-free quantification of RNA-seq data. Tools such as Sailfish (Patro et al. 2014), Salmon (Patro et al. 2017), and kallisto (Bray et al. 2016) rely on a colored de Bruijn graph (implemented using a hash table) to represent and quantify sets of transcripts per genes.
Microbial genomics
Cortex (Iqbal et al. 2012), which introduced the concept of colored de Bruijn graphs, was used to study the host diversity and dynamics of Staphylococcus aureus substrains using whole-genome sequencing (Young et al. 2012). Then, several papers demonstrated how sets of k-mer sets could be used to mine and analyze collections of microbial samples or genomes, whether they be strains of the same genera (e.g., 16,000 strains of Salmonella) using VARI-Merge (Muggli et al. 2019), microbiomes (e.g., 286,997 genomes from the human microbiome), or more extensive microbial data (e.g., 469,654 bacterial, viral, and parasitic data sets from the ENA) using BIGSI (Bradley et al. 2019). For example, GenomeTrakr (Timme et al. 2018) was developed to coordinate international efforts in sequencing whole genomes of foodborne pathogens. Indexing and querying this and other databases could lead to improved surveillance of pathogenic bacteria and thus elucidate the effectiveness of interventions that attempt to control them.
Subsequently, k-mer indices have been used to follow the spread of antimicrobial resistance (AMR) genes and plasmids across bacterial populations. The BIGSI authors also searched for plasmid sequences bearing AMR and initiated a study in an index containing a variety of microbial genomes. They identified some of these plasmids spread across different genera. Other AMRs, such as SNPs associated with fluoroquine resistance, were studied across 100,000 Salmonella genomes with Bifrost (Luhmann et al. 2020).
Lastly, an effort was proposed to build a comprehensive human gut microbiome resource with the help of a set of k-mer set structure. Cultured genomes and metagenomes assembled from metagenomics data were combined in a BIGSI index to create the Unified Human Gastrointestinal Genome index (Almeida et al. 2020). This resource aims at exploration and enables looking for contigs sequences, genes, or genetic variants.
Genome dynamics
In a study of fine-scale recombination landscape in birds, Cortex was used to de novo call variants in zebra finch raw data sets, bypassing the low-quality state of current genome resources (Singhal et al. 2015). Recently, a novel phylogeny approach was introduced by building a colored de Bruijn graph (Wittler 2020) (using Bifrost) on a set of genomes (assembled or reads) and traverses the structure to extract phylogenetic signal. This approach bypasses the usual multiple genome alignment step.
As an aside, tools like Mash (Ondov et al. 2016) perform sketching of data sets (i.e., construct small sets of short k-mers that constitute signatures of data sets), in order to compute ecological distances between data sets. Because sketching uses specific techniques that do not rely on the entire k-mer sets (see a related review: Marçais et al. 2019), we consider them outside the scope of this study.
Finally, beyond these applications, other topics are starting to be explored: integrated variant calling across large-scale gene, plasmid, and transposon searches (Blackwell et al. 2019; Bradley et al. 2019; Miller et al. 2020), bacterial pan-genome indexation (Muggli et al. 2019), and gene fusion and pan-cancer analysis (Yu et al. 2018).
Query model
Here, we describe the types of queries that are supported by the surveyed methods.
Let be a collection of n data sets. Let S be a nucleic sequence of arbitrary length such as a gene or a transcript. Note that S can, in principle, be as short as a single k-mer, but in practice, it is often a sequence longer than k. The aim is to determine the presence of S in each data set of .
The most elementary type of queries supported by all methods in this survey consist in reporting every data set Di ∈ which contains a query k-mer. It can be naturally extended to a longer query sequence S by querying each element of the set Q of all k-mers present in S. One can see that, if S is present in a data set, then every element of Q is present as well. However the converse is not true: k-mers in Q may possibly correspond to different sequences within a data set and S may actually be absent. Consider the two k-mers ACT and CTG (k = 3) and assume they are present in two different reads within a single data set. A query sequence ACTG would then be reported as present in that data set, regardless of whether the sequence is truly found as part of a single read. Despite this potential shortcoming, this is widely considered to be a reasonable approximation, due to k being long enough to make such false-positive events unlikely.
In a seminal work, Solomon and Kingsford (2016) proposed to report every data set Di ∈ in which a proportion of at least θ k-mers of Q appear, that is, |Di ∩ Q| / |Q ≥ θ. Here, θ can be seen as a stringency parameter for the search. This query model is motivated by events such as sequencing errors and variants, which reduce the number of common k-mers between a query and a target. Thus, it is interesting and often necessary to report when only a fraction of the k-mers from a query sequence are present in a data set. Typically, θ is set between 0.7 and 0.9 (Solomon and Kingsford 2016). Also, the typical k-mer size range seen in applications is 21–31.
Building blocks
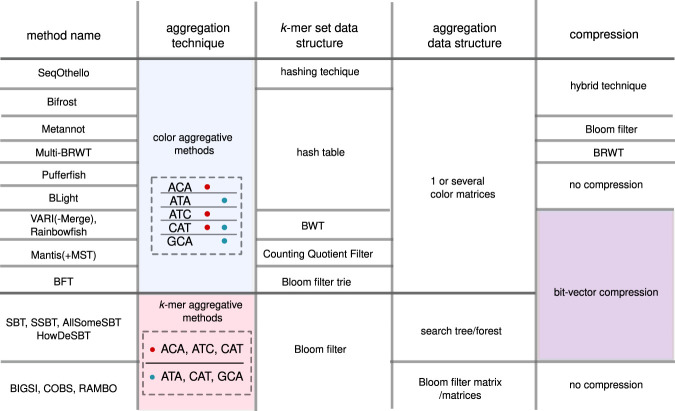
We view the storage of a set of k-mer sets as having four possible components. These components are: the underlying data structure used to represent a single set; the strategy used to aggregate k-mers across different sets; the data structure used to store this aggregation; and the compression strategy used. See Figure 2 for an illustration of this view. Most of the novelty in the methods comes in the aggregation strategy and in the data structure used to support it. The other two components are used more as building blocks. In this section, we will cover these two building blocks.
Figure 2.
Overview of set of k-mer sets building blocks. We classified strategies in color-aggregative approaches and k-mer aggregative approaches (second column). The top row of the figure indicates the general categories of components of each method: the type of k-mer set; the way multiple sets are combined together; and an optional compression scheme. Each next row describes one of the surveyed methods. The cells in this figure are methodological choice, potentially common across methods; hence many cells are joined.
k-mer set data structures
A set of k-mers is a collection of k-mers that are deduplicated and unordered. It will be enough to consider them as black boxes that support all or a subset of the following operations:
membership, that is, testing whether a k-mer is in the set;
insertion and/or deletion of a k-mer.
However, methods to represent k-mer sets are not all equivalent in terms of features and performance. We briefly review their main characteristics in the rest of this section but refer the reader to the recent survey by Chikhi et al. (2019) for further details.
Most methods rely on bit vectors to store the presence or absence of k-mers in data sets. A bit vector is an array of bits; for example, 00101 represents a bit vector of length 5. A 0 is used to indicate that the k-mer is absent, and a 1 indicates that it is present. A bit vector could be used to record the data sets in which a given k-mer appears or, alternatively, all the k-mers that are contained in a given data set. However, with a growing number of data sets and k-mers, using plain bit vectors is generally too simplistic, and often compression or other tricks are also incorporated. One example is the Bloom filter (Bloom 1970), which is a way to store a set as a bit vector using many fewer bits than the naive approach (see Box 1).
Box 1. Technical definitions.
Hashing, hash functions. Mathematical functions that are used to associate elements (e.g., k-mers) to numbers (e.g., positions in an array).
Bloom filters (BFs). Bit vectors that record the presence or absence of elements within a set, with some approximation, using hashing.
Counting quotient filters (CQFs). Similar in nature to Bloom filters but differ by their hashing strategy. CQFs support membership queries of elements in a set, and also counting elements in a multiset.
Minimal perfect hash functions (MPHFs). Functions that associate a fixed set of elements to the range of consecutive integers from 0 to the number of elements, in a highly space-efficient way.
See Supplemental Box S1 for detailed illustrations of BF, CQF, and a hashing method inspired by MPHF techniques called Othello.
Burrows–Wheeler transform (BWT). A text transformation algorithm. Given an arbitrary text, such as a DNA sequence, BWT rearranges it in a way that enhances its compression and permits indexing. The transformation is reversible, allowing the text to be efficiently recovered.
Graph definitions
A graph (see A in the figure below) is a pair of two sets V and E. Elements of V are nodes (in blue), and elements of E are pairs of related nodes called edges (in orange and red).
A path in a graph is a sequence of edges that connects a sequence of distinct nodes (the example shows a path drawn between nodes 1, 2, 3, and 4 through red edges).
A tree (B in the figure below) is a particular graph in which any two nodes are connected by exactly one path. A forest is a disjoint union of trees (C in the figure below). A subtree (circled in gray in B) is a subset G′ and E′ of a tree T = (G, E).
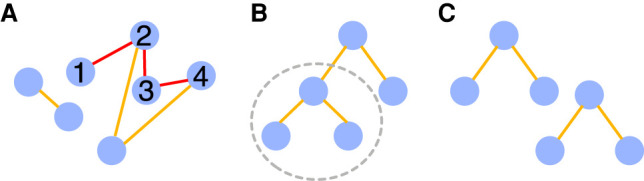
A trie is a tree that allows to efficiently store and query a set of words. Wavelet tries (Grossi and Ottaviano 2012) are designed to store compressed sequences.
A de Bruijn graph (DBG) is a graph where nodes are k-mers and there exists a directed edge from vertex u to v if the last k−1 characters of u are the same as the first k−1 characters of v. A compacted de Bruijn graph is a different graph than the DBG, which, however, represents the same k-mer information by merging unambiguous paths.
See Supplemental Box S2 for an example of DBG and compacted DBG.
Some methods view a k-mer set as a de Bruijn graph (DBG) (see Box 1). These two views, k-mer sets and DBGs, are (in some sense) equivalent as they intrinsically represent the same information.
Data structures for representing k-mer sets (DBG or not) can further be divided into two categories: membership data structures and associative data structures. The first category only informs about the presence or absence of k-mers, for example, as in the case of a Bloom filter (BF). The second category associates pieces of information to k-mers, akin to how dictionaries link words to their definitions. Some examples of associative data structures include hash tables and counting quotient filters (CQF) (Box 1; Bender et al. 2012; Pandey et al. 2017; Almodaresi et al. 2019).
Some data structures (e.g., CQFs, BOSS) can represent sets in an exact way, whereas others (e.g., Bloom filters) represent them in a probabilistic way, meaning that the structures can return false positives (i.e., meaning that a k-mer is sometimes falsely reported as present in the set when in fact it is absent). These false positives lead to an overestimation in the number of k-mers detected as present in a set. Although this is an undesirable effect, it can be partly mitigated as we will see in section, “Background and method intuition.”
The main reason such advanced data structures are considered, instead of those provided in the standard libraries of programming languages, is space efficiency. Bloom filters and CQFs approximately require a byte for each element in the set, that is, less than the size of the element itself. Similarly, optimized representations of DBGs (Bowe et al. 2012; Chikhi and Rizk 2013; Boucher et al. 2015), which are also representations of k-mer sets, aim for near-optimal space efficiency. Exact and probabilistic data structures offer a trade-off between space and accuracy. This is a crucial aspect, as the volume of data typically exceeds what can be processed using unoptimized data structures.
Compression
To further optimize space usage, different compression techniques have been applied to sets of k-mer sets. Bloom filters and bit vectors are amenable to a number of compression techniques because they are represented in bits. They can be sparse (i.e., when most of the bits are 0's) or dense (i.e., when most of the bits are 1's). Compression methods exploit these properties.
Bit vector compression
Bit vectors can be efficiently stored using bit-encoding techniques that exploit their sparseness or redundancy. The most prevalent of the methods in this survey are RRR (Raman et al. 2002) or Elias-Fano (EF) (Fano 1971; Elias 1974; Ottaviano and Venturini 2014). The principle behind these is to find runs of 0's and to encode them in a more efficient manner, reducing the size of the original vectors. Other techniques such as Roaring bitmaps (Lemire et al. 2016) adjust different strategies to subparts of the vectors. Wavelet trees (Grossi et al. 2003) generalized compression of vectors on larger alphabets (i.e., not just 0's and 1's but, e.g., a's, b's, c's, etc.). More advanced techniques deriving from the same concept were also proposed specifically for sets of k-mer sets (Karasikov et al. 2019).
Delta-based encoding
When two sets share many elements, it may be more advantageous to store only one along with the differences with the other. For instance, rather than storing two (possibly compressed) bit vectors, one can only store the first bit vector explicitly along with a list of positions that need to be inverted to obtain the second vector.
This list of positions can itself be encoded as a bit vector, with a bit set to 1 if and only if the bit is at the location of a difference between the two vectors. This bit vector is expected to be more sparse than the original encoding, allowing better compression. Such a scheme is usually called “delta-based encoding” in the literature.
Hybrid techniques
In hybrid approaches, a collection of bit vectors is split into different buckets, where each bucket contains bit vectors with similar features. Compression within each bucket is performed using a suitable technique selected from a pool of feature-specific ones. An illustration of these techniques is provided in Supplemental Box S4.
Color-aggregative methods
The methods that we will survey are split into two categories. Color-aggregative methods index the union set of k-mers, which is the joint set of all k-mers that appear in all the data sets. Instead, k-mer aggregative methods index each data set separately, then build an aggregation data structure to distribute queries. A few methods that escape this categorization will be presented separately.
Color-aggregative methods gather and index the union set of k-mers, then associate information to each k-mer to record its data set(s) of origin. A practical advantage of color-aggregative methods is that a k-mer that appears in many samples will appear only once in the union set. This greatly reduces redundancy in the representation of k-mers but introduces the need to store additional color information. In this subsection, we give a brief background and history of the methods that fall into this category.
Color matrix
A color of a given k-mer is frequently used in the literature to identify a data set containing the k-mer, assuming each data set is given a unique color. A color set is the set of colors associated with a k-mer. It is convenient to represent a color set using a bit vector. Here, fixing an ordering of the data sets, a 1 at position i in the bit vector indicates the presence of the k-mer in the ith data set and 0 its absence. Given n k-mers and c data sets, the color matrix is an n × c matrix of bits which describe the presence or absence of each k-mer (in the rows) in each data set (in the columns). For an example, see Box 2.
Box 2. Representation of colors in color-aggregative methods.
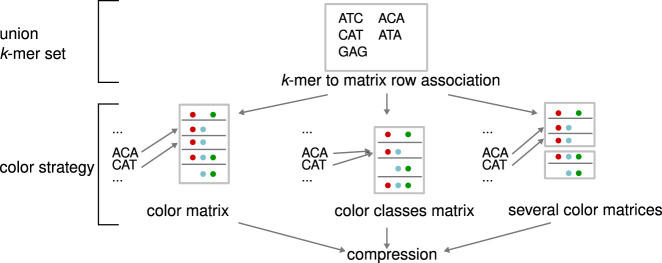
A color matrix represents the presence of n k-mers across c data sets (in the above figure, n = 5, c = 3). Different schemes have been introduced to encode such matrices. In particular, a color class is a set of colors that is common to one or more k-mers. In other words, in the color matrix, there may be identical rows, then the corresponding k-mers belong to the same color class. One may “deduplicate” the n rows of the color matrix into m < n color classes (here, m = 4). Then, color class identifiers are introduced as intermediaries between k-mers and color classes. (To go further, frequently used color classes can be referenced using fewer bits by using small integers as identifiers.)
Color-aggregative methods are generally composed of three parts. First, a set of all k-mers, built using either a DBG or an ad hoc representation. Second, a correspondence between k-mers and colors in the form of a color matrix (left, “color strategy” row), color classes (middle), or several color matrices (right). Finally, k-mer sets and/or colors may be further compressed. In the two first columns’ strategies, compression is based on one of the techniques from the section, “Compression.” In the third column, different techniques may be used for different matrices.
Background
The first color-aggregative method was proposed by Iqbal et al. (2012) in the Cortex software. It implements a relatively straightforward associative data structure that maps k-mers to colors. A colored DBG is a DBG of the union set of k-mers, where each vertex is labeled with the color set of the corresponding k-mer. Iqbal et al. used a colored DBG built on a set of individuals from a population to detect SNPs and other short variants; such events are reflected in the graph by a pair of short paths that share their start and end nodes. This enabled detection of genetic variation in a population without the use of a reference genome. Cortex consumes an inordinate amount of RAM when the total number of distinct k-mers exceeds tens of billions. This main drawback motivated more recent works improving the efficiency of the colored DBG.
We note that, later in this survey, we will not restrict the term colored DBG to the original work from Iqbal et al. but will extend it to any explicit DBG implementation that associates color sets to k-mers. Colored DBGs are only implemented in the class of color-aggregative methods. Conversely, as we will see later, some color-aggregative methods do not implement a colored DBG.
Later methods
The first color-aggregative methods that improved upon the memory- and time-efficiency of Cortex were Bloom filter trie (BFT) (Holley et al. 2016) and Vari (Muggli et al. 2017). These methods achieved a significant reduction in representation size via different strategies. After the introduction of these methods, subsequent improvements were made with the development of Rainbowfish (Almodaresi et al. 2017), Multi-BRWT (Karasikov et al. 2019), Mantis (Pandey et al. 2018), SeqOthello (Yu et al. 2018), Mantis + MST (Almodaresi et al. 2019), and Vari-Merge (Muggli et al. 2019). Most of these recent techniques rely on a more careful encoding of the colors of each k-mer, which takes advantage of redundancy in the data.
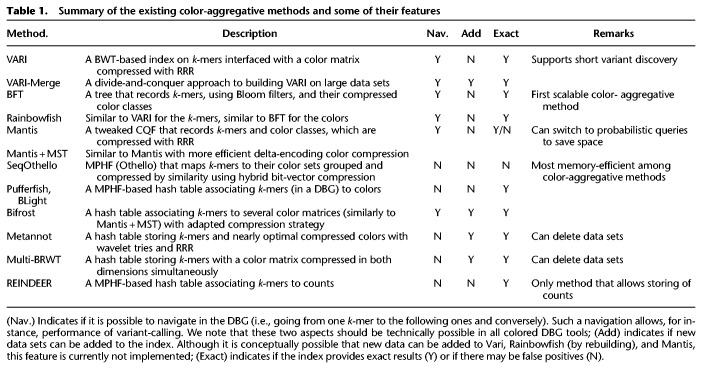
A summary of the main features of color-aggregative methods is presented in Table 1. Their methodological strategies are presented in more detail in Supplemental Box S6.
Table 1.
Summary of the existing color-aggregative methods and some of their features
Methods based on a color matrix
The representation of the DBG used by Vari (Muggli et al. 2017) is a BWT implementation referred to as BOSS (Boucher et al. 2015). We will not go into the technical details here (see Supplemental Files and Supplemental Box S3 for more information); it is sufficient to see BOSS as a rearrangement of the original data that enables indexing and compression. In order to add color information in Vari, a compressed color matrix is constructed row-by-row.
Later, Vari-Merge (Muggli et al. 2019) was introduced to construct colored DBGs for very large data sets, which can also be updated with new data. Two other methods, Pufferfish (Almodaresi et al. 2018) and BLight (Marchet et al. 2020b) put emphasis on the k-mer indexing technique in order to efficiently store DBGs in memory and use a simple color matrix to represent the colored DBG. It is worth noting that BLight shares similarities with Kraken (Wood and Salzberg 2014), a taxonomic classifier. Indeed, it can be seen as a colored de Bruijn graph of k-mers with labels to their genome of origin.
Methods based on color classes
In many applications, such as human RNA-seq indexing (Solomon and Kingsford 2016), it is expected that many data sets share a large number of k-mers. This redundancy can be exploited to reduce the color encoding size, through color classes. When colors are seen as bit vectors, the color classes are defined simply as deduplicated bit vectors. Thus, two k-mers having the same color sets are associated with a single color class instead of two identical bit vectors (see Box 2). Compression may be achieved by representing the color matrix as a compressed bit vector.
Bloom Filter Trie (Holley et al. 2016) uses a different approach to storing the DBG than Vari but also aims at representing a DBG. BFT introduced the idea of color classes, and a more detailed description of its inner workings is provided in Supplemental Box S5. Rainbowfish (Almodaresi et al. 2017) mixes ideas from Vari and BFT. Mantis (Pandey et al. 2018) introduces another strategy (the CQF) (see Box 1) for storing the DBG in a space-efficient manner. Initially, CQFs were introduced to record counts associated with k-mers, but in Mantis, the structure instead stores color sets. Mantis + MST (Almodaresi et al. 2019), an extension of Mantis, takes advantage of the insight that many color classes are frequently similar to each other, because many k-mers occur in relatively similar sets of sequences. Thus, it proposes a more efficient encoding of colors.
Methods based on several matrices
SeqOthello (Yu et al. 2018) does not explicitly represent a DBG but rather stores a probabilistic set of k-mers using a hashing method inspired by MPHF techniques called Othello (see Supplemental Box S1). SeqOthello proposes to group similar color profiles, then uses a suitable compression technique depending on the sparsity of each group. It may wrongly associate a data set to an alien k-mer, instead of correctly returning that such k-mer belongs to no data set. For a query that consists of many k-mers (such as genes or transcripts), errors can be mitigated because false positives are unlikely to all point to the same data set(s). This property will also be used in k-mer aggregative structures and will be further discussed in the section, “Background and method intuition.”
Recently, another construction strategy for color-aggregation was proposed in Bifrost (Holley and Melsted 2020). As in BLight and Pufferfish, Bifrost uses a compacted DBG (introduced in, e.g., Chikhi et al. 2016; Minkin et al. 2016; see Supplemental Box S2) to more efficiently represent the sequences than a set of individual k-mers. In addition, we note these methods are similar to Mantis and SeqOthello in terms of the underlying hash-based strategies, and the differences are detailed in Supplemental Box S6.
Other methods
Some techniques evade the above categorization and have focused on specific aspects of color-aggregative methods memory optimization. The growing number of colors (or classes) motivated works to further reduce space through lossy compression. In Metannot (Mustafa et al. 2019) and Multi-BRWT (Karasikov et al. 2019), the main contribution is not the data structure used to store the graph but the one used to store colors. Metannot explores two strategies for color compression. One of them is probabilistic: in order to reduce false positives, color sets queries are corrected by taking the intersection with other color sets from neighboring k-mers in the DBG. Multi-BRWT improves upon standard bit-encoding representation (such as RRR, EF).
Colored DBGs have been used to perform RNA-seq quantification (Patro et al. 2014, 2017; Bray et al. 2016) by associating colors to individual genes as opposed to data sets. Yet, such methods still require a pseudo-alignment step to recover abundance information from the reads. Recently, REINDEER (Marchet et al. 2020a) proposed a color-aggregative index which also records abundance, bypassing the need to align reads in order to recover abundances. It relies on BLight, to which it adds novel features in indexing and a more advanced color matrix with color classes and compression.
Queries
Given that current implementations use k-mers that fit within (extended) computer words (∼21–63), the query time bottleneck comes mainly from random memory accesses, neglecting the time taken to calculate and hash the k-mers. Hash-based methods perform very fast color queries: retrieving information relative to a single k-mer requires only a constant number of memory accesses. The methods whose underlying DBG is BOSS (e.g., Vari, Rainbowfish, Vari-Merge) are expected to show a lower throughput. Indeed, the retrieval of a k-mer requires on the order of k memory accesses.
k-mer aggregative methods
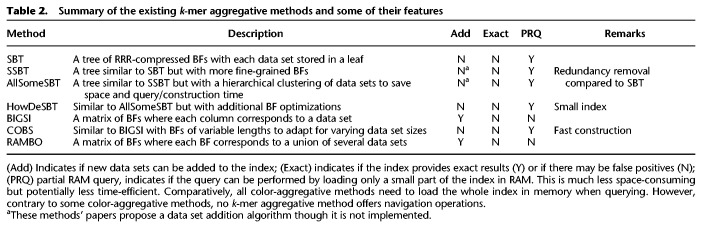
We now turn to a completely different class of data structures. Unlike previously mentioned methods, k-mer aggregative methods do not pool k-mers from all data sets in order to build an index. Rather, they first process data sets separately and then aggregate them in different ways. A summary of these methods’ features appears in Table 2.
Table 2.
Summary of the existing k-mer aggregative methods and some of their features
Background and method intuition
All the k-mer aggregative methods surveyed work by storing the k-mers of each data set in a separate Bloom filter, that is, using one BF per data set. A BF is a probabilistic data structure that sometimes returns false positives; that is, the BF may report that a k-mer belongs to a certain data set when it really does not. In the query model that we defined in the section, “Query model,” the θ parameter allows to partially mitigate this problem by considering the results of multiple k-mer queries. Indeed, the false-positive rate for a sequence decreases exponentially with the number of k-mer queries (Solomon and Kingsford 2016; Bingmann et al. 2019). For the values of θ used in practice, the false-positive rate of an individual BF can be set as high as 50% without degradation of query performance on sequences that are much longer than k (Solomon and Kingsford 2016).
Prior to construction, unlike color-aggregative methods, most k-mer aggregative methods (except COBS) need to know in advance how large is the largest data set, in terms of the number of distinct k-mers, to ensure that BFs are appropriately sized. The common BF size is chosen according to a desired false-positive rate.
k-mer aggregative methods summary
Sequence Bloom Trees (SBTs)
These are a family of related techniques detailed across multiple publications (Solomon and Kingsford 2016, 2018; Sun et al. 2017; Harris and Medvedev 2020), adapted to bioinformatics from a previously known hierarchical structure of BFs (Bloofi) (Crainiceanu and Lemire 2015). The tree structure represents a hierarchical clustering of the data sets, for example, one obtained using k-mer similarity across data sets. In the original SBT (Solomon and Kingsford 2016), each leaf corresponds to an individual data set, and each internal node is a BF that represents all the k-mers of the data sets descendant from it. Split-Sequence Bloom Trees (SSBT) (Solomon and Kingsford 2018) and AllSomeSBT (Sun et al. 2017) simultaneously proposed to instead store two BFs per internal node, each one separately containing the k-mers present in (or, respectively, absent from) all the descendants. HowDeSBT (Harris and Medvedev 2020) further improved the space utilization and provided the first analytical analysis of the running time and memory usage of the various SBT approaches. These recent improvements (Sun et al. 2017; Solomon and Kingsford 2018; Harris and Medvedev 2020) greatly reduced the space and query time compared to the original SBT (see Supplemental Box S8 for a comparison of SBT flavors).
Matrix strategies
An orthogonal approach was proposed in BIGSI (Box 3B; Bradley et al. 2019). As a first approximation, BIGSI can be seen as the concatenation of many BFs, forming a color matrix. The matrix is stored in row-major order, that is, row-by-row, so that each row appears as a consecutive block and can be efficiently queried. A closely related work is presented as a part of DREAM-Yara (Dadi et al. 2018), where BFs are interleaved in order to efficiently retrieve the same position of several BFs (see Supplemental Box S8). BIGSI was later improved, speed- and memory-wise, by COBS (Bingmann et al. 2019).
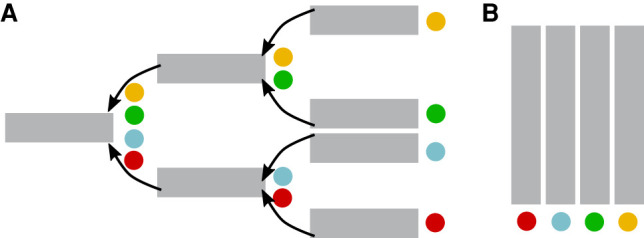
Box 3. Techniques for k-mer aggregation.
Data structures
In k-mer aggregative strategies, Bloom filters representing each of the data sets are organized in either a tree or a matrix structure. In the example below, there are four data sets (red, blue, green, and yellow), and the gray rectangles represent Bloom filters.
(A) Tree strategy. A search tree is constructed, where each leaf is a data set and internal nodes represent groups of data sets. Data sets with similar BFs can be clustered to reside in the same subtree. In the original SBT approach (Solomon and Kingsford 2016), each node stores exactly one BF, containing all the k-mers present in the data sets of its subtree. For a leaf, this is simply the k-mers in the corresponding data set. Later versions of SBTs (Sun et al. 2017; Solomon and Kingsford 2018; Harris and Medvedev 2020) store more sophisticated data at each node, though they still rely on BFs.
(B) Matrix strategy. The BFs from all the data sets are concatenated column-wise to obtain a matrix similar to a color matrix. A row in the matrix roughly corresponds to a k-mer (more precisely, to the position indicated by the hash value of a k-mer). In the original BIGSI approach (Bradley et al. 2019), all BFs have exactly the same size. In COBS (Bingmann et al. 2019), data sets of comparable cardinality are grouped into bins, leading to a collection of matrices of different sizes.
Queries
Consider an example query composed of three k-mers with a threshold θ = 2/3, where, for simplicity, each k-mer corresponds to a single location in the BF.
(A) Tree strategy. Conceptually, one starts at the root node and then explores down the tree, always checking all the children of a node before moving to another node (breadth-first strategy). A counter of k-mers that have been determined to be present or absent is maintained for the query as it propagates down the tree. If either of the counters exceeds a certain threshold, the search does not propagate further down the subtree of that node. For example, in panel A below, black bars in the BF represent the presence of three queried k-mers. Considering that θ = 2/3 of the k-mers should be present, the query is pruned at the yellow/green nodes because not enough present k-mers are found. Only the red data set is returned as containing the query.
(B) Matrix strategy. In BIGSI, each k-mer corresponds to a single row in the matrix, which is then extracted and summed column by column to obtain a vector where each element contains the number of k-mers occurring in the corresponding data set. Again, in panel B below, black bars in the BF represent the presence of three queried k-mers. The red data set will be the only one returned as containing the query.
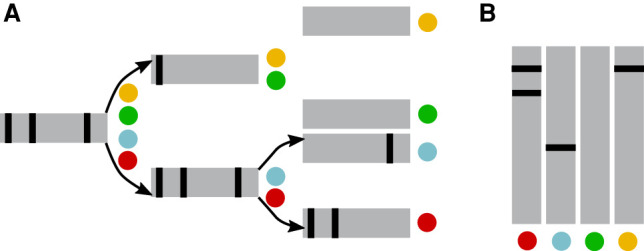
Detailed examples can be found in Supplemental Box S7. RAMBO (Yan et al. 2019) appears, at first glance, related to BIGSI, as it is also a matrix of BFs. However, RAMBO is actually closer to SBTs: each BF in the RAMBO matrix represents several data sets but not in a hierarchical fashion. More details are provided in the Supplemental Files and Supplemental Box S8.
Queries
In SBTs, a query containing several k-mers Q starts at the root and propagates down the tree. At any node, the information stored at that node is used to determine which k-mers of Q are determined in all descendants of the node. Depending on the SBT flavor, a determined k-mer may be for sure present, or for sure absent, in all descendants. The k-mers which are determined are discarded from Q as the query propagates down the tree (see Box 3). When enough k-mers become determined, the search can be pruned, that is, not carried further down the tree.
In matrix approaches, a k-mer query extracts a bit vector indicating its presence across (see Box 3). For a set of k-mers Q, the bit vector for each k-mer in Q is constructed, and bitwise operations on these vectors are performed to answer the whole query.
Other schemes
Other unpublished tools have considered different techniques for storing and indexing sets of k-mer sets. kamix (https://github.com/jaudoux/kamix) uses SAMtools's BGZF library (block-compressed gzip) to store and index a k-mer matrix. From the same author, kad (https://github.com/jaudoux/kad) uses a RocksDB database to store a list of k-mers and counts.
BEETL (Cox et al. 2012) is a technique that stores inside a BWT all sequences (i.e., not k-mers, but the original data) from a sequencing data set. BEETL was able to compress and index 135 GB of raw sequencing data into an 8.2-GB space (on disk for storage, or in memory for queries). A variant, BEETL-fastq (Janin et al. 2014), also enabled the performance of efficient sequences searches and was also applied to the representation of multiple data sets.
Population BWT (Dolle et al. 2017) is also a scheme based on BWT geared toward the indexing of thousands of raw sequencing data sets. The BWT allows querying k-mers of any length and additionally gives access to the position of each k-mer occurrence within the original reads (note, however, that reads need to be error-corrected).
Recently, compressed structures able to compress full-text were proposed as proofs-of-concept for indexing and querying collections of biological data sets (Cobas et al. 2020) for presence/absence and abundance. However, at the time of this writing, such indices have been tested on a few dozens of close bacterial strains, not yet on raw reads data.
Performances overview
Index construction on human RNA-seq samples
Indexing data sets of a similar type, such as RNA-seq samples from the same species, was one of the first applications proposed in the literature of sets of k-mer sets and remains one of the main benchmarks for these tools. Table 3, based on Supplemental Tables S1 and S2, reports the performance of most of the recent tools on a collection of human RNA-seq data sets (2652 RNA-seqs from the original SBT article [https://www.cs.cmu.edu/~ckingsf/software/bloomtree/srr-list.txt]). This table was constructed by gathering results from three recent articles (Yu et al. 2018; Bradley et al. 2019; Harris and Medvedev 2020). As the articles use different hardware and slightly different parameters, a direct comparison of the tools is challenging. Instead, Table 3 presents a summary of the best possible performance that can be currently achieved on the given data sets. Supplemental Table S3 also presents a summary of the methods’ time complexities.
Table 3.
Overview of the best achievable performance in terms of space and time requirements to build indices
The data processing time column refers to the time necessary to convert the original sequence files to the k-mer set indices (Bloom filters/Othello). The maximum external memory column corresponds to the peak disk usage when building the index. The time column is the time required to build the set of k-mer sets index (on one processor). The index size column is the final index size.
The data processing phase, where the k-mer sets are constructed and initialized, often takes significant time across all methods. It is usually not presented as a bottleneck because it is viewed that this step can be computed while downloading the samples.
Regarding query times, each method has used different experimental setups, making comparisons difficult, for example, using transcript batches of different sizes (100−10,000). We refer the reader to the experimental benchmark in Harris and Medvedev (2020), which compares the average query times for randomly selected batches, effects of warming the cache, and maximum peak memory for queries. Finally, we note that the information output by a query can vary from one implementation to another and that the maximum supported value for k-mer size is also implementation-dependent.
Indexing bacterial genomes
We now turn to the indexing of large collections of bacterial data sets. Table 3 summarizes the benchmark published in the COBS article (Bingmann et al. 2019). Methods that were reported to perform the best in the previous section remain the most efficient, and most recent methods tend to show the best performance. BIGSI, AllSomeSBT, and COBS queries are fast. We note that COBS construction time is very low (< 1 min), in part because it has been run using 80 threads. SSBT and COBS also have low RAM consumption. An advantage of HowDeSBT is the small size of the index on disk. This demonstrates that highly diverse data sets, in terms of k-mer contents, can also be efficiently stored in variants of SBTs.
Indexing human genome sequencing data
To the best of our knowledge, only two methods (BEETL-fastq and Population BWT) have been applied to the representation of full read information from cohorts of whole human genomes. BEETL-fastq represented 6.6 TB of human reads in FASTQ format in 1.7 TB of indexed files. Population BWT managed to index (in a lossy way) 87 Tbp of data, corresponding to 922 billion reads from the 1000 Genomes Project. After read correction and trimming, the authors obtained a set of 53 billion distinct reads (4.9 Tbp) and indexed it with a BWT stored with 464 GB on disk (requiring 561 GB of main memory for query). Metadata (e.g., sample information for each read) was stored in a 4.75-TB database.
Given the apparent difficulty of constructing large-scale indices on human sequencing data sets, we conclude that this is not yet a mature operation. Therefore, we did not provide a detailed comparison with other indexing techniques.
Discussion
General observations can be derived from the comparison we have presented in this survey.
SBT approaches were designed for collections with high k-mer redundancy, such as human RNA-seq. In contrast, BIGSI and COBS focused on indexing heterogeneous k-mer sets, such as k-mers originating from various bacteria. Experiments in Bingmann et al. (2019) demonstrated that SBTs like HowDeSBT could also perform well on this type of data. A trade-off exists between the construction time in favor of COBS and index size in favor of the SBTs. As shown in the COBS paper, resizing BFs allows saving memory, but the latest SBT flavors also have a lightweight memory footprint because compressing BFs can achieve a similar effect as resizing. Smaller BFs also increased the false-positive rate of COBS in comparison to other BF-based techniques (Bingmann et al. 2019).
It is also important to note that, for many methods, queries are approximate, although a number of color-aggregative methods support exact queries. Some colored DBG implementations (Vari and Vari-Merge) support additional features such as SNP and short variant discovery and graph traversal. New query types should also be considered. For instance, recording k-mer counts (with REINDEER) instead of presence or absence is likely to assist gene expression studies.
Color-aggregative methods and BIGSI/COBS seem better suited to query large sequences. Indeed, in these methods, the bottleneck for a single query is loading the index into memory. Then, the rest of the query consists in hashing k-mers, roughly in constant time per each k-mer. Henceforward, once the index is loaded in memory, batches of queries or large queries can be answered very rapidly. Query speeds depend on the method and its implementation. For instance, in some data structures such as the CQF in Mantis, consecutive k-mers are likely to appear nearby in memory, thus reducing the number of cache misses during a query. A drawback is that these structures are usually more memory-consuming than SBTs. Moreover, in the case of SBTs, BIGSI, and COBS, large queries allow mitigation of the underlying BF false-positive rate. SBTs and COBS do not need to load the entirety of the index into memory at query time because the query iteratively prunes irrelevant data sets. That is why SBTs are more suitable for short queries, whereas for large queries, k-mer look-ups become a bottleneck. For very large queries (e.g., the k-mers from a whole sequencing experiment), only AllSomeSBT (Sun et al. 2017) has an efficient specialized algorithm. The type of queries proposed by Solomon and Kingsford (2016), which has been widely adopted across SBT flavors, relies on the threshold θ to determine if a sequence matches a data set. This threshold controls the sensitivity of matches with respect to sequence identity and sequencing errors. It would benefit from being further explored from a biological point of view. For instance, a single substitution in a base is covered by k different k-mers. If the indexed sequences differ from the query on that substitution, these k-mers will not be found in the structure, and if the value of θ is too high, the match could be missed.
Although there have been extensive empirical benchmarks to compare the performance of the different methods, analytical comparisons of their performance have been limited (see Harris and Medvedev 2020 for an example, though it is limited to only SBTs). The difficulty in using worst-case analysis to analyze performance in this case is that the methods are really designed to exploit the properties of real collections, and worst-case analysis is therefore not helpful. Progress can be made by coming up with appropriate models to capture the essential properties of real data and analyzing the methods using those models.
We note that there are several issues that lie outside this survey but merit mention the selection of k and the presence of sequencing errors. The value of k is well-known to control sensitivity and specificity of the methods. Too small of a value of k decreases the sensitivity and too large of a value of k decreases the specificity. Automatically selecting the best k value was studied in the context of genome assembly (Chikhi and Medvedev 2014) but, to the best of our knowledge, not yet for indexing collections of read data sets. An additional issue related to this survey is the presence or absence of sequencing errors, which result in k-mers that have a low number of occurrences. To address this issue, some methods (such as Cortex) filter k-mers with a low frequency by default, whereas others require user intervention.
The data structures surveyed in this paper should be seen as initial attempts from the community toward being able to routinely query the hundreds of thousands of samples deposited in public repositories (e.g., SRA) or private ones. An essential next step would be to have user-friendly tools. User friendliness can be seen from different perspectives. First, one may try to cast more concrete biological questions into simplified k-mer queries that can then be asked to the indices. Second, the results of queries could be presented in a manner that is more suitable to biologists rather than their current form, consisting mainly of the output of k-mer queries. For instance, a list of reads contained in the indexed data sets could be output for further investigation. However, indexing reads is more challenging, and this direction would require new developments for the structures to scale. Third, special attention given to user interfaces could help broaden the usage of these methods. Web interfaces are challenging to maintain in the long run (the group maintaining BIGSI proposed one: http://www.bigsi.io/); thus, another solution could be to provide offline precomputed indices. This way, users would only download some chunks of interest from the index for further investigation.
Competing interest statement
The authors declare no competing interests.
Supplementary Material
Acknowledgments
This work was supported by ANR Transipedia (ANR-18-CE45-0020) and INCEPTION (PIA/ANR-16-CONV-0005). This material is based upon work supported by the National Science Foundation under Grants No. 1453527 and 1439057 to P.M. This work was supported by the National Science Foundation under Grant No. 1618814 and the National Institutes of Health, National Institute of Allergy and Infectious Diseases Grant No. R01AI141810-01 to C.B. We thank Jan Holub for feedback on the BOSS section and Daniel Gautheret for his comments and corrections.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.260604.119.
References
- Almeida A, Nayfach S, Boland M, Strozzi F, Beracochea M, Shi ZJ, Pollard KS, Sakharova E, Parks DH, Hugenholtz P, et al. 2020. A unified catalog of 204,938 reference genomes from the human gut microbiome. Nat Biotechnol 10.1038/s41587-020-0603-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almodaresi F, Pandey P, Patro R. 2017. Rainbowfish: a succinct colored de Bruijn graph representation. In Proceedings of the Seventeenth International Workshop on Algorithms in Bioinformatics, Boston Dagstuhl Publishing, Saarbrücken/Wadern, Germany. [Google Scholar]
- Almodaresi F, Sarkar H, Srivastava A, Patro R. 2018. A space and time-efficient index for the compacted colored de Bruijn graph. Bioinformatics 34: i169–i177. 10.1093/bioinformatics/bty292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almodaresi F, Pandey P, Ferdman M, Johnson R, Patro R. 2019. An efficient, scalable and exact representation of high-dimensional color information enabled via de Bruijn graph search. In Proceedings of the International Conference on Research in Computational Molecular Biology, Washington, pp. 1–18. Springer, New York. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender MA, Farach-Colton M, Johnson R, Kraner R, Kuszmaul BC, Medjedovic D, Montes P, Shetty P, Spillane RP, Zadok E. 2012. Don't thrash: how to cache your hash on flash. PVLDB 5: 1627–1637. [Google Scholar]
- Bingmann T, Bradley P, Gauger F, Iqbal Z. 2019. COBS: a COmpact Bit-sliced Signature index. In Proceedings of the Twenty-sixth Int'l Symposium on String Processing and Information Retrieval, Segovia, Spain, pp. 285−303. [Google Scholar]
- Blackwell G, Iqbal Z, Thomson N. 2019. Evolution and spread of bacterial transposons. Access Microbiol 1 10.1099/acmi.ac2019.po0568 [DOI] [Google Scholar]
- Bloom BH. 1970. Space/time trade-offs in hash coding with allowable errors. Commun ACM 13: 422–426. 10.1145/362686.362692 [DOI] [Google Scholar]
- Boucher C, Bowe A, Gagie T, Puglisi SJ, Sadakane K. 2015. Variable-order de Bruijn graphs. In Proceedings of the 2015 Data Compression Conference, Snowbird, Utah, pp. 383–392. [Google Scholar]
- Bowe A, Onodera T, Sadakane K, Shibuya T. 2012. Succinct de Bruijn graphs. In Proceedings of the Twelfth International Workshop on Algorithms in Bioinformatics, Ljubljana, Slovenia, pp. 225–235. Springer, New York. [Google Scholar]
- Bradley P, den Bakker HC, Rocha EP, McVean G, Iqbal Z. 2019. Ultrafast search of all deposited bacterial and viral genomic data. Nat Biotechnol 37: 152–159. 10.1038/s41587-018-0010-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray NL, Pimentel H, Melsted P, Pachter L. 2016. Near-optimal probabilistic RNA-seq quantification. Nat Biotechnol 34: 525–527. 10.1038/nbt.3519 [DOI] [PubMed] [Google Scholar]
- Byron SA, Van Keuren-Jensen KR, Engelthaler DM, Carpten JD, Craig DW. 2016. Translating RNA sequencing into clinical diagnostics: opportunities and challenges. Nature Reviews Genetics 17: 257–271. 10.1038/nrg.2016.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi R, Medvedev P. 2014. Informed and automated k-mer size selection for genome assembly. Bioinformatics 30: 31–37. 10.1093/bioinformatics/btt310 [DOI] [PubMed] [Google Scholar]
- Chikhi R, Rizk G. 2013. Space-efficient and exact de Bruijn graph representation based on a Bloom filter. Algorithms Mol Biol 8: 22 10.1186/1748-7188-8-22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi R, Limasset A, Medvedev P. 2016. Compacting de Bruijn graphs from sequencing data quickly and in low memory. Bioinformatics 32: i201–i208. 10.1093/bioinformatics/btw279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi R, Holub J, Medvedev P. 2019. Data structures to represent a set of k-long DNA sequences. arXiv:1903.12312 [cs.DS].
- Clarke L, Zheng-Bradley X, Smith R, Kulesha E, Xiao C, Toneva I, Vaughan B, Preuss D, Leinonen R, Shumway M, et al. 2012. The 1000 Genomes Project: data management and community access. Nat Methods 9: 459–462. 10.1038/nmeth.1974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobas D, Mäkinen V, Rossi M. 2020. Tailoring r-index for metagenomics. arXiv:2006.05871v1 [cs.DS].
- Cook CE, Lopez R, Stroe O, Cochrane G, Brooksbank C, Birney E, Apweiler R. 2019. The European Bioinformatics Institute in 2018: tools, infrastructure and training. Nucleic Acids Res 47: D15–D22. 10.1093/nar/gky1124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox AJ, Bauer MJ, Jakobi T, Rosone G. 2012. Large-scale compression of genomic sequence databases with the Burrows–Wheeler transform. Bioinformatics 28: 1415–1419. 10.1093/bioinformatics/bts173 [DOI] [PubMed] [Google Scholar]
- Crainiceanu A, Lemire D. 2015. Bloofi: multidimensional Bloom filters. Inf Syst 54: 311–324. 10.1016/j.is.2015.01.002 [DOI] [Google Scholar]
- Dadi TH, Siragusa E, Piro VC, Andrusch A, Seiler E, Renard BY, Reinert K. 2018. DREAM-Yara: an exact read mapper for very large databases with short update time. Bioinformatics 34: i766–i772. 10.1093/bioinformatics/bty567 [DOI] [PubMed] [Google Scholar]
- Dolle DD, Liu Z, Cotten M, Simpson JT, Iqbal Z, Durbin R, McCarthy SA, Keane TM. 2017. Using reference-free compressed data structures to analyze sequencing reads from thousands of human genomes. Genome Res 27: 300–309. 10.1101/gr.211748.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elias P. 1974. Efficient storage and retrieval by content and address of static files. Journal of the ACM 21: 246–260. 10.1145/321812.321820 [DOI] [Google Scholar]
- Fano RM. 1971. On the number of bits required to implement an associative memory. In Computation Structures Group Memo, Vol. 61 MIT Project MAC Computer Structures Group, Cambridge, MA. [Google Scholar]
- Grossi R, Ottaviano G. 2012. The wavelet trie: maintaining an indexed sequence of strings in compressed space. In Proceedings of the Thirty-first ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, Scottsdale, AZ, pp. 203–214. [Google Scholar]
- Grossi R, Gupta A, Vitter JS. 2003. High-order entropy-compressed text indexes. In Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, pp. 841.–. Society for Industrial and Applied Mathematics, Philadelphia. [Google Scholar]
- Harris RS, Medvedev P. 2020. Improved representation of sequence bloom trees. Bioinformatics 36: 721–727. 10.1093/bioinformatics/btz662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holley G, Melsted P. 2020. Bifrost: highly parallel construction and indexing of colored and compacted de Bruijn graphs. Genome Biol 21: 249 10.1186/s13059-020-02135-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holley G, Wittler R, Stoye J. 2016. Bloom Filter Trie: an alignment-free and reference-free data structure for pan-genome storage. Algorithms Mol Biol 11: 3 10.1186/s13015-016-0066-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iqbal Z, Caccamo M, Turner I, Flicek P, McVean G. 2012. De novo assembly and genotyping of variants using colored de Bruijn graphs. Nat Genet 44: 226–232. 10.1038/ng.1028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janin L, Schulz-Trieglaff O, Cox AJ. 2014. BEETL-fastq: a searchable compressed archive for DNA reads. Bioinformatics 30: 2796–2801. 10.1093/bioinformatics/btu387 [DOI] [PubMed] [Google Scholar]
- Karasikov M, Mustafa H, Joudaki A, Javadzadeh-No S, Rätsch G, Kahles A. 2019. Sparse binary relation representations for genome graph annotation. In Proceedings of the International Conference on Research in Computational Molecular Biology, Washington, pp. 120–135. Springer, New York. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lappalainen T, Sammeth M, Friedländer MR, ‘t Hoen PAC, Monlong J, Rivas MA, Gonzàlez-Porta M, Kurbatova N, Griebel T, Ferreira PG, et al. 2013. Transcriptome and genome sequencing uncovers functional variation in humans. Nature 501: 506–511. 10.1038/nature12531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leinonen R, Sugawara H, Shumway M, on behalf of the International Nucleotide Sequence Database Collaboration. 2011. The Sequence Read Archive. Nucleic Acids Res 39: D19–D21. 10.1093/nar/gkq1019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemire D, Ssi-Yan-Kai G, Kaser O. 2016. Consistently faster and smaller compressed bitmaps with Roaring. Softw Pract Exp 46: 1547–1569. 10.1002/spe.2402 [DOI] [Google Scholar]
- Luhmann N, Holley G, Achtman M. 2020. BlastFrost: fast querying of 100,000 s of bacterial genomes in Bifrost graphs. bioRxiv 10.1101/2020.01.21.914168 [DOI] [PMC free article] [PubMed]
- Marçais G, Solomon B, Patro R, Kingsford C. 2019. Sketching and sublinear data structures in genomics. Ann Rev of Biomed Data Sci 2: 93−118. 10.1146/annurev-biodatasci-072018-021156 [DOI] [Google Scholar]
- Marchet C, Iqbal Z, Gautheret D, Salson M, Chikhi R. 2020a. REINDEER: efficient indexing of k-mer presence and abundance in sequencing datasets. In Proceedings of the 28th Annual Conference on Intelligent Systems for Molecular Biology, Montreal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchet C, Kerbiriou M, Limasset A. 2020b. Efficient exact associative structure for sequencing data. bioRxiv 10.1101/546309 [DOI] [PubMed]
- The MetaSUB International Consortium. 2016. The Metagenomics and Metadesign of the Subways and Urban Biomes (MetaSUB) International Consortium inaugural meeting report. Microbiome 4: 24 10.1186/s40168-016-0168-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EA, Elnekave E, Flores-Figueroa C, Johnson A, Kearney A, Munoz-Aguayo J, Tagg KA, Tschetter L, Weber BP, Nadon CA, et al. 2020. Emergence of a novel Salmonella enterica serotype reading clonal group is linked to its expansion in commercial turkey production, resulting in unanticipated human illness in North America. mSphere 5: e00056-20 10.1128/mSphere.00056-20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minkin I, Pham S, Medvedev P. 2016. TwoPaCo: an efficient algorithm to build the compacted de Bruijn graph from many complete genomes. Bioinformatics 33: 4024–4032. 10.1093/bioinformatics/btw609 [DOI] [PubMed] [Google Scholar]
- Muggli MD, Bowe A, Noyes NR, Morley PS, Belk KE, Raymond R, Gagie T, Puglisi SJ, Boucher C. 2017. Succinct colored de Bruijn graphs. Bioinformatics 33: 3181–3187. 10.1093/bioinformatics/btx067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muggli MD, Alipanahi B, Boucher C. 2019. Building large updatable colored de Bruijn graphs via merging. Bioinformatics 35: i51–i60. 10.1093/bioinformatics/btz350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustafa H, Schilken I, Karasikov M, Eickhoff C, Rätsch G, Kahles A. 2019. Dynamic compression schemes for graph coloring. Bioinformatics 35: 407–414. 10.1093/bioinformatics/bty632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ondov BD, Treangen TJ, Melsted P, Mallonee AB, Bergman NH, Koren S, Phillippy AM. 2016. Mash: fast genome and metagenome distance estimation using MinHash. Genome Biol 17: 132 10.1186/s13059-016-0997-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottaviano G, Venturini R. 2014. Partitioned Elias-Fano indexes. In Proceedings of the Thirty-seventh International ACM SIGIR Conference on Research and Development in Information Retrieval, Gold Coast, QLD, Australia, pp. 273.–. ACM, New York. [Google Scholar]
- Pandey P, Bender MA, Johnson R, Patro R. 2017. A general-purpose counting filter: making every bit count. In Proceedings of the 2017 ACM International Conference on Management of Data, Chicago, pp. 775.–. ACM, New York. [Google Scholar]
- Pandey P, Almodaresi F, Bender MA, Ferdman M, Johnson R, Patro R. 2018. Mantis: a fast, small, and exact large-scale sequence-search index. Cell Syst 7: 201–207.e4. 10.1016/j.cels.2018.05.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patro R, Mount SM, Kingsford C. 2014. Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms. Nat Biotechnol 32: 462–464. 10.1038/nbt.2862 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patro R, Duggal G, Love MI, Irizarry RA, Kingsford C. 2017. Salmon provides fast and bias-aware quantification of transcript expression. Nat Methods 14: 417–419. 10.1038/nmeth.4197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman R, Raman V, Rao SS. 2002. Succinct indexable dictionaries with applications to encoding k-ary trees and multisets. In Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, pp. 233–242. ACM/SIAM, New York: /Philadelphia. [Google Scholar]
- Singhal S, Leffler EM, Sannareddy K, Turner I, Venn O, Hooper DM, Strand AI, Li Q, Raney B, Balakrishnan CN, et al. 2015. Stable recombination hotspots in birds. Science 350: 928–932. 10.1126/science.aad0843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon B, Kingsford C. 2016. Fast search of thousands of short-read sequencing experiments. Nat Biotechnol 34: 300–302. 10.1038/nbt.3442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon B, Kingsford C. 2018. Improved search of large transcriptomic sequencing databases using split sequence bloom trees. J Comput Biol 25: 755–765. 10.1089/cmb.2017.0265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C, Harris RS, Chikhi R, Medvedev P. 2017. Allsome Sequence Bloom Trees. In Proceedings of the Twenty-first Annual International Conference on Research in Computational Molecular Biology, Hong Kong, China, Vol. 10229, pp. 272–286. [Google Scholar]
- Timme RE, Rand H, Leon MS, Hoffmann M, Strain E, Allard M, Roberson D, Baugher JD. 2018. GenomeTrakr proficiency testing for foodborne pathogen surveillance: an exercise from 2015. Microb Genom 4: e000185 10.1099/mgen.0.000185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomczak K, Czerwińska P, Wiznerowicz M. 2015. The Cancer Genome Atlas (TCGA): an immeasurable source of knowledge. Contemp Oncol 19: A68–A77. 10.5114/wo.2014.47136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbull C, Scott RH, Thomas E, Jones L, Murugaesu N, Pretty FB, Halai D, Baple E, Craig C, Hamblin A, et al. 2018. The 100,000 Genomes Project: bringing whole genome sequencing to the NHS. BMJ 361: k1687 10.1136/bmj.k1687 [DOI] [PubMed] [Google Scholar]
- Wittler R. 2020. Alignment- and reference-free phylogenomics with colored de Bruijn graphs. Algorithms Mol Biol 15: 4 10.1186/s13015-020-00164-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DE, Salzberg SL. 2014. Kraken: ultrafast metagenomic sequence classification using exact alignments. Genome Biol 15: R46 10.1186/gb-2014-15-3-r46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan M, Gupta G, Coleman B, Treangen T, Shrivastava A. 2019. Sub-linear sequence search via a repeated and merged Bloom filter (RAMBO): indexing 170 TB data in 14 hours. arXiv:1910.04358 [q-bio.GN].
- Young BC, Golubchik T, Batty EM, Fung R, Larner-Svensson H, Votintseva AA, Miller RR, Godwin H, Knox K, Everitt RG, et al. 2012. Evolutionary dynamics of Staphylococcus aureus during progression from carriage to disease. Proc Natl Acad Sci USA 109: 4550–4555. 10.1073/pnas.1113219109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y, Liu J, Liu X, Zhang Y, Magner E, Lehnert E, Qian C, Liu J. 2018. SeqOthello: querying RNA-seq experiments at scale. Genome Biol 19: 167 10.1186/s13059-018-1535-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.