Greater strength of selection and higher proportion of beneficial amino acid changing mutations in humans compared with mice and Drosophila melanogaster

Abstract

Quantifying and comparing the amount of adaptive evolution among different species is key to understanding how evolution works. Previous studies have shown differences in adaptive evolution across species; however, their specific causes remain elusive. Here, we use improved modeling of weakly deleterious mutations and the demographic history of the outgroup species and ancestral population and estimate that at least 20% of nonsynonymous substitutions between humans and an outgroup species were fixed by positive selection. This estimate is much higher than previous estimates, which did not correct for the sizes of the outgroup species and ancestral population. Next, we jointly estimate the proportion and selection coefficient (p⁺ and s⁺, respectively) of newly arising beneficial nonsynonymous mutations in humans, mice, and Drosophila melanogaster by examining patterns of polymorphism and divergence. We develop a novel composite likelihood framework to test whether these parameters differ across species. Overall, we reject a model with the same p⁺ and s⁺ of beneficial mutations across species and estimate that humans have a higher p⁺s⁺ compared with that of D. melanogaster and mice. We show that this result cannot be caused by biased gene conversion or hypermutable CpG sites. We discuss possible biological explanations that could generate the observed differences in the amount of adaptive evolution across species.

Since the inception of molecular population genetics, there has been tremendous interest in quantifying the amount of adaptive evolution in different organisms. The neutral theory of molecular evolution postulated that beneficial mutations are rare and that many of the substitutions between species are neutral (Kimura 1983). One early challenge to this theory originated from a comparison of polymorphisms and divergence at synonymous and nonsynonymous sites in Drosophila (Fay et al. 2002; Smith and Eyre-Walker 2002). Under neutral models, the ratio of nonsynonymous to synonymous changes should remain equal when comparing polymorphisms (i.e., differences within species) and divergence (i.e., differences between species). In contrast to this prediction, a genome-wide excess of nonsynonymous divergence between species was observed, a pattern indicative of an abundance of positive selection in Drosophila. Smith and Eyre-Walker (2002) proposed a statistic, α, which is the proportion of nonsynonymous substitutions between species that can be attributed to positive selection. Their approach has found that at least 40% of nonsynonymous substitutions have been fixed by positive selection in Drosophila (Smith and Eyre-Walker 2002).

Since the publication of the original study, α has been estimated from different species across the tree of life (Fay 2011). Estimates of α vary tremendously across species, tending to be higher in insects (Andolfatto 2005; Eyre-Walker and Keightley 2009) but much lower in primates and plants (Boyko et al. 2008; Eyre-Walker and Keightley 2009; Gossmann et al. 2010). In these latter species, formal tests have been unable to reject the hypothesis that α is zero (i.e., no positive selection) (Boyko et al. 2008; Foxe et al. 2008; Eyre-Walker and Keightley 2009). It is not clear why α varies across species. One possibility is that α is higher for species with larger population sizes, which could occur if adaptation is mutation limited. Here, species with larger population sizes would have a higher rate of beneficial mutations. The fixation probability of a given beneficial mutation also would be higher in species with larger population size, but this effect is likely to only be important for very weakly beneficial mutations. Evidence indicates that, in some cases, α is correlated with population size. For example, Phifer-Rixey et al. (2012) found that estimates of α were higher for species of mice that have larger population sizes compared with species with smaller population sizes. Further, there is a positive correlation between α and population size when comparing different species of sunflowers (Strasburg et al. 2011) and from phylogenetically diverse taxa (Gossmann et al. 2012). More recently, Galtier (2016) found a positive correlation between α and effective population size for 44 animal species. Additional evidence that there is more positive selection in larger populations stems from analyses of selection at linked sites. Corbett-Detig et al. (2015) found increased evidence for selection at linked sites in species with larger population sizes, although the mechanism driving this pattern is not entirely clear. Further, Nam et al. (2017) have suggested that across primates, species with larger population sizes experienced more selective sweeps.

Although evidence suggests that adaptation could be mutation limited and that this could be driving the variation in α across species, other factors can influence the α statistic (Messer and Petrov 2013; Rousselle et al. 2018). As the denominator of α is the total number of observed differences between species, it is sensitive to the fixation of weakly deleterious mutations. For two populations with the same number of beneficial substitutions, the one with a higher number of substitutions owing to weakly deleterious mutations will have a lower α. Indeed, because the number of fixed weakly deleterious mutations is inversely related to population size (Ohta 1973, 1992), this effect could drive the correlation between α and population size. In support of this prediction, Galtier (2016) found that the rate of adaptive divergence relative to neutral divergence (omega-a) (Gossmann et al. 2012) showed no correlation with population size. Similar arguments have been made by Phifer-Rixey et al. (2012). Further, for humans, it has been suggested that α has been underestimated owing to the presence of weakly beneficial mutations segregating as polymorphisms (Galtier 2016; Uricchio et al. 2019). Indeed, methods that account for weakly beneficial mutations segregating as polymorphisms infer slightly higher values of α = 0.24 between humans and chimpanzee and α = 0.135 in the human lineage (Galtier 2016; Uricchio et al. 2019). In addition, population sizes of the outgroup and ancestral population determine the rate of fixation of weakly deleterious mutations in the outgroup lineage and in the ancestral population and could potentially influence the estimate of α (McDonald and Kreitman 1991; Eyre-Walker 2002; Rousselle et al. 2018).

Other studies quantified positive selection by focusing on the proportion of beneficial mutations (p⁺) and their selection coefficients (s⁺). Boyko et al. (2008) found that by assuming a fraction (0%–1.86%) of new mutations is positively selected, they could better match the frequency spectrum of polymorphisms and the counts of human–chimpanzee divergence. Models with weaker selection coefficients for beneficial mutations tended to have a higher proportion of positively selected mutations than models with stronger selection (Boyko et al. 2008). Several studies also have estimated p⁺ and s⁺ in Drosophila species and mice (Sella et al. 2009; Schneider et al. 2011; Elyashiv et al. 2016; Keightley et al. 2016; Campos et al. 2017; Booker and Keightley 2018). However, there has not been a systematic comparison across species.

Here we compare the amount of adaptive evolution in primates, rodents, and Drosophila. We use two complementary approaches that quantify different aspects of the adaptive process. First, we use improved modeling of weakly deleterious mutations and demographic models, particularly correcting for the sizes of outgroup species and ancestral population to infer α. Second, we jointly estimate p⁺ and s⁺ of newly arising beneficial mutations by examining patterns of polymorphism and divergence. We develop a composite likelihood framework to test whether these parameters differ across taxa. This approach enables a more direct comparison of beneficial mutations across species and is less confounded by the fixation of weakly deleterious mutations.

Results

Estimates of α for multiple species using the MK method

We first estimated α from coding regions of primates, rodents, and Drosophila. We analyzed published genomic data sets to obtain counts of synonymous and nonsynonymous polymorphisms (P_S and P_N) and divergent sites between species (D_S and D_N). For computation of α in humans, we used chimpanzee and macaque as outgroup species. For mice and D. melanogaster, we used rat and Drosophila simulans as the outgroup species, respectively.

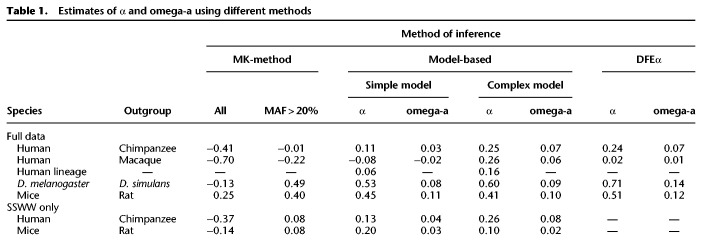
An extension of the McDonald–Kreitman (MK) test was used to estimate α (Table 1; Supplemental Table S1; Smith and Eyre-Walker 2002). To examine the effect of slightly deleterious mutations on α, we filtered the data with several minor allele frequency (MAF) cutoffs (Supplemental Table S2; Fay et al. 2001; Charlesworth and Eyre-Walker 2008; Messer and Petrov 2013). For example, after removing low-frequency polymorphisms with MAF <20%, the estimated α is close to zero for the human–chimpanzee comparison (Table 1), consistent with previous estimates (Boyko et al. 2008; Eyre-Walker and Keightley 2009). However, for the human–macaque comparison, α is −0.22 (Table 1), suggesting that the choice of outgroup species could greatly influence α. In contrast, for the D. melanogaster–D. simulans and mouse–rat comparisons, the estimated values of α are 49% and 40%, respectively, with the MAF filter at 20% (Table 1). Both of these estimates are comparable to previous studies (Andolfatto 2005; Eyre-Walker and Keightley 2009; Phifer-Rixey et al. 2012). These results suggest that the proportion of substitutions fixed by positive selection varies drastically across species.

Table 1.

Estimates of α and omega-a using different methods

Model-based inference of α

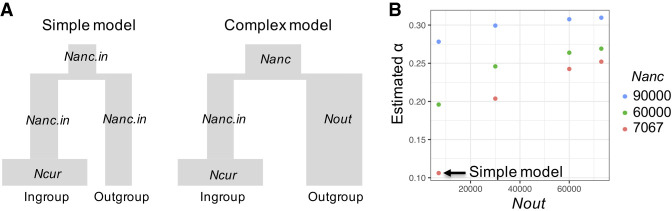
Model-based approaches estimate α by contrasting the observed number of nonsynonymous differences between species (D_NO) with the number expected under a demographic model and a distribution of fitness effects (DFE) including only neutral and deleterious mutations (D_NE) (Supplemental Table S3; Loewe et al. 2006; Boyko et al. 2008; Eyre-Walker and Keightley 2009; Haddrill et al. 2010). The excess of observed D_NO compared with the predicted D_NE is attributed to fixations driven by positive selection. These methods assume that the population sizes of outgroup species and the ancestral population of the ingroup and outgroup are the same as the ancestral size of the ingroup population (Nanc.in). We refer to this demographic model as the Simple model (Fig. 1A).

Figure 1.

The ancestral and outgroup population sizes greatly influence α. (A) Schematic demographic models illustrate the Simple and Complex models with associated parameters. In the Simple model, the size of the ancestral population (Nanc) and the size of the outgroup (Nout) are assumed to be the same as the ancestral size of the ingroup (Nanc.in). This assumption is relaxed in the Complex model. (B) Effect of Nanc and Nout on estimates of α for humans using the chimpanzee as an outgroup. Colors denote different values of Nanc. Arrow points to the estimate of α from the Simple model, where Nanc = Nout = Nanc.in = 7067.

By using the Simple model, we estimated that α = 11% for humans and chimpanzees. This estimate is comparable to the inference by Boyko et al. (2008). When we use macaque as the outgroup species, we estimated that α is negative (Table 1). Although it is possible that this difference could reflect distinct evolutionary events experienced by different outgroups, it could also be an artifact of the modeling assumptions. Previous estimates of the human–chimpanzee ancestral population size (Nanc) range from 12,000 to 125,000 using different data sets and methods (Chen and Li 2001; Hobolth et al. 2007; Burgess and Yang 2008; Prado-Martinez et al. 2013; Schrago 2014). The estimated chimpanzee population size (Nout) is around 30,000 (Supplemental Table S4; Fischer et al. 2004; Hvilsom et al. 2012; Prado-Martinez et al. 2013). However, the ancestral size inferred for the human lineage using human polymorphism data is 7067, which is much smaller than all previous estimates of Nanc and Nout. Using values of Nanc and Nout that are too small likely biases estimates of α because more of the nonsynonymous substitutions are incorrectly attributed to the fixation of weakly deleterious mutations, causing α to be underestimated.

To more accurately model the larger Nanc and Nout, we use the Complex model, which allows Nout and Nanc to differ from Nanc.in (Fig. 1A). For humans, the larger Nanc is very ancient; thus, it does not affect the polymorphism pattern within humans (confirmed by coalescent simulations) (see Supplemental Text). We calculated the number of substitutions fixed in the ingroup, outgroup, and ancestral populations (Methods). We first explored how Nout and Nanc affect the inferred α. For the human–chimpanzee comparison, the inferred α changes with different values of Nout and Nanc. Larger values result in larger estimates of α (Fig. 1B). For example, when Nout = 30,000 (Fischer et al. 2004; Hvilsom et al. 2012; Prado-Martinez et al. 2013) and Nanc = 60,000 (Chen and Li 2001; Hobolth et al. 2007; Prado-Martinez et al. 2013), supported by many previous studies (Supplemental Table S4), α is approximately 24.6%. When using other values of Nout and Nanc within the ranges of previous estimates (Supplemental Table S4), the corresponding estimates of α may differ, but remain above 20% (Fig. 1B). We next revisited the human–macaque comparison under the Complex model (Supplemental Fig. S1), using Nout = 73,000 (Hernandez et al. 2007; Xue et al. 2016), Nanc = 48,000 (McVicker et al. 2009), and changing the ingroup population size to 60,000 at human–chimpanzee divergence time to match what we modeled in human–chimpanzee (Supplemental Table S5). Here we infer that ∼26.0% of human–macaque nonsynonymous substitutions were fixed by positive selection, which is comparable to what we found for the human–chimpanzee analysis. These estimates of α for primates using the more realistic Complex demographic model are much higher than previous estimates, implying that there is a greater contribution of positive selection to nonsynonymous divergence than previously appreciated.

Similarly, we estimated α for Drosophila and rodents using the Complex demographic model. For Drosophila, it had been inferred that D. simulans have slightly larger N_e than D. melanogaster (Andolfatto et al. 2011), so we set Nout to be 1.5× the current population size of D. melanogaster (Ncur) at the species’ split (Supplemental Table S5). For mice, a previous study estimated that the outgroup rat species has an effective population size about fivefold lower than that of wild house mice (Ness et al. 2012). Thus, we set the Nout to be 0.2× Ncur of mice (Supplemental Table S5). Because there is limited knowledge of the population sizes of the ancestor of D. melanogaster and D. simulans and of the ancestor of mice and rat, for these two comparisons, we assume Nanc = Nout. By using these Complex models for D. melanogaster–D. simulans and mouse–rat, we estimated their α to be 60% and 41%, compared with 53% and 45% using the Simple model, respectively (Table 1; for 95% confidence intervals, see Supplemental Table S1). The differences between these estimates reflect the importance of accurately modeling the population size of outgroup species for calculations of α.

We estimated α for substitutions that occurred exclusively on the human lineage, using the human–macaque alignment to polarize sequence differences between human and chimpanzee. We estimate that α = 6.2% using the Simple model and 16.0% using the Complex model (Table 1; Supplemental Text).

To compare our estimates of α to those from another model-based method that assumes Nanc = Nout = Nanc.in, we used DFE-alpha, to infer α for our three species pairs. Using this method, α is estimated to be 24% and 2% for humans using chimpanzee and macaque as outgroup, respectively; 71% for D. melanogaster–D. simulans; and 51% for mouse–rat (Table 1). These estimates are all higher compared with estimates from Simple demographic models. However, the estimates of α for primates differ significantly depending on whether the macaque or chimpanzee is used as the outgroup for humans.

In addition, we calculated omega-a for both the Simple model and the Complex model for all taxa (Table 1). We find similar patterns of omega-a as for α. First, using the Complex models, estimates of omega-a for primates are similar (i.e., 0.06 or 0.07) regardless of outgroup. Second, the estimate of omega-a for primates is higher using the Complex model than the Simple model. Across taxa, primates have the lowest estimate of omega-a, compared with Drosophila (0.09) and rodents (0.10) using the full data set.

Testing whether p⁺ and s⁺ differ across species

We next estimated the proportion and selection coefficient of new beneficial mutations. For each species, we estimate the proportion of new mutations that are beneficial (p⁺) and their selection coefficient (s⁺) jointly using a grid search approach. We then test whether these two parameters differ across species.

The number of nonsynonymous differences between a pair of species (D_N) is assumed to be Poisson-distributed (Sawyer and Hartl 1992), with rate parameter equal to

$$E[D_N]=2N\mu [\int G(s)u(s)(1-p^{+})+u(s^{+})p^{+}],$$ (1)

where G(s) is the DFE of deleterious and neutral mutations from Huber et al. (2017), u(s) is the fixation probability (Kimura 1962) of deleterious and neutral mutations, u(s⁺) is the fixation probability of beneficial mutations, and p⁺ is the proportion of new mutations that are beneficial. We then use a Poisson log-likelihood (LL) function for D_N in each species and a series of likelihood ratio tests (LRTs) to determine whether p⁺ and s⁺ differ across primates, rodents, and Drosophila (see Methods).

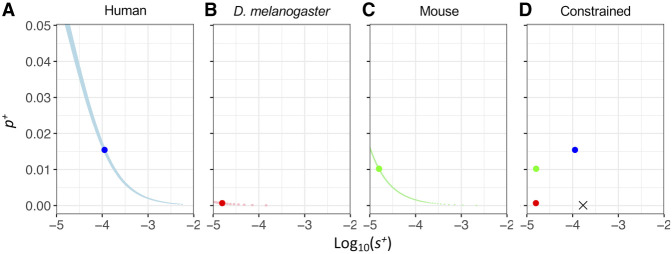
By using this framework, we find that the full model H1, in which each taxon is allowed to have its own p⁺ and s⁺, fits D_N significantly better than the constrained null model, where p⁺ and s⁺ are constrained to be the same across all three taxa (LRT statistic Λ = 124,974, df = 4, P < 10⁻¹⁶) (Fig. 2A–D; Supplemental Fig. S2; Supplemental Table S6). We also compared p⁺ and s⁺ between pairs of taxa (i.e., primate vs. rodent; primate vs. Drosophila; rodent vs. Drosophila). In all pairwise tests, the model in which each species has its own p⁺ and s⁺ fits the observed D_N significantly better than a model in which p⁺ and s⁺ are constrained to be the same in the tested taxa (Supplemental Table S6). Many combinations of p⁺ and s⁺ values show similar LLs (Fig. 2A–C), suggesting the two parameters are not separable. Models with a larger s⁺ have a lower proportion of positively selected mutations (p⁺) than models with a smaller s⁺.

Figure 2.

Log-likelihood (LL) surfaces for p⁺ and s⁺ for different species: (A) human; (B) D. melanogaster; and (C) mouse. (D) The constrained model (H0), in which p⁺ and s⁺ are constrained to be the same across all three taxa. LLs are calculated using a grid search method of log₁₀(s⁺) in the range of −5 to −2 and p⁺ in the range of 0%–7.5%. Blue denotes human; red, D. melanogaster; and green, mouse. The large points represent the MLE for each species; the black cross in panel D represents the MLE of the constrained model; and the lighter colors show grid points within three LL units of each MLE. The Complex model is used for each species, and we use the chimpanzee as the outgroup for humans.

We next investigated whether when allowing p⁺ to differ across primates, rodents, and Drosophila, a model with the same s⁺ could fit all species. This is shown in conditional likelihood plots, where when assuming the same s⁺ for all species, humans would need a higher proportion of beneficial mutations compared with mice and D. melanogaster to match the observed D_N (Fig. 3A). When we constrain p⁺ to be the same for all species, s⁺ is larger in humans compared with that in mice and D. melanogaster (Fig. 3B).

Figure 3.

Conditional LL surfaces: (A) maximizing p⁺ given particular values of s⁺ and (B) maximizing s⁺ given particular values of p⁺. Only grid points within three LL units of the MLEs for each parameter for each species are shown. Light blue denotes human; pink, D. melanogaster; and light green, mouse.

Motivated by the observation that p⁺ and s⁺ cannot be reliably estimated separately, we estimated a composite parameter p⁺s⁺, the product of p⁺ and s⁺. We find clear evidence that, regardless of the model of ancestral demography or outgroup, humans have a significantly higher p⁺s⁺ than do D. melanogaster and mice (Fig. 4). The LL curves are quite peaked and have little overlap across species. Thus, approximate 95% confidence intervals on p⁺s⁺ do not overlap across species, implying more positive selection in humans than in D. melanogaster and mice.

Figure 4.

The composite parameter p⁺s⁺, capturing the proportion of beneficial mutations and the strength of selection, differs across species. LL curves for p⁺s⁺ in the three species. Red denotes the inference for D. melanogaster; green, the inference for mouse; blue, the inference for human using the chimpanzee as the outgroup; and purple, the inference for human using the macaque as the outgroup. Lighter colors denote the Simple model. Darker colors denote the Complex model, which better models the ancestral demography and population size of the outgroup. Note that regardless of which demographic model is used, the LL curves from the different species do not overlap within the top 500 LL units, suggesting p⁺s⁺ is significantly different among taxa.

Testing whether γ⁺ and p⁺ differ across species

Humans, D. melanogaster, and mice have drastically different population sizes, which can influence the efficacy of selection within each species. Thus, we next examined whether the selection coefficient scaled by current population size (γ⁺ = 2Ns⁺) and p⁺ differ across primates, rodents, and Drosophila.

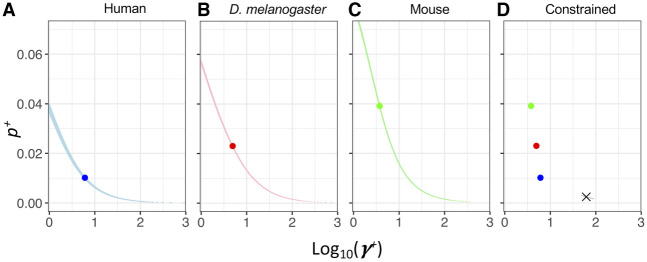
We find that the full model (H1) in which each taxon has its own γ⁺ and p⁺ fits the observed D_N significantly better than the constrained model (H0) in which γ⁺ and p⁺ are constrained to be the same across all three taxa (LRT statistic Λ = 3541, df = 4, P < 10⁻¹⁶) (Fig. 5A–D; Supplemental Fig. S2; Supplemental Table S6). We also compared γ⁺ and p⁺ between pairs of taxa. For the human–D. melanogaster and human–mice pairs, the models in which each species has its own γ⁺ and p⁺ fit the observed D_N significantly better than a model in which γ⁺ and p⁺ are constrained to be the same in the tested two taxa (Supplemental Table S6), regardless of outgroup. However, we cannot reject the hypothesis that mice and D. melanogaster have same γ⁺ and p⁺ (Supplemental Table S6). Similar to what was seen above for p⁺ and s⁺, a ridge of parameter values have similar LLs (Fig. 5A–C). Models with larger γ⁺ tended to have a lower proportion of positively selected mutations than models with smaller γ⁺, suggesting the two parameters are not separable. The relative ordering of the MLEs of p⁺ across species considering γ⁺ is not necessarily the same as that for the s⁺ results because the population sizes differ across species.

Figure 5.

LL surfaces for p⁺ and γ⁺ for different species: (A) human; (B) D. melanogaster; and (C) mouse. (D) The constrained model, H0, in which p⁺ and γ⁺ are constrained to be the same across all three taxa. LLs are calculated using a grid search method of log₁₀(γ⁺) in the range of 0–3 and p⁺ in the range of 0%–7.5%. Blue denotes human; red, D. melanogaster; and green, mouse. The large points represent the MLE for each species; the black cross in panel D represents the MLE of the constrained model; and the lighter colors show grid points within three LL units of each MLE. The Complex model is used for each species, and we use chimpanzee as the outgroup for humans.

We next investigated whether it is possible that either γ⁺ or p⁺ is the same across taxa while the other parameter varies. With the same γ⁺ for all species, humans would need a lower proportion of beneficial mutations compared with that of mice and D. melanogaster to fit the observed D_N (Supplemental Fig. S3A). When we constrain p⁺ to be the same for all taxa, humans have a smaller γ⁺ for beneficial mutations (Supplemental Fig. S3B). Furthermore, because it is challenging to reliably estimate p⁺ and γ⁺ separately, we also estimated a composite parameter p⁺γ⁺, the product of p⁺ and γ⁺. We find that p⁺γ⁺ is not as distinct across different taxa as is p⁺s⁺. In the Complex models, humans have a smaller p⁺γ⁺ than do mice. However, the LL curves of p⁺γ⁺ overlap between D. melanogaster and mice and between D. melanogaster and humans, suggesting they are not significantly different (Supplemental Fig. S4).

Effects of biased gene conversion and hypermutable CpG sites

Biased gene conversion (BGC) is the preferred transmission of G/C alleles (S indicates strong alleles) at the expense of A/T alleles (W indicates weak alleles). This process is common in mammals (Duret and Galtier 2009; Lachance and Tishkoff 2014; Bolívar et al. 2016) but is not as evident in D. melanogaster (Robinson et al. 2014; Jackson et al. 2017). Further, methylated CpG sites in mammals have a higher mutation rate to T alleles owing to deamination of the C nucleotide (Duncan and Miller 1980; Sved and Bird 1990). Both factors could possibly bias comparisons of selection between mammals and insects.

To test whether BGC and hypermutable CpG sites drive the observed pattern of positive selection across primates, rodents, and Drosophila, we filtered primate and rodent data to keep only strong-to-strong or weak-to-weak mutations (herein called SSWW mutations), which are not affected by BGC and are not CpG changes (Supplemental Text; Supplemental Fig. S5). We then reinferred α. For primates, α is comparable to that without filtering (Table 1). For rodents, however, α is substantially lower than before filtering, suggesting that BGC and CpG mutational processes may account for some of the nonsynonymous differences between the mouse and rat. We also calculated omega-a using SSWW mutations. When using the Complex models, omega-a for primates is slightly higher than that before filtering, whereas for rodents, it is much lower than before filtering (Table 1).

After removing the effect of BGC and CpG sites in primates and rodents, we again quantify the strength and proportion of new beneficial mutations across all three taxa. A model in which each taxon has its own p⁺ and s⁺ fits the observed D_N significantly better than a model in which p⁺ and s⁺ are constrained to be the same across all three taxa (LRT statistic Λ = 825, df = 4, P < 10⁻¹⁶) (Supplemental Fig. S6A–D; Supplemental Table S6). Models comparing each pair of taxa (e.g., primates vs. rodents; primates vs. Drosophila; rodents vs. Drosophila) suggest that each taxon has its own unique p⁺ and s⁺, regardless of demography (Supplemental Table S6). Allowing p⁺ to differ across taxa, a model with the same s⁺ across all taxa could fit the data and vice versa. When we constrain s⁺ to be the same for all species, humans still have the highest proportion of new beneficial mutations (Supplemental Fig. S6E). Constraining p⁺ to be the same for all species, humans have the largest selection coefficient (Supplemental Fig. S6F).

Similarly, the model in which each taxon has its own p⁺ and γ⁺ fits the observed D_N significantly better than a model in which p⁺ and γ⁺ are constrained to be the same across all three taxa (LRT Λ = 4496, df = 4, P < 10⁻¹⁶) (Supplemental Table S6; Supplemental Fig. S7). Models comparing each pair of taxa suggest that each taxon has its own unique p⁺ and γ⁺, regardless of demography (Supplemental Table S6). Allowing p⁺ to differ across species, a model with the same γ⁺ across all taxa could fit the data and vice versa. When we constrain γ⁺ to be the same for all species, D. melanogaster has the highest proportion of beneficial new mutations, and mice have the lowest proportion. When we constrain p⁺ to be the same for all species, D. melanogaster has the largest γ⁺, and mice have the smallest γ⁺ (Supplemental Fig. S7).

Last, we estimated two composite parameters, p⁺s⁺ and p⁺γ⁺, for SSWW mutations. Humans again have a significantly higher p⁺s⁺ than do D. melanogaster and mice (Supplemental Fig. S8), suggesting more positive selection in humans than in D. melanogaster and mice. Similar to the full data set, p⁺γ⁺ is not as distinct across different species as p⁺s⁺. We find that under the Complex model, humans and D. melanogaster have a significantly (i.e., the LL curves do not overlap within two units of the MLEs) larger p⁺γ⁺ than mice, and the LL curves of p⁺γ⁺ for humans and D. melanogaster overlap near the MLEs (Supplemental Fig. S8).

Discussion

We have quantified the amount of adaptive evolution in multiple species with varying degrees of complexity and population size using two different approaches. First, we examined the proportion of nonsynonymous substitutions fixed by positive selection and found that this proportion is higher in Drosophila than in rodents and primates, consistent with prior work (Andolfatto 2005; Boyko et al. 2008; Eyre-Walker and Keightley 2009; Fay 2011). However, after correcting for the population sizes of the outgroup and ancestral population, we infer that α is much higher in primates than what was inferred in previous studies. Second, we show that the proportion of and strength of positive selection on new beneficial mutations differs across species. The species with the smaller population size and greater complexity (i.e., humans) has stronger and/or more abundant new beneficial mutations than the other two species with much larger population sizes (i.e., mice and D. melanogaster). These results are robust to the choice of outgroup, BGC, and hypermutable CpG sites.

One major advantage of our method to infer α over previous similar approaches from Boyko et al. (2008) and DFE-alpha (Eyre-Walker and Keightley 2009) is that we allow the outgroup and ancestral population sizes to differ from the ancestral population size of the ingroup. The population size of the outgroup matters because it affects the fixation probability of weakly deleterious alleles in the outgroup lineage (Ohta 1973, 1992; Kimura 1983). The size of the ancestral population matters because it determines the amount of variation in the ancestral population that can then contribute to divergence between species. Larger values of Nanc mean that the ratio of nonsynonymous to synonymous polymorphism in the ancestral population will be smaller because proportionally fewer deleterious mutations will be segregating. All else being equal, the smaller ratio of nonsynonymous to synonymous polymorphism in the ancestral population will lead to a lower ratio of nonsynonymous to synonymous divergence. As such, the number of nonsynonymous substitutions attributed to weakly deleterious mutations is highly affected by the population sizes of the outgroup and ancestral population, affecting estimates of α. By using more realistic population sizes, the α estimates we obtained for primates are similar when using chimpanzee or macaque as outgroup species. This is strong evidence that our method is more accurate, as all the other methods give drastically different estimates of α using these two different outgroups. Eyre-Walker and Keightley (2009) also suggested that α in humans could be as high as 0.31 if the effective population size of humans and macaques was much higher than 10,000 until very recently, foreshadowing our current estimates. The increased accuracy of the Complex model applies to the estimation of other parameters of adaptive evolution, including but not limited to omega-a. Future studies of adaptive substitutions should carefully consider ancestral and outgroup population sizes and use statistical methods that model them realistically.

Here we have quantified adaptive evolution from two different perspectives. First, we estimate the proportion of adaptive nonsynonymous substitutions between species, α. This statistic measures the endpoint where a number of factors such as demography, genetic drift, and natural selection all come into play. Second, we estimate p⁺ and s⁺ of newly arising beneficial mutations. This approach aims to understand the properties of new beneficial mutations, the beginning point where beneficial mutations appear and enter the population. Thus, it is possible that these two approaches can yield qualitative opposite results. Indeed, we have shown that D. melanogaster has the largest values of α, but the smallest p⁺s⁺.

We previously found that 15% of nonsynonymous mutations in humans are weakly beneficial (Huber et al. 2017). Because Huber et al. (2017) only analyzed polymorphism data, they did not consider strongly beneficial mutations that became substitutions between species. Our present study leverages genome sequences of several related species pairs to estimate the proportion of strongly beneficial (s⁺ > 10⁻⁵) mutations along with the strength of selection acting on them. Weakly beneficial mutations are already accounted for in our model using the DFE from Huber et al. (2017) as they likely segregate as polymorphisms. We find that humans have a higher p⁺s⁺ than D. melanogaster, mirroring the qualitative trend seen for weakly beneficial mutations in Huber et al. (2017). In the context of human evolution, it has been shown that segregating weakly beneficial mutations could result in an underestimate of α (Galtier 2016; Uricchio et al. 2019). Thus, α in humans could be even higher if adaptive polymorphisms are taken into account. However, our approach of modeling the complex demography in the outgroup and ancestral populations should correct for some of the bias in inferring α owing to weakly beneficial mutations segregating as polymorphisms. Modeling the complex demography reduces the number of fixations from nearly neutral mutations that are treated in our model as nonadaptive, including those from segregating weakly beneficial mutations.

Our estimate of α for human lineage is 16.0% using the Complex demographic model, which is comparable to the estimate of human-lineage α by Uricchio et al. (2019), despite the use of different analytical approaches. α is expected to be lower on the human lineage compared with the chimpanzee or macaque lineage owing to the higher proportion of weakly deleterious amino acid substitutions on the human lineage to their smaller population size (Ohta 1973, 1992). For D. melanogaster, by using the Complex model, we estimate p⁺γ⁺ to be ∼0.1, which is within a factor of two of a previous estimate of Keightley et al. (2016). For mice, using the Complex model, we estimate p⁺γ⁺ to be ∼0.15, which is somewhat greater than the value of ∼0.05 inferred by Booker and Keightley (2018) and 0.05–0.06 by Campos et al. (2017). The differences in estimates could be because of the use of different methods and models, such as our detailed modeling of the ancestral and outgroup population sizes.

We make several key modeling assumptions. First, we assume that the DFE is the same between the ingroup and outgroup for each pair of species (e.g., humans and chimpanzee have the same DFE). This assumption could be relaxed by using only polymorphism data to infer the beneficial DFE (Tataru et al. 2017), although not including divergence to an outgroup species reduces power to infer positive selection (Booker 2020). Second, our inference of p⁺ and s⁺, as well as related approaches (Schneider et al. 2011; Campos et al. 2017; Tataru et al. 2017; Booker and Keightley 2018), makes the assumption of selection starting from a single mutation, because we use the fixation probability of a mutation introduced as a single copy. Selection on standing variation (i.e., one type of soft sweep) might bias the parameter estimates, although the meaning of p⁺ and s⁺ are not as clear under models with soft sweeps. However, α should be accurately estimated if the beneficial mutations reach fixation. Furthermore, as our approach only focuses on strongly beneficial mutations that contribute to divergence, it is not sensitive to types of selection in which mutations do not reach fixation. These include another type of soft sweeps (Pritchard et al. 2010), in which multiple independent beneficial mutations in the same gene are selected simultaneously but no mutation becomes fixed, as well as polygenic adaptation, in which beneficial alleles only slightly increase in frequency, without reaching fixation. Another limitation comes from the model itself. It has been suggested that models in which s⁺ does not change over time may not model the complexity of adaptive walks, in which the first beneficial mutation may have a greater effect on fitness than subsequent beneficial mutations (Gillespie 2004; Lourenço et al. 2013). Thus, our estimates of p⁺ and s⁺ should be interpreted as the average values over time and over genetic backgrounds, rather than literal values that have stayed constant over time. In fact, our findings show that p⁺ and s⁺ have changed over deep evolutionary time, pointing to their dynamic nature. Furthermore, as shown by the ridges on the LL surfaces (Figs. 2A–C, 5A–C), our method cannot separately infer p⁺ and s⁺ (as well as p⁺ and γ⁺). Other types of data and analyses could potentially separately estimate p⁺ and s⁺ or γ⁺. Andolfatto (2007) and Campos et al. (2017) suggested that large values of s⁺ and γ⁺ with smaller values of p⁺ are required to generate a negative relationship between synonymous diversity and nonsynonymous divergence. Such parameter values could still be consistent with our estimates of composite parameters p⁺s⁺ and p⁺γ⁺. In addition, there likely is a distribution of s⁺, which could include a relatively smaller proportion of strongly beneficial mutations that generate the sweep effect on synonymous diversity.

If adaptation is mutation limited, more beneficial mutations are expected in organisms with larger population sizes. This view was not supported by conceptual arguments by Gillespie (2004) who suggested that the rate of environment change will matter more than the population size in determining the rate of adaptive evolution. The simulation study by Lourenço et al. (2013) that considered a changing DFE over time in the context of a Fisher's geometric model found that the population size was only weakly related to α. Instead, the rate at which the environment changed was an important predictor of the amount of adaptive evolution, as environmental shifts moved the population from the fitness optimum, creating the opportunity for new beneficial mutations. Further, Rousselle et al. (2020) recently found a weak negative correlation between the amount of adaptive evolution and the amount of genetic diversity in modern populations, which supports the models of Lourenço et al. (2013) and Gillespie (2004). However, not all studies are in agreement on the role of the environment as Connallon and Clark (2015) found that environmental heterogeneity reduces the fraction of beneficial mutations by inflating the standardized mutation size in a Fisher's geometric model. Lourenço et al. (2013) also found that organismal complexity, here defined as the number of phenotypes under selection, was a key predictor of the amount of adaptive evolution within species. Through a “cost of complexity,” more complex organisms have a harder time adapting to new environmental conditions because of the additional constraints imposed by the increased number of traits under selection. As such, adaptive walks require more beneficial mutations (Orr 1998).

Our results presented here are in broad agreement with the conceptual model of Lourenço et al. (2013). Specifically, we do not find that species with larger population sizes (i.e., D. melanogaster) have more beneficial mutations. Instead, we find that p⁺s⁺ is higher in humans than in D. melanogaster or mice. Second, although it is hard to precisely define organismal complexity, previous work has found more protein–protein interactions in humans than in Drosophila (Valentine et al. 1994; Stumpf et al. 2008), suggesting that humans may be more complex than Drosophila. If this is the case, then our findings of a higher p⁺s⁺ in humans than D. melanogaster and mice support the arguments from Lourenço et al. (2013) that adaptive walks after an environmental shift are less efficient and require more steps (i.e., beneficial mutations) in more complex organisms, leading to a higher p⁺s⁺ in complex organisms. Additionally, differences in the degree of environmental change across species could also contribute to the disparate inferences of p⁺s⁺ across taxa. Although it is hard to say which species have experienced more environmental shifts, species with longer generation times, like primates, may experience more environmental change per generation than species with shorter generation times, like Drosophila or rodents (Romiguier et al. 2014; Rousselle et al. 2020). Another possibility is that the selection coefficient per year is similar across species (Charlesworth 1994; Chevin 2011). This could occur if the selection coefficient is related to interactions with the environment on a per-year timescale. Under such a model, the per-generation selection coefficient, as we measure here, would be larger in species with longer generation times. Our finding of a higher p⁺s⁺ in primates than in Drosophila is consistent with these predictions, although it is not possible from our analyses to conclusively favor any particular explanation.

Methods

Polymorphism and divergence data for humans, mice, and D. melanogaster

For humans, we used polymorphism data from 112 individuals from Yoruba in Ibadan, Nigeria (YRI) from The 1000 Genomes Project (The 1000 Genomes Project Consortium 2012). Published genome alignments of human and chimpanzee (hg19/panTro4), and human and Macaca mulatta (hg19/rheMac3) were downloaded from the UCSC Genome Browser (http://hgdownload.soe.ucsc.edu/goldenPath/hg19/). As coding regions in hg19 are well annotated, use of more recent genome builds would not affect our conclusions. For D. melanogaster, we used the Drosophila Population Genomics Project phase 3 data, including 197 African D. melanogaster lines from Zambia, Africa (Lack et al. 2015). For divergence, D. melanogaster and D. simulans genic alignments (Dmel v5/Dsim v2) were extracted from the multispecies alignments from Hu et al. (2013). Only autosomal regions were used in our analysis. Human and D. melanogaster polymorphism data were filtered and down-sampled to 100 chromosomes as described by Huber et al. (2017).

For mice, raw data were downloaded for 10 Mus musculus castaneus individuals that were collected in the northwest Indian state of Himachal Pradesh (Halligan et al. 2010, 2013). Reads were mapped against mouse genome mm9 using BWA (Li and Durbin 2009) and Stampy (Lunter and Goodson 2011). As coding regions in mm9 are well annotated, use of more recent genome builds would not affect our conclusions. Duplicate reads were marked using Picard, and further preprocessing was performed following GATK best practice guidelines (McKenna et al. 2010). Variants were called using the GATK UnifiedGenotyper and filtered using the GATK VQSR using Affymetrix Mouse Diversity Genotyping Array sites (Yang et al. 2009). We further filtered the data set to only retain sites with a sample size of at least 16 chromosomes and down-sampled all sites to a sample size of 16 chromosomes using the hypergeometric probability distribution. Published genome alignments of mice and rat (mm9/rn5) were downloaded from UCSC (http://hgdownload.soe.ucsc.edu/goldenPath/mm9/vsRn5/axtNet/). For each species, polymorphism and divergence data were intersected, and only coding regions shared by both data sets were used in our analysis.

In total, 19.1 Mb of coding sequences for primates, 26.6 Mb of coding sequences for rodents, and 15.8 Mb of coding sequences for Drosophila were included. The nonsynonymous and synonymous total sequence lengths (L_NS, L_S) were estimated using multipliers of L_NS = 2.85 × L_S in D. melanogaster and L_NS = 2.31 × L_S in mammals from Huber et al. (2017). Human variants were annotated using the SeattleSeq Annotation pipeline (http://snp.gs.washington.edu/SeattleSeqAnnotation138/). Mice and Drosophila variants were annotated using SnpEeff v3.6 using the mice NCBIM37.66 annotation database and the D. melanogaster BDGP5.75 annotation database, respectively. Sites that are annotated as near-splice, or loss of function, were removed. The ratio of nonsynonymous/synonymous differences between human and chimp sequences in our data set is approximately 0.65, which is consistent with several previous reports from different data sets (Bustamante et al. 2005; Torgerson et al. 2009; Enard et al. 2014).

Model-based estimates of α

Model-based estimates of α require a demographic model and a DFE for neutral and deleterious mutations to predict the D_NE that is accounted for by such mutations. For primates and Drosophila, we used demographic and DFE parameters from Huber et al. (2017; Supplemental Table S3). For rodents, we conducted our own inference of these parameters by summarizing the polymorphism data in mice by the folded SFS (Supplemental Text).

To compute the expected divergence between species, we computed the divergence accumulated in the ingroup population, outgroup population, and ancestral population separately and summed them. The divergence in the ingroup and outgroup population is a function of divergence time, effective population size, mutation rate, and selection coefficient and was calculated according to equation 13 in Sawyer and Hartl (1992). We computed the expected divergence under a gamma DFE model by Monte Carlo integration using 1 million gamma-distributed selection coefficients. The contribution of the ancestral population to divergence between two species was computed numerically based on the diffusion equation, using prfreq (Boyko et al. 2008) and assuming the same gamma DFE. These calculations are implemented in our program predicDiv (Supplemental Code). For both the Simple and the Complex models, we first estimate the divergence times (Supplemental Table S5) that fit the observed number of synonymous differences between a pair of species because there is a wide range of divergence times from the literature for each species. Here the number of synonymous differences equals 2 × divergence time × mutation rate. Second, using this divergence time, demography, and DFE inferred from Huber et al. (2017), or as described above for mice, we estimated the expected number nonsynonymous differences (D_NE) according to equation 13 of Sawyer and Hartl (1992; Boyko et al. 2008). Then, α and omega-a are calculated as

$$\alpha =\frac{D_{NO}-D_{NE}}{D_{NO}},$$ (2)

$$omeg{a}_a=\frac{D_{NO}-D_{NE}}{Ds}/\left(\frac{L_{NS}}{L_S}\right),$$ (3)

where D_NO is the observed number of nonsynonymous differences between species, and D_S is the observed number of synonymous differences between species. The 95% CIs of α were calculated by parametric bootstrapping through resampling 10,000 draws of D_N using a Poisson distribution with mean of D_NO.

DFE-alpha

Data files and the program v2.15 were downloaded from the following link: http://www.homepages.ed.ac.uk/pkeightl//dfe_alpha/download-dfe-alpha.html. Folded synonymous and nonsynonymous SFSs were used as input in the inferences. The est_alpha_omega program was used to estimate the proportion of adaptive divergence.

Composite likelihood approach for testing whether p⁺ and s⁺ differ across species

We first used predicDiv and prfreq to generate a look-up table for the expected number of nonsynonymous differences between species for a range of s⁺ for each species. We focused on this range to capture strongly advantageous mutations. Given a demographic model, we assume a substitution rate according to equation 13 in Sawyer and Hartl (1992). The contribution of the ancestral population to the divergence between two species is computed by numerically solving the diffusion equation using predicDiv and prfreq (Boyko et al. 2008). For each species, we then searched a grid of values of log₁₀(s⁺) (−5 to −2) and p⁺(0%–7.5%). We are interested in this range of strong s⁺ because weakly beneficial mutations still segregating as polymorphisms and are accounted for by the DFE fit to the SFS. We use a Poisson LL function to calculate the LL for each combination of s⁺ and p⁺. We find the MLE of s⁺ and p⁺ for each taxon under each demographic model that maximizes the LL and best fit the observed D_N. This is the full model (H1) in which each taxon (i.e., primates, rodent, and Drosophila) is allowed to have its own s⁺ and p⁺. In the constrained model (H0), two or three taxa have the same s⁺ and p⁺. The LL of the constrained model is the sum of LL for each s⁺ and p⁺ for each taxon under comparison. We then found the MLE for the constrained model and the likelihood ratio between H1 and H0.

Composite likelihood approach for testing whether p⁺ and γ⁺ differ across species

Similarly, we used predicDiv and prfreq (Boyko et al. 2008) to generate a look-up table for the expected number of nonsynonymous differences for a range of γ⁺ for each taxon under each demographic model. For each species, we performed a grid search of log₁₀(γ⁺) (0–3) and p⁺(0%–7.5%). Note that because effective population sizes differ over several orders of magnitude across our three taxa, we are searching across drastically different ranges of s⁺ compared with our previous inference described above. We again use a Poisson LL function to calculate the LL for each combination of γ⁺ and p⁺ and use a similar LRT as described above for s⁺ and p⁺.

Composite parameters p⁺s⁺ and p⁺γ⁺

We examined two composite parameters, the product of p⁺ and s⁺ and the product of p⁺ and γ⁺ for each taxon. Multiple combinations of parameters could give the same product p⁺s⁺ and p⁺γ⁺and distinct combinations could have different LL. Thus, we found the values of p⁺ and s⁺ that gave the highest LL for each p⁺s⁺ value (and similarly each p⁺ and γ⁺for each p⁺γ⁺). Values of log₁₀(p⁺s⁺) and p⁺γ⁺were rounded to three digits before this comparison.

Conditional LLs

To examine whether primates, rodents, and Drosophila could have the same s⁺ or p⁺, we examined the conditional LLs. To make the conditional LL curve for p⁺, for each s⁺ value, we find the p⁺ that maximizes the LL, as well as the p⁺ values that have a LL within three LL units of this maximum LL for this s⁺ (i.e., p⁺|s⁺). To make the conditional LL curve for s⁺, for each p⁺ value, we look for the s⁺ that maximizes the LL as well as the s⁺ values that have a LL within three LL units of this maximum LL for this p⁺ (i.e., s⁺|p⁺). The same approach was used to construct the conditional LL curve for p⁺ and γ⁺.

Filtering to only include sites not affected by BGC or CpG hypermutation

We repeated our analyses only including SSWW mutations because these changes were not affected by BGC or increased mutation rates owing to deamination of methylated CpG sites. To do this, we adjusted the mutation rates to include only SSWW sites (Supplemental Text). We also reinferred the demographic parameters and DFE using only SSWW mutations in rodents (Supplemental Text) because the SFS for SSWW mutations differed from that of the full data.

Software availability

predicDiv is available as Supplemental Code and also at GitHub (https://github.com/LohmuellerLab/predicDiv).

Competing interest statement

The authors declare no competing interests.