Genome-wide prediction of DNA mutation effect on nucleosome positions for yeast synthetic genomics

Abstract

Genetically modified genomes are often used today in many areas of fundamental and applied research. In many studies, coding or noncoding regions are modified in order to change protein sequences or gene expression levels. Modifying one or several nucleotides in a genome can also lead to unexpected changes in the epigenetic regulation of genes. When designing a synthetic genome with many mutations, it would thus be very informative to be able to predict the effect of these mutations on chromatin. We develop here a deep learning approach that quantifies the effect of every possible single mutation on nucleosome positions on the full Saccharomyces cerevisiae genome. This type of annotation track can be used when designing a modified S. cerevisiae genome. We further highlight how this track can provide new insights on the sequence-dependent mechanisms that drive nucleosomes’ positions in vivo.

The first genetically modified organisms were created in the seventies, shortly after Cohen et al. developed the DNA recombination technology (Cohen et al. 1973). This has been the foundation of biotechnology which is now a flourishing domain both in fundamental research and industrial applications (Russo 2003). The recent development of game changing technologies such as CRISPR and DNA oligonucleotide de novo synthesis now opens the way to major genome rewriting projects (Ostrov et al. 2019). A first paradigmatic example of this effort, the Saccharomyces cerevisiae 2.0 (Sc 2.0) project (Richardson et al. 2017), will soon deliver the first example of a complete synthetic eukaryotic genome. Several projects are now starting with the aim to design more synthetic genomes (Ostrov et al. 2019) that could reach even the scale of the human genome. In the field of genomic engineering, the first step is to design the DNA sequence of interest, either resulting from very few edits of the wild-type sequence, or from a more extensive genome rewriting, or even from the introduction of DNA sequences coming from a different organism. When introduced in the cell, this sequence will be interpreted by the cellular machinery, and the resulting activity can be unpredictable. To date, there is no way to know whether the nucleosomes will assemble and position themselves on the DNA as expected, whether they will be modified or not by enzymes, or whether the chromatin will fold in space in an appropriate way. Because experimentally testing a huge quantity of trial sequences is cumbersome, if not unfeasible, computational tools are a good alternative to optimize the design of synthetic sequences so that they can fold into a functional chromatin in vivo. Although this is a complex problem, the solution could come from the recent uptake of deep neural networks.

In parallel to the evolution of experimental genome editing techniques, the explosion of the amount of data available together with algorithmic advances and the use of graphical processing units (GPUs) (Shi et al. 2016) enabled the development of deep neural networks in many different contexts. This led to several breakthroughs in domains such as computer vision (Krizhevsky et al. 2012; Girshick et al. 2014; Long et al. 2015), speech recognition (Hannun et al. 2014), and machine translation (Wu et al. 2016). As a data-driven domain, genomics followed the trend, and pioneering studies (Alipanahi et al. 2015; Zhou and Troyanskaya 2015) have demonstrated the effciency of deep neural networks to annotate the genome with functional marks directly by interpreting the DNA sequence. The application of deep neural networks to genomics is growing at a high pace, and it can now be considered as a state of the art computational approach to predict genomics annotations (Quang et al. 2015; Kelley et al. 2016, 2018; Kim et al. 2016; Min et al. 2016; Jones et al. 2017; Umarov and Solovyev 2017; Eraslan et al. 2019; Zou et al. 2019). One of the advantages of deep neural networks is their ability to predict a learned annotation on a variation of the genome, that is, to predict the effect of mutations.

In this work, we report the use of deep learning to estimate the effect on nucleosome positions of changing each single nucleotide of the S. cerevisiae genome into another nucleotide. The nucleosome positioning in S. cerevisiae has been extensively studied in the past by MNase-seq. This protocol relies on the enzymatic digestion of the linker DNA between nucleosomes and the sequencing of the protected DNA (Zhang et al. 2011; Hughes and Rando 2015; Krietenstein et al. 2016). Several studies pointed toward a close link between gene regulation and nucleosome positions (Tsankov et al. 2010; Hughes et al. 2012). The role of the DNA sequence in the nucleosome positioning process has been a longstanding debate. To assess this question, a pioneering study (Segal et al. 2006) showed evidence for the existence of motifs negatively correlated with nucleosome positions (Iyer and Struhl 1995; Anderson and Widom 2001; Raisner et al. 2005). Kaplan et al. (2009) developed a statistical method to predict the nucleosome density from the DNA sequence, emphasizing the preferential positioning of nucleosomes on specific DNA statistical motifs. Numerous computational methods (for review, see Teif 2016) were developed afterward to predict the positions of nucleosomes from the DNA sequence. Recently, deep neural networks were also applied to discriminate between 147-bp-long sequences bound by a nucleosome and 147-bp-long sequences without any nucleosomes (Di Gangi et al. 2018; Zhang et al. 2018).

Building on these previous works, we use here convolutional neural networks (CNNs) to predict the experimental nucleosome density (i.e., the results of the MNase protocol) for every position on the S. cerevisiae genome from the raw DNA sequence. The model reproduces well the characteristic nucleosome depletion around transcription start sites (TSSs) as well as the typical periodic nucleosomal pattern on gene bodies. We then use the model as an in silico model of the yeast machinery to predict the effect of every single mutation along the genome. In doing so, we assign to every nucleotide a score representing its importance regarding the nucleosome positioning process. This genomic track is accessible at GitHub (https://github.com/etirouthier/NucleosomeDensity/blob/master/Results_nucleosome/mutasome_scerevisiae.bw) and can be used freely by others, when designing genetically modified yeast, to anticipate the effect of induced mutations on nucleosome positioning. We also use this track to analyze the DNA motifs that present a high mutation score, corresponding to motifs that are important for nucleosome positioning.

Results

Quality of the prediction

The first goal of this study is to accurately predict the nucleosome density directly from the DNA sequence. We use a CNN model whose input is defined by a one-hot-encoded DNA sequence of a given length L and whose output is the nucleosome local density associated with the nucleotide found in center of the input sequence. Several approaches aiming at extracting nucleosome positions from the nucleosome density have been proposed (e.g., Chen et al. 2013, 2014), but our goal here is to predict the experimental output—that is, the continuous nucleosome density—rather than the nucleosome positions that can be inferred from this experimental density. We present in this section a quantitative evaluation of the prediction quality.

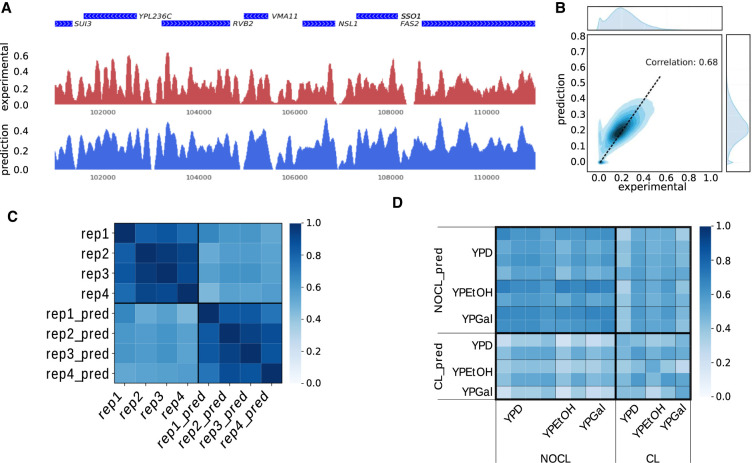
A typical experimental result, such as the one of Hughes et al. (2012), exhibits a locally periodic signal, with depleted regions preferentially found in inter-genic regions (Fig. 1A, red signal). We train a CNN (refer to Methods for details) using the experimental nucleosome density of all chromosomes but the Chr 16, which is kept aside as a test set. A length L = 2000 bp of the input sequence was chosen, and all sequences of length L obtained with a 1-bp sliding window on each chromosomes are used for training (Chr 1 to Chr 13), validation (Chr 14 and Chr 15), and test (Chr 16). The prediction on Chromosome 16 matches the experimental density, both in genic and inter-genic regions (Fig. 1A, blue signal). A quantitative comparison between the two signals on the whole chromosome is displayed in Figure 1B. Our method reaches a Pearson's correlation of 0.68 between prediction and experiment, a value comparable with the results obtained by state-of-the-art CNN-based methods on other tracks annotating the human genome, such as DNase sensitivity or histone modifications (Kelley et al. 2018).

Figure 1.

Evaluation of the predicted nucleosome density. (A) Comparison between experimental (red) and predicted (blue) nucleosome densities in a region of Chromosome 16. Genes are shown in blue on top of the two tracks (data from Hughes et al. 2012). (B) Density plot of the predicted nucleosome density in function of the experimental nucleosome density. The correlation between the two signals is 0.68. The distributions of the values of these two tracks on Chromosome 16 are also shown at the top (experimental) and on the right (prediction). (C) Cross-correlation between nucleosome densities on Chromosome 16 for four technical replicates (data from Kaplan et al. 2009) and four predictions obtained with models trained on each of the four replicates (e.g., rep1_pred is obtained with a model trained on the rep1 nucleosome density). (D) Cross-correlation between nucleosome densities for 13 experiments and 13 predictions with models trained on each of the 13 experimental densities (experimental densities are on the horizontal axis, predicted densities on the vertical axis). The 13 experiments were carried out using different growth media (namely YPD, YPEtOH, and YPGal). Two different cross-linking conditions were used (cross-linking of nucleosomes on DNA prior to MNase digestion: CL; or no cross-link: NOCL).

To investigate the generalizability of our results, we trained four CNNs models independently on four experimental replicates from a different data set (Kaplan et al. 2009). The Pearson's correlation between predictions (0.85 ± 0.05) is in the same range as the correlation between experimental replicates (0.87 ± 0.07). These values are constantly higher than the correlation between predictions and experiments (0.58 ± 0.05) which is itself lower than the correlation of 0.68 we obtained with the Hughes et al. data set above (Fig. 1C; Hughes et al. 2012). An important control is that the performance obtained by comparing the predicted density with the experimental density coming from the data set used for training the model is not significantly higher than the performance obtained by comparing the predicted density with the experimental densities from data sets which were not used for training (i.e., correlation between rep1_pred [as defined on Fig. 1C], and rep1 is comparable to the correlation of rep1_pred with the three other experimental densities). The model thus filters a large part of the replicates variability, which indicates a good generalizability of the results.

Training a network is a nondeterministic process. We trained four networks on the same data set and looked at the variability in predictions. We found that this variability can vary locally and is correlated with the experimental variability observed between replicates (Supplemental Fig. S1). This indicates that using CNN could also be valuable to find regions of higher or lower confidence in experimental data.

To further investigate the generalizability of our models, we trained independently CNNs on experimental densities obtained under different experimental conditions (Kaplan et al. 2009). Those conditions are the growth medium (YPD, YPEtOH, YPGal) and the presence or absence of a formaldehyde cross-linking step in the experimental protocol. For each condition, several technical replicates are available. All the model-predicted densities do not correlate significantly better with the experimental densities that were obtained with the same growth medium as compared to the density that were used to train the model. This points toward an overall similar nucleosome positioning in these different growth conditions (Fig. 1D). We next focus on regions surrounding the GAL1-10 promoters, which are known to exhibit a different nucleosome occupancy profile in YPD versus YPGal (Supplemental Fig. S2). Our prediction captures the nucleosome depletion at these gene promoters in YPGal (highlighted in light blue on Supplemental Fig. S2) but fails to reproduce the strong positioning of specific nucleosomes neighboring these promoters in YPD (highlighted in light gray on Supplemental Fig. S2). The model thus learns some of the growth medium-specific patterns at locations where the nucleosome density changes significantly between experimental protocols.

The models trained on experimental results including or lacking a cross-linking step produce quite different predictions when applied on the Chromosome 16 sequence. The models that were trained with an experimental density lacking a cross-linking step are predicting densities that correlate, on average, better (0.59) with experimental densities obtained with no cross-linking step than with experimental densities obtained using a cross-linking step (0.49). Similarly, predicted densities obtained with a model trained on cross-linked data correlate, on average, better with experimental densities obtained with cross-link (0.45 vs. 0.39). The globally lower correlation values obtained using experiments that include a cross-linking step show that this step generates modifications in the experimental nucleosome density that cannot be predicted from the sequence alone. This suggests that this step can alter the nucleosome profile in a nonreproducible way.

For the sake of comparison of our CNN-based method with previously proposed CNN-based method for predicting nucleosome positions from DNA sequences, we used two previously proposed networks (Di Gangi et al. 2018; Zhang et al. 2018) to predict the nucleosome density over the entire Chromosome 16. We found a correlation between prediction and experiment of 0.43 and 0.40 to be compared with 0.68 obtained with our model trained and tested on the Hughes et al. (2012) data set. The lower performance of previously published methods for this task is expected because both methodologies were designed as classifiers which discriminate between fragments of DNA containing a nucleosome and fragments of DNA devoid of nucleosomes, whereas our method is designed to predict directly the nucleosome density over a whole chromosome. All methods nevertheless reproduce accurately inter-genic nucleosome-depleted regions, but our method reproduces with more accuracy the locally periodic density observed between depleted regions (see Supplemental Fig. S3).

Studying the effect of input length L on the predicted nucleosome phasing at TSSs

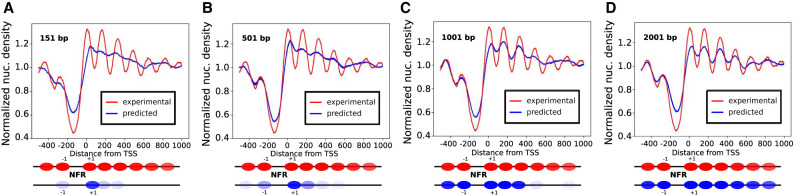
Whereas specific DNA-binding proteins usually recognize short DNA motifs, nucleosomes are positioned by a combination of several other mechanisms, including DNA local flexibility and shape, as well as the presence of neighboring nucleosomes (Mavrich et al. 2008; Tsankov et al. 2010; Zhang et al. 2011; Hughes et al. 2012; Riposo and Mozziconacci 2012). The length L of the input sequence in our model is thus an important parameter that can change the performance of the CNN. We display on Figure 2 a comparison between the predicted and experimental metagene profiles (i.e., nucleosome density averaged over TSS regions) for different input lengths (L = 151, 501, 1001, and 2001 bp). The experimental nucleosome density exhibits a characteristic pattern when averaged over TSS regions: a region with a low density, known as the nucleosome-depleted region (NDR), precedes the TSS position. Further nucleosomes are regularly spaced with a periodicity of 167 bp on the gene body (Mavrich et al. 2008; Riposo and Mozziconacci 2012). This pattern reflects the molecular mechanisms at work in nucleosome positioning. Nucleosomes are excluded from regions preceding TSSs, which are enriched with RNA polymerase. These regions act as barriers around which nucleosomes tend to stack upon each other, either due to thermal noise (Mavrich et al. 2008), or to chromatin remodelers (Lieleg et al. 2015) and local attraction between nucleosome faces (Riposo and Mozziconacci 2012). How accurately this characteristic pattern is reproduced by the model is hereafter used as a qualitative measure.

Figure 2.

Influence of the input length L on the pattern of the predicted nucleosome density in TSS regions. Average predicted (blue) and experimental (red) nucleosome density in TSS regions. The predicted nucleosome density is here obtained with CNN models trained with different values of L ([A]: 151 bp, [B]: 501 bp, [C]: 1001 bp, [D]: 2001 bp). The other hyperparameters of the network are the same. Nucleosome positions (in red for the experimental and blue for the predicted densities) are sketched below the curves. +1 and −1 refer to the first nucleosomes before and after the NDR.

The CNN model is able to identify and predict the NDR for all values of the input length L. This result is expected because short DNA motifs such as poly(A) motifs are known to exclude nucleosomes from these regions. However, the prediction of the periodical pattern has a strong dependence on the input length L. For L = 151 bp (which corresponds to a single nucleosome), the model is not able to recover the periodical pattern (Fig. 2A); the correlation between the predicted and the experimental metagene profiles is nevertheless high—it reaches 0.9 (Supplemental Fig. S4). For L = 501 bp (approximately three nucleosomes), a periodical pattern starts to appear, and the first nucleosome after the TSS is well positioned (Fig. 2B); this improvement can be quantified by the correlation between metagene profiles which increases to 0.93. For L = 1001 bp (six nucleosomes), the periodical pattern improves, and the first three nucleosomes after the TSS are well positioned (Fig. 2C); the correlation between the metagene profiles reaches 0.95. The best prediction quality is obtained for L = 2001 bp, which corresponds to 12 nucleosomes, the typical size of longer genes. For this particular length of the input, the characteristic nucleosome pattern in TSS regions is well reproduced by our network (Fig. 2D); the correlation between the metagene profiles is accordingly increased to 0.97. Further increasing the input length does not change the performances significantly, whereas it penalizes the training process due to an increasing need for computational memory. The global correlation between experimental and predicted densities over the whole chromosome increases from 0.63 to 0.68 (Supplemental Fig. S7) when the input length L increases.

Genome transfection of Kluyveromyces lactis in S. cerevisiae

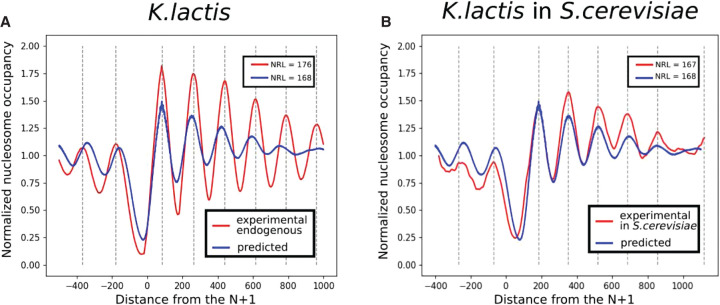
Hughes et al. (2012) transfected pieces of the Kluyveromyces lactis genome into S. cerevisiae and measured the nucleosomal density with MNase-seq in order to compare the nucleosome positioning mechanisms in different species. Following their idea, we try to predict the nucleosome density in a different yeast species to further assess the generality of the model. The model trained on S. cerevisiae is first used to predict the nucleosome density on Chromosome F of K. lactis. Results are presented in Figure 3, where the predicted density averaged over TSSs is compared with two different experimental densities (Fig. 3A): the nucleosome density on Chromosome F of K. lactis (Fig. 3B) and the nucleosome density on Chromosome F of K. lactis transfected in S. cerevisiae. The CNN is able to capture accurately the NDR in K. lactis while being trained on S. cerevisiae. We conclude that DNA sequence motifs that determine NDR are similar between those two species. If we consider now the periodical pattern on the gene body, we can see that the prediction on K. lactis displays a periodical pattern, but the value of the period, called nucleosomal repeat length (NRL), is the same as in S. cerevisiae (167 bp), whereas it should be 176 bp, as observed in K. lactis. The predicted density is indeed similar to the experimental nucleosome density obtained on the transfected K. lactis sequences in S. cerevisiae. Our model is able to predict the behavior of the cell machinery of S. cerevisiae for the task of positioning nucleosomes on an exogenous genome.

Figure 3.

Predictions on the Kluyveromyces lactis genome compared with experiments. The prediction of the model, trained on Saccharomyces cerevisiae and applied on Chromosome F of K. lactis, is compared with the experimental data obtained by Hughes et al. (2012). The signal around every TSS is aligned with respect to the first nucleosome downstream from the TSS and averaged. (A) Endogenous context (Chr F of K. lactis in K. lactis). (B) Transfected context (Chr F of K. lactis in S. cerevisiae).

Having carefully characterized the behavior of our model across replicates, experimental conditions, and DNA sequences from different species, we now wish to use it to predict the effect of single mutations on the nucleosome positions.

Predicting the effect of single mutations

With our model in hand, it is now possible to predict the nucleosome positions resulting from a mutation in the genome. The rationale behind this is that the more important a nucleotide is regarding nucleosome positioning, the more the effect of a mutation of this nucleotide will modify the predicted nucleosome density. In order to find positions on the genome associated with such modifications, we generate all the possible single mutations along the genome and assign to every position a mutation score. This mutation score represents the Z-normalized distance between the nucleosome density predicted with and without mutation. Training several CNNs by letting aside from the training set each time the chromosome on which the prediction will be made, we computed the mutation score across the whole genome (see Methods for details).

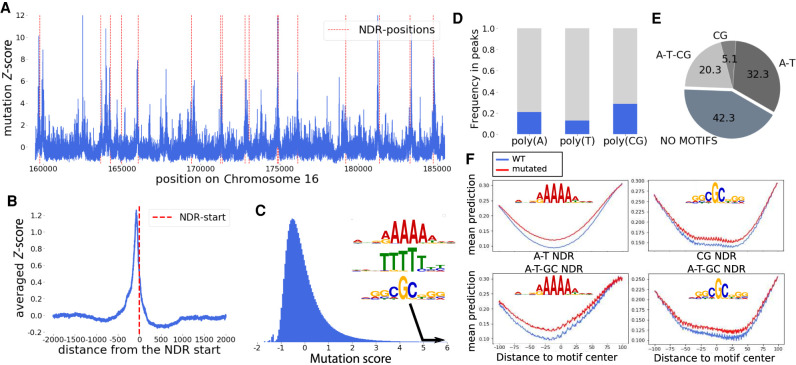
A typical example of the mutation score along a region of Chromosome 16 with representative peaks at specific positions is outlined in Figure 4A. Those peaks often coincide with NDRs, represented as red dotted lines in Figure 4A. Aligned and averaged around every NDR start, the mutation score displays a peak centered on the NDR (Fig. 4B). This result highlights the fundamental role of the NDR in nucleosome positioning.

Figure 4.

Effect of single mutations on the nucleosome density. (A) The mutation score on a region of Chromosome 16. NDRs are shown with red dotted lines. (B) Average of the mutation score aligned on all NDR starts. On average, the mutation score is peaking in the NDR, showing the major role of those regions in the nucleosome positioning process. (C) The distribution of the mutation score, as well as the three motifs enriched in the DNA sequences found in peaks with high mutation scores. (D) Proportion of poly(A), poly(T), and poly(CG) motifs in the genome that correspond with a high mutation score. (E) Proportion of four groups of NDR:NDR containing only poly(A/T) motifs (referred to as A-T), containing only poly(CG) like motifs (CG), containing both poly(A) and poly(CG) like motifs (A-T-CG), and NDR harboring none of these motifs. (F) Effect of a mutation in the poly(A/T) and poly(CG) motifs found in NDRs on the nucleosome density in A-T and CG NDRs, respectively (top), and in A-T-CG NDRs (bottom).

The distribution of the mutation score (Fig. 4C) exhibits a narrow peak with over 90% of the values falling between −1 and +1 standard deviations, to be compared with 68% expected for a normal distribution. The distribution also features a long tail toward positive values corresponding to mutations having a strong impact on nucleosome positioning. In the following, we focus on mutations with a score above 5, representing 0.6% of the genome.

To investigate the existence of DNA motifs for nucleosome positioning (Segal et al. 2006), we analyze the motifs found at these high mutation score positions. We collect all 15-bp sequences surrounding a nucleotide with a high mutation score and extract from them overrepresented motifs (see Methods). Those motifs can be separated into two groups. The first group corresponds to poly(A) and the second group corresponds to poly(CG) (Fig. 4C).

The first group, poly(A), has previously been shown to be overrepresented in NDRs and to have a role in nucleosome exclusion from these regions (Suter et al. 2000; Anderson and Widom 2001; Raisner et al. 2005; Segal and Widom 2009). This effect has been proposed to be in part due to the natural stiffness of the poly(A) stretches (Iyer and Struhl 1995) and is enhanced and modulated by active nucleosome remodeling (Zhang et al. 2011; de Boer and Hughes 2014). An important player in this process is the Remodeling the Structure of Chromatin (RSC) complex, which has been shown in vitro to clear promoters by removing nucleosomes from poly(A) sequences (Krietenstein et al. 2016).

The second group, poly(CG), also corresponds to the binding sequence of a subunit of the RSC (RSC3) (Badis et al. 2008). These sequences are found preferentially ∼100 bp upstream of TSSs (see Supplemental Fig. S5). Mutation of the RSC3 protein has been shown to result in an increase in nucleosome occupancy at NDRs which contained a poly(CG) motif, suggesting that these sequences can exclude nucleosomes as well (Badis et al. 2008).

The roles of poly(A) and poly(CG) have previously been described only in NDRs upstream of TSSs, and our findings are in line with these previous results. Indeed, only a fraction of those core motif occurrences result in a significantly high mutation score (21% for poly[A], 13% for poly[T], and 29% for poly[CG]) (Fig. 4D). These sites are enriched in NDRs: when the motifs are present within gene bodies, their predicted impact on nucleosome positions is weaker.

We next ask whether all NDRs have poly(A) or poly(CG) motifs and find that almost 60% of the NDRs harbor at least one of these motifs (Fig. 4E). Approximately 40% of the NDRs harbor motifs coming from one group only, but the two groups are not mutually exclusive, because ∼20% of the NDRs harbor motifs coming from both kinds, that is, one poly(A) and one poly(CG) (Fig. 4E). We next investigate the relative position of these motifs relative to the TSS. Poly(A) and poly(CG) motifs are typically located 120 and 140 bp upstream of the TSS (Supplemental Fig. S5). When both sites are present within a NDR, the poly(A) is, on average, moved further away from the TSS (160 bp). The position of the start site of the NDR does not depend on the group of motifs present: the NDR always starts, on average, 75 bp upstream of the TSS (Supplemental Fig. S5).

To investigate more quantitatively the effect of disrupting these motifs within the NDR, we compute the averaged predicted nucleosome density in a 200-bp region centered on all motif instances within NDRs with and without mutations in the motif. A mutation of a nucleotide in either a poly(A) or poly(CG) motif results in an increase of the nucleosome density in the vicinity of the mutation (Fig. 4F). A similar effect is seen for the complementary motifs poly(T) and poly(GC). This effect does not depend on the fact that one or two different motifs are found within a NDR. We conclude that, in agreement with previously reported experimental results, these two motifs are involved in the depletion of nucleosomes. Using this methodology, we do not find any motifs that would position nucleosomes by attracting them, that is, motifs for which a mutation would locally reduce the nucleosome density.

Predicting the effect of multiple mutations

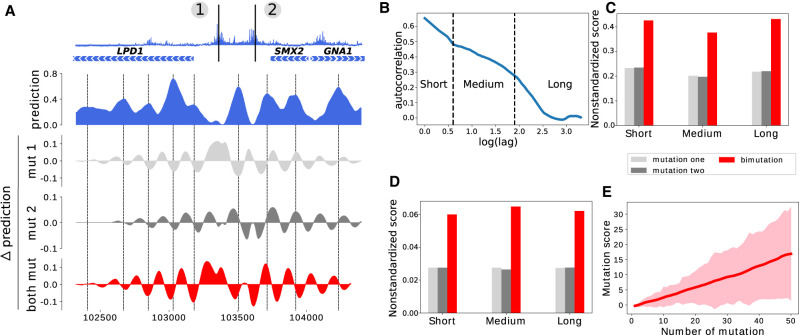
When designing synthetic genomes, one often needs to make several mutations in a given region. We therefore set out to investigate qualitatively the effect on the prediction of the nucleosome occupancy of having two or more mutations. We chose for illustration purposes a region of Chromosome 16 displaying two high mutation score positions in an inter-genic region (Fig. 5A, top). The two sites, numbered 1 and 2, fall into two NDRs that flank a well-positioned nucleosome. We computed the variation in predicted nucleosome occupancy that resulted in mutating each one of the sites or mutating both sites. Mutation of site 1 results in a partial loss of the corresponding NDR. Nucleosome occupancy decreases at nucleosomal peaks in the vicinity of the mutation (indicated with dotted lines on Fig. 5A) and increases in linker regions. Mutation of site 2 induces a wider opening of the corresponding NDR as well as a sliding of the two neighboring nucleosomes away from the NDR. When mutating both sites, this results in a nontrivial combination of the two variations, leading to an overall higher perturbation of the nucleosomal occupancy than for one mutation alone.

Figure 5.

Effect of mutating multiple nucleotides. (A) Illustration of the effect of two mutations on nucleosome occupancy on a locus of Chromosome 16; (top) mutation score over the region, (blue) predicted nucleosome occupancy for the wild-type sequence, (light gray and gray) local variation of the prediction obtained when mutating position 1 or 2, respectively, (red) local variation of the prediction obtained when mutating both positions. Nucleosome occupancy peaks are highlighted with dashed lines. (B) Autocorrelation of the mutation score (semi-log-10 plot). Three different regimes can be identified, separated by dashed lines. (C) Average nonstandardized mutation score obtained by mutating 16,000 randomly sampled single nucleotides presenting a high mutation score (>5, light gray), by mutating, one by one, all nucleotides that are found closer than 500 bp to these mutations (gray), and by mutating all pairs of nucleotides that are closer than 500 bp (red). Mutation scores are separated in three categories based on the distance between the two mutated nucleotides: less than 5 bp (Short), between 5 bp and 90 bp (Medium), and between 90 bp and 500 bp (Long). (D) Same as C but for nucleotides with a low mutation score (<1). (E) Evolution of the mutation score with the number of mutations with a low mutation score. All mutations considered here—taken individually—have a score <1. The solid line represents the average mutation score, and the width of the line represents the standard deviation of the distribution of mutation scores.

We then set out to quantify the average effect of having two mutations at high-scoring mutation sites. We reasoned that the combination of two mutations may depend on the distance between these mutations. Based on the autocorrelation of the mutation score (Fig. 5B), we defined three different types of comutations: the first one for mutations that are closer than 5 bp corresponds to mutations in the same motif; the second one for mutations which are found between 5 and 90 bp away corresponds to mutations within a cluster of motifs; and the third one corresponds to mutations which are found between 90 and 500 bp. Note that by construction of our network, mutations which are found at a distance greater than two input sequence lengths (here, 4000 bp) will be independent, so that the mutation score for the two mutations will be the sum of mutation score for each mutation taken independently. In order to evaluate the effect of two mutations and compare this effect with the effect of single mutations, we selected 1000 loci with high (>5) mutation scores on each chromosome and computed their average mutation score (Fig. 5C, light gray). For all these mutations, we investigated the effect of high-scoring mutations that were found within 5 bp (Short) by computing their average nonstandardized mutation score (Fig. 5C, gray). We then compared these two values with the average nonstandardized score obtained by mutating both the primary and secondary mutations (Fig. 5C, red). We used here nonstandardized scores which are always positive and additive by construction, whereas standardized scores are not. This procedure was repeated for mutations found between 5 and 90 bp away (red, Medium) as well as for mutations found between 90 and 500 bp away (red, Long). We conclude that the effect of having two mutations of high mutation score within a region can be, on average, approximated by the sum of the effect of each mutation taken independently and that this effect does not depend on the distance between mutations. The sum of the mutation score of each mutation and the mutation score associated with their simultaneous mutations are strongly correlated (0.75 for short-, 0.70 for medium-, and 0.80 for long-distance comutations) (Supplemental Fig. S6A–C). As a recommendation for genome design, we thus advise changing as few nucleotides as possible with high mutation scores.

When repeating a similar analysis for low mutation score nucleotides (score < 1) (Fig. 5D), we also found that mutating two nucleotides with low mutation score impacts, on average, the nucleosome occupancy in the proportions one would expect by adding the mutation scores for each mutation. The sum of the nonstandardized mutation score of each mutation and the mutation score of the comutations are also strongly correlated (0.73 for short-, 0.82 for medium-, and 0.97 for long-distance comutations) (Supplemental Fig. S6D–F). On average, mutating two such nucleotides leads to a standardized mutation score of 1, still much below the highest scores that can be obtained by changing some specific nucleotides with high mutation scores. Nevertheless, when adding more and more mutations within the same region, the mutation score can reach values as high as 15, that is, scores obtained when mutating two high-score nucleotides (Fig. 5E). As a guideline for design, our analysis shows that, on average, 20 low-score mutations have a similar effect as compared to one high-score mutation.

These figures can serve as a baseline to evaluate the effect of a specific sequence design on nucleosome positions, but in the case of a massive editing of many nucleotides, we recommend running a full prediction of nucleosome occupancy on the designed sequence in order to check for the potentially unwanted effects on nucleosome positioning.

Discussion

In this study, we used deep learning to generate a genomic track that leverages MNase-seq experimental results in order to predict the potential changes of nucleosome positioning resulting from mutating any base pair in the S. cerevisiae genome. A similar procedure can, in principle, be done for any genomic track. The benefits of this track are twofold. First, it can give some guidelines to create a synthetic genome without modifying nucleosome positions in an unwanted manner. Second, the results can be used to better understand how nucleosomes are positioned by the underlying DNA sequence.

The study of the predicted nucleosome phasing at TSSs as a function of the input length of the network gives us more precise information. A network whose inputs are too short is able to capture the position of the NDR whereas it is not able to capture the periodicity in the pattern of nucleosome positions away from the NDR (Fig. 3). This observation leads to two conclusions: NDRs are hard-coded by DNA motifs, whereas the DNA sequence wrapped around nucleosomes is not suffcient to precisely set their positions. In a cross-species context, in which the network is trained in S. cerevisiae and the predictions are made on the K. lactis genome, the periodicity is wrongly predicted to be the one of S. cerevisiae, whereas the NDRs are well predicted. These observations reveal the importance of the conserved DNA motifs residing in the NDRs in the process of nucleosome exclusion upstream of the TSSs. Studying the influence of single mutations all along the genome allows us to confirm this mechanism and to point out these specific motifs. Poly(A) and poly(CG) are, in agreement with earlier experimental studies (Suter et al. 2000; Anderson and Widom 2001; Raisner et al. 2005; Badis et al. 2008; Krietenstein et al. 2016), shown to be the core motifs preventing nucleosomes from binding in the NDRs. Although our study confirms the role of these core motifs, it also outlines that not all of these motifs in the genome are important for nucleosome positioning. We also show that other positions along the genome can play a role in this process. A general guideline for designing a synthetic yeast genome would be to preserve nucleotides that present a high mutation score. For a quantitative anticipation of effects of mutation, the mutation score track is available at GitHub (https://github.com/etirouthier/NucleosomeDensity/blob/master/Results_nucleosome/mutasome_scerevisiae.bw).

Of course, the procedure used here in yeast for nucleosome positioning can be extended to other genomic tracks and other species. Whereas we have validated here the high potential of this approach by studying how the DNA sequence drives nucleosome positioning in yeast, we anticipate that it will be a very valuable tool to study nucleosome positioning rules in more complex organisms and ultimately in human. This would, for instance, empower the community to ask whether some mutations frequently associated with diseases have a predominant role in positioning nucleosomes. Several issues will need to be solved to achieve this aim. The first is mappability; because many genomic regions are repetitive, the nucleosome density cannot be measured on these sequences, and this needs to be explicitly taken into account during training. The second is the size of the genome. The human genome is more than 200 times longer than the yeast genome. This has two impacts. The first is the coverage of the MNase experiment. The best coverage achieved for human cells is about 30 reads per nucleosome, whereas it is usually 10 times higher in a standard yeast experiment (cf. Valouev et al. 2011 and Kaplan et al. 2009). Last but not least, nucleosome spacing in human depends both on the cell type considered as well as on the location on the genome. The nucleosomal spacing is 167 bp in yeast, and the nucleosomal density shows only minor changes in different growth conditions (Supplemental Fig. S2). In human, the spacing can change along the genome as well as in different cell types, taking values ranging from 178 to 205 bp (Valouev et al. 2011). We expect that these issues can be solved by using more sophisticated network architectures as well as increasing the computing power and that future developments in deep learning algorithms will become a game-changing technology for genome writing.

Methods

Data accession and preprocessing

We use the reference genome sacCer3 of S. cerevisiae, available at: http://hgdownload.soe.ucsc.edu/goldenPath/sacCer3/bigZips/.

MNase-seq experimental results are available through NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession numbers GSM552910 and GSE13622 (Kaplan et al. 2009). Data for K. lactis used in the present study have been obtained from Tsankov et al. (2010) and are available at GEO under accession number GSE21960. The experimental averaged nucleosome density in the TSS regions was obtained from the study of Hughes et al. (2012) and is available at GEO under accession number GSM953761.

To obtain the nucleosome density from single-end reads, we take the beginning of each read and add one count for each base pair in a region of 100 bp in the direction of the read. We then truncate the obtained nucleosome density to a threshold—the 99th percentile of the distribution of density scores—and divide the density by the threshold. This finally yields a density signal comprised between zero and one. We prepare input sequences of 151, 301, 501, 1001, 1501, and 2001 bp for every position in the genome except for Chromosome 16 to define the training (Chromosome 1 to 13) and validation (Chromosome 14 and 15) sets. We thus generate 10,613,042 input sequences among which those corresponding to a nucleosomal density equal to zero are excluded (as they correspond to nonuniquely mappable sequences). Each input sequence is then labeled with the nucleosome density value found at its central position.

Model architecture and training

We implement the CNN using the Keras library (https://keras.io) and TensorFlow (Abadi et al. 2016) as back-end. A RTX 2080 Ti GPU is used to improve training speed. We use the adaptive moment estimation algorithm (Adam) to compute adaptive learning rates for each parameter and a batch size of 512.

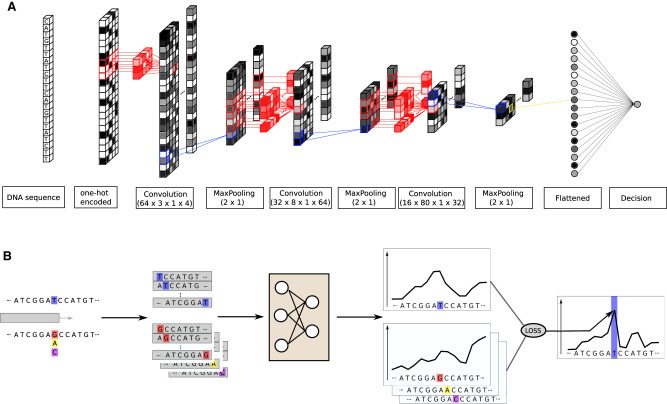
Our CNN architecture (see Fig. 6A) consists of three convolutional layers with, respectively, 64, 16, and 8 kernels of shape (3 × 1 × 4), (8 × 1 × 64), and (80 × 1 × 16). The stride is equal to 1. Our model takes inputs of shape (L, 1, 4), the last dimension representing the four nucleotides.

Figure 6.

CNN architecture and mutation score computation. (A) The model is trained to predict the nucleosome density at the center position of a 2001-bp-long DNA sequence. It contains three convolutional layers with max-pooling, batch-normalization, and dropout. The final convolutional layer output is flattened and fed to a single output neuron. (B) We test all the possible mutations at the position indicated in blue, here a T, and predict the nucleosome density around this position with and without mutations. The mutation score is the Z-normalized sum of the distance between the wild-type density and all the mutated type. The loss function used to train the network is used to compute the distance.

The first and second layer kernels identify 20-bp-long motifs which will play a role in the local affnity of the DNA sequence for nucleosomes. It is known, for instance, that poly(A) will disfavor nucleosome formation, whereas an ∼10-bp periodic enrichment of AA/TT/TA dinucleotides that oscillate in phase with each other and out of phase with GC dinucleotides will increase the affnity of the sequence for nucleosomes (Segal et al. 2006). The third layer is designed to capture long-range information (coming from several nucleosomes) in order to grasp the nucleosomes stacking one against another (Riposo and Mozziconacci 2012).

The ReLU function is applied to the outputs of convolutional layers, which are then entered into a max-pooling layer with pooling size (2 × 1). After each max-pooling layer, batch-normalization is applied as well as a dropout with a ratio of 0.2. Finally, the output of the last layer is flattened and connected to the output layer containing one neuron through a single perceptron and using a linear activation function to make predictions. We tested several other architectures before choosing the one described above, and a full recapitulation of hyper-parameters values which were tested is presented in Supplemental Table S1.

The loss function combines the Pearson's correlation (corr) between the prediction and the target and the mean absolute error (MAE) between them (loss = MAE[ŷ, y] + 1−corr[ŷ, y], with ŷ being the model prediction and y the target). The rationale for using this combined loss function is that we get a faster convergence and better final values both for the MAE and the correlation than using only one of them as a loss function (see Supplemental Fig. S7).

An early stopping procedure is applied during training to prevent models from overfitting. The loss function is calculated on the validation set at every epoch to evaluate the generalizability of the model. The training procedure is stopped if the validation loss does not decrease at all for five epochs and the model parameters are set back to their best performing value. The training procedure usually lasts 15 to 20 epochs.

TSS alignment

For Figure 2, genes positions of the studied species are download from the Ensembl fungi browser (ftp://ftp.ensemblgenomes.org/pub/fungi/release-46/gff3/saccharomyces_cerevisiae/Saccharomyc es_cerevisiae.R64-1-1.46.gff3.gz). The alignment on the TSS is simply made by taking a window of [−500, 1000] bp around every TSS and by averaging the signal.

Figure 3 displays the average nucleosome density in the TSS region realigned on the first nucleosome downstream from the TSS as previously performed by Hughes et al. (2012).

NDR determination

The NDR positions are defined as in Tsankov et al. (2010). Briefly, the signal is firstly modified by setting to zero all the positions with a value lower than 40% of the mean value, so that DNA linkers appear as a series of zeros. NDRs are then defined as the first linkers longer than 60 bp upstream of each TSS. If no suffciently long linker is found closer than 1000 bp away from the TSS, the first zero is set as the beginning of the NDR.

Mutation score

To assign a mutation score to every position on the genome, we use the methodology displayed on Figure 6B. All the three possible mutations at a given position (highlighted in blue) are performed. The wild type and the three mutated genomes are used to predict the nucleosome density. Predictions are made on the complete range in which the mutation can affect the model, that is, ±1000 bp around the mutated position. Then, using the training loss function, we compute the distance between the wild type local density and all the three mutated type local densities. By summing these three distances, we assign a score to the mutated position. This score is then Z-normalized within each chromosome to give the mutation score. This score reflects how the nucleosome density was perturbed by the mutation at the chosen position. Knowing that the nucleosome positions are not directly encoded in the underlying DNA sequence, we take long-range perturbations into account using this methodology.

For the track presented along with the manuscript, the mutation score on Chromosome N is the average of three mutation scores obtained with three models independently trained on all the chromosomes with the exclusion of Chromosome N. Although only a small fraction of the training set is suffcient to reach the maximum of accuracy (Supplemental Fig. S8), we chose to use all sequences for training to improve the reproducibility of the mutation scores. We finally obtain a robust mutation score, as two independently computed scores reach a correlation of 0.88 (Supplemental Fig. S9). In this regard, it is good practice to train several models independently and to use the average of the prediction scores to assess the effect of a mutation.

Motif analysis

We make the assumption that a nucleotide assigned a high mutation score belongs to a motif that plays a role in the nucleosome positioning process. Every nucleotide assigned with a mutation score >5 is considered to be the center of a 15-bp important motif. All those loci are collected (64,610 loci) and aggregated when they intersect (23,585 loci). We then use MEME (Bailey et al. 2015) to extract significant motif logos from those loci. We used the following options: meme -oc outdir -nmotifs 10 -dna sacCer3peakseq.fa. MEME is commonly used to extract binding site logos from the DNA windows underlying peaks of ChIP-seq data; we use it to extract meaningful logos from the DNA windows containing nucleotides with high mutation scores.

Software availability

The mutation score track is available at GitHub (https://github.com/etirouthier/NucleosomeDensity/blob/master/Results_nucleosome/mutasome_scerevisiae.bw) and as Supplemental Code. All of the code necessary to reproduce the results is accessible at GitHub (https://github.com/etirouthier/NucleosomeDensity.git) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.