A classification of countries and regions by degree of the spread of coronavirus based on statistical criteria

Abstract

This paper presents models of the spread of SARS-CoV-2 coronavirus in individual countries and globally in 2020 based on the statistical characteristics of the spread in the given countries or regions (in particular, in Hubei province). Through modeling, we attempt to achieve a goal which is of vital interest to societies in a pandemic catastrophe, and to answer the question of what stage of spread the epidemic has reached in a given country. The country classifier we developed is based on the relative variability indicator of the confirmed cases variable. This classification indicator is compared with a set of data-driven thresholds, the crossing of which determines the degree of spread of the epidemic in a given country. The article was written between April 2020, when the pandemic had been suppressed in China and was raging in Europe and the USA, and August 2020, as a new wave of local resumed outbreaks appeared in many countries. We contend that the spread phases are predictable based on statistical similarity. There are four phases of epidemic spread: growth, duration, suppression and re-outbreak. The authors’ Matlab software, which allows simulations of the spread of coronavirus in any country based on data published by CSSE, is available in the public GitHub repository.

1. Introduction

Our aim is to address the statistical aspect of the spread of SARS-CoV-2 coronavirus in various countries by building a model based on the variability of the most commonly used variables. In an analysis of the sources of data on SARS-CoV-2 coronavirus, one should first of all acknowledge a commonly used web application in the form of an interactive dashboard, located at https://www.arcgis.com/apps/opsdashboard/index.html, which allows the status of the pandemic to be viewed anywhere in the world. This site is a result of the work of three employees of the Center for Systems Science and Engineering (CSSE) (2020) at the University of John Hopkins in Baltimore – Ensheng Dong, Hongru Du and Lauren Gardner, who published key information in the Lancet Infectious Diseases on 19 Feb 2020 regarding the launch of the dashboard (Dong et al., 2020). This dashboard is an important informational and sometimes spiritual support for many societies, institutions, research facilities and governments. Of course, this contains pure statistical information, of a more technical than medical, microbiological or clinical nature. All the collected data (from many healthcare organizations, including the WHO, CDC, ECDC, Worldometer (2020), etc.) are updated daily and are available through the GitHub repository. Currently, the dashboard is used by millions of people, being one of the most important open sources of statistical data concerning the pandemic.

Similar knowledge and data are also provided by two other notable sources - the work of Roser et al. (2020) and the sources of worldometers.info, which contain many varied data and charts. In the literature on SARS-CoV-2 coronavirus, there are a large number of publications on the first SARS-CoV virus outbreak (detected in 2003), among which works on the medical, clinical and epidemiological aspects of the disease predominate. Examples are articles written by e.g. Du et al., 2005, Yen et al., 2006, Takeda-Shitaka et al., 2004, Liu et al., 2003, Nasir and Rehman, 2017. Of course, there are fewer peer-reviewed publications so far about the second SARS-CoV-2 virus outbreak (detected in 2019), than about the first epidemic, which adopt the same microbiological approach; however, we can consider, e.g. Xu et al., 2020, Huang et al., 2020, Benvenuto et al. (2020) or Zhao S. et al. (2020). Moreover, the preprint literature on SARS-CoV-2 is expanding rapidly. In addition to the undoubtedly important medical aspects of the spread of SARS-CoV-2, presented above, societies in many countries expect information on statistics regarding the duration of the epidemic, periods in which the number of cases doubled, the average number of infections from one patient, the expected number of patients, deaths, etc. Therefore, in this work, motivated by these expectations, the authors deal only with the statistical aspect of the spread of SARS-CoV-2 in various countries.

The ongoing epidemic is a challenge for scientists creating spread models because data available in many countries (including the US) is still on an early growth trajectory, and the epidemiological features of the new coronavirus have not yet been fully explained. Few papers have been published that attempt to apply a statistical approach to modeling the spread of the virus. These include, for example, the work of Nesteruk (2020), in which an attempt is made to use the SIR (Susceptible-Infected-Recovered) model for short-term data (only for China). This work should be treated as preliminary estimates for long-term forecasts of the spread based on more complex mathematical models. They require identification and calculations of unknown parameters. Also, taking a statistical approach, Wu et al., 2020, Wu et al., 2020, use the SIRD (Susceptible-Infected-Recovered-Dead) model for major Chinese cities. Both of these studies, as well as others of similar content, e.g. Zhao and Chen (2020) or Roosa et al. (2020), Li et al. (2020), Yang et al. (2020) were published in January and February 2020 and are among the first studies of this type and predict the rapid spread of the virus throughout the world.

In the following months of the epidemic, further analyses, such as that of Elmousalami & Hassanien (2020), confirmed the rapid and exponential spread of the virus. Fanelli & Piazza (2020) showed a certain regularity in the spread of the epidemic in three countries (China, Italy, France). Their analysis suggests that models can be used to collect quantitative data on the spread of the epidemic, especially the size and timing of the peak of infection. The analysis of data under the SIRD model indicates that the kinetic parameter describing the recovery rate seems to be independent of the country, while the percentages of infections and deaths appear to be more variable. Accurate insights on the mathematical modeling of coronavirus can be attributed to Kucharski (2020), both in his popular science publications (as in New Scientist) and as an epidemiologist (Kucharski et al., 2020).

The traditional epidemiological models indicated above require very detailed data for analysis. Because of this, Fu et al. (2020) proposed using Boltzmann's approach to estimate the potential number of infections in China. Only daily measurements of the cumulative number of confirmed cases of SARS-CoV-2 were used.

It should be mentioned that the current prevailing pandemic has also attracted interest from researchers in the field of computer science / artificial intelligence. One outcome of this interest is a methodology proposed by Fong et al. (2020) for forecasting the spread of the epidemic for a small sample of data. Their results show that the proposed polynomial neural network can be useful in generating a critical outbreak prognosis when a small amount of data is available.

Many interesting papers, published in the form of preprints, have yet to be reviewed. These works were especially important in March-April 2020, after which peer-reviewed articles began to appear. For example, in the Research Gate resources, under the tag “Covid-19”, thousands of such preprints, messages or open projects can be found. Some of them directly relate to the topics covered in this article. Attempts are being made to forecast changes in the spread of the virus within specific countries or geographical regions. For example, the problem of forecasting for several states of Brazil is dealt with by a team of Brazilian researchers (Ribeiro et al., 2020). Quite good results were obtained for short-term, several-day forecasts on extinction predictions, MAP accuracy of 5–7%. Several AI methods were used, including Random Forest, SVR and the ARIMA model. Gupta & Pal (2020) are attempting a 30-day forecast for India based on the ARIMA model. The result of their research is a growing spectrum of model errors, growing along with the forecasting horizon. Other researchers – Petropoulos and Makridakis (2020), present a model for forecasting on a 10-day horizon; however, with larger errors than in the works just cited. A group of Slovenian scientists similarly presents less accurate models for 4 selected countries (Perc et al., 2020). In another work, Bhatnagar (2020) presents the modeling of the spread of the epidemic in India and other countries using a clustering method. Finally, Roy and Roy Bhattacharya (2020) use differential equation systems to simulate virus propagation in India taking into account local conditions.

All the above-mentioned works are characterized by the presentation of mathematical models based on existing statistical data. Most use CSSE resources as the base data (Dong et al., 2020). Despite the short time since the first cases of SARS-CoV-2 were discovered, the first studies comparing (from a medical/clinical/epidemiological point of view) the SARS-CoV and SARS-CoV-2 epidemics have already been published. These include the work of Wilder-Smith et al. (2020), which shows that preventive measures (isolating patients, etc.) adopted for the first version of the virus may not necessarily be effective at present. This is mainly due to the different scale of the spread of the virus: in 2003, the number of detected infections reached about 8000 people. Currently, it was already close to 2 million infected in the first days of writing this article, and up to 20 million in the final development phase of this work. On the other hand, with regard to the statistical approach, we could find no comparative publications covering both epidemics. Many scientists are attempting to predict the degree of the spread of coronavirus based on models developed after the 2003 epidemic (Dye & Gay, 2003). However, as with comparisons at the medical level, the models used so far may not be effective for SARS-CoV-2.

Given the relatively short time since the outbreak of the pandemic, the point where peer-reviewed literature pertaining directly to the pandemic can represent a coherent response has not yet been reached. The subject is still evolving, and the discourse is changing moment by moment as we discover new information about the pandemic, thus it is challenging to enter into that discourse in the way we normally conceive to do so within the scientific paradigm, but we endeavor to do so here. For example, in July 2020, there was an epidemic phase in several countries that we had not anticipated in April - the phase of local re-outbreaks. Most available studies are brief on-line publications with sparing use of editorial procedures, but this does not necessarily undermine their reliability and substantive value.

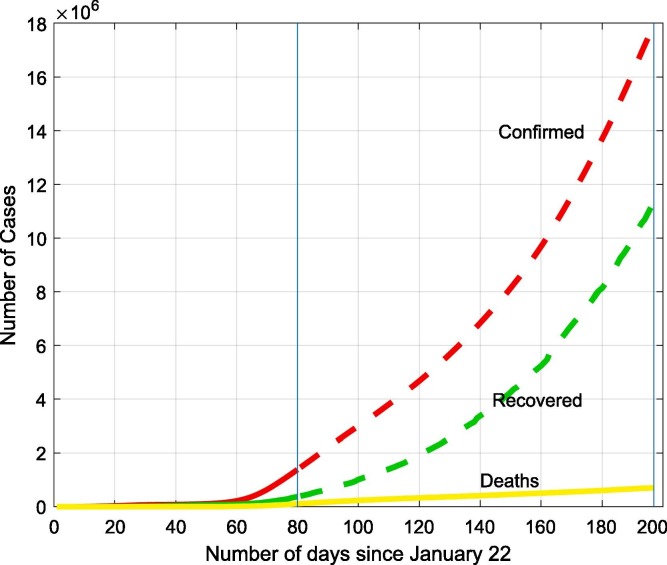
Because the global situation is extremely dynamic, we include Fig. 1, Fig. 2 to capture the moment this work is presented on the timeline. The first (Fig. 1) is the state of change in Hubei province, which symbolizes the outbreak of the pandemic, the second (Fig. 2) presents global cumulative curves published by the CSSE – Confirmed, Recovered, Deaths.

Fig. 1.

Three observed variables in Hubei province at the time of writing this work. The course of the curves clearly indicates epidemic suppression.

Fig. 2.

Three observed variables on a global scale for all the world at the time of writing the article. Compared to the situation in Hubei (Fig. 1), we observe the pandemic in the explosive phase.

The graphs show two completely extreme situations in the spread of the pandemic - an almost suppressed epidemic in Hubei province (Fig. 1) and its most dynamic phase in the world, driven by the United States and several major European countries - Spain, Italy, France, Germany and the United Kingdom (Fig. 2) until around day 80 of the pandemic, and then via Brazil, India, Russia and other countries up to around 200 days (from January 22, 2020). The graph (Fig. 2) shows a huge increase in the number of confirmed cases globally from day 80 to day 200. Globally, the pandemic is in a phase of strong growth. In some countries and regions, it may be better, e.g. as in Hubei province (as before).

The formation of each of these curves is accompanied by many controversies, measurement methods, and factors accounted for differently in different countries. We do not intend to attempt to account for any inconsistencies between the facts and the CSSE statistics.

2. Model for monitoring the spread of the virus based on the relative daily number of increases in cases

In the first of the two considered models, the authors searched for an indicator that would take into account changes in the basic variables measured and published by the WHO and CSSE – Confirmed, Recovered and Deaths. Such changes are of course observed and presented, e.g. the relative and absolute daily increase [worldometers.info]. The problem is that with the huge diversity of locales (countries or regions), the values of these variables are difficult to compare directly with each other and it is even more difficult to forecast their future trajectory.

The whole world is passionate about the trajectory of these variables over time, and with no specifically agreed definitions, the search continues for similarities between the spread in a given country compared with the so-called Chinese, Italian or US models. At the time of the beginning of writing (April – May 2020), these countries represented the three most characteristic patterns of the spread of the virus. The Hubei pattern, describing the spread of coronavirus in suppression, the Italian pattern, which could, perhaps, be described as the beginning of the end of epidemic growth and the US pattern - the virus in the phase of rapid growth.

Searching for a solution to determine the phase of the spread of the SARS-CoV-2 epidemic in a given country, regardless of the absolute values of the three basic variables, the authors focused on analyzing only one time series - the number of confirmed cases measured once a day. Treating this variable $\mathit{Conf}$ (Confirmed) as the basic one, a variable was introduced that depends on the instantaneous current maximum value in the $\mathit{Conf}(t)$ time series. Therefore, the variable $Y_i^m$ represents the highest value in the time series for each day $i=1,2,...,N$, whereas in the series ending on the $i$-th day, this value can only occur at the end of the series for $i=N$, because $\mathit{Conf}$ is the cumulative event variable, i.e. a non-decreasing variable.

$Y_j^m$ therefore increases monotonically with $i$ from a certain value and adopts a constant value - the highest in the whole time series.

$$Y_j^m=\max y_j,j=1,2,\cdots ,i,\mathrm{f}\mathrm{o}\mathrm{r}i=1,2,\cdots ,N,$$ (1)

where: $N$ - the number of columns of the $\mathit{Conf}$ variable matrix (number of observation days).

Let us denote the base time series, e.g. $\mathit{Conf}(t)$ as $y(t)$. This series is sampled once a day (just as CSSE data is presented) and is denoted as $y(i),i=1,2,\cdots ,N$.

Let us also define daily increases in this series as:

$$\mathit{yp}\left(i\right)=y\left(i\right)-y(i-1),\mathrm{f}\mathrm{o}\mathrm{r}i=2,3,\cdots ,N$$ (2)

and refer them to the previously specified maximum value of $Y_j^m$ as:

$$\mathit{Yp}(i)=\frac{\mathit{yp}(i)}{Y_j^m}$$ (3)

The $\mathit{Yp}$ variable turns out to be very selective if we wish to distinguish the stages of the spread of coronavirus in different countries. Fig. 3 shows an example of 10 countries with $\mathit{Yp}$ plots taken on the same day.

Fig. 3.

Graphs of $\mathit{Yp}$ index variability for different countries and regions. The graphs show the spread of SARS-CoV-2 in the suppression stage (with a green marker) and in the phase of intensive growth (without a green marker).

The figure shows the graphs of the $\mathit{Yp}$ variable for different countries / regions clearly differing in the spread phase of the coronavirus. It is possible to align the charts on which the epidemic is suppressed and those on which it strongly grows.

Assuming that the $\mathit{Yp}$ indicator will be a variable determining the diagnosis of the epidemic phase in a given country, the problem appeared of the dependence of these phases on the constantly changing maximum $Y_j^m$. This variability would be particularly unfavorable for the moment (date) of diagnosis of the first phase of the epidemic - the phase of advanced growth. It would be advisable for this moment to have a fixed date and be a parameter of historical importance for a given country. A continuous change of the maximum $Y_j^m$ after each reading of new data would consequently cause a continuous change of the position of this point on the timeline.

Therefore, it was decided to introduce a criterion for recognizing the first phase of the epidemic that would be independent of the number of columns in the $\mathit{Conf}$ matrix (independent of the data read).

The epidemic in each country registered in the CSSE matrices begins at different times, therefore its beginning is formally recognized after the appearance of non-zero values in the $\mathit{Conf}$ matrix for a given country.

Let $D_n$ denote the day on which the first non-zero $\mathit{Conf}$ value appeared for a given country:

$$D_n=iz|Conf\left(iz-1\right)=0\mathrm{a}\mathrm{n}\mathrm{d}Conf\left(i\right)>0,\mathrm{f}\mathrm{o}\mathrm{r}i=iz,iz+1,\cdots$$ (4)

Let us also introduce the concept of the reference day occurring $d_r$ days after $D_n$:

$$D_r=D_n+d_r$$ (5)

On the day $D_r$, the ordinate $\mathit{Conf}(D_r)$ will appear on each $\mathit{Conf}$ curve (for each country on a different day).

A more complete explanation of the relationship between $D_r$, and $d_r$ is explained in the Discussion. In particular, Fig. 8 illustrates this, using the example of the beginning of the epidemic in the USA. This is the case of the most rapid growth of Conf in the history of the pandemic. Let us now return to the consideration of the relative changes of Conf defined by (3).

Fig. 8.

Illustration of the formation of the first threshold on the Conf curve on the example of the confirmed cases variable for the USA.

Referring to $\mathit{yp}(i)$, according to (2), let us introduce the variable - relative daily increment, related to the ordinate $\mathit{Conf}(D_r)$:

$$\mathit{Yb}=\frac{yp\left(i\right)}{\mathit{Conf}(D_r)}$$ (6)

Let us now introduce the concept of the first ${\mathit{th}}_u$ threshold, the exceeding by the variable $\mathit{Yb}$ from the bottom of which will mean the $\mathit{Conf}$ curve entering the phase of dynamic growth.

$$\exists j(Yb\left(j\right)>{\mathit{th}}_u),j\in (\mathrm{i}=1,2,\cdots ,\mathrm{N})$$ (7)

In the studies, the results of which are presented here, the reference value was $d_r$ = 14 days and the threshold value ${\mathit{th}}_u$ = 1.0. This means that the phase of dynamic epidemic growth for a given country began on the day of the occurrence of daily increases in $yp\left(i\right)$ exceeding the ordinate of $D_r$. Observing the charts, we find that for some countries this happens very quickly (after a few days), and for other countries after several dozen days.

These differences, as the interval between the red and blue markers, can be seen in Fig. 3, Fig. 6. For example, the epidemic spread rapidly in Belgium, Brazil, Italy, Russia (Fig. 3), Uruguay, Slovenia and Luxembourg (Fig. 6). In turn, slow changes in the dynamics of the epidemic can be noticed, for example, in Poland (Fig. 3) and Cameroon (Fig. 6).

Fig. 6.

Occurrence of the fourth phase of the epidemic for selected countries in the $\mathit{Yp}$ indicator graphs.

With this definition of the beginning of the first phase (4), (5), (6), (7), it will always start for a given country on the same day, regardless of the day of observation of $N$.

After defining the first phase of the epidemic, thresholds based on the rate of relative increments $\mathit{Yp}$ were introduced for the determination of the subsequent phases of the epidemic according to (3).

To make a formal distinction between these stages (phases), the concepts of three additional thresholds were introduced:

• -the ${\mathit{th}}_m$ threshold for the duration of the epidemic, which, if exceeded from the top, implies the exit from the dynamic growth phase (phase 1) and the duration phase (phase 2) until the upper phase of suppression (phase 3) is reached;
• -the lower threshold ${\mathit{th}}_d$, the crossing from above of which indicates that the epidemic is being suppressed;
• -the ${\mathit{th}}_r$ threshold of re-outbreak, which, if exceeded from below, indicates the appearance of the fourth phase of the epidemic ${\mathit{th}}_r$.

Considering the range of $\mathit{Yp}$ variability for most countries, it was empirically determined that the stage of the epidemic (phase) is well extracted from the data when these thresholds have the following values:

${\mathit{th}}_m=0.010$;

${\mathit{th}}_d=0.005$;

${\mathit{th}}_r=2{\mathit{th}}_d$.

When generating the graphs in Fig. 3, such threshold values were set for all the considered countries and regions. The application of thresholds for each of the sub-charts (countries) in Fig. 3 resulted in the appearance of the proper marker for such a chart.

If the following condition was met:

$$\exists j(Yb\left(j\right)>{\mathit{th}}_u),j\in (\mathrm{i}=1,2,\cdots ,\mathrm{N}),$$ (8)

then the value 1 was assigned to a certain variable which signaled exceeding the threshold ${\mathit{th}}_u$:

$$E({\mathit{th}}_u)=1$$

For this value $i=j$ (on the $j$-th day of the simulation), a blue marker was placed on the ordinate with the value ${\mathit{th}}_u$. This meant that the given graph recorded a state of strong growth, hereinafter referred to as phase 1.

Let us continue to study changes over time on the indicator $\mathit{Yp}(i)$ chart. If such a simulation day $j$ was found for which another condition was met:

$$\exists j\left(Yp\left(j\right)<{\mathit{th}}_m\right)\wedge E\left({\mathit{th}}_m\right)=1,j\in (\mathrm{i}=1,2,\cdots ,\mathrm{N})$$ (9)

it was considered that at this value $i=j$, the upper threshold was exceeded in the return movement for the abscissa $j$ and the ordinate ${\mathit{th}}_m$ and the graph entered phase 2. This is understood as a transient phase (phase 2) and was not marked on the graph.

On the other hand, if the changes in the chart were continued towards a decrease in $\mathit{Yp}(i)$ until the condition was met:

$$\exists j\left(Yp\left(j\right)<{\mathit{th}}_d\right)\wedge E\left({\mathit{th}}_m\right)=1,j\in (\mathrm{i}=1,2,\cdots ,\mathrm{N})$$ (10)

then a green marker would be placed on the chart and the epidemic would go to the state referred to as phase 3 - the epidemic suppression phase. At this time, two markers would appear on the chart - blue and green. In terms of the state of advancement of the epidemic, this would mean the beginning of its gradual suppression in a given country/region.

In the final stage of the research, around July 2020, the fourth phase of the epidemic began to appear. Formally, this can be registered as the fulfillment of the condition:

$$\exists j\left(Yp\left(j\right)>{\mathit{th}}_r\right)\wedge E\left({\mathit{th}}_d\right)=1,j\in (\mathrm{i}=1,2,\cdots ,\mathrm{N})$$ (11)

At this time, a magenta marker appeared on the chart (the beginning of phase 4).

The epidemic phase identification model defined in this way was subjected to multiple simulations using the constantly changing data published by the CSSE. Conclusions regarding the distribution of epidemic phases among countries changed constantly.

The results of these studies are presented in the next chapter.

3. Results of the study of the COVID-19 epidemic phase identification model

The research was carried out with the primary focus of generating graphs of the index of relative daily increments of the $\mathit{Conf}$ variable for different countries. As mentioned, Fig. 3 presents these graphs for 10 selected countries. The Matlab program published by the authors in the GitHub repository allows us to choose any country for analysis. In this paper, countries were selected that are socially important in some sense. These are either large countries or those initially heavily affected by the epidemic.

In the course of the research, it turned out that some phases appeared as a result of an accidental deviation, not confirmed by the further course of the curve. Therefore, the algorithm for identifying the epidemic phase was modified by using ConfMA - the moving average of the Conf variable.

The moving average of the $\mathit{Conf}$ values was calculated using a window of length, e.g. $L=7$ days:

$$ConfMA\left(i\right)=\sum _{i-L}^{i}Conf\left(i\right),\mathrm{f}\mathrm{o}\mathrm{r}i=L,L+1,L+2,\cdots ,N$$ (12)

In further considerations, the variable $ConfMA\left(i\right)$ was written as $y\left(i\right).$

Fig. 3 shows the results of the identification of the epidemic phase in 10 countries, showing a large variation in the plots of the analyzed $\mathit{Yp}$ index - an indicator of relative changes in the daily number of confirmed cases. In as many as 6 out of 10 countries, the third phase of the epidemic - its suppression, has been achieved. Unfortunately, for one of these cases - Japan, it turned out to be the beginning of the second wave of the epidemic, signaled by the magenta marker.

Four of these countries experienced the first or second phase of the epidemic, which in practice means a continuous increase or a continuation without any specific end.

The ten graphs in Fig. 3 show how clear the differences are between the $\mathit{Yp}$ plots. They are much larger than the differences in the $\mathit{Conf}$ charts published by the CSSE. It is enough to compare, for example, France with Brazil or Japan with Poland.

In the graphs in Fig. 3, the red marker marks the beginning of non-zero time series values. The $\mathit{Conf}$ matrices published by the CSSE add subsequent lines to these matrices from January 22 starting due to the time shift from many zeros. The red marker just marks the beginning of non-zero values in a given row, i.e. the beginning of the initiation of the epidemic in a given country. Fig. 3 also shows the first case of exceeding the ${\mathit{th}}_r$ threshold and entering the phase of epidemic re-outbreak among the considered countries. Such is the case of Japan, which is additionally considered in Fig. 4 . This graph shows very clearly both the thresholds initiating the next phase of the epidemic and the first changes in the $\mathit{Yp}$ index within a given phase. The violent course of the fourth phase of the epidemic is very dynamic and certainly disturbing for Japanese society. It occurred following a total lull of over a month (phase three, from the green marker).

Fig. 4.

Epidemic spread phases for Japan. The magenta marker indicates that the ${\mathit{th}}_r$ threshold has been exceeded following the suppression phase, and Japan is entering the re-outbreak phase.

For such defined phases of the spread of the epidemic in individual countries, a simulation was carried out on the $\mathit{Conf}$ matrix to determine the epidemic phases for all countries and regions for which the number of cases on the day of the beginning of this study (80 days from 22 Jan) exceeded 1000 (confirmed cases), and on the day of the final stage of research (exactly 197 days from 22 Jan).

The results are shown in Table 1, Table 2 .

Table 1.

Phases of the spread of the SARS-CoV-2 epidemic in particular countries/regions in the first half of April 2020.

Phase 1 Dynamic growth	Egypt, Kuwait, Mexico, Moldova, United Arab Emirates, United Kingdom, United States
Phase 2 Intermediate phase	Algeria, Argentina, Armenia, Austria, Azerbaijan, Belarus, Belgium, Brazil, Canada (Quebec), Chile, Colombia, Croatia, Czechia, Denmark, Dominicana, Ecuador, Finland, France, Germany, Greece, Hungary, Iceland, Indonesia, Iran, Iraq, Ireland, Israel, Italy, Japan, Lithuania, Malaysia, Morocco, Netherlands, New Zealand, Norway, Pakistan, Panama, Peru, Philippines, Poland, Portugal, Romania, Russia, Saudi Arabia, Serbia, Singapore, South Africa, Spain, Sweden, Switzerland, Thailand, Turkey
Phase 3 Suppression phase	Bahrain, Bosnia and Herzegovina, Australia (New South Wales), Australia (Victoria), Canada (Alberta), China (Hubei), China (Hunan), Estonia, Hong Kong, India, Luxembourg, South Korea, Qatar, Slovenia, Ukraine

Table 2.

Phases of the spread of the SARS-CoV-2 epidemic in particular countries/regions in the first half of August 2020.

Phase 1 Dynamic growth	Argentina, Bolivia, Bosnia, Bulgaria, Colombia, India, Indonesia, Iraq, Kazakhstan, Mexico, Montenegro, Namibia, Philippines, Poland, Romania, South Africa, United States
Phase 2 Intermediate phase	Armenia, Azerbaijan, Bahrain, Bangladesh, Brazil, Chile , Colombia, Croatia, Moldova, Paraguay, Peru, Russia,
Phase 3 Suppression phase	Austria, Belarus, Belgium, Brazil, Hubei, Cuba, Estonia, Denmark, France, Germany, Hungary, Iceland, Italy, Lithuania, New Zealand, Pakistan, Portugal, Sudan, Sweden, Turkey, United Kingdom
Phase 4 Relapse of epidemic phase	Benin, Burkina Faso, Cameroon, Croatia, Cyprus, Congo, Ecuador, Gabon, Greece, Iran, Israel, Japan, Luxembourg, North Makedonia, Serbia, Slovenia, Slovakia, Uruguay, Zambia

The tables indicate a large migration of countries between the various phases of the epidemic.

Phases 1 and 3 are easy to identify and the unambiguity of their designation is beyond discussion. In April, when we started work on this article, we wrote: no case of a rapid revival of Phase 3 of the epidemic has been noted. It, therefore, was considered as having achieved a permanent state. This is the statement from April. Studies on these considerations appear in many cited papers, and sometimes this threat was directly described, e.g. Shunqing and Yuanyuan (2020). Of course, today, no one doubts the possibility of re-outbreaks of the epidemic because they have become more and more numerous, as in Table 2.

Equally unambiguous as Phase 3 is the definition of Phase 1. It is accompanied by decisive, increasing relative increments, manifested as a rapidly growing number of cases. Phase 2, on the other hand, is more difficult to determine, but it was introduced to observe some fluctuations in growth and even local decreases in $\mathit{Yp}$, to signal approaching the maximum number of cases.

In this context, Phase 4 is also quite easy to notice after the agreed threshold is set. In practice, it was found that this threshold was exceeded quite strongly, so the identification of the fourth phase is rather unambiguous. The study of Phase 4 will undoubtedly be an increasingly important scientific challenge.

Fig. 5 shows the changes in confirmed cases for 8 selected countries in which the epidemic is in Phase 4.

Fig. 5.

Confirmed cases charts for eight selected countries with a clearly marked increase heralding the fourth phase of the epidemic.

These countries were not chosen by accident, but were selected to show the initiation of the fourth phase by changing the Conf curve in a variety of ways: by a marked increase after the suppression phase (Japan, Israel, Croatia), by an increase after a not very pronounced suppression (Serbia, North Macedonia), by an epidemic outbreak after a slow rise (Zambia). Many countries have and will have the syndrome of a subtle appearance of the fourth phase, as in the case of Spain in Fig. 5.

Fig. 5 clearly shows increases in the final phase of the charts. According to the authors, the visualization of growth by means of the $\mathit{Yp}$ index is much clearer. Just compare the sub-plots for Japan from Fig. 5 and from Fig. 4. Fig. 4 clearly shows the phases of the epidemic, while Fig. 5 shows their extraction is definitely more difficult, although the phases of growth and suppression and then re-outbreak can be seen.

The same sharp increases indicating the emergence of the fourth phase of the epidemic are shown in Fig. 6 . However, in the $\mathit{Yp}$indicator graphs, the magenta marker marks the beginning of this phase. According to the authors, such a visualization is more accessible to the reader.

Several other countries are shown here, including two from Africa and two from South America.

As a summary of the research on the model, we include Fig. 7 on the changes in the $\mathit{Yp}$ index for the Chinese province of Hubei, whose capital Wuhan has become a symbol of the birth of the global pandemic. Referring to Fig. 1, we see a sharp increase in the epidemic to about 50 days after its outbreak, and then the suppression phase that lasts until today, August 2020. For the first 50 days, the changes in the $\mathit{Yp}$ index have been visualized as shown in Fig. 7.

Fig. 7.

Graphs of the $\mathit{Yp}$ index variability presented every 5 days for Hubei province.

In the chart, in a relatively short period, in comparison with other countries, all phases of the epidemic except the last one occur.

4. Discussion

The aim of the article is to try to find an indicator or indicators that allow the degree of the spread of the SARS-CoV-2 epidemic in different countries to be assessed. This pandemic is spreading throughout the world, allowing us to observe the infected countries chronologically. For this reason, a question frequently asked today is - whose trail are we following? Which model in the countries infected so far will be similar to our model for the pandemic spread? In this regard, the work is in the form of a prognosis through the detection of the epidemic phase and a comparison with patterns in other countries, more advanced in the spread of the virus. There are already many publications devoted to the problem of time series forecasting (mainly confirmed cases), which are also cited in this work. The surprising majority do not consider the qualitative changes which take place in a time series as expected by the media and public opinion. As a rule, what is important is what will happen next, and at what stage, phase, wave, etc. is the epidemic in our country. Regardless of what these phases will be called, their distinction will be socially important. The pandemic is arguably the most important social event for many decades. Introducing the $\mathit{Yp}$ index instead of a cumulative time series makes it easier to perceive these changes. This objective, especially considering the $\mathit{Yp}$ indicator, seems to have been achieved.

Let us discuss the initiation of the four-phase model presented here, firstly returning to the explanation of the moment the first threshold is crossed and a given country enters into the phase of epidemic growth, defined by (4), (5), (6), (7). Fig. 8 shows the confirmed cases curve for the USA. The first non-zero point on this curve appeared on the eighth day after the start of the CSSE recording (red marker). Two weeks after that date, a reference ordinate was issued in accordance with the principles discussed in Chapter 2. For the case under consideration - for the USA, it was on day 8 + $d_r$ = 22 days (for $d_r$ = 14). On the chart, the value of the Conf variable on that day was 11 cases. In the same graph, yellow-colored bars are placed with their heights corresponding to daily increments on the Conf curve. Condition (7) for the assumed ${\mathit{th}}_u$ = 1 was met in this example on day 43. On that day, an ordinate was set ending with the issuance of a blue marker, which signifies the country's entry into the phase of dynamic growth. In the case of the USA, this phase fully deserves its name, as in no case has there so far been such a sharp increase.

A significant advantage of such an arbitrary definition of this point is its independence from any future events. For a given case, the blue marker for any new data will always appear at the same point – here, for the USA. For other countries, this point will also be fixed, of course on a different day. It should be emphasized that both $d_r$ = 14 days and ${\mathit{th}}_u$ = 1 are arbitrarily determined values. However, it was necessary to adopt some values, the same for all countries, to compare the waveforms of Yp. Those mentioned above are the result of attempts to ensure good visualization of the waveforms and they are considered by the authors to be congruent.

A separate explanation is required for the selection of the $\mathit{Yp}$ index as being more favorable than the directly observed confirmed cases for determining the epidemic phases in individual countries. Fig. 9, Fig. 10 show the spread of the virus in the intentionally selected four countries. Fig. 9 shows the confirmed cases for Brazil, Russia, Italy and Japan for the first 150 days of the pandemic. These countries represent the 4 phases of the pandemic, despite the fact that observation is made at exactly the same time. According to the definitions proposed in this paper, these phases are successively achieved as a result of the spread of the epidemic. It should be understood as follows - Brazil is in the first phase of continuous dynamic growth and has not yet reached the second phase. This is clearly seen in Fig. 10 - where the Conf curves are converted to $\mathit{Yp}$according to (3).

Fig. 9.

Examples of plots of the confirmed cases (Conf) variable for four different countries in four different epidemic phases sequentially from 1. (Brazil) to 4. (Japan). On the ordinate axis, Conf is expressed as real numbers, not normalized.

Fig. 10.

Graphs of the $\mathit{Yp}$ indicator - relative daily gains in confirmed cases for 4 countries representing different phases of the spread of the virus.

In the sub-plot for Russia (Fig. 9), Phase 2 is defined, which is not visible for Russia in Fig. 10, but the representation of these changes in Fig. 9 is clearly different. The chart for Russia in Fig. 9 shows the fulfillment of the condition (9), which means that the second phase has started. For the third country under consideration – Italy, a clear flattening of the Conf chart can be seen in Fig. 9, but only in Fig. 10, according to the criteria proposed in this paper, is it possible to determine the moment when the extinction of the epidemic begins.

A comparison of these two sets of graphs for the same countries seems to allow a better visualization of the epidemic phases by means of the indicator of relative daily increases $\mathit{Yp}$.

We have already mentioned the variable relationship between the $\mathit{Yp}$ indicator and the threshold indicating the beginning of the epidemic growth phase in a given country. A particularly valuable property of the $\mathit{Yp}$ indicator is its relatively small variability, allowing for a comparison of the changes between countries / regions differing in absolute changes by even 2–3 orders of magnitude.

In order to verify these changes directly on the Conf variable graph, an additional comparison of Conf curves was performed in the range of 0–80 days from the start of publication by the CSSE, and from day 81 till today, i.e. up to day 127 of the pandemic (from January 22).

There is a clear convergence of conclusions from observing the Conf charts in Fig. 11 and the Yp indicator charts. Fig. 11 also shows differences in the perception of the epidemic phase in the Conf charts. For the initial pandemic period, Fig. 11 clearly shows the rising nature of the curves – in fact, for all countries / regions except Hubei, Korea, and Italy's slightly protracted flattening. Probably at that moment, Iran is misleading because the end of the red fragment of the chart suggests another continuation.

Fig. 11.

Charts of the confirmed cases variable for the same countries / regions as in the previous figures. The figure illustrates the thesis that for some cases (countries) the further course of the Conf curve cannot be predicted. Despite very similar courses over a specific interval (e.g. expressed in red), their continuation (shown in blue) is completely different.

After a few weeks (exactly 47 days, between the 80th and 127th day), the clearly rising sections of the curves (in the figure – in blue) remained only in the three mentioned countries – Iran, Poland and the USA. It is worth noting the correction of data made by the CSSE for France, (which led to the appearance of two curves side by side). This correction is not relevant to the overall conclusions.

There are also obviously other different kinds of weakness and difficulty which affect building the $\mathit{Conf}(t)$ curve. The way sick people are registered is far from standardized globally. It depends on many factors, principally the number and type of tests performed and the resulting number of hidden and asymptomatic cases of the disease. It is also controversial to include or exclude pandemic deaths accompanied by co-morbidities. The authors are aware of these systemic inaccuracies; however, in order to carry out any inference process, even one with such measurement errors, we decided to treat the data in the “as is” state.

It is also worth noting that despite all the respect for and gratitude to the CSSE institute, their method of presenting data does not facilitate their analysis. For many months, their daily publications were accompanied by constant changes in the order of lines in the $\mathit{Conf}$, $\mathit{Rec}$ and $\mathit{Dea}$ matrices resulting from the need to add new countries in which the virus appeared or to change the order, e.g. from chronological to alphabetical.

Among the latest publications in July and August 2020, there are more and more works devoted to the second wave of the pandemic and the methods for its forecasting. Among the peer-reviewed works, one should mention, for example, those such as Paiva et al., 2020, Wieczorek et al., 2020, Feroze, 2020, Vaishnav and Vajpai, 2020. This latter work is about forecasts for India, which appears to be a country of unlimited trends. Among the preprints, it is worth mentioning the article by Duan et al. (2020), focused precisely on the issue of new epidemic outbreaks.

The work allows the time-varying classification of countries and regions in terms of the local severity of the SARS-CoV-2 pandemic. Particularly reliable is the classification in terms of Phase 1 – growth and Phase 3 – suppression. Taking into account the recent publications mentioned, also the fourth phase seems easily noticeable.

5. Conclusions

The presented classifier based on the variability of the $\mathit{Yp}$ indicator, the relative increase in the number of Conf, seems to be a good tool to determine the state of the epidemic in a given country. The conclusion of prime significance to the authors is the opportunity to express concern for their own country - Poland. According to the results presented, e.g. in Fig. 3, Fig. 6, Poland is far from a state of suppression of the epidemic. Meanwhile, for purely political reasons, further reductions in social restrictions, contrary to the obvious statistical data are announced regardless of the reality. Among the countries concerned, similar conclusions can also be expressed in relation to the USA and Iran. The characteristics $\mathit{Yp}(t)$ of the Iranian epidemic are particularly worrying, as there is a re-increase in infections, not yet seen in other cases.

South America is the world's new focal point for the pandemic. Countries such as Brazil, Peru, Mexico or Chile should be carefully monitored. Studies which are not published here point to a worrying growing number of Phase 1 or 2 infections according to the model. The model presented here will probably offer a chance in the near future to assess the degree of development of the pandemic in Africa on the global scale.

Table 2 shows a number of African countries in the fourth phase of the epidemic. These generally small countries have a low number of confirmed infections (South Africa is the exception) and yet have already reached the suppression phase followed by a renewed outbreak. This phenomenon may increase in the coming months. Similarly, the enormous numbers of confirmed cases in South America or India began with very small numbers of cases.

The Balkan states, with similar eruptions after the suppression period, are also worrying. Tourism and tourists have been blamed for these outbreaks.

The division of the spread of the epidemic into 4 phases is presented here according to the author's proposal, valid in August 2020. It is impossible to predict what will happen next. It can be assumed that in the countries that are in an earlier phase than the third phase, we will notice a trend towards suppression. The question is when? In the countries entering the fourth phase, the question is what next? Will the cycle repeat itself? There is more and more talk in the media about the impending second wave of the virus. This is the popular name for the second outbreak of the epidemic, expected in the autumn. In our opinion, the fourth phase in some countries already shows this.

Regardless of how the epidemic changes in different countries, it is worth trying to classify because the phases have a natural sequence. It should also be remembered that the world as a whole today, in August 2020, is in a phase of unstoppable growth of the pandemic.

The authors have made their Matlab script available in the public GitHub repository together with instructions on how to observe the spread of the epidemic in any selected country for current CSSE data – https://github.com/awilin/covid. We encourage readers to update the data themselves by downloading them from the repository of the CSSE institute (also available on GitHub) and using our software.

This work was not financially supported, with the exception of the proofreading process mentioned below, and is the result of the fascination for independent research and the motivation of the authors.

CRediT authorship contribution statement

Antoni Wilinski: Conceptualization, Methodology, Software, Writing - original draft, Supervision. Eryk Szwarc: Data curation, Software, Validation, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.