Abstract
Motivation
Next-generation amplicon sequencing is a powerful tool for investigating microbial communities. A main challenge is to distinguish true biological variants from errors caused by amplification and sequencing. In traditional analyses, such errors are eliminated by clustering reads within a sequence similarity threshold, usually 97%, and constructing operational taxonomic units, but the arbitrary threshold leads to low resolution and high false-positive rates. Recently developed ‘denoising’ methods have proven able to resolve single-nucleotide amplicon variants, but they still miss low-frequency sequences, especially those near more frequent sequences, because they ignore the sequencing quality information.
Results
We introduce AmpliCI, a reference-free, model-based method for rapidly resolving the number, abundance and identity of error-free sequences in massive Illumina amplicon datasets. AmpliCI considers the quality information and allows the data, not an arbitrary threshold or an external database, to drive conclusions. AmpliCI estimates a finite mixture model, using a greedy strategy to gradually select error-free sequences and approximately maximize the likelihood. AmpliCI has better performance than three popular denoising methods, with acceptable computation time and memory usage.
Availability and implementation
Source code is available at https://github.com/DormanLab/AmpliCI.
Supplementary information
Supplementary material are available at Bioinformatics online.
1 Introduction
High throughput sequencing has revolutionized the study of microbial communities. A common strategy characterizes samples by amplifying and sequencing biomarker genes, like 16S rRNA or fungal internal transcribed spacer. These biomarkers are both conserved for amplification and uniquely hypervariable, so deep amplicon sequencing can reveal the detailed composition of microbial communities.
Biomarker utility is degraded by sequencing errors, polymerase chain reaction (PCR) amplification errors and natural genetic variation (Knight et al., 2018). To account for these factors, a typical first step of microbiome analysis is to resolve the data into operational taxonomic units (OTUs), clusters of sequences with 97% or greater similarity. There are many methods for identifying OTUs (Callahan et al., 2017), roughly classifiable into closed-reference methods, which use a reference database of known organisms, or de novo methods. However, when applied to mock communities, it is widely found that both types of methods cannot accurately identify true OTUs in a sample (Edgar, 2017; Huse et al., 2007, 2010; Kopylova et al., 2016; Nearing et al., 2018; Quince et al., 2009).
OTUs are problematic entities, lacking both biological and physical interpretability. They only roughly approximate biological species, genera or higher taxa, and they do not represent true, error-free sequences in the sample. Thus, OTU-based methods are prone to both false positives and negatives, reporting errors as OTUs and missing real biological sequence variation, such as single-nucleotide polymorphisms (Callahan et al., 2017). The empirical 97% threshold (Konstantinidis and Tiedje, 2005; Stackebrandt and Goebel, 1994) fails to achieve genus- or species-level resolution (Edgar, 2018; Schloss and Westcott, 2011). There are distinct species with more than 97% similar 16S rRNA (Johnson et al., 2019; Stackebrandt and Ebers, 2006) and strains whose 16S rRNA locally differ by more than 3% (Rossi-Tamisier et al., 2015).
Illumina amplicon sequence data support de novo single-nucleotide resolution (Callahan et al., 2016). Modern methods strive to identify all unique sequences in a sample (Amir et al., 2017; Callahan et al., 2016; Edgar, 2016b; Eren et al., 2013, 2015; Hathaway, 2018 ; Mysara et al., 2016; (Tikhonov, 2015) ). Such denoising methods make no biological judgment on taxonomy, but simply remove or correct sequence errors and, sometimes, PCR errors. The denoised sequences are called amplicon sequence variants (ASVs) (Callahan et al., 2016), sub-OTUs (Amir et al., 2017) or zero-radius OTUs (Edgar, 2016b). Their higher resolving power, lower false-positive rates and greater inter-sample consistency have made denoising methods the recommended tool for biomarker gene analysis (Callahan et al., 2017; Knight et al., 2018; Nearing et al., 2018).
There are currently three widely used denoising methods (Nearing et al., 2018). UNOISE3 (Edgar, 2016b) and Deblur (Amir et al., 2017) ignore the quality information and greedily select true sequences assuming conservative error rates. DADA2 (Callahan et al., 2016) uses a greedy, hierarchical divisive clustering algorithm based on a probabilistic error model, while accounting for averaged quality score information. Only DADA2 infers error rates from data, a potential advantage, since experimental conditions affect error profiles (Tikhonov, 2015) .
We introduce AmpliCI, amplicon clustering inference, a model-based algorithm for denoising Illumina amplicon data. The statistical model underlying AmpliCI is a finite mixture model, which for computational feasibility, is maximized using an approximate, greedy scheme. Like DADA2, AmpliCI uses a formal model for sequencing errors, but it retains higher resolving power by not averaging quality scores among reads with identical sequences. AmpliCI considers both substitution and indel errors, estimating substitution error parameters directly from the sample. We test our method on simulated, mock and real datasets. AmpliCI shows better performance than current algorithms, particularly achieving higher accuracy for highly related sequences.
2 Materials and methods
2.1 Statistical model
We start with read set and quality set , containing n sequences of base calls and quality scores. We assume that the data are independent draws from a K-component mixture distribution, where the kth component is generated by the true sequence (haplotype) . The likelihood function for fixed K is
| (1) |
where are the unknown source sequences, parameters are the mixing proportions , the true haplotypes and parameters , dictating how quality scores , treated as observed covariates, impact the read likelihood.
The conditional probability is calculated based on the pairwise alignment between the read and the source haplotype . Since substitution errors greatly exceed insertion or deletion (indel) errors in Illumina sequencing (Schirmer et al., 2016), we use a simple model to penalize indels. We assume an insertion can occur before or a deletion at any one of the lk positions in the kth haplotype at a very small, constant rate δ. Assuming these events are independent, the number di of observed indel events in the ith read may be approximately modeled as a truncated Poisson distribution,
| (2) |
We ignore indel lengths, assuming all plausible lengths are equally likely. Technically, because reads have fixed lengths, indels are neither independent nor their lengths ignorable, but the approximation should be good for short indels, small δ and by treating 3′ terminal indels as necessary consequences of earlier indels. Finally, assuming errors are independent across sites, the conditional probability is
| (3) |
where j indexes positions in haplotype and the aligned read/quality sequences. The term is the probability of generating nucleotide rij from hkj with quality score qij at alignment position j, understood to be 1 when rij is a deletion. Like DADA2 (Callahan et al., 2016), we estimate the log probabilities , for each choice of hkj and rij in , using LOcally Estimated Scatterplot Smoothing (LOESS) regression on the quality scores (details in Section 2.4).
2.2 Greedy haplotype selection
Maximizing the likelihood (Equation 1) is very difficult (Melnykov and Maitra, 2010). Two key assumptions motivate approximate maximization. Capitalizing on low Illumina error rates, we assume (1) all true haplotypes appear at least once without error and (2) error-containing reads that match a true haplotype are overwhelmingly sourced from more abundant haplotypes. Under (1), unique sample sequences with positive true proportions are true haplotypes. Assumption (2) yields rough, rapid estimates.
Suppose the true haplotypes are for some sequence . The observed abundance of comprises the true abundance plus the number of misreads from other haplotypes to read minus the number of sequence misreads (Supplementary Fig. S1),
If we take the expectation of both sides, then
where is the misread probability of sequence , which if are sequence homogeneous, yields method-of-moments estimator
| (4) |
where is the observed abundance. Equation (4) estimates for all unique , but it requires the haplotypes . We use our assumptions and ideas from Deblur and UNOISE2 to incrementally find haplotypes and .
For convenience, we reindex the data. Given M unique sequences , sorted from highest to lowest observed abundance , grouping reads by unique sequence induces a partition on the read and quality sets. Subset contains reindexed reads , with reindexed quality scores in . DADA2 similarly groups reads, but averages quality scores in subset m (Callahan et al., 2016). Retention of original quality scores is an important distinction, increasing sensitivity by allowing AmpliCI to detect members of that are likely misreads of other haplotypes.
Let = be the expected scaled true abundances (shortened to scaled abundances) we aim to estimate. Value is the expected number of error-free reads of true sequence . Assuming the most frequent unique sequence is a haplotype, and no matching reads are misreads, we start by setting and estimator . Given k haplotypes so far, the th haplotype will be some , whose scaled abundance estimate is computed as
where we condition on the current haplotypes and use the quality scores of the reads matching the mth unique sequence . This estimate is obtained assuming the haplotypes are , which is clearly incorrect in early iterations. However, the approximation is essential for computation (Yang et al., 2011) and is reasonable under assumption (2). Further derivations in Supplementary Material S1 yield estimation function
| (5) |
with given by Equation (3). Estimate is a fixed point of Equation (5) (Supplementary Material S2), which can be found through fixed point iteration (Supplementary Material S3).
For approximately maximizing Equation (1), our algorithm (Fig. 1) proposes candidate as the sequence with highest estimated scaled abundance . It is not only a likely haplotype, but also the haplotype most likely distorting the observed abundance of other candidates. Whether we accept the proposed candidate is a model selection issue.
Fig. 1.
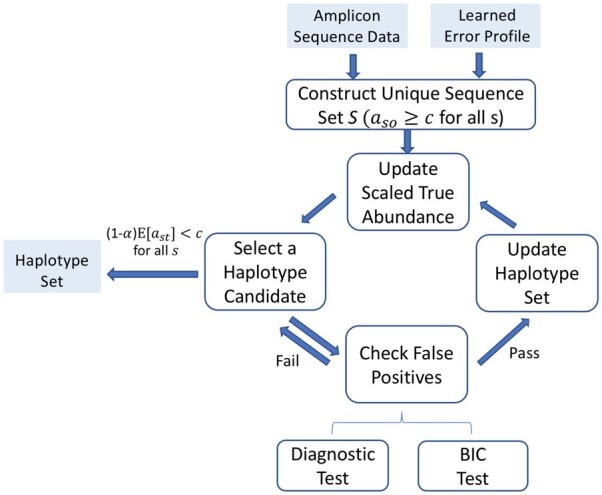
AmpliCI: inferring ASVs from samples. (1) Construct unique sequence set , and put the most abundant unique sequence in haplotype set . (2) Given the current haplotypes , the scaled abundances are estimated for each remaining unique sequence via update function (5), and the haplotype candidate with highest scaled abundance is selected. (3) Verify the approximate BIC improves and the diagnostic probability pmz is small enough, and update . Otherwise, permanently discard candidate and select the next most abundant candidate. (4) Repeat (2)–(3) until the scaled abundance of all remaining unique sequences are below the user-determined abundance threshold c. (5) Output the K haplotypes
To assess model goodness of fit with haplotype , we require an approximate Bayesian Information Criterion (BIC) to improve (Supplementary Material S5). Surviving candidates are then diagnosed for contamination (Supplementary Material S6). Briefly, we assume contamination introduces z (default 1) copies of the candidate . If it is ‘easy’ to generate all remaining copies as misreads of haplotypes in , then we doubt is a haplotype. To quantify the ease of this event, we compute assuming the misreads follow a Poisson Binomial distribution. Small values of pmz indicate it is not easy to explain the observed count without haplotype . We require (default ε = 0.001/M for M unique candidate sequences). When candidate fails to improve the BIC or pmz exceeds the threshold, we permanently reject and consider next most abundant candidates. If is accepted, the haplotype set is updated, , and the process repeats. The algorithm iterates until there are K haplotypes in and all remaining candidate sequences are screened out or have estimated scaled abundances below a second threshold c (default 2).
2.3 Abundance estimation
An important secondary goal of a denoising algorithm is abundance estimation, which is required for chimera detection (Edgar, 2016a) and many downstream analyses (Knight et al., 2018). AmpliCI uses the final, estimated scaled abundances for this purpose. Assuming sequence-independent misread rate for all , these values are directly proportional to the true haplotype abundances. However, with a fully probabilistic model such as AmpliCI, it is possible to imagine more sophisticated methods for abundance quantification. These issues and the related issues are discussed in Supplementary Material S7.
2.4 Implementation
We implement AmpliCI in the C language. By default, the indel error rate is , consistent with previous estimates (Schirmer et al., 2016). Here, we describe the estimation of the remaining error parameters and how we avoid the computational expense of all-against-all alignments.
Quality scores do not perfectly predict error rates (Tikhonov, 2015) , but they strongly correlate with errors (Callahan et al., 2016), even if the exact relationship can vary by dataset (Ma et al., 2019). In our experience, it is important to estimate sample error properties before denoising. AmpliCI independently learns the error profile for each sample, after demultiplexing (Supplementary Material S4). Briefly, initializing error rates to Phred error probabilities (Ewing and Green, 1998),
| (6) |
where for all , we alternate adding a haplotype with AmpliCI and estimating error rates by weighted LOESS regression with default settings until parameters stabilize. The final estimates are used in a second run of AmpliCI without error rate estimation.
Since the cost of Needleman–Wunsch alignment (see Section 2.1) is high, we implement an alignment-free strategy by default, where conditional probability (Equation 3) is calculated without pairwise alignment. This strategy decreases the average runtime on simulated datasets (Section 2.6) from 0.89 s (--align option) to 0.06 s. It works because sequencing indel errors are rare. However, for small abundance threshold c, the approach will select indel-containing reads. To mitigate this problem, once a haplotype candidate is selected, we recalculate its scaled abundance based on the pairwise alignments (scores: gap , match , mismatch for transition and –3 for transversion) to each current haplotype. If the scaled abundance drops below the threshold c, which is expected for indel misreads, the candidate haplotype is permanently dropped.
2.5 Setting run parameters
AmpliCI exposes several parameters to user adjustment, most importantly c, z and ϵ. The threshold c > 1 on scaled abundance (option --abundance) affects sensitivity and runtime. It eliminates candidate haplotypes with estimated scaled abundance (and consequently observed abundance) below c. Integer (option --contaminants) and the threshold ϵ on pmz (option --diagnostic) affect the sensitivity. Varying ϵ alters the specificity/sensitivity tradeoff. A positive z appears important for eliminating low-level contaminants in real datasets. A haplotype cannot be detected unless it produces at least (default 2) perfect reads.
2.6 Data simulation
Synthetic datasets are simulated from a model like that of read simulator ART (Huang et al., 2012). For the simulation with most easily detected haplotypes, we simply use the K = 12 most abundant haplotypes from the Extreme mock dataset (Callahan et al., 2016), but for the other synthetic datasets, we first simulate 12 haplotypes on a star-shaped phylogeny, under the Jukes–Cantor model (Jukes and Cantor, 1969) rooted with the consensus sequence of the 12 Extreme sequences. Similarity between haplotypes is controlled by the branch length cd in the star phylogeny (Supplementary Table S1), plus a requirement of distinct haplotypes. The relative abundance of the 12 haplotypes are , implying unbalanced clusters. For each read, we randomly pick one haplotype given the mixing proportions, simulate the quality scores from a read position-specific empirical quality score distribution, and simulate nucleotides independently assuming Phred quality scores (Equation 6). The mixing proportions, quality score distribution and γhr in the Phred error probabilities are the maximum likelihood estimates obtained by Expectation–Maximization (EM) optimization of the mixture model (Equation 1) for 3000 random reads from the Extreme mock dataset (Callahan et al., 2016) with fixed, known haplotypes and initialized with . The insertion/deletion rates are set to per position. The simulation error model is related but not identical to the AmpliCI error model, and importantly, we do not enforce the additional AmpliCI assumptions. We simulate 3000 reads per synthetic dataset at five different similarity levels.
2.7 Analysis of mock and real datasets
We examine three mock datasets, Extreme (Callahan et al., 2016), Even1 and Stag1 from Mock5 (Bokulich et al., 2015, 2016) and one real vaginal microbiome dataset (MacIntyre et al., 2015) (Table 1). Most denoisers are part of a complete analysis pipeline, including both pre- and post-processing steps. The pipeline we use is shown in Supplementary Figure S2. To facilitate comparison, especially for mock data, we equalize as much as possible in these pipelines, though see Supplementary Material S10.
Table 1.
Information on tested datasets
| Method | Property | Dataset |
|||
|---|---|---|---|---|---|
| Extreme | Even1 | Stag1 | Vagina | ||
| NA | Region | V4 | V4 | V4 | V1–V2 |
| Length (nt) | 250 | 250 | 250 | 300 | |
| No. strains | 27 | 21 | 21 | – | |
| No. reads | 2.0M | 1.0M | 1.3M | 2.1M | |
| DADA2 | t (s) | 2252.0 | 1487.6 | 1266.0 | 343.1 |
| Mem (MB) | 12576.8 | 4043.4 | 6137.1 | 2747.3 | |
| Deblur | t (s) | 2211.2 | 708.0 | 937.8 | 1591.2 |
| Mem (MB) | 6658.0 | 1265.4 | 2138.3 | 648 | |
| UNOISE3 | t (s) | 11.7+1.4 (13.1) | 4.2+0.2 (4.4) | 5.7+0.3 (6.0) | 10.4+1.9 (12.3) |
| Mem (MB) | 1245.6 | 671.5 | 926.6 | 1304.6 | |
| AmpliCI | t (s) | 73.0+423.3 (496.3) | 53.7+2738.7 (2792.4) | 72.1+2725.9 (2798.0) | 32.2+133.6 (165.8) |
| Mem (MB) | 3924.5 | 5171.9 | 6884.7 | 64.8 | |
Note: All datasets contain 16S rRNA gene amplicon sequences generated on the Miseq platform. For DADA2 and Deblur: time recorded for the whole workflow. For UNOISE3: time recorded for data compression (-fastx_uniques) and denoising (-unoise3). For AmpliCI: time recorded for error estimation and haplotype inference. Total time in parentheses.
NA, not Applicable; Length (nt), read length in nucleotides; No. strains, number of known strains in mock community; No. reads, total number of reads in dataset; t, running time; mem, maximum resident set size.
Only forward reads of each sample are input to the denoisers. Even1 and Stag1 are demultiplexed out of the Mock5 dataset using QIIME1 (Caporaso et al., 2010) script split_libraries_fastq.py and default settings. We download the real data already demultiplexed. We truncate reads at 240 nt and discard shorter reads. We remove reads that contain any quality score less than 3 or ambiguous nucleotide ‘N’. The resulting datasets are used as the same input for all algorithms.
Denoiser output is often processed to remove chimera sequences and other artifacts. For analyses on mock datasets, we run Deblur with neither positive nor negative prefiltering (Amir et al., 2017). For mock datasets, we use the standalone UCHIME3 de novo method (Edgar, 2016a) to remove chimeras for all denoisers except UNOISE3, which uses an embedded version. Additional pipeline deviations for real datasets are described in Section 3.
3 Results
We compare AmpliCI with three prevalent denoising methods: DADA2 (Callahan et al., 2016), UNOISE3 (Edgar, 2016b) and Deblur (Amir et al., 2017). Summary information of all algorithms is given in Supplementary Table S3. An abundance threshold like c exists in most methods, except DADA2, where we mimic results by post hoc removal of haplotypes with observed abundance less than c. The AmpliCI default contamination diagnostic threshold was roughly trained on subsets of the Extreme dataset, but it proved to be a liberal threshold. Without running AmpliCI again, we removed haplotypes with diagnostic probability after chimera removal and labeled the result AmpliCI-con.
3.1 Simulated datasets
We compare the ability of the denoisers and a well-known OTU-based method UPARSE (Edgar, 2013) to recover true haplotypes and read assignments on synthetic data, using abundance threshold c = 2 and all other default parameters. Since Deblur does not have a read assignment method, we use USEARCH v11.0 (Edgar, 2010) to assign reads to Deblur haplotypes. For AmpliCI, we assign reads to the cluster with maximum posterior assignment probability [Supplementary Eq. (S6) in Supplementary Methods S7]. For assessing accuracy of read assignments, we compute the Adjusted Rand Index (ARI) (Hubert and Arabie, 1985).
Figure 2 and Supplementary Table S1 show method performance on five replicate datasets under six simulation conditions, where we vary haplotype similarity. For datasets with 0.80 mean haplotype similarity, all denoising algorithms perform well. As mean haplotype similarity increases, performance declines for all algorithms, but AmpliCI achieves the highest ARI and sensitivity. UNOISE3 is the only denoiser to identify false positives, a total nine in seven of 30 simulated datasets. Additional analysis of the simulated datasets is given in Supplementary Material S8.
Fig. 2.
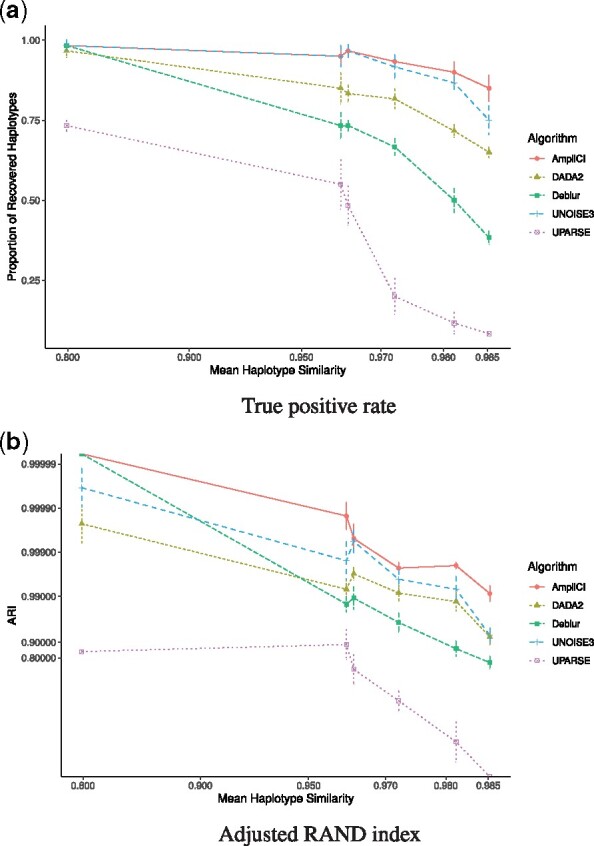
Mean (a) proportion of detected haplotypes ± standard error and (b) ARI ± standard error for six levels of simulated haplotype similarity. For each level, the x coordinate is set to the mean haplotype similarity of the five simulated datasets. Mean haplotype similarity (x axis) and ARI plotted on logit scale; ARI standard error computed by the delta method.
3.2 Mock datasets
We analyze the forward reads of three mock datasets, real samples of known microbial communities, widely used for microbiome method benchmarking. To screen low abundance contaminants and handle the peculiar noise patterns of real data, denoising algorithms take extra steps to screen putative haplotypes. All algorithms, including AmpliCI, overestimate the chance of read errors (see Section 4). In addition, Deblur and UNOISE3 recommend setting a high abundance threshold. While a high threshold can reduce the number of false positives, it also reduces method sensitivity. In contrast, DADA2 sets a low threshold of two and tests the evidence in support of candidate haplotypes, accepting new haplotypes only if its P-value falls below , a highly conservative choice. We compare both a low (2) and high (10) abundance threshold on all methods, and present results for default AmpliCI and conservative AmpliCI-con.
Table 2 shows the result when true positives (TP) only include estimated haplotypes that are a 100% match to the provided mock reference sequences. AmpliCI achieves more or equal true haplotypes with fewer false haplotypes. With low abundance threshold two, AmpliCI-con performs better than all other methods on all three datasets. AmpliCI-con, though designed for fine-scale resolution, continues to perform best at high abundance threshold 10 on the Extreme and Even1 datasets. Although Deblur achieves the best performance on the Stag1 dataset with c = 10, AmpliCI and DADA2 find one more true haplotype and Deblur is the worst denoiser in simulation. Additional interpretation of the comparison study on mock datasets is given in Supplementary Material S9.
Table 2.
Results on three mock datasets
| Data | Method | c | Outcome |
||||||
|---|---|---|---|---|---|---|---|---|---|
| TP | TN | FP | FN | Sens. | Prec. | MCC | |||
| Extreme | DADA2 | 2 | 26 | 40817 | 48 | 3 | 0.897 | 0.351 | 0.561 |
| UNOISE3 | 2 | 27 | 40728 | 137 | 2 | 0.931 | 0.165 | 0.391 | |
| AmpliCI | 2 | 26 | 40807 | 58 | 3 | 0.897 | 0.310 | 0.526 | |
| AmpliCI-con | 2 | 26 | 40832 | 33 | 3 | 0.897 | 0.441 | 0.628 | |
| Deblur | 2 | 21 | 40815 | 50 | 8 | 0.724 | 0.296 | 0.462 | |
| DADA2 | 10 | 21 | 40845 | 20 | 8 | 0.724 | 0.512 | 0.609 | |
| UNOISE3 | 10 | 21 | 40851 | 14 | 8 | 0.724 | 0.600 | 0.659 | |
| AmpliCI | 10 | 21 | 40851 | 14 | 8 | 0.724 | 0.600 | 0.659 | |
| AmpliCI-con | 10 | 21 | 40852 | 13 | 8 | 0.724 | 0.618 | 0.669 | |
| Deblur | 10 | 16 | 40855 | 10 | 13 | 0.552 | 0.615 | 0.582 | |
| Even1 | DADA2 | 2 | 23 | 16403 | 40 | 0 | 1.000 | 0.365 | 0.603 |
| UNOISE3 | 2 | 22 | 16403 | 40 | 1 | 0.956 | 0.355 | 0.582 | |
| AmpliCI | 2 | 23 | 16423 | 20 | 0 | 1.000 | 0.535 | 0.731 | |
| AmpliCI-con | 2 | 23 | 16427 | 16 | 0 | 1.000 | 0.590 | 0.768 | |
| Deblur | 2 | 21 | 16424 | 19 | 2 | 0.913 | 0.525 | 0.692 | |
| DADA2 | 10 | 23 | 16418 | 25 | 0 | 1.000 | 0.479 | 0.692 | |
| UNOISE3 | 10 | 22 | 16441 | 2 | 1 | 0.957 | 0.917 | 0.936 | |
| AmpliCI | 10 | 23 | 16440 | 3 | 0 | 1.000 | 0.885 | 0.940 | |
| AmpliCI-con | 10 | 23 | 16442 | 1 | 0 | 1.000 | 0.958 | 0.979 | |
| Deblur | 10 | 21 | 16443 | 0 | 2 | 0.913 | 1.000 | 0.955 | |
| Stag1 | DADA2 | 2 | 21 | 21887 | 73 | 2 | 0.913 | 0.223 | 0.451 |
| UNOISE3 | 2 | 21 | 21888 | 72 | 2 | 0.913 | 0.226 | 0.453 | |
| AmpliCI | 2 | 21 | 21887 | 73 | 2 | 0.913 | 0.223 | 0.451 | |
| AmpliCI-con | 2 | 21 | 21906 | 54 | 2 | 0.913 | 0.280 | 0.505 | |
| Deblur | 2 | 21 | 21900 | 60 | 2 | 0.913 | 0.259 | 0.486 | |
| DADA2 | 10 | 18 | 21931 | 29 | 5 | 0.783 | 0.383 | 0.547 | |
| UNOISE3 | 10 | 17 | 21956 | 4 | 6 | 0.739 | 0.810 | 0.773 | |
| AmpliCI | 10 | 18 | 21936 | 24 | 5 | 0.783 | 0.429 | 0.579 | |
| AmpliCI-con | 10 | 18 | 21950 | 10 | 5 | 0.783 | 0.643 | 0.709 | |
| Deblur | 10 | 17 | 21958 | 2 | 6 | 0.739 | 0.895 | 0.813 | |
Note: Results on three mock datasets, Extreme, Mock5 Even1 and Mock5 Stag1, treating reference sequences of the mock communities as the gold standard. Abundance threshold c is set as 2 or 10. AmpliCI uses default contamination diagnostics (see Section 2); AmpliCI-con results are after applying a post hoc filter on the contamination diagnostic threshold .
TP, true positives; TN, true negatives; FP, false positives; FN, false negatives; Sens., sensitivity; Prec., precision; MCC, Matthew’s correlation coefficient. Bold numbers indicate best performance for the dataset/c combination.
3.3 Real dataset
The real dataset we analyze consists of 157 samples collected from 42 British women in a longitudinal study of the vaginal microbiome during and after pregnancy (MacIntyre et al., 2015). DADA2 estimates the error profile from the first several samples until the cumulative number of nucleotides and uses the same error profile to infer haplotypes in each sample independently. Then chimera detection is performed by its default algorithm. Deblur also infers haplotypes from each sample independently with the per-sample abundance threshold 2 (option –min-size) and cross-sample abundance threshold 10 (option –min-reads). UNOISE3 pools all samples together and infers haplotypes with abundance threshold 8 (option -minsize). AmpliCI estimates error profiles and infers haplotypes independently per sample. Then chimeras are detected per sample using default UCHIME3 de novo (Edgar, 2016a). We run AmpliCI with abundance threshold c = 2, but post hoc filter with summed scaled abundance threshold 8 or 10 across all samples to better compare with UNOISE3 and Deblur.
Without a known reference, we evaluate the results by aligning estimated haplotypes against the Silva v132 rRNA gene database ( Quast, 2012 ). Figure 3 shows that the total number of haplotypes with a 100% match in the database are similar among the different algorithms, although no two methods agree perfectly. Haplotypes without 100% matches in the reference database, which could be true biological variants or false positives generated during PCR and sequencing, are not inferred with as much agreement among the algorithms. Overall, AmpliCI is closest in predictions to Deblur, UNOISE3, then DADA2, although it should be noted that because more potential haplotypes are screened under the default settings for DADA2, UNOISE3, then Deblur, there are also more opportunities to disagree in precisely the methods we find to most disagree.
Fig. 3.

Venn diagrams of haplotypes discovered in the vaginal microbiome dataset (MacIntyre et al., 2015) by AmpliCI, AmpliCI-con, DADA2, UNOISE3 and Deblur. Haplotypes with a 100% match to the Silva v132 rRNA gene database (Quast et al., 2012) are shaded. AmpliCI and AmpliCI-con compared to (a) DADA2 with abundance threshold c = 2, (b) UNOISE3 with c = 2 and cross-sample abundance threshold and (c) Deblur with c = 2 and cross-sample abundance threshold
3.4 Run time and memory analysis
Table 1 displays the time and memory usage of the four algorithms on the three mock and one real datasets. The GNU time command provides user time and maximum memory usage on a server with an Intel(R) Xeon(R) CPU E3-1241 v3 @ 3.50 GHz. For algorithms within a pipeline, we report only the timing and memory usage for the major steps of denoising. For UNOISE3 and Deblur, statistics were computed with chimera detection via UCHIME de novo embedded in the denoising step, but chimera detection is a relatively insignificant contributor to resource usage.
For datasets containing a single sample (the three mock datasets), the time and memory usage of AmpliCI increases in the number of reads and haplotypes. AmpliCI resource usage is far higher on Even1 and Stag1 than Extreme because though there are fewer reads, there are many small clusters generated by chimeras. Though AmpliCI is not the most efficient algorithm, it uses less resources than Deblur and DADA2 on Extreme, and roughly the same resources on Even1 and Stag1. On the multisample vaginal microbiome, Deblur has the highest run time and DADA2 has the highest memory usage. UNOISE3 triumphs in computational and memory efficiency, beating all other methods.
4 Discussion
We propose AmpliCI, a likelihood-based denoiser of Illumina amplicon sequence data under the mixture model framework. We have shown that AmpliCI is better than three other popular denoising methods on most performance metrics, and retains acceptable computation time and memory usage. Here, we discuss the advantages of AmpliCI as well as the persistent challenges (minor limitations discussed in Supplementary Material S11) that remain for all amplicon sequence denoising methods.
4.1 Likelihood-based inference with quality score
It is logical to formulate denoising as a clustering problem (Callahan et al., 2016; Edgar, 2016b), where all members of a cluster are reads of the same true sequence. If sequencing errors are a homogeneous disturbance of the true sequences, then the high sequencing depth supports using a homogeneous finite mixture model (McLachlan and Peel, 2000). Quince et al. (2009) recognized this possibility when proposing a finite mixture model for the fluorescent signals emitted by amplicon sequences processed on the 454 sequencer, but AmpliCI appears to be the first finite mixture model proposed for denoising Illumina amplicon data. AmpliCI shares several similarities with DADA2 (Callahan et al., 2016), which also models errors as homogeneous disturbances on unknown true sequences, but DADA2 is not formulated as a mixture model, and the two methods take different strategies to overcome the computational challenges.
Model-based clustering is plagued by the dual computational challenges of choosing the number of clusters and global optimization, especially challenging when sample sizes number in the millions and clusters in the hundreds to thousands. AmpliCI adopts an approximate maximization strategy, selecting likely true haplotypes in a greedy fashion. DADA2 does not formulate a likelihood, instead using its error model to devise a divisive clustering algorithm based on diagnostic tests. AmpliCI and DADA2 use nearly identical error models, but DADA2 compresses data at the unique sequence level, discarding the quality score information of individual reads and treating unique sequences as conditionally independent observations within clusters. In AmpliCI and as appropriate for the mixture model formulation, the reads are treated as conditionally independent observations within clusters.
Using an estimated error model that considers quality scores should increase the resolution of both AmpliCI and DADA2 over other methods, such as UNOISE3 and Deblur, that use fixed thresholds and ignore quality scores. Further, AmpliCI should achieve better resolution than DADA2 by not compressing the reads into unique sequences and by capitalizing on the likelihood principle. The higher resolution of AmpliCI is confirmed in our simulation study, where it clearly and reproducibly detects more correct true sequences than any other method, most notably when there is little separation between the true sequences.
4.2 Error models and their limitations
Quality scores cannot be simply interpreted as Phred scores (Ewing and Green, 1998). In real data, sample quality, library preparation methods, PCR conditions and sequencing platforms generate datasets that disrupt information communicated by Phred quality scores in sample-specific ways (Bender et al., 2018; Ma et al., 2019; Schirmer et al., 2016). Quality information may be further invalidated by predenoising filters, which clip low-quality tails of reads and discard short reads. Such filtering is recommended (Caporaso et al., 2011) because read quality and length can have large impact on the downstream analysis, especially diversity estimation (Bokulich, 2013) . Simply converting quality scores to Phred error probabilities can indeed be disastrous: AmpliCI is overrun with haplotype predictions (858 compared to 29 when using estimated errors with abundance threshold c = 15 on the Extreme dataset).
The error models inside Deblur and UNOISE3 are fixed across samples, ignore the differences in substitution miscalls (transitions A ↔ G and T ↔ C are usually more common than transversions), and ignore quality scores all together (Ma et al., 2019; Schirmer et al., 2016; (Tikhonov, 2015) ). While DADA2 and AmpliCI estimate and use quality score-based error models, they do not account for all the patterns in sequencing errors. Systematic sequencing errors have been identified in Illumina data, including high error rates near certain three nucleotide motifs and inverted repeats (Nakamura et al., 2011; Schirmer et al., 2016). Even worse, real data are replete with additional false signals (contaminants, propagated PCR errors) that mimic true haplotypes.
Methods can handle this complexity by (1) modeling it, (2) assuming error rates high enough to bury it in the noise, (3) discarding low abundance variants, or (4) making conservative decisions. We are aware of no method that has successfully done (1), and all remaining strategies sacrifice resolving power. UNOISE3 and Deblur adopt strategies (2) and (3) by setting conservative error rates and recommending high abundance thresholds. Less obviously, but to lesser degree, both AmpliCI and DADA2 also adopt (2) and (3). Neither considers singletons as possible haplotypes by default, and because they use an approximate strategy to estimate error rates before all haplotypes have been determined, the error rates are overestimated. A better strategy is to invent better error models (1), while applying conservative decisions (4) to overcome remaining deficiencies. A careful comparison of method performance on all three mock datasets, shows that AmpliCI has achieved a better trade-off in decision errors by more accurately modeling the per-read sequencing process. Higher-resolution denoisers will be achieved through better understanding and models for the as yet untackled noise in amplicon sequencing.
Supplementary Material
Acknowledgements
The authors thank Heliang Shi for previous work on Ampliclust, an EM algorithm for maximization of Equation (1). An earlier version of this paper won the American Statistical Association Section on Statistics in Genomics and Genetics’ 2020 Student Paper Competition. The authors thank the reviewers for their helpful comments.
Funding
This work was supported in part by the United States Department of Agriculture (USDA) National Institute of Food and Agriculture (NIFA) Hatch project IOW03617. The content of this paper is however solely the responsibility of the authors and does not represent the official views of the NIFA or USDA.
Conflict of Interest: none declared.
Contributor Information
Xiyu Peng, Department of Statistics, Ames, IA 50011, USA; Interdepartmental Program in Bioinformatics and Computational Biology, Ames, IA 50011, USA.
Karin S Dorman, Department of Statistics, Ames, IA 50011, USA; Interdepartmental Program in Bioinformatics and Computational Biology, Ames, IA 50011, USA; Department of Genetics, Development and Cell Biology, Iowa State University, Ames, IA 50011, USA.
References
- Amir A. et al. (2017) Deblur rapidly resolves single-nucleotide community sequence patterns. mSystems, 2, e00191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender J.M. et al. (2018) Quantification of variation and the impact of biomass in targeted 16S rRNA gene sequencing studies. Microbiome, 6, 155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokulich N.A. et al. (2013) Quality-filtering vastly improves diversity estimates from Illumina amplicon sequencing. Nat. Methods, 10, 57–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokulich N.A. et al. (2015) A standardized, extensible framework for optimizing classification improves marker-gene taxonomic assignments. PeerJ PrePrints, 3, e934v2. [Google Scholar]
- Bokulich N.A. et al. (2016) mockrobiota: a public resource for microbiome bioinformatics benchmarking. mSystems, 1, e00062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callahan B.J. et al. (2016) DADA2: high-resolution sample inference from Illumina amplicon data. Nat. Methods, 13, 581–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callahan B.J. et al. (2017) Exact sequence variants should replace operational taxonomic units in marker-gene data analysis. ISME J., 11, 2639–2643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caporaso J.G. et al. (2010) QIIME allows analysis of high-throughput community sequencing data. Nat. Methods, 7, 335–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caporaso J.G. et al. (2011) Global patterns of 16S rRNA diversity at a depth of millions of sequences per sample. Proc. Natl. Acad. Sci. USA, 108, 4516–4522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. (2010) Search and clustering orders of magnitude faster than BLAST. Bioinformatics, 26, 2460–2461. [DOI] [PubMed] [Google Scholar]
- Edgar R.C. (2013) UPARSE: highly accurate OTU sequences from microbial amplicon reads. Nat. Methods, 10, 996–998. [DOI] [PubMed] [Google Scholar]
- Edgar R. (2016. a) UCHIME2: improved chimera prediction for amplicon sequencing. 10.1101/074252. [DOI]
- Edgar R.C. (2016. b) UNOISE2: improved error-correction, 10.1101/081257. [DOI]
- Edgar R.C. (2017) Accuracy of microbial community diversity estimated by closed- and open-reference OTUs. PeerJ, 5, e3889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. (2018) Updating the 97% identity threshold for 16S ribosomal RNA OTUs. Bioinformatics, 34, 2371–2375. [DOI] [PubMed] [Google Scholar]
- Eren A.M. et al. (2013) Oligotyping: differentiating between closely related microbial taxa using 16S rRNA gene data. Methods Ecol. Evol., 4, 1111–1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eren A.M. et al. (2015) Minimum entropy decomposition: unsupervised oligotyping for sensitive partitioning of high-throughput marker gene sequences. ISME J., 9, 968–979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewing B., Green P. (1998) Base-calling of automated sequencer traces using phred. II. Error probabilities. Genome Res., 8, 186–194. [PubMed] [Google Scholar]
- Hathaway N.J. et al. (2018) SeekDeep: single-base resolution de novo clustering for amplicon deep sequencing. Nucleic Acids Res., 46, e21–e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W. et al. (2012) ART: a next-generation sequencing read simulator. Bioinformatics, 28, 593–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert L., Arabie P. (1985) Comparing partitions. J. Classif., 2, 193–218. [Google Scholar]
- Huse S.M. et al. (2007) Accuracy and quality of massively parallel DNA pyrosequencing. Genome Biol., 8, R143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huse S.M. et al. (2010) Ironing out the wrinkles in the rare biosphere through improved OTU clustering. Environ. Microbiol., 12, 1889–1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson J.S. et al. (2019) Evaluation of 16S rRNA gene sequencing for species and strain-level microbiome analysis. Nat. Commun., 10, 5029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes T.H., Cantor C.R. (1969) Evolution of protein molecules. In: Munro H.N., Allison J.B. (eds.) Mammalian Protein Metabolism, Vol. 3. Academic Press, New York, pp. 21–132. [Google Scholar]
- Knight R. et al. (2018) Best practices for analysing microbiomes. Nat. Rev. Microbiol., 16, 410–413. [DOI] [PubMed] [Google Scholar]
- Konstantinidis K.T., Tiedje J.M. (2005) Genomic insights that advance the species definition for prokaryotes. Proc. Natl. Acad. Sci. USA, 102, 2567–2572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopylova E. et al. (2016) Open-source sequence clustering methods improve the state of the art. mSystems, 1, e00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X. et al. (2019) Analysis of error profiles in deep next-generation sequencing data. Genome Biol., 20, 50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacIntyre D.A. et al. (2015) The vaginal microbiome during pregnancy and the postpartum period in a European population. Sci. Rep., 5, 8988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan G.J., Peel D. (2000) Finite Mixture Models. Wiley Series in Probability and Statistics. Wiley, New York. [Google Scholar]
- Melnykov V., Maitra R. (2010) Finite mixture models and model-based clustering. Stat. Surv., 4, 80–116. [Google Scholar]
- Mysara M. et al. (2016) IPED: a highly efficient denoising tool for Illumina MiSeq paired-end 16S rRNA gene amplicon sequencing data. BMC Bioinformatics, 17, 192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura K. et al. (2011) Sequence-specific error profile of Illumina sequencers. Nucleic Acids Res., 39, e90–e90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nearing J.T. et al. (2018) Denoising the denoisers: an independent evaluation of microbiome sequence error-correction approaches. PeerJ, 6, e5364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quast C. et al. (2012) The SILVA ribosomal RNA gene database project: improved data processing and web-based tools. Nucleic Acids Res., 41, D590–D596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quince C. et al. (2009) Accurate determination of microbial diversity from 454 pyrosequencing data. Nat. Methods, 6, 639–641. [DOI] [PubMed] [Google Scholar]
- Rossi-Tamisier M. et al. (2015) Cautionary tale of using 16S rRNA gene sequence similarity values in identification of human-associated bacterial species. Int. J. Syst. Evol. Microbiol., 65, 1929–1934. [DOI] [PubMed] [Google Scholar]
- Schirmer M. et al. (2016) Illumina error profiles: resolving fine-scale variation in metagenomic sequencing data. BMC Bioinformatics, 17, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schloss P.D., Westcott S.L. (2011) Assessing and improving methods used in operational taxonomic unit-based approaches for 16S rRNA gene sequence analysis. Appl. Environ. Microbiol., 77, 3219–3226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stackebrandt E., Ebers J. (2006) Taxonomic parameters revisited: tarnished gold standards. Microbiol. Today, 33, 152–155. [Google Scholar]
- Stackebrandt E., Goebel B.M. (1994) Taxonomic note: a place for DNA-DNA reassociation and 16S rRNA sequence analysis in the present species definition in bacteriology. Int. J. Syst. Evol. Microbiol., 44, 846–849. [Google Scholar]
- Tikhonov M. et al. (2015) Interpreting 16S metagenomic data without clustering to achieve sub-OTU resolution. ISME J., 9, 68–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X. et al. (2011) Repeat-aware modeling and correction of short read errors. BMC Bioinformatics, 12, S52. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


