FANCY: fast estimation of privacy risk in functional genomics data

Abstract

Motivation

Functional genomics data are becoming clinically actionable, raising privacy concerns. However, quantifying privacy leakage via genotyping is difficult due to the heterogeneous nature of sequencing techniques. Thus, we present FANCY, a tool that rapidly estimates the number of leaking variants from raw RNA-Seq, ATAC-Seq and ChIP-Seq reads, without explicit genotyping. FANCY employs supervised regression using overall sequencing statistics as features and provides an estimate of the overall privacy risk before data release.

Results

FANCY can predict the cumulative number of leaking SNVs with an average 0.95 R² for all independent test sets. We realize the importance of accurate prediction when the number of leaked variants is low. Thus, we develop a special version of the model, which can make predictions with higher accuracy when the number of leaking variants is low.

Availability and implementation

A python and MATLAB implementation of FANCY, as well as custom scripts to generate the features can be found at https://github.com/gersteinlab/FANCY. We also provide jupyter notebooks so that users can optimize the parameters in the regression model based on their own data. An easy-to-use webserver that takes inputs and displays results can be found at fancy.gersteinlab.org.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

With the surge of genomics data and the decreasing cost of sequencing (Sboner et al., 2011), genome privacy is an increasingly important area of study. Traditional DNA sequencing, functional genomics (Harmanci and Gerstein, 2018) and molecular phenotype (Harmanci and Gerstein, 2016; Schadt et al., 2012) datasets create quasi-identifiers, which in turn can be used to re-identify or characterize individuals without their consent. The surge in widely available functional genomics data increases correlations between phenotype and genotype datasets, which amplifies the possibility of re-identification and characterization of the individuals who participate in these studies. Functional genomics data allow for a detailed characterization of disease states and susceptibility, and broad dissemination of this data can promote key scientific advances. Unlike DNA sequencing, functional genomics experiments are not performed for genotyping purposes (rather, for understanding phenotypes and basic biology). Yet, they still yield next-generation sequencing reads containing a substantial amount of patients’ variants, which raises privacy concerns. Thus, there is a trade-off between utility and privacy when it comes to sharing functional genomics data. This trade-off can be difficult for scientists to navigate. For example, scientific funding agencies’ data-sharing and privacy policies about controlled-access can prevent the release of data, sometimes as late as after the relevant article has published (NIH, 2018).

In contrast to DNA sequencing-based data, such as genome-wide association study (GWAS), few tools currently exist to assess the risk of privacy loss from functional genomics data. In order to protect patient privacy while promoting scientific progress through data-sharing, it is essential that we develop robust methods for making these assessments. Such assessments may bolster informed consent and empower scientists to plan functional genomics experiments with patient privacy in mind. Previous studies suggest that 30–80 independent single nucleotide polymorphisms (SNPs) can be enough to re-identify an individual (Lin et al., 2004). Although the majority of genome-wide functional genomics datasets will likely contain more than 80 SNPs, the number of required SNPs to re-identify individuals are highly dependent on the number of individuals sequenced in other databases. It is envisioned that more individuals will be sequenced moving forward and more SNPs will be needed to re-identify individuals in these databases. Therefore, estimating the number of SNPs leaked in omics datasets is important for understanding the risk of privacy. In addition, another privacy risk to the participants is the risk of characterization, i.e. the risk of inferring stigmatizing phenotypes by using the genotype–phenotype relationship. Clearly, the more variants leaked, the greater the chances of being characterized (e.g. through GWAS overlap). In this sense, knowing the number of variants that leak in a given functional genomics dataset helps us to understand the loss of privacy.

Before the release of data from a functional genomics experiment, it is essential to be able to rapidly quantify the number of leaking variants. This is particularly important as different assays target different regions of the genome with different coverage profiles [e.g. RNA sequencing (RNA-Seq) targets expressed exons, whereas H3K27ac chromatin immunoprecipitation sequencing (ChIP-Seq) targets the non-coding genome on the promoter and enhancer regions] and depth profiles (i.e. some assays have spread out peaks while others are more punctuated). The quantification of the number of leaking variants is possible by genotyping the raw sequences and overlapping them with gold-standard genotypes (e.g. those obtained from whole-genome sequencing). The use of a gold-standard is necessary because functional genomics data alone provides a less reliable picture of an individual’s genotypes, and may lead to false positives due to the targeted nature of the assays. For example, it has been shown that the variants called using RNA-Seq data of 432 individuals from the gEUVADIS project (Lappalainen et al., 2013) have a precision of $\sim 10\%$ (Gursoy et al., 2019). The limitations of directly genotyping the functional genomics dataset are (i) the large resources required for genotyping-in principle, it is possible to genotype the raw reads with current genotyping tools, but an average variant calling pipeline would need to be radically re-parameterized to suit different assays, as traditional genotyping software are typically optimized for whole-genome sequencing and (ii) the need for a gold-standard genotype dataset belonging to the patient to check the correctness of the called variants, which may not be readily available in every case.

In this study, we developed $\text{FANCY}$, a supervised learning method to infer the number of leaking single nucleotide variants (SNVs) from reference-aligned functional genomics data. Our primary goal was to quantify the SNV leaks in raw sequences without needing genotyping or a gold-standard genotype list. We built a Gaussian Process Regression (GPR) model that takes the assay type, sequencing features, such as mean depth ($\overline{d}$) and breadth (b) of the coverage, and the statistical properties of the depth distribution, such as standard deviation(σ), skewness ($\pm s$) and kurtosis(k) as input, and predicts the cumulative number of leaking SNVs. $\text{FANCY}$ can separately estimate the number of rare and common variants, and outputs each estimated number with a predicted upper and lower bound in the 95% confidence level. In addition to estimating privacy risk, $\text{FANCY}$ can be used to plan functional genomics experiments; for a target number of SNVs, one can back-calculate the required sequencing statistics. The privacy risk assessment is of critical value when the number of leaking variants is low, as in critical ranges, leakage of a few additional variants can change the status of the privacy risk from ‘can be shared’ to ‘cannot be shared’. Therefore, we also trained our model with data that has SNV leakage fewer than 1000 variants to obtain more accurate results in the lower ranges. This model is called ${\text{FANCY}}_{\text{low}}$. A user can first predict the leakage with $\text{FANCY}$. If the number of predicted SNVs is below 1000, the user can then use ${\text{FANCY}}_{\text{low}}$ to fine-tune the accuracy of the prediction.

In addition to $\text{FANCY}$, we also developed a Random Forest classifier plug-in that predicts the type of assay [RNA-Seq versus Assay for Transposase-Accessible Chromatin using sequencing (ATAC-Seq) versus ChIP-Seq] used to obtain a given dataset by using the sequencing statistics as features. This kind of reverse identification of data may be useful to the community for samples with missing metadata.

2 Materials and methods

2.1 $\text{FANCY}$ details

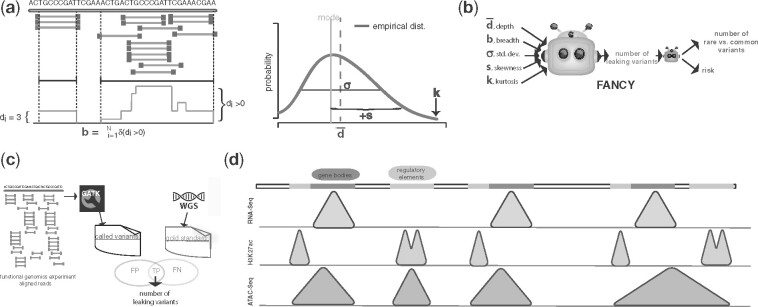
$\text{FANCY}$ is a two-step method. The first step is a regression framework that uses a GPR model with a Matern kernel (Rasmussen and Williams, 2006). We obtained the features as follows: we first aligned the raw functional genomics reads to the reference genome [bwa (Li and Durbin, 2009) is used for ChIP and ATAC-seq data; STAR (Dobin et al., 2013) is used for RNA-Seq data]. We then calculated the depth per base pair using samtools (Li et al., 2009) and calculated the following statistics: depth ($\overline{d}$) and breadth (b) of the coverage, and the statistical properties of the depth distribution, such as standard deviation(σ), skewness ($\pm s$) and kurtosis(k) (Fig. 1a). For the true number of SNVs, we used GATK (DePristo et al., 2011; Van der Auwera et al., 2013) (with appropriate parameterization for each assay type) to call the SNVs. After filtering low-quality SNVs as suggested by the GATK Best Practices (DePristo et al., 2011; Van der Auwera et al., 2013), we overlapped the remaining SNVs with the gold-standard SNVs generated from whole-genome sequencing data to obtain the true number of leaking SNVs (Fig. 1c). The second step is the estimation of rare versus common variants. We divided the 1000 Genomes data (The 1000 Genomes Project Consortium, 2010) into rare and common categories based on minor allele frequency of the SNVs. For each individual in the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2010), given an assay, we found the rare variant density and used the mean density of all individuals with the predicted number of total leaking variants to estimate the number of rare versus common variants.

Fig. 1.

Details of FANCY. (a) The schematic of the features of FANCY: average depth; breadth, i.e. number of nucleotides represented with at least one read; first, second and third moment of the depth distribution (SD, skewness and kurtosis). If the distribution is skewed to the right-hand side of the mode (mean is larger than the mode), the skewness is positive. It is negative if the mean is smaller than the mode. (b) The schematic of inputs and outputs of FANCY. (c) The process of determining true number of leaking variants from functional genomics reads. (d) The regions represented by each assay type. The reads of RNA-Seq are concentrated on the gene bodies, H3K27ac ChIP-Seq is concentrated on the non-coding genome (enhancers and promoters), and because ATAC-Seq covers the open chromatin, the reads are concentrated on both coding and non-coding regions

${\text{FANCY}}_{\text{low}}$ uses the same regressor with the same set of features. However, the training data used in ${\text{FANCY}}_{\text{low}}$ contains leaking SNVs up to 1000 to increase the accuracy when the number of leaking variants is low.

2.2 Gaussian process regression

GPR is a supervised learning method that is based on learning fitting functions to a given set of training data. In comparison, traditional regression models learn the parameters of a given function. GPR is a non-parametric method used to calculate the probability distribution over all functions that fit the data instead of calculating the probability distribution of a specific function’s parameters. The advantage of using GPR is its ability to provide uncertainty estimations at a given confidence level. The disadvantage of this method is the computational complexity, which makes it infeasible for large datasets. Since the sequencing statistics relate to the number of inferred variants differently in different regimes and for different assays (Fig. 1c), the relationship between features and the number of leaking variants cannot be modeled by general mathematical approaches, such as generalized linear models (Fig. 2). A Gaussian process can be defined by its mean and covariance functions as

$$f(x)\sim (\mu (x),\sum (x)).$$

Fig. 2.

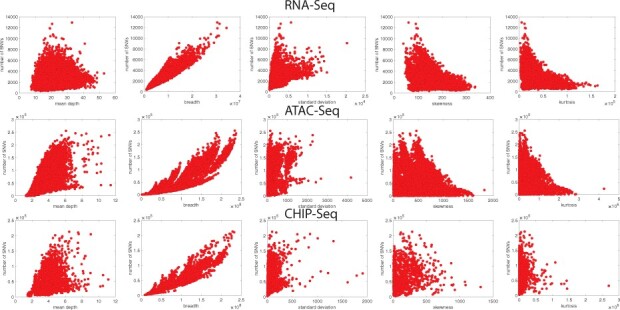
Relationship between sequencing statistics and number of leaking variants. Overall, breadth of the coverage has the highest correlation with the number of leaking variants, while other statistics still show a decent correlation

A Gaussian process assumes that the distribution of the values of functions $p(f(x_1),f(x_2),\dots ,f(x_N))$ at a set of points $(x_1,x_2,\dots ,x_N)$ is jointly Gaussian with a mean $\mu (x)$ and covariance $\sum (x)$, where $\sum _{ij}=k(x_i,x_j)$. K is a kernel function, which determines the similarity between data points x_i and x_j. If these points are deemed similar by the kernel, we expect the output of the functions at these points to be similar as well. For each x_i, y_i in our training dataset, we can write a function $f(x_i)$ such that

$$y_i=f_i(x_i)+{ϵ}_i,$$

where ${ϵ}_i\sim N(0,{\sigma }^2)$. Therefore, for any input vector $(x_1,x_2,\dots ,x_N)$, f(x) has a joint Gaussian distribution. The covariance (kernel) function k is generally taken as Gaussian (i.e. squared exponential kernel). However, in this application, we found that a Matern kernel performs better. We used 5-fold cross-validation to avoid over-fitting and a separate test dataset to validate our model. We tried other regression models, such as linear regression with and without interactions, different regression trees, neural networks and support vector machine (SVM) regression models. GPR outperformed other models in training [both in terms of root-mean-squared error (RMSE) and R², P-value <${10}^{-}2$; see Table 1 for results and Supplementary Tables S1 and S2 for statistics]. We have also compared the training times of different regression models in Supplementary Table S3.

Table 1.

Comparison of different regression model performances on training dataset

Model	RMSE	R  2
Linear regression	8066.4±7.03	0.96
Decision tree	5559.0±90.82	0.98
Boosted tree	66518.8±8.19	0.98
Bagged tree	5148.4±37.86	0.98
SVM	5754.5±13.96	0.99
NeuralNet	8190.7±799.37	0.99
GPR	4302.3±14.20	0.96

2.3 Dataset

We used RNA-Seq data from 432 individuals generated by the gEUVADIS project (Lappalainen et al., 2013), H3K27ac ChIP-Seq data from 100 individuals generated by the PsychENCODE Consortium (Wang et al., 2018), ATAC-Seq data from 344 individuals generated by the BrainGVEX project(Wang et al., 2018) and ATAC-Seq data from 288 individuals generated by the PsychENCODE Consortium (Wang et al., 2018). We then used the GATK Best Practices from RNA-Seq and DNA data (DePristo et al., 2011; Van der Auwera et al., 2013) to call SNVs and small insertions and deletions (Fig. 3). We treated each chromosome separately, which resulted in 25 152 data points. In total, we had 13 537 data points from ATAC-Seq, 9456 data points from RNA-Seq and 2159 from ChIP-Seq. We randomly divided the entire dataset in half to use as training and test sets, which preserved the ratio of each assay type in training and test sets. We used 5-fold cross-validation while training on the training dataset to prevent over-fitting. We also separately validated our model by using 308 data points from the RNA-Seq study by Kilpinen et al. (2013). Since there is an imbalance in the number of datapoints coming from different assays, we wanted to understand if such imbalance is affecting our model selection. To this end, we repeatedly sub-sampled 2159 data points from the RNA-Seq and ATAC-Seq categories (to match it to the most under-represented category of ChIP-Seq) and trained multiple regression models. We found that GPR is still the best regression model with the smallest RMSE in each case (P-value <${10}^{-}2$; see Table 2 for results and Supplementary Tables S4 and S5 for statistics).

Fig. 3.

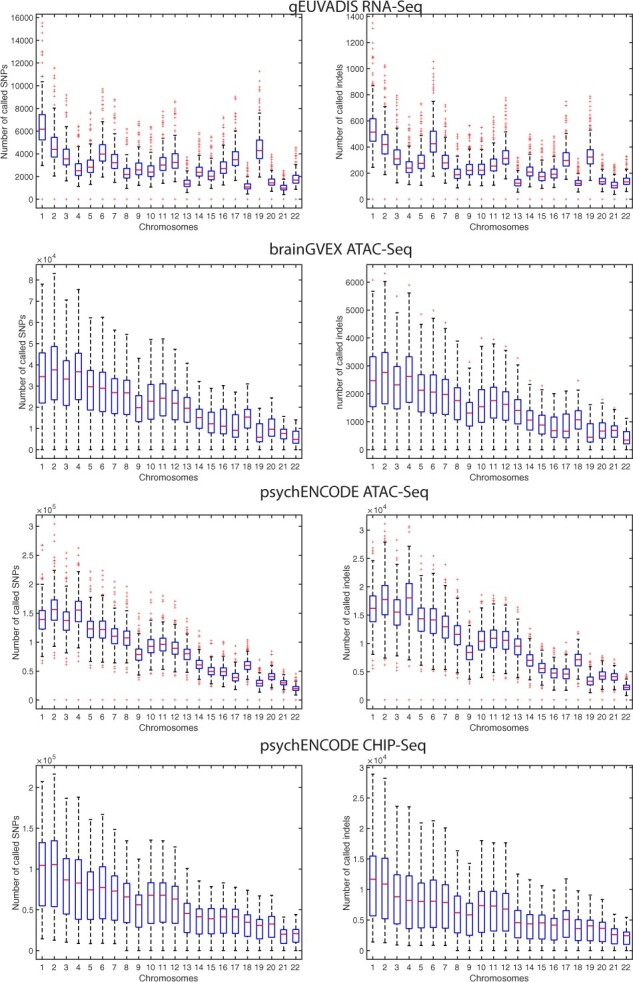
Distribution of the number of called SNPs and indels from functional genomics data. We used the GATK Best Practices from RNA-Seq and DNA data to call SNVs and small insertions and deletions

Table 2.

Comparison of different regression model performances when the training data are sub-sampled

Model	RMSE	R  2
Linear regression	6714.5±21.74	0.95
Decision tree	7133.8±121.86	0.94
Boosted tree	6708.1±53.98	0.95
Bagged tree	6923.6 ±135.39	0.95
SVM	7903.8±197.08	0.93
NeuralNet	8376.1±973.26	0.92
GPR	5474.1±65.74	0.97

2.4 Random Forest details

Random Forest was used as a plug-in to $\text{FANCY}$ in order to predict the assay type of the data from the sequencing statistics in the case that metadata is missing. Random Forest classifiers combine several decision trees that use multiple subsets of data from a training sample to produce better predictive performance than that of a single decision tree. The advantage of a Random Forest classifier is that it handles high dimensionality in data, as well as missing values. It works via the following principles: assume we have an observation y_i and the feature associated with it is $x_{i,j}$. Here, $i=1,\mathrm{..},N,\hspace{0.17em}j=1,\dots ,M$ and N and M are the number of observations and features, respectively. We first take a subset from N number of training data randomly with replacement. We then take a subset of M features randomly. We split the node iteratively by finding the feature associated with the best split. With this iteration, we grow the largest tree. We then repeat these steps to aggregate n number of trees to create our Random Forest. We generated 30 trees using a 5-fold cross-validation and an independent test set to validate our model.

3 Results

Genotyping from DNA sequences is the process of comparing the DNA sequence of an individual to that of the reference human genome. To be able to successfully genotype, one needs a substantial depth of sequencing reads for each base pair. According to the Lander–Waterman statistics for DNA sequencing, when random chunks of DNA are sequenced repeatedly, the depth per base pair follows a Poisson distribution with a mean that can be estimated from the read length, number of reads and the length of the genome (Lander and Waterman, 1988). For example, as RNA-Seq aims to sequence expressed genes, one would expect that sequencing depth per base pair does not follow Poisson statistics. Genotyping using reads from RNA-Seq experiments is biased toward variants that are in the exonic regions. Conversely, ChIP-Seq is biased against RNA-Seq, as it targets non-coding genome, such as promoters and enhancers (see Fig. 1d).

We hypothesized that the statistical properties of the depth per base pair distribution are strong indicators of the number of variants that can be inferred from functional genomics data. We used a total of six sequencing features: (i) the average depth per base pair ($\overline{d}$); (ii) the total fraction of the genome that is represented at least by one read [i.e. the breadth, $b=\sum _{i=1}^N\delta (d_i)$, such that $\delta (d_i)=1$ if $d_i>0$, b = 0 otherwise and N is the total number of nucleotides in the genome]; (iii) the SD of the depth distribution; (iv) skewness (i.e. whether the distribution is larger on the right or left side of the mean); (v) kurtosis (i.e. whether or not the depth distribution has big tails); and (vi) the type of the experiment (i.e. RNA-Seq, ATAC-Seq or ChIP-Seq).

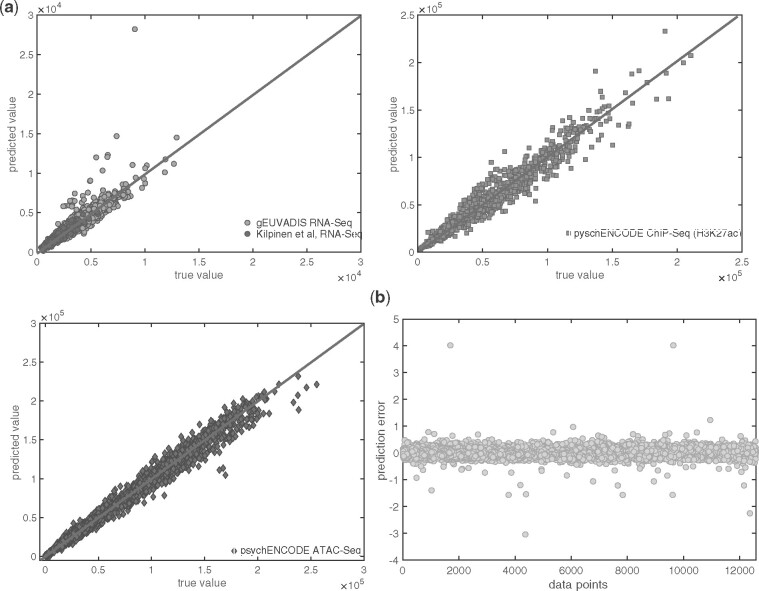
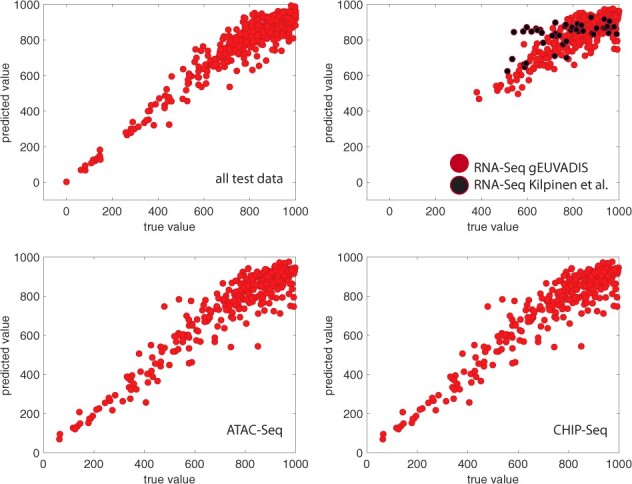
FANCY predicts the cumulative number of leaking SNVs with an R² of 0.99 for training (with 5-fold cross-validation) and 0.90 for independent test RNA-Seq, 0.99 for independent test ATAC-Seq and 0.99 for independent test ChIP-Seq datasets (Fig. 4 and Table 3). We used mean squared error as our loss function in the regression model (see Tables 1–3 for RMSE). Our predictions are in strong agreement with the true number of leaking variants in all the independent test datasets (Fig. 4a). To easily interpret the performance of our predictions, we calculated the deviation from the true values by calculating $\delta =(y_p-y_r)/y_r$, where y_p is the predicted value and y_r is the real value of the number of SNPs. The negative values indicate under-prediction (i.e. the number of predicted SNVs is lower than the true number of leaking SNVs). On average, we had 8% prediction error for all of the independent test sets (Fig. 4b).

Fig. 4.

Details of FANCY. (a) The performance of FANCY on the independent test datasets. (b) The ratio of the error in the predictions with respect to true values. Negative values indicate that the predicted values are lower than the true values, and positive values indicate the predicted values are greater than the true values. Zero indicates perfect prediction

Table 3.

The maximum and minimum number of variants leaked in each experiment and the RMSE of our predictions in these test datasets

Assay	Number of test	Max. number	Min. number	Total number	RMSE
	data points	of variants	of variants	of variants
RNA-Seq	4740	12 928	379	12 062 696	422.76
ATAC-Seq	6753	238 481	65	339 606 218	4503.10
ChIP-Seq	1082	210 567	2665	57 921 174	5381.22

We also assessed the performance of our model on RNA-Seq data that was obtained using different experimental protocols. We were able to test FANCY on poly-A minus, poly-A plus and total RNA-Seq data obtained by different labs. The selection of these test datasets was limited by the number of available functional genomics datasets with accompanying WGS data (required for the validation of our model). We found that our model works equally well with independent datasets obtained using different protocols than those used to obtain the training data (R² 0.97–0.98, see Fig. 5).

Fig. 5.

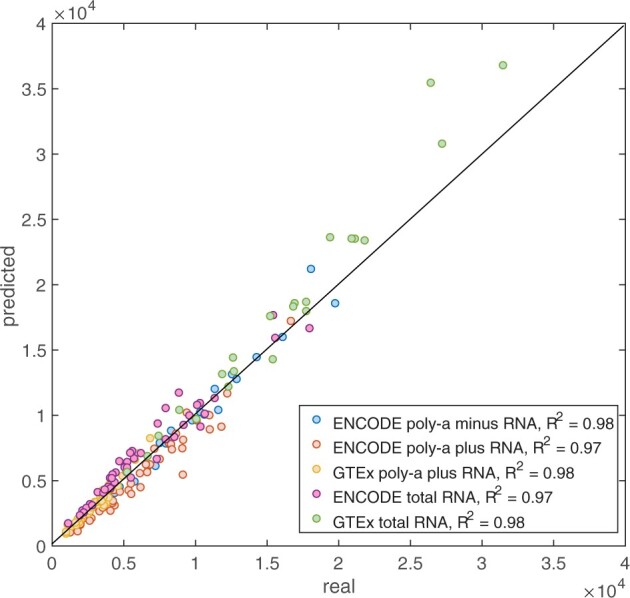
Performance of FANCY on different RNA-Seq protocols. The performance of FANCY on the independent test RNA-Seq datasets that were obtained using different protocols and in different labs & consortia

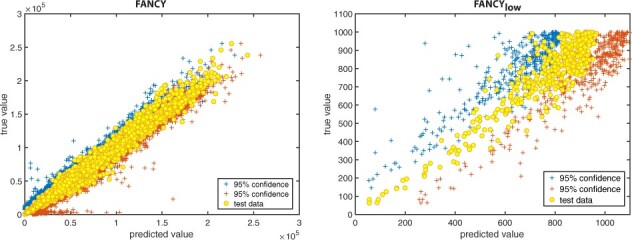
If a functional genomics experiment is leaking more than 1000 variants, the associated privacy risk for re-identification and characterization is at the maximum, regardless of the absolute value of the number of variants. However, re-identification might require a lower number of leaking variants than characterization. Thus, the risk assessment for re-identification can be more valuable for experiments that are leaking a low number of variants, as mis-predicting these values only slightly may result in the release of private data. Thus, we developed another regression model (see Section 2) that aims to predict the leakage more precisely when the number of leaking variants is low. This second model had an RMSE of 75.64, 74.8 and 74.0 for independent test RNA-Seq, ATAC-Seq and ChIP-Seq datasets, respectively, in which the maximum number of leaking variants is 1000 (Figs 6). We also calculated the number of under-predicted (predicted value is lower than true value) leaking variants and found that we have no under-predicted leaking variants when the total number of leaking variants is lower than 400, and only three under-predicted leaking variants when the total number of leaking variants is between 400 and 500. Moreover, both FANCY and ${\text{FANCY}}_{\text{low}}$ can also output the number of leaking variants within 95% confidence interval (Fig. 7).

Fig. 7.

Predicted versus true values within 95% confidence level

Fig. 6.

Performance of ${\text{FANCY}}_{\text{low}}$ when the number of leaked variants is <1000. Performance for the test dataset, RNA-Seq, ATAC-Seq and ChIP-Seq are shown separately. For RNA-Seq, we validated our model with two datasets, shown in red and black. (Color version of this figure is available at Bioinformatics online.)

To further understand the role of the features on the prediction performance, we did a ‘leave one feature out’ test and found that the mean depth ($\overline{d}$) and breadth (b) of the coverage had the greatest effect on the performance of the predictor (Fig. 8a) 8. We then created predictors by using only (i) mean depth, (ii) breadth and (iii) mean depth and breadth as the features. However, these predictors performed worse than the original model (Fig. 8a). These results show that although breadth is the highest contributing feature, all of our features contributed to the final model; indeed, the RMSE is the lowest when we use all of the features (Fig. 8a, see Supplementary Table S6 for the statistics). We further changed the depth cut-off used for defining the breadth of the coverage from 1 to 2, 4 and 8 and re-trained a model using the 9456 data points from RNA-Seq data. We found that although overall performance of the regression slightly improved, the best performance was still obtained when we used all of the features (Supplementary Fig. S1). This is likely because the correlation between the breadth (feature) and the number of SNPs (outcome) is only slightly improved when we use different thresholds (Supplementary Fig. S2). In addition to estimating privacy risk, FANCY can also be used to plan functional genomics experiments (i.e. for a target number of callable SNVs, one can back-calculate the required sequencing statistics). This can be done by using the empirical depth distribution of available data from different assays and calculating the required number of reads to reach the desired statistical properties, such as mean depth, skewness and kurtosis. Moreover, we also developed a Random Forest classifier as a plug-in that predicts the type of the assay (RNA-Seq versus ATAC-Seq versus ChIP-Seq) by using the sequencing statistics as features, which can be broadly useful to the community for characterizing samples with missing metadata. This classifier has an average accuracy of 96.8%, precision of 94.9%, recall of 90.2% and F1 score of 93.3% (Fig. 8b).

Fig. 8.

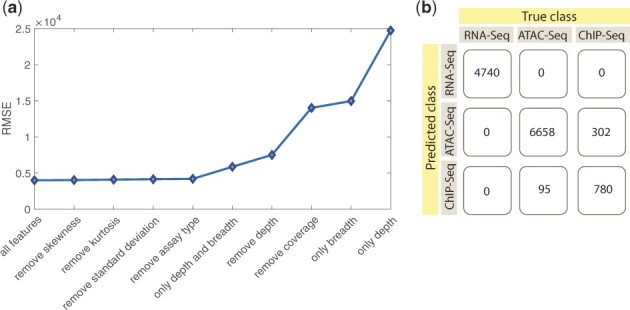
Feature importance and classifier performance. (a) Lower RMSE corresponds to better predictions. The difference between the first five points on the figure is smaller compared to other data points, however, lowest RMSE is still observed when using all the features in the model. (b) A Random Forest Classifier is developed to predict the type of the experimental assay by using sequencing statistics as features. Here we show the performance of this classifier

4 Discussion

How can we quantify the privacy risk that accompanies collection and sharing of functional genomics data? In this study, we addressed this question with FANCY, a model using GPR followed by rare versus common variant estimation to predict the number of total leaking variants in a functional genomics dataset. We showed that this prediction can be generated with high accuracy without relying on genotyping or a gold-standard genotype list, which requires significant resources to obtain and may not always be obtainable for every individual. We determined that the depth and breadth of sequencing coverage had the greatest influence on the predictor, and that using all of the features yielded the most accurate prediction. Not only does FANCY quantify the risk of privacy leaks from an existing dataset, but it also allows experimentalists to design functional genomics sequencing experiments, before collecting data, with the goal of obtaining a desired number of variants.

In this study, we used available data types from different projects, including RNA-Seq, ATAC-Seq and ChIP-Seq H3K27ac. However, as sequencing costs decrease, we will soon have access to a surge of datasets from a wider range of experimental protocols using large cohorts of individuals (e.g. 10x single-cell RNA-Seq, different ChIP-Seq targets, etc.). Therefore, we also provide users our workflow and source code, which can be used as a base framework to adapt prediction methods according to the ever evolving privacy landscape.

FANCY can also be used to accelerate sharing of functional genomics datasets. Functional genomics researchers may want to share their data alongside their published results. However, funding agencies’ data-sharing policies typically require extensive privacy risk assessments before the data are released. These assessments can be lengthy and costly, and can significantly delay data release (sometimes until after the relevant article has been published) (Mailman et al., 2007). Our tool will allow for fast assessments of privacy risk in functional genomics datasets, which will permit faster release of data. After FANCY, further assessments may be done of the data with significant risk.

If a functional genomics dataset leaks more than 1000 variants, the risk of re-identifying an individual from that dataset is maximized. However, when the number of leaking variants is low, the qualitative measurements of sharing risk commonly given in consent documents may not be accurate and will not give the individual a sense of the true risk of privacy loss. Therefore, we designed ${\text{FANCY}}_{\text{low}}$, a specially modified version of FANCY with improved precision just for a low number of leaking variants. Given that an individual’s privacy is at stake, it was important to minimize under-predictions of leaking variants as this could lead to a dataset being labeled safe to share when it actually permits re-identification.

Privacy protection is the core goal of developing FANCY and related tools, but they have other uses in genomics research. In cases where whole-genome sequence data are missing, e.g. FANCY can also be used to determine whether SNP calling is possible using a particular dataset. Additionally, our Random Forest Classifier, which we developed alongside FANCY, can be used to identify the kind of experiment a dataset came from in the case of missing metadata. This latter tool does not protect privacy, but helps to maximize data utility.

One limitation of the current version of FANCY is the lack of joint predictions of the same sample from different assays. We envision that in the future multiple assays will be performed on samples from the same individuals. In other words, a single data type may not leak enough variants for privacy to be a concern, but a combination of different functional genomics data can pose significant privacy risk. Some of these assays likely contain overlapping SNPs, but such overlap can easily be estimated by using the overlapping signal coverage and incorporated into the FANCY framework.

We understand that genome privacy is a complex issue and can be discussed beyond the number of leaking SNVs. For example, data from an experiment may leak a small number of SNVs, but when overlapped with GWAS results can reveal sensitive information about the individual, such as risk for a particular stigmatizing disease. Because the SNVs obtained from functional genomics experiments are likely present in the functional regions of the genome, we believe that quantifying the number of leaked SNVs will be a useful initial assessment of the risk of privacy loss.

We also think that our training data will be useful to the community. For example, even before mapping the reads to the genome, one can look at the training data to see roughly how many reads in an assay type lead to how much leakage in order to have a rough estimate and then perform the mapping and FANCY calculations if more precision is needed.

The privacy risk associated with human DNA sequencing has been acknowledged for years. Yet, as scientists have become increasingly interested in a more diverse set of experimental human omics data, it is critical to develop companion tools to assess the privacy risk of those data. In this study, we contribute FANCY to the toolbox. Importantly, these tools must be convenient for scientists to use and easy for patients/individuals to understand. FANCY requires only a few files and can be run easily from the command line. Furthermore, we set up a simple web page, which allows users to input statistics about their dataset and runs FANCY to output a leakage prediction and qualitative privacy risk assessment. These user-friendly components are a key benefit of FANCY, and require no private information to be input to our servers, making it convenient for experimentalists to rapidly assess the risk of privacy before they release the data.

Funding

This work is supported by US National Institutes of Health K99 HG010909 and R01 HG010749 grants and and by AL Williams Professorship funds.

Conflict of Interest: none declared.