Theoretical model for the diclofenac release from PEGylated chitosan hydrogels

Abstract

Controlled drug delivery systems are of utmost importance for the improvement of drug bioavailability while limiting the side effects. For the improvement of their performances, drug release modeling is a significant tool for the further optimization of the drug delivery systems to cross the barrier to practical application. We report here on the modeling of the diclofenac sodium salt (DCF) release from a hydrogel matrix based on PEGylated chitosan in the context of Multifractal Theory of Motion, by means of a fundamental spinor set given by 2 × 2 matrices with real elements, which can describe the drug-release dynamics at global and local scales. The drug delivery systems were prepared by in situ hydrogenation of PEGylated chitosan with citral in the presence of the DCF, by varying the hydrophilic/hydrophobic ratio of the components. They demonstrated a good dispersion of the drug into the matrix by forming matrix-drug entities which enabled a prolonged drug delivery behavior correlated with the hydrophilicity degree of the matrix. The application of the Multifractal Theory of Motion fitted very well on these findings, the fractality degree accurately describing the changes in hydrophilicity of the polymer. The validation of the model on this series of formulations encourages its further use for other systems, as an easy tool for estimating the drug release toward the design improvement. The present paper is a continuation of the work ‘A theoretical mathematical model for assessing diclofenac release from chitosan-based formulations,’ published in Drug Delivery Journal, 27(1), 2020, that focused on the consequences induced by the invariance groups of Multifractal Diffusion Equations in correlation with the drug release dynamics.

1. Introduction

Controlled drug delivery is a science field that attracts increased attention of researchers due to the impact on human health. While for the systemic administration of the drugs, the most used administration route, the therapeutic effect exerts indiscriminately on the entire body leading to side effects, the controlled drug release targets the affected sites of the body, increasing the drug bioavailability and limiting the negative effects (Chari, 2008). This is of particular importance for cancer therapy, which involves drugs with high cytotoxic effects (Park, 2014; Kuen et al., 2020).

A pathway for the controlled release of the drugs is their encapsulation into an injectable matrix, which assures their administration and the prolonged-release directly into tumors. Hydrogels are the most important matrix for this aim, due to the intrinsic physical peculiarities such as porosity, high hydrophilicity, biocompatibility, and similarity with the biological tissues (Pertici et al., 2019). Among them, the ones based on chitosan occupy a special place due to the compositional and mechanical similarity of chitosan with the extracellular matrix (Sultankulov et al., 2019). Starting from these premises, chitosan-based hydrogels are largely investigated as a matrix for the controlled drug delivery systems, and continuous attention is directed to the development of new biocompatible formulations to meet the requirements for in vivo applications (Bhattarai et al., 2010; Ailincai et al., 2018; Craciun et al., 2019). In this view, in the last years, our group developed a new strategy for the preparation of biocompatible chitosan-based hydrogels by using natural monoaldehydes as physico-chemical crosslinkers. It was demonstrated that, by the reaction of chitosan polyamine with monoaldehydes, dynamic polyimines are formed which due to the imination and transamination reactions along with hydrophilic/hydrophobic segregation, self-assemble into three-dimensional networks forming hydrogels. This was proved as a great strategy to transform chitosan into materials with tuned properties, by a simple choice of the suitable aldehydes (Ailincai et al., 2016; Iftime et al., 2017; Marin et al., 2017; Olaru et al., 2018; Ye et al., 2020). The hydrogels prepared via this method displayed a good ability to anchor drugs and to release them in a controlled manner (Ailincai et al., 2018; Craciun et al., 2019; Ailincai, Mititelu-Tartau, et al., 2020; Iftime, Mititelu Tartau, et al., 2020). To further improve the properties of the matrix, PEGylated chitosan was considered instead of chitosan. This decision has been taken considering the PEG hydrophilicity and its well-established safety which made it a valuable candidate for drug delivery applications that passed the clinical trials (Bonora & Drioli, 2008; D’souza & Shegokar, 2016; Vijayan et al., 2019). By grafting poly(ethylene glycol) and citral on the chitosan backbone, new biocompatible hydrogels were obtained. Due to the PEG they showed improved hydrophilicity and thixotropic properties, promising to become an excellent matrix for local injection of the drugs to the tumor sites (Ailincai, Mititelu-Tartau, et al., 2020). To investigate their ability to act as a matrix for prolonged release of the drugs, the PEGylated chitosan hydrogels were used as a matrix for the encapsulation of diclofenac sodium salt (DCF). DCF was preferred as a model drug, due to the fact that besides the well-known anti-inflammatory activity, recent preclinical and clinical investigations revealed its anticancer activity on many tumor cell lines (Pantziarka et al., 2016). This activity was attributed to the presence of the electron-withdrawing halogens, similar to many other antitumor drugs, offering the opportunity to consider it as a model for antitumor drugs (Isanbor & O’Hagan, 2006; Marin et al., 2013).

The preliminary investigation of these drug delivery systems indicated in vivo biocompatibility and the ability to release the drug in a prolonged manner along with the slow biodegradation of the matrix (Ailincai, Mititelu-Tartau, et al., 2020). This encouraged us to further investigate the drug delivery mechanism in order to understand the phenomena which govern the drug release, allowing the development of the formulation design. To do this, a mathematical model based on the Multifractal Theory of Motion was established. Various solutions of the model based on the consequences induced by the SL(2R) invariance groups in the form of kink, soliton, antisoliton, breather, etc. are correlated with the drug release mechanisms.

2. Experimental

Materials

Citral (95%), low molecular weight chitosan (217 kDa, DA: 85%), O-[2-(6-Oxocaproylamino)ethyl]-O′-methylpolyethylene glycol 2000, phosphate buffer saline (pH = 7.4), diclofenac sodium salt (DCF) and ethanol were purchased from Sigma Aldrich and used as received.

Synthesis of the drug delivery systems

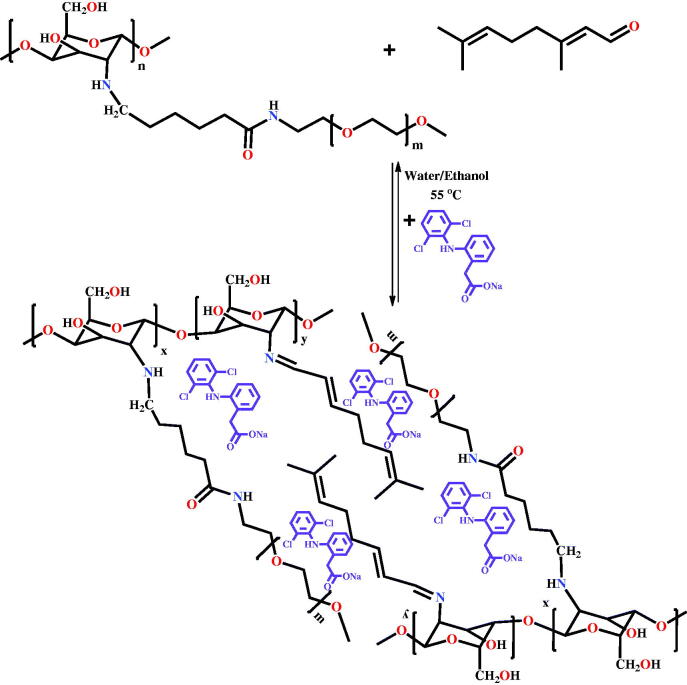
Drug delivery systems were obtained via the acid condensation reaction of the free amino groups of two hydrolytically stable PEGylated chitosan with the aldehyde group of citral in the presence of DCF (Scheme 1) (Ailincai, Mititelu-Tartau, et al., 2020). The two PEGylated chitosan derivatives were previously synthetized by the acid condensation reaction of the chitosan with PEG-aldehyde in the amine/aldehyde molar ratio of 40/1 and 50/1, respectively, followed by reductive amination, as described in the reference Ailincai, Mititelu-Tartau, et al., (2020). Four drug delivery systems were obtained by the acid condensation of the two PEGylated chitosan derivatives with citral, in the presence of the DCF drug. In order to obtain drug delivery systems with different properties, the DCF amount was kept constant, while the crosslinking density was changed by modifying the molar ratio between amine and aldehyde functionalities, to give formulations with different content of PEG. In Figure 1 were given the codes of the formulations and the number of their components. It should be highlighted that this in situ encapsulation method assured the encapsulation of the entire amount of drug (Figure 1). Further, the preservation of the activity of the drug by encapsulation into these hydrogels was proved by in vivo drug delivery somatic pain testing, which was performed using tail-flick assay on mice (Ailincai, Mititelu-Tartau, et al., 2020).

Scheme 1.

Synthesis of the formulations

Figure 1.

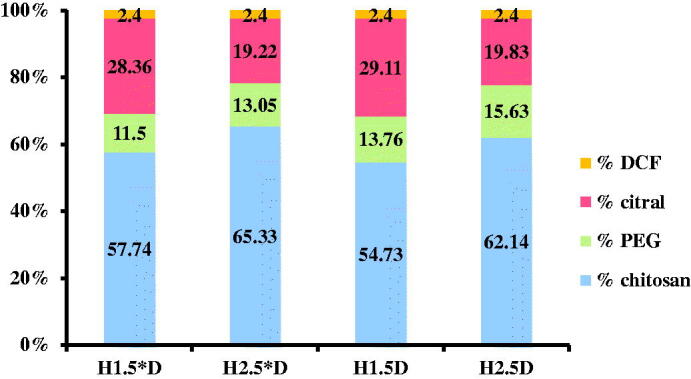
Composition of the drug delivery systems and their codes.

Methods

The PEGylated chitosan derivatives and the drug delivery systems have been obtained by freezing them in liquid nitrogen and further lyophilization using a LABCONCO Free Zone Freeze Dry System equipment, in working conditions −54 °C and 1.510 mbar, for 24 h.

ATR-FTIR spectra of the drug delivery systems (H1.5D; H2.5D; H1.5*D; H2.5*D) were recorded using an FTIR Bruker Vertex 70 Spectrophotometer equipped with a ZnSe single reflection ATR accessory.

Wide-angle X-ray diffraction (WAXD) was performed on a Bruker D8 Advance diffractometer at 36 kV and 30 mA, using Ni filtered Cu-Ka radiation (λ = 0.1541 nm). The diffractograms were recorded in the 2°–40° range, at room temperature, on pellets obtained by pressing a certain amount of sample using a hydraulic press (5 N/m²).

The investigations of the supramolecular architecture of the systems were realized by polarized optical microscopy (POM), using a Leica DM 2500 microscope.

The morphology of the samples was evaluated with a field emission scanning electron microscope (Scanning Electron Microscope SEM EDAX – Quanta 200) at an accelerated electron energy of 10 eV.

The monitoring of the in vitro release kinetics was performed in phosphate buffer saline (PBS) (pH = 7.4), at human body temperature, 37 °C. The obtained drug delivery systems (H1.5D; H2.5D; H1.5*D; H2.5*D) were used for the in vitro release experiments, following a previously used experimental procedure (Pantziarka et al., 2016; Ailincai, Mititelu-Tartau, et al., 2020) Pieces of xerogels with a mass of 62 mg, containing 1.5 mg of DCF drug were immersed into 10 mL of PBS. After different time intervals, 2 mL of supernatant were withdrawn and replaced with fresh PBS, to keep the same sink conditions. The concentration of the drug in the removed supernatant was determined by UV-vis spectroscopy, by measuring the absorbance of the characteristic absorption band of DCF at 275 nm and fitting on a calibration curve. The calibration curve was previously drawn by measuring the absorbance for different solutions of DCF with well-known concentrations and by the graphical representation of the absorbance as a function of concentration (Ailincai, Mititelu-Tartau, et al., 2020). The cumulative drug release was calculated using the following mathematical equation:

$$\%\mathrm{ }\text{DCF}\mathrm{ }=\mathrm{ }\left[\left(10C_n+2\Sigma C_{n-1}\right)/m_0\right]\times 100$$

where C_n and C_n−1 are the concentrations of the drug in the supernatant after n and n − 1 withdrawing steps, respectively, while m₀ = 1.5 mg, corresponding to the amount of DCF loaded in the samples. The experiments were done in triplicate and the values are given as the mean value of three independent measurements. The absorbance of the DCF drug was measured using a Perkin Elmer Lambda 35 UV-Vis spectrophotometer.

Mathematical model

In the past years, a wide range of theoretical models aiming at describing drug release mechanisms has been developed. The first type of models are empirical and semi-empirical models. The most used ones are the zero-order model, Higuchi model, Hixson–Crowell model, Korsmeyer–Peppas model, first-order model, etc. (Fisher et al., 2010; Peppas & Brannon-Peppas, 2010; Tiwari et al., 2012; Patra et al., 2018). There are also kinetic models, based on the usual conservation laws, developed on spaces with integer dimensions (Tiwari et al., 2012) or kinetic models, based on the conservation laws, developed on spaces with a non-integer dimension, explicitly written through fractional derivatives (Kosmidis et al., 2003; Agop & Merches, 2019). Recently, a new generation of theoretical models has arisen, based on Scale Relativity, either in the monofractal dynamics as in the case of Nottale (Nottale, 2011), or in the multifractal dynamics as is the case for the Multifractal Theory of Motion (Agop et al., 2004; Agop & Murgulet, 2007; Agop et al., 2008; Colotin et al., 2009; Paun et al., 2010; Merches & Agop, 2016; Agop & Paun, 2017; Bujoreanu et al., 2017; Cobzeanu et al., 2017; Irimiciuc et al., 2018, 2020). In such a context, supposing that, from both structural and functional perspectives, the polymer–drug complex system is assimilated to a multifractal system (Iftime, Dobreci, et al., 2020; Ailincai, Dorobanțu, et al., 2020; Iancu et al., 2020) the wide ranges of drug release dynamics can be described through the movement of the so-called polymer-drug complex system structural units on multifractal curves. Accepting multifractality as a fundamental property in drug release dynamics (and since multifractality is induced through stochasticity (Jackson, 1993; Cristescu, 2008; Mandelbrot, 1982)), the drug release dynamics can be associated to various flow regimes of a stochastic fluid at various scale resolutions (multifractal fluid). Then, for a large temporal scale resolution, with respect to the inverse of the highest Lyapunov exponent (Mandelbrot, 1982; Jackson, 1993; Cristescu, 2008), the deterministic trajectories of the polymer–drug system structural units can be replaced by a collection of potential trajectories (virtual trajectories), while the concept of definite trajectories can be replaced by that of probability density. In such a context, a multifractal probability density conservation law will become functional for the drug release dynamics, in the form of a diffusion-type equation at various scale resolutions (multifractal diffusion equations) (Iftime, Dobreci, et al., 2020):

$${\partial }_t\rho =2\lambda {\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }_l{\partial }^l\rho$$ (1)

where

$${\partial }_t=\frac{\partial }{\partial t},\mathrm{ }{\partial }_l=\frac{\partial }{\partial X^l},\mathrm{ }{\partial }_l{\partial }^l=\frac{\partial }{\partial X^l}\left(\frac{\partial }{\partial X^l}\right)$$ (2)

In the above relation, $\rho$ is the multifractal probability density, $X^l$ with $l=1,\mathrm{ }2,\mathrm{ }3$ are the multifractal spatial coordinates, $t$ is a non-multifractal temporal coordinate having the affine parameter role on the movement curves, $dt$ is the scale resolution, $\lambda$ is a coefficient associated to the multifractal to non-multifractal transition, $f\left(\alpha \right)$ is the singularity spectrum of order $\alpha$ and $\alpha$ is the singularity index through which the fractal dimension D_F is specified (for D_F we can use any definitions – Kolmogorov fractal dimension, Hausdorff–Besikovich fractal dimension, etc. (Mandelbrot, 1982); it is regularly found that D_F < 2 for correlative processes and D_F > 2 for non-correlative processes). From such a perspective, through $f\left(\alpha \right)$ it is possible to identify not only the drug release volumes that are characterized by a certain fractal dimension (i.e. the case of mono-fractal drug release dynamics) but also the drug release quantity for which the fractal dimension is situated in an interval of values (i.e. the case of multifractal drug release dynamics). More than that, for the same $f\left(\alpha \right),$ it is possible to identify classes of universality in the drug release dynamics laws, even when regular or strange attractors have various aspects (Jackson, 1993; Cristescu, 2008).

In a recent paper (Iftime, Dobreci, et al., 2020), operating with Equation (1), it has been shown that specific mechanisms of the release dynamics of the polymer–drug complex system (i.e. Fickian-type diffusion, non-Fickian-type diffusion, degradation of matrix, dissolution of matrix, etc.), can be ‘mimed’ as multifractal fluid diffusion modes (at various scalar resolutions). Then, $\rho \left(t\right)/{\rho }_{\mathrm{\infty }}$ was assimilated to the fraction of dissolved drug, that is, $M\left(t\right)/M_{\mathrm{\infty }}\equiv \rho \left(t\right)/{\rho }_{\mathrm{\infty }},$ where $M\left(t\right)$ is the amount of drug dissolved in time $t$ and $M_{\mathrm{\infty }}$ is the total amount of drug dissolved, when the pharmaceutical dosage form is released.

Now, new data regarding release dynamics, complementary to the class of solutions associated with Equation (1) (generated through initial and boundary conditions), can also be given on the base of the transformation groups (which leave invariant the Equation (1)) (Jaynes, 1973; Mazilu & Skyrmions, 2012; Merches & Agop, 2016; Agop & Paun, 2017). These transformation groups constitute, in the most general case of the one-dimensional drug release dynamics, a realization of the Lie group $SL\left(2R\right),$ through the action (Mazilu et al., 2020):

$$t\mathrm{\prime }\to \frac{\alpha t+\beta }{\gamma t+\delta },\mathrm{ }X\mathrm{\prime }\to \frac{X}{\gamma t+\delta }\mathrm{ }$$ (3)

where $\alpha ,$ $\beta ,$ $\gamma$ and $\delta$ are real elements.

Let us consider that, in accordance with general mathematical procedures from (Jaynes, 1973; Kosmidis et al., 2003; Peppas & Brannon-Peppas, 2010; Mazilu & Skyrmions, 2012), the release dynamics may be generally described with the help of a 2 × 2 matrix, with real elements. In a polymer–drug type system, it is obvious that the problem revolves around a family of such matrices, each of them describing the dynamics of a complex system entity (structural unit). The interactions between the complex system entities can then be expressed through relations between the representative matrices. These relations must contain certain parameters that characterize the structure of the polymer–drug complex system, adequate to the description of the drug release dynamics.

Therefore the matrix which generates an unharmonic curve (Mazilu & Skyrmions, 2012), is a 2 × 2 matrix with real elements, written in the form:

$$\widehat{\mathrm{M}}=\left(\begin{array}{cc}\alpha & \beta \\ \gamma & \delta \end{array}\right)$$ (4)

The elements of this matrix contain, in an unspecified form, both the physical parameters of the complex system of polymer–drug type implying release dynamics and the possible initial conditions of the release dynamics. More precisely, the elements of the matrix in Equation (4) depend on the scale resolution in the sense of the Multifractal Theory of Motion (the release curves are continuous and non-differentiable, that is, multifractal curves) (Merches & Agop, 2016; Agop & Paun, 2017; Mazilu et al., 2020). In such a conjecture, the results to be obtained will also be in a sense of the previously-mentioned theory.

A set of such matrices, with variable elements, may be admitted as relevant for the release dynamics, for example by means of a fundamental spinor set, given by 2 × 2 matrices which describe the release dynamics. This description is analogous with the spinor description of space–time (Penrose, 1960).

In such a situation, any 2 × 2 matrix of form in Equation (4) can be written as a linear combination with real coefficients, which implies two special matrices, specifically the unity matrix $\widehat{U}$ and a null-trace matrix $\widehat{I}$(from involution), meaning:

$$\widehat{M}=\lambda \widehat{U}+\mu \widehat{I}$$ (5)

The involution $\widehat{I}$ has some important properties, such as its squared form is a multiple of $\widehat{U}$ and the fixed points of its homographic action are the ones of matrix $\widehat{M}.$

In Equation (5), there exists the liberty to choose a parameterization in which the squared form of $\widehat{U}$ can be the unity matrix, up to a sign. In this case the elements of $\widehat{I}$ maybe expressed with the help of only two parameters, which represent the asymptotic directions of matrix $\widehat{M}.$ If the asymptotic directions are complex, being of the form $u\pm iv,$ the representation of the matrix $\widehat{I}$ through asymptotic directions is of a spherical type. Then, satisfying the afore-mentioned properties (a) and (b) implies, for the matrix $\widehat{I},$ the form:

$$\widehat{I}=\frac{1}{v}\left(\begin{array}{cc}-u& -u^2-v^2\\ 1& u\end{array}\right),\mathrm{ }\widehat{I}=-\widehat{U}\mathrm{ }$$ (6)

Such a representation of the release dynamics has an important advantage. When analyzing the physics of the problem, the model allows an explicit differential description of the release dynamics, through matrix geometry, identic to the metric geometry of space at a certain moment, the hyperbolic geometry of the second type (in a Barbilian sense (Barbilian, 1971; Barbilian, 1974)).

The representation of release dynamics through 2 × 2 matrices leads to a natural matrix of the matrices’ space, for example, the Killing–Cartan metric of $SL(2R)$-type algebra of these matrices (Cartan, 2001; Mazilu & Skyrmions, 2012; Mazilu et al., 2020). The basic co-vectors of such geometry are, in the general case of matrix in Equation (4), given by the external differential forms as follows:

$$\begin{array}{c}{\omega }^1=\frac{\alpha d\beta -\beta d\alpha }{\Delta },\mathrm{ }{\omega }^2=\frac{\alpha d\gamma -\gamma d\alpha }{\Delta },\mathrm{ }{\omega }^3=\frac{\beta d\gamma -\gamma d\beta }{\Delta }\\ \Delta =\alpha \gamma -{\beta }^2\end{array}$$ (7)

In the parameterization given through Equations (5) and (6), Equation (7) becomes:

$${\omega }^1=\frac{1}{v}d\Phi +{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2\Phi \frac{du}{v^2}-\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi \frac{dv}{v^2}{\omega }^2=2\frac{u}{v}d\Phi +2{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2\Phi \frac{\mathit{udu}+\mathit{vdv}}{v^2}+2\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi \frac{\mathit{vdu}-\mathit{udv}}{v^2}{\omega }^3=\frac{u^2+v^2}{v}d\Phi +{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2\Phi \frac{\left(u^2-v^2\right)du+2u\mathit{vdv}}{v^2}+\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi \frac{2u\mathit{vdu}-\left(u^2-v^2\right)dv}{v^2}$$ (8)

where:

$$\hspace{0.17em}\text{tan}\hspace{0.17em}\Phi =\frac{\mu }{\lambda }\mathrm{ }$$ (9)

Related to these co-vectors, the metric is given by the squared form as follows:

$$d{s}^2={\omega }^1{\omega }^3-{\left(\frac{{\omega }^2}{2}\right)}^2=d{\Phi }^2-\hspace{0.17em}{\text{sin}}^2\Phi \frac{d{u}^2+d{v}^2}{v^2}\mathrm{ }$$ (10)

As such, for as long as the polymer–drug complex system is represented defined by the core property that physics admits as being essential – which is the release dynamic – its description mode is a metric geometry. In this case, the metric is given through (10), where $\Phi$ is an arbitrary ‘phase,’ and $u$ and $v$ are ‘coordinates’ obtained from the (local) dynamic of the polymer–drug complex system, in the way previously described.

Such a metric approach for the release dynamics can be certainly delegated to harmonic maps, from the polymer–drug complex system to space. As soon as the mapping mode of the polymer–drug complex system on the space available its disposal is solved, the quantities$\mathrm{ }\Phi ,$ $u,$ and $v$ – and, the elements of the matrix family which represent the polymer–drug complex-system – are obtained. In principle, a ‘position’ function will be sufficient to correctly define a specific quantity of the polymer–drug complex system.

The difficulty of representing the polymer–drug complex system in this form is overcome through the harmonic map $X=\left(X_1,X_2,X_3\right)\to \xi =\left({\xi }^1,{\xi }^2,{\xi }^3\right)$ which can provide a set of quantities as functions of spatial coordinates. Let it be considered the function corresponding to the harmonic mapping principle (Misner et al., 2017; Xi, 2018):

$$J=\frac{1}{2}\iint \int d^{3}X\sqrt{\left|h\right|}\mathrm{ }{h}^{il}\left(X\right)\frac{\partial {\xi }^{\mu }\partial {\xi }^{\nu }}{\partial X^i\partial X^l}{g}_{\mu \nu }\left(\xi \right)$$ (11)

where $h$ is the space metric and $g$ is the associated metric of the polymer–drug complex system. Canceling the first-degree variation of this functional, in relation to the spatial coordinates, gives the sought harmonic map. Taking into account the fact that space is Euclidean and using Equation (9) for the metric tensor associated with the polymer–drug complex system, for the integrand of Equation (11) the expression will be as follows:

$$\sqrt{\left|h\right|}\mathrm{ }{h}^{il}\left(X\right)\frac{\partial {\xi }^{\mu }\partial {\xi }^{\nu }}{\partial X^i\partial X^l}{g}_{\mu \nu }\left(\xi \right)\equiv {\partial }_l{\Phi \partial }^l\Phi -{\left(\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi }{v}\right)}^2\left[{\partial }_l{u\partial }^{l}u+{\partial }_l{\nu \partial }^l\nu \right]$$ (12)

where the usual notation ${\partial }_l$ denotes the gradient. The Euler equations corresponding to the functional Equation (12) are as follows:

$$\begin{array}{c}{\partial }_l{\partial }^l\Phi +\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi \frac{{\partial }_{l}u{\partial }^{l}u+{\partial }_{l}v{\partial }^{l}v}{v^2}=0\\ {\partial }_i\left(\frac{{\partial }_{l}u}{v^2}\right)=0,\mathrm{ }{\partial }_i\left(\frac{{\partial }_{l}v}{v^2}\right)+\frac{{\partial }_{l}u{\partial }^{l}u+{\partial }_{l}v{\partial }^{l}v}{v^2}=0\end{array}$$ (13)

The last two equalities of Equation (13) represent a harmonic map from the Euclidean space to the hyperbolic plane (Lobacevsky plane), in the Beltrami–Poincaré representation.

As a consequence of these equalities, there will be:

$${\partial }_i\left(\frac{{\partial }_{l}u{\partial }^{l}u+{\partial }_{l}v{\partial }^{l}v}{v^2}\right)=0$$ (14)

This means that the scalar quantity under the gradient ${\partial }_i$ is constant in space, but at the same time positive, being a sum of two squares of a real quantity.

Let this quantity be denoted as $m^2,$ where $m$ is real. The first equality in (13) becomes 3-dimensional Sine–Gordon type equation (in a multifractal sense):

$${\partial }_l{\partial }^l\Phi +m^2\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi =0$$ (15)

It extension on a space–time manifold (in a multifractal sense) through a generalized mapping principle of Equation (11) type implies the functionality of a 4-dimensional Sine–Gordon type equation (in a multifractal sense):

$$\mathrm{\square }\Phi +m^2\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi =0$$ (16)

where $\square$ is the d’Alembert-type operator (in a multifractal sense). For the standard Sine–Gordon equation, see Jackson (1993) and Cristescu (2008).

A solution of the equation (13) can be given relatively simply, if it is assumed that the quantities depend on the ‘localization’ on the space–time manifold by means of the linear form (the ansatz in a multifractal sense (Mazilu & Skyrmions, 2012; Skyrme, 1994)):

$$\xi =a_1{X}_1+a_2{X}_2+a_3{X}_3+a_4{X}_4=V_{0}t$$ (17)

where $X_1,$ $X_2,$ $X_3$ are the spatial coordinates and, $X_4$ is the time. As such, Equation (16) becomes:

$$\frac{d^2\Phi }{d{\xi }^2}+\frac{m^2}{a^2}\hspace{0.17em}\text{sin}\hspace{0.17em}\Phi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi =0$$ (18)

where:

$$a^2=a_1^2{+a}_2^2{+a}_3^2{+a}_4^2$$ (19)

Further on, Equation (18) is multiplied by $\frac{d\Phi }{d\xi },$ after which it can be integrated and leads to the following expression:

$${\left(\frac{d\Phi }{d\xi }\right)}^2+\frac{m^2}{a^2}\hspace{0.17em}{\text{sin}}^2\Phi =b^2$$

where $b$ is an integration constant which is assumed to be real. As such, $\xi$ is an elliptic integral of the first kind (Angheluta, 1957):

$$b\left(\xi -{\xi }_0\right)=\pm {\int }_0^{\mathit{arcsin}Z}\frac{dc}{\sqrt{\left(1-z^2\right)\left(1-s^2{z}^2\right)}}$$ (20)

of modulus:

$$s^2=\frac{m^2}{b^2{a}^2},\mathrm{ }0\le s\le 1$$ (21)

where $z=\hspace{0.17em}\text{sin}\hspace{0.17em}\mathrm{ }\mathrm{\Phi },$ ${\xi }_0$ is an integration constant assumed to be real, while $\Phi$ becomes the sn Jacobi elliptic function of the same modulus (Equation (21)),

$$\Phi =sn\left[b\left(\xi -{\xi }_0\right);s\right]$$ (22)

The elliptic Equation (22) degenerates both in the limit $s\to 0,$ the situation in which it implies the periodic mode (in a multifractal sense):

$$\Phi \to \hspace{0.17em}\text{sin}\hspace{0.17em}\left[b\left(\xi -{\xi }_0\right);s\to 0\right],$$ (23)

as well as in the limit $s\to 1,$ the situation in which it implies the kink mode (in a multifractal sense):

$$\Phi \to \tanh \left[b\left(\xi -{\xi }_0\right);s\to 1\right]$$ (24)

Finally, admitting that $\mathrm{\Phi }$ is a measure of a drug release degree though Equation (19), (i.e. the usual $M(t)/M_{\mathrm{\infty }}$ in normalized coordinates) it results that the release process in a complex drug–polymer system can be dictated by release modes (i.e. those described through Jacobi elliptical function).

3. Results and discussions

3.1. Formulation characterization

A deep investigation by FTIR, X-ray diffraction, polarized light microscopy, and scanning electron microscopy was performed in order to reveal the structural and supramolecular particularities of the formulations.

FTIR spectra confirmed that the hydrogelation process was the result of the formation of the imine units and their supramolecular ordering, by the occurrence of the specific vibration band of the imine units at 1645 cm⁻¹ and of the vibration band characteristic to the intra- and inter-molecular H-bonds around 3400 cm⁻¹. Besides, the presence of the drug into formulations was confirmed by the presence of characteristic vibrations bands of the diclofenac (Ailincai, Mititelu-Tartau, et al., 2020).

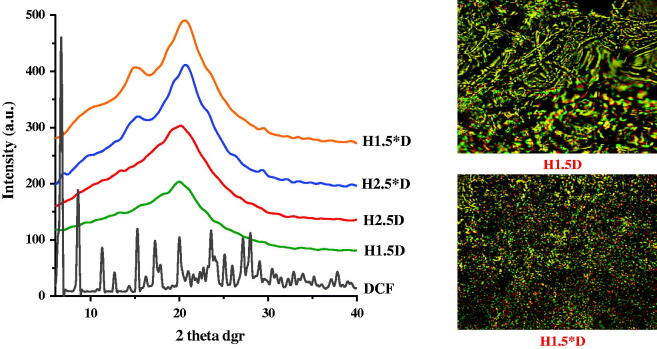
With the aim to investigate the supramolecular architecture of the drug delivery systems and also to evaluate the form in which the drug was encapsulated into the polymeric matrix, X-ray diffraction has been performed. As it could be observed in Figure 2, all the diffractograms displayed broad diffraction peaks with a maximum around 21°, which was attributed based on the literature data to the semicrystalline state of the matrix (Iftime et al., 2017; Marin et al., 2017; Olaru et al., 2018). No reflection corresponding to the drug was clearly observed, suggesting that the drug crystallization into this matrix did not occur. This can be explained by taking into consideration the strong interactions which may establish between the matrix and the drug, which in this case seems to be stronger than the drug–drug interactions. Consequently, it was estimated that matrix-drug fractal entities were formed during the hydrogelation process.

Figure 2.

WXRD diffractograms of the drug delivery systems and DCF drug model and POM images (magnification: 200×) of representative drug delivery systems.

Polarized optical microscopy images of the formulation confirmed the X-ray diffraction data. All the samples presented birefringence, the signature of an ordering degree characteristic to the semicrystalline state (Figure 2). The continuous birefringence allowed us to conclude that the supramolecular matrix-drug fractal entities were dispersed into the samples in a quite uniform manner, leading to the appearance of a continuous texture due to their superposing across the sample (Marin et al., 2013).

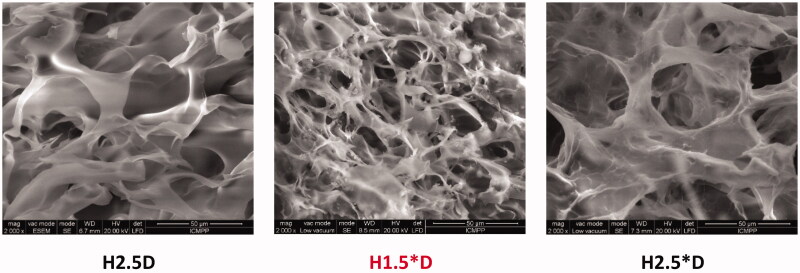
SEM images displayed a porous microstructure forming interconnected micrometric pores with thick walls (Figure 3). The microstructure of the samples was quite homogenous in the entire mass, with no obvious drug crystals in the pores. This indicated that the encapsulation of the drug occurred mainly inside the pores’ walls, at the nanometric level.

Figure 3.

SEM microphotographs of representative drug delivery systems.

These data allowed us to conclude that: (i) DFC was dispersed into the hydrogel matrix as submicrometric crystals, eventually, as molecules, anchored by H-bonds, probably forming matrix-drug fractal entities; (ii) the formulations have microporous morphology; (iii) the drug was uniformly dispersed into the hydrogel matrix, more exactly into the hydrogel walls.

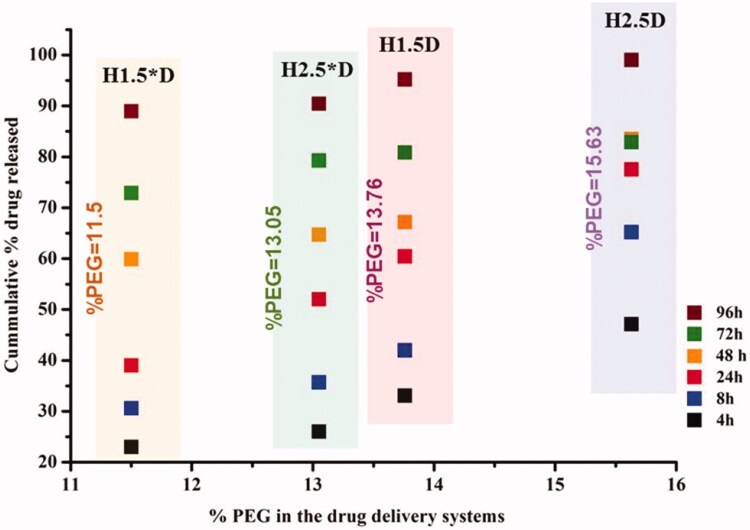
The investigation of the in vitro drug delivery behavior showed that the composition of the formulations and their morphologic particularities significantly influenced the drug release, especially in the first stage. Thus, the sample with a higher content of PEG and lower crosslinking density (H2.5D) showed the most abrupt burst release effect (release of ∼65%), while the sample with the lower PEG content and the higher crosslinking degree (H1.5*D) displayed the lowest burst release effect (release of ∼30%). The different release rate appeared to be related to the hydrophilicity of the systems; the systems containing a higher content of PEG were more hydrophilic and prompted a faster erosion by dissolution favoring a more rapid drug release (Figure 4).

Figure 4.

The graphical representation of the PEG percent of samples versus the cumulative drug release, measured in an environmental mimicking physiologic conditions (pH = 7.4, 37 °C).

The fitting of the release data on five traditional mathematical models (Zero order, First order, Korsmeyer–Peppas, Higuchi, and Hixson–Crowell) gave excellent correlation coefficients (R² = 0.97−0.99) (see supporting information) indicating a complex drug delivery mechanism governed by the matrix particularities and drug encapsulation peculiarities, but not a clear conclusion could be drawn. Consequently, a new theoretical mathematical model based on the Fractal Theory of Motion was developed in order to investigate the drug release from a series of four formulations based on DCF dispersed into a hydrogel matrix of PEGylated chitosan crosslinked with citral.

3.2. Multifractal simulation of the drug release process

The complexity of the release processes (i.e. drug diffusion, erosion of polymer matrix, drug solubility, etc.) can be expressed through non-linear behaviors of the release dynamic in the complex system drug–polymer, the explicit presentation of these non-linearities is a parabola through the modulus s if the elliptical functions sn. Therefore, the linear behaviors of the release process (induced by weak type interactions between the composing components of the polymer–drug system) can be expressed through periodic type release modes (Equation (23)) while the nonlinear behaviors induced by strong interactions between the components of the system can be expressed through kin-type release modes (Equation (24)). The latter fits well with the empirical data and with the usual dependences reported in the literature. The solution (Equations (19)–(21)) represents release modes that contain multifractal behavior of the release dynamics in a global sense.

Without giving up of the ansatz in a multifractal sense, the Sine–Gordon type equation (in a multifractal sense), both through separation and intervention of some normalized coordinates (in the sense$\mathrm{ }\eta =a_1{X}_1\leftrightarrows ,\mathrm{ }\tau =a_4{X}_4$), all of these based on specific operational procedures (Merches & Agop, 2016; Agop & Paun, 2017), also implies the following special solutions (Jackson, 1993; Cristescu, 2008):

1. soliton (+) and antisoliton (−) modes (in a multifractal sense):

   $${\Phi }_1\left(\eta ,\tau ,\alpha \right)=4\mathit{arctan}\left[\hspace{0.17em}\text{exp}\hspace{0.17em}\left(\pm \frac{\tau -\alpha \eta }{\sqrt{1-{\alpha }^2}}\right)\right],\mathrm{ }0\le \alpha <1$$ (25)
2. breather modes – localized oscillating modes (in a multifractal sense):

   $${\Phi }_2\left(\eta ,\tau ,q\right)=4\mathit{arctan}\left\{\sqrt{\frac{q}{1-q}}\left[\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\sqrt{1-q}\tau \right)}{\cosh \left(q\eta \right)}\right]\right\},\mathrm{ }0<q<1$$ (26)

These can be assimilated to a soliton–antisoliton oscillating pairs (in a multifractal sense). In Equations (25) and (26) a₁ and a₄ are characteristic parameters of the release process (for instance, a₁ is a specific wavenumber and a₄ is a specific velocity), while through constants $\alpha$ and q are detailed the local release processes. The special solution (Equations (25) and (26)) are presenting an explicit manner the local behaviors in a multifractal sense, of the release dynamics of the complex system polymer–drug. These solitons and antisolitons (in a multifractal sense) release mode (Equation (25)) describe local un-localized behavior of the release dynamics, while the breather type release modes (in a multifractal sense) (Equation (26)) describes localized behaviors.

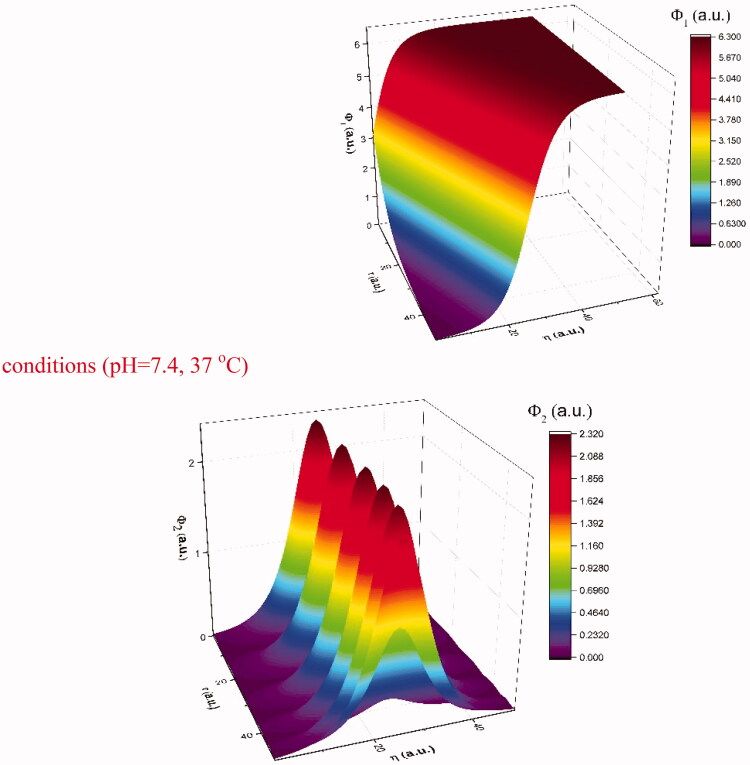
In Figure 5 we have represented the 3D representations of soliton modes (left side) and breather modes (right side). We can see that these to depict two types of localized behavior that the model predicts will be found in drug-release related scenarios. The soliton mode is in line with the classical approach and we can see that it follows well the global behavior of the investigated conditions. This means that the release is controlled and increases over time both locally and globally. A peculiar scenario can be seen for the breather modes. There is a periodic burst type release localized around the release surfaces. Globally these should not be seen as it does not completely affect the general behavior of the polymer–drug matrix. However, we do see in Figure 6 that the data presents some waves in the time span of 10–70 h. This means that although the steep increase and the saturated regions are still seen as in our previous reports the transitions here seem to be described better by a combination of the two modes predicted by our model with the contribution ratio from each mode strongly depending on the fractality degree of the system.

Figure 5.

3D representations of soliton modes (Equation (22)) (left side) and breather modes (Equation (23)) (right side).

Figure 6.

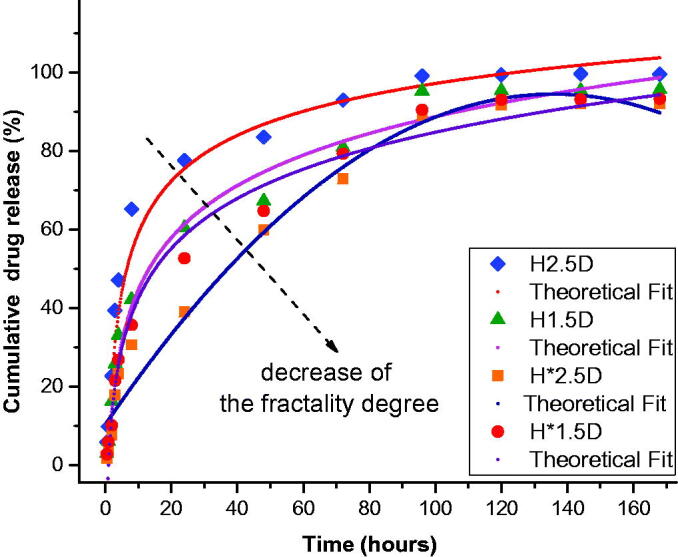
Theoretical fit of the empirical data using the multifractal mathematical model.

In order to confirm the predictions made by our multifractal model, we used Equation (24) to fit the empirical data. Each theoretical fit leads to an R² > 97%, which validates our model for long-time release dynamics. The results are presented in Figure 6. We can observe that the fractality degree, extracted from the fit, decreases with the decrease of PEG concentration. This is in good agreement as a faster release would indeed assume a high density of interaction between the released drug molecules and the environment. Therefore now, by contrasting the empirical data with an understanding of the fractality degree we can now say that the fractality degree can accurately describe the changes in hydrophilicity of the polymer. A lower fractality degree as we can see (green) will also be more susceptive to a breather periodic burst type release, while a higher fractality leads to a release pattern defined mainly by the soliton mode. Based on the existent literature (Craciun et al., 2019; Ailincai, Mititelu-Tartau, et al., 2020; Iftime, Mititelu Tartau, et al., 2020), the burst effect in the first release stage can be attributed to the faster dissolution of the bigger drug crystals. In this time-span breather-type solution more accurately depicts the drug release process. We stated that for low fractality systems (Figure 4 – H*2.5D and H*1.5D) breather-type of release is dominant as the existence of a low density of large drug crystals will generate a fast release with limited interactions with the medium. With the increase of the hydrophilicity and thus of the fractality degree in the same time-span the drug release scenario it is depicted better by the steep increase (Figure 4 – H2.5D and H1.5D). The steep increase defined by a soliton-type solution and the inhibition of the breather modes could also be a sign for the increase in larger crystals density in the matrix. For longer time-scales the progressive release of the second stage is attributed to the slower dissolution of the drug encapsulated as nanocrystals or even as single molecules, which were stronger anchored in the hydrogel matrix. The transition is seen faster for high fractality systems that are described by soliton-type release where the presence of multiple large release sources mediates the whole process transitioning to the quasi-stationary regime.

4. Conclusions

Based on the notion that the fractal theory of motion is invariant to the homographic transformations, the release dynamics were described through 2 × 2 matrices with real elements. Using the 2 × 2 matrix properties and the Killing–Cartan formalism for obtaining the SL(2R) invariant metrics through a harmonic mapping procedure we showed that the release dynamics can be described by a multifractal Sine–Gordon type equation. The solution of the equation, in its most general form, specifies the fact that the release modes are of elliptic type. The degeneration of the elliptic solution leads to the Kink type release mode, which described the global drug-release behavior. The particular solution of soliton–antisoliton and breather type describe the local drug release behaviors. Therefore, the solition–antisoliton solution corresponds to the nonlocalized drug-release mechanism while the breather solution corresponds to the localized mechanism. This multifractal mathematical model was developed in order to stimulate the release of DCF from a PEGylated chitosan matrix for a better understanding of the rules governing this process and thus to further improve it for in vivo applications. The mathematical model has been applied for a series of drug delivery systems prepared by in situ dispersion of the drug into a PEGylated chitosan matrix. The systems proved the formation of the drug/matrix fractals and an in vitro drug release rate in dependence to the hydrophilicity degree. The mathematical model demonstrated a good correlation supporting the influence of the matrix hydrophilicity on the drug release rate.

Funding Statement

The research leading to these results has received funding from the Romanian National Authority for Scientific Research, MEN-UEFISCDI grant, project number PN-III-P1-1.2-PCCDI2017-0569 (10PCCDI/2018).

Disclosure statement

No potential conflict of interest was reported by the author(s).