Approaches to inferring multi-regional interactions from simultaneous population recordings

Abstract

Most past studies of neural representations and dynamics have focused on recordings from single brain areas. However, growing evidence of brain-wide, parallel representations of cognitive variables suggests that analyzing neural representations and dynamics in individual brain areas can benefit from understanding the context of multi-regional interactions that support them. Moreover, perturbation experiments revealed that the manner in which these parallel representations interact with each other can differ dramatically across different pairs of brain areas. Recent advances in recording technology offer a potentially powerful substrate to study how multi-regional interactions coordinate neural representations in individual brain areas and dictate behavior on a single-trial basis through simultaneous recordings of multiple brain areas. We review pragmatic approaches to studying multi-regional interactions and illustrate them in the concrete context of a rodent delayed response task paradigm.

Introduction

Advances in our ability to record activity of large populations of neurons [1-6] have enabled neuroscience to complement single-neuron-based analysis with analyses of population activity. Similarly, though the existence of widespread task relevant signals has been known for decades [7-14], recent electrophysiological [3,5] and imaging techniques [2,4] that have dramatically facilitated the ability to record populations of neurons in each of several brain areas open the door to population-level analysis of multi-regional populations. Indeed, in organisms that have a relatively small number of neurons, ranging from C. elegans and leeches to (larval) fruit flies and zebrafish, it has been possible to simultaneously record from (nearly) all neurons in the brain or a large fraction of neurons in the central nervous system [15-31]. Even for animals with a considerably more neurons, simultaneous recordings of multiple brain areas are becoming more common. In rodents, wide-field calcium imaging has been increasingly popular in studying the cortex-wide neural dynamics and representations [32-38], although it typically does not offer true cellular resolution. Electrophysiological recordings and two-photon calcium imaging offer single neuron resolution across multiple areas and have been recently used to study encoding patterns across regions and their interactions [39-43]. Such simultaneous multi-regional recordings have been also performed in non-human primates [44-58], and are expected to become more common as recording technology improves [59-61].

These recordings have demonstrated even more clearly that task-related neural activity is present across many cortical and subcortical areas even in seemingly simple cognitive tasks in both rodents [32,34-39,41,42,62-76] and primates [7-14,44,46-48,51,77-93]. Focusing on one example, in a delayed response task where mice are trained to report the identity of sensory stimulus after a delay period, neural activity encoding the task stimulus has been observed across a wide range of cortical and subcortical areas [94-100]. Moreover, beyond just encoding of similar task-related features, significant correlations have been observed between many of those areas. In addition, perturbations to these areas revealed that interactions between areas qualitatively differ from area to area. For instance, the left and right hemispheres of the anterior lateral motor cortex (ALM) can each maintain their selectivity when the other hemisphere is (optogenetically) silenced. Each hemisphere provides input to the perturbed hemisphere to recover its selectivity, making ALM robust to unilateral (but not bilateral) perturbations [100]. In contrast, the ALM and thalamus do not have such robustness; perturbations to either of them abolish selectivity in the other [96]. Interactions between ALM and cerebellum appear more complicated; while silencing either tends to diminish selectivity in the other, transient photostimulation of the cerebellum leads to a decrease of selectivity in some ALM neurons and an increase in others, suggesting a persistent change in population coding [94]. This suggests that a full understanding of neural computation may in many cases require dissecting and understanding the diverse interactions between multiple brain areas.

Here, we present an overview of existing and emerging approaches to the study of multi-regional interactions in the brain. Before we begin, it is important to discuss our position in terms of what is the nature of these interactions and what is the goal of inferring them. A term that is often used in this context is “functional connectivity”. We purposefully do not use this term since we feel it implies a single, well-defined underlying quantity that may be difficult to infer, but is in itself a concrete, specific entity. Rather, the term we chose, influence, more accurately captures our opinion that though there are of course specific patterns of within- and between-population connectivity and particular single neuron and synaptic non-linearities that can be, in principle, described as specific time-varying effective connectivity, it is not realistic in most cases to expect to be able to capture these in full detail in the near future. Instead, a more reasonable conceptual model starts from the position that since we are forced to have a more coarse-grained description, there naturally are diverse ways to arrive at it, or multiple approaches to quantify different aspects of the mutual relationship between two sets of dynamics, a position more accurately evoked by the use of the term “influence”.

Perhaps more important still is the question of why extract such quantities, regardless what we choose to term them. From the position that it is possible to treat interactions between populations as a concrete underlying entity, this has a straightforward answer. It is a property of the system and it is useful to infer it, just like it is useful to quantify the charge of an object by studying changes in an electric field. From our perspective that treating interactions as a unique, discoverable underlying entity is not realistically possible, the emphasis is different. The reason to perform these analyses, of describing the interaction of populations of neurons in a particular way, is the promise that these different coarse-grained measures of influence capture aspects of the organization of population dynamics that are useful for understanding downstream phenomena. For instance, whether quantifiable differences in between-brain-area influence across animals predicts different behavior or different encoding of task-related information. Such predictions provide confidence that describing the interaction between populations through a particular lens is a useful step in understanding the organization of population dynamics on a larger scale.

Single-neuron-based and population-based measures

Even without population-level recordings, simultaneous recordings from multiple areas can be analyzed for pairwise interactions between neurons across two brain areas. Analysis of pairs of neurons across brain areas can reveal different types of information transmission For example, cross-correlation analyses have been applied to simultaneous recordings of the amygdala and dorsal anterior cingulate cortex (dACC) in monkeys performing an aversive-conditioning task where the cue-outcome contingency is reversed after they have learned the original contingency [49]. The analyses suggested that one type of “surprise signal” that encodes the difference between the expected and actual outcome (referred to as “unsigned prediction error (PE)”) first emerges in the amygdala and then is relayed to the dACC, while another type of surprise signal (referred to as “signed PE”) is propagated in the opposite direction. Such analyses of interactions between individual neurons in different brain areas can be very informative, and perhaps even sufficient for addressing certain types of questions regarding multi-regional interactions.

In addition, there is also a rich history of studying interactions between brain regions using alternative signals such as fMRI [101-106] or field potentials [107-114]. These are not the focus of this review and we refer the reader to other reviews for these subjects [115-118],

In general, there are both practical and conceptual reasons to complement single-neuron-based analyses with population level analyses in the context of multi-regional interactions. First, many analyses will depend on relating single-trial activity in one population to another. Single neurons, particularly in areas with low firing rates, have limited signal-to-noise (SNR) which may hamper single-trial analyses. Switching to the population level, one can selectively pool across neurons in a way that ameliorates SNR. Second, in many brain areas, representations are highly distributed across a population of neurons, and individual neurons tend to have mixed selectivity for a number of task-related variables [119-124]. If interactions are organized according to task-related representations, studying interactions between pairs of neurons in different areas with mixed selectivity may conflate analyses. Third, in a related but more general point, interactions between two brain areas may primarily occur in a low-dimensional subspace of population activity in each area, as shown in recent studies [56,100]. Population activity projected onto such a subspace may be highly correlated between the two areas due to their interactions, but population activity orthogonal to it may be much less correlated. In such cases, studying interactions between pairs of individual neurons will not provide a clear picture of how the two areas interact. Instead, the natural strategy would be to first identify these subspaces where multi-regional interactions primarily occur, and then study interactions between population activity projected on these subspaces. Fourth, on a more practical note, when we record from a large number of neurons, estimating all pairwise measures will be cumbersome and may easily lead to overfitting. To avoid overfitting, some kind of dimensionality reduction will have to be applied to population activity before modeling interactions. Lastly, neurons recorded in a given session are typically a random sparse sampling of the neuronal population in the area. From session to session and animal to animal the particular sampling may vary. Using the sampled neurons to estimate underlying population level measures may ameliorate subsampling.

Population level measures of multi-regional interactions

The activity of two populations of neurons can be analyzed in multiple ways to derive measures of influence. Given our point of view that the success of a particular measure of influence is empirical, it is natural to consider multiple different ways to define population-to-population influence. One could imagine a myriad of possible analyses, but broadly speaking two general properties of analyses are in our view of central importance: (i) whether they are static or sensitive to time (ii) whether they use the full population activity or specific subspaces. The former distinction is straightforward; some approaches bin activity at different time points and then treat bins as just different samples regardless of the time from which they were extracted, whereas other techniques take into account the temporal order of data. For the latter, while it may seem natural to allow a technique to have access to the full activity of a brain area, when the amount of data (e.g., number of trials in trial-based behavioral experiments) is limited, it may be more effective to narrow down the space of population activity first, for instance by choosing only patterns of activity that correlate with a set of behavioral features.

We begin by discussing approaches that use only specific subspaces. A key reason to start by describing these approaches is that if the subspace chosen is one dimensional, i.e., we use a weighted sum to reduce the activity across multiple neurons to a single number per time point, then we would end up with a single entity, an effective single population unit per area, allowing us to connect to the rich history of studying pairwise between-single-unit measures. Starting by dimensionality reduction naturally leads to the question of which subspace should one use, or which component of population activity should one focus on?

Patterns of activity that are tied to the animal’s behavior in the task are in our opinion a natural generic choice for the component of population activity to concentrate on with regard to influence between brain areas. Such decoders have been shown to capture aspects of the state of behavior-related computations [100,125] and therefore between brain area influence that affects them may be more directly interpretable. To be more specific, we will illustrate such analyses through the example of a delayed response task paradigm (Figure 1a). We will specifically consider the delayed response task paradigm initiated in [99] and followed up by many recent studies including [94-100,126,127]. In this delayed response task, mice are given a binary sensory stimulus, e.g., a pole at two possible locations, and have to report its identity after a delay period that typically spans a few seconds, by licking one of two ports (left or right port) where water rewards are delivered on correct trials (Figure 1a). To successfully perform the task, mice must maintain a persistent representation of the stimulus or upcoming choice during the delay period in some brain area. A series of studies recording from different brain areas have revealed that such representations are not isolated in one area but distributed across a wide range of cortical and subcortical areas [94,96,99,100].

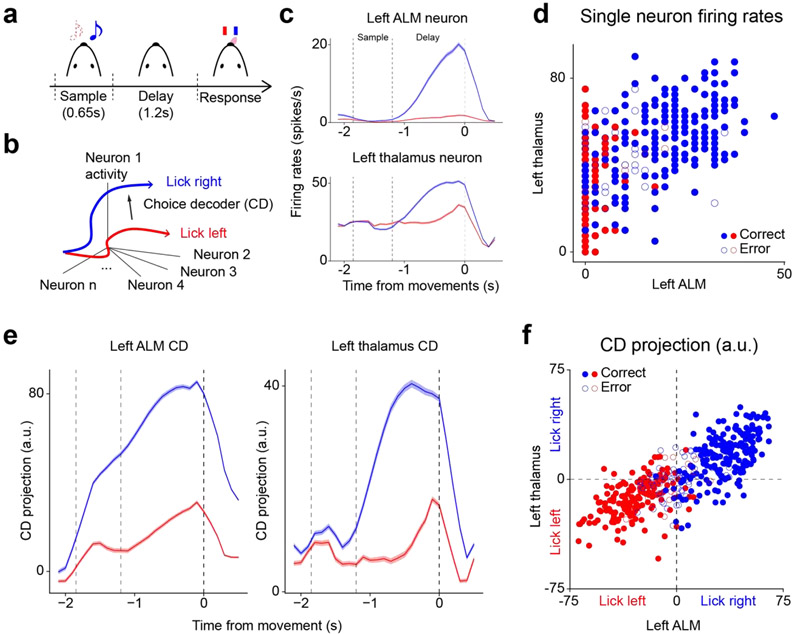
Figure 1. Single neuron vs. population level measures.

a. A schematic of the delayed response task. Head-fixed mice discriminate auditory tones and respond “lick right” or “lick left” after a delay.

b. A schematic for the choice decoder (CD), a vector in activity space that maximally separates the “lick left” and “lick right” activity trajectories.

c. Peri-stimulus time histograms (PSTH) of two example neurons in ALM and thalamus. Blue, “lick right” trials; red, “lick left” trials. Dashed lines delineate behavioral epochs as in a. Error bars indicate s.e.m. across trials.

d. Single-trial activity of the two example neurons shown in d. Blue, “lick right” trials; red, “lick left” trials. Solid circles, correct trials; open circles, error trials. Compared to c, single-trial activity of the individual neurons tends to be more grainy due to the discrete nature of spikes, which could potentially degrade the signal-to-noise ratio of choice decoding. Moreover, choice decoding from individual neurons is generally inferior to choice decoding from population activity when the choice information is encoded in a distributed manner.

e. Time traces of projections of population activity onto CD in ALM and thalamus. Blue, “lick right” trials; red, “lick left” trials. Dashed lines delineate behavioral epochs as in a. Error bars indicate s.e.m. across trials.

f. Single-trial projections onto CD in ALM and thalamus. Dashed lines indicate the decision boundary of CD in each area. Blue, “lick right” trials; red, “lick left” trials. Solid circles, correct trials; open circles, error trials. The projections in each area are centered with respect to the decision boundary. The decision boundaries divide the space of the joint state of CDs in the two areas into four quadrants. The bottom left and top right quadrants correspond to the case where the two areas agree in their prediction of the upcoming choice. On the other hand, the bottom right and top left quadrants correspond to the case where they disagree with each other.

A key behavioral property in the delayed response task is the animal’s choice and choice decoders link particular patterns of neural activity to choices the animal makes on individual trials. To be concrete, we will consider linear decoders, which are not only easily interpretable but have also turned out to be highly accurate not only in normal behavior but also when perturbation scrambles activity [100]. On a more technical note, without priors on the structure of population activity the decoder is not fully defined. A straightforward linear decoder may be obtained by taking the vector of the difference between the “lick left” and “lick right” trial-average activity (Figure 1b). Alternatively, one may derive a linear decoder using linear discriminant analysis, which can in principle yield better decoding accuracy by incorporating the covariance of population activity. In practice, though, it may in fact yield worse accuracy if the sample estimate of the covariance is noisy due to a limited number of trials. Here, for simplicity we will use the former. A second important detail is that we can either train a choice decoder at each time point separately, i.e., a time-dependent decoder, or a time-independent decoder defined by averaging activity across time or concatenating different time points as different samples. In practice, one can start with instantaneous decoders, analyze their similarity and use this similarity to define times over which decoders can be averaged. In the case of the delayed response task we found that instantaneous decoders are very similar across the delay period (and similar between the sample and delay period, but not the delay and response period) [100]. Hence, we will use for simplicity a decoder averaged across the entire delay period.

Three analyses that have featured centrally in single-neuron-based analyses are noise correlations, signal correlations and cross correlations. The first two are static, the third dynamic. We discuss the first two and their population level analogues below and return to the third later. A more comprehensive review of these analyses at the single-neuron level is given in [128].

Noise correlation between neurons is defined as the trial-to-trial correlation between the firing rates of two neurons conditioned on the external stimulus [129,130] (Figure 1c,d). Similarly, one can study the correlation between the single-trial state of decoders across pairs of brain areas (Figure 1e,f). One way to visualize the correlation between the single-trial state of decoders across two areas is to generate a two-dimensional scatter plot where the x-axis represents the choice decoder projection in one area and the y-axis the choice decoder projection in another area (Figure 1f). Each dot in this plot would correspond to the joint state of the decoders in a single trial. When a trial is in either the upper right or lower left quadrants, the two areas agree, and when it is in either the upper left or lower right quadrants, they disagree. From these, one can extract the population-level equivalent of noise correlations by considering correlations only within trials of a specific task condition.

Single-neuron-based signal correlation refers to the correlation between the tuning curves of two neurons and thus measures the similarity between their trial-averaged responses to external stimuli [131]. In binary decision-making tasks signal correlations are somewhat impoverished since the tuning curve has only two values, as there are only two conditions. However, in binary tasks there is an interesting population level analogue, the degree to which choices predicted from different areas are correlated, which we refer to as “choice correlation”. Intuitively speaking, pairs of brain areas that partake in the same distributed choice encoding should always agree on their choice predictions whether or not their predictions are correct, whereas pairs that do not partake in the same distributed encoding may be completely independent from each other. In other words, the fraction of trials in which decoders agree can be a useful metric for how linked is the encoding of two regions (Figure 1f). Though we described choice correlations starting from signal correlations, we note that strictly speaking choice correlation mixes properties of both signal and noise correlations.

To better illustrate these approaches we performed a preliminary analysis based on choice decoders in the left ALM and thalamus, whose reciprocal connections generate recurrent excitation involved in maintaining selectivity in both areas [96]. It reveals that while the two areas are in consensus for most trials, they do disagree as well (Figure 1f). When they disagree, ALM tends to predict the choice more accurately, which is consistent with previous observations that ALM causally dictates the upcoming choice in this task [99,100]. On the other hand, when they agree, their choice predictions are rarely incorrect. In cases where more than two areas are simultaneously recorded, it would be also interesting to see whether the choice might be determined by a “majority vote” among those areas on a trial-by-trial basis. If so, that would suggest that the upcoming choice is likely determined not by any single area but by a joint state of multiple areas. In addition, there is clear correlation between the single-trial states of the decoders in the two areas even when one examines trials from a single condition alone (Figure 1f)

While we introduced these measures through choice decoders, this was just one example of a one-dimensional subspace. Even still considering task-related subspaces, tasks may have multiple features of interest. For instance, in the delayed response task, there is a distinction between the instructed choice (i.e., the stimulus type) and the actual choice the animal makes, and they may be differently encoded across areas. One can define decoders for these other task variables and study projections onto them.

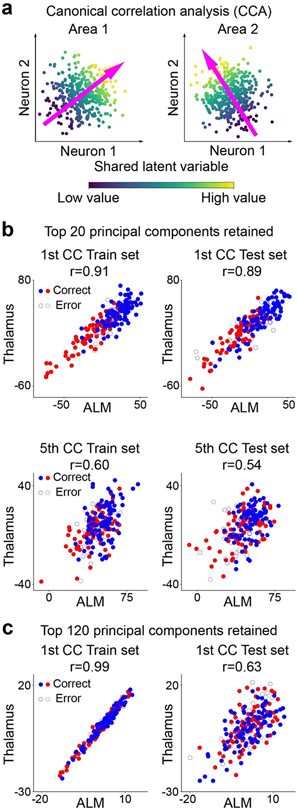
Returning to our classification of approaches in terms of subspace vs. full activity, the second class of models does not pre-specify subspaces of interest, but rather uses the full space of population recordings. One way to use the full space of recordings is to directly search for components in the population activity space of each brain area that capture a particular form of interaction. The most straightforward of such approaches is canonical correlation analysis (CCA) [132,133]. In a nutshell, CCA can be used to identify a series of pairs of linear components, or directions, in the activity space of the two brain areas, such that the correlation of population activity projected onto these directions is maximized (Figure 2a). The pairs of directions are called canonical components. Once the first canonical components are identified, we can identify the second canonical components by projecting out the first canonical components from the population activity in each area, and then maximizing the correlation between the remaining population activity in the two areas. Similar procedures can be repeated to obtain the third canonical components and so on (Figure 2b). CCA therefore identifies in an unbiased way the subspaces in which population activity is strongly correlated between the two areas. A related technique called partial least squares [134,135] can also be used to find directions of correlation between brain areas. CCA is a decades old classical technique with important caveats such as sensitivity to overfitting (Figure 2c), and numerous variants, such as non-linear generalizations [136-139], have been developed.

Figure 2. Canonical correlation analysis (CCA) as a way to extract latent states relevant for multi-regional interactions.

a. A schematic for CCA. Population activity of area 1 and 2 have a shared latent variable, for example due to a common input or direct interaction. This leads to shared trial-to-trial variability in their population activity. The objective of CCA is to discover the direction in the activity space of each area in which shared trial-to-trial variability resides. CCA achieves this by finding a direction in the activity space of each of the two areas such that their projections are maximally correlated across trials (the first CCA component). Once the first CCA components are calculated, the second CCA components can be found by subtracting out from each dataset the projection on the first CCA component. This procedure can be repeated to obtain the third CCA components and so on.

b. Top, Projections onto the first CCA components of ALM and thalamus, separated into trials used to compute CCA components (train trials), and held-out trials (test trials). Blue, “lick right” trials; red, “lick left” trials. Solid circles, correct trials; open circles, error trials. To avoid overfitting, dimensionality reduction is first performed on population activity in each area by performing principal component analysis, keeping only the first 20 principal components and applying CCA to the principal component scores. Bottom, Projections onto the fifth CCA components of ALM and thalamus for train and test trials. The correlation between the two areas is significantly weaker along these directions than the first CCA components.

c. Same as the top row of b, but when dimensionality reduction is weaker, keeping the first 120 principal components during the delay period. When the dimensionality of the neural data is not sufficiently low compared to the number of trials, CCA can easily suffer from overfitting, resulting in large differences in correlation between the train and test trials.

Dynamic perspectives on multi-regional interactions

The approaches we discussed above, were static in nature. A straightforward example of a more dynamical approach that has been used frequently in single neuron bases analyses is cross correlation. Namely, computing trial-to-trial correlations across different time lags [49,140]. Intuitively, if neuron A is presynaptic to neuron B, a spike of neuron A could trigger a spike of neuron B, after a certain time lag. Therefore, their spike trains would be maximally correlated when the spike train of neuron B is offset by this time lag relative to that of neuron A. In other words, one assumes that by identifying the existence of a peaked cross correlation and the sign of the time lag, one can infer a potential influence between two neurons and possibly its direction (though of course such lags may be due to a common input arriving at two neurons with a different delay). Along similar lines, cross-correlation analysis can be performed on projections on the decoders to compute relative time lags of choice-selective activity between brain areas to infer potential influence.

More generally though, a versatile approach to quantify how multi-regional influence shapes dynamics is through predictive modeling of single trial activity. For clarity, we first describe a single neuron variant. Such a predictive approach explicitly models the future activity of a neuron as a function of external stimuli, the past activity of other neurons and the past activity of the neuron itself. A particularly successful application of a detailed predictive modeling approach was presented in [141], which studied in vitro the responses of an isolated population of parasol ganglion cells from the macaque retina to binary white noise. In their model, each neuron was assigned a stimulus filter, corresponding to the spatio-temporal receptive field of the cell, a post-spike filter, which describes how the past activity of the cell affects its future activity, and a set of coupling filters, which capture the influence of other neurons’ past activity. The model not only reproduced known facts regarding single neuron responses, such as the center-surround receptive field organization, but also revealed patterns of single-neuron interactions which correctly predicted the spiking synchrony. For example, the model inferred that the closer two neurons’ receptive field centers were the more strongly they influenced each other, thus the more synchronized the spikes, a prediction which was confirmed in the data.

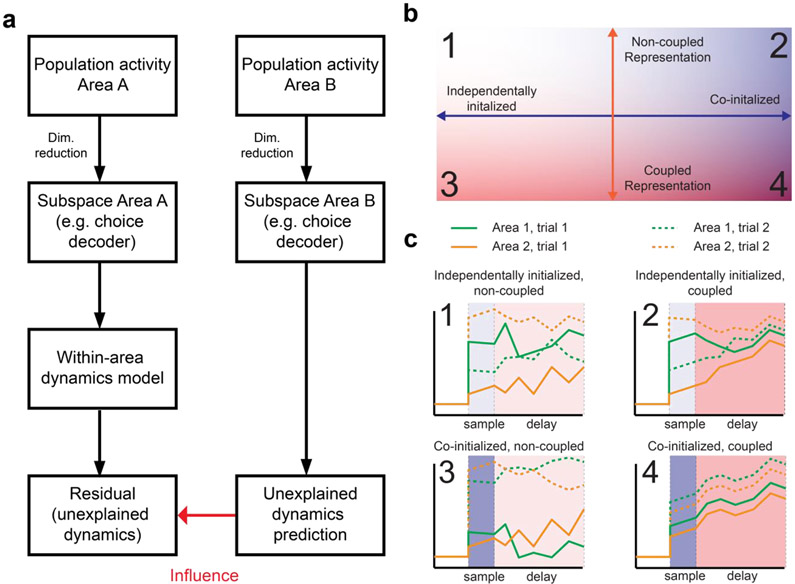
In the population-level equivalent, a predictive model describes the future activity of an area as a combination of past dynamics of that area and activity in other areas. Though numerous approaches can be employed, intuitively speaking, such a model assesses influence of one brain area on another by the ability to predict unexpected deviations in the latent dynamics of one brain area (the modeled area) from the just-preceding activity in another brain area (the influencing area) (Figure 3a). In other words, we first predict the dynamics of the modeled area from its own past history, then detect deviations from the predicted dynamics and then determine whether these deviations can be themselves reliably predicted from the state of the influencing area. While it is possible in principle to use a more detailed model as above with potential coupling from and to every recorded neuron, such models are likely to overfit and it is likely more appropriate to perform predictive modeling on latent states of population activity in each area. The latent states could be just the leading principal components, could represent task-related activity, such as the choice decoder projections, or projections on a subspace through which two brain areas primarily communicate [56].

Figure 3. A schematic of predictive model analysis for multi-regional interactions and interpretations in terms of co-initialization and dynamic coupling.

a. Flow chart for predictive model analysis at the population level. To infer influence of Area B on Area A, we measure how much of future activity in Area A that cannot be predicted from its own past activity, can be predicted from past activity in Area B. More specifically, we first model the within-area dynamics of Area A to predict its future activity. The residual of this within-area prediction is then predicted from Area B, the performance of which defines a measure of influence from Area B to A. To avoid potential overfitting, one can first apply dimensionality reduction to the raw population activity in each area and focus on task-relevant activity components (such as the projection onto CD).

b. Correlated activity across brain areas could be described through co-initialization of two brain areas (Quadrant 2), dynamic coupling between them (Quadrant 3), or a combination of both (Quadrant 4).

c. Schematics of single-trial trajectories of activities in the two areas illustrating each condition. Population activity in each area is assumed to be projected onto a low-dimensional subspace of interest, such as CD. Green, area 1; orange, area 2. Solid lines, trial 1; dashed lines, trial 2. Top left, independently initialized, non-coupled (Quadrant 1). The initial states of the two areas during the sample period are uncorrelated, and they evolve independently from each other. Top right, independently initialized, coupled (Quadrant 2). While the initial states of the two areas are uncorrelated, their interactions tend to make their states more correlated over time. Bottom left, co-initialized, non-coupled (Quadrant 3). While the initial states of the two areas are correlated, their subsequent states gradually become more independent. Bottom right, co-initialized, coupled (Quadrant 4). The states of the two areas remain highly correlated across both the sample and delay period.

This approach is similar in spirit to the idea of Granger causality, and a large body of work has pursued such approaches in the fMRI [101-106,115-117] and field potential [107-111,113,118] literature. In the context of electrophysiological or optical recordings, studies along this line have been much rarer and mostly concerned with interactions between individual neurons in one brain area [141-143], presumably due to the technical difficulty of simultaneous recordings from multiple areas. However, due to recent advances in recording techniques, the application of this approach to multi-regional electrophysiological recordings is starting to emerge [56,57].

While latent states of interest can be specified before training a predictive model as explained above, they may also be learned jointly with the predictive model itself. The latent states so obtained could potentially describe multi-regional interactions in a less biased manner. For example, in contrast to CCA, which only incorporates instantaneous correlations across two areas, other methods of extracting latent states have been developed that can potentially incorporate the temporal structure of influence between two areas [56,57]. These approaches will be useful especially when we do not have much prior knowledge about neural representations or dynamics in the areas of interest (e.g., because the task involves a large number of cognitive/behavioral variables or the neurons exhibit complex responses).

High-level, more interpretable descriptors for multi-regional interactions

While we described each analysis above as a stand-alone measure, it is potentially beneficial to relate the approaches described above to more high-level, interpretable descriptions of the relation between dynamics in two areas. For example, the dynamics of activity in two brain areas can be analyzed in terms of: co-initialization and dynamic coupling (Figure 3b,c). That is, whether: representations are co-initiated or independently initiated and whether representations evolve over time independently or in synchrony. In more detail, as sensory information is incorporated into representations across brain areas, some brain areas will have their representations initiated at a roughly equivalent state whereas others will be initiated more independently and may start therefore at more distant states. In the context of the delayed response task, the degree of this initial similarity can be quantified based on, say, the choice-conditioned correlation during the sample period where the stimulus is given to the animal (Figure 3b, horizontal axis and 3c). At the same time, the state of a representation will fluctuate over time, especially during the delay period when no new sensory information is presented. These fluctuations may be correlated, leading the representations to become more congruent, or uncorrelated, leading them to be more disparate. This can be quantified for example by the increase in the choice-conditioned correlation over time, or the correlation of fluctuations across time (Figure 3b, vertical axis, and 3c).

Concluding remarks

In this review we introduced approaches to quantifying the relation between simultaneously recorded dynamics in two brain areas. As we emphasized above, dimensionality reduction and latent space model approaches are likely to be central to future studies of multi-regional interactions.

Most latent space approaches implicitly regard neurons in a brain area as a homogeneous population. However, important additional insight may be gained by taking cell types into account. For example, in the context of the delayed response task discussed above, it was found that distinct cell types in ALM, despite being spatially intermingled, project to different cortical and subcortical areas, have disparate population selectivity, and play a role in either maintaining preparatory activity or triggering movements [95,98]. Such knowledge of how different cell types project to different areas could be used to perform more judicious pooling for population level measures. Moreover, learning process may differentially affect interactions between neurons depending on their cell type, potentially yielding different distributions of connections that predictive models could take into account [143].

While most latent space models used in practice for analyzing neural data are linear (or only mildly nonlinear), ultimately the brain is a highly nonlinear dynamical system, and linear models will no longer be a good enough approximation at some point. The limited number of trials in a behavioral experiment is the universal factor that hampers the use of nonlinear models, but some recent attempts, such as [144], are encouraging. We hope that continuing advances in deep learning will bring further progress in this direction.

Ending by coming back to the elephant in the room, a key issue in the study of multi-regional interactions is their interpretation. As described above, there are numerous a priori reasonable models one could use. Part of the reason to describe multiple approaches as we have done is that it is an open question which measures of influence will end up being useful metrics of large-scale organization, as evidenced by their ability to predict between-animal differences in behavior, large-scale encoding patterns, or responses to perturbations and in particular targeted perturbations [126,145]. Though there are promising initial results, to what extent such predictions can be extracted, and which influence measures yield the most robust predictions is very much an open research question.

Highlights.

• In many behavioral tasks important task-related variables can be decoded from multiple brain areas and diverse interactions between brain areas have been found by perturbation experiments

• Recent advances in technology allows us to simultaneously record from these brain areas. Leveraging these simultaneous recordings to infer interactions between brain areas remains a substantial analytical challenge

• We review between-single-neuron measures of influence and discuss how they can be extended to the population level to measure interactions between brain areas