Causal Mediation Programs in R, Mplus, SAS, SPSS, and Stata

Abstract

Mediation analysis is a methodology used to understand how and why an independent variable (X) transmits its effect to an outcome (Y) through a mediator (M). New causal mediation methods based on the potential outcomes framework and counterfactual framework are a seminal advancement for mediation analysis, because they focus on the causal basis of mediation analysis. There are several programs available to estimate causal mediation effects, but these programs differ substantially in data set up, estimation, output, and software platform. To compare these programs, an empirical example is presented, and a single mediator model with XM interaction was estimated with a continuous mediator and a continuous outcome in each program. Even though the software packages employ different estimation methods, they do provide similar causal effect estimates for mediation models with a continuous mediator and outcome. A detailed explanation of program similarities, unique features, and recommendations are discussed.

Mediation models are fundamental structural equation models (SEMs) because they are used to investigate a core aspect of SEM--how an independent variable, X, is related to an outcome variable, Y, through a mediator variable, M (Judd & Kenny, 1981; MacKinnon, 2008, 2020; Sobel, 1982). The mediation model is a primary topic in all major books on SEM (Bollen, 1989; Kline, 2015; Little, 2013). The central role of mediating hypotheses in many research fields, including psychology, sociology, and epidemiology, has driven the development of improved mediation methods over the last thirty years. A seminal methodological development for mediation focuses on the estimation of causal mediation effects based on a counterfactual or potential outcomes approach to mediation analysis. These methods clarify the causal basis of mediation, which is a topic raised in many different criticisms of mediation analysis (Bullock, Green, & Ha, 2010; MacKinnon, 2008, 2020; Sobel, 2008). These new methods have been called revolutionary because they focus on assessing the causal basis of structural relations among variables. As summarized by Gary King, “More has been learned about causal inference in the last few decades than the sum total of everything that had been learned about it in all prior recorded history.” (King, 2015; cited in Morgan and Winship (2015), back cover).

The development of causal mediation analysis has led to an explosion of new software programs, routines, and macros for SAS, Stata, SPSS, R, and Mplus (Discacciati, Bellavia, Lee, Mazumdar, & Valeri, 2019; Emsley & Liu, 2013; L. K. Muthén & Muthén, 1998/2017; SAS Institute, 2018; Steen, Loeys, Moerkerke, & Vansteelandt, 2017; Tingley, Yamamoto, Hirose, Keele, & Imai, 2014; Valeri & Vanderweele, 2013). The programs use different software platforms, different estimation methods, and have varying capabilities. So far, no paper has provided an overview of the estimation methods and capabilities of these programs for estimating causal mediation effects. This paper is not meant to be an exhaustive review of all capabilities of each macro or software environment, but an overview of the capabilities that are central to the estimation and interpretation of causal mediation effects.

Single Mediator Model

There are several software programs available for the estimation of causal mediation effects, including the Valeri and Vanderweele (2013) SAS and SPSS mediation macros, the Stata PARAMED macro, PROC CAUSALMED in SAS, the Med4Way macro in Stata, the MODEL INDIRECT statement in Mplus, the mediation R package, and the MedFlex R package. All of these programs require the estimation of two regression equations as input to estimate the causal effects for the single mediator model (Imai, Keele, & Tingley, 2010; B. O. Muthén, Muthén, & Asparouhov, 2017; VanderWeele & Vansteelandt, 2009):

$$M=i_1+aX+e_1$$ (1)

$$Y=i_2+c^{\prime }X+bM+hXM+e_2$$ (2)

Where Equation 1 represents the effect of X on M (a coefficient). Equation 2 represents the effect of X on Y adjusted for M (c’ coefficient), the effect of M on Y adjusted for X (b coefficient), and the effect of the XM interaction on Y (h coefficient). The magnitude of the h coefficient indicates how much the effect of X on Y (c’) varies across mediator levels (M) and how much the effect of M on Y (b) varies across treatment levels (X). The i₁ and i₂ terms in Equations 1 and 2 represent intercepts, and the e₁ and e₂ terms represent residuals. It is assumed that e₂ and e_1, X and e₁, X and e₂, and M and e₂ are uncorrelated, that the variables are measured without error, that the correct temporal order is observed (e.g., X→M→Y rather than X→Y→M), and that there are no common causes of M and Y (MacKinnon, 2008, 2020). The h coefficient in Equation 2 approaches zero when there is no XM interaction. In this situation, Equation 2 can be estimated without the XM variable. For our running example we estimated a mediation model with XM interaction and without covariates. Code for mediation models without XM interaction, and for covariate-adjusted mediation models with XM interaction are provided in the supplementary materials. In the next section, the causal mediated effect definitions and the causal assumptions are described.

Causal Mediation Analysis

Causal mediation analysis is based on the potential outcomes framework and the more general counterfactual framework (Holland, 1986; Rubin, 1974). These frameworks provide general definitions and assumptions to identify causal effects in both randomized experiments and nonrandomized studies. One of the acknowledged strengths of these causal effect definitions and assumptions is that they are not based on any specific estimation method and are therefore nonparametric. They can therefore be applied to any mediation model, including models with continuous and categorical variables, and models with treatment-mediator (XM) interactions.

The causal effect definitions are based on the assumption that each individual unit has a potential outcome value for each level of treatment (Holland, 1986; Rubin, 1974). For example, assuming the treatment X is a binary variable with two levels, X = 0 and X = 1, each individual unit (denoted as i) has an outcome value Y had they been at level X = 0 (i.e., Y_i(0)) and a Y value had they been at level X = 1 (i.e., Y_i(1)). The individual-level causal effect is then Y_i(1) – Y_i(0). However, it is impossible to observe the outcome for each individual under both conditions. That is, Y_i(0) but not Y_i(1) will be observed for an individual assigned to level X = 0, whereas Y_i(1) but not Y_i(0) will be observed for an individual assigned to level X = 1. This inability to obtain outcome measures for one individual in each condition at the same time is referred to as the “fundamental problem of causal inference” (Holland, 1986). However, under the assumption that the treatment and control groups are exchangeable in the absence of confounding, the causal treatment effect can be estimated at the average-level, i.e., E[Y_i(1)-Y_i(0)].

When applied to mediation models, the average-level potential outcome values for Y are defined and estimated based on varying mediator levels in addition to the varying treatment levels. That is, E[Y_i(0, m)] indicates the individual’s Y value observed in the control group while fixing the mediator at a predetermined value m, and E[Y_i(1, m)] indicates the individual’s Y value observed in the treatment group while fixing the mediator at a predetermined value m. The mediator can also be held constant at the value that would have been observed had the individual been in the control group, i.e., M_i(0), or had the individual been in the intervention group, i.e., M_i(1). This extends the potential outcomes to E[Y_i(1, M_i(1))]), E[Y_i(1, M_i(0))]), E[Y_i(0, M_i(1))]), and E[Y_i(0, M_i(0))]). For example, the potential outcome E[Y_i(1, M_i(1))]) indicates the average outcome value for individuals in the treatment group, whose mediator value is fixed at the value that would have been observed had they been in the treatment group. It is possible to observe E[Y_i(1, M_i(1))]) for individuals in the treatment group, and E[Y_i(0, M_i(0))]) for individuals in the control group. However, the two potential outcomes E[Y_i(1, M_i(0))]) and E[Y_i(0, M_i(1))]) cannot be observed at the individual level, but can be estimated at the average level.

The causal direct, indirect, and total effects are defined as the difference between two potential outcomes. In total, six causal effects are defined: 1) total natural indirect effect; 2) pure natural indirect effect; 3) total natural direct effect; 4) pure natural direct effect; 5) controlled direct effect; and 6) total effect. The total natural indirect effect (TNIE) is the effect of X on Y through M, when the direct effect is held constant at the treatment-group level X = 1; TNIE = E[Y_i(1, M_i(1)) − Y_i(1, M_i(0))]. The pure natural indirect effect (PNIE) is the effect of X on Y through M, when the direct effect is held constant at the control-group level X = 0; PNIE = E[Y_i(0, M_i(1)) − Y_i(0, M_i(0))]. The total natural direct effect (TNDE) is the effect of X on Y, while fixing each individual’s mediator to the value that would naturally have been observed had the individual been in the treatment group (i.e., M_i(1)); TNDE = E[Y_i(1, M_i(1)) − Y_i(0, M_i(1))]. The pure natural direct effect (PNDE) is the effect of X on Y, while fixing each individual’s mediator to the value that would naturally have been observed had the individual been in the control group (i.e., M_i(0)); PNDE = E[Y_i(1, M_i(0)) − Y_i(0, M_i(0))]. The controlled direct effect (CDE) is the effect of X on Y, while fixing the mediator for all individuals at a predetermined value m; CDE = E[Y_i(1, m) − Y_i(0, m)]. The total effect (TE) is the effect of X on Y and equals the sum of the TNDE and the PNIE or, equivalently, the sum of the PNDE and the TNIE; i.e., TE = E[Y_i(1, M_i(1)) − Y_i(0, M_i(0))].

The potential outcomes framework provides a general approach to decompose effects in the mediation model. By providing two indirect effect definitions, i.e., the TNIE and PNIE, and three direct effect definitions, i.e., the TNDE, PNDE, and CDE, causal mediation analysis naturally incorporates XM interaction in the effect estimates. When there is an XM interaction, the treatment-outcome effect differs across mediator levels, and the mediator-outcome effect differs across treatment levels. The TE can then be decomposed into the direct and indirect effect using various decompositions, with up to four components, i.e., the CDE, PNIE, reference interaction, and mediated interaction. The CDE is the part of the TE that is not due to interaction nor mediation, the PNIE is the part that is solely due to mediation, the reference interaction is the part that is solely due to interaction, and the mediated interaction is the part that is due to both interaction and mediation (for more details see VanderWeele (2014)). When there is no XM interaction or other non-linearities, e.g., a binary outcome, the TNDE = PNDE, and the TNIE = PNIE.

Identification Assumptions for Indirect and Direct Effects

VanderWeele and Vansteelandt (2009) described four no-unmeasured confounder assumptions for the nonparametric identification of indirect effects in the single mediator model:

1. No unmeasured confounders of the X – Y relation conditional on pretreatment covariates C, i.e., Y_i(x, m)∐X_i|C_i;

2. No unmeasured confounders of the M – Y relation conditional on treatment and pretreatment covariates C, i.e., Y_i(x, m)∐M_i|X_i, C_i;

3. No unmeasured confounders of the X – M relation, conditional on pretreatment covariates C, i.e., M_i(x)∐X_i|C_i;

4. No measured or unmeasured confounders of the M – Y relation affected by X conditional on pretreatment covariates C, i.e., Y_i(x, m)∐M_i(x*)|C_i.

Assumption 1 and 3 are satisfied in expectation when X represents random assignment to an experimental condition. Assumption 2 is not satisfied when X represents random assignment to an experimental condition, because individuals still self-select their mediator value given their observed treatment and covariate values. See Figure 1 for a depiction of the single mediation model and how baseline covariates may affect the X, M, and Y relations. More details on the single mediator model with baseline covariates are included in the supplemental materials. For the remainder of this manuscript, we will focus on the single mediator model with XM interaction and assume there are no baseline covariates that need to be adjusted for. In the next section, we describe the running data example, and the available software packages to estimate causal mediation effects.

Figure 1.

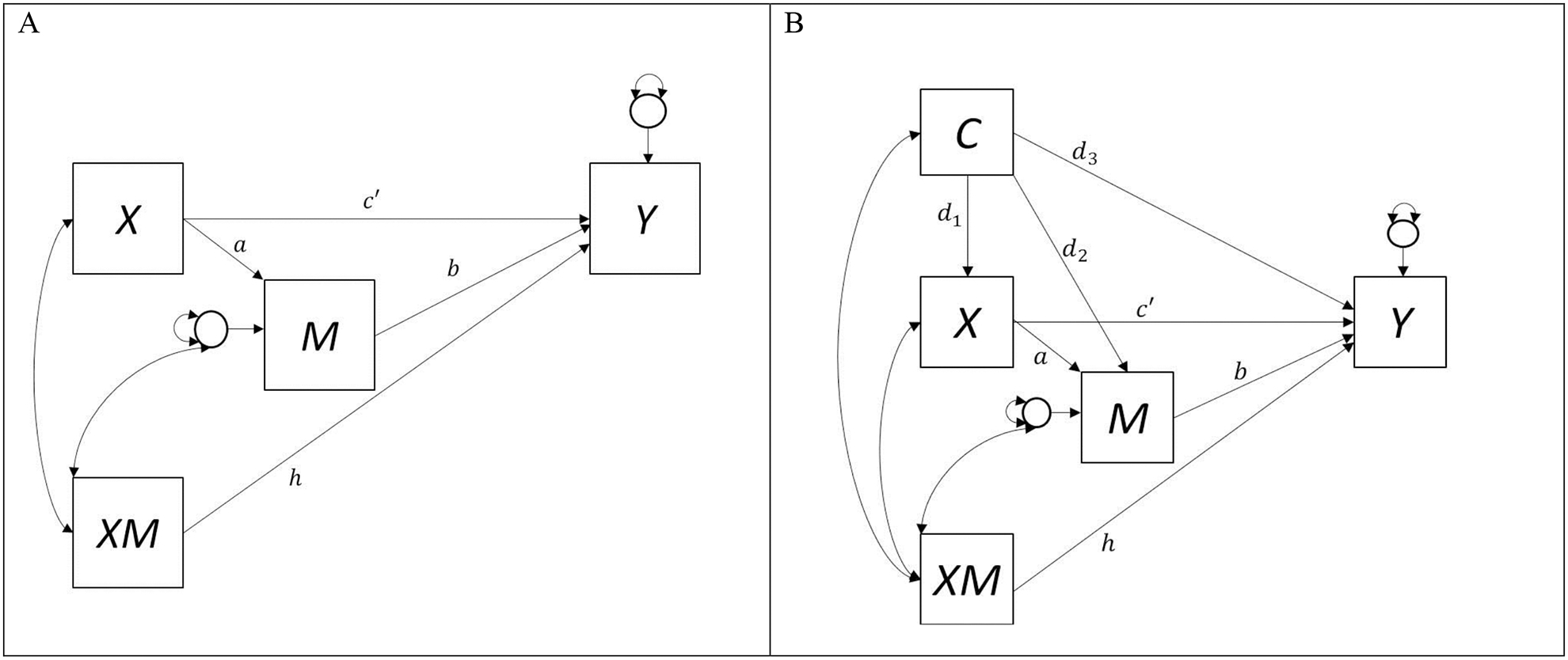
(A) Path diagram depicting the single mediator model with treatment by mediator interaction (XM). (B) Path diagram depicting the single mediator model with treatment by mediator interaction (XM) and baseline covariate (C) confounding the X-M, M-Y, and X-Y relations.

Empirical example

Data from the Athletes Training and Learning to Avoid Steroids (ATLAS; Goldberg et al. 1996) program were used to compare the output of the different software packages. ATLAS was designed to reduce high school football players’ use of anabolic steroids compared to a control group by engaging students in healthy nutrition and strength training alternatives. MacKinnon et al. (2001) investigated twelve mediators of the ATLAS program on three outcomes. Our example uses ATLAS program versus control (X) as the exogenous variable and strength training self-efficacy as the outcome (Y), which was a composite variable created by averaging the responses to six items, such as “I know how to train with weights to become stronger.”, on 7-point Likert scales (M = 5.88, SD = 1.08, Min = 1.00, Max = 7.00). The mediator (M) was knowledge of the effects of anabolic androgenic steroids (AAS) which was a composite variable created by summing the responses to two items (M = 10.86, SD = 5.07, Min = 0.00, Max = 18.00). The first item was “Please mark any of the effects or benefits that you believe anabolic steroids can cause:” which included response options such as “ more arguments and fights” and “improve physically”. The second item was “Please mark whether or not you think these health problems can readily be caused by anabolic steroids:” which included response options such as “liver disease” and “heart disease”. Additional information about the constructs can be found in Table 1 in the supplementary materials. The sample size was 1,191 after listwise deletion of the original 1,506 observations. Listwise deletion was used to simplify the discussion of the results therefore substantive conclusions should be approached with caution. In the example codes, the variable representing the ATLAS program is named “ngroup”, the mediator variable is named “ncknwas”, the outcome variable is named “ncstrtrn”, and the XM interaction term is named “groupknw”.

Valeri and Vanderweele (2013) SAS and SPSS Macros and Stata PARAMED

The Valeri and VanderWeele (VVW) SAS and SPSS mediation macros (Valeri & Vanderweele, 2013, 2015) and the Stata PARAMED macro (Emsley & Liu, 2013) provide researchers a general program for the estimation of causal mediation effects based on various linear and non-linear regression models for Equations 1 and 2, and with and without XM interaction. The VVW and Stata PARAMED macros start by estimating the parameters of regression Equations 1 and 2, and subsequently use these parameters to estimate the causal mediation effects (see Table 1 for an overview of these causal estimators) (VanderWeele & Vansteelandt, 2009). Example VVW SAS macro code used for the empirical example is presented here:

Table 1.

Regression-based estimators of the causal indirect, direct, and total effects for models with a continuous mediator and a continuous outcome.

Effect	Potential outcomes notation	Causal estimator
TNIE	E[Yi(1, Mi(1)) − Yi(1, Mi(0))]	ba + ha
PNIE	E[Yi(0, Mi(1)) − Yi(0, Mi(0))]	ba
TNDE	E[Yi(1, Mi(1)) − Yi(0, Mi(1))]	c’ + hi1+ ha
PNDE	E[Yi(1, Mi(0)) − Yi(0, Mi(0))]	c’ + hi1
CDE	E[Yi(1, m) − Yi(0, m)]	c’ + hm
TE	E[Yi(1, Mi(1)) − Yi(0, Mi(0))]	c’ + hi1 + ba + ha

Abbreviations: TNIE, total natural indirect effect; PNIE, pure natural indirect effect; TNDE, total natural direct effect; PNDE, pure natural direct effect; CDE, controlled direct effect; TE, total effect.

Title ‘single mediator model with XM interaction and continuous y’; %mediation(data=atlas,yvar=ncstrtrn,avar=ngroup,mvar=ncknwas,cvar=,a0=0,a1=1,m=0,nc=,yreg=linear, mreg=linear, interaction=true,casecontrol=,output=full, c=,boot=true,cens=); run;

The dataset name is specified after data, the outcome variable is specified after yvar, the treatment variable is specified after avar, and the mediator variable is specified after mvar, cvar is used to specify a list of covariates. a0 and a1 denote the control group and treatment group values of X if X is a binary variable, or two reference values if X is a continuous variable. m is used to specify the m value that the CDE is estimated at, which we set to zero for the example. In practice, the CDE may be estimated at theoretically interesting or clinically relevant values of the mediator (Pearl, 2001). It is also possible to estimate the CDE at the mean value of the mediator or +/− 1 standard deviation units above/below the mean of the mediator (MacKinnon, 2008, 2020). nc is used to specify the number of baseline covariates entered in the analysis and yreg and mreg are used to specify the outcome and mediator models are linear, respectively. We specified interaction=true to estimate the XM interaction in Equation 2, casecontrol is used to specify if the data are from a case-control study, output=full is used to have the macro output all causal mediation effect estimates, and c is used to specify at which covariate values the conditional causal effects need to be estimated. When no covariate values are specified under c the causal effects are estimated at the mean covariate values. boot=true was specified to get 95% percentile bootstrap confidence intervals, and cens is used to specify whether the outcome variable is censored (only available in the SAS version of the macro). Percentile bootstrapping is a computer intensive method that creates an empirical distribution of the causal effect estimates by resampling from the observed dataset many times with replacement and estimating the causal effect in each resampled dataset (Bollen & Stine, 1990). Percentile bootstrapping then uses the effect estimate at the 2.5^th percentile of the distribution as the lower limit of the 95% confidence interval and the estimate at the 97.5^th percentile as the upper limit of the 95% confidence interval.

The SPSS version of the VVW mediation macro is presented here:

DEFINE !path()”C:/Users/mvalente/Downloads/” !ENDDEFINE. *Single mediator model with XM interaction and continuous Y. mediation data=‘C:/Users/mvalente/Downloads/DATA.sav’/yvar=ncstrtrn/avar=ngroup/mvar=ncknwas/cvar= /NC=0/a0=0/a1=1/m=0/yreg=LINEAR/mreg=LINEAR/interaction=TRUE/boot=TRUE/nobs=1191/Output=FULL/c=‘.

The SPSS version of the VVW mediation macro is largely the same as the SAS version. It is important to specify the location the macro will save the relevant effect estimates, which is accomplished by running the first two lines of code. If bootstrap standard errors and confidence intervals are specified in the SPSS version, an additional input nobs= is used to specify the number of observations in the observed dataset (Valeri & Vanderweele, 2013). It is important to specify NC=0 if there are no covariates in the model.

The Stata PARAMED macro code for the example is presented here:

paramed ncstrtrn, avar(ngroup) mvar(ncknwas) cvars() a0(0) a1(1) m(0) yreg(linear) mreg(linear) boot reps(1000) seed(1234) full

The syntax for Stata PARAMED is very similar to the VVW macros, so in an effort to save journal space we will not provide a detailed explanation of each macro input. One important difference between the VVW and PARAMED macros is that the PARAMED macro provides bias-corrected bootstrap confidence intervals when the boot option is used as opposed to the percentile bootstrap confidence intervals provided in the VVW macro output. The bias-corrected bootstrap uses the percentiles from the percentile bootstrap, but applies a correction to the upper and lower limits to take into account the bias in the central tendency of the effect estimate. Of these two bootstrapping methods, the percentile bootstrap procedure is generally preferred because it has higher statistical power than the normal theory confidence intervals and more accurate Type 1 error rates for the PNIE in a single mediator model with no XM interaction than bias-corrected bootstrap (Mackinnon, Lockwood, & Williams, 2004). Another difference is that the VVW macro in SAS facilitates a wider range models for Equation 2 than the PARAMED macro and the SPSS version of the VVW macro (see Table 2 for more details). The macros use complete-cases only when there is missing data.

Table 2.

Features of the causal mediation software packages

	Outcome model	Mediator model	Treatment variable	Standard errors/ Confidence intervals	Missing Data	Sensitivity Analysis	Multiple Mediators	Latent variables	Moderated mediation
VVW	Linear, logistic, Poisson, negative binomial, Cox, or accelerated failure time (exponential or Weibull).a	Linear or logistic.	Binary or continuous.	Delta method or percentile bootstrap.	Complete case analysis only.	No	No	No	No
PARAMED	Linear, logistic, Poisson, negative binomial.	linear or logistic.	Binary or continuous.	Delta method, bias-corrected bootstrap.	Complete case analysis only.	No	No	No	No
CAUSALMED 9.4 TS1M6	Linear, logistic, Poisson, negative binomial.	linear or logistic.	Binary or continuous.	Delta method, normal-based bootstrap, percentile bootstrap, or bias-corrected bootstrap.	Complete case analysis only.	No	No	No	No
Med4Way	Linear, logistic, Poisson, negative binomial, log-binomial, Cox, or accelerated failure time (exponential or Weibull).	linear or logistic.	Binary or continuous.	Delta method, normal-based bootstrap, percentile bootstrap, bias-corrected bootstrap, or bias-corrected and accelerated bootstrap.	Complete case analysis only.	No	No	No	No
Model Indirect (Mplus 8.4)	Linear, (ordered) logistic, (ordered) probit, censored, Poisson, or negative binomial.b	Linear, (ordered) logistic, (ordered) probit, or censored.b	Binary or continuous.	Delta method, percentile bootstrap, bias-corrected bootstrap. Robust standard errors, Bayesian credible intervals.	Multiple imputation, maximum likelihood, or complete case analysis.	Yes	Yes, only overall indirect effect estimates are provided assuming no interactions between mediators.	Yes	Yes
Mediation (version 4.5)	Linear, (ordered) logistic, (ordered) probit, Poisson, Cox, accelerated failure time, tobit, quantile regression, generalized additive model, or (generalized) mixed-effects.c	Linear, (ordered) logistic, (ordered) probit, Poisson, Cox, accelerated failure time, quantile regression, generalized additive model, or (generalized) mixed-effects.c	Binary, continuous, or multicategorical.	Quasi-Bayesian Monte Carlo, percentile bootstrap, or bias-corrected and accelerated bootstrap. Robust standard errors.	Complete case analysis or multiple imputation for the input models using standard multiple imputation functions	Yes	Yes, overall indirect effect estimates are provided assuming no interactions between mediators.	No	Yes
Medflex (version 0.6–6)	Linear, logistic, probit, or Poisson.d	Imputation-based approach: linear, logistic, probit, Poisson, multinomial logistic, ordinal logistic.d Weighting-based approach: linear, logistic, probit, Poisson, multinomial logistic.d	Binary, continuous, or multicategorical.	Normal-based bootstrap, percentile bootstrap, bias-corrected bootstrap, or bias-corrected and accelerated bootstrap. Robust standard errors.	Default for weighting-based approach is complete case analysis. Imputation-based approach uses imputation of missing values conditional on treatment, mediator, and baseline covariates. Multiple imputation is supported for both approaches.	No	Yes, overall indirect effect estimates are provided.	No	Yes

^aCox and accelerated failure time models are only facilitated in the SAS macro (Valeri & VanderWeele, 2015).

^bA two-part outcome model can be estimated using a combination of the Model Indirect command and the Model Constraint command. A multinomial mediator can be assumed using the Model Constraint command. Mplus uses the latent variable response formulation for categorical dependent variables.

^cThe quasi-Bayesian approximation cannot be used if the mediator model is specified as a quantile regression model or a generalized additive model or if the outcome model is specified as a generalized additive model or an ordered logistic (probit) model. See Tingley et al., 2014 for additional information and the specific R packages that can be used to fit the mediator and outcome models.

^dSee Steen et al., 2017 for additional information and the specific R packages that can be used to fit the mediator and outcome models.

SAS PROC CAUSALMED

The SAS PROC CAUSALMED procedure follows the same steps in the estimation of the causal mediation effects as the VVW and PARAMED macros. It first estimates the parameters of Equations 1 and 2 and then uses these estimated parameters to compute the causal mediation effects using the estimators in Table 1 (SAS Institute, 2018). PROC CAUSALMED provides three different types of bootstrap confidence intervals: bias-corrected, normal-based, and percentile bootstrap. The normal-based bootstrap confidence intervals assume that the bootstrap estimates of the causal effects follow a normal distribution. This may not be accurate when the causal effect estimates are a non-linear function of regression coefficients (e.g., the product of two regression coefficients does not necessarily follow a normal distribution; Meeker, Cornwell, and Aroian (1981)). Therefore, percentile bootstrap confidence intervals are preferred (Mackinnon et al., 2004).

In addition to the causal mediation effects, PROC CAUSALMED provides various TE decompositions. The code used for the empirical example is presented here:

PROC CAUSALMED DATA=atlas pALL ALPHA=.05;  CLASS ngroup/DESCENDING;  MODEL ncstrtrn = ngroup | ncknwas;  MEDIATOR ncknwas = ngroup;  EVALUATE “CDE@0” ncknwas=0;  BOOTSTRAP CI (ALL) NBOOT = 1000; quit;

We specified the active dataset by using DATA=atlas. By specifying pALL, all possible output is provided and ALPHA=.05 sets the alpha level for significance testing to 0.05. CLASS ngroup/DESCENDING is used to specify X as a categorical variable with the lowest-coded level as the reference level. MODEL ncstrtrn = ngroup | ncknwas estimates Equation 2 and MEDIATOR ncnkwas = ngroup estimates Equation 1. The EVALUATE “CDE@0” ncknwas=0 statement is used to estimate the CDE at the mediator value of zero. The BOOTSTRAP CI (ALL) NBOOT = 1000 statement is used to output all possible bootstrap confidence intervals based on 1000 bootstrap resamples (See Table 2 for more details). When there is missing data, SAS PROC CAUSALMED relies on complete-case only analysis. The causal effects are by default estimated conditional on the mean covariate value, unless other covariate values are specified by the user.

Stata Med4Way

The Stata Med4way macro (Discacciati et al., 2019) is most similar to SAS PROC CAUSALMED. The primary aim of Med4Way is to provide researchers with output from the four-way decomposition of the TE and therefore does not provide the option to estimate the single mediator model without an XM interaction. The output of the Med4Way macro contains CDE, PNIE, and TE estimates, as these are components of the four-way decomposition, but does not contain TNIE, PNDE, and TNDE estimates. Med4way code for the example is presented here:

med4way ncstrtrn ngroup ncknwas, a0(0) a1(1) m(0) yreg(linear) mreg(linear) bootstrap reps(1000) seed(1234) fulloutput estat bootstrap, all

The syntax for Med4way is similar to PARAMED and therefore will not be discussed in detail. The estat bootstrap, all command outputs normal-based, bias-corrected bootstrap, and bias-corrected and accelerated bootstrap confidence intervals. The Med4way macro uses complete-cases only when there is missing data (See Table 2). The causal effects are by default estimated conditional on the mean covariate values, unless other covariate values are specified by the user.

Mplus Model Indirect

The Model Indirect command in Mplus follows similar steps as the previous software programs when estimating the causal mediation effects (B. O. Muthén et al., 2017; L. K. Muthén & Muthén, 1998/2017). First, the parameters in Equations 1 and 2 are estimated and then these parameter estimates are used to compute the causal mediation effects. The previous software programs use OLS to estimate the regression parameters when Equations 1 and 2 are estimated based on a continuous mediator or outcome, but Mplus has many estimator options; with the default being maximum likelihood (see Table 2 for more details). Code that was applied to the empirical example is presented here:

TITLE: Comparison cont Y with XM; DATA: FILE= atlas.txt; VARIABLE: NAMES = id ngroup ncknwas ncstrtrn groupknw; USEVAR = ngroup ncknwas ncstrtrn groupknw; ANALYSIS: estimator=ml; type=general; bootstrap=1000; MODEL: ncknwas on ngroup; ncstrtrn on ngroup ncknwas groupknw; MODEL INDIRECT: ncstrtrn mod ncknwas(0) groupknw ngroup; OUTPUT: SAMPSTAT CINTERVAL(bootstrap);

The dataset was specified using DATA: FILE= atlas.txt, the variables names are id ngroup ncknwas ncstrtrn groupknw, and USEVAR = ngroup ncknwas ncstrtrn groupknw specifies the variables used in this specific analysis. ANALYSIS: is used to specify estimator=ml for maximum likelihood, type=general for the estimation of linear regressions. Bootstrap=1000 is used to specify 1,000 bootstrap resampled datasets. MODEL: ncknwas on ngroup is used to estimate Equation 1 and ncstrtrn on ngroup ncknwas groupknw is used to estimate Equation 2. MODEL INDIRECT: ncstrtrn mod ncknwas(0) groupknw ngroup is used to specify the causal mediation effects with XM interaction, and the CDE estimated conditional on a mediator value of zero. OUTPUT: SAMPSTAT is used to get sample statistics in the output and CINTERVAL(bootstrap) is used to specify percentile bootstrap confidence intervals. Mplus has a variety of missing data handling techniques including full-information maximum likelihood and multiple imputation (L. K. Muthén & Muthén, 1998/2017). By default, Mplus uses maximum likelihood and therefore uses all available data. The causal effects are by default estimated conditional on the covariate value of zero, unless the covariates have been centered at a different level. Finally, it is possible to use the Mplus Model Constraint command to estimate the causal mediation effects (B. O. Muthén et al., 2017).

R – Mediation Package

The mediation package in R provides estimates of the Average Direct Effect (ADE) (treated) (i.e., TNDE), the ADE (control) (i.e., PNDE), the Average Causal Mediated Effect (ACME) (treated) (i.e., TNIE), the ACME (control) (i.e., PNIE), and TE, but not of the CDE (Tingley et al., 2014). First, the R mediation package estimates the parameters of Equations 1 and 2 using the lm function (see Table 2 for other options). Second, it computes predicted values for each of the four potential outcomes for each observation. Third, the causal mediation effects are computed as the difference in the predicted potential outcomes (e.g., PNIE = Y_i((0, M_i(1)) − Y(0, M_i(0))). for each observation and then the average is estimated (for more details see Imai et al., 2010). Code applied to the empirical example is presented here:

model.m1=lm(ncknwasñgroup, data=atlas) model.y2cont=lm(ncstrtrnñgroup+ncknwas+ngroup*ncknwas, data= atlas) model2cont=mediate(model.m1, model.y2cont, treat=“ngroup”, mediator=“ncknwas”,boot = TRUE, boot.ci.type=“perc”, conf.level=.95, sims=1000) summary(model2cont)

model.m1 is the R object that contains the estimated linear regression parameters in Equation 1 with data= atlas specifying the name of the dataset for the analysis. model.y2cont is the R object that contains the estimated linear regression parameters in Equation 2. The primary function of the mediation package is mediate, which requires the name of the R object for the mediator and outcome models (model.m1 and model.y2cont, respectively). The intervention variable is specified after treat=, and the mediator variable is specified after mediator=. boot=”TRUE”, boot.ci.type”perc”, conf.level=.95, sims=1000 are used to specify 95% percentile bootstrapped confidence interval based on 1,000 bootstrap resamples. If boot=”FALSE” is specified, the sims argument specifies the number of simulations used to estimate standard errors and confidence intervals using a quasi-Bayesian Monte Carlo method. The summary(model2cont) provides the output of the mediate function. The mediation R package uses complete-cases for the mediator equation (model.m1) and the outcome equation (model.y2cont) by default, but does have capabilities to estimate the causal mediation effects on imputed datasets (see Tingley et al. 2014 for more details). The causal effects are by default averaged over the covariate distributions but can also be estimated conditional on specific covariate values.

R – medflex Package

The medflex package in R provides estimates of the TNDE, PNDE, TNIE, PNIE, and TE, but not of the CDE (Steen et al., 2017). The causal effects in medflex are estimated based on natural effect models. In these models, the natural direct and indirect effects are each represented by a single regression coefficient. To estimate the natural direct and indirect effect in one model, data is required for the potential outcome values observed under both treatment values. Whereas only one potential outcome value is observed for each subject, medflex uses a weighting-based approach or an imputation-based approach to estimate the unobserved potential outcomes. The weighting-based approach requires the researcher to estimate Equation 1 and the natural effect model. The imputation-based approach requires the researcher to estimate Equation 2 and the natural effect model (Steen et al. (2017); See supplemental materials for more details on how medflex estimates the parameters of the natural effect models). Code for the imputation-based approach is presented here:

expData2 <-neImpute(ncstrtrnñgroup*ncknwas, data= atlas) neMod2 <-neModel(ncstrtrnñgroup0*ngroup1, expData = expData2, se=“bootstrap”, nBoot = 1000) neMod2eff<-neEffdecomp(neMod2) summary(neMod2eff) confint(neMod2eff, level=.95, type=“perc”)

The function neImpute imputes the unobservable potential outcomes using Equation 2 which is specified ncstrtrnñgroup*ncknwas using the atlas dataset. The neModel function estimates the causal mediation effects, specified by yñgroup0*ngroup1. The expData command uses the imputed dataset created in the previous step (expData=expData2). Se=”bootstrap” and nBoot=1000 specifies that the standard errors and confidence intervals are estimated based on 1,000 resamples. The neEffdecomp function decomposes the causal effect estimates from the object neMod2 in order to output the results in terms of the PNDE, TNDE, PNIE, TNIE, and TE. The summary(neMod2eff) provides the output of the neEffdecomp function. The confint function with level=.95 and type=“perc” was applied to the neMod2eff object to estimate 95% percentile bootstrap confidence intervals for the causal mediation effects. The confint function internally calls the boot.ci function in R to produce bootstrapped confidence intervals. Code for the weighting-based approach is presented here:

xm<-neWeight(ncknwas~factor(ngroup),data= atlas) xmmod<-neModel(ncstrtrnñgroup0*ngroup1,expData=xm, se=“bootstrap”, nBoot=1000) causeff<-neEffdecomp(xmmod) summary(causeff) confint(causeff, type=“perc”, level=0.95)

The code for the weighting-based approach is similar to the code for the imputation-based approach, only the first line of the code differs. The function neWeight in the first line of the code creates a weight for each observation based on the estimated Equation 1. This weight is computed as the propensity to observe the mediator value in the counterfactual condition divided by the propensity to observe the mediator value in the observed condition. Medflex uses complete-cases only analysis when there is missing data but has the option to estimate the causal mediation effects on imputed datasets (see Table 2). As in Mplus, the causal effects are by default estimated conditional on the covariate value of zero, unless the covariates have been centered at a different level.

Estimates and Computational Time

The VVW, PARAMED, Causalmed, Model Indirect, the mediation R package, and the imputation-based approach in the medflex R package provided nearly identical estimates of the TNIE, PNIE, TNDE, PNDE, and TE (see Table 3). The VVW, PARAMED, Causalmed, Model Indirect provided identical estimates of the CDE. Med4way only provided estimates of the PNIE, CDE, and TE which were nearly identical to the estimates obtained from the other programs except for the weighting-based approach in the medflex R package. The results for the weighting-based approach in the medflex R package were similar to the results from the other programs, but not identical. The PNIE of the ATLAS program on strength training self-efficacy through its effect on knowledge of the effects of AAS was 0.203 holding the direct effect constant at the control-group level, and the TNIE was 0.177 holding the direct effect constant at the intervention-group level. Both the PNIE and TNIE were statistically significant, based on the 95% confidence intervals. The PNDE of the ATLAS program on strength training self-efficacy, while holding each subject’s mediator constant at the control group value was 0.125, and the TNDE holding each subject’s mediator constant at the intervention group value was 0.099. Neither the PNDE nor the TNDE were statistically significant according to most outputs based on the 95% confidence intervals, except for the PNDE estimate based on the mediation R package, and the TNDE estimate based on the weighting-based approach in the medflex R package. The CDE of the ATLAS program on strength training self-efficacy, while holding each subject’s mediator constant at zero, was 0.114 according to all outputs. Based on the 95% confidence intervals, the CDE was only significant according to the Med4way output. The total effect of the ATLAS program on strength training self-efficacy was 0.302, and was statistically significant according to all outputs based on the 95% confidence intervals.

Table 3.

Causal effect estimates with 95% percentile bootstrap confidence intervals for the empirical data example.

Program
Effect	VVWa	PARAMEDb	Causalmed	Med4way	Mplus Model Indirect	Mediation	Medflex
PNIE	0.203 [0.148, 0.268]	0.203 [0.141, 0.267]	0.203 [0.143, 0.273]	0.203 [0.142, 0.268]	0.203 [0.147, 0.273]	0.203 [0.144, 0.270]	Imputed: 0.203 [0.141,0.270] Weighted: 0.182 [0.128, 0.249]
TNIE	0.177 [0.116, 0.250]	0.177 [0.118, 0.247]	0.177 [0.115, 0.245]	N/A	0.177 [0.114,0.247]	0.177 [0.113, 0.250]	Imputed: 0.177 [0.119,0.253] Weighted: 0.198 [0.125, 0.277]
PNDE	0.125 [−0.006, 0.251]	0.125 [−0.002,0.255]	0.126 [−0.001, 0.255]	N/A	0.125 [−0.006,0.248]	0.125 [<0.001,0.250]	Imputed: 0.125 [−0.006, 0.246] Weighted: 0.104 [−0.029, 0.250]
TNDE	0.099 [−0.020, 0.217]	0.098 [−0.020, 0.209]	0.099 [−0.024, 0.207]	N/A	0.099 [−0.022,0.213]	0.098 [−0.012,0.220]	Imputed: 0.099 [−0.016,0.212] Weighted: 0.120 [0.004, 0.244]
CDE	0.114 [−0.001, 0.231]	0.114 [−0.003,0.233]	0.114 [−0.009, 0.2252]	0.114 [<0.001, 0.234]	0.114 [−0.011, 0.230]	N/A	N/A
TE	0.302 [0.178, 0.429]	0.302 [0.176, 0.417]	0.302 [0.174, 0.422]	0.302 [0.184, 0.423]	0.302 [0.173, 0.417]	0.302 [0.187, 0.420]	Imputed: 0.302 [0.176, 0.415] Weighted: 0.302 [0.181, 0.429]

^aThe effect estimates and confidence intervals come from two separate runs of the macro. The first run consisted of bootstrap = false so the effect estimates represent the observed sample effect estimates and not bootstrap estimates. The second run consisted of bootstrap = true to obtain percentile bootstrap confidence intervals for the effect estimates.

^bConfidence intervals are 95% bias-corrected bootstrap confidence intervals.

All programs ran on a Dell Optiplex 7450 AIO with an Intel Core i7–6700 CPU @3.4 GHz running Windows 10 Enterprise 64-bit operating system. The estimation of the causal effects took the SAS version of the VVW mediation macro 4 minutes and two seconds, the SPSS version of the VVW mediation macro took two minutes and 40 seconds, PARAMED took 17 seconds, Proc Causalmed took 1 second, Med4Way took one minute, Mplus took less than 1/100^th of a second, the mediation R package took 8 seconds, the imputation-based approach in the medflex R package took 14 seconds, and the weighting-based approach in the medflex R package took 12 seconds. Mplus was therefore the fastest program and the SAS version of the VVW mediation macro was the slowest program. All estimates of computing time were rounded to the nearest second.

Discussion

The proliferation of new software for the estimation of causal mediation effects highlights the need for a review of their capabilities, to increase the application of these important new methods. The purpose of this paper was to provide researchers with information on how to estimate causal mediation effects based on their own data and recommendations for which software to use. We explained how each software program handles the estimation of causal mediation effects for the single mediator model with XM interaction, and described additional program features.

Evaluation and Recommendations

For a single mediator model with binary X, continuous M and Y, and XM interaction, the software programs provided nearly identical effect estimates, similar bootstrapped confidence intervals, and had similar computation times. For this model, any program is satisfactory for estimating causal mediation effects. The adequacy of the software programs, however, diverges on a few key topics. First, in the presence of missing data that is not missing completely at random (MCAR), it is preferred to use either maximum likelihood or multiple imputation. Mplus offers users the option to use maximum likelihood, or multiple imputation. The mediation R package and medflex R package allow researchers to handle missing data using multiple imputation. In the presence of missing data, researchers are therefore recommended to use either Mplus Model Indirect, mediation R package, or medflex. Second, if X, M, and/or Y represent unobserved variables, Mplus offers the possibility to treat these constructs as latent variables using a theoretically and statistically validated measurement model (B. O. Muthén et al., 2017; L. K. Muthén & Muthén, 1998/2017). Third, the mediation and medflex R packages are recommended when researchers have a multi-categorical treatment variable as these are the only two packages that provide causal mediation effect estimates for this situation. Finally, the medflex R package provide researchers with modeling options that may be robust to potential misspecifications of the mediator or outcome models depending on which modeling choice is made (imputation vs. weighting). For more information about these modeling choices, researchers are encouraged to read Steen et al. (2017).

Future improvements for Causal Mediation Software

There is no single software package that provides researchers with all features described in Table 2 of this paper. There are four main areas of improvement. First, the causal effect estimation for multiple mediator models is limited. The multiple mediator functions currently available are limited because they do not estimate path-specific mediated effects. Second, the causal effect estimation for multilevel models needs further development, as currently the only software package that includes multilevel analysis is the mediation R package (Tingley et al., 2014). Third, causal effect estimation for longitudinal models are needed because these models allow researchers to take time-lags into account when estimating causal mediation effects. Fourth, more development is needed for causal effect estimation based on non-parametric models. A major strength of causal mediation analysis is that its effect definitions do not rely on any specific estimation method (Pearl, 2001). For models with a continuous mediator and outcome, causal and traditional mediation analysis have been shown to provide similar effect estimates (MacKinnon, Valente, & Gonzalez, 2020; Miočević, Gonzalez, Valente, & MacKinnon, 2018; Rijnhart, Twisk, Chinapaw, de Boer, & Heymans, 2017). However, non-parametric causal mediation analysis is preferred over traditional mediation analysis when the parametric assumptions are violated. Overall, there is a compelling need for an improvement in the causal mediation software before this important new methodology can be broadly applied to all common mediation models.

Overall, researchers are encouraged to use causal mediation analysis, because of its strength in defining general causal indirect and direct effects (Pearl, 2001; VanderWeele & Vansteelandt, 2009). The overview, comparison, and recommendations of specific software programs provided in this paper, make it easier for researchers to apply causal mediation methods and interpret causal mediation effects. Ultimately, the application of causal mediation methods to substantive research questions can help improve the understanding of causal mechanisms.