Abstract
The physico-mechanical properties of nanoscale lipid vesicles (e.g., natural nano-vesicles and artificial nano-liposomes) dictate their interaction with biological systems. Understanding the interplay between vesicle size and stiffness is critical to both the understanding of the biological functions of natural nano-vesicles and the optimization of nano-vesicle-based diagnostics and therapeutics. It has been predicted that, when vesicle size is comparable to its membrane thickness, the effective bending stiffness of the vesicle increases dramatically due to both the entropic effect as a result of reduced thermal undulation and the nonlinear curvature elasticity effect. Through systematic molecular dynamics simulations, we show that the vesicle membrane thins and softens with the decrease in vesicle size, which effectively counteracts the stiffening effects as already mentioned. Our simulations indicate that the softening of nano-vesicles results from a change in the bilayer’s interior structure - a decrease in lipid packing order - as the membrane curvature increases. Our work thus leads to a more complete physical framework to understand the physico-mechanical properties of nanoscale lipid vesicles, paving the way to further advances in the biophysics of nano-vesicles and their biomedical applications.
Keywords: Lipid membrane, Vesicle, Curvature, Elastic modulus, Stiffness, Molecular simulation
1. Introduction
Nanoscale vesicles primarily consisted of phospholipid molecules exist in both natural and synthetic forms. Exosomes, now termed small extracellular vesicles (sEV) [1], are endogenous lipid-bound vesicles with a diameter less than 150 nm. They serve as communication vehicles by transferring membrane-bound and cytosolic proteins, as well as lipids and RNA between cells in multiple physiological and pathological processes [2]. Examples include transferring placental trophoblast biomolecules to increase viral resistance of recipient cells , enabling T-cell activation by dendritic cells as part of the defensive immune response, and regulating angiogenesis by tumor cells during tumor progression [3–7]. The molecular information carried by sEVs makes them a potential diagnostic tool [8]. In addition, the potential of nanoscale vesicles as next-generation nanoparticulate drug-delivery carriers has been extensively studied [9,10] along with their artificial counterparts, namely nanoliposomes or small unilamellar vesicles [11]. Recent studies have illustrated that both the size and the stiffness of lipid vesicles significantly regulate their interaction with biological systems, especially during tumor penetration and endocytosis by cells [12–16]. Understanding the potential coupling between the vesicle size and stiffness is critical for constructing a complete picture of the biological functions of sEVs as well as to optimize the design of lipid vesicle-based diagnostic and therapeutic applications.
Mechanical properties of large lipid vesicles, such as red blood cells and artificial giant unilamellar vesicles (1–200 μm), have been well described by the Canham-Helfrich’s theoretical framework in which the lipid membrane is modeled as an elastic sheet with zero thickness undergoing elastic deformation [17–19]. According to this classic membrane model, one can easily predict that the total bending energy of a spherical vesicle is independent of the vesicle size. The dependence of vesicle stiffness on vesicle size emerges from the following two considerations. First, the translational and rotational entropy contributions due to thermal fluctuation of a finite-sized vesicle make the free energy of a vesicle logarithmically scale with the vesicle size [20,21]. Second, when the vesicle size is comparable with the membrane thickness, the contribution from large curvature, nonlinear elasticity becomes significant and surges with the decrease in vesicle size [22–24]. Both the entropic and the nonlinear effects suggest the stiffening of the lipid vesicle as the vesicle size decreases.
In this study, we have performed detailed molecular dynamics (MD) simulations using Martini coarse-grained force field [25,26] to elucidate how lipid packing and mechanical properties are regulated by the vesicle size. We have simulated planar lipid bilayers as well as vesicles of two different outer diameters (17 nm and 24 nm). The 17 nm vesicle lies in the range of 10–20 nm diameter that we have previously predicted as the lower bound for vesicle sizes [24]. The 24 nm vesicles are 1.5 times bigger than the 17 nm ones and are closer to the natural sEV size. Considering that phosphatidylcholine (PC) and phosphatidylethanolamine (PE) are two of the most common phospholipid types in biological membranes, our model membranes are composed of either di-myristoyl-phosphatidylcholine (DMPC) or di-myristoyl-phosphatidylethanolamine (DMPE) lipids. By simulating a series of swelling experiments and correcting the Laplace’s law for the finite-membrane thickness effect, we have characterized both the stress state and mechanical properties of the lipid vesicles. We have identified a membrane softening effect as the membrane curvature increases, which counteracts the stiffening schemes established previously [23] and renders a more complete physical framework for understanding the physico-mechanical properties of nanoscale lipid vesicles.
2. Methods
2.1. MD simulations of planar lipid bilayers and vesicles
MD simulations were carried out for DMPC and DMPE lipid bilayers in both planar and vesicle forms using the coarse-grained MARTINI force-field version 2.2 implemented in the GROMACS version 2018.2 software [27–29]. In the MARTINI model, about four non-hydrogen atoms are grouped into one bead, and thus the 14 carbon atoms in each DM tail of DMPC or DMPE lipids are mapped to three beads and four water molecules into one bead. DMPC lipid features an NC3 head-group while DMPE features an NH3 group, the latter being able to form hydrogen bonds with neighbouring PE head-groups. This is reflected by the lower Lennard-Jones potential minimum at the equilibrium distance between two NH3 beads compared to that between two NC3 beads in the MARTINI force-field.
The initial configurations and simulation set-up files for planar lipid bilayers and vesicles were generated using the Martini Bilayer Maker and Martini Vesicle Maker [30], respectively, within the CHARMM-GUI web-based platform [31]. Planar bilayers were generated with 1024 lipids per monolayer, and 3 nm-thick water layers above and below the bilayer. Lipid vesicles were generated with an initial outer diameter of 7.5 nm for small vesicles and 11.25 nm for large vesicles with six, symmetrically placed 2-nm-diameter pores to facilitate the exchange of inner and outer water as well as possible lipid flip-flops between the inner and outer leaflets. After energy minimization steps, MD simulations were carried out with progressively reduced restraints on lipid head-group positions as the simulation time-step increased from 2 to 20 fs. During equilibration of vesicles, the pores were progressively closed by reducing the strength of position restraints. Unrestrained simulations were subsequently carried out for at least 0.5 μs.
Electrostatic interactions were computed using Reaction-Field method with dielectric constant of 15 and cut-off distance of 1.1 nm. Van der Waals interactions were computed using cut-off method with the same distance of 1.1 nm. System temperature was maintained at 310 K with the Velocity-rescale thermostat, whereas pressure was maintained at 1 bar with the Parrinello-Rahman barostat with semi-isotropic coupling for bilayers (X-Y plane coupled separately from the Z or bilayer normal direction) and isotropic coupling for vesicles, with time-constant of 12 ps and compressibility of 4.5 × 10−5 bar−1.
2.2. Calculation of lipid bilayer physical properties
Bilayer thickness was calculated as the difference in the mean locations of PO4 beads between the two leaflets. Distributions of PO4 bead positions were extracted from the respective simulation trajectories. For planar bilayer, the bead positions were taken relative to the center of mass of the bilayer along the normal direction of the bilayer. For vesicles, the bead positions were taken relative to the center of the vesicle along the radial direction. The area per lipid for planar bilayers was computed from the time-averaged simulation box area divided by the number of lipids in each monolayer. For vesicles, the inner (Rin) and outer (Rout) radii of the vesicle were estimated based on the respective PO4 bead positions of each leaflet. The inner and outer surface areas were computed and divided by the number of lipids in each leaflet in the final configuration to obtain the area per lipid for each leaflet. Both the bilayer thickness and area per lipid obtained for the planar bilayers are consistent with previously reported results [32]. The physical properties of vesicles were summarized in Table S1. The radius at the interface of the inner and outer leaflets (Rcore) was determined based on the mean of the distribution of lipid tail beads (C3A and C3B). Note that Rcore values are close to the average of inner and outer radii.
2.3. Calculation of pressure profiles
The GROMACS-LS v2016.3 program [33,34] was used with default settings to post-process simulation trajectories (with particle positions and velocities saved every 100 ps) to obtain the time-averaged Hardy stress tensor at every grid point on a spatial grid (default grid spacing of 0.1 nm) covering the entire simulation box. The simulation trajectories had to be adjusted to make the center of mass of the bilayer or vesicle remain at the center of the simulation box. The Hardy stress tensor σij (i, j = x, y, z) is a sum of contributions from kinetic (due to particle momentum) and potential (due to inter-particle forces) components [33]. The output files containing stress tensor values at each grid point in the simulation domain from GROMACS-LS were processed by the Pressure-Tools programs for planar bilayers and vesicles [35], which averaged the pressure tensor (pij = −σij) values at grid points with the same z coordinate value (i.e. in the x-y plane) to give pij(z) for planar bilayers. The normal component of the pressure profile of the planar membrane was then given by PN(z) = pzz(z) whereas the lateral component was given by PL(z) = pxx(z) = pyy(z) . For vesicles, the program transformed the pressure tensor to the spherical coordinate system and averaged over grid points within spherical shells of radius r, with coordinate origin at the vesicle center. The vesicle pressure profile components were radial and tangential in this case, given by PR(r) = prr(r) and PT(r) = pθθ (r) = pφφ (r), respectively [35]. The inner pressure is then calculated as the average of the radial and tangential pressure profile values from the location at r = 2.5 nm till the rise of the first tangential pressure profile peak. The outer pressure is calculated similarly from r = 11 to 20 nm for 17 nm vesicles and r = 15 to 20 nm for 24 nm vesicles and confirmed to be close to 1 bar.
2.4. Estimation of the membrane elastic modulus
For the estimation of membrane tension and elastic modulus of planar DMPC and DMPE bilayers, we first stretched each bilayer to different tension levels by specifying a negative value for pressure PL in the bilayer plane [36]. The membrane tension was then calculated from the external pressure applied to the system as σ = LZ(PZ − PL), where LZ and PZ are the size of the simulation box and the pressure in the direction perpendicular to the bilayer plane, respectively. We varied PL from −5 bar to −30 bar while maintaining PZ at 1 bar. The membrane tension values were then plotted against the fractional change in the membrane area and the elastic modulus KA taken as the slope of the linear regression fit to the curve at small area strains [37,38].
To estimate the elastic modulus of vesicle membranes, equilibrated lipid vesicles were swelled by increasing the water density in their inner core. We first removed the largest water core of the equilibrated vesicle that do not overlap with lipid head-groups. A water sphere of the same diameter generated using PackMol [39,40] with a density ranging from 1.1 to 2.25 times higher than the standard density was inserted into the centre of the hollowed vesicle, leading to a reconstituted vesicle with higher inner water density. The reconstituted vesicles were subsequently subjected to 7 equilibration phases, whereby Phases 1 and 2 are energy minimization phases and Phases 3 to 7 are MD phases (1 ns duration each with simulation time-step increasing from 2 to 20 fs). The resultant pressure profile was calculated and the difference between inner and outer pressures (see Section 2.3) were used to determine the membrane tension following either classic Laplace law or the corrected equation. The vesicle elastic modulus KA was then obtained from the slope of the linear regression fit to the plot of membrane tension against vesicle area strain (A − A0)/A0, where A0 is the vesicle area at zero membrane tension obtained by extrapolating the linear regression fit to membrane tension against vesicle area data to zero tension. The corresponding bilayer thickness of each vesicle at tensionless state was similarly obtained for use in the estimation of bending modulus from elastic modulus from tension vs area strain curves.
3. Results and Discussion
3.1. The effect of vesicle curvature on the structural properties of the lipid membrane
The representative equilibrated configurations of our simulated planar bilayers and vesicles are shown in Fig. 1(a). Compared with planar bilayers, the sharp distributions of the locations of PO4 beads suggest suppressed shape fluctuation of lipid vesicles (Fig. S1(a)). We observe that membrane curvature enhances the asymmetry of lipid organization across the bilayer. For both DMPC and DMPE membranes, the ratio of the number of lipids in the outer leaflet to that in the inner leaflet is always larger than 1.0 and consistently increases with membrane curvature (Table S1 and Fig. S1(b)), which is facilitated by lipid flip-flops during equilibration. Both DMPC and DMPE membranes exhibit a decrease in the thickness as the membrane curvature increases (Fig. 1(b)). This curvature-regulated membrane thinning phenomenon is consistent with previous studies using dissipative particle dynamics [41].
FIG. 1.
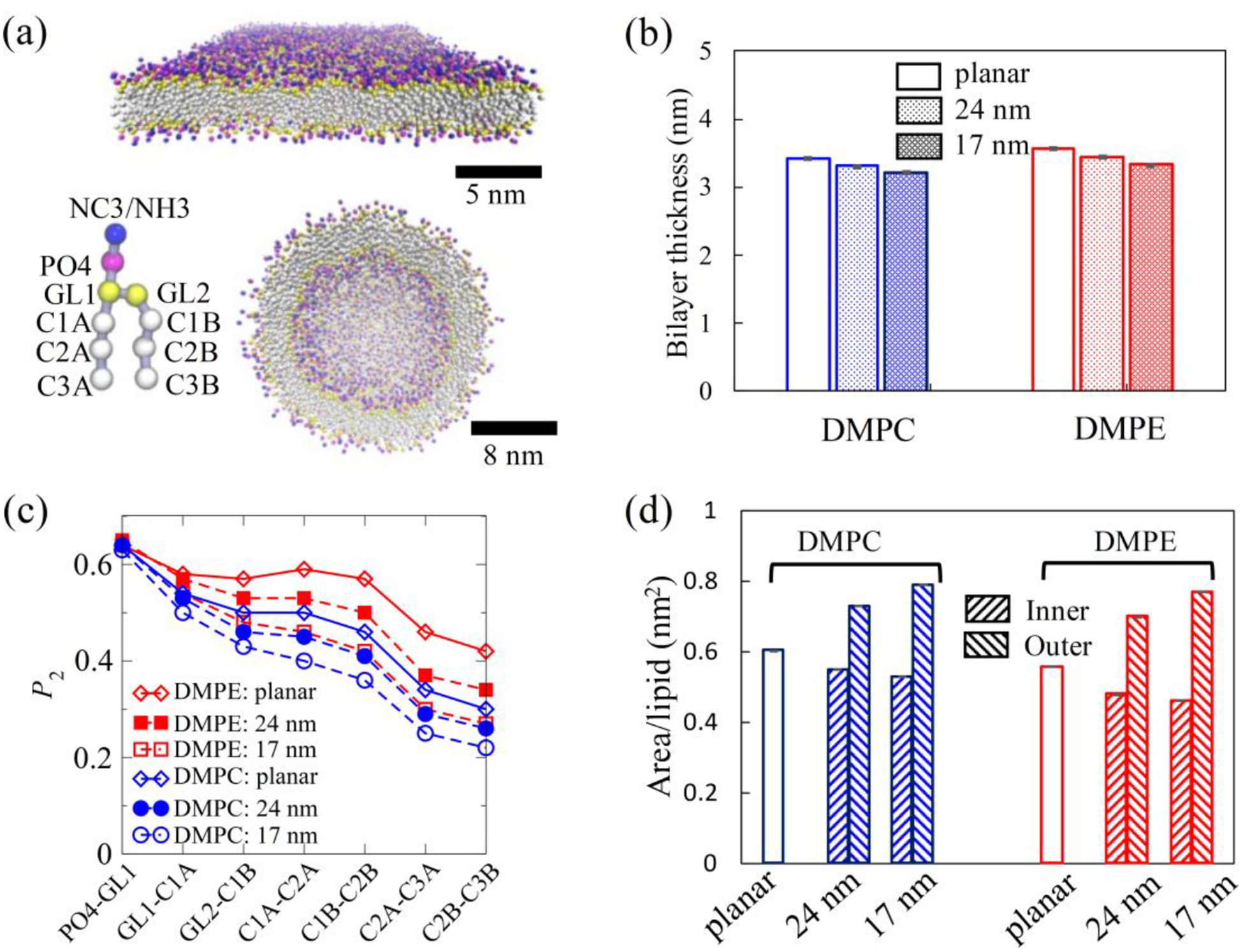
Curvature-regulated structural properties of lipid bilayers. (a) Molecular simulation snapshots of equilibrated planar (top) and vesicular (bottom) MARTINI coarse-grained lipid bilayers. Inset shows particles in each MARTINI lipid, with hydrophilic head group particles being NC3 for DMPC or NH3 for DMPE. (b) Membrane thickness of planar lipid bilayers and lipid vesicles with outer diameters of 24 nm and 17 nm, where membrane thickness is defined based on the locations of head group PO4 particles. (c) Order parameter of the bonds along each lipid molecule averaged over all lipid molecules and over 100 ns of simulation time in planar and vesicle simulations. (d) Area/lipid of planar lipid bilayers, and of inner and outer monolayers in DMPC/DMPE vesicles.
The thinning of the membrane with curvature is directly correlated with the observed decrease in the order parameter of lipid tails (Fig. 1(c)). The order parameter of the bonds along each lipid molecule was calculated according to the following definition: P2 = (3cos2〈θ〉 − 1)/2, where θ is defined as the angle between the bond vector and the bilayer normal for planar bilayers while as the angle between bond vector and radial vector from vesicle center to the middle of the bond for vesicles. The low order parameters suggest that both our DMPC and DMPE membranes are in the fluid phase at 310 K (Fig. 1(c) and Fig. S2(a–b)). At a lower temperature of 282 K, the planar DMPE membrane has much higher order parameters, implying that the lipids are in the gel phase (Fig. S2(a)). Both planar DMPE and DMPC membranes are in the gel phase at the even lower temperature of 270 K. In contrast, the 17 nm vesicles show no significant increase in the lipid order as the temperature is lowered, suggesting that they remain in the fluid phase. The suppression effect on the global gel formation by the strong curvature agrees with a prior simulation study whereby a coarse-grained model of a 20 nm DPPC vesicle at 265 K was found to remain in the fluid phase over hundreds of nanoseconds whereas its planar counterpart entered the gel phase [42].
Curvature-induced reduction in the lipid order parameter is observed in both inner and outer leaflets (Fig. S2(c–d)). However, in contrast to DMPE vesicles whose inner leaflets are more ordered than their outer leaflets, an opposite trend is observed in DMPC vesicles of the same size. The order parameter data suggest that DMPE lipids prefer the inner leaflet of vesicles due to their smaller and more attractive head-groups, whereas the reverse is true for DMPC. As suggested by the difference in the average area occupied by each lipid (Fig. 1(d)), the lipid packing of the inner leaflet becomes tighter as the curvature increases, while an opposite trend is observed for the outer leaflet, indicating that the outer and inner leaflets are in different stress states. In general, DMPE vesicles are relatively thicker, more ordered and packed more tightly than their DMPC counterparts due to the more attractive interactions among the DMPE head groups.
3.2. The effect of vesicle curvature on the stress state of the lipid membrane
For planar bilayers, the in-plane pressure profiles show deep, but symmetric negative peaks from both the inner and outer monolayers which represent the localized membrane stress due to the attractive interactions between lipid head-group particles (Fig. 2(a) and (d)). Similar pressure profiles have been observed in previous studies [33,35]. The large positive region between the negative peaks arises from the lipid tail repulsion within the hydrophobic core of the bilayer. However, the pressure normal to the bilayer plane does not show any significant spatial variation.
FIG. 2.
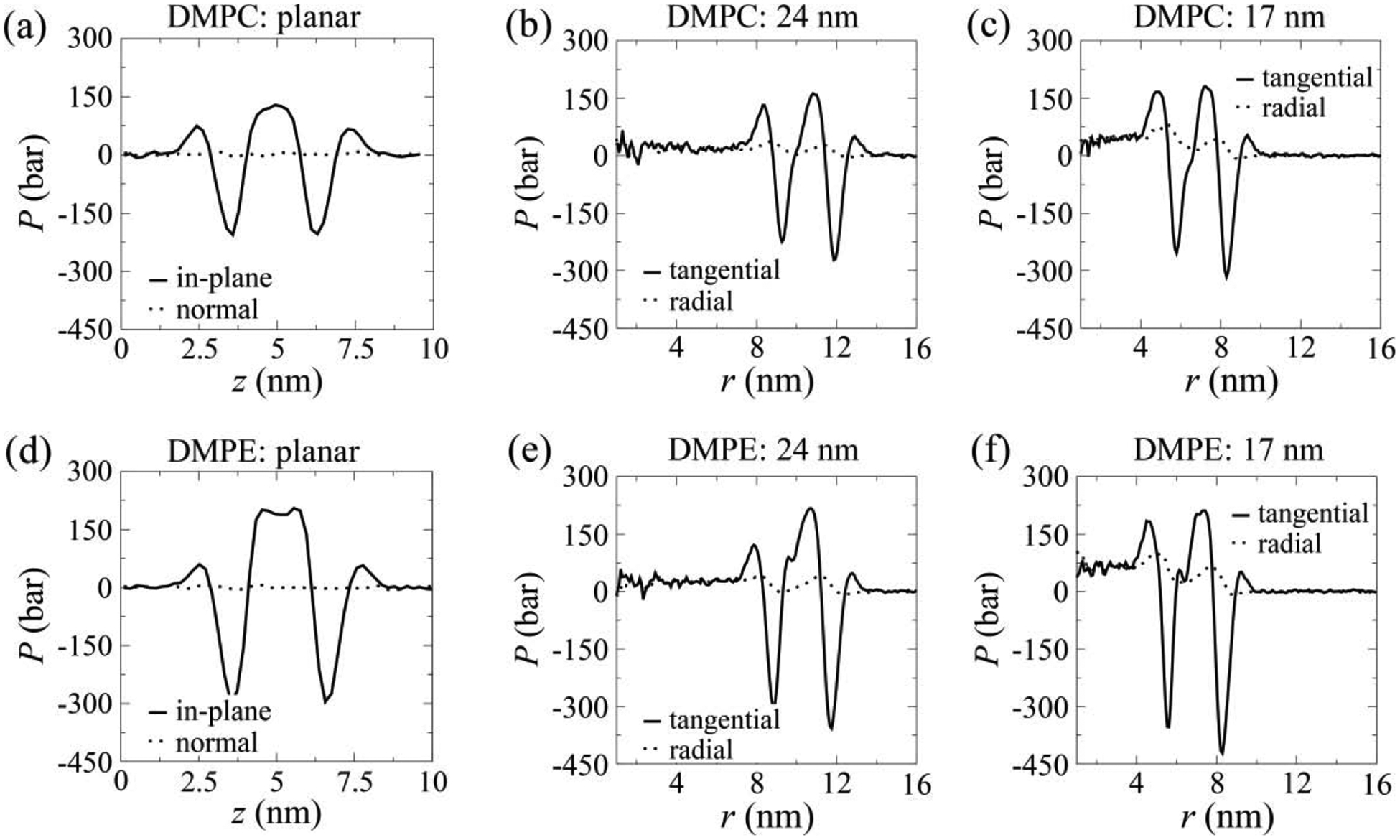
Pressure profiles of equilibrated DMPC (a–c) and DMPE (d–f) bilayers.
In contrast to planar bilayers, the enhanced physical asymmetry by the membrane curvature of vesicles leads to an asymmetric pressure profile across the lipid bilayer. In the vesicles, both the tangential and radial pressure profiles exhibit significant asymmetries between the inner and outer monolayers. First, the tangential pressure profiles of both DMPC (Fig. 2(b–c)) and DMPE (Fig. 2(e–f)) vesicles feature a relatively deeper peak in the outer leaflet than that in the inner one, indicating that the outer membrane leaflet is under a higher membrane tensile stress. The peaks become progressively deeper than that in planar bilayer as the vesicle size decreases, suggesting that membrane stress increases with membrane curvature. The negative pressure peaks of DMPE membranes are always deeper than the DMPC ones in agreement with the stronger attractive interactions among DMPE head-group particles. Second, vesicles show unequal peak tangential pressures between the inner and outer vesicle leaflets, with the inner pressure being relatively higher. Our large DMPC vesicle has an inner pressure of 18 bar, and the small DMPC vesicle has a higher pressure of 47 bar. Corresponding values for large and small DMPE vesicles are 26 bar and 65 bar, respectively. Given that the pressure outside vesicles is at 1 bar, the nanoscale vesicles are sustaining a substantially large pressure difference across their lipid bilayers. To verify that the large pressure difference is not caused by possible insufficient relaxation during equilibration, we have formed a DMPC vesicle by self-assembly (see SM for simulation details). The self-assembled vesicle shows a similar pressure profile as the constructed ones (Fig. S3).
For micron-sized vesicles, we can imaginarily cut a spherical vesicle at the equator and the membrane tension (σ) can be readily obtained based on the force balance between the forces stemming from the surface stresses and the force from the pressure difference inside and outside the vesicle (ΔP = Pin − Pout) [43]:
| (1) |
where the first term inside the brackets is the spontaneous tension, and R, κ and H0 are the radius of the curvature at the midplane of the lipid bilayer, the bending modulus and the spontaneous mean curvature of the vesicle membrane, respectively. Although a non-zero spontaneous curvature presents due to the asymmetric number of lipids in the inner and outer leaflets, the spontaneous tension is expected to make a negligible contribution because of the fact that lipid exchange via flip-flops between the two leaflets has been allowed to release the spontaneous tension during the equilibration phases. We confirm that the curvature of equilibrated vesicles is quite close to the spontaneous curvature, resulting in a minor spontaneous tension (< 1 mN/m) that contributes < 5% compared to the membrane tension (see SM and Table S3). Note that the contributions by the spontaneous tension were estimated using the bending stiffness of planar lipid bilayers. Since the membranes of lipid vesicles are relatively softer than planar bilayers (see more details in Section 3.3), the actual contributions by the spontaneous tension terms are expected to be even smaller. Hence, Eqn. (1) reduces to the well-known Laplace’s law after omitting the spontaneous tension term.
However, the assumption that the membrane thickness is negligible compared to the vesicle size in the Laplace’s law is clearly violated in the case of nano-vesicles. For example, the small DMPC vesicle in our study has a membrane thickness of ~3 nm and an outer radius of ~8.5 nm. To correct the finite-membrane thickness effect, we consider that the inner and outer pressures act on the inner and outer surfaces of the vesicle, respectively, and the corrected force balance leads to a corrected expression for membrane tension as (see SM for more details; Fig. S4):
| (2) |
where Rin and Rout are the inner and outer radii of the vesicle, respectively. Note that we have followed the general practice to treat the midplane of the lipid bilayer as the reference surface within the membrane. Equation (2) reduces to the Laplace’s law when the membrane is treated as a zero-thickness film, i.e., Rin = Rout = R. As shown in Fig. 3, the membrane tension obtained with our correction using Eqn. (2) is lower than that from the Laplace’s law by Eqn. (1), for both 24 nm diameter and 17 nm diameter DMPC or DMPE vesicles. Nevertheless, both methods show that the small vesicle’s membrane is under a higher tension than the large ones with DMPE membrane featuring a higher tension than their DMPC counterparts. Since membrane tension closely regulates both the configuration and lateral mobility of membrane-embedded proteins, such as large mechanosensitive channels [44] and voltage-gated potassium channel KvAP [45,46], the dependence of membrane tension on the vesicle size may serve as a mechanism for maintaining vesicle homeostasis.
FIG. 3.
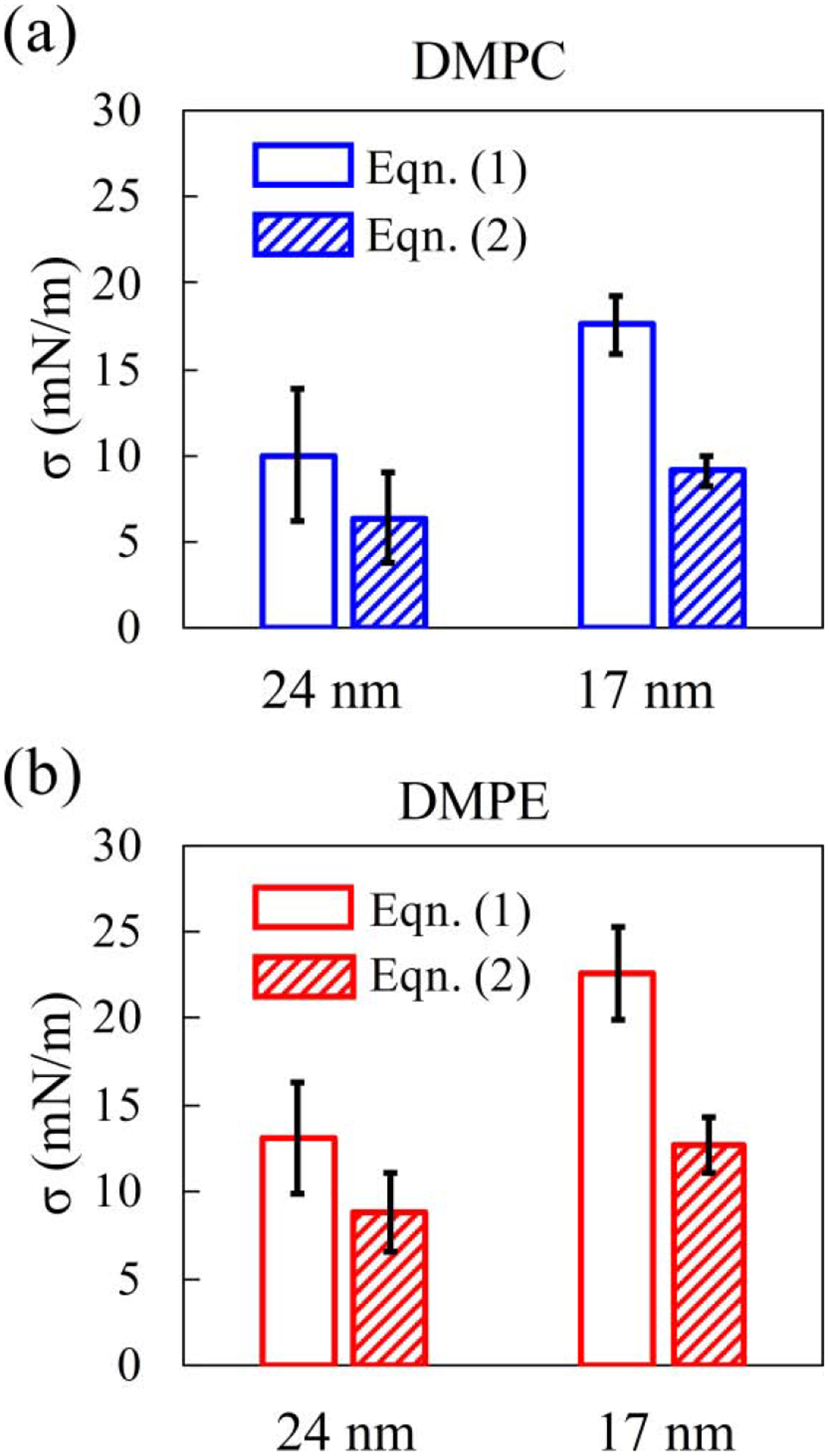
Membrane tension of equilibrated DMPC (a) and DMPE (b) vesicles obtained based on pressure difference across the vesicle membranes using Eqns. (1) and (2) in the main text.
3.3. The effect of vesicle curvature on the mechanical properties of the lipid membrane
To illustrate how the curvature-regulated lipid organization affects their mechanical properties, we calculate the elastic and bending moduli for both planar lipid bilayer and closed vesicles. The elastic moduli (KA) of planar bilayers were estimated by stretching the bilayer to different area strains and KA is determined as the slope of the linear regression line to the membrane tension vs area strain curves at low strain levels (Fig. S5). Our approach to obtaining KA potentially avoids the issue with system-size dependence observed with the projected area fluctuation method [47,48]. The KA value of our coarse-grained DMPC bilayer (248 mN/m) is close to the values obtained from both simulations of a near-atomistic bilayer model [48] and experiments based on micropipette aspiration of giant vesicles [38].
We then obtain the elastic moduli of vesicle membranes by virtually swelling our nano-vesicles to various extents to obtain membrane tension vs area strain curves (resembling osmotic swelling [37]). Swelling of equilibrated nano-vesicles is induced by replacing their inner cores with water molecules packed at higher densities, followed by equilibration simulations (see Methods for more details; Fig. S6). The vesicle size increases during induced swelling and stabilizes after equilibration. The pressure profile of each swelled vesicle is computed and the pressure difference between the inside and outside of the vesicle is extracted to calculate the corresponding membrane tension. The tangential pressure profile peaks become increasingly more negative with the swelling level, implying an increase in membrane tensile stresses due to swelling (Figs. S7 and S8).
The pressure difference across the bilayer membrane increases with the swelling level, which translates to an increase of the membrane tension. The membrane tension increases linearly with the vesicle area under low swelling conditions for both stress values from Eqn. (1) and from Eqn. (2), and nonlinear correlation is observed when the vesicle is swelled excessively (Fig. S9). However, the membrane tension with correction is always lower than that without correction. In addition, the membrane thickness decreases with increased swelling (Fig. S10). The same trend has previously been reported by Lin et al. using a different coarse-grained model [49]. The elastic modulus KA is extracted by fitting the linear region in the stress vs area strain curves (Fig. S11) [37,38]:
| (3) |
where σeqm and Aeqm are the membrane tension and surface area of swelled vesicles after equilibration, respectively, and A0 is the surface area of the same vesicle at zero membrane tension state. The A0 value is obtained for each vesicle by extrapolating the linear regression lines in the area-membrane tension plot to zero tension (Fig. S9). The membrane elastic modulus may also be extracted from the force-indentation curves for giant unilamellar vesicles (GUVs) as detailed by Schäfer et al. [50], however, theoretical analysis carried out by Tang et al. indicates that such a process is not trivial for pressurized elastic fluid nano-vesicles [51]. The membrane bending moduli of our vesicles are estimated from the elastic moduli using KB = KA(h0 − 1)2/24 based on the polymer brush model [38], where h0 is the bilayer thickness of the membrane at zero tension. We have assumed that the relation between the two moduli which was derived for GUVs (15–30 μm in diameter) is valid for our nanoscale vesicles. The h0 values are obtained by extrapolating the thickness-membrane tension plots for all the vesicles (Fig. S10). Our predicted KB value of 14.1 kBT for DMPC bilayer is close to the experimental value of 13.4 kBT [38]. Although the membrane bending stiffness may also be determined by analyzing the shape fluctuation of micron-sized GUVs [52], the largely suppressed fluctuation makes this approach less suitable for nano-vesicles.
As shown in Fig. 4, both the elastic and bending moduli obtained using the Laplace’s law (Eqn. (1)) reduce with the increase in membrane curvature. Our correction to the Laplace’s law leads to even larger reductions, indicating a strong curvature-regulated membrane softening effect. We have performed a simple sensitivity analysis by placing the reference surface used in the calculation of the membrane tension at different locations within the membrane for the DMPC vesicles. As we move the reference surface from the inner surface of the vesicle to the outer surface, the estimated elastic moduli obtained using Laplace’s law shows opposing trends; but with Eqn. (2), the moduli are always smaller for the smaller vesicle (Table S4). In other words, the curvature-regulated softening effect is observed regardless the location of the reference surface with Eqn. (2). This mechanical softening effect is consistent with the lowering of lipid tail ordering as the curvature increases. A similar decease in lipid order parameter with membrane curvature has been reported previously by Lin et al. [41]. However, in their study, the elastic moduli of lipid vesicles were found to increase with the membrane curvature, which is in stark contrast to our observations, despite similar observations of thinner and more disordered membranes for smaller vesicles. In their attempt to consider the finite-membrane thickness effect on membrane tension, the two leaflets were treated as two zero-thickness surfaces and the interfacial tensions in the inner and outer monolayers were assumed to be equal. However, as we have shown in Fig. 2, the outer monolayer of vesicles always exhibits a deeper in-plane pressure peak than the inner one, which suggests a higher interfacial tension in the outer monolayer. Symmetric pressure profiles are observed only for planar bilayers (Fig. 2(a) and (d)). Such a fundamental difference in pressure profiles between vesicles and planar bilayers has been shown previously [35]. Hence, the validity of the assumptions made by Lin et al. is questionable for nano-vesicles. Curvature softening of gel-phase lipid membranes has been previously identified by comparing the shape of buckled membranes with that of their fluid-phase counterparts [53]. However, it is fundamentally different from the mechanical softening effect presented in this work for the following reasons. First, both our DMPC and DMPE membranes are in liquid phase as suggested by their low order parameters (Fig. 1(c)). In addition, the membrane curvature of lipid vesicles is caused by the asymmetry in lipid number between the two leaflets facilitated by lipid flip-flops, while the curved membrane structure in the work by Diggins IV et al. was induced by mechanical compression.
FIG. 4.
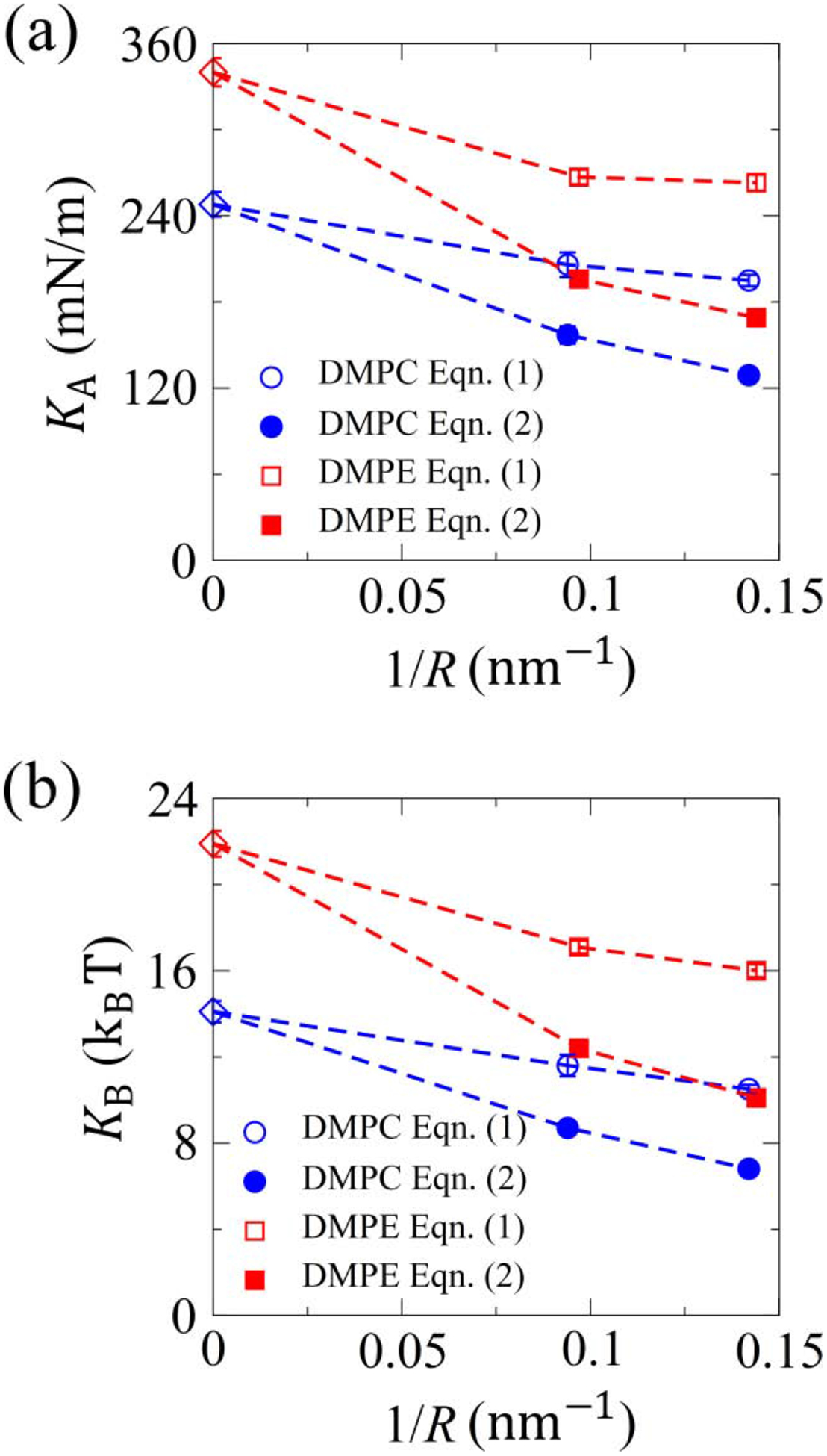
Curvature-regulated mechanical properties of lipid bilayers. (a) Variation of elastic modulus (KA) with the bilayer curvature. (b) Variation of bending modulus (KB) with the bilayer curvature. The data for planar bilayer (zero curvature) are shown as reference using diamond symbols with DMPC in blue and DMPE in red.
4. Conclusions
In conclusion, by performing systematic coarse-grained MD simulations of planar bilayer membranes and nano-vesicles, our results suggest that the lipid membrane thins and softens with an increase in curvature. This curvature-regulated membrane softening effect is fundamentally different from the scheme that controls the softening or stiffening of other common nanostructures (e.g., nanowires [54–57], nanofilms [58–61], and nanodroplets [62]). The novel mechanical properties of solid nanomaterials typically result from the difference in stress condition between the bulk and the free surface [63]. In contrast, the softening of lipid vesicles results from the change in the lipid tail ordering and membrane thickness. Our study demonstrates that this curvature-regulated membrane softening effect counteracts the stiffening schemes established previously [23] and renders a more complete physical framework for understanding the physico-mechanical properties of nanoscale lipid vesicles (see SM and Fig. S12). Considering that vesicle stiffness plays an important role in regulating their interaction with biological systems, we expect that taking this membrane softening effect into consideration will allow more faithful prediction to understand the biological function of sEVs and to harness the design of nano-vesicle-based therapeutics.
Supplementary Material
Acknowledgements
Y.S., K.J.H. and C.H. acknowledge the financial support by the NIH Eunice Kennedy Shriver National Institute of Child Health and Human Development (grant R01HD086325). K.J.H. would like to acknowledge financial support from Nanyang Technological University (start-up grant M4082428.050). C.H. would also like to acknowledge financial support from Nanyang Technological University (start-up grant M4082352.050) and the Ministry of Education, Singapore, under its Academic Research Fund Tier 1 (M4012229.050). The computational work for this article was fully performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Supplemental Material
The SM contains additional details of the methods and analyses performed.
References
- [1].Théry C, Witwer KW, Aikawa E, Alcaraz MJ, Anderson JD, Andriantsitohaina R, Antoniou A, Arab T, Archer F, Atkin-Smith GK, Ayre DC, Bach JM, Bachurski D, Baharvand H, Balaj L, Baldacchino S, Bauer NN, Baxter AA, Bebawy M, Beckham C, Bedina Zavec A, Benmoussa A, Berardi AC, Bergese P, Bielska E, Blenkiron C, Bobis-Wozowicz S, Boilard E, Boireau W, Bongiovanni A, Borràs FE, Bosch S, Boulanger CM, Breakefield X, Breglio AM, Brennan M, Brigstock DR, Brisson A, Broekman MLD, Bromberg JF, Bryl-Górecka P, Buch S, Buck AH, Burger D, Busatto S, Buschmann D, Bussolati B, Buzás EI, Byrd JB, Camussi G, Carter DRF, Caruso S, Chamley LW, Chang YT, Chaudhuri AD, Chen C, Chen S, Cheng L, Chin AR, Clayton A, Clerici SP, Cocks A, Cocucci E, Coffey RJ, Cordeiro-da-Silva A, Couch Y, Coumans FAW, Coyle B, Crescitelli R, Criado MF, D’Souza-Schorey C, Das S, de Candia P, De Santana EF, De Wever O, del Portillo HA, Demaret T, Deville S, Devitt A, Dhondt B, Di Vizio D, Dieterich LC, Dolo V, Dominguez Rubio AP, Dominici M, Dourado MR, Driedonks TAP, Duarte FV, Duncan HM, Eichenberger RM, Ekström K, EL Andaloussi S, Elie-Caille C, Erdbrügger U, Falcón-Pérez JM, Fatima F, Fish JE, Flores-Bellver M, Försönits A, Frelet-Barrand A, Fricke F, Fuhrmann G, Gabrielsson S, Gámez-Valero A, Gardiner C, Gärtner K, Gaudin R, Gho YS, Giebel B, Gilbert C, Gimona M, Giusti I, Goberdhan DCI, Görgens A, Gorski SM, Greening DW, Gross JC, Gualerzi A, Gupta GN, Gustafson D, Handberg A, Haraszti RA, Harrison P, Hegyesi H, Hendrix A, Hill AF, Hochberg FH, Hoffmann KF, Holder B, Holthofer H, Hosseinkhani B, Hu G, Huang Y, Huber V, Hunt S, Ibrahim AGE, Ikezu T, Inal JM, Isin M, Ivanova A, Jackson HK, Jacobsen S, Jay SM, Jayachandran M, Jenster G, Jiang L, Johnson SM, Jones JC, Jong A, Jovanovic-Talisman T, Jung S, Kalluri R, ichi Kano S, Kaur S, Kawamura Y, Keller ET, Khamari D, Khomyakova E, Khvorova A, Kierulf P, Kim KP, Kislinger T, Klingeborn M, Klinke DJ, Kornek M, Kosanović MM, Kovács ÁF, Krämer-Albers EM, Krasemann S, Krause M, Kurochkin IV, Kusuma GD, Kuypers S, Laitinen S, Langevin SM, Languino LR, Lannigan J, Lässer C, Laurent LC, Lavieu G, Lázaro-Ibáñez E, Le Lay S, Lee MS, Lee YXF, Lemos DS, Lenassi M, Leszczynska A, Li ITS, Liao K, Libregts SF, Ligeti E, Lim R, Lim SK, Linē A, Linnemannstöns K, Llorente A, Lombard CA, Lorenowicz MJ, Lörincz ÁM, Lötvall J, Lovett J, Lowry MC, Loyer X, Lu Q, Lukomska B, Lunavat TR, Maas SLN, Malhi H, Marcilla A, Mariani J, Mariscal J, Martens-Uzunova ES, Martin-Jaular L, Martinez MC, Martins VR, Mathieu M, Mathivanan S, Maugeri M, McGinnis LK, McVey MJ, Meckes DG, Meehan KL, Mertens I, Minciacchi VR, Möller A, Møller Jørgensen M, Morales-Kastresana A, Morhayim J, Mullier F, Muraca M, Musante L, Mussack V, Muth DC, Myburgh KH, Najrana T, Nawaz M, Nazarenko I, Nejsum P, Neri C, Neri T, Nieuwland R, Nimrichter L, Nolan JP, Nolte-’t Hoen ENM, Noren Hooten N, O’Driscoll L, O’Grady T, O’Loghlen A, Ochiya T, Olivier M, Ortiz A, Ortiz LA, Osteikoetxea X, Ostegaard O, Ostrowski M, Park J, Pegtel DM, Peinado H, Perut F, Pfaffl MW, Phinney DG, Pieters BCH, Pink RC, Pisetsky DS, Pogge von Strandmann E, Polakovicova I, Poon IKH, Powell BH, Prada I, Pulliam L, Quesenberry P, Radeghieri A, Raffai RL, Raimondo S, Rak J, Ramirez MI, Raposo G, Rayyan MS, Regev-Rudzki N, Ricklefs FL, Robbins PD, Roberts DD, Rodrigues SC, Rohde E, Rome S, Rouschop KMA, Rughetti A, Russell AE, Saá P, Sahoo S, Salas-Huenuleo E, Sánchez C, Saugstad JA, Saul MJ, Schiffelers RM, Schneider R, Schøyen TH, Scott A, Shahaj E, Sharma S, Shatnyeva O, Shekari F, Shelke GV, Shetty AK, Shiba K, Siljander PRM, Silva AM, Skowronek A, Snyder OL, Soares RP, Sódar BW, Soekmadji C, Sotillo J, Stahl PD, Stoorvogel W, Stott SL, Strasser EF, Swift S, Tahara H, Tewari M, Timms K, Tiwari S, Tixeira R, Tkach M, Toh WS, Tomasini R, Torrecilhas AC, Tosar JP, Toxavidis V, Urbanelli L, Vader P, van Balkom BWM, van der Grein SG, Van Deun J, van Herwijnen MJC, Van Keuren-Jensen K, van Niel G, van Royen ME, van Wijnen AJ, Vasconcelos MH, Vechetti IJ, Veit TD, Vella LJ, Velot É, Verweij FJ, Vestad B, Viñas JL, Visnovitz T, Vukman KV, Wahlgren J, Watson DC, Wauben MHM, Weaver A, Webber JP, Weber V, Wehman AM, Weiss DJ, Welsh JA, Wendt S, Wheelock AM, Wiener Z, Witte L, Wolfram J, Xagorari A, Xander P, Xu J, Yan X, Yáñez-Mó M, Yin H, Yuana Y, Zappulli V, Zarubova J, Žėkas V, ye Zhang J, Zhao Z, Zheng L, Zheutlin AR, Zickler AM, Zimmermann P, Zivkovic AM, Zocco D, Zuba-Surma EK, Minimal information for studies of extracellular vesicles 2018 (MISEV2018): a position statement of the International Society for Extracellular Vesicles and update of the MISEV2014 guidelines, J. Extracell. Vesicles 7 (2018) 1535750 10.1080/20013078.2018.1535750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Margolis L, Sadovsky Y, The biology of extracellular vesicles: the known unknowns, PLoS Biol. 17 (2019) 1–12. 10.1371/journal.pbio.3000363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Simons M, Raposo G, Exosomes - vesicular carriers for intercellular communication, Curr. Opin. Cell Biol 21 (2009) 575–581. 10.1016/j.ceb.2009.03.007. [DOI] [PubMed] [Google Scholar]
- [4].Raposo G, Stoorvogel W, Extracellular vesicles: exosomes, microvesicles, and friends, J. Cell Biol 200 (2013) 373–383. 10.1083/jcb.201211138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Delorme-Axford E, Donker RB, Mouillet J-F, Chu T, Bayer A, Ouyang Y, Wang T, Stolz DB, Sarkar SN, Morelli AE, Sadovsky Y, Coyne CB, Human placental trophoblasts confer viral resistance to recipient cells., Proc. Natl. Acad. Sci. U. S. A 110 (2013) 12048–12053. 10.1073/pnas.1304718110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Rak J, Microparticles in cancer, Semin. Thromb. Hemost 36 (2010) 888–906. 10.1055/s-0030-1267043. [DOI] [PubMed] [Google Scholar]
- [7].Mallegol J, Van Niel G, Lebreton C, Lepelletier Y, Candalh C, Dugave C, Heath JK, Raposo G, Cerf-Bensussan N, Heyman M, T84-Intestinal epithelial exosomes bear MHC class II/peptide complexes potentiating antigen presentation by dendritic Cells, Gastroenterology. 132 (2007) 1866–1876. 10.1053/j.gastro.2007.02.043. [DOI] [PubMed] [Google Scholar]
- [8].Ouyang Y, Bayer A, Chu T, Tyurin V, Kagan V, Morelli AE, Coyne CB, Sadovsky Y, Isolation of human trophoblastic extracellular vesicles and characterization of their cargo and antiviral activity, Placenta. 47 (2016) 86–95. 10.1016/j.placenta.2016.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Batrakova EV, Kim MS, Using exosomes, naturally-equipped nanocarriers, for drug delivery, J. Control. Release 219 (2015) 396–405. 10.1016/j.jconrel.2015.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Luan X, Sansanaphongpricha K, Myers I, Chen H, Yuan H, Sun D, Engineering exosomes as refined biological nanoplatforms for drug delivery, Acta Pharmacol. Sin 38 (2017) 754–763. 10.1038/aps.2017.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Díaz MR, Vivas-Mejia PE, Nanoparticles as drug delivery systems in cancer medicine: emphasis on RNAi-containing nanoliposomes, Pharmaceuticals. 6 (2013) 1361–1380. 10.3390/ph6111361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhang S, Li J, Lykotrafitis G, Bao G, Suresh S, Size-dependent endocytosis of nanoparticles, Adv. Mater 21 (2009) 419–424. 10.1002/adma.200801393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Andar AU, Hood RR, Vreeland WN, Devoe DL, Swaan PW, Microfluidic preparation of liposomes to determine particle size influence on cellular uptake mechanisms, Pharm. Res 31 (2014) 401–413. 10.1007/s11095-013-1171-8. [DOI] [PubMed] [Google Scholar]
- [14].Takechi-Haraya Y, Goda Y, Sakai-Kato K, Control of liposomal penetration into three-dimensional multicellular tumor spheroids by modulating liposomal membrane rigidity, Mol. Pharm 14 (2017) 2158–2165. 10.1021/acs.molpharmaceut.7b00051. [DOI] [PubMed] [Google Scholar]
- [15].Yi X, Shi X, Gao H, Cellular uptake of elastic nanoparticles, Phys. Rev. Lett 107 (2011) 1–5. 10.1103/PhysRevLett.107.098101. [DOI] [PubMed] [Google Scholar]
- [16].Hui Y, Yi X, Hou F, Wibowo D, Zhang F, Zhao D, Gao H, Zhao C, Role of nanoparticle mechanical properties in cancer drug delivery, ACS Nano. 13 (2019) 7410–7424. 10.1021/acsnano.9b03924. [DOI] [PubMed] [Google Scholar]
- [17].Canham PB, The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell, J. Theor. Biol 26 (1970) 61–81. 10.1016/S0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- [18].Helfrich W, Elastic properties of lipid bilayers: theory and possible experiments, Zeitschrift Fur Naturforsch. - Sect. C J. Biosci 28 (1973) 693–703. 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- [19].Seifert U, Configurations of fluid membranes and vesicles, Adv. Phys 46 (1997) 13–137. 10.1080/00018739700101488. [DOI] [Google Scholar]
- [20].Helfrich W, Size distributions of vesicles: the role of the effective rigidity of membranes, J. Phys 47 (1986) 321–329. 10.1051/jphys:01986004702032100. [DOI] [Google Scholar]
- [21].Morse DC, Milner ST, Fluctuations and phase behavior of fluid membrane vesicles, Europhys. Lett 26 (1994) 565–570. 10.1209/0295-5075/26/8/002. [DOI] [Google Scholar]
- [22].V Manyuhina O, Shklyarevskiy IO, Jonkheijm P, Christianen PCM, Fasolino A, Katsnelson MI, Schenning APHJ, Meijer EW, Henze O, Kilbinger AFM, Feast WJ, Maan JC, Anharmonic magnetic deformation of self-assembled molecular nanocapsules, Phys. Rev. Lett 98 (2007) 146101 10.1103/PhysRevLett.98.146101. [DOI] [PubMed] [Google Scholar]
- [23].Ahmadpoor F, Sharma P, Thermal fluctuations of vesicles and nonlinear curvature elasticity -- implications for size-dependent renormalized bending rigidity and vesicle size distribution, Soft Matter. 12 (2016) 2523–2536. 10.1039/c5sm02769a. [DOI] [PubMed] [Google Scholar]
- [24].Huang C, Quinn D, Sadovsky Y, Suresh S, Hsia KJ, Formation and size distribution of self-assembled vesicles, Proc. Natl. Acad. Sci 114 (2017) 2910–2915. 10.1073/pnas.1702065114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Marrink SJ, de Vries AH, Mark AE, Coarse grained model for semiquantitative lipid simulations, J. Phys. Chem. B 108 (2004) 750–760. 10.1021/jp036508g. [DOI] [Google Scholar]
- [26].Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH., The MARTINI forcefield: coarse grained model for biomolecular simulations, J. Phys. Chem. B 111 (2007) 7812–7824. [DOI] [PubMed] [Google Scholar]
- [27].Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX. 1 (2015) 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- [28].Páll S, Abraham MJ, Kutzner C, Hess B, Lindahl E, Tackling exascale software challenges in molecular dynamics simulations with GROMACS, in: Markidis S, Laure E (Eds.), Solving Softw. Challenges Exascale, Springer, Cham, 2015: pp. 3–27. 10.1007/978-3-319-15976-8_1. [DOI] [Google Scholar]
- [29].Pronk S, Páll S, Schulz R, Larsson P, Bjelkmar P, Apostolov R, Shirts MR, Smith JC, Kasson PM, van der Spoel D, Hess B, Lindahl E, GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit, Bioinformatics. 29 (2013) 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Qi Y, Ingo HI, Cheng X, Lee J, Marrink SJ, Im W, CHARMM-GUI Martini Maker for coarse-grained simulations with the Martini force field, J. Chem. Theory Comput 11 (2015) 4486–4494. 10.1021/acs.jctc.5b00513. [DOI] [PubMed] [Google Scholar]
- [31].Jo S, Kim T, Iyer VG, Im W, CHARMM-GUI: a web-based graphical user Interface for CHARMM, J. Comput. Chem 29 (2008) 1859–1865. 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- [32].Arnarez C, Uusitalo JJ, Masman MF, Ingólfsson HI, De Jong DH, Melo MN, Periole X, De Vries AH, Marrink SJ, Dry martini, a coarse-grained force field for lipid membrane simulations with implicit solvent, J. Chem. Theory Comput 11 (2015) 260–275. 10.1021/ct500477k. [DOI] [PubMed] [Google Scholar]
- [33].Vanegas JM, Torres-Sánchez A, Arroyo M, Importance of force decomposition for local stress calculations in biomembrane molecular simulations, J. Chem. Theory Comput 10 (2014) 691–702. 10.1021/ct4008926. [DOI] [PubMed] [Google Scholar]
- [34].Torres-Sánchez A, Vanegas JM, Arroyo M, Examining the mechanical equilibrium of microscopic stresses in molecular simulations, Phys. Rev. Lett 114 (2015) 258102 10.1103/PhysRevLett.114.258102. [DOI] [PubMed] [Google Scholar]
- [35].Ollila OHS, Risselada HJ, Louhivuori M, Lindahl E, Vattulainen I, Marrink SJ, 3D Pressure field in lipid membranes and membrane-protein complexes, Phys. Rev. Lett 102 (2009) 1–4. 10.1103/PhysRevLett.102.078101. [DOI] [PubMed] [Google Scholar]
- [36].Leontiadou H, Mark AE, Marrink SJ, Molecular dynamics simulations of hydrophilic pores in lipid bilayers, Biophys. J 86 (2004) 2156–2164. 10.1016/S0006-3495(04)74275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Ul S, Shibly A, Ghatak C, Abu M, Karal S, Experimental Estimation of Membrane Tension Induced by Osmotic Pressure, Biophys. J 111 (2016) 2190–2201. 10.1016/j.bpj.2016.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Rawicz W, Olbrich KC, Mcintosh T, Needham D, Evans E, Effect of chain length and unsaturation on elasticity of lipid bilayers, Biophys. J 79 (2000) 328–339. 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Martinez L, Andrade R, Birgin EG, Martinez J, Packmol: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem 30 (2009) 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- [40].Martinez J, Martinez L, Packing optimization for the automated generation of complex system’s initial configurations for molecular dynamics and docking, J. Comput. Chem 24 (2003) 819–825. 10.1002/jcc.10216. [DOI] [PubMed] [Google Scholar]
- [41].Lin CM, Li CS, Sheng YJ, Wu DT, Tsao HK, Size-dependent properties of small unilamellar vesicles formed by model lipids, Langmuir. 28 (2012) 689–700. 10.1021/la203755v. [DOI] [PubMed] [Google Scholar]
- [42].Marrink SJ, Risselada J, Mark AE, Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model, Chem. Phys. Lipids 135 (2005) 223–244. 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- [43].Deserno M, Fluid lipid membranes: from differential geometry to curvature stresses, Chem. Phys. Lipids 185 (2015) 11–45. 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- [44].Sukharev S, Betanzos M, Chiang C-S, Guy HR, The gating mechanism of the large mechanosensitive channel MscL, Nature. 409 (2001) 720–724. 10.1038/35055559. [DOI] [PubMed] [Google Scholar]
- [45].Quemeneur F, Sigurdsson JK, Renner M, Atzberger PJ, Bassereau P, Lacoste D, Shape matters in protein mobility within membranes, Proc. Natl. Acad. Sci. U. S. A 111 (2014) 5083–5087. 10.1073/pnas.1321054111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Morris RG, Turner MS, Mobility measurements probe conformational changes in membrane proteins due to tension, Phys. Rev. Lett 115 (2015) 1–5. 10.1103/PhysRevLett.115.198101. [DOI] [PubMed] [Google Scholar]
- [47].Doktorova M, LeVine MV, Khelashvili G, Weinstein H, A new computational method for membrane compressibility: bilayer mechanical thickness revisited, Biophys. J 116 (2019) 487–502. 10.1016/j.bpj.2018.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Waheed Q, Edholm O, Undulation contributions to the area compressibility in lipid bilayer simulations, Biophys. J 97 (2009) 2754–2760. 10.1016/j.bpj.2009.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Lin CM, Wu DT, Tsao HK, Sheng YJ, Membrane properties of swollen vesicles: growth, rupture, and fusion, Soft Matter. 8 (2012) 6139–6150. 10.1039/c2sm25518a. [DOI] [Google Scholar]
- [50].Schäfer E, Vache M, Kliesch TT, Janshoff A, Mechanical response of adherent giant liposomes to indentation with a conical AFM-tip, Soft Matter. 11 (2015) 4487–4495. 10.1039/c5sm00191a. [DOI] [PubMed] [Google Scholar]
- [51].Tang X, Shi X, Gan Y, Yi X, Nanomechanical characterization of pressurized elastic fluid nanovesicles using indentation analysis, Extrem. Mech. Lett 34 (2020) 100613 10.1016/j.eml.2019.100613. [DOI] [Google Scholar]
- [52].Faizi HA, Reeves CJ, Georgiev VN, Vlahovska PM, Dimova R, Fluctuation spectroscopy of giant unilamellar vesicles using confocal and phase contrast microscopy, Soft Matter. 16 (2020) 8996–9001. 10.1039/d0sm00943a. [DOI] [PubMed] [Google Scholar]
- [53].Diggins IV P, McDargh ZA, Deserno M, Curvature softening and negative compressibility of gel-phase lipid membranes, J. Am. Chem. Soc 137 (2015) 12752–12755. 10.1021/jacs.5b06800. [DOI] [PubMed] [Google Scholar]
- [54].Li X, Ono T, Wang Y, Esashi M, Ultrathin single-crystalline-silicon cantilever resonators: fabrication technology and significant specimen size effect on Young ‘ s modulus, Appl. Phys. Lett 83 (2003) 3081 10.1063/1.1618369. [DOI] [Google Scholar]
- [55].Xiong Q, Duarte N, Tadigadapa S, Eklund PC, Force-deflection spectroscopy: a new method to determine the young’s modulus of nanofilaments, Nano Lett. 6 (2006) 1904–1909. 10.1021/nl060978f. [DOI] [PubMed] [Google Scholar]
- [56].Zhu Y, Xu F, Qin Q, Fung WY, Lu W, Mechanical properties of vapor-liquid-solid synthesized silicon nanowires, Nano Lett. 9 (2009) 3934–3939. 10.1021/nl902132w. [DOI] [PubMed] [Google Scholar]
- [57].Li P, Liao Q, Wang Z, Lin P, Zhang Z, Yan X, Zhang Y, AFM investigation of nanomechanical properties of ZnO nanowires, RSC Adv. 5 (2015) 33445–33449. 10.1039/c5ra01688f. [DOI] [Google Scholar]
- [58].Cao G, Chen X, Energy analysis of size-dependent elastic properties of ZnO nanofilms using atomistic simulations, Phys. Rev. B 76 (2007) 165407 10.1103/PhysRevB.76.165407. [DOI] [Google Scholar]
- [59].Fedorchenko AI, Wang AB, Cheng HH, Thickness dependence of nanofilm elastic modulus, Appl. Phys. Lett 94 (2009) 2007–2010. 10.1063/1.3120763. [DOI] [Google Scholar]
- [60].Wang W, Niu L, Zhang Y, Lin E, Tensile mechanical behaviors of cubic silicon carbide thin films, Comput. Mater. Sci 62 (2012) 195–202. 10.1016/j.commatsci.2012.05.035. [DOI] [Google Scholar]
- [61].Li J, Wang A, Narsu B, Yun G, Gao Z, Liu D, Surface elasticity and surface slice thickness effects on the elastic properties of nanofilms, Appl. Phys. A 125 (2019) 1–7. 10.1007/s00339-019-2726-2. [DOI] [Google Scholar]
- [62].Evangelopoulos AEAS, Glynos E, Koutsos V, Elastic modulus of a polymer nanodroplet: theory and experiment, Langmuir. 28 (2012) 4754–4767. 10.1021/la2049037. [DOI] [PubMed] [Google Scholar]
- [63].Kramer D, Weissmüller J, A note on surface stress and surface tension and their interrelation via Shuttleworth’s equation and the Lippmann equation, Surf. Sci 601 (2007) 3042–3051. 10.1016/j.susc.2007.05.005. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


