Dynamics of fractional order COVID-19 model with a case study of Saudi Arabia

Abstract

The novel coronavirus disease or COVID-19 is still posing an alarming situation around the globe. The whole world is facing the second wave of this novel pandemic. Recently, the researchers are focused to study the complex dynamics and possible control of this global infection. Mathematical modeling is a useful tool and gains much interest in this regard. In this paper, a fractional-order transmission model is considered to study its dynamical behavior using the real cases reported in Saudia Arabia. The classical Caputo type derivative of fractional order is used in order to formulate the model. The transmission of the infection through the environment is taken into consideration. The documented data since March 02, 2020 up to July 31, 2020 are considered for estimation of parameters of system. We have the estimated basic reproduction number $({\mathcal{R}}_0)$ for the data is $1.2937$. The Banach fixed point analysis has been used for the existence and uniqueness of the solution. The stability analysis at infection free equilibrium and at the endemic state are presented in details via a nonlinear Lyapunov function in conjunction with LaSalle Invariance Principle. An efficient numerical scheme of Adams-Molten type is implemented for the iterative solution of the model, which plays an important role in determining the impact of control measures and also sensitive parameters that can reduce the infection in the general public and thereby reduce the spread of pandemic as shown graphically. We present some graphical results for the model and the effect of the important sensitive parameters for possible infection minimization in the population.

Introduction

The fatal disease called a coronavirus (COVID-19) has grown beyond the expectation of everyone and seems to stay around for months or even years. The rapid spread of the virus with a high level of severity has become an unprecedented threat for the public health. To understand the mechanism of this virus and its possible eliminations, the researchers and scientists are looking to discover some treatments and vaccinations for its eliminations. The source of transmission is mainly through the droplets and person to person contact. To reduce the infection spread, the wearing of mask, stay at home, social distancing and wash the hands regularly are the highly recommended. Still the coronavirus infection spreading and according to the recent updates, over $20.2$ million are infected with 787,909 deaths globally so far [20], [13].

Like other countries, the rapid spreading of COVID-19 in Saudi Arabia; in which by the 30 of July 2020, an accounted 288609 confirmed cases of infected people, with 252035 recovered, and 3167 lost their lives as well as the severe economic hardship. The first case reported in Saudi Arabia was on second March 2020 while the second case has been reported on March 14 by the entry of the person from Iran via Bahrain [11]. After these cases, the government make plans and other preventive measure for the infection further spread. In this regard, a strict lock-down and curfew were announced, as a results the educations sector and the business markets were closed, flights suspended, Ummrah and Hajj are restricted to a certain number of people. The development of the vaccine and the possible control of the infections, the researchers and the biologists around the globe started thinking to have some vaccine for the disease elimination. The virologists are focusing their attention on vaccine ongoing trials, many to developing the vaccine and also a specific treatment mechanism to prevent the spread of this deadly virus.

The researchers around the world focus to study the coronavirus infection in different scenarios. Some were studying the statistical tools to understand the infected cases and to find some relationships that can be used further to help the infection minimization. Some studying the virus biologically and to think for some vaccine developments. Besides this, the others who developing mathematical models in terms of mathematics and to predict the infection eradication stage. The mathematical models are were considered in fast for many infectious diseases and its outbreak. Like corona infection, the authors used the theory of differential equations to formulate mathematical models with different characteristics and provided useful results for its eliminations.

Mathematical modeling is a valuable tool to study very effectively the disease spread and its control. In this regard the researchers around the world presented many useful mathematical models in the last few decades to study the dynamics of infectious diseases and to determine some useful strategies for the better elimination of infection. The compartmental models along with real cases are more helpful to provide useful information about a particular disease outbreak. Several mathematical models are considered in literature in order to investigate and analyze the complex transmission pattern of the novel ongoing COVID-19 pandemic, see [18], [19], [28], using ordinary, stochastic and delay differential equations. More briefly, the COVID-19 dynamics through a mathematical with Pakistani data and with the impact of public interventions are studied in [23]. The most three high infected countries due to corona virus and its dynamics are briefly studied in [15]. Recently, the authors in [3] investigated a new COVID-19 compartmental model involving the environmental viral concentration in order to study the corona virus infection and its dynamics. The authors obtained the model parameters in [3] for the coronavirus data of Saudi Arabia. Further, they constructed the transmission model under the assumption that the people exposed to the infection can also transmit the virus to the community.

The fractional mathematical models that are regarding the generalized model and considered useful for modeling purposes in epidemiology. Various benefits can be obtained from a fractional order system in the sense of best data fitting, information about its memory and to identify the best possible value of the fractional order than can best describe the model for the real cases. In addition, the hereditary properties, it makes the models constructed in fractional derivatives more strong and useful for describing the real phenomenon. It is useful than the ordinary order and with the benefit of cross over behaviors. Different mathematical models with the effect of non-locality and with other interesting results are proposed in [16], [2] and the references therein. Mathematical models where the authors proposed different fractional derivatives, see [5], [21], [17], and its applications, see [9], [6], [25]. Among the existing fractional order derivatives, the Caputo derivative gaining much interest and is widely used in problems arising in science and engineering. A vast literature is available on the application of Caputo type derivative. For instance, in [24], the Caputo fractional derivative is utilized in order to analyze the tuberculoses infection. The application of Caputo fractional derivative to a non-linear model of biochemical see [1] and the Hepatitis B virus with the use of hospitalization class, see [25]. In epidemiology, the Caputo fractional derivative is applied as a useful tool to provides a better understanding of disease dynamics. The dynamics of tuberculous (TB) in Pakistan was studied using the Caputo mathematical model in [24]. The authors in [24] showed that the Caputo model provides a better approximation to the reported infected cases. Recently, a number of Caputo-fractional order model are formulated to explore the transmission dynamics of novel coronavirus infection [22], [7], [8]. Some other mathematical models that addressed the coronavirus disease are studied in [4]. For example, the dynamical analysis of coronavirus model using lockdown effect has been analyzed in [4]. Using the real cases reported in Pakistan have been analyzed through a fractional mathematical model given in [7].

Motivated by the above discussion, the goal of the present work is to adopt the use of Caputo fractional-order time derivative to analyze the dynamics of COVID-19 in Saudi Arabia within the given period March 02, 2020 till July 31, 2020. We will study the model qualitatively to show the disease eradication using the important sensitive parameters. We extend the integer-order mathematical model recently studied in [3] to fractional order using Caputo derivative. The reproduction number shall be evaluated for the updated estimated and fitted model parameters. We can show more interesting results and its theoretically and its justifications numerically in the form of graphs. The effect of fractional order values on model as a graphically will be shown. This paper can be categorized with the sections is as follows: In Section “Basics of fractional calculus and model descriptions”, we give the basics related to the fractional calculus and the model descriptions. The results of the system, existence and uniqueness shown in Section “Analysis of the fractional model” while the stability analysis of the model are discussed in Section “Iterative solution and stability analysis”. We presented the graphical results with discussion in Section “Results and discussion” and concluding the findings in Section “Conclusion”.

Basics of fractional calculus and model descriptions

We give here in brief the essential definitions regarding fractional calculus and the model description in fractional derivative. The following important definitions are considered that will be utilized as a application to our proposed study.

Definition 2.1

Consider $y\in C^n$ be function, then the well known classical Caputo derivative having fractional order $\alpha$ in $(n-1,n)$ where $n\in \mathbb{N}$ [21] is defined as:

$${}^C{D}_t^{\alpha }(y(t))=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_0^t{y}^n(\varrho ){(t-\varrho )}^{n-\alpha -1}d\varrho ,$$

clearly ${}^C{D}_t^{\alpha }(y(t))$ tends to $y\prime (t)$ as $\alpha \to 1$.

Definition 2.2

The Corresponding integral with fractional order $\alpha >0$ of the function $y:{\mathbb{R}}^{+}\to \mathbb{R}$ is described as follows:

$$I_t^{\alpha }(y(t))=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^{t}y(\varrho ){(t-\varrho )}^{\alpha -1}d\varrho ,0<\alpha <1,t>0\text{.}$$

Definition 2.3

The Atangana-Baleanu operator (ABC) developed with the help of generalized Mittag-Leffler function is defined as [5]:

$${{}^{\mathit{ABC}}}_a{D}_t^{\alpha }(y(t))=\frac{\mathit{ABC}(\alpha )}{(1-\alpha )}{\int }_a^t{y}^{\prime }(\varrho )E_{\alpha }\left[-\alpha \frac{{(t-\varrho )}^{\alpha }}{1-\alpha }\right]d\varrho ,\alpha \in [0,1]\text{.}$$

Definition 2.4

The integral for the Definition 2.3 is given by:

$${{}^{\mathit{ABC}}}_a{I}_t^{\alpha }(y(t))=\frac{1-\alpha }{\mathit{ABC}(\alpha )}y(t)+\frac{\alpha }{\mathit{ABC}(\alpha )\mathrm{\Gamma }(\alpha )}{\int }_a^{t}y(\varrho ){(t-\varrho )}^{\alpha -1}d\varrho ,$$

where $\alpha \in [0,1)$.

Definition 2.5

Let $y^{\ast }$ denotes the equilibrium point of the Caputo fractional model then:

$${}^C{D}_t^{\alpha }y(t)=h(t,y(t)),\alpha \in (0,1),\mathit{iff}h(t,y^{\ast })=0\text{.}$$

Model descriptions

We consider here to generalize the COVID-19 model with the description of memory effects by using the Caputo derivative. For this purpose, we divide the total populations of humans at any time t in five different sub-classes. These sub-classes include, the susceptible $S(t)$, exposed $E(t)$, asymptomatic infected (no clinical symptoms but infect healthy people) $A(t)$, having disease symptoms and infected people or symptomatic infected $I(t)$ and the recovered individuals $R(t)$. The environmental class given by $B(t)$ shows the concentration of virus in the environment. Then, the following is the representations of the corona virus model in terms of fractional differential equations:

$$\left\{\begin{array}{c}{}^C{D}_{0,t}^{\alpha }S(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }S\prime (\varrho )d\varrho ,\hfill \\ \hfill \\ {}^C{D}_{0,t}^{\alpha }E(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }E\prime (\varrho )d\varrho ,\hfill \\ \hfill \\ {}^C{D}_{0,t}^{\alpha }I(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }I\prime (\varrho )d\varrho ,\hfill \\ \hfill \\ {}^C{D}_{0,t}^{\alpha }A(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }A\prime (\varrho )d\varrho ,\hfill \\ \hfill \\ {}^C{D}_{0,t}^{\alpha }R(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }R\prime (\varrho )d\varrho ,\hfill \\ \hfill \\ {}^C{D}_{0,t}^{\alpha }B(t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\varrho )}^{-\alpha }B\prime (\varrho )d\varrho \text{.}\hfill \end{array}\right)$$ (1)

The COVID-19 model in Caputo operator form is;

$$\left\{\begin{array}{c}{}^C{D}_{0,t}^{\alpha }S(t)=\mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-\nu S,\hfill \\ {}^C{D}_{0,t}^{\alpha }E(t)=\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-(\mu +\nu )E,\hfill \\ {}^C{D}_{0,t}^{\alpha }I(t)=(1-\omega )\mu E-\left(\nu +{\nu }_1+{\varphi }_1\right)I,\hfill \\ {}^C{D}_{0,t}^{\alpha }A(t)=\omega \mu E-\left(\nu +{\varphi }_2\right)A,\hfill \\ {}^C{D}_{0,t}^{\alpha }R(t)={\varphi }_{1}I+{\varphi }_{2}A-\nu R,\hfill \\ {}^C{D}_{0,t}^{\alpha }B(t)={\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B,\hfill \end{array}\right)$$ (2)

with the corresponding initial conditions (ICs) defined as:

$$\begin{array}{cc}\hfill S(0)=& S_0⩾0,E(0)=E_0⩾0,I(0)=I_0⩾0,\hfill \\ \hfill A(0)=& A_0⩾0,R(0)=R_0⩾0,B(0)=B_0⩾0\text{.}\hfill \end{array}$$ (3)

The birth rate of humans population and the natural mortality rate is considered as $\mathrm{\Lambda }$ and $\nu$ respectively. The parameters ${\beta }_i$ for $i=1,2,3$ are used to describe the disease transmission rates through the direct transmission from the exposed, symptomatic and asymptomatic infected individual respectively. Whereas, ${\beta }_4$ shows the virus transmission rate from the environment or contaminated surfaces. The symptoms develop in exposed individuals at the rate $(1-\omega )\mu$ they become infected and join $I(t)$ class while the remaining do not show any (or having mild) symptoms enter to asymptomatic class. The recovery rate in infected and asymptomatic class is ${\varphi }_1$ and ${\varphi }_2$ respectively. The people die at the rate ${\nu }_1$ from infected compartment. The concentration rate ${\phi }_i$ for $i=1,2,3$, contributed by E(t), I(t) and asymptomatic infected people to the environment and removal rate from the environment is $\psi$. In system (2), the net human population at time t is described by the term $N(t)$. Moreover, $N(t)=S(t)+E(t)+I(t)+A(t)+R(t)$. By adding them, we observe

$$\begin{array}{cc}\hfill {}^C{D}_t^{\alpha }N(t)=& {}^C{D}_t^{\alpha }S(t)+{}^C{D}_t^{\alpha }E(t)+{}^C{D}_t^{\alpha }I(t)+{}^C{D}_t^{\alpha }A(t)+{}^C{D}_t^{\alpha }R(t),\hfill \\ \hfill =& \mathrm{\Lambda }-\nu N-{\nu }_{1}I⩽\mathrm{\Lambda }-\nu N,\hfill \end{array}$$

we obtain

$$N(t)⩽N(0)E_{\alpha ,1}(-\nu t^{\alpha })+\mathrm{\Lambda }{t}^{\alpha }{E}_{\alpha ,\alpha +1}(-\nu t^{\alpha })\text{.}$$

Therefore, we have

$${\displaystyle \underset{}{\lim }}t\to \infty N(t)⩽\frac{\mathrm{\Lambda }}{\nu }\text{.}$$

The feasible region $\mathrm{\Omega }$, shown by

$$\mathrm{\Omega }=\left\{(S(t),E(t),I(t),A(t),R(t))\in {\mathbb{R}}_{+}^5:N(t)⩽\frac{\mathrm{\Lambda }}{\nu },B(t)\in {\mathbb{R}}_{+}:\frac{\mathrm{\Lambda }}{\nu }\frac{{\phi }_1+{\phi }_2+{\phi }_3}{\psi }\right\}\text{.}$$

Corollary 1

Suppose, $g(y)\in C[a_1,b_1]$ and ${}^C{D}_t^{\alpha }y(h)\in (a_1,b_1]$ , where $\alpha \in (0,1]$ . Then if

$$\begin{array}{c}\hfill (i).{}^C{D}_t^{\alpha }y(h)⩾0,\forall h\in (a_1,b_1),\mathit{then}y(h)\mathit{is}\mathit{non}-\mathit{decreasing}\text{.}\\ \hfill (\mathit{ii}).{}^C{D}_t^{\alpha }y(h)\le 0,\forall h\in (a_1,b_1),\mathit{then}y(h)\mathit{is}\mathit{non}-\mathit{increasing}\text{.}\end{array}$$

Parameter estimation

In order to parameterize the biological parameters of the proposed model by considering the reported infected cases of corona virus in Saudi Arabia for the given period starting from March 02 till 31 July 2020 (the peak time of COVID-19), we make use of the well-known least square fitting technique. The birth rate denoted by $\mathrm{\Lambda }$ and the natural mortality rate $\nu$ are estimated from literature [12] as can be found in the table given below. The total population of KSA is $N(0)=34813871$ and the average life span is $1/74.87$ years. The other parameters of the model under consideration are estimated from the real data of the aforementioned period in KSA. Consequently, using the estimated and fitted parameters the reproduction number is evaluated ${\mathcal{R}}_0\approx 1.2937$. The predicted curve is depicted in Fig. 1 , which provides a reasonable fitting curve to the actual cumulative infected cases. The Table 1 describes the parameters values estimated from the real data.

Fig. 1.

Model fitting versus data: circle denotes real cases while bold line model fit for $\alpha =1$.

Table 1.

Real data based fitted values of parameters along with biological description.

Parameter	Description	Value (per day)	Reference
$\mathrm{\Lambda }$	Recruitment rate	$N(0)\times \nu$	Estimated
$\nu$	Mortality rate	$1/(74.7\times 365)$	[12]
${\beta }_1$	Contact rate between E and S compartments	$0.1233$	Fitted
${\beta }_2$	Contact rate between I and S compartments	$0.0542$	Fitted
${\beta }_3$	Contact rate between A and S compartments	$0.0020$	Fitted
${\beta }_4$	Contact rate between B and S compartments	$0.1101$	Fitted
$\mu$	Incubation period	$0.1980$	Fitted
$\omega$	The fraction of individuals that move to $A(t)$	$0.3085$	Fitted
${\nu }_1$	Infection induced mortality rate of I individuals	$0.0104$	Fitted
${\varphi }_1$	Rate of recovery form I	$0.3680$	Fitted
${\varphi }_2$	Rate of recovery form A	$0.2945$	Fitted
${\phi }_1$	Virus concentration from E to B	$0.2574$	Fitted
${\phi }_2$	Virus concentration from I to B	$0.2798$	Fitted
${\phi }_3$	Virus concentration from A to B	$0.1584$	Fitted
$\psi$	Removal of virus from environment	$0.3820$	Fitted

Analysis of the fractional model

In this section, we investigate some basic and necessary mathematical features of the proposed model (2). To present the existence as well as the uniqueness (EU) of the problem solutions, we proceed as follow:

Existence and uniqueness (EU) of the model solution

This subsections explores the EU of the solution for Caputo operator with the help of fixed point theory. For this purpose, let $\mathcal{B}(\mathcal{G})$ denoting a Banach space consists of real valued continuous functions over the interval $\mathcal{G}=[0,a]$ with norm defined by $\Vert S\Vert ={\mathit{sup}}_{t\in \mathcal{G}}|S(t)|,\Vert E\Vert ={\mathit{sup}}_{t\in \mathcal{G}}|E(t)|,\Vert I\Vert ={\mathit{sup}}_{t\in \mathcal{G}}|I(t)|,\Vert A|={\mathit{sup}}_{t\in \mathcal{G}}|A(t)|,\Vert R|={\mathit{sup}}_{t\in \mathcal{G}}|R(t)|$ and $\Vert B\Vert ={\mathit{sup}}_{t\in \mathcal{G}}|B(t)|$, and the norm $\Vert (S,E,I,A,R,B)\Vert =\Vert S\Vert +\Vert E\Vert +\Vert I\Vert +\Vert A\Vert +\Vert R\Vert +\Vert B\Vert$.

Proof

System (2) gets the following for after utilizing the Caputo integral

$$\begin{array}{cc}\hfill S(t)=& S(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{\mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-\nu S\right\},\hfill \\ \hfill E(t)=& E(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-(\mu +\nu )E\right\},\hfill \\ \hfill I(t)=& I(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{(1-\omega )\mu E-\left(\nu +{\nu }_1+{\varphi }_1\right)I\right\},\hfill \\ \hfill A(t)=& A(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{\omega \mu E-\left(\nu +{\varphi }_2\right)A\right\},\hfill \\ \hfill R(t)=& R(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{{\varphi }_{1}I+{\varphi }_{2}A-\nu R\right\},\hfill \\ \hfill B(t)=& B(0)+{}^C{\mathbf{I}}_{0,t}^{\alpha }\left\{{\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B\right\}\text{.}\hfill \end{array}$$

Now by definition (2.2),

$$\left\{\begin{array}{c}S(t)=S(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_1(\varsigma ,S(\varsigma ))d\varsigma ,\hfill \\ E(t)=E(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_2(\varsigma ,E(\varsigma ))d\varsigma ,\hfill \\ I(t)=I(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_3(\varsigma ,I(\varsigma ))d\varsigma ,\hfill \\ A(t)=A(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_4(\varsigma ,A(\varsigma ))d\varsigma ,\hfill \\ R(t)=R(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_5(\varsigma ,R(\varsigma ))d\varsigma ,\hfill \\ B(t)=B(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_6(\varsigma ,B(\varsigma ))d\varsigma ,\hfill \end{array}\right)$$ (4)

where the kernels are,

$$\begin{array}{cc}\hfill K_1(t,S(t))=& \mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-\nu S,\hfill \\ \hfill K_2(t,E(t))=& \left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-(\mu +\nu )E,\hfill \\ \hfill K_3(t,I(t))=& (1-\omega )\mu E-\left(\nu +{\nu }_1+{\varphi }_1\right)I,\hfill \\ \hfill K_4(t,A(t))=& \omega \mu E-\left(\nu +{\varphi }_2\right)A,\hfill \\ \hfill K_5(t,R(t))=& {\varphi }_{1}I+{\varphi }_{2}A-\nu R,\hfill \\ \hfill K_6(t,B(t))=& {\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B\text{.}\hfill \end{array}$$

The expressions $K_1(t,S(t)),K_2(t,E(t)),K_3(t,I(t)),K_4(t,A(t))$ $K_5(t,R(t))$ and $K_6(t,B(t))$ fulfil the Lipschitz conditions with $S(t),E(t),I(t),A(t),R(t)$ and $B(t)$ having an upper bound. Let the two function $S(t)$ and $S^{\ast }(t)$ into consideration, and in similar manner for other functions. we have

$$\Vert K_1(t,S(t))-K_1(t,S^{\ast }(t))\Vert =\Vert (\frac{1}{N}\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)+\nu )(S(t)-S^{\ast }(t))\Vert \text{.}$$

Now assuming $l_1=\Vert (\frac{1}{N}\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)+\nu )\Vert$, and continuing in the same way for the remaining equations, we get

$$\begin{array}{cc}\hfill \Vert K_1(t,S(t))-K_1(t,S^{\ast }(t))\Vert ⩽& l_1\Vert S(t))-S^{\ast }(t)\Vert ,\hfill \\ \hfill \Vert K_2(t,E(t))-K_2(t,E^{\ast }(t))\Vert ⩽& l_2\Vert E(t))-E^{\ast }(t)\Vert ,\hfill \\ \hfill \Vert K_3(t,I(t))-K_3(t,I^{\ast }(t))\Vert ⩽& l_3\Vert I(t))-I^{\ast }(t)\Vert ,\hfill \\ \hfill \Vert K_4(t,A(t))-K_4(t,A^{\ast }(t))\Vert ⩽& l_4\Vert A(t))-A^{\ast }(t)\Vert ,\hfill \\ \hfill \Vert K_5(t,R(t))-K_5(t,R^{\ast }(t))\Vert ⩽& l_5\Vert R(t))-R^{\ast }(t)\Vert ,\hfill \\ \hfill \Vert K_6(t,B(t))-K_6(t,B^{\ast }(t))\Vert ⩽& l_6\Vert B(t))-B^{\ast }(t)\Vert ,\hfill \end{array}$$

where $l_1,l_2,l_3,l_4,l_5$ and $l_6$ denote the respective Lipschitz constants to the functions $K_1,K_2,K_3,K_4,K_5$ and $K_6$. Hence, the Lipschitz condition are satisfied. The equations in (4) can be shown recursively as:

$$\left\{\begin{array}{ccc}{S}_n(t)\hfill & =\hfill & S(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_1(\varsigma ,S_{n-1}(\varsigma ))d\varsigma ,\hfill \\ E_n(t)\hfill & =\hfill & E(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_2(\varsigma ,E_{n-1}(\varsigma ))d\varsigma ,\hfill \\ I_n(t)\hfill & =\hfill & I(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_3(\varsigma ,I_{n-1}(\varsigma ))d\varsigma ,\hfill \\ A_n(t)\hfill & =\hfill & A(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_4(\varsigma ,A_{n-1}(\varsigma ))d\varsigma ,\hfill \\ R_n(t)\hfill & =\hfill & R(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_5(\varsigma ,R_{n-1}(\varsigma ))d\varsigma ,\hfill \\ B_n(t)\hfill & =\hfill & B(0)+\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}{K}_6(\varsigma ,B_{n-1}(\varsigma ))d\varsigma \text{.}\hfill \end{array}\right)$$ (5)

The corresponding difference among the successive terms along with the initial conditions of model will takes the form;

$$\begin{array}{cc}\hfill {\Phi }_{S,n}(t)=& S_n(t)-S_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_1(\varsigma ,S_{n-1}(\varsigma ))-K_1(\varsigma ,S_{n-2}(\varsigma )))d\varsigma ,\hfill \\ \hfill {\mathrm{\Phi }}_{E,n}(t)=& E_n(t)-E_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_2(\varsigma ,E_{n-1}(\varsigma ))-K_2(\varsigma ,E_{n-2}(\varsigma )))d\varsigma \hfill \\ \hfill {\mathrm{\Phi }}_{I,n}(t)=& I_n(t)-I_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_3(\varsigma ,I_{n-1}(\varsigma ))-K_3(\varsigma ,I_{n-2}(\varsigma )))d\varsigma ,\hfill \\ \hfill {\mathrm{\Phi }}_{A,n}(t)=& A_n(t)-A_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_4(\varsigma ,A_{n-1}(\varsigma ))-K_4(\varsigma ,A_{n-2}(\varsigma )))d\varsigma ,\hfill \\ \hfill {\mathrm{\Phi }}_{R,n}(t)=& R_n(t)-R_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_5(\varsigma ,R_{n-1}(\varsigma ))-K_5(\varsigma ,R_{n-2}(\varsigma )))d\varsigma ,\hfill \\ \hfill {\mathrm{\Phi }}_{B,n}(t)=& B_n(t)-B_{n-1}(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\varsigma )}^{\alpha -1}(K_6(\varsigma ,B_{n-1}(\varsigma ))-K_6(\varsigma ,B_{n-2}(\varsigma )))d\varsigma \text{.}\hfill \end{array}$$

It is noted that, $S_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{S,j}(t),E_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{E,j}(t),I_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{I,j}(t),A_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{A,j}(t),R_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{R,n}(t),B_n(t)={\mathrm{\Sigma }}_{j=0}^n{\mathrm{\Phi }}_{B,n}(t)$. Now, we consider that;

$$\begin{array}{cc}\hfill {\Phi }_{S,n-1}(t)=& S_{n-1}(t)-S_{n-2}(t),{\mathrm{\Phi }}_{E,n-1}(t)=E_{n-1}(t)-E_{n-2}(t),\hfill \\ \hfill {\mathrm{\Phi }}_{I,n-1}(t)=& I_{n-1}(t)-I_{n-2}(t),{\mathrm{\Phi }}_{A,n-1}(t)=A_{n-1}(t)-A_{n-2}(t),\hfill \\ \hfill {\mathrm{\Phi }}_{R,n-1}(t)=& R_{n-1}(t)-R_{n-2}(t),{\mathrm{\Phi }}_{B,n-1}(t)=B_{n-1}(t)-B_{n-2}(t),\hfill \end{array}$$

we get the following,

$$\begin{array}{cc}\hfill \Vert {\mathrm{\Phi }}_{S,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_1{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{S,n-1}(\varsigma )\Vert d\varsigma ,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{E,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_2{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{E,n-1}(\varsigma )\Vert d\varsigma ,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{I,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_3{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{I,n-1}(\varsigma )\Vert d\varsigma ,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{A,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_4{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{A,n-1}(\varsigma )\Vert d\varsigma ,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{R,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_5{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{R,n-1}(\varsigma )\Vert d\varsigma ,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{B,n}(t)\Vert ⩽& \frac{1}{\mathrm{\Gamma }(\alpha )}{l}_6{\int }_0^t{(t-\varsigma )}^{\alpha -1}\Vert {\mathrm{\Phi }}_{B,n-1}(\varsigma )\Vert d\varsigma \text{.}\hfill \end{array}$$

Hence, $S(t),E(t),I(t),A(t),R(t)\mathit{andB}(t)$ describe the bounded functions and the expressions $K_1,K_2,K_3,K_4,K_5$ and $K_6$ satisfy the Lipschitz condition. □

Theorem 3.1

The Caputo COVID-19 epidemic model has a unique solution for $t\in [0,a]$ if

$$\frac{1}{\mathrm{\Gamma }(\alpha )}{l}_{j}m<1,j=1,\dots ..6\text{.}$$

Proof

It is observed that $S(t),E(t),I(t),A(t),R(t)$ and $B(t)$ are bounded and the expressions $K_1,K_2,K_3,K_4,K_5$ and $K_6$ fulfil the Lipschitz condition. By recursive principle the above equation implies:

$$\begin{array}{cc}\hfill \Vert {\mathrm{\Phi }}_{S,n}(t)\Vert ⩽& \Vert S_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_1\right)}^n,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{E,n}(t)\Vert ⩽& \Vert E_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_2\right)}^n,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{I,n}(t)\Vert ⩽& \Vert I_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_3\right)}^n,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{A,n}(t)\Vert ⩽& \Vert A_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_4\right)}^n,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{R,n}(t)\Vert ⩽& \Vert R_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_5\right)}^n,\hfill \\ \hfill \Vert {\mathrm{\Phi }}_{B,n}(t)\Vert ⩽& \Vert B_0(t)\Vert {\left(\frac{m}{\mathrm{\Gamma }(\alpha )}{l}_6\right)}^n\text{.}\hfill \end{array}$$

Therefore the sequence exist and obey the conditions describes $\Vert {\mathrm{\Phi }}_{S,n}(t)\Vert \to 0,\Vert {\mathrm{\Phi }}_{E,n}(t)\Vert \to 0,\Vert {\mathrm{\Phi }}_{I,n}(t)\Vert \to 0,\Vert {\mathrm{\Phi }}_{A,n}(t)\Vert \to 0,\Vert {\mathrm{\Phi }}_{R,n}(t)\Vert \to 0$, and $\Vert {\mathrm{\Phi }}_{B,n}(t)\Vert \to 0$, as $n\to \infty$.

$$\begin{array}{cc}\hfill \Vert S_{n+l}(t)-S_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_1^j=\frac{Y_1^{n+1}-Y_1^{n+l+1}}{1-Y_1},\hfill \\ \hfill \Vert E_{n+l}(t)-E_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_2^j=\frac{Y_1^{n+1}-Y_2^{n+l+1}}{1-Y_2},\hfill \\ \hfill \Vert I_{n+l}(t)-I_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_3^j=\frac{Y_1^{n+1}-Y_3^{n+l+1}}{1-Y_3},\hfill \\ \hfill \Vert A_{n+l}(t)-A_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_4^j=\frac{Y_1^{n+1}-Y_4^{n+l+1}}{1-Y_4},\hfill \\ \hfill \Vert R_{n+l}(t)-R_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_5^j=\frac{Y_1^{n+1}-Y_5^{n+l+1}}{1-Y_5},\hfill \\ \hfill \Vert B_{n+l}(t)-B_n(t)\Vert ⩽& {\displaystyle \sum _{j=n+1}^{n+l}}{Y}_6^j=\frac{Y_1^{n+1}-Y_6^{n+l+1}}{1-Y_6}\text{.}\hfill \end{array}$$

So by hypothesis, $\frac{1}{\mathrm{\Gamma }(\alpha )}{l}_{j}m<1$, and $S_n,E_n,I_n,A_n,R_n,B_n$ is the cauchy sequence. Hence, complete the desired result for the fractional-order model (2) is reached. □

Iterative solution and stability analysis

To establish the results in details, we provide the following results:

Theorem 4.1

Let $(\mathcal{B},\Vert .\Vert )$ denoting a Banach space and $G^{\ast }$ defines a self map on $\mathcal{B}$ . Further, $z_{n+1}=h(G^{\ast },z_n)$ shows the recursive expression while $\mathcal{C}(G^{\ast })$ denoting the fixed point set upon $G^{\ast }$ . Further, by defining $\Vert y_{n+1}^{\ast }-h(G^{\ast },y_n^{\ast })\Vert$ such that $\left\{y_n^{\ast }\subseteq \mathcal{B}\right\}$ . Then, the iterative approach, $y_{n+1}=h(G^{\ast },y_n),G^{\ast }$ is stable if ${\lim }_{n\to \infty }{c}_n=0$ , that is ${\lim }_{n\to \infty }{c}_n^{\ast }=p^{\ast }$ for $z_{n+1}=G^{\ast }$ where, n is taken as the Picard’s iteration then $G^{\ast }$ iteration is stable. The theorem can be summarized as below:

$(\mathcal{B},\Vert .\Vert )$ defines a Banach space and $G^{\ast }$ be a self-map upon $\mathcal{B}$ , then for all $x,y\in \mathcal{B}$ , we have

$$\begin{array}{cc}\hfill S_{n+1}(t)=& S_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-\nu S\right\}\right\},\hfill \\ \hfill E_{n+1}(t)=& E_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-(\mu +\nu )E\right\}\right\},\hfill \\ \hfill I_{n+1}(t)=& I_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{(1-\omega )\mu E-\left(\nu +{\nu }_1+{\varphi }_1\right)I\right\}\right\},\hfill \\ \hfill A_{n+1}(t)=& A_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\omega \mu E-\left(\nu +{\varphi }_2\right)A\right\}\right\},\hfill \\ \hfill R_{n+1}(t)=& R_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{{\varphi }_{1}I+{\varphi }_{2}A-\nu R\right\}\right\},\hfill \\ \hfill B_{n+1}(t)=& B_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{{\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B\right\}\right\}\text{.}\hfill \end{array}$$

Let $\mathcal{P}$ defines a self map, then we have

$$\begin{array}{cc}\hfill \mathcal{P}[S_n(t)]=& S_{n+1}(t)=S_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-\nu S\right\}\right\},\hfill \\ \hfill \mathcal{P}[E_n(t)]=& E_{n+1}(t)=E_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B\right)\frac{S}{N}-(\mu +\nu )E\right\}\right\},\hfill \\ \hfill \mathcal{P}[I_n(t)]=& I_{n+1}(t)=I_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{(1-\omega )\mu E-\left(\nu +{\nu }_1+{\varphi }_1\right)I\right\}\right\},\hfill \\ \hfill \mathcal{P}[A_n(t)]=& A_{n+1}(t)=A_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\omega \mu E-\left(\nu +{\varphi }_2\right)A\right\}\right\},\hfill \\ \hfill \mathcal{P}[R_n(t)]=& R_{n+1}(t)=R_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{{\varphi }_{1}I+{\varphi }_{2}A-\nu R\right\}\right\}\hfill \\ \hfill \mathcal{P}[B_n(t)]=& B_{n+1}(t)=B_n(t)+{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{{\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B\right\}\right\}\text{.}\hfill \end{array}$$

$\mathcal{P}$ is stable if the following conditions are satisfied $\left\{1-\mathrm{\Lambda }-{\beta }_1\left(Q_1+Q_2\right)f_1-{\beta }_2\left(Q_1+Q_3\right)f_2-{\beta }_3\left(Q_1+Q_4\right)f_3-{\beta }_4\left(Q_1+Q_6\right)f_4-\nu K_1\right\}<1,\left\{1-{\beta }_1\left(Q_1+Q_2\right)f_5+{\beta }_2\left(Q_1+Q_3\right)f_6+{\beta }_3\left(Q_1+Q_4\right)f_7+{\beta }_4\left(Q_1+Q_6\right)f_8-(\mu +\nu )K_2\right\}<1,\left\{1-((1-\omega )\mu -\left(\nu +{\nu }_1+{\varphi }_1\right))K_3\right\}<1,\left\{1-(\omega \mu -\left(\nu +{\varphi }_2\right))K_4\right\}<1,\left\{1-({\varphi }_1+{\varphi }_2-\nu )K_5\right\}<1,\left\{1-K_6({\phi }_1+{\phi }_2+{\phi }_3-\psi )\right\}<1$ .

Proof

Since the map $\mathcal{P}$ is a fixed point, therefore, we evaluate the following equation

$$\left\{\begin{array}{ccc}\mathcal{P}[S_n(t)]-\mathcal{P}[S_m(t)]\hfill & =\hfill & S_n(t)-S_m(t),\hfill \\ \mathcal{P}[E_n(t)]-\mathcal{P}[E_m(t)]\hfill & =\hfill & E_n(t)-E_m(t),\hfill \\ \mathcal{P}[I_n(t)]-\mathcal{P}[I_m(t)]\hfill & =\hfill & I_n(t)-I_m(t),\hfill \\ \mathcal{P}[A_n(t)]-\mathcal{P}[A_m(t)]\hfill & =\hfill & A_n(t)-A_m(t),\hfill \\ \mathcal{P}[R_n(t)]-\mathcal{P}[R_m(t)]\hfill & =\hfill & R_n(t)-R_m(t),\hfill \\ \mathcal{P}[B_n(t)]-\mathcal{P}[B_m(t)]\hfill & =\hfill & B_n(t)-B_m(t)\text{.}\hfill \end{array}\right)$$ (6)

Taking the norm of both sides of above equation

$$\begin{array}{cc}\hfill \Vert \mathcal{P}[S_n(t)]-\mathcal{P}[S_m(t)]\Vert =& \Vert {\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\mathrm{\Lambda }-\left({\beta }_1{E}_n+{\beta }_2{I}_n+{\beta }_3{A}_n+{\beta }_4{B}_n\right)\frac{S_n}{N}-\nu S_n\right\}\right\}\hfill \\ \hfill & -{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\mathrm{\Lambda }-\left({\beta }_1{E}_m+{\beta }_2{I}_m+{\beta }_3{A}_m+{\beta }_4{B}_m\right)\frac{S_m}{N}-\nu S_m\right\}\right\}\hfill \\ \hfill & +S_n(t)-S_m(t)\Vert \text{.}\hfill \end{array}$$

After simplification, we have

$$\begin{array}{cc}\hfill \Vert \mathcal{P}[S_n(t)]-\mathcal{P}[S_m(t)]\Vert ⩽& \Vert S_n(t)-S_m(t)\Vert +{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\Vert {\beta }_1{S}_n(E_n-E_m)\Vert \right)\right)\hfill \\ \hfill & +\Vert {\beta }_1{E}_n(S_n-S_m)\Vert +\Vert {\beta }_2{S}_n(I_n-I_m)\Vert +\Vert {\beta }_2{I}_n(S_n-S_m)\Vert \hfill \\ \hfill & +\Vert {\beta }_3{S}_n(A_n-A_m)\Vert +\Vert {\beta }_3{A}_n(S_n-S_m)\Vert +\Vert {\beta }_4{S}_n(B_n-B_m)\Vert \hfill \\ \hfill & \left(\left(+\Vert {\beta }_4{B}_n(S_n-S_m)\Vert \frac{1}{N}-\Vert \nu (S_n-S_m)\Vert \right\}\right\}\text{.}\hfill \end{array}$$

Now it assumed that,

$$\begin{array}{c}\hfill \Vert E_n(t)-E_m(t)\Vert \cong \Vert S_n(t)-S_m(t)\Vert ,\\ \hfill \Vert I_n(t)-I_m(t)\Vert \cong \Vert S_n(t)-S_m(t)\Vert ,\\ \hfill \Vert A_n(t)-A_m(t)\Vert \cong \Vert S_n(t)-S_m(t)\Vert ,\\ \hfill \Vert B_n(t)-B_m(t)\Vert \cong \Vert S_n(t)-S_m(t)\Vert ,\end{array}$$

after substituting the above relation, we have

$$\begin{array}{cc}\hfill \Vert \mathcal{P}[S_n(t)]-\mathcal{P}[S_m(t)]\Vert ⩽& \Vert S_n(t)-S_m(t)\Vert +{\mathcal{L}}^{-1}\left\{\frac{1}{s^{\alpha }}\mathcal{L}\left\{\Vert {\beta }_1{S}_n(S_n-S_m)\Vert \right)\right)\hfill \\ \hfill & +\Vert {\beta }_1{E}_n(S_n-S_m)\Vert +\Vert {\beta }_2{S}_n(S_n-S_m)\Vert +\Vert {\beta }_2{I}_n(S_n-S_m)\Vert \hfill \\ \hfill & +\Vert {\beta }_3{S}_n(S_n-S_m)\Vert +\Vert {\beta }_3{A}_n(S_n-S_m)\Vert +\Vert {\beta }_4{S}_n\Vert (S_n-S_m)\Vert \hfill \\ \hfill & \left(\left(+\Vert {\beta }_4{B}_n(S_n-S_m)\Vert \frac{1}{N}-\Vert \nu (S_n-S_m)\Vert \right\}\right\}\text{.}\hfill \end{array}$$

Because the sequences $S_n(t),E_m(t),I_m(t),A_m(t)$, and $B_m(t)$ are convergent and bounded, their exist five different constant $S_1>0,S_2>0,S_3>0,S_4>0$ and $S_5>0$ for all t. Hence we have $\Vert S_n(t)\Vert <|S_1\Vert ,\Vert E_m(t)\Vert <\Vert S_2\Vert ,\Vert I_m(t)\Vert <\Vert S_3\Vert ,\Vert A_m(t)\Vert <\Vert S_4\Vert ,\Vert B_m(t)\Vert <\Vert S_5\Vert ,(m,n)\in \mathbb{N}\times \mathbb{N}$.

By the relation we can attain

$$\begin{array}{cc}\hfill \Vert \mathcal{P}(S_n(t))-\mathcal{P}(S_m(t))\Vert ⩽& \left[1-\mathrm{\Lambda }-{\beta }_1\left(Q_1+Q_2\right)f_1-{\beta }_2\left(Q_1+Q_3\right)f_2\right)\hfill \\ \hfill & \left(-{\beta }_3\left(Q_1+Q_4\right)f_3-{\beta }_4\left(Q_1+Q_6\right)f_4-\nu K_1\right]\Vert S_n(t)-S_m(t)\Vert ,\hfill \\ \hfill \mathcal{P}[E_n(t)]-\mathcal{P}[E_m(t)]⩽& \left[1-{\beta }_1\left(Q_1+Q_2\right)f_5+{\beta }_2\left(Q_1+Q_3\right)f_6+{\beta }_3\left(Q_1+Q_4\right)f_7\right)\hfill \\ \hfill & \left(+{\beta }_4\left(Q_1+Q_6\right)f_8-(\mu +\nu )K_2\right]\Vert E_n(t)-E_m(t)\Vert ,\hfill \\ \hfill \mathcal{P}[I_n(t)]-\mathcal{P}[I_m(t)]⩽& \left[1-((1-\omega )\mu -\left(\nu +{\nu }_1+{\varphi }_1\right))K_3\right]\Vert I_n(t)-I_m(t)\Vert ,\hfill \\ \hfill \mathcal{P}[A_n(t)]-\mathcal{P}[A_m(t)]⩽& \left[1-(\omega \mu -\left(\nu +{\varphi }_2\right))K_4\right]\Vert A_n(t)-A_m(t)\Vert ,\hfill \\ \hfill \mathcal{P}[R_n(t)]-\mathcal{P}[R_m(t)]⩽& \left[1-({\varphi }_1+{\varphi }_2-\nu )K_5\right]\Vert R_n(t)-R_m(t)\Vert ,\hfill \\ \hfill \mathcal{P}[B_n(t)]-\mathcal{P}[B_m(t)]⩽& \left[1-({\phi }_1+{\phi }_2+{\phi }_3-\psi )K_6\right]\Vert B_n(t)-B_m(t)\Vert \text{.}\hfill \end{array}$$

Hence, the proof is complete. □

Disease free equilibrium (DFE) and the basic reproduction number

We obtain the basic reproduction number of the system (2) and its equilibrium point at the disease free case. Let the disease free equilibrium DFE of the system (2) denoted by ${\mathcal{E}}_0^{**}=(S^0,E^0,I^0,A^0,R^0,B^0)$, and can be obtained by setting, ${}^C{D}_t^{\alpha }S(t)={}^C{D}_t^{\alpha }E(t)={}^C{D}_t^{\alpha }I(t)={}^C{D}_t^{\alpha }A(t)={}^C{D}_t^{\alpha }R(t)={}^C{D}_t^{\alpha }B(t)=0$. Solving these equations at the disease free state, we get

$${\mathcal{E}}_0^{**}=\left(\frac{\mathrm{\Lambda }}{\nu },0,0,0,0,0\right)\text{.}$$ (7)

In order to get the expression for the basic reproduction number ${\mathcal{R}}_0$ of the system (2), we apply the technique known as the next generation method [26]. The well-known next-generation procedure is utilized in order to derive the basic reproductive number ${\mathcal{R}}_0$ for the model (2). Let $x={(E,I,A,B)}^T$, then the necessary matrices are

$$\mathcal{F}=\left(\begin{array}{c}\hfill \frac{{\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A+{\beta }_{4}B)S}{N}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\mathcal{V}=\left(\begin{array}{c}\hfill (\mu +\nu )E\hfill \\ \hfill (\nu +{\nu }_1+{\varphi }_1)I-(1-\omega )\mu E\hfill \\ \hfill (\nu +{\varphi }_2)A-\omega \mu E\hfill \\ \hfill \psi B-{\phi }_{1}E-{\phi }_{2}I-{\phi }_{3}A\hfill \end{array}\right)\text{.}$$

Now, for linearization the Jacobian of above matrices at disease free-state is:

$$\mathbf{F}=\left(\begin{array}{cccc}\hfill {\beta }_1\hfill & \hfill {\beta }_2\hfill & \hfill {\beta }_3\hfill & \hfill {\beta }_4\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\mathbf{V}=\left(\begin{array}{cccc}\hfill \mu +\nu \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -(1-\omega )\mu \hfill & \hfill \nu +{\nu }_1+{\varphi }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\omega \mu \hfill & \hfill 0\hfill & \hfill \nu +{\varphi }_2\hfill & \hfill 0\hfill \\ \hfill -{\phi }_1\hfill & \hfill -{\phi }_2\hfill & \hfill -{\phi }_3\hfill & \hfill \psi \hfill \end{array}\right)\text{.}$$

We have

$${\mathbf{FV}}^{-1}=\left(\begin{array}{cccc}\hfill \frac{{\beta }_1}{k_1}+\frac{k_3\mu \psi (1-\omega ){\beta }_2}{k_1{k}_2{k}_3\psi }+\frac{\omega \mu {\beta }_3}{k_1{k}_3}+d_1\hfill & \hfill \frac{{\beta }_2}{k_2}+\frac{{\beta }_4{\phi }_2}{k_2\psi }\hfill & \hfill \frac{{\beta }_3}{k_3}+\frac{{\beta }_4{\phi }_3}{k_3\psi }\hfill & \hfill \frac{{\beta }_4}{\psi }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{.}$$

Where, for simplicity we take

$$k_1=\mu +\nu ,k_2=\nu +{\nu }_1+{\varphi }_1,k_3=\nu +{\varphi }_2,d_1=\frac{{\beta }_4(k_2{k}_3{\phi }_1+k_3\mu {\phi }_2-k_3\mu \omega {\phi }_2+k_2\mu \omega {\phi }_3)}{k_1{k}_2{k}_3\psi }\text{.}$$

Thus, the expression of ${\mathcal{R}}_0$ in term of model parameters is obtained as:

$$\begin{array}{cc}\hfill {\mathcal{R}}_0=& \frac{k_2\mu \omega ({\beta }_4{\phi }_3+{\beta }_3\psi )+k_2{k}_3({\beta }_4{\phi }_1+{\beta }_1\psi )+\mu k_3(1-\omega )({\beta }_4{\phi }_2+{\beta }_2\psi )}{k_1{k}_2{k}_3\psi },\hfill \\ \hfill =& {\mathcal{R}}_1+{\mathcal{R}}_2+{\mathcal{R}}_3,\hfill \end{array}$$ (8)

where

$${\mathcal{R}}_1=\frac{\mu (1-\omega )({\beta }_4{\phi }_2+{\beta }_2\psi )}{k_1{k}_2\psi },{\mathcal{R}}_2=\frac{\mu \omega ({\beta }_4{\phi }_3+{\beta }_3\psi )}{k_1{k}_3\psi },{\mathcal{R}}_3=\frac{{\beta }_4{\phi }_1+{\beta }_1\psi }{k_1\psi }\text{.}$$

Local stability of DFE

In order to study the local asymptotical stability of the system (2), we give the following result:

Theorem 4.2

For any two positive integers $n_1^{\ast },n_2^{\ast }$ with $\mathit{gcd}(n_1^{\ast },n_2^{\ast })=1$ where $\alpha =\frac{n_1^{\ast }}{n_2^{\ast }}$ and $M=n_2^{\ast }$ . Then, the system (2) is LAS if $|\mathit{arg}(\lambda )|>\frac{\pi }{2M}$ for every root of $\lambda$ that defined by the following equation,

$$\mathit{det}(\mathit{diag}[{\lambda }^{M\alpha }{\lambda }^{M\alpha }{\lambda }^{M\alpha }{\lambda }^{M\alpha }{\lambda }^{M\alpha }{\lambda }^{M\alpha }]-J({\mathcal{E}}_0^{**}))=0\text{.}$$ (9)

Proof

Now the Jacobian of system (2) at ${\mathcal{E}}_0^{**}$ is:

$$J({\mathcal{E}}_0^{**})=\left(\begin{array}{cccccc}\hfill -\nu \hfill & \hfill -{\beta }_1\hfill & \hfill -{\beta }_2\hfill & \hfill -{\beta }_3\hfill & \hfill 0\hfill & \hfill -{\beta }_4\hfill \\ \hfill 0\hfill & \hfill -k_1+{\beta }_1\hfill & \hfill {\beta }_2\hfill & \hfill {\beta }_3\hfill & \hfill 0\hfill & \hfill {\beta }_4\hfill \\ \hfill 0\hfill & \hfill \mu (1-\omega )\hfill & \hfill -k_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mu \omega \hfill & \hfill 0\hfill & \hfill -k_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\varphi }_1\hfill & \hfill {\varphi }_2\hfill & \hfill -\nu \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\phi }_1\hfill & \hfill {\phi }_2\hfill & \hfill {\phi }_3\hfill & \hfill 0\hfill & \hfill -\psi \hfill \end{array}\right)\text{.}$$

Expanding the matrix (9) gives,

$${({\lambda }^m+\nu )}^2({\lambda }^{4m}+c_1{\lambda }^{3m}+c_2{\lambda }^{2m}+c_3{\lambda }^m+c_4)=0\text{.}$$ (10)

The repeated two eigenvalues are $-\nu ,-\nu$, contains negative real part. We used the polynomial in (10) and estimating the remaining eigenvalues by obtaining the coefficients given below:

$$\begin{array}{cc}\hfill c_1=& k_1+k_2+k_3+\psi -{\beta }_1,\hfill \\ \hfill c_2=& k_1{k}_2(1-\frac{{\beta }_2\mu (1-\omega )}{k_1{k}_2})+k_1{k}_3(1-\frac{{\beta }_3\mu \omega }{k_1{k}_3})+k_1\psi (1-\frac{{\beta }_4{\phi }_1+{\beta }_1\psi }{k_1\psi })\hfill \\ \hfill & +(k_2+k_3)(\psi -{\beta }_1)+k_2{k}_3,\hfill \\ \hfill c_3=& k_1{k}_2(1-{\mathcal{R}}_1)\psi +k_1{k}_3(1-{\mathcal{R}}_2)\psi -{\beta }_2\mu k_3(1-\omega )-{\beta }_3\mu k_2\omega -(k_2+k_3)({\beta }_4{\phi }_1+{\beta }_1\psi )\hfill \\ \hfill & -{\beta }_1{k}_2{k}_3+k_2{k}_3+k_2{k}_3\psi +k_1{k}_2{k}_3,\hfill \\ \hfill c_4=& k_1{k}_2{k}_3\psi (1-{\mathcal{R}}_0)\text{.}\hfill \end{array}$$

Clearly, $a_i$ are all positive for $i=1,..,4$ if ${\mathcal{R}}_0<1$. The Routh-Hurtwiz criteria can be used further to satisfy the conditions and make it sure the asymptotical stability of the system (2). This computation can be done easily through some computational software. The argument of the roots of equation ${({\lambda }^m+\nu )}^2=0$ are

$$\mathit{arg}({\lambda }_k)=\frac{\pi }{m}+k\frac{2\pi }{m}>\frac{\pi }{M}>\frac{\pi }{2M},\mathit{where}k=0,1,2,\dots .,(m-1)\text{.}$$

Similar approach can be adopted to show that the argument of the roots of Eq. (10) are all greater than $\frac{\pi }{2M}$ if ${\mathcal{R}}_0<1$. Moreover, we can find an argument less than $\frac{\pi }{2M}$ for ${\mathcal{R}}_0>1$. Thus disease-free equilibrium is LAS for ${\mathcal{R}}_0<1$. □

Lemma 4.1

The system (2) is unstable at the disease-free equilibrium if ${\mathcal{R}}_0>1$ .

Global stability of DFE

The Lyapunov function approach will be used to proceed the results for GAS of proposed model at disease free-state. For this we state and prove theorem:

Theorem 4.3

The DFE of the system (1) in fractional derivative is GAS if ${\mathcal{R}}_0<1$ .

Proof

We present the Lyapunov function defined below by establishing the above result:

$$\mathbb{G}(t)=f_{1}E+f_{2}I+f_{3}A+f_{4}B,$$ (11)

where the coefficients $f_j>0$, for $j=1,\dots ,4$, denoting the arbitrary positive constants, and later in the proof we can assign appropriate values. Applying the Caputo-fractional derivative on $\mathbb{G}(t)$, together with the use of the model (2), we have,

$${}^C{D}_t^{\alpha }\mathbb{G}(t)=f_1{}^C{D}_t^{\alpha }E+f_2{}^C{D}_t^{\alpha }I+f_3{}^C{D}_t^{\alpha }A+f_4{}^C{D}_t^{\alpha }B,$$ (12)

$$\begin{array}{cc}\hfill {}^C{D}_t^{\alpha }\mathbb{G}(t)=& f_1\left\{\lambda S(t)-k_{1}E(t)\right\}+f_2\left\{(1-\omega )\mu E(t)-k_{2}I(t)\right\}\hfill \\ \hfill & +f_3\left\{\mu \omega E(t)-k_{3}A(t)\right\}+f_4\left\{{\phi }_{1}E(t)+{\phi }_{2}I(t)+{\phi }_{3}A-\psi B(t)\right\},\hfill \\ \hfill ⩽& \left\{f_1{\beta }_2-f_2{k}_2+f_4{\phi }_2\right\}I(t)+\left\{f_1{\beta }_3-f_3{k}_3+f_4{\phi }_3\right\}A(t)\hfill \\ \hfill & +\left\{f_1({\beta }_1-k_1)+f_2(1-\omega )\mu +f_3\mu \omega +f_4{\phi }_1\right\}E(t)+\left\{f_1{\beta }_4-f_4\psi \right\}B(t),S⩽N,\hfill \\ \hfill ⩽& \left\{f_1{\beta }_2-f_2{k}_2+f_4{\phi }_2\right\}I(t)+\left\{f_1{\beta }_3-f_3{k}_3+f_4{\phi }_3\right\}A(t)\hfill \\ \hfill & +f_1{k}_1\left\{\frac{f_1{\beta }_1+f_2(1-\omega )\mu +f_3\mu \omega +f_4{\phi }_1}{f_1{k}_1}-1\right\}E(t)+\left\{f_1{\beta }_4-f_4\psi \right\}B(t)\text{.}\hfill \end{array}$$

Now choosing

$$f_1=k_2{k}_3\psi ,f_2=k_3({\beta }_4{\phi }_2+{\beta }_2\psi ),f_3=k_2({\beta }_4{\phi }_3+{\beta }_3\psi ),f_4=k_2{k}_3{\beta }_4\text{.}$$

$${}^C{D}_t^{\alpha }\mathbb{G}(t)⩽k_1{k}_2{k}_3\psi \left({\mathcal{R}}_0-1\right)E\text{.}$$ (13)

Hence ${}^C{D}_t^{\alpha }\mathbb{G}(t)\le 0$, if ${\mathcal{R}}_0<1$. ${}^C{D}_t^{\alpha }\mathbb{G}(t)=0$ if and only if $E=I=A=B=0$. Thus $(E,I,A,B)\to (0,0,0,0)$  as  $t\to \infty$ and model (2) implies that $S\to \frac{\mathrm{\Lambda }}{\nu }$, and $R\to 0$  as $t\to \infty$. It can be followed from the results given in [27], the solution of system (2) with non-negative ICs tends to ${\mathcal{E}}_0^{**}$ whenever $t\to \infty$ in $\mathrm{\Omega }$. So, the system (2) at ${\mathcal{E}}_0^{**}$ is GAS. □

The endemic equilibrium

In order to find the endemic equilibrium (EE) of the model (2), we denote it by

$${\mathcal{E}}_1^{**}=(S^{**},E^{**},I^{**},A^{**},R^{**},B^{**}),$$

where, $N^{**}=(S^{**}+E^{**}+I^{**}+A^{**}+R^{**})$. The system (2) gives the following results at a steady state:

$$\begin{array}{cc}\hfill S^{**}=& \frac{\mathrm{\Lambda }}{{\lambda }^{\ast }+\nu },\hfill \\ \hfill E^{**}=& \frac{{\lambda }^{\ast }\mathrm{\Lambda }}{k_1({\lambda }^{\ast }+\nu )}=\frac{{\lambda }^{\ast }{S}^{**}}{k_1},\hfill \\ \hfill I^{**}=& \frac{\mu (1-\omega ){\lambda }^{\ast }\mathrm{\Lambda }}{k_1{k}_2({\lambda }^{\ast }+\nu )}=\frac{(1-\omega )\mu E^{**}}{k_2}=\frac{(1-\omega ){\lambda }^{\ast }{S}^{**}}{k_1{k}_2},\hfill \\ \hfill A^{**}=& \frac{\mu \omega {\lambda }^{\ast }\mathrm{\Lambda }}{k_1{k}_3({\lambda }^{\ast }+\nu )}=\frac{\mu \omega E^{**}}{k_3}=\frac{\mu \omega {\lambda }^{\ast }{S}^{**}}{k_1{k}_3},\hfill \\ \hfill R^{**}=& \frac{{\varphi }_1{I}^{**}+{\varphi }_2{Q}^{**}}{\nu }=({\varphi }_1(1-\omega )+{\varphi }_2\mu \omega )\frac{{\lambda }^{\ast }{S}^{**}}{\nu k_1{k}_2{k}_3},\hfill \\ \hfill B^{**}=& \frac{{\phi }_1{E}^{**}+{\phi }_2{I}^{**}+{\phi }_3{A}^{**}}{\psi }\text{.}\hfill \end{array}$$ (14)

Further, at endemic steady-state,

$${\lambda }^{\ast }=\frac{{\beta }_1{E}^{**}+{\beta }_2{I}^{**}+{\beta }_3{A}^{**}+{\beta }_4{B}^{**}}{N^{**}}\text{.}$$ (15)

Substituting (14) in (15), and after simplification, we get

$$F({\lambda }^{\ast })=d_1{\lambda }^{\ast }+d_2,$$

where,

$$\begin{array}{cc}\hfill d_1=& \psi (\mu k_3(1-\omega )({\varphi }_1+\nu )+k_2(\mu \omega ({\varphi }_2+\nu )+\nu k_3)),\hfill \\ \hfill d_2=& \nu k_1{k}_2{k}_3\psi (1-{\mathcal{R}}_0)\text{.}\hfill \end{array}$$

If ${\mathcal{R}}_0>1$, then a unique EE exist.

Lemma 4.2

The system (2) has a unique EE $({\mathcal{E}}_1^{**})$, whenever ${\mathcal{R}}_0>1$.

Global asymptotical stability (GAS) of EE

We wish to establish the global asymptotical stability of the system (2) for the special case when the contact rate (${\beta }_4)=0$, and induced mortality is negligible (${\nu }_1)=0$, then, the following modal is presented:

$$\left\{\begin{array}{c}{}^C{D}_{0,t}^{\alpha }S(t)=\mathrm{\Lambda }-\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A\right)\frac{S}{N}-\nu S,\hfill \\ {}^C{D}_{0,t}^{\alpha }E(t)=\left({\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A\right)\frac{S}{N}-(\mu +\nu )E,\hfill \\ {}^C{D}_{0,t}^{\alpha }I(t)=(1-\omega )\mu E-\left(\nu +{\varphi }_1\right)I,\hfill \\ {}^C{D}_{0,t}^{\alpha }A(t)=\omega \mu E-\left(\nu +{\varphi }_2\right)A,\hfill \\ {}^C{D}_{0,t}^{\alpha }R(t)={\varphi }_{1}I+{\varphi }_{2}A-\nu R,\hfill \\ {}^C{D}_{0,t}^{\alpha }B(t)={\phi }_{1}E+{\phi }_{2}I+{\phi }_{3}A-\psi B,\hfill \end{array}\right)$$ (16)

where,

$$\lambda (t)=\frac{{\beta }_{1}E+{\beta }_{2}I+{\beta }_{3}A}{N}\text{.}$$

We obtain from system (16) that $N(t)\to \frac{\mathrm{\Lambda }}{\nu }$as $t\to \infty$. So, we get

$${\lambda }_1(t)={\beta }_1^{\ast }E+{\beta }_2^{\ast }I+{\beta }_3^{\ast }A,{\beta }_1^{\ast }=\frac{{\beta }_1\nu }{\mathrm{\Lambda }},{\beta }_2^{\ast }=\frac{{\beta }_2\nu }{\mathrm{\Lambda }},{\beta }_3^{\ast }=\frac{{\beta }_3\nu }{\mathrm{\Lambda }}\text{.}$$ (17)

The associated reproduction number ${\mathcal{R}}_{01}$ of the reduced model with (17) is:

$${\mathcal{R}}_{01}=\frac{k_{20}(k_3{\beta }_1+\omega \mu {\beta }_3)+k_3\mu {\beta }_2(1-\omega )}{k_1{k}_{20}{k}_3}\text{.}$$ (18)

The following results at steady state for model (16) are,

$$\left\{\begin{array}{ccc}\mathrm{\Lambda }\hfill & =\hfill & ({\lambda }_1^{\ast }+\nu )S^{***},\hfill \\ k_1{E}^{***}\hfill & =\hfill & {\lambda }_1^{\ast }{S}^{***},\hfill \\ k_{20}{I}^{***}\hfill & =\hfill & (1-\omega )\mu E^{***},\hfill \\ k_3{A}^{***}\hfill & =\hfill & \mu \omega E^{***}\text{.}\hfill \end{array}\right)$$ (19)

$${\lambda }_1^{\ast }=({\beta }_1^{\ast }{E}^{***}+{\beta }_2^{\ast }{I}^{***}+{\beta }_3^{\ast }{A}^{***}),k_{20}=\nu +{\varphi }_1\text{.}$$

Theorem 4.4

The reduced system (16) at the (EE) ${\mathcal{E}}_1^{***}$ is globally asymptotically stable in $\mathrm{\Omega }$ , if ${\mathcal{R}}_{01}>1$ .

Proof

Defining a non-linear Lyapunov function for the system (16), and then by taking its time fractional derivative, we have the following result,

$$\begin{array}{cc}\hfill {}^C{D}_t^{\alpha }\mathcal{G}(t)=& \left(1-\frac{S^{***}}{S}\right){}^C{D}_t^{\alpha }S(t)+\left(1-\frac{E^{***}}{E}\right){}^C{D}_t^{\alpha }E(t)+\frac{k_1}{(1-\omega )\mu }\left(1-\frac{I^{***}}{I}\right){}^C{D}_t^{\alpha }I(t)\hfill \\ \hfill & +\frac{k_1}{\mu \omega }\left(1-\frac{A^{***}}{A}\right){}^C{D}_t^{\alpha }A(t),\hfill \\ \hfill =& \left(1-\frac{S^{***}}{S}\right)\left(\mathrm{\Lambda }-{\lambda }_{1}S-\nu S\right)+\left(1-\frac{E^{***}}{E}\right)\left({\lambda }_{1}S-k_{1}E\right)\hfill \\ \hfill & +\frac{k_1}{(1-\omega )\mu }\left(1-\frac{I^{***}}{I}\right)\left((1-\omega )\mu E-k_{20}I\right)+\frac{k_1}{\mu \omega }\left(1-\frac{A^{***}}{A}\right)\left(\omega \mu E-k_{3}A\right)\text{.}\hfill \end{array}$$

From (19), we have

$$\begin{array}{cc}\hfill \left(1-\frac{S^{***}}{S}\right){}^C{D}_t^{\alpha }S(t)=& \left(1-\frac{S^{***}}{S}\right)\left(({\lambda }_1^{\ast }+\nu )S^{***}-({\lambda }_1+\nu )S\right),\hfill \\ \hfill =& {\beta }_1^{\ast }{S}^{***}{E}^{***}\left(1-\frac{S^{***}}{S}-\frac{\mathit{ES}}{E^{***}{S}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_2^{\ast }{S}^{***}{I}^{***}\left(1-\frac{S^{***}}{S}-\frac{\mathit{IS}}{I^{***}{S}^{***}}+\frac{I}{I^{***}}\right)\hfill \\ \hfill & +{\beta }_3^{\ast }{S}^{***}{A}^{***}\left(1-\frac{S^{***}}{S}-\frac{\mathit{AS}}{A^{***}{S}^{***}}+\frac{A}{A^{***}}\right)\hfill \\ \hfill & +\nu S^{***}\left(2-\frac{S^{***}}{S}-\frac{S}{S^{***}}\right)\text{.}\hfill \end{array}$$ (20)

$$\begin{array}{cc}\hfill \left(1-\frac{E^{***}}{E}\right){}^C{D}_t^{\alpha }E(t)=& \left(1-\frac{E^{***}}{E}\right)\left(\lambda S-{\lambda }^{\ast }{S}^{***}\frac{E}{E^{***}}\right)\hfill \\ \hfill =& {\beta }_1^{\ast }{S}^{***}{E}^{***}\left(1-\frac{S}{S^{***}}-\frac{E}{E^{***}}+\frac{\mathit{ES}}{E^{***}{S}^{***}}\right)\hfill \\ \hfill & +{\beta }_2^{\ast }{S}^{***}{I}^{***}\left(1-\frac{E}{E^{***}}-\frac{E^{***}\mathit{IS}}{{\mathit{EI}}^{***}{S}^{***}}+\frac{\mathit{IS}}{I^{***}{S}^{***}}\right)\hfill \\ \hfill & +{\beta }_3^{\ast }{S}^{***}{A}^{***}\left(1-\frac{E}{E^{***}}-\frac{E^{***}\mathit{AS}}{{\mathit{EA}}^{***}{S}^{***}}+\frac{\mathit{AS}}{A^{***}{S}^{***}}\right)\text{.}\hfill \end{array}$$ (21)

$$\begin{array}{cc}\hfill \left(\frac{k_1}{\mu (1-\omega )}\right)\left(1-\frac{I^{***}}{I}\right){}^C{D}_t^{\alpha }I(t)=& k_1\left(1-\frac{I^{***}}{I}\right)\left(E-E^{***}\frac{I}{I^{***}}\right),\hfill \\ \hfill =& {\lambda }^{\ast }{S}^{***}\left(1-\frac{I}{I^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}+\frac{E}{E^{***}}\right),\hfill \\ \hfill =& {\beta }_1^{\ast }{S}^{***}{E}^{***}\left(1-\frac{I}{I^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_2^{\ast }{S}^{***}{I}^{***}\left(1-\frac{I}{I^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_3^{\ast }{S}^{***}{A}^{***}\left(1-\frac{I}{I^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}+\frac{E}{E^{***}}\right)\text{.}\hfill \end{array}$$ (22)

$$\begin{array}{cc}\hfill \left(\frac{k_1}{\mu \omega }\right)\left(1-\frac{A^{***}}{A}\right){}^C{D}_t^{\alpha }A(t)=& \left(\frac{k_1}{\mu \omega }\right)\left(1-\frac{A^{***}}{A}\right)\left(\mu \omega E-\mu \omega E^{***}\frac{A}{A^{***}}\right),\hfill \\ \hfill =& {\lambda }^{\ast }{S}^{***}\left(1-\frac{A}{A^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right),\hfill \\ \hfill =& {\beta }_1^{\ast }{S}^{***}{E}^{***}\left(1-\frac{A^{***}E}{E^{***}A}-\frac{A}{A^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_2^{\ast }{S}^{***}{I}^{***}\left(1-\frac{A}{A^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_3^{\ast }{S}^{***}{A}^{***}\left(1-\frac{A}{A^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\text{.}\hfill \end{array}$$ (23)

after substituting, we get

$$\begin{array}{cc}\hfill {}^C{D}_t^{\alpha }\mathcal{G}(t)=& {\beta }_2^{\ast }{S}^{***}{I}^{***}\left(4-\frac{S^{***}}{S}-\frac{A}{A^{***}}-\frac{E^{***}\mathit{IS}}{{\mathit{EI}}^{***}{S}^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_3^{\ast }{S}^{***}{A}^{***}\left(4-\frac{S^{***}}{S}-\frac{I}{I^{***}}-\frac{E^{***}\mathit{AS}}{{\mathit{EA}}^{***}{S}^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\hfill \\ \hfill & +{\beta }_1^{\ast }{S}^{***}{E}^{***}\left(4-\frac{S^{***}}{S}-\frac{I}{I^{***}}-\frac{A}{A^{***}}-\frac{S}{S^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}\left(1-\frac{I}{I^{***}}\right)\right)\hfill \\ \hfill & \left(-\frac{A^{***}E}{{\mathit{AE}}^{***}}\left(1-\frac{A}{A^{***}}\right)\right)+\nu S^{***}\left(2-\frac{S^{***}}{S}-\frac{S}{S^{***}}\right)\text{.}\hfill \end{array}$$ (24)

We have the following fact,

$$\left(2-\frac{S^{***}}{S}-\frac{S}{S^{***}}\right)\le 0\text{.}$$

Further, if

$$\left\{\begin{array}{c}\left(4-\frac{S^{***}}{S}-\frac{A}{A^{***}}-\frac{E^{***}\mathit{IS}}{{\mathit{EI}}^{***}{S}^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\le 0,\hfill \\ \left(4-\frac{S^{***}}{S}-\frac{I}{I^{***}}-\frac{E^{***}\mathit{AS}}{{\mathit{EA}}^{***}{S}^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}-\frac{A^{***}E}{{\mathit{AE}}^{***}}+\frac{E}{E^{***}}\right)\le 0,\hfill \\ \left(4-\frac{S^{***}}{S}-\frac{I}{I^{***}}-\frac{A}{A^{***}}-\frac{S}{S^{***}}-\frac{I^{***}E}{{\mathit{IE}}^{***}}\left(1-\frac{I}{I^{***}}\right)-\frac{A^{***}E}{{\mathit{AE}}^{***}}\left(1-\frac{A}{A^{***}}\right)\right)\le 0\text{.}\hfill \end{array}\right)$$ (25)

Hence, ${}^C{D}_t^{\alpha }\mathcal{G}(t)\le 0$ for ${\mathcal{R}}_{01}$. Thus, by Lasalle invariance principle,

$${\displaystyle \underset{t\to \infty }{\lim }}S(t)=S^{***},{\displaystyle \underset{t\to \infty }{\lim }}E(t)=E^{***},{\displaystyle \underset{t\to \infty }{\lim }}I(t)=I^{***},{\displaystyle \underset{t\to \infty }{\lim }}A(t)=A^{***},{\displaystyle \underset{t\to \infty }{\lim }}R(t)=R^{***},{\displaystyle \underset{t\to \infty }{\lim }}B(t)=B^{***}\text{.}$$

So, every solution associated to the model (16) approaches to its unique endemic equilibrium. So, whenever ${\mathcal{R}}_0>1$, the system (16) at (${\mathcal{E}}_1^{**}$) is globally asymptotically stable. □

Conjecture 1

The unique EE of the system described in (2) is GAS in $\mathrm{\Omega }$, if ${\mathcal{R}}_0>1$, in $\mathrm{\Omega }$.

Results and discussion

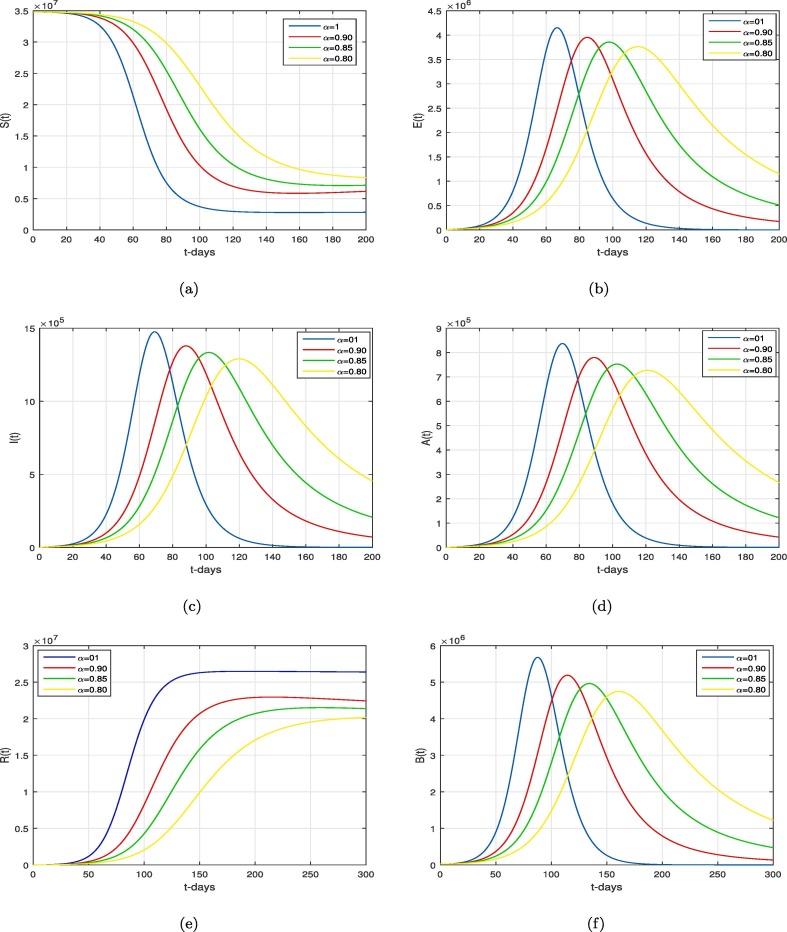
We present the simulation and discussion for the Caputo COVID-19 model (2) in the given section. We consider the numerical results given in Table 1 for the numerical results. The proposed fractional model is solved numerically using the method described in details in [10], [14]. The biological parameters estimated from COVID-19 confirmed cases and tabulated in Table 1 to assess the dynamics of novel COVID-19 pandemic in KSA. In order to analyze the role of different parameters and memory index in the dynamical behavior of the disease incidence, we varied various values of the key parameters of the model and the $\alpha$. The dynamics of proposed COVID-19 model (2) are shown graphically by taking the time unit in days. Fig. 2 describes the model differen component solution graphically for various values of $\alpha$. It can be seen that the healthy individuators increases while the non-healthy individuals that shown by different compartments are decreasing with the decrease of the value of $\alpha$. The influence of the contact rates ${\beta }_1$ and ${\beta }_4$ on the dynamics of only symptomatically-infected people are illustrated in Fig. 3, Fig. 4 respectively. This behavior is interpreted for two values of the order of Caputo operator i.e., $\alpha =1,0.90$. It is found that by decreasing the contact rates to its estimated baseline for two distinct values of $\alpha$, we can see a significant decrease. Although, a comparative faster decrease is observed in the infected population for $\alpha =0.90$. But, the peaks of infection curves occur at the longer period of time in this case. The role of viral concentration on the COVID-19 incidence is depicted in Fig. 5 . By decreasing the virus concentration rate, one can observe the decrease in the infected compartments as shown in Fig. 5. Fig. 6 shows that decay in the infected population due to decreasing the removal rate $\psi$. The behavior is even more prominent for a smaller value of fractional order $\alpha$ as can be seen in 6(b-d).

Fig. 2.

Simulation of the system (2) for various values of $\alpha$.

Fig. 3.

The impact of Contact rate ${\beta }_1$ on infected COVID-19 individuals for $\alpha =1,\alpha =0.90$.

Fig. 4.

The impact of Contact rate ${\beta }_4$ on infected COVID-19 individuals for $\alpha =1,\alpha =0.90$.

Fig. 5.

The impact of virus concentration $({\phi }_1=0.2574,0.2074,0.1574,0.1074)$ on infected individuals for $\alpha =1,\alpha =0.90$.

Fig. 6.

The impact of $\psi$ on infected individuals for $\alpha =1,\alpha =0.85,\alpha =0.75,\alpha =0.65$.

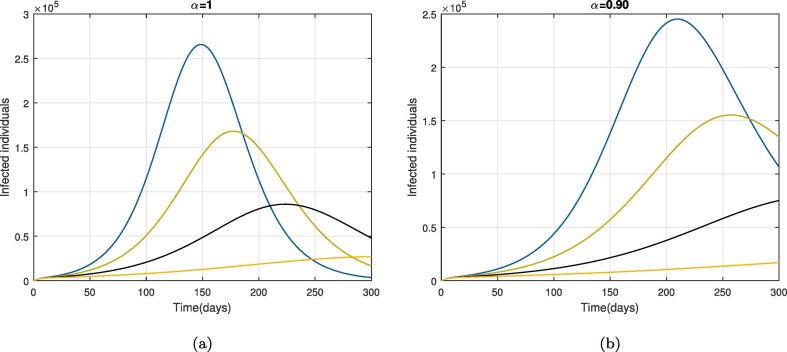
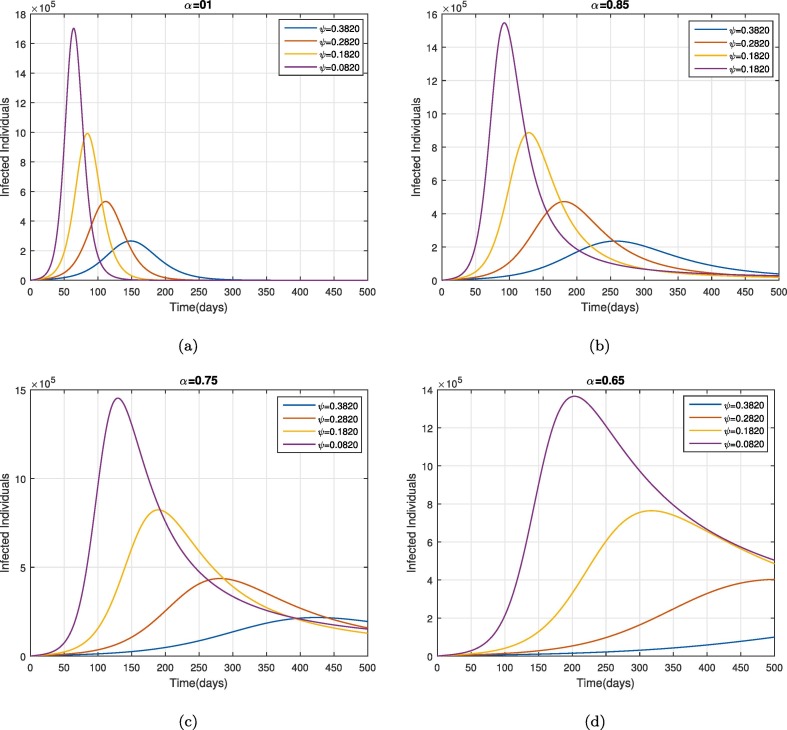
Moreover, we also investigated the impact of some parameters on the dynamical behavior of cumulative symptomatic and asymptomatic infected cases. The impact of contact rates ${\beta }_1$ and ${\beta }_4$ on the cumulative symptomatic and asymptomatic people is shown in Fig. 7 and Fig. 8 respectively. The reduction in these parameters can reduce the cumulative symptomatic and asymptomatic people significantly as can be seen in Fig. 7, Fig. 8. This reveals that the disease incidence can be reduced following protective measures i.e., using a facemask, sanitizer, glues, etc. through disinfection spry in order to reduce the environmental viral load. Furthermore, the decrease in the cumulative symptomatic and asymptomatic population on the reduction in the virus concentration rate ${\phi }_1$ due to exposed people is depicted in 9 . This behavior becomes more prominent for smaller values of $\alpha$ as shown in 9(b-c). From Fig. 10 the role of removal rate of the virus from the environmental (via disinfection spray etc.), is observed and seems to be more feasible for small values of the fractional operator $\alpha$.

Fig. 7.

The impact of ${\beta }_1$ on cumulative symptomatic and asymptomatic COVID-19 individuals for $\alpha =1,\alpha =0.90$.

Fig. 8.

The impact of ${\beta }_4$ on cumulative symptomatic and asymptomatic individuals for $\alpha =1,\alpha =0.90$.

Fig. 9.

The parameter ${\phi }_1=0.2574,0.2074,0.1574,0.1074$ impact on cumulative infected and asymptomatic cases for $\alpha =1,\alpha =0.95,\alpha =0.90$.

Fig. 10.

The parameter $\psi$ on cumulative symptomatic and asymptomatic cases for $\alpha =1,\alpha =0.85,\alpha =0.75,\alpha =0.60$.

Conclusion

We established a mathematical model for the understanding the corona virus infection in the Kingdom of Saudi Arabia through a fractional mathematical model in Caputo sense. We considered the real cases reported in the Kingdom have been analyzed and obtained a reasonable fit to the data. The environmental impact on the COVID-19 incidence is taken into consideration. Initially, the model in integer order were considered and then the fractional order operator with the power law kernel were applied for its generalization. We provided the related properties for the fractional model. The threshold quantity ${\mathcal{R}}_0$ and parameters were estimated from the reported COVID-19 cases in Saudi Arabia with the help of nonlinear least square procedure and we found that ${\mathcal{R}}_0=1.2937$. The stability analysis at the DFE and EEP are explored in detailed. We used a numerical scheme for the solution of the fractional order model and presented the graphical results. The predictor corrector scheme of Adams Molten type is utilized and studied the influence of various parameters by varying to its baseline value for distinct values of $\alpha$. The dramatic reduction in the disease burden was observed with an enhancement in contact tracing policy. The impact of variation in the environmental viral load due to symptomatic and asymptomatic COVID-19 infected individuals is analyzed graphically. It is observed that by reducing the viral contribution in the environment by asymptomatic infected individuals (i.e.,${\phi }_3$) decrease the disease burden significantly. We also depicted the impact of variation in the removal rate of virus from the environment (or surfaces) graphically on the disease prevalence. In overall simulation results, that the sensitive parameters decrease the infection in the population very fast. Such important parameters that can be considered as a control for the infection eradication in the population. The present work can be extended by using the cases in the state of Saudi Arabia with the second wave in more recent introduced fractal-fractional operators.

CRediT authorship contribution statement

Yu-Ming Chu: Writing - review & editing, Conceptualization, Methodology, Visualization. Aatif Ali: Conceptualization, Methodology, Visualization, Investigation. Muhammad Altaf Khan: Conceptualization, Visualization, Writing - review & editing. Saeed Islam: Visualization, Writing - review & editing, Writing - original draft. Saif Ullah: Writing - original draft, Conceptualization, Methodology, Visualization, Investigation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.