Stationary distribution and probability density function of a stochastic SVIS epidemic model with standard incidence and vaccination strategies

Abstract

Considering the great effect of vaccination and the unpredictability of environmental variations in nature, a stochastic Susceptible-Vaccinated-Infected-Susceptible (SVIS) epidemic model with standard incidence and vaccination strategies is the focus of the present study. By constructing a series of appropriate Lyapunov functions, the sufficient criterion ${\mathcal{R}}_0^s>1$ is obtained for the existence and uniqueness of the ergodic stationary distribution of the model. In epidemiology, the existence of a stationary distribution indicates that the disease will be persistent in a long term. By taking the stochasticity into account, a quasi-endemic equilibrium related to the endemic equilibrium of the deterministic system is defined. By means of the method developed in solving the general three-dimensional Fokker-Planck equation, the exact expression of the probability density function of the stochastic model around the quasi-endemic equilibrium is derived, which is the key aim of the present paper. In statistical significance, the explicit density function can reflect all dynamical properties of an epidemic system. Next, a simple result of disease extinction is obtained. In addition, several numerical simulations and parameter analyses are performed to illustrate the theoretical results. Finally, the corresponding results and conclusions are discussed at the end of the paper.

1. Introduction

1.1. Research background

It is well established that many infectious diseases have a critical influence on global social economies and human health. More precisely, the detailed statistics reported by the World Health Organization (WHO) show that approximately one-third of all deaths worldwide are caused by various epidemics. Recently, the global outbreak of COVID-19 with high transmission has also increased awareness of the importance of preventing and controlling infectious diseases. In epidemiology, mathematical models have provided several effective approaches to describe the characteristics and spread of epidemics in the last hundred years. In 1927, by dividing the population into two clusters, which includes people susceptible to the disease and infected individuals, Kermack and McKendrick [1] initially proposed the classical susceptible-infected-susceptible (SIS) epidemic model and established the corresponding threshold theory. Since then, various realistic ordinary differential equations (ODEs) have been extended to analyze and control the transmission of diseases [2], [3], [4], [5], [6], [7], [8]. For instance, Hove-Musekwa and Nyabadza [4] developed a HIV/AIDS model with active screening of disease carriers and obtained the corresponding basic reproduction number. Considering the effect of vertical infection, Tuncer and Martcheva [6] formulated a hepatitis B model with acute infection and carriers.

With the accelerated development of science and technology, vaccination comprises a common precaution that reduces the infection rate and even immunizes against some contagious diseases, such as measles, cholera, and tuberculosis [9]. According to a 2005 WHO report, the eradication of smallpox has been considered the most spectacular success of routine vaccination. Thus, some basic epidemic models with vaccination strategies have been studied in the last several decades [9], [10], [11], [12], [13]. In [9], Liu et al. obtained the global stability of equilibria and analyzed the effect of pulse vaccination. Gao et al. [11] proposed mixed vaccination strategies in the SIRS epidemic model with seasonal variability on infection. However, the vast majority of infection processes are caused by person-to-person contact. As Ma and Wang [2] described, the classical bilinear incidence rate is reasonably assumed by the simple mass-action law. From Anderson and May [14], Hethcote [15], this law is a good approximation for some communicable diseases, such as dengue fever and avian influenza. However, studies (see, e.g., [16], [17]) have shown that the underlying assumption of homogeneous mixing and homogeneous environmental for several sexually transmitted diseases, e.g., HIV/AIDS and syphilis, may be invalid. In addition, owing to the psychological effect, susceptible individuals may tend to reduce the number of contacts with the infected per unit time as the numbers of the infected individuals increase [18], [19]. As a result, the corresponding adequate incidence rate should be modified as a nonlinear form. More importantly, Anderson and May [20], [21] pointed out that various epidemic models with standard incidence are suitable for human beings and some gregarious animals.

Given the above, a SVIS epidemic system with standard incidence and vaccination is the focus of the present study.

1.2. Deterministic SVIS model and dynamical properties

The total population $N\left(t\right)$ is divided into three compartments, namely susceptible people $S\left(t\right),$ infected individuals $I\left(t\right),$ and vaccinees $V\left(t\right)$ that are in the vaccination process at time $t$. Then, the corresponding deterministic SVIS epidemic model with standard incidence and vaccination strategies takes the form

$$\{\begin{array}{c}{\displaystyle \frac{dS\left(t\right)}{dt}=\Lambda -(\mu +\vartheta )S-\frac{\beta SI}{N}+\gamma V+\delta I,}\hfill \\ {\displaystyle \frac{dV\left(t\right)}{dt}=\vartheta S-(\mu +\gamma )V,}\hfill \\ {\displaystyle \frac{dI\left(t\right)}{dt}=\frac{\beta SI}{N}-(\mu +\alpha +\delta )I,}\hfill \end{array}$$ (1.1)

where $\Lambda$ denotes the recruitment rate of the susceptible, $\beta$ is the effective contact rate, $\mu$ depicts the natural death rate of the population, $\alpha$ denotes the additional death rate due to the disease, $\vartheta$ is the vaccination rate of the susceptible, $\gamma$ denotes the immunity loss coefficient of the vaccinated, and $\delta$ reflects the recovery rate of the infected. In epidemiology, these biological parameters are assumed to be positive.

Following similar results described by Ma and Zhou [22], the corresponding basic reproduction number of system (1.1) takes the form

$${\mathcal{R}}_0=\frac{\beta (\mu +\gamma )}{(\mu +\gamma +\vartheta )(\mu +\alpha +\delta )}.$$ (1.2)

By defining a positive invariant set ${\mathcal{D}}_0=\left\{(S,V,I)|S\ge 0,V\ge 0,I\ge 0,S+V+I\le \frac{\Lambda }{\mu }\right\},$ two possible equilibria and their dynamical properties are then given as follows.

$•$ Assuming that ${\mathcal{R}}_0\le 1,$ the disease-free, $E_0=(S^0,V^0,I^0)=(\frac{\Lambda (\mu +\gamma )}{\mu (\mu +\gamma +\vartheta )},\frac{\Lambda \vartheta }{\mu (\mu +\gamma +\vartheta )},0),$ are then globally asymptotically stable in ${\mathcal{D}}_0$.

$•$ If ${\mathcal{R}}_0>1,$ there is a unique endemic equilibrium $E^{+}=(S^{+},V^{+},I^{+}),$ where $I^{+}=\frac{\Lambda ({\mathcal{R}}_0-1)}{\mu +(\mu +\alpha )({\mathcal{R}}_0-1)},S^{+}=\frac{\Lambda (\mu +\gamma )}{(\mu +\gamma +\vartheta )[\mu +(\mu +\alpha )({\mathcal{R}}_0-1)]},V^{+}=\frac{\Lambda \vartheta }{(\mu +\gamma +\vartheta )[\mu +(\mu +\alpha )({\mathcal{R}}_0-1)]}$. Moreover, $E^{+}$ is globally asymptotically stable in ${\mathcal{D}}_0,$ but $E_0$ is unstable.

1.3. Stochastic SVIS epidemic model

In fact, Truscott and Gilligan [23] pointed out that the spread of infection, travel of populations, and design of control strategies are critically perturbed by some environmental variations. Therefore, it is more reasonable to construct a corresponding stochastic model to reveal the epidemiological characteristics of infectious diseases by comparison with the deterministic model. Notably, there are various possible approaches to simulate the random effects from biological significance and mathematical perspective [24]. For instance, making use of the fatal properties and multiplex networks, Zhu et al. [25], Jia et al. [26] studied the SIR epidemic spreading process and analyzed individual decision-making behavior. In 2002, the most classical assumption that random changes always fluctuate around some average values due to continuous disturbances in nature, adopted by Mao et al. [27], became a common way of describing environmental variations. Moreover, the above random fluctuations are all assumed to be types of white noise. Therefore, many authors have formulated the relevant stochastic differential equations (SDEs) with linear noises for the transmission of various epidemics [28], [29], [30], [31], [32], [33], [34], [35], [36]. As an example, Qi and Jiang [29] studied the impact of virus carrier screening and actively seeking treatment on the dynamical behavior of a stochastic HIV/AIDS epidemic model with bilinear incidence. In [34], Shi and Zhang focused on the corresponding stochastic avian influenza system and investigated the existence of the unique ergodic stationary distribution. In addition, several dynamical analyses of the stochastic SIS models or epidemic systems with vaccination have been conducted [37], [38], [39], [40]. In [37], Zhao and Jiang creatively proposed a general theory about extinction and persistence in mean based on a stochastic SIS epidemic model with vaccination. Zhang and Jiang [39] obtained sufficient conditions for a stochastic SIS system with saturated incidence and double epidemic diseases. By taking the periodicity effect into account, they still investigated a stochastic SVIR epidemic model with vaccination strategies, and derived the criteria for the existence of non-trivial positive periodic solution [40]. Given the above, in the present study it is assumed that the environmental noises are separately proportional to the compartments $S,V$ and $I$. Then, the corresponding system (1.1) with the stochastic perturbations is described by

$$\{\begin{array}{c}{\displaystyle dS\left(t\right)=[\Lambda -(\mu +\vartheta )S-\frac{\beta SI}{N}+\gamma V+\delta I]dt+{\sigma }_{1}Sd{B}_1\left(t\right),}\hfill \\ {\displaystyle dV\left(t\right)=[\vartheta S-(\mu +\gamma \left)V\right]dt+{\sigma }_{2}Vd{B}_2\left(t\right),}\hfill \\ {\displaystyle dI\left(t\right)=[\frac{\beta SI}{N}-(\mu +\alpha +\delta )I]dt+{\sigma }_{3}Id{B}_3\left(t\right),}\hfill \end{array}$$ (1.3)

where $B_1\left(t\right),B_2\left(t\right)$ and $B_3\left(t\right)$ are three independent standard Brownian motions (or Wiener processes), with ${\sigma }_i^2>0(i=1,2,3)$ denoting their intensities.

From the perspective of biomathematics, the existence and ergodicity of stationary distribution indicates that an infectious disease will prevail and persist in long-term development. More importantly, the corresponding probability density function of the stationary distribution can reflect all statistical properties of the individuals $S,V$ and $I$. It can be regarded as a great intersection of epidemiological dynamics and statistics. It should be pointed out that there are relatively few studies devoted to the explicit expression of probability density function due to the difficulty of solving the corresponding Fokker-Planck equation. To the best of our ability, several general methods of solving the corresponding algebraic equations are developed herein that are equivalent to the Fokker-Planck equation, and the exact expression of density function is derived.

The rest of this paper is organized follows. In Section 2, several mathematical notations and important lemmas for the dynamical analyses of system (1.3) are presented. The sufficient conditions for the existence and uniqueness of the ergodic stationary distribution of system (1.3) are obtained in Section 3. By means of the developed approaches in solving the general three-dimensional Fokker-Planck equation, the exact expression of the probability density function for the stationary distribution is derived in Section 4. In Section 5, several simple criteria for the disease extinction of system (1.3) are given. In Section 6, several numerical simulations are performed, together with parameter analyses to validate the theoretical results. Finally, the corresponding result discussions and main conclusions are shown, compared with existing articles, at the end of the paper.

2. Preliminaries and necessary lemmas

Throughout the paper, let $\{\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P}\}$ be a complete probability space with a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ with a filtration ${\left\{{\Gamma }_t\right\}}_{t\ge 0}$ satisfying the usual conditions (i.e., it is increasing and right continuous, while ${\Gamma }_0$ contains all $\mathbb{P}$-null sets. Assuming that $A_{m\times n}$ is a real matrix, let $A^{\tau }$ be the transpose matrix of $A$. If $m=n,$ $A^{-1}$ depicts the inverse matrix of $A$. The reader is referred to Mao [41] for detailed descriptions. For convenience, let ${\mathbb{R}}^n$ be the $n$-dimensional Euclidean space, and

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{+}^n& =& \left\{(x_1,...,x_n)\right|x_k>0,1\le k\le n\},\hfill \\ \hfill {\Xi }_n& =& (\frac{1}{n},n)\times (\frac{1}{n},n)\times (\frac{1}{n},n).\hfill \end{array}$$

Clearly, the values $S,V$ and $I$ that satisfy system (1.3) are required to be positive for the corresponding dynamical behavior. To this end, the existence of uniqueness of the global positive solution of system (1.3) is described by the following Lemma 2.1.

Lemma 2.1

For any initial value$(S\left(0\right),V\left(0\right),I\left(0\right))\in {\mathbb{R}}_{+}^3,$there is then a unique solution$\left(S\right(t),V(t),I(t\left)\right)$of the system(1.3)on$t\ge 0,$and the solution will remain in${\mathbb{R}}_{+}^3$with probability 1 (a.s.).

The detailed proof is almost the same as those in Zhou et al. [28], and thus it is omitted here. Next, let $X\left(t\right)$ be a homogeneous Markov process defined on ${\mathbb{R}}^n$ that satisfies the following SDE,

$$dX\left(t\right)=\varphi \left(X\left(t\right)\right)dt+\sum _{k=1}^l{g}_k\left(X\right)d{B}_k\left(t\right),$$

where the diffusion matrix $H\left(x\right)=\left({\overline{a}}_{ij}\left(x\right)\right),$ and ${\overline{a}}_{ij}\left(x\right)={\sum }_{k=1}^l{g}_k^{\left(i\right)}\left(x\right)g_k^{\left(j\right)}\left(x\right)$. Then, the corresponding ergodicity theory and the existence of stationary distribution are described by the following Lemma 2.2.

Lemma 2.2

(Has’miniskii[42]) The Markov process$X\left(t\right)$has a unique ergodic stationary distribution$\varpi (·),$if there exists a bounded domain${\mathbb{D}}_0\subset {\mathbb{R}}^n$with a regular boundary$\Gamma$and the following are true.

$\left({\mathcal{A}}_1\right)$. In the domain${\mathbb{D}}_0$and some neighborhood thereof, the smallest eigenvalue of the diffusion matrix$H\left(x\right)$is bounded away from zero.

$\left({\mathcal{A}}_2\right)$. There is a non-negative$C^2$-function$U\left(X\right(t\left)\right)$such that$\mathcal{L}V\left(X\right(t\left)\right)$is negative for any${\mathbb{R}}^n\setminus {\mathbb{D}}_0$.

Then, for any$x\in {\mathbb{R}}^n$and integral function$\phi (·)$with respect to the measure$\varpi (·),$it follows that

$$\mathbb{P}\{\underset{t\to \infty }{\lim }\frac{1}{t}{\int }_0^t\phi \left(X\left(t\right)\right)dt={\int }_{{\mathbb{R}}^n}\phi \left(x\right)\varpi \left(dx\right)\}=1.$$

By Zhou et al. [28], two important lemmas of solving the special algebraic equations are given as follows.

Lemma 2.3

([28]) Let${{\rm Y}}_1$be a symmetric matrix, for the three-dimensional algebraic equation$G_0^2+A_0{{\rm Y}}_1+{{\rm Y}}_1{A}_0^{\tau }=0,$where$G_0=diag(1,0,0),$

$$A_0=\left(\begin{array}{ccc}-p_1& -p_2& -p_3\\ 1& 0& 0\\ 0& 1& 0\end{array}\right).$$ (2.1)

If$p_1>0,$$p_3>0$and$p_1{p}_2-p_3>0,$then${{\rm Y}}_1$is positive definite, which follows

$${{\rm Y}}_1=\left(\begin{array}{ccc}\frac{p_2}{2(p_1{p}_2-p_3)}& 0& -\frac{1}{2(p_1{p}_2-p_3)}\\ 0& \frac{1}{2(p_1{p}_2-p_3)}& 0\\ -\frac{1}{2(p_1{p}_2-p_3)}& 0& \frac{p_1}{2p_3(p_1{p}_2-p_3)}\end{array}\right)$$

Lemma 2.4

([28]) Consider the three-dimensional algebraic equation$G_0^2+B_0{{\rm Y}}_2+{{\rm Y}}_2{B}_0^{\tau }=0,$where${{\rm Y}}_2$is a symmetric matrix,$G_0=diag(1,0,0),$

$$B_0=\left(\begin{array}{ccc}-q_1& -q_2& -q_3\\ 1& 0& 0\\ 0& 1& q_{33}\end{array}\right).$$ (2.2)

Assuming that$q_1>0$and$q_2>0,$then${{\rm Y}}_2$is positive semi-definite, which takes the form

$${{\rm Y}}_2=\left(\begin{array}{ccc}\frac{1}{2q_1}& 0& 0\\ 0& \frac{1}{2q_1{q}_2}& 0\\ 0& 0& 0\end{array}\right).$$

Finally, combining Lemmas 2.3–2.4 and the Routh-Hurwitz criterion [43], two general theories are developed in solving the similar algebraic equations, i.e., Lemmas 2.5 and 2.6.

Lemma 2.5

For the three-dimensional algebraic equation$G_1^2+C_0{{\rm Y}}_3+{{\rm Y}}_3{C}_0^{\tau }=0,$where${{\rm Y}}_3$is a symmetric matrix,$G_1=diag(a_0,0,0)(a_0\ne 0)$

$$C_0=\left(\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ 0& c_{22}& c_{23}\\ 0& c_{32}& c_{33}\end{array}\right).$$ (2.3)

If$c_{11}<0,$then${{\rm Y}}_3$is a positive semi-definite matrix of the form

$${{\rm Y}}_3=\left(\begin{array}{ccc}-\frac{a_0^2}{2c_{11}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$

Lemma 2.6

For any real matrices$A={\left(a_{ij}\right)}_{3\times 3},\Pi =diag({\alpha }_1^2,{\alpha }_2^2,{\alpha }_3^2),$where${\alpha }_i>0(i=1,2,3)$. Assume that${\Sigma }_0$is a symmetric matrix, for the three-dimensional algebraic equation

$$\Pi +A{\Sigma }_0+{\Sigma }_0{A}^{\tau }=0.$$ (2.4)

By defining the characteristic polynomials of$A$as${\psi }_A\left(\lambda \right)={\lambda }^3+r_1{\lambda }^2+r_2\lambda +r_3,$if$A$has all negative real part eigenvalues – that is,$r_1>0,r_3>0,r_1{r}_2-r_3>0$– then${\Sigma }_0$is positive definite.

Remark 1

From Zhou et al. [28], $A_0$ and $B_0$ are called standard $R_1$ and $R_2$ matrices, respectively. Similarly, it is assumed that $C_0$ is a standard $R_3$ matrix. In addition, subsection (I) of Appendix A gives the detailed proof of Lemma 2.5. The corresponding proof of Lemma 2.6 and the special form of ${\Sigma }_0$ are shown in subsection (II) of Appendix A.

3. Stationary distribution and ergodicity of system (1.3)

In this section, the focus is on the sufficient conditions for the existence and ergodicity of stationary distribution for system (1.3). Moreover, one must guarantee that the results have no difference from those in the deterministic system (1.1). Define

$${\mathcal{R}}_0^s=\frac{\mu \beta (\mu +\gamma +\frac{{\sigma }_2^2}{2})}{[(\mu +\frac{{\sigma }_1^2}{2})(\mu +\gamma +\frac{{\sigma }_2^2}{2})+\vartheta (\mu +\frac{{\sigma }_2^2}{2})](\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})}.$$ (3.1)

Theorem 3.1

Assuming that ${\mathcal{R}}_0^s>1,$ then the solution $\left(S\right(t),V(t),I(t\left)\right)$ of system (1.3) with any initial value $(S\left(0\right),V\left(0\right),I\left(0\right))\in {\mathbb{R}}_{+}^3$ is ergodic and has a unique stationary distribution $\varpi (·)$ .

Proof

By Lemma 2.1, for any initial value $(S\left(0\right),V\left(0\right),I\left(0\right))\in {\mathbb{R}}_{+}^3,$ system (1.3) has a unique global positive solution $(S\left(t\right),V\left(t\right),I\left(t\right))\in {\mathbb{R}}_{+}^3$. Then, the proof of Theorem 3.1 is divided into the following two steps: (i) construct a pair of a $C^2$-Lyapunov function $U(S,V,I)$ and bounded domain ${\mathbb{D}}_{ϵ}$ such that $\mathcal{L}U\le -1$ for any $(S,V,I)\in {\mathbb{R}}_{+}^3\setminus {\mathbb{D}}_{ϵ},$ and (ii) validate the condition $\left({\mathcal{A}}_1\right)$ of Lemma 2.2. Step 1. Consider a suitable $C^2$-function $W(S,V,I)$ in the form

$$W(S,V,I)=M_0(S+V+I-a_1\ln S-a_1{a}_2\ln V-a_3\ln I)-\ln S-\ln V+(S+V+I),$$

where $a_1,a_2,a_3$ are all positive constant and are determined in (3.4), and $M_0=\frac{\Lambda +2\mu +\gamma +\vartheta +\frac{{\sigma }_1^2+{\sigma }_2^2}{2}+2}{3\Lambda (\sqrt[3]{{\mathcal{R}}_0^s}-1)}>0,$ which indicates

$$-3M_0\Lambda (\sqrt[3]{{\mathcal{R}}_0^s}-1)+\Lambda +2\mu +\gamma +\vartheta +\frac{{\sigma }_1^2+{\sigma }_2^2}{2}=-2.$$ (3.2)

Define, for simplicity,

$$W_1=S+V+I-a_1\ln S-a_1{a}_2\ln V-a_3\ln I,W_2=-\ln S-\ln V,W_3=S+V+I.$$

Applying It$\widehat{o}$’s formula to $W_1,$ which is shown in subsection (III) of Appendix B, obtains

$$\begin{array}{cc}\hfill \mathcal{L}{W}_1=& \Lambda -\mu N-\alpha I-a_1[\frac{\Lambda }{S}-\frac{\beta I}{N}+\frac{\gamma V}{S}+\frac{\delta I}{S}-(\mu +\vartheta +\frac{{\sigma }_1^2}{2})]\hfill \\ & -a_1{a}_2[\frac{\vartheta S}{V}-(\mu +\gamma +\frac{{\sigma }_2^2}{2})]-a_3[\frac{\beta S}{N}-(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})]\hfill \\ \hfill \le & \Lambda -(\mu N+\frac{a_1\Lambda }{S}+\frac{a_3\beta S}{N})+a_1(\mu +\vartheta +\frac{{\sigma }_1^2}{2})+a_3(\mu +\alpha +\delta +\frac{{\sigma }_2^2}{2})\hfill \\ & -(\frac{a_1\gamma V}{S}+\frac{a_1{a}_2\vartheta S}{V})+a_1{a}_2(\mu +\gamma +\frac{{\sigma }_2^2}{2})+\frac{a_1\beta I}{N}\hfill \\ \hfill \le & \Lambda -3\sqrt[3]{a_1{a}_3\Lambda \mu \beta }-2\sqrt{a_1^2{a}_2\vartheta \gamma }+a_1(\mu +\vartheta +\frac{{\sigma }_1^2}{2})+a_3(\mu +\alpha +\delta +\frac{{\sigma }_2^2}{2})+a_1{a}_2(\mu +\gamma +\frac{{\sigma }_2^2}{2})+\frac{a_1\beta I}{N}.\hfill \end{array}$$ (3.3)

Choosing $a_1,a_2$ and $a_3$ such that

$$a_2{(\mu +\gamma +\frac{{\sigma }_2^2}{2})}^2=\gamma \vartheta ,a_1[(\mu +\vartheta +\frac{{\sigma }_1^2}{2})-\frac{\gamma \vartheta }{\mu +\gamma +\frac{{\sigma }_2^2}{2}}]=a_3(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})=\Lambda ,$$ (3.4)

which means $a_1=\frac{\gamma \vartheta }{{(\mu +\gamma +\frac{{\sigma }_2^2}{2})}^2},$ $a_2=\frac{\Lambda }{\mu +\vartheta +\frac{{\sigma }_1^2}{2}-\frac{\gamma \vartheta }{\mu +\gamma +\frac{{\sigma }_2^2}{2}}}$ and $a_3=\frac{\Lambda }{\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2}},$ one can obtain

$$\mathcal{L}{W}_1\le 2\Lambda +a_1[(\mu +\vartheta +\frac{{\sigma }_1^2}{2})-\frac{\gamma \vartheta }{\mu +\gamma +\frac{{\sigma }_2^2}{2}}]-3\sqrt[3]{\frac{a_1{\Lambda }^2\mu \beta }{\mu +\alpha +\delta +\frac{{\sigma }_2^2}{2}}}+\frac{a_1\beta I}{N}=3\Lambda -3\Lambda \sqrt[3]{{\mathcal{R}}_0^s}+\frac{a_1\beta I}{N}=-3\Lambda (\sqrt[3]{{\mathcal{R}}_0^s}-1)+\frac{a_1\beta I}{N}.$$ (3.5)

Applying It$\widehat{o}$’s formula to $W_2,W_3$ similarly obtains

$$\begin{array}{cc}\hfill \mathcal{L}{W}_2=& [-\frac{\Lambda }{S}+(\mu +\vartheta +\frac{{\sigma }_1^2}{2})+\frac{\beta I}{N}-\frac{\gamma V}{S}-\frac{\delta I}{S}]-\frac{\vartheta S}{V}+(\mu +\gamma +\frac{{\sigma }_2^2}{2})\hfill \\ \hfill \le & -\frac{\Lambda }{S}-\frac{\vartheta S}{V}+\frac{\beta I}{N}+2\mu +\gamma +\vartheta +\frac{{\sigma }_1^2+{\sigma }_2^2}{2},\hfill \end{array}$$ (3.6)

$$\mathcal{L}{W}_3=\Lambda -\mu (S+I)-(\mu +\alpha )I\le \Lambda -\mu N.$$ (3.7)

Additionally, note that $W(S,V,I)$ is a continuous function satisfying

$$\underset{l\to +\infty ,(S,V,I)\in {\mathbb{R}}_{+}^3\setminus {\Xi }_l}{lim\; inf}W(S,V,I)=+\infty .$$

Hence, $W(S,V,I)$ has a minimum value $W_0$. Defining a non-negative $C^2$-function $U(S,V,I):{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}^1$ by

$$U(S,V,I)=W(S,V,I)-W_0,$$

and combining (3.2) and (3.5)–(3.7), it can be shown that

$$\mathcal{L}U\le -3M_0\Lambda (\sqrt[3]{{\mathcal{R}}_0^s}-1)+\frac{a_1{M}_0\beta I}{N}-\frac{\Lambda }{S}-\frac{\vartheta S}{V}+\frac{\beta I}{N}+(\Lambda +2\mu +\gamma +\vartheta +\frac{{\sigma }_1^2+{\sigma }_2^2}{2})-\mu N=-2+\frac{(a_1{M}_0+1)\beta I}{S+V+I}-\frac{\Lambda }{S}-\frac{\vartheta S}{V}-\mu (S+V+I).$$ (3.8)

Next, the corresponding compact subset ${\mathbb{D}}_{ϵ}$ is contructed by

$$D_{ϵ}=\{(S,V,I)\in {\mathbb{R}}_{+}^3|S\ge ϵ,V\ge {ϵ}^2,I\ge {ϵ}^3,S+V+I\le \frac{1}{ϵ}\},$$

where $ϵ>0$ is a sufficiently small constant such that the following inequalities hold:

$$-2+(a_1{M}_0+1)\beta -\frac{\min (\Lambda ,\vartheta ,\mu )}{ϵ}\le -1,$$ (3.9)

$$-2+(a_1{M}_0+1)\beta ϵ\le -1.$$ (3.10)

For convenience, consider the following four subsets of ${\mathbb{R}}_{+}^3\setminus {\mathbb{D}}_{ϵ}$:

$$\begin{array}{ccc}\hfill {\mathbb{D}}_{1,ϵ}^c& =& \{(S,V,I)\in {\mathbb{R}}_{+}^3|S<ϵ\},{\mathbb{D}}_{2,ϵ}^c=\{(S,V,I)\in {\mathbb{R}}_{+}^3|V<{ϵ}^2,S\ge ϵ\},\hfill \\ \hfill {\mathbb{D}}_{3,ϵ}^c& =& {\displaystyle \{(S,V,I)\in {\mathbb{R}}_{+}^3|I<{ϵ}^3,V\ge {ϵ}^2\},{\mathbb{D}}_{4,ϵ}^c=\{(S,V,I)\in {\mathbb{R}}_{+}^3|S+V+I>\frac{1}{ϵ}\}.}\hfill \end{array}$$

Now, it must be shown that

$$\mathcal{L}U\le -1,\forall (S,V,I)\in {\mathbb{D}}_{i,ϵ}(i=1,2,3,4).$$

Case 1. If $(S,V,I)\in {\mathbb{D}}_{1,ϵ},$ by (3.8)–(3.9), one can derive

$$\mathcal{L}U\le -2+(a_1{M}_0+1)\beta -\frac{\Lambda }{S}\le -2+(a_1{M}_0+1)\beta -\frac{\min (\Lambda ,\vartheta ,\mu )}{ϵ}\le -1.$$

Case 2. For any $(S,V,I)\in {\mathbb{D}}_{2,ϵ},$ it follows from (3.8)–(3.9) that

$$\mathcal{L}U\le -2+(a_1{M}_0+1)\beta -\frac{\vartheta S}{V}\le -2+(a_1{M}_0+1)\beta -\frac{\min (\Lambda ,\vartheta ,\mu )}{ϵ}\le -1.$$

Case 3. Assuming that $(S,V,I)\in {\mathbb{D}}_{3,ϵ},$ by (3.8)–(3.9) it can be seen that

$$\mathcal{L}U\le -2+\frac{(a_1{M}_0+1)\beta I}{V}\le -2+(a_1{M}_0+1)\beta ϵ\le -1.$$

Case 4. If $(S,V,I)\in {\mathbb{D}}_{1,ϵ},$ from (3.8) and (3.10), one has

$$\mathcal{L}U\le -2+(a_1{M}_0+1)\beta -\mu (S+V+I)\le -2+(a_1{M}_0+1)\beta -\frac{\min (\Lambda ,\vartheta ,\mu )}{ϵ}\le -1.$$

Notably, ${\mathbb{R}}_{+}^3\setminus {\mathbb{D}}_{ϵ}={\bigcup }_{i=1}^4{\mathbb{D}}_{i,ϵ}$. Hence, one equivalently obtains

$$\mathcal{L}U\le -1,\forall (S,V,I)\in {\mathbb{R}}_{+}^3\setminus {\mathbb{D}}_{ϵ}.$$

Therefore, the condition $\left({\mathcal{A}}_2\right)$ of Lemma 2.2 holds. The corresponding diffusion matrix is given by

$$H=\left(\begin{array}{ccc}{\sigma }_1^2{S}^2& 0& 0\\ 0& {\sigma }_2^2{V}^2& 0\\ 0& 0& {\sigma }_3^2{I}^2\end{array}\right).$$

Clearly, $H$ is a positive-definite matrix. Then, the assumption $\left({\mathcal{A}}_1\right)$ of Lemma 2.2 also holds.

Given the above, the global positive solution $\left(S\right(t),V(t),I(t\left)\right)$ of system (1.3) follows a unique ergodic stationary distribution $\varpi (·)$. This completes the proof of Theorem 3.1. □

Remark 2

Under ${\mathcal{R}}_0^s>1,$ the existence of the ergodic stationary distribution for system (1.3) is derived. This reveals that the contagious disease will prevail and persist in a population. Furthermore, from the expressions of ${\mathcal{R}}_0^s$ and ${\mathcal{R}}_0,$ it can be obtained that ${\mathcal{R}}_0^s\le {\mathcal{R}}_0,$ and the sign holds if and only if ${\sigma }_1={\sigma }_2={\sigma }_3=0$. Consequently, not only does this reveal that random fluctuations have a critical effect on the spread of epidemic, but it also indicates that ${\mathcal{R}}_0^s$ is a unified threshold of the disease persistence of systems (1.1) and (1.3).

4. Probability density function analysis

By Theorem 3.1, one obtains that the global solution $\left(S\right(t),V(t),I(t\left)\right)$ of system (1.3) follows a unique ergodic stationary distribution $\varpi (·)$. This section is devoted to deriving the explicit expression of the density function of the distribution $\varpi (·)$ while ${\mathcal{R}}_0^s>1$. In fact, the result will present a wide range of possibilities for the further development of epidemiological dynamics. Before this, two necessary transformations of system (1.3) should be first introduced.

4.1. Two important transformations of system (1.3)

(I) (Logarithmic transformation): Let ${(u_1,u_2,u_3)}^{\tau }={(\ln S,\ln V,\ln I)}^{\tau },$ Employing It$\widehat{o}$’s formula, it follows from system (1.3) that

$$\{\begin{array}{c}{\displaystyle d{u}_1=[\Lambda e^{-u_1}-(\mu +\vartheta +\frac{{\sigma }_1^2}{2})-\frac{\beta e^{u_3}}{e^{u_1}+e^{u_2}+e^{u_3}}+\gamma e^{u_2-u_1}+\delta e^{u_3-u_1}]dt+{\sigma }_{1}d{B}_1\left(t\right),}\hfill \\ {\displaystyle d{u}_2=[\vartheta e^{u_1-u_2}-(\mu +\gamma +\frac{{\sigma }_2^2}{2})]dt+{\sigma }_{2}d{B}_2\left(t\right),}\hfill \\ {\displaystyle d{u}_3=[\frac{\beta e^{u_1}}{e^{u_1}+e^{u_2}+e^{u_3}}-(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})]dt+{\sigma }_{3}d{B}_3\left(t\right).}\hfill \end{array}$$ (4.1)

By taking the random effect into consideration, another critical value is defined: ${\mathcal{R}}_0^c=\frac{\beta (\mu +\gamma +\frac{{\sigma }_2^2}{2})}{(\mu +\gamma +\epsilon +\frac{{\sigma }_2^2}{2})(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})}$. Moreover, if ${\mathcal{R}}_0^c>1,$ then the quasi-stable equilibrium $E^{*}=(S^{*},V^{*},I^{*}):=(e^{u_1^{*}},e^{u_2^{*}},e^{u_3^{*}})\in {\mathbb{R}}_{+}^3$ is determined by the following Eq. (4.2):

$$\{\begin{array}{c}{\displaystyle \Lambda e^{-u_1^{*}}-(\mu +\vartheta +\frac{{\sigma }_1^2}{2})-\frac{\beta e^{u_3^{*}}}{e^{u_1^{*}}+e^{u_2^{*}}+e^{u_3^{*}}}+\gamma e^{u_2^{*}-u_1^{*}}+\delta e^{u_3^{*}-u_1^{*}}=0,}\hfill \\ {\displaystyle \vartheta e^{u_1^{*}-u_2^{*}}-(\mu +\gamma +\frac{{\sigma }_2^2}{2})=0,}\hfill \\ {\displaystyle \frac{\beta e^{u_1^{*}}}{e^{u_1^{*}}+e^{u_2^{*}}+e^{u_3^{*}}}-(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})=0.}\hfill \end{array}$$ (4.2)

For convenience, let ${\mu }_i=\mu +\frac{{\sigma }_i^2}{2}$ for any $i=1,2,3$. As a result, it can be derived by (4.2) that $V^{*}=\frac{\vartheta S^{*}}{{\mu }_2+\gamma },I^{*}=\frac{({\mu }_2+\gamma +\vartheta )({\mathcal{R}}_0^c-1)S^{*}}{{\mu }_2+\gamma },N^{*}=S^{*}+V^{*}+I^{*}=\frac{\beta S^{*}}{{\mu }_3+\alpha +\delta },$ where $S^{*}=\frac{\Lambda ({\mu }_2+\gamma )}{{\mu }_1({\mu }_2+\gamma )+\vartheta {\mu }_2+({\mu }_3+\alpha )({\mu }_2+\gamma +\vartheta )({\mathcal{R}}_0^c-1)}$.

Notably, it is easily obtained that ${\mathcal{R}}_0^s<{\mathcal{R}}_0^c$. This then indicates that $E^{*}\in {\mathbb{R}}_{+}^3$ if ${\mathcal{R}}_0^s>1$. In addition, if there is no stochastic noise in system (1.3), i.e., model (1.1), then $E^{*}=E^{+}=(S^{+},V^{+},I^{+})$.

(II) (Equilibrium offset transformation): Given the above, let $X={(x_1,x_2,x_3)}^{\tau }=(u_1-u_1^{*},u_2-u_2^{*},u_3-u_3^{*})$; thus, the corresponding linearized system of (4.1) takes the form

$$\{\begin{array}{c}d{x}_1=(-a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3)dt+{\sigma }_{1}d{B}_1\left(t\right),\hfill \\ d{x}_2=(a_{21}{x}_1-a_{21}{x}_2)dt+{\sigma }_{2}d{B}_2\left(t\right),\hfill \\ d{x}_3=[(a_{32}+a_{33})x_1-a_{32}{x}_2-a_{33}{x}_3]dt+{\sigma }_{3}d{B}_3\left(t\right),\hfill \end{array}$$ (4.3)

where

$$a_{11}=\frac{\Lambda +\gamma V^{*}+\delta I^{*}}{S^{*}}-\frac{\beta S^{*}{I}^{*}}{{\left(N^{*}\right)}^2},a_{12}=\frac{\gamma V^{*}}{S^{*}}+\frac{\beta V^{*}{I}^{*}}{{\left(N^{*}\right)}^2}>0,a_{13}=\frac{\delta I^{*}}{S^{*}}-\frac{\beta (S^{*}+V^{*})I^{*}}{{\left(N^{*}\right)}^2},$$

$$a_{21}={\mu }_2+\gamma >0,a_{32}=\frac{\beta S^{*}{V}^{*}}{{\left(N^{*}\right)}^2}>0,a_{33}=\frac{\beta S^{*}{I}^{*}}{{\left(N^{*}\right)}^2}>0.$$

4.2. Density function of stationary distribution $\varpi (·)$

Theorem 4.1

For any initial value $(S\left(0\right),V\left(0\right),I\left(0\right))\in {\mathbb{R}}_{+}^3,$ if ${\mathcal{R}}_0^s>1,$ then the stationary distribution $\varpi (·)$ around $E^{*}$ follows a unique log-normal probability density function $\Phi (S,V,I),$ which is given by

$$\Phi (S,V,I)={\left(2\pi \right)}^{-\frac{3}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}}){\Sigma }^{-1}{(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}})}^{\tau }},$$ (4.4)

where $\Sigma$ is a positive definite matrix, and the special form of $\Sigma$ is given as follows.

$\left(1\right)$ . If $m_1\ne 0,m_2\ne 0$ and $a_{13}\ne 0,$ then

$$\Sigma ={\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }+{\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+{\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(M_3{J}_3\right)}^{-1}\right]}^{\tau }.$$

$\left(2\right)$ . If $m_1\ne 0,m_2\ne 0$ and $a_{13}=0,$ then

$$\Sigma ={\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }+{\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+J_4^{-1}{\Theta }_4{\left(J_4^{-1}\right)}^{\tau }.$$

$\left(3\right)$ . If $m_1\ne 0,m_2=0$ and $a_{13}\ne 0,$ then

$$\Sigma ={\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }+a_{32}^2{\sigma }_2^2{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}{\Theta }_3{\left[{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+{\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(M_3{J}_3\right)}^{-1}\right]}^{\tau }.$$

$\left(4\right)$ . If $m_1\ne 0$ and $m_2=a_{13}=0,$ then

$$\Sigma ={\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }+a_{32}^2{\sigma }_2^2{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}{\Theta }_3{\left[{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+J_4^{-1}{\Theta }_4{\left(J_4^{-1}\right)}^{\tau }.$$

$\left(5\right)$ . If $m_1=0,m_2\ne 0$ and $a_{13}\ne 0,$ then

$$\Sigma =a_{21}^2{\sigma }_1^2{\left({\tilde{H}}_1{J}_1\right)}^{-1}{\Theta }_1{\left[{\left({\tilde{H}}_1{J}_1\right)}^{-1}\right]}^{\tau }+{\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+{\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(M_3{J}_3\right)}^{-1}\right]}^{\tau }.$$

$\left(6\right)$ . If $m_1=a_{13}=0$ and $m_2\ne 0,$ then

$$\Sigma =a_{21}^2{\sigma }_1^2{\left({\tilde{H}}_1{J}_1\right)}^{-1}{\Theta }_1{\left[{\left({\tilde{H}}_1{J}_1\right)}^{-1}\right]}^{\tau }+{\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+J_4^{-1}{\Theta }_4{\left(J_4^{-1}\right)}^{\tau }.$$

$\left(7\right)$ . If $m_1=m_2=0$ and $a_{13}\ne 0,$ then

$$\Sigma =a_{21}^2{\sigma }_1^2{\left({\tilde{H}}_1{J}_1\right)}^{-1}{\Theta }_1{\left[{\left({\tilde{H}}_1{J}_1\right)}^{-1}\right]}^{\tau }+a_{32}^2{\sigma }_2^2{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}{\Theta }_3{\left[{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+{\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(M_3{J}_3\right)}^{-1}\right]}^{\tau }.$$

$\left(8\right)$ . If $m_1=m_2=a_{13}=0,$ then

$$\Sigma =a_{21}^2{\sigma }_1^2{\left({\tilde{H}}_1{J}_1\right)}^{-1}{\Theta }_1{\left[{\left({\tilde{H}}_1{J}_1\right)}^{-1}\right]}^{\tau }+a_{32}^2{\sigma }_2^2{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}{\Theta }_3{\left[{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+J_4^{-1}{\Theta }_4{\left(J_4^{-1}\right)}^{\tau },$$

with

$$J_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -\frac{a_{32}+a_{33}}{a_{21}}& 1\end{array}\right),J_2=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right),J_3=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& \frac{a_{12}}{a_{32}}& 1\end{array}\right),J_4=\left(\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right),$$

$${\Theta }_0=\left(\begin{array}{ccc}\frac{r_2}{2(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right),{\Theta }_1=\left(\begin{array}{ccc}\frac{1}{2w_1}& 0& 0\\ 0& \frac{1}{2w_1{w}_2}& 0\\ 0& 0& 0\end{array}\right),{\Theta }_3=\left(\begin{array}{ccc}\frac{1}{2w_3}& 0& 0\\ 0& \frac{1}{2w_3{w}_4}& 0\\ 0& 0& 0\end{array}\right),$$

$$H_1=\left(\begin{array}{ccc}{a}_{21}{m}_1& -(a_{21}+a_{33})m_1& a_{33}^2\\ 0& m_1& -a_{33}\\ 0& 0& 1\end{array}\right),{\tilde{H}}_2=\left(\begin{array}{ccc}-a_{32}& -a_{33}-a_{12}-\frac{a_{12}{a}_{33}}{a_{32}}& a_{32}+a_{33}\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),$$

$$H_2=\left(\begin{array}{ccc}-a_{32}{m}_2& -(a_{11}+a_{33})m_2& {(a_{11}-a_{12}-\frac{a_{12}{a}_{33}}{a_{32}})}^2+m_2(a_{32}+a_{33})\\ 0& m_2& -a_{11}+a_{12}+\frac{a_{12}{a}_{33}}{a_{32}}\\ 0& 0& 1\end{array}\right),{\Theta }_4=\left(\begin{array}{ccc}\frac{1}{2a_{33}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$

$${\tilde{H}}_1=\left(\begin{array}{ccc}{a}_{21}& -a_{21}& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),H_3=\left(\begin{array}{ccc}{a}_{13}{a}_{21}& -a_{21}(a_{11}+a_{21})& a_{21}(a_{12}+a_{21})\\ 0& a_{21}& -a_{21}\\ 0& 0& 1\end{array}\right),$$

and

$$m_1=\frac{a_{33}(a_{21}-a_{32}-a_{33})}{a_{21}},m_2=a_{13}+\frac{a_{12}(a_{11}-a_{33})}{a_{32}}-\frac{a_{12}^2(a_{32}+a_{33})}{a_{32}^2},$$

$${\varrho }_1=a_{21}{m}_1{\sigma }_1,{\varrho }_2=-a_{32}{m}_2{\sigma }_2,{\varrho }_3=a_{13}{a}_{21}{\sigma }_3,$$

$$r_1=a_{11}+a_{21}+a_{33},r_2=a_{21}(a_{11}-a_{12}+a_{33})+[a_{11}{a}_{33}-a_{13}(a_{32}+a_{33})],r_3=a_{21}{a}_{33}(a_{11}-a_{12}-a_{13}),$$

$$w_1=a_{11}+a_{21},w_2=a_{21}(a_{11}-a_{12}-a_{13}),w_3=a_{12}+a_{21}+a_{33}+\frac{a_{12}{a}_{33}}{a_{32}},w_4=\frac{a_{21}{a}_{32}{a}_{33}(a_{11}-a_{12}-a_{13})}{a_{32}(a_{11}-a_{12})-a_{12}{a}_{33}}.$$

Proof

For convenience and simplicity, let $B\left(t\right)={(B_1\left(t\right),B_2\left(t\right),B_3\left(t\right))}^{\tau }$ and

$$M=\left(\begin{array}{ccc}{\sigma }_1^2& 0& 0\\ 0& {\sigma }_2^2& 0\\ 0& 0& {\sigma }_3^2\end{array}\right),A=\left(\begin{array}{ccc}-a_{11}& a_{12}& a_{13}\\ a_{21}& -a_{21}& 0\\ a_{32}+a_{33}& -a_{32}& -a_{33}\end{array}\right).$$

Hence, system (4.3) can be rewritten as $dX=AXdt+MdB\left(t\right)$. By the theory of Gardiner [44], the unique density function $\Phi \left(X\right)$ around the quasi-endemic equilibrium $E^{*}$ satisfies the following Fokker-Plauck equation:

$$-\sum _{k=1}^3\frac{{\sigma }_k^2}{2}\frac{{\partial }^2\Phi }{\partial x_k^2}+\frac{\partial }{\partial x_1}\left[\right(-a_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3\left)\Phi \right]+\frac{\partial }{\partial x_2}\left[\right(a_{21}{x}_1-a_{21}{x}_2\left)\Phi \right]+\frac{\partial }{\partial x_3}\left[\right((a_{32}+a_{33})x_1-a_{32}{x}_2-a_{33}{x}_3\left)\Phi \right]=0.$$ (4.5)

Since the diffusion matrix $M$ is a constant matrix, Roozen [45] pointed out that $\Phi \left(X\right)$ can be described by a quasi-Gaussian distribution, i.e., $\Phi \left(X\right)=c_0{e}^{-\frac{1}{2}XQ{X}^{\tau }},$ where $c_0>0$ is determined by the normalized condition ${\int }_{R_{+}^3}\Phi \left(X\right)dX=1$ and $Q$ is a symmetric matrix.

Substituting these results into (4.5), one can obtain that $Q$ obeys the algebraic equation $Q{M}^{2}Q+A^{\tau }Q+QA=0$. If $Q$ is a inverse matrix, by letting $\Sigma =Q^{-1},$ an equivalent equation is given by

$$M^2+A\Sigma +\Sigma A^{\tau }=0.$$ (4.6)

Next, it will be proved that $A$ has all negative real-part eigenvalues. The characteristic polynomial of $A$ is defined as $\psi \left(\lambda \right)={\lambda }^3+p_1{\lambda }^2+p_2\lambda +p_3,$ where

$$r_1=a_{11}+a_{21}+a_{33},r_2=a_{21}(a_{11}-a_{12}+a_{33})+[a_{11}{a}_{33}-a_{13}(a_{32}+a_{33})],r_3=a_{21}{a}_{33}(a_{11}-a_{12}-a_{13}).$$

By the expressions of $S^{*},V^{*},I^{*}$ and $N^{*},$ it can be shown that

$$\begin{array}{cc}& \text{(i)}.a_{11}=({\mu }_1+\vartheta )+\frac{\beta I^{*}}{N^{*}}-\frac{\beta S^{*}{I}^{*}}{{\left(N^{*}\right)}^2}=({\mu }_1+\vartheta )+\frac{\beta (V^{*}+I^{*})I^{*}}{{\left(N^{*}\right)}^2}>0,\hfill \\ & \text{(ii)}.a_{11}-a_{12}-a_{13}=[\frac{\Lambda +\gamma V^{*}+\delta I^{*}}{S^{*}}-\frac{\beta S^{*}{I}^{*}}{{\left(N^{*}\right)}^2}]-[\frac{\gamma V^{*}}{S^{*}}+\frac{\beta V^{*}{I}^{*}}{{\left(N^{*}\right)}^2}]-[\frac{\delta I^{*}}{S^{*}}-\frac{\beta (S^{*}+V^{*})I^{*}}{{\left(N^{*}\right)}^2}]=\frac{\Lambda }{S^{*}}>0,\hfill \\ & \text{(iii)}.a_{12}{a}_{33}-a_{13}{a}_{32}=\frac{\beta S^{*}}{{\left(N^{*}\right)}^2}(\frac{\gamma V^{*}{I}^{*}}{S^{*}}+\frac{\beta V^{*}{I}^{*}}{N^{*}}-\frac{\delta V^{*}{I}^{*}}{S^{*}})=\frac{({\mu }_3+\gamma +\alpha )\beta V^{*}{I}^{*}}{{\left(N^{*}\right)}^2}>0,\hfill \\ & \text{(iv)}.a_{11}-a_{12}+a_{33}>\frac{\Lambda }{S^{*}}+\frac{\delta I^{*}}{S^{*}}-\frac{\beta V^{*}{I}^{*}}{{\left(N^{*}\right)}^2}>\frac{({\mu }_3+\alpha +\delta )({\mathcal{R}}_0^c-1)}{{\mu }_2+\gamma }[({\mu }_2+\gamma )+\frac{\vartheta ({\mathcal{R}}_0^c-1)}{{\mathcal{R}}_0^c}]>0.\hfill \end{array}$$

Consequently, it follows from (i)–(iv) that

$$\begin{array}{cccc}\left(1\right).\hfill & \hfill r_1& =& a_{11}+a_{21}+a_{33}>0,r_3=a_{21}{a}_{33}(a_{11}-a_{12}-a_{13})>0,\hfill \\ \left(2\right).\hfill & \hfill r_2& =& a_{21}(a_{11}-a_{12}+a_{33})+[a_{11}{a}_{33}-a_{13}(a_{32}+a_{33})]\hfill \\ & & >& (a_{12}+a_{13})a_{33}-a_{13}(a_{32}+a_{33})\hfill \\ & & =& a_{12}{a}_{33}-a_{13}{a}_{32}>0.\hfill \end{array}$$

$$\left(3\right).r_1{r}_2-r_3=(a_{11}+a_{21}+a_{33})\{a_{21}(a_{11}-a_{12}+a_{33})+[a_{11}{a}_{33}-a_{13}(a_{32}+a_{33})]\}-a_{21}{a}_{33}(a_{11}-a_{12}-a_{13})=a_{11}{r}_2+a_{21}[(a_{11}+a_{33})a_{33}-a_{13}{a}_{32}]+a_{33}[a_{11}{a}_{33}-a_{13}(a_{32}+a_{33})]=a_{11}{r}_2+a_{21}{a}_{33}(a_{11}-a_{12}+a_{33})+a_{33}^2(a_{11}-a_{12}-a_{13})+(a_{21}+a_{33})(a_{12}{a}_{33}-a_{13}{a}_{32})>a_{11}{r}_2>0.$$

Combining the above (1)-(3) and Lemma 2.6, that $\Sigma$ of Eq. (4.6) is positive definite can be derived.

However, following the corresponding proof of Lemma 2.6, which is shown in subsection (II) of Appendix A, the exact expression of $\Sigma$ is given. First, by the finite independent superposition principle, (4.6) can be equivalently transformed into the sum of solution to the following algebraic sub-equations,

$$M_k^2+A{\Sigma }_k+{\Sigma }_k{A}^{\tau }=0,$$

where $M_1=diag({\sigma }_1,0,0),M_2=diag(0,{\sigma }_2,0),M_3=diag(0,0,{\sigma }_3),$ and the symmetric matrices ${\Sigma }_k(k=1,2,3)$ are their respective solutions. Clearly, $\Sigma ={\Sigma }_1+{\Sigma }_2+{\Sigma }_3$. Now, the special expression of $\Sigma$ are derived by the following three steps.

Step 1. For the algebraic equation

$$M_1^2+A{\Sigma }_1+{\Sigma }_1{A}^{\tau }=0,$$ (4.7)

denote $A_1=J_{1}A{J}_1^{-1},$ where the elimination matrix $J_1$ and $A_1$ are derived by

$$J_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -\frac{a_{32}+a_{33}}{a_{21}}& 1\end{array}\right),A_1=\left(\begin{array}{ccc}-a_{11}& a_{12}+\frac{a_{13}(a_{32}+a_{33})}{a_{21}}& a_{13}\\ a_{21}& -a_{21}& 0\\ 0& m_1& -a_{33}\end{array}\right),$$

where $m_1=\frac{a_{33}(a_{21}-a_{32}-a_{33})}{a_{21}}$. By the value of $w_1,$ the relevant discussion is divided into two subcases:

$$\left(\mathbf{i}\right).m_1\ne 0,\left(\mathbf{ii}\right).m_1=0.$$

Case (i). If $m_1\ne 0,$ in view of the method introduced in Zhou et al. [28], it is assumed that $B_1=H_1{A}_1{H}_1^{-1},$ where the standardized transformation matrix is

$$H_1=\left(\begin{array}{ccc}{a}_{21}{m}_1& -(a_{21}+a_{33})m_1& a_{33}^2\\ 0& m_1& -a_{33}\\ 0& 0& 1\end{array}\right).$$ (4.8)

By direct calculation, one obtains

$$B_1=\left(\begin{array}{ccc}-r_1& -r_2& -r_3\\ 1& 0& 0\\ 0& 1& 0\end{array}\right),$$

where $r_1,r_2$ and $r_3$ are the same as above. Furthermore, one can equivalently transform Eq. (4.7) into

$$\left(H_1{J}_1\right)M_1^2{\left(H_1{J}_1\right)}^{\tau }+B_1\left[\left(H_1{J}_1\right){\Sigma }_1{\left(H_1{J}_1\right)}^{\tau }\right]+\left[\left(H_1{J}_1\right){\Sigma }_1{\left(H_1{J}_1\right)}^{\tau }\right]B_1^{\tau }=0.$$

Letting ${\Theta }_0={\varrho }_1^{-2}\left(H_1{J}_1\right){\Sigma }_1{\left(H_1{J}_1\right)}^{\tau },$ where ${\varrho }_1=a_{21}{m}_1{\sigma }_1,$ we obtain

$$G_0^2+B_1{\Theta }_0+{\Theta }_0{B}_1^{\tau }=0.$$

Noting that A has all negative real-part eigenvalues, then $B_1$ is a standard $R_1$ matrix. By Lemma 2.3, this means that ${\Sigma }_0$ is positive definite, which takes the form

$${\Theta }_0=\left(\begin{array}{ccc}\frac{r_2}{2(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right).$$ (4.9)

Therefore, ${\Sigma }_1={\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }$.

Case (ii). If $m_1=0,$ i.e., $a_{21}=a_{32}+a_{33},$ ${\tilde{B}}_1={\tilde{H}}_1{A}_1{\tilde{H}}_1^{-1}$ is defined, where another standardized transformation matrix ${\tilde{H}}_1$ and ${\tilde{B}}_1$ are obtained by

$${\tilde{H}}_1=\left(\begin{array}{ccc}{a}_{21}& -a_{21}& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),{\tilde{B}}_1=\left(\begin{array}{ccc}-w_1& -w_2& -{\xi }_1\\ 0& 1& 0\\ 0& 0& -a_{33}\end{array}\right),$$ (4.10)

where $w_1=a_{11}+a_{21},w_2=a_{21}(a_{11}-a_{12}-a_{13}),$ and ${\xi }_1$ is abbreviation. Obviously, ${\tilde{B}}_1$ is a standard $R_2$ matrix. Additionally, (4.7) can be equivalently transformed into

$$\left({\tilde{H}}_1{J}_1\right)M_1^2{\left({\tilde{H}}_1{J}_1\right)}^{\tau }+{\tilde{B}}_1\left[\left({\tilde{H}}_1{J}_1\right){\Sigma }_1{\left({\tilde{H}}_1{J}_1\right)}^{\tau }\right]+\left[\left({\tilde{H}}_1{J}_1\right){\Sigma }_1{\left({\tilde{H}}_1{J}_1\right)}^{\tau }\right]{\tilde{B}}_1^{\tau }=0.$$

By letting ${\Theta }_1={\left(a_{21}{\sigma }_1\right)}^{-2}\left({\tilde{H}}_1{J}_1\right){\Sigma }_1{\left({\tilde{H}}_1{J}_1\right)}^{\tau },$ it can be simplified as

$$G_0^2+{\tilde{B}}_1{\Theta }_1+{\Theta }_1{\tilde{B}}_1^{\tau }=0.$$

In view of Lemma 2.4, ${\Theta }_1$ is described by

$${\Theta }_1=\left(\begin{array}{ccc}\frac{1}{2w_1}& 0& 0\\ 0& \frac{1}{2w_1{w}_2}& 0\\ 0& 0& 0\end{array}\right).$$ (4.11)

Hence, ${\Sigma }_1=a_{21}^2{\sigma }_1^2{\left({\tilde{H}}_1{J}_1\right)}^{-1}{\Theta }_1{\left[{\left({\tilde{H}}_1{J}_1\right)}^{-1}\right]}^{\tau }$. Step 2. Consider the algebraic equation

$$M_2^2+A{\Sigma }_2+{\Sigma }_2{A}^{\tau }=0.$$ (4.12)

For the corresponding elimination matrix $J_2,J_3,$ $A_2=J_{2}A{J}_2^{-1}$ is defined, where $J_2,J_3$ and $A_2$ are obtained by

$$J_2=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right),J_3=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& \frac{a_{12}}{a_{32}}& 1\end{array}\right),A_2=\left(\begin{array}{ccc}-a_{21}& -\frac{a_{12}{a}_{21}}{a_{32}}& a_{21}\\ -a_{32}& -a_{33}-a_{12}-\frac{a_{12}{a}_{33}}{a_{32}}& a_{32}+a_{33}\\ 0& m_2& -a_{11}+a_{12}+\frac{a_{12}{a}_{33}}{a_{32}}\end{array}\right),$$

where $m_2=a_{13}+\frac{a_{12}(a_{11}-a_{33})}{a_{32}}-\frac{a_{12}^2(a_{32}+a_{33})}{a_{32}^2}$. Similarly, the following two sub-conditions are considered:

$$\left(\mathbf{1}\right).m_2\ne 0,\left(\mathbf{2}\right).m_2=0.$$

Case (1). If $m_2\ne 0,$ let $B_2=H_2{A}_2{H}_2^{-1},$ where the relevant standardized transformation matrix

$$H_2=\left(\begin{array}{ccc}-a_{32}{m}_2& -(a_{11}+a_{33})m_2& {(a_{11}-a_{12}-\frac{a_{12}{a}_{33}}{a_{32}})}^2+m_2(a_{32}+a_{33})\\ 0& m_2& -a_{11}+a_{12}+\frac{a_{12}{a}_{33}}{a_{32}}\\ 0& 0& 1\end{array}\right).$$ (4.13)

In fact, one still derives

$$B_2=B_1=\left(\begin{array}{ccc}-r_1& -r_2& -r_3\\ 1& 0& 0\\ 0& 1& 0\end{array}\right),$$

which means that $B_2$ is also a standard $R_1$ matrix. By letting ${\Theta }_2={\varrho }_2^{-2}\left(H_2{J}_2\right){\Sigma }_2{\left(H_2{J}_2\right)}^{\tau },$ where ${\varrho }_2=-a_{32}{m}_2{\sigma }_2,$ (4.12) is then equivalent to the following equation:

$$G_0^2+B_2{\Theta }_2+{\Theta }_2{B}_2^{\tau }=0.$$

By Lemma 2.3 and the result of A having all negative real-part eigenvalues again, it can be shown that

$${\Theta }_2={\Theta }_0=\left(\begin{array}{ccc}\frac{r_2}{2(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right).$$

In other words, ${\Sigma }_2={\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }$.

Case (2). If $m_2=0,$ let ${\tilde{B}}_2={\tilde{H}}_2{A}_2{\tilde{H}}_2^{-1},$ where the corresponding standardized transformation matrix ${\tilde{H}}_2$ and ${\tilde{B}}_2$ are given by

$${\tilde{H}}_2=\left(\begin{array}{ccc}-a_{32}& -a_{33}-a_{12}-\frac{a_{12}{a}_{33}}{a_{32}}& a_{32}+a_{33}\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),{\tilde{B}}_2=\left(\begin{array}{ccc}-w_3& -w_4& -{\xi }_2\\ 0& 1& 0\\ 0& 0& -a_{11}+a_{12}+\frac{a_{12}{a}_{33}}{a_{32}}\end{array}\right),$$

where $w_3=a_{12}+a_{21}+a_{33}+\frac{a_{12}{a}_{33}}{a_{32}},w_4=\frac{a_{21}{a}_{32}{a}_{33}(a_{11}-a_{12}-a_{13})}{a_{32}(a_{11}-a_{12})-a_{12}{a}_{33}},$ and ${\xi }_2$ is also shorthand. Similarly, ${\tilde{B}}_2$ is a standard $R_2$ matrix. By defining ${\Theta }_3={\left(a_{32}{\sigma }_2\right)}^{-2}\left({\tilde{H}}_2{J}_2\right){\Sigma }_2{\left({\tilde{H}}_2{J}_2\right)}^{\tau },$ (4.12) is then equivalent to

$$G_0^2+{\tilde{B}}_2{\Theta }_3+{\Theta }_3{\tilde{B}}_2^{\tau }=0.$$

According to Lemma 2.4, ${\Theta }_1$ takes the form

$${\Theta }_3=\left(\begin{array}{ccc}\frac{1}{2w_3}& 0& 0\\ 0& \frac{1}{2w_3{w}_4}& 0\\ 0& 0& 0\end{array}\right).$$ (4.14)

Then, ${\Sigma }_2=a_{32}^2{\sigma }_2^2{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}{\Theta }_3{\left[{\left({\tilde{H}}_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }$.

Step 3. For the following algebraic equation,

$$M_3^2+A{\Sigma }_3+{\Sigma }_3{A}^{\tau }=0,$$ (4.15)

and for the following elimination matrix $J_3,$ let $A_3=J_{4}A{J}_4^{-1},$ where $J_4$ and $A_3$ are given by

$$J_4=\left(\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right),A_3=\left(\begin{array}{ccc}-a_{33}& a_{32}+a_{33}& -a_{32}\\ a_{13}& a_{12}& -a_{11}\\ 0& a_{21}& -a_{21}\end{array}\right).$$

Hence, (4.15) can be equivalently transformed into

$$J_4{M}_3^2{J}_4^{\tau }+B_3{\Theta }_4+{\Theta }_4{B}_3^{\tau }=0,$$ (4.16)

where ${\Theta }_4=J_4{\Sigma }_3{J}_4^{\tau }$. Similarly, the proof is divided into two subcases by the value of $a_{13}$. Case (I). If $a_{13}\ne 0,$ consider the corresponding standardized transformation matrix

$$H_3=\left(\begin{array}{ccc}{a}_{13}{a}_{21}& -a_{21}(a_{11}+a_{21})& a_{21}(a_{12}+a_{21})\\ 0& a_{21}& -a_{21}\\ 0& 0& 1\end{array}\right).$$

Letting $B_3=H_3{A}_3{H}_3^{-1},$ that $B_3=B_1$ is still derived. Hence, an equivalent algebraic equation of (4.16) is described as follows:

$$\left(H_3{J}_4\right)M_3^2{\left(H_3{J}_4\right)}^{\tau }+B_3\left[\left(H_3{J}_4\right){\Sigma }_3{\left(H_3{J}_4\right)}^{\tau }\right]+\left[\left(H_3{J}_4\right){\Sigma }_3{\left(H_3{J}_4\right)}^{\tau }\right]B_3^{\tau }=0.$$

Denoting ${\Theta }_5={\varrho }_3^{-2}\left(H_3{J}_4\right){\Sigma }_3{\left(H_3{J}_4\right)}^{\tau },$ where ${\varrho }_3=a_{13}{a}_{21}{\sigma }_3,$ the last equation can be also simplified as

$$G_0^2+B_1{\Theta }_5+{\Theta }_5{B}_1^{\tau }=0.$$

Similarly, one obtains

$${\Theta }_5={\Theta }_0=\left(\begin{array}{ccc}\frac{r_2}{2(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right).$$

Consequently, ${\Sigma }_3={\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(H_3{J}_4\right)}^{-1}\right]}^{\tau }$.

Case (II). If $a_{21}=0,$ then $A_3$ is a standard $R_3$ matrix. Noting that $J_4{M}_3^2{J}_4^{\tau }={\sigma }_3^2{G}_0^2$=diag$({\sigma }_3^2,0,0),$ by Lemma 2.5, one can obtain

$${\Theta }_4=J_4{\Sigma }_3^2{J}_4^{\tau }=\left(\begin{array}{ccc}\frac{{\sigma }_3^2}{2a_{33}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$

Based on $a_{33}>0,$ then ${\Theta }_4$ is a positive semi-definite matrix, which means that ${\Sigma }_3=J_4^{-1}{\Theta }_4{\left(J_4^{-1}\right)}^{\tau }$.

In summary, the special form of $\Sigma$ is divided into eight cases by the different values of $m_1,m_2$ and $a_{13},$ which is shown in Theorem 4.1. Finally, in view of the relation of systems (4.1) and (4.3), the stationary distribution $\varpi (·)$ around $E^{*}$ then has a unique log-normal probability density function

$$\Phi (S,V,I)={\left(2\pi \right)}^{-\frac{3}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}}){\Sigma }^{-1}{(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}})}^{\tau }}.$$

Therefore, this completes the proof. □

Remark 3

If ${\mathcal{R}}_0^s>1,$ Theorem 4.1 shows that the stationary distribution $\varpi (·)$ around $E^{*}$ has the unique log-normal density function $\Phi (S,V,I)$. This reflects the stochastic permanence of system (1.3) from one side. In addition, that ${\mathcal{R}}_0^s={\mathcal{R}}_0^c={\mathcal{R}}_0$ if ${\sigma }_i=0(i=1,2,3)$ is obtained.

5. Extinction of system (1.3)

As is known, all of the properties of disease persistence of system (1.3) are reflected by Theorems 3.1 and 4.1. For a comprehensive study, a simple extinction result of system (1.3) is described by the following Theorem 5.1.

Theorem 5.1

For any initial value$(S\left(0\right),V\left(0\right),I\left(0\right))\in {\mathbb{R}}_{+}^3,$if${\mathcal{R}}_0^d=\frac{\beta }{\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2}}<1,$then the solution$\left(S\right(t),V(t),I(t\left)\right)$of system(1.3)follows:

$$\underset{t\to +\infty }{lim\; sup}\frac{\ln I\left(t\right)}{t}\le (\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})({\mathcal{R}}_0^d-1)<0,a.s.,$$ (5.1)

which means that the epidemic of system(1.3)will go to extinction with probability 1 (a.s.).

Proof

Employing It$\widehat{o}$’s formula to $\ln I\left(t\right),$ one obtains

$$d\ln I\left(t\right)=[\frac{\beta S\left(t\right)}{N\left(t\right)}-(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})]dt+{\sigma }_{3}d{B}_3\left(t\right).$$ (5.2)

Integrating from 0 to $t$ and dividing by $t$ on both sides of (5.1), it can be seen that

$$\begin{array}{cc}\hfill \frac{\ln I\left(t\right)}{t}\le & \frac{\ln I\left(0\right)}{t}+\frac{1}{t}{\int }_0^t[\frac{\beta S\left(u\right)}{N\left(u\right)}-(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})]du+\frac{{\int }_0^t{\sigma }_{3}d{B}_3\left(u\right)}{t}\hfill \\ \hfill \le & \frac{\ln I\left(0\right)}{t}+\frac{1}{t}{\int }_0^t[\beta -(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})]du+\frac{{\int }_0^t{\sigma }_{3}d{B}_3\left(u\right)}{t}\hfill \\ \hfill =& \frac{\ln I\left(0\right)}{t}+(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})({\mathcal{R}}_0^d-1)+\frac{{\int }_0^t{\sigma }_{3}d{B}_3\left(u\right)}{t}.\hfill \end{array}$$ (5.3)

Next, by the strong law of large numbers [1], one derives

$$\underset{t\to +\infty }{\lim }\frac{{\int }_0^t{\sigma }_{3}d{B}_3\left(u\right)}{t}=0,a.s.$$ (5.4)

Taking the superior limit of $t\to +\infty$ on both sides of (5.3), the assertion (5.1) can then be obtained by (5.4). Moreover, from the expressions of ${\mathcal{R}}_0^s$ and ${\mathcal{R}}_0^s,$ one can obtain that ${\mathcal{R}}_0^d\le {\mathcal{R}}_0^s$.

Consequently, the proof of Theorem 5.1 is confirmed. □

6. Simulations and parameter analyses

In this section, by means of the well-known higher-order method developed by Milstein [46], the corresponding discretization equation of system (1.3) is obtained in the form

$$\{\begin{array}{c}{\displaystyle S^{k+1}=S^k+[\Lambda -(\mu +\vartheta )S^k-\frac{\beta S^k{I}^k}{S^k+V^k+I^k}+\gamma V^k+\delta I^k]\Delta t+\frac{{\sigma }_1^2}{2}{S}^k({\xi }_k^2-1)\Delta t+{\sigma }_1{S}^k\sqrt{\Delta t}{\xi }_k}\hfill \\ {\displaystyle V^{k+1}=V^k+[\vartheta S^k-(\mu +\gamma )V^k]\Delta t+\frac{{\sigma }_2^2}{2}{V}^k({\eta }_k^2-1)\Delta t+{\sigma }_2{V}^k\sqrt{\Delta t}{\eta }_k}\hfill \\ {\displaystyle I^{k+1}=I^k+[\frac{\beta S^k{I}^k}{S^k+V^k+I^k}-(\mu +\alpha +\delta )I^k]\Delta t+\frac{{\sigma }_3^2}{2}{I}^k({\zeta }_k^2-1)\Delta t+{\sigma }_3{I}^k\sqrt{\Delta t}{\zeta }_k,}\hfill \end{array}$$ (6.1)

where the time increment $\Delta t>0,$ and ${\xi }_k,{\eta }_k,and{\zeta }_k$ are three independent Gaussian random variables that follow the distribution $N(0,1)$ for $k=1,2,...,n$. Furthermore, $(S^k,V^k,I^k)$ is the corresponding value of the $k$th iteration of the discretization equation. From AI-Darabsah [13], Zhao and Jiang [37], Liu et al. [38], Zhang and Jiang [39], Arino et al. [47], and the detailed data of the Central Statistical Office of Zimbabwe (CSZ), the corresponding realistic statistics of system (1.3) are shown in Table 1 . Next, several empirical examples are provided to focus on the following five aspects.

Table 1.

List of biological parameters of system (1.3).

Parameters	Description	Unit	Value	Source
$\Lambda$	Recruitment rate of population	per day	$\ge 0.5$	[38], [39]
$\beta$	Transmission rate of susceptible individuals	per day	[0.390,0.432]	[13]
$\mu$	Natural death rate of population	per day	$[2.74,6.85]\times {10}^{-5}$	[47],CSZ data
$\alpha$	Disease mortality of infected people	per day	$\frac{1}{0.6\times 365}$	[13]
$\delta$	Recovery rate	None	[0.01,0.2]	Estimated
$\gamma$	Immune loss rate of vaccinated individuals	None	0.2	[37]
$\vartheta$	Vaccination rate of susceptible individuals	None	[0.371,0.436]	[13]

(i) The existence of the ergodic stationary distribution of system (1.3) while ${\mathcal{R}}_0^s>1$.

(ii) The exact expression and verification of the unique log-normal density function for the stationary distribution under ${\mathcal{R}}_0^s>1$.

(iii) The influence of random fluctuations on the disease persistence of system (1.3).

(iv) The effects of the main parameters of system (1.3) on the disease dynamics.

(v) The corresponding dynamical behavior of system (1.3) if ${\mathcal{R}}_0^d<1$.

6.1. Dynamical behavior of system (1.3) if ${\mathcal{R}}_0^s>1$

Example 6.1

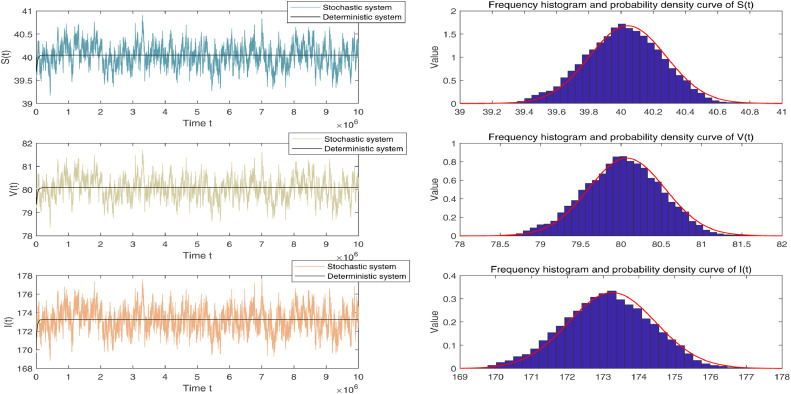
By Table 1, letting the environmental noise intensities $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$ and main parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.05,0.2,0.4),$ one then obtains

$${\mathcal{R}}_0=\frac{\beta (\mu +\gamma )}{(\mu +\gamma +\vartheta )(\mu +\alpha +\delta )}=2.44>1,{\mathcal{R}}_0^s=\frac{\mu \beta (\mu +\gamma +\frac{{\sigma }_2^2}{2})}{[(\mu +\frac{{\sigma }_1^2}{2})(\mu +\gamma +\frac{{\sigma }_2^2}{2})+\vartheta (\mu +\frac{{\sigma }_2^2}{2})](\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})}=2.43>1.$$

It follows from Theorem 3.1 that system (1.3) admits a unique ergodic stationary distribution $\varpi (·)$. The left-hand column of Fig. 1 can be seen to validate it. By Theorem 4.1, the stationary distribution $\varpi (·)$ around the quasi-endemic equilibrium $E^{*}$ has a unique log-normal density function $\Phi (S,V,I)$. Moreover, it is calculated that

$$m_1=0.0246\ne 0,m_2=-27.8515\ne 0,a_{13}=0.1196\ne 0,$$

which means

$$\begin{array}{ccc}\hfill \Sigma & =& {\varrho }_1^2{\left(H_1{J}_1\right)}^{-1}{\Theta }_0{\left[{\left(H_1{J}_1\right)}^{-1}\right]}^{\tau }+{\varrho }_2^2{\left(H_2{J}_3{J}_2\right)}^{-1}{\Theta }_0{\left[{\left(H_2{J}_3{J}_2\right)}^{-1}\right]}^{\tau }+{\varrho }_3^2{\left(H_3{J}_4\right)}^{-1}{\Theta }_0{\left[{\left(M_3{J}_3\right)}^{-1}\right]}^{\tau }\hfill \\ & =& {10}^{-4}\times \left(\begin{array}{ccc}0.3524& 0.3498& 0.3947\\ 0.3498& 0.3538& 0.3882\\ 0.3947& 0.3882& 0.4970\end{array}\right).\hfill \end{array}$$

By direct calculation, one can obtain that $E^{*}=(S^{*},V^{*},I^{*})=(40.0428,173.2562,80.0736)$. Then, the corresponding marginal density functions of $S\left(t\right),V\left(t\right)$ and $I\left(t\right)$ are separately given as follows.

$$\text{(1)}.P_1\left(S\right)=\frac{\partial \Phi }{\partial S}=67.204e^{-14188.4(\ln S-3.69)},\text{(ii)}.P_2\left(V\right)=\frac{\partial \Phi }{\partial V}=67.07e^{-14132.2(\ln V-5.15)},$$

$$\text{(iii)}.P_3\left(I\right)=\frac{\partial \Phi }{\partial I}=56.59e^{-10060.4(\ln I-4.38)}.$$

The curves of (i)-(iii) are shown in the right-hand column of Fig. 1. Obviously, this greatly illustrates Theorem 4.1 from the side.

Fig. 1.

Left-hand column shows simulation of compartments $S\left(t\right),V\left(t\right),$ and $I\left(t\right)$ in deterministic system (1.1) and stochastic system (1.3) with noise intensities $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$ and main parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.05,0.2,0.4),$ respectively. Right-hand column shows frequency histogram and corresponding marginal density function curves of individuals $S,V,$ and $I$.

Combining Remarks 3.1–4.1 and Theorem 5.1, one can derive that all random perturbations ${\sigma }_1,{\sigma }_2,$ and ${\sigma }_3$ have a critical influence on the dynamical behavior of system (1.3). Therefore, the corresponding parameter analyses of the above three white noises are shown by Example 6.2.

6.2. Impact of random noises ${\sigma }_i(i=1,2,3)$ on disease extinction and the existence of stationary distribution

Example 6.2

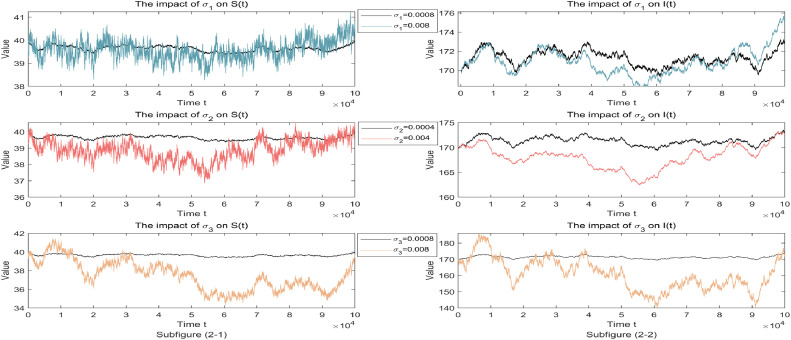
One chooses the epidemiological parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.05,0.2,$ 0.4) and considers the following four subcases of stochastic perturbations:

$$\left(\mathbf{i}\right).({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008),\left(\mathbf{ii}\right).({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.008,0.0004,0.0008),$$

$$\left(\mathbf{iii}\right).({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.004,0.0008),\left(\mathbf{iv}\right).({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.008).$$

First, it should be pointed out that the above four subcases (i)–(iv) all guarantee the existence of a stationary distribution, which has an ergodicity property. For convenience and simplicity, only the population intensities of susceptible and infected individuals are focused on, which are presented in subfigures (2-1) and (2-2) of Fig. 2 , respectively. By only increasing the perturbation intensities of the vaccinated individuals (or infected individuals), i.e., the larger ${\sigma }_2$ (or ${\sigma }_3$), then the disease infection will be effectively inhibited. In contrast, by only increasing the perturbation intensity of the susceptible individuals, a great destabilizing influence on the population numbers of $S$ and $I$ manifests.

Fig. 2.

Corresponding simulation of partial compartments $S\left(t\right)$ and $I\left(t\right)$ of stochastic system (1.3) under noise intensities $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008),(0.008,0.0004,0.0008),(0.0008,0.004,0.0008)$ and $(0.0008,0.0004,0.008),$ respectively. Other fixed parameters: $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.05,0.2,0.4)$.

Next, by Zhu et al. [25], Jia et al. [26], the impact of the main parameters of system (1.3) on the individual decision-making behavior is studied. From the expressions of ${\mathcal{R}}_0^s$ and ${\mathcal{R}}_0^d,$ the disease persistence and extinction of system (1.3) are critically affected by the transmission rate $\beta$ and vaccination rate $\vartheta$. Thus, the following Examples 6.3 and 6.4 will reveal the impact. In addition, the corresponding effect of the recruitment rate $\Lambda$ on the dynamical behavior of system (1.3) is also shown in Example 6.5.

6.3. Impact of transmission rate $\beta$ on dynamics of system (1.3)

Example 6.3

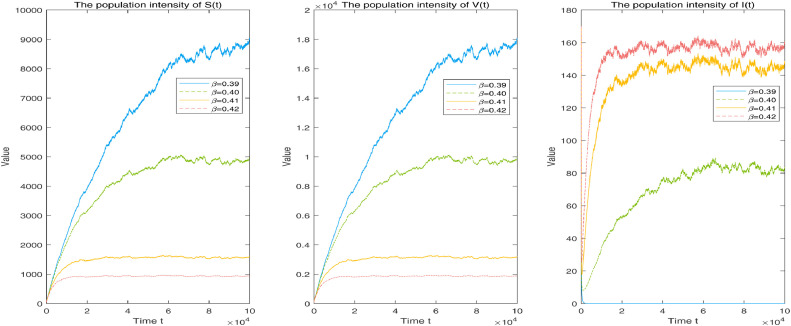
Choosing the epidemiological parameters $(\Lambda ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,3\times {10}^{-5},0.00457,0.128,0.2,0.4)$ and random noises $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$ and considering the subcases of transmission rate $\beta =0.39,0.40,0.41$ and 0.42, the corresponding numbers of the solution $\left(S\right(t),V(t),I(t\left)\right)$ to system (1.3) are described in Fig. 3 . Clearly, a small transmission rate can lead to reduction of disease infection and even elimination, such as $\beta \le 0.39$ per day.

Fig. 3.

Corresponding population numbers of solution $\left(S\right(t),V(t),I(t\left)\right)$ to system (1.3) with transmission rates of $\beta =0.39,0.40,0.41,$ and 0.42, respectively. Other given parameters: $(\Lambda ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,3\times {10}^{-5},0.00457,0.128,0.2,0.4)$ and $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$.

6.4. Impact of vaccination rate $\vartheta$ on dynamics of system (1.3)

Example 6.4

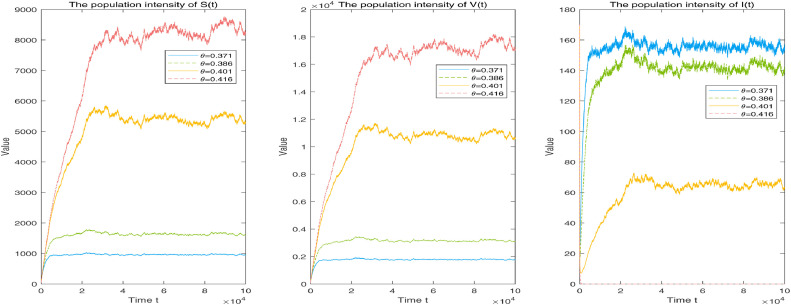
Assuming that the parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma )=(0.8,0.4,3\times {10}^{-5},0.00457,0.128,0.2)$ and stochastic perturbations $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008),$ for the corresponding subcases of vaccination rate $\vartheta =0.371,0.386,0.401,$ and 0.416, the corresponding solutions $\left(S\right(t),V(t),andI(t\left)\right)$ to system (1.3) are shown in Fig. 4 . Similarly, a small vaccination rate can control the disease infection more effectively than a large one.

Fig. 4.

Corresponding simulation of solution $\left(S\right(t),V(t),I(t\left)\right)$ to system (1.3) with vaccination rate $\vartheta =0.371,0.386,0.401,$ and 0.416, respectively. Other fixed parameters: $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma )=(0.8,0.4,3\times {10}^{-5},0.00457,0.128,0.2)$ and $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$.

6.5. Impact of recruitment rate $\Lambda$ on dynamics of system (1.3)

Example 6.5

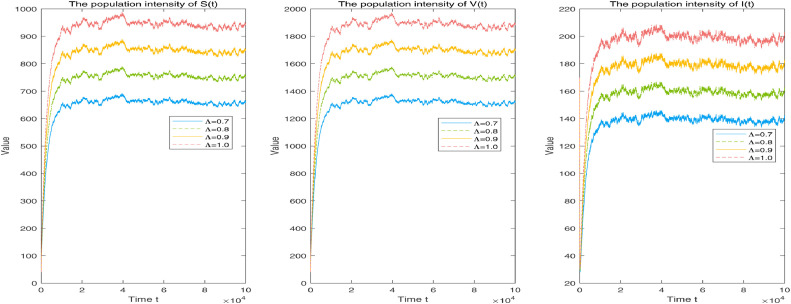
Letting the dynamical parameters be $(\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.4,3\times {10}^{-5},0.00457,0.128,0.2,0.4)$ and stochastic fluctuations be $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008),$ and considering the sub-conditions of recruitment rate $\Lambda =0.7,0.408,0.9,$ and 1.0, the corresponding intensities of the compartments $S,V,$ and $I$ of system (1.3) are reflected in Fig. 5 . Obviously, as the parameter $\Lambda$ increases to 1 from 0.7, the spread and infection of an epidemic can be effectively controlled by the small recruitment rate.

Fig. 5.

Corresponding population intensities of individuals $S,V,$ and $I$ of system (1.3) with recruitment rate $\Lambda =0.7,0.8,0.9,$ and 1.0, respectively. Other given parameters: $(\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.4,3\times {10}^{-5},0.00457,0.128,0.2,0.4)$ and $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.0008,0.0004,0.0008)$.

6.6. Dynamical behaviors of system (1.3) under ${\mathcal{R}}_0^d<1$

Example 6.6

Considering the stochastic noises $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.01,0.01,0.78)$ and main parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.13,0.2,0.38),$ one can then obtain

$${\mathcal{R}}_0=\frac{\beta (\mu +\gamma )}{(\mu +\gamma +\vartheta )(\mu +\alpha +\delta )}=1.0249>1,{\mathcal{R}}_0^d=\frac{\beta }{\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2}}=0.9116<1,{\mathcal{R}}_0^s=0.1179<1.$$

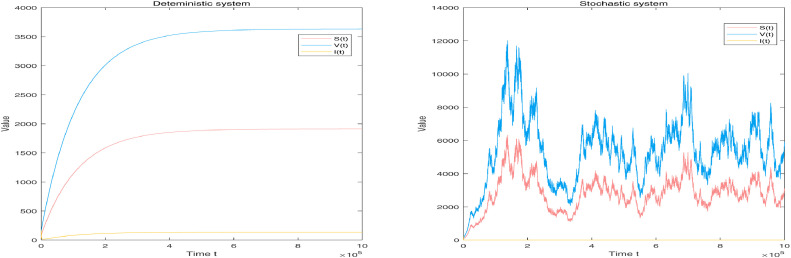
By Theorem 3.1, one cannot derive the existence of the ergodic stationary distribution of system (1.3). In contrast, it follows from Theorem 5.1 that the disease of stochastic system (1.3) will be extinct in a long term. In addition, the deterministic model (1.1) has a globally asymptotically stable endemic equilibrium $E^{+}$. On the one hand, these results validate the fact that large white noises lead to disease elimination from the side. On the other hand, the large random fluctuation ${\sigma }_3(i.e.,\frac{{\sigma }_3}{{\sigma }_1}=\frac{{\sigma }_3}{{\sigma }_2}=78>>1)$ indicates that it is necessary to isolate and control the infected individuals during the outbreak of an epidemic. These results are verified by Fig. 6 .

Fig. 6.

Corresponding population numbers of solution $\left(S\right(t),V(t),I(t\left)\right)$ to system (1.3) with random perturbations $({\sigma }_1,{\sigma }_2,{\sigma }_3)=(0.01,0.01,0.78)$ and main parameters $(\Lambda ,\beta ,\mu ,\alpha ,\delta ,\gamma ,\vartheta )=(0.8,0.4,3\times {10}^{-5},0.00457,0.13,0.2,0.38)$.

For epidemiological study, combining the above numerical simulations and parameter analyses, several reasonable and effective measures to reduce the threat of infectious diseases to human life, and even eliminate the epidemic, are provided. The special approaches are the following.

(i) Several reasonable policies of joint prevention and control are implemented to reduce the population mobility in differential risk epidemic areas. Then, the small recruitment rate $\Lambda$ may lead to the elimination of disease (see Fig. 5).

(ii) Controlling the activities of the susceptible individuals in highly pathogenic areas to decrease the contact rate of population. Hence, $\beta \to 0^{+}$ can be guaranteed, which means ${\mathcal{R}}_0^s<1$ and ${\mathcal{R}}_0^d<1$ (see Fig. 3).

(iii) Developing several effective vaccines and carrying out other prophylactic measures to improve the immune rate of disease (see Fig. 4).

7. Conclusions and result discussions

7.1. Conclusions

The corresponding theoretical results of this paper are the following.

(i) By Theorem 3.1, system (1.3) admits a unique ergodic stationary distribution $\varpi (·)$ under

$${\mathcal{R}}_0^s=\frac{\mu \beta (\mu +\gamma +\frac{{\sigma }_2^2}{2})}{[(\mu +\frac{{\sigma }_1^2}{2})(\mu +\gamma +\frac{{\sigma }_2^2}{2})+\vartheta (\mu +\frac{{\sigma }_2^2}{2})](\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})}.$$

(ii) By taking the effect of random perturbations into account, a quasi-endemic equilibrium $E^{*}$ related to $E^{+}$ is defined while ${\mathcal{R}}_0^c=\frac{\beta (\mu +\gamma +\frac{{\sigma }_2^2}{2})}{(\mu +\gamma +\epsilon +\frac{{\sigma }_2^2}{2})(\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2})}>1$. In view of the expressions of ${\mathcal{R}}_0^c$ and ${\mathcal{R}}_0^s,$ it is further proved that the stationary distribution $\varpi (·)$ around $E^{*}$ has a log-normal density function in the following form:

$$\Phi (S,V,I)={\left(2\pi \right)}^{-\frac{3}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}}){\Sigma }^{-1}{(\ln \frac{S}{S^{*}},\ln \frac{V}{V^{*}},\ln \frac{I}{I^{*}})}^{\tau }},$$

where the special form of $\Sigma$ is shown in Theorem 4.1. (iii) The disease of system (1.3) will go to extinction with probability 1 if ${\mathcal{R}}_0^d=\frac{\beta }{\mu +\alpha +\delta +\frac{{\sigma }_3^2}{2}}<1$. The above results (i) and (ii) reflect the stochastic persistence and ergodicity of the epidemic. Moreover, the corresponding disease extinction of system (1.3) is described by result (iii).

7.2. Result discussions

In this paper, combining the great effect of vaccination and the unpredictability of environmental fluctuations in the real world, a stochastic SVIS infectious disease model with vaccination and standard incidence is the object of concern. Adopting the descriptions in [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], linear perturbation, which is the most intuitive assumption of a random effect, is similarly taken into consideration in this paper. Subsequently, several dynamical properties of stochastic system (1.3) are analyzed, such as the existence and uniqueness of a global positive solution, existence and ergodicity of a stationary distribution, and disease elimination. By comparison with the existing results ([28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40]), several highlights developed in the present study are detailed in the following two points.

$•$ As is known, the endemic equilibrium and basic reproduction number, two important results of a deterministic epidemic, reflect disease permanence and elimination. Similarly, for the corresponding stochastic model, the existence of stationary distribution indicates the stochastic positive equilibrium state. In this paper, it is first proved that stochastic system (1.3) admits a unique ergodic stationary distribution under the critical value ${\mathcal{R}}_0^s>1$. It should be pointed out that ${\mathcal{R}}_0^s>1$ is a unified threshold for the disease persistence of systems (1.1) and (1.3). Moreover, the sufficient condition ${\mathcal{R}}_0^d<1$ is obtained for the disease extinction of system (1.3). Both ${\mathcal{R}}_0^s>1$ and ${\mathcal{R}}_0^d<1$ reveal that the dynamical behavior of system (1.3) is critically affected by the random fluctuations, i.e., ${\sigma }_1,{\sigma }_2,$ and ${\sigma }_3$. In view of the method of controlling variables and numerical simulations, this means that a large white noise leads to the disease eradication, while a small one guarantees stochastic permanence. In addition, by the main parameter analyses, several effective measures to stop the spread of an epidemic are provided.

$•$ It is generally accepted that the existence of an ergodic stationary distribution incurs difficulty in studying more exact statistical properties. Hence, this paper is devoted to obtaining the corresponding probability density function for further dynamical investigation. The results of Zhou et al. [28] are further perfected and general solving theories of algebraic equations with respect to the three-dimensional Fokker-Planck equation are developed, which are described in Lemmas 2.5 and 2.6. By taking the effect of stochasticity into account again, the quasi-endemic equilibrium $E^{*}$ corresponding to the endemic equilibrium $E^{+}$ is defined. For practical application, the exact expression of the log-normal three-dimensional density function $\Phi (S,V,I)$ of system (1.3) is given. Furthermore, it is worth mentioning that the methods and theories developed herein are still suitable for the case of the diffusion matrix $M$ being positive semi-definite, such as delay stochastic differential equations [32], [48].

Several remaining issues are now proposed and analyzed. First, by virtue of the limitation of the present mathematical approaches for epidemiological dynamics, a value gap exists between ${\mathcal{R}}_0^s$ and ${\mathcal{R}}_0^d,$ and it is unfortunate that difficulty is encountered in obtaining the most precise threshold for disease extinction and persistence. Second, the impact of telegraph noises and periodicity on the dynamics of system (1.3) should also be studied; the reader is referred to [30], [34], [45], [49], [50]. These problems are expected to be studied and solved as planned future work.

CRediT authorship contribution statement

Baoquan Zhou: Validation, Software, Formal analysis, Writing - original draft, Writing - review & editing. Daqing Jiang: Conceptualization, Investigation, Methodology, Writing - review & editing. Yucong Dai: Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Tasawar Hayat: Conceptualization, Writing - review & editing. Ahmed Alsaedi: Investigation, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Appendix A.  

(I) (Proof of Lemma 2.5): Consider the algebraic equation $G_1^2+C_0{{\rm Y}}_3+{{\rm Y}}_3{C}_0^{\tau }=0,$ where ${{\rm Y}}_3$ is a symmetric matrix. Letting ${{\rm Y}}_3:={\left({\kappa }_{ij}\right)}_{3\times 3},$ by direct calculation one has

$${{\rm Y}}_3=\left(\begin{array}{ccc}{\kappa }_{11}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$ (A.1)

where ${\kappa }_{11}=-\frac{a_0^2}{2c_{11}}$. If $c_{11}<0,$ then it means that ${{\rm Y}}_3$ is a positive semi-definite matrix. The proof is then completed.

(II) (Proof of Lemma 2.6): Denote

$${\Pi }_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),{\Pi }_2=\left(\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right),{\Pi }_3=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right).$$

Let ${\Sigma }_i(i=1,2,3)$ be the solutions of the following algebraic equations, respectively:

$${\Pi }_i+A{\Sigma }_i+{\Sigma }_i{A}^{\tau }=0.$$

Obviously, one can obtain

$${\Sigma }_0={\alpha }_1^2{\Sigma }_1+{\alpha }_2^2{\Sigma }_2+{\alpha }_3^2{\Sigma }_3.$$

Before proving the positive definiteness of ${\Sigma }_0,$ the following two theories of matrix algebra should be described first.

$\left(T_1\right)$. The positive definiteness of the matrix is not affected by the inverse congruence transformation.

$\left(T_2\right)$. The similarity transformation does not change the eigenvalues of the matrix.

For convenience and simplicity, an important notation is introduced as follows. For the same dimensional square matrix $A$ and $B,$ define

$$A⪰B:A-B\text{is}\text{at}\text{least}\text{a}\text{positive}\text{semi-definite}\text{matrix}.$$

Given the above, it is easily derived that $A$ is also positive definite if $B$ is a positive definite matrix.

First, consider the following algebraic equation,

$${\Pi }_1+A{\Sigma }_1+{\Sigma }_1{A}^{\tau }=0,$$ (A.2)

after which the relevant proof can be divided into the following two conditions:

$$\left({\mathcal{B}}_1\right).a_{21}=a_{31}=0,\left({\mathcal{B}}_2\right).a_{21}\ne 0\text{or}{a}_{31}\ne 0.$$

Next, one must demonstrate that the elements $a_{21}$ and $a_{31}$ have the equivalent status in $A$. Let $\tilde{A}=F_{1}A{F}_1^{-1}:={\left({\tilde{a}}_{ij}\right)}_{3\times 3},$ where $\tilde{A}$ and the invertible matrix $F_1$ are given by

$$F_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),\tilde{A}=\left(\begin{array}{ccc}{a}_{11}& a_{13}& a_{12}\\ a_{31}& a_{33}& a_{32}\\ a_{21}& a_{23}& a_{22}\end{array}\right),$$

respectively. Hence, (A.2) can be equivalently transformed as

$$F_1{\Pi }_1{F}_1^{\tau }+\tilde{A}\left(F_1{\Sigma }_1{F}_1^{\tau }\right)+\left(F_1{\Sigma }_1{F}_1^{\tau }\right){\tilde{A}}^{\tau }=0.$$ (A.3)

By defining ${\tilde{\Pi }}_1=F_1{\Pi }_1{F}_1^{\tau },{\tilde{\Sigma }}_1=F_1{\Sigma }_1{F}_1^{\tau },$ it can be noticed that

$$\text{(i)}.{\tilde{\Pi }}_1={\Pi }_1,\text{(ii)}.{\tilde{\Sigma }}_1\text{and}{\Sigma }_1\text{have}\text{the}\text{same}\text{positive}\text{definiteness}.$$

In addition, ${\tilde{a}}_{21}=a_{31},{\tilde{a}}_{31}=a_{21}$. Therefore, the validation is completed. Namely, one must only discuss the following two cases, which are equivalent to conditions $\left({\mathcal{B}}_1\right)$ and $\left({\mathcal{B}}_2\right),$ respectively:

$$\left({\mathcal{C}}_1\right).a_{21}=a_{31}=0,\left({\mathcal{C}}_2\right).a_{21}\ne 0.$$

Case $\left({\mathcal{C}}_1\right)$. If $a_{21}=a_{31}=0,$ by directly solving Eq. (A.2), one obtains

$${\Sigma }_1=\left(\begin{array}{ccc}-\frac{1}{2a_{11}}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right):={\Delta }_{11}.$$

Since $A$ has all negative real part eigenvalues, by the similarity invariance of ${\psi }_A\left(\lambda \right),$ it indicates that

$${\lambda }^3+r_1{\lambda }^2+r_2\lambda +r_3={\psi }_A\left(\lambda \right)=(\lambda -a_{11})[{\lambda }^2-(a_{22}+a_{33})\lambda +(a_{22}{a}_{33}-a_{23}{a}_{32})].$$

Consequently, ${\phi }_A\left(\lambda \right)$ has an eigenvalue ${\lambda }_1=a_{11},$ which has a negative real part. By $a_{11}\in \mathbb{R},$ then $a_{11}<0$. In other words, ${\Delta }_{11}$ is positive semi-definite. Moreover,

$${\Sigma }_1⪰{\Delta }_{11}.$$ (A.4)

Case $\left({\mathcal{C}}_2\right)$. If $a_{21}\ne 0,$ let ${\omega }_0=a_{32}+\frac{a_{31}(a_{33}-a_{22})}{a_{21}}-\frac{a_{23}{a}_{31}^2}{a_{21}^2}$.

$•$ If ${\omega }_0=0,$ which means $a_{21}(a_{21}{a}_{32}-a_{22}{a}_{31})-a_{31}(a_{31}{a}_{23}-a_{21}{a}_{33})=0,$ let $\widehat{A}=\left(F_3{F}_2\right)A{\left(F_3{F}_2\right)}^{-1},$ where

$$F_2=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -\frac{a_{31}}{a_{21}}& 1\end{array}\right),F_3=\left(\begin{array}{ccc}{a}_{21}& a_{22}+\frac{a_{23}{a}_{31}}{a_{21}}& a_{23}\\ 0& 1& 0\\ 0& 0& 1\end{array}\right).$$

Thus, (A.2) can be equivalently rewritten as

$$\left(F_3{F}_2\right){\Lambda }_1{\left(F_3{F}_2\right)}^{\tau }+\widehat{A}\left[\left(F_3{F}_2\right){\Sigma }_1{\left(F_3{F}_2\right)}^{\tau }\right]+\left[\left(F_3{F}_2\right){\Sigma }_1{\left(F_3{F}_2\right)}^{\tau }\right]{\widehat{A}}^{\tau }=0.$$ (A.5)

Denoting ${\widehat{\Pi }}_1=\left(F_3{F}_2\right){\Pi }_1{\left(F_3{F}_2\right)}^{\tau }$ and ${\widehat{\Sigma }}_1=\left(F_3{F}_2\right){\Sigma }_1{\left(F_3{F}_2\right)}^{\tau },$ one computes

$${\widehat{\Pi }}_1=\left(\begin{array}{ccc}{a}_{21}^2& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\widehat{A}=\left(\begin{array}{ccc}-{\xi }_1& -{\xi }_2& -{\xi }_3\\ 1& 0& 0\\ 0& 0& a_{33}-\frac{a_{23}{a}_{31}}{a_{21}}\end{array}\right),{\widehat{\Sigma }}_1=\left(\begin{array}{ccc}\frac{a_{21}^2}{2{\xi }_1}& 0& 0\\ 0& \frac{a_{21}^2}{2{\xi }_1{\xi }_2}& 0\\ 0& 0& 0\end{array}\right),$$

where the parameters ${\xi }_k(k=1,2,3)$ can be obtained by (A.5). Because their sign is the only object of concern, they are omitted here. Furthermore, the characteristic polynomial ${\psi }_A\left(\lambda \right)$ follows from $\widehat{A}$ that

$${\psi }_A\left(\lambda \right)=(\lambda -a_{33}+\frac{a_{23}{a}_{31}}{a_{21}})({\lambda }^2+{\xi }_1\lambda +{\xi }_2).$$

By the condition that $A$ has all negative real part eigenvalues, it thus means that the equation ${\lambda }^2+{\xi }_1\lambda +{\xi }_2=0$ has two negative real part roots. By the Routh-Hurwitz stability criterion [43], it can be shown that

$${\xi }_1>0,{\xi }_2>0.$$ (A.6)

In view of

$${\widehat{\Sigma }}_1=\left(\begin{array}{ccc}\frac{a_{21}^2}{2{\xi }_1}& 0& 0\\ 0& \frac{a_{21}^2}{2{\xi }_1{\xi }_2}& 0\\ 0& 0& 0\end{array}\right)=\left(\begin{array}{ccc}\frac{a_{21}^2}{2{\xi }_1}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)+\left(\begin{array}{ccc}0& 0& 0\\ 0& \frac{a_{21}^2}{2{\xi }_1{\xi }_2}& 0\\ 0& 0& 0\end{array}\right):=L_1+L_2,$$

one hence obtains

$$\begin{array}{cc}\hfill {\Sigma }_1=& {\left(F_3{F}_2\right)}^{-1}{\widehat{\Sigma }}_1{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }={\left(F_3{F}_2\right)}^{-1}(L_1+L_2){\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ \hfill =& {\left(F_3{F}_2\right)}^{-1}{L}_1{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }+{\left(F_3{F}_2\right)}^{-1}{L}_2{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ \hfill =& \left(\begin{array}{ccc}\frac{1}{2{\xi }_1}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)+{\left(F_3{F}_2\right)}^{-1}{L}_2{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ \hfill :=& {\Delta }_{12}+{\left(F_3{F}_2\right)}^{-1}{L}_2{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }.\hfill \end{array}$$ (A.7)

By means of ${\xi }_1>0$ and ${\xi }_2>0,$ it is derived that ${\Delta }_{12},L_2$ and ${\left(F_3{F}_2\right)}^{-1}{L}_2{\left[{\left(F_3{F}_2\right)}^{-1}\right]}^{\tau }$ are all positive semi-definite. It is then implied that

$${\Sigma }_1⪰{\Delta }_{12}.$$ (A.8)

$•$ If ${\omega }_0\ne 0,$ let $\overline{A}=\left(F_4{F}_2\right)A{\left(F_4{F}_2\right)}^{-1},$ where the invertible matrix $F_4$ is given by

$$F_4=\left(\begin{array}{ccc}{a}_{21}{\omega }_0& (a_{22}+a_{33}){\omega }_0& {(a_{33}-\frac{a_{23}{a}_{31}}{a_{21}})}^2+a_{23}{\omega }_0\\ 0& {\omega }_0& a_{33}-\frac{a_{23}{a}_{31}}{a_{21}}\\ 0& 0& 1\end{array}\right).$$

Denoting ${\overline{\Pi }}_1=\left(F_4{F}_2\right){\Lambda }_1{\left(F_4{F}_2\right)}^{\tau },{\overline{\Sigma }}_1=\left(F_4{F}_2\right){\Sigma }_1{\left(F_4{F}_2\right)}^{\tau },$ (A.2) can then be equivalently transformed into the following equation:

$${\overline{\Pi }}_1+\overline{A}{\overline{\Sigma }}_1+{\overline{\Sigma }}_1{\overline{A}}^{\tau }=0.$$ (A.9)

Similarly, by direct calculation, one obtains that ${\widehat{\Pi }}_1=diag({\left(a_{21}{\omega }_0\right)}^2,0,0),$ and

$$\widehat{A}=\left(\begin{array}{ccc}-r_1& -r_2& -r_3\\ 1& 0& 0\\ 0& 1& 0\end{array}\right),{\widehat{\Sigma }}_1={\left(a_{21}{\omega }_0\right)}^2\left(\begin{array}{ccc}\frac{r_2}{2(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right),$$

where $r_1,r_2,r_3$ are the same as those in Lemma 2.6. Considering

$${\overline{\Sigma }}_1={\left(a_{21}{\omega }_0\right)}^2\left(\begin{array}{ccc}\frac{1}{2r_1}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)+{\left(a_{21}{\omega }_0\right)}^2\left(\begin{array}{ccc}\frac{r_1}{2r_3(r_1{r}_2-r_3)}& 0& -\frac{1}{2(r_1{r}_2-r_3)}\\ 0& \frac{1}{2(r_1{r}_2-r_3)}& 0\\ -\frac{1}{2(r_1{r}_2-r_3)}& 0& \frac{r_1}{2r_3(r_1{r}_2-r_3)}\end{array}\right):=L_3+L_4,$$

one can therefore derive, by a similar method as that described in (A.7),

$$\begin{array}{ccc}\hfill {\Sigma }_1& =& {\left(F_4{F}_2\right)}^{-1}{\overline{\Sigma }}_1{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }={\left(F_4{F}_2\right)}^{-1}(L_3+L_4){\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ & =& {\left(F_4{F}_2\right)}^{-1}{L}_3{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }+{\left(F_4{F}_2\right)}^{-1}{L}_4{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ & =& \left(\begin{array}{ccc}\frac{1}{2r_1}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)+{\left(F_4{F}_2\right)}^{-1}{L}_4{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }\hfill \\ & :=& {\Delta }_{13}+{\left(F_4{F}_2\right)}^{-1}{L}_4{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }.\hfill \end{array}$$

Noting that ${\Delta }_{13},L_4$ and ${\left(F_4{F}_2\right)}^{-1}{L}_4{\left[{\left(F_4{F}_2\right)}^{-1}\right]}^{\tau }$ are all positive semi-definite, one then has

$${\Sigma }_1⪰{\Delta }_{13}.$$ (A.10)

Consequently, by (A.4), (A.8) and (A.10), a constant ${\eta }_1>0$ always exists such that

$${\Sigma }_1⪰\left(\begin{array}{ccc}{\eta }_1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$ (A.11)

In addition, for the following two algebraic equations,

$$\text{(i)}.{\Pi }_2+A{\Sigma }_2+{\Sigma }_2{A}^{\tau }=0,\text{(ii)}.{\Pi }_3+A{\Sigma }_3+{\Sigma }_3{A}^{\tau }=0,$$

and letting ${\tilde{\Pi }}_2=F_5{\Pi }_2{F}_5^{\tau },{\tilde{\Pi }}_3=F_6{\Pi }_3{F}_6^{\tau },{\tilde{\Sigma }}_2=F_5{\Sigma }_2{F}_5^{\tau },{\tilde{\Sigma }}_3=F_6{\Sigma }_3{F}_6^{\tau },and{A}_2=F_{5}A{F}_5^{-1},A_3=F_{6}A{F}_6^{-1},$ where

$$F_5=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right),F_6=\left(\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right).$$

Noting that ${\tilde{\Pi }}_2={\tilde{\Pi }}_3={\Pi }_1,$ by a method similar to that shown in (A.2), one can see that

$${\tilde{\Sigma }}_2⪰\left(\begin{array}{ccc}{\eta }_2& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),{\tilde{\Sigma }}_3⪰\left(\begin{array}{ccc}{\eta }_3& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),$$

where the constants ${\eta }_2>0and{\eta }_3>0$; that is to say,

$${\Sigma }_2=F_5^{-1}{\tilde{\Sigma }}_2{F}_5^{-1}⪰\left(\begin{array}{ccc}0& 0& 0\\ 0& {\eta }_2& 0\\ 0& 0& 0\end{array}\right),{\Sigma }_3=F_6^{-1}{\tilde{\Sigma }}_3{F}_6^{-1}⪰\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& {\eta }_3\end{array}\right).$$ (A.12)

In summary, it can be derived that

$${\Sigma }_0={\alpha }_1^2{\Sigma }_1+{\alpha }_2^2{\Sigma }_2+{\alpha }_3^2{\Sigma }_3⪰\left(\begin{array}{ccc}{\alpha }_1^2{\eta }_1& 0& 0\\ 0& {\alpha }_2^2{\eta }_2& 0\\ 0& 0& {\alpha }_3^2{\eta }_3\end{array}\right).$$

Given the above definitions and discussions, ${\Sigma }_0$ is a positive-definite matrix. This completes the proof.

(III). (SED Preliminaries): For the above complete probability space $\{\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P}\},$ it is assumed that $B\left(t\right)$ is an $n$-dimensional standard Brownian motion defined on it. Consider the following $n$-dimensional SDE,

$$dX\left(t\right)=f(X\left(t\right),t)dt+g(X\left(t\right),t)dB\left(t\right),\text{for}t\ge t_0$$

, with the initial value $X\left(t_0\right)=X_0\in {\mathbb{R}}^n$. A common differential operator $\mathcal{L}$ is given by

$$\mathcal{L}=\frac{\partial }{\partial t}+\sum _{k=1}^n{f}_k(X,t)\frac{\partial }{\partial X_k}+\frac{1}{2}\sum _{i,j=1}^n{\left[g^{\tau }(X,t)g(X,t)\right]}_{ij}\frac{{\partial }^2}{\partial X_i\partial X_j}.$$

Letting the operator $\mathcal{L}$ act on a function $V\in C^{2,1}({\mathbb{R}}^n\times [t_0,+\infty ];{\mathbb{R}}_{+}^1),$ one has

$$\mathcal{L}V(X\left(t\right),t)=V_t(X\left(t\right),t)+V_x(X\left(t\right),t)f(X\left(t\right),t)+\frac{1}{2}trace\left[g^{\tau }(X\left(t\right),t)V_{xx}(X\left(t\right),t)g(X\left(t\right),t)\right],$$

where $V_t=\frac{\partial V}{\partial t},$ $V_x=(\frac{\partial V}{\partial x_1},...,\frac{\partial V}{\partial x_n})$ and $V_{xx}={\left(\frac{{\partial }^{2}V}{\partial x_i\partial x_j}\right)}_{n\times n}$. If $X\left(t\right)\in {\mathbb{R}}^n,$ one has

$$dV(X\left(t\right),t)=\mathcal{L}V(X\left(t\right),t)dt+V_x(X\left(t\right),t)g(X\left(t\right),t)dB\left(t\right).$$