Modeling the influence of working memory, reinforcement, and action uncertainty on reaction time and choice during instrumental learning

Abstract

What determines the speed of our decisions? Various models of decision-making have focused on perceptual evidence, past experience, and task complexity as important factors determining the degree of deliberation needed for a decision. Here, we build on a sequential sampling decision-making framework to develop a new model that captures a range of reaction time (RT) effects by accounting for both working memory and instrumental learning processes. The model captures choices and RTs at various stages of learning, and in learning environments with varying complexity. Moreover, the model generalizes from tasks with deterministic reward contingencies to probabilistic ones. The model succeeds in part by incorporating prior uncertainty over actions when modeling RT. This straightforward process model provides a parsimonious account of decision dynamics during instrumental learning and makes unique predictions about internal representations of action values.

Introduction

Life is full of decisions, and decisions take time. Consider a labored deliberation in the cheese section of a grocery store - do you opt for your old stand-by, the Irish Cheddar, or take a risk on a fragrant Roquefort? Or maybe the Gouda? Research on decision-making typically focuses on the choices people make (which cheese?), though studying decision time can also shed light on underlying cognitive processes. In our grocery example, several factors may influence decision time: For instance, decision time could be affected by both how much you like a particular option over the others (which can become stronger with experience), but also the total number of options there are to choose from (which will vary in different contexts).

Most preferences emerge via learning, suggesting that learning models could be useful for explaining decision latencies. Indeed, a body of recent research (Fontanesi et al., 2019; Frank et al., 2015; Miletić et al., 2020; Pedersen et al., 2017; Shahar et al., 2019) has attempted to combine models derived from reinforcement learning (RL) theory with a class of sequential sampling process models derived from perceptual decision-making – “evidence accumulation" models – which account for choice and RT data simultaneously. In evidence accumulation models, such as Ratcliff's drift diffusion model (DDM; Ratcliff, 1978) or Brown and Heathcote's Linear Ballistic Accumulator (LBA; Brown & Heathcote, 2008), RT is determined by the accumulation of evidence for different choices, where accumulators move towards a decision boundary. Evidence accumulation models are traditionally used to fit RT distributions in decision-making tasks, where human and other animal subjects have to, for instance, integrate noisy evidence over time to make perceptual discriminations (Ratcliff & Rouder, 1998; Shadlen & Newsome, 1996; Usher & McClelland, 2001), perform categorical classifications (Nosofsky & Palmeri, 1997; Sewell et al., 2019), or choose between well-known items with different subjective values (Busemeyer et al., 2019). These sequential sampling models provide good fits to RT data, and provide a link between psychological processes and neural mechanisms. For example, the incremental accumulation of perceptual evidence has been linked to parametric changes in the spiking of cortical neurons (Shadlen & Newsome, 1996).

Recent studies directly linking evidence accumulation with reinforcement learning (Fontanesi et al., 2019; Frank et al., 2015; Pedersen et al., 2017; Shahar et al., 2019) have used tasks where subjects have to choose between two actions to maximize probabilistic rewards. These models suggest that the rate of accumulation may be proportional to differences in the learned value of actions: If two actions have similar values, internal evidence accumulation (and thus choice RT) will be slow relative to a situation where one action is strongly preferred over the other. Because of this principled relationship between RT and choice, sequential sampling models can also be leveraged for fitting choice data, providing a more mechanistic account of the decision-making process compared to simpler choice policies (e.g., softmax).

To our knowledge, however, no modeling effort that links RL and RT has addressed the full range of established choice RT effects. These effects include the set size effect, where increasing the number of choice options drives a logarithmic increase in RT (“Hick's Law"; Hick, 1952; Rabbitt, 1968), repetition effects (i.e., attenuated RT when a choice stimulus is repeated; Bertelson, 1965), delay effects (i.e., changes in RT based on how long ago a choice stimulus was last observed; Hyman, 1953; Remington, 1969), and learning and set size interactions (i.e., gradual reductions in RT and the attenuation of set size effects over time; Davis et al., 1961; Mowbray & Rhoades, 1959; Proctor & Schneider, 2018; Schneider & Anderson, 2011). Although some memory-based accumulation models can capture set size effects (Pearson et al., 2014), they often do not address learning or repetition effects. In contrast, the aforementioned RL-based DDM models (Frank et al., 2015; Pedersen et al., 2017) can capture choices and RT distributions, but are not suited for capturing set size effects, as they are usually designed for two-alternative forced-choice tasks. One short-term memory model built on the ACT-R framework (Schneider & Anderson, 2011) was able to capture Hick's Law and learning-related RT effects, but did not model RT distributions. A recent neural model provides a normative account of multi-alternative decision-making that captures set size effects, but does not address learning (Tajima et al., 2019). Taking inspiration from these previous efforts, we propose a simple model of choice and RT that can capture this range of behavioral phenomena.

Furthermore, we test two specific hypotheses about RT and instrumental learning by analyzing two previous behavioral data sets and performing one new experiment. First, we test the idea that choice RT is best modeled by taking into account both a labile working memory process and a slow RL process that operate in parallel during learning. Previous work has shown that choices during instrumental learning are best explained by simultaneous contributions from both of these systems (A. G. E. Collins & Frank, 2012). Second, we posit a key latent variable that modulates decision time: a prior uncertainty over actions, where the speed of action selection is influenced by an internal estimate of action uncertainty averaged over all states.

Results

Task and behavior overview

Even in simple tasks, multiple cognitive processes may be recruited to optimize our decisions. For instance, a driver approaching an intersection has to select well-practiced motor movements to slow the vehicle at the proper rate, while also guiding attentional control to various external factors as they decide which lane to enter (e.g., the position of neighboring cars, the distance until the next turn, etc.). Various studies show that decision-making in a simple laboratory stimulus-response learning task is best modeled by accounting for these two systems, exemplified by, respectively, RL and working memory (A. G. E. Collins & Frank, 2012). Specifically, when human subjects learn deterministic stimulus-response mappings, they appear to rely on short-term memory of recent trial outcomes, in addition to gradual, implicit consolidation of the correct stimulus-response map.

The trade-off between these qualitatively distinct processes may be influenced by set size (the number of stimulus-response instances to be learned), where lower set sizes lead to more working memory-driven learning and higher set sizes lead to more RL-driven learning. A dualprocess model that captures this idea – the RLWM model – has been shown to provide a better fit to choice data in these tasks than models that postulate a single learning mechanism (A. G. E. Collins et al., 2014, 2017; A. G. E. Collins & Frank, 2018; A. G. E. Collins & Frank, 2012). However, the RLWM model was not developed to account for RT data. Here we build on this body of work to provide a more complete model that captures both choice and RT, and we also extend this model to stochastic learning contexts with probabilistic reward feedback. We start by describing the laboratory task, previous behavioral findings, and the RLWM model introduced in previous studies.

The standard version of the RLWM task (Fig. 1A; A. G. E. Collins et al., 2014, 2017; A. G. E. Collins & Frank, 2018; A. G. E. Collins & Frank, 2012) proceeds as follows: Subjects are instructed to learn which of three responses is associated with a particular image to maximize reward. Stimuli are presented in a pseudorandomized sequence within a block of trials, and subjects are required to respond to each stimulus with a button press (either the “j”, “k”, or “l” keys on a keyboard) in under 1.5 seconds. When a stimulus appears and the correct response is made, a reward of “+1" points is earned; when an incorrect response is made, no reward is earned. In the standard version of this task, rewards are deterministic – each stimulus is associated with one correct response (however, see below for results of a probabilistic version of the task). Each stimulus is seen 9-12 times per block.

Figure 1. RLWM task and behavioral signatures.

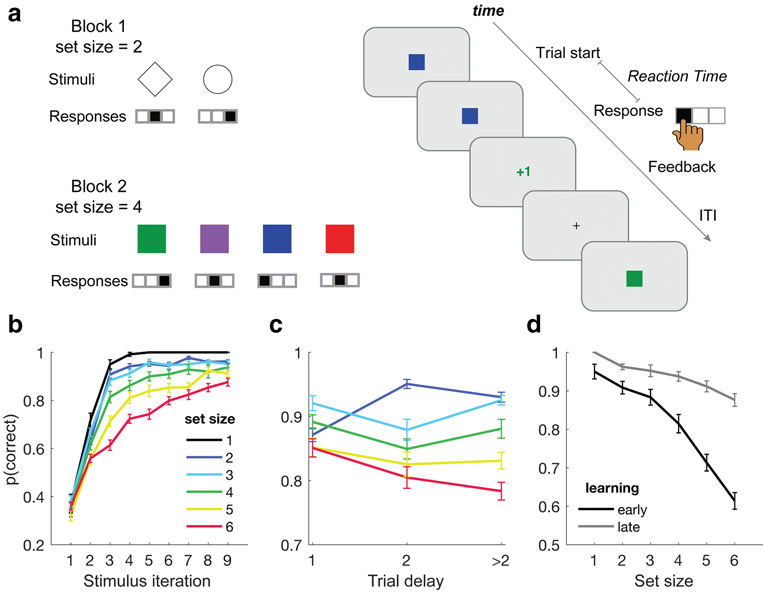
(A) Task design. In the RLWM task, subjects learn stimulus-response associations over several blocks of trials. Two example blocks are shown, each with a different set size, or the number of associations to be learned in that block. Regardless of set size, three actions are available. Stimuli are presented in a pseudo-randomized sequence, and each stimulus is seen 9 times within a block. (B) Learning, plotted as a function of stimulus iteration, is less robust as set size increases. (C) A greater number of intervening trials between responses to a specific stimulus decreases performance. The effect of this trial-based delay is stronger in higher set sizes. (D) The effect of set size on performance is most pronounced early in learning versus late in learning. All error bars = 95% CIs. Data from Collins & Frank, 2018.

Critically, each block is associated with a particular set size, which represents the number of distinct stimulus-response pairs to be learned during that block. Moreover, to discourage subjects from trying to infer correct actions for unseen stimuli (e.g., via process-of-elimination), different stimulus-response “mappings” are used within set sizes. For example, in one set size 3 block, each of the three stimuli could be associated with exactly one of the 3 available response buttons, while in another set size 3 block, two stimuli could be associated with one response, with the third stimulus associated with a second response and no stimuli associated with the third response.

The first key behavioral result is the effect of set size on performance: Average learning curves at each set size are shown in Figure 1B. Subjects learn to select correct actions in all set sizes, but they are slower to learn at higher set sizes. This negative effect of set size on performance has multiple possible sources: First, it could be the result of interference between stimulus representations or value decay within the RL system, where higher set sizes lead to a greater degree of interference. A non-mutually exclusive proposal is that subjects also recruit working memory processes in this task, and that the restrictive capacity limitations of working memory account for most of the set size effects observed (A. G. E. Collins & Frank, 2012). Indeed, support for the latter has been observed in computational (A. G. E. Collins & Frank, 2012), neuropsychological (Collins et al., 2014), and neurophysiological studies (Collins et al., 2017; Collins & Frank, 2018).

Similarly, delay (i.e., the number of trials since the current stimulus was last responded to) also has a negative effect on performance (Figure 1C), and subjects' performance at different delays interacts with set size, where longer delays at higher set sizes leads to relatively weaker performance. This result reflects a form of sequential learning effects (Lohse et al., 2020) that are consistent with trial- or time-based decay (i.e., forgetting) of items held in short-term memory (Posner & Keele, 1967).

Lastly, the magnitude of the adverse influence of set size on performance diminishes with practice (Figure 1D). This suggests that subjects may cache learned associations over time, perhaps reducing their reliance on more costly, capacity-limited executive functions. We note that the behavioral effects depicted in Figure 1 (A. G. E. Collins & Frank, 2018) have been replicated across several different studies using this task (A. G. Collins et al., 2014, 2017; A. G. Collins & Frank, 2012).

Collins and Frank (2012) formalized the concept of working memory (WM) and reinforcement learning (RL) working in parallel in a simple learning model, the RLWM model. In the RLWM model, two modules learn the stimulus-response contingencies (i.e., state-action values) over time.

The RLWM model of choice

The learning of stimulus-action values is modeled using a variant of a standard RL model (Sutton & Barto, 1998). The task consists of two main variables - the state, s (i.e., the stimulus on the screen), and the action, a (i.e., the button pressed). The action-value in a given state, Q(s, a), is updated on each trial, t, using the delta rule (Rescorla & Wagner, 1972):

$$Q_{t+1}(s,a)=Q_t(s,a)+\alpha {\delta }_t$$ (1)

$${\delta }_t=r-Q_t(s,a)$$ (2)

where α is the learning rate, δ is the reward prediction error, and r is the (binary) reward received.

In the basic RLWM model of choice, values are transformed into probabilities, or “weights”, with the softmax function,

$$p(a\mid s)=\frac{e^{Q(s,a)\beta }}{{\Sigma }_i{e}^{{}^{Q(s,a_i)\beta }}}$$ (3)

where β constitutes the inverse temperature parameter, and the sum in the denominator is taken over the three possible actions, a_i.

The RLWM model captures the parallel recruitment of working memory (WM) and reinforcement learning (RL) by training two simultaneous learning modules (Figure 2A). The RL module is characterized by Equations 1-2. The WM module learns stimulus-response associations (W), and is formally similar to Equations 1-2 albeit with a fixed learning rate of α_WM = 1:

$$W_{t+1}(s,a)=W_t(s,a)+{\alpha }_{{}_{WM}}(r-W_t(s,a))=r$$ (4)

Figure 2. Model overview and comparisons.

(A) Schematic diagram of the RLWM model of choice. A working memory (WM) module deterministically learns stimulus-response associations, with trial-based forgetting. A reinforcement learning (RL) module learns stimulus-action associations with standard reward prediction error based RL. WM and RL are differentially weighted to produce an action policy. (B) Schematic diagram of the Linear Ballistic Accumulator (Brown & Heathcote, 2008), where responses compete to produce a choice and a reaction time. (C-F) Model comparisons, showing (C) mean BIC differences relative to the winning model, (D) BIC differences between the best and second-best model for each individual, and (E, F) a leave-1-block out validation comparison procedure. Sorting of individuals in (F) matches the ordering in (D). LL = cross-validated log-likelihood. Error bars = 95% CIs.

Thus, the WM module has, in principle, perfect learning of the observed outcome, which makes it qualitatively distinct from a gradual RL process. Critically, however, working memory is vulnerable to short-term forgetting after updating is performed: The model captures trial-by-trial decay of W,

$$W_t(s_j,a_i)=W_t(s_j,a_i)+\varphi \left(W_0-W_t(s_j,a_i)\right)$$ (5)

where ϕ draws W (over all stimuli j and actions i) toward their initial values, $W_0=\frac{1}{n_A}$, where n_A is the number of actions (in this task, 3).

Separate WM and RL policies (π^WM and π^RL) are computed using the softmax function (Equation 3), and are then combined in the calculation of the final policy via a weighted sum,

$$\pi =w{\pi }^{WM}+(1-w){\pi }^{RL}$$ (6)

where w approximates how much WM should contribute to the decision (Figure 2A). This parameter is determined by two free parameters, the working memory capacity (i.e., resource limit) C, and the initial WM weighting ρ,

$$w=\rho \ast min\left(1,\frac{C}{n\_S_k}\right)$$ (7)

where n_S represents the set size in block k. In short, this equation says that the influence of WM on choice is reduced if the set size exceeds WM capacity C. This weighting step, and the free parameters C and ρ, are critical for capturing the quantitative and qualitative effects of set size on performance in this task (A. G. E. Collins & Frank, 2012).

Lastly, the model also captures learning biases, in particular, the neglect of negative feedback consistently observed in this task: When an action is incorrect and thus generates a negative prediction error (i.e., δ < 0), the learning rate α is reduced multiplicatively:

$$\alpha =\gamma \alpha$$ (8)

where γ controls the degree of perseveration (higher values cause less perseveration, and lower values more). Perseveration occurs for both the RL and WM modules; in the latter case, the fixed learning rate of 1 is scaled by γ.

Previous work has shown that the RLWM model successfully recapitulates the learning curves of human subjects performing this task, and does so better than various other candidate models (e.g., RL-only models, as well as RL models including mechanisms that capture qualitative set size effects, such as RL models with individual learning rates for each set size, simple RL models with forgetting, interference, credit assignment limitations, or other noise mechanisms, etc.; A. G. E. Collins et al., 2014, 2017; A. G. E. Collins & Frank, 2018; A. G. E. Collins & Frank, 2012). Critically, the final output of the RLWM model is π, which represents the action policy. We note here that instead of referring to the quantities represented in the policy as probabilities, as they’re typically referred to in RL, we will refer to them as weights given to each of the three possible responses. In several of the models described below, we extend the function of these weights to serve as the input to an accumulation process, allowing us to model both choice and RT.

Expanding the RLWM choice model to RTs

In settings with binary choices, the drift-diffusion model (DDM) is often used to model choice and RT (Frank et al., 2015; Pedersen et al., 2017; Ratcliff, 1978; Ratcliff & McKoon, 2008). While powerful, this model is not particularly well-suited to situations where there are more than n_A = 2 available actions. A similar evidence accumulation model, the Linear Ballistic Accumulator, or LBA (Figure 2B; Brown & Heathcote, 2008), can easily accommodate any number of actions (n_A = 1, 2, 3,…∞). The LBA shares many key properties with the DDM, although within-trial accumulation is simplified to a noiseless linear process.

Accumulation via the LBA is schematized in Figure 2B. Parameter A corresponds to the upper limit of a uniform distribution from which the starting point (or bias) of the accumulator is drawn. The parameter b corresponds to the boundary of accumulation (i.e., the threshold at which the accumulator terminates and generates a reaction time). The parameter t₀ determines the “non-decision time”, commonly interpreted as time taken for visual processing of the stimulus and motor execution (not shown).

The density function associated with the ith accumulator in the LBA is given by (Brown & Heathcote, 2008):

$$PD{F}_i(t)=f_i(t){\prod }_{j\ne i}\left(1-F_j(t)\right)$$ (9)

where F_j(t) is the cumulative probability function associated with all other competing accumulators, j ≠ i. Here, the probability density of a response time for a particular accumulator is normalized by the probability of the agent making the response associated with that particular accumulator, with other accumulators (competing actions) not having reached threshold. The termination time distribution function for the ith accumulator to be the first to reach threshold (f_i) is the given by the probability density function:

$$f_i(t)=\frac{1}{A}\left[-v_i\Phi \left(\frac{b-A-t{v}_i}{tsv}\right)+sv\varphi \left(\frac{b-A-t{v}_i}{tsv}\right)+v_i\Phi \left(\frac{b-t{v}_i}{tsv}\right)-sv\varphi \left(\frac{b-t{v}_i}{tsv}\right)\right]$$ (10)

where the drift rate is drawn from the normal N(v_i, sv), and ϕ and Φ refer to, respectively, the Gaussian distribution’s density and cumulative probability functions. Further details concerning the LBA distribution specifications and their mathematical derivations can be found in Brown & Heathcote (2008).

We have thus far presented two separate modeling frameworks – the RLWM model of learning and the LBA model of reaction time (Figure 2A, B). How should we connect these two models to capture both learning and RT in our instrumental learning task?

We start with a baseline model inspired by previous work connecting reinforcement learning processes with the DDM. In these other models, the difference between learned Q-values of two competing actions directly scales a single mean drift rate v of a diffusion process (Frank et al., 2015; Pedersen et al., 2017). Thus, when two action values are far apart, RT will be short, and when two values are close, RT will be long. Directly replicating that model with an LBA, which instead has individual accumulators for each action, is not possible; however, individual drift rates can be scaled proportionally by their associated action weights.

The first model we tested (the π model) posits a nonlinear relationship between latent action weights and accumulation rates. In the π model, weights of each action scale the drift rate of their associated accumulators: Each drift rate mean parameter v_i is directly multiplied by the associated weight π_i of each action i on trial t:

$$v_{i,t}=\eta {\pi }_{i,t}$$ (11)

where η is a scaling parameter (simply allowing for the scaling of all drift rates across subjects). Critically, this model performs softmax normalization (Equation 3) to compute π and thus to determine the accumulation drift rates associated with each action; this step reflects the assumption that a non-linearity (i.e., the transformation of Q and W into weights) governs both the differential weighting of Q and W and the relationship between action value and reaction time. This aspect of the model is consistent with similar recent work (Fontanesi et al., 2019), as well as assumptions from the actor-critic framework (Sutton & Barto, 1998), where state-action weights in the striatum govern decision latency.

Consider that the time needed for a decision should not only be affected by the difference of one action’s value over another (e.g., a strong preference for eating chocolate ice cream versus vanilla), but, more generally, the uncertainty over all relevant actions (e.g., choosing between ten flavors that are all similarly valued). Indeed, uncertainty is thought to be a key ingredient in capturing choice RT (Hyman, 1953). Thus, we hypothesized that drift rates should vary as a function of two quantities: First, individual accumulation rates should be affected by the estimated weight of each action i given the current state (π_i), as reflected in the π model above. Second, we intuited that prior uncertainty over actions (i.e., over their average weights over all stimuli within a block) would also influence decision time. That is, the time it takes to select an action in a given state may be affected to some degree by the distribution of average action weights across all states. Thus, if the average weights of the three possible actions across all states are very similar, we should expect maximum uncertainty, and a slow RT. This prior uncertainty term (H_prior) was modeled by first computing an average policy ($\stackrel{\rightharpoonup }{\pi }{}^{{}^{\mu }}$), which requires averaging action weights for each action i over each state/stimulus k (π_i,k) across all n_S possible states/stimuli:

$$\stackrel{\rightharpoonup }{\pi }{}_i^{\mu }=\frac{1}{nS}{\sum }_{k=1}^{n\_S}{\pi }_{i,k}$$ (12)

This simple averaging step thus collapses latent action weights into a single 1 X n_A vector that putatively represents the probability of choosing each of the three actions prior to encoding the current trial’s stimulus. Then, to ascertain the degree of uncertainty over this prior, the Shannon entropy (Shannon, 1948) is computed on this vector, inspired by classic work on RT and uncertainty (Hyman, 1953). (We note here that using inverse variance instead of entropy to quantify uncertainty produced qualitatively similar results.):

$$H_{prior}=-{\sum }_{i=1}^3\stackrel{\rightharpoonup }{\pi }{}_i^{\mu }lo{g}_2\left(\stackrel{\rightharpoonup }{\pi }{}_i^{\mu }\right)$$ (13)

Because action weights change with learning, the quantity above will take on a unique value for each trial t. To illustrate, if the current block was a set size 4 block, the three-element vector $\stackrel{\rightharpoonup }{\pi }{}^{{}^{\mu }}$ used to compute H_prior is the column-wise average over a 4 X 3 matrix of states X actions.

Finally, we incorporate the uncertainty quantity from Equation 13 into the evidence accumulation rate for the ith accumulator using division:

$$v_{i,t}=\eta \left(\frac{{\pi }_{i,t}}{H_{prior,t}}\right)$$ (14)

Thus, in this model, all three drift rates are scaled down equally by the degree of uncertainty associated with taking any particular action in that trial. This heuristic could be interpreted as capturing conflict between actions, which occurs at the level of their prior probabilities going into each trial. We hypothesized that this additional consideration would help the model better estimate RTs. We refer to this as the π_H model.

We also tested two additional control models, the Q model and the π_H-RL model. In the Q model, we tested an alternative assumption where latent variables from the separate RL (Q-values) and WM (W stimulus-response associations) modules linearly scale drift rates. Thus, we exclude the step where those values are nonlinearly transformed with the softmax function (Equation 3). These quantities are still differentially weighted according to Equation 6 to reflect respective WM and RL contributions across different set sizes. However, the mean accumulation rate for each accumulator (v_i) corresponding to each action i is directly proportional to the weighted Q and W quantities for each action (V_i) on trial t:

$$v_{i,t}=\eta V_{i,t}$$ (15)

Lastly, the π_H-RL model was included to test the utility of including a working memory module in the underlying learning process (A. G. E. Collins & Frank, 2012). This model is identical to the π_H model, but only a single action policy is learned (Equations 1 and 2). In this model, the three working memory-related free parameters – capacity (C), weighting (ρ), and decay (ϕ) – are not included.

In all four models, choices and RTs are fit simultaneously. That is, a model’s fit to subjects’ RTs determines its likelihood during the fitting process, and the probability of a given RT is linked to the probability of the choice associated with that RT (Equation 9; Brown & Heathcote, 2008). Models were fit to the data using maximum likelihood estimation by minimizing the negative log likelihood using the MATLAB function fmincon. Fit quality was determined using both the Bayesian Information Criterion (BIC ; Schwarz, 1978), as well as a leave-p-out cross-validation procedure (see Methods for further details on model fitting, parameter recovery, validation, and model simulation).

Model comparisons

The π_H model assumes that action uncertainty modulates RTs and choices. To test this claim we compared it to the three other variants highlighted above (π, Q, and π_H-RL), performing model fitting on a previously-published data set (data set 1; N = 40; A. G. E. Collins & Frank, 2018). As shown in Figure 2C, the π_H model fit the RT data better than the other three models (i.e., lower BIC values; all average BIC differences > 120; protected exceedance probability = 1.0). Figure 2D shows individual BIC comparisons of the π_H model versus the second-best model, the π model, for each subject. Best fit parameter values for all models are shown in Table S1.

We also performed a cross-validation comparison analysis (Figure 2E, F): Models were fit to individual subject's RT data, leaving out the last block from each set size as a test set. The π_H model outperformed the alternatives in this analysis as well (paired t-tests on cross-validated log-likelihoods, all p's < 0.001). We additionally performed a simulation and fitting procedure, using the best-fit parameters, to test how well differentiated the four models were from one another (see Methods; Wilson & Collins, 2019). As suggested by the confusion matrix in Figure S1, the four models were reliably separable.

The specific implications of our model comparisons (Figure 2C-F) are as follows: First, the π_H-RL model did not perform as well as any of the other models. This echoes previous work showing that modeling parallel WM and RL systems better describes behavior in this task versus modeling a single RL system alone (A. G. E. Collins et al., 2014, 2017; A. G. E. Collins & Frank, 2018; A. G. E. Collins & Frank, 2012). Here, we extend this finding to RT data. Second, as predicted, the π model outperformed the Q model, showing that incorporating a nonlinearity (e.g., via the softmax) better captures the relationship between latent value estimates and evidence accumulation rates, consistent with previous work (Fontanesi et al., 2019). Finally, the π_H model outperformed all other models. This suggests that prior uncertainty over actions has a measurable influence on subjects’ behavior in this task.

We emphasize that the model comparisons highlighted in Figure 2 reflect how well the models fit the RT distributions, which, in the LBA architecture are also linked to subjects' choices (Brown & Heathcote, 2008). Thus, this analysis reflects each model's ability to characterize both RT and choice data simultaneously.

Parameter recovery

Although the π_H model performed well in the fitting procedure, this does not guarantee that the model is well identified. To investigate the model’s identifiability, we performed a parameter recovery experiment, simulating choices and RTs using the best-fit parameters from the fitting procedure, and then attempting to fit the resulting synthetic data to recover those parameters (see Methods).

The π_H performed well in the recovery experiment, showing consistent recovery of all 8 of its free parameters (Figure S2). Moreover, the π_H model recovered 4 of the 5 parameters of the underlying RLWM learning model significantly better than the RLWM model recovered those free parameters when fit to the same choice data (for statistics see Figure S2). This improvement in recovery supports recent findings showing that leveraging RT data in addition to choice data in RL tasks improves the identifiability of underlying RL parameters (Ballard & McClure, 2019; Shahar et al., 2019).

For completeness, we conducted an additional control analysis: In all tested models, the non-decision time parameter t₀ – which is meant to capture the portion of the RT that involves perception of the stimulus as well as motor execution – was fixed at 150 ms. We also fit a version of the π_H model where t₀ was allowed to freely vary (Figure S3). In this fitting analysis we found that t₀ traded-off with various other model parameters, and also tended to take on values well below biologically reasonable minimum human RTs (i.e., < 100 ms), even when fitting constraints were altered or additional rapid RTs were screened. Moreover, as shown in Figure S3, while allowing t₀ to vary freely improved the model fit versus having a fixed t₀, as was expected, parameter recovery was modestly but consistently attenuated. We note that the main results and conclusions of our study are not significantly altered by using a fixed versus a free t₀ parameter.

Model simulations

To validate the π_H model, we used simulations to test its ability to produce qualitative choice and RT behavior that echoed subjects’ behavior. We simulated the model using the best fit parameters from the fitting procedure.

The model was able to capture the learning time course of reaction times in each set size, showing the expected facilitation of RTs as learning progressed (Figure 3A). Moreover, the model mimicked the effect of set size on performance in the task (Figure 3B), consistent with previous models fit on choices only (A. G. E. Collins & Frank, 2012). We note that our model did not successfully capture RTs in the earliest stimulus iterations, particularly in the lower set sizes (we return to this point in the Discussion).

Figure 3. RT and choice learning curves with model simulations.

Mean RT time courses (A) and choice performance (B) for each set size, showing subject data (solid lines) and model simulated data (dashed lines). Error shading = 95% CIs. Data from Collins & Frank, 2018.

The π_H model also mimicked the logarithmic relationship between set size and average RT (i.e., Hick's Law, also known as the Hick/Hyman Law), as shown in Figure 4A. The π_H model outperformed the π model in capturing this relationship (t-test comparing regression coefficients between modeled and observed Hick's Law slopes: t(39) = 8.23, p < 0.001). The π model approximated a sigmoidal set size effect rather than a logarithmic one, suggesting a misspecification in the relationship between action policies and RT. This fundamental error in the π model occurs because the π model essentially re-capitulates, in RTs, the effect of set size on choice performance (Figure 1B). That is, in the choice data, the larger set size effects are present in the higher set sizes, whereas in the RT data, the larger set size effects are present in the lower set sizes. The result presented in Figure 4A suggests that the action uncertainty term is critical for capturing the set size effect in RTs. As illustrated in Figure 4B, the quantity computed in Equation 14 (which sets the drift rates), here depicted using simulations from the fitted model, decreases exponentially as a function of set size. Taken together, these results echo the classic finding that uncertainty is a key element in the effect of set size on RT (Hyman, 1953).

Figure 4. Set size effects.

(A) Average RTs across set sizes form subject data (filled triangles), the π_H model (unfilled triangles), and the π model (unfilled circles). (B) Simulated policy of chosen action i divided by the prior uncertainty, as specified in Equation 13, across set sizes. Simulations are averaged across simulated subjects. Error bars = 95% CIs.

To further understand why the inclusion of an action uncertainty term helped the π_H model perform better than the more straightforward π model, we next looked at how RTs differed between different stimulus-response (S-R) mappings within each set size.

Recall that in set sizes greater than 1, subjects could be faced with different S-R mappings within particular set sizes (see Methods). That is, in one set size 4 block, two stimuli could map onto one of the response buttons, another two stimuli could map onto a second response, and no stimuli could map onto the third response. For simplicity, we can notate this mapping as [0 2 2], where each number in this vector represents the number of stimuli assigned to each of the three possible actions (we note here that the order of responses in this notation is not consequential, as actual button assignments were randomized across blocks). In contrast, on a different set size 4 block, two stimuli could map onto one of the responses, and the remaining two stimuli could each separately map onto one of each of the remaining two responses (i.e., a [1 1 2] mapping). Overall, in all n_S > 1 blocks subjects experienced a total of 12 possible mappings (Figure 5).

Figure 5. S-R mapping effects.

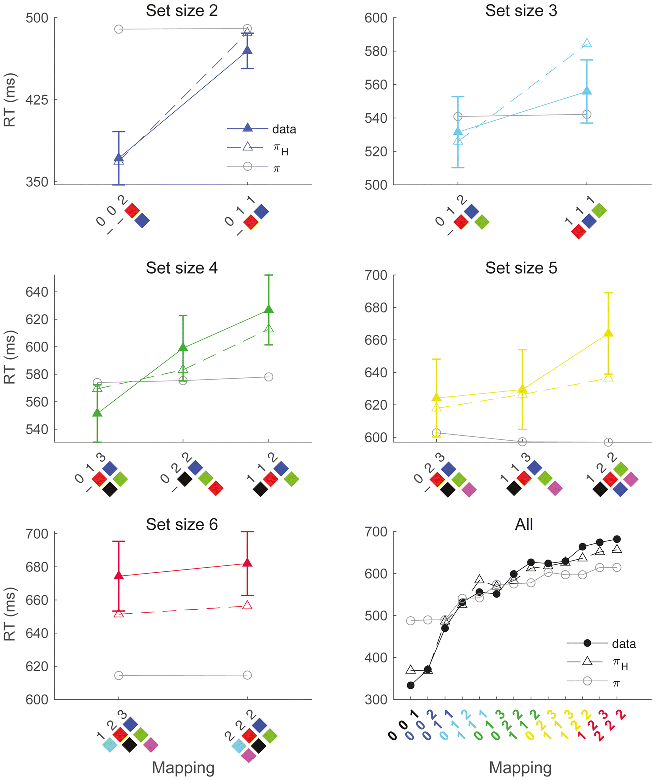
Different stimulus-response (S-R) mappings were used within each set size (n_S > 1). Mappings on the x-axis refer to the specific assignment of stimuli to their associated responses – each response could be associated with 0-3 stimuli depending on the particular mapping and set size. S-R mappings are notated by a sorted 3-element vector describing the number of stimuli associated with each response (the order of values in this notation does not reflect the actual response buttons used). Mappings are also visually schematized, where each colored square represents a single stimulus (note that specific stimuli were never repeated across blocks). Error bars = 95% CIs.

Crucially, after some learning has occurred, different S-R mappings within a set size should be associated with different degrees of action uncertainty. To illustrate, if we imagine a situation where a subject has perfect knowledge of the correct S-R associations, the entropy over the average policy (Equation 13) for a [0 2 2] mapping will be H([0/4 2/4 2/4]) = 1 bit, and for a [1 1 2] mapping will be H([1/4 1/4 2/4]) = 1.5 bits. Thus, the π_H model will tend to predict a higher RT in the latter condition, even though both conditions have an identical set size. In contrast, the π model predicts no such distinction.

Figure 5 shows average RTs (with 95% confidence intervals) for each mapping within each set size, as well as average simulated RTs from both the π_H and π models. As expected, the π_H model was able to capture within-set-size variance in RTs while the π model was not. Crucially, significant RT mapping effects were not limited to comparisons between mappings with a different number of 0’s (i.e., blocks where one action was not associated with any stimuli). For example, RTs were significantly lower in the set size 5 [1 1 3] mapping versus the set size 5 [1 2 2] mapping (t(39) = 2.56, p = 0.01), and the set size 4 [0 1 3] mapping versus set size 4 [0 2 2] mapping (t(39) = 4.69, p < 0.001). These results are consistent with the action uncertainty account and rule out potential action “pruning” strategies as an explanation of our results.

To quantify these effects independent of the modeling analysis, we entered subjects’ mean RTs for each block into a repeated-measures ANOVA, with independent variables for the set size and for the S-R mapping entropy given an idealized asymptotic action policy (as described above). We observed robust main effects of set size (F(1,39) = 1124.00, p < 0.001), mapping entropy (F(1,39) = 228.10, p < 0.001), and a significant (negative) interaction (F(1,39) = 13.97, p < 0.001). Critically, these findings could not be explained by differences in the proportion of correct/incorrect trials between mappings: First, a similarly robust main effect of mapping entropy on RT was observed when this analysis was restricted to correct trials (F(1,39) = 352.80, p < 0.001). Moreover, when the above ANOVA was performed with choice performance (i.e., probability correct) as the dependent variable instead of RT, we unsurprisingly observed a significant (negative) main effect of set size (F(1,39) = 98.45, p < 0.001), but we did not observe significant effects of mapping entropy (F(1,39) = 2.32, p = 0.14) nor any interaction (F(1,39) = 0.00, p = 0.98).

Linking back to our observations in Figure 4, the findings in Figure 5 may partly explain the model’s ability to capture overall set size effects on RT: The key role of uncertainty echoes classic interpretations of Hick’s Law that point to uncertainty over the probability of the stimulus as the main determinant of RT (Hyman, 1953); here, this idea is extended to uncertainty over internal representations of action values learned via reinforcement, as stimulus appearance probability was identical within set sizes.

Figure 6A and B show full distributions of pooled subject RT data (bars) and the distribution of pooled simulation data (black lines), for, respectively, correct and incorrect trials, collapsed over set sizes. The model’s ability to capture RT distributions across set sizes is further illustrated by comparing the simulated and observed RT data quantiles within each set size (Figure 6C).

Figure 6. RT distributions.

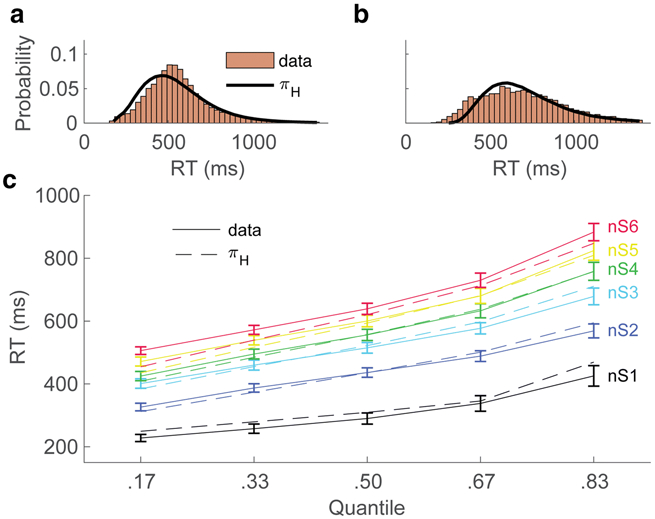
Model and data RT distributions for correct (A) and incorrect (B) trials, collapsed over set sizes. (C) RT quantile data and model simulations over five cumulative probability bins. Error bars = 95% CIs.

We illustrate the model’s ability to fit the data at the level of individual subjects in Figure 7. The model appeared to perform well at the level of fitting individuals, shown in the fit to five example subjects’ RT distributions, RT time courses, and choice learning curves (Figure 7; ordered from top to bottom by membership in choice performance quantiles computed on the group).

Figure 7. Example individual model fits.

Five subjects were randomly selected for display after sorting subjects into five quantiles based on average choice performance, with one subject selected from each bin (top to bottom ordering reflects increasing choice performance). Left column: full RT distributions. Center column: RT time courses. Right column: Choice learning time courses. Solid lines: data. Dashed lines: model.

We hypothesized that due to working memory limitations, evidence accumulation speed should decrease as a function of the number of intervening trials between successive presentations of a given stimulus, and thus RT would increase. The effect of these delays on average RT is shown in Figure 8A for subjects (purple triangles) and model simulations (black triangles), collapsed across set sizes. As predicted, the model approximated the effects of trial delay on RT.

Figure 8. Delay, repetition, and learning effects.

(A) Subject delay effects on RT (purple), and model simulated delay effects (black). (B) Subject repetition effects, and model repetition effects. (C) The effect of practice on the Hick's Law function over time. (D) Effects of trial delay on human and model choice performance, separated by early and late learning phases. Error bars = 95% CIs.

It follows from the delay effects that repeated presentations of a stimulus should produce relatively fast RTs. Repetition RT effects of this nature have been widely documented (Bertelson, 1965; Campbell & Proctor, 1993; Hale, 1969; Proctor & Schneider, 2018). In this analysis, we examined subjects' RTs when they responded to the same stimulus two trials in a row. Consistent with our predictions, the model replicated the effect of repetition on RT (Figure 8B).

One widely documented amendment to Hick's Law is the effect of practice (Davis et al., 1961; Mowbray & Rhoades, 1959; Proctor & Schneider, 2018). That is, if a learner is thought to have proceduralized stimulus-response contingencies, Hick's effect should be attenuated or even abolished. This can be quantified as a decrease in the slope of a linear function, where the x-variable is defined as log₂(set size) and the y-variable is the average RT in each set size. The attenuation of this slope should occur on long learning time scales, especially in higher set sizes like those used in classic studies (e.g., Hick, 1952). Given the relatively brief blocks in our task, we thus chose to analyze the late phase of learning for this analysis (iterations 7, 8, and 9).

We predicted that in this later phase of learning, where working memory retrieval processes presumably become less important, the slope of the log-linear set size effect would decrease because the reinforcement learning system has begun to cache a stimulus-response map (McDougle & Taylor, 2019). Consistent with previous work, the log-linear slope of the set size effect significantly decreased over time (t-test on regression coefficients of slope change: t(39) = 2.29, p = 0.03; Figure 8C). The model produced a qualitatively similar decrease in the set size effect (black triangles), reflecting the effect of practice on crystalizing action policies and attenuating set size effects.

As shown in Figure 1C, trial-based delay has a marked effect on choice performance, especially in higher set sizes. Here, to capture interactions between delay and learning, we operationalized delay as the previous time a given stimulus was responded to (A. G. Collins & Frank, 2012), and separated choice data into an early learning phase (iteration < 5) and a late learning phase (iteration ≥ 5). As learning progressed, the effect of delay was attenuated (t-test on regression coefficients of delay effect slope change from early to late learning: t(39) = 3.35, p = 0.002). This attenuation is potentially due to a gradual trade-off between working memory and RL systems. As shown in Figure 8D, the model also approximates this process.

Taken together, the results of our model simulations suggest that the π_H model provides a parsimonious account of learning and decision-making processes in our task, accounting for a variety of choice and reaction time phenomena. One concern in any behavioral study is the replicability of the main behavioral trends. In our case, we have multiple data sets from previous studies using the same task in independent samples of subjects. We demonstrate the replicability of the task’s average behavioral trends, and illustrate the model’s ability to capture these trends, as follows (Figure S4): We took the average of the π_H model parameters derived from fitting the model to data set 1 (n = 40; A. G. E. Collins & Frank, 2018), then we simulated the π_H model with those average parameter values on the block and stimulus sequences subjects experienced in data set 2 (n = 79; A. G. Collins & Frank, 2012). The behavioral trends were similar in the two data sets, and the π_H model was able to capture RT time courses, set size effects on choice, Hick’s Law, and RT distributions in this separate group of subjects (Figure S4). This result is expected – if the behavior is replicated across experiments, the model’s ability to capture trends in that behavior should be replicated as well. More importantly, the simulated π_H model also fit better than the simulated π model on these out-of-set data (average BIC difference: 22.21; protected exceedance probability: 0.97), further favoring the former model over the latter.

Model performance in probabilistic learning

Having established that the π_H model can characterize various choice and RT effects in a simple deterministic instrumental learning task, we next wanted to test the model’s ability to capture data in a probabilistic learning context. The vast majority of research on traditional choice RT effects use simple deterministic tasks, where stimulus-response associations are fixed and often explicitly explained to subjects (Hick, 1952; Hyman, 1953; Proctor & Schneider, 2018), or perceptual discriminations have a ground truth correct answer (Ratcliff & McKoon, 2008). On the other hand, RL tasks typically involve stochastic reward schedules (Pedersen et al., 2017). Because our model characterizes RT as a function of probabilistic action policies acquired via reinforcement learning and short-term memory maintenance, it should, in theory, generalize to situations where rewards are not perfectly reliable. In this context, in addition to set size effects, the reliability of stimulus-response associations should influence RT in a similar manner (i.e., by decreasing stimulus-action weights and generally increasing uncertainty). The goal of this experiment was to test the hypotheses that a) the concept of concurrent working memory and RL processes would generalize to a stochastic learning setting (i.e., the RLWM framework), and b) the π_H extension of the RLWM model would capture the effects of probabilistic feedback on both RT and choice.

In a new experiment (Figure 9A) we modified our deterministic instrumental learning task by adding two reliability conditions: In the High-prob condition, the “correct” response to a stimulus was rewarded on 92% of trials, and an incorrect response was rewarded on 8% of trials. In the Low-Prob conditions, the correct response was rewarded on 77% of trials, and an incorrect response was rewarded on 23% of trials. In both cases, either of the two incorrect responses could produce a reward on the pre-designated low-probability trials. Two set sizes, 3 and 6, were used, creating a 2 X 2 design (Figure 9A; see Methods for further details of the task).

Figure 9. Probabilistic task.

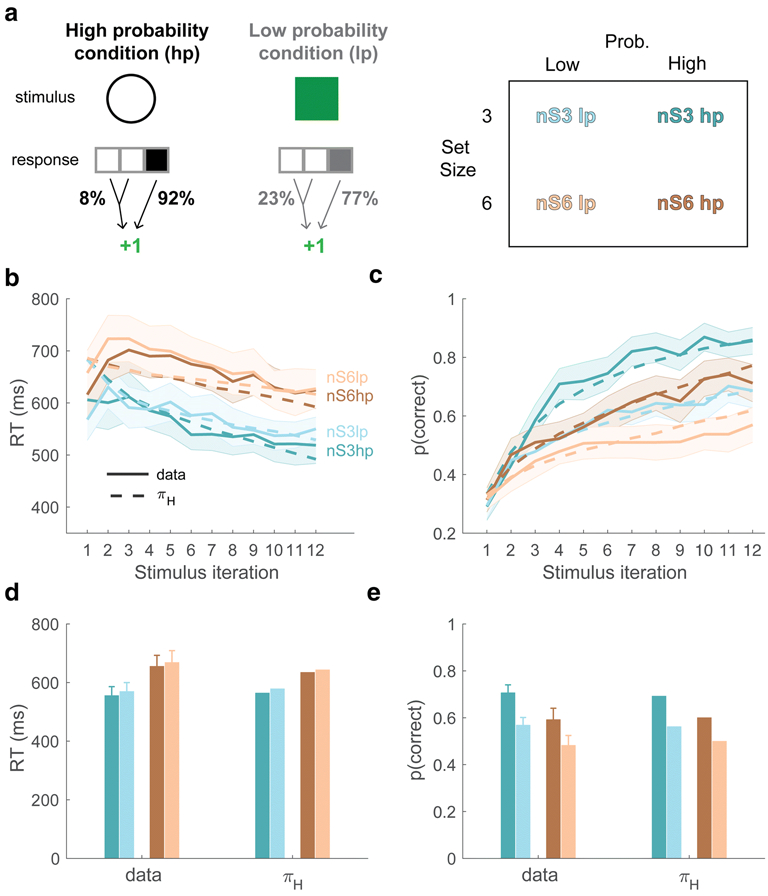
(A) In this task, subjects learn stimulus-response associations under varying degrees of reward reliability given the correct action, and under two set sizes (nS = 3 and nS = 6). Subject data and fitted model simulations, showing RT (B) and choice (C) learning curves, as well as average RT (D) and choice (E) performance across the set size and probability conditions. Error bars and shading = 95% CIs.

We performed two separate repeated-measures ANOVAs to quantify the effects of set size and feedback reliability on reaction time and choice performance in the probabilistic context. In terms of RT (Figure 9B, D), we observed a significant main effect of set size (F(1,33) = 55.99, p < 0.001), but no significant effect of reliability (F(1,33) = 0.73, p = 0.79) nor any interaction (F(1,33) = 0.26, p = 0.61). In terms of choice (Figure 9C, E), as predicted, we observed both significant set size (F(1,33) = 31.56, p < 0.001) and reliability main effects (F(1,33) = 105.4, p < 0.001), but a nonsignificant interaction (F(1,33) = 1.77, p = 0.19). The strong effect of set size on learning in the probabilistic context suggests that putative working memory recruitment in our task may not be contingent on there being deterministic stimulus-response associations.

To test the generalizability of the π_H model, we fit it to these new data. As predicted, the model was able to approximate the time courses of subjects’ reaction times (Figure 9B, dashed lines) and learning curves (Figure 9C, dashed lines) in this probabilistic setting (fit parameter values are presented in Table S1). In particular, the model was able to recapitulate the result where feedback reliability and set size have comparable effects on choice, but the effect of reliability on RT is much weaker than the effect of set size on RT (Figure 9D). These results endorse the generalizability of our model, suggesting that the underlying action policy, if modeled accurately, can predict RT and choice dynamics across experimental contexts. (We note here that the mapping analysis shown in Figure 5 could not be conducted on the probabilistic experiment, as only a single mapping was used within each set size.)

Relative to the deterministic experiment, we observed several significant changes in fit π_H parameter values in the probabilistic experiment: First, as predicted, the learning bias to neglect negative feedback (as captured in the γ parameter) was significantly higher in the probabilistic experiment (Mann-Whitney U tests, comparing fitted values from the probabilistic versus the deterministic experiment, p < 0.001). Moreover, the weight given to the working memory module (ρ) was lower in the probabilistic context (p < 0.001), while the reinforcement learning rate (α) did not differ between conditions (p = 0.49). Interestingly, the capacity parameter (C) was higher in the probabilistic task (p = 0.003), as was the accumulation rate scaling factor (η; p = 0.01). No other parameters differed significantly between experiments (all p’s > 0.24).

In terms of the unexpected bi-directional differences between the key working memory parameters (ρ and C) across experiments, we note that these parameters can be difficult to independently estimate when there are only two set sizes (as in the probabilistic experiment). However, using Equation 7, the actual weight given to the working memory (WM) module during learning can be directly computed using these two free parameters. As shown in Figure S5, we found significantly greater WM weighting in the deterministic experiment (data set 1) versus the probabilistic experiment in both set size 3 (2-sample t-tests; t(72) = 6.55, p < 0.001) and set size 6 (t(72) = 4.13, p < 0.001). Moreover, the decrease in WM weighting from set size 3 to set size 6 was larger in the deterministic versus probabilistic experiment (t(72) = 6.88, p < 0.001), also indicating less reliance on WM in the probabilistic experiment.

Discussion

Choice and reaction time are tightly intertwined aspects of decision making. Here, using a novel evidence accumulation reinforcement learning (RL) model, we show that leveraging both choice and reaction time (RT) data can help shed light on a variety of behavioral phenomena, including effects of repetition, delay, and set size on RT, and the interaction of working memory and reinforcement during instrumental learning.

The results presented here provides further support to the hypothesis that working memory and RL act in concert during instrumental learning (A. G. E. Collins & Frank, 2012). Our model expands this idea into the more mechanistic framework of evidence accumulation. Evidence accumulation models have provided many insights in the domain of perceptual decision making tasks (Ratcliff & McKoon, 2008), and recent efforts have extended this class of models to instrumental learning (Fontanesi et al., 2019; Frank et al., 2015; Miletić et al., 2020; Pedersen et al., 2017). This is an important development, as RL models generally characterize choice policies using simple functions like the softmax or rigid “greedy” policies. However, these characterizations of the choice process are clearly oversimplifications, and do not make predictions about RT. Our model suggests that the concurrent operation of working memory and RL, as well as an internal representation of action uncertainty, shape RT.

Simultaneously modeling choice and RT can provide practical benefits that modeling each in isolation cannot. For instance, recent work shows that incorporating RT data during model fitting improves the estimation of RL model parameters (Ballard & McClure, 2019). We replicated this result, demonstrating that our combined choice/RT model led to improved recovery of both the RL and working memory parameters (Figure S2). In general, rich RT data, while often neglected in reinforcement learning tasks, can be leveraged to better understand the underlying cognitive and neural processes driving decision making. Furthermore, when attempting to characterize RL model parameters in the clinical setting, as in the burgeoning field of computational psychiatry (Huys et al., 2016), achieving more reliable parameter estimates could improve the replicability of between-group comparisons and clinical interpretations.

One critical component of our model is prior action uncertainty (Equation 13). This value represents the effect that uncertainty over the full action policy space (i.e., over all states) has on an agent's reaction time. Incorporating this value in our model was critical for accurately capturing the effect of different stimulus-response mappings on RT (Figure 5), appeared to aid in the modeling of set size effects (Figure 4), and also lead to an improved fit to the data when compared to models omitting this quantity (Figure 2). Normatively, the average action policy (Equation 12) used in our uncertainty heuristic could be interpreted as the Bayes-optimal policy going into a trial, before the state/stimulus is observed. Even though our states/stimuli have virtually no observation noise (as they were all saliently different colors, objects, shapes etc.; see Methods), this prior policy still appeared to exert an influence on RT.

At the process-level, one interpretation of the uncertainty heuristic we used in the π_H model is that it approximates a form of competition between actions (Usher & McClelland, 2001). In our model, this conflict is implemented by decreasing all drift rates based on the degree of action uncertainty (Equation 14). One speculative process-level extension of this is that uncertainty-related RT effects in our task are the result of proactive, versus reactive, cognitive control processes being recruited before each trial (Braver, 2012). At the neural level, this could perhaps be implemented by top-down parallel preparation of actions.

The results depicted in Figure 4 also speak to the psychological processes underlying Hick's Law (Proctor & Schneider, 2018). One common explanation is that the law represents the amount of time it takes subjects to extract the (Shannon) information related to a stimulus. For instance, RT is affected by the probability that a given stimulus will be presented within a specific trial sequence (Hyman, 1953). If we assume a uniform distribution of stimulus presentations, as used in our task, these stimulus probabilities will decrease with set size because the probability that a stimulus appears is 1/n_S, with n_S reflecting the number of stimuli that could be seen in a block. Leveraging this simple fact could explain both the basic set size effect, as well as the effect of delays and repetitions on choice RT (Hyman, 1953). However, this particular explanation of Hick's Law does not address the learning of S-R associations, nor uncertainty over actions versus stimuli (exemplified in, respectively, the numerator and denominator of the values depicted in Figure 4B). Our findings, particularly on within-set-size S-R mapping effects (Figure 5), suggest that a more generalized account of Hick's Law should incorporate both trial-by-trial learning dynamics and, critically, uncertainty over learned action weights (Wifall et al., 2016). We note that a learning-based approach to explaining Hick's Law has been taken before – Schneider and Anderson (Schneider & Anderson, 2011) proposed an elegant model within the ACT-R framework to capture set size RT effects. They were able to show that Hick's Law, and the impact of practice and repetition on RTs, could be linked to the effects of load, time, and forgetting in short term memory.

Another important detail in our model is the proposed nonlinear relationship between latent action values and the rate of evidence accumulation, operationalized by a sigmoidal transfer function (Equation 3) that transforms those values into weights, which are then used to set accumulation rates. This step is inspired by the RL actor-critic framework, which suggests that while ventral striatum (the critic) tracks state values and enables prediction error computations, the dorsal striatum (the actor) instead tracks stimulus-action weights (Joel et al., 2002; O’Doherty et al., 2004; Sutton & Barto, 1998). Consistent with our model, some theories support a nonlinear relationship between values represented in the critic system and striatal state-action weights represented in the “actor” system (A. G. E. Collins & Frank, 2014). This nonlinearity can be captured by a softmax transfer function such as that used in our model, which, importantly, improved the model fit (see Fontanesi et al., 2019 for a similar conclusion). Moreover, the use of a softmax function could be interpreted as a simplified implementation of lateral inhibition between competing actions (Usher & McClelland, 2001).

The ability of the π_H model to also capture probabilistic stimulus-response learning (Figure 9) has several implications. First, this result shows that the model is flexible enough to capture learning in different task contexts. Second, our results show that the underlying hypothesis of concurrent working memory and RL contributions to instrumental learning, which has to date only been tested via tasks with deterministic feedback (A. G. E. Collins et al., 2014, 2017; A. G. E. Collins & Frank, 2018; A. G. E. Collins & Frank, 2012), may generalize to a probabilistic setting. However, we note that do not have direct evidence that working memory strategies are leveraged in the probabilistic task.

Interestingly, the cross-experiment comparisons supported our expectation that working memory is given a lower weight in the probabilistic context (Figure S5), suggesting that if working memory strategies are leveraged here, they may have a weaker influence on decisions. Further research could attempt to better model working memory processes in these probabilistic settings by going beyond the simplified one-trial-back algorithm presented here (Equation 4). One approach could be to model learned associations held in working memory as probabilistic hypotheses rather than deterministic stimulus-response associations. Lastly, we observed no significant change in the reinforcement learning rate (α) between deterministic and probabilistic contexts. This suggests that the slower learning observed in the probabilistic task may primarily be a consequence of noisier explicit working memory strategies, though this should be more fully explored in future research.

We note several limitations in this study.

First, our model was clearly ineffective at capturing RTs in the earliest iterations of each block (Figure 3A). This was partly expected, as action values are initialized to the same number in all set sizes (1/3); thus, both the action weights and prior uncertainty over actions were identical in the first trial of every block, leading to similar RTs across blocks. Why, then, did we observe a set size effect in subjects’ RTs at the start of the block? First, subjects are likely guessing on most of these early trials (Schaaf et al., 2019), and this kind of un-directed exploration (Wilson et al., 2014) is not explicitly specified in our models. We also speculate that some subjects may covertly name or label stimuli early in the block, especially in the higher set sizes, and associate those labels with their guesses – strategies like this could appear as early as the first iteration because subjects are informed about the upcoming set size before each block begins and shown a preview of the full set of images. In some situations, subjects could even perform deterministic hypothesis-testing strategies in the early phases of a learning block (e.g., trying each finger from left to right; Mohr et al., 2018). Despite these caveats and alternative learning strategies, our model was still able to closely approximate the time course of subjects' reaction times and choices (Figures 3, 7, and 9).

Second, our model also appeared to underestimate variance in RT distributions, particularly for incorrect trials (Figure 6B), and to underestimate the RT set size effect (Figure 6C). The reason for this is not clear, although we note that there were clear variations in fit quality on the individual level (Figure 7). Moreover, the model tended to overestimate RTs in the set size 1 condition. This was partly expected, as a true decision process would not be needed once subjects learned the correct action in the set size 1 condition (rather, they simply needed to detect the appearance of the stimulus). These fitting limitations may relate to model misspecification as discussed above; subjects likely leverage additional learning and hypothesis-testing strategies (e.g., systematic guesses, pre-planning responses) that are simply not specified in our modeling approach.

Another limitation of our modeling effort is the requirement to fix certain parameters, namely, non-decision time t₀, the noise parameter s_v, and the softmax sensitivity parameter β. Although fixing versus fitting these parameters did not alter the main conclusions of our study, we made decisions to fix these parameters for several reasons: First, as shown in Figure S3, fitting t₀ provided an expected increase in fit quality at the expense of interpretability and model recoverability. If and how different experimental conditions may influence non-decision time in our task is an issue for future model development. In terms of the noise parameter s_v, previous studies have shown that fixing this parameter is important for LBA model identifiability (Donkin et al., 2009), a finding we replicated in our own control analyses (not shown). Lastly, fixing β at a relatively high value is important for identifiability and recovery of the RLWM choice model (A. G. E. Collins, 2018).

Evidence accumulation has been directly linked to specific neural dynamics underlying decision making. Most prominently, this has been demonstrated in activity profiles of neural populations that may reflect the accumulation of perceptual evidence (Shadlen & Newsome, 1996, see also Latimer et al., 2015). Recent evidence also suggests that neurons in the striatum, a key substrate in reinforcement learning and decision making, perform evidence accumulation during decision-making (Yartsev et al., 2018). Future human physiological studies, perhaps using techniques with high temporal resolution (e.g., intracranial electroencephalography), could attempt to measure putative neural accumulation processes at play during instrumental learning and action selection.

Conclusion

Here we presented a model of choice and RT that captures decision-making behaviors in two stimulus-response learning tasks. The model was able to capture a variety of RT and choice phenomena, including set size, repetition, delay, and practice effects, and was effectively validated with multiple methods. Modeling RT and choice together improved the estimation of underlying reinforcement learning parameters and incorporating internal estimates of action uncertainty in the model markedly improved model fit and validation. Lastly, the model was able to characterize choice and RT in both deterministic and probabilistic feedback contexts. Our results suggest that modeling choice and RT together can provide a more nuanced account of instrumental learning.

Methods

Behavioral task

The protocol for all behavioral tasks was approved by the institutional review board at Brown University. Details of subject samples for data set 1 and the out-of-sample data set (data set 2, Figure S4) can be found in the original source papers (respectively, A. G. E. Collins & Frank, 2018; A. G. Collins & Frank, 2012). Forty-one subjects were recruited for the probabilistic task (data set 3; mean age = 21, 23 females). Given the increased difficulty of the probabilistic task, seven subjects were excluded for having average choice performance that was at or below the chance level (0.33) for selection of the optimal action (i.e., the one most likely to be rewarded for a given stimulus), leaving a sample of 34 (mean age = 20.97, 20 females) for the model fitting analysis of the probabilistic task.

The basic structure of the task is depicted in Figure 1A. The task was administered as follows: Subjects were seated in front of a computer monitor and made responses on an external USB computer keyboard. Subjects were instructed by the experimenter to learn which of three responses was associated with each presented image, in order to maximize earned rewards. On correct trials, positive feedback (“+1”) was displayed centrally in green font; on incorrect trials, negative feedback (“0”) was displayed centrally in red font. On trials where subjects responded too slowly, a “Too Slow” warning appeared in red font on the center of the screen. Across experiments and analyses, trials where responses were too slow (1.33%) or overly rapid (<150 ms, 0.75%) were excluded.

Each experiment was divided into several blocks of trials, and each block was associated with a particular set of images and a particular set size, defined by the number of stimulus-response pairs to be learned in that block. The number of actions was held constant across all blocks at 3. Key press responses were made with the dominant hand, and required pressing one of three adjacent keys (e.g. j, k, or l) with the index, middle, or ring finger, respectively. To discourage process-of-elimination strategies, in set sizes over 1 the correct actions were not always evenly distributed among the stimuli (e.g., in some set size three blocks, each action could be correct for exactly one stimulus, while in other blocks, one action could be correct for two of the stimuli, one could be correct for the third stimulus, and the third action could be correct for no stimuli). Twelve such mappings were used overall and are each depicted in Figure 5.

Before each block, all of the images to be learned about in that block were centrally displayed in a tiled layout on the screen (e.g., all 3 images if set size = 3) for subjects to familiarize themselves with the stimuli before the block began. On each trial, one image was displayed at a time in the center of the computer screen over a black background (visual angle of stimulus, ~8°). Subjects had a maximum of 1400 ms to respond to the image. For data sets 1 (N = 40; A. G. E. Collins & Frank, 2018) and 2 (N = 79; A. G. E. Collins & Frank, 2012), the correct stimulus-response contingencies were consistent throughout the block. That is, the correct action for a given stimulus would always yield a reward, and both of the two incorrect actions for that stimulus would never yield a reward. Within a block, each stimulus was presented a minimum of 9 times and a maximum of 15 times (data sets 1 and 2); the block ended either after n_S × 15 trials, or when subjects reached a performance criterion whereby they had selected the correct action for three of the four last iterations. The specific sequence of stimuli within a block was pseudorandomized. Stimuli within a given block were drawn from a single category (e.g. scenes, fruits, animals), and stimuli never repeated across blocks. In data set 1, 22 blocks were completed (set sizes 1-6); in data set 2 (Figure S4), 18 blocks were completed (set sizes 2-6).

The probabilistic experiment (N = 34; data set 3) had a similar design to the deterministic experiments, but with two key differences: First, only two set sizes were used (set sizes 3 and 6) with only one S-R mapping per set size ([0 1 2] and [2 2 2]). Second, two different feedback “reliability” conditions were introduced: In the High-prob condition, the “correct” response to a stimulus was rewarded 92% of the time, and an incorrect response (either of the other two actions) was rewarded 8% of the time. In the Low-Prob conditions, the correct response was rewarded 77% of the time, and an incorrect response was rewarded 23% of the time. That is, subjects still had to learn which action was the most rewarded for each stimulus, but the solution was not deterministic. The specific trials in which unreliable reward feedback was given were predetermined. Exactly twelve iterations of each stimulus were presented per block, and 14 blocks were completed in total.

Model fitting and model comparison

Models were fit to reaction time data using maximum likelihood estimation, specifically by minimizing the negative log likelihood using the MATLAB function fmincon. All RTs were specified in milliseconds. Initial parameter values were randomized across fitting iterations, and 40 iterations were used per fitting run to avoid local minima. Parameter constraints were defined as follows: α = [0,1]; γ = [0,1]; ϕ = [0,1]; ρ = [0,1]; C = [2,5]; η = [0,3]; A = [0,500]; b = [0,600]; and b > A. The s_v parameter was fixed at 0.1; fixing this parameter has been shown to significantly improve LBA model identifiability (Heathcote et al., 2019). (We note that our model comparison results were similar when allowing s_v to freely vary, but identifiability was strongly weakened for the other LBA parameters.) Inverse temperature β was fixed at 50 for all fits and simulations, consistent with previous studies (A. G. E. Collins & Frank, 2018). The non-decision time parameter t₀ was subtracted from RT data before fitting and was fixed at 150 ms (data set 1 and the probabilistic experiment; Table S1) or 225 ms (data set 2; Figure S4). All Q and W values were initialized at 1/3 for all fitting iterations and simulations.

Model comparisons were conducted using two methods: First, we fit models on subjects' full data sets and compared them using the Bayesian Information Criterion (Schwarz, 1978), plotting mean BIC differences with standard errors (Figure 2), reporting the mean BIC differences of the best model versus its competitors, and computing the protected exceedance probability (Stephan et al., 2009) of the winning model (using the MATLAB spm_BMS function from the SPM toolbox; https://www.fil.ion.ucl.ac.uk/spm). Second, we also computed a cross-validated likelihood measure: This value was determined by a leave-p-out cross-validation procedure, where models were fit to each subject on a reduced data set that left out the last block of each set size, after which a log-likelihood was computed on the six left-out blocks using the parameters gleaned from the fit.

Model simulation

For simulations, the mean accumulation rate (v) is computed for each action i (Equations 11-14), which is shaped by the modeled learning of stimulus-response associations (Equations 1-8). The ith accumulator's starting point k is drawn from a uniform distribution on the interval [0, A] and the drift rate d is drawn from a normal distribution, N(v, s_v). The time to threshold and the simulated choice can then be directly computed,

$$T_i=\frac{b-k_i}{d_i}+t_0$$ (16)

$$a=min(T)$$ (17)

where the chosen action a corresponds to the accumulator that generates the minimum RT across the three accumulators (i.e., the winning accumulator). Simulated accumulators with negative drift rates, which are possible given that drift rates are normally distributed, were disqualified from reflecting the winning action, and simulated trials that produced an RT that exceeded the experimentally enforced maximum RT (1400 ms) were re-run until that constraint was satisfied. Model simulations were performed 100 times per simulated subject then averaged.

Parameter recovery and model separability

We performed a model separability analysis by computing a model confusion matrix as follows: Choices and RTs were simulated 40 times for each of the four models using the best-fit parameters gleaned from fitting each model to each of the 40 individual subjects. Each model was then fit to each of the four sets of simulations (using 40 starting points of randomized parameter initializations per fit and selecting the best result), in an attempt to recover the underlying model that produced the simulated data. In each case, the optimal outcome is for the winning model in the fitting procedure to match the model that was originally used to simulate the underlying synthetic data (Wilson & Collins, 2019). After fitting, we plotted a confusion matrix using the proportion of simulations best fit by each model (Figure S1). We performed this analysis using both the AIC (Akaike, 1974) and BIC metrics and found that the BIC-based confusion matrix resulted in better model separability. Therefore, we used the BIC for our model comparisons, though all main findings were similar with the AIC.

We also performed a parameter recovery experiment to measure model identifiability (Figure S2). In this analysis, after fitting each model, we simulated data using either the π_H model (which simulates choices and RTs) or the basic RLWM model of (choices only; A. G. Collins & Frank, 2012). We then attempted to recover the free parameters by fitting the resulting choice/RT data (again using 40 starting points of randomized parameter initializations and selecting the best fit). Resulting Spearman correlations were computed and compared across models using the Fisher r-to-z transformation. Parameters were depicted in scatter plots to visualize recovery success (Figures S2 and S3).

Supplementary Material

13423_2020_1774_MOESM1_ESM

Figure S1. Model Confusion Matrix. Each of the four tested models were used to simulate a synthetic data set (RTs and choices) and were then fit to each set of simulations in an attempt to recover the underlying model (see Methods for details). The heat map depicts the proportion of simulations best fit by each model (according to the BIC).

Figure S2. Parameter recovery. (A) RT and choice data from the π_H model were simulated to generate 40 synthetic data sets, using the best fit parameters from the 40 subjects in data set 1 (Collins & Frank, 2018). These data were then fit with the π_H model in an attempt to recover the ground-truth parameter values. Parameters include the reinforcement learning rate α, the working memory decay rate ϕ, the initial working memory weight ρ, negative prediction error learning modulation γ, working memory capacity C, evidence accumulation rate scaling factor η, the upper evidence Bound, and the upper initial bias boundary A. Correlation coefficients (Spearman) are specified in the title of each subplot. (B) Same as (A), but for recovery of the RLWM parameters. Here, the RLWM choice model (Collins & Frank, 2012) was fit to subjects’ choices, then choices were simulated using those parameters, and, lastly, recovery was attempted. We note that the RLWM model does not model RTs. Correlations between simulated and fit parameters were compared across models with the Fisher r-to-z transform. Recovery of the π_H model was significantly better than the RLWM model for the RL learning rate α (p = 0.006), working memory decay ϕ (p = 0.02), working memory weight ρ (p < 0.001), and working memory capacity C (p < 0.001). No significant difference in recovery was found between the models for negative prediction error learning rate scaling factor γ (p = 0.56).

Figure S3. Model comparison and parameter recovery for π_H model with a free t₀ parameter. (A) Allowing for a freely varying t₀ parameter improved model fit. (B) RT and choice data from the π_H model were simulated and fit as described above (Figure S2), but with the non-decision time parameter t₀ set as a freely varying parameter rather than fixed at 150 ms. Model recovery was generally successful with a freely varying t₀, however, recovery was attenuated for 7/8 parameters relative to the original π_H model.

Figure S4. Performance of the model on out-of-sample data. (A) The π_H model was fit on data from data set 1 (Collins & Frank, 2018). Then, average fit parameter values were used to simulate data from data set 2 (Collins & Frank, 2012). Here we depict model and data RT (A) and choice (B) learning curves, Hick’s Law (C), and RT distribution quantiles (D). Error shading and error bars = 95% CIs.

Figure S5. Differential weighting of the working memory (WM) module between deterministic (data set 1) and probabilistic learning contexts. The π_H model determines the weighting of the WM learning module using the ρ and C parameters. After fitting the model, the weighting of WM can be directly computed using the equation depicted on the x-axes above (Equation 7 in main text). Histograms of WM weightings are shown for each experiment, at set size 3 (left) and set size 6 (right). Between-subject comparisons are restricted to set sizes 3 and 6 as these were the set size conditions used in the probabilistic experiment. WM weighting was significantly higher in the deterministic experiment (data set 1) in both set size 3 (t(72) = 6.55, p < 0.001) and set size 6 blocks (t(72) = 4.13, p < 0.001). Moreover, the decrease in WM weighting from set size 3 to set size 6 was larger in the deterministic versus probabilistic context (t(72) = 6.88, p < 0.001).

Table S1. Parameter values. Mean fit parameter values, +/− standard deviation of the mean. We note that the s_v and t₀ parameters were fixed for all models. The fifth row (π_H PROB) refers to the fit parameters of the π_H model for the probabilistic feedback experiment (Figure 8).