Computational Models of Cardiac Hypertrophy

Abstract

Cardiac hypertrophy, defined as an increase in mass of the heart, is a complex process driven by simultaneous changes in hemodynamics, mechanical stimuli, and hormonal inputs. It occurs not only during pre- and post-natal development but also in adults in response to exercise, pregnancy, and a range of cardiovascular diseases. One of the most exciting recent developments in the field of cardiac biomechanics is the advent of computational models that are able to accurately predict patterns of heart growth in many of these settings, particularly in cases where changes in mechanical loading of the heart play an import role. These emerging models may soon be capable of making patient-specific growth predictions that can be used to guide clinical interventions. Here, we review the history and current state of cardiac growth models and highlight two main limitations of current approaches with regard to future clinical application: their inability to predict the regression of heart growth after removal of a mechanical overload, inability to account for evolving hemodynamics, and inability to incorporate known growth effects of drugs and hormones on heart growth. Next, we outline growth mechanics approaches used in other fields of biomechanics and highlight some potential lessons for cardiac growth modeling. Finally, we propose a multiscale modeling approach for future studies that blends tissue-level growth models with cell-level signaling models to incorporate the effects of hormones in the context of pregnancy-induced heart growth.

1. Introduction

Over the course of a lifetime, the heart dramatically modulates its size and shape in response to a combination of mechanical and chemical stimuli. During development, the embryonic heart develops from a single tube into a four-chamber pump, a process primarily driven by cell proliferation (hyperplasia). After birth, the postnatal heart continues to grow, increasing in mass by two orders of magnitude, primarily through increases in cell size (hypertrophy) (Taber and Perucchio, 2004). In adulthood, a healthy heart continues to adapt its mass and shape in response to increased loading and hormonal stimuli. Exercise can induce reversible heart growth, with endurance and strength-trained athletes exhibiting larger left ventricular dimensions compared to age-matched controls (Pluim et al., 2000) and normalization of dimensions after cessation of training (Maron and Pelliccia, 2006). During pregnancy, circulating hormone levels surge as the maternal cardiac output increases by 50% (Hunter and Robson, 1992) and left ventricular mass by 30% (Savu et al., 2012), only to return to nonpregnant levels within two weeks postpartum. Cardiovascular disease also induces a range of patterns of heart growth, some of which are at least partially reversible following correction of the underlying pathology. Conditions such as hypertension or a stenotic aortic valve that impose a pressure overload by increasing the pressure the left ventricle (LV) must generate to eject blood typically trigger an increase in mass and thickening of the LV wall, a pattern known as concentric hypertrophy. In some respects, this response is physiologically adaptive, allowing the LV to generate higher pressures. Yet increased cardiac mass is also an independent predictor of poor outcomes in patients with aortic stenosis (Beach et al., 2014; Mihaljevic et al., 2008), suggesting that hypertrophy in these settings has both benefits and costs. Other conditions such as valvular regurgitation and myocardial infarction can place a volume overload on the heart, forcing the LV to pump higher volumes of blood at relatively normal pressures. Volume overload typically triggers eccentric hypertrophy, a pattern of growth in which the LV circumference increases much faster than the wall thickness, often resulting in dilated heart failure and eventual death.

Cardiac hypertrophy is a complex process, driven by simultaneous changes in mechanical and hormonal stimuli, interacting through a complex network of intracellular pathways within cardiac muscle cells (cardiomyocytes) that lead to increased sarcomeric protein synthesis and assembly, and an increase in cell size. Experiments in cultured cells and transgenic animals have identified many different individual stimuli that can drive hypertrophy and revealed details of the underlying signaling cascades (Heineke and Molkentin, 2006). Other aspects of the process, particularly how hypertrophic signaling results in lengthening of myocytes during eccentric hypertrophy and thickening of myocytes during concentric hypertrophy, remain unclear (Kehat et al., 2011; You et al., 2017). However, even as molecular details remain under investigation, phenomenological models that rely on changes in mechanics to predict patterns of growth have proven surprisingly powerful. Thus, we are at an exciting stage where state-of-the-art growth models are able to predict patterns of heart growth due to multiple mechanical perturbations. These successes raise the possibility of applying computational models clinically to predict the time course of heart growth and remodeling in individual patients, and to aid in the efforts of designing effective, patient specific interventions and therapies for various types of heart disease.

The objective of this manuscript is to review the history and current state of cardiac growth models and highlight two main limitations of current approaches with regard to future clinical application: their inability to predict the regression of heart growth after removal of a mechanical overload, their inability to account for evolving hemodynamics, and their inability to incorporate known growth effects of drugs and hormones on heart growth. Next, we outline growth mechanics approaches used in other fields of biomechanics and highlight some potential lessons for cardiac growth modeling. Finally, we propose a new multiscale framework to incorporate the effects of hormones in the context of pregnancy-induced heart growth.

2. Predictive computational models of heart growth

2.1. Kinematic growth framework

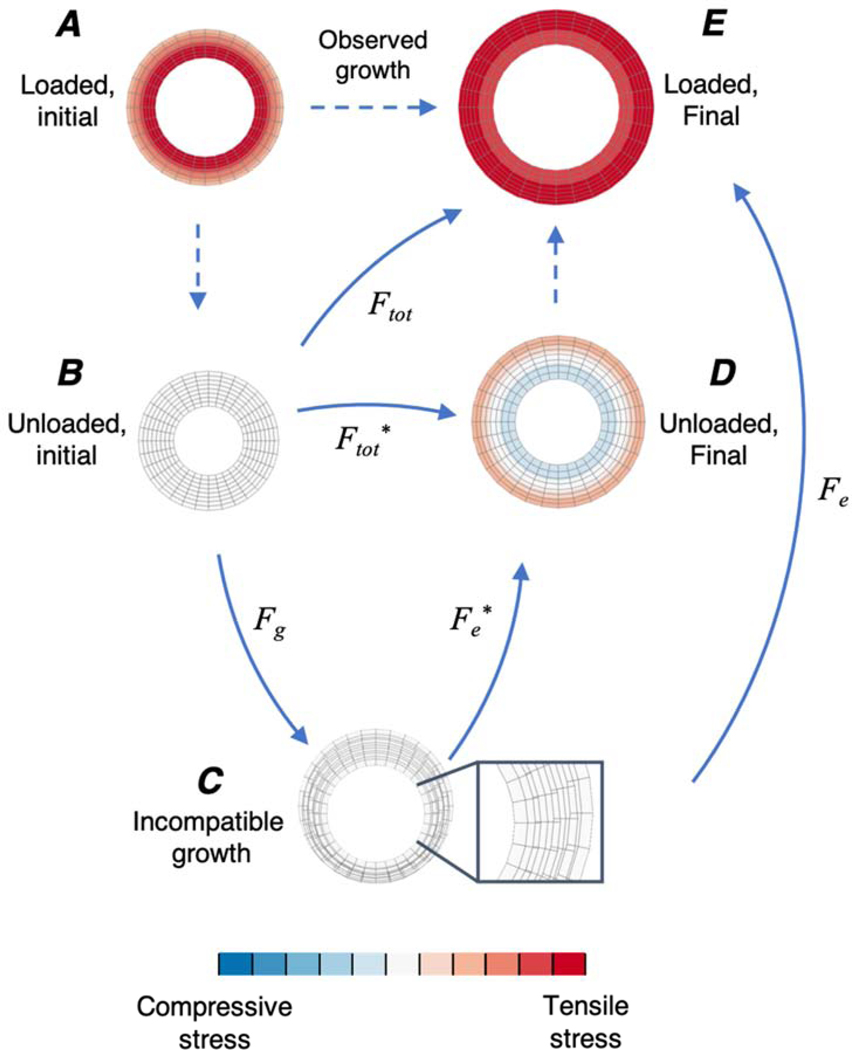
Computational modeling of growth requires a framework for tracking how addition and subtraction of material within a tissue changes the stresses and strains present in that tissue. The vast majority of cardiac growth modeling studies to date have employed the framework proposed by Rodriguez et al. in 1994 (Rodriguez et al., 1994). Their framework decomposes the total observable deformation due to growth (F_tot) as a product of two deformation tensors (Fig. 1) – a growth deformation tensor (F_g) and an elastic deformation tensor (F_e). Within this framework, F_g is a diagonal tensor that represents the changes in dimensions that would arise due to addition or removal of material in a stress-free state. However, in many situations the configuration that results after application of F_g is physically incompatible (Fig. 1C). An elastic deformation F_e* is then applied to restore compatibility and continuity, and in general introduces stresses (Fig. 1C, D, E). When this framework is used to describe the growth of a tissue in the absence of external loads (Fig. 1B, C, D), the initial configuration is assumed to be stress-free and the final configuration is the residually stressed, unloaded state. In the presence of external loads (Fig. 1A, C, E), these initial and final configurations are both subjected to additional elastic deformations due to loading and it is these loaded reference (Fig. 1A) and grown states (Fig. 1E) that are typically observed experimentally or clinically. As discussed below, based on experimental evidence that changes in mechanics can induce heart growth, a number of investigators have proposed and implemented a range of mathematical (phenomenological) relationships that relate mechanical stimuli to the components of F_g in the Rodriguez framework to model various cases of heart growth (Table 1). In these models, stimuli such as stress and strain drive growth, which in turn alters F_e and tissue stresses even under a fixed external load, creating feedback loops that in some cases lead to a new, stable steady-state and in others produce runaway growth.

Figure 1:

Finite element simulations of a pressurized cylinder demonstrating the different states of the kinematic growth framework. Top row describes growth under an applied load and second row describes growth in the absence of load (see text). Colors depict induced stresses from growth and loading with blue representing compressive and red representing tensile stresses. Initial state (before growth) of the cylinder under load (A) and with the load removed in a stress-free state, assuming no residual stresses are present (B). Applying a growth deformation (F_g) in a stress-free state can induce incompatible growth (C). Inset in (C) shows overlap between meshes. In the absence of external loads, F_e* is applied to restore compatibility, which introduces residual stresses (D). When external loads are present (i.e. as observed in vivo), F_e also incorporates additional deformations due to loading, resulting in the final grown and loaded state (E).

Table 1:

Summary of cardiac growth modeling studies using the kinematic growth framework.

Growth stimulus	Reference	Process(es) modeled	Patterns of growth	Geometry	Boundary conditions	Species	Data used to tune/select growth parameters	Independent predictions not used to tune model
Stress	(Lin and Taber, 1995)	Embryonic development	Concentric and eccentric	Thick-walled cylinder	ED pressure	Chick embryo	Wall volume changes from control and banded embryonic chick ventricles	Residual stress from opening angle experiment
	(Taber, 1998)	Embryonic development, pressure overload, volume overload	Concentric and eccentric	Thin-walled cylinder	ES pressure and ED radius	Chick embryo	Known physiology and qualitative agreement with experimental observations	N/A
	(Ramasubramanian et al., 2008)	Embryonic development	Eccentric	2D Finite element model	Applied force	Chick embryo	Qualitative agreement with experimental observations	N/A
	(Göktepe et al., 2010a)	Athlete’s heart	Isotropic	Finite element model (truncated ellipsoid biventricular)	Experiment al LV pressure cycle	Human geometry, Porcine pressures and material properties	Known physiology and qualitative agreement with experimental observations	N/A
	(Rausch et al., 2011)	Hypertension	Concentric	Finite element model (truncated ellipsoid biventricular)	Linear pressure increase	Human geometry, Porcine pressures and material properties	Quantitative agreement with clinical heart growth in hypertensive patients	N/A
	(Klepach et al., 2012)	Myocardial infarction and infarct removal	Eccentric	Finite element model (patient specific LV)	Constant pressure	Human	Cardiomyocyte changes in patients and rabbits with dilated cardiomyopathy	N/A
	(Bianco, 2018)	Mild aortic stenosis	Concentric	Finite element model (Truncated ellipsoid LV)	Pressurevolume loop model	Canine	Growth parameters based on Göktepe et al., 2010a. Compares electromechanical feedback with and without growth	N/A
Strain	(Arts et al., 2005)	Pressure overload	Concentric and eccentric	One fiber sphere model	Adaptive circulation model	Human (adult and fetal)	Known physiology and qualitative agreement with clinical observations	N/A
	(Kroon et al., 2008)	Volume overload	Isotropic	Finite element model (Truncated ellipsoid LV)	Constant EDP	Canine	Induced a 30% volume change	N/A
	(Kerckhoffs, 2012)	Postnatal growth	Eccentric and Concentric	Finite element model (Truncated ellipsoid LV)	Constant EDP	Rat (newborn)	Cross-fiber growth rate set to 1/3 of fiber growth rate. Qualitative and quantitative agreement with organ level growth trends and cellular dimensions in rats	N/A
	(Kerckhoffs et al., 2012a)	Aortic stenosis and mitral regurgitation	Eccentric and Concentric	Finite element model (MRI based biventricular)	Circulation model	Canine	Mixed qualitative and quantitative match to aortic stenosis and mitral regurgitation experiments in canines	N/A
	(Kerckhoffs et al., 2012b)	Left bundle branch block	Eccentric and Concentric	Finite element model (MRI based biventricular)	Circulation model	Canine	Quantitative match to experimental data in canines with left bundle branch block	N/A
	(Lee et al., 2015a)	Volume overload and reverse remodeling	Isotropic	Thick-walled cylinder and finite element model (Truncated ellipsoid and MRI based LV)	ED pressure cycles	Human	Qualitative agreement to clinical and experimental observations of forward and reverse growth due to volume overload	N/A
	(Genet et al., 2015)	Physiological residual stress	Isotropic	Finite element model (MRI based LV)	Constant pressure	Human	Quantitative match to opening angle experiments in pig hearts	N/A
	(Genet et al., 2016)	Pressure and volume overload	Eccentric and Concentric	Finite element model (4 chamber Living Heart Model)	Constant pressure	Human	Qualitative agreement to clinical observations of eccentric and concentric growth	N/A
	(Lee et al., 2015b)	Myocardial infarction	Eccentric	Finite element model (MRI based LV)	Windkessel model	Human	Qualitative agreement with clinical and experiments of infarct stiffening	N/A
	(Witzenburg and Holmes, 2018)	Aortic stenosis, mitral regurgitation, and myocardial infarction	Eccentric and Concentric	Thin-walled sphere	Circulation model	Canine	Canine aortic banding and mitral regurgitation experiments	Independent canine aortic banding and mitral regurgitation experiments
	(Peirlinck et al., 2019)	Mitral regurgitation	Eccentric	Finite element model (patient specific LV)	Increasing EDV	Porcine	Growth rates observed in experimental volume overload in rabbits	Quantitative agreement with myocyte dimensions for each animal
	(Arumugam et al., 2019)	LV Freewall pacing	Eccentric and Concentric	Finite element model (MRI based biventricular)	Windkessel model	Human	Quantitative match to electrical pacing experiments in canines	Regional differences in growth
	(Yoshida et al., 2020)	Aortic banding and unbanding	Eccentric and Concentric	Finite element model (MRI based biventricular)	Circulation model	Canine	Calibrated to match forward growth in canine aortic banding experiment	Qualitative agreement with clinical and experimental observations after release of pressure overload
Combination of stress and strain (or work)	(Taber and Chabert, 2002)	Development before and after birth	Eccentric and Concentric	Thick-walled cylinder	ED and ES pressure	Chick embryo	Qualitative match to growth in developing chick embryo	Quantitative agreement with opening angle experiments in normal and banded hearts
	(Göktepe et al., 2010b)	Pressure overload and volume overload	Eccentric and Concentric	Finite element model (truncated ellipsoid biventricular)	Constant pressure	Human	Qualitative agreement with clinical observations	N/A
	(Arts et al., 2012)	Volume overload, hypertension, decreased contractility	Eccentric and Concentric	TriSeg Model (three spherical segments, (Lumens et al., 2009))	Adaptive circulation model	Human	For each candidate stimulus, growth parameters were optimized for stability	Qualitative agreement with clinical and experimental observations

ED: end-diastolic, ES: end-systolic, LV: left ventricle, MRI: magnetic resonance imaging

2.2. Proposed mechanical signals that drive heart growth

It is clear that changes in mechanical environment can be transduced by myocytes and produce growth, but the underlying intracellular mechanisms are still not fully understood. Here, we limit our discussion to the mechanical signals that have been proposed and successfully utilized to predict growth. In 1975, Grossman et al. (Grossman et al., 1975) hypothesized that the heart increases its wall thickness in response to pressure overload in order to normalize systolic stresses. Like many subsequent hypotheses about the drivers of growth, Grossman’s concept was motivated by an experimental observation: he computed estimated wall stresses for patients with elevated LV pressures due to aortic stenosis and compared them to estimates in normal controls. The pressure-overloaded patients had normal peak systolic wall stresses, due to a significantly higher LV wall thickness that offset the elevated LV pressure in the stress calculation. Combining his data with other similar observations in the literature, Grossman reasoned that concentric hypertrophy might be driven by systolic wall stress, creating a feedback loop that produced a new steady-state once wall stress was normalized. Inspired by these early observations, many cardiac growth models have employed stress as the driver of growth (Table 1). Stress-driven growth has been utilized to capture growth during development (Lin and Taber, 1995; Ramasubramanian et al., 2008; Taber, 1998; Taber and Perucchio, 2004), wall thickening due to pressure overload induced by aortic stenosis or hypertension (Bianco, 2018; Rausch et al., 2011), cavity dilation in response to myocardial infarction (Klepach et al., 2012), and isotropic growth in response to significant amounts of exercise (Göktepe et al., 2010a).

Grossman also proposed that diastolic stresses might drive eccentric hypertrophy (circumferential growth with little change in wall thickness), although he also recognized that eccentric hypertrophy would further increase diastolic stresses. Emery and Omens confirmed that computed wall stresses remained elevated during eccentric hypertrophy in rats, while diastolic strains returned to normal by 6 weeks, and argued that diastolic strain would therefore be a more appropriate driver for eccentric growth in computational models (Emery and Omens, 1997). Since that time, many cardiac growth laws have employed strain as the mechanical driver of growth (Table 1). Strain-driven growth has been used to predict responses to pressure overload (Arts et al., 2005; Genet et al., 2016), volume overload (Genet et al., 2016; Kroon et al., 2008; Peirlinck et al., 2019), as well as post-natal heart growth (Kerckhoffs, 2012) and the origin of residual stresses (Genet et al., 2015). More recently, some of these growth laws have been extended to capture chamber dilation in response to myocardial infarction (Lee et al., 2015b) and dyssynchrony (Arumugam et al., 2019). Of particular interest is the strain-based growth relationship proposed by Kerckhoffs et al. (Kerckhoffs et al., 2012a), which was able to predict responses to both pressure and volume overload with a single set of growth parameters, and to predict regional differences in growth in the presence of simulated dyssynchrony (Kerckhoffs et al., 2012b). While the comparisons to data were somewhat qualitative in these early papers, Witzenburg and Holmes implemented a version of the Kerckhoffs law in a compartmental model of the heart and circulation and showed that it could quantitatively match remodeling data from multiple independent canine studies of pressure overload, volume overload, and myocardial infarction with a single set of growth parameters (Witzenburg and Holmes, 2018).

Not surprisingly, other models have employed combinations of stress and strain or related quantities such as mechanical work. One study proposed a combination of stress and strain to describe growth during embryonic heart development (Taber and Chabert, 2002). Another used strain to drive eccentric growth due to volume overload and stress to drive concentric growth due to pressure overload (Göktepe et al., 2010b). Arts et al. (Arts et al., 2012) designed a modeling study to test combinations of eight different mechanical signals including measures of stress, strain, and work in response to volume overload, hypertension, and decreased contractility of the heart. They determined that a combination of four different measures of stresses performed the best in predicting eccentric and concentric growth.

The complexity of these computational models varies between studies. Geometric complexity in the studies listed in Table 1 ranges from thin-walled cylinders (Taber, 1998) to anatomically accurate MRI-derived finite element models. In addition to geometry, these studies span a range of hemodynamic complexity from simple passive inflation to represent changes in end-diastolic pressure to models that fully couple the heart to a circuit model of the circulation to account for changes in hemodynamics. Recently, our group and others have highlighted the importance of hemodynamics on heart growth. In the case of dyssynchrony due to left bundle branch block, Kerckhoffs et al. (Kerckhoffs et al., 2012b) demonstrated that their model only matched experimentally reported growth when they represented the hemodynamic compensation required to maintain a constant mean arterial pressure. Work from our group has also demonstrated that a compartmental growth model, where complex changes in hemodynamics were taken into account while the geometry of the left ventricle was simplified to a thin-walled sphere, was able to quantitatively predict the time course of heart growth much faster but with similar accuracy compared to a traditional finite element model (Witzenburg and Holmes, 2018).

2.3. Stability of heart growth

As discussed above, one of the considerations investigators have often employed when formulating hypotheses about mechanical drivers of growth is that the system should be stable, returning to a new steady-state after growth normalizes the inciting stimulus. The data are more complicated. Heart size clearly reaches a steady-state as children grow into adulthood or when adapting to a new exercise routine. On the other hand, eccentric hypertrophy in response to volume overload or myocardial infarction often produces runaway dilation leading to heart failure. Another complicating factor when modeling these responses is that most models do not fully represent other control systems such as reflex control of hemodynamics that feed back to modulate cardiac growth as it progresses. Thus, in practice it has proven difficult to formulate growth laws that can match both stable growth and runaway growth observed in various physiologic and pathologic situations. We recently compared the responses of eight published cardiac growth laws to prescribed cyclic stretches representing mechanics typical of pressure and volume overload and found that only two of the laws could return to homeostasis in both simulations (Witzenburg and Holmes, 2017). Accordingly, many published growth models incorporate a growth limiting function, where the rate of growth approaches unity when a component of F_g reaches a pre-defined value (Göktepe et al., 2010a, 2010b; Kerckhoffs et al., 2012a, 2012b; Klepach et al., 2012; Rausch et al., 2011). Kroon et al. (Kroon et al., 2008) investigated an alternate approach, incrementally updating the reference configuration after each growth step to represent the evolution of the homeostatic setpoint of the mechanical sensing systems due to turnover of the underlying cellular components. This modification produced a decrease in growth stimulus over time, which led to overall attenuation of growth compared to a simulation where a fixed reference configuration was chosen. As discussed below, we recently implemented an evolving homeostatic setpoint in an attempt to better reproduce observed regression of hypertrophy following relief of pressure overload and observed a similar reduction in the stimulus for concentric hypertrophy (Yoshida et al., 2020).

3. Limitations of current cardiac growth models

3.1. Predicting reversal of heart growth after therapies

Despite encouraging successes, there are particular situations where current approaches for modeling cardiac hypertrophy fall short. As we look ahead to clinical applications of computational cardiac growth models, the ability to predict the regression of heart growth is critical, since clinical questions often center on whether or how a patient’s heart will reverse its growth after an intervention, such as a valve replacement/repair (Siegel et al., 2011; Whitlow et al., 2012) or cardiac resynchronization therapy to treat dyssynchronous heart failure (Brignole et al., 2013; St John Sutton, 2003). Kinematic growth models lead to atrophy when the growth stimulus becomes negative, which occurs when elastic strains or stresses drop below homeostatic values, leading to growth stretches that are less than one. We would expect these models to correctly predict atrophy when an intervention directly reduces strains or stresses below a homeostatic baseline, such as during experimental unloading of the heart by heterotopic transplantation (Didié et al., 2013; Ono and Lindsey, 1969). However, our group recently demonstrated that in certain situations, the kinematic growth framework does a poor job of capturing heart growth reversal after a clinical intervention. We simulated pressure-overload hypertrophy and regression following imposition and then relief of aortic constriction in dogs. We employed the strain-based growth law proposed by Kerckhoffs et al. (Kerckhoffs et al., 2012a), which performed the best in a head to head comparison of eight proposed growth laws (Witzenburg and Holmes, 2017) and was able to correctly predict patterns of “forward” growth (hypertrophy) in response to multiple perturbations including pressure overload, volume overload, and myocardial infarction in our previous simulations (Witzenburg and Holmes, 2018). When we matched the hemodynamics and forward growth reported in the canine pressure-overload experiments, then matched the hemodynamics associated with unloading, the Kerckhoffs law could not replicate the regression of hypertrophy typically observed with relief of pressure overload (Yoshida et al., 2020). Furthermore, our analysis demonstrated that unless the growth setpoint was allowed to evolve, any stress or strain-based growth laws used within a kinematic growth framework would perform similarly. However, we were able to correctly predict both hypertrophy and regression by incorporating an evolving growth setpoint in the governing growth equations; as discussed further in Section 4.2, the evolution of growth setpoints is a key feature of other approaches to modeling growth and may better reflect some aspects of the underlying biology. In the case of volume overload, a finite element model using the kinematic growth framework was able to predict growth reversal (atrophy) if simulated LV pressure was reduced (Lee et al., 2015a). However, studies of the MitraClip device for repair of mitral regurgitation have found significant reverse remodeling (Whitlow et al., 2012) with no change in LV pressure (Siegel et al., 2011).

3.2. Accounting for growth of individual tissue constituents

In many cases of cardiac growth, cardiomyocyte hypertrophy is accompanied by fibrosis and remodeling of the extracellular matrix (de Boer et al., 2019; Niestrawska et al., 2020). In its classical formulation, the kinematic growth framework does not account for differences in growth between individual constituents (cardiomyocytes, collagen, elastin, etc.). In a recent study of hypertrophy and regression following pressure overload and unloading (Yoshida et al., 2020), we investigated the effect of fibrosis by inducing a 20% increase in passive stiffness of the myocardium but found it had no effect on growth predictions. In what settings accounting for these changes in composition or material properties is necessary to correctly predict growth remains an open question.

3.3. Accounting for evolving hemodynamics

The studies on regression of hypertrophy discussed in the previous section add even more weight to the growing body of evidence that correctly modeling hemodynamics is an essential step when formulating and testing growth laws. In our own simulations of pressure-overload relief, we found that a strain-based kinematic growth law with a fixed growth setpoint could generate regression of hypertrophy under some hemodynamic conditions, but not under the actual hemodynamic conditions reported following relief of pressure overload in experiments. Together with data showing that matching the evolution of hemodynamics is often critical to correctly predicting hypertrophy (see section 2.2), these modeling results suggest that growth models that aim to prospectively predict the effects of interventions on heart growth will need to incorporate realistic models (Beard et al., 2013) of how the hemodynamic loads placed on the heart will evolve in response to those interventions and to ongoing growth and remodeling.

3.3. Incorporating effects of hormones and commonly used drugs

Another limitation of current approaches to modeling heart growth is the inability to capture the effects of hormones that are known to enhance or attenuate heart growth and the modulation of hypertrophy by drugs such as beta-adrenergic and angiotensin inhibitors commonly used to treat cardiovascular disease. Cardiomyocyte growth is driven by a complex network of intracellular signaling pathways (Heineke and Molkentin, 2006; Ryall et al., 2012). In vitro experiments demonstrate the ability of various hormones and drugs to induce cardiomyocyte hypertrophy in the absence of mechanical stimuli, as well as the potential of stretch to induce hypertrophy in the absence of hormones. Ryall et al. (Ryall et al., 2012) constructed a computational model of the intracellular signaling pathways associated with many of these reported responses and showed that the signaling pathways that transduce myocyte stretch overlap with those that respond to hypertrophy-associated hormones and chemokines (Ryall et al., 2012). Recently, this model was further refined and validated by recapitulating in vivo heart growth in 52 transgenic and 4 double-transgenic mouse models (Frank et al., 2018). Furthermore, experiments such as aortic banding that are often used to calibrate growth models are known to alter not only heart mechanics but also the levels of many hypertrophy-associated hormones (Kamal et al., 2014; Liao et al., 2003; Lindpaintner et al., 1987; Lorell and Carabello, 2000; Rapacciuolo et al., 2001; Schunkert et al., 1990; Yamazaki et al., 1995). Thus, calibrations of mechanics-based growth laws against experimental data likely incorporate both mechanical and hormonal influences on growth, and such laws would be expected to perform poorly if the hormonal environment changes. This is a particular concern in considering potential clinical applications of growth laws, since patients with cardiovascular disease typically receive different combinations of drugs that act on pathways such as beta-adrenergic and angiotensin signaling that are known to modulate hypertrophy. Additionally, gender differences in heart growth and heart failure are well-established (Mendelsohn, 2005; Regitz-Zagrosek and Kararigas, 2017) but modeling studies that consider the role of sex and steroid hormones on cardiac growth are lacking. As discussed in more detail in Section 5, multiscale approaches that combine models of organ-level LV mechanics with models of cellular-level signaling may provide a useful way to address these complexities as growth modeling moves towards the clinic.

4. Growth approaches used in other tissues and fields of study and lessons learned

Most models of cardiac growth reviewed above are conceptually similar – they employ the kinematic growth framework from Rodriguez et al. (Rodriguez et al., 1994) and drive growth using various combinations of mechanical stimuli. By contrast, mathematical modeling of growth more broadly has a long history involving a variety of conceptual approaches, from early studies in plants (see Cowin, 2011 (Cowin, 2011) for a very interesting review) and bone to recent work in systems biology. While we cannot provide a comprehensive review of all of this literature here, we highlight a few examples of concepts first applied in other tissues and fields of study that might prove useful in future models of cardiac growth.

4.1. Bone growth modeling

There is a rich history of computational growth modeling in the field of bone biomechanics. Originally formulated design orthopedic implants, a number of continuum mechanics models were formulated to capture “Wolff’s Law” – a phenomenon where trabecular bone structures adapt by increasing its mass density in response to increased loading. Many of the basic mathematical concepts used to model growth of other tissues originate from these works including phenomenological laws that define remodeling rates as functions of stress, strain, or strain energy density (see (Cowin, 1993) for a detailed review on this topic) as well as the concept of adaptive remodeling setpoints (Cowin, 1984). Cowin also highlighted the need for more mechanistic models that simulate how mechanical signals are transduced into cellular responses (Cowin, 2004).

A major area of interest in bone research is the development of osteoporosis due to estrogen deficiency in postmenopausal women (Schiessl et al., 1998). Accordingly, some computational modeling studies have focused on incorporating the effects of estrogen and mechanics on bone growth (See Klein-Nulend et al, 2015 for a review on this topic (Klein-Nulend et al., 2015)). Specifically, Ruimerman et al. (Ruimerman et al., 2005) simulated postmenopausal osteoporosis by increasing bone resorption rates and found that the resulting loss of bone volume fraction increased remodeling rates due an increase in mechanical stimulus.

4.2. Constrained mixture modeling approaches

Another popular approach for modeling growth is the constrained mixture model proposed by Humphrey and Rajagopal (Humphrey and Rajagopal, 2002). In their original manuscript, Humphrey and Rajagopal proposed a continuum mechanics framework to account for the differences in production and degradation rates of various tissue constituents (cells, collagen, elastin, proteoglycans, etc.), which are constrained to deform together. In this framework, each constituent evolves its own natural (unstressed) configuration as new materials are produced in the current (grown) configuration and old materials are degraded. Modeling these processes leads to the evolution of the reference state of the composite mixture due to growth.

The constrained mixture framework has been diversely applied within the fields of arterial biomechanics, musculoskeletal biomechanics, and tissue engineering (Miller et al., 2015; Soares and Sacks, 2016). For more details, readers are referred to other review papers on this topic (Ateshian and Humphrey, 2012; Myers and Ateshian, 2013). The strength of this framework is its incorporation of biologically realistic turnover of individual tissue components, in contrast to the purely phenomenological whole-tissue growth simulated by the kinematic growth framework. More recently, mixture approaches have been extended to incorporate interactions between biology and mechanics. Lattore et al. (Latorre et al., 2019; Latorre and Humphrey, 2018) developed a mechanical-inflammation model the effects of both mechanics and inflammatory cell burden were incorporated into the mass production equation. Using their model, the authors were able to capture both favorable mechano-adaptation and fibrotic maladaptation in an animal model of hypertension.

In application to cardiac growth, the constrained mixture approach offers features that can address some of the limitations of current kinematic growth models addressed above. First, the constrained mixture approach explicitly accounts for new constituents (with new reference configurations) replacing old constituents with unique deposition and degradation rates. Modeling these processes can then lead to new homeostatic states that are different from the original ungrown configuration. In the kinematic growth framework, a similar effect can only be achieved by allowing the growth setpoint to adapt over time. Based on our finding that an evolving growth setpoint is necessary to predict observed regression of heart growth following relief of pressure overload (Yoshida et al., 2020), a constrained mixture approach may be better suited to modeling post-treatment regression of cardiac hypertrophy. Second, the mixture theory framework allows for the division between different tissue constituents, whereas the classical applications of the kinematic growth framework only account for bulk growth of the composite tissue. Since fibrosis of the myocardium is often associated with heart growth, implementing mixture approaches to separately model accumulation of collagen and cardiomyocyte hypertrophy could have important advantages (Niestrawska et al., 2020).

Despite its advantages, one of the practical challenges in the application of constrained mixture models is their computational complexity. For example, a 3D finite element implementation of this framework requires tracking each constituent’s stress-free configuration in each element at each growth time step. Therefore, there have been few studies that employ 3D finite-element implementations of the constrained mixture approach (Valentín et al., 2013). Nevertheless, Ateshian and co-workers (Ateshian and Ricken, 2010) formulated a finite element implementation of constrained mixture growth, which is available in the open source finite element software, FEBio (http://febio.org). Some authors have proposed the use of a hybrid approach combining constrained mixture growth with the kinematic growth framework (Cyron and Humphrey, 2017), where the mass turnover of each constituent is temporally homogenized (Cyron et al., 2016) or mass/shape change is represented kinematically by tracking the evolution of “recruitment” stretch (Eriksson et al., 2014). These approaches could be a promising next step for modeling cardiac growth mechanics.

4.3. Systems biology models of growth

The biology underlying cardiomyocyte hypertrophy has been extensively studying, and systems biology models that incorporate much of that knowledge have begun to emerge. Specifically, Saucerman and coworkers have focused on the intracellular signaling pathways through which stretch and hormones interact (Frank et al., 2018; Ryall et al., 2012) as well as how stretch directly affect mechano-sensitive cell receptors and downstream signaling pathways (Tan et al., 2017) that lead to hypertrophy. These network models are developed by integrating data across many studies about known biological pathways that drive cardiomyocyte hypertrophy. Such models have the potential for exciting clinical applications, as they are able to predict the influences of and even interactions among drugs that alter cardiomyocyte growth. One disadvantage, however, is that current models are able predict changes in mass, but not in myocyte shape, as the pathways that lead to differences in shape (i.e. myocyte lengthening leading to eccentric growth vs. thickening leading to concentric growth) are still unclear. Nevertheless, as described below, integrating these models with mechanics-based approaches holds great promise for predicting heart growth in settings where mechanics, hormonal environment, and/or drug treatments all interact.

4.4. Thermodynamic growth approaches

Whereas the systems biology models described in the previous section make detailed mechanistic predictions of changes in mass without accounting for changes in myocyte shape, a recently published model based on thermodynamic principles (Cohen et al., 2019) specifically addresses changes in myocyte shape. Based on previous computational models developed to capture stress fiber remodeling in fibroblasts (Vigliotti et al., 2016), this thermodynamic framework proposes that a cardiomyocyte will grow or shrink by adding or removing sarcomere units to balance the total energy between mechanical work, internal energy, and entropy of the cardiomyocyte. In its first implementation, the model was able to qualitatively capture experimental trends from cultured cardiomyocytes, suggesting potential promise for explaining the differences in myocyte shape change in response to pressure and volume overload.

5. Integrating systems biology with mechanics for pregnancy induced heart growth

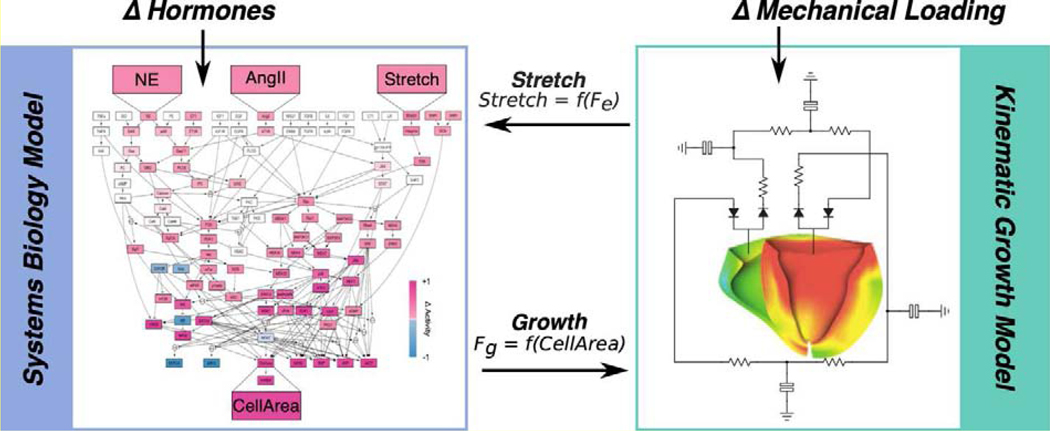
As outlined above, developments in other fields of study (Section 4) have the potential to address limitations of current approaches for cardiac growth models (Section 3). In particular, multiscale models where cell-level systems biology models are coupled with a mechanics-based growth framework are an exciting approach for investigating interactions between biology and mechanics (Sree and Tepole, 2020). Here, we propose a multiscale modeling approach for future studies that couples a systems biology model of cell-level cardiomyocyte growth (Section 4.3) with a tissue-level kinematic growth framework (Section 2.1) to understand how mechanics and biology interact to drive pregnancy induced heart growth.

Pregnancy stands at the interface of biology and mechanics. Over nine months of pregnancy, circulating hormone levels surge by up to 10 times (Tulchinsky et al., 1972). Pregnancy presents a cardiovascular challenge to the mother, as her cardiac output increases by 50%, her blood volume increases 60%, and systemic resistance decreases by 20% - only to return to nonpregnant levels by 2 weeks postpartum (Hunter and Robson, 1992). Within the field of pregnancy research, there is a critical need to understand how these pregnancy hormones and changes in hemodynamics interact during pregnancy. Maternal death rates in the United States have increased over the last 25 years (Kassebaum et al., 2016) and cardiovascular conditions remain as the leading cause of pregnancy-related deaths (Creanga et al., 2017).

Two of the main pregnancy hormones, estrogen and progesterone are known to attenuate and induce hypertrophy, respectively as demonstrated in both in vitro and in vivo studies (Babiker et al., 2006, 2004; Bhuiyan et al., 2009; Chen et al., 2011; Chung et al., 2013, 2012; Cui et al., 2011; Donaldson et al., 2009; Kilić et al., 2009; Liu et al., 2006; Patten et al., 2008; Pedram et al., 2013, 2005; Van Eickels et al., 2001). Therefore, to understand pregnancy-induced heart growth, it is critical to consider changes in both mechanics and hormones, as outlined in the proposed multiscale growth model (Figure 2). Within this proposed multiscale growth model, the actions of estrogen and progesterone on the intracellular signaling pathways leading to growth can be incorporated into a systems biology model. A lumped-parameter circulation model can be used to simulate changes in the maternal hemodynamics to solve for the boundary conditions of the mechanical finite element model. Accordingly, this multiscale modeling approach can be used to account for the simultaneous changes in hemodynamics and circulating hormone levels. The amount of growth predicted by the systems biology model for a particular level of stretch and circulating hormones can be fed into the finite element model as a growth deformation (F_g) to change the geometry of the heart, which can solve for changes in stretches due to growth experienced by the cell. To close the loop, changes in stretches can be fed back into the systems biology model and used to predict changes in growth. By modeling the interactions between hormones and mechanics using this approach, we aim to identify the critical intracellular pathways that drive pregnancy induced growth. These future studies could have important clinical applications such as developing new therapies for pregnancy-related heart conditions, including heart failure in women towards the end of pregnancy or immediately postpartum (peripartum cardiomyopathy). Outside of pregnancy, this model also has potential applications in explore sex differences in heart failure, including elucidating the mechanisms through which estrogen protects premenopausal women from cardiovascular disease (Stampfer et al., 1991) and to design effective therapies.

Figure 2:

Proposed multiscale cardiac growth model. A systems biology signaling network model of cardiomyocyte growth (Ryall et al., 2012) is coupled to a kinematic growth based finite element model to understand interactions between hormones and mechanical signals that drive growth. The network model predicts the amount of growth due to a particular level of stretch and circulating hormone inputs and outputs a CellArea, which is fed into the finite element model as a growth stretch in one or more directions (F_g). Changes in stretches due to growth and mechanical loading (F_e) is then fed back into the network model to close the loop.

6. Conclusions

In conclusion, mechanics-based growth models have been successfully used to model cardiac hypertrophy in response to altered loading in a wide variety of conditions. However, these models have been less successful in predicting regression of hypertrophy in response to treatments that relieve mechanical overloads. Furthermore, standard approaches provide no good way to incorporate the effects of hormones and drugs that influence growth and are frequently altered in clinical settings. Emerging computational modeling approaches such as constrained mixture growth models, systems biology models of networks of intracellular signaling pathways underlying growth, and thermodynamics-based models that can predict cardiomyocyte shape changes have the potential to address many of the main limitations of the standard kinematic growth framework for modeling growth. To illustrate this potential, we propose here a multiscale modeling approach for pregnancy-induced cardiac growth, wherein a systems biology model is coupled to a mechanics-based finite element model and circulation, to better understand how hormones and mechanics interact to drive hypertrophy and regression.