Using Multimodel Inference/Model Averaging to Model Causes of Covariation Between Variables in Twins

Abstract

Objective:

To explore and apply multimodel inference to test the relative contributions of latent genetic, environmental and direct causal factors to the covariation between two variables with data from the classical twin design by estimating model-averaged parameters.

Methods:

Behavior genetics is concerned with understanding the causes of variation in phenotypes and the causes of covariation between two or more phenotypes. Two variables may correlate as a result of genetic, shared environmental or unique environmental factors contribute to variation in both variables. Two variables may also correlate because one or both directly cause variation in the other. Furthermore, covariation may result from any combination of these sources, leading to 25 different identified structural equation models. OpenMx was used to fit all these models to account for covariation between two variables collected in twins. Multimodel inference and model averaging were used to summarize the key sources of covariation, and estimate the magnitude of these causes of covariance. Extensions of these models to test heterogeneity by sex are discussed.

Results:

We illustrate the application of multimodel inference by fitting a comprehensive set of bivariate models to twin data from the Virginia Twin Study of Psychiatric and Substance Use Disorders. Analyses of body mass index and tobacco consumption data show sufficient power to reject distinct models, and to estimate the contribution of each of the five potential sources of covariation, irrespective of selecting the best fitting model. Discrimination between models on sample size, type of variable (continuous versus binary or ordinal measures) and the effect size of sources of variance and covariance.

Conclusions:

We introduce multimodel inference and model averaging approaches to the behavior genetics community, in the context of testing models for the causes of covariation between traits in term of genetic, environmental and causal explanations.

INTRODUCTION

Data from the classical twin design, i.e., from monozygotic and dizygotic twins, are commonly used to estimate the role of genetic and environmental factors in explaining variation and covariation in human traits. Typically, univariate (or mono-phenotype) modeling proceeds by fitting a standard biometrical model with three sources of variance (A: additive genetic factors, C: shared environmental factors and E: unique environmental factors, known as the ACE model) to twin data, and examining the significance of each of the sources of variance by fitting submodels (Maes 2005) or estimating likelihood-based confidence intervals (Neale et al. 1997). This is a manageable task as it requires fitting only three (AE, CE and E) submodels when the model has up to three sources of variance. Note that alternatively, models may include dominance genetic variance D instead of C, although additional relatives types would be needed to estimate both sources of variance simultaneously. When each twin is measured on two variables (referred to hereafter as bivariate) context, these models are extended to estimate the contributions of ACE variance components to the covariance between traits, in addition to the ACE components of each of the two variables. Furthermore, the covariance between the two traits may be modeled as direct causal paths, instead of or in addition of shared latent factors. Thus there are five parameters to consider when describing the covariance between two variables. We show in Appendix I that all models with any three of these parameters are identified (i.e., fitting them will yield a unique estimate for each parameter. For example, bidirectional causation and genetic correlation or pleiotropy. However, selecting the best model from the 25 possible models and submodels remains a challenge. Accordingly, we explore model averaging as a statistical method that may help to obtain a balanced overall view of the processes that may have generated the data.

For many years, the Cholesky decomposition of covariance matrices was popular in Behavior Genetics. The model specifies that covariance between m variables is due to m factors which have a factor loading pattern where the first factor affects all variables, the second affects all except the first variable, and so on until the last factor (which influences only the last variable). Models for twin data would assume this structure for covariance due to each of the A, C and E components of variance, so it became known as the ‘triple Cholesky’. While the model is suitable for longitudinal data, several articles have noted statistical problems (Carey 2005, Wu et al. 2013, Verhulst et al. 2019).

Typically, submodels are tested, either based on pre-set hypotheses or on results from the fitted model, and/or confidence intervals around the model parameters are estimated. Results sections generally include estimates of the best fitting model with confidence intervals, although sometimes results from a full model with confidence intervals on all parameters are also presented. In some studies, direction of causation models are chosen to test more directly whether the data are consistent with one variable being a direct cause of the other variable. These direction-of-causation (DOC) models may or may not be compared with models estimating sources of covariance directly (Heath et al. 1993, Duffy et al. 1994). Model selection is usually done by likelihood ratio tests or by selecting the model with the best parsimony measure, often operationalized as the lowest Akaike’s Information Criterion (AIC) or Bayesian Information Criterion (BIC). However, in many instances, no single model stands out as more strongly supported by the data than are others. Selection of a best-fitting model becomes difficult, and resolution between alternatives may require collection of more data with either the same design or an extended one. Such worthwhile efforts typically take considerable time and money, and the impatient or impoverished researcher may lack either or both. This raises the question as to whether novel statistical methods can provide a glimpse of what such efforts would bring. The aim here is not to provide a comprehensive simulation study of multiple methods, but simply to explore one of them in the context of real data from a genetically-informative study.

The method used here is multimodel inference, which deals specifically with these types of scenarios where many alternative models could be fitted to a dataset (Burnham et al. 2004). These methods may be especially useful in cases where not all parameters of interest can be estimated simultaneously due to under-identification of the full model. The approach involves fitting all possible (identified) bivariate twin models that include different combinations of the parameters of interest. AIC (minus twice the log-likelihood of the data minus twice the degrees of freedom) is calculated for each of the alternative models. These statistics can then be used to obtain average parameter estimates by weighting them according to their AIC fit. This process of model-averaging thus generates an averaged picture of the parameter estimates, along with their standard errors. It also allows to obtain simultaneous estimates of more parameters than would ordinarily be identified, and typically estimated in alternative models.

In the paper, we illustrate the use of multimodel inference and model averaging in a bivariate analysis of genetically informative data with a focus on exploring the sources of covariation between two variables. Our aims are to: i) show how to fit the 25 alternative identified bivariate twin models and submodels; ii) evaluate which sources of covariance are most consistent with the data through multimodel inference; iii) estimate the magnitude of each of the sources of covariation using model averaging; iv) explore the covariance between obesity and smoking quantity; and v) consider the statistical power to reject alternative models. We chose obesity and smoking quantity because both variables are at times analyzed as continuous or as binary/ordinal measures.

METHODS

Subjects

The phenotypic data analyzed here were collected from twins participating in the Virginia Adult Twin Study of Psychiatric and Substance Use Disorders, a study of ~8000 adult male and female same sex and opposite sex twin pairs ascertained from a population-based twin registry (Kendler et al. 2006). For these analyses, data were extracted from the first wave of the female study for height & weight, and the third and fourth waves for smoking behaviors. In the male and opposite sex twin pairs study (the MMMF study), height and weight data came from waves 1 and 2, and smoking data form waves 2 and 3.

Measures

We chose to analyze two continuous variables, first body mass index (BMI, calculated from self-report weight/height²), a commonly used measure of obesity. Second, we used number of cigarettes or their equivalent for alternative tobacco products smoked per day, a measure of tobacco quantity (ITOB). We set non-smokers to zero for these illustrative analyses, even though we are aware that number of cigarettes smoked is conditional on having initiated smoking and should ideally be analyzed as a conditional variable (Maes et al. 2004, Neale et al. 2006a, Neale et al. 2006b). We further generated ordinal and binary variables by placing thresholds on the continuous distributions of BMI (BMIo=0: bmi<18.5, 1: bmi>=18.5 & <25, 2: bmi>=25 & <30, 3: bmi>=30 for the ordinal measure; BMIb=0: bmi<25, 1: bmi>=25 for the binary measure). For ITOB, we also created a four-category variables (ITOBo) with 0 for those who have not initiated tobacco, 1 for those who smoked fewer than 10 cigarettes (or equivalents in alternative tobacco products), 2 for having smoked between 10 and 30 cigarette equivalents per day, and 3 for smoking more than 30 cigarettes per day; and a binary variable (ITOBb), where those in the first two categories were scored 0 versus those in the upper two categories scored 1. Binary variables were created to have an approximately even split.

Statistical Analyses

Sources of covariation

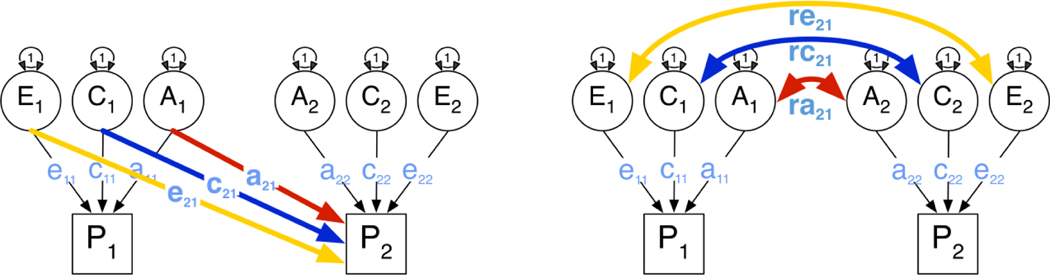
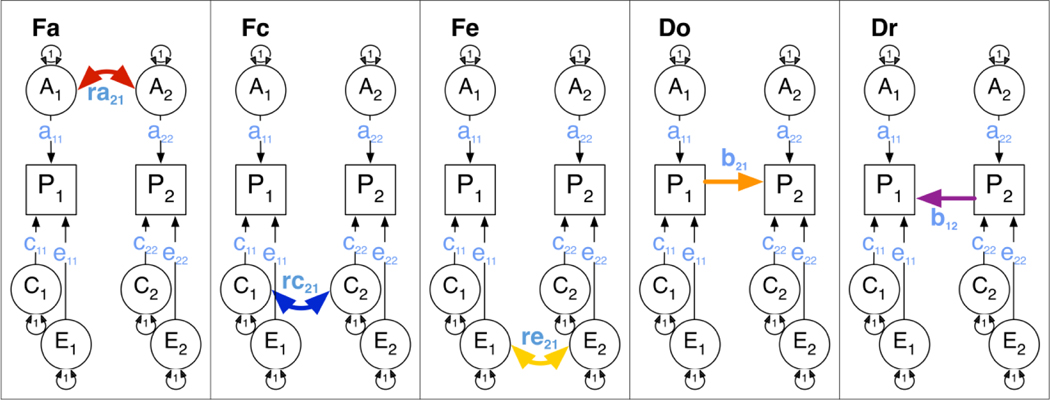
Structural equation modeling of genetically informative data was used to model the contributions of genetic and environmental factors to the liability of two variables, assuming an underlying threshold model when fitting to binary or ordinal data (Neale et al. 1992). Additive genetic factors A refer to the cumulative small effects of a large number of genetic loci. Shared (or between-family) environmental effects C make nuclear family members relatively more similar, whereas unique (or within-family) environmental factors E are unique to individuals within a family and contribute to differences between family members. Traditional bivariate twin models assume that each of the three sources of variance (ACE) contribute to the variances of each of the phenotypes as well as to their covariance, typically parameterized as a ‘triple Cholesky’ decomposition. Models can be re-parameterized as correlated factor models. Figure 1 shows alternative representations of a model for bivariate twin data. A separate class of bivariate twin models often applied to two variables are the causal models (Heath, Kessler 1993), which can be used to test whether the data are consistent with: i) a direct causal effect of one variable on the other, or ii) vice-versa, or iii) reciprocal causation between the two variables. It is important to note that twin data can reject simple models about the direction of causation between two variables, even with cross-sectional data, and that power to discriminate between alternative models increases with the difference between the MZ and the DZ correlations for the two variables. Covariation between two variables of interest can thus result from shared genetic factors, parameterized as a correlation between the latent genetic factors of two variables (ra). In addition to or alternatively, shared environmental factors may contribute to variance in both phenotypes, as represented by rc, and similarly can unique environmental factors (re). Finally, there may be a direct causal path from variable one to variable two, referred to as b₂₁, or there may be reverse causation, referred to as b₁₂. These five sources of covariance are illustrated in Figure 2.

Figure 1:

Alternative representations of bivariate twin models: triple Cholesky (top) and correlated factors model (bottom)

Figure 2:

Sources of covariation, identifiable with data from the classical twin design, representing 5 of the 25 identified bivariate submodels

Model selection

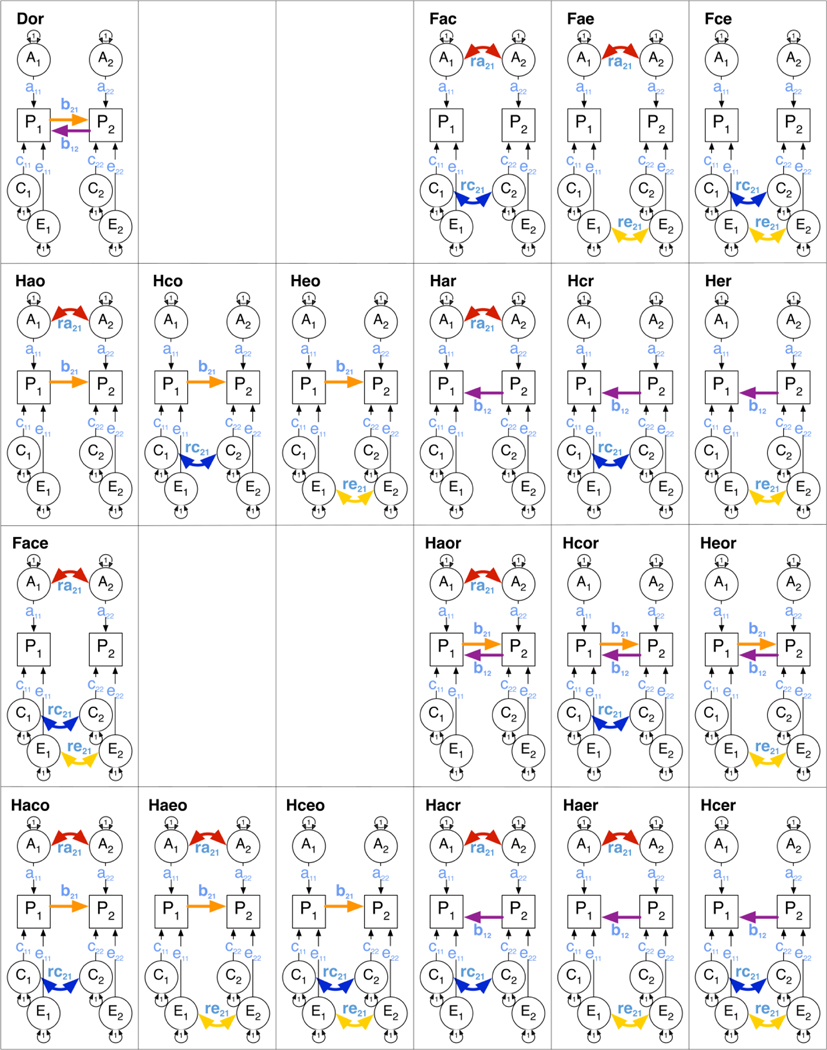
In most situations where one is interested in understanding the etiology of a correlation between two variables, there is little a priori knowledge of which sources of variance might contribute, or the relative strengths of these influences. This agnostic situation often leads investigators to several flawed strategies to distill the model fitting results. A researcher may arbitrarily pick a full correlated factors model or a causal model with assumed direction of causation, or may fit submodels by dropping some parameters based on, e.g., their statistical significance or interpretability. Others may proceed by systematically testing all submodels or a limited set of specific hypotheses. Here, we instead take a more a-theoretical approach. We fit all possible identified models, i.e., all models with up to three of the five specified sources of covariance (ra, rc, re, b₂₁ & b₁₂), resulting in 25 models. The first set includes only one of the five sources. The second set of ten models includes any two of the five sources, and the third includes three sources (see Figure 3). Models with more than three parameters are not identified. The mxCheckIdentification(see Appendix 1) function in the OpenMx package (Neale et al. 2016) shows that models including any combination of up to three sources of covariance are identified with data from the classical twin study. Thus, we set out to fit each of the 25 possible models to our continuous and derived categorical variables and to obtain empirical evidence of the best fitting model(s). The estimates from these models are then weighted by their degree of support (better fitting models get heavier weights) using multi-model inference to deliver model-averaged estimates. The different measures were used to illustrate model averaging for three types of data.

Figure 3:

Models with any two (top) or any three (bottom) sources of covariation between two variables

Multimodel inference and model averaging

We use multimodel inference methods to summarize the goodness-of-fit of the models and to calculate weights used in model averaging to obtain the ‘best’ estimates of the parameters of interest (Burnham, Anderson 2004, Symonds et al. 2011, Kirkpatrick et al. 2015). Multimodel inference uses AIC to compare different models by rank ordering models by AIC and calculating the difference (Δ) in AIC of each model and the model with the lowest AIC. This difference in AIC is then translated into an Akaike weight which has a value between 0 and 1 with the sum of the Akaike weights of all models being 1, and can be interpreted as the probability that a given model is the model that best approximates the data. Models with Δ less than 2 are typically considered as good as the best model, those with Δ greater than 10 are substantially poorer than the best AIC model. Multimodel inference approaches also generate a ‘confidence set’ of best approximating models by summing the Akaike weights of ranked models until the cumulative weight exceeds 0.95 (or alternative chosen level), concluding that one of the models in this set is the best approximating model (Symonds, Moussalli 2011). We can also use the model weights to assess the relative importance of each of the relevant parameters, by summing the Akaike weights for each model that includes the parameter. These summed weights can be considered as probabilities that the parameter is in the best fitting model. The best estimates of the model parameters are derived from weighted averages of the parameter values across models, a procedure known as model averaging. We used full-model averaging where inference is based on all models by summing the products of Akaike weights with the estimates from each model, so that models that do not include a particular parameter (because it was set to zero) do not contribute to the calculation of the average estimate of that parameter.

Model Specification in OpenMx

Twenty-five genetic models were evaluated, starting with a ‘triple correlated factors’ model, which is a fully saturated biometrical genetic factor ACE model, specified as correlated factors ra, rc, and re. The remaining set of 24 models can be grouped in sets of three each. The first set includes any two of the three correlated factors, followed by a set of models including only one of the three correlated factors. Next are a series of hybrid models that include at least one correlated factor, and at least one causal path. This series includes two sets of three models, each with two correlated factors, and one causal path, a set of three models with one of the correlated factors and two causal paths, and two sets of three models, each with one correlated factor, and one causal path. Finally included are the three DOC models with only one or two causal paths. Scripts for the analyses were written for OpenMx (Neale, Hunter 2016, Boker et al. 2011) and are available online at http://hermine-maes.squarespace.com (Maes 2018). These scripts incorporate a recently released model averaging function in OpenMx, called mxModelAverage(). This function (see Appendix 2) generates tables of: Akaike weights for each of the fitted models, model-wise estimates and sampling variances, and model-averaged point estimates and their standard errors. To calculate model-average estimates, only models are included in which the parameter is freely estimated. Models were specified as correlated factors models, which result in non-negative estimates of the variance components. Although models with direct variance estimation have better statistical properties for testing significance of model parameters (Wu, Neale 2013, Visscher 2006), model averaging methods implemented in OpenMx currently do not allow negative variances.

Sex Limitation

A common feature of behavior genetic models is testing for sex differences in the means and variance components. We illustrate this by considering data on female and male twin pairs separately or jointly. In the latter case, standard tests for sex differences in the magnitude and nature of the sources of variance are incorporated. The simplest model constrains parameters pertaining to variances and covariances across sex (no sex differences in variances and covariances). Quantitative sex differences can be tested by estimating separate parameters for male and female variance components and causal paths (Neale, Cardon 1992, Neale et al. 2006c). To evaluate additional qualitative sex differences, covariances across males and females between genetic or shared environmental factors can be estimated freely in opposite sex twin pairs. As is the case in testing sex heterogeneity for a single variable using the classical twin design, there is not enough information to simultaneously estimate the correlation between genetic factors across sex and that between shared environmental factors. Instead alternative models are fitted estimating the degree of overlap in either genetic or shared environmental factors across sex. In practice, we can evaluate the significance of sex differences in the first of the 25 models by fitting four sex-limitation models (no sex differences, quantitative sex differences only, and adding genetic or shared environmental qualitative sex differences), to guide fitting models to both sexes simultaneously. The main effects of sex and other potential covariates are straightforward to include in these models.

RESULTS

Descriptive Statistics

Data on BMI were available for 7,840 twins (3,455 females, 4,385 males) and on tobacco quantity for 6,516 twins (2,774 females, 3,742 males). Table 1 presents means for continuous variables (Table 1a) and frequencies for derived ordinal and binary variables (Table 1b). The continuous variables were divided by a constant to obtain variances near 1 to aid optimization. Observed values were higher for males and females for both BMI and tobacco quantity. Table 2 shows the pattern of twin correlations (cross-twin within-trait, Table 2a), which suggested primarily genetic influences and unique environmental influences on both variables and minor contributions of shared environmental factors. Phenotypic (within-twin cross-trait) correlations (Table 2b) and cross-twin cross-trait correlations (Table 2c) between BMI & ITOB suggested modest covariation between the two traits with different patterns for females, males and opposite sex twins. Note that these variables were chosen as illustrative examples.

Table 1:

Descriptive Statistics for continuous (1a) and ordinal/binary (1b) measures of BMI and ITOB for total sample and by sex

1a

	Variable	N	Mean	StdDev	Minimum	Maximum
total	BMI	7840	24.77	4.51	14.41	54.64
	BMIc	7840	6.19	1.13	3.60	13.66
	ITOB	6516	15.77	18.77	0.00	165.60
	ITOBc	6516	0.79	0.94	0.00	8.28
female	BMI	3455	23.31	4.69	14.41	51.60
	BMIc	3455	5.83	1.17	3.60	12.90
	ITOB	2774	11.70	15.21	0.00	80.00
	ITOBc	2774	0.58	0.76	0.00	4.00
male	BMI	4385	25.93	4.00	15.39	54.64
	BMIc	4385	6.48	1.00	3.85	13.66
	ITOB	3742	18.79	20.51	0.00	165.60
	ITOBc	3742	0.94	1.03	0.00	8.28

1b

	total			female			male
BMIo	7840	N	%	3455	N	%	4385	N	%
0		260	3.32		224	6.48		36	0.82
1		4224	53.88		2351	68.05		1873	42.71
2		2460	31.38		564	16.32		1896	43.24
3		896	11.43		316	9.15		580	13.23
BMIb		N	%		N	%		N	%
0		4484	57.19		2575	74.53		1909	43.53
1		3356	42.81		880	25.47		2476	56.47
ITOBo	6516	N	%	2774	N	%	3742	N	%
0		1474	22.62		942	33.96		532	14.22
1		2021	31.02		798	28.77		1223	32.68
2		1884	28.91		749	27		1135	30.33
3		1137	17.45		285	10.27		852	22.77
ITOBb		N	%		N	%		N	%
0		3495	53.64		1740	62.73		1755	46.9
1		3021	46.36		1034	37.27		1987	53.1

BMI: body mass index; BMIo: ordinal BMI measure; BMIb: binary BMI measure

ITOB: tobacco quantity: ITOBo: ordinal ITOB measure; ITOBb: binary ITOB measure

Table 2:

Product-moment, polychoric & tetrachoric correlations for measures of BMI and ITOB by zygosity and sex: twin (within-trait cross-twin) correlations (2a), phenotypic (cross-trait within-twin) correlations (2b) and cross-trait cross-twin correlations (2c)

2a

	MZ	DZ		MZf	DZf	MZm	DZm	Dzo
BMI	0.64	0.41	BMI	0.81	0.38	0.73	0.30	0.31
BMIo	0.59	0.43	BMIo	0.79	0.37	0.73	0.32	0.32
BMIb	0.70	0.48	BMIb	0.84	0.47	0.75	0.37	0.34
ITOB	0.51	0.34	ITOB	0.61	0.36	0.59	0.27	0.24
ITOBo	0.64	0.40	ITOBo	0.76	0.45	0.68	0.32	0.28
ITOBb	0.68	0.49	ITOBb	0.73	0.61	0.79	0.42	0.31

2b

	total	female	male		same-sex	female	male
BMI-ITOB	0.10	0.03	0.08	BMI-ITOB	0.11	0.02	0.09
BMIo-ITOBo	0.11	0.01	0.07	BMIo-ITOBo	0.14	0.00	0.10
BMIb-ITOBb	0.10	0.01	0.05	BMIb-ITOBb	0.10	−0.02	0.08

2c

	MZ	DZ		MZf	DZf	MZm	DZm	Dzo
BMI-ITOB	0.03	0.09	BMI-ITOB	0.04	0.02	0.13	0.04	0.09
BMIo-ITOBo	0.02	0.11	BMIo-ITOBo	0.05	−0.02	0.15	0.04	0.07
BMIb-ITOBb	−0.02	0.10	BMIb-ITOBb	0.03	−0.04	0.15	0.06	0.07

MZ: monozygotic twins; DZ: dizygotic twins; m: male; f: female; o: opposite sex twins

Model fitting and model averaging

First, we illustrate the process of fitting the 25 alternative bivariate models to BMI-ITOB data of female twins, and generating multimodel statistics and model-averaged parameter estimates. Fit statistics of the 25 models were rank ordered starting with the one with the lowest value of AIC (see Table 3a). Delta AIC values were calculated as the difference in AIC between each of the models and the most parsimonious one. Models with cumulative Akaike weights up to .95 are considered to be in the Confidence set. Akaike weights were summed for all models that contain a parameter of interest to generate a probability that that parameter was in the best fitting model. When fitting bivariate models to data of MZ & DZ same-sex female twins (N= 1139 twin pairs), results suggested little discrimination between alternative models as shown by delta AIC values less than 4, and most models (23 out of 25) being considered in the confidence set. Note that for females the phenotypic correlation between the two traits was small and not significantly different from 0, resulting in each of the five possible covariance parameters doing equally well in accounting for it, as shown by probabilities of ~.40 for each of the five sources of covariance to be in the best fitting model. In this situation, simpler models (those with fewer parameters that generate covariance) did better as they are less penalized when calculating AIC. Results from analyses in same-sex male data (N= 1,497 twin pairs) were more informative. First, several models could be rejected based on the difference in fit, resulting in 17 models included in the confidence set. The models retained had mostly two or three sources of covariance. The best fitting models are most likely to include the ra parameter (p=.57), suggesting that at least some genetic factors were shared between the traits, with an equal chance of including re, b₂₁ & b₁₂ (p=.50).

Table 3:

Model fitting and model averaging results of bivariate models to data of females (3a), and males (3b) for continuous measures of BMI & ITOB

3a

model	AIC	delta	Akaike Weight	inConfidenceSet		ra	rc	re	b21	b12
Fe	9031.36	0.00	0.07	*	0.07	0.00	0.00	0.07	0.00	0.00
Fc	9031.60	0.24	0.06	*	0.13	0.00	0.06	0.00	0.00	0.00
Her	9031.70	0.33	0.06	*	0.19	0.00	0.00	0.06	0.00	0.06
Fce	9031.70	0.33	0.06	*	0.25	0.00	0.06	0.06	0.00	0.00
Fae	9031.74	0.38	0.06	*	0.31	0.06	0.00	0.06	0.00	0.00
Hao	9031.74	0.38	0.06	*	0.36	0.06	0.00	0.00	0.06	0.00
Heo	9031.74	0.38	0.06	*	0.42	0.00	0.00	0.06	0.06	0.00
Har	9031.78	0.42	0.06	*	0.48	0.06	0.00	0.00	0.00	0.06
Dor	9031.84	0.48	0.05	*	0.53	0.00	0.00	0.00	0.05	0.05
Fa	9031.94	0.57	0.05	*	0.59	0.05	0.00	0.00	0.00	0.00
Hcr	9032.02	0.66	0.05	*	0.64	0.00	0.05	0.00	0.00	0.05
Dr	9032.40	1.04	0.04	*	0.68	0.00	0.04	0.00	0.00	0.04
Do	9032.49	1.13	0.04	*	0.72	0.00	0.00	0.00	0.04	0.00
Hco	9032.62	1.26	0.04	*	0.75	0.00	0.04	0.00	0.04	0.00
Fac	9033.56	2.20	0.02	*	0.78	0.02	0.02	0.00	0.00	0.00
Face	9033.62	2.26	0.02	*	0.80	0.02	0.02	0.02	0.00	0.00
Haco	9033.62	2.26	0.02	*	0.82	0.02	0.02	0.00	0.02	0.00
Hceo	9033.62	2.26	0.02	*	0.84	0.00	0.02	0.02	0.02	0.00
Hacr	9033.62	2.26	0.02	*	0.87	0.02	0.00	0.00	0.00	0.02
Haer	9033.62	2.26	0.02	*	0.89	0.02	0.00	0.02	0.00	0.02
Haor	9033.62	2.26	0.02	*	0.91	0.02	0.00	0.00	0.02	0.02
Hcor	9033.62	2.26	0.02	*	0.93	0.00	0.02	0.00	0.02	0.02
Heor	9033.62	2.26	0.02	*	0.96	0.00	0.00	0.02	0.02	0.02
Hcer	9033.62	2.26	0.02			0.00	0.02	0.02	0.00	0.02
Haeo	9033.74	2.38	0.02			0.02	0.00	0.02	0.02	0.00
			1.00			0.38	0.38	0.44	0.38	0.40

3b

model	AIC	delta	Akaike Weight	inConfidenceSet		ra	rc	re	b21	b12
Dor	14757.76	0.00	0.10	*	0.10	0.00	0.00	0.00	0.10	0.10
Heo	14757.76	0.00	0.10	*	0.19	0.00	0.00	0.10	0.10	0.00
Fae	14757.76	0.01	0.10	*	0.29	0.10	0.00	0.10	0.00	0.00
Har	14757.76	0.01	0.10	*	0.38	0.10	0.00	0.00	0.00	0.10
Her	14757.76	0.01	0.10	*	0.48	0.00	0.00	0.10	0.00	0.10
Hao	14757.77	0.01	0.10	*	0.57	0.10	0.00	0.00	0.10	0.00
Fa	14758.91	1.15	0.05	*	0.62	0.05	0.00	0.00	0.00	0.00
Hceo	14759.74	1.99	0.04	*	0.66	0.00	0.04	0.04	0.04	0.00
Heor	14759.75	1.99	0.04	*	0.70	0.00	0.00	0.04	0.04	0.04
Haor	14759.75	1.99	0.04	*	0.73	0.04	0.00	0.00	0.04	0.04
Hcor	14759.75	1.99	0.04	*	0.77	0.00	0.04	0.00	0.04	0.04
Hacr	14759.76	2.00	0.04	*	0.80	0.04	0.00	0.00	0.00	0.04
Haco	14759.76	2.00	0.04	*	0.84	0.04	0.04	0.00	0.04	0.00
Haeo	14759.76	2.00	0.04	*	0.87	0.04	0.00	0.04	0.04	0.00
Face	14759.76	2.01	0.04	*	0.91	0.04	0.04	0.04	0.00	0.00
Haer	14759.76	2.01	0.04	*	0.94	0.04	0.00	0.04	0.00	0.04
Hcer	14759.77	2.01	0.03	*	0.98	0.00	0.03	0.03	0.00	0.03
Fac	14760.90	3.14	0.02			0.02	0.02	0.00	0.00	0.00
Fc	14766.27	8.51	0.00			0.00	0.00	0.00	0.00	0.00
Hco	14767.35	9.59	0.00			0.00	0.00	0.00	0.00	0.00
Fce	14767.82	10.06	0.00			0.00	0.00	0.00	0.00	0.00
Do	14768.17	10.41	0.00			0.00	0.00	0.00	0.00	0.00
Hcr	14768.20	10.45	0.00			0.00	0.00	0.00	0.00	0.00
Dr	14772.31	14.55	0.00			0.00	0.00	0.00	0.00	0.00
Fe	14777.12	19.36	0.00			0.00	0.00	0.00	0.00	0.00
			1.00	0.57			0.20	0.50	0.50	0.50

Twenty-five genetic models were evaluated, starting with a ‘triple correlated factors’ model, referred to here as Face, with F referring to correlated Factors, and ace to ra, rc, and re respectively. Submodels include any two of three correlated factors (Fac, Fae, Fce), or one of three correlated factors (Fa, Fc, Fe). The three DOC models (acronyms starting with D) include one or two causal paths where o refers to the b₂₁ path and r to the b₁₂ path (Dor, Do & Dr). Hybrid models (acronyms starting with H) include one or two correlated factors, and one or two causal paths: 6 models with 2 correlated factors and 1 causal path, (Haco, Haeo Hceo, Hacr, Haer, Hcer), 3 models with 1 correlated factor and 2 causal paths (Haor, Hcor, Heor), and 6 models with 1 correlated factor and 1 causal path (Hao, Hco Heo, Har, Hcr, Her).

Testing sex limitation

When analyzing both sexes jointly and including opposite sex twins, we evaluated first whether sources of variance and covariance in males and females were of the same magnitude (quantitative sex differences) and the same kind (qualitative sex differences, where either genetic or shared environmental correlations across sex are estimated). We fitted the four sex limitation models using the triple correlated factors model. When quantitative and qualitative sex differences were found, these parameters were included in the remaining 24 alternative models. Although it is theoretically possible to fit all 25 models in all 4 sex difference scenarios, we reduced the model set to focus on the causal and correlational relationships rather than on sex differences. We present results for fitting the 25 models under two of the four sex limitation scenarios: only quantitative sex differences, and including additional qualitative sex differences by estimating the genetic correlations across sex. When allowing only quantitative sex differences, 13 models were retained in the confidence set and the probability that the best fitting model contained ra was .71, with the next most likely parameter accounting for covariance being b₂₁ at .56 probability. In models with both quantitative and qualitative sex differences, thus estimating more parameters, 15 models were in the confidence set with an .84 probability that ra was included in the best fitting model. In analyses that include tests of sex heterogeneity, models in the confidence set were more likely to include ra than any other parameter to account for the covariation between the variables, similar to the results from the male only analyses. Furthermore, most models with only one parameter accounting for covariance between variables did not make it into the confidence set, suggesting that at least two parameters are necessary to account for the observed covariance.

Modeling continuous, ordinal or binary variables

In addition to fitting the set of 25 models to continuous variables, we fitted them to ordinal and binary measures derived from the continuous ones for three main reasons, to: illustrate the practical use of the scripts, to evaluate ii) the consistency of the results and iii) the power to discriminate between alternative models. Results are presented in Table 4. We repeated the series of analyses with data of females (top left) and males (top right) separately, followed by analyzing males and females jointly to allow testing for heterogeneity by gender (bottom half of table 4). We show results for both the full sex limitation model (quantitative and qualitative genetic sex differences, bottom left) and a quantitative sex differences model only (bottom right), as the former fit best for the continuous measures and the latter for the ordinal/binary measures. For each analysis we present models ranked by their AIC value (with the best fitting model first), the fit of the first model and difference in fit compared to the first model. Models considered to be in the confidence set according to the multimodel inference criteria are bolded. When comparing results for continuous, ordinal or binary measures, typically the number of models in the confidence set increased for ordinal/binary scenarios. Except for the analyses in females only, the same models appeared consistently outside the confidence set. The rank order of the models (from best to least well fitting) was far from consistent across type of variable analyzed, possibly due to small differences in AIC, suggesting limited discrimination between models.

Table 4:

Model fitting results of bivariate models to data of females (3a), males (3b), jointly with full sex limitation (3c) and with quantitative sex differences only (3d) for continuous, ordinal and binary measures of BMI & ITOB

con	AIC & Δ	ord	AIC & Δ	bin	AIC & Δ	con	AIC & Δ	ord	AIC & Δ	bin	AIC & Δ
Fe	9031.36	Fe	7379.84	Fe	3933.83	Dor	14757.76	Fa	12324.89	Fc	7077.78
Fc	0.24	Har	0.98	Dr	0.05	Heo	0.00	Her	0.46	Dor	1.00
Her	0.33	Fae	1.06	Fc	0.08	Her	0.01	Hao	0.47	Fce	1.13
Fce	0.33	Hao	1.06	Do	0.14	Fae	0.01	Heo	0.48	Fa	1.55
Fae	0.38	Heo	1.06	Fa	0.18	Har	0.01	Fae	0.48	Hco	1.65
Heo	0.38	Her	1.13	Dor	1.47	Hao	0.01	Har	0.48	Hcr	1.71
Hao	0.38	Fa	1.24	Har	1.66	Fa	1.15	Dor	0.52	Heo	1.98
Har	0.42	Fc	1.25	Fac	1.82	Hceo	1.99	Fac	1.91	Her	1.98
Dor	0.48	Dr	1.30	Hao	1.87	Heor	1.99	Face	2.45	Fac	2.00
Fa	0.57	Do	1.33	Fce	1.96	Haor	1.99	Hceo	2.45	Fae	2.01
Hcr	0.66	Fce	1.47	Her	1.99	Hcor	1.99	Hacr	2.45	Hao	2.01
Dr	1.04	Dor	1.61	Fae	1.99	Hacr	2.00	Heor	2.45	Har	2.18
Do	1.13	Hcr	2.43	Heo	2.00	Haco	2.00	Hcer	2.45	Face	2.99
Hco	1.26	Hco	2.72	Hcr	2.05	Haeo	2.00	Haco	2.45	Hcer	2.99
Fac	2.20	Face	2.98	Hco	2.06	Face	2.01	Hcor	2.46	Hceo	2.99
Hacr	2.26	Haor	2.98	Face	3.42	Haer	2.01	Haor	2.46	Haco	2.99
Haco	2.26	Haco	2.98	Hcor	3.42	Hcer	2.01	Haer	2.46	Hacr	2.99
Hceo	2.26	Haer	2.98	Hacr	3.42	Fac	3.14	Haeo	2.48	Haer	2.99
Hcor	2.26	Hceo	2.98	Haco	3.42	Fc	8.51	Fc	3.43	Hcor	2.99
Heor	2.26	Hacr	2.98	Hcer	3.42	Hco	9.59	Hco	4.85	Haor	2.99
Face	2.26	Hcor	2.98	Hceo	3.42	Fce	10.06	Hcr	5.17	Heor	3.00
Haor	2.26	Hcer	2.98	Heor	3.42	Do	10.41	Fce	5.31	Haeo	3.34
Haer	2.26	Heor	2.99	Haer	3.42	Hcr	10.45	Do	5.99	Dr	3.35
Hcer	2.26	Haeo	3.06	Haor	3.42	Dr	14.55	Dr	7.46	Do	3.93
Haeo	2.38	Fac	3.24	Haeo	3.44	Fe	19.36	Fe	15.85	Fe	7.45
Fae	38358.34	Hcor	31523.38	Fc	17743.78	Har	38366.31	Hcor	31521.33	Hao	17744.04
Har	0.02	Har	1.17	Fce	2.13	Hceo	0.21	Hacr	0.58	Har	0.10
Hao	0.08	Dor	1.21	Fa	4.08	Haeo	0.21	Haco	0.96	Haco	0.26
Fa	1.47	Fce	1.27	Hcor	4.29	Hcor	0.53	Face	2.57	Fa	0.93
Heor	1.78	Fae	1.30	Fac	5.35	Haco	0.77	Har	2.72	Fae	1.10
Face	1.94	Hao	1.30	Hceo	5.40	Hao	0.77	Hceo	3.57	Hacr	1.22
Haco	1.94	Fa	1.53	Hcer	5.64	Hacr	0.93	Haor	3.58	Hceo	1.74
Hacr	1.96	Fc	1.74	Har	5.85	Face	1.07	Hao	4.54	Fac	2.09
Fac	3.18	Hceo	2.42	Hao	5.87	Fae	1.19	Fae	4.77	Hcer	2.10
Haeo	3.94	Hcr	2.58	Fae	6.04	Haor	2.34	Fac	5.30	Face	2.14
Haor	3.94	Heor	2.87	Heor	6.82	Hcer	2.85	Heor	5.58	Hcor	2.17
Haer	3.95	Face	3.09	Her	6.89	Haer	2.85	Haer	6.09	Haeo	2.53
Hcor	4.09	Haco	3.11	Face	7.12	Her	3.61	Hcer	6.13	Haor	2.81
Hceo	4.27	Hco	3.14	Haco	7.12	Heor	3.73	Heo	6.67	Haer	3.23
Hcer	5.22	Hacr	3.17	Heo	7.25	Heo	5.48	Dor	6.86	Heor	3.32
Fce	5.44	Hcer	3.27	Hacr	7.31	Fac	6.86	Her	7.00	Her	3.71
Fc	5.72	Fac	3.54	Haer	8.09	Dor	7.35	Haeo	8.20	Heo	3.82
Hcr	5.98	Her	4.26	Haor	8.10	Fa	8.20	Fc	8.36	Hco	4.87
Hco	6.84	Heo	4.93	Dr	8.29	Do	20.50	Hco	10.04	Dr	5.03
Her	7.50	Haor	5.10	Dor	8.40	Hco	21.87	Fa	10.71	Dor	5.20
Heo	9.78	Haer	5.23	Haeo	8.46	Dr	23.79	Fce	11.05	Do	5.31
Dor	11.32	Haeo	5.31	Hco	8.49	Hcr	25.12	Hcr	11.75	Fc	5.33
Do	23.65	Do	13.69	Do	8.69	Fc	26.88	Do	16.67	Hcr	6.52
Dr	26.96	Dr	14.27	Hcr	9.95	Fe	28.14	Dr	17.49	Fe	7.19
Fe	31.68	Fe	17.34	Fe	10.53	Fce	28.89	Fe	20.23	Fce	9.17

AIC: Akaike’s Information Criterion for first model; Δ: difference in AIC compared to first model; models including ra highlighted

Graphing model-averaged parameter estimates

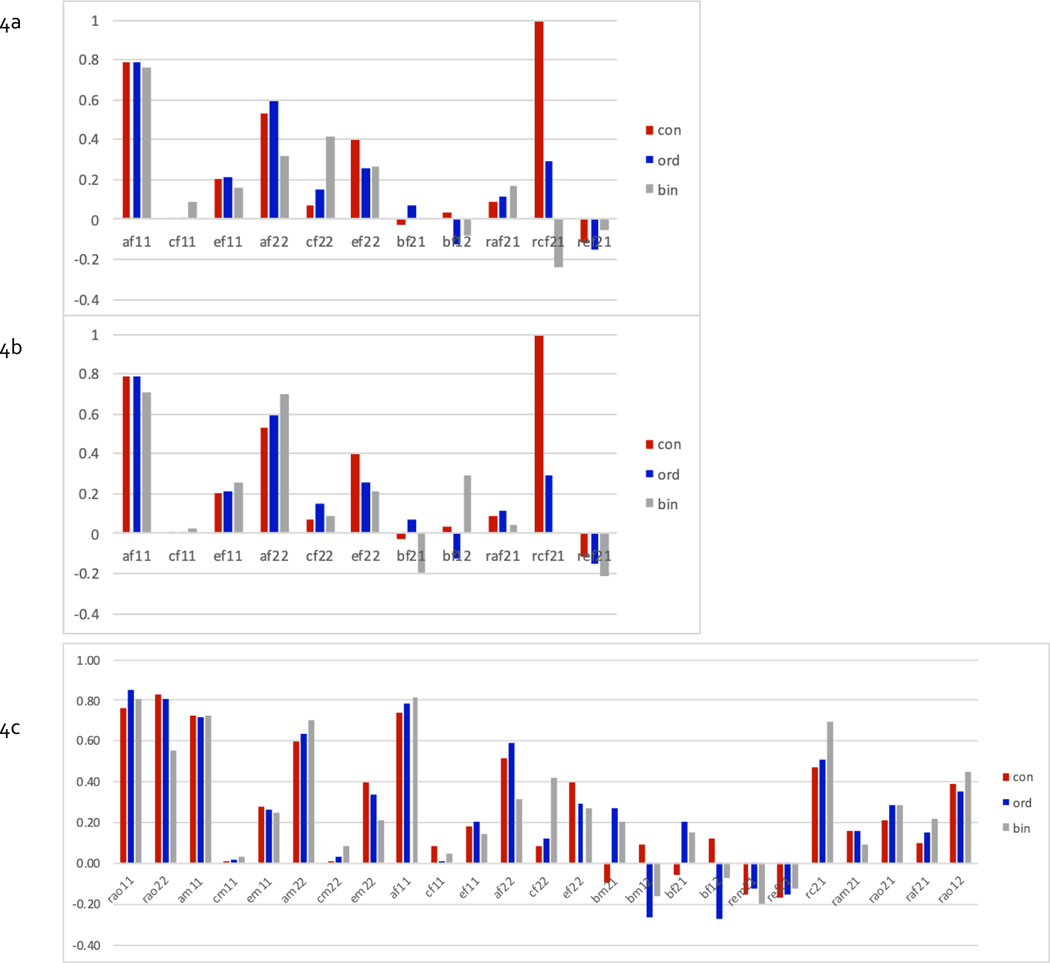
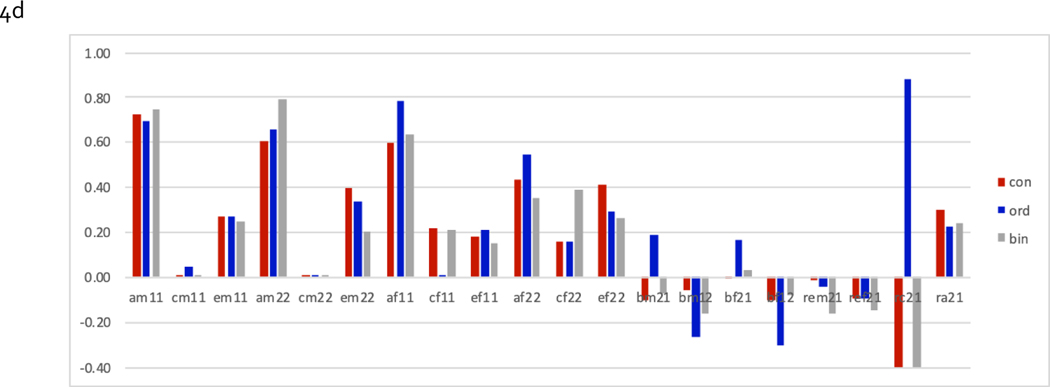
Finally, we present model averaged parameter estimates, where estimates of parameters of each of the models are weighted by their AIC, a ‘penalized’ goodness-of-fit index, in Figure 4 (4a: females, 4b: males, 4c: males & females with full sex limitation and 4d:males & female with quantitative sex differences). Figures 4a & 4b show the proportions of variance accounted for by genetic (a², shared environmental c² and unique environmental e² factors for the first variable (here BMI), the proportions for the second variable (here ITOB), and the parameters accounting for covariance (ra, rc, re, b₂₁ & b₁₂) between the two variables. Note that the latter five can go negative, possibly resulting in cancelling each other out when looking at phenotypic correlations. For females, genetic factors accounted for most of the variance (~.8 for BMI, ~.6 for ITOB), with negligible shared environmental contributions for BMI but suggestive for ITOB. Estimates of genetic covariance were consistently positive, those for unique environmental covariance consistently negative, and those for shared environmental covariance inconsistent & unstable, likely due to the lack of shared environment variance for BMI. However, none of the covariance paths, including causal path estimates, was significant. The pattern of results for males was similar, except that there was no evidence of c² for ITOB either. When dropping c² from the model altogether, the estimated positive genetic covariance and negative unique environmental covariance approached significance, but causal paths remained non-significant and were inconsistent across the two levels of measurement (results not shown).

Figure 4:

Model-averaged parameter estimates from fitting bivariate models to data of females (4a), males (4b), jointly with full sex limitation (4c) and with quantitative sex differences only (4d) for continuous, ordinal and binary measures of BMI & ITOB (need to add error bars)

Graphs for estimates of full sex limitation models include additional parameters, starting with estimates of the genetic correlations across sex for each variable, followed by a², c² and e² variance components for the two variables for males and females, and the parameters accounting for covariance between variables. The latter include sex-specific causal paths in both directions, sex-specific unique environmental covariance, shared environmental covariance constrained across sex, and four genetic covariance parameters depending across sex. In the quantitative sex differences model, genetic correlations across sex are fixed to 1 and genetic covariance parameters constrained to be equal across sex. Given that none of the covariance parameters is statistically significant in these analyses, we limit our discussion of the results to the fact that the genetic covariance between BMI and ITOB approached significance, which was consistent with most models in the confidence set across analyses including ra.

Estimating power for bivariate models

We simulated data with the same pattern of correlations as the real data example to evaluate the power to discriminate between alternative models. As any combination of three parameters out of ra, rc, re, b₂₁ & b₁₂ can account for any pattern of covariation between two measures, we only list power to reject models with one or two of the five parameters (see Table 5, associated OpenMx script in appendix 3). The real data example had sufficient power to reject most models with a single parameter accounting for the covariance than with two parameters. Furthermore, power is greater to reject ra, rc or re, compared to causal paths b₂₁ & b_12.

Table 5:

Power to reject models based on simulated data, corresponding to the pattern of correlations observed for real data example.

	simulation parameters
vA1	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8
vC1	0	0	0	0	0	0	0	0	0
vE1	0.2	0.2	0.2	0.2	0.2	0.2	0.2	0.2	0.2
vA2	0.55	0.55	0.55	0.55	0.55	0.55	0.55	0.55	0.55
vC2	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
vE2	0.4	0.4	0.4	0.4	0.4	0.4	0.4	0.4	0.4
ra	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
rc	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8
re	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
b21	−0.2	−0.2	−0.2	0	0	0	0.2	0.2	0.2
b12	−0.2	0	0.2	−0.2	0	0.2	−0.2	0	0.2
fit	4551.22	4330.78	4118.98	4330.78	4330.78	4330.78	4118.98	4330.78	4551.22
	power to reject models including sources of covariance
b21	0.48	0.09	0.87	0.53	0.1	0.9	0.48	0.09	0.87
b12	0.37	0.42	0.37	0.08	0.09	0.08	0.77	0.81	0.77
ra	1	0.12	1	0.97	0.6	1	0.11	1	1
rc	1	0.66	1	1	0.91	1	0.4	1	1
re	1	0.93	0.1	0.46	0.71	1	0.94	1	1
b21 & b12	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
b21 & ra	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
b21 & rc	0.34	0.08	0.67	0.39	0.09	0.73	0.34	0.08	0.67
b21 & re	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
b12 & ra	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
b12 & rc	0.17	0.2	0.17	0.07	0.08	0.07	0.42	0.48	0.42
b12 & re	0.05	0.05	0.05	0.05	0.05	0.05	0.06	0.06	0.06
ra & rc	1	0.13	1	0.98	0.66	1	0.12	1	1
ra & re	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
rc & re	0.94	0.38	0.05	0.11	0.27	0.86	0.44	0.98	1

DISCUSSION

Most prior genetic epidemiological modeling of the causes of covariation between two variables measured in twins have used one of two approaches. Usually, a triple Cholesky decomposition model is fit, followed up with fitting submodels based on a stated hypothesis or more or less well defined criteria. Within this approach, non-significant parameters may be fixed to zero to obtain a better fitting model. Occasionally, direction of causation models are fit, typically with a particular direction of causation. Most reports then present parameter estimates and confidence intervals of the best fitting or most parsimonious model. Sometimes a full model’s estimates would also be included with confidence intervals, leading to potentially non-significant parameters being retained, but resulting in less bias in estimates of the significant parameters. This strategy may, by chance, result in the selection of the best possible model, in terms of goodness-of-fit and parsimony, for the data, and the most accurate parameter estimates, but it also may not.

The multimodel inference approach presented in this paper attempts to avoid bias due to selective model fitting, but rather fits a set of identified models to the same data, selects all the models that are consistent with the data, and calculates the model averaged parameters by taking into account the goodness-of-fit of all considered models. We illustrated here how this can be done with data from the classical twin design, and how it can be extended to testing for heterogeneity (by sex) using the opensource software OpenMx for which scripts are freely available.

Even though causes of covariation between obesity and smoking behavior are of substantial interest, the current application was chosen for illustrative purposes, and we therefore did not go into the background literature on this topic nor discussed the results in light of previous findings. However, results from the range of analyses and associated power analyses performed provide some insight into modeling the causes of covariation using the classical twin design, in particular with respect to the power of these studies as a function of sample size, type of variable analyzed and accommodation for sex heterogeneity. Due to the relative complexity of the model and the vast number of possible scenarios and values to consider for each of the parameters of the model, a formal simulation study is beyond the scope of this paper. The results confirm those of previous studies, that stronger conclusions can be drawn from studies using continuous measures compared to those using ordinal or binary measures (Neale et al. 1994). Genuinely continuous measures yield both greater power to discriminate between alternative models, and more precise parameter estimates. A more novel finding is that with reasonable sample sizes of pairs for typical twin studies, the power to discriminate between alternative models likely depends on the magnitude and the nature of the phenotypic covariance between the two measures, and will be explored with other data and other variables for which evidence of covariation exists.

In summary, we chose to present the multimodel framework using real data, to illustrate the use of these new features in OpenMx (Neale, Hunter 2016, Boker, Neale 2011). This paper hopes to introduce multimodel inference and model averaging approaches to the behavior genetics community, in the context of testing models for the causes of variation and covariation in traits in term of genetic, environmental and causal explanations.

Limitations

This study should be interpreted in the context of some potential limitations. First, nicotine use is a complex variable. As noted above, biometrical models for data on substance use should ideally differentiate between substance initiation and quantity once initiated, as the liabilities to them may not be unidimensional. In principle, a better approach would be a trivariate analysis including initiation as a separate variable in the model (and code use quantity as missing data). However, doing so would greatly increase the model’s complexity and decrease its value as an illustration. We intend to extend the current methods to incorporate such types of analysis. Second, the statistical power of any study depends heavily on sample size. Although the data analyzed here come from a well-powered population-based study, the sample still required voluntary participation, and the females-only part of the study occurred several years prior to that of males. The larger sample of male-male and opposite sex pairs than female-female, was by design due to the lower statistical power to study disorders such as depression that occur with lower frequency in males. Although the design may have been sub-optimal for detecting sex differences in BMI and smoking, they were found for means, variances and components of variance. Furthermore, it was clear from the current analyses that power is also substantially greater when analyzing continuous measures versus ordinal or binary measures, consistent with previous simulation studies (Neale, Eaves 1994). However, it is important not to analyze ordinal variables as if they were continuous, because doing so violates methodological assumptions necessary for robust estimation of effect sizes and accurate statistical inference. It should also be noted that DOC models have not been used extensively as their power depends heavily on differential genetic architecture of the phenotypes under study (Heath, Kessler 1993). Finally, we note that ‘there is no such thing as a free lunch ‘in model-fitting. Model averaging appears to help distinguish between models and may support a model that could not be identified by the data being analyzed. It is, alas, no substitute for improving research design by including other types of relative, repeated measures, or experimental interventions. It is through the combination of these approaches that consistency across multiple lines of evidence may be achieved. Such agreement is prerequisite for the safe application of empirical scientific results to health care policy.