Estimating global visual field indices in glaucoma by combining macula and optic disc OCT scans using 3D convolutional neural networks

Abstract

Purpose:

To evaluate the accuracy at which visual field global indices could be estimated from Optical Coherence Tomography (OCT) scans of the retina using deep neural networks, and to quantify the contributions to the estimates by the macula (MAC) and the optic nerve head (ONH).

Design:

Observational cohort study.

Participants:

10,370 eyes from 109 healthy, 697 glaucoma suspect, and 872 glaucoma patients (10,370 in total) over multiple visits (median=3).

Methods:

3D convolutional neural networks were trained to estimate global visual field indices derived from automated Humphrey perimetry (SITA 24-2) tests, using OCT scans centered on MAC, ONH, or both (MAC+ONH) as inputs.

Main Outcome Measures:

Spearman’s rank correlation coefficients, Pearson’s correlation coefficient, and absolute errors, calculated for two indices: Visual Field Index (VFI) and Mean Deviation (MD).

Results:

MAC+ONH achieved 0.76 Spearman’s correlation coefficient and 0.87 Pearson’s correlation for VFI and MD respectively. Median absolute error was 2.7 for VFI and 1.57 dB for MD. Separate MAC or ONH estimates were significantly less correlated and less accurate. Accuracy was dependent on OCT signal strength and on the stage of glaucoma severity.

Conclusions:

The accuracy of global visual field indices estimate is improved by integrating information from MAC and ONH in advanced glaucoma, suggesting that structural changes of the two regions have different timecourses in the disease severity spectrum.

Précis

Global indices of visual field could be estimated from Optical Coherence Tomography scans using deep neural networks. Combining macular and optic nerve head scans was more effective in advanced glaucoma.

Glaucoma is a progressive neurodegenerative disease that can result in irreversible loss of sight, caused by the loss of retinal ganglion cells and their axons. A comprehensive understanding of the relationship between visual functions and retinal structure is critical for developing effective strategies for managing the disease, because clinicians use both structural measures derived from retinal scans and functional measures derived from visual field tests to monitor the progression of glaucoma. However, the complex relationship between the two is not fully understood, and sometimes conflicting.^1,2

The extent to which functional measures can be estimated from structural scans of the retina has important clinical implications. If structure-function relationship could be accurately encapsulated in quantitative models, surrogates of visual field test outcomes could be derived from retinal scans, which would allow practitioners to make clinical judgements in functional terms, but without some of the inherent limitations of visual field testing (such as the subjective nature of the test, high test-to-test variability, relatively long testing time, and the requirement for an isolated environment to conduct the test). Previous efforts in characterizing structure-function relationship have concentrated on correlating visual field test outcomes with measures derived from anatomical features such as the thickness of the retinal nerve fiber layer (RNFL) and/or the macular ganglion cell layer.^3–15 In contrast to the traditional approach, in this study, we used deep convolutional neural networks¹⁶ to estimate global indices derived from visual field tests using Optical Coherence Tomography (OCT) scans of the retina. Instead of explicitly segmenting the OCT images into retinal layers with pre-assumptions on relevant indicators, in our approach, the neural networks were free to learn any relevant image feature in the OCT scans, and use nonlinear combinations of these features to produce estimates, and therefore establish structure-function relationship in a more comprehensive, flexible manner. Recent research has explored the use of deep convolutional networks in the study of structure-function relationship.^3,4,17 In this work, we concentrated on the use of 3D convolutional filters to take full advantage of the volumetric nature of OCT scans.

We examined the factors that influenced the performance of the networks in detail. In particular, we quantified estimation accuracy at different levels of glaucoma severity, and examined the effectiveness of integrating structural information from two specialized regions of retina that are routinely imaged in clinics: the macula (MAC) and the optic nerve head (ONH). While glaucoma has been often considered a disease that primarily affects the ONH, recent studies have highlighted the significance of the macula.¹⁸ In particular, it has been shown that structural changes of the macula can be observed at the early stage of glaucoma, and may have higher dynamic range at the advanced stage^19–21, where the peripapillary RNFL thickness measured at the ONH exhibits the “floor effect”.^22,23 Investigating the effectiveness of combining structural information from both regions is therefore important for developing methods suitable for the long-term monitoring of glaucoma progression.

Methods

This observational study was conducted in accordance with the tenets of the Declaration of Helsinki and the Healthy Insurance Portability and Accountability Act. The Institutional Review Board of New York University and the University of Pittsburgh approved the study, and all participants gave written consent before participation.

Data

1678 participants were studied longitudinally (median number of visits: 3; range 1-14), forming a dataset with 10,370 pairs of MAC-centered and ONH-centered OCT cubes. All participants underwent a comprehensive ophthalmic examination. The participants were included in the study according to the following inclusion criteria: best-corrected visual acuity of 20/60 or better, refractive error between −6.00 and 3.00 diopters, and reliable visual field test results (see below). Participants were excluded based on the following exclusion criteria: history of intraocular surgery without cataract, glaucoma, laser surgery (participants were allowed to have these surgeries even during the follow-up period), or a combination thereof; diagnosis of diabetes; or diagnosis of a posterior pole pathologic condition other than glaucoma. The visual field of each eye was tested with the Swedish interactive thresholding algorithm 24-2 perimetry (SITA standard; Humphrey Field Analyzer; Zeiss, Dublin, CA). Only test that met the following criteria were included in the dataset: fixation loss<20%, false positive rate<20%, false negative rate<20%. Two global visual field indices commonly used to monitor the progression of glaucoma, visual field index (VFI) and mean deviation (MD), were calculated. OCT scans were acquired with Cirrus spectral-domain OCT scanners (Zeiss). The scans had physical dimensions of 6x6x2 mm with a corresponding size of 200x200x1024 voxels per volume. Scans with signal strength less than 6 were discarded. For training the neural networks, the scans were downsized to 64x64x128 voxels. The laterality of the OCT cubes was normalized: OCT cubes obtained in the right eye were flipped with respect to the vertical axis.

The participants in the dataset (summarized in Table 1) were healthy subjects (6.5%), glaucoma suspects (41.5%), and patients diagnosed with a variety of glaucoma subtypes (52.0%). Glaucoma suspect eyes were defined as eyes with normal visual field test results with any of the following criteria: intraocular pressure of 22 to 30 mmHg, asymmetric optic nerve head cupping, or both; abnormal optic nerve head appearance; or an eye that was the contralateral eye of unilateral glaucoma. Glaucomatous eyes were those with at least 2 consecutive abnormal visual field test results, which was defined as tests featuring a cluster of 3 or more adjacent points in the pattern deviation plot depressed more than 5 dB, or 2 adjacent points depressed more than 10 dB and pattern standard deviation or glaucoma hemifield test results outside normal limits.

Table 1.

Dataset characteristics

# of OCT cube pairs	10,370
# of unique eyes	3,014
# of subjects	1,678
Mean age in years (SD)	63.5 (±12.2)
% of females	54.9%
Median # of visits	3
# of subjects in subsets:
Glaucoma (%)	872 (52.0%)
Suspects (%)	697 (41.5%)
Healthy (%)	109 (6.5%)

# of cube pairs in subsets:		median MD	median VFI
Glaucoma (%)	6,042 (59.4%)	−3.45	94
Suspects (%)	3,703 (36.4%)	−1.00	99
Healthy (%)	427 (4.2%)	−0.54	99
All		−2.07	97

MD = mean deviation; OCT = optical coherence tomography; SD = standard deviation; VFI = visual field index

Neural network

The neural network (illustrated schematically in Fig. 1A), based on previous work,²⁴ consisted of two regional networks that analyzed the MAC and the ONH cube separately. Information from the networks was integrated by concatenating the outputs of the two regional networks after they were pooled by global averaging pooling (GAP). Each of the regional networks had 5 convolutional layers (CONV), each with 32 volumetric filters with ReLU activations and were batch-normalized. The parameters of the filters are summarized in Fig. 1B. The network had three outputs (using sigmoid nonlinearity), which were fully connected to the GAP layer: an output that had access to information from both regional networks, and two outputs with access only to the individual regional network. The combined network had ~700,000 parameters in total. The sigmoid function used on the output units entails that the ranges of the estimates were bounded. We scaled our inputs/outputs such that VFI estimates were limited to the range of (−12.5, 112.5), whereas MD estimates were limited to (−37.5, 7.5) in dB. This is why the networks tend to overestimate at the low ends and underestimate at the high ends of the VFI and MD. The GAP layer was used in the calculation of “attention maps”²⁵ to visualize regions in the OCT scans that contribute more strongly to the models’ outputs. The GAP layer calculates the averaged activations of each channels of the last CONV layer, to estimate the relative contributions to the network’s outputs by each channel. The 3D activation patterns of each channel in the last CONV layer were then weighted by the GAP outputs and summed. The results were scaled to the size of the original OCT scans and displayed as heat maps (e.g., Fig. 9). To visualize the 3D attention maps in en face view, we summed the maps across the z-dimension.

Figure 1.

A, The architecture of the neural network. The elements shaded in pink represent feature maps of the convolutional layers. B, Parameters of the 3D filters for each of the convolutional layers. CONV = convolutional layer; GAP = global average pooling; MAC = macula; ONH = optic nerve head.

Figure 9.

Representative examples of attention maps in en face view, highlighting retinal regions strongly contributing to the MAC+ONH estimates of VFI. A, An example map for a healthy subject. B and C, Example maps for two eyes with primary open angle glaucoma. N = nasal; S = superior; VFI = visual field index; MAC and ONH = macular and optic nerve head scans; POAG = primary open angle glaucoma.

Neural network training

Two separate networks with the architecture described above were trained to estimate MD and VFI. The sum of the root mean square errors of the three outputs was minimized using Adam RMSprop with Nesterov momentum. The size of the mini-batch was 8. For all layers, dropout of entire feature maps was used to prevent overfitting. The dataset was split into a 80% training set, 10% validation set, and 10% test set in 8-fold cross-validation. The split was performed based on individual participants, to ensure that performance evaluation was not affected by the correlations between the two eyes of the same patient, or among multiple visits of the same patient. For each fold, the weights of the network were saved at the epoch where the RMS error of the validation set was smallest (early stopping).

Estimation variability

Repeated OCT scans were acquired in many of the scanning sessions (2 to 9 repeats, median = 2). Only one MAC+ONH pair per session was included in the main dataset. To evaluate the variability of the trained neural networks’ outputs, we created a separated dataset consisting of the repeated scans associated with images in the test set of the first cross-validation fold. This dataset had 755 pairs of MAC+ONH scans in total, from 363 unique sessions.

Statistics

All statistics was performed in R. Linear mixed-effect model analyses were performed with the lme4 and lmerTest package.^26,27 The correlation between the estimated and the measured values was quantified by Spearman’s rank correlation coefficient and Pearson’s correlation coefficient. The accuracy of the estimates was quantified using two summary statistics, the median and the third quartile (Q3) of the absolute errors |ε|. Two summary statistics were used because the distributions of |ε| were heavily skewed, and because the relationship of the three outputs was dependent on the magnitude of the error.

Results

Representative examples of the neural networks’ outputs, plotted against the measured values (ground truth), are illustrated in Figure 2. Table 2, which quantifies the neural networks’ overall performance, indicates that estimates based on combined MAC and ONH inputs (MAC+ONH) were more correlated with the measured values, when compared with estimated values based on either region alone. This was true for estimating VFI and MD (one-sided Wilcoxon signed-rank test; P<0.011 for all comparisons).

Figure 2.

The networks’ outputs on the test set, compared against the measured values. Only the results from one of the 8 validation folds are plotted. The upper row illustrates the estimates for VFI, whereas the lower row illustrates the estimates for MD. dB = decibel; MAC = macula; MD = mean deviation; ONH = optic nerve head; VFI = visual field index.

Table 2.

The overall performances of the networks evaluated on the test sets

VFI estimation
	Spearman’s r	Pearson’s ρ	median |ε|	Q3 |ε|
MAC	0.74±0.03	0.84±0.04	3.11±0.24	7.97±0.65
ONH	0.73±0.05	0.86±0.04	3.53±0.73	7.35±0.73
MAC+ONH	0.76±0.04	0.87±0.03	2.70±0.27	6.88±0.40
MD estimation
	Spearman’s r	Pearson’s ρ	median |ε| dB	Q3 |ε| dB
MAC	0.75±0.02	0.83±0.04	1.63±0.12	2.58±0.15
ONH	0.72±0.04	0.85±0.04	1.86±0.19	2.54±0.15
MAC+ONH	0.76±0.03	0.86±0.03	1.57±0.13	2.35±0.15

The number following ± represents the standard deviation across the 8 folds; median |ε| = median absolute error; Q3 |ε| = the third quartile absolute error; dB = decibel; VFI = visual field index; MAC = estimation based on macular scan; MAC+ONH = estimation based on macular and optic nerve head scans; MD = mean deviation; ONH = estimation based on optic nerve head scan.

Figure 3A, B illustrates the distributions of the absolute error of the estimation |ε|. As the error distributions were non-symmetrical with long tails, we quantified the accuracy of the estimates at two points: the median and the third quartile (Q3) of |ε|. (Fig. 3C, D). In general, MAC+ONH had smaller errors than MAC or ONH for all comparisons (one-sided Wilcoxon signed-rank test, P<0.007 for all tests), except that the difference between MAC+ONH and MAC was not significantly different for median MD (P=0.097). In addition, we observed that the relationship between MAC and ONH was dependent on the magnitude of the error. For smaller errors (measured with median |ε|), the trend was that MAC was more accurate than ONH, but the reverse was true for larger errors (measured with Q3|ε|).

Figure 3.

A and B, The distributions of the absolute estimation error |ε| for MAC, ONH, and MAC+ONH. Estimates across the 8 folds were collapsed. C and D, The medians and the third quartiles (Q3) of |ε|, evaluated on the test sets. C and D illustrate the results for VFI and MD respectively. The bars represent mean values across the 8 folds, and the circles represent values for the individual fold. Values calculated from the same fold are connected by line segments. Statistically significant comparisons (p<0.05) are indicated by the asterisks. dB = decibel; VFI = visual field index; MAC, ONH, MAC+ONH = estimation based on the macula scan, optic nerve head scan, and both; MD = mean deviation.

The pattern that MAC+ONH had smaller or comparable errors than MAC or ONH was consistently observed in healthy participant, glaucoma suspects and glaucoma patients (Figure 4).

Figure 4.

A and B, The median absolute errors (|ε|) for healthy participants, glaucoma suspects, and glaucoma patients. The red horizontal lines indicate the values for the entire testing set, as reported in Table 2. The bars represent means and standard deviation. C and D, The distributions of VFI and MD for each cohort in the dataset. The proportions indicated are percentages of samples in each of the three cohorts. dB = decibel; VFI = visual field index; MAC, ONH, MAC+ONH = estimation based on the macula scan, optic nerve head scan, and both; MD = mean deviation.

The accuracy of the estimates was dependent on signal strength of the OCT. Figure 5 shows that scans with higher signal strength on the average produced smaller median |ε|.

Figure 5.

A, The distribution of MAC signal strength in the test sets. B, The median absolute errors of MAC for VFI, stratified by the signal strength. C, the same as B, but for MD. D, E, F, the same as A, B, C, but for ONH. The red lines indicate median errors across all signal strengths. The bar charts illustrate means and standard deviations across the 8 folds on the test sets. dB = decibel; MD = mean deviation; ONH = estimation based on optic nerve head scan; VFI = visual field index.

Furthermore, estimation accuracy was also dependent on the measured values of the indices. We divided the full ranges of VFI and MD into five segments, using the 1^st of the 16-, 8-, 4, and 2-quantile of their values as boundaries, and calculated median |ε| and Q3|ε| within each segment. Figure 6 shows that both metrics decreased with the values of the index. Furthermore, MAC appeared to be on the average more accurate than ONH at the high end (VFI>97, MD>−2.24 dB); but the reverse was true for the rest of the 5 segments. And finally, MAC+ONH improved the accuracy of the other two mainly at the low end (VFI<67, MD<−12 dB).

Figure 6.

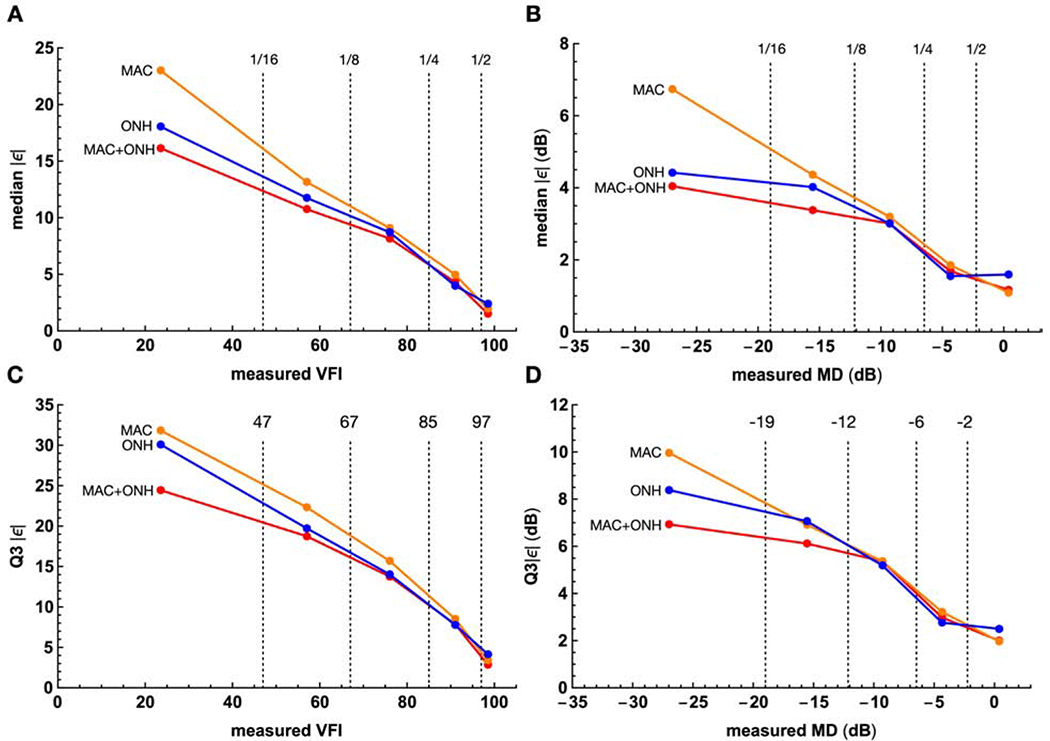
The relationships between the measured VFI and MD, and the accuracy of the estimates. The entire ranges of the VFI and MD are divided to 5 segments with boundaries (dashed vertical lines) set to the 1 of the 16-, 8-, 4-, and 2-quantile. These boundaries are denoted 1/16, 1/8, 1/4, and 1/2 in the upper row, with their values given in the lower row. Within each segment, the mean values across the 8-fold test sets are plotted. Columns: plots for VFI (left column) and MD (right column). Rows: plots for accuracy quantified with the median (top row) and the third qaurtile (bottom row) of the absolute error. median and Q3 |ε| = the median and the third quartile absolute error. dB = decibel; VFI = visual field index; MAC, ONH, MAC+ONH = estimation based on macula scans, the optic nerve head scans, and both; MD = mean deviation.

To quantify the relationships among MAC, ONH, and MAC+ONH on a sample-by-sample basis, we pooled the estimates from all folds, and plotted the differences between the MAC+ONH errors and the ONH errors, Δ|ε| = |ε|_MAC+ONH − |ε|_ONH, against the measured VFI in Figure 7A. The points were scattered (due to the noisy nature of visual field tests), but in the lower VFI segment, MAC+ONH appeared to be more accurate than ONH, because Δ|ε| tended to be more negative. The relationships between Δ|ε| and VFI, for each of the 5 segments, was established with a linear mixed-effect model, treating individual eyes as random intercepts to account for the effects of multiple visits. The mean Δ|ε| (the red curve in Fig. 7A) was estimated by the model as:

$$\Delta |\epsilon |=-4.521+0.06937*\text{vfi}+1.700*\text{seg}(\text{vfi})-0.02564*\text{vfi}*\text{seg}(\text{vfi})$$

where vfi is the measured VFI, and seg(vfi) encodes the segments (integers from 0 to 4). The interaction between VFI segment and slope was significant (P < 0.001). The model confirmed that MAC+ONH were on average more accurate than ONH, for VFI lower than 47, and that the lower bound of the mean Δ|ε| was about 5. In addition, there was also a slight MAC+ONH advantage at highest segment.

Figure 7.

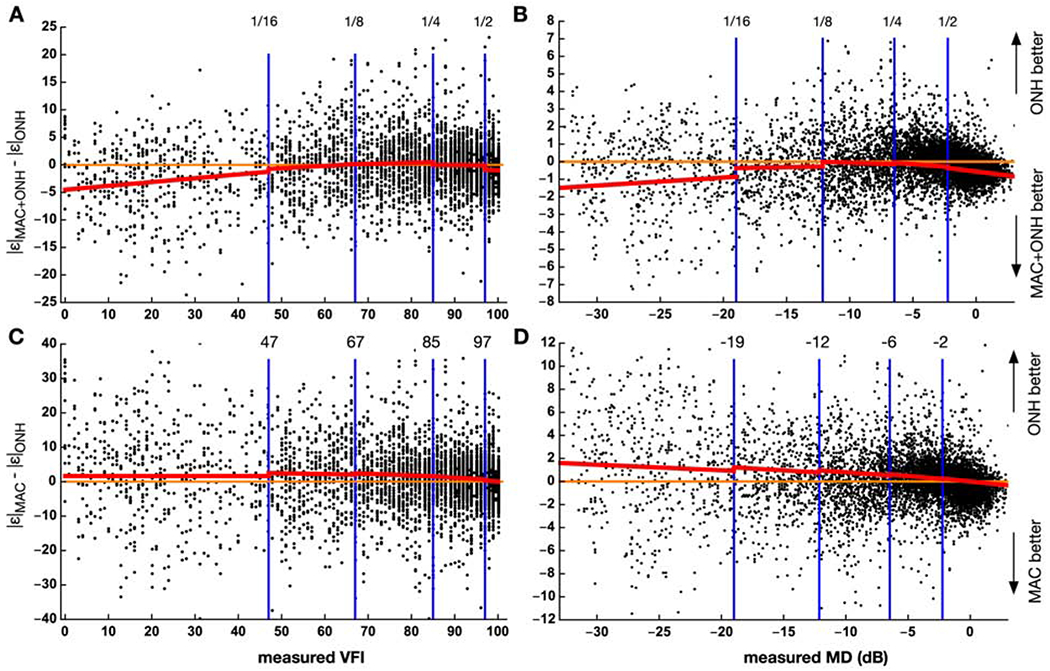
The dots represent the differences in absolute error for individual samples, pooled across the 8 folds test sets. The top row compares MAC+ONH against ONH, whereas the bottom row compares MAC against ONH. The left column plots results for VFI, and the right plots results for MD. The range of VFI and MD was divided into 5 segments, as in Figure 5. The red curves are the estimated mean values in each segment, given by the linear mixed-effect models. |ε|_MAC, |ε|_ONH, |ε|_MAC+ONH = the absolute error of the estimates based on the macula scan, the optic nerve head scan, and both. dB = decibel; MAC, ONH, MAC+ONH = estimation based macular scans, optic nerve head scans, and both; MD = mean deviation. VFI = visual field index.

A similar pattern was also observed for MD (Fig. 7B). Mean Δ|ε| was estimated

$$\Delta |\epsilon |=0.04529*\text{md}-0.1401*\text{seg}(\text{md})-0.03379*\text{md}*\text{seg}(\text{md})$$

The interaction was significant (P < 0.001). This model suggests that combining MAC with ONH was effective primarily for MD<−19 dB, and that the upper bound of the difference was about 1.5 dB. We also observed some improvements for MD > −2 dB.

Using the same procedure to compare MAC with ONH (Fig. 7C, D), we concluded that on the average, ONH was more accurate than MAC, except at the highest segment, where the accuracy of the two was similar. Previously in Figure 3C, D, we observed a small MAC advantage over ONH, based on the median errors of the entire population, but this advantage was not evident under the mixed-linear model analysis (Fig. 7C, D). We therefore did not find strong evidence for MAC advantage for the estimation of visual function.

The variability of the estimation across repeated OCT scans during the same session was quantified with the standard deviation of the neural networks’ outputs. The median values for MAC, ONH, and MAC+CONH were 1.1, 0.7, and 0.8 respectively for VFI, and 0.42 dB, 0.29 dB, and 0.30 dB respectively for MD. The variability was smaller the variability of visual field tests.²⁸ Like accuracy, estimation variability was also dependent on the severity of the disease (Fig. 8).

Figure 8.

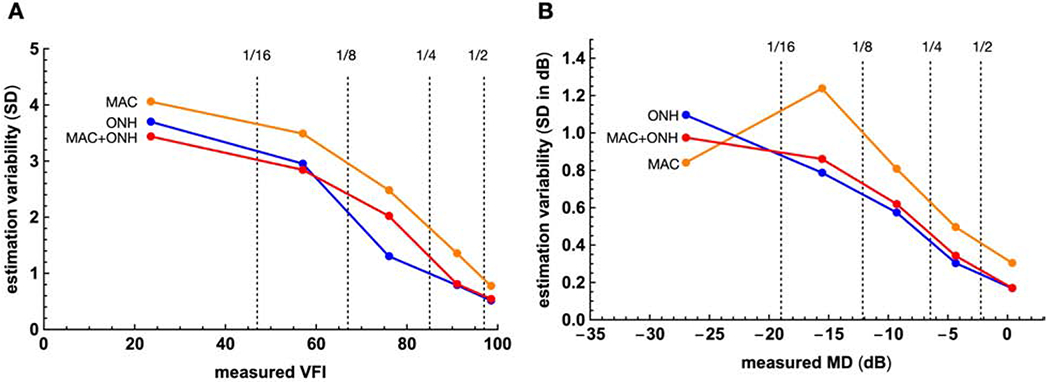
The relationships between the measured VFI and MD, and the variability of the estimates. The ranges of the VFI and MD are divided to 5 segments as in Figure 4. dB = decibel; VFI = visual field index; MAC, ONH, MAC+ONH = estimation based on macula scans, the optic nerve head scans, and both; MD = mean deviation, SD = standard deviation.

To gain insights about the 3D features learned by the networks, we used “attention maps”²⁵ to highlight retinal regions that contributed most strongly to the networks’ estimates. In Figure 9, the 3D attention maps are displayed in en face view to illustrate how they were affected by the severity of visual field damage. The figure shows strong activations surrounding the arcuate in the ONH scans and regions surrounding the macula in the MAC scans. Comparing the three maps, it can be appreciated that the severity of glaucoma is associated with the total volume of highlighted regions: the healthy eye (Fig. 9A) showed activations in large areas, whereas in the eye with advanced primary open angle glaucoma, the highlighted areas are sparse and isolated.

Discussions

We took a neural network approach to investigate the possibility of using structure to estimate function as a strategy that would allowing clinicians to interpret retinal scans in functional terms, while avoiding some of the well-known problems of visual field tests, such as the relatively long testing time. The networks were trained and evaluated on a large clinical dataset encompassing healthy subjects, glaucoma suspects, and patients of various glaucoma subtypes, to capture the diversity of structure-function relationship in clinical settings. The approach requires no image registration, segmentation and other preprocessing steps, making it efficient for the study of very large image datasets. We report promising results as a first step towards that goal, and analyzed factors that need to be taken into account in the interpretation of the estimates, such as OCT signal strength (Fig. 5), the severity of glaucoma (Fig. 6), and estimation variability (Fig. 8)

In this study, we focused on estimating global visual field indices because they are commonly used to monitor glaucoma in the clinic. Previous studies, on the other hand, estimated the threshold sensitivities of each individual point in visual field tests.^3–7,11 Although the tasks are not equivalent (ours being a simpler problem), we made an effort to approximately compare the current results to the averaged values reported in previous studies. Guo et al. (2017)⁵, for example, estimated the individual thresholds of SITA 24-2 test outcomes, using wide-field layer thickness maps derived from 9 OCT scans, and reported Pearson’s correlation coefficient in the range of 0.5 to 0.85 (average 0.74). In comparison, the Pearson’s correlation coefficients of our MD-estimation network were 0.83, 0.85, and 0.86 for MAC, ONH, and MAC+ONH respectively. The average root mean square error of our MD estimation was 2.35 dB, which also compared favorably to the 5.42 dB reported by Guo et al. (2017). Recent applications of deep learning methods have improved the performance of structure to function estimation. A recent study by Christopher et al. (2019)¹⁷, for example, used 2D convolutional network to estimate MD from en face OCT scans, and achieved R²=0.7 and MAE=2.5dB. These values are comparable to the performance of our MAC+ONH network, which correspond to R²=0.7 and MAE=2.3dB. It should be noted that estimation accuracy depends on the composition of the dataset (Fig. 4). A common dataset is therefore needed to evaluate the performance of different estimation techniques.

This study quantified the contributions of two distinctive regions of the retina to visual function: the macula and the ONH. The macula is devoted to the processing of the central visual field (<8° in eccentricity), which is probed by only 16 out of 54 points (~30%) in the SITA 24-2 perimetry.¹⁸ It was therefore surprising that macular scans alone could produce estimates that were close to the accuracy of OHN estimates. The fact that typical OCT scans, despite the small window of view (6 mm x 6mm enface), carry reliable information about global visual field functions suggests a significant degree of structural redundancy across the retina.

Since VFI is weighted to give more emphasis on the central visual field,²⁹ we expected that the VFI-estimation task would exhibit some level of macular advantage, compared to the MD-estimation task, but we did not find strong evidence for such a difference. The lack of blood vessels in the macula could potentially lead to smaller estimation errors or lower variability, but we also did not find strong evidence for this possibility.

A notable finding is that the estimation error tended to increase as visual function deteriorated (Fig. 6) – an observation that has also been reported by others.^5,6,11 This pattern is likely contributed by a number of factors including the skewed distribution of VFI/MD in the training set, the increased variability of visual field test results in advanced glaucoma²⁸, and the reduced dynamic range of RNFL thickness in advanced glaucoma.^22,23 This relationship explains why the performance of the networks was different for the different subsets (Fig. 4A, B): the distributions of the measured indices were concentrated in the high ends for healthy participants (Fig. 4C, D), entailing lower errors. Glaucoma patients, on the other hand, had a wide range of VFI and MD, entailing a broader distribution of errors. Furthermore, because VFI and MD were heavily concentrated in the high ends of the spectrum (Fig. 4C, D), this relationship explains why the overall error distributions were skewed (Fig. 3A, B).

In conclusion, we demonstrated that the accuracy for low index values could be improved by combing MAC with ONH (Fig. 7A, B). Recent findings suggest that the thickness of retinal ganglion cell and the inner plexiform layer at the macula has a large dynamic range in advanced glaucoma, and therefore might be more informative about visual function. ^19–21 This observation is not necessarily contradicted by the fact that MAC did not outperform ONH in advanced glaucoma in our study, because the estimation of low visual field indices requires information about the peripheral visual field, which is not well represented in the macula. Our findings emphasize that it is the complementary information at MAC and ONH that increases in advanced glaucoma. Therefore, to increase the accuracy of functional estimation at advanced glaucoma, combining information from the two regions is important. It should be noted that our models consistently overestimated MD and VFI in advanced glaucoma. The overestimations of the MAC and ONH models were reduced by MAC+ONH (Fig. 6), but the combination did not fully eliminate the bias. The bias might be due to the skewed distributions of MD and VFI in the dataset, which might have prevented the networks from fully compensating the floor effects in the OCT scans. Further studies using datasets with higher numbers of advanced glaucoma patients are needed to address this issue.

Abbreviations and Acronyms:

CONV

convolutional layer

GAP

global average pooling

MAC

macula

dB

decibel

MD

median deviation

OCT

optical coherence tomography

ONH

optic nerve head

Q3

the third quartile

ReLU

rectified linear unit

RNFL

retinal nerve fiber layer

SITA

Swedish interactive thresholding algorithm

VFI

visual field index