Abstract
Background:
Genome-wide association studies (GWAS) have demonstrated that psychopathology phenotypes are affected by many risk alleles with small effect (polygenicity). It is unclear how ubiquitously evolutionary pressures influence the genetic architecture of these traits.
Methods:
We partitioned SNP heritability to assess the contribution of background (BGS) and positive selection, Neanderthal local ancestry, functional significance, and genotype networks in 75 brain-related traits (8,411≤N≤1,131,181, mean N=205,289). We applied binary annotations by dichotomizing each measure based on top 2%, 1%, and 0.5% of all scores genome-wide. Effect size distribution features were calculated using GENESIS. We tested the relationship between effect size distribution descriptive statistics and natural selection. In a subset of traits, we explore the inclusion of diagnostic heterogeneity (e.g., number of diagnostic combinations and total symptoms) in the tested relationship.
Results:
SNP-heritability was enriched (false discovery rate q<0.05) for loci with elevated BGS (7 phenotypes) and in genic (34 phenotypes) and loss-of-function (LoF)-intolerant regions (67 phenotypes). These effects were strongest in GWAS of schizophrenia (1.90-fold BGS, 1.16-fold genic, and 1.92-fold LoF), educational attainment (1.86-fold BGS, 1.12-fold genic, and 1.79-fold LoF), and cognitive performance (2.29-fold BGS, 1.12-fold genic, and 1.79-fold LoF). BGS (top 2%) significantly predicted effect size variance for trait-associated loci (σ2 parameter) in 75 brain-related traits (β=4.39×10−5, p=1.43×10−5, model r2=0.548). Considering the number of DSM-5 diagnostic combinations per psychiatric disorder improved model fit (σ2 ~ BTop2% × Genic × diagnostic combinations; model r2=0.661).
Conclusions:
Brain-related phenotypes with larger variance in risk locus effect sizes are associated with loci under BGS. We show exploratory results suggesting that diagnostic complexity may also contribute to increase the polygenicity of psychiatric disorders.
Keywords: diagnostic heterogeneity, natural selection, background selection, complex traits, psychiatry, partitioned heritability
Introduction
Genome-wide association studies (GWAS) have identified numerous common genetic variants underlying thousands of human health and disease phenotypes (Buniello, et al. 2019). Psychiatric, neurological, and mental health related disorders and phenotypes have been investigated by large-scale GWAS, revealing substantial polygenicity, with small effects of loci across the genome contributing additively to a phenotype (Zhang, et al. 2018).
Background selection (BGS), the selective removal of alleles across the genome that confer deleterious effects, has been widely detected in the loci associated with mental health and behavior (Ward and Kellis 2012; Gazal, et al. 2017; Pardinas, et al. 2018; Zeng, et al. 2018; O’Connor, et al. 2019). The effects of BGS are visible in the contribution of common and rare risk loci to overall trait heritability estimates: complex trait SNP-based heritability (SNP-h2) is generally distributed evenly in common variants across the genome but is nonuniformly distributed across rare variants (O’Connor, et al. 2019). These recent findings suggest that BGS has directly contributed to the degree of polygenicity of complex phenotypes and this relationship appears to be particularly strong in brain-related traits (Zeng, et al. 2018; O’Connor, et al. 2019). Because of the extremely complex genetic architecture of multifactorial brain-related phenotypes, the sample sizes needed to maximize explainable SNP-h2 exceed several million (Zhang, et al. 2018). Even estimating these required sample sizes is further complicated by the effects of phenotype heterogeneity, which serves to reduce power for the detection of loci in GWAS, and is a systematic feature of diagnosed mental health conditions such as psychiatric disorders (Manchia, et al. 2013; Kulminski, et al. 2016).
Since gene discovery can provide information about disease biology and identify potential treatment targets, it is imperative to study both of these potential genotype-phenotype origins. In other words, it is essential to investigate how evolution and diagnostic heterogeneity independently and interactively contribute to the polygenicity of traits related to mental health and disease. The goal of the present study was to extend previous studies of BGS and other evolutionary pressures on complex traits (Gazal, et al. 2017; Pardinas, et al. 2018; O’Connor, et al. 2019) to investigate how indicators of natural selection influences polygenicity across 75 brain phenotypes. We focus on brain-related phenotypes in this investigation due to evidence of (1) the influence of natural selection on the structure of the modern human brain (Neubauer, et al. 2018) and (2) the relationship between structural features of the brain and cognition, behavior, and psychopathology (Zhao, et al. 2019). Since diagnostic heterogeneity could also contribute to the degree of polygenicity observed in psychiatric disorders, we also investigated how the addition of heterogeneous trait definitions may contribute to genomic risk locus discovery. We find that both BGS and clinical heterogeneity increase the variance of effect size for risk loci associated with complex traits, including psychiatric disorders.
Materials and Methods
Datasets
GWAS summary association data were accessed from the Psychiatric Genomics Consortium (PGC), Social Science Genetic Association Consortium (SSGAC), UK Biobank (UKB), and UKB Brain Imaging Genetics (BIG) Consortium. All datasets were formatted as standard input for Linkage Disequilibrium Score Regression (LDSC). SNP-h2 was calculated for all traits. For case/control phenotypes, SNP-h2 was calculated using effective sample sizes and converted to liability scale using population and sample prevalence reported in the respective publications (Table 1). The 1000 Genomes Project Europeans (Auton, et al. 2015) were used as the LD reference panel. Due to its complex LD structure, the major histocompatibility complex region of the genome was removed from munged summary statistics. Traits were selected for partitioning (see Partitioned Heritability) based on SNP-h2 z-score ≥ 7 (Tables S1 and S2) as previously recommended (Finucane, et al. 2015). To evaluate the impact of psychiatric disorder diagnostic heterogeneity on effect size distribution, we used psychiatric disorder heterogeneity features described in the Supplemental Methods.
Table 1. Functional annotation enrichments.
Three phenotypes whose observed scale SNP-based heritability (SNP-h2) estimates demonstrated significant (q<0.05) enrichment of loci in genic and loss-of-function (LoF) intolerant regions of the genome.
| Trait | Genic SNP-h2 Fold Enrichment (p) | LoF Intolerance SNP-h2 Fold Enrichment (p) |
|---|---|---|
| Schizophrenia | 1.16 (5.46×10−11) | 1.92 (8.80×10−21) |
| Educational Attainment | 1.12 (1.70×10−10) | 1.79 (8.65×10−23) |
| Cognitive Performance | 1.12 (2.71×10−9) | 1.79 (6.26×10−29) |
Partitioned Heritability
SNP-h2 partitioning(Finucane, et al. 2015) was performed with LDSC using 75 baseline LD genomic annotations from Gazel, et al. (Gazal, et al. 2019) characterizing important molecular properties such as allele frequency distributions, conserved regions of the genome, and regulatory elements. We created additional genome-wide annotations for genic (Lek, et al. 2016), loss-of-function (LoF) intolerant (Lek, et al. 2016), positively selected (Sabeti, et al. 2007; Grossman, et al. 2010; Grossman, et al. 2013), negatively selected (McVicker, et al. 2009; Huber, et al. 2016), and Neanderthal-introgressed (Sankararaman, et al. 2014; Durvasula and Sankararaman 2019) positions using per-SNP measurements obtained directly from the original publications. Detailed information of these evolutionary annotations is reported in the Supplementary Methods. Here, we report a brief description. To annotate LoF intolerant regions of the genome, we assigned a probability of loss-of-function intolerance (pLI) score to each gene based on the ExAC database (Lek, et al. 2016). One measure of BGS was tested. The B-statistic describes reduction in local allele diversity as a consequence of purifying selection. In other words, B of a neutral site describes the ratio of effective population size at that site versus the effective population size in the absence of BGS (McVicker, et al. 2009). We tested SNP-h2 enrichment based on three measures of positive selection: integrated haplotype score (iHS) (Voight, et al. 2006), cross-population extended haplotype homozygosity based on European and African ancestries from the 1000 Genomes Project (XP-EHH) (Sabeti, et al. 2007), the composite of multiple signals (CMS; long haplotypes, differentiated alleles, and high frequency derived alleles) (Grossman, et al. 2010; Grossman, et al. 2013). Neanderthal local ancestry (LA) quantified by comparing Neanderthal and contemporary human genomes was used to quantify the contribution of Neanderthal ancestry to the phenotypes investigated (Sankararaman, et al. 2014; Durvasula and Sankararaman 2019). Annotations also were generated for summary data describing genotype networks (i.e., a collection of genotypes and their relatedness) across the genome (Dall’Olio, et al. 2014; Dall’Olio, et al. 2015). In line with previous studies (Vitti, et al. 2013; Huber, et al. 2016; Pardinas, et al. 2018), annotations of evolutionary pressures were analyzed as bins of the top 2%, top 1%, and top 0.5% of scores genome-wide. Enrichments were interpreted as follows: (i) fold-enrichment values <1 indicated SNP-h2 depletion attributed to an annotation, and (ii) fold-enrichments >1 indicated SNP-h2 enrichment attributed to an annotation. Unless otherwise noted, we report h2(C) and associated p-values for each enrichment which corresponds to heritability enrichment of SNPs in a genomic annotation. These values are considered generally robust to the number of annotations in a model.
Effect Size Distribution
Descriptive statistics of the effect size distribution for loci associated with complex traits were the main dependent variable of interest in this study. We calculated descriptive statistics of trait-associated loci effect size distribution described by Zhang, et al. (Zhang, et al. 2018).
The GENESIS (GENetic Effect-Size distribution Inferences from Summary-level data) R package was used to determine effect size distribution descriptive statistics for brain-related traits (Zhang, et al. 2018). As per developer guidelines (Zhang, et al. 2018), all GWAS for brain-related traits were filtered to include only Hapmap3 SNPs (Altshuler, et al. 2010); SNPs were removed if (i) their effective sample sizes were less than 0.67 times the 90th percentile of the per-SNP sample size distribution, (ii) they fell within the major histocompatibility region (these were removed due to the complex LD structure of this region), and (iii) they had extremely large effect sizes (per-SNP effect z-scores>80). Descriptive statistics of effect size distribution were defined as follows: (i) πc is the proportion of susceptibility SNPs per trait, (ii) σ2 is the variance parameter for non-null SNPs, and (iii) a is the parameter describing all residual effects not captured by the variance of effect-sizes (e.g., population stratification, underestimated effects of extremely small effect size SNPs, and/or genomic deflation) (Zhang, et al. 2018). Zhang, et al. (Zhang, et al. 2018) compared two- and three-component models of effect size distribution assuming 99% of SNPs in complex trait GWAS are null and the effect sizes for the remaining 1% of non-null SNPs follow a normal distribution centered around zero (two-component) or a mixture normal distribution (three-component). Results from Zhang, et al. (Zhang, et al. 2018) support the use of two-component models for autism spectrum disorder, bipolar disorder, major depressive disorder, schizophrenia, college completion, neuroticism, cognitive performance, and intelligence quotient. We therefore considered only the two-component model to calculate effect size distribution descriptive statistics for the brain-related phenotypes analyzed in this study.
Non-Parametric Correlation and Regression Tests
We used Spearman’s rho (ρ) to test the correlation between SNP-h2, effect size distribution descriptive statistics, enrichment measures, and diagnostic heterogeneity measures in the following ways: (i) z-score-converted dependent (e.g., effect size distribution descriptive statistics) and independent measures (e.g., enrichments and diagnostic heterogeneity), (ii) z-score-converted dependent measure and unstandardized independent measures, and (iii) unstandardized measures for all trait features studied herein. With this design, we evaluate the influence of polygenic architecture and GWAS power in relation to natural selection and diagnostic heterogeneity measures. Unless otherwise noted, we discuss results using z-score-converted independent and dependent variables but provide all correlations in the corresponding supplementary information. Similarly to the LDSC method that hinges on the relationship between marginal effect sizes and the tagging effects of LD (Bulik-Sullivan, et al. 2015), we used non-parametric regression tests including median-based linear regression (MBLM; y~x; https://cran.r-project.org/web/packages/mblm/index.html), local regression (locally-estimated scatterplot smoothing or LOESS: y~x1+x2+xn; https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/loess), and generalized additive models (GAM: y~x1+x2+…+xn and y~x1×x2×…×xn; https://cran.rproject.org/web/packages/gam/index.html) to evaluate the predictive capabilities of linear and additive models on an outcome variable of interest. MBLM computes all lines between each pair of data points and reports the median of the slopes of these lines. Model r2 values are not reported due to the median-based nature of the test; however, MBLM slopes and p-values for each slope are reported. GAMs were evaluated using nominally significant MBLM predictors. When multiple binary versions of the same genomic annotation were significant predictors of the outcome variable by MBLM (e.g., enrichment of loci in the top 2%, 1%, and 0.5% of B-statistics were all significant predictors of outcome Y), the genomic annotation with the lowest p-value was included in GAM. GAMs are accompanied by generalized cross-validation (GCV) scores representing mean square error of the model. GCVs associated with GAM estimate the model prediction error without performing formal cross-validation in an out-sample (Wood 2004, 2011; MARRA and WOOD 2012; Wood 2013; Wood, et al. 2016). GCVs closer to zero represent better fitting models. The analysis of variance (ANOVA; anova.gam) feature in the mgcv (Wood, et al. 2016) R package was used to evaluate significant differences in model fit.
Results
A total of 75 brain traits were sufficiently heritable, based on observed-scale SNP-h2 z-score ≥ 7, for partitioning based on evolutionarily relevant functional annotations of the genome (Table S1). These phenotypes were grouped into eleven categories based on general trait similarities: anxiety and related, brain imaging, cognition, cross disorder, depressive and related, eating, externalizing behavior, family adversity, internalizing behavior, neurodevelopmental, and substance use and related (Table S1).
Enrichment of Genic and Loss-of-Function Intolerance
The SNP-h2 estimates of 39 and 69 phenotypes out of the 75 evaluated were nominally significantly enriched for genic and LoF-intolerant loci, respectively, 34 and 67 of which survived false discovery rate (FDR) multiple testing correction (q<0.05; Figure 1 and Table S1). The top three significant phenotypes were the same for both annotations: schizophrenia, educational attainment, and cognitive performance (Table 1). The greatest magnitude of SNP-h2 enrichment of genic loci was observed in the GWAS of T1-weighted left-plus-right caudate volume (enrichment=1.32-fold, p=0.003). The SNP-h2 for GWAS of confiding adult relationship (enrichment=2.31-fold, p=1.16×10−4) and recent easy annoyance (enrichment=2.31-fold, p=1.60×10−5) demonstrated the greatest LoF-intolerance enrichment magnitude.
Figure 1. Enrichment of natural selection and functional annotation measures.
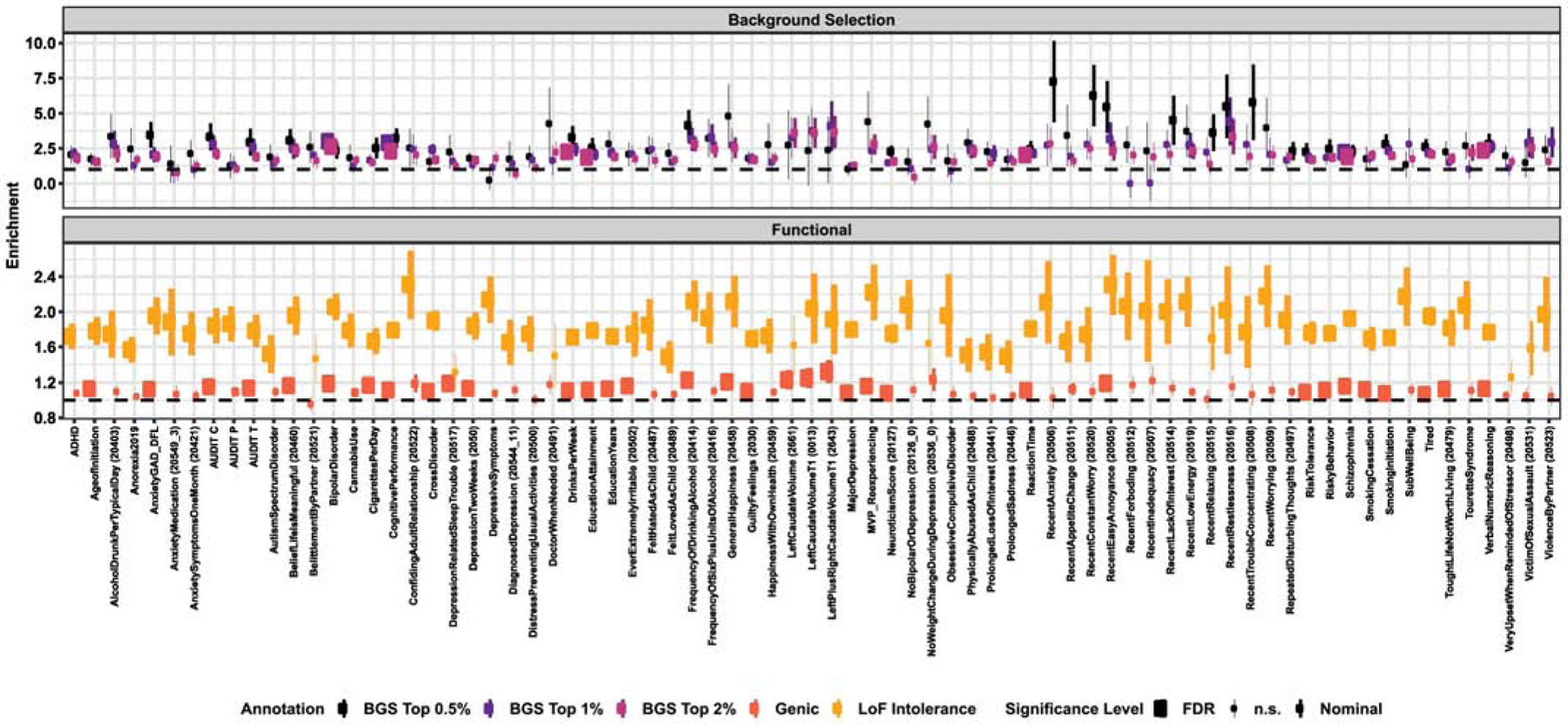
Significant enrichments of genic and loss-of-function (LoF) intolerant loci (A) and three genomic annotations of background selection (BGS). Both panels list phenotypes in descending order from highest to lowest magnitude enrichment for the most abundant annotation (i.e., LoF intolerance in panel A and top 2% of BGS scores in panel B). All phenotypes listed were at least nominally significant (p<0.05) and solid circles indicate that the enrichment survived multiple testing correction (q<0.05). Error bars represent the 95% confidence interval around each enrichment estimate.
When phenotypes were binned into eleven domains (Table S1), the brain imaging category demonstrated significantly higher enrichment of SNP-h2 attributed to genic loci than cognition (difference in mean=0.174, q=1.47×10−5), depressive and related (difference in mean=0.125, q=0.002), internalizing behavior (difference in mean=0.130, q=0.001), and substance use and related (difference in mean=0.158, q=1.46×10−5) phenotype categories. There was no significant difference in enrichment of LoF intolerance loci by phenotype category (ANOVA p=0.149). Thirty-two phenotypes demonstrated FDR significant enrichment of both genic and LoF intolerant loci (q<0.05); there was a strong overlap between genic and LoF intolerant enrichment magnitudes (ρ=0.490, p=0.003; Figure S1).
We next tested whether significant genic and LoF intolerance enrichments were influenced by trait heritability as a proxy representation of effective population size per phenotype. Genic (ρ=0.950, p=2.20×10−16) and LoF-intolerant (ρ=0.890, p=2.20×10−16) enrichment z-scores were significantly positively correlated with trait SNP-h2 z-scores (Figure S1). These results were recapitulated in unstandardized correlations where enrichment magnitude for genic and LoF-intolerance annotations was significantly negatively correlated with trait SNP-h2 z-score (SNP-h2 z-score versus genic enrichment: ρ=−0.790, p=3.52×10−10; SNP-h2 z-score versus LoF intolerance enrichment: ρ=−0.300, p=0.015; Figure S1). In other words, GWAS for phenotypes with higher confidence SNP-h2 estimates tend to show higher confidence enrichment estimates, but these estimates tend to approach 1 (i.e., minimal enrichment). The former observation is expected and suggests that the more accurately trait SNP-h2 is estimated, the more accurately that SNP-h2 can be partitioned (Finucane, et al. 2015). The latter observation is perhaps unexpected and may suggest that the magnitude of SNP-h2 enrichment attributed to functional annotation is nonuniformly a function of proxy measures of sample size up to a certain level of trait SNP-h2, visually estimated here to be an approximate SNP-h2 z-score = 15.
Enrichment of Background Selection
The GWAS of 48 phenotypes demonstrated nominally significant enrichment of BGS in at least one of the genomic annotations created (i.e., top 2%, 1%, and/or 0.5% of B-statistic genome-wide; Figure 1). Elevated BGS was detected at the level of FDR significance (q<0.05) in the GWAS of seven phenotypes, all of which demonstrated at least nominally significant BGS enrichment at all three genomic annotations and when using the B-statistic as a continuous annotation (Table 2). Three of these phenotypes also demonstrated depletion of positive selective pressures at various levels of thresholding each annotation of the genome: (i) the SNP-h2 of cognitive performance was depleted of SNPs in the top 2% of CMS scores (0.112-fold depletion, p=0.002) and SNPs in the top 1% of iHS scores (0.207-fold depletion, p=0.012), (ii) schizophrenia was depleted of SNPs in the top 2% of XP-EHH scores (0.216-fold depletion, p=0.005) and SNPs in the top 0.5% of CMS scores (−0.426-fold depletion, p=0.018), and (iii) verbal numeric reasoning was depleted for SNPs in the top 2% of XP-EHH scores (0.190-fold depletion, p=0.023), SNPs in the top 2% of CMS scores (0.101-fold depletion, p=0.028), SNPs in the top 0.5% of CMS scores (−0.310-fold depletion, p=0.043), SNPs in the top 2% of iHS scores (0.371-fold depletion, p=0.001), and SNPs in the top 1% of iHS scores (−0.334-fold depletion, p=0.002). Because BGS results in reduced genetic variation, enrichment of BGS and depletion of positive selection may be interpreted as evidence for the effect of BGS on complex traits; however, this result relies on tests for ongoing and partial selective sweeps and will require neutral-model comparisons against these and other positive selection tests.
Table 2. Background selection enrichments.
Seven phenotypes whose observed scale SNP-based heritability (SNP-h2) estimates demonstrated significant enrichment (q<0.05) of background selection (BGS) in at least one genomic annotation of per-SNP B-statistic measures. FDR significant observations (q<0.05) are in bold text.
| Trait | BGS (top 2%) SNP-h2 Fold Enrichment (p) | BGS (top 1%) SNP-h2 Fold Enrichment (p) | BGS (top 0.5%) SNP-h2 Fold Enrichment (p) |
|---|---|---|---|
| Bipolar Disorder | 2.62 (2.01×10−6) | 3.01 (4.31×10−6) | 2.36 (0.021) |
| Cognitive Performance | 2.29 (1.81×10−8) | 2.90 (7.31×10−6) | 3.24 (0.001) |
| Drinks Per Week | 2.25 (8.33×10−7) | 2.43 (0.004) | 3.29 (0.006) |
| Educational Attainment | 1.86 (9.69×10−6) | 2.04 (0.001) | 2.53 (0.003) |
| Schizophrenia | 1.90 (7.29×10−6) | 2.23 (6.04×10−6) | 2.27 (0.007) |
| Reaction Time | 2.02 (1.33×10−7) | 2.13 (0.001) | 2.44 (0.018) |
| Verbal Numeric Reasoning | 2.35 (8.63×10−8) | 2.63 (2.21×10−4) | 2.81 (0.017) |
We next tested whether BGS enrichment z-scores were associated with SNP-h2 z-scores (like those observations with genic and LoF intolerant loci). There were significant positive associations between SNP-h2 z-scores and BGS z-scores at all three genomic partitions: SNP-h2 versus BGSTop2%: ρ=0.911, p=2.20×10−16, SNP-h2 versus BGSTop1%: ρ=0.856, p=1.7×10−9, SNP-h2 versus BGSTop0.5%: ρ=0.751, p=9.81×10−6. Correlations reiterate observations from genic and LoF intolerance correlations where those phenotypes with high confidence SNP-h2 estimates (e.g., SNP-h2 z-score greater than ~15) generally showed no relationship between SNP-h2 and BGS enrichment (Figure S2).
Enrichment of Neanderthal Introgression
The SNP-h2 of UK Biobank neuroticism score was significantly depleted of SNPs in the top 2% of Neanderthal LA: 0.358-fold depletion, p=8.61×10−6. This phenotype also exhibited nominally significant enrichment of SNPs demonstrating evidence of BGS in the top 2% of B-statistic (1.57-fold enrichment, p=0.003) and top 0.5% of B-statistic (2.28-fold enrichment, p=0.002). It has been shown that per-SNP measures of Neanderthal LA and B-statistic were significantly correlated (Sankararaman, et al. 2014) however we demonstrate, with the τc statistic calculated in LDSC (Finucane, et al. 2015; Pardinas, et al. 2018), that enrichment of Neanderthal LA in the UKB phenotype neuroticism score was independent of all other annotations of the genome investigated in this study (p=1.41×10−4) (Dannemann and Kelso 2017).
Correlates of Effect Size Distribution
We used the non-parametric Spearman ρ to evaluate linear relationships between effect size distribution parameters (πc, σ2, and a; Figure 2 and Figure S3) and (i) BGS, (ii) genic and LoF intolerance, (iii) trait SNP-h2 (considering liability-scale SNP-h2 for binary traits), and (iv) diagnostic heterogeneity (psychiatric disorders only). The phenotype attributes total symptoms and diagnostic combinations were obtained from Olbert, et al. (Olbert, et al. 2014) and describe how the total number of DSM-5 criteria per psychiatric disorder contributes to diagnostic heterogeneity.
Figure 2. Complex trait effect size distribution curves.
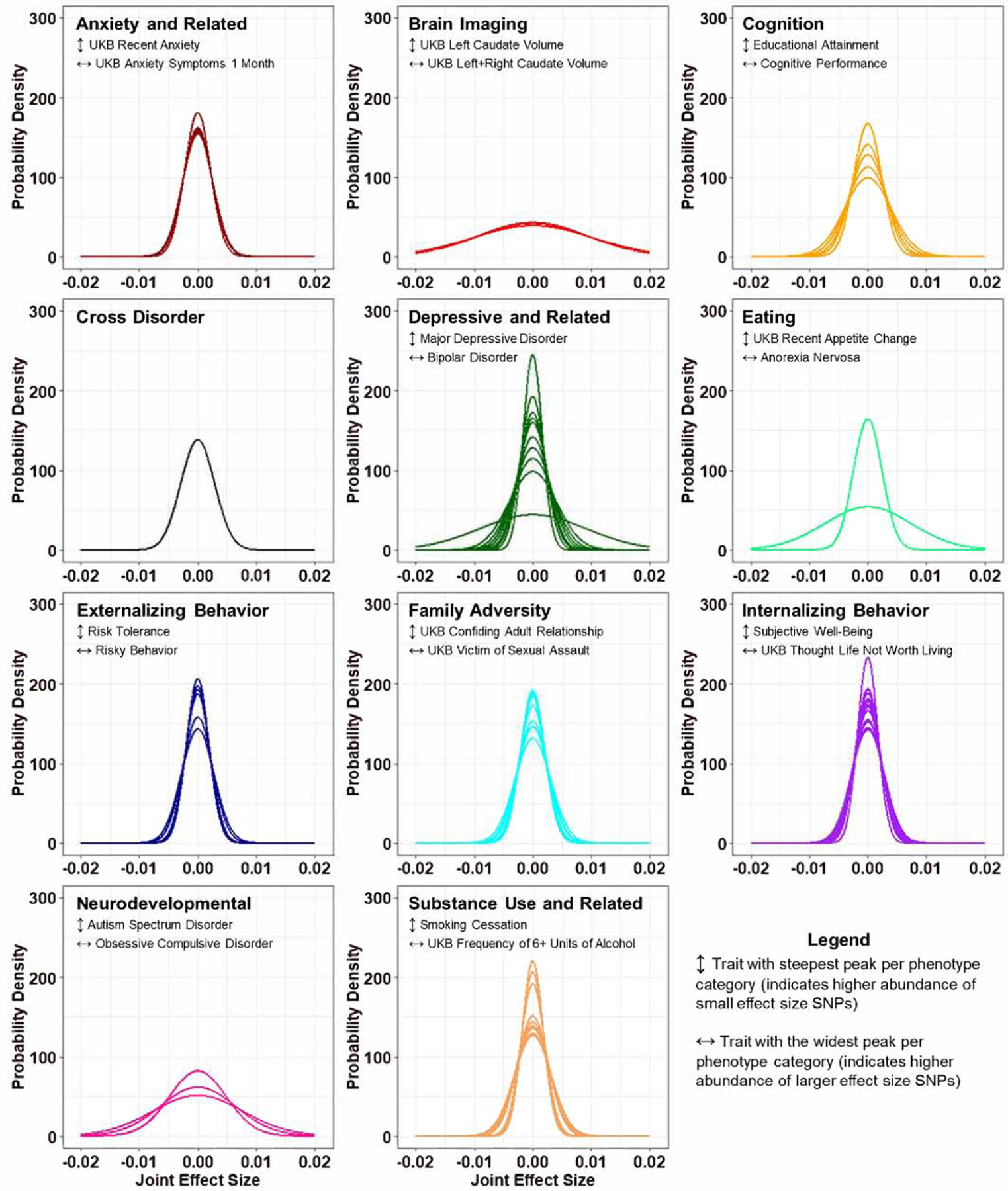
Effect size distribution curves derived from GWAS summary statistics for 75 mental health and disease phenotypes using the GENESIS R package. Phenotypes were grouped into eleven categories (Table S1). The phenotype corresponding to the steepest curve (↕) and the widest curve (↔) are identified in each subplot.
Three effect size distribution outliers were detected with measurements of at least three standard deviations from the mean (Figure 2). First, left plus right caudate volume (z-score=3.06) was an outlier with respect to σ2, highlighting a wide distribution of variant effect sizes underlying this phenotype. Second, anorexia nervosa (z-score=3.75) and bipolar disorder (z-score=5.78) were outliers with respect to the a parameter, suggesting possible residual population stratification underlying these GWAS. Notably, neither phenotype was an outlier with respect to their intercept from LDSC: anorexia nervosa intercept=1.03±0.010 and bipolar disorder intercept=1.01±0.008 relative to an expected intercept of 1 (Yengo, et al. 2018). We observed significantly reduced πc (pdiff=7.52×10−4) for major depressive disorder, which is likely attributed to large changes in (i) effective sample size and (ii) phenotype definition used herein relative to those used in Zhang, et al. (Ripke, et al. 2013; Wray, et al. 2018; Zhang, et al. 2018; Howard, et al. 2019). Estimates for schizophrenia, bipolar disorder, and autism spectrum disorder, and cognitive performance were not significantly different from those reported in Zhang, et al. (Zhang, et al. 2018).
There were no statistically significant differences in correlation when outliers were removed (Supplementary Information) so all reported correlations included the complete sample. Genic and LoF-intolerance enrichment z-scores significantly predicted all three effect size parameters (ρπc_genic=0.851, p=2.20×10−16; ρπc_LoF=0.600, p=4.68×10−7; ρσ2_genic=0.862, p=2.20×10−16; ρσ2_LoF=0.599, p=5.07×10−7; ρa_genic=0.798, p=5.72×10−9; ρa_LoF=0.736, p=2.20×10−16; Figure S3). We observed no relationship between LoF-intolerance and effect size distribution; however, enrichment of genic loci was negatively correlated with πc (ρπc_genic=−0.682, p=1.52×10−6) and positively correlated with σ2 (ρσ2 genic=0.546, p=2.33×10−4). This suggests that SNP-h2 enrichment attributed to genic loci (i) decreases the number of detectable risk loci and (ii) increases the variance associated with effect size estimates for detectable risk loci.
Using only phenotypes with at least nominal enrichment of BGS, all three effect size distribution parameter z-scores were nominally correlated with BGS enrichment z-scores: πc (ρπc_Btop2%=0.557, p=3.59×10−7; ρπc_Btop1%=0.557, p=5.49×10−7; ρπc_Btop0.5%=0.575, p=1.26×10−7), σ2 (ρσ2_Btop2%=0.514, p=3.39×10−6; ρσ2_Btop2%=0.549, p=5.16×10−7; ρσ2_Btop0.5%=0.613, p=9.80×10−9), and a (ρa_Btop2%=0.688, p=2.20×10−16; ρa_Btop1%=0.632, p=9.18×10−10; ρa_Btop0.5%=0.543, p=7.49×10−7; Figure S3). Unstandardized analyses reveal that higher BGS enrichment generally associated with reduced proportion of risk loci (πc; ρπc_Btop2%=−0.493, p=0.002; ρπc_Btop1%=−0.462, p=0.012), increased variance among those non-null risk loci (σ2; ρσ2_Btop2%=0.413, p=0.009), and decreased residual effects (e.g., population stratification, underestimated effects of extremely small effect size SNPs, and/or genomic deflation) as measured by the a parameter (ρa_ Btop0.5%=−0.642, p=5.50×10−4). These results highlight the relative importance of BGS on detection of genetic risk for complex phenotypes. Considering psychiatric diagnoses only, there were no detectable correlative relationships between measures of heterogeneity (total symptoms and diagnostic combinations) and effect size distribution (πc, σ2, and a).
Predicting Effect Size Distribution
We next tested the ability of each trait property (BGS, genic and LoF intolerance enrichment, and heterogeneity features) to predict effect size distribution descriptive statistics (πc, σ2, and a) using MBLM method (Siegel 1982) (Figure 3). For this analysis, Spearman correlations were not used to inform MBLM testing because of potential effects of (i) confounder bias, (ii) collider bias, and/or (iii) incidental cancellation potentially resulting in (a) a correlated independent variable not predicting an effect size distribution descriptive statistic or (b) an uncorrelated independent variable predicting an effect size distribution descriptive statistic. Therefore, enrichment of genic, LoF intolerant, and all partitions of BGS were used in MBLM to predict πc, σ2, and a regardless of their pairwise correlations. Though highly correlated with effect size distributions (Figures S1 and S2), SNP-h2 was not used to predict effect size distribution parameters because it represents effective population size in case-control phenotypes, which varies considerably across phenotypes.
Figure 3. Predicting effect size distribution with natural selection, functional annotation, and phenotype heterogeneity.
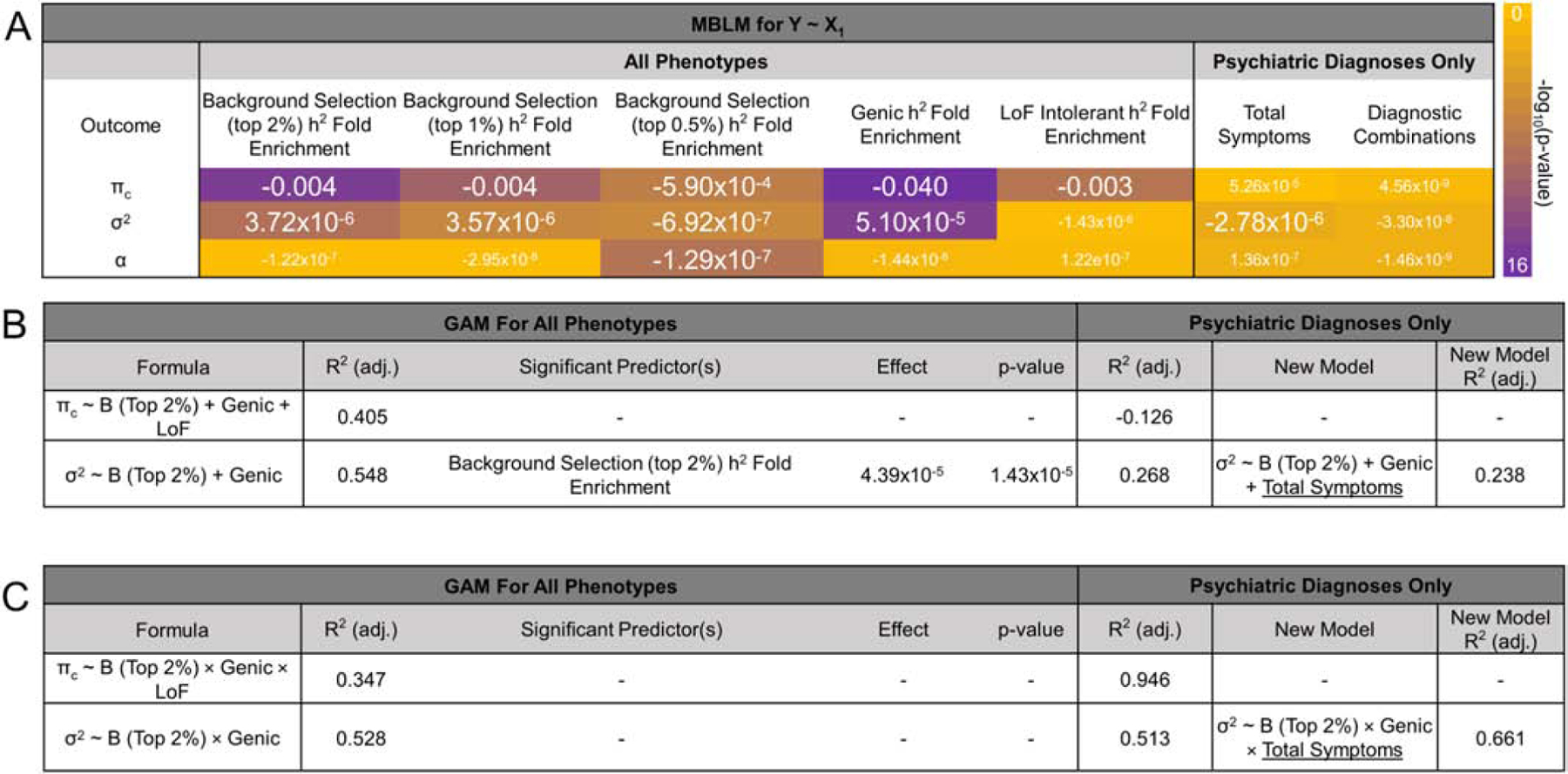
Summary of models predicting effect size distribution parameters. (A) Median-based linear models (MBLM) for predicting effect size distribution descriptive statistics with a single unstandardized independent variable. Larger font indicates at least nominal significance for the respective effect of each independent variable on the outcome effect size distribution descriptive statistic. (B and C) Generalized (GAM) additive (B) and interactive (C) models of effect size distribution descriptive statistics using individually significant predictors of each metric (from A). Prior to testing the addition of heterogeneity information, each model was re-evaluated in psychiatric disorders only.
After multiple testing correction, πc (i.e., proportion of susceptibility loci) was predicted by enrichment of genic, LoF intolerant, and all three BGS partitions (Figure 3). After multiple testing correction, the σ2 parameter (i.e., the variance parameter for non-null SNPs) was predicted independently by enrichment of all three BGS partitions and genic loci. In the additive model of σ2, BGS (top 2% of B-statistic) was the only significant predictor (β=4.39×10−4, p=1.43×10−5; r2=0.548). In the absence of out-sample cross-validation, GCV estimates associated with model fit (r2) represent a prediction error estimate whereby smaller GCV values indicate greater model fit. For the additive model of σ2, we observed a very small prediction error in the model fit, GCV=5.79×10−10. Interactive models of πc and σ2 generally explained comparable variances in the outcome variable of interest but lack significant individual or interactive predictors: πc~BTop2%×Genic×LoF r2=0.347, GCV=2.72×10−5 and σ2~BTop2%×Genic r2=0.528, GCV=4.80×10−10. The a parameter (i.e., residual effects not captured by the variance of effect-sizes) was only predicted by SNP-h2 enrichment attributed to loci in the top 0.5% of B-statistic scores (MBLM β=−1.29×10−7, p=2.48×10−5).
Exploration of how diagnostic heterogeneity may contribute to risk locus effect size distribution is described in Supplementary Results, Figure 3, and Table S1.
Discussion
Brain phenotypes, including psychiatric disorders, cognition, psychopathology, and structural elements typically demonstrate narrow effect size distributions (i.e., normal distributions with most data points distributed tightly around zero) supporting that they are (i) highly polygenic and (ii) the additive result of SNPs conferring small effects (Zhang, et al. 2018). Here we investigated how these effect sizes and their distribution are shaped by natural selection. Notably, this study is not designed to formally test per-SNP or per-locus evidence of selection against a neutral evolution hypothesis nor evaluate evidence of polygenic adaptation between populations and therefore we do not report evidence of positively or negatively selected regions of the genome such as those described previously (Ovaskainen, et al. 2011; Berg and Coop 2014). Conversely, we applied a thresholding approach to define “selected” versus “not selected” sites, as performed previously (Pardinas, et al. 2018), using per-SNP or per-locus descriptive statistics defined in the European population (Voight, et al. 2006; Sabeti, et al. 2007; McVicker, et al. 2009; Grossman, et al. 2010; Grossman, et al. 2013; Dall’Olio, et al. 2014; Sankararaman, et al. 2014; Wagner, et al. 2014; Dall’Olio, et al. 2015; Durvasula and Sankararaman 2019).
The concept of genome-wide flattening was used to demonstrate that low-frequency variants contribute less to the polygenicity of a trait than common variants, and that negative selection constrains effect sizes for these common variants (O’Connor, et al. 2019). Flattening describes the reduced effect size distributions for complex traits subjected to BGS, resulting in a highly polygenic architecture consisting of many loci with relatively small effects. Using common genetic variation and measures of effect size distributions describing (i) the proportion of non-null risk loci, (ii) the variance of non-null risk loci effect size estimates, and (iii) the residual variance not attributed to non-null risk loci, we converge on comparable findings and confirmed the detection of BGS influencing schizophrenia risk (Pardinas, et al. 2018). We extend this observation to 48 other psychopathology phenotypes and identify traits whose risk loci exhibit an overrepresentation of BGS. Seven phenotypes (bipolar disorder, cognitive performance, drinks per week, educational attainment, schizophrenia, reaction time, and verbal numeric reasoning) survived multiple testing correction, suggesting a significant influence of BGS on their common genetic variation. We also detect an overabundance of genic and LoF intolerant loci contributing to phenotype SNP-h2, implying that functionally important regions of the genome contribute the most to SNP-h2 (Lek, et al. 2016; Pardinas, et al. 2018; Hujoel, et al. 2019; O’Connor, et al. 2019). Importantly, we demonstrate that while partitioning the heritability of suitably powered phenotypes (h2 z>7) with LDSC power biases still exist in enrichments using brain related phenotypes. As the heritability estimate per phenotype becomes more accurate (h2 z increases), the accuracy of evolutionary and functional annotation enrichment improved even though the estimates approached 1. In context we believe this finding reinforces a discipline-wide initiative to establish more carefully defined phenotypes which reduce GWAS heterogeneity and improve estimates of trait heritability (Tropf, et al. 2017; Dahl, et al. 2019; Gallois, et al. 2019).
Three phenotypes demonstrated enrichment of BGS, genic, and LoF intolerance: cognitive performance, educational attainment, and schizophrenia. The persistence of risk-conferring (i.e., deleterious) loci in regions of the genome intolerant to mutation and at common frequency may at first be viewed as paradoxical. We and others hypothesize that this paradox could be attributed to BGS, which selectively removes haplotypes from the population that contain large effect deleterious mutations (Comeron, et al. 2008; Charlesworth 2012). This in turn reduces genetic diversity and allows for small-effect variants (or haplotypes) to rise in frequency to the levels of common variation detected by GWAS (Comeron, et al. 2008; Charlesworth 2012; North and Beaumont 2015; Lek, et al. 2016; Pardinas, et al. 2018). We believe this scenario is why some studies detect evidence of positive selection at traits like schizophrenia (Xu, et al. 2015; Srinivasan, et al. 2016; Polimanti and Gelernter 2017), while our present study, and others (Pardinas, et al. 2018), observe evidence for background selection when analyzing both selective mechanisms.
We next evaluated the ability of BGS, genic, and LoF intolerance enrichments to predict the effect size distributions. We identified two models for predicting the variance parameter (σ2) of effect size distributions using BGS and genic locus enrichment: (i) an additive model explaining 54.8% of the variance in σ2 and (ii) an interactive model explaining 52.8% of the variance in σ2. These data explicitly quantify the effects of natural selection on the distribution of effects sizes underlying GWAS of complex traits. However, they do not suggest that BGS acts directly on the analyzed phenotypes. They may instead point to strong effects of BGS on pleiotropic regions of the genome shared by these phenotypes (Gazal, et al. 2017). Only the interactive model performed modestly well when tested in psychiatric disorders only, explaining 51.3% of the variance in σ2. After incorporating phenotype heterogeneity information, 66.1% of variance in the σ2 parameter for psychiatric disorders was explained by the interaction between BGS, loci in genic regions of the genome, and the total number of symptoms included in psychiatric disorder diagnosis, though this improvement over the model excluding total symptom count was not significant.
Our study has four primary limitations. First, a model predicting the effect size distribution variance parameter (σ2) of psychiatric disorders is inherently limited in the number of observations contributing to the development of said model. The scarcity of data contributing to model training likely drives this model towards overfitting and a lack of generalizability, even via cross-validation. This is a difficult issue to tackle, however, due to (i) the motivation to increase the training set size, (ii) decisions of appropriate test set size, (iii) lack of large numbers of psychiatric disorders to test and (iv) potential biases from genetic correlation across psychiatric disorders. We do not attempt to cross validate this model due to a lack of data to do so, but we do demonstrate that the original model of interactive effects between genic and BGS loci persisted in psychiatric disorders. Second, two psychiatric disorders (anorexia nervosa and bipolar disorder) were statistical outliers with respect to a, which captures residual variance in effect size estimates. Though not evident by their LDSC intercept estimates, it is possible that these analyses harbor residual population stratification requiring longer LD-blocks to resolve (Byrne, et al. 2020). Third, we use psychopathology SNP-h2 enrichment values to make predictions about effect size distribution outcomes. The precise magnitude of enrichment may change depending on (i) LDSC model structure (Finucane, et al. 2015; Gazal, et al. 2017; Gazal, et al. 2019; Hujoel, et al. 2019; Speed and Balding 2019; Speed, et al. 2020), (ii) genetic correlation within and between phenotype categories, and, as we demonstrate, (iii) robust SNP-h2 z-scores. Therefore, this model will require further refinement as GWAS for complex phenotypes continue to grow and detailed evaluation of possible external confounders not adjusted for in each GWAS. Finally, it is important to note that prior studies report evidence of positive selection in schizophrenia common variant risk (Xu, et al. 2015; Srinivasan, et al. 2016; Polimanti and Gelernter 2017). Our finding, and others, oppose those findings but do not explicitly test for any selective pressure against a neutral hypothesis. We hypothesize that background selection may confound these observations these instances require (1) formal testing of CMS, XP-EHH, and iHS against neutral hypotheses, (2) testing a wider assortment of positive selection measures, and (3) testing these effects in schizophrenia correlates.
In summary we demonstrate that genetic risk effect sizes for psychopathology phenotypes are ubiquitously influenced by BGS. We attempted to extend this observation to psychiatric disorders, which may be affected by diagnostic heterogeneity. These results provide genetic and evolutionary evidence in favor of the continuous and/or intermediate phenotype approaches to studying the genetics of psychiatric disorders and complex phenotypes more generally. These data begin to unravel questions of “how” and “why” human brain-related GWAS suffer a substantial burden from large sample size requirements to identify risk loci by demonstrating how the combined effects of functional regions and natural selection influence SNP effect size distributions.
Supplementary Material
Highlights.
We used association statistics from large-scale genome-wide association studies of 75 brain-related phenotypes to investigate the polygenicity of human brain phenome
The effect of purifying selection and functional significance are ubiquitous across the polygenic architectures of brain health and disease
The diagnostic complexity also contributes to the high polygenicity of psychiatric disorders
Acknowledgements
This study was supported by the Simons Foundation Autism Research Initiative (SFARI Explorer Award: 534858), the American Foundation for Suicide Prevention (YIG-1-109-16), the National Institutes of Health (R21 DC018098 and R21 DA047527), and the National Center for PTSD of the U.S. Department of Veterans Affairs. This research is supported in part by the Department of Veterans Affairs Office of Academic Affiliations Advanced Fellowship Program in Mental Illness Research and Treatment, the Department of Veterans Affairs National Center for Post-Traumatic Stress Disorder Clinical Neurosciences Division, and the VA Connecticut Healthcare System. The views expressed here are the authors’ and do not necessarily represent the views of the Department of Veterans Affairs or the NIH.
List of Abbreviations
- GWAS
genome-wide association study
- ADHD
attention deficit hyperactivity disorder
- DSM-5
Diagnostic and Statistical Manual of Mental Disorders, 5th Edition
- PTSD
posttraumatic stress disorder
- PGC
Psychiatric Genomics Consortium
- SSGAC
Social Science Genetic Association Consortium
- UKB
United Kingdom Biobank
- BIG
Brain Imaging Genetics
- LDSC
Linkage Disequilibrium Score Regression software
- h2
observed-scale heritability
- LD
linkage disequilibrium
- LoF
loss-of-function
- SNP
single nucleotide polymorphism
- ExAC
Exome Aggregation Consortium
- pLI
probability of loss-of-function intolerance score
- BGS
background selection
- B B
statistic
- EHH
extended haplotype homozygosity
- iHS
integrated haplotype score
- XP
EHH cross-population extended haplotype homozygosity
- CMS
composite of multiple signals
- LA
local ancestry
- GENESIS
GENetic Effect-Size distribution Inferences from Summary-level data software
- MBLM
median-based linear model
- GAM
generalized additive model
- LOESS
locally-estimated scatterplot smoothing
- GCV
generalized cross-validation score
- ANOVA
analysis of variance
- FDR
false discovery rate
- PCL
posttraumatic stress disorder (PTSD) Checklist
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors declare no competing interests.
References
- Altshuler DM, Gibbs RA, Peltonen L, Altshuler DM, Gibbs RA, Peltonen L, Dermitzakis E, Schaffner SF, Yu F, Peltonen L, et al. 2010. Integrating common and rare genetic variation in diverse human populations. Nature 467:52–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auton A, Brooks LD, Durbin RM, Garrison EP, Kang HM, Korbel JO, Marchini JL, McCarthy S, McVean GA, Abecasis GR. 2015. A global reference for human genetic variation. Nature 526:68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg JJ, Coop G. 2014. A Population Genetic Signal of Polygenic Adaptation. PLOS Genetics 10:e1004412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulik-Sullivan BK, Loh PR, Finucane HK, Ripke S, Yang J, Patterson N, Daly MJ, Price AL, Neale BM. 2015. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet 47:291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buniello A, MacArthur JAL, Cerezo M, Harris LW, Hayhurst J, Malangone C, McMahon A, Morales J, Mountjoy E, Sollis E, et al. 2019. The NHGRI-EBI GWAS Catalog of published genome-wide association studies, targeted arrays and summary statistics 2019. Nucleic Acids Res 47:D1005–D1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne RP, van Rheenen W, van den Berg LH, Veldink JH, McLaughlin RL. 2020. Dutch population structure across space, time and GWAS design. bioRxiv:2020.2001.2001.892513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B 2012. The effects of deleterious mutations on evolution at linked sites. Genetics 190:5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron JM, Williford A, Kliman RM. 2008. The Hill-Robertson effect: evolutionary consequences of weak selection and linkage in finite populations. Heredity (Edinb) 100:19–31. [DOI] [PubMed] [Google Scholar]
- Dahl A, Cai N, Ko A, Laakso M, Pajukanta P, Flint J, Zaitlen N. 2019. Reverse GWAS: Using genetics to identify and model phenotypic subtypes. PLoS Genet 15:e1008009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dall’Olio GM, Bertranpetit J, Wagner A, Laayouni H. 2014. Human genome variation and the concept of genotype networks. PLoS One 9:e99424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dall’Olio GM, Vahdati AR, Bertranpetit J, Wagner A, Laayouni H. 2015. VCF2Networks: applying genotype networks to single-nucleotide variants data. Bioinformatics 31:438–439. [DOI] [PubMed] [Google Scholar]
- Dannemann M, Kelso J. 2017. The Contribution of Neanderthals to Phenotypic Variation in Modern Humans. Am J Hum Genet 101:578–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durvasula A, Sankararaman S. 2019. A statistical model for reference-free inference of archaic local ancestry. PLoS Genet 15:e1008175.31136573 [Google Scholar]
- Finucane HK, Bulik-Sullivan B, Gusev A, Trynka G, Reshef Y, Loh PR, Anttila V, Xu H, Zang C, Farh K, et al. 2015. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat Genet 47:1228–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallois A, Mefford J, Ko A, Vaysse A, Julienne H, Ala-Korpela M, Laakso M, Zaitlen N, Pajukanta P, Aschard H. 2019. A comprehensive study of metabolite genetics reveals strong pleiotropy and heterogeneity across time and context. Nat Commun 10:4788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazal S, Finucane HK, Furlotte NA, Loh PR, Palamara PF, Liu X, Schoech A, Bulik-Sullivan B, Neale BM, Gusev A, et al. 2017. Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat Genet 49:1421–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazal S, Marquez-Luna C, Finucane HK, Price AL. 2019. Reconciling S-LDSC and LDAK functional enrichment estimates. Nat Genet 51:1202–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossman SR, Andersen KG, Shlyakhter I, Tabrizi S, Winnicki S, Yen A, Park DJ, Griesemer D, Karlsson EK, Wong SH, et al. 2013. Identifying recent adaptations in large-scale genomic data. Cell 152:703–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossman SR, Shlyakhter I, Karlsson EK, Byrne EH, Morales S, Frieden G, Hostetter E, Angelino E, Garber M, Zuk O, et al. 2010. A composite of multiple signals distinguishes causal variants in regions of positive selection. Science 327:883–886. [DOI] [PubMed] [Google Scholar]
- Howard DM, Adams MJ, Clarke TK, Hafferty JD, Gibson J, Shirali M, Coleman JRI, Hagenaars SP, Ward J, Wigmore EM, et al. 2019. Genome-wide meta-analysis of depression identifies 102 independent variants and highlights the importance of the prefrontal brain regions. Nat Neurosci 22:343–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber CD, DeGiorgio M, Hellmann I, Nielsen R. 2016. Detecting recent selective sweeps while controlling for mutation rate and background selection. Mol Ecol 25:142–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hujoel MLA, Gazal S, Hormozdiari F, van de Geijn B, Price AL. 2019. Disease Heritability Enrichment of Regulatory Elements Is Concentrated in Elements with Ancient Sequence Age and Conserved Function across Species. Am J Hum Genet 104:611–624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulminski AM, Loika Y, Culminskaya I, Arbeev KG, Ukraintseva SV, Stallard E, Yashin AI. 2016. Explicating heterogeneity of complex traits has strong potential for improving GWAS efficiency. Sci Rep 6:35390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lek M, Karczewski KJ, Minikel EV, Samocha KE, Banks E, Fennell T, O’Donnell-Luria AH, Ware JS, Hill AJ, Cummings BB, et al. 2016. Analysis of protein-coding genetic variation in 60,706 humans. Nature 536:285–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manchia M, Cullis J, Turecki G, Rouleau GA, Uher R, Alda M. 2013. The impact of phenotypic and genetic heterogeneity on results of genome wide association studies of complex diseases. PLoS One 8:e76295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MARRA G, WOOD SN. 2012. Coverage Properties of Confidence Intervals for Generalized Additive Model Components. Scandinavian Journal of Statistics 39:53–74. [Google Scholar]
- McVicker G, Gordon D, Davis C, Green P. 2009. Widespread genomic signatures of natural selection in hominid evolution. PLoS Genet 5:e1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neubauer S, Hublin JJ, Gunz P. 2018. The evolution of modern human brain shape. Sci Adv 4:eaao5961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- North TL, Beaumont MA. 2015. Complex trait architecture: the pleiotropic model revisited. Sci Rep 5:9351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connor LJ, Schoech AP, Hormozdiari F, Gazal S, Patterson N, Price AL. 2019. Extreme Polygenicity of Complex Traits Is Explained by Negative Selection. Am J Hum Genet 105:456–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olbert CM, Gala GJ, Tupler LA. 2014. Quantifying heterogeneity attributable to polythetic diagnostic criteria: theoretical framework and empirical application. J Abnorm Psychol 123:452–462. [DOI] [PubMed] [Google Scholar]
- Ovaskainen O, Karhunen M, Zheng C, Arias JMC, Merilä J. 2011. A New Method to Uncover Signatures of Divergent and Stabilizing Selection in Quantitative Traits. Genetics 189:621–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardinas AF, Holmans P, Pocklington AJ, Escott-Price V, Ripke S, Carrera N, Legge SE, Bishop S, Cameron D, Hamshere ML, et al. 2018. Common schizophrenia alleles are enriched in mutation-intolerant genes and in regions under strong background selection. Nat Genet 50:381–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polimanti R, Gelernter J. 2017. Widespread signatures of positive selection in common risk alleles associated to autism spectrum disorder. PLoS Genet 13:e1006618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripke S, Wray NR, Lewis CM, Hamilton SP, Weissman MM, Breen G, Byrne EM, Blackwood DH, Boomsma DI, Cichon S, et al. 2013. A mega-analysis of genome-wide association studies for major depressive disorder. Mol Psychiatry 18:497–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabeti PC, Varilly P, Fry B, Lohmueller J, Hostetter E, Cotsapas C, Xie X, Byrne EH, McCarroll SA, Gaudet R, et al. 2007. Genome-wide detection and characterization of positive selection in human populations. Nature 449:913–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankararaman S, Mallick S, Dannemann M, Prufer K, Kelso J, Paabo S, Patterson N, Reich D. 2014. The genomic landscape of Neanderthal ancestry in present-day humans. Nature 507:354–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel AF. 1982. Robust Regression Using Repeated Medians. Biometrika 69:242–244. [Google Scholar]
- Speed D, Balding DJ. 2019. SumHer better estimates the SNP heritability of complex traits from summary statistics. Nat Genet 51:277–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D, Holmes J, Balding DJ. 2020. Evaluating and improving heritability models using summary statistics. Nat Genet 52:458–462. [DOI] [PubMed] [Google Scholar]
- Srinivasan S, Bettella F, Mattingsdal M, Wang Y, Witoelar A, Schork AJ, Thompson WK, Zuber V, Winsvold BS, Zwart JA, et al. 2016. Genetic Markers of Human Evolution Are Enriched in Schizophrenia. Biol Psychiatry 80:284–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tropf FC, Lee SH, Verweij RM, Stulp G, van der Most PJ, de Vlaming R, Bakshi A, Briley DA, Rahal C, Hellpap R, et al. 2017. Hidden heritability due to heterogeneity across seven populations. Nat Hum Behav 1:757–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitti JJ, Grossman SR, Sabeti PC. 2013. Detecting natural selection in genomic data. Annu Rev Genet 47:97–120. [DOI] [PubMed] [Google Scholar]
- Voight BF, Kudaravalli S, Wen X, Pritchard JK. 2006. A map of recent positive selection in the human genome. PLoS Biol 4:e72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner AK, Scanlon JM, Becker CR, Ritter AC, Niyonkuru C, Dixon CE, Conley YP, Price JC. 2014. The influence of genetic variants on striatal dopamine transporter and D2 receptor binding after TBI. J Cereb Blood Flow Metab 34:1328–1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward LD, Kellis M. 2012. Evidence of abundant purifying selection in humans for recently acquired regulatory functions. Science 337:1675–1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood SN. 2011. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 73:3–36. [Google Scholar]
- Wood SN. 2013. A simple test for random effects in regression models. Biometrika 100:1005–1010. [Google Scholar]
- Wood SN. 2004. Stable and Efficient Multiple Smoothing Parameter Estimation for Generalized Additive Models. Journal of the American Statistical Association 99:673–686. [Google Scholar]
- Wood SN, Pya N, Säfken B. 2016. Smoothing Parameter and Model Selection for General Smooth Models. Journal of the American Statistical Association 111:1548–1563. [Google Scholar]
- Wray NR, Ripke S, Mattheisen M, Trzaskowski M, Byrne EM, Abdellaoui A, Adams MJ, Agerbo E, Air TM, Andlauer TMF, et al. 2018. Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression. Nat Genet 50:668–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu K, Schadt EE, Pollard KS, Roussos P, Dudley JT. 2015. Genomic and network patterns of schizophrenia genetic variation in human evolutionary accelerated regions. Mol Biol Evol 32:1148–1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yengo L, Yang J, Visscher PM. 2018. Expectation of the intercept from bivariate LD score regression in the presence of population stratification. bioRxiv:310565. [Google Scholar]
- Zeng J, de Vlaming R, Wu Y, Robinson MR, Lloyd-Jones LR, Yengo L, Yap CX, Xue A, Sidorenko J, McRae AF, et al. 2018. Signatures of negative selection in the genetic architecture of human complex traits. Nat Genet 50:746–753. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Qi G, Park JH, Chatterjee N. 2018. Estimation of complex effect-size distributions using summary-level statistics from genome-wide association studies across 32 complex traits. Nat Genet 50:1318–1326. [DOI] [PubMed] [Google Scholar]
- Zhao B, Luo T, Li T, Li Y, Zhang J, Shan Y, Wang X, Yang L, Zhou F, Zhu Z, et al. 2019. Genome-wide association analysis of 19,629 individuals identifies variants influencing regional brain volumes and refines their genetic co-architecture with cognitive and mental health traits. Nat Genet 51:1637–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


