Abstract
To perform their functions, transcription factors and DNA-repair/modifying enzymes randomly search DNA in order to locate their specific targets on DNA. Discrete-state stochastic kinetic models have been developed to explain how the efficiency of the search process is influenced by the molecular properties of proteins and DNA as well as by other factors such as molecular crowding. These theoretical models not only offer explanations on the relation of microscopic processes to macroscopic behavior of proteins, but also facilitate the analysis and interpretation of experimental data. In this review article, we provide an overview on discrete-state stochastic kinetic models and explain how these models can be applied to experimental investigations using stopped-flow, single-molecule, nuclear magnetic resonance (NMR), and other biophysical and biochemical methods.
Keywords: Diffusion, Dynamics, Kinetics, Protein-DNA interactions, Target search
1. Introduction
In cells, genomic DNA molecules are gigantic polymers containing millions to billions of nucleotide residues. To regulate particular genes, transcription factors must locate functional target sites within particular regulatory regions in the genome [1]. For maintaining the genomic integrity, DNA-repair enzymes must detect damages buried among numerous intact nucleotide residues of the genome [2]. These DNA-binding proteins specifically recognize particular structural signatures in DNA. They can also interact with nonspecific sites on DNA. Although the interactions are weaker for individual nonspecific sites, the vast quantity of nonspecific DNA segments compensates for their weak affinity. Kinetic and thermodynamic efficiencies for the proteins to bind to their functional targets on DNA are strongly influenced by prior interactions with non-target sites on genomic DNA [3–6].
Target search processes of DNA-binding proteins have been intensively studied in the past five decades. Since Riggs et al. discovered astonishingly rapid target location by the lac repressor in 1970 [7], the mechanisms allowing the DNA-binding proteins to efficiently locate their targets on DNA have been studied both experimentally and theoretically [8–27]. Arguably the most impactful work in this area was a series of papers published in 1981 by Berg, Winter, and von Hippel [28–30]. These researchers theorized some of the key concepts for protein translocation on DNA and used them to explain biochemical data on the lac repressor. They hypothesized that proteins search for their targets on DNA via several translocation modes such as sliding and hoping. This work was remarkable in that these hypothetical concepts were postulated when only a very limited number of experimental methods and no crystal structures of protein-DNA complexes were available. Now, sliding of proteins on DNA is a well-established fact, which has been directly observed for many DNA-binding proteins in vitro and even in vivo by single-molecule methods [8,10,14,19–21,31]. Other methods such as nuclear magnetic resonance (NMR) spectroscopy [13,32], stopped-flow fluorescence [33–35], and elaborate biochemical approaches [36–42] also provide rich and quantitative information about how proteins locate their targets on DNA.
In the 21st century, remarkable progress has also been made in understanding the molecular mechanisms of target DNA search processes (e.g. reviewed in Refs. [15, 18, 23, 25, 43]). A large number of theoretical studies has utilized the so-called chemical-kinetic or discrete-state stochastic models for binding of proteins at nonspecific sites on DNA [5,44–57]. For convenience, we refer to them as discrete-state stochastic kinetic models. The main advantage of these models is that exact analytical expression for the mean search times can be obtained, as recently reviewed [25]. Many features of target DNA search (e.g., impacts of sequence heterogeneity, crowding, traps, DNA-looping, protein conformational fluctuations) were theoretically investigated obtaining the search time as an analytical function of experimentally measured parameters (rates, diffusion constants, length of DNA, etc.) for underlying processes and configurations [44–54,56].
Importantly, because the discrete-state stochastic kinetic models can provide testable predictions, they can also facilitate experimental studies of the target DNA search processes. By incorporating the models into experimental investigations, kinetic rate constants and other parameters relevant to protein translocation on DNA can be determined. The analytical functions of target search kinetics are particularly useful for such experimental investigations. In this review article, we provide an overview on discrete-state stochastic kinetic models, physical meaning of involved parameters, and experimental applications of the models. Showing some examples, we explain how these theoretical models can facilitate experimental analysis and interpretation of various biophysical and biochemical observations on the search processes.
2. Discrete-state stochastic kinetic models for protein translocation on DNA
2.1. Justification for discrete states
In discrete-state stochastic kinetic models for protein translocation on DNA, discrete states are defined for proteins being bound nonspecifically at different sites on DNA. One might rather suppose that protein translocation on DNA should occur in a continuous (as opposed to discrete) manner. Coarse-grained molecular dynamics simulations elegantly display continuous movements of proteins on DNA (e.g. Refs. [58–63]). Sliding of proteins on DNA is a random-walk process that is typically regarded as one-dimensional (1D) diffusion [28]. In the free state, a protein molecule undergoes diffusion in a three-dimensional (3D) diffusion. Obviously, it would be unreasonable to assume discrete states at different positions for the protein undergoing 3D diffusion in a solution. One may wonder why discrete states can be assumed for a protein undergoing 1D diffusion along DNA. What justifies the use of the discrete-state models?
Unlike 3D diffusion, sliding is not a barrierless process. In other words, for the protein to slide to an adjacent site, the protein molecule must first break interactions with nucleotides at the current site. Solution NMR studies on nonspecific DNA complexes showed that despite perpetual changes in binding sites, nonspecific DNA complexes of proteins share many structural features with the corresponding specific DNA complexes with the targets [64–69]. In nonspecific DNA complexes, intermolecular ion pairs should be formed between protein basic side chains and DNA phosphates. The protein molecule must transiently break all of these ions pairs when it moves from one site to another on DNA. The requirement of breaking all ion pairs could represent an energy barrier for sliding [70]. In fact, for many proteins, the 1D diffusion coefficient for the sliding on DNA is ~102–103 fold smaller than the 3D diffusion coefficient calculated with the Stokes-Einstein equation that gives the diffusion coefficient as a function of the hydrodynamic radius, viscosity, and temperature. This fact implies the presence of energy barriers for translocation of a protein along DNA. Upon overcoming a barrier, the protein can slide to an adjacent site and may form ion pairs with a shifted set of DNA phosphates. These energy barriers clearly define different protein states, allowing for successful use of discrete-state stochastic models.
2.2. Example model
Fig. 1A depicts an example of the discrete-state stochastic kinetic models for target DNA search by proteins. Similar, but more elaborate models were also developed to account for the effect of semi-specific sites viewed as traps, sequence heterogeneity, crowding, protein conformational dynamics and DNA looping [44–54,56]. The model shown in Fig. 1A involves two types of DNA duplexes whose concentrations and configurations are different. One of the DNA duplexes contains a total of L sites, of which only the m-th site from an edge is a target of the protein, and all others are nonspecific sites. The other DNA duplex (referred to as the ‘competitor DNA’) contains a total of M nonspecific sites and no target. This model can represent various systems, including one involving target-containing and non-target-containing segments separated by nucleosomes (Fig. 1B). Individual sites on each DNA are overlapped and shifted by a single base pair (bp) from adjacent sites (Fig. 1C). For example, for a 100-bp DNA and a protein that covers a 10-bp region, the number of sites L is 91 (=100 − 10 + 1).
Fig. 1.
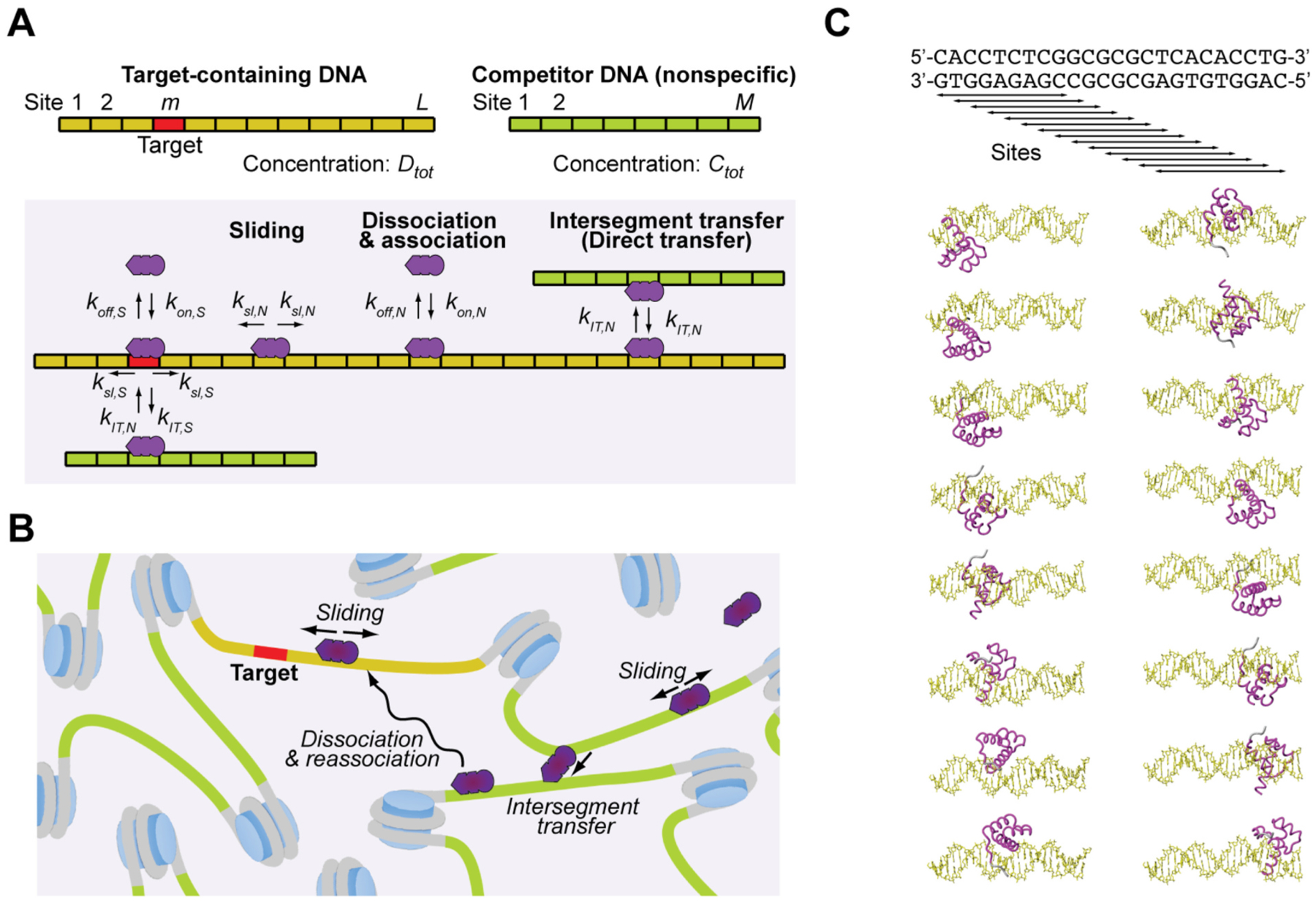
A discrete-state stochastic kinetic model for target DNA search by proteins. (A) Sites and processes involved in the model. The system involves two types of DNA duplexes: one containing a target and the other nonspecific sites only. (B) Target search on linker DNA between nucleosomes. This can be modeled by the system shown in Panel A. (C) Nonspecific binding sites for a protein on B-form DNA. Each site is overlapped and shifted by 1 bp from adjacent sites.
This model involves the kinetic rate constants for dissociation, association, sliding, and intersegment transfer. The rate constants for the specific complex and the nonspecific complexes are separately defined, for which the subscripts ‘S’ and ‘N’ are used, respectively. The parameters used in this model are summarized in Table 1. The model involves the intrinsic (as opposed to apparent) association rate constants kon,N and kon,S, the dissociation rate constants koff,N and koff,S, the first-order rate constants ksl,N and ksl,S for sliding, and the second-order rate constants kIT,N and kIT,S for intersegment transfer (also known as direct transfer) between nonspecific sites on two distinct DNA duplexes.
Table 1.
Parameters for the model shown in Fig. 1.
| Parameters | Symbols | Units |
|---|---|---|
| Kinetic rate constants | ||
| Apparent rate constant for target association | ka | M−1 s−1 |
| Intrinsic associate rate constantsa | kon,N (kon,S) | M−1 s−1 |
| Intrinsic dissociate rate constantsa | koff,N (koff,S) | s−1 |
| Sliding for a nonspecific site to an adjacent sitea | ksl,N (ksl,S) | s−1 |
| Rate constant for intersegment transfera | kIT,N (kIT,S) | M−1 s−1 |
| DNA parameters | ||
| Number of sites in the target-containing DNA segment | L | (unitless) |
| Position of the target | m | (unitless) |
| Number of sites in the nonspecific DNA segment | M | (unitless) |
| Number of possible protein orientations for each nonspecific site (1 or 2) | ϕ | (unitless) |
| Base-pair thickness (3.4 Å) | lb | m |
| Concentrations | ||
| Total concentration of target-containing DNA segment | Dtot | M |
| Total concentration of nonspecific DNA segment | Ctot | M |
| Total protein concentration | Ptot | M |
Subscripts ‘S’ and ‘N’ in these symbols are for ‘specific’ and ‘nonspecific’ sites, respectively.
2.3. Relation to one-dimensional diffusion coefficient for sliding
In the discrete-state stochastic kinetic model presented above, ksl,N is defined as the rate constant for sliding from one site to an adjacent site. However, it is practically difficult to directly observe each step of sliding because the distance separating two neighboring sites is very short, 0.34 nm, the thickness of 1 base pair (bp). For example, although single-molecule analysis can provide a 1D diffusion coefficient D1 for sliding, the spatiotemporal resolution of single-molecule methods is not high enough to detect a shift of the protein’s position by 1 bp via sliding. The rate constant ksl,N for a single-step sliding from one site to an adjacent site is directly related to the 1D diffusion coefficient D1 as follows [33]:
| (1) |
where lb is the length of 1 bp along the DNA axis (i.e., lb = 3.4 × 10−10 m).
The derivation of Eq. 1 is straightforward but worth describing here because it was not discussed previously. By definition, the diffusion coefficient D1 is related to the mean squared displacement <x2> as follows:
| (2) |
For a discrete-state system, since adjacent sites are overlapped and shifted by 1 bp (see Fig. 1C), the mean squared displacement of a protein along the DNA axis from the initial position is given by:
| (3) |
where j represents an index for each site; pj represents the probability of finding the protein at the site j; and i is the site index for the protein’s initial position. This probability pj is defined for a consecutive sliding process and ∑pj = 1. During the consecutive sliding process from the initial association with DNA until dissociation, the differential equation for the time evolution of pj for each site (but not for the ends of DNA) is:
| (4) |
Neglecting the two ends, which is valid for long DNA chains when pj for the end sites are small, Eqs. 3 and 4 give the time derivative of <x2>:
| (5) |
This expression can be rearranged as follows,
| (6) |
Eqs. 2 and 6 together lead to Eq. 1.
Eq. 1 provides an important connection between continuum models and discrete models for protein translocation on DNA. This relation is also useful when the discrete-state stochastic models are applied to interpret experimental data. In literature, D1 is often given in bp2s−1 units instead of m2s−1 units. When D1 is given in bp2s−1 units, it is numerically equivalent to ksl,N. For example, the D1 coefficient for the Egr-1 zinc-finger protein at 110 mM KCl was measured to be 6.1 × 105 bp2s−1 [34]. This is equivalent to ksl,N = 6.1 × 105 s−1 and also corresponds to D1 = 7.1 × 10−14 m2s−1.
2.4. Analytical expression of target search kinetics
An important feature of discrete-state stochastic kinetic models is that they can provide analytical expression for the search kinetics [25]. The first-passage theory and backward master equations for probability density functions [71] can give an analytical expression for the mean search time T0 for an initially unbound protein molecule to reach a target [56]. Macroscopically, is related to the apparent rate constant for the protein-target association (ka) and corresponds to the product between ka and the concentration of the target DNA. This relation of to ka was confirmed through numerical simulations for ensemble populations of individual states by solving the rate equations for the same system [33].
An exact analytical expression for the apparent second-order rate constant (ka) for the target association is available for the model shown in Fig. 1A. Although the full derivation is rather complicated [34], the final expression for ka is remarkably simple and it has a very clear physical meaning:
| (7) |
The parameter S represents an acceleration (S > 1) of target association through the antenna effect (see Section 2.5); ρ represents a deceleration (0 < ρ < 1) via trapping of proteins at nonspecific sites outside the antenna; and the parameter η represents an acceleration (η > 1) via intersegment transfer. These parameters are given as follows [34]:
| (8) |
| (9) |
| (10) |
In Eq. 8, Kd,N(=koff,N/kon,N) is the dissociation constant for each nonspecific site. The parameter ϕ is the number of possible orientations for each nonspecific site. Due to structural pseudo-C2 symmetry for DNA, proteins that bind as a monomer to DNA can take two opposite orientations. This corresponds to ϕ = 2. For symmetric dimers, ϕ = 1. For example, for monomeric proteins, specific association with a target site occurs only in one of the two possible orientations, and the binding to the same site in the opposite orientation is regarded as nonspecific. In Eq. 10, y is a function of the sliding length λ (in bp; unitless):
| (11) |
The sliding length λ represents the mean length of sliding (in base pairs; unitless) and is given by [28]:
| (12) |
The parameter τN is the mean residence time of a protein bound to DNA nonspecifically. In the absence of intersegment transfer, the mean residence time τN is:
| (13) |
In the presence of the intersegment transfer mechanism, the time τN is shorter and given by:
| (14) |
Although details are obviously model-dependent, Eq. 7 captures some general features of the target DNA search kinetics. In the following subsections, based on the presented discrete-state stochastic kinetic model, we will explain the effects and factors that impact the search kinetics (Table 2).
Table 2.
Effects and factors relevant to target search efficiency.
| Parameters | Symbols | Units | Equations |
|---|---|---|---|
| Acceleration & deceleration factors | |||
| Antenna size | S | (unitless) | Eqs. 10–15 |
| Deceleration by trapping | ρ | (unitless) | Eq. 8 |
| Acceleration by intersegment transfer | η | (unitless) | Eq. 9 |
| Sliding parameters | |||
| One-dimensional diffusion coefficient for sliding | D1 | m2s−1 | Eq. 1 |
| Sliding length | λ | bp (unitless) | Eq. 12 |
| Mean time for sliding | τn | s | Eqs. 13, 14 |
2.5. Sliding length and antenna effect
To understand the target DNA search kinetics, the sliding length λ (also known as the scanning length) is important. The sliding length corresponds to the average distance that a protein can slide without dissociating from DNA [28]. It is relatively easy to measure through experiments (see Sections 3.1 and 3.2). The sliding length λ is directly related to the antenna effect (represented by the parameter S), one of the direct determinants of target search kinetics. Fig. 2A depicts the physical meanings of the parameter S and the sliding length λ. Let’s consider a system with a target located in a middle of a long DNA segment. If a protein associates with a nonspecific site more than λ bp apart from the target, the protein molecule is likely to dissociate from DNA before reaching the target via the sliding mechanism. If the protein binds to a nonspecific site within λ bp from the target, the protein can reach target through sliding. In other words, nonspecific sites within ±λ bp can capture the protein and lead it to the target through sliding. In such a case, the target search kinetics is accelerated by a factor of up to 2λ. This effect, which is referred to as the antenna effect, depends on the position of the target and the DNA length. The parameter S represents S-fold acceleration by the antenna effect. Hereafter, we referred to S as the antenna size.
Fig. 2.
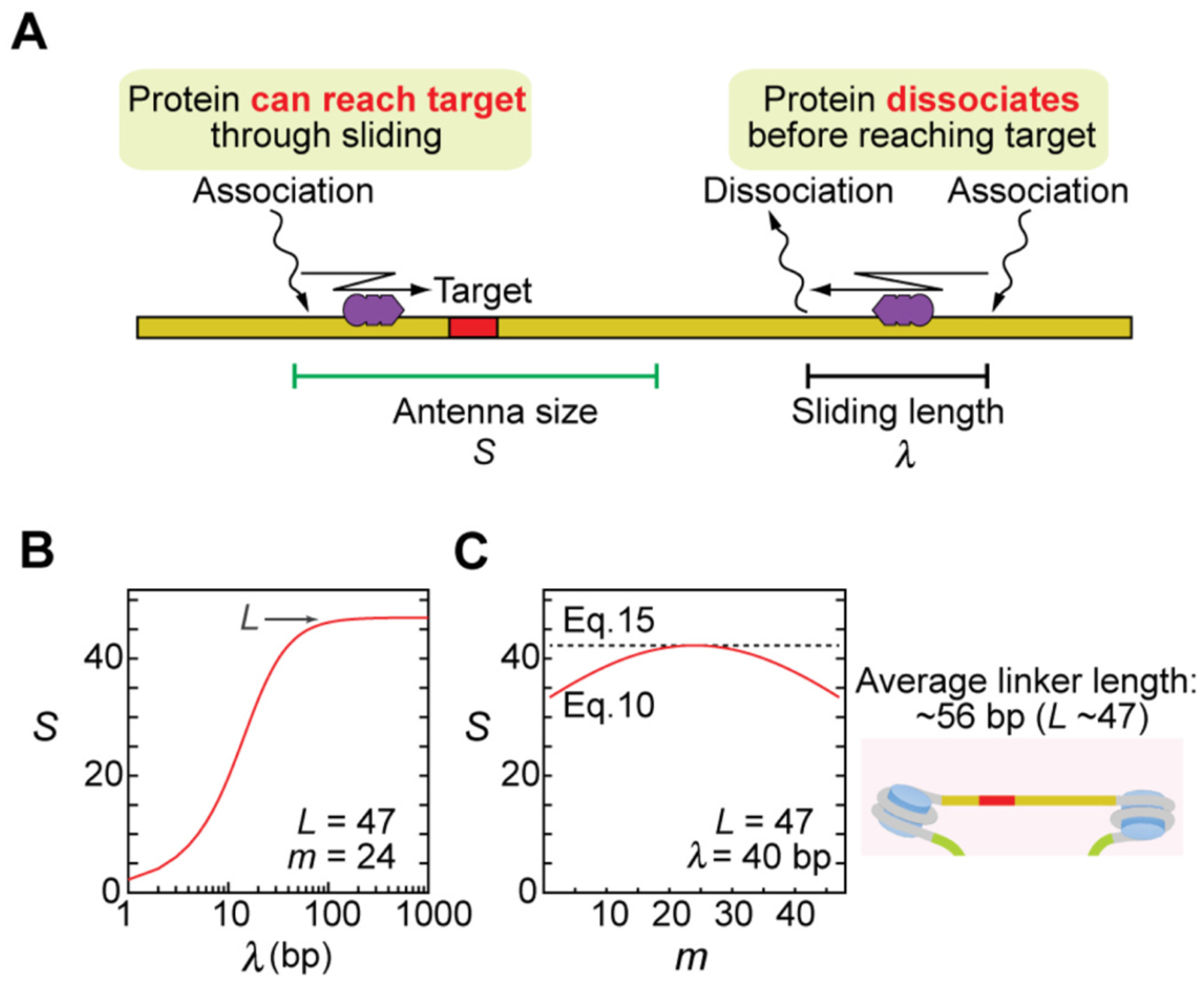
The antenna size S and the sliding length λ. (A) Physical meanings of the antenna size S and the sliding length λ. When a protein binds to a nonspecific site outside of the antenna, the protein does not reach the target through sliding. (B) Dependence of the antenna size S on the sliding length λ. Note that S ≈ L when λ » L. (C) Dependence of the antenna size S on the target position m. For Panels B and C, L = 47 was used, which corresponds to an approximate number of sites in a linker DNA segment of the average length in nuclei of human cells.
Eq. 10 gives an exact expression of the antenna size S to the target position, the number of sites, and the sliding length. A less exact, but intuitively clearer form of S is also available. If the target position is near the middle of the DNA duplex (i.e., m ≈ L/2), S becomes virtually independent of m and is reduced to [18,28]:
| (15) |
The maximum value of S is 2λ, which is achieved when the target-containing DNA is much longer than the sliding length. Under this limit, the antenna is spanned by up to the sliding length λ on each side of a target (Fig. 2A). If the target-containing DNA segment is short and λ » L, then S is virtually the same as L (Fig. 2B). In this limit, the entire DNA segment becomes the antenna. In other words, even if the protein exhibits a very long sliding length, the antenna size cannot exceed the size of the target-containing DNA segment. For example, the average length of linkers between nucleosome particles in human cells is only 56-bp [72]. Short lengths of linkers certainly limit the antenna effect. Although Eq. 15 is intuitively useful, this approximation is not valid when the target is located closer to an edge of DNA. Even in such as cases, Eq. 10 accurately provides the antenna size S. Fig. 2C compares values of S calculated with Eqs.15 and 10, showing how S depends on the target position m. Compared to those near the middle of a DNA segment, positions near a DNA edge give a smaller S and therefore should exhibit slower target association with the protein. The difference between the sliding length λ and the antenna size S can also be explained by using the following arguments. The parameter S gives the average number of distinct sites visited by the protein before the dissociation from DNA. Thus, the antenna size cannot be less than one, while the sliding length can go below one. Even if the protein cannot slide after association to the DNA molecule it will check the association site if it is a target one or not. Similarly, the antenna size cannot be larger than L while it is possible to have λ > L. In this case, the protein can move on DNA by visiting the same sites multiple times.
2.6. Trapping effect
When proteins are bound to distant nonspecific sites and are unable to reach a target through sliding, these proteins are essentially trapped at non-productive positions. In the analytical expression of the apparent target association rate constant ka (Eq. 7), the parameter ρ represents the population of proteins that are not trapped at non-productive positions. When ρ is small, the trapping effect is strong, and the search kinetics is slow. The term ϕL – S in Eq. 2 corresponds to the number of nonspecific sites outside the antenna on the target-containing DNA duplex, and (ϕL – S)Dtot + ϕMCtot corresponds to the net overall concentration of nonspecific sites. The parameter ρ is virtually independent of S when the amount of competitor DNA is much larger than the target-containing DNA (i.e., Dtot « Ctot). Kd,N represents the dissociation constant for a nonspecific complex and is given by koff,N/kon,N. It should be noted that the denominator in Eq. 8 is in a form of a partition function based on the equilibrium constant for the protein: the first term (i.e., 1) corresponds to the statistical weight for the free state as the reference state; the second term is for the proteins bound to non-antenna regions of target-containing DNA; and the third term is for the proteins bound to competitor DNA. From this form, it is obvious that the parameter ρ represents the fraction of protein molecules that are not trapped by any non-productive positions during the target search process. In terms of diffusion, the parameter ρ represents the population of proteins undergoing 3D diffusion. Through 3D diffusion, the protein can arrive at the antenna or it can directly reach the target, although with a smaller probability. The protein can reach the target through sliding from the antenna without dissociating from nonspecific DNA.
2.7. Impact of intersegment transfer
Although intersegment transfer has been neglected in many studies on target DNA search processes, some theoretical studies suggest that this translocation mechanism plays an important role in the search kinetics [73–75]. Because intersegment transfer requires an intermediate where a protein molecule transiently bridges two DNA duplexes [28], this mechanism is significant for multi-domain or multi-subunit DNA-binding proteins. If there is no intersegment transfer, proteins can transfer to target-containing DNA segment only through dissociation, 3D diffusion, and re-association. Through the intersegment transfer mechanism, proteins can directly transfer from one DNA segment to another without going through the free state. As previously explained [33], intersegment transfer can be treated as a phenomenological second-order process. The model shown in Fig. 1A involves the second-order rate constant kIT,N for intersegment transfer from nonspecific site. The parameter η represents acceleration of target search through intersegment transfer. If intersegment transfer is much faster than dissociation [i.e., kIT,N(ϕLDtot + ϕMCtot) » koff,N], thenη » 1 and intersegment transfer can substantially increase the apparent target association rate constant ka and accelerate the search kinetics. The contribution of intersegment transfer can in principle exceed the contribution of sliding (i.e., η > S), especially for systems with high density of DNA and short segments. Since two DNA ends of each nucleosome particle are apart by only ~60 Å, proteins might be able to bypass the roadblock of nucleosome via intersegment transfer [69].
3. Experimental applications
The simultaneous presence of multiple processes poses a challenge in experimental studies on the target search mechanisms. The discrete-state stochastic kinetic models can greatly facilitate analyses and interpretation of various experimental data. Here, we describe how these models can be applied to experimental studies of target DNA search by proteins.
3.1. Ensemble kinetics experiments
Various biochemical and biophysical techniques can be used to measure the kinetics of the target search process whereby DNA-binding proteins locate their specific targets on DNA in the abundant presence of nonspecific DNA. The discrete-state stochastic kinetic model shown in Fig. 1A can be applied to ensemble kinetics experiments (e.g., fluorescence-based stopped-flow experiments) for quantitative investigations of the target DNA search processes under various conditions.
3.1.1. DNA length dependence of target association
In conjunction with the discrete-state stochastic kinetic model, DNA length dependence data for target association kinetics allows for precise determination of the sliding length λ. When the length dependence is studied, the apparent target association rate constant ka is measured for some DNA duplexes of different lengths, varying L, the number of sites on target-containing DNA. Since the equations of the parameters S, ρ, and η (i.e., Eqs. 3–5) contain L, all of these parameters will be affected when L is changed in experiments. However, if the amount of the competitor DNA is much larger than the target-containing DNA, satisfying LDtot « MCtot, then ρ and η become virtually independent of L, and the length dependence of ka will arise solely from the length dependence of S. Under such conditions, the sliding length λ can be accurately determined from the length-dependent ka data alone, because S involves only λ and two DNA configurational parameters m and L. As an example, Fig. 3 shows the length-dependence data of the target association kinetics measured for the Egr-1 zinc-finger protein at 110 mM KCl by a stopped-flow method [34]. In this case, longer DNA exhibited significantly faster target association for lengths between 33 and 88 bp, whereas DNA duplexes longer than 88 bp resulted in almost the same target association kinetics. This is because additional nonspecific sites far from the antenna do not increase the chance for the protein to reach the target via sliding. Through fitting using Eqs. 7–14, the sliding length λ was determined to be 44 ± 3 bp in this case. Because the target site was close to the edge, the exact analytical form of S (i.e., Eq. 10) was used.
Fig. 3.
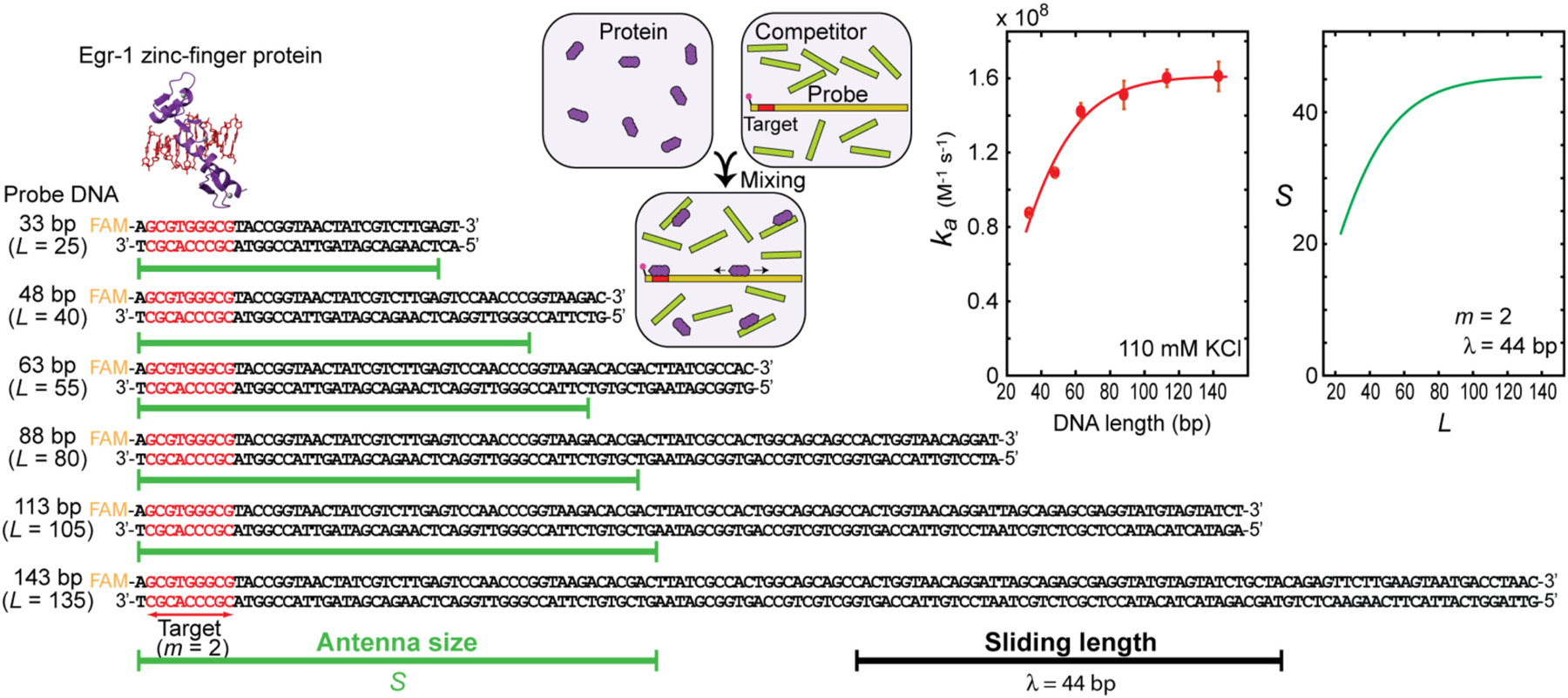
Determination of the sliding length λ from experimental data of the DNA length-dependence of the apparent association rate constant ka. The data of the apparent kinetic rate constant for target association of the Egr-1 zinc-finger protein at 110 mM KCl are shown [34]. This protein is the DNA-binding domain of the human transcription factor Egr-1 and comprises three zinc fingers (Egr-1 residues 335–423). The target association kinetics was measured for 33, 48, 65, 88, 113, and 143-bp DNA duplexes. The nucleotide sequences of these DNA duplexes are shown. The target-containing probe DNA was 2.5 nM in each kinetic measurement. The solutions also contained a far larger amount of 28-bp nonspecific competitor DNA (2000 nM). The experimental ka data are shown by red circles in the graph on the left-hand side. The best-fit curve is shown by a red solid line. The sliding length was determined to be 44 ± 3 bp through nonlinear least-squares fitting to the ka data. The corresponding length is indicated by a black bar below the DNA sequences. Green bars represent the antenna sizes S calculated for individual target-containing DNA duplexes and indicates the region of S sites, including the target. The length of each green bar is (the length of the target) + S – 1 bp. Shown on the right-hand side is a graph indicating the dependence of S on the number of sites L for the system of m = 2 and λ = 44 bp. Eq. 10 was used for this graph.
The discreate-state stochastic kinetic model can also allow for determination of the 1D diffusion coefficient D1 (also the rate constant ksl,N; see Eq. 1) for sliding and the rate constant koff,N and kon,N, if the dissociation constant Kd,N and the rate constant kIT,N for intersegment transfer are available from other experiments. There are experimental methods to determine the dissociation constant Kd,N for a nonspecific site. Methods to determine the rate constant kIT,N are also available, as described below. Thus, the DNA-length dependence data can provide comprehensive information about sliding and dissociation & re-association processes.
3.1.2. Experimental analysis of intersegment transfer
Discrete-state stochastic kinetic models also facilitate experimental investigations of intersegment transfer. There are several different experimental approaches to investigate intersegment transfer [33–35,66,69,76–81]. These approaches require kinetic measurements at varied concentrations of competitor DNA and can be categorized into two types.
One of the approaches to determine kIT,N is through measurements of apparent rate constants for transfer of the protein from a complex to competitor DNA at various concentrations. A typical experiment for these measurements involves a mixing of the protein-DNA complex and competitor DNA at concentrations much higher than Kd,N, satisfying koff « kon,N[D]. This inequality ensures that the rate-limiting step in the dissociation & reassociation process is dissociation. Since dissociation is a first-order process, the apparent dissociation rate constant should be independent of the competitor DNA concentration in the absence of intersegment transfer. However, in the presence of intersegment transfer, the apparent dissociation rate constant is linearly dependent on the competitor DNA concentration, and the apparent rate constant is given by koff,N + kIT,NϕMCtot. The rate constant kIT,N for intersegment transfer can be determined from this dependence. It should be noted that the second term is proportional to the number of sites M on the competitor DNA. When the efficiency of intersegment transfer is discussed, the number of nonspecific sites on competitor DNA should be taken into account.
The other type of the experimental approaches utilizes target association kinetics at various concentrations of competitor DNA [33,34]. In the absence of intersegment transfer (i.e., kIT,N = 0 and η = 1), the ka constant is inversely proportional to Ctot when the concentration of the competitor DNA is much higher than that of the target-containing DNA (i.e., Dtot « Ctot) [82]. This inverse proportionality arises from the parameter ρ (see Eq. 8). At a higher concentration of competitor DNA, the protein can be trapped at nonspecific sites more easily, which slows down the target association process. However, intersegment transfer can counteract this trapping effect [33]. Upon an increase in the concentration of competitor DNA, intersegment transfer becomes faster and the parameter η increases (see Eq. 9), which also increases the ka constant. The increase in the parameter η also affect the antenna size S. Due to these effects, the dependence of ka on Ctot becomes substantially deviate from the proportionality to . Using Eqs. 5–14, the rate constant kIT,N for intersegment transfer can be determined from ka data at various Ctot concentrations.
3.1.3. Salt concentration dependence of target search kinetics
Because electrostatic interactions are crucial for protein-DNA association [70], the kinetics and thermodynamics of protein-DNA interactions strongly depend on the salt concentration used in experiments [29,34,64,67,83–88]. The counterion condensation theory predicts a linear relationship between logKd and log[salt] for the dissociation constants of protein-DNA complexes [85,86] and a similar linear relationship between logk and log[salt] for some kinetic rate constants relevant to protein-DNA constants [89]. In either case, the salt concentration dependence of these parameters is predicted to be monotonic. However, the salt-concentration dependence of the apparent rate constants (ka) for target search kinetics is not monotonic and there exists a salt concentration that maximizes the efficiency of the target DNA search. For the lac repressor and the Egr-1 zinc-finger protein, the target search kinetics is fastest at a physiological ionic strength and slower at lower or high ionic strengths [29,34]. The salt concentration dependence of the ka rate constant measured for the Egr-1 zinc-finger protein at various concentrations of KCl is shown in Fig. 4A.
Fig. 4.
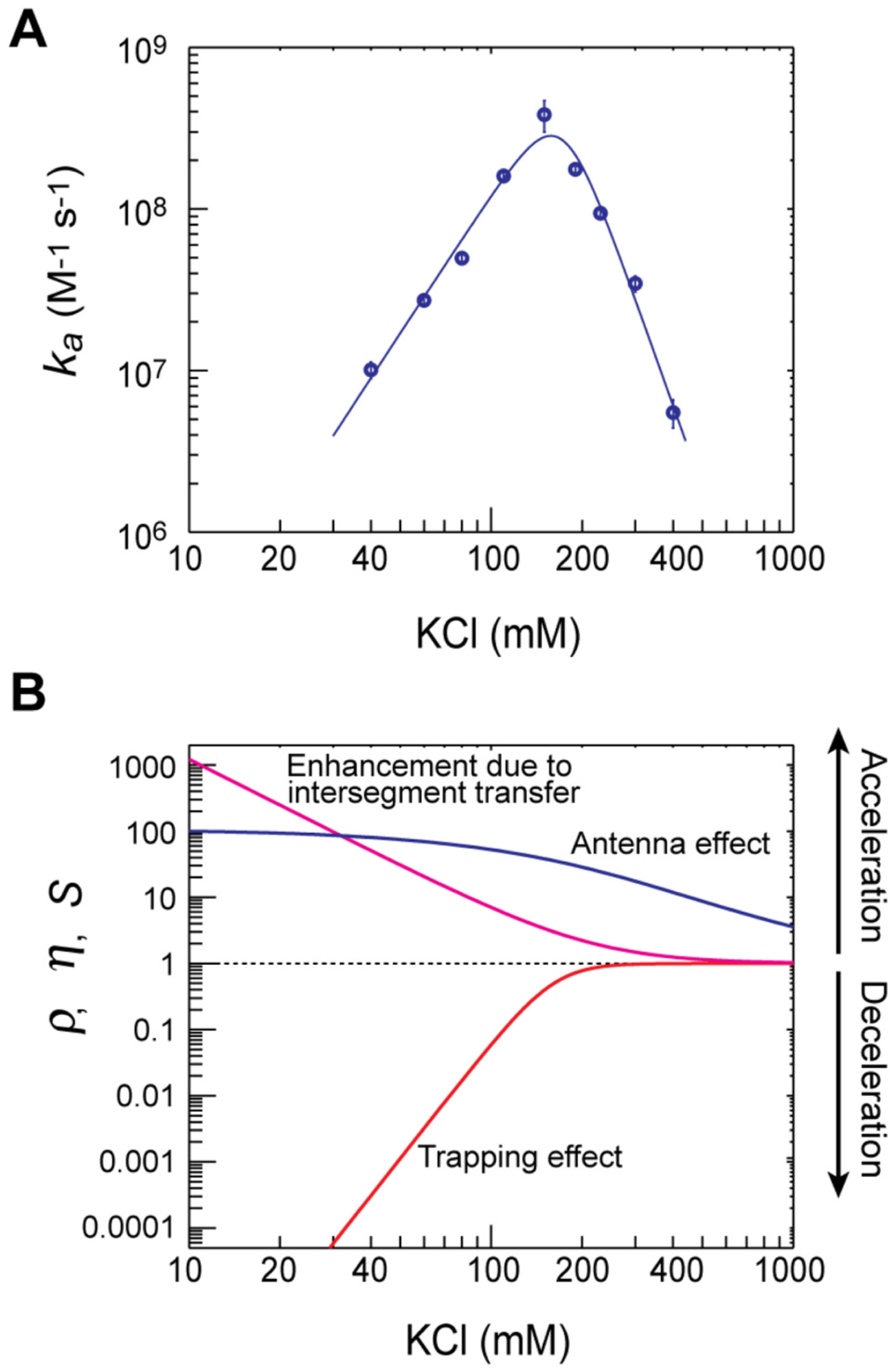
Salt concentration dependence of the target search kinetics for the Egr-1 zinc-finger protein. (A) The apparent target association rate ka measured for the Egr-1 zinc-finger protein at various concentrations of KCl. The stopped-flow experiments were conducted using a 113-bp DNA containing an Egr-1 recognition sequence (Dtot = 2.5 nM) and a nonspecific 28-bp DNA (Ctot = 2000 nM). (B) Salt concentration dependence of the parameters S, η, and ρ. The parameter S represents the antenna size (see Section 2.5); η represents an acceleration by intersegment transfer; and ρ represents a deceleration by trapping of protein at nonspecific DNA. These parameters were calculated from the experimental data on the rate constants ksl,N, koff,N and kIT,N, and the dissociation constant Kd,N for the Egr-1 zinc-finger protein along with Eqs. 8–10. The following conditions were used: L = 105 sites, M = 20 sites, and m = 2 were used. Ionic-strength dependence represented by logk = a log [KCl] + b was assumed for ksl,N, koff,N, kIT,N, and Kd,N, and the parameters a and b were calculated from the salt-dependence data for these constants. Adopted from Esadze et al. [34].
The salt concentration dependence can be explained using the equations for the discrete-state stochastic kinetic model. Based on experimental data, the parameters ρ, η, and S for the Egr-1 zinc-finger protein were calculated (Fig. 4B). The parameters S and η are decreasing functions of ionic strength, and the antenna effect and intersegment transfer substantially accelerate the target search kinetics at low ionic strengths. In contrast, the parameter ρ is an increasing function of ionic strength, and the trapping effect substantially decelerates the target search kinetics at low ionic strengths. The rate constants for electro-statically assisted macromolecular association (such as kon,N) are typically a decreasing function of ionic strength [90,91]. The rate constant ka as the product Sρηkon,N (Eq. 6) is therefore maximized at a particular ionic strength as shown in Fig. 4A.
3.2. Single-molecule experiments
In the 21st century, single-molecule fluorescence tracking of proteins bound to DNA has gained widespread popularity in the biophysical field [8,10,14,19–21,31]. The tacking for thousands of proteins molecules bound to DNA allows for quantitative analysis of sliding and dissociation. From the trajectory data, the mean squared displacement <x2> along DNA axis can be obtained for proteins sliding on DNA. For a simple diffusion process, the mean squared displacement <x2> is a linear function of time and the slope corresponds to 2D1 (see Eq. 2). Therefore, the single-molecule fluorescence tracking data directly provide the 1D diffusion coefficient D1 for sliding. Through histogram analysis of the ‘bound time’ between the initial association and the final dissociation of the protein, the dissociation rate constant koff,N can also be determined. The sliding length λ can also be determined using the D1 and koff,N data along with Eqs. 12 and 13. Discrete-state stochastic kinetic models can provide additional information. From D1 data, one can estimate the mean time of protein at a nonspecific site before sliding to either adjacent site. This is given by based on Eq. 1. If the measured 1D diffusion coefficient is D1 = 6 × 10−14 m2s−1, it suggests that the protein spends ~1 μs at each nonspecific site before sliding to an adjacent site (i. e., a shift by 1 bp, 0.34 nm). This information from the discrete-state stochastic kinetic model is useful because it is beyond the current highest spatiotemporal resolution of single-molecule techniques (~20 nm, ~500 μs; Ref. [92]). Based on Eq. 10, the antenna size S for a target in a particular DNA segment (e.g., a linker between two nucleosomes) can also be calculated. In other words, from the single-molecule data on proteins bound to nonspecific DNA, the discrete-state stochastic kinetic model can provide information about the extent of acceleration of target association kinetics via the sliding mechanism. This is important for understanding how the microscopic processes affect the efficiency in target DNA search by proteins.
3.3. NMR experiments
NMR spectroscopy is well suited to study dynamics of biological macromolecules at atomic and molecular levels and can provide spatiotemporal information on their dynamics [93]. The capabilities of NMR spectroscopy are actively being expanded with new technologies such as ultra-high field magnets (with 1H frequencies up to 1.2 GHz), 13C/15N direct-detection triple-resonance cryogenic probes, and dynamic nuclear polarization methods [94]. More challenging, dynamic systems of biological macromolecules can be studied with current NMR techniques. Some NMR-based approaches have been developed for investigating the target DNA search by proteins [13,32]. Structural information on the proteins scanning DNA can be obtained through NMR experiments [64–69]. For example, conformational mobility of particular domains or moieties within the proteins bound to DNA can be investigated. NMR spectroscopy also allows for investigations of ion-pair dynamics involving basic side chains at protein-DNA interfaces [95–98].
Some NMR methods can provide kinetic information about protein translocation on DNA. The discrete-state stochastic kinetic model of protein translocation on DNA can be incorporated directly into a master equation for NMR spectroscopy [99]. Due to the timescale of protein translocation on DNA, the McConnell equation [100,101] can be used to describe the behavior of nuclear magnetization for discrete states involved in the search process. Since proteins and DNA at chemical equilibrium are used and the concentrations of individual species remain constant in typical NMR experiments, any second-order processes can be dealt with a pseudo-first-order treatment, enabling the use of a kinetic matrix even for second-order processes (Fig. 5). By numerically solving NMR master equations incorporating the kinetic matrix for protein translocation on DNA, one can learn how the translocation process influences NMR data for proteins that are nonspecifically bound to DNA. Kinetic information about sliding, dissociation, and intersegment transfer can be obtained through this approach, as demonstrated for the Hox-D9 homeodomain [99]. In principle, the discrete-state stochastic kinetic model for protein translocation on DNA can readily be implemented into the equations on N-site exchange systems for CPMG R2 relaxation [100], R1ρ relaxation [102], cross-saturation [103], and paramagnetic relaxation enhancement (PRE) [104].
Fig. 5.
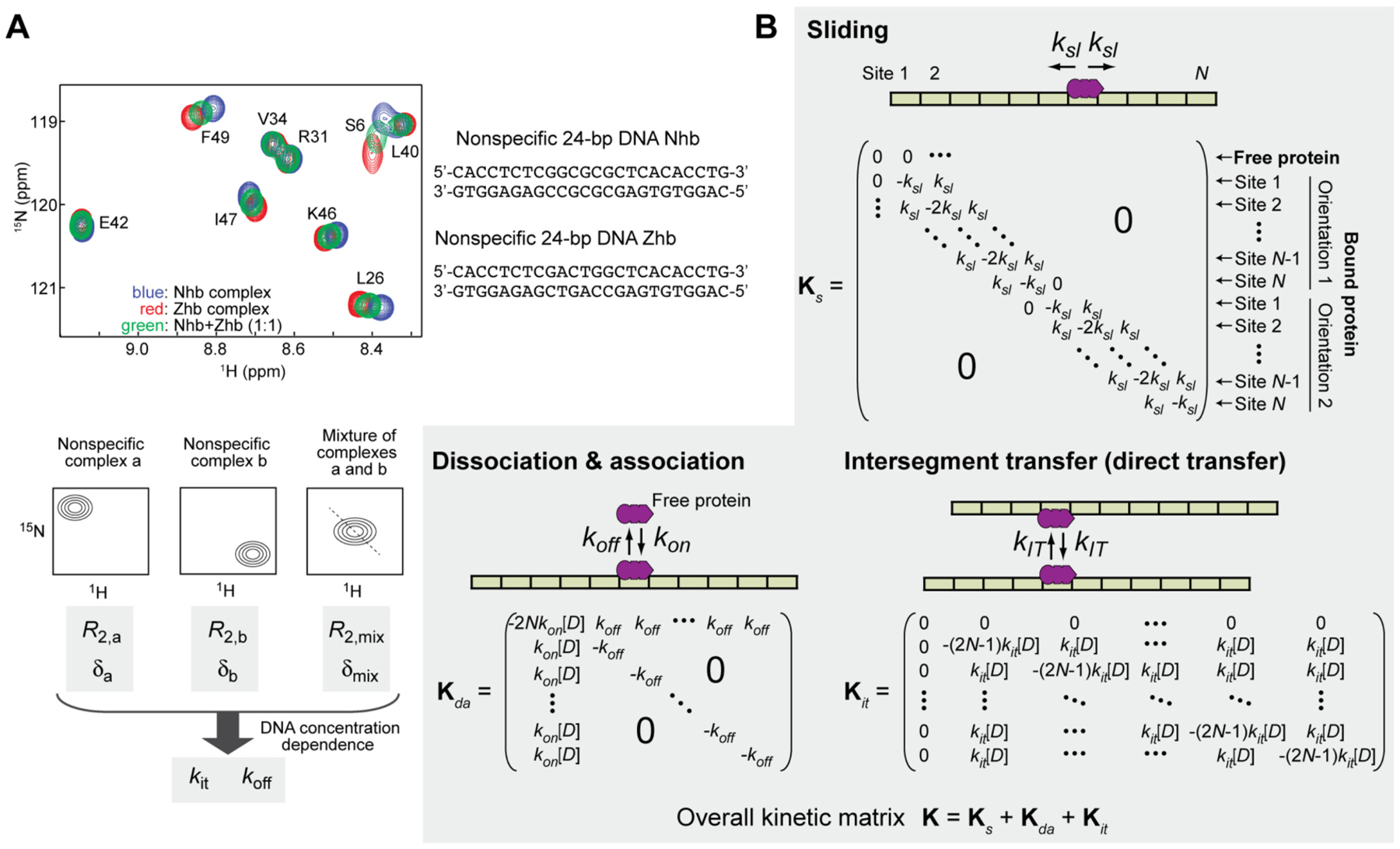
Discrete-state stochastic kinetic models can be incorporated into the McConnell equations for NMR investigations of protein translocation on DNA. (A) NMR spectra recorded for two nonspecific DNA complexes of the HoxD9 homeodomain and for a mixture of the two complexes. From NMR relaxation data for these samples, kinetic rate constants for protein translocation on DNA can be determined. (B) Kinetic matrices for protein translocation on DNA. NMR experiments are conducted using solutions at chemical equilibrium, which does not alter macroscopic concentrations of chemical species. Due to the constant concentrations of involved species in the NMR experiments, even second-order processes can be treated with a kinetic matrix for the McConnell equations. Adopted from Sahu et al. [99] with permission from the American Chemical Society.
3.4. Dissecting impacts of mutations on search kinetics
The discrete-state stochastic kinetic models can also facilitate in-depth investigations into how protein mutations impact the target DNA search because these models allow for the determination of various parameters for the underlying processes (Tables 1 and 2). Depending on mutations, different molecular properties may be impacted. Some mutations cause an increase in the diffusion coefficient D1 for sliding on DNA [68,105]. Such an increase in D1 (or ksl) does not necessarily cause a longer sliding length λ because dissociation could also be faster when the energy barrier for sliding is lower. Some mutations in the Egr-1 zinc-finger protein were found to modulate intersegment transfer [68]. Mutations can also shift the conformational equilibrium that governs the kinetic and thermodynamic properties of protein molecules during the target search process, as discussed for p53, TUS, and λ repressor proteins [106].
3.5. Limitations of discrete-state stochastic kinetic models
Although discrete-state stochastic kinetic models are useful for experimental investigations of target DNA search processes, experimentalists should be aware of some limitations of these models. The model shown in Fig. 1A assumes identical properties for each nonspecific site. This assumption simplifies the experimental analysis. However, actual properties of individual sites could be more or less different, depending on DNA sequence. If a DNA segment used in an experiment is supposed to be nonspecific but actually contains some sites whose affinities are substantially higher than others, these high-affinity sites will affect the search kinetics [48,107,108]. Another assumption for typical discrete-state stochastic kinetic models is that once a protein molecule dissociates from DNA, all sites have equal chance of association with the protein. It can be argued that this is the result of the fact that the 3D diffusion is much faster than the 1D diffusion and protein can reach all sites on DNA via the bulk diffusion. In reality, proximal sites should have a higher chance [109,110]. The assumption of equal probability of re-association may be valid only for dilute systems and may not be applicable to systems with high DNA density. Experiments should be designed so that the assumptions for the employed model are valid enough. Nonetheless, it should also be noted that the advantage of discrete-state stochastic models is that they are flexible and can take into account these effects. For example, the sequence heterogeneity [52], conformational switching [45,49], the presence of other proteins [54], and DNA looping [44,51,53] have been already incorporated into discreate-state stochastic kinetic models in the previous theoretical studies. In principle, these modified models can be used in experimental analysis, though such applications remain to be examined.
4. Conclusions
Mainly from a perspective of experimental applications, we have provided an overview of discreate-state stochastic kinetic models for target DNA search by proteins. These simple theoretical models provide the explicit relations of underlying processes to macroscopic kinetics of the target DNA search processes. Incorporating these models into the analyses of experimental data is relatively straightforward and can greatly facilitate various experimental studies on the target DNA search process. The analytical expressions of the search kinetics for these models allow for fitting calculations to determine various parameters such as the sliding length, the 1D diffusion coefficient for sliding, and the kinetic rate constants for microscopic processes from experimental data. But most importantly, this theoretical method significantly clarifies the details of molecular mechanisms for protein-DNA interactions. We hope that this review will encourage researchers to take advantage of these models for their experimental or theoretical studies on target DNA search processes.
Acknowledgements
This work was supported by Grant R35-GM130326 (to J.I.) from the National Institutes of Health; and Grants CHE-1953453 (to A.B.K.), MCB-1941106 (to A.B.K.), and MCB-2026805 (to J.I.) from the National Science Foundation. A.B.K. also acknowledges the support from the Center for Theoretical Biological Physics sponsored by the National Science Foundation (Grant PHY-2019745). We thank Channing Pletka for editing our manuscript.
Footnotes
Declaration of Competing Interest
None.
References
- [1].Alberts B, Johnson A, Lewis J, Morgan D, Martin R, Roberts K, Walter P, Control of gene expression, in: Molecular Biology of the Cell, Garland Science, New York, 2014, pp. 369–438. [Google Scholar]
- [2].Lord CJ, Ashworth A, The DNA damage response and cancer therapy, Nature 481 (2012) 287–294. [DOI] [PubMed] [Google Scholar]
- [3].Bottani S, Veitia RA, Hill function-based models of transcriptional switches: impact of specific, nonspecific, functional and nonfunctional binding, Biol. Rev. Camb. Philos. Soc 92 (2017) 953–963. [DOI] [PubMed] [Google Scholar]
- [4].Crocker J, Noon EP, Stern DL, The soft touch: low-affinity transcription factor binding sites in development and evolution, Curr. Top. Dev. Biol 117 (2016) 455–469. [DOI] [PubMed] [Google Scholar]
- [5].Gerland U, Moroz JD, Hwa T, Physical constraints and functional characteristics of transcription factor-DNA interaction, Proc. Natl. Acad. Sci. U. S. A 99 (2002) 12015–12020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].von Hippel PH, Revzin A, Gross CA, Wang AC, Non-specific DNA binding of genome regulating proteins as a biological control mechanism: I. The lac operon: equilibrium aspects, Proc. Natl. Acad. Sci. U. S. A 71 (1974) 4808–4812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Riggs AD, Bourgeois S, Cohn M, The lac represser-operator interaction: III. Kinetic studies, J. Mol. Biol 53 (1970) 401–417. [DOI] [PubMed] [Google Scholar]
- [8].Cuculis L, Schroeder CM, A single-molecule view of genome editing proteins: biophysical mechanisms for TALEs and CRISPR/Cas9, Annu. Rev. Chem. Biomol. Eng 8 (2017) 577–597. [DOI] [PubMed] [Google Scholar]
- [9].Esadze A, Stivers JT, Facilitated diffusion mechanisms in DNA base excision repair and transcriptional activation, Chem. Rev 118 (2018) 11298–11323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Gorman J, Greene EC, Visualizing one-dimensional diffusion of proteins along DNA, Nat. Struct. Mol. Biol 15 (2008) 768–774. [DOI] [PubMed] [Google Scholar]
- [11].Halford SE, Marko JF, How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res 32 (2004) 3040–3052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Howard MJ, Wilson SH, DNA scanning by base excision repair enzymes and implications for pathway coordination, DNA Repair (Amst) 71 (2018) 101–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Iwahara J, Zandarashvili L, Kemme CA, Esadze A, NMR-based investigations into target DNA search processes of proteins, Methods 148 (2018) 57–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Kamagata K, Itoh Y, Subekti DRG, How p53 molecules solve the target DNA search problem: a review, Int. J. Mol. Sci 21 (2020) 1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Kolomeisky AB, Physics of protein-DNA interactions: mechanisms of facilitated target search, Phys. Chem. Chem. Phys 13 (2011) 2088–2095. [DOI] [PubMed] [Google Scholar]
- [16].Lee AJ, Wallace SS, Hide and seek: how do DNA glycosylases locate oxidatively damaged DNA bases amidst a sea of undamaged bases? Free Radic. Biol. Med 107 (2017) 170–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Liu Z, Tjian R, Visualizing transcription factor dynamics in living cells, J. Cell Biol 217 (2018) 1181–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mirny L, Slutsky M, Wunderlich Z, Tafvizi A, Leith J, Kosmrlj A, How a protein searches for its site on DNA: the mechanism of facilitated diffusion, J. Phys. A Math. Theor 42 (2009) 401335. [Google Scholar]
- [19].Monico C, Capitanio M, Belcastro G, Vanzi F, Pavone FS, Optical methods to study protein-DNA interactions in vitro and in living cells at the single-molecule level, Int. J. Mol. Sci 14 (2013) 3961–3992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mueller F, Stasevich TJ, Mazza D, McNally JG, Quantifying transcription factor kinetics: at work or at play? Crit. Rev. Biochem. Mol. Biol 48 (2013) 492–514. [DOI] [PubMed] [Google Scholar]
- [21].Persson F, Barkefors I, Elf J, Single molecule methods with applications in living cells, Curr. Opin. Biotechnol 24 (2013) 737–744. [DOI] [PubMed] [Google Scholar]
- [22].Presman DM, Ball DA, Paakinaho V, Grimm JB, Lavis LD, Karpova TS, Hager GL, Quantifying transcription factor binding dynamics at the single-molecule level in live cells, Methods 123 (2017) 76–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Sheinman M, Benichou O, Kafri Y, Voituriez R, Classes of fast and specific search mechanisms for proteins on DNA, Rep. Prog. Phys 75 (2012), 026601. [DOI] [PubMed] [Google Scholar]
- [24].Shimamoto N, One-dimensional diffusion of proteins along DNA. Its biological and chemical significance revealed by single-molecule measurements, J. Biol. Chem 274 (1999) 15293–15296. [DOI] [PubMed] [Google Scholar]
- [25].Shvets AA, Kochugaeva MP, Kolomeisky AB, Mechanisms of protein search for targets on DNA: theoretical insights, Molecules 23 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Von Hippel PH, Berg OG, Facilitated target location in biological systems, J. Biol. Chem 264 (1989) 675–678. [PubMed] [Google Scholar]
- [27].Vuzman D, Levy Y, Intrinsically disordered regions as affinity tuners in protein-DNA interactions, Mol. BioSyst 8 (2012) 47–57. [DOI] [PubMed] [Google Scholar]
- [28].Berg OG, Winter RB, Von Hippel PH, Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory, Biochemistry 20 (1981) 6929–6948. [DOI] [PubMed] [Google Scholar]
- [29].Winter RB, Berg OG, Von Hippel PH, Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor-operator interaction: kinetic measurements and conclusions, Biochemistry 20 (1981) 6961–6977. [DOI] [PubMed] [Google Scholar]
- [30].Winter RB, von Hippel PH, Diffusion-driven mechanisms of protein translocation on nucleic acids. 2. The Escherichia coli repressor–operator interaction: equilibrium measurements, Biochemistry 20 (1981) 6948–6960. [DOI] [PubMed] [Google Scholar]
- [31].Tafvizi A, Mirny LA, van Oijen AM, Dancing on DNA: kinetic aspects of search processes on DNA, Chemphyschem 12 (2011) 1481–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Clore GM, Exploring translocation of proteins on DNA by NMR, J. Biomol. NMR 51 (2011) 209–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Esadze A, Iwahara J, Stopped-flow fluorescence kinetic study of protein sliding and intersegment transfer in the target DNA search process, J. Mol. Biol 426 (2014) 230–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Esadze A, Kemme CA, Kolomeisky AB, Iwahara J, Positive and negative impacts of nonspecific sites during target location by a sequence-specific DNA-binding protein: origin of the optimal search at physiological ionic strength, Nucleic Acids Res 42 (2014) 7039–7046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Itoh Y, Murata A, Takahashi S, Kamagata K, Intrinsically disordered domain of tumor suppressor p53 facilitates target search by ultrafast transfer between different DNA strands, Nucleic Acids Res 46 (2018) 7261–7269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Esadze A, Rodriguez G, Weiser BP, Cole PA, Stivers JT, Measurement of nanoscale DNA translocation by uracil DNA glycosylase in human cells, Nucleic Acids Res 45 (2017) 12413–12424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Gowers DM, Wilson GG, Halford SE, Measurement of the contributions of 1D and 3D pathways to the translocation of a protein along DNA, Proc. Natl. Acad. Sci. U. S. A 102 (2005) 15883–15888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Jack WE, Terry BJ, Modrich P, Involvement of outside DNA sequences in the major kinetic path by which EcoRI endonuclease locates and leaves its recognition sequence, Proc. Natl. Acad. Sci. U. S. A 79 (1982) 4010–4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Kim JG, Takeda Y, Matthews BW, Anderson WF, Kinetic studies on Cro repressor-operator DNA interaction, J. Mol. Biol 196 (1987) 149–158. [DOI] [PubMed] [Google Scholar]
- [40].Porecha RH, Stivers JT, Uracil DNA glycosylase uses DNA hopping and short-range sliding to trap extrahelical uracils, Proc. Natl. Acad. Sci. U. S. A 105 (2008) 10791–10796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Rau DC, Sidorova NY, Diffusion of the restriction nuclease EcoRI along DNA, J. Mol. Biol 395 (2010) 408–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Schonhoft JD, Stivers JT, Timing facilitated site transfer of an enzyme on DNA, Nat. Chem. Biol 8 (2012) 205–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Brackley CA, Cates ME, Marenduzzo D, Effect of DNA conformation on facilitated diffusion, Biochem. Soc. Trans 41 (2013) 582–588. [DOI] [PubMed] [Google Scholar]
- [44].Felipe C, Shin J, Loginova Y, Kolomeisky AB, The effect of obstacles in multisite protein target search with DNA looping, J. Chem. Phys 152 (2020), 025101. [DOI] [PubMed] [Google Scholar]
- [45].Kochugaeva MP, Berezhkovskii AM, Kolomeisky AB, Optimal length of conformational transition region in protein search for targets on DNA, J. Phys. Chem. Lett 8 (2017) 4049–4054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Kochugaeva MP, Shvets AA, Kolomeisky AB, On the mechanism of homology search by RecA protein filaments, Biophys. J 112 (2017) 859–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Lange M, Kochugaeva M, Kolomeisky AB, Protein search for multiple targets on DNA, J. Chem. Phys 143 (2015) 105102. [DOI] [PubMed] [Google Scholar]
- [48].Lange M, Kochugaeva M, Kolomeisky AB, Dynamics of the protein search for targets on DNA in the presence of traps, J. Phys. Chem. B 119 (2015) 12410–12416. [DOI] [PubMed] [Google Scholar]
- [49].Shin J, Kolomeisky AB, Molecular search with conformational change: one-dimensional discrete-state stochastic model, J. Chem. Phys 149 (2018) 174104. [DOI] [PubMed] [Google Scholar]
- [50].Shin J, Kolomeisky AB, Target search on DNA by interacting molecules: first-passage approach, J. Chem. Phys 151 (2019) 125101. [DOI] [PubMed] [Google Scholar]
- [51].Shin J, Kolomeisky AB, Facilitation of DNA loop formation by protein-DNA nonspecific interactions, Soft Matter 15 (2019) 5255–5263. [DOI] [PubMed] [Google Scholar]
- [52].Shvets AA, Kolomeisky AB, Sequence heterogeneity accelerates protein search for targets on DNA, J. Chem. Phys 143 (2015) 245101. [DOI] [PubMed] [Google Scholar]
- [53].Shvets AA, Kolomeisky AB, The role of DNA looping in the search for specific targets on DNA by multisite proteins, J. Phys. Chem. Lett 7 (2016) 5022–5027. [DOI] [PubMed] [Google Scholar]
- [54].Shvets AA, Kolomeisky AB, Crowding on DNA in protein search for targets, J. Phys. Chem. Lett 7 (2016) 2502–2506. [DOI] [PubMed] [Google Scholar]
- [55].Slutsky M, Mirny LA, Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential, Biophys. J 87 (2004) 4021–4035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Veksler A, Kolomeisky AB, Speed-selectivity paradox in the protein search for targets on DNA: is it real or not? J. Phys. Chem. B 117 (2013) 12695–12701. [DOI] [PubMed] [Google Scholar]
- [57].Zhou HX, Rapid search for specific sites on DNA through conformational switch of nonspecifically bound proteins, Proc. Natl. Acad. Sci. U. S. A 108 (2011) 8651–8656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Givaty O, Levy Y, Protein sliding along DNA: dynamics and structural characterization, J. Mol. Biol 385 (2009) 1087–1097. [DOI] [PubMed] [Google Scholar]
- [59].Kanada R, Terakawa T, Kenzaki H, Takada S, Nucleosome crowding in chromatin slows the diffusion but can promote target search of proteins, Biophys. J 116 (2019) 2285–2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Marcovitz A, Levy Y, Frustration in protein-DNA binding influences conformational switching and target search kinetics, Proc. Natl. Acad. Sci. U. S. A 108 (2011) 17957–17962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Tan C, Terakawa T, Takada S, Dynamic coupling among protein binding, sliding, and DNA bending revealed by molecular dynamics, J. Am. Chem. Soc 138 (2016) 8512–8522. [DOI] [PubMed] [Google Scholar]
- [62].Vuzman D, Azia A, Levy Y, Searching DNA via a “Monkey Bar” mechanism: the significance of disordered tails, J. Mol. Biol 396 (2010) 674–684. [DOI] [PubMed] [Google Scholar]
- [63].Vuzman D, Levy Y, DNA search efficiency is modulated by charge composition and distribution in the intrinsically disordered tail, Proc. Natl. Acad. Sci. U. S. A 107 (2010) 21004–21009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Iwahara J, Clore GM, Detecting transient intermediates in macromolecular binding by paramagnetic NMR, Nature 440 (2006) 1227–1230. [DOI] [PubMed] [Google Scholar]
- [65].Iwahara J, Schwieters CD, Clore GM, Characterization of nonspecific protein-DNA interactions by 1H paramagnetic relaxation enhancement, J. Am. Chem. Soc 126 (2004) 12800–12808. [DOI] [PubMed] [Google Scholar]
- [66].Iwahara J, Zweckstetter M, Clore GM, NMR structural and kinetic characterization of a homeodomain diffusing and hopping on nonspecific DNA, Proc. Natl. Acad. Sci. U. S. A 103 (2006) 15062–15067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Kalodimos CG, Biris N, Bonvin AM, Levandoski MM, Guennuegues M, Boelens R, Kaptein R, Structure and flexibility adaptation in nonspecific and specific protein-DNA complexes, Science 305 (2004) 386–389. [DOI] [PubMed] [Google Scholar]
- [68].Zandarashvili L, Esadze A, Vuzman D, Kemme CA, Levy Y, Iwahara J, Balancing between affinity and speed in target DNA search by zinc-finger proteins via modulation of dynamic conformational ensemble, Proc. Natl. Acad. Sci. U. S. A 112 (2015) E5142–E5149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Zandarashvili L, Vuzman D, Esadze A, Takayama Y, Sahu D, Levy Y, Iwahara J, Asymmetrical roles of zinc fingers in dynamic DNA-scanning process by the inducible transcription factor Egr-1, Proc. Natl. Acad. Sci. U. S. A 109 (2012) E1724–E1732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Yu B, Pettitt BM, Iwahara J, Dynamics of ionic interactions at protein–nucleic acid interfaces, Acc. Chem. Res 53 (2020) 1802–1810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Redner S, A Guide to First-Passage Processes, Cambridge University Press, Cambridge, 2001. [Google Scholar]
- [72].Valouev A, Johnson SM, Boyd SD, Smith CL, Fire AZ, Sidow A, Determinants of nucleosome organization in primary human cells, Nature 474 (2011) 516–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Hu T, Shklovskii BI, How a protein searches for its specific site on DNA: the role of intersegment transfer, Phys. Rev. E Stat. Nonlinear Soft Matter Phys 76 (2007), 051909. [DOI] [PubMed] [Google Scholar]
- [74].Schmidt HG, Sewitz S, Andrews SS, Lipkow K, An integrated model of transcription factor diffusion shows the importance of intersegmental transfer and quaternary protein structure for target site finding, PLoS One 9 (2014), e108575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Sheinman M, Kafri Y, The effects of intersegmental transfers on target location by proteins, Phys. Biol 6 (2009), 016003. [DOI] [PubMed] [Google Scholar]
- [76].Doucleff M, Clore GM, Global jumping and domain-specific intersegment transfer between DNA cognate sites of the multidomain transcription factor Oct-1, Proc. Natl. Acad. Sci. U. S. A 105 (2008) 13871–13876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Fried MG, Crothers DM, Kinetics and mechanism in the reaction of gene regulatory proteins with DNA, J. Mol. Biol 172 (1984) 263–282. [DOI] [PubMed] [Google Scholar]
- [78].Iwahara J, Clore GM, Direct observation of enhanced translocation of a homeodomain between DNA cognate sites by NMR exchange spectroscopy, J. Am. Chem. Soc 128 (2006) 404–405. [DOI] [PubMed] [Google Scholar]
- [79].Lieberman BA, Nordeen SK, DNA intersegment transfer, how steroid receptors search for a target site, J. Biol. Chem 272 (1997) 1061–1068. [DOI] [PubMed] [Google Scholar]
- [80].Sidorova NY, Scott T, Rau DC, DNA concentration-dependent dissociation of EcoRI: direct transfer or reaction during hopping, Biophys. J 104 (2013) 1296–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Takayama Y, Clore GM, Interplay between minor and major groove-binding transcription factors Sox2 and Oct1 in translocation on DNA studied by paramagnetic and diamagnetic NMR, J. Biol. Chem 287 (2012) 14349–14363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Lin SY, Riggs AD, Lac repressor binding to non-operator DNA: detailed studies and a comparison of eequilibrium and rate competition methods, J. Mol. Biol 72 (1972) 671–690. [DOI] [PubMed] [Google Scholar]
- [83].Bujalowski W, Overman LB, Lohman TM, Binding mode transitions of Escherichia coli single strand binding protein-single-stranded DNA complexes. Cation, anion, pH, and binding density effects, J. Biol. Chem 263 (1988) 4629–4640. [PubMed] [Google Scholar]
- [84].Kawasaki M, Hosoe Y, Kamatari YO, Oda M, Naïve balance between structural stability and DNA-binding ability of c-Myb R2R3 under physiological ionic conditions, Biophys. Chem 258 (2020) 106319. [DOI] [PubMed] [Google Scholar]
- [85].Privalov PL, Dragan AI, Crane-Robinson C, Interpreting protein/DNA interactions: distinguishing specific from non-specific and electrostatic from nonelectrostatic components, Nucleic Acids Res 39 (2011) 2483–2491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Record MT, Anderson CF, Lohman TM, Thermodynamic analysis of ion effects on binding and conformational equilibria of proteins and nucleic-acids: roles of ion association or release, screening, and ion effects on water activity, Q. Rev. Biophys 11 (1978) 103–178. [DOI] [PubMed] [Google Scholar]
- [87].Record MT Jr., de Haseth PL, Lohman TM, Interpretation of monovalent and divalent cation effects on the lac repressor-operator interaction, Biochemistry 16 (1977) 4791–4796. [DOI] [PubMed] [Google Scholar]
- [88].Vo T, Albrecht AV, Wilson WD, Poon GMK, Quantifying length-dependent DNA end-binding by nucleoproteins, Biophys. Chem 251 (2019) 106177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Lohman TM, DeHaseth PL, Record MT Jr., Analysis of ion concentration effects of the kinetics of protein-nucleic acid interactions. Application to lac repressor-operator interactions, Biophys. Chem 8 (1978) 281–294. [DOI] [PubMed] [Google Scholar]
- [90].Schreiber G, Fersht AR, Rapid, electrostatically assisted association of proteins, Nat. Struct. Biol 3 (1996) 427–431. [DOI] [PubMed] [Google Scholar]
- [91].Vijayakumar M, Wong KY, Schreiber G, Fersht AR, Szabo A, Zhou HX, Electrostatic enhancement of diffusion-controlled protein-protein association: comparison of theory and experiment on barnase and barstar, J. Mol. Biol 278 (1998) 1015–1024. [DOI] [PubMed] [Google Scholar]
- [92].Subekti DRG, Murata A, Itoh Y, Takahashi S, Kamagata K, Transient binding and jumping dynamics of p53 along DNA revealed by sub-millisecond resolved single-molecule fluorescence tracking, Sci. Rep 10 (2020) 13697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Cavanagh J, Fairbrother JW, Palmer GA, Rance M, Skelton JN, Protein NMR Spectroscopy: Principles and Practice, Second ed., Elsevier Academic Press, 2007. [Google Scholar]
- [94].Arthanari H, Takeuchi K, Dubey A, Wagner G, Emerging solution NMR methods to illuminate the structural and dynamic properties of proteins, Curr. Opin. Struct. Biol 58 (2019) 294–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Anderson KM, Esadze A, Manoharan M, Brüschweiler R, Gorenstein DG, Iwahara J, Direct observation of the ion-pair dynamics at a protein-DNA Interface by NMR spectroscopy, J. Am. Chem. Soc 135 (2013) 3613–3619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Chen CY, Esadze A, Zandarashvili L, Nguyen D, Pettitt BM, Iwahara J, Dynamic equilibria of short-range electrostatic interactions at molecular interfaces of protein-DNA complexes, J. Phys. Chem. Lett 6 (2015) 2733–2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Esadze A, Chen C, Zandarashvili L, Roy S, Pettitt BM, Iwahara J, Changes in conformational dynamics of basic side chains upon protein-DNA association, Nucleic Acids Res 44 (2016) 6961–6970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Nguyen D, Hoffpauir ZA, Iwahara J, Internal motions of basic side chains of the Antennapedia Homeodomain in the free and DNA-bound states, Biochemistry 56 (2017) 5866–5869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Sahu D, Iwahara J, Discrete-state kinetics model for NMR-based analysis of protein translocation on DNA at equilibrium, J. Phys. Chem. B 121 (2017) 9548–9556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Allerhand A, Thiele E, Analysis of Carr-Purcell spin-Echo NMR experiments on multiple-spin systems. II. The effect of chemical exchange, J. Chem. Phys 45 (1966) 902–916. [Google Scholar]
- [101].McConnell HM, Reaction rates by nuclear magnetic resonance, J. Chem. Phys 28 (1958) 430–431. [Google Scholar]
- [102].Koss H, Rance M, Palmer AG 3rd, General expressions for R1rho relaxation for N-site chemical exchange and the special case of linear chains, J. Magn. Reson 274 (2017) 36–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Ueda T, Takeuchi K, Nishida N, Stampoulis P, Kofuku Y, Osawa M, Shimada I, Cross-saturation and transferred cross-saturation experiments, Q. Rev. Biophys 47 (2014) 143–187. [DOI] [PubMed] [Google Scholar]
- [104].Clore GM, Iwahara J, Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules and their complexes, Chem. Rev 109 (2009) 4108–4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Blainey PC, van Oijen AM, Banerjee A, Verdine GL, Xie XS, A base-excision DNA-repair protein finds intrahelical lesion bases by fast sliding in contact with DNA, Proc. Natl. Acad. Sci. U. S. A 103 (2006) 5752–5757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Leven I, Levy Y, Quantifying the two-state facilitated diffusion model of protein-DNA interactions, Nucleic Acids Res 47 (2019) 5530–5538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Kemme CA, Esadze A, Iwahara J, Influence of quasi-specific sites on kinetics of target DNA search by a sequence-specific DNA-binding protein, Biochemistry 54 (2015) 6684–6691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Kemme CA, Marquez R, Luu RH, Iwahara J, Potential role of DNA methylation as a facilitator of target search processes for transcription factors through interplay with methyl-CpG-binding proteins, Nucleic Acids Res 45 (2017) 7751–7759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [109].Pulkkinen O, Metzler R, Distance matters: the impact of gene proximity in bacterial gene regulation, Phys. Rev. Lett 110 (2013) 198101. [DOI] [PubMed] [Google Scholar]
- [110].Wunderlich Z, Mirny LA, Spatial effects on the speed and reliability of protein-DNA search, Nucleic Acids Res 36 (2008) 3570–3578. [DOI] [PMC free article] [PubMed] [Google Scholar]


