When CAT is not an Option: Complementary Methods of Test Abbreviation for Neurocognitive Batteries

Abstract

Introduction:

In the era of large-scale population genetic studies, there is an obvious need for maximally efficient measurement of neuropsychiatric phenomena. A proven method—computerized adaptive testing (CAT)—is not feasible for all types of tests, necessitating alternative methods of increasing test efficiency.

Methods:

We compared (and combined) two methods for abbreviating rapid test forms using two tests unamenable to CAT (a Continuous Performance Test [CPT] and an n-back test [NBACK]). N=9,498 participants (mean age 14.2 years; 52% female) were administered the tests, and abbreviation was accomplished using methods that answer two complementary questions: 1) what happens to standard error of measurement as items are removed, and 2) what happens to scores’ correlations with validity criteria as items are removed. The first question was investigated using quasi-CAT simulation, while the second was investigated using bootstrapped confidence intervals around full-form-short-form comparisons.

Results:

Results for the two methods overlapped, suggesting that the CPT could be abbreviated to 102 stimuli (57% of original) and NBACK could be abbreviated to 78 stimuli (87% of original) with the maximum acceptable loss of precision and minimum acceptable relationships with validity criteria.

Conclusions:

This combination of two test-abbreviation methods (a novel quasi-CAT simulation method and successive item removal) show promise for use in other types of tests, and the divergent results for the CPT and NBACK demonstrate the methods’ ability to detect when a test should not be shortened at all (or only minimally). We recommend the two methods be used in combination, because they emphasize complementary aspects of measurement quality: precision (reliability) and validity.

Today, it is possible to learn someone’s entire genome from a single blood draw (or even less invasively), allowing collection of genetic data with almost no cost to the study participant. Thus, one of the biggest roadblocks to large-scale genomic research is not acquiring the genetic material as such, but rather the time it takes to measure everything else, including psychological traits (e.g., cognitive ability, psychopathology, etc.), demographic information, medical histories, general biometrics (blood pressure, height, weight, etc.), biological samples (hair, stool, blood, saliva, etc.), and perhaps even neuroimaging protocols. Taking cognition as an example, even the most well-established neurocognitive test batteries used in large-scale genomic studies (e.g., Penn Computerized Neurocognitive Battery, Cambridge Neuropsychological Test Automated Battery, etc.) (Gur, R. C. et al., 2001; Gur, Ruben C. et al., 2010; Robbins et al., 1994) take about one hour to complete. Combined with the need to collect demographics, clinical symptoms, neuroimaging, and countless other variables on a large number of participants (~10,000+), one hour is often too long. The result is usually a compromise whereby the researchers choose a more limited number of tests, sacrificing breadth of measurement to fit within the time constraints.

The pressure to minimize test/scale administration time is felt especially by research groups who administer collections of tests—test batteries—on a regular basis. If there is a good method for decreasing administration time, it could be applied to all tests in a battery, cumulatively resulting in large time savings. One method to decrease administration time is computerized adaptive testing (CAT) (Chang, 2015; Wainer, 2000), which incorporates methods from item response theory (IRT) (Embretson & Reise, 2009) to build item banks and administer only the most informative items to examinees. IRT allows characterization of individual test items (e.g. their difficulty), which enables a real-time testing algorithm to determine which item from an item bank will provide the most information about an examinee, given the examinee’s current estimated trait level. For example, if nothing is known about the examinee, his/her ability could be assumed to be average, and the algorithm would choose the best item for someone of average ability. Once that person responds to the item, his/her trait can be estimated based on that one response, and the next item administered will be the one that is optimal at the newly estimated trait level. This targeted item administration means fewer items must be administered to achieve any given level of measurement error than if the items were administered sequentially. This method has proven useful in saving administration time and maximizing precision¹ (Gibbons et al., 2012; Mizumoto et al., 2019; Yudien et al., 2019), especially since building CATs has become more cost effective (e.g. Scalise & Allen, 2015).

However, computerized adaptive testing is not appropriate for all types of tests. For example, a test might require someone to freely recall words from a list of words just read aloud by a proctor. In this case, the test is just one item scored as a count (“Recall as many words as you can”), which is not appropriate for CAT. Another example would be a test that is not self-paced. For example, continuous performance tests (CPTs) (Riccio, Lowe, & Reynolds, 2004) and n-back tests (requiring participants to remember stimuli presented n spaces “back” in a display sequence; Owen, McMillan, Laird, & Bullmore, 2005) both present stimuli rapidly and continue presenting stimuli regardless of whether the participant responds. This presentation of stimuli independent of examinee behavior is obviously not amenable to CAT. Thus, research groups hoping to create an abbreviated version of an entire battery (collection of tests) can expect some of their tests to be unamenable to CAT. Although there are IRT models designed for signal-detection-like tests (Thomas et al., 2018), these models have not yet been linked to computerized adaptive testing or used for test abbreviation as such. An obvious question is, if we are dealing with a test for which “CAT is not an option”, why simulate CAT administrations of it (which we do below)? The answer is that CAT would be good for these tests except for their speed (~1 second or less per stimulus), which is an unalterable characteristic of the tests. However, simply because CAT is not feasible does not mean item parameters cannot be estimated and used in informative simulations.

The creation of short/abbreviated test forms has been a goal of psychometricians for decades, and there are several well-established methods for doing so. These include selecting items that correlate most strongly with the full scale (e.g. Francis et al., 1992; Geil, 1945; Straus & Douglas, 2004), selecting items that most improve relationships with external validity criteria (Bae & Cho, 2004), removing items that demonstrate bias (Bann et al., 2012), selecting items that have high factor loadings (Bagley & Mallick, 1978; Joseph et al., 2004), selecting items that have a desirable² spread of difficulty parameters (Calamia et al., 2011; Cole et al., 2004), selecting items based on expert human input rather than quantitative analysis (e.g. Harris, 1975; Whitman et al., 2013), and, quite often, combinations of the above (Manos et al., 2011; Peters et al., 2012; Sturm et al., 2017). The two combined methods used in the present study (described below) most closely match the first, second, fourth, and fifth approaches mentioned above: correlation with full form, correlation with validity criteria, high factor loadings (IRT discrimination parameters), and desirable spread of difficulty parameters. This approach most closely matches those described by Reise and Henson (2000), Hol et al. (2007), and Choi et al. (2010). This combined approach is unique not in its coverage of so many criteria (a common approach), but in its combined treatment of item discrimination and difficulty (via CAT simulation; see below). Some existing methods account for item difficulty, but these tend to either ignore item discrimination (Calamia et al., 2011; Hibbard et al., 2005) or subjectively choose items that span the difficulty continuum without tying those parameters to any other criteria or approaches used (e.g. Colledani et al., 2019).

The aim of the present study was to use two methods—one based on score validity (first and second approaches in above paragraph) and the other based on standard error of measurement (fourth and fifth in above paragraph)—to create optimal short-forms for two rapid tests on the Penn Computerized Neurocognitive Battery, the Penn Continuous Performance Test (CPT) and NBACK test. We used data from a large neurodevelopmental cohort to compare these two methods and examine their utility to create more economical neurocognitive assessments when the tests are not amenable to CAT.

Methods

Participants

Participants were part of the Philadelphia Neurodevelopmental Cohort (PNC) (Calkins et al., 2014; Calkins et al., 2015; Moore, T. M. et al., 2016; Satterthwaite et al., 2014; Satterthwaite et al., 2016), which included youth (age 8–21) recruited through an NIMH-funded Grand Opportunity study characterizing clinical and neurobehavioral phenotypes in a genotyped, prospectively accrued community cohort. All study participants previously consented for genomic studies when they presented for pediatric services within the Children’s Hospital of Philadelphia (CHOP) health care network. At that time, they provided a blood sample for genetic studies, authorized access to Electronic Medical Records, and gave written informed consent/assent to be recontacted for future studies. Of the 50,540 genotyped subjects, 18,344 met criteria necessary to be included in the study (listed below) and were randomly selected, with stratification for age, sex, and ethnicity. A total of 9,498 enrolled in the study between 11/2009 –12/2011 and were included in this analysis.

The sample included children in stable health, proficient in English, and physically and cognitively capable of participating in an interview and performing the computerized neurocognitive testing. Youths with disorders that impaired motility or cognition (e.g., significant paresis or palsy, intellectual disability) were excluded. Notably, participants were not recruited from psychiatric clinics, and the sample is not enriched for individuals seeking psychiatric help. Participants provided informed consent/assent after receiving a complete description of the study and the Institutional Review Boards at Penn and CHOP approved the protocol. Table 1 shows the demographic characteristics of the sample, as well as rates of common mental disorders.

Table 1.

Sample Demographic and Basic Lifetime Clinical Information.

Variable	Mean (SD)
Age, months (SD)	170.3 (43.9)
Prop. Female	0.52
Prop. African American	0.33
Prop. Caucasian	0.56
Prop. Hispanic	0.07
Avg. Parent Edu., yrs. (SD)	14.3 (2.3)
Prop. with Depression	0.12
Prop. with GAD	0.03
Prop. with OCD	0.03
Prop. with Psychosis	0.04
Prop. with ADD	0.18

Note. Prop = proportion; yrs = years; SD = standard deviation; GAD = generalized anxiety disorder; OCD = obsessive-compulsive disorder; ADD = attention deficit disorder.

Measures

Continuous Performance Test.

The Penn CPT (Gur et al., 2010) measures vigilance and visual attention independent of working memory or perceptual factors. Vertical and horizontal lines in 7-segment displays appear on the screen at a rate of one second each. The participant is instructed to press the spacebar when the lines are configured as complete numbers (first half of task) or complete letters (second half of task) and to not press when the lines are not complete numbers or letters, respectively. Each half lasts 1.5 minutes, and during each one-second response window, the stimulus is presented for only 300 milliseconds (leaving 700 milliseconds of blank screen). If a stimulus is shown and the examinee behaves correctly (press in the case of targets, don’t press in the case of foils), that “item” is a correct response. For the validity-centered method (successive item removal; see below), the key outcome was d-prime, defined as the z-transform of the hit rate (proportion of targets for which the participant correctly pressed the space bar) minus the z-transform of the false alarm rate (proportion of foils for which the participant incorrectly pressed the space bar). For example, if someone correctly pressed the space bar on 99% of the targets and incorrectly pressed the space bar on 20% of the foils, his/her d-prime would be Z(0.99) – Z(0.20) = 2.33 – (−0.84) = 2.33 + 0.84 = 3.17. For the precision-centered method (CAT simulation), the key piece of information is the standard error of the score, which is obtained by traditional expectation-maximization (Bock & Aitkin, 1981) latent trait scoring.

n-Back.

The Penn Letter n-Back Test (NBACK) (Ragland et al., 2002) measures working memory, the ability to maintain and update goal-related information. Participants attend to a continual series of letters that flash on the screen (one at a time) and press the spacebar according to three different rules (0-back, 1-back, and 2-back). During the 0-back condition, the participant is instructed to simply respond to a currently present target (“X”). During the 1-back condition, the participant is instructed to press the spacebar when the letter on the screen is the same as the previous letter. During the 2-back condition, the participant is instructed to press the spacebar when the letter on the screen is the same as the letter before the previous letter (i.e., 2 letters back). In all trials, the inter-stimulus interval (ISI) is 2.5 seconds, and the stimuli (letters) are presented for 0.5 seconds each. The participant practices all three principles before testing. If a stimulus is shown and the examinee behaves correctly (press in the case of targets, don’t press in the case of foils), that “item” is a correct response. Scoring of the NBACK was the same as the scoring of the CPT, where the NBACK also has clear targets and foils.

Clinical Assessment.

An in-person interview based on the structured Schedule for Affective Disorders and Schizophrenia for School-Age Children (GOASSESS) evaluated lifetime history of clinical symptoms (Calkins et al., 2014; Calkins et al., 2015) across major psychopathology domains. Participants were assessed dimensionally and categorically and had to have significant symptoms associated with distress that affected functioning to score high on specific domains of mood/anxiety, fear, externalizing behavior, and psychosis. The procedures used for obtaining the dimensional clinical scores are described in Shanmugan et al. (2016, Supplement) and Moore et al. (2019)³. Briefly, item-factor analysis was performed on 112 clinical symptoms extracting four theoretical factors—three described by Krueger (1999), plus psychosis—where those factors were allowed to correlate. Of the four dimensional factors (Anxious-Misery, Fear, Externalizing, and Psychosis), only Psychosis was used here due to its unambiguous and well-established associations with cognition. The clinical assessment also included the Children’s Global Assessment Scale (CGAS) (Shaffer et al., 1983).

Approximation of Socioeconomic Status.

Socioeconomic status was approximated using neighborhood-level characteristics obtained by geocoding participants’ addresses to census and crime data in the Philadelphia area. Neighborhood characteristics were measured at the block-group level and included median family income, percent of residents who are married, percent of real estate that is vacant, and several others; see Moore et al. (2016) for further details.

Analysis

The first method of test abbreviation (Simulated Successive Item-Removal; SSIR) involved simulating test administrations as successive numbers of items were removed and examining the effect of item-removal on the criterion validity of total scores. The second method (CAT Simulation Method) involved calibrating items using IRT and simulating the number of stimuli needed to achieve various levels of precision (indicated by standard error of measurement).

Simulated Successive Item Removal (SSIR) Method.

The SSIR method focuses on what happens when test items/stimuli are removed. Specifically, what happens to the relationship between test scores and important criteria (e.g., ADHD severity) when successive items are removed? For example, if we find that scores on a 100-item test correlate −0.25 with ADHD severity, we want to know what happens to that −0.25 correlation when 1 item is removed (i.e., only 99 items are administered) compared to the full test version. Items are successively removed until the point (e.g., going from 82 items to 81 items) where removal of one additional item decreases the magnitude of the −0.25 correlation beyond what would be considered acceptable (see below for description of unacceptable levels). This point—where the score-criterion relationship is deflated to an unacceptable level—is the point at which the test is “too short.” Using this information, a short form can be constructed that comprises just enough items to achieve an acceptable relationship with ADHD score (indicating acceptable measurement precision).

The Simulated Successive Item Removal method for the CPT proceeded as follows:

1. Item order was scrambled (as in real administrations of the CPT), and d-prime was calculated for the full test plus each successive short form (e.g., d-prime after the last item is removed, d-prime after the last two items are removed, etc.), for a total of 89 short-form scores.

2. Bivariate relationships were calculated between the full-form d-prime and each of the short-form’s d-prime (full-short correlations).

3. Bivariate relationships were calculated between the full-form d-prime and the following validity criteria: age, global assessment of functioning (CGAS), socioeconomic status, psychosis (severity) score, and total score on a working memory test (NBACK).

4. The same bivariate relationships above were calculated for all short-form scores.

5. The above four steps were repeated 1,000 times to obtain a distribution of each bivariate relationship.

6. For each short-form (e.g., one item removed, two items removed, etc.), the relationships with validity criteria were compared to the same relationships using the full test by taking the ratio of the correlations. A ratio of 1.0 would mean the full-form and short-forms have exactly the same correlation with the validity criterion, and deviations (up or down) from 1.0 would suggest a difference between the correlations. Consistent with the common (albeit arbitrary) 0.90 cutoff (e.g. Baker et al., 2019; Dunkel et al., 2005; Jamison et al., 2007; Ward et al., 2018) for what is considered an acceptable correlation of a short-form with its corresponding original form (i.e. a 10% lower correlation), we used 10% as the maximum acceptable difference between short- and long-form criterion correlations. That is, if 0.90 or 1.10 fell within two standard deviations of the ratio of correlations between the full test and a validity criterion, that short form was considered too short. For each short form and for each validity criterion (completely crossed), we obtained a distribution of ratios of correlations, and if the ratio was not between > 0.90 and < 1.10 with 95% confidence, the short-form was considered an insufficient substitute for the full form.

7. For each short-form (e.g., one item removed, two items removed, etc.), the distribution of correlations with the full-form (short-full correlations) was examined. If 0.90 (the minimum acceptable) was contained within two SDs of the distribution, the short-form was considered too short.

For the NBACK, the steps described were the same, with two exceptions. Item order for a given form is important for the NBACK because the correctness of a response depends on previous stimuli. Therefore, the item order was preserved, and variation across simulations was produced by random row sampling (random sampling of exactly half of the response vectors). In addition, correlations with the CPT were used as validity criteria in bivariate relationships.

CAT Simulation Method.

Introduced⁴ by Moore et al. (2015) and building on the work of Reise and Henson (2000) and Choi et al (2010), the CAT-simulation method of short-form creation used here has shown promise in both cognitive (Bezdicek et al., 2018; Roalf et al., 2016) and non-cognitive (Lawson, Moore, Okamura, Becker-Haimes, & Beidas, 2020; Saine et al., 2020) assessments. This method uses IRT, which is the measurement theory underlying and facilitating CAT. Details of IRT (Embretson & Reise, 2009) and CAT (Wainer, 2000) are beyond the present scope. Principally, IRT takes the focus away from evaluating psychometric properties of the test as a whole (e.g. global reliability) and instead focuses on characterizing each individual item (e.g., difficulty of the item, how well the item can discriminate between test-takers with high versus low scores). These item characteristics, in combination, determine how much information an item provides about a person at any given trait level. Further details of IRT are provided in the Supplement, but a key point here is that IRT is the basis for Computerized Adaptive Testing (CAT). The item characteristics mentioned above can be estimated for multiple items (e.g., all items on a test), which composes an “item bank”, the group of items from which a CAT algorithm can choose if the test is administered adaptively. Establishing an item bank also allows one to simulate what would happen if a test were taken adaptively (as a CAT), and this simulation is the basis of the CAT-simulation method used here. After simulating CAT administrations, one can look post hoc at how often each item was administered; the items administered most often can be considered the “best” items and should be included on the short form. Here, we use a variation of the CAT-simulation method in which we determined the number of items necessary to achieve a predetermined precision goal (e.g., SEM< 0.30), rather than selecting the specific items providing the most information (on average). That is, whereas the CAT-simulation method of creating a short-form usually involves selecting items based on exposure (frequency of administrations), in this case that exposure is fixed (random exposure in the case of the CPT, and sequential exposure in the case of the N-BACK). Indeed, the only “CAT” characteristic of the simulated tests in this case is that they have a standard-error based termination criterion, which depends on IRT item parameter estimates.

In summary, the CAT-simulation method finds items that have an optimal⁵ combination of discrimination and difficulty—high discrimination, with difficulty within a reasonable range. Discrimination measures the differential capability of an item, such that a high discrimination value indicates that an item provides a high capability to differentiate subjects. High discrimination is desirable because it indicates that an item can distinguish among more fine-grained levels of the trait than if it had low discrimination. Having difficulty parameters within a reasonable range avoids items answered correctly/incorrectly by almost everyone (too easy or too difficult). Consider two hypothetical items: item #1 has a discrimination of 1.0 (normal) and difficulty of 0.0 (average); item #2 has a discrimination of 2.0 (high) and difficulty of 2.0 (high). So, item #2 has better discrimination than item #1, but item #1 has better difficulty (within typical range). So how do we determine which item should be selected for a short-form? The obvious problem is that researchers will usually not be able to “eyeball” a table of item parameter estimates and determine which combination is optimal, and thus a practical way is to simulate what would happen if a computer algorithm (CAT) were selecting these items based on information, which is inversely related to standard error of measurement. If the algorithm selects an item at any given time, it means that item was indeed the absolute best of all options in the item bank, so an item that is selected often is a good item. It is worth reiterating that, as with the use of the word “optimal” above, the assertion that “an item that is selected often is a good item” here depends on some assumptions. For example, in real-world CAT applications, it is sometimes advantageous to limit exposure of some items and promote exposure of others—i.e. to prevent item under- or overexposure (Eggen, 2001; Revuelta & Ponsoda, 1998).

The CAT-simulation method proceeded as follows:

1. Dimensionality of the test was assessed to determine whether a unidimensional IRT model can be used. Specifically, the ratio of first to second eigenvalues was examined to determine whether there was any possibility of unidimensionality; if so (e.g. eigenvalue ratio > 3.0), follow-up tests would have been performed (parallel analysis and fit of the unidimensional model) to confirm the unidimensionality (see Slocum-Gori & Zumbo, 2011). If multidimensionality was detected—i.e., a unidimensional IRT model was inappropriate—the optimal number of factors was determined in preparation for a multidimensional model. The planned tests for the number of factors included the minimum average partial method (Velicer, 1976), scree test (Cattell, 1966), and parallel analysis with Glorfeld correction (using 99^th percentile) (Glorfeld, 1995). However, in the present case involving targets and foils, both theory (targets vs. foils) and the clean 2-factor solution (all targets on one factor and all foils on another factor) suggested 2-factors.

2. In the present data, multidimensionality was detected (ratios of 1^st:2^nd eigenvalues = 1.94, 1.17, 1.94, 2.11, and 2.51 for the CPT Numbers, CPT Letters, NBACK 0-back, NBACK 1-back, and NBACK 2-back, respectively), and item responses were therefore calibrated using a bifactor (Reise, 2012) IRT model, where each item loaded on its specific factor (targets or foils) and on a general factor comprising all items. Parameter estimates for the general factor are used here, and intercepts were transformed to conventional IRT difficulty parameters using Equation 9 in Cai (2010).

3. The parameter estimates for the general factor obtained from #2 above were input to Firestar (Choi, 2009), which simulates test administrations. Normally, CAT simulation follows some versions of the typical CAT procedure: select item based on maximum information at current trait estimate, re-estimate ability based on response, select best item based on new ability estimate, etc. Here, however, the simulated test administrations proceeded non-adaptively—i.e., item-selection was random for the CPT and sequential for the NBACK—and the administrations stopped after a predetermined number of items (depending on the simulation condition). Unlike in Moore et al. (2015), where the goal was to find which items were selected most often during the simulations, the goal here was to determine the standard error of measurement we could expect (on average) after administration of x items. It is all part of the same CAT-simulation procedure, and the focus on test precision here (rather than selecting specific items) is due to the fact that the stimuli are (by design) administered randomly in the final test. We are trying to minimize the number administered randomly.

Age Associations.

The sample used here had a fairly wide age range (8 – 21 years), and most importantly, this age range is one of rapid and complex neurodevelopment. Theoretically, the only effect of age is to improve or worsen performance (in this sample, improve), which would have no effect on the metrics used here (measurement precision and correlations with criteria). However, age could have other effects as well—e.g. the relationship between cognitive performance and a given criterion might be weaker/stronger in older participants than in younger participants. This age effect would affect our outcome metrics. For thoroughness, we therefore performed the SSIR method described above after splitting the sample into younger (8 – 14 years) and older (15 – 21 years) groups.

Results

SSIR Method

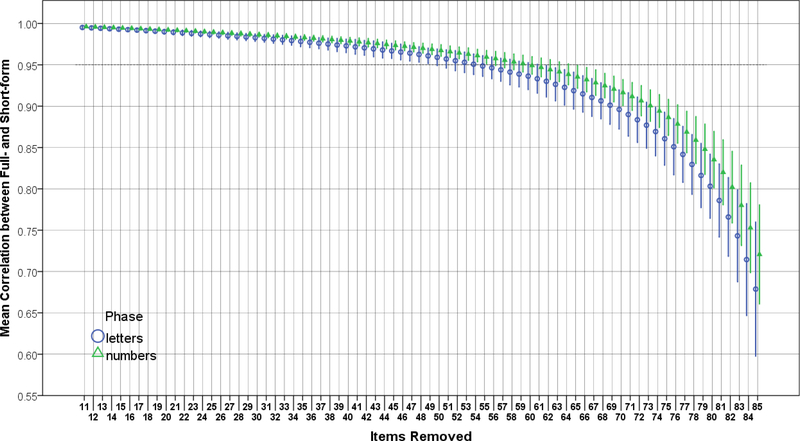
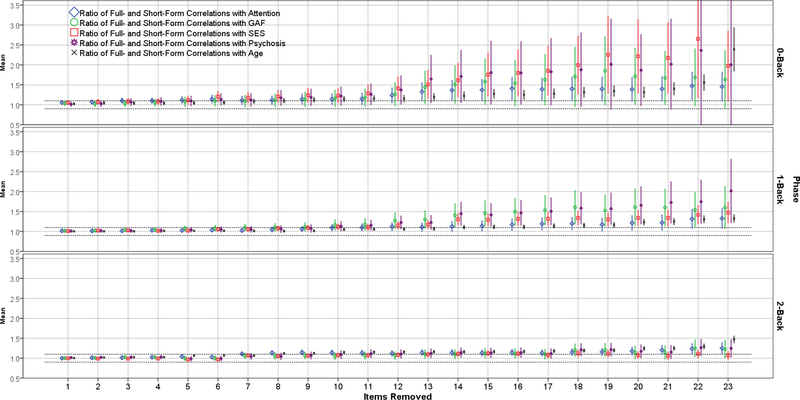
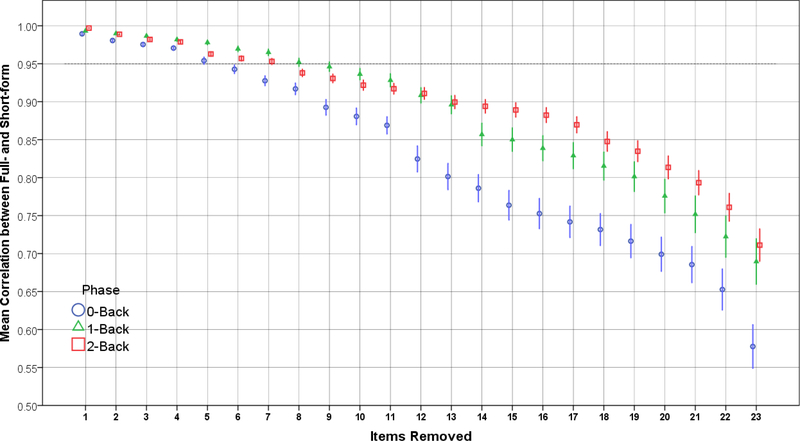
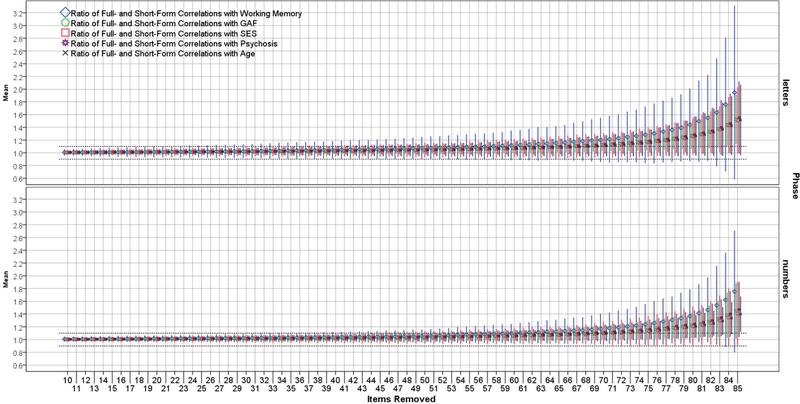
Figures 1–4 show the results of the SSIR method for the CPT and NBACK. Figures 1 and 2 show changes to correlations between full- and short-forms as items are removed. For the CPT (Figure 1), the correlation stays fairly steady until >55 items are removed, at which point the correlation plummets. Thus, the optimal number of items (point where the correlation 95% CI first includes 0.95) for the CPT letters and numbers, respectively, were 41 (46% of original) and 35 (39%). For the NBACK (Figure 2), there is a more uniform decline in full-short correlations as items are removed, such that the short forms quickly become too short as items are removed. The optimal number of items for the NBACK 0-back, 1-back, and 2-back, respectively, were 26 (87% of original), 23 (77%), and 24 (80%). Figures 3 and 4 show what happens to short-form correlations with validity criteria (compared to full-form) as items are removed. For both tests, the ratio of full-form to short-form correlations increases as items are removed. That is, the full form shows stronger correlations with validity criteria, and this difference (reflected in a ratio) increases as items are removed. The focal points on Figures 3 and 4 are the places where the 2SD error bars touch the dotted lines at 1.10 and 0.90, because these points indicate the limit of shortening for the test.

Figure 1.

Mean Correlation between Short-Form and Full-Form Versions of the CPT, by Phase.

Figure 4.

Ratios of Criterion Validity Correlations Using the Full-Form and Short-Forms of the NBACK, by Phase.

Figure 2.

Mean Correlation between Short-Form and Full-Form Versions of the NBACK, by Phase.

Figure 3.

Ratios of Criterion Validity Correlations Using the Full-Form and Short-Forms of the CPT, by Phase.

Table 2 shows the results of these analyses—i.e., the recommended number of items for a short-form—corresponding to Figures 1–4. Two overall patterns are apparent. First, the suggested CPT length (mean across phases = 53% of original) is much shorter than the suggested NBACK length (mean 83% of original). Second, the suggested test length does not differ substantially across validity criteria. The lowest average suggested length (64.4%) comes from analyses using Age, while the highest average suggested length (78.2%) comes from analyses using the convergent validity criterion (working memory predicting attention, and vice versa). Based on the results in Table 2 and using the 10% rule described in Methods (point where CI of correlation ratio includes 0.90 or 1.10), we suggest that the minimum acceptable lengths of CPT letters phase, CPT numbers phase, NBACK 0-back, NBACK 1-back, and NBACK 2-back, are 51 (57%), 43 (48%), 28 (93%), 23 (77%), and 24 (80%) items, respectively.

Table 2.

Number of Items Necessary to Achieve Satisfactory Levels of Criterion Validity (Relative to Full-Form) and Short-Full Correlation.

Criterion Validity
Test & Phase	Convergent	CGAS	SES	Psychosis	Age	Full-Short Correlation
CPT letters	69 (77%)	42 (47%)	55 (61%)	48 (53%)	53 (59%)	41 (46%)
CPT numbers	55 (61%)	40 (44%)	48 (53%)	43 (48%)	39 (43%)	35 (39%)
NBACK 0-back	29 (97%)	28 (93%)	29 (97%)	28 (93%)	25 (83%)	26 (87%)
NBACK 1-back	23 (77%)	27 (90%)	24 (80%)	25 (83%)	18 (60%)	23 (77%)
NBACK 2-back	24 (80%)	24 (80%)	24 (80%)	24 (80%)	23 (77%)	24 (80%)

Note. CGAS = Children’s Global Assessment Scale; SES = socio-economic status; CPT = Continuous Performance Task.

Age Associations.

Supplementary Figure S2 shows the same analyses as presented in Figure 3 but split by age. Two points are worth noting. First, the functions for older and younger participants are mostly overlapping until the midpoint (~40 items removed). However—and this is the second point—there does appear to be some consistent separation between the older and younger participants in the Letters portion (blue curve slightly above red curve). Supplementary Figure S3 shows the same analyses as above, but for the NBACK. As for the CPT, there is very little separation between the older and younger groups (red and blue curves) until the midpoint (~11 items removed). Notably, some of the differences become quite large after this midpoint. However, unlike for the CPT, there is no consistent difference between the curves—i.e. red appears above blue about as often as the opposite.

CAT Simulation Method

Supplementary Tables S1 and S2 show the item parameter estimates (normal metric; D = 1.702) for the NBACK (mean discrimination = 0.80; mean difficulty = −1.96) and CPT (mean discrimination = 0.48; mean difficulty = −1.22). Of note for the NBACK, discrimination parameters were substantially higher for the targets (mean = 1.35) than for the foils (mean = 0.53), which was also true for the difficulty parameters (mean for targets = −1.52; mean for foils = −2.18). Differences for the CPT were similar but subtler (mean target & foil discrimination = 0.55 & 0.44; mean target & foil difficulty = −1.07 & −1.29). One noticeable difference between the parameter estimates of the NBACK and CPT is that the former appear to depend on a stimulus’ position in the sequence (i.e. which stimulus was displayed immediately before) while the latter appear to depend more on characteristics of the stimulus itself. The stimuli in Table S2 are “blocked” into sets of 5, such that the first five rows are the same stimulus presented at successively later (though random) times; for example, items 1, 2, 3, 4, and 5 are the same stimulus and could be administered, for example, in random positions 3, 10, 55, 56, 81, and 90, respectively. To take an extreme example, items 121 through 125 all have near-zero discrimination parameters, indicating that this specific stimulus is a poor indicator of the ability to correctly reject the non-target. (Indeed, the stimulus is a non-letter that looks very much like a letter.) When this stimulus was administered during the simulations, it left the standard error of measurement essentially unchanged, meaning it is a “dead weight” item that takes up time but adds nothing⁶.

Table 3 shows the item exposure results using the CAT-simulation method of test abbreviation. The numbers of items necessary to achieve six levels of precision (from very high precision to minimum acceptable) are shown for each test and phase. Taking the fourth row (Max. SEM = 0.45) as an example, the second column gives the equivalent test-level reliability⁷ (0.80) followed by (going from left to right) the recommended lengths of the CPT Numbers phase (can be shortened to 69% of original), CPT letters phase (76% of original), NBACK 0-back (97%), NBACK 1-back (92%), and NBACK 2-back (92%). Across the six levels of precision, going from extreme to minimum acceptable (top to bottom of Table 3), the mean recommended short-form lengths were 98%, 95%, 90%, 85%, 80%, and 73% of the original test, a relatively linear decrease. Consistent with the results from the SSIR method reported above, the results in Table 3 suggest that the CPT can be shortened substantially, whereas the NBACK cannot. Using “moderate” precision as the cutoff for an acceptable short form, the suggested test lengths of CPT letters phase, CPT numbers phase, NBACK 0-back, NBACK 1-back, and NBACK 2-back are 62, 69, 29, 28, and 28, respectively. Taken together, these results, combined with the SSIR method, suggest that we can create a CPT that is 57% of its original length and an NBACK that is 87% of its original length.

Table 3.

Number of Stimuli Necessary to Reach Six Levels of Measurement Precision for the CPT and NBACK.

		Items Needed
Precision		CPT		NBACK
Max. SEM	α Equivalent†	Numbers	Letters	0-back	1-back	2-back
0.30	0.91 (extreme)	84.4 (94%)	88.8 (99%)	29.6 (99%)	29.6 (99%)	30.0 (100%)
0.35	0.88 (high)	78.4 (87%)	83.7 (93%)	29.4 (98%)	29.0 (97%)	29.6 (99%)
0.40	0.84	71.0 (79%)	76.9 (85%)	29.1 (97%)	28.4 (95%)	28.8 (96%)
0.45	0.80 (moderate)	62.0 (69%)	68.6 (76%)	29.0 (97%)	27.7 (92%)	27.7 (92%)
0.50	0.75	52.1 (58%)	59.4 (66%)	28.9 (96%)	27.1 (90%)	26.5 (88%)
0.55	0.70 (min. acceptable)	41.1 (46%)	49.4 (55%)	28.9 (96%)	25.9 (86%)	24.9 (83%)

Note. CPT = Continuous Performance Task; SEM = standard error of measurement; max = maximum;

^†standard error of measurement and internal consistency reliability (here, Cronbach’s α) are related by the equation SEM = SD_scores × sqrt(1 − α), which can be reduced to SEM = sqrt(1 − α) in the normal IRT metric in which SD_scores is assumed to be 1.0 without further information (SD = standard deviation).

Discussion

In this study, we compared a method of test abbreviation using correlations with full forms and validity criteria to a precision-based method using CAT simulation. Results from the validity-based method were largely consistent with those from the CAT-simulation method using the lowest reliability cutoff (SEM < 0.55). For the CPT, the validity-based method suggested that the test could be shortened by about half of its original length for letters and numbers, respectively, while the CAT-simulation method suggested almost identical percentages. Both offer substantial savings in administration time. For the NBACK, results were not as consistent, with the CAT-simulation results being more conservative. For the 0-, 1-, and 2-back, the validity-based method suggested almost no abbreviation; the CAT-simulation method suggested the same. Both methods indicate that the time savings are negligible, and if this test is used, it should be administered in its entirety. Further research is needed to determine the cause of the discrepancy for the NBACK, as it could be related to the fixed order of the task, difficulty of the task, or other factors.

This study had some notable limitations. First, there are many test types not amenable to CAT, and we only examined two relatively similar, rapid, signal-detection-like tests. It is unknown whether applying these methods will be as effective or feasible for other types of tests not amenable to CAT, such as the trail-making tests (Reitan, 1955), tests that change answer key logic mid-test (e.g., Penn Conditional Exclusion Test; Kurtz, Ragland, Moberg, & Gur, 2004), or list-learning tests involving free recall (Claparède, 1918). A second limitation is that the methods presented here do not obviate the need to make subjective decisions when building a short-form. Any decision to use a specific precision level cutoff (e.g., SEM < 0.40) or validity criterion cutoff will be at least partly subjective and based on the specific needs of the study. A third limitation is that the age range used here (8 – 21) is a unique period of human development (including puberty). It is possible that some of the effects, especially the relationships among scores and validity criteria, tend to be higher or lower for this age group (or a sub-group within this one) compared to the general population. Indeed, our analyses separating the age groups (Supplementary Figures S2 and S3) confirmed some of the above. Specifically, for the CPT Letters portion, the test forms (full versus long) tend to diverge more quickly in the older than in the younger group, such that application of the present method in a younger group would suggest the test can be shortened more than if it were done in an older group. For the NBACK, while there was no systematic difference between the older and younger groups, the differences became large and unpredictable after ~10 items were removed (right sides of panels in Figure S2). We therefore urge researchers to apply this method in the full age range for which the short-form is intended. Otherwise, the inevitable (and unmodeled) effects of age could have unintended consequences. A fourth limitation is that, while the abbreviated test forms used here save considerable time in aggregate, the time savings on an individual level is negligible (1–2 minutes). A fifth limitation is that the assumptions are made throughout that: 1) higher discrimination is always better, and 2) the trait will always be normally distributed with mean=0 and standard deviation=1. However, violations of #2 are so common in nature as to need no further explanation, and counterexamples of #1 were suggested and demonstrated by Chang & Ying (1999) and Hua & Chang (2001). Finally, it is both a potential limitation and a cautionary note that some tests (especially neurocognitive) are designed with examinee fatigue in mind; abbreviating the test might change the nature of what is being measured. For example, one aspect of the original version of the Continuous Performance Test used here is that it was quite long and therefore measured some aspect of examinee stamina for sustained attention. If the test was intentionally designed that way (to measure stamina as well as attention), careful thought needs to be given to whether it is necessary to maintain the same measurement properties as the original. If so, abbreviation might not be an option.

In sum, overall results provide some evidence in favor of using dual test-abbreviation methods for certain tests that are not amenable to traditional CAT, especially if those tests are rapid and include signal-detection-like properties (i.e., detecting and reacting to targets versus foils). Here, these novel methods were able to shorten the length of a continuous performance test by approximately half, while the time savings on an n-back measure were minimal. Future studies should examine the utility of these methods in additional computerized neurocognitive measures given in large studies. Given the scale of many current genomic and international studies, the total time savings from creation of short-forms is potentially vast. For example, the Penn Continuous Performance Test used here takes 5.3 minutes to administer. If we abbreviate it to 3.3 minutes (2 minutes saved, a conservative estimate by the present results), administration to ~500,000 people (e.g., in the UK Biobank) (Sudlow et al., 2015) would mean ~16,667 hours (1.9 years) of examinee time saved from abbreviating just one test. This consideration highlights the tremendous potential for increasing assessment efficiency, which could free up time and resources for more impactful uses or for gathering data on a broader range of behavioral domains.