IN VIVO ESTIMATION OF MURINE IRIS STIFFNESS USING FINITE ELEMENT MODELING

Abstract

The iris plays an important role in certain types of glaucoma, including primary angle-closure glaucoma and pigmentary glaucoma. Iris mechanics are also important in influencing trabecular meshwork deformation in response to intraocular pressure changes in some animal species. Although mice are widely used to study ocular disease, including glaucoma, the in vivo biomechanical properties of the murine iris are unknown. Thus, the primary objective of this study was to estimate murine iris biomechanical stiffness. We used optical coherence tomography (OCT) images of the anterior segment of living mice (n=13, age = 7.3 ± 3.2 [mean ± SD] months) at sequentially increasing IOP levels, observing IOP-dependent iris deformations. We then used an inverse finite element model to predict iris deformations under the same conditions, estimating iris stiffness by maximizing agreement between OCT data and numerical simulations. Our results show an in vivo murine iris stiffness of 96.1 ± 54.7 kPa (mean ± SD), which did not correlate with age but was dependent on gender. Our results further showed strong evidence of reverse pupillary block, with mean posterior chamber pressure remaining at approximately 12 mmHg even as anterior chamber pressure was set to much higher levels. Our approach to monitoring iris stiffness in vivo is applicable to study potential changes of iris stiffness in various pathophysiological conditions and thus has significant potential for clinical care of ocular disease involving iris biomechanics.

1. INTRODUCTION

The iris plays important roles in certain types of glaucoma. Specifically, in some patients with narrow iridocorneal angles, the iris can bow anteriorly and impede aqueous humor drainage. Obstruction of the outflow pathways causes an increase in IOP, which can lead to primary angle closure glaucoma (PACG). In pigmentary glaucoma (PG) and pigment dispersion syndrome (PDS), the iris is abnormally located so that pigment is released from the posterior iris by mechanical contact with the zonules^1–3. In general, the configuration of the iris depends on its mechanical properties, and it is therefore important to have information about iris stiffness to understand how iris mechanics may contribute to these conditions. Further, iris movement influences trabecular meshwork behavior, especially in species with extensive trabecular meshwork-iris connections, such as rodents. This relationship can be an important confounding factor when assessing trabecular meshwork stiffness in situ using a recently proposed imaging-based approach⁴, and thus knowledge of iris mechanical stiffness is useful for carrying out this assessment.

Several groups have studied iris stiffness in vivo in rabbits and humans^5,6, as well as conducting ex vivo studies in animals^7–10 and humans¹¹. However, to our knowledge, there are no measurements of in vivo iris stiffness in mice, even though the mouse is widely used in ophthalmology research. Thus, the objective of this study was to estimate murine iris stiffness in vivo. For this purpose, we used OCT images of anterior segment of mouse eye and an inverse finite element modeling approach.

2. MATERIAL AND METHODS

Before providing details below, we first describe the overall workflow (Fig. 1). We acquired OCT scans of the anterior segment in mice, observing iris deformation as IOP was changed (Fig. 1A and 1B). The OCT scans were used to construct a 3-dimensional axisymmetric finite element model (Fig. 1C) and a structural analysis was conducted to predict iris deformation due to IOP change; this predicted deformation was then compared to the observed deformation from OCT data (Fig. 1D). Finally, we used an optimization algorithm to vary the stiffness of the iris to best match the iris deformation as predicted by the finite element model to the measured OCT data.

Figure 1.

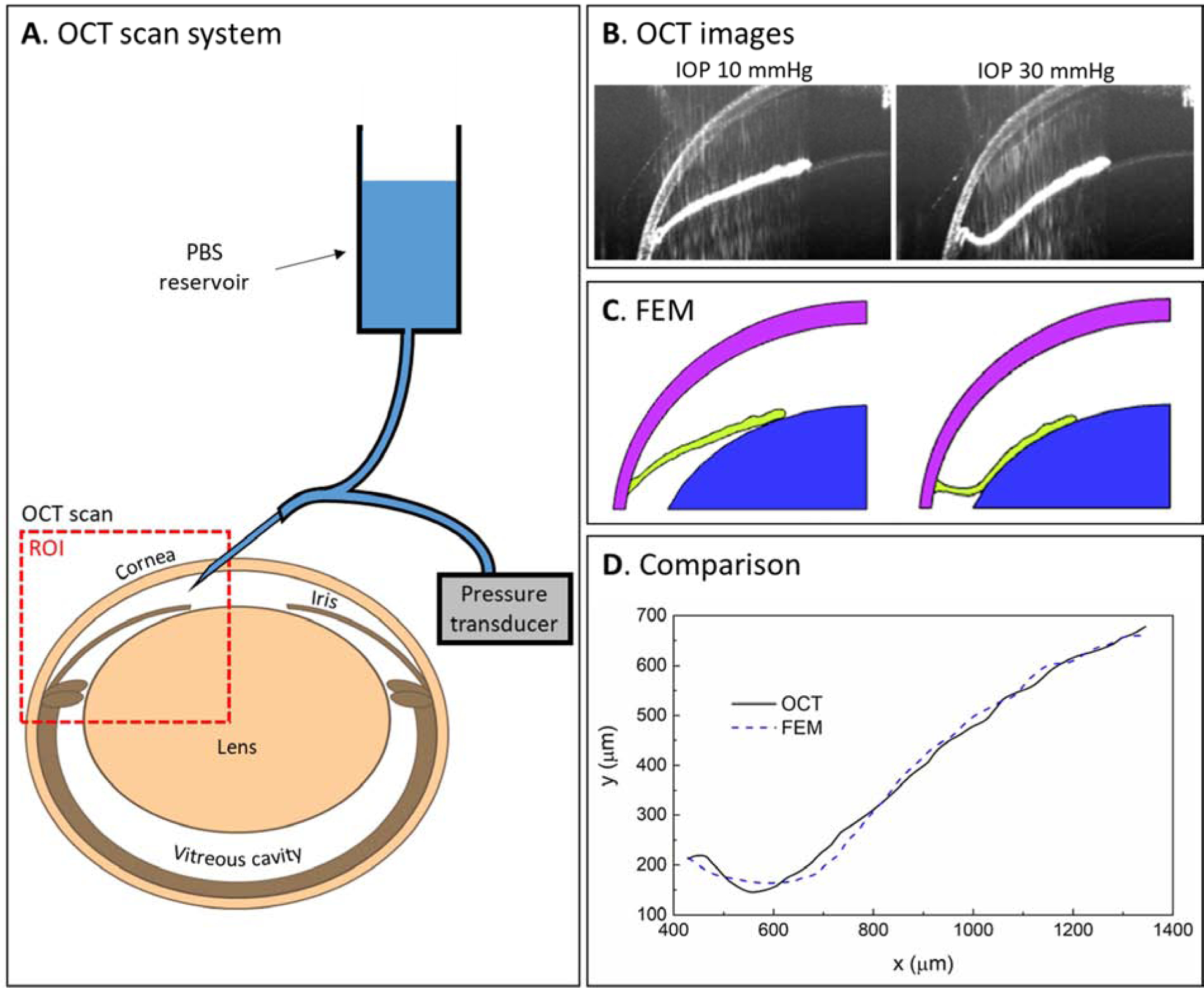
Workflow for murine iris stiffness estimation in vivo. A. OCT scans of the anterior segment of mouse eyes were acquired at several IOP levels, as set by a reservoir. B. Representative OCT images showing iris deformation as IOP was changed from 10 mmHg (left) to 30 mmHg (right panel). The visualized region corresponds approximately to the red dashed box in panel A. C. Finite element model of the anterior segment of the eye, based on the OCT images. An IOP change was applied to the surfaces enclosing the anterior chamber to predict the iris (green) deformation. D. The profiles of the anterior iris as observed in OCT scans (black solid line) and as predicted by FEM (blue dashed line) were compared to determine the iris stiffness that resulted in the best match between the profiles. ROI = region of interest, FEM = finite element model.

2.1. Animals

C57BL/6 (C57) mice (both males and females) were used in the current study. The animals were handled in accordance with an approved protocol (A001-19-01, Institutional Animal Care and Use Committee of Duke University) and in compliance with the Association for Research in Vision and Ophthalmology (ARVO) Statement for the Use of Animals in Ophthalmic and Vision Research. The mice were purchased from the Jackson Laboratory (Bar Harbor, Maine, USA), bred/housed in clear cages and kept in housing rooms at 21°C with a 12h:12h light:dark cycle.

2.2. OCT scans:

Ostensibly healthy C57BL/6 mice (n=13, 4 males and 9 females, age = 7.3 ± 3.2 months, [mean ± SD]) were anesthetized using ketamine (100mg/kg) plus xylazine (10 mg/kg). Anesthesia was maintained with ketamine (60 mg/kg) every 20 min by IP administration. In each animal, a microneedle was inserted into the anterior chamber of the right eye as described in details in previous publications^4,12–15. This needle was connected to both a reservoir and pressure transducer to control and monitor IOP, respectively. The right eye was imaged by OCT on a single nasal plane of the anterior segment at IOP levels of 10, 12, 15, 17, 20, 25, and 30 mmHg. The time interval between each scan was about 1–2 min, which was sufficiently short to ensure that the drainage of aqueous humor (~60–130 nl/min¹⁶) was relatively small compared to the iris displacement (~1uL) observed in the OCT images. The OCT images included part of the cornea/sclera, the iris from its root to the pupillary margin, and part of the lens.

To assess the spatial (circumferential) variation of the mechanical behavior of the iris, OCT images were acquired at two circumference sites (nasal and temporal) sequentially in four of the 13 mice (animal numbers 05, 06, 07 and 09). To assess the repeatability of the method, we conducted a test-retest study in which three mice (animal numbers 11, 12 and 13) were scanned twice sequentially at the same site (nasal). In all of the above tests, the eyes were imaged once at the nasal site as described above, then were returned to an IOP of 10 mmHg for 5 minutes, which was enough time for tissues to return to their original configurations. A second scan set, i.e. images at 10, 12, 15, 17, 20, 25, and 30 mmHg, was then acquired at a temporal site (for the spatial variation test) or at the nasal site (for the repeatability test). Thus, in total we acquired 20 sets of OCT images from 13 mouse eyes, including 4 sets from temporal locations and 3 sets of “retest” nasal site images.

2.3. Finite element model:

For each mouse eye, the OCT images at an IOP of 10 mmHg were used to create a subject-specific finite element model of the anterior segment. The margins of the lens and cornea were manually delineated as segments of ellipses, as assumed in previous studies in human eyes^17–19. This ellipsoidal delineation showed good agreement with tissue margins seen in OCT images (Fig 2A). The iris margin was delineated using an iterative automatic thresholding technique based on the isodata algorithm²⁰, as implemented in ImageJ (version 1.52a). To account for 3D effects, we treated the eye as axisymmetric and rotated the delineated 2D image about a symmetry axis by 1 degree to create a 3D “wedge” computational domain that is compatible with the FEBio open-source suite²¹. The symmetry axis was defined as the line connecting the apices of the cornea and lens in the OCT scans. The resulting 3D model was meshed using hexahedral finite elements (ICEM CFD 19.1; ANSYS, Inc, Fig. 2B), with only one element in the circumferential direction to minimize computational cost. We conducted a mesh convergence test and found that the results were sensitive to mesh density in the iris, but were less sensitive to mesh density in other regions (Fig. A1, Appendix).

Figure 2.

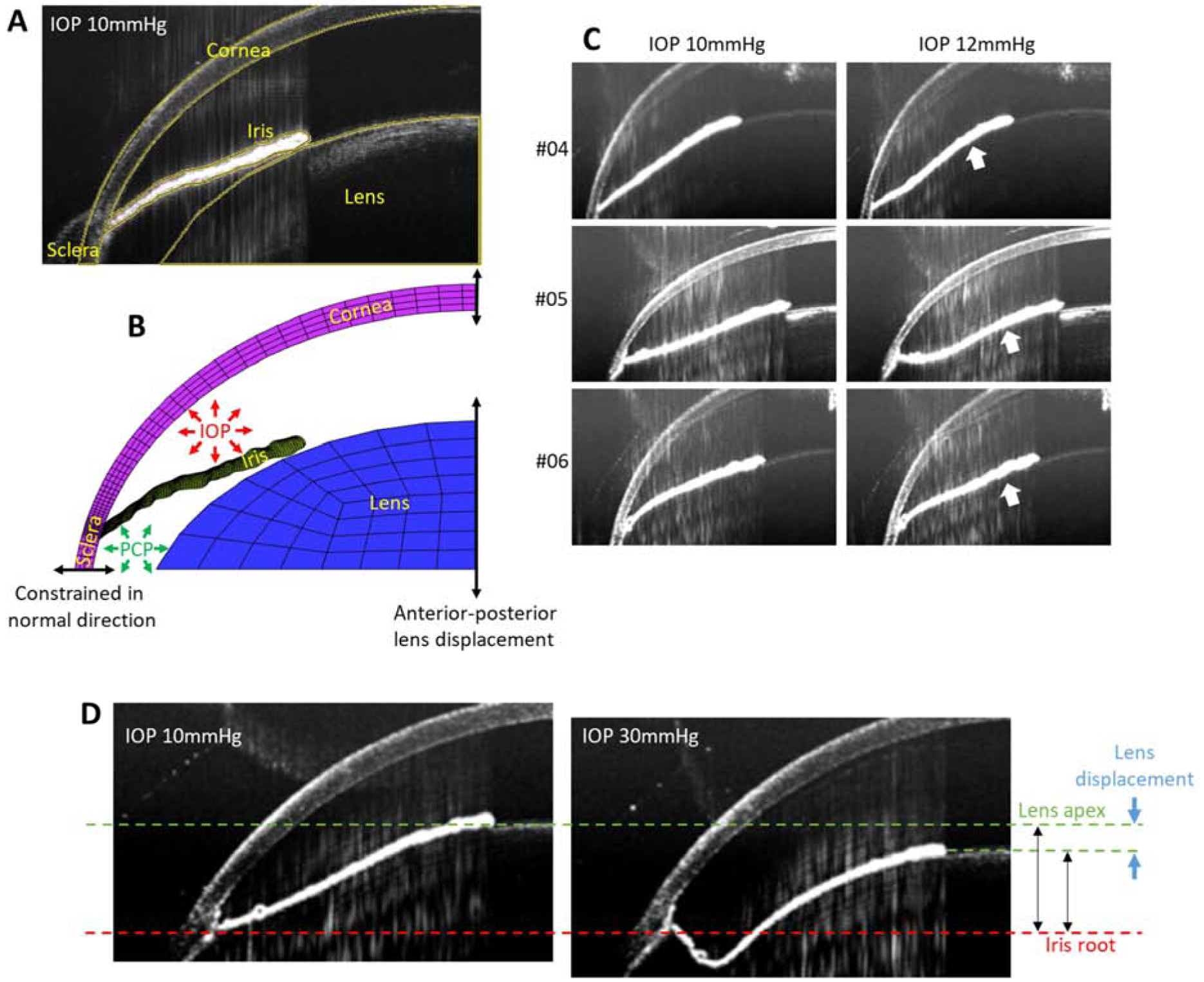
A. Delineation of anatomical structures within the anterior mouse eye (yellow lines) from an OCT scan at an IOP of 10 mmHg, including the cornea, sclera, iris and lens. B. Finite element model of the anterior region of a mouse eye based on the delineated OCT geometry, showing the applied boundary conditions. C. OCT scans at IOPs of 10 mmHg (left) and 12 mmHg (right panels) for several representative mouse eyes (animal numbers 04, 05 and 06) showing reverse pupillary block (white arrows) at an IOP of 12 mmHg. D. OCT scans at 10 mmHg (left panel) and 30 mmHg (right panel) showing the change (blue arrows) in the relative anterior-posterior distance between the lens apex (green dashed line) and the iris root (red dashed line), used to specify an anterior-posterior lens displacement in the finite element simulations.

2.3.1. Loading conditions.

The IOP, which was controlled and known during the experiments, was applied as a stress to the tissue surfaces enclosing the anterior chamber in the computations. It is also necessary to specify the posterior chamber as part of the calculations, yet this pressure could not be experimentally measured due to the small size of the mouse eye. Thus, we determined this pressure as part of the computations, as follows. The OCT images indicated that the iris-lens channel began to occlude for IOPs less than 12 mmHg, as judged by the pupillary margin of the iris closely following the contour of the lens at an IOP of 12mmHg for all mice (Fig. 2C). According to a previous study in the same mouse strain²², the flow rate versus perfusion pressure relationship differed depending on whether the infusion needle tip was inserted into the anterior chamber (AC), as in our experiments, or the posterior chamber (PC). Specifically, when the needle tip was in the AC, severe reverse pupillary block was observed as IOP increased, while when the needle tip was in the PC, there was not. This result and our OCT observations together suggest that the posterior chamber pressure (PCP) likely differed from anterior chamber pressure in this study due to reverse pupillary block as IOP increased. It is reasonable to assume that PCP increases monotonically with IOP, since an increased IOP displaces the iris posteriorly which in turn induces a PCP increase. However, the exact relationship between IOP and PCP in the situation where reverse pupillary block is involved is unknown, and thus we assumed a fairly general non-linear relationship of the form

$$PC{P}_i-PC{P}_{ref}=\left(PC{P}_{max}-PC{P}_{ref}\right){\left(\frac{IO{P}_i-IO{P}_{ref}}{IO{P}_{max}-IO{P}_{ref}}\right)}^{\beta }$$

where β is an unknown non-linearity factor, and PCP_ref and IOPCP_ref represent PCP and IOP at a reference state where there is open communication between the anterior and posterior chambers, i.e. at the state where the pressure in these chambers is essentially the same. Having the same reference pressure when there is open communication is consistent with previous studies showing that the pressure difference between the anterior and posterior chambers is very small, i.e. less than 0.1 mmHg when the iris-lens gap is open¹⁷ and remains small when slight reverse pupillary block occurs due to conditions such as corneoscleral indentation or spontaneous blinking^18,23. Based on the above argument, we took IOP_ref = PCP_ref = 10 mmHg. PCP_i represents the PCP when IOP is set to IOP_i, where the subscript i indicates the experimental pressure step. In our experiments, i lay in the range [1 − max], corresponding to IOP_i in the range [12, 15, 17, 20, 25, 30] mmHg. The exception was animal numbers 01 and 02, where the 25 mmHg pressure step was not recorded. The above formulation includes two unknowns: PCP at the maximum pressure (final pressure step), PCP_max, and the non-linearity factor, β We determined these unknowns during our inverse finite element modeling procedure.

2.3.2. Modeling constraints:

The boundaries lying on the symmetry axis were constrained to move only in the anterior-posterior direction. The equatorial boundary of the cornea/sclera was assumed to be constrained in its normal direction, i.e. the sclera was allowed to expand radially at this location but not to displace in the anterior-posterior direction. In other words, the equatorial boundary of the cornea/sclera, and the iris root attached near this location, were taken as a reference location for anterior-posterior deformations. Experimentally, it was observed that the lens moved in the anterior-posterior direction relative to the iris root as IOP was changed (Fig 2D). We therefore determined a subject-specific lens displacement from the OCT images as follows. We identified the position of the lens apex and the iris root at IOPs of 10 mmHg and 30 mmHg, and calculated the change in the distance between the lens apex and iris root as a net anterior-posterior displacement of the lens relative to iris root (Fig. 2D).

We assumed that the difference in pressures between the anterior and posterior chambers drove the anterior-posterior displacement of the lens, and thus interpolated relative lens displacements at IOPs between 10 and 30 mmHg as follows

$$d_{\mathit{\text{lens}},i}=d_{\mathit{\text{lens}},\mathit{\text{max}}}\left(\frac{\mathit{\text{IO}}{P}_i-PC{P}_i}{IO{P}_{\mathit{\text{max}}}-PC{P}_{\mathit{\text{max}}}}\right)$$

where d_lens,i is the relative lens displacement at pressure step i and other notation is as above.

We assumed that only normal forces acted between the posterior surface of the iris and the anterior lens, neglecting any friction between these surfaces.

2.3.3. Material models:

We observed that the radial contour length of the iris changed slightly during the experiment as IOP was increased, due presumably to changes in the radial and/or dilator muscle tone. We quantified this change by measuring the iris arc length for each eye at each IOP and normalizing this length by the iris contour length at an IOP of 10 mmHg. We then averaged these normalized lengths over all IOP steps to obtain a single value representing the iris’ radial length change for each eye during the experiment. Some studies have accounted for the effect of iris muscle tone on stiffness of the iris by considering dilation in response to light^6,24. In this study, however, the ambient light intensity was not strictly controlled during OCT imaging, although all experiments were conducted under standard room lights in the same location and thus light conditions did not vary significantly. In addition, whether there is an active response of iridial muscles to changes in IOP is unknown, although we did not see a consistent trend towards mydriasis or miosis as IOP was increased (see Results). Therefore, it was impossible to know the exact state of iridial muscle tone in this study. Rather than including the unknown effects of active muscles in our finite element model, we instead modeled the iris as a passive tissue, with the stiffness representing an effective average due to contributions from both passive and active iridial components. Specifically, the iris was modeled as an incompressible, isotropic, hyperelastic neo-Hookean material, described by the energy density function, W = C₁(I₁ − 3), where I₁ is the first invariant of the right Cauchy-Green deformation tensor and C₁ is a material property to be determined by the inverse finite element method.

The lens was treated as a rigid body, since it is much stiffer than tissues attached to it and thus would tend to displace rather than deform as IOP is changed. The cornea/sclera was modeled as an incompressible, hyperelastic neo-Hookean material with a stiffness of 4050 kPa, an average of the values reported in a previous study²⁵.

2.4. Inverse finite element method.

We used inverse finite element modeling to determine three quantities for each mouse: PCP at the final step of the experiment, PCP_max, the non-linearity factor, β, and the iris material coefficient C₁. We assumed a starting set of values for PCP_max, β, and C_1, predicted iris deformation due to IOP changes, and compared the predicted iris deformation to the OCT data. Specifically, we computed two-dimensional coordinates of points on the delineated upper surface of the iris relative to the left and bottom margin of each OCT image as vertical and horizontal coordinate axes, respectively. The FEM and OCT result for each eye at each IOP step were aligned to minimize the root mean square difference between them to account for potential inconsistency of relative positions of the coordinate axis in OCT images over IOPs (see Fig. 2D as an example). We then compared the anterior-posterior positions of the aligned iridial profiles as observed from OCT images (y_OCT) and predicted by FEM (y_FEM) by the objective function $f_{\mathit{\text{obj}}}=\left[{\sum }_{i=1}^{\mathit{\text{max}}}{\left(\sqrt{{{\sum }_{j=1}^n\left(y_{\mathit{\text{OCT}},j}-y_{\mathit{\text{FEM}},j}\right)}^2/n}\right)}_j\right]/\mathit{\text{max}}$, which is essentially a root mean square difference (RMSD) between the profiles averaged over all IOP steps. The subscript j refers to uniformly distributed locations along the radial direction, n is the number of such locations (= 100), i refers to the IOP steps, and max is the number of such steps (= 5 for animal numbers 01 and 02, 6 for other animals). Optimization was conducted using the surrogate algorithm²⁶ implemented in Matlab to find the values of PCP_max, β, C₁ that minimized f_obj. The optimization process was repeated with different initial guesses for 6 out of 13 eyes to test the uniqueness of the optimized parameter values. In this study, we report stiffness as the equivalent Young’s modulus (E) calculated as E = 6 C₁. Statistical analysis was conducted for 13 eyes in the nasal position excluding repeat tests for the same eye unless stated otherwise.

3. RESULTS

The iris bowed posteriorly as IOP was increased, and this deformation was generally well-predicted by the FEM model, although there were some discrepancies near the iris root at higher IOPs (Fig. 3). The mean RMSD between OCT data and FEM prediction over all IOPs for all eyes was 12.6 ± 3.5 um, corresponding to 11.0 ± 3.8 % of the maximum anterior-posterior deformation of the iris from IOP of 10 mmHg to 30 mmHg, as measured in OCT images.

Figure 3.

OCT images of the anterior segment of a representative mouse eye (animal number 05) overlain with optimized FEM results (yellow lines) at different IOP levels. This eye showed a median value for the mean RMSD between OCT data and FEM prediction relative to the maximum anterior-posterior deformation of the iris from IOP of 10 mmHg to 30 mmHg, and thus can be considered representative.

We measured the change in radial length of the iris during IOP steps, related to mydriasis/miosis and hence iris muscle tone. There was no consistent trend in normalized iris radial length change over the course of the experiment, with a mean normalized iris length of 1.00 ± 0.03 (mean ± SD, 20 tests from 13 eyes), which was not significantly different from 1 (Fig. 4A, p=0.94). In other words, we did not observe a consistent trend towards either mydriasis or miosis during the experiment, even though most mice showed either a small amount of mydriasis or a small amount of miosis.

Figure 4.

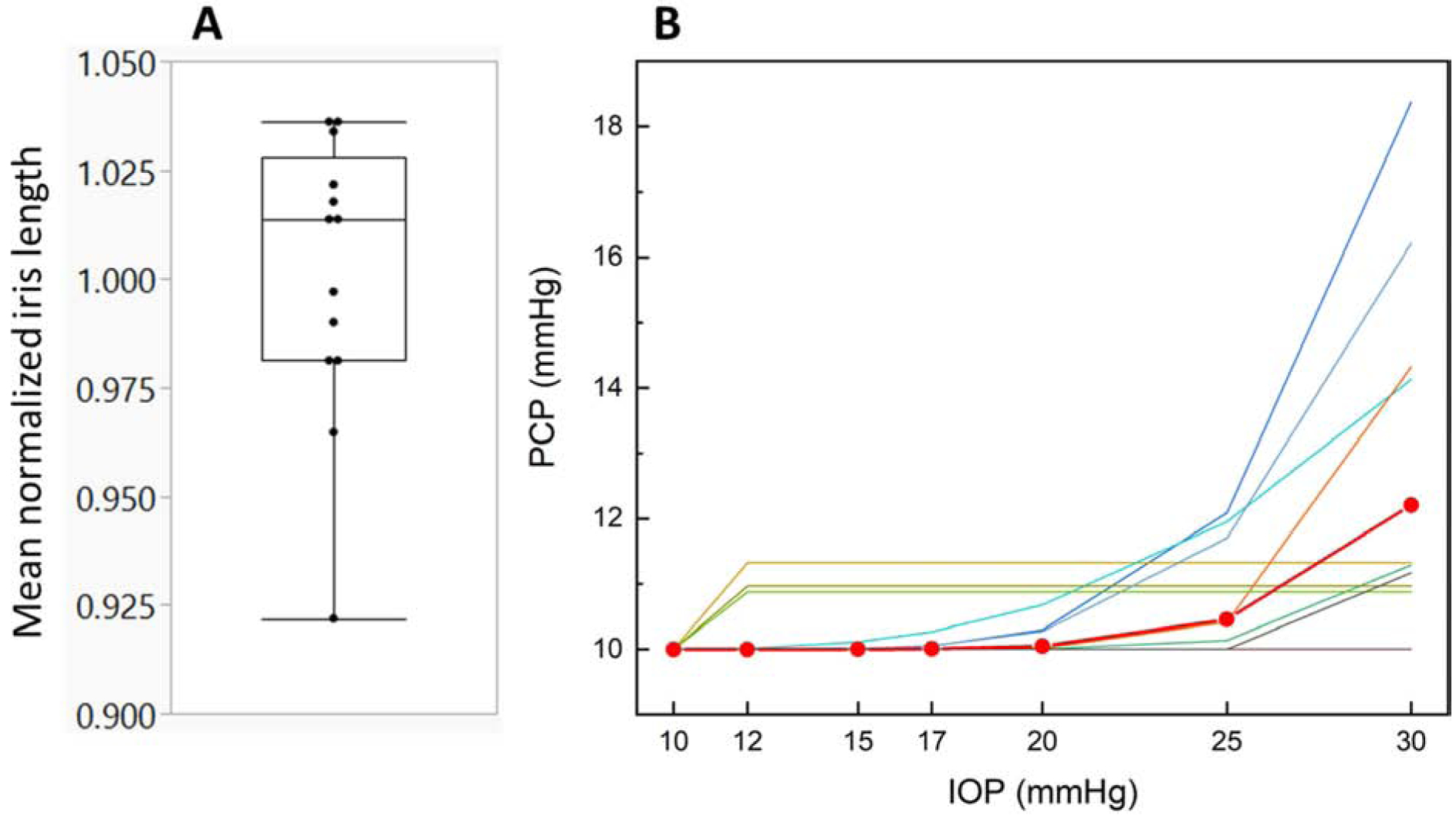
A. Distribution of mean normalized iris lengths observed from OCT images. Values less than 1 indicates mydriasis (iris shortening radially during the experiment), while values larger than 1 represent miosis. No consistent trend towards mydriasis or miosis during the experiment was observed. The box represents the 25^th to 75^th quantile, the horizontal bar within the box indicates the median, and the horizontal bars outside the box show the minimum and maximum values. B. Predicted posterior chamber pressures (PCPs) as IOP was increased. The lines represent individual eyes and the red line with circular symbols represents the mean PCP change averaged over all 13 eyes.

We estimated PCP_max as 12.2 ± 2.7 mmHg (mean ± SD, n=13), indicating that there was a large difference between anterior and posterior chamber pressures, as expected, and that reverse pupillary block typically occurred around 12 mmHg, consistent with previous observations²² (Fig. 4B). However, this behavior was heterogenous: in 6 of 13 eyes, PCPs were predicted to increase nonlinearly as IOP was increased (β > 1), in 3 eyes PCP was constant after the first pressure step, and in 4 eyes, PCP did not change over the experiment (PCP_max = PCP_ref = 10 mmHg). Averaged over all eyes where PCP changed during the course of the experiment, the nonlinearity factor β was 5.5 ± 6.7 (mean ± SD, n=9).

The estimated iris stiffnesses for 13 eyes in the nasal position (excluding repeat tests for the same eye) was 96.1 ± 54.7 kPa (mean ± SD). Repeat optimization of the parameters with a different starting guess for 6 eyes showed a mean difference in estimated iris stiffness of only 3.8% as compared to the first optimization, indicating that the optimization produced robust parameter values that were relatively independent of starting guess. There were no outliers and the estimated stiffnesses were well fit by a normal distribution (Anderson-Darling goodness of fit test, p=0.743, Fig. 5A). Age did not correlate with the stiffness estimates (r²= 0.11 p=0.2582, Fig. 5B). In contrast, the estimated iris stiffness was dependent on gender, showing that females had significantly stiffer iris than males (p=0.0363, Fig. 5C).

Figure 5.

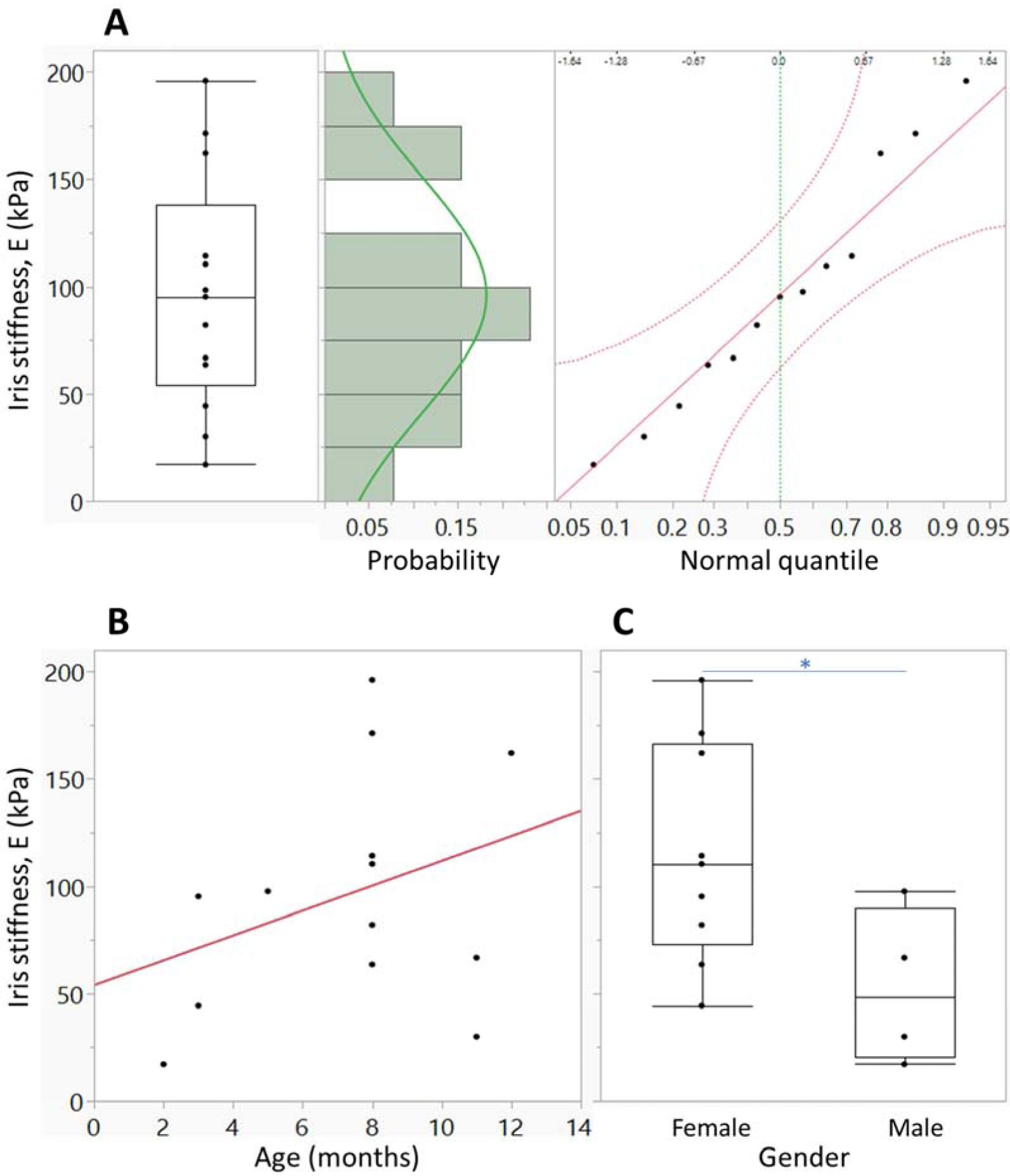
A. Distribution of the estimated iris stiffnesses for mouse eyes in the nasal position (n=13). The results from temporal scans and the repeat scans were excluded to avoid statistical bias in evaluating the distribution. The box (left panel) represents the 25^th to 75^th quantile, the horizontal bar within the box indicates the median, and the horizontal bars outside the box show the minimum and maximum values. Based on a histogram of stiffness estimates with a green line representing a normal distribution fit to the estimated stiffness (middle panel) and a normal quantile plot (right panel), we do not have sufficient evidence to conclude that the stiffness distribution does not follow a normal distribution (Anderson-Darling goodness of fit test p=0.743). B. Relationship between the estimated iris stiffness and mouse age. Red line represents the linear fit to the data. Mouse age is not significantly correlated with the estimated stiffness (p=0.85). C. Dependence of estimated iris stiffness on mouse gender. The interpretation of the plots is as in panel A. Female mice have stiffer iris than males (p=0.0363, two-tailed t-test).

For the four eyes that were scanned at both nasal and temporal locations, there was no consistent trend in estimated iris stiffnesses between the nasal and temporal locations (p=0.122, paired t-test, n= 4 pairs) although all eyes showed some spatial variation in stiffness (Table 1). In the test-retest study, the mean difference between stiffnesses obtained from two scans in the nasal region was 12.5% (Table 1) and there was no consistent trend between the 1^st and 2^nd tests (p=0.3599, paired t-test, n=3 pairs). The mean difference between the estimated PCP_max for the 1^st and 2^nd tests including both of the spatial variation test and the repeatability test was 10%.

Table 1.

Effects of location on iris stiffness (measurements on the same eye at different scanning locations) and results of the test-retest study.

Effects of location (different scan locations in same eye)				Test-retest at the same scan location
Subject number	1st – Nasal (kPa)	2nd –Temporal (kPa)	% difference from average	Subject number	1st – Nasal (kPa)	2nd –Nasal (kPa)	% difference from average
5	67	55	±9.7	11	64	54	±8.5
6	30	29	±1.0	12	114	80	±17.6
7	82	57	±17.6	13	17	21	±11.3
9	95	50	±31.4
mean	70	49	±14.9	mean			±12.5

4. DISCUSSION

We present a new methodology to estimate iridial stiffness of living mice. Using a subject-specific inverse FEM approach that was based on OCT images acquired as IOP was changed, we found that irideal stiffness was 96.1 ± 54.7 kPa. This value should be considered as an “effective bending stiffness” of the intact iris that incorporates the mechanical behavior of both the passive and active iridial components, and determines the biomechanical response of the iris to the IOP changes by bending. This information will be useful for future studies of iris biomechanics. We further found that iris stiffness did not correlate with age, although our subjects spanned a limited range of ages and thus more animals from larger range of ages need to be studied to confirm this phenomenon. Iris stiffness depended on gender, showing a larger stiffness in females than in males. This trend of gender difference in iris stiffness is opposite to previously reported gender differences in stiffness of other ocular tissues (cornea^27,28 and optic nerve sheath²⁹), showing a larger tissue stiffness in males than in females. Importantly, our finding is consistent with the relationship between gender, PACG, and iris biomechanics, in which females are at higher risk for PACG compared to males^30,31 and PACG patients have stiffer iris compared to healthy subjects⁶, although the exact mechanism of how gender difference affects iris stiffness and how the iris stiffness plays a role in PACG were unclear.

In Table 2, we compare our values to previous reports of iris stiffness in other species. Zang et al.⁵ used an approach similar to ours to estimate leporine iridial stiffness. Direct comparison with their data is difficult since the material model they used was different than ours (Ogden vs. neo-Hookean), but when their estimated model parameters are converted into an equivalent stiffness using a uniaxial tensile test assumption, their instantaneous stiffness was 500 kPa at a stretch ratio of one; a value about four times larger than ours. Their effective stiffness rapidly increases to almost infinity as the stretch increases, due to the very non-linear behavior of the Ogden model vs the neo-Hookean model we used for this study. We also tested the Ogden model in our study (data not presented) but it failed to give better agreement between OCT and FEM than the simple neo-Hookean model. In another study, Pant et al.⁶ accounted for both the passive and active muscles to estimate human iris stiffness by examining iridial response to light. However, they had to assume a magnitude for the active muscle stress and only could provide a normalized iris stiffness value of 0.97 ± 0.40 (mean ± SD) which is defined by the ratio between the iris stiffness, E, and the assumed active muscle stress (σ_act). They reported an iris stiffness of 38.8 ± 15.8 kPa (mean ± SD) by assuming 40 kPa of active muscle stress, which is difficult to measure in vivo. Since they found that the ratio, E/σ_act remained constant over a tested range of assumed muscle stress (0 – 400 kPa), an active muscle stress of about 100 kPa corresponds to an iris stiffness value of 97± 40 kPa (mean ± SD), similar to our estimate. As well, our estimation of iris stiffness was comparable to Heys and Barocas⁷, who measured the stiffness of bovine iris ex vivo using a uniaxial tensile test. They showed that the iris is anisotropic, with the azimuthal stiffness being much greater than in the radial direction (760 kPa vs. 27 kPa). In our case, the direction of loading and deformation was neither purely azimuthal nor radial, and thus our stiffness value between their two extremes seems reasonable.

Table 2.

Reported iris stiffnesses in various species. Equivalent stiffness for neo-Hookean material model was evaluated by E = 6 C₁. The equivalent stiffness for the Ogden model was estimated as the tangent modulus as stretch λ varied from 1 to 1.5.

References	Species	# of samples	Material model	Model parameter, Mean ± SD	Equivalent stiffness E, Mean ± SD (kPa)
Current study	Mouse	13	Neo-Hookean	C1 = 16± 9.1 kPa	96.1 ± 54.7
Zhang et al. 20145	Rabbit	6	Ogden	μ1 = 86.1 ± 8 kPa	500 to infinity (stretch λ from 1 to 1.5)
				α1 = 54.3 ± 12.7
				μ2 = 75.4 ± 20 kPa
				α2 = 48.1 ± 15.8
Pant et al. 20186	Human	8	Passive (neo-Hookean) + Active muscle stress σact	$\frac{E}{{\sigma }_{\mathit{\text{act}}}}=0.97\pm 0.40$	97 ± 40 (When σact = 100 kPa assumed)
Heys and Barocas 19997	Cattle	25	Linear elastic		Azimuthal 760 ± 550 Radial 27 ± 16

The iris profile near the pupillary margin seemed to be mainly determined by the lens contour, consistent with the presence of reverse pupillary block (Fig. 3). Thus, our stiffness values primarily characterize the material properties of the region near the iris root. However, our iris model is a 3-dimensional axisymmetric structure similar to an inclined annular plate or a cone that is azimuthally constrained and supported by the lens just at its pupillary margin. Therefore the predicted iris contour, even including the section near the pupillary margin, depends on a combination of azimuthal and radial deformation of the whole iris. Specifically, for the iris near the root to deform posteriorly, radial elongation of the iris and/or the azimuthal expansion of the iris near the pupillary margin must be involved, which in turn would determine the position of the iris tip relative to lens. In other words, the observed deformation near the iris root depends not only on tissue material properties near the root but also on the stiffness of the whole iris, including the pupillary margin.

Due to the small size of the mouse eye, it was not feasible to measure PCP during the experiment. We predicted PCP changes during the experiments using the inverse FEM approach, showing only a mild increase of PCP in most eyes (a 2.2 mmHg increase in average from the reference state [PCP_ref = 10 mmHg]) as IOP increased by 20 mmHg above the reference state (IOP_ref = 10 mmHg). This strongly suggests the presence of reverse pupillary block during the experiments, causing an imbalance in pressures between the anterior and posterior chambers, driving the iris to bow posteriorly.

It is interesting to consider an approximate calculation where the change in posterior chamber pressure is estimated by using the volume displaced by the iris at an IOP of 30 mmHg as observed in OCT images. By using the iris contours at 10 and 30 mmHg and assuming circumferential symmetry, the estimated volume displaced by iris motion was ~ 1 μL. Using this volume, and the previously reported value for compliance of the mouse eye (0.086 μL/mmHg)³², the predicted change in PCP was of order 20 mmHg or more, which is much greater than the value obtained by inverse finite element fitting and not consistent with the observed (posterior) direction of iris bowing. This large discrepancy strongly suggests that during imposed transient IOP changes and associated transient iris movement, the lens-iris diaphragm was not entirely closed, likely allowing a small amount of fluid to leak locally and transiently from the posterior chamber to the anterior chamber until a steady state was attained, i.e. the real process possibly includes some dynamic behavior so that the situation is much more complicated than the lens-iris junction being either just entirely sealed or opened, thus resulting in a PCP less than expected if the lens-iris diaphragm was entirely sealed during the experiment.

We did not account for the effects of active muscles in the iris and considered the iris as a homogeneous, isotropic material in our study. Although the iris is known to show inhomogeneous and anisotropic biomechanics 9, inclusion of such effects in our model was not warranted without detailed knowledge of animal-specific material properties, since adding more fitting parameters may increase the chance of overfitting or losing uniqueness. Future studies should consider the incorporation of such effects. During experiments, the iris shortened radially in some eyes, while other eyes showed no change or even radial lengthening (Fig. 4A). Overall, there was no consistent trend, strongly suggesting that there is no effect of IOP on iris radial length and hence iridial muscle tone. However, anesthesia applied to the mice during the experiments may have induced decrease of muscle tone as reported in a previous study³³ and thus affected the estimated iridial stiffness, which needs to be studied in detail in a future study. It also would be worth applying our approach to the eyes with eye drops such as pilocarpine and atropine that causes miosis and mydriasis, respectively not only to control the experimental condition but also to study further about the level of active muscle stress and its effect on iridial behavior.

No consistent trend of spatial variation of iris stiffness was observed when comparing temporal and nasal locations, although only a small number of eyes was reliably tested. Specifically, the average difference between the nasal and temporal stiffnesses in the same eye was ±14.9%. The averaged variability between the test-retest for the same eye at the same location (nasal) was ±12.5%, which we suggest is reasonable for in vivo testing, especially since it is significantly less than the population coefficient of variation (population standard deviation divided by the population mean) of 56.9%.

This study has some limitations in addition to those noted above. First, we used the same corneal material property value for all subjects. However, changes in this value would have only a small effect on our results because the cornea is much stiffer than iris, consistent with OCT images which showed minimal corneal deformation (Fig. 3). Second, we did not account for friction between the iris and the lens, although we expect this effect to be small due to fluid trapped between these two tissues. Third, the axis of symmetry may not be located exactly on the plane of OCT images. Although the experimenter tried to keep a consistent angle during the imaging process, there may be some errors when specifying the axis of symmetry. Fourth, we assumed that iris root motion was purely translational; however, it has been reported in a previous study³⁴ that due to the anisotropy of limbal tissues, the iris root may rotate as well as translate when IOP changes. The rotation of the iris root and limbal deformation could apply load on zonular fibers and thus on the lens, eventually affecting iris deformation during our experiment. Such effects are worth exploring in future studies. Finally, there may be some distortion in the OCT images. There have been some reports showing various sources of distortion when imaging the anterior segment of the eye and there also have been some efforts to correct such distortion^35–37. Such a correction would be worth investigating in future studies.

Highlights.

• Iridial stiffness, important in anterior segment biomechanics, is unknown in mice.

• We developed a method to estimate in vivo murine iris stiffness using OCT.

• In vivo murine iris stiffness was 96.1 ± 54.7 kPa (mean ± SD).

• In vivo murine iris stiffness did not correlate with age but depended on gender.

APPENDIX

Figure A1.

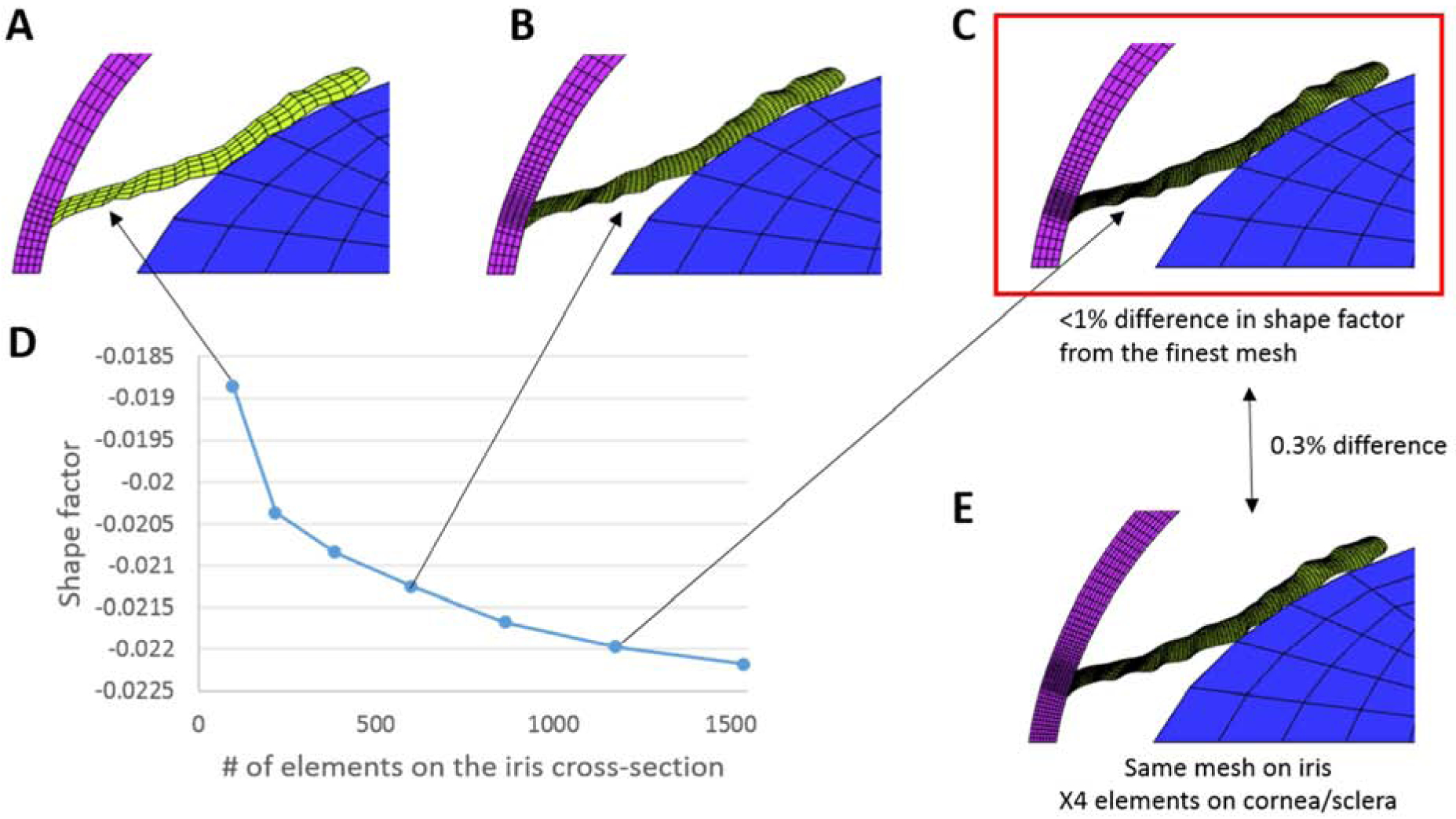
Mesh convergence test. A-C. Models created with coarse, medium, and fine meshes for the iris, respectively. D. Computed shape factor at an IOP 30 mmHg versus iris mesh density. The shape factor quantifies the iris bowing and was defined as follows: the coordinates of points on the iris upper surface were normalized by iris chord length (the distance between the iris root and tip), and then fit by a quartic polynomial (y = fit(x)). The shape factor (S) was calculated by integrating the fitted polynomial over the iris chord: $S={\int }_0^1\text{fit}(x)dx$ identical material properties were used for all simulations. The shape factor obtained using the fine mesh in panel C differed by < 1% as compared to the result with finest mesh tested (last point on the graph in panel D). Thus, the fine mesh in panel C was used as the production mesh for this study. E. A model incorporating the same iris mesh as in panel C, but having four times more elements in the cornea/sclera than the mesh in panel C. The shape factor differed by less than 0.3 % vs. the result with the fine mesh in panel C, showing a smaller effect of mesh density for the cornea/sclera as compared to the iris. For all tested meshes, the mesh density for the lens was not changed and remained relatively coarse because the lens was considered as a rigid body that simply translated in the anterior-posterior direction as IOP changed, acting as a non-penetrating rigid constraint on the location of the posterior surface of the iris.