Genetic and Environmental Influences on Stressful Life Events and their Associations with Executive Functions in Young Adulthood: A Longitudinal Twin Analysis

Abstract

Although stress is frequently considered an environmental factor, dependent stressful life events (SLEs) -- stressors that result from one’s actions or behaviors -- may in fact be evoked by a genetic liability. It has been suggested that dependent SLEs may be partially caused by poor executive function (EFs), higher-level cognitive abilities that enable individuals to implement goal-directed behavior. We investigated the possibility of genetic and environmental overlap between SLEs and EFs in a longitudinal twin study. We found high genetic stability in the number of dependent SLEs from age 23 to age 29, suggesting that the number of dependent stressors show persistence across time due to their genetic etiology. In addition, there was a nominally significant negative genetic correlation between a Common EF latent factor and dependent SLEs at age 23. The genetic stability of dependent SLEs and association with Common EF provides insight into how some behaviors may lead to persistent stress.

Introduction

Stress can lead to a range of health problems, affecting both physical and mental health (Cohen, Tyrrell, & Smith, 1993; Conway, Hammen, & Brennan, 2012). Although stress is frequently considered an environmental factor, dependent stressful life events (SLEs)-- stressors that result from one’s own actions or behaviors, such as trouble with relationships or work -- may be evoked partially by a genetic liability to put oneself in stressful situations (Bemmels et al., 2008). In contrast, independent SLEs -- stressors that are random and uncontrollable, such as one’s parent dying or a natural disaster -- have smaller heritabilities (Bemmels et al., 2008). Behavior genetic research typically shows genetic influences on traits to be stable over time, whereas environmental influences on traits are often more time specific (e.g., Briley & Tucker-Drob, 2017; Nes et al., 2007). Snyder and Hankin (2016) posited that dependent SLEs may be at least partially caused by poor executive function abilities (EFs), higher-level cognitive abilities that enable individuals to implement goal-directed behavior. Thus, the moderate heritability of dependent events and their potential association with EFs suggests that there may be some stability in the number of dependent events occurring over time, which has implications for understanding related negative health outcomes. However, little is known about the stability of dependent and independent events and their genetic and environmental associations with EFs across time.

In the current study, we use longitudinal twin data on SLEs (specifically, the number of negative dependent and independent stressful events endorsed) and EFs at ages 23 and 29 years old to address the following questions:

1. Do dependent SLEs have higher heritability and more stability across time, compared to independent SLEs?

2. Do dependent SLEs have stronger phenotypic and genetic associations with EFs, compared to independent SLEs?

3. Is the relationship between number of SLEs and EFs bidirectional? i.e., do dependent SLEs and EFs prospectively predict each other in a longitudinal cross-lag model?

We preregistered this study. Hypotheses and methods can be viewed at https://osf.io/tcb94. Our hypotheses regarding the etiology of SLEs and associations with EF were preregistered. Here, we additionally examined the stability of SLEs as an implication of our hypothesis about genetic etiology.

Genetic and Environmental Etiology of Stressful Life Events

Hammen (1991) proposed the stress generation theory as an explanation for why some people are more likely to experience stress. Broadly, this theory posits that individuals who are depressed may evoke, ruminate on, or remember stressful situations in their environment more than non-depressed individuals. Supporting this hypothesis, depressed individuals are likely to suffer more dependent, interpersonal stressors, but not more likely to experience more independent stressors (Hammen, 2006).

The idea that individuals’ characteristics or predispositions may in part evoke stressful experiences is supported by twin research. In particular, some stressful events may result from active and/or evocative gene-environment correlations, in which individuals select and evoke environments that reflect their genetics (Scarr & McCartney, 1983; Kendler & Baker, 2007). Gene-environment correlations are indicated when a putatively environmental measure shows evidence for genetic influences (i.e., is heritable). Most prior twin literature that compares sum scores for dependent and independent SLEs find number of dependent SLEs to be more heritable; both dependent and independent SLE counts often show non-shared environmental influences as well (dependent SLE h²= 19–51%; independent SLE h²= 0–18%) (Billig et al., 1996; Plomin et al., 1990; Rice et al., 2003; Sobolewski et al., 2001; Boardman et al., 2011).

This prior evidence for greater genetic influences on dependent events than independent events has potential implications for the stability of individual differences in stressful experiences across time. In particular, if dependent SLEs are moderately heritable and due in part to an individual’s characteristics and behaviors, one would expect individual differences in the number of those types of stressors to be moderately stable across the lifespan. In contrast, one might not expect the number of independent stressors to be stable across time. Despite the consensus that some types of events are partially genetically evoked, there has been little investigation of the stability of these types of events. Existing evidence is inconsistent; Eaton (1978) found, when looking at both positive and negative events, the total number of life events experienced to be uncorrelated across time. Billings and Moos (1982), however, examined positive and negative events separately and did find some evidence for temporal consistency in number and type of events longitudinally. Thus, this question warrants further study, especially in the context of dependent and independent SLEs.

Associations between Stressful Events and Executive Function Abilities

There is growing evidence supporting the partial genetic nature of dependent SLEs, but less research on characteristics that are genetically associated with experiencing greater number of dependent SLEs. Here, we investigate the possibility that heightened vulnerability for stress generation may be associated with worse EFs. Snyder and Hankin (2016) reported results consistent with a model in which the link between self-reported EF and internalizing symptoms was mediated by stress and rumination. In another study, they examined EFs with a battery of EF tasks. Specifically, they used the latent unity/diversity model of EF (Friedman & Miyake, 2017) to test associations with a transdiagnostic liability for psychopathology (a P factor), with mediating mechanisms of dependent stress and rumination. In a subsequent study corroborating those findings, Snyder et al. (2019) found a significant indirect effect of a Common EF latent variable on internalizing symptoms via dependent SLEs and rumination in older youth. Combined with evidence that EFs are highly heritable (Friedman et al., 2016), genetic influences on individual differences in EFs may at least partially underlie the genetic influences on dependent SLEs. However, given that EFs are multifaceted, it is important to consider which components of EF may be most related to stress.

The most commonly studied EFs are response inhibition (avoiding a dominant or automatic response), working memory updating (maintaining and updating relevant information), and mental set shifting (rapidly switching between two tasks). These three EFs, though separable, are moderately correlated, and the unity/diversity model (Friedman & Miyake, 2017) captures this structure. In this model, a Common EF latent factor captures covariance across all EF tasks, whereas Updating-specific and Shifting-specific latent factors capture remaining covariance among updating and shifting tasks, respectively, after Common EF variance is removed. The Common EF factor captures all the covariance across inhibiting tasks, so there is no inhibiting-specific factor. The Common EF factor is thought to capture the ability to maintain and implement goals (Friedman & Miyake, 2017), an ability that is required by all EF tasks. These EF latent variables have been shown to be highly stable and heritable from late adolescence to early adulthood (Friedman et al., 2016).

We hypothesize that lower Common EF may lead to more dependent events, but not more independent events, because worse Common EF, evidenced by poor planning and lack of goal-directed behavior, might lead to interpersonal or character-reflective stressful situations (Snyder et al., 2019). Billig et al. (1996) found dependent life events, but not independent or familial events, to be significantly heritable, and the phenotypic correlation with personality to be partially genetically mediated. The authors suggested a genetic predisposition may lead some to engage in behaviors that bring about negative life events. We hypothesize here that at least part of this genetic predisposition may be accounted for by poor Common EF evoking dependent but not independent SLEs.

Conversely, cognitive resources devoted to prolonged rumination about stressful situations (either dependent or independent) may impair Common EF (Williams et al., 2009). Any negative event may lead to a cognitive load (both in lab tasks and outside the lab, potentially due to rumination; Snyder et al., 2019), but, as mentioned above, we do not expect individual characteristics or behaviors to evoke random, independent SLEs. Therefore, we expect the association between dependent SLEs and Common EF to be bidirectional, but the relationship between independent SLEs and Common EF to be unidirectional, leading to a stronger association of Common EF with dependent SLEs than independent SLEs at each time point.

Previous analyses on the EF data used in this study indicate high heritability for all three EF latent variables (Friedman et al., 2016). Thus, we hypothesize that the relation between number of dependent SLEs and Common EF will be primarily genetic in origin. It may also be somewhat environmentally mediated, but because environmental influences on Common EF are small, environmental covariance should not account for much of the phenotypic relationship. Conversely, we expect number of independent SLEs will be most explained by environmental influences, and therefore have a smaller negative association with Common EF; those associations should be primarily environmentally mediated as they are more random events than dependent SLEs.

While some positive events may still induce stress (e.g., getting married or having a child), we focus here on negative events because of our hypothesis that lower EF may lead to a greater number of negative SLEs, but not necessarily a greater number of positive SLEs. Therefore, in the context of this paper, when we refer to dependent or independent SLEs, we only include negative events.

Method

Participants

Participants were same-sex twins from the ongoing Colorado Longitudinal Twin Study (LTS; Rhea et al., 2013; Corley et al., 2019). Twins were recruited through the Colorado Department of Health between 1986 and 1990. Participants were part of the Colorado Twin Registry (CTR) and have participated in several studies of emotional and cognitive development from as young as 5-months old to the current wave. We used life events data from the Center for Antisocial Drug Dependence (CADD) at the University of Colorado (referred to as “age 23”) and from the Colorado Twin and Adoption Study of Life Course Development (CATSLife; referred to as “age 29”).

The total number of individuals with data from one or both of the age 23 and age 29 assessments was 789 (416 female, 373 male; 726/789 identified as White and 715/789 identified as having non-Hispanic ancestry). There were 418 MZ and 371 DZ individuals; 387 complete pairs and 15 singletons. The mean age of the age 23 wave was 22.80 (SD= 1.27), and the mean age of the age 29 data was 29.21 (SD= 1.18). These two time-points were optimal to use because LTS participants completed longitudinal EF batteries at the same time as the life events questionnaires, as part of a separate study on EFs (Rhea et al., 2013).

Measures

EFs.

Participants completed a battery of EF tasks assessing response inhibiting, working memory updating, and mental set shifting. The nine age-23 tasks (antisaccade, stop-signal, Stroop, keep track, letter memory, spatial n-back, number-letter, color-shape and category-switch) and data analyses were described in depth by Friedman et al. (2016), and the six age-29 tasks (antisaccade, Stroop, keep track, letter memory, number-letter, and category-switch) were described by Reineberg et al. (2018), so we only briefly describe them here.

The inhibition tasks involved avoiding a dominant response (antisaccade: avoiding saccading to a cue on one side of the screen, instead immediately saccading to the opposite side in time to identify a briefly appearing target digit before it is masked; stop-signal: avoiding a practiced categorization of an arrow when it turns red; Stroop: naming colors of words instead of reading the words). The updating tasks involved adding and removing information from working memory (keep-track: recalling the most recent exemplars of target categories from a serially presented list of words from 6 categories; letter memory: rehearsing the last four letters in a sequence of up to 13 letters; spatial n-back: indicating whether locations match those n(2 or 3)-trials previous). Lastly, the shifting tasks involved quickly switching between subtasks according to a given cue (number-letter: depending on where on the screen a number-letter pair appeared, categorizing the number even or odd or the letter as consonant or vowel; color-shape: depending on a cue letter (C or S) above a shape on a colored square, categorizing the shape as circle or triangle, or the color as red or green; category switch: depending on a cue symbol appearing above a word, categorizing the word as something bigger than a soccer ball or living or non-living).

Life Events.

At age 23, participants completed an online version of the 75-item Life Events Checklist (LEC) (Sarason et al., 1978). On the first 60 items, participants indicated whether they experienced a certain life event in the past year. On items 61–75, participants indicated whether they had ever experienced each of the 15 more serious life events, such as mother, spouse, or child passing away.

At age 29, participants completed an online version of the 85-item Psychiatric Epidemiology Research Interview (PERI; Dohrenwend et al., 1978). The initial 70 items asked if the participant experienced a certain life event in the past year, and if so to rate how undesirable it was on a scale from 1 to 7 (1 being neutral and 7 being extremely undesirable). Similar to the LEC, the last 15 items (71–85) assessed lifetime adversity. The LEC and PERI items were largely overlapping, with 26 unique items between them. See Supplemental Table SI for a list of all events and endorsement rates per item.

Coding.

The life events data were coded independently by four raters at the Institute for Behavioral Genetics at the University of Colorado Boulder (two graduate students and two professors). Coders rated events on 5-point scales as dependent or independent: 1=completely independent (random) to 5=completely dependent (almost certainly due to characteristics or behavior of the individual); and negative or positive: 1=very positive to 5=very negative, with 3=neutral.

Each rater categorized each event as dependent (rating of 3–5) or independent (rating of 1–2), then we calculated the mode based on the four independent raters’ ratings to determine if an event was dependent or independent. For example, if three raters rated an item as dependent, and one rated the item as independent, we categorized the event as dependent. For positive/negative only, we counted a rating of 3 as neutral. For example, if three raters rated an item as positive and one rater rated an item neutral, we categorized the event as positive. However, if three raters rated an item neutral and one rated the item positive, we categorized the event as positive, according to the valence. Similarly, if two raters rated an item neutral and two rated the item positive, we categorized the event as positive.

Because of our interest in potentially harmful consequences of stressful life events and relations to EFs, we focus here only on negative events, not positive. Variables created were “negative dependent SLEs” and “negative independent SLEs,” but we refer to here as simply “dependent SLEs” and “independent SLEs.” We did not include items in the negative dependent and negative independent variables if raters were split 50/50 across dependent and independent (LEC and PERI n=1) or if all raters rated the item neutral (LEC n=3, PERI n=4).

At age 23, there were 24 past-year negative dependent events, 7 past-year negative independent events, 3 lifetime negative dependent events, and 16 lifetime negative independent events. At age 29, there were 32 past-year negative dependent events, 8 past-year negative independent events, 2 lifetime negative dependent events, and 12 lifetime negative independent events.

Our preregistration plan included negative life events and an aggregate of all life events. We created variables for “total SLEs” at both ages 23 and 29, which were sums of all past-year and lifetime positive, negative, and neutral events experienced per individual. The total SLEs were not significantly correlated with any EF variables (rs= −13–.04, ps= .047 to .890), and their heritabilities mostly reflected dependent SLEs (h²= .67), as 50 out of 74 and 64 out of 85 total events were dependent at ages 23 and 29, respectively. In addition, the total SLEs variables introduced multi-collinearity into models that included all stress variables, so for the majority of analyses, we focused only on negative dependent and independent SLEs.

Reliability.

Inter-rater reliability was calculated based on the proportion of categorical matches for each item between raters. If three raters rated an item as dependent (rated a 3, 4, or 5) and one rater rated the item independent (rated a 1 or 2), the item had a 0.75 proportion match. For positive/negative only we counted a rating of 3 as its own category: neutral. So, if two raters deemed an item neutral (rated it a 3), and two raters deemed an item positive (rated a 1 or 2), the item had a 0.50 proportion match. Our interrater reliability was very good; for dependent/independent, average categorical percent agreement was 97.87%, and for negative/positive, it was 94.68%.

At age 29, the participants rated valence of life events if those events happened to them (1=positive/neutral to 7=extremely undesirable). To verify ratings, we correlated the average positive/negative score from our raters and the average participant rating of those items. The average participant positive/negative rating of the 70 past-year items for age 29 was a significant predictor (r= .88, p<0.001) of the average of the independent raters’ scores. We decided to classify variables based on independent raters because only the age 29, and not the age 23, stressful life events data collected information on valence of events experienced and we wanted to maintain consistency across ages.

Binning.

The life events count data were not normally distributed, with many zeros. Derks et al. (2004) demonstrated ACE twin analyses of right-skewed data are often biased (downward for shared-environment and upward for non-shared environment) and transforming the data does not reduce this bias but may be avoided by using categorical data. Thus, we binned all stressful life events variables using the same criteria for both time points. Negative dependent past year variables were binned as 0, 1–2, 3+ events; negative independent past year variables were binned as 0, 1+ events; negative dependent lifetime variables were binned as: 0, 1+ events; negative independent lifetime variables were binned as: 0, 1+ events; and total events variables were binned as: 0–6, 7–10, 11+ events. These bins were selected to maximize the number of categories with reasonable sample sizes per bin across ages; see Supplemental Table SII for bins.

Statistical Analyses

Analyses were completed with raw data in Mplus 8 (Muthen & Muthen, 1998–2018) using the means and variances adjusted weighted least squares (WLSMV) estimator because of the ordinal life events data. We used confirmatory fit index (CFI) > 0.95 and root-mean-square error of approximation (RMSEA) < 0.06 as indicators of good model fit (Hu & Bentler, 1998). To test significance of parameters, we used p-values of the z-statistic, which is the ratio of each parameter estimate to its standard error, for phenotypic analyses, and chi-square difference tests for genetic models. For all analyses presented in the main text, we used an alpha level of .0083 to correct for multiple testing. We decided upon this alpha because there were six main classes of variables: three latent EFs and two stress classes; 3×2= 6, and .05/6= .0083. We report all nominally significant findings in the Supplemental Materials. For all models with stress, we included sex as a covariate and modelled its effect on the categorical stress variables. For phenotypic models with EF, we included sex as a covariate on the indicator task variables. For genetic models with EF, we regressed each EF task on sex and used the residuals instead of raw data for the analysis to reduce model complexity.

Phenotypic Model Parameterization.

A phenotypic nested factors (orthogonal bifactor) model was used to model the EF factors at both waves. In this model, all tasks load onto a Common EF latent factor, the updating tasks load onto an Updating-specific latent factor and the switching tasks load onto a Shifting-specific latent factor (Friedman et al., 2016). The latent factors do not correlate in the model, so the specific factors can be interpreted as residual covariance among updating and shifting tasks, after accounting for the variance due to Common EF. The nested factors model with latent EFs was included in all subsequent phenotypic and genetic analyses here. We describe the EF data and models for both waves in more depth in the Supplemental Materials.

Phenotypic models used the TYPE=COMPLEX function, which uses a weighted likelihood function and sandwich estimator to correct for twin non-independence and gives corrected standard errors and chi-squares robust to nonindependence (Rebollo, de Moor, Dolan & Boosma, 2006). We analyzed each wave of data separately to obtain correlations between the EF latent variables and stress variables.

To estimate associations between EFs and SLEs across timepoints, controlling for the initial association between the two variables, we analyzed both waves together with two cross-lagged panel models. One model included only past year SLEs and the other model only lifetime SLEs, see Figure 1. In both models, dependent SLEs at 23 was allowed to predict dependent SLEs and all three EFs at 29, and independent SLEs at 23 was allowed to predict independent stress and all three EFs at 29. Because the EF latent factors are orthogonal, each EF at 23 was allowed to predict its respective EF at 29 but did not correlate with other EFs within or across timepoints. Dependent and independent SLEs were allowed to correlate with each other as well as with each EF latent factor within both timepoints. The residual variance of Updating-specific EF at age 29 was zero, so it was not allowed to correlate with other variables.

Fig. 1.

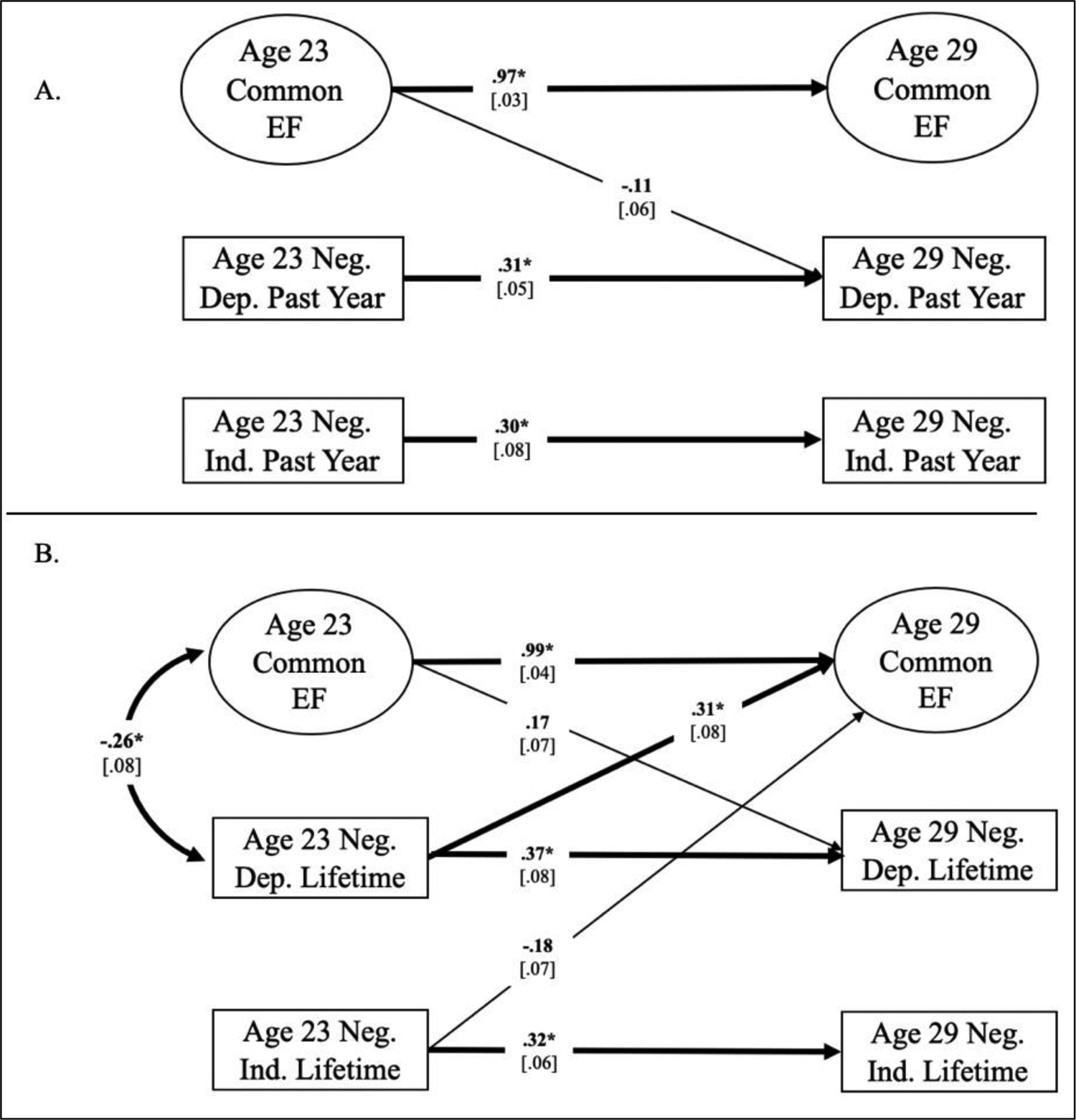
Phenotypic cross-lagged panel models of stress variables and Common Executive Function (Common EF). Panel A shows a model with Common EF and past year stress variables; panel B shows a model with Common EF and lifetime stress variables. Numbers on cross paths are standardized regression coefficients and numbers on double headed arrows are correlation estimates (standard errors are in brackets). For simplicity, only parameters that were at least nominally significant are pictured, the EF measurement model is not shown and Updating-specific and Shifting-specific EF latent factors are not pictured, although they were included in the model. The full models are presented in Figure S4 in the Supplemental Materials. Also not shown are the non-significant regression paths from age 23 EFs to both age 29 stress variables, regression paths from both age 23 stress variables to age 29 EFs, and correlations between each EF and both stress variables within age 23 and age 29, although these were included in the model; Table SX in the Supplemental Materials presents all non-significant regression and correlation coefficients. Thicker lines and * indicate p< .0083; boldface type and thinner lines indicate p< .05.

While our conceptualization of EFs includes Updating and Shifting-specific factors, we were most interested in the relationships of a Common EF latent factor with the number of SLEs experienced. There is more reason to hypothesize Common EF would be related to SLEs, as it encompasses covariance across all EF tasks and more broadly represents the ability to maintain and implement goals. Thus, for simplicity, we focus our discussion on Common EF and SLEs, and do not present Updating-specific and Shifting-specific results even though they were included in models with EF. However, because our preregistration made hypotheses regarding Updating and Shifting-specific abilities, we present those hypotheses and results in the Supplemental Materials.

Genetic Model Parameterization.

For twin analyses, we fit ACE models, where A represents additive genetic variance, C represents shared environmental variance and E represents non-shared environmental variance, which includes random measurement error for non-latent variable. A correlates at 1.0 for MZ twins and 0.5 for DZ twins, C correlates at 1.0 for all twin pairs, and E does not correlate within twin pairs by definition. We first fit univariate ACE models for all stress variables and EFs and report those variance component and model fit statistics in Table I and Supplemental Table SIV.

Table I.

Twin correlations, univariate ACE, ADE and sub-model estimates for stress variables & Common EF

		Twin Correlations		Standardized Paths			Model Fit					Diff test p
Stress Variable		MZ	DZ	A	C/D	E	χ2	df	p	CFI	RMSEA
1. Age 23 Dependent	ACE	.42 [.08]	.16 [.09]	.63 [.13]	.00 [20]	.77 [.05]	8.47	10	.58	1.0	.00	-
	ADE	-	-	.46 [.27]	.45 [.28]	.77 [.05]	8.25	10	.60	1.0	.00	-
2. Age 23 Dependent LT	ACE	.42 [.13]	.18 [.18]	.58 [.22]	.00 [.25]	.76 [.08]	7.16	6	.31	.94	.03	-
	ADE	-	-	.32 [.29]	.56 [.30]	.74 [.08]	6.98	6	.32	.95	.03	-
	AE	-	-	.63 [.11]	-	.76 [.08]	7.14	7	.41	.99	.01	.99
	E	-	-	-	-	.98 [.01]	18.41	8	.02	.59	.13	.00
3. Age 29 Dependent	ACE	.23 [.10]	.08 [.11]	.46 [.18]	.00 [.20]	.89 [.05]	6.81	10	.74	1.0	.00	-
	AE	-	-	.46 [.11]	-	.89 [.05]	6.84	11	.81	1.0	.00	.85
	E	-	-	-	-	1.0 [.00]	5.61	12	.43	.89	.10	.02
4. Age 29 Dependent LT	ACE	.33 [.12]	.17 [.14]	.58 [.24]	.02 [.30]	.81 [.07]	6.35	6	.39	.96	.02	-
	AE	-	-	.58 [.11]	-	.81 [.07]	6.32	7	.50	1.0	.00	.99
	E	-	-		-	1.0 [.00]	15.52	8	.05	.23	.07	.00
5. Age 23 Independent	ACE	−.03 [.15]	−.04 [.16]	0 [.15]	.00 [.12]	1.0 [.03]	3.57	6	.74	1.0	.00	-
6. Age 23 Independent LT	ACE	.62 [.08]	.25 [.12]	.78 [.11]	.00 [.21]	.63 [.06]	5.30	6	.51	1.0	.00	-
	ADE	-	-	.61 [.30]	.50 [.32]	.62 [.07]	5.02	6	.54	1.0	.00	-
	AE	-	-	.78 [.05]	-	.63 [.06]	5.26	7	.63	1.0	.00	.62
7. Age 29 Independent	ACE	.27 [.15]	.05 [.15]	.48 [.33]	.00 [.21]	.88 [.07]	9.25	6	.16	.00	.06	-
	AE	-	-	.48 [.16]	-	.87 [.08]	9.26	7	.23	.00	.04	.99
	E	-	-	-	-	1.0 [.01]	12.37	8	.14	.00	.06	.08
8. Age 29 Independent LT	ACE	.46 [.11]	.29 [.13]	.53 [.26]	.37 [.25]	.75 [.07]	4.43	6	.62	1.0	.00	-
	AE	-	-	.66 [.08]	-	.73 [.07]	4.65	7	.70	1.0	.00	.62
	CE	-	-	-	.59 [.07]	.79 [.05]	5.15	7	.64	1.0	.00	.40
	E	-	-	-	-	.99 [.01]	24.41	8	.00	.40	.11	.00
9. Age 23 Total Events	ACE	.30 [.11]	−.09 [.16]	.67 [.07]	.00 [.07]	.73 [.05]	11.93	10	.29	.96	.03	-
	ADE		-	.00 [.29]	.70 [.21]	.71 [.05]	9.69	10	.46	1.0	.00	-
10. Age 29 Total Events	ACE	.46 [.08]	.17 [.11]	.67 [.12]	.00 [.17]	.74 [.05]	7.92	10	.64	1.0	.00	-
11. Age 23 Common EF	ACE	.85 [.04]	.46 [.09]	.90 [.08]	.20 [.25]	.39 [.07]	420.26	320	.00	.95	.04	-
12. Age 29 Common EF	ACE	.93 [.04]	.27 [.12]	.96 [.02]	.00 [.05]	.29 [.08]	222.68	142	.00	.92	.06	-
	ADE	-	-	.41 [.34]	.87 [.25]	.28 [.08]	219.13	142	.00	.92	.06	-

Standard errors in brackets, bootstrapped for the ACE and ADE paths. Twin correlations do not include sex as a covariate, but sex was included as a covariate in the twin models; ACE and ADE paths may not sum to 1 to the extent that sex accounted for variance (estimates not shown). Significance of twin correlation determined with z-tests (Wald tests); significance of ACE and ADE influences determined with 1 df chi-square difference tests (diff test p) shown in rows with sub-models below full ACE model. All difference tests were compared to the full ACE model, so are based on a chi-square with 1 df for AE or CE models, and with 2 df for E models. C was not estimated for Common EF age 29 model. See Supplemental Figures S2 and S3 and Supplemental SVI for full results of the age 29 EF model, and Friedman et al (2016) for the age 23 EF model. EF = executive function; MZ = monozygotic twins, DZ = dizygotic twins; A = additive genetic; C = shared environmental; D = dominant genetic; E = nonshared environmental variance (including measurement error); LT = lifetime; 23 and 29 indicate mean ages of assessment. Boldface type indicates p< .05. Dashes indicate the parameter was not estimated.

Genetic and environmental models of EF latent factors at age 23 have been presented in Friedman et al. (2016), so we summarize those models in the Supplemental Materials. ACE models of EF latent factors at age 29 have not yet been published, so they are also presented in the Supplemental Materials (Figures S2 and S3). ADE models, where D represents nonadditive genetic variance and correlates at 1.0 for MZ twins and 0.25 for DZ twins, were fit in cases where MZ correlations were greater than 2 times the DZ correlations.

To decompose genetic and environmental components between SLEs, we ran a series of bivariate Cholesky decompositions and only included C for variables where C was estimated > 0 at the univariate level. If C was estimated at 0 for one of the variables at the univariate level, we did not estimate rCs with that variable. Because dropping nonsignificant non-zero parameters in twin models can bias other parameters (i.e. dropping C will upwardly bias A), we reproduced these decompositions without dropping C parameters and rCs in the Supplemental Materials (Table SVI). For all genetic analyses we included bootstrapped standard errors for reference, but based significance assessments on chi-square difference (Δχ²) tests, because they are invariant across alternative parameterizations (e.g., estimating ACE variances vs. ace paths) whereas tests based on estimated standard errors are not (Neale, Heath, Hewitt, Eaves & Fulker, 1989).

For EF–stress Cholesky decompositions, we fit AE models and focused on significant phenotypic relationships. Age 23 latent EFs show little C influence so we did not estimate C in EF-SLE bivariate genetic analyses (Friedman et al., 2016), but reproduce all decompositions with C in the Supplemental Materials. We also did not estimate correlations with Updating-specific E variance at age 23 because it explained less than 2% of the variance. In genetic models with EF latent variables, all EF tasks had specific A and E components. For age 29 EF we tested whether C was significant at the task level; model fit did not change significantly without any individual task C, all Δχ²(1)< 1.33, ps> .250, or when we removed all task-specific and latent-variable Cs from the model, Δχ²(9)= 1.322, p= .998, so we used AE models for age 29 EFs with SLEs.

We calculated bivariate genetic and environmental correlations (rA and rE) by taking the standardized A/E cross-path from the first variable to the second variable, divided by the square root of the total genetic/non-shared environmental variance for the second variable. We also reproduced these decompositions without dropping C and rC parameters in the Supplemental Materials (Table SVII); however, as there was little to no evidence for C in any EF latent variable at these timepoints, we ran into several model convergence issues and ended up having to drop some C parameters, as indicated in that Table.

Power Analysis.

Given our relatively low sample size for behavioral genetic data, we ran Monte Carlo simulations in MPlus to consider power for our main analyses assuming an alpha of 0.05. In our sample of 789 individuals, we had 80% power to detect a phenotypic correlation as low as −.15 between a 2-threshold categorical SLE variable and the Common EF latent factor at age 23. Our sample of 402 twin pairs (213 MZ, 189 DZ) has power of 15%, 28%, 54%, 81% and essentially 100% to detect heritabilities of .25, .36, .49, .64 and .81 for a 2-threshold categorical SLE variable in a full ACE model. However, under the same assumptions, our sample has power of 20%, 52%, 88%, and essentially 100% to detect heritabilities of .09, .16, .25, and .36 of a 2-threshold categorical SLE variable in an AE model. The power to detect genetic correlations between Common EF and SLEs is slightly lower and depends on the heritability of the SLEs. Given that the heritability of dependent SLEs often ranges from 19–51%, we had 80% power to detect genetic correlations as low as 0.20–0.30, depending on the genetic variance of dependent SLEs. As the heritability of independent SLEs is typically much lower (0–18%), we only had 80% power to detect a genetic correlation as low as 0.30–0.40 between Common EF and independent SLEs.

Results and Discussion

Do dependent SLEs have higher heritability and more stability across time?

To examine whether our data reflect previous literature on dependent and independent SLEs, we decomposed the variances of SLEs into genetic and environmental influences with univariate ACE models. We also decomposed the covariances across time to investigate whether there is genetic and/or environmental stability in SLEs. Based on previous research, we hypothesized that dependent SLEs would be explained by both additive genetic and non-shared environmental influences, whereas independent SLEs would be explained primarily by non-shared environmental influences. We also hypothesized that dependent SLEs would show higher genetic stability than independent SLEs, because dependent SLEs are often more heritable.

As shown by full ACE models in Table I, we largely replicated previous literature. Dependent SLEs had moderate heritability estimates (a²= .34–.40), with the exception of negative dependent past-year SLEs at age 29 (a²= .21). Although only one of these was statistically significant in a full ACE models, the other three dependent SLE variables became significantly heritable in AE models. This pattern suggests heritability of dependent SLEs because all but one of the Cs were estimated at zero in the full ACE model, and it was not significant.

Somewhat surprisingly, independent SLEs generally had similar or larger heritability estimates in ACE models (a²= .00–.61) compared to dependent SLEs. Although independent lifetime SLEs at age 29 was not significantly heritable in the full ACE model, A was significant in an AE model. The only timepoint where our hypothesis of greater heritability for dependent SLEs was confirmed was age 23 past year (dependent a²=.40; independent a²=.00).

All dependent SLE variables were also influenced to a large extent by non-shared environment in ACE models (e²= .57–.78); this result was expected because prior literature consistently shows non-shared environment to be a main influence in all life events. Similarly, and consistent with prior literature, all negative independent SLE variables were substantially explained by non-shared environmental influences in ACE models (e²= .40–1.0). Additionally, shared environmental influences were low and non-significant for all variables (c²= .00–.23), which is not surprising given the ages of assessment. Overall, the additive genetic and non-shared environmental variance was similar across all types of SLE variables, which did not confirm our hypothesis that dependent SLEs would have higher heritabilities than independent SLEs.

Given the twin correlations, ADE models were run for age 23 dependent SLEs, age 23 dependent lifetime SLEs, age 23 independent lifetime SLEs, age 23 total SLEs, and age 29 Common EF. Nonadditive genetic influences were not significant for most of these models, and age 23 total SLEs reflected a biologically implausible model (all genetic effects were dominant, with no additive genetic variance). Given that power to detect D in this classic twin design is low, we cannot not rule out genetic dominance or epistasis (Posthuma & Boomsma, 2000).

At the phenotypic level, both dependent and independent SLEs were moderately stable, which makes sense given the moderate heritability of most SLE variables in this analysis. Figure 1 shows the past year and lifetime cross-lagged panel models where age 23 SLEs predicted age 29 SLEs (dependent SLEs cross wave β_{past year}= .31, p<.001, β_lifetime= .37, p<.001; independent SLEs cross wave β_{past year}= .30, p<.001, β_lifetime= .32, p<.001). Constraining the cross-wave regression paths between dependent and independent SLEs to be equal resulted in non-significant difference tests, Δχ²(1)_{past year}= 0.02, p=.900; Δχ²(1)_lifetime= 0.28, p=.595. Thus, we do not have evidence to conclude that dependent SLEs are phenotypically more stable than independent SLEs.

If dependent SLEs are partially influenced by genetics, we would expect stability in the relative number of dependent SLEs experienced across time, and the shared variance between dependent SLEs across time to be mostly genetic rather than reflecting environmental influences that tend to be short lived. In contrast, if the number of independent SLEs is more influenced by nonshared environment, they would likely not be stable across time, due to the more typical time-specific effects of nonshared environment. However, because both additive genetic influences and phenotypic stability were similar across dependent and independent SLEs, we might expect these data to reflect genetic stability for both types of SLEs.

Table II presents the key cross-wave rAs and rEs between SLE variables. Figure 2 shows the bivariate decompositions between dependent past year SLEs at age 23 and 29 (Panel A) and independent past year SLEs at age 23 and 29 (Panel B). Here we compare the bivariate heritabilities with bootstrapped standard errors (from the MPlus cinterval(bootstrap) option) and not the rGs; the bivariate heritability is more informative because in some cases genetic correlations were 1 or close to 1, but the heritability of one of the traits was near zero.

Table II.

Genetic and environmental stability of stress variables across waves

Bivariate Decomposition	rA	rE	Biv A	Biv E	Pheno r
Age 23 Dependent-Age 29 Dependent	.94* [.15]	.07 [.09]	.28* [.06]	.05 [.06]	.32* [.05]
Age 23 Dependent LT-Age 29 Dependent LT	.78* [.22]	−.03 [.17]	.29* [.09]	−.02 [.10]	.28* [.08]
Age 23 Independent-Age 29 Independent	1.0 [.87]	.20 [.13]	.05 [.07]	.17 [.11]	.22* [.08]
Age 23 Independent LT-Age 29 Independent LT	.55* [.17]	.01 [.18]	.29* [.09]	.00 [.08]	.29* [.06]

Shared environment (C) correlations were not estimated in decompositions but these same decompositions without dropping all other C parameters are reproduced in Supplemental Table SVI. rA=genetic correlation; rE=nonshared environmental correlation; BivA= bivariate heritability—the phenotypic correlation explained by the genetic correlation; Biv E= bivariate nonshared environmentality—the phenotypic correlation explained by the nonshared environmental correlation; 23 and 29 indicate mean ages of assessment; LT=lifetime stress variable. For each pair of variables, Biv A + Biv E equals the model phenotypic correlations, which are very close to those in Supplemental Table SIII (significance of Pheno r determined by Table III for consistency).

^*p< 0083, boldface p< .05; determined with chi-square difference tests dropping the relevant Cholesky cross-paths, but bootstrapped standard errors shown in brackets for reference. When standard errors disagree with chi-square difference tests, we deemed significance from chi-square difference tests.

Fig. 2.

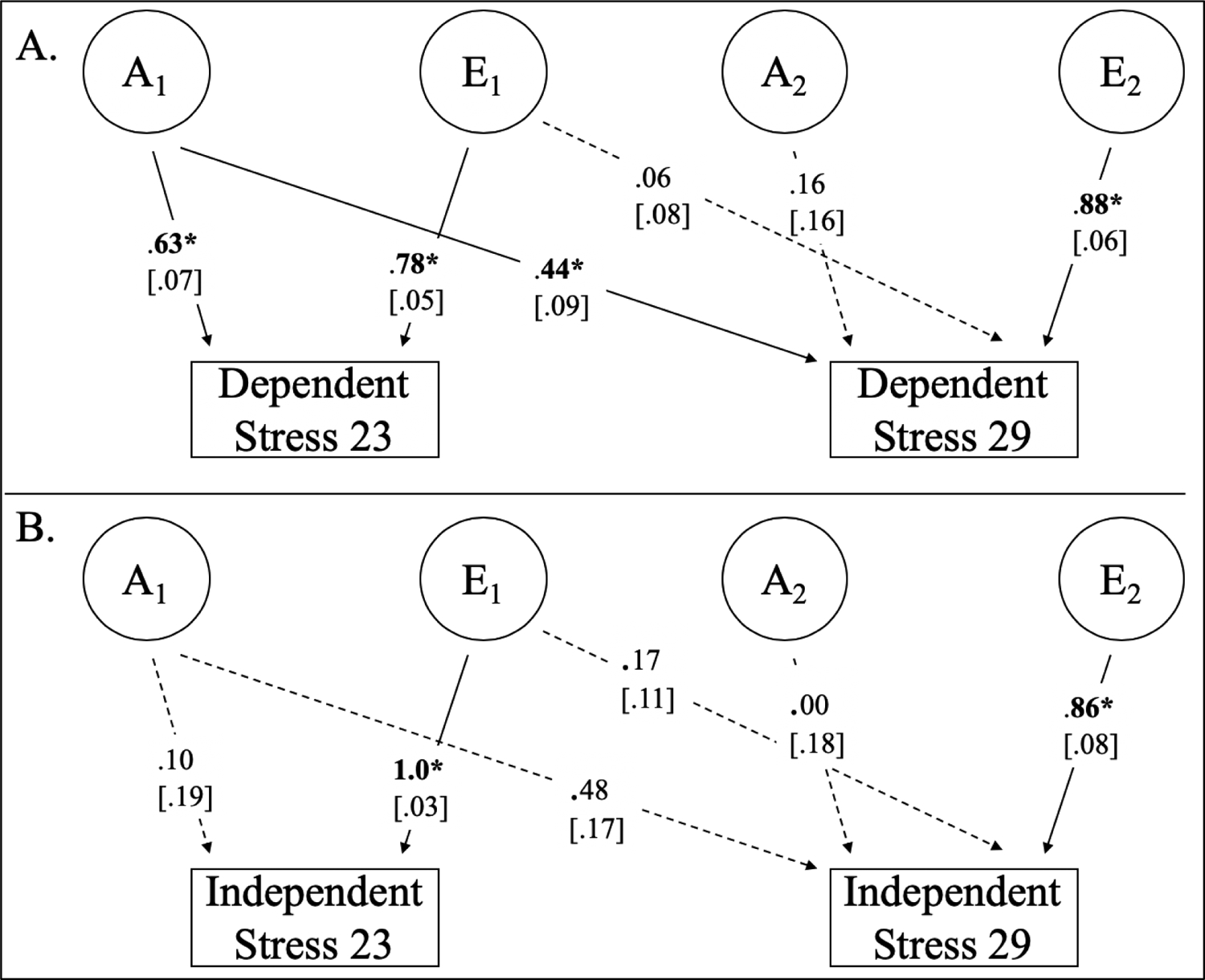
ACE models of stability of stress variables from age 23 and 29. Panel A shows a Cholesky decomposition of dependent past-year stress variables at ages 23 and 29. Panel B shows a Cholesky decomposition of independent past-year stress variables at ages 23 and 29. Shared environment (C) was only estimated if univariate models showed non-zero C estimates. For simplicity, only one twin is depicted. Standardized estimates are shown, significance was determined by dropping the relative path and computing a 1 degree of freedom chi square difference test, with bootstrapped standard errors in brackets for reference. When standard errors disagree with chi-square difference tests, we deemed significance from chi-square difference tests. *p< .0083; boldface type indicate p< .05; dashed lines indicate p>.05.

The age 23 dependent SLEs-age 29 dependent SLEs bivariate heritability (bivA=.278, 95% CI=.141, .374) was higher than the age 23 independent SLEs-age 29 independent SLEs bivariate heritability (bivA=.047, 95% CI=−.111, .173). Based on Zou (2007)¹, we estimated the 95% CI for the difference (.231) as .045 to .416. As the lower bound did not include zero, it suggests that the bivariate heritability is significantly higher for dependent than independent life events. However, the bivariate heritabilities for lifetime SLEs were similar to each other (23 dependent lifetime SLEs-29 dependent lifetime SLEs bivA=.292, 95% CI=.084, .437; 23 independent lifetime SLEs-29 independent lifetime SLEs bivA=.288, 95% CI=.120, .420). The 95% CI for their difference (.004) was −.242 to .251, suggesting that the bivariate heritability between dependent lifetime SLEs is not higher than for independent lifetime SLEs.

All combinations of cross-wave SLE rAs and rEs are presented in Supplemental Table SVIX. Additionally, we reproduced the bivariate SLE decompositions from Table II in Supplemental Table SVI without dropping C parameters. The only discrepancy was that the correlation between age 23 dependent and age 29 dependent SLEs became only nominally significant (rA= 1.0, p=.009).

Are dependent SLEs more phenotypically and genetically associated with EFs, compared to independent SLEs?

We hypothesized that number of dependent SLEs would be more related to Common EF than independent SLEs because those who have difficulty carrying out goal-directed behavior and controlling impulses may have more incidences of stressful situations brought about by those characteristics. Table III presents correlations between SLEs and Common EF from a model where all stress variables were allowed to correlate with all three EFs within and across waves, χ²(145)= 204.77, p< .001, CFI= .974, RMSEA= .023. See Supplemental Table SIII for phenotypic correlations of all SLE variables.

Table III.

Phenotypic correlations of stress variables with Common EF

	Correlation with Common EF
Stress Variable	Age 23	Age 29
1. Age 23 Dependent	−.09 [.06]	−.08 [.07]
2. Age 23 Dependent Lifetime	−.14 [.08]	−.04 [.06]
3. Age 29 Dependent	−.14 [.06]	−.03 [.07]
4. Age 29 Dependent Lifetime	.05 [.07]	.15 [.07]
5. Age 23 Independent	.00 [.07]	−.02 [.08]
6. Age 23 Independent Lifetime	−.07 [.06]	−.04 [.06]
7. Age 29 Independent	−.01 [.07]	−.01 [.07]
8. Age 29 Independent Lifetime	.07 [.07]	.10 [.07]

Standard errors in brackets. Models included all executive function (EF) latent variables, but only results with Common EF are shown here. All stress variables were allowed to correlate with each other as well as all EF latent variables. χ²(145)= 204.774, p=.0008, RMSEA= .023, CFI= .974. *p< .0083, boldface type indicates p<.05.

No correlations were statistically significant after multiple correction in the SLE and EFs correlational model. A surprising pattern in the nominally significant results was that dependent SLEs at age 29 was negatively correlated with Common EF at age 23 (r= −.14, p=.015), but dependent lifetime SLEs at age 29 was positively correlated with Common EF at age 29 (r=.15, p=.036). The opposite direction of these correlations is difficult to explain as Common EF at age 23 and 29 were highly correlated (r=.97 p<.0001), and dependent SLEs at age 29 and dependent lifetime SLEs at age 29 were moderately correlated (r=.32, p=.0001). One or both of these correlations could reflect a false positive, given that they did not meet correction for multiple tests.

In addition, we constrained the correlations between dependent SLEs and Common EF to be equal to the correlations between independent SLEs and Common EF, and no chi-square difference tests were significant, Δχ²s(1)= 0.00–2.47, ps= .116–.947. Thus, we do not have evidence to conclude that Common EF is phenotypically more related to the number of dependent SLEs compared to independent SLEs. Although dependent SLEs were not more phenotypically related to Common EF than independent SLEs, we ran bivariate genetic models of SLEs and EFs to see if the associations reflect different etiologies.

Individual differences in EFs are both heritable and stable by late adolescence, but as shown in Friedman et al. (2016), still sensitive to environmental influences. We reproduced the unity/diversity EF model used in Friedman et al. (2016) at age 23 with the age 29 data. See Table I for univariate ACE estimates and MZ/DZ correlations of Common EF at both age 23 and 29, and the Supplemental Materials for a brief description of the age 23 EF data and full description of the genetic and phenotypic model of latent EFs at age 29 (Figures S1–S3).

We expected associations between EFs and number of dependent SLEs to be mostly genetic and associations between EFs and number of independent SLEs to be mostly environmental. Table IV presents genetic and environmental correlations between SLEs and Common EF, as well as the bivariate heritability and environmentality (the phenotypic correlations predicted by the genetic and non-shared environmental correlations). Although dependent SLEs at age 23 was nominally genetically correlated with Common EF at age 23 (rA= −.29, se=.13) as was independent lifetime SLEs and Common EF at age 23 (rA= −.21 se=.10), no associations survived multiple correction. There were no major differences in these decompositions when we did not drop C parameters (see Supplemental Tables SVII).

Table IV.

Genetic and environmental correlations between stress variables and Common EF

Stress variable	With 23 Common EF					With 29 Common EF
	rA	rE	Biv A	Biv E	Pheno r	rA	rE	Biv A	Biv E	Pheno r
1. Age 23 Dependent	−.29 [.13]	.33 [.34]	−.17 [.07]	.08. [05]	−.09 [.06]	−.15 [.16]	.05 [.26]	−.09 [.09]	.02 [.07]	−.07 [.07]
2. Age 23 Dependent Lifetime	−.28 [.17]	.07 [.50]	−.17 [.10]	.02 [.08]	−.16 [.08]	−.16 [.22]	.27 [.34]	−.10 [.12]	.08 [.09]	−.02 [.09]
3. Age 29 Dependent	−.21 [.19]	−.15 [.41]	−.09 [.08]	−.04 [.06]	−.13 [.06]	−.38 [.24]	.31 [.24]	−.16 [.09]	.11 [.07]	−.06 [.07]
4. Age 29 Dependent Lifetime	.02 [.17]	.16 [.44]	.01 [.08]	.04 [.07]	.05 [.07]	−.03 [.21]	.45 [.26]	−.01 [.10]	.14 [.08]	.13 [.07]
5. Age 23 Independent	−.58 [.47]	.08 [.44]	−.04 [.08]	.02 [.07]	−.01 [.07]	.19 [.37]	−.15 [.30]	.03 [.09]	−.06 [.09]	−.02 [.08]
6. Age 23 Independent Lifetime	−.21 [.10]	.55 [.31]	−.16 [.08]	.11 [.05]	−.05 [.06]	−.10 [.13]	−.10 [.37]	−.07 [.10]	−.02 [.07]	−.10 [.07]
7. Age 29 Independent	−.14 [.26]	.18 [.45]	−.07 [.10]	.05 [.08]	−.02 [.08]	−.02 [.30]	.02 [.35]	−.01 [.12]	.01 [.10]	.00 [.09]
8. Age 29 Independent Lifetime	.06 [.14]	.13 [.47]	.04 [.09]	.03 [.07]	.07 [.07]	.05 [.17]	.17 [.35]	.03 [.10]	.05 [.08]	.08 [.08]

Estimates are derived from Cholesky decompositions. Shared environmental (C) correlations were not estimated because of zero or near-zero C variances for executive functions (EF) and stress. Models included all EF latent variables, but only results with Common EF are shown here. rA= genetic correlation; rE= nonshared environmental correlation; Biv A= bivariate heritability—the phenotypic correlation explained by the genetic correlation; Biv E=bivariate nonshared environmentality—the phenotypic correlation explained by the nonshared environmental correlation. For each pair of variables, Biv A + Biv E equals the model phenotypic correlations, Pheno r, which are very close to those in Table III (significance of Pheno r determined by Table III for consistency). *p<.0083, boldface type indicates p<.05; determined with chi-square difference tests dropping the relevant Cholesky cross-paths but bootstrapped standard errors are shown in brackets for reference. When standard errors disagree with chi-square difference tests, we deemed significance from chi-square difference tests.

Do dependent SLEs and EFs prospectively predict each other in a longitudinal cross-lag model?

Although we found few phenotypic relationships between latent EFs and number of SLEs, one of our main questions was whether relationships between stress and EFs are bidirectional. Thus, even though significant phenotypic correlations between number of SLEs and EFs were few and small, we estimated two longitudinal cross-lagged models: one for past year stress variables and one for lifetime stress variables. We hypothesized there might be a bidirectional relationship between number of dependent SLEs and Common EF across time; however, if a relationship existed between number of independent SLEs and Common EF it would only be unidirectional such that more independent SLEs would lead to later lower Common EF because of the potential for stressors to impair EF via a mechanism such as rumination. Although Common EF is highly stable, there is evidence for change in early adulthood (Friedman et al., 2016), particularly attributable to new nonshared environmental influences. This change, though limited, leaves room for the possibility of effects of stress on Common EF, particularly to the extent that those effects are environmental.

The past-year cross-lagged model fit well, χ²(110) = 175.18, p< .001, CFI= .968, RMSEA= .027; Figure 1A, but no associations were significant after multiple testing correction, consistent with the correlational model. See Supplemental Table SX for nominal associations.

The lifetime SLE cross-lagged panel model also fit well, χ²(110) = 181.07, p<0.001, CFI= .965, RMSEA= .029; Figure 1B. Within age 23, controlling for independent lifetime SLEs, dependent lifetime SLEs correlated with Common EF (r= −.26, p= .001). Across time, controlling for independent lifetime SLEs, dependent lifetime SLEs at age 23 significantly predicted EF at age 29 (EF β= .31, p= .0001). See Supplemental Table SX for nominal associations.

It is surprising that these associations emerged in the longitudinal cross-lagged panel model given the modest stability of dependent SLEs and lack of associations in the cross-sectional correlational model. One possibility is that small effects at the later time point were more likely to be significant due to large reductions in error achieved by including the stability paths, which were highly stable for EFs. The positive effect of number of dependent SLEs at age 23 on Common EF at age 29 could be due to the relation of dependent SLEs with Common EF at timepoint 2 not being as strong as at timepoint 1, despite the stability in both SLEs and Common EF. We cannot conclude much from these results given the dearth of other significant findings in both the correlational and cross-lagged model.

General Discussion

This study examined the etiology and stability of individual differences in the number of dependent and independent SLEs, and their cross-sectional and longitudinal associations with EF latent variables. We replicated previous research (Billig et al., 1996; Rice et al., 2003; Sobolewski et al., 2001; Kendler et al., 1999; Silberg et al., 2001, Plomin et al., 1990) finding that the number of dependent SLEs had both genetic and non-shared environmental influences, whereas, inconsistent with most prior literature, the number of independent SLEs had moderate genetic and non-shared environmental influences. Extending this literature, we found that both past year and lifetime number of dependent SLEs showed significant genetic stability across waves. Although we did also find significant genetic stability across waves for number of lifetime independent SLEs, some stability in the number of lifetime events reported across waves is not surprising. Comparing confidence intervals demonstrated dependent SLEs had a higher bivariate heritability than independent SLEs for past year but not lifetime variables.

The finding of genetic stability is still novel and important; to our knowledge, prior literature has not investigated this topic. Much of the literature treats stress as a purely environmental factor, but our results and prior studies suggest that different types of stressors have distinct etiologies. This distinction may have large implications for the relationships of stress with other biological and behavioral outcomes such as stress response or psychopathology.

We hypothesized dependent SLEs may have a bidirectional negative relationship with Common EF, such that more stress may lead to worse EF, and worse EF may also bring about more stress. However, we did not find significant negative longitudinal phenotypic relationships between number of dependent SLEs and Common EF after multiple testing correction. In a model of lifetime SLEs, dependent SLEs at age 23 positively predicted Common EF at age 29. In most cases, dependent SLEs and EFs also did not exhibit the negative genetic relationship we hypothesized, but we did find a nominally significant negative genetic correlation (rA= −.29, se=.19) between dependent SLEs at age 23 and Common EF at 23 indicating more research should be done on this topic.

Another common classification scheme of SLEs is network vs. personal SLEs, where network SLEs reflects stress that may be introduced into one’s life via someone close to them, and personal SLEs are those that directly happen to the individual (Kendler, Karkowski & Prescott, 1999). While these categories do not translate immediately to independent and dependent SLEs, the general idea is similar in that personal and dependent SLEs may both be partially evoked by certain characteristics of the individual, but personal SLEs may also be completely independent and random. One would expect neither network nor independent SLEs to be evoked by the individual in most cases, although network SLEs might be dependent to the extent that the characteristics and behaviors of individuals with whom one associates are related to one’s own characteristics (e.g., assortative mating). Our finding of genetic stability of dependent SLEs may have implications to be extended to personal SLEs, as they have also been found to have genetic influences (Colodro-Conde et al., 2018). It is important for future work to consider the types of SLEs being analyzed and that not all SLEs should be treated as purely environmental.

Limitations and future directions.

Some of the major limitations of this study come from the SLE measures. Our SLE variables had non-normal distributions, so to correct for this we binned them into ordinal variables. However, not all of the variables had the same binning criteria because many of them showed different distributions. It is possible that the measures we used did not adequately capture variation in dependent and independent past year and lifetime SLEs. Also, there were fewer independent life events items overall compared to dependent life events items (27 and 33 items respectively); this was especially evident in the past year variables (8 independent items compared to 28 dependent items). It is also possible that our community-based sample was a relatively low-stress sample.

A related limitation is that the SLE data is perhaps less consistent or reliable than desirable. Of the 15 independent lifetime SLE items endorsed at age 23 that had a similar item at age 29, 41% of the time individuals who endorsed a lifetime event at age 23 endorsed the same event at age 29. While the concordance of endorsement rate was 100% for the item “found out cannot have children,” it was still surprisingly low for other items, such as “father died” or “suffered miscarriage” (63% and 47% respectively). It is not unreasonable that the items “had serious accident or injury” or “child had serious accident or injury” had relatively low concordance of endorsement rates (33% and 0% respectively), because the endorsement rates at age 23 were small and what one considers a serious accident or injury could change over the years. The low concordance of endorsement rates could also be attributed to the large time lag, as perhaps some of the events endorsed at age 23 were not remembered at age 29, or that participants did not pay attention to the instructions that discerned between past year and lifetime events.

While this is a limitation with the data, we also consider it a valuable opportunity to further analyze the reliability of longitudinal stressful life events data. Many similar studies are cross-sectional and thus do not have the chance to conduct this type of analysis. Our findings of low reliability, which likely translates to increased error variance and non-shared environmental influences in genetic analyses, are important for the stressful life event literature to consider going forward.

Finally, although the longitudinal assessments were a major advantage, the time lag of 5–6 years between waves also may not have been optimal to look at changes in SLEs and EFs. It is possible that a shorter time lag would reveal more robust effects and associations across time.

Although we did not find support for a relationship between dependent SLEs and EFs, as Snyder and Hankin (2016) did, EFs have been suggested as transdiagnostic risk factors for psychopathology via dependent SLEs (Snyder et al., 2019). Therefore, a logical next step could be to look at SLEs in relation to both EFs and psychopathology in a genetically informative design. In addition, given suggestion from brain data that stress may have distinct impacts on cognitive outcomes at different points in the lifespan (Lupien et al., 2009), similar analyses in a younger, still developing sample may yield different patterns of results.

Conclusions

This study added to the literature of SLEs and EF by utilizing twin models to look at dependent and independent SLEs and latent EF variables in a longitudinal analysis. Notably, we found genetic stability in individual differences in the number of past year dependent SLEs experienced from age 23 to age 29, demonstrating that certain types of negative SLEs may be partially genetically evoked and more persistent across time. Although not as strong as expected, the association between dependent SLEs and EFs needs to be investigated further. The genetic stability of dependent SLEs and small but significant negative genetic association with early adult Common EF may provide insight regarding the kinds of behaviors that may lead to more persistent stressors.