Structured layer surface segmentation for retina OCT using fully convolutional regression networks

Abstract

Optical coherence tomography (OCT) is a noninvasive imaging modality with micrometer resolution which has been widely used for scanning the retina. Retinal layers are important biomarkers for many diseases. Accurate automated algorithms for segmenting smooth continuous layer surfaces with correct hierarchy (topology) are important for automated retinal thickness and surface shape analysis. State-of-the-art methods typically use a two step process. Firstly, a trained classifier is used to label each pixel into either background and layers or boundaries and non-boundaries. Secondly, the desired smooth surfaces with the correct topology are extracted by graph methods (e.g., graph cut). Data driven methods like deep networks have shown great ability for the pixel classification step, but to date have not been able to extract structured smooth continuous surfaces with topological constraints in the second step. In this paper, we combine these two steps into a unified deep learning framework by directly modeling the distribution of the surface positions. Smooth, continuous, and topologically correct surfaces are obtained in a single feed forward operation. The proposed method was evaluated on two publicly available data sets of healthy controls and subjects with either multiple sclerosis or diabetic macular edema, and is shown to achieve state-of-the art performance with sub-pixel accuracy.

1. Introduction

Optical coherence tomography (OCT), which uses light waves to rapidly obtain 3D retina images, is widely used in the clinic. Retinal layers are important biomarkers for retinal diseases like diabetic macular edema (DME) (Chiu et al., 2015) or neurological diseases like multiple sclerosis (MS) (Saidha et al., 2011b; Rothman et al., 2019). Global disease progression for MS can be assessed by both peripapillary retinal nerve fiber layer (pRNFL) and ganglion cell plus inner plexiform layer (GCIP) thicknesses (Saidha et al., 2011a, 2012). Since manually segmenting these images is time consuming, fast automated retinal layer segmentation tools are routinely used instead. A major goal of an automated segmentation tool is to obtain smooth, continuous retinal layer surfaces with the correct anatomical ordering as shown in Fig. 1; these results can then be used for thickness analysis (Antony et al., 2016a) or surface shape analysis (Lee et al., 2017b).

Fig. 1.

A B-scan with nine manually delineated retinal surfaces separating the following retinal layers: the retinal nerve fiber layer (RNFL); the ganglion cell layer (GCL) combined with the inner plexiform layer (IPL), denoted as GCIP; the inner nuclear layer (INL); the outer plexiform layer (OPL); the outer nuclear layer (ONL), the inner segment (IS); the outer segment (OS); and the retinal pigment epithelium (RPE). Surfaces between these layers are identified by hyphenating their acronyms. The other named surfaces are: the inner limiting membrane (ILM); the external limiting membrane (ELM); and Bruch’s Membrane (BM). Finally, above the RNFL is the vitreous and below the BM is the choroid.

State-of-the-art methods are usually based on a two step process: pixel-wise labeling and post processing. In the first step, a trained classifier (e.g, random forest (RF) or deep network) is used for coarse pixel-wise labeling; there are two types of classifiers. In the first, the classifier labels each pixel as being one of the layer classes, a lesion (including edema or fluid), or background. Two problems with these pixel-wise labeling schemes are that layer topology is not guaranteed and that continuous and smooth surfaces separating the retinal layers are not obtained. Roy et al. (2017) used a fully convolutional network (FCN) to label each pixel into eight layer classes, edema, and background; Lee et al. (2017a) and Schlegl et al. (2018) each used an FCN to segment retinal edema and fluids; and Venhuizen et al. (2017) used an FCN to segment the whole retina without segmenting each layer. The second type of classifier labels pixels as surfaces (i.e., boundaries between retinal layers or between the retina and its background) or background (i.e., non-boundaries). Examples of this include RFs (Lang et al., 2013, 2015), convolutional neural networks (CNNs) (Fang et al., 2017), and recurrent neural networks (RNN) (Kugelman et al., 2018). They classify the center pixel of a patch as being a surface or background. Patch based classification is computationally inefficient compared to FCNs, but classifying the one-pixel wide surface across the whole image using an FCN can have class imbalance issues.

The second step in typical retinal layer segmentation methods is a post processing of the surface classification results using either level sets (Carass et al., 2014; Novosel et al., 2015; Carass and Prince, 2016; Novosel et al., 2017; Liu et al., 2018, 2019) or graph methods (Garvin et al., 2009; Chiu et al., 2010; Lang et al., 2013, 2014, 2015; Antony et al., 2014, 2016b; Lang et al., 2017) to obtain final smooth, continuous, and topologically correct surfaces. In order to build a topologically correct graph (Garvin et al., 2009; Lang et al., 2013), surface distances and smoothness constraints, which are spatially varying, are empirically assigned and the final surfaces are extracted using a minimum s-t cut. Building the graph, as shown in (Li et al., 2006), is not trivial. A simpler shortest path graph method (Chiu et al., 2010) was used by (Fang et al., 2017; Kugelman et al., 2018). However, this method extracts each surface separately, which does not guarantee retinal layer ordering especially at the fovea where the distance between the surfaces can be zero. We summarize the aforementioned methods in Fig. 2.

Fig. 2.

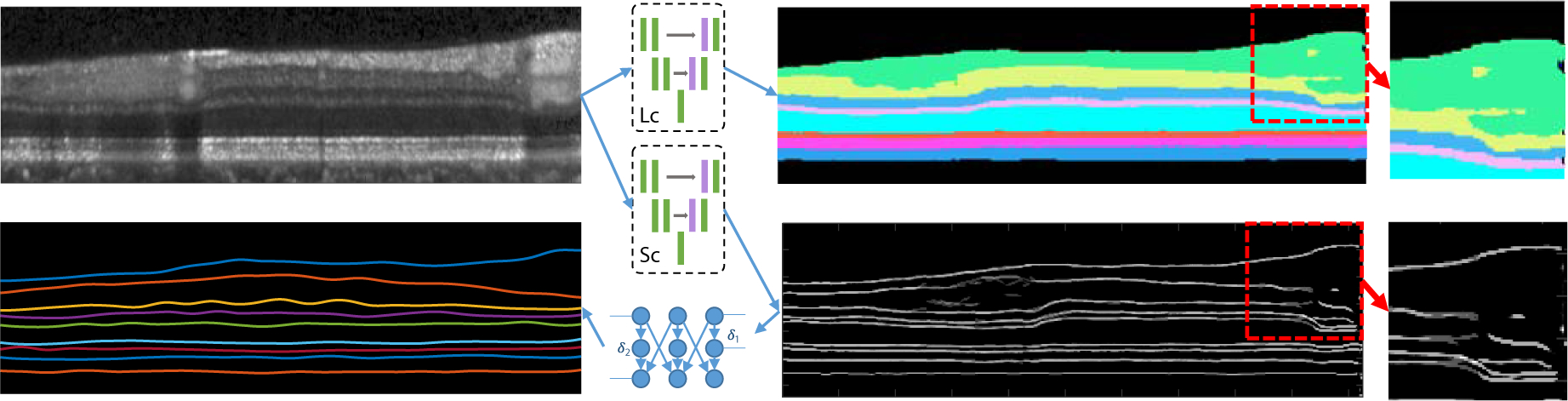
An illustration of conventional pixel-wise labeling schemes. A deep network layer classifier (Lc) classifies each pixel into each layer class or background, but the layer topology is not guaranteed as shown in the red dotted box. A deep network surface classifier (Sc) classify each pixel into each surface class or background, but the generated surfaces may be discontinuous. The final structured surfaces are extracted using graph based post processing. The classification results are multiple probability maps but are combined in a single image for visualization simplicity.

Whereas the retinal layers have strict anatomical orderings, methods that use pixel-wise labeling can have incorrect layer topologies, as shown in Fig. 2. For example, the pixels labeled as GCIP (GCL+IPL) should not have smaller row indexes than the pixels labeled as RNFL (see Fig. 1 for layer definitions) on the same A-scan, since the RNFL is above the GCIP (in this conventional OCT presentation of the human retina). Pixel-wise labeling methods like a conventional FCN do not explicity guarantee the correct topological relationships of the retinal layers. To address this general issue, Ravishankar et al. (2017) used an auto-encoder to learn object shape priors and BenTaieb and Hamarneh (2016) used a special training loss to incorporate object topological relationships. On the other hand, He et al. (2017) used a post-processing network to iteratively correct the retinal layer topology. These methods can alleviate segmentation topology problems but they cannot guarantee the layer orderings and the final surfaces are implied but not directly obtained.

An alternate strategy, is to directly focus on the retinal layer surfaces. For retinal OCT images, each such surface intersects with each image column (A-scan) at only one position; thus, for a B-scan image with N columns, a surface can be represented by a 1D vector of length N representing the surface position at a certain column. As long as the surfaces satisfy the topological ordering at every column, the layer segmentation bounded by the surfaces is guaranteed to maintain the proper ordering. However, unless otherwise constrained, algorithms that focus on labeling the surface pixels will often have discontinuities, as shown in Fig. 2, and the result is also not topologically correct.

The aforementioned limitations of pixel-wise labeling are solved with model-based post-processing like graph methods (Garvin et al., 2008; Lang et al., 2013). However, such methods currently cannot be integrated into a deep network, and thus cannot be optimized end to end together with the pixel-wise classifier. Also, the inference for the graph limits the time efficiency and flexibility of the deep learning pipeline. Moreover, graph methods require special hand tuning of parameters for optimal use, which can be cohort and pathology specific (Lang et al., 2017). These attributes make the graph methods harder to optimize when large lesions exist within the layers or when the retinal geometry is otherwise unusual. He et al. (2019b) use a second network to replace the graph method to obtain smooth, topology-guaranteed surfaces, but the fully connected regression requires much more computation and is performed as a post-processing step, which could render the initial segmentation sub-optimal.

In this paper, we propose a unified framework for structured layer surface segmentation which can output smooth structured continuous layer surfaces with the correct topology in an end-to-end deep learning scheme; an earlier version of this work was reported in He et al. (2019a) which we have extended and validated in this work. We use an FCN to model the position distribution of the surfaces and use a soft-argmax method to infer the final surface positions. The proposed fully convolutional regression method can obtain sub-pixel surface positions in a single feed forward propagation without any fully-connected layers (thus requiring fewer parameters than He et al. (2019b)). Our network has the benefit of: 1) being trained end-to-end; 2) improving accuracy against the state-of-the-art; and 3) being light-weight because it does not use a fully-connected layer for regression. We also perform a surface slope analysis to show that the surface connectivity is well constrained, even without explicit constraints, as in the graph methods.

2. Method

As shown in Fig. 3, our network has two output branches. The first branch outputs a pixel-wise labeling segmentation of layers and lesions and the second branch models the distribution of surface positions and outputs the positions of each surface at each column (A-scan). These two branches share the same feature extractor: a residual U-Net (Ronneberger et al., 2015). The input to the network is a three-channel image. One channel is the original flattened OCT image (Lang et al., 2016, 2018), and the other two inputs are the normalized spatial positions of each pixel to provide additional spatial information, see Fig. 3.

Fig. 3.

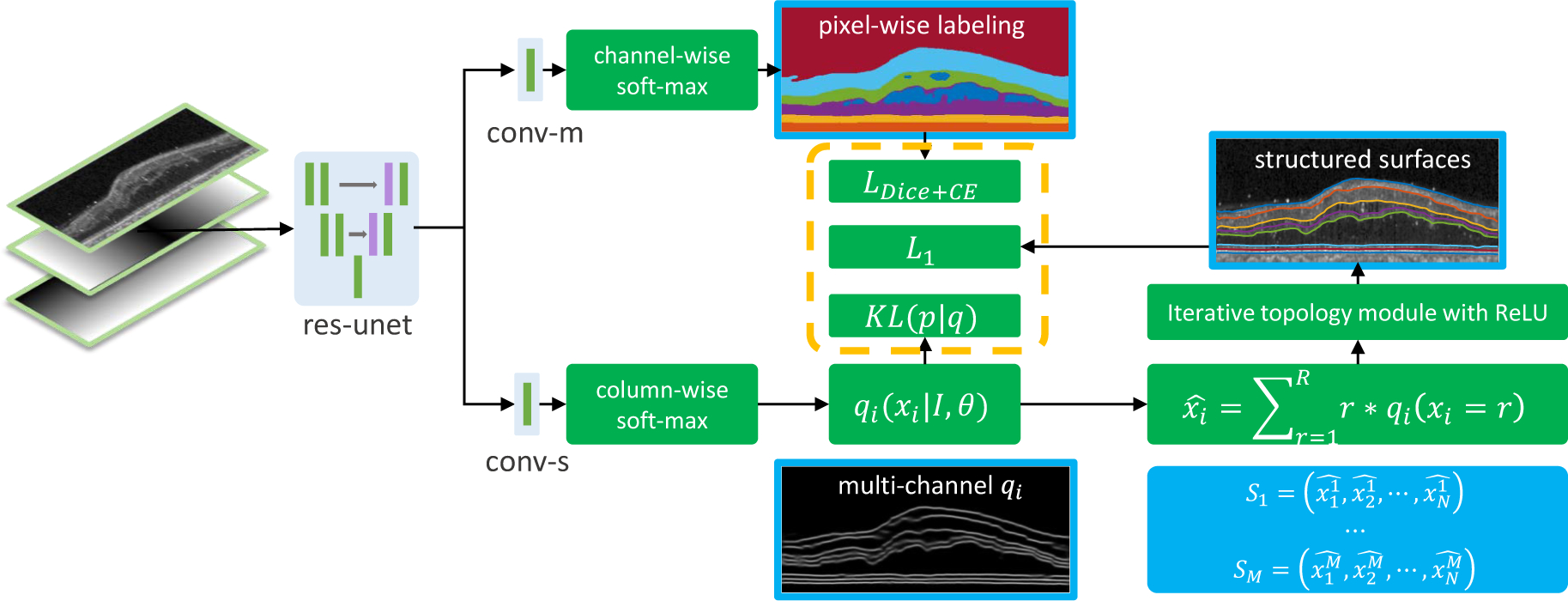
A schematic of the proposed method. The input is a three channel image (flattened B-scan, normalized x and y coordinates). The features extracted by the res-unet (a residual U-Net) are shared by the two output branches. The top branch (conv-m) uses channel-wise softmax to output segmentation probability maps for the layers, backgrounds (choroid or vitreous), and lesions. The bottom branch (conv-s) uses column-wise soft-max to produce variational q_i’s and then uses soft-argmax and iterative ReLU to produce M structured surfaces.

2.1. Preprocessing

The input 3D OCT scan has blood vessel shadows removed and is contrast enhanced (Girard et al., 2011). To reduce memory usage and normalize surface positions to a certain range, we estimate Bruch’s membrane (BM) using an intensity gradient method (Lang et al., 2013) and shift (with interpolation) each column of the original B-scan (size of R_o × N) vertically such that the BM has the same depth position at each column. We then crop the image from 60 microns (around 15 pixels) below BM to R pixels above that position. We refer to this modified image of size R × N, as being flattened (Lang et al., 2016, 2018). Each pixel in the image has a row and column index j and i. We normalize j and i to [0, 1] and [−0.5, 0.5], respectively, with j/R and (i − N/2)/N. These two normalized coordinate maps are concatenated with the flattened image as the second and third network inputs.

2.2. Surface position modeling

Given a B-scan image, I, and a ground truth surface represented by row indexes $x_1^g,\dots ,x_N^g$ across N columns (correspondingly N A-scans), a conventional pixel-wise labeling scheme builds a surface probability map H. A deep network $f(\cdot ;\mathcal{W})$, with weights $\mathcal{W}$, is trained to predict H by minimizing the sum of a conventional pixel-wise loss $\mathcal{L}$ over each pixel,

$$\text{minimize}\sum _{i,j}\mathcal{L}\left(H^{i,j}(I),f^{i,j}(I;\mathcal{W})\right)$$

where,

$$H^{i,j}(I)=\{\begin{array}{ll}1,\hfill & i=(1,\dots ,N),j=x_i^g,\hfill \\ 0,\hfill & \text{ else. }\hfill \end{array}$$

Ideally, a surface will be continuous across the image and intersect each column only once. However, the generated probability map may produce zero or multiple positions with high prediction probability in a single column, thus breaking this condition. Extreme class imbalance between the one-pixel-wide boundary and non-boundary pixels may also cause problems during classification.

In contrast to the pixel-wise labeling scheme, we want to model the surface position distribution p = p(x₁, … , x_N, I), where x_i is a random variable representing the surface depth (row) position for each column i. Surface properties, like smoothness, are encoded within the joint distribution and a sample from p is a likely surface segmentation. A training pair ($x_1^g,\cdots ,x_N^g$, I) can be considered to be a sample from p. However, sampling each x_i from the joint distribution p is hard, so we use the idea of Variational Bayesian methods (Fox and Roberts, 2012) by approximating p with:

$$q={\Pi }_{i=1}^N{q}_i\left(x_i\mid I;\theta \right)p(I).$$

For an input image I, the network generates N independent surface position distributions q_i(x_i|I;θ), i = 1, ⋯ , N at each column. θ are the network parameters to be trained by minimizing the K-L divergence between the data distribution p and q. It is easier to sample the x_i’s given the simpler independent q_i’s. To train the network by minimizing the K-L divergence using the input image I and ground truth $x_i^g$’s, we have

$$\begin{gathered} \underset{\theta }{\text{argmin}}\text{\hspace{0.17em}K-L}(p\Vert q) \\ ={\underset{\theta }{\text{argmin}}}_{\overrightarrow{\mathit{x}},I}p\left(x_1,\cdots ,x_N,I\right)\text{log}\frac{p\left(x_1,\cdots ,x_N,I\right)}{{\prod }_{i=1}^N{q}_i\left(x_i\mid I;\theta \right)p(I)}, \\ ={\underset{\theta }{-\text{argmin}}}_{\overrightarrow{\mathit{x}},I}p\left(x_1,\cdots ,x_N,I\right)\sum _{i=1}^N\text{log\hspace{0.17em}}{q}_i\left(x_i\mid I,\theta \right), \\ =\underset{\theta }{-\text{argmin}}\underset{\overrightarrow{\mathit{x}},I~p}{\text{E}}\left(\sum _{i=1}^N\text{log}{q}_i\left(x_i\mid I,\theta \right)\right), \end{gathered}$$ (1)

where $\overrightarrow{\mathit{x}}$ is a vector of surface positions at N columns and is sampled from data distribution p. In a stochastic gradient descent training scheme, the expectation in Equation (1) can be removed with a training sample ($x_1^g,\cdots ,x_N^g$, I) and the position $x_i^g$ of the i^th column is rounded to the image grid, which can only be an integer from 1 to the image row number R. Thus the loss becomes,

$${\mathcal{L}}_{\text{CE}}=-\sum _{i=1}^N\sum _{j=1}^R𝟙\left(x_i^g=j\right)\text{log\hspace{0.17em}}{q}_i\left(x_i^g\mid I,\theta \right),$$ (2)

where $\mathbb{1}\left(x_i^g=j\right)$ is an indicator function. Equation (2) is the cross entropy loss for a single surface. For the case of segmenting multiple surfaces, we use the network to output M such q_i’s. In practice, each q_i is a discrete distribution of length R and their values sum up to one. We use the deep network to output M feature maps (each map has the same size as the input image) for the M surfaces. A column-wise softmax is performed independently on these M feature maps to generate surface position probabilities q_i(x_i|I;θ), i = 1, … , N for each column and each surface. An intuitive explanation of the proposed formulation is: Instead of classifying each pixel into surfaces or backgrounds, we are selecting a row index at each column for each surface.

2.3. Independent inference

The deep network outputs marginal conditional distributions q_i(x_i|I, θ) for column i, so the exact inference of the boundary position at column i from q_i can be performed independently. We can use the maximum a posterior (MAP) estimator to obtain the final surface position x_i with the maximum q_i, however, the maximum operation is not differentiable. Instead, we use a fully differentiable estimator of minimum mean square error (MMSE); this is equivalent to the differentiable soft-argmax operation which has been used in keypoint localization (Honari et al., 2018). We use the soft-argmax to estimate the final surface position $x_i^{sa}$ at each column i, readily computed as

$$x_i^{sa}=\sum _{r=1}^{R}r{q}_i(r\mid I,\theta ).$$

Thus, we directly obtain the surface positions from the network with a differentiable operation. An example is shown in Fig. 5.

Fig. 5.

An example of the structured surface prediction. The left image shows that a surface can be represented by the row index at each column and the surface is defined on the grid (generated by either graph methods or manual selection). The right image shows that the surface position can be a float value (thus the accuracy is not limited by the pixel resolution), and the exact position for each column can be inferred independently by the network output q_i’s. With q₁ and q₂ being directly computed in this case.

Since every $x_i^{sa}$ is fully differentiable, we further regularize the q_i’s by directly encouraging the soft-argmax of q_i to be the ground truth, $x_i^g$, with a smooth L1 loss,

$${\mathcal{L}}_{\text{L}1}=\sum _{i=1}^{N}0.5d_i^2𝟙\left(\left|d_i\right|<1\right)+\left(\left|d_i\right|-0.5\right)𝟙\left(\left|d_i\right|\ge 1\right),$$

where,

$$d_i=x_i^{sa}-x_i^g.$$

We add this extra loss and note that a smooth L1 is a better surface distance measurement than cross entropy. To explain this, consider a ground truth surface s(x) and two predictions p_A(x) = s(x) + c_A and p_B(x) = s(x) + c_B, where c_A > c_B > 0 are constants. The surface prediction B is better than A; however, the cross entropy loss will be the same for both. L1 loss does not have this problem and will choose p_B over p_A. Additionally, the cross entropy loss requires us to round the ground truth, x^g, to the image grid thus reducing the resolution of the approach. In contrast, the L1 loss can use float values.

2.4. Topology guarantee module

The layer boundaries within the retina have a strict anatomical ordering. For M surfaces s₁, … , s_M from the inner to the outer retina, the anatomy requires,

$$s_1(i)\le s_2(i)\le \cdots \le s_M(i),i=1,\dots ,N,$$ (3)

where s_m(i) is the position of the m^th surface at the i^th column. The soft-argmax operation produces exact surfaces s₁, … , s_M but may not satisfy the ordering constraint of Equation (3). To solve this problem, our deep network outputs the first surface s₁ (ILM surface) and we update subsequent surfaces iteratively to guarantee the ordering with the following additional constraint,

$$s_j(i)=s_{j-1}(i)+\text{ReLU}\left(s_j(i)-s_{j-1}(i)\right).$$

These operations (addition, subtraction, and ReLU activation) are implemented as a deep network output layer, thus guaranteeing the topology during both the training and testing stages.

2.5. Pixel-wise labeling

Our multi-task network has two output branches. The first branch (conv-s) described above outputs the correctly ordered surfaces whereas the second branch (conv-m) outputs pixel-wise labeling for both layers and lesions, as well as the background labels of choroid and vitreous. These two branches share the same feature extractor. The pixel-wise labeling scheme has topological problems with biologically structured layers. However, lesions (fluid or edema) that appear at different locations and with different shapes cannot be assigned a fixed topology and thus pixel-wise labeling is appropriate. Thus, during testing, we only use the lesion prediction from the pixel-wise labeling branch. A combined differentiable Dice and cross entropy loss (Roy et al., 2017) is used for the output of this branch. C is the total number of classes, g_c(x) and p_c(x) are the ground truth and predicted probability, respectively, that pixel x belongs to class c. Since Ω_c is the number of pixels in class c, our pixel-wise labeling loss is

$$\begin{gathered} {\mathcal{L}}_{\text{Dice}+\text{CE}}=\sum _{c=1}^C\sum _{x\in {\Omega }_c}{w}_c(x)g_c(x)\text{log}\left(p_c(x)\right) \\ -\frac{1}{C}\sum _{c=1}^C\frac{ϵ+{\sum }_{x\in {\Omega }_i}2g_c(x)p_c(x)}{ϵ+{\sum }_{x\in {\Omega }_c}{g}_c{(x)}^2+p_c{(x)}^2}. \end{gathered}$$

Here, ϵ = 0.001 is a smoothing constant that also prevents division by zero and w_c(x) is a weighting function for each pixel (Roy et al., 2017), with a higher weight for the pixels around lesions and surfaces. The final network training loss is,

$$\mathcal{L}=w_1*{\mathcal{L}}_{\text{Dice}+\text{CE}}+w_2*{\mathcal{L}}_{\text{CE}}+w_3*{\mathcal{L}}_{\text{L}1},$$

where w₁, w₂, and w₃ are weighting hyper-parameters which are set to one in training.

2.6. Network structure

The detailed network structure is shown in Fig. 4. The input is a three-channel image and the basic block for the whole network is a res-block. A 3 × 3 convolution (C₀) is used on the res-block input with 64 output channels. Then two 3 × 3 convolutions (64 channel input and 64 channel output) with batch normalization and parametric ReLU (prelu) between them are used. The result is then batch normalized, added to the C₀ output, activated with prelu, and used as the res-block output. The network includes a shared feature extractor (res-unet) and two output heads: conv-m for the pixel-wise masks estimation and conv-s for the surface estimation. The res-unet is a modification of the U-Net (Ronneberger et al., 2015). It consists of three levels of 2 × 2 maxpooling and three levels of 2 × 2 bilinear upsampling. The convolutions in the original U-Net are replaced with the res-block and the output channel number is fixed to 64 in the res-unet. The output 64 channel feature map from the res-unet is then shared by two output branches. The first branch, conv-m, has a res-block with 32 output channels and a 1×1 convolution to classify each pixel as either 8 layers, 2 background labels (vitreous and choroid), or lesions (fluids or edema). The second branch, conv-s, has the same structure as conv-m except the output channel has 9 feature maps for 9 surfaces. A column-wise softmax is applied on each feature map to produce the variational surface position distributions q_i’s for each surface.

Fig. 4.

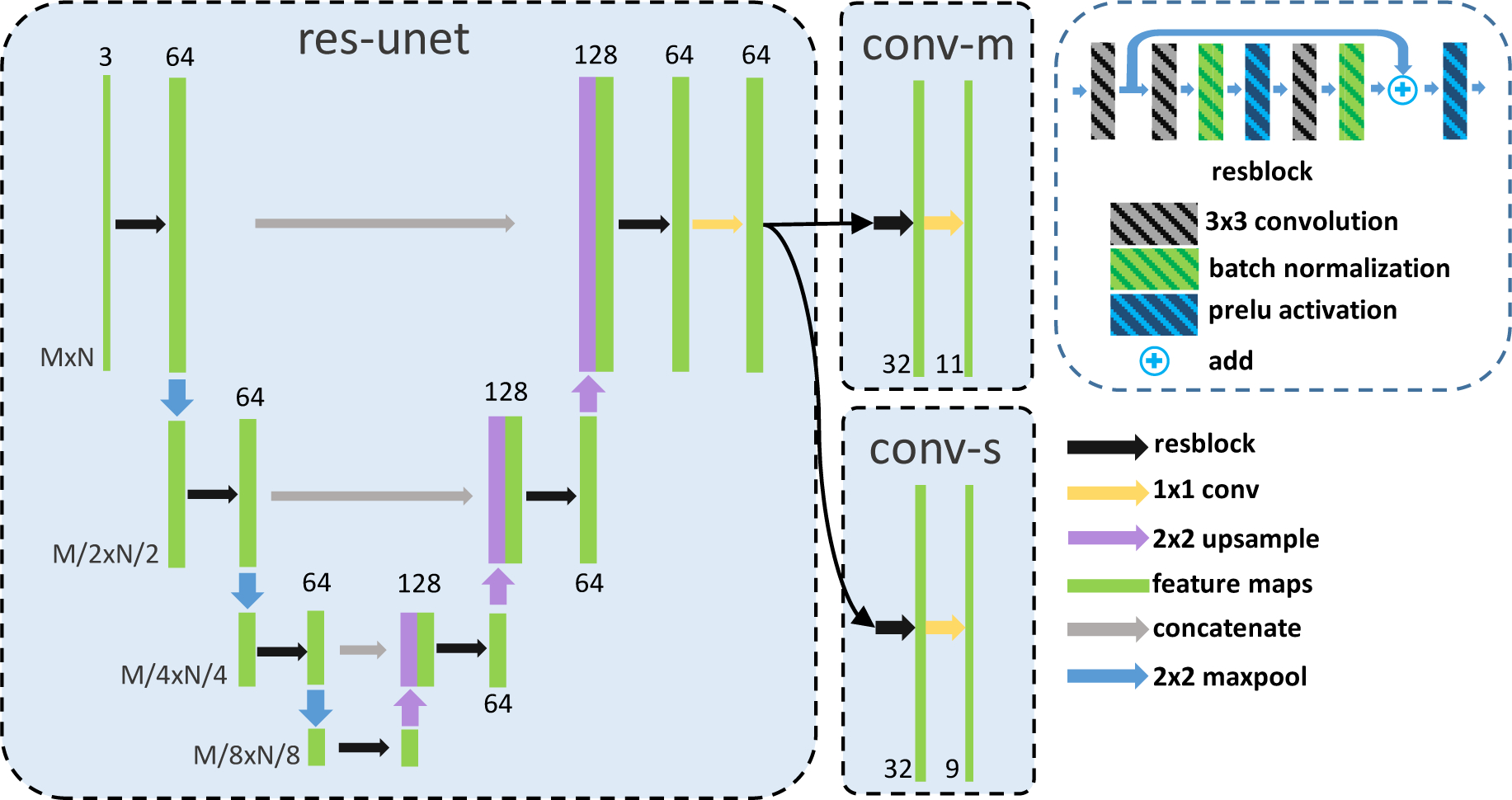
Detailed network structure of res-unet, conv-m, and conv-s shown schematically in Fig. 3. The res-unet is a residual U-Net with four downsamplings and four upsamplings which consists of the residual blocks (each has three 3 × 3 convolutions, a parametric ReLU, and a batch normalization). Two output branches (conv-m, conv-s) consist of a residual block and a 1 × 1 final output layer.

3. Experiments

The proposed method was validated on two publicly available data sets. The first data set (He et al., 2019c) contains 14 healthy controls (HC) and 21 people with MS (PwMS); MS subjects exhibit mild thinning of retinal layers. Some PwMS images contain microcystic macular edema (MME) but the retinal layer structure of all the images is intact in the data set. The data is OCT macula data acquired on a Heidelberg Spectralis scanner with nine surfaces manually delineated in each scan. These surfaces are illustrated in Fig. 1. The surface between the GCL and IPL is not visible and is thus not delineated. Each of the 35 subjects have 49 B-scans of size 496 × 1024. The lateral and axial resolution, and the B-scan distances are 5.8 μm, 3.9 μm, and 123.6 μm, respectively. Following the train/test split in He et al. (2018), the last 6 HCs and last 9 PwMS are used for training (735 B-scans) and the other 20 subjects are used for testing (980 B-scans). Within the 15 training subjects, we used the first HC and first two PwMS for network training validation.

The second data set (Chiu et al., 2015) contains 110 B-scans (496 × 768) from 10 diabetic macular edema (DME) patients (each of which has 11 B-scans). The first five patients are rated as having severe macular edema with damaged retinal structures. Eight retinal surfaces and macular edema have been manually delineated; these are the same surfaces in Fig. 1 with the exception of the ELM, which is not delineated. To accommodate this, we changed the final output channel of the network branches conv-m and conv-s to 10 and 8, respectively, but we kept the other hyper-parameters the same as the experiments for HC and PwMS.Following the 50%−50% train/test split in (Chiu et al., 2015; Rathke et al., 2017; Karri et al., 2016; Roy et al., 2017), we trained on the last 55 B-scans until training convergenced and tested on the challenging first 55 B-scans which have large edema.

The preprocessing¹ was performed within Matlab. In particular, the B-scans from the HC/PwMS, and DME data set were flattened and cropped to the sizes 128 × 1024 and 224 × 768, respectively. The deep network was implemented using Python and Pytorch. The following hyper-parameters are the same for both data sets. We trained the network with an Adam optimizer with an initial learning rate of 10⁻⁴, weight decay of 10⁻⁴, and a minibatch size of 2. The training image was augmented with horizontal flipping and vertical scaling both with probability 0.5 (the scaled image were cropped to the same size before scaling).

3.1. Surface position prediction accuracy

3.1.1. HC and PwMS data set

We compare our proposed method with several base-lines: AURA toolkit, RNet, ReLayNet, and SP. The AURA toolkit (Lang et al., 2013) is a graph based method and it is the state-of-the-art compared to other publicly available tools, as shown in Bhargava et al. (2015); Tian et al. (2016). It uses a random forest to perform patch based surface pixel classification and graph methods (Garvin et al., 2008) for the final structured surface extraction. RNet (He et al., 2019b) is a regression deep network which is used as a post-processing step to obtain topology guaranteed smooth surfaces from layer segmentation maps. ReLayNet (Roy et al., 2017) is a variation on U-Net and only outputs layer maps and as such retinal surfaces are not obtained explicitly. Since the retinal layer structures are intact (which means the ground truth segmentation maps between adjacent layers do not have gaps or overlaps), we obtain the final surface positions by summing up the output layer maps in each column. The shortest path (SP) algorithm (Chiu et al., 2010; Fang et al., 2017; Kugelman et al., 2018) is also used for comparison noting that we extracted the final surfaces using SP on our predicted q_i’s (as shown in Fig. 3). All of these baseline methods were retrained on the same data as our proposed method. The mean absolute distances (MADs) and rooted mean square error (RMSE) between predicted surface position and manual delineation along each column for each method are shown in Table 1 (with mean and variance calculated over the 980 test B-scans). We performed a Wilcoxon rank sum test between our result and the best result of the four baseline methods for each surface; p-values smaller than 0.05 are labeled with a star (*) in Table 1.

Table 1.

Mean absolute distance (MAD), root mean square error (RMSE), and standard deviation (Std. Dev.) in μm evaluated on 980 manually delineated B-scans of 9 surfaces, comparing AURA toolkit (Lang et al., 2013), R-Net (He et al., 2018), ReLayNet (Roy et al., 2017), SP (shortest path on our surface probabilities), and our proposed method. Depth resolution is 3.9 μm. Numbers in bold are the best in that row. We compare our result with the best result of the other 4 methods for each surface using Wilcoxon rank sum test (mean MAD and RMSE per B-scan, in total 980 sample values (980 test B-scans)).

	MAD (Std. Dev.)
Boundary	AURA	R-Net	ReLayNet	SP	Ours
ILM	2.37 (0.69)	2.38 (1.22)	3.17 (1.08)	2.70 (0.70)	2.41 (0.81)
RNFL-GCL	3.09 (1.22)	3.10 (1.29)	3.75 (1.59)	3.38 (1.29)	2.96* (1.70)
IPL-INL	3.43 (1.02)	2.89 (0.90)	3.42 (0.90)	3.11 (1.03)	2.87* (1.69)
INL-OPL	3.25 (0.95)	3.15 (0.98)	3.65 (0.92)	3.58 (1.58)	3.19 (1.49)
OPL-ONL	2.96 (1.29)	2.76 (1.26)	3.28 (1.33)	3.07 (1.37)	2.72* (1.70)
ELM	2.69 (0.84)	2.65 (1.05)	3.04 (0.86)	2.86 (0.89)	2.65 (1.14)
IS-OS	2.07 (0.96)	2.10 (1.03)	2.73 (0.71)	2.45 (0.67)	2.01 (0.88)
OS-RPE	3.77 (1.71)	3.81 (1.89)	4.22 (2.06)	4.10 (2.12)	3.55* (1.73)
BM	2.89 (2.37)	3.71 (2.47)	3.09 (1.62)	3.23 (1.64)	3.10* (2.21)
Overall	2.95 (1.23)	2.95 (1.34)	3.37 (1.23)	3.16 (1.25)	2.83* (1.48)
	RMSE (Std. Dev.)
Boundary	AURA	R-Net	ReLayNet	SP	Ours
ILM	2.97 (0.95)	2.94 (1.59)	3.87 (1.74)	3.29 (0.88)	3.00 (1.35)
RNFL-GCL	4.24 (2.00)	4.18 (2.34)	5.15 (2.78)	4.48 (2.29)	4.02* (2.59)
IPL-INL	4.38 (1.50)	3.73 (1.30)	4.41 (1.46)	4.01 (1.58)	3.80 (2.74)
INL-OPL	4.14 (1.26)	3.96 (1.26)	4.60 (1.31)	4.50 (2.59)	4.12 (2.46)
OPL-ONL	3.99 (2.05)	3.65 (1.94)	4.26 (2.05)	4.04 (2.30)	3.69 (2.75)
ELM	3.28 (0.98)	3.24 (1.24)	3.69 (0.98)	3.50 (1.34)	3.29 (1.62)
IS-OS	2.54 (1.10)	2.58 (1.24)	3.25 (0.78)	2.99 (0.96)	2.51 (1.32)
OS-RPE	4.68 (1.93)	4.62 (2.11)	5.10 (2.21)	5.01 (2.33)	4.34 (1.92)
BM	3.43 (2.46)	4.25 (2.56)	3.72 (1.77)	3.85 (1.76)	3.66* (2.28)
Overall	3.74 (1.58)	3.68 (1.73)	4.23 (1.68)	3.96 (1.78)	3.60* (2.11)

A star (*) is shown on our results if the p-value is smaller than 0.05 for that surface.

3.1.2. DME data set

We compared our results with three graph based methods (for final surface extraction): Chiu et al. (2015), Rathke et al. (2017), and Karri et al. (2016). Due to the existence of edema, extracting continuous layer surfaces from layers and edema segmentation maps is non-trivial, so we compared the lesion Dice scores with Roy et al. (2017), which is a modified U-Net. However, we ignore the positions where Chiu et al. (2015)’s result or the manual delineation are missing. The boundary MAD is shown in Table 2 (the reported numbers for Rathke et al. (2017) are from the corresponding paper). It can be observed that we achieve better surface segmentation accuracy than the state-of-the-art graph based methods. Our network has an extra branch for layer and lesion segmentation (the layer segmentation maps are not used); however, Rathke et al. (2017)’s and Karri et al. (2016)’s method can only output layer surfaces. Accordingly, we should only compare the diabetic macular edema Dice score from Chiu et al. (2015), ReLayNet, and our method, which are 0.56, 0.7, and 0.7 respectively. Qualitative results are shown in Fig. 7.

Table 2.

Mean absolute distance (MAD) in μm for eight surfaces (and the mean of those eight surfaces) evaluated on 55 manually delineated scans comparing Chiu et al. (2015), Karri et al. (2016), Rathke et al. (2017), and our proposed method. Numbers in bold are the best in that column. Our method is best for six of the eight surface, and is best overall.

	Mean	ILM	RNFL-GCL	IPL-INL	INL-OPL	OPL-ONL	IS-OS	OS-RPE	BM
Chiu et al. (2015)	7.82	6.59	8.38	9.04	11.02	11.01	4.84	5.74	5.91
Karri et al. (2016)	9.54	4.47	11.77	11.12	17.54	16.74	4.99	5.35	4.30
Rathkeetal. (2017)	7.71	4.66	6.78	8.87	11.02	13.60	4.61	7.06	5.11
Our Method	6.70	4.51	6.71	8.29	10.71	9.88	4.41	4.52	4.61

Fig. 7.

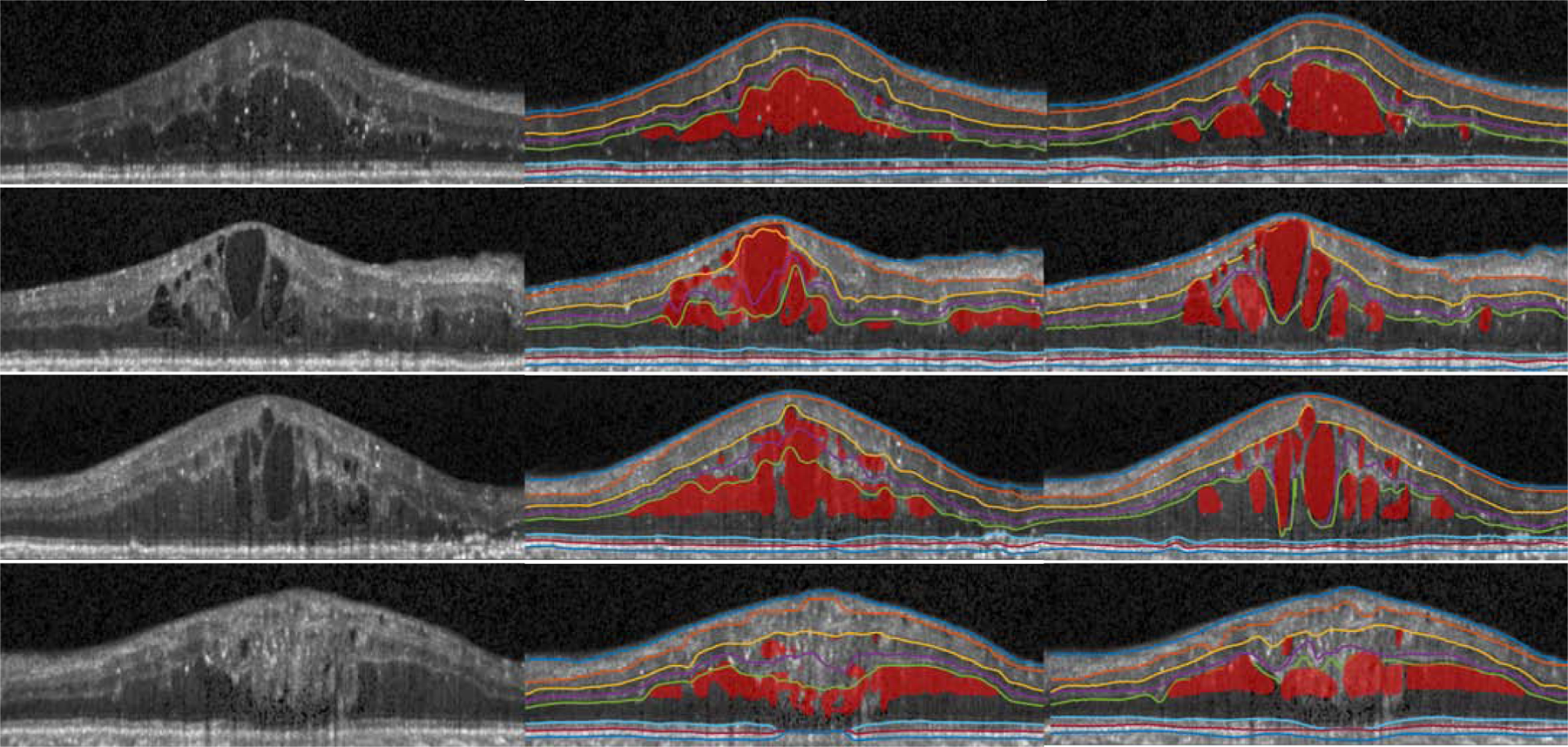
Visualization of the OCT original image (left), our results (middle), and the manual segmentation (right) from four B-scans of the diabetic macular edema subjects.

3.2. Surface smoothness and connectivity analysis

Graph-based methods impose hard constraints on the smoothness of their generated surfaces, which are typically hand tuned on a data set by data set basis. In contrast, deep network based approaches do not offer any guarantees on the smoothness of the output surfaces-such methods often assume that extracting surfaces from pixel-wise labeling is trivial. However, smooth surfaces are important for shape analysis, surface based registration, and visualization. As defined in graph based methods (Li et al., 2006; Garvin et al., 2008), a feasible surface satisfies task-specific smoothness constraints which guarantee surface connectivity. The (2D) B-scan smoothness constraint at column i for surface s, can be written as,

$$\Delta (i)=|s(i+1)-s(i)|\le {\delta }_x\forall i,$$

where Δ(i), is the absolute slope and the smoothness constraint δ_x could vary according to different positions or surfaces and the absolute surface difference within adjacent columns. Graph-based methods generally have manually selected δ_x. As previously stated, our method has no hard constraints on the absolute slope, Δ(i). The soft-argmax inference is performed on individual columns of q_i’s, but the q_i’s are generated by the deep network which has 3 × 3 convolutions and down-samplings; thus, the smoothness constraints between adjacent columns are learnt implicitly from the ground truth. To explore the smoothness of the proposed method, we plot the histogram of the surface slope s(i + 1) − s(i) in Fig. 8. For the HC/PwMS data set, we have 1023 (columns) × 9 (surfaces) × 980 (B-scans) surface points for which we can compute slope; correspondingly for the DME data set, we have 499 (columns) × 8 (surfaces) × 55 (B-scans) surface points. For graph methods, s(i + 1) − s(i) is constrained to a pre-defined δ_x; in the case of shortest path δ_x = 1, which equates to the surface changing by one voxel (s(i+1)−s(i) = ±1) or staying flat (s(i + 1) − s(i) = 0). Since graph methods already have such constraints, we do not include them in Fig. 8. Instead we plot our method, the ground truth manual delineation, and the naive approach of taking the maximum a posterior (MAP) over the q_i’s (select the the index that has maximum surface probability along each column). This MAP approach is essentially a trivial step to extract surfaces from conventional pixel-wise labeling results, as in the work of Li et al. (2019).

Fig. 8.

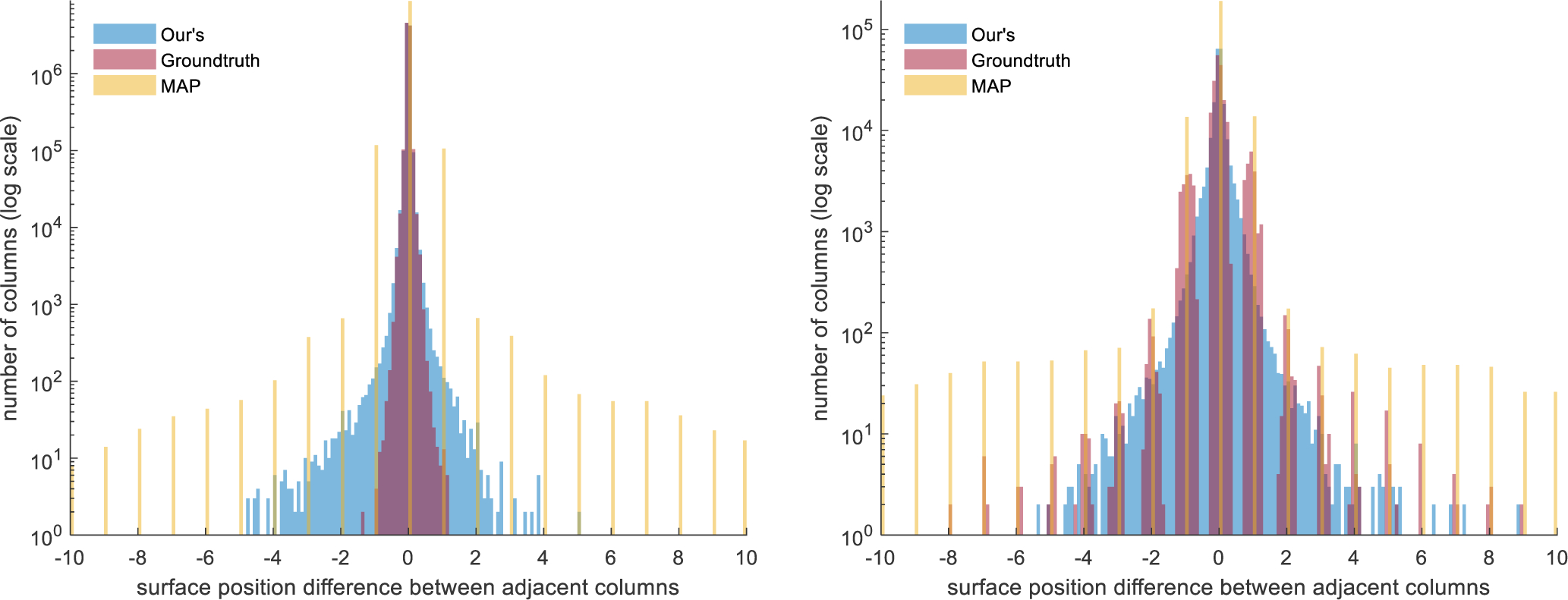
Histogram of the surface distance between adjacent columns |s_j(x_i +1) − s_j(x_i)| for our method, the proposed soft-argmax inference from q_i’s (Ours), manual delineation (Groundtruth), and maximum a posterior from the q_i’s (MAP). Left: The histogram for the HC/PwMS data set. Right: The histogram for the DME data set. Note the y-axis uses a log-scale.

Since we do not have hard constraints on Δ(i), we examine the number (#) of outlier positions that have large absolute slope, which is #i where Δ(i) > δ_x. For the HC/PwMS data set, as we expect smooth uninterrupted surfaces, we threshold #i’s with δ_x = {3, 4, 5}, as well as reporting the maximum Δ(i) for the three reported methods. See Table 3 for the breakdown of these results. For the DME cohort, we expect larger jumps in the surfaces due to the edema. Thus, we threshold the #i’s with δ_x = {5, 10} with the results also reported in Table 3. For the HC/PwMS data set, the results show that the largest absolute slope Δ(i) for our method is 5.08 pixels, whereas the MAP based approach reaches 83 pixels. For our method, .00828% columns have an absolute slope larger than 3 pixels–less than 90 columns. For the DME data set, our method aligns well with the ground truth surface slope histogram and the maximum Δ(i) is 10.44 pixels. Figure 9 gives an example of obtaining smooth surfaces from our q_i’s in the presence of large edema.

Table 3.

The surface absolute slope Δ (i) = |s (i + 1) s (i)| statistics of the HC PwMS and DME data sets. The table lists the max Δ (i) (Max) for our method, manual delineation (GT), and maximum a posterior (MAP). The total number of sample points for the HC/PwMS data set is 9.0 × 10⁶ and for the DME cohort the number is 2.2 × 10⁵. The number of columns with Δ (i) > δ_x are listed for different thresholds, for the HC/PwMS data set we use δ_x = {3, 4, 5} and for the DME data set we use δ_x = {5, 10}.

HC/PwMS	Ours	GT	MAP
Max Δ(i)	5.08	1.36	83
#Δ(i) > 3	83	0	934
#Δ(i) > 4	22	0	711
#Δ(i) > 5	2	0	586
DME
Max Δ(i)	10.44	26.9	179
#Δ(i) > 5	40	89	799
#Δ(i) > 10	2	35	406

Fig. 9.

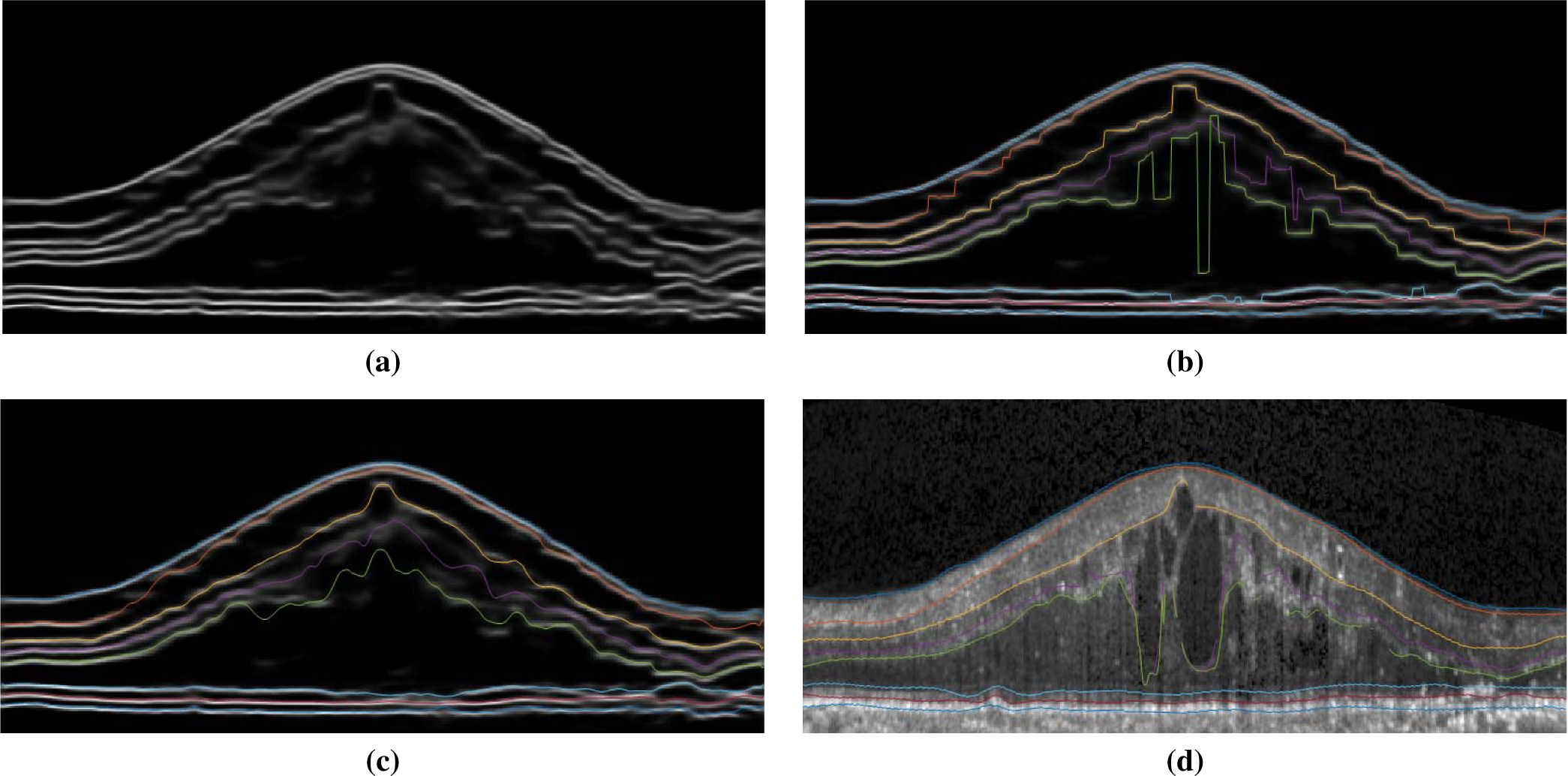
An example of continuous surface extraction: (a) Shown are the summed q_i’s for all eight channels corresponding to the eight surfaces.We note that the edema area has lower surface prediction probability. (b) Extracted surfaces using MAP from the q_i’s, overlaid on the image from (a). This is similar to the naive method of finding maximum probability position per column for each surface/layer using pixel-wise classification. (c) Using our proposed soft-argmax method, the surfaces remain smooth. (d) The groundtruth delineation.

4. Discussion and Conclusion

In this paper, we propose a novel method of using deep networks for structured layer surface segmentation from retina OCT. The proposed network formulates the multiple layer surface segmentation as a surface position modeling problem and performs the inference using variational methods. Compared to post-processing using graph methods, our method is learned end-to-end and the fully differentiable soft-argmax operation generates sub-pixel surface positions in a single feed forward propagation. The surface prediction accuracy meets or exceeds the state-of-the-art and the surface position prediction is a float value, which gives it the ability to produce sub-pixel segmentation. The surface smoothness (connectivity) is also well maintained without hard smoothness constraints as shown in Table 3. Meanwhile, the generated surfaces have the correct layer ordering, which is guaranteed by the network both in the training and testing stages. The conventional pixel-wise labeling scheme cannot guarantee the topology as shown in Fig. 10 nor obtain smooth surfaces with simple methods like MAP as shown in Figs. 8 and 9.

Fig. 10.

On the left, an example topology error (white box) from our pixel-wise labeling branch can be seen. On the right, we see the topologically correct segmentation as generated by the surface output branch of our method.

There are also limitations of our work. Our network works on each B-scan individually; thus, the smoothness learned by the network is limited to 2D, while 3D graph based methods (Garvin et al., 2008; Lang et al., 2013) can guarantee inter B-scan smoothness. This problem can be solved by extending our network to 3D or leverage adjacent B-scan information within the network. Although the network can obtain highly accurate structured surfaces, unlike model-based post-processing, our method is more prone to be affected by outlier images with bad quality or artifacts with limited training data. Our topology module is integrated into the deep network and is not a post-processing step, but it updates surfaces iteratively from top to bottom which has a risk of affecting lower surfaces with bad upper surface estimates. A more sophisticated topology module needs to be proposed in the future.

Overall, we propose a pure data driven method of structured retinal surface segmentation from OCT image data. The method has the potential to be adapted for other structured terrain-like surface segmentation problems (Li et al., 2006) in medical imaging.

Fig. 6.

Visualization of shortest path (top), AURA (second from top), our result (third from top), and manual segmentation (bottom) from a healthy control. Our result is smooth and produces sub-pixel surface prediction, while shortest path generates surfaces on image grids.

Highlights.

• A novel formulation of deep network to output continuous, smooth and topology correct surfaces without post-processing

• End-to-end optimization of multiple structured surface segmentation

• An effective multitask deep network for retinal layer surface and lesion segmentation