Tunable Chiral Optics in All-Solid-Phase Reconfigurable Dielectric Nanostructures

Abstract

Subwavelength nanostructures with tunable compositions and geometries show favorable optical functionalities for the implementation of nanophotonic systems. Precise and versatile control of structural configurations on solid substrates is essential for their applications in on-chip devices. Here, we report all-solid-phase reconfigurable chiral nanostructures with silicon nanoparticles and nanowires as the building blocks in which the configuration and chiroptical response can be tailored on-demand by dynamic manipulation of the silicon nanoparticle. We reveal that the optical chirality originates from the handedness-dependent coupling between optical resonances of the silicon nanoparticle and the silicon nanowire via numerical simulations and coupled-mode theory analysis. Furthermore, the coexisting electric and magnetic resonances support strong enhancement of optical near-field chirality, which enables label-free enantiodiscrimination of biomolecules in single nanostructures. Our results not only provide insight into the design of functional high-index materials but also bring new strategies to develop adaptive devices for photonic and electronic applications.

Graphical Abstract

Chirality is ubiquitous as human hands are the most recognized chiral objects in our daily life. Many molecules such as amino acids, proteins, sugars, and DNA are also chiral, which are essential in biology, chemistry, medicine, and medical engineering. Recently, nanoscale chiral structures with intriguing chiroptical properties have attracted tremendous interest in many emerging applications, such as chiral sensing,^1–3 enantioselective detection and separation,^4,5 spin state manipulation,⁶ and valleytronics.^7–9 These chiral structures are usually composed of plasmonic antennas, dielectric particles, or their hybrid to facilitate the light-matter interactions through strong local field enhancement and thus improve the performance of devices impressively.¹⁰

The chiroptical response of chiral structures is largely determined by the arrangement of the building blocks. Conventional chiral structures are static with fixed configurations and optical response, which are not suitable for applications in tunable systems and multifunctional devices. Lately, active chiral structures, where the optical chirality can be on-demand controlled, have triggered research interest for advanced applications, such as polarization conversion, biomolecular sensing, optical communication, as well as enantioselective synthesis and catalysis.¹¹ Along this line, several solution-based techniques have been proposed. For instance, DNA nanotechnologies permit the fabrication of dynamic plasmonic chiral nanostructures, where the external stimuli (e.g., light, strand displacement, pH) can further regulate their configurations.^12–15 In another method, reconfigurable chiral metamolecules can be assembled from individual colloidal nanoparticles in the solution in a laser-generated opto-thermoelectric field.¹⁶ However, these solution-based approaches come down with undesired capillary forces as well as Brownian motion of nanoparticles, which largely limits their implementation of reliable and stable devices.

Dynamic modulation of optical properties on solid substrates will significantly boost the development of on-chip active devices and solid-state microelectromechanical systems. The integration of phase-change materials with chiral structures have been exploited to alter their chiroptical response based on refractive index control.^17,18 However, the tuning range of this method is limited as the structural configuration remains unchanged. Alternatively, chiral metasurfaces based on magneto-optical materials also show controllable chiroptical properties by externally applied magnetic fields.^19,20 In addition, strain- or pressure-induced structural deformation has been adopted to regulate chiroptical properties with a broader tuning range and reversible handedness control.^21,22 However, since mechanical deformation or magnetic field is applied to whole structures, fully site-specific dynamic control of the individual structural elements at the nanoscale remains elusive.

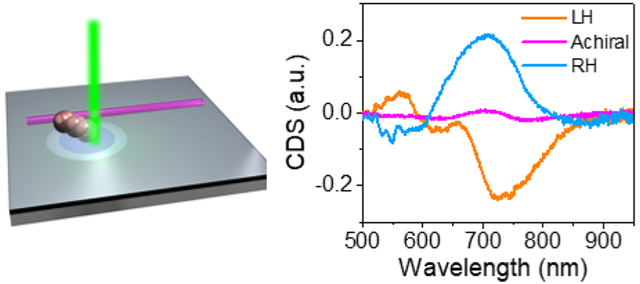
Herein, we demonstrate all-solid-phase reconfigurable chiral nanostructures, where the geometry and chiroptical properties can be dynamically tailored and fully controlled on a solid substrate without liquid media. Our chiral nanostructures consist of a silicon nanoparticle (SiNP) and a silicon nanowire (SiNW) as the building blocks, which are assembled by optothermally gated photon nudging technique (Figure 1a, also see Figure S1 for the experimental setup).²³ Briefly, we modulate the particle-substrate interactions by introducing a thin layer of thermally responsive cetyltrimethylammonium chloride (CTAC) between the particle and substrate. An increase in temperature (>350 K, Figure S2) resulted from optical heating of the SiNP leads to a localized order-disorder transition of surrounding CTAC from the solid phase to a quasi-liquid structure. Meanwhile, optical scattering forces nudge the SiNP away from the laser beam (see more detailed mechanisms in Figure S3). It should be noted that optical forces can push the SiNP under any polarizations (Figure S4), enabling the effective manipulation of SiNPs in all directions on the substrate. In addition, by translating the laser beam or the substrate, it is simple to transport a SiNP to the target position adjoining the SiNW to form chiral nanostructures (Figure S5). The geometry of chiral structures can be further tailored by transporting the SiNP along the SiNW, rendering large and tunable chiroptical responses. Owing to the large size contrast between the diameter of SiNPs and the length of SiNWs, a broad, continuous tuning range is obtained by placing the SiNP at different positions near the SiNW. Figure 1c,d shows dark-field optical micrographs and scanning electron microscope (SEM) images of the optically assembled chiral nanostructures, where left-handed (LH) and right-handed (RH) structures are corresponding to L-shaped and mirror-L-shaped patterns, respectively. The handedness of chiral structures is determined by the location of the SiNP against the SiNW (see Figure S6 for clarification). LH and RH nanostructures exhibit handedness-dependent optical responses to circularly polarized light (Figure 1b and Figure S7), which will be discussed in detail in the following context.

Figure 1.

Assembly of solid-phase dielectric chiral nanostructures. (a) Schematic showing the assembly of LH chiral structure. (b) The measured CDS spectra of the assembled chiral nanostructures in panels c and d. (c,d) Schematic, optical, and SEM images of the assembled LH (c) and RH (d) chiral nanostructures. Scale bars: 1 μm.

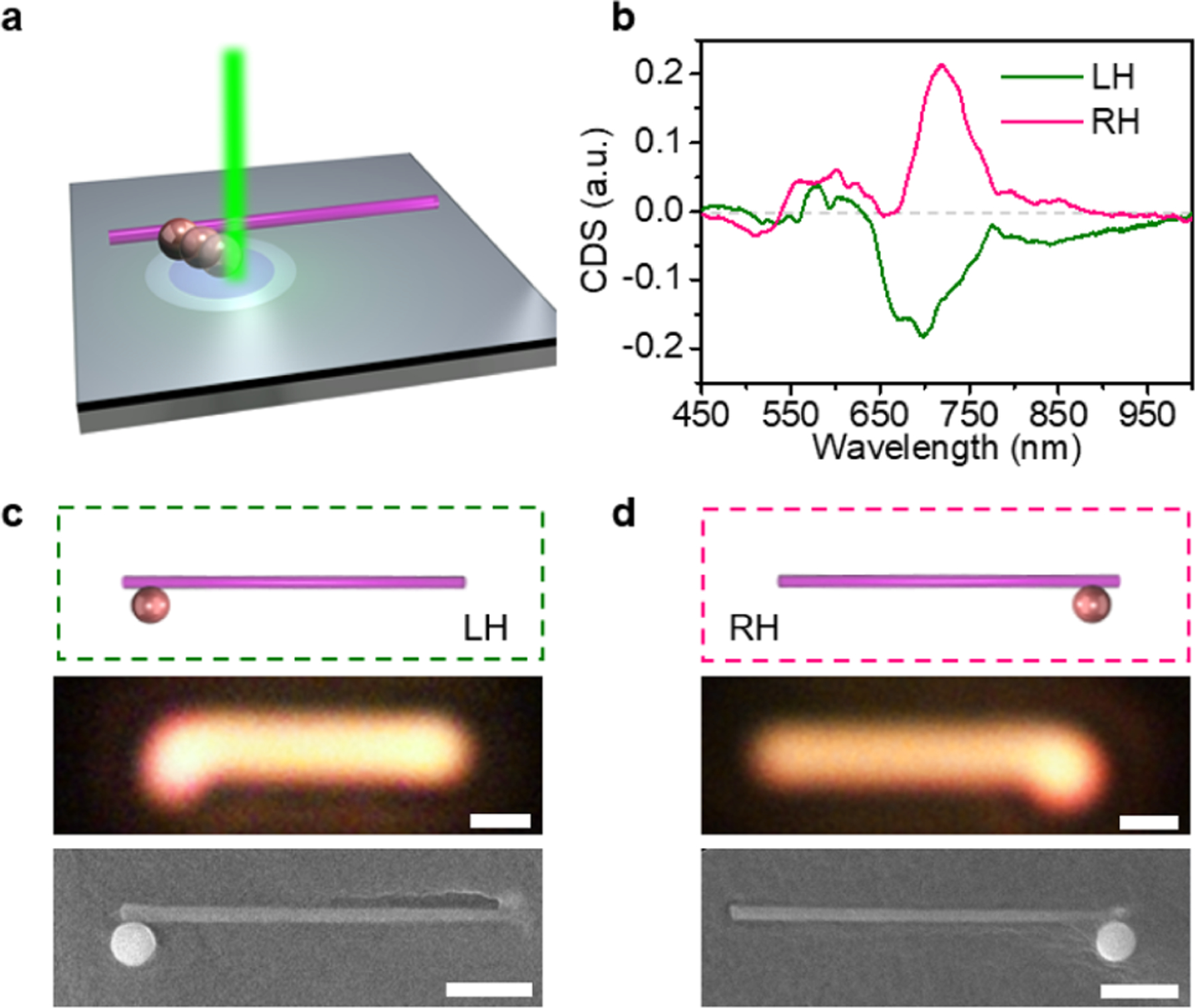
To account for the observed chiral optical response, we first examine each individual building blocks. Specifically, such chiral nanostructures are composed of a hydrogenated amorphous SiNP (~500 nm in diameter, Figure S8) and a single-crystalline SiNW (~5 μm in length and ~170 nm in diameter) with high refractive indexes (~4 at the visible wavelengths; see Supporting Information Experimental Details for the preparation). In contrast to their plasmonic counter-parts,^24–26 dielectric nanostructures feature low material loss, pronounced magnetic resonances at the wavelengths of both visible and near-infrared regimes, and high compatibility with integrated electronics based on complementary metal-oxide-semiconductor.^27–30 Figure 2a shows the measured scattering spectrum of a single SiNP (see Supporting Information Experimental Details for the measurement details). Two major peaks at 620 and 745 nm are mainly attributed to the magnetic octupole (MO) and magnetic quadrupole (MQ) resonances, respectively (see Figure S9 for the fitting), which are consistent with the calculated results in Figure 2c by Mie theory (see SI Note S1 for more details).³¹ The sharp MQ and MO scattering peaks confirm the low dissipative nature of hydrogenated amorphous SiNP in the visible and near-infrared range.³² The scattering spectrum of a single SiNW shows two peaks at 520 and 700 nm (Figure 2b), which also agrees well with the calculated result (Figure 2d and see SI Note S1 for more details). The peak at 700 nm corresponds to the magnetic dipole (MD) resonance of the SiNW (inset in Figure 2d).³³ The experimental and calculated spectra are also in good agreement with the FDTD simulation results (Figure S10). We note that the high-quality Mie resonance here is important for enhanced light-matter interactions, which, after the assembly, could promise the large chiroptical response as further revealed numerically later.

Figure 2.

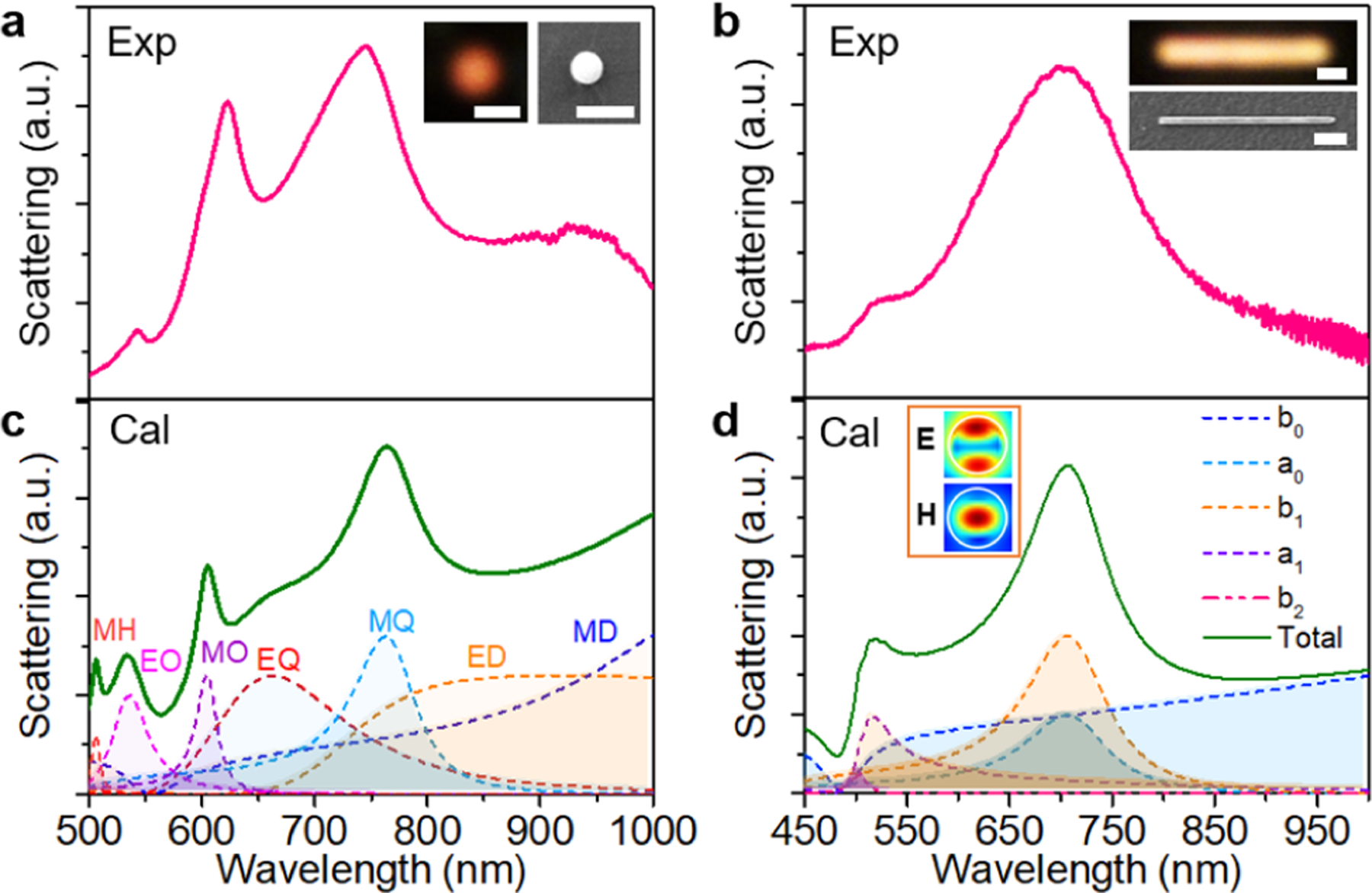
Building blocks of chiral structures. (a,b) Experimental scattering spectra of a SiNP (a) and a SiNW (b). The insets show the corresponding optical and SEM images. Scale bars: 1 μm. (c) Scattering spectra of a 500 nm SiNP along with multipole decomposition calculated with Mie theory. MD, magnetic dipole; ED, electric diploe; MQ, magnetic quadrupole; EQ, electric quadrupole; MO, magnetic octupole; EO, electric octupole; and MH, magnetic hexadecapole. (d) Calculated scattering spectra and multipole decomposition of a SiNW with a diameter of 165 nm. Inset shows the electric and magnetic field distribution in the cross section of the SiNW at 700 nm.

Now, we discuss the tunable chiroptical responses of the assembled nanostructures. Figure 3a schematically presents the assembly of reconfigurable chiral nanostructures with opposite handedness. First, achiral SiNPs and SiNWs as the building blocks were randomly dispersed on the substrate (Figure 3b and Figure S11). To form a chiral nanostructure, we optically nudge a SiNP to the vicinity of a SiNW, which breaks the mirror symmetry. By nudging the nearby SiNP along the SiNW from one end to the other, we transformed the SiNP-SiNW structure from LH to achiral and RH in sequence (Figure 3c–e). The far-field optical scattering spectra (in a forward mode) of the assembled structures were measured with left-handed and right-handed circularly polarized (LCP and RCP) light focused at the connection area between the SiNP and SiNW. We then calculated the circular differential scattering (CDS) spectra from the measurements (see Supporting Information Experimental Details). First, we observed that, compared to RCP incidence, the LH structure has a stronger scattering peak at ~730 nm under LCP light (Figure 3g), resulting in a negative CDS peak (Figure 3f). As a result of a simple argument of mirror geometry, the RH nanostructure exhibits an anticipated handedness-flipped chiroptical response (Figure 3f,i), suggesting the enantiomeric characteristic of the assembled nanostructures. As expected, the achiral nanostructure exhibits no optical chirality due to the restored mirror symmetry (Figure 3h). Second, the most significant chiroptical response (near the wavelength 720 nm) happens at the maximal spectral overlap of the strong Mie resonance between the SiNW (MD resonance) and the SiNP (MQ resonance), hinting the origins of the enhanced optical chirality from the Mie resonance coupling, which will be further supported in the following numerical simulations. In addition, compared to the single SiNW under circularly polarized lights (Figure S11), the scattering peak in all LH, RH, and achiral structures shows a blue shift (from ~745 to ~730 nm), which indicates the coupling between the SiNW and the SiNP at Mie magnetic resonances.^34,35 We last remark that the chiroptical response can also be modified by flipping the SiNP from one side to the other side of the SiNW (Figure S12) with similar results as described above. By manipulating the SiNP on the substrate, we can dynamically reverse and turn ON/OFF the optical chirality of the chiral nanostructures, enabling the development of on-chip active chiroptical devices.

Figure 3.

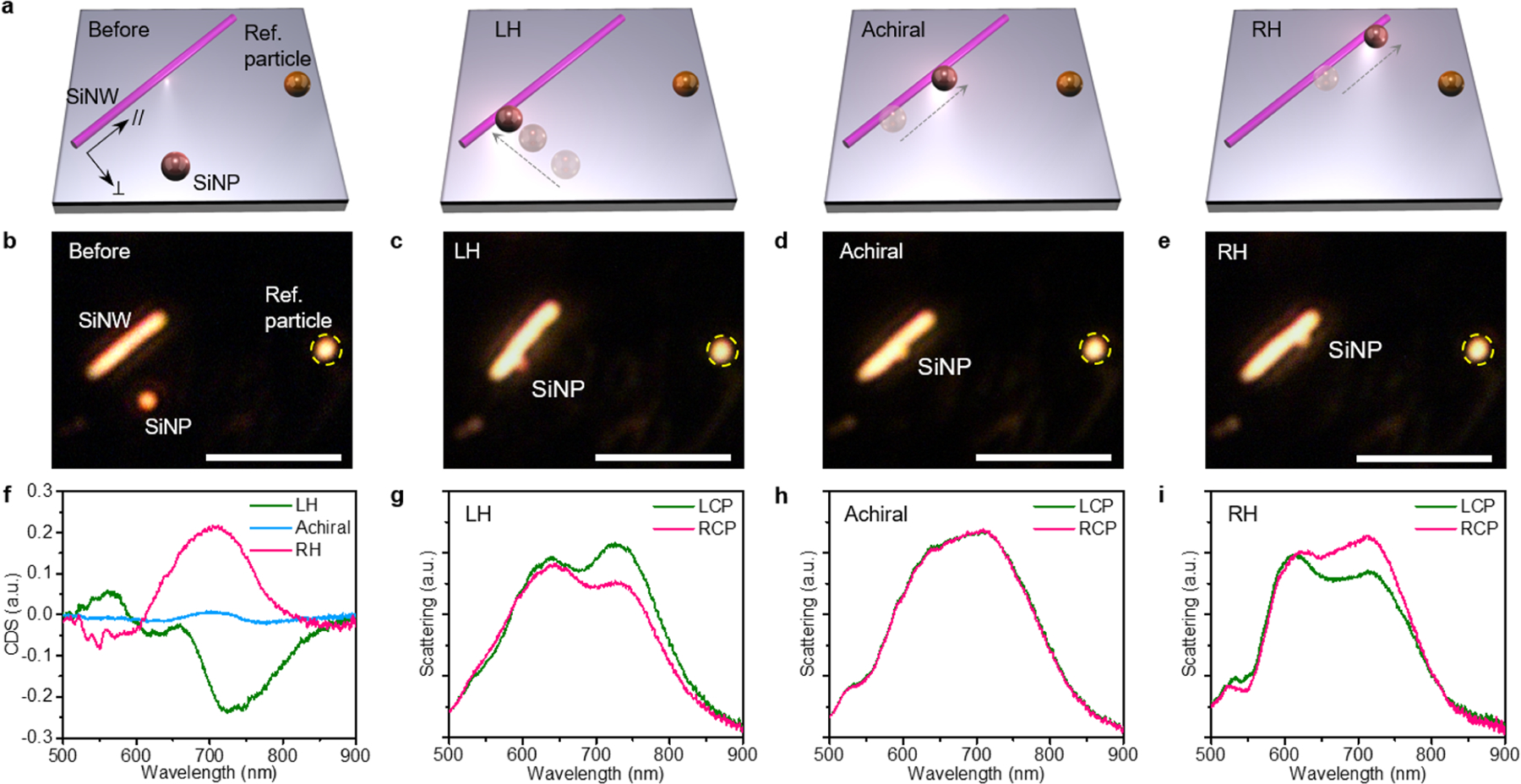
Reconfigurable construction on a solid substrate. (a) Schematic illustration of on-demand assembly of the SiNP-SiNW nanostructure with LH, achiral, or RH configuration. (b–e) Optical images of dispersed building blocks (b), LH (c), achiral (d), and RH (e) structures. All scale bars are 5 μm. (f) CDS spectra of LH, achiral, and RH structures. (g–i), Optical scattering spectra of LH (g), achiral (h), and RH (i) structures under LCP and RCP illumination.

To further interpret the chiroptical responses, we performed full-wave numerical simulations using the finite-difference time-domain (FDTD) method (see Supporting Information Experimental Details). The simulated scattering spectra of all the structures are in good agreement with the experimental data with two major peaks at ~620 and ~740 nm (Figure S13). Taking the LH structure as an example, a polarization-sensitive behavior can be clearly identified in which the LCP light can be scattered more effectively at peak positions (Figure 4a). The calculated CDS spectra based on the simulation also present handedness-flipped responses with two peaks for LH and RH assemblies (Figure 4b), which are very consistent with the experimental data in Figure 3f. Previous studies revealed that the coupling between magnetic resonances could lead to strong electric field enhancement in the gap of the silicon dimer, which is strongly affected by the polarization of the incident beam.^34–36 In our case, this polarization-dependent modulation of scattering intensity can be attributed to the tailored chiral coupling between the SiNP and SiNW at magnetic resonances, as illustrated by the simulated electric field distributions (Figure 4c–f).¹⁰ By comparing Figure 4 panel c with panel d, a more pronounced hotspot at the gap between the SiNP and the SiNW is distinctly observed for LCP incidence at 740 nm, which indicates the stronger electric field enhancement and chirality-selective optical scattering. In contrast, for the achiral structure the electric field distributions under LCP and RCP irradiation are identical (Figure 4e,f), leading to the same optical scattering spectra under the light with opposite circular polarizations. Similarly, stronger electric field enhancement is observed for the LH structure under LCP incidence at 620 nm (Figure S14). The differential electric field distributions under LCP and RCP light are also plotted for clear comparison (Figure S15). In addition, we simulated the electric field components along the SiNW (E_//) and perpendicular to the SiNW (E_⊥) to further unravel the chiral couplings in the assemble nanostructures (Figure S16). The results show that the E_⊥ has a brighter hotspot in the SiNP-SiNW gap and exhibits a distinct chiroptical response, while the E_// is weak in the gap and insensitive to the handedness of the incident beam. This result is because the electric field across the gap between two dielectric nanoparticles is dominant over other components.³⁶ The electric dipole moment in the SiNP can induce strong E_⊥ in the gap, and the field enhancement is dependent on the handedness of the incident light. Finally, it should be mentioned that no remarkable asymmetric response in magnetic field distributions is observed at the gap (Figure S17). The reason is that the magnetic fields mainly localize inside the SiNW and SiNP, and thus the magnetic field enhancement in the gap brought by the coupling between SiNW and SiNP is weaker compared to the electric field.³⁴

Figure 4.

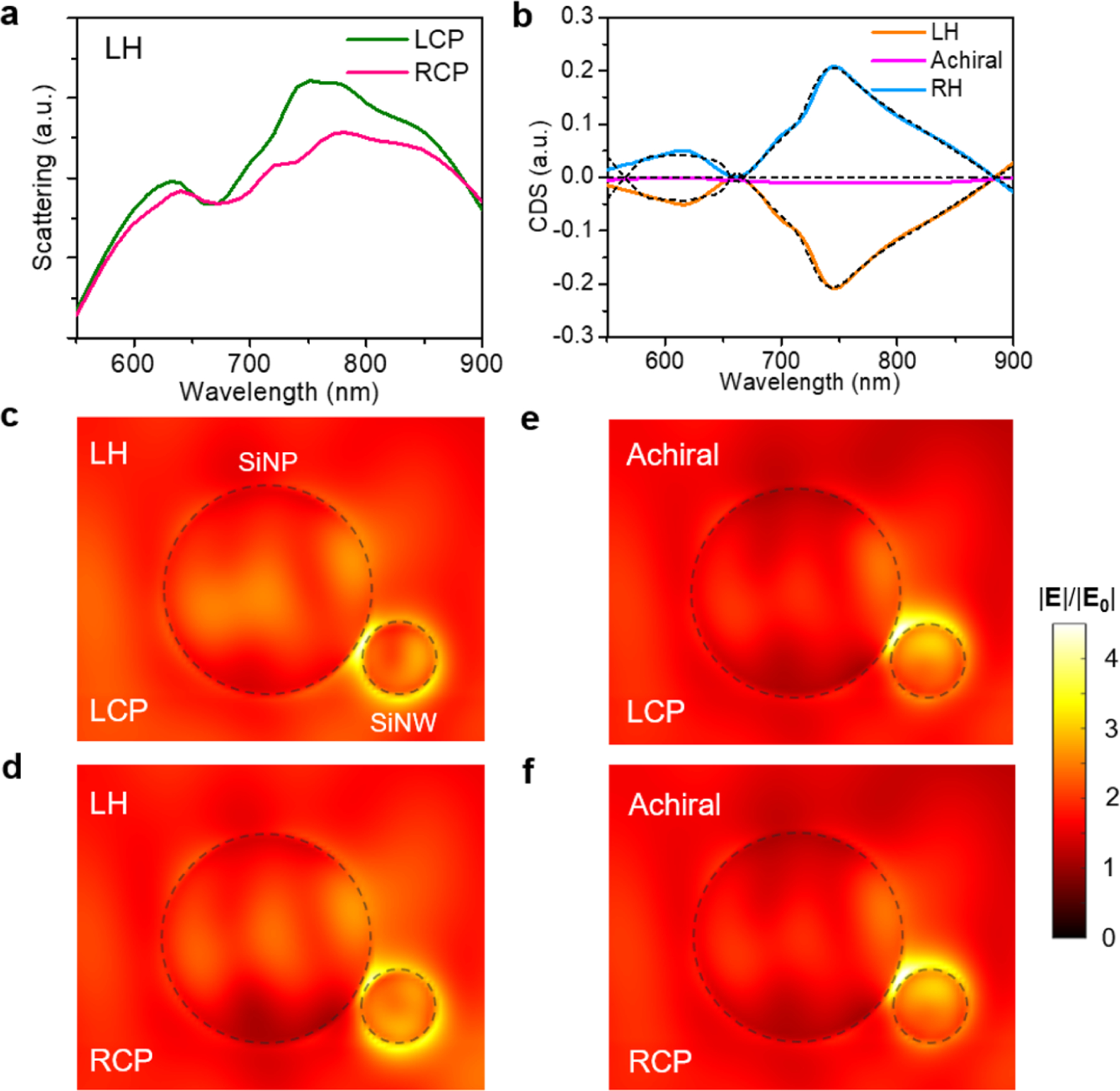
FDTD simulation and coupled-mode theory analysis. (a) Simulated scattering spectra of the LH structure under LCP and RCP illumination. (b) Simulated CDS spectra of LH, achiral, and RH structures. The black dashed lines are the fitting curves via the coupled-mode theory. (c,d) The electric field distributions in the LH structure at 740 nm induced by LCP (c) and RCP (d) incidence. (e,f) The electric field distributions in achiral structure at 740 nm induced by LCP (e) and RCP (f) incidence. All electric field distributions are cut at the cross-sectional plane of the SiNW passing through the center of the SiNP.

Next, coupled-mode theory (CMT) is adopted to provide an intuitive understanding of the origins of the chiral response of the assembled nanostructures, as inspired by the Born-Kuhn model for the description of chiral media.^37,38 In our theoretical model, the system consists of two optical resonators, that is, the SiNP and the SiNW, which involve two dominant bare modes of energy-normalized amplitudes a_n, n = 1,2. For simplicity, we assume that they are of equal resonance (angular) frequency ω₀ and coupled with the strength ξ. For the scattering experiment, we consider that the system is coupled with three channels within which the first two support the light of two distinguished polarizations connected with the source while the third for the detector. Correspondingly, propagating through these channels, inputs and output are respectively represented by 3 × 1 complex vectors |S₊⟩ and |S₋⟩ consisting of flux-normalized wave amplitudes. Indeed, other propagating channels can be accounted for as additional radiation losses and incorporated in a Hermitian matrix Γ describing all of the dissipation processes of the resonators. Under these considerations, the interaction between the incoming waves, the resonators, and the outgoing waves can be modeled as³⁹

$$\frac{\text{d}\mathit{\text{a}}}{\text{d}t}=(i\Omega -\Gamma )\mathit{\text{a}}+D{(\theta )}^{\text{T}}|S_{+}\rangle$$ (1)

$$|S_{-}\rangle =K(\theta )|S_{+}\rangle +D(\theta )\mathit{\text{a}}$$ (2)

where $\mathit{\text{a}}=\left(\begin{array}{l}{a}_1\hfill \\ a_2\hfill \end{array}\right)$ and $\Omega =\left(\begin{array}{ll}{\omega }_0\hfill & \xi \hfill \\ \xi \hfill & {\omega }_0\hfill \end{array}\right)$. K(θ) and D(θ) represent the direct nonresonance scattering and couplings between the modes and the channels, respectively. They depend on an effective phase difference θ due to wave interactions in the structure of finite sizes^40,41 and can be controlled by the relative positions of the SiNP and the SiNW. The CMT fitting curves are very consistent with the numerical simulations (Figure 4b), indicating that the optical chirality results from the couplings between the optical resonances in the SiNP and the SiNW (see SI Note S2 for more details). In addition, the coupling between the resonance modes under LCP and RCP illumination is determined by the phase difference between the SiNP and the SiNW. For LH and RH structures with mirrored geometries, the opposite phase difference leads to a handedness-flipped optical response under circularly polarized light.⁴² The CMT analysis further suggests that the maximal chiroptical response should happen at the largest degree of broken mirror symmetry with the largest phase difference, which, in our case, corresponds to the position of the SiNP near the end of the SiNW.

Last, as a case study, we show the practical applications of chiral sensing in our system with unique advantages brought by all-solid-phase assembly. Dielectric nanostructures are well-known to support the strong enhancement of both electric and magnetic fields, which leads to a remarkable enhancement of near-field optical chirality. The optical chirality C is defined as⁴³

$$C\equiv \frac{{\epsilon }_0}{2}\cdot \nabla \times E+\frac{1}{2{\mu }_0}B\cdot \nabla \times B$$ (3)

where ε₀ and μ₀ are the permittivity and permeability of free space, respectively; and E and B are the local electric and magnetic fields, respectively. The parameter C thus determines the degree of chiral asymmetry in the rate of excitation of a chiral molecule.⁴³ We simulated the electromagnetic field distributions at the plane normal to the light incident direction (Figure S18) and calculated the corresponding optical chirality. Under the irradiation with different circular polarization states, the optical chirality fields in chiral structures show opposite signs (Figure S19), which can induce strong polarization-dependent interactions between chiral molecules and the chiral structures (Figure 5a). Consequently, the adsorption of chiral molecules on the chiral structures results in asymmetric modification of the local refractive index and thus asymmetric peak shifts upon LCP and RCP light illumination.⁴⁴

Figure 5.

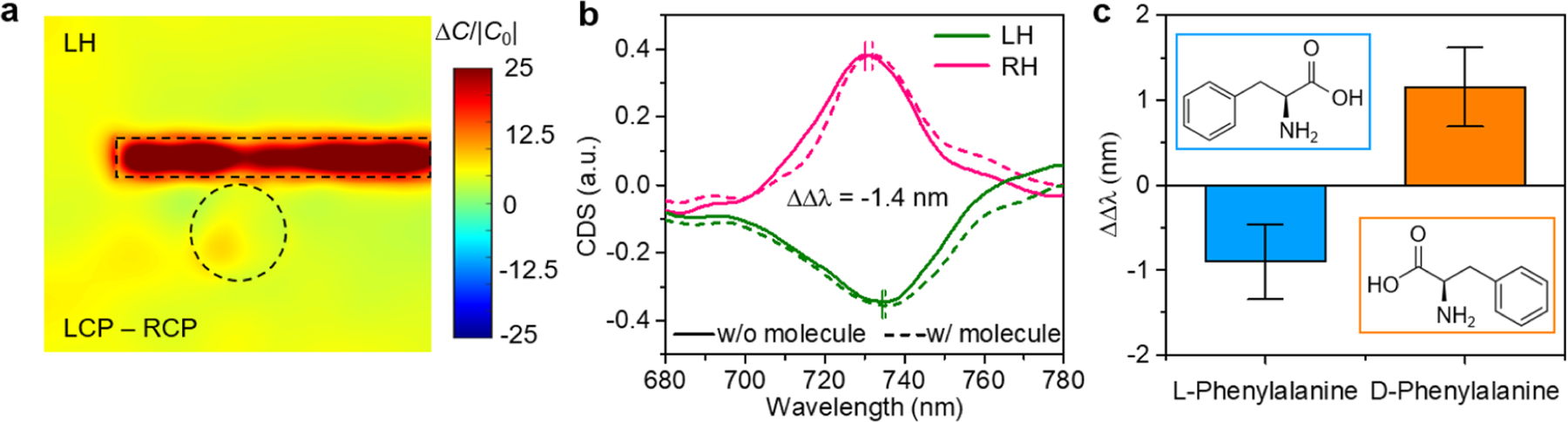
Enhanced chiral sensing. (a) Differential optical chirality mapping in the LH structure at 740 nm under LCP and RCP illumination. C₀ is the chirality for circularly polarized light without the nanostructure. (b) CDS spectra of the LH and RH structures before and after the adsorption of l-phenylalanine. (c) ΔΔλ values for l-Phenylalanine and d-Phenylalanine. The opposite signs of ΔΔλ values reveal the opposite handedness of l-phenylalanine and d-phenylalanine. Insets show the chemical structures of the chiral molecules.

We demonstrated the chiral sensing capability of the assembled chiral nanostructures using two enantiomers of phenylalanine (2 mg mL⁻¹) as the sample analytes (see Supporting Information Experimental Details). Phenylalanine is an essential α-amino acid, and l-phenylalanine is frequently used for the synthesis of pharmaceutically active chemicals and the diagnosis of phenylketonuria.⁴⁵ We measured the peak shifts of CDS spectra (Δλ_LH andΔλ_RH for LH and RH structures, respectively) induced by the chiral molecules and calculated the dissymmetric factor ΔΔλ = Δλ_LH – Δλ_RH (Figure 5b), which reflects the structural chirality of the adsorbed molecules.⁴⁶ The ΔΔλ has a positive value (1.16 ± 0.47 nm) for d-phenylalanine, whereas it is negative (−0.90 ± 0.44 nm) for l-phenylalanine (Figure 5c and Figure S20). The detection concentration is comparable to plasmonic metamaterials and superior to the conventional chiroptical spectroscopy, reflecting the good figure of merit of all-dielectric chiral nanostructures. We also remark that our system is in all solid phase, which further brings new advantages of stability and reliability against the sensing systems fabricated by solution-based methods.

In summary, we have demonstrated handedness-dependent coupling in reconfigurable dielectric nanostructures on solid substrates without requiring liquid media. The configuration of the nanostructures can be largely tailored to tune their chiroptical properties. Using numerical simulation and coupled-mode theory analysis, we elucidated the coupling between Mie resonances of the SiNP and SiNW as the origin of chirality in our nanostructures. We envision that this study will bring new insights and possibilities in various chiroptical applications, such as enantiodiscrimination and polarization conversion, for the development of safer drugs and advanced optical tools. In addition, as a general method to construct reconfigurable nanostructures on the solid substrate, our strategy will also enable the versatile fabrication of adaptive on-chip nanodevices for a wide range of photonic and electronic applications.