Summary
Area V4 is the first object-specific processing stage in the ventral visual pathway, just as area MT is the first motion-specific processing stage in the dorsal pathway. For almost 50 years, coding of object shape in V4 has been studied and conceived in terms of flat pattern processing, given its early position in the transformation of 2D visual images. Here, however, in awake monkey recording experiments, we found that roughly half of V4 neurons are more tuned and responsive to solid, 3D shape-in-depth, as conveyed by shading, specularity, reflection, refraction, or disparity cues in images. Using 2-photon functional microscopy, we found that flat- and solid-preferring neurons were segregated into separate modules across the surface of area V4. These findings should impact early shape processing theories and models, which have focused on 2D pattern processing. In fact, our analyses of early object processing in AlexNet, a standard visual deep network, revealed a similar distribution of sensitivities to flat and solid shape in layer 3. Early processing of solid shape, in parallel with flat shape, could represent a computational advantage discovered by both primate brain evolution and deep network training.
Keywords: vision, primate, cortex, 3D, V4, shape, object, ventral pathway, neural coding, deep network
eTOC BLURB
Brain representation of solid shape has been demonstrated only in final stages of the visual object pathway. Here, Srinath et al. show that solid shape coding actually emerges in early-stage area V4. Similar findings in visual deep networks suggest that rapid conversion of flat images to 3D reality is an effective general strategy for vision.
Introduction
Here, we studied neural coding of solid shape, i.e. explicit (easy-to-read) representation of volume-occupying object structure, like the head, torso, shoulders, limbs, and feet of a quadrupedal animal. Solid, volumetric shape perception is derived from multiple, converging cues for the depth structure (like shading, texture, and stereopsis) and the image boundaries of visible object surfaces. In any one image, these visible surfaces are restricted to a hemisphere of possible orientations, like the near side of the moon. The rest of the object surface and the volume enclosed by the surfaces are inferred from the perceived depth structure and boundaries of the visible surface, combined with implicit prior knowledge about shape probabilities based on learning during visual experience [1–5]. One strong prior is curvature continuity, which comes into play particularly at object boundaries. If the cylindrical curvature of a torso or limb is fairly constant up to the object boundary, and that boundary coincides with the transition of surface orientation from visible to occluded, it is highly improbable that surface curvature changes precisely at that specific boundary, which is randomly determined by a single viewpoint. Based on this, we perceive that the surface continues in depth and encloses a volume. This is true even without experience of specific object categories, as in the case of unfamiliar animals with unusual shapes. If, however, this precise convergence of surface depth structure and object boundary is violated, we perceive a rumpled surface with a cut edge rather than a solid shape.
Solid shape coding, or shape-in-depth, is a complex, high-dimensional geometric domain. It is distinct from position-in-depth of individual visual features, a simple one-dimensional property encoded as early as primary visual cortex (V1), on the basis of binocular disparity [6–8]. Solid shape is known to be encoded in the final stages of the ventral, object-processing pathway [9,10], in anterior inferotemporal cortex (AIT) [11–16]. The geometric tuning dimensions for solid shape coding in AIT include surface orientation, surface curvature, object-centered position, medial axis orientation, and medial axis curvature. AIT neurons typically encode multiple shape motifs in these dimensions, and respond strongly to any object shapes that combine those motifs [11,12].
It has long been thought that solid shape coding emerges only at the end of the ventral pathway, in AIT [15,16], and that depth information in early and intermediate stages like V4 and PIT, which includes signals for fine-scale and relative depth based on disparity and shading cues [17–26], does not extend to robust, explicit signals for shape-in-depth [24,27]. This would make sense considering the complex computations required for deriving solid shape from 2D images, which might require many processing steps in the ventral pathway network. Accordingly, shape coding in earlier ventral pathway stages has been studied and characterized for decades in terms of flat, planar shape, including boundary contours and spatial frequencies [28–45].
Here, though, we found explicit, robust coding of solid shape much earlier than AIT, in area V4, the first object-specific cortical stage. We used single-unit electrophysiology to show that many V4 neurons are explicitly tuned for the 3D geometry of simple, individual solid shape fragments, providing signals that could ultimately support more complex shape-in-depth representation in AIT. The tuning dimensions are equivalent to those studied in AIT [11,12]. (The size and complexity of the shape fragments encoded is more limited, as is natural given smaller receptive fields in V4, but this result could have been influenced by greater constraints on the complexity of stimuli in this experiment.) This tuning was robust across a number of image changes and depth cues, as in AIT. Moreover, using 2-photon functional microscopy, we found that flat and solid shape coding are segregated across the surface of V4 into separate modules. These results have two major implications. First, transformation of flat image information into solid shape signals occurs from the beginning rather than only at the end of object-specific processing, suggesting that early solid shape extraction has a strong computational advantage for real-world vision. Second, flat and solid shape information are processed in parallel channels. This may reflect the independent importance, even in a 3D world, of 2D surface patterns, for object recognition, material perception, shadow interpretation, biological signaling, and camouflage penetration.
Results
Area V4 encodes both flat and solid shape information
We used a probabilistic genetic stimulus algorithm, in which higher response stimuli give rise to partially morphed descendants in subsequent stimulus generations [11–14,32], to focus sampling of responses of individual V4 neurons within a wide domain of solid and flat shapes that could not be effectively explored with systematic or random sampling. Experiments began with a first generation (Gen 1) of 80 random stimuli (Figure 1A), divided into two lineages of 40 each (left and right columns). These stimuli were created with a probabilistic procedure for constructing smoothly joined configurations of solid object parts (Methods and Supplementary Figure 1A). The result was a wide variety of solid, multi-part, branching shapes with naturalistic, biological appearances. These stimuli were presented in the V4 neuron’s receptive field while the monkey performed a fixation task. The average response rate for each stimulus is represented by the color of the surrounding border (referenced to the scale at the upper right), with bright red corresponding to 26 spikes/s in this case. Stimuli in each block are ordered by descending response strength from the upper left to the lower right.
Figure 1. Area V4 encodes solid shape information—introductory example.
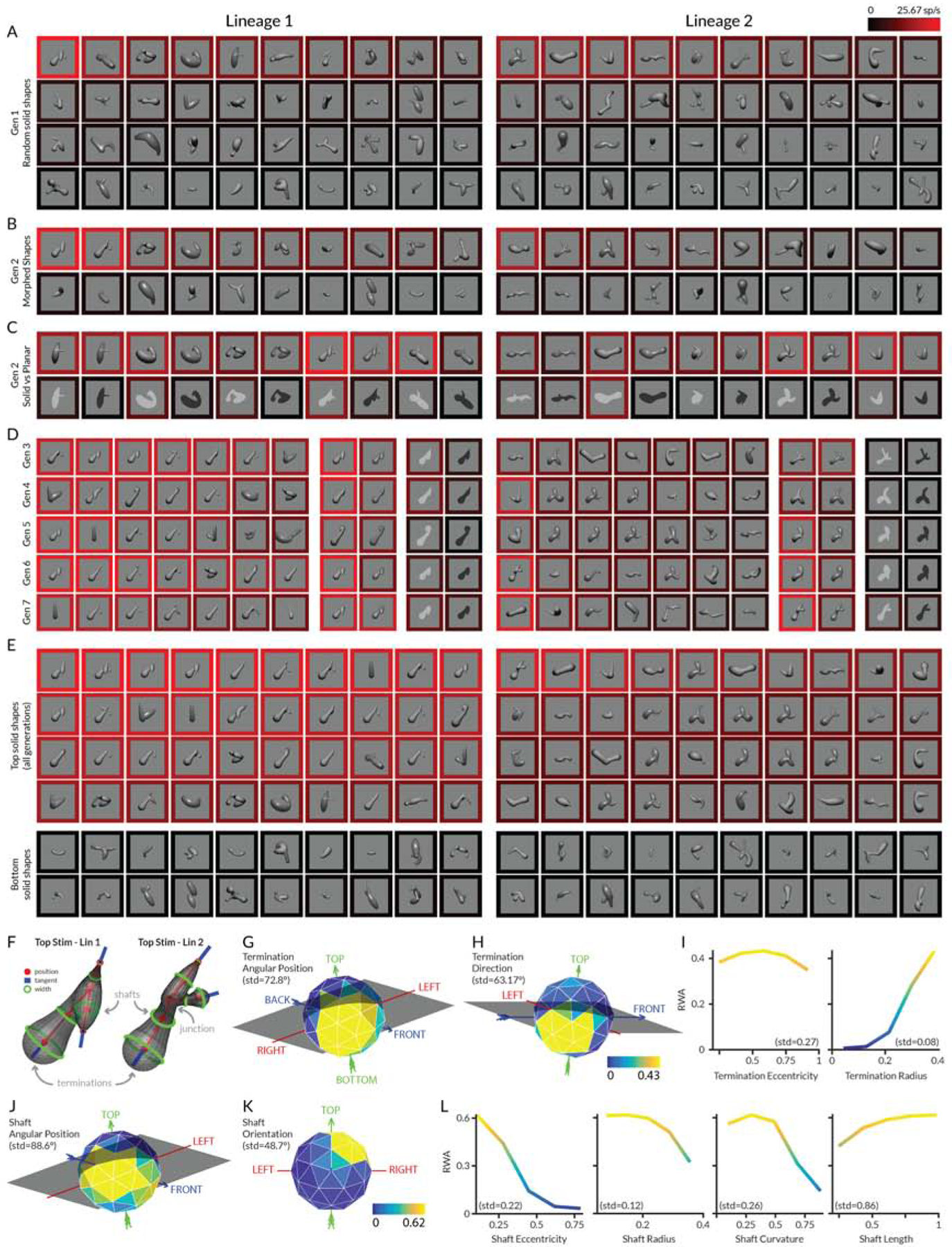
(A) First generation (Gen 1) of 40 random stimuli per lineage. Each stimulus was rendered with a lighting model based on either a matte or polished surface illuminated by an infinite distance point source from the viewer’s direction. Stimuli were centered on and sized to fit within the previously mapped receptive field of an individual V4 neuron and flashed in random order for 750 ms each (interleaved with 250 ms blank periods), against a uniform gray background, while the monkey performed a fixation task. The response rate for each stimulus was calculated as the average number of spikes/s across the 750 ms presentation periods and across 5 repetitions of each stimulus. The neuron’s average response to each stimulus is represented by the color of the surrounding border, referenced to the scale at the upper right, with bright red corresponding to 26 spikes/s. Stimuli in each block are ordered by descending response strength from the upper left to the lower right. (B) Half of Gen 2 comprised partially morphed descendants of ancestor stimuli from Gen 1 plus additional random stimuli. (C) The other half of Gen 2 comprised tests of high response Gen 1 stimuli rendered as solid vs. flat shapes. (D) Highest response stimuli and example solid/flat comparisons in Gen 3–7. (E) Highest and lowest response stimuli across all generations. (F) Parameterization of shaft, junction, and termination shape. (G–L) Response weighted average (RWA) analysis of response strength. Each panel shows average normalized response strength as a function of geometric dimensions used to describe shaft or termination shape. Each plot represents a slice through the RWA at the location of the overall RWA peak across all dimensions (rather than a collapsed average across the other dimensions). Spherical (object-centered position and termination direction) and hemispherical dimensions (shaft orientation) are shown as spherical polygons, in some cases tilted and rotated to reveal the tuning peak. The arrows and labels (LEFT, RIGHT, TOP, BOTTOM, BACK, FRONT) indicate the original directions in the stimulus from the monkey’s point of view. Normalized response strength is indexed to a color scale for shafts (below K) and a color scale for terminations (below H). Color is a redundant cue for response strength in the Cartesian plots. See also Figure S1.
The second generation (Gen 2) of each lineage was created by partial morphing of ancestor stimuli from Gen 1. The probability of a Gen 1 stimulus producing descendants was a function of its response rate, which thus serves as the fitness metric for the genetic algorithm. This strategy ensures denser sampling in higher response regions of shape space. Half of Gen 2 comprised morphed descendants (16 in each lineage, Figure 1B) and newly generated random stimuli (4 in each lineage). The highest response stimulus in Gen 1 lineage 1 in this case gave rise to two visually similar, high response descendants in Gen 2 lineage 1.
The other half of Gen 2 (Figure 1C) comprised 10 high response stimuli drawn from Gen 1 (5 per lineage) and presented in four conditions: solid shapes rendered with matte surfaces, solid shapes rendered with polished surfaces (producing specular highlights in addition to shading), flat (planar) shapes with bright contrast, and flat shapes with dark contrast. The flat shapes are similar to stimuli used previously to measure contour shape tuning [29–37]. The evolving solid stimuli simultaneously test for responses to their 2D self-occlusion boundaries, providing an efficient way to explore both domains simultaneously. We did not evolve flat stimuli independently in these tests. (We were unable to discover a method for generating solid shapes with natural self-occlusion boundaries from randomly created flat shapes.) Basing the flat stimuli on the solid shapes ensures that they have a naturalistic contour boundary that could correspond to the self-occlusion boundary of a smooth real-world object, and thus are more likely to drive V4 neurons adapted for the natural world. In addition, responses to flat and solid versions of the same shapes were highly correlated for most neurons, showing that evolution in either domain would be effective for identifying the tuning peak in the other domain, regardless of relative absolute response rates (see below). Finally, we obtained essentially identical flat/solid preference distributions with a standardized, matched flat/solid stimulus set in our 2-photon functional microscopy experiments (see below).
Subsequent generations were constructed in the same way as Gen 2, drawing ancestors from all previous generations. Figure 1D shows the 7 highest response stimuli in each lineage from each subsequent generation (3–7), along with an example stimulus rendered in the four conditions. Visually similar descendants of the original Gen 1, lineage 1 top stimulus consistently evoked the strongest responses. A smaller number of visually similar stimuli evolved independently in lineage 2. Solid stimuli consistently evoked higher responses from this neuron than corresponding flat stimuli.
We used a simple index to compare solid and flat (planar) shape responses:
where n is the total number of shapes tested in both solid and flat versions, rs,i is the response to a solid version of the ith stimulus (either matte or polished, whichever was higher on average across stimuli), and rp,i is the response to a planar/flat version of the same stimulus (either dark or bright, whichever was higher on average). Solid preference (SP) varies from −1 for neurons responsive only to flat stimuli, to 0 for neurons equally responsive to solid and flat versions, to 1 for neurons responsive only to solid stimuli. For this neuron, solid preference = 0.568, meaning that solid shape responses were on average about twice as strong as 2D shape responses.
Our next analysis step was to quantify the shape information encoded by the neuron’s responses, in order to demonstrate focused tuning for 3D shape geometry that could contribute to downstream representations in AIT and to solid shape perception itself. The highest response solid stimuli across all generations (Figure 1E) included a straight shaft with a bulbous termination pointing toward and positioned near the lower left of the object. Tuning for this solid shape motif was broad, with more moderate responses to stimuli with partially different geometry (e.g. changes in shaft orientation or surface radius). To parameterize these shape characteristics, we defined a geometric space with dimensions for object-relative position, orientation, length, cross-sectional radius, and curvature of medial axis shafts, junctions, terminations, and their surrounding surfaces (Figure S1A,B). Each stimulus was defined as a set of points in this space corresponding to its constituent elements (Figure S1C). Thus the geometric descriptions of the highest response shapes from lineages 1 and 2 (Figure 1F) include the position, orientation, radius, curvature, and length of the long diagonal shaft, as well as the position, direction, and radius of the bulbous termination.
We smoothed these points with Gaussian functions and weighted them by the response value of the stimulus (Supplementary Figure 1C). We summed the response-weighted points across stimuli in each lineage (Supplementary Figure 1D), and divided this by the unweighted sampling matrix, to normalize for uneven sampling due to the probabilistic and biasing nature of the genetic algorithm. Finally, we calculated the dot product of the response-weighted, normalized averages for the two lineages [32]. This ensured that the final response-weighted average (RWA) comprised only shape-tuning energy that evolved independently in both lineages.
The RWA for this example neuron clearly corresponded to the shaft and termination geometry visible in its highest response stimuli (Figure 1E,F). For terminations, tuning for object-relative position was centered below, behind, and leftward of object center of mass (Figure 1G). Tuning for termination direction centered toward leftward/downward (Figure 1H). Terminations with larger radii evoked stronger responses (Figure 1I). For shafts, object-relative position tuning was likewise below, leftward, and rearward of object center (Figure 1J). Shaft orientation tuning centered on diagonals running from top/forward/right to bottom/rearward/left (Figure 1K), consistent with termination direction tuning. (Shaft orientation, which has no inherent directionality and thus occupies only a hemispherical domain, is plotted here only in the hemisphere facing the viewer.) Tuning for shaft radius favored lower values (Figure 1L). Altogether, these tuning functions define a peak corresponding to the narrow shaft and bulbous termination pointing left/downwards that characterizes the highest response stimuli.
Four additional examples of tuning for 3D shape are presented in Figure 2. For each neuron, the highest response stimuli tested in all four conditions are shown (Figures 2A,C,E,G). The RWA is represented by tuning functions along the strongest dimensions for that neuron, and a scatterplot shows the relationship between observed responses and responses in the RWA (Figures 2B,D,F,H). The RWA is not presented as a cross-validated tuning model, since it was fit to the entire dataset and not tested outside that dataset. The RWA thus serves only to show that the responses observed in the GA-evolved stimuli can be described well with response-weighted linear models on a straightforward geometric domain. The first example neuron (Figures 2A,B) responded to shafts and terminations directed toward the upper right back. The second example (Figures 2C,D) responded to curved shafts with a vertical orientation. The third example (Figures 2E,F) responded to medial axis junctions positioned to the right and opening toward the left and back (the direction of the junction bisector). The fourth example (Figures 2G,H) responded to medial axis junctions positioned near the bottom right and opening toward the left. In each case, responses were strongest for solid shapes.
Figure 2. Area V4 encodes solid shape information—additional examples.
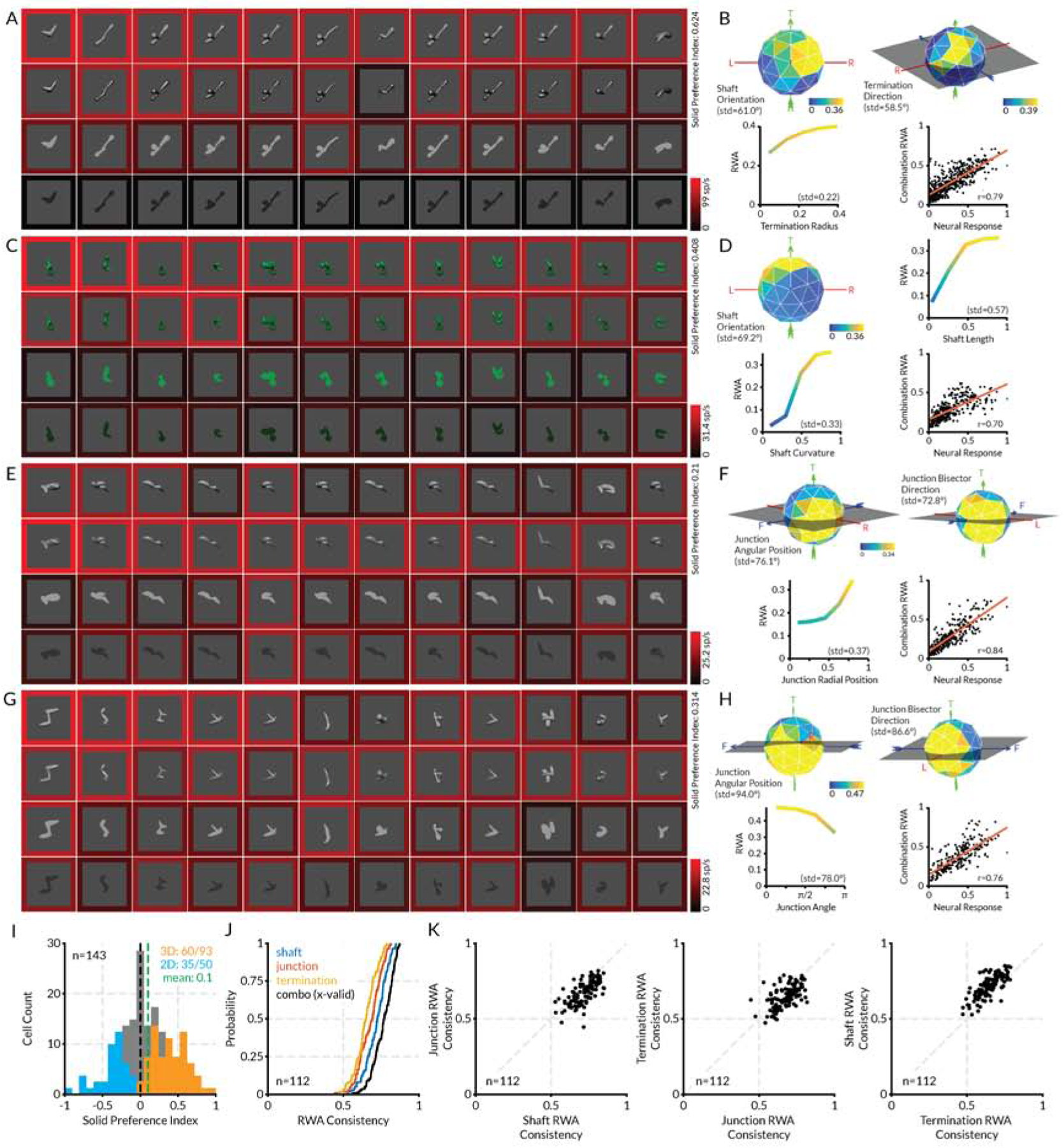
(A) Highest response stimuli (columns) for the first example neuron, tested in four rendering conditions (rows). Scale bar at bottom right indexes the border color representation of average neural response to each stimulus. (B) Plots of RWA strength for this neuron, selected to highlight dimensions with strongest tuning, plus a scatterplot of RWA responses vs. observed responses. (C–H) Plots for the three other example neurons. Details as in (a) and (b). (I) Histogram distribution of solid shape preference index (SP). Values significantly greater or less than 0 (t-test, two-tailed, p < 0.05) are plotted in orange and blue, respectively. (J) Cumulative distributions of RWA/observed correlations for shaft, junction, and termination RWAs. (K) Comparisons of prediction accuracies for shaft, junction, and termination RWAs. See also Figure S2.
As in these examples, the majority of V4 neurons in our sample were more responsive to solid shapes than to flat shapes, and solid shape tuning was described well by RWAs. Figure 2I shows that 94/143 cells (65.7%) had an solid preference value greater than 0 (preferred solid shapes on average). The observed responses to evolved solid stimuli were strongly correlated with the corresponding weighted, smoothed averages in the RWAs (Figure 2J), with an average r of 0.78. RWAs based on shaft parameters typically captured more variance than RWAs based on junctions or terminations (Figure 2K). In addition, RWAs across the population had focused tuning peaks that occupied a restricted region of the overall tuning domain (Figure S2).
Nevertheless, a substantial fraction of V4 neurons responded more strongly to flat shapes (Figure 3). This makes sense, since flat image patterns represent the object’s self-occlusion boundary, which is a major cue for its solid shape [1–5]. Even solid-selective neurons typically responded at lower levels to flat shapes with isomorphic contours (e.g. Figure 1), consistent with self-occlusion boundaries contributing to solid shape perception. In addition, flat shape patterns on surfaces remain important for other aspects of perception, e.g. for distinguishing coloration patterns on plants and animals. There is even evidence that the ventral pathway compensates for surface distortions due to solid shape to recover veridical 2D surface patterns [51].
Figure 3. Area V4 encodes flat shape information—example.
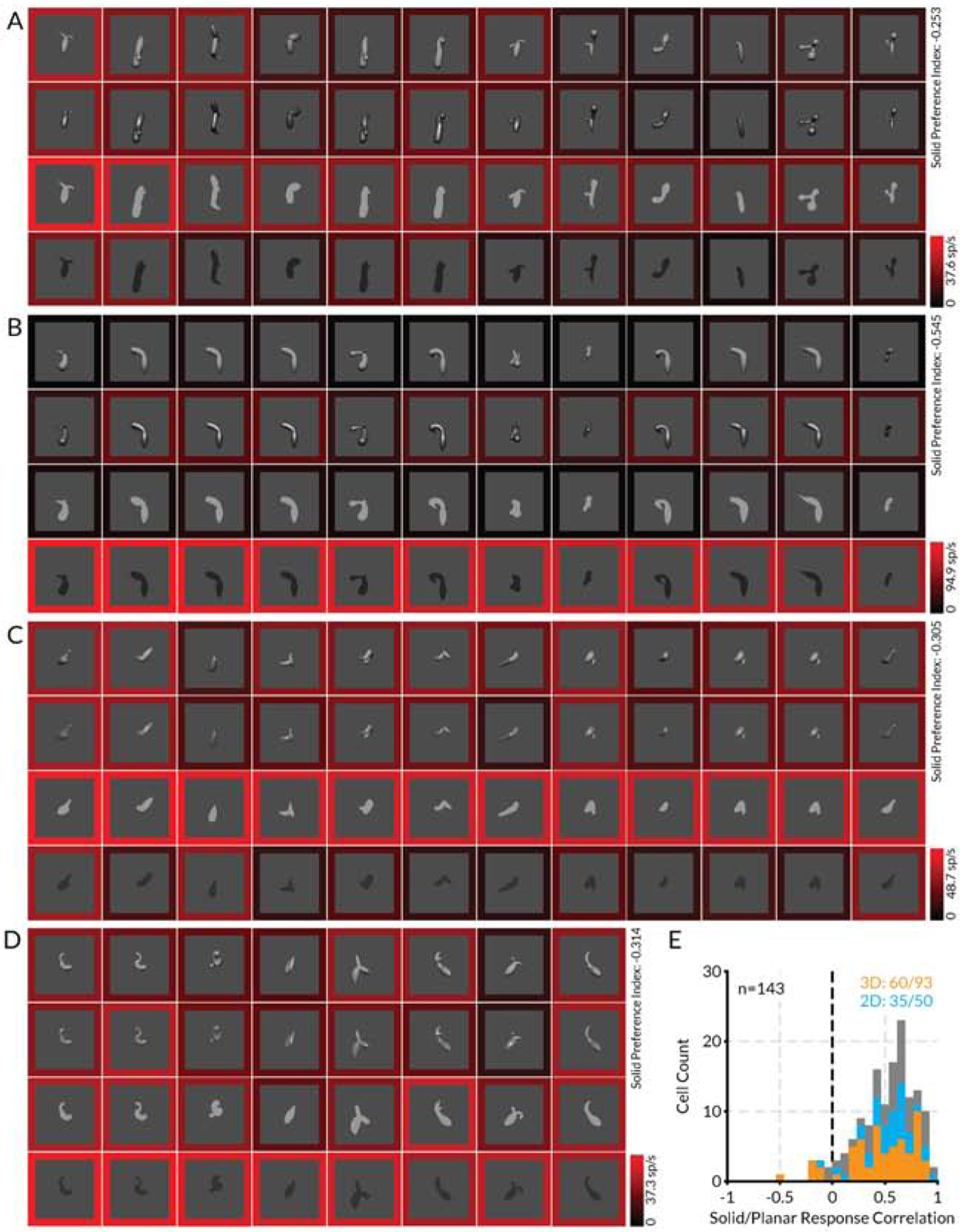
(A–D) Highest response stimuli (columns) for four example neurons, tested in four rendering conditions (rows), showing stronger responses to flat shapes. Scale bar at bottom right of each plot indexes the border color representation of average neural response to each stimulus. (E) Distribution of correlation values between highest response solid rendering condition (either shading or specular) and highest response flat rendering condition (either bright or dark) across all stimuli tested in the four rendering conditions.
The many neurons with higher responses to flat shapes verify that our experimental method, in which 2D boundary shape coevolved with shading and specularity cues, was competent to identify tuning peaks even for neurons with higher responses to flat stimuli. In addition, we found that tuning patterns were highly correlated across flat and solid rendering conditions for most neurons (Figure 3E), meaning that successful identification of the tuning peak in either one of these domains would ensure finding the peak in the other domain.
V4 solid shape coding generalizes across different image cues
We performed several post hoc tests to confirm that many V4 neurons are selective for solid shape per se rather than some associated low-level image feature (Figure 4, example neurons on the left, population results on the right). First, we varied the contrast of high response shapes from the genetic algorithm to ensure that high solid shape responses did not just reflect a specific contrast sensitivity peak. The four example neurons in Figure 4A show how solid shape preferring individual V4 neurons tuned for different contrast ranges remained strongly selective for solid shapes, even vs. much brighter and darker flat shapes. The majority of solid shape preferring neurons with significantly positive solid preference (SP) values in the genetic algorithm (t-test, two-tailed, p < 0.05) tested in this way correspondingly had larger responses to solid shape averaged across contrast variations (i.e., fell in the upper right quadrant of Figure 4B). The average solid preference value across contrasts for the tested neurons was 0.26 (Figure 4C) which was significantly greater than 0 (t-test, two-tailed, p < 0.05). Thus, we conclude that contrast differences do not explain preference for solid shape stimuli.
Figure 4. V4 solid shape coding generalizes across different image cues.
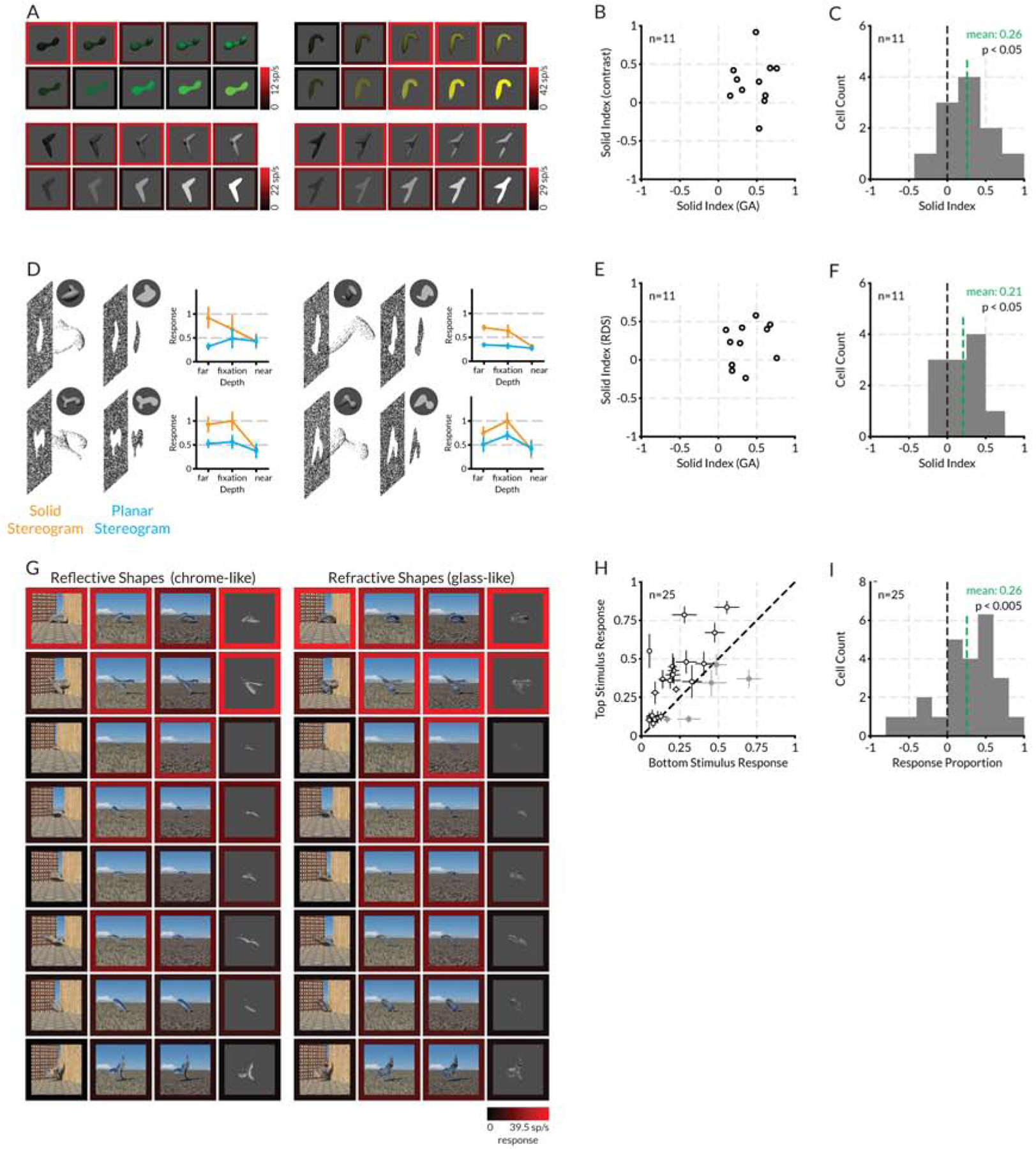
(A) Comparison of solid and flat stimulus responses across a range of figure/background contrasts, for four example solid-preferring V4 neurons. In each case, responses to solid stimuli, within an optimum contrast range, were stronger, as shown by the brighter red surrounds (indexed to the color scale bars on the bottom right of each plot). (B) Scatterplot of solid preference values for 11 neurons with significantly positive solid preference values in the genetic algorithm dataset (randomization t-test, two-tailed, p < 0,05), tested across contrasts as in (A). (C) Histogram of solid preference values for the same 11 neurons. The mean solid preference value for these neurons in the genetic algorithm was 0.46 and this was significantly greater than 0 (t-test, two- tailed, p <0.001). The mean solid preference value in the contrast test, based on averaging responses across the full contrast ranges, was 0.26 and this was significantly greater than 0 (t-test, two-tailed, p < 0.05). (D) Diagrams and normalized response plots for four example V4 neurons, comparing responses to solid vs. planar random dot stereogram versions of high response stimuli from the genetic algorithm experiment, presented at three stereoscopic depths relative to the fixation plane. Bars indicate standard error of the mean across 5 repetitions. (E) Scatterplot of solid preference values for 11 neurons with significantly positive solid preference values in the genetic algorithm dataset (randomization t-test, two-tailed, p < 0,05), tested with solid and planar stereograms as in (D). (F) Histogram of solid preference values for the same 11 neurons. The mean solid preference value for these neurons in the genetic algorithm was 0.37 and this was significantly greater than 0 (t-test, two-tailed, p <0.001). The mean solid preference value in the random dot stereogram test, based on averaging responses across depths, was 0.21 and this was significantly greater than 0 (t-test, two-tailed, p < 0.05). (G) Responses of a single example solid-preferring V4 neuron to 8 stimuli (rows, in descending order of response strength in the original genetic algorithm dataset) in four chrome-like renderings and four glass-like renderings (columns). Response levels are indicated by border color, indexed to the scale bar at lower right. (H) Scatterplot of average responses of 25 neurons tested in the same way, to the top vs. bottom genetic algorithm stimuli, averaged across the refraction and reflection rendering conditions (e.g., the top and bottom rows in (C)). (I) Histogram of response proportion index values for the same 25 neurons. The RP mean across the 25 neurons was 0.26 and this was significantly greater than 0 (t-test, two-tailed, p < 0.005). See also Figure S3.
We also tested whether selectivity for solid shape was maintained in the absence of any monocular image cues, by using random dot stereograms (RDSs) to create shape percepts based entirely on binocular disparity. Pure disparity in stereograms supports solid shape perception [47] and disparity and shading together provide more accurate shape information [48]. We used random dot stereograms to create solid and flat versions of high response stimuli (Figures 4D,S3), centered in depth either at, in front of, or behind the fixation plane (with the background offset even further behind the fixation plane). For four example neurons (not the same as in Figure 4A), responses remained higher for solid shapes behind and at the fixation plane. Responses to both solid and flat shapes were low for near disparities, perhaps because they were closer to the fusion limit in the range of our V4 receptive field eccentricities (1–4°). The majority of neurons with significantly positive solid preference values in the genetic algorithm (t-test, two-tailed, p < 0.05) tested in this way (we did not succeed in testing a meaningful number of neurons with significantly negative preferences) had larger responses to solid shape in the stereograms (Figure 4E, upper right quadrant), and the average solid preference value of 0.21 (Figure 4F) was significantly greater than 0 (t-test, two-tailed, p < 0.05). Thus, solid preference persisted in the absence of any monocular image cues.
Finally, we tested whether selectivity for 3D shape was maintained across more unusual monocular image cues. In our basic genetic algorithm experiment, we based perceptual 3D shape on shading and specularity, which are highly informative cues for shape in depth in the natural world. In the post hoc test shown here for a single neuron, we selected a range of high through low response 3D shapes from the genetic algorithm experiment (Figure 4G, rows). We then rendered these shapes with reflection and refraction cues, by simulating glass-like and chrome-like versions of the same 3D shapes against blank or naturalistic backgrounds (Figure 4G, columns). Refraction and reflection patterns support strong 3D shape perception regardless of the environment being refracted or reflected, possibly based on higher derivatives of pattern compression produced by surface curvature [49,50]. In fact, recognition of such materials requires 3D shape information [51–53].
The Figure 4G example maintains high responses under some though not all of the rendering conditions, showing that this neuron can provide information about shape from reflection and shape from refraction, but not in an entirely robust or invariant way. For 25 neurons tested in this way, the differential between the top response row and the bottom response row was maintained in 20 cases (Figure 4H, upper left triangle). We quantified the differences between average top and bottom stimulus responses across rendering conditions with a response proportion index:
where rt,i is the response to the top shape in rendering condition i, and rb,i is the response to the bottom shape in rendering condition i. The RP mean across the 25 neurons was 0.26 and this was significantly greater than 0 (t-test, two-tailed, p < 0.005) (Figure 4I). Thus, V4 neurons preserve some information about solid shape across unusual shape-in-depth cues where shading and highlights are entirely absent.
Area V4 micro-organization includes flat and solid shape modules
Micro-organization across the cortical surface is a signature of important neural tuning dimensions throughout the primate brain [54–81]. Clustering of neurons with related tuning is likely to reduce wiring costs, improve temporal precision, and enable addressability for feed-forward and feedback connections [82–87]. We used 2-photon functional microscopy in anesthetized monkeys to examine the micro-organization of solid and flat shape selectivity across 300–400 um imaging regions in upper layer II/III of area V4 of the foveal/para-foveal region (1–4° eccentricity) of the lower field representation at the ventral end of the prelunate gyrus (Figure 5A; comparable to the region targeted by our neural recording experiments). We injected sulforhodamine (SR101) [88] to discriminate neurons from glia and Oregon Green BAPTA (OGB) [89,90] to measure calcium fluorescence transients associated with neural spiking responses. We measured calcium changes in response to flashed or drifting L- or C- shaped stimuli presented at a variety of 3D orientations (Figure 5B,C, Figures S4,S5) in order to span a finite shape domain within a short time period. These stimuli contain many or most of the shape motifs (shafts, terminations, junctions at various orientations and object-centered positions) for which neurons were tuned in the electrophysiology experiment. They were shown with and without shading cues in order to contrast responses to solid and flat stimuli. However, this limited stimulus set is insufficient to characterize tuning with the precision of the genetic algorithm procedure used in electrophysiology experiments.
Figure 5. Area V4 micro-organization includes flat and solid shape modules—introductory example.
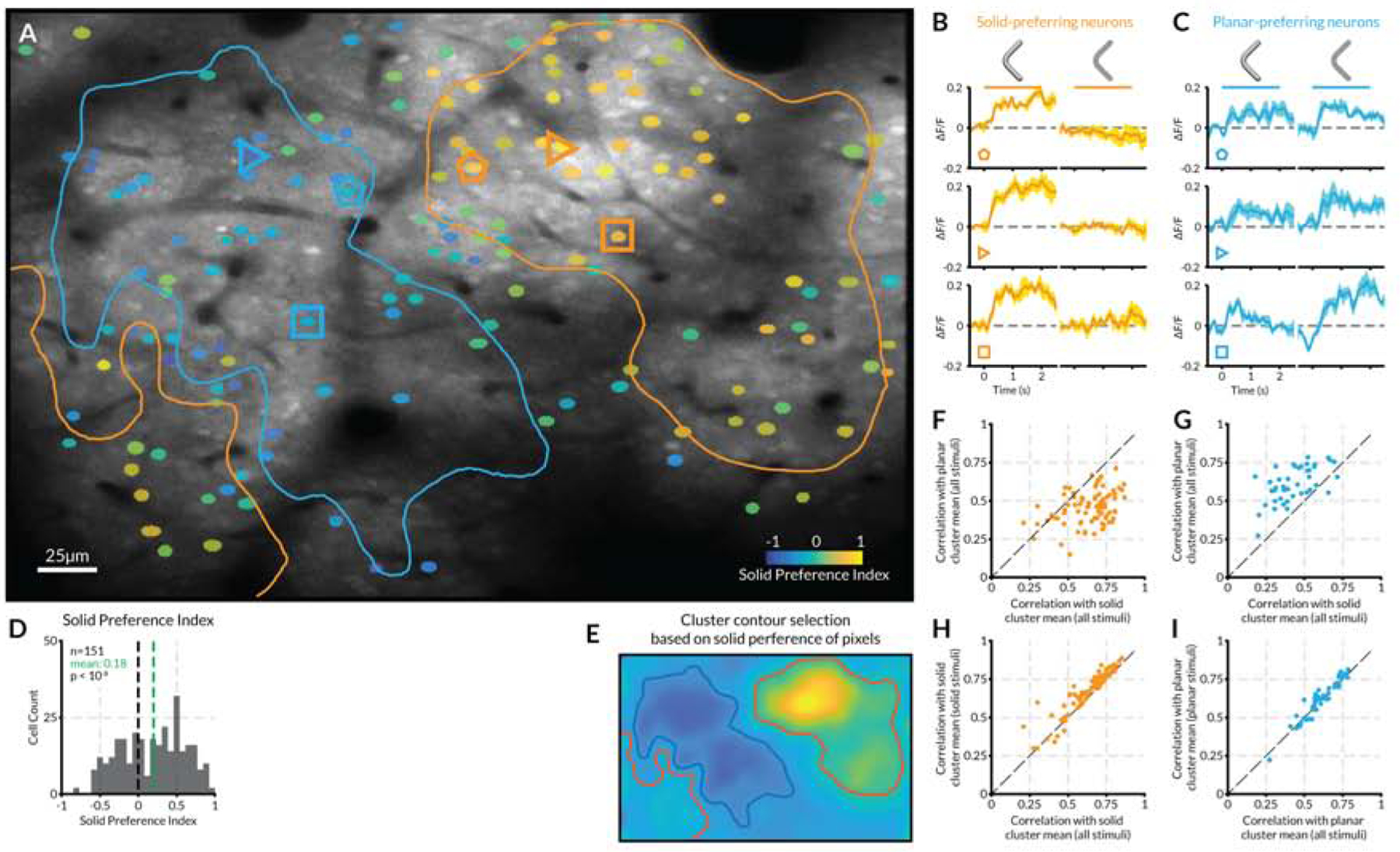
(A) Anatomical average image of a section of V4 cortical surface (anatomical scale bar at lower left). Neurons with significant (based on multiple tests; see STAR Methods) fluorescent responses to stimuli (Figure S4) are overlaid with a color indexing their preference for flat (blue) or solid (yellow) stimuli (SP; see solid preference scale bar at lower right). (B) Peri-stimulus time fluorescence plots for example solid-preferring neurons indicated by orange polygons in (A). Horizontal bars span the 2 s stimulus presentation period for solid (left) and flat (right) stimuli. (C) Example flat-preferring neurons; details as in (B). (D) Distribution of solid preference values for neurons in this region. The mean solid preference value of 0.18 is significantly greater than 0 (t-test, two-tailed, p < 10−6). (E) Smoothed map of pixels solid preference values in this imaging region, used as the basis for drawing cluster boundaries (see STAR Methods) shown in (A). (F) Correlations of stimulus response patterns for neurons in the upper right solid cluster (orange contour in (A)) with the average response pattern in that solid cluster (horizontal axis) vs. the average response pattern in the planar cluster (blue contour in (A)). (G) Correlations of stimulus response patterns for neurons the planar cluster (blue contour in (A)) with solid and planar cluster averages. (H) Correlations of solid cluster neurons with solid cluster average across all stimuli (horizontal axis) vs. solid stimuli only (vertical axis). (I) Correlations of planar cluster neurons with planar cluster average across all stimuli (horizontal axis) vs. planar stimuli only (vertical axis).
For some neurons, solid shapes evoked much stronger fluorescence changes than flat shapes (Figure 5B). Other neurons responded more strongly to flat shapes (Figure 5C). We used our standard solid preference index to compare the summed responses across solid shapes vs. flat shapes. The distributions of solid preference values varied across imaging regions but showed a similar combination of solid- and flat-preferring neurons (Figure 5D). Plotting the solid preference values for identified neurons across anatomical images revealed separate clustering of solid and flat preference types (Figure 5A). We generated cluster boundaries based on the pixel-wise solid preference values for the same neurons, combining signals from neuropil and cell bodies (Figure 5E). For each cluster, we calculated an average response pattern across all stimuli for identified neurons only. Within the large solid cluster at the upper right in Figure 5A, the response patterns of most neurons were highly correlated with the solid cluster average, and correlations with the planar (flat) cluster average were substantially lower (Figure 5F). Within the planar cluster at the left, neurons were highly correlated with the planar cluster average, and less correlated with the solid cluster average (Figure 5G). These differential correlations were not simply due to different responses to the solid and planar stimuli in each cluster. Solid cluster neurons show similarly high correlations to the response pattern across solid stimuli alone (Figure 5H), and planar cluster neurons showed similarly high correlations to the response pattern across planar stimuli alone (Figure 5I). This indicates that, within clusters, shape tuning is similar across neurons. Thus, these clusters might represent modules for specific flat and solid shape motifs of the types seen in Figures 1–3, representing combined clustering for the geometric dimensions (object-centered position, orientation/direction, surface curvature, etc.) we tested in our experiments. We observed similar results in other imaging regions and in other monkeys (Figure 6).
Figure 6. Area V4 micro-organization includes flat and solid shape modules—additional examples.
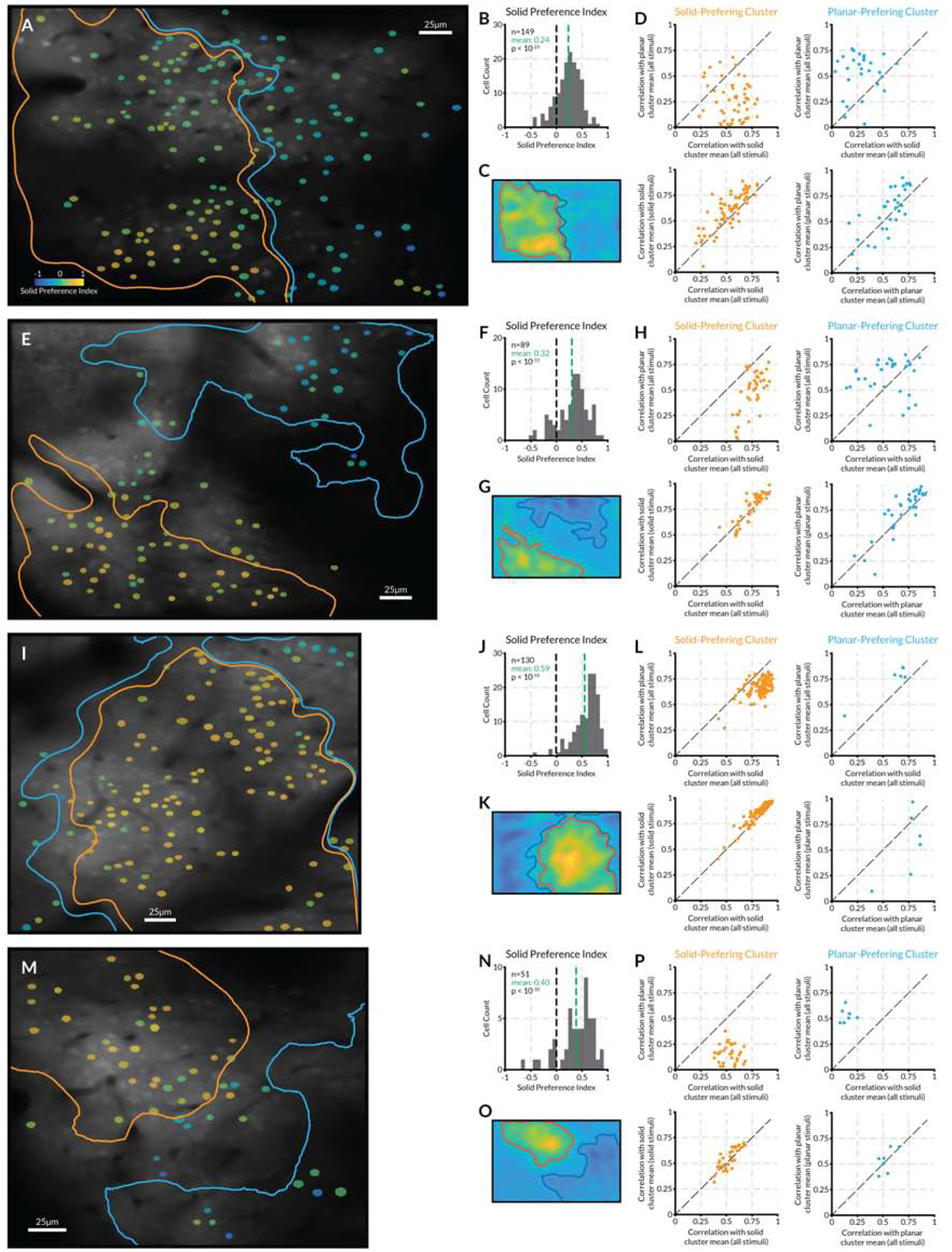
(A–D, E–H, I–L) Three imaging regions studied with flashing stimuli (Figure S4), as in Figure 5. Details as in Figure 5. (M–P) Imaging region studied with drifting stimuli (Figure S5). These data leave open questions about distribution of cluster sizes across larger surface regions, relationship of clusters to organization for other tuning dimensions in V4, and depth profiles of clusters, which would require electrophysiology to measure.
AlexNet layer 3 neurons exhibit similar flat and solid shape tuning
AlexNet [91] and other moderately deep networks trained on ImageNet categorization are promising models for the ventral pathway hierarchy, with intermediate layers providing the closest potential matches to V4 [92,93]. We performed a strong test of this idea, by measuring whether AlexNet manifests the same kind of individual neuron solid shape selectivity observed in V4. First, we searched for direct correlations between the responses of individual V4 neurons to their genetic algorithm stimuli and the responses of individual AlexNet neurons to the same stimuli (Figure S6). The highest correlation AlexNet neurons were found in layer 3, confirming its homology to area V4. The majority of these layer 3 neurons exhibited stronger responses to 3D stimuli, like their V4 counterparts.
On this basis, we investigated 2D and 3D shape tuning in AlexNet layer 3 with independent genetic algorithm experiments. These tests involved essentially the same protocol used for V4, but comprised more generations (since testing time was unlimited) and more variation in size and position of stimuli within the image (so that size and position would be optimized during stimulus evolution, since we did not define the AlexNet layer 3 neuron receptive field before the experiment as we did in V4). Genetic algorithm experiments and RWA analyses revealed tuning for solid shape geometry that was remarkably similar to what we observed in V4 (Figure 7A–F). The top example layer 3 neuron (Figure 7A,B) was tuned for solid shafts tilted toward the upper right and positioned near the bottom relative to object center. Activations were stronger for solid stimuli vs. flat stimuli with the same boundary contours. The second example (Figure 7C,D) was tuned for large radius shafts tilted toward the upper left with sharp (small radius) terminations directed toward the upper left. This neuron responded nearly exclusively to solid stimuli. The bottom example (Figure 7E,F) responded to small radius junctions positioned at the upper right of object center, with the concavity bisector pointing downwards, i.e. for the thin hooks near the top of the high response solid stimuli stimuli. Responses to flat stimuli were low, though slightly higher when the thin hook was visible in profile.
Figure 7. AlexNet layer 3 neurons exhibit similar flat and solid shape tuning.
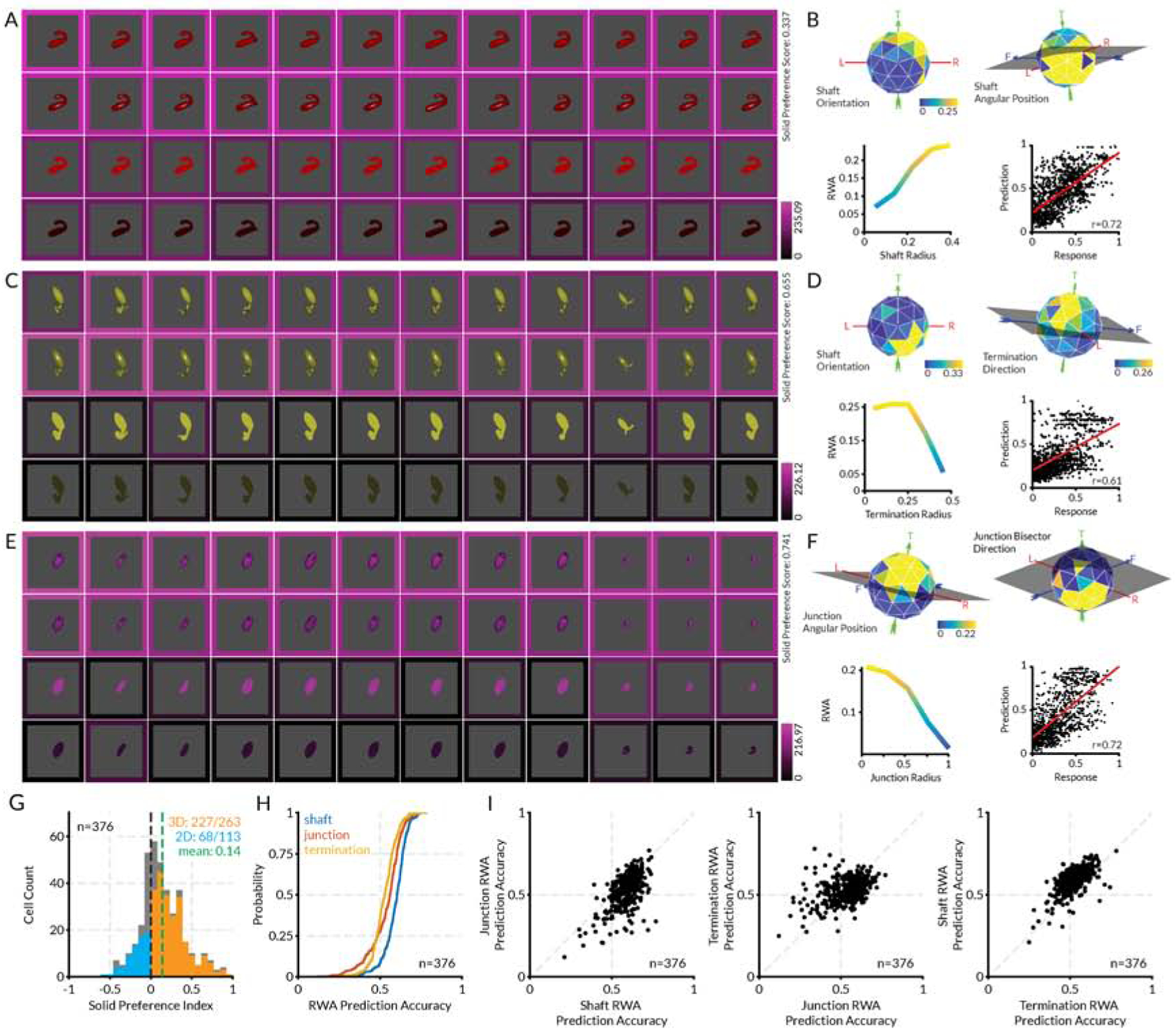
(A) Highest response stimuli (columns) for an example layer 3 neuron, tested in four rendering conditions (shading, shading + specularity, bright flat, dark flat, rows). (B) RWA plots for this unit, selected to highlight dimensions with strongest tuning, plus a scatterplot of RWA values vs. observed activations. (C–F) Two additional example layer 3 neurons. Details as in (A) and (B). (G) Distribution of solid preference values for 376 unique layer 3 neurons. The mean value of 0.15 was significantly greater than 0 (t-test, two-tailed, p < 10−21). (H) Cumulative distributions of correlations between observed activations by genetic algorithm stimuli and values in RWAs based on the geometry of shafts, junctions, and terminations. (I) Scatterplots comparing correlations with observed activations and RWAs based on shafts, junctions, and termination. See also Figure S6.
The distribution of solid and flat shape tuning in AlexNet layer 3 was remarkably similar to the distribution in V4 (Figure 7G; compare Figure 2I). RWA analyses of layer 3 genetic algorithm responses yielded values that were strongly correlated with observed activations, with r-values above 0.5 in most cases (Figure 7H). As in V4, shaft tuning was somewhat more predictive than tuning for junctions or terminations (Figures 7H–I). These analyses show that AlexNet, like the primate object pathway, represents a combination of flat and solid shape just two stages beyond an initial bank of 2D Gabor-like filters.
DISCUSSION
We found that area V4, the first object-specific cortical stage, and the main source of inputs to subsequent stages in the ventral pathway, is tuned not only for flat, 2D image patterns, but also for solid, 3D shape, which defines the structure of most objects in the natural world. This indicates that solid shape representation is a major aspect of early/intermediate object processing in the brain. It shows that the brain quickly converts 2D image information into 3D representations of physical reality. Conceivably, this information originates from V4, a hypothesis supported by the similar solid shape tuning we observed in layer 3 of AlexNet, which is strictly feedforward, like most current deep networks. But it is also possible that the tuning we observed is influenced by feedback connections from anterior ventral pathway and/or dorsal pathway areas involved in depth processing [94]. The relationship of V4 3D signals to 3D shape processing in the rest of the brain remains an open question to be explored in future experiments.
Our study constitutes a break from the long history of studying V4 in terms of flat shape processing [28–43]. It also directly conflicts with previous studies concluding that neither V4 [24] nor PIT (posterior inferotemporal cortex) [90], the next ventral pathway stage after V4 [9,10], encode 3D shape to any significant degree. The stimuli in those studies were a limited set of curved surfaces, with sharply cut 2D boundaries and various degrees of convex or concave surface curvature at one orientation, toward or away from the viewer. Here, in contrast, we used a genetic algorithm to explore a large space of solid naturalistic 3D shapes, with self-occlusion boundaries rather than cut edges, comprising multiple parts that varied across the full ranges of many geometric dimensions: shaft orientation, shaft length, shaft curvature, junction direction, termination direction, surface orientation, maximum surface curvature, minimum surface curvature, and max/min surface curvature orientation. This far wider exploration of more naturalistic geometry presumably explains why we found such strong responsiveness and clear tuning to 3D shape.
We used a number of control tests to rule out alternate explanations for the observed solid shape tuning. Solid shape preference was preserved on average across a wide range of contrasts. The on average preservation of tuning across reflective and refractive cues for depth structure shows that it did not depend exclusively on the shading/specularity cues. The on average preservation of solid shape preference in random dot stereograms shows that, at least for many cells, it did not depend exclusively on monocular cues of any kind, ruling out any low-level cues not based on disparity, including spatial frequency and texture tuning (since internal texture is balanced between the flat and solid stereograms, by equating the distribution of dots in the image plane, regardless of stimulus surface angles).
This work builds upon, and does not replace, previous discoveries about flat, 2D shape representation in V4. On the contrary, our recording and functional microscopy data show that flat and solid shape are processed in parallel, and the distinction is important enough that 2D and 3D shape processing appear to be segregated into modules across the surface of V4. This is consistent with the independent ecological importance of 3D shape for understanding object structure, mechanics, and physics, vs. 2D shape for processing object boundaries, figure/ground and occlusion relationships, object identity under conditions where depth cues are absent, biological signaling with surface patterns, and biological camouflage with surface patterns.
These previous studies have shown that V4 neurons are selective for contour fragments within larger shapes [30,32]. They are tuned for the orientation, curvature, and object-centered position of those fragments. Thus, at the population level, V4 neurons encode an entire object boundary in terms of its constituent contour fragments, how they are oriented, their degree of convex or concave curvature, and their spatial arrangement relative to object center [31]. This dimensionality is the 2D complement to the solid shape tuning dimensions measured here.
Contour orientation is a circular slice through the spherical surface orientation domain at the self-occlusion boundary. Contour curvature is a one-dimensional slice through the two-dimensional surface curvature domain, which comprises the maximum and minimum cross-sectional curvatures. Angular position relative to object center in the image plane is a circular slice through the spherical relative position dimension measured here for solid shape.
This dimensional similarity is consistent with our results showing a close relationship between flat and solid shape processing. The distributions of solid shape preference (SP) values we observed with recording and functional microscopy were continuous, with peaks near 0. And in some imaging regions (Figure 5F,G; Figure 6H,L), many neural response patterns in solid and flat cluster regions were highly correlated (above 0.5) with neighboring flat and solid cluster averages, respectively. This makes sense since 2D self-occlusion boundary shape is strongly related to solid shape and thus serves as a potent cue for solid shape [1–5], especially when depth cues are degraded or absent. In addition, flat and solid shape must often be processed together, for example when interpreting surface patterns distorted by surface shape and orientation changes, a problem that appears to be resolved in anterior inferotemporal cortex (AIT) [46].
The emergence of clear neural tuning for solid, 3D shape motifs in area V4, just two stages beyond V1, where 2D image patterns are processed with Gabor-like filters or kernels, calls for rethinking ideas about early and intermediate visual processing, at the theoretical and computational levels. Currently, deep networks trained to categorize object photographs are considered to be the most promising models for ventral pathway processing. A drawback to deep networks is the opacity of their underlying algorithms. However, Pospisil, Pasupathy and Bair [95] showed how artificial neurons in AlexNet [91] can be studied just like neurons in the brain, with stimulus sets that reveal tuning for visual characteristics. They found neurons in AlexNet with tuning functions corresponding to V4 tuning for 2D shape fragments. Here, we used a similar approach to study tuning for flat and solid shape in AlexNet. Consistent with other evidence [92,93], we found that convolutional layer 3 in AlexNet had the closest correspondence to V4 tuning. And, we found a similar distribution of tuning for flat and solid shape among layer 3 neurons, even though AlexNet is only trained on an object categorization task that would not appear to require internal representation of 3D shape.
The finding of explicit tuning for solid shape motifs in the third stage of AlexNet, so similar to tuning in the third stage of primate ventral pathway, suggests that early 3D shape representation may be a powerful general solution for object vision. It also adds substantial weight to the idea that moderately deep networks are accurate models for ventral pathway processing mechanisms. This finding of one type of correspondence with one deep network is preliminary, but it points toward further directions for investigating the brain and deep networks in parallel.
STAR ★ METHODS
RESOURCE AVAILABILITY
Lead Contact
Requests for resources should be directed to and will be fulfilled by the Lead Contact, Charles E. Connor (connor@jhu.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
The datasets/code supporting the current study have been deposited in a public Github repository https://github.com/ramanujansrinath/V4_solid_flat_data_code. This repository contains Matlab code to generate each figure in this publication and corresponding data. Further requests for data and analysis software can be sent to the corresponding author.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Electrophysiology
Two adult male rhesus macaques (Macaca mulatta) weighing 8.0 and 11.0 kg were used for the awake, fixating, electrophysiology experiments. They were singly housed during training and experiments.
Two-photon Imaging
Three juvenile male rhesus macaques (Macaca mulatta) aging between 15–21 months and weighing between 3.0 and 4.0 kg were used for anesthetized two-photon imaging experiments. They were singly housed before the experiments and were not involved in any prior procedures.
All procedures were approved by the Johns Hopkins Animal Care and Use Committee and conformed to US National Institutes of Health and US Department of Agriculture guidelines.
METHOD DETAILS
Electrophysiology
Behavioral task
Both monkeys were head-restrained and trained to maintain fixation within a 0.5deg window (radius) surrounding a 0.25deg square sprite (fixation spot) displayed on a monitor 60cm away for juice reward. Eye positions for both eyes were monitored with a dual-camera, infra-red eye tracker (ISCAN, Inc, Woburn, MA). In trials requiring stereoscopic fusion, separate images were shown in left and right eyes via cold mirrors. In trials not requiring stereoscopic fusion, the same images were shown. Stereo fusion was monitored with a random-dot stereogram search task.
Neural recording
The electrical activity of 169 (114 and 55 respectively from the two monkeys) well-isolated neurons was recorded using epoxy-coated tungsten electrodes (FHC Microsystems), processed with TDT RX5 Amplifier (TDT, Inc, Alachua, FL). Single electrodes were lowered through a metal guide tube into dorsal V4, targeted with a custom-built electrode drive. Area V4 was identified on the basis of structural MRI, the sequence of sulci as the electrode was lowered, and the visual response characteristics of the neurons. The neurons receptive field properties (size, position, and color preference) were mapped using 2D sprites (bars and random planar shapes) under experimenter control.
Visual stimulus construction and morphing
Solid stimuli were constructed using a procedure similar to Hung et al. Briefly, stimuli were generated by connecting 2–4 medial axial components. The skeletal structure – limb configuration, limb lengths, curvatures, and widths were randomly generated. The width profile of each limb was generated using a quadratic function fit to the randomly generated width at the mid-point and the two ends. Limb junctions were smoothed using a gaussian kernel on the 3D position and normal for every face. During the experiment, the stimuli were morphed by adding, deleting, or replacing limbs, or changing the length, orientation, curvature, or width of the limbs. Additionally, the position, size, and 3D orientation of the object were also changed probabilistically. Planar shapes were generated by turning off shading/lighting in OpenGL.
Adaptive stimulus algorithm
Each neuron was studied using two independent lineages of evolving solid shapes (see figure 1). The first generation consisted of 40 randomly generated solid stimuli (matte or shiny shading) in each lineage. Each subsequent generation was divided into two parts - shape evolution and solid shape preference testing. For shape evolution, 16 stimuli were randomly selected for morphing from the previous generation − 6 from the stimuli from the top 10% response range, 4 from the next 20%, 3 from the next 20%, 2 from the next 20%, and 1 from the bottom 10%. An additional 4 randomly generated stimuli were added to the pool. For solid/planar preference testing, the top 5 stimuli from the previous generation were rendered in solid matte, solid shiny, planar high contrast, and planar low contrast versions. The contrast of the planar stimuli were chosen to be the average contrast across solid matte and shiny shapes. This algorithm allowed us to not only to test each neuron’s solid shape tuning based on its responses to the stimuli, but also simultaneously test its solid shape preference. Neurons were tested with 80–440 randomly generated and morphed stimuli. For the 143 neurons studied with two or more generations of the adaptive algorithm (102 of 114 and 41 of 55 neurons from the two monkeys respectively), the solid preference score was calculated as:
where rs,i and rp,i are the solid and planar shape responses for the ith stimulus out of n stimuli. The Pearson’s correlation between the planar (rp,i) and solid (rs,i) shape responses for each neuron are plotted in figure 3E.
Post-hoc stimulus selection and construction
After the evolutionary testing procedure, 4–8 stimuli were sampled from the high (top 20%), medium, and low (bottom 20%) response ranges to be tested with the following post-hoc tests (see figure 3).
Contrast:
Each stimulus was rendered as a planar shape with 5 levels of increasing contrast or a solid matte shape with 5 levels of increasing surface brightness.
Stereogram:
The visible parts of each solid (or planar) shape were selected to generate a solid (or planar) stereogram by randomly placing dots at the appropriate depth. This shape was then translated in depth relative to the fixation spot. A set of random background dots were placed behind the shape (at the farthest depth). 3–5 relative disparities were tested for each neuron.
Naturalistic stimuli:
Each selected stimulus was rendered with a smooth, purely reflective or purely refractive (index 2.0) shader in Blender. It was then placed in a closed (surrounded by walls and a floor) or in an open (field of grass or textured ground) environment. The textures were selected from online texture libraries.
Two-photon Imaging
Animal preparation and dye injections
We followed standard procedures described previously59. Briefly, animals were anesthetized with ketamine (10mg/kg IM) and pre-treated with atropine (0.04mg/kg, IM). Throughout the experiment, anesthesia was maintained with sufentanil citrate (4–20μg/mg/h, IV), supplemented with isoflurane (0.5–2%) during surgeries. The animal was paralyzed with pancuronium bromide (0.15mg/kg/hr, IV) and artificially ventilated with a small animal respirator (Ugo Basile). Dexamethasone (0.1mg/kg, IM) and cefazolin (25mg/kg, IV) were administered to prevent infections and swelling. EEG, EKG, SpO2, EtCO2, respiration, heart rate, and body temperature were monitored continuously to maintain the appropriate depth of anesthesia and ensure animal health throughout the experiment. The animal’s head was held by a head post implanted at the start of the procedure. For imaging, a custom imaging well was attached to the skull over V4. Small craniotomies and durotomies were made within this well for imaging.
A dye solution of 2mM Oregon Green BAPTA 2-AM, 10% DMSO, 2% pluronic, and 25% sulforhodamine 101 (ThermoFisher Scientific) in ACSF was loaded into a glass pipette, with was lowered into cortex at an ~ 45° angle using a micro-manipulator (Sutter Instruments) under microscopic guidance. Several injections of the dye solution were made into a single durotomy using a Picospritzer pressure injection system (Parker Hannifin). After a ~1 hr waiting period, the craniotomy was covered with 1.5% Type III Agarose (Millipore Sigma) and a glass coverslip (Warner Instruments) was inserted under the craniotomy to reduce vertical motion artifacts due to breathing. Horizontal motion artifacts were removed post-hoc. Most imaging data was collected at cortical depths of ~100–200μm.
Before the imaging experiment, both eyes were covered with contact lenses to protect them from drying. Refraction of the eyes was determined for the stimulus display at 60cm from the eyes based on electrophysiological recording of a patch of V1 cortex. In this procedure, neural responses to oriented gratings at several spatial frequencies were recorded with ophthalmic lenses of different strengths placed in front of each eye. Lenses which optimized responses to the highest spatial frequency gratings were then chosen for each eye.
Two-photon microscope
Two-photon microscopy was performed using a Neurolabware microscope coupled to a Ti:Sapphire laser (Coherent Chameleon Ultra II). We used Scanbox (Dario Ringach, Neurolabware) for data acquisition. A 16X water-immersion objective (Nikon; 0.8 NA lens and 3mm working distance) was mounted on a movable stage with one rotational and three translational degrees of freedom for easy placement perpendicular to the imaging region. Imaging was performed at an excitation wavelength of 920 nm at a frame rate of 15.5Hz. Emission was collected using a green (510 nm center, 84 nm band) and a red (630 nm center, 92 nm band) filter (both from Semrock).
Visual Stimulus Generation
A set of solid and planar shape stimuli were used to test shape tuning properties. All stimuli were generated with OpenGL rendering of solid shapes with a single light source placed above the virtual camera. The 3D models for solid shape stimuli were generated from sections of simple geometric components (cylindrical tubes and hemispheric terminations). Flat, planar stimuli were generated by disabling OpenGL lighting.
Visual Stimulus Presentation
Stimuli were presented using the Psychophysics Toolbox extension for MATLAB (Mathworks Inc.). The toolbox was also used to synchronize visual stimulus presentation with two-photon image acquisition. The stimuli were presented on a 120Hz 24” LCD display (Viewsonic) gamma-corrected using a Photo Research spectroradiometer. A set of receptive field (RF) localizing stimuli (gratings, bars, 2D shapes) were presented and the average receptive field of neurons in the imaging region was determined using online analysis. The stimulus display was approximately centered on the RF location.
In one animal, visual stimulus set 1 (C-shaped and L-shaped, see Figure S3) was flashed within the RF for 1–2 s followed by a blank gray screen for 1–3s (see time courses in Figure 5). Five blank trials (gray screen) were also randomly presented during the experiment. The long stimulus and inter-stimulus durations was matched to the slow time course of OGB responses and acquisition rate. Each stimulus was repeated 5–10 times.
In the other two animals, visual stimulus set 2 (L-shaped, see Figure S4) was drifted across the full field of view. Stimuli in set 2 were drifted for 2 cycles plus the approximate diameter of the receptive field in the direction indicated by the L-bend and orthogonally offset between drifts in 11 increments spanning the height of the stimuli plus the approximate diameter of the receptive field.
Image pre-processing and segmentation
An anatomical reference image was created for each imaging region by averaging uniformly sampled frames across the experiment duration. For longer experiments, several reference images were created. For in-plane movement correction, each frame was correlated with the reference image and a horizontal and vertical shift was found. These shifts were applied to the frame to yield a stable recording. This correction was applied to each frame before further analyses. A binary cell segmentation mask was created for the imaging region by manually encircling cells in the reference image. Glia cells were discounted based on selective labeling with SR101 (cells present in both red and green channels were rejected). The response of each neuron in each frame was computed by the product of the movement-corrected frame with the neuron’s binary mask. Each imaging region yielded ~25–200 neurons. The fluorescence time-course (ΔFn(t)) of each neuron for each stimulus trial was calculated as: where t = 0 represents the stimulus onset, fn(t) is the measured fluorescence response of the nth neuron, and is the average response of the neuron in the baseline period (t > −1200ms and t < −100ms). The stimulus response of each neuron was calculated as the average ΔFn(t) for t > 100ms and t < toff + 600ms (where toff is the time of stimulus offset).
QUANTIFICATION AND STATISTICAL ANALYSIS
Electrophysiology
Solid Shape Preference Index
For the adaptive sampling experiment, SI was calculated as described in equation 1 above. A randomization test was used to determine the significant solid or planar shape responses for each neuron. For each neuron, for each stimulus, the responses of the matte and polished solid shape responses and high and low contrast planar shape responses were randomized. SI was calculated with the resultant response set. This procedure was repeated 10000 times to obtain a distribution of 10000 solid indices. The neuron’s actual SI was then compared with the top and bottom 2.5 percentile of this SI distribution to obtain the p-value for significantly solid or planar responses. For the main experiment and post-hoc tests, all distributions of SI were determined to be significantly greater than 0 using Student’s t-test.
Response-weighted averaging (RWA) analysis
The RWA analysis was performed independently on each lineage on neurons studied with more than 80 solid stimuli (more than three generations) per lineage.
For metric shape analysis, each shape was divided into its constituent limbs and each limb was described in terms of the geometry of its terminal end and its shaft (figure 1F and S1A–B). Additionally, the junctions between pairs of limbs were also independently parameterized. These geometric constructs were parameterized using their position relative to the center of the shape, their orientation in 3D space, and their lengths, curvatures, and radii.
Based on these parameterizations, RWA matrices were constructed – one each for shafts, terminations, and junctions – such that each element of these matrices is a bin that represents a specific part of any shape (figure S1C). The dimensions of each of these matrices are the geometrical parameters (figure S1C) used to describe the shape fragment. For example, the termination matrix has four dimensions – 3D angular position (80 bins on an icosahedral surface), 3D radial position (5 bins), 3D direction (80 bins on an icosahedral surface), and radius (5 bins). To populate these matrices, for each shape, several response-weighted gaussians (centered at the bins occupied by every shape fragment in a solid shape) were iteratively summed into the matrices (figure S1D). After repeating this for every shape, each matrix was normalized with a non-response-weighted matrix. Finally, the RWA matrices obtained from each independent lineage were multiplied bin-by-bin to produce an accurate representation of neural tuning. These lineage-product RWA matrices were used in all further analyses and visualizations.
Each RWA matrix was used to estimate responses to the full set of solid shape stimuli presented during the experiment to determine RWA consistency with neural responses. Because the responses of most cells were well estimated by all three RWA matrices (figure 2J and 2K), a linear combination of these predictions was fit to obtain the final measure of RWA consistency. This linear combination was cross-validated with 10-fold cross validation and the predicted response for each stimulus was determined from the set where it was held out. These predicted responses are plotted against neural responses in figure 2, and the distribution of correlations between cross-validated predictions and neural responses are plotted in figure 2J.
The standard deviation of each parameter around the peak RWA was calculated as:
where bi is the ith bin, bpeak is the bin with the peak RWA, Ri is the RWA in the ith bin, and dist(bi,bpeak) is the distance between the center of the ith bin and the bin with the peak RWA. This distance can be linear (for shaft length, curvature, etc.), circular (junction subtense, planar rotation), or spherical (angular position, orientation, etc.).
Two-photon Imaging
For imaging regions with stimulus set 1, only cells that passed a t-test (p < 0.05) between the best and worst stimulus condition were included in further analyses. This statistic was only used for rejecting neurons that were unresponsive to any stimuli in this set and no additional per-neuron or population analyses were performed based on this rejection. For imaging regions with stimulus set 2, since each stimulus drifted across the screen in each trial (time) and was displaced in the orthogonal direction across trials (space), this created a 2D matrix of responses. To effectively capture the significance of neural response across time and spatial shifts, a two-sample, two-dimensional Kolmogorov-Smirnov test was calculated across time and stimulus displacement between the best and worst stimulus condition. Only cells that passed the 2D KS-test (p < 0.05) were included in further analyses. The solid preference index for each neuron in an imaging region was calculated as described above for the electrophysiology analysis. Regions that contained fewer than 10 significantly responsive neurons were rejected.
Spatial Clustering Analysis
To group neurons in an imaging region into meaningful spatial clusters, a pixel map of SP was created (see figure 5E) i.e. each pixel was assigned an SP score using the same formula as above. The map was then smoothed with a broad 2D Gaussian kernel using the MATLAB function imgaussfilt with a standard deviation of 20, normalized, and a contour map was generated. The 2D contours from this contour map provided cluster candidates. All contours went through a 3-stage selection/rejection criterion. Stage 1: Contours that contained fewer than four neurons or were smaller than 10% of the size of the imaging region in area or were too complex (ratio of the area of the contour to the area of the convex hull of the contour was less than 0.95) were rejected first. Stage 2: For remaining contours that contained the same neurons, the most complex contours were rejected. Stage 3: For the remaining contours, concentric contours were identified and the largest contour with the least SP kurtosis (fourth moment of the distribution of SP of neurons within a contour) was chosen. This ensured a homogeneous distribution of SP values within the selected clusters
Correlation Analysis
The population average response for each cluster was calculated as the average of the responses of all significantly responsive neurons within the cluster to all stimuli, solid stimuli only, and planar stimuli only. These average response patterns were compared with the response pattern of each neuron within the same cluster or neurons of the adjacent cluster. The correlations thus obtained are plotted in Figures 5 and 6.
AlexNet Analysis
Comparison of AlexNet nodes with V4 neurons
For each neuron recorded from V4, the solid and planar shape stimuli were collated as an image set. Then, for each ReLU layer in AlexNet, the images were scaled and positioned within the theoretical receptive field of the nodes in the layer and their activations were obtained. These activations were compared with the V4 neuron and the best correlated node was chosen (supplementary figure 6D). A solid shape preference score was calculated (same as for the V4 neurons, above) based on these activations (supplementary figure 6H). RWA matrices were constructed (in the same way as for the V4 neurons, above) and used to predict node activations (supplementary figure 6C and 6F).
Adaptive stimulus algorithm with AlexNet nodes
All 384 AlexNet ReLU layer 3 nodes were considered for this analysis. To find the color preference of the node, it was tested with an initial set of solid and planar shapes rendered in matte and specular shading (for solid shapes) and two different contrast levels (for planar shapes) in seven different colors. The shape color was chosen based on the mean activation across all solid and planar shapes. (Three nodes were not activated by any stimulus in this initial set and were discarded from further analysis.) A modified adaptive shape morphing experiment was run on every node. This experiment was identical to the one run for V4 neurons except for the following modifications. The experiment ran for 20 generations across two lineages with 40 stimuli in each generation. The initial generation of 40 random solid stimuli were randomized in scale and position within the theoretical receptive field of the node. The second generation consisted of 32 random shapes (with random positions and scales) and 8 morphed stimuli. The number of random shapes decreased exponentially to 0 by the 20th generation and the probability of morphs increased concomitantly. Of the morphs, the number of shape morphs (adding, removing, and replacing limbs, and changing the radius profile of limbs) increased exponentially from 0 in the second generation to 40 in the 20th generation. The rest of the stimuli were scale and position morphs of stimuli presented in previous generations. Additionally, as in the V4 experiment, the top 5 stimuli from each generation were presented as matte and specular solid shapes and low and high contrast planar shapes in the next generation to test for solid shape preference. In total, each node was studied with 800 solid shape stimuli using the adaptive algorithm and additionally with 380 solid and planar tetrads. Five nodes had non-zero responses to fewer than 120 stimuli (3 effective generations) and were discarded.
After this experiment, node activations to solid shapes were used to generate RWA matrices for shafts, junctions and terminations, and a cross-validated linear combination of response predictions to the full stimulus set was fit to obtain the final prediction of node activations (same as for V4 neurons).
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| Rhesus Macaques (Macaca mulatta) | Johns Hopkins University | N/A |
| Software and Algorithms | ||
| MATLAB | MathWorks | mathworks.com/products/matlab.html |
| Psychophysics Toolbox 3 | Psychtoolbox.org | psychtoolbox.org |
| LWJGL + OpenGL | Khronos/BSD | lwjgl.org |
| Python | Python Software Foundation | python.org |
| Blender | Blender Foundation | blender.org |
| Textures and materials | Blender Market and CGTextures | textures.com/terms-of-use.html, https://www.blendermarket.com/page/royalty-free-license |
| Data Acquisition | ||
| Tungsten microelectrodes | FHC, Inc, Bowdoin, ME | fh-co.com |
| TDT RX5 Amplifier | TDT, Inc, Alachua, FL | tdt.com/systems/neurophysiology-systems/ |
| ISCAN Eye tracking system | ISCAN, Inc, Woburn, MA | iscaninc.com |
| Scanbox | Neurolabware, Los Angeles, CA | scanbox.orgneurolabware.com |
| Chameleon 2 Ti-Sa Laser | Coherent Inc., Palo Alto, CA | www.coherent.com |
HIGHLIGHTS.
Brain coding of solid shape emerges at the beginning, not end, of object processing
Early-stage area V4 processes flat and solid shape in parallel, in distinct modules
Artificial deep visual networks (AlexNet) also encode solid shape in early layers
ACKNOWLEDGMENTS
This work was supported by NIH grant R01EY029420 and ONR grant N000141812119. We thank William Nash, William Quinlan, and Justin Killibrew, and Ofelia Garalde for technical assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Koenderink JJ (1984). What does the occluding contour tell us about solid shape? Perception 13, 321–330. [DOI] [PubMed] [Google Scholar]
- 2.Richards WA, Dawson B, and WhittingDton D (1986). Encoding contour shape by curvature extrema. J. Opt. Soc. Amer. A 3, 1483–1491. [DOI] [PubMed] [Google Scholar]
- 3.Richards WA, Koenderink JJ, and Hoffman DD (1987). Inferring three-dimensional shapes from two-dimensional silhouettes. J. Opt. Soc. Amer. A 4, 1168–1175. [Google Scholar]
- 4.Beusmans JMH, Hoffman DD, and Bennett BM (1987). Description of solid shape and its inference from occluding contours. J. Opt. Soc. Amer. A 4, 1155–1167. [Google Scholar]
- 5.Tse PU (2002). A contour propagation approach to surface filling-in and volume formation. Psych. Rev 109, 91–115. [DOI] [PubMed] [Google Scholar]
- 6.Barlow HB, Blakemore C, and Pettigrew JD (1967). The neural mechanism of binocular depth discrimination. J. Physiol 193, 327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hubel DH, and Wiesel TN (1970). Stereoscopic vision in macaque monkey: cells sensitive to binocular depth in area 18 of the macaque monkey cortex. Nature 225, 41–42. [DOI] [PubMed] [Google Scholar]
- 8.Poggio GF, and Fischer B (1977). Binocular interaction and depth sensitivity in striate and prestriate cortex of behaving rhesus monkey. J. Neurophysiol 40, 1392–1405. [DOI] [PubMed] [Google Scholar]
- 9.Felleman DJ, and Van Essen DE (1991). Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex 1, 1–47. [DOI] [PubMed] [Google Scholar]
- 10.Kravitz DJ, Saleem KS, Baker CI, Ungerleider LG, and Mishkin M (2013). The ventral visual pathway: an expanded neural framework for the processing of object quality. Trends Cog. Sci 17, 26–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yamane Y, Carlson ET, Bowman KC, Wang Z, and Connor CE (2008). A neural code for three-dimensional object shape in macaque inferotemporal cortex. Nat. Neurosci 11, 1352–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hung CC, Carlson ET, and Connor CE (2012). Medial axis shape coding in macaque inferotemporal cortex. Neuron 74, 1099–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vaziri S, Carlson ET, Wang Z, and Connor CE (2014). A channel for 3D environmental shape in anterior inferotemporal cortex. Neuron 84, 55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vaziri S, and Connor CE (2016). Representation of gravity-aligned scene structure in ventral pathway visual cortex. Curr. Biol 26, 766–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Janssen P, Vogels R, and Orban GA (2000a). Selectivity for 3D shape that reveals distinct areas within macaque inferior temporal cortex. Science 288, 2054–2056. [DOI] [PubMed] [Google Scholar]
- 16.Janssen P, Vogels R, and Orban GA (2000b). Three-dimensional shape coding in inferior temporal cortex. Neuron 27, 385–97. [DOI] [PubMed] [Google Scholar]
- 17.Hinkle DA, and Connor CE (2001). Disparity tuning in macaque area V4. Neuroreport 12, 365–369. [DOI] [PubMed] [Google Scholar]
- 18.Hinkle DA, and Connor CE (2002). Three-dimensional orientation tuning in macaque area V4. Nat. Neurosci 5, 665–670. [DOI] [PubMed] [Google Scholar]
- 19.Hinkle DA, and Connor CE (2005). Quantitative characterization of disparity tuning in ventral pathway area V4. J. Neurophysiol 94, 2726–2737. [DOI] [PubMed] [Google Scholar]
- 20.Watanabe M, Tanaka H, Uka T, and Fujita I (2002). Disparity-selective neurons in area V4 of macaque monkeys. J. Neurophysiol 87, 1960–1973. [DOI] [PubMed] [Google Scholar]
- 21.Tanabe S, Doi T, Umeda K, and Fujita I (2005). Disparity-tuning characteristics of neuronal responses to dynamic random-dot stereograms in macaque visual area V4. J. Neurophysiol 94, 2683–2699. [DOI] [PubMed] [Google Scholar]
- 22.Umeda K, Tanabe S, and Fujita I (2007). Representation of stereoscopic depth based on relative disparity in macaque area V4. J. Neurophysiol 98, 241–252. [DOI] [PubMed] [Google Scholar]
- 23.Shiozaki HM, Tanabe S, Doi T, and Fujita I (2012). Neural activity in cortical area V4 underlies fine disparity discrimination. J. Neurosci 32, 3830–3841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hegdé J, and Van Essen DC (2005). Role of primate visual area V4 in the processing of 3-D shape characteristics defined by disparity. J. Neurophysiol 94, 2856–2866. [DOI] [PubMed] [Google Scholar]
- 25.Fang Y, Chen M, Xu H, Li P, Han C, Hu J, Zhu S, Ma H and Lu HD (2019). An orientation map for disparity-defined edges in area V4. Cerebral Cortex 29, 666–679. [DOI] [PubMed] [Google Scholar]
- 26.Arcizet F, Jouffrais C, and Girard P (2009). Coding of shape from shading in area V4 of the macaque monkey. BMC Neurosci. 10, 140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Alizadeh AM, Van Dromme IC, and Janssen P (2018). Single-cell responses to three-dimensional structure in a functionally defined patch in macaque area TEO. J. Neurophysiol 120, 2806–2818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kobatake E, and Tanaka K (1994). Neuronal selectivities to complex object features in the ventral visual pathway of the macaque cerebral cortex. J. Neurophysiol 71, 856–867. [DOI] [PubMed] [Google Scholar]
- 29.Pasupathy A, and Connor CE (1999). Responses to contour features in macaque area V4. J. Neurophysiol 82, 2490–2502. [DOI] [PubMed] [Google Scholar]
- 30.Pasupathy A, and Connor CE (2001). Shape representation in area V4: position-specific tuning for boundary conformation. J. Neurophysiol 86, 2505–2519. [DOI] [PubMed] [Google Scholar]
- 31.Pasupathy A, and Connor CE (2002). Population coding of shape in area V4. Nat. Neurosci 5, 1332–1338. [DOI] [PubMed] [Google Scholar]
- 32.Carlson ET, Rasquinha RJ, Zhang K, and Connor CE (2011). A sparse object coding scheme in area V4. Curr. Biol 21, 288–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bushnell BN, Harding PJ, Kosai Y, and Pasupathy A (2011). Partial occlusion modulates contour-based shape encoding in primate area V4. J. Neurosci 31, 4012–4024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bushnell BN, and Pasupathy A (2012). Shape encoding consistency across colors in primate V4. J. Neurophysiol 108, 1299–1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kosai Y, El-Shamayleh Y, Fyall AM, and Pasupathy A (2014). The role of visual area V4 in the discrimination of partially occluded shapes. J. Neurosci 34, 8570–8584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Oleskiw TD, Pasupathy A, and Bair W (2014). Spectral receptive fields do not explain tuning for boundary curvature in V4. J. Neurophysiol 112, 2114–2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.El-Shamayleh Y, and Pasupathy A (2016). Contour curvature as an invariant code for objects in visual area V4. J. Neurosci 36, 5532–5543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gallant JL, Braun J, and Van Essen DC (1993). Selectivity for polar, hyperbolic, and Cartesian gratings in macaque visual cortex. Science 259, 100–103. [DOI] [PubMed] [Google Scholar]
- 39.Gallant JL, Connor CE, Rakshit S, Lewis JW, and Van Essen DC (1996). Neural responses to polar, hyperbolic, and Cartesian gratings in area V4 of the macaque monkey. J. Neurophysiol 76, 2718–2739. [DOI] [PubMed] [Google Scholar]
- 40.David SV, Hayden BY, and Gallant JL (2006). Spectral receptive field properties explain shape selectivity in area V4. J. Neurophysiol 96, 3492–3505. [DOI] [PubMed] [Google Scholar]
- 41.Touryan J, and Mazer JA (2015). Linear and non-linear properties of feature selectivity in V4 neurons. Front. Syst. Neurosci 9, 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Okazawa G, Tajima S, and Komatsu H (2015). Image statistics underlying natural texture selectivity of neurons in macaque V4. Proc. Natl. Acad. Sci 112, E351–E360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Okazawa G, Tajima S, and Komatsu H (2016). Gradual development of visual texture-selective properties between macaque areas V2 and V4. Cerebral Cortex 27, 4867–4880. [DOI] [PubMed] [Google Scholar]
- 44.Brincat SL & Connor CE (2004) Underlying principles of visual shape selectivity in posterior inferotemporal cortex. Nat. Neurosci 7, 880–886. [DOI] [PubMed] [Google Scholar]
- 45.Brincat SL & Connor CE (2006) Dynamic shape synthesis in posterior inferotemporal cortex. Neuron 49, 17–24. [DOI] [PubMed] [Google Scholar]
- 46.Ratan Murty NA, and Arun SP (2016). Seeing a straight line on a curved surface: decoupling of patterns from surfaces by single IT neurons. J. Neurophysiol 117, 104–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.De Vries SC, Kappers AM, and Koenderink JJ (1993). Shape from stereo: A systematic approach using quadratic surfaces. Percept. Psychophys, 53, 71–80. [DOI] [PubMed] [Google Scholar]
- 48.Cryer JE, Tsai PS, and Shah M (1995). Integration of shape from shading and stereo. Pattern Recognit. 28, 1033–1043. [Google Scholar]
- 49.Fleming RW, Torralba A, and Adelson EH (2004). Specular reflections and the perception of shape. Journal of vision, 4(9), 10–10. [DOI] [PubMed] [Google Scholar]
- 50.Fleming R, Li Y, and Adelson E (2008). Image statistics for 3D shape estimation. J. Vis 8, 76–76. [Google Scholar]
- 51.Anderson BL, and Kim J (2009). Image statistics do not explain the perception of gloss and lightness. J. Vis 9, 10–10. [DOI] [PubMed] [Google Scholar]
- 52.Kim J, Marlow P, and Anderson BL (2011). The perception of gloss depends on highlight congruence with surface shading. J. Vis 11, 4–4. [DOI] [PubMed] [Google Scholar]
- 53.Marlow P, Kim J, and Anderson BL (2011). The role of brightness and orientation congruence in the perception of surface gloss. J. Vis 11, 16–16. [DOI] [PubMed] [Google Scholar]
- 54.Mountcastle VB (1997). The columnar organization of the neocortex. Brain 120, 701–22. [DOI] [PubMed] [Google Scholar]
- 55.Mountcastle VB (1957). Modality and topographic properties of single neurons of cat’s somatic sensory cortex. J. Neurophysiol 20, 408–434. [DOI] [PubMed] [Google Scholar]
- 56.Hubel DH, and Wiesel TN (1968). Receptive fields and functional architecture of monkey striate cortex. J. Physiol 195, 215–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hubel DH, and Wiesel TN (1977). Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc. R. Soc. Lond. B 198, 1–59. [DOI] [PubMed] [Google Scholar]
- 58.Blasdel GG, and Salama G (1986). Voltage-sensitive dyes reveal a modular organization in monkey striate cortex. Nature 321, 579–585. [DOI] [PubMed] [Google Scholar]
- 59.Ts’o DY, Frostig RD, Lieke EE, and Grinvald A (1990). Functional organization of primate visual cortex revealed by high resolution optical imaging. Science 249, 417–20. [DOI] [PubMed] [Google Scholar]
- 60.Bartfeld E, and Grinvald A (1992). Relationships between orientation-preference pinwheels, cytochrome oxidase blobs, and ocular-dominance columns in primate striate cortex. Proc. Natl. Acad. Sci. U. S. A 89, 11905–11909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Obermayer K, and Blasdel GG (1993). Geometry of Orientation and Ocular Dominance Columns in Monkey Striate Cortex. J. Neurosci 13, 4114–4129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Nauhaus I, Nielsen KJ, Disney AA, and Callaway EM (2012). Orthogonal micro-organization of orientation and spatial frequency in primate primary visual cortex. Nat. Neurosci 15, 1683–1690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Nauhaus I, Nielsen KJ, and Callaway EM (2016). Efficient Receptive Field Tiling in Primate V1. Neuron 91, 893–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Malach R, Tootell RBH, and Malonek D (1994). Relationship between Orientation Domains, Cytochrome Oxidase Stripes, and Intrinsic Horizontal Connections in Squirrel Monkey Area V2. Cereb. Cortex 4, 151–165. [DOI] [PubMed] [Google Scholar]
- 65.Xiao Y, Wang Y, and Felleman DJ (2003). A spatially organized representation of colour in macaque cortical area V2. Nature 421, 535–539. [DOI] [PubMed] [Google Scholar]
- 66.Chen G, Lu HD, and Roe AW (2008). A map for horizontal disparity in monkey V2. Neuron 58, 442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lu HD, Chen G, Tanigawa H, and Roe AW (2010). A Motion Direction Map in Macaque V2. Neuron 68, 1002–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Felleman DJ, Lim H, Xiao Y, Wang Y, Eriksson A, and Parajuli A (2015). The Representation of Orientation in Macaque V2: Four Stripes Not Three. Cereb. Cortex 25, 2354–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Albright T, Desimone R, and Gross CG (1984). Columnar organization of directionally selective cells in visual area MT of the macaque. J. Neurophysiol 51, 16–31. [DOI] [PubMed] [Google Scholar]
- 70.DeAngelis GC, and Newsome W (1999). Organization of disparity-selective neurons in macaque area MT. J. Neurosci 19, 1398–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Malonek D, Tootell RBH, and Grinvald A (1994). Optical Imaging Reveals the Functional Architecture of Neurons Processing Shape and Motion in Owl Monkey Area MT. Proc. R. Soc. Lond. B Biol. Sci 258, 109–119. [DOI] [PubMed] [Google Scholar]
- 72.Diogo ACM, Soares JGM, Albright TD, and Gattass R (2002). Two-dimensional map of direction selectivity in cortical visual area MT of Cebus monkey. An. Acad. Bras. Ciênc 74, 463–476. [DOI] [PubMed] [Google Scholar]
- 73.Diogo ACM, Soares JGM, Koulakov A, Albright TD, and Gattass R (2003). Electrophysiological Imaging of Functional Architecture in the Cortical Middle Temporal Visual Area of Cebus apella Monkey. J. Neurosci 23, 3881–3898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Diogo ACM, Lima B, Soares JGM, Gattass R, Diogo ACM, Lima B, Soares JGM, and Gattass R (2020). Tangential distribution of cell type and direction selectivity in monkey area MT. An. Acad. Bras. Ciênc 92. [DOI] [PubMed] [Google Scholar]
- 75.Britten KH (1998). Clustering of response selectivity in the medial superior temporal area of extrastriate cortex in the macaque monkey. Vis. Neurosci 15, 553–558. [DOI] [PubMed] [Google Scholar]
- 76.Tanigawa H, Lu HD, and Roe AW (2010). Functional organization for color and orientation in macaque V4. Nat. Neurosci 13, 1542–1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.An X, Gong H, Qian L, Wang X, Pan Y, Zhang X, Yang Y, and Wang W (2012). Distinct functional organizations for processing different motion signals in V1, V2, and V4 of macaque. J. Neurosci 32, 13363–13379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Li P, Zhu S, Chen M, Han C, Xu H, Hu J, Fang Y, and Lu HD (2013). A Motion Direction Preference Map in Monkey V4. Neuron 78, 376–388. [DOI] [PubMed] [Google Scholar]
- 79.Wang G, Tanaka K, and Tanifuji M (1996). Optical imaging of functional organization in the monkey inferotemporal cortex. Science 272, 1665–8. [DOI] [PubMed] [Google Scholar]
- 80.Wang G, Tanifuji M, and Tanaka K (1998). Functional architecture in monkey inferotemporal cortex revealed by in vivo optical imaging. Neurosci. Res 32, 33–46. [DOI] [PubMed] [Google Scholar]
- 81.Tsunoda K, Yamane Y, Nishizaki M, and Tanifuji M (2001). Complex objects are represented in macaque inferotemporal cortex by the combination of feature columns. Nat. Neurosci 4, 832–838. [DOI] [PubMed] [Google Scholar]
- 82.Knudsen E, Lac S, and Esterly S (1987). Computational maps in the brain. Annu. Rev. Neurosci 10, 41–65. [DOI] [PubMed] [Google Scholar]
- 83.Swindale NV, Cynader MS, and Matsubara J (1990). Cortical cartography: a two- dimensional view In Computational Neuroscience, Schwartz EL, ed. (Cambridge, MA: MIT Press; ), pp. 232–241. [Google Scholar]
- 84.Koulakov A, and Chklovskii D (2001). Orientation Preference Patterns in Mammalian Visual Cortex: A Wire Length Minimization Approach. Neuron 29, 519–527. [DOI] [PubMed] [Google Scholar]
- 85.Chklovskii DB, and Koulakov AA (2004). Maps in the brain: what can we learn from them? Annu. Rev. Neurosci 27, 369–92. [DOI] [PubMed] [Google Scholar]
- 86.Jin J, Wang Y, Swadlow HA, and Alonso JM (2011). Population receptive fields of ON and OFF thalamic inputs to an orientation column in visual cortex. Nat. Neurosci 14, 232–238. [DOI] [PubMed] [Google Scholar]
- 87.Nauhaus I, and Nielsen KJ (2014). Building maps from maps in primary visual cortex. Curr. Opin. Neurobiol 24, 1–6. [DOI] [PubMed] [Google Scholar]
- 88.Nimmerjahn A, Kirchhoff F, Kerr JND, and Helmchen F (2004). Sulforhodamine 101 as a specific marker of astroglia in the neocortex in vivo. Nat. Methods 1, 31–37. [DOI] [PubMed] [Google Scholar]
- 89.Stosiek C, Garaschuk O, Holthoff K, and Konnerth A (2003). In vivo two-photon calcium imaging of neuronal networks. Proc. Natl. Acad. Sci 100, 7319–7324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Ohki K, Chung S, Kara P, Huebener M, Bonhoeffer T, and Reid RC (2006). Highly ordered arrangement of single neurons in orientation pinwheels. Nature 442, 925–928. [DOI] [PubMed] [Google Scholar]
- 91.Krizhevsky A, Sutskever I, and Hinton GE (2012). Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst 25,1097–1105). [Google Scholar]
- 92.Yamins DL, and DiCarlo JJ (2016). Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci 19, 356–365. [DOI] [PubMed] [Google Scholar]
- 93.Bashivan P, Kar K, and DiCarlo JJ (2019). Neural population control via deep image synthesis. Science 364, 6439. [DOI] [PubMed] [Google Scholar]
- 94.Janssen P, Verhoef BE, and Premereur E (2018). Functional interactions between the macaque dorsal and ventral visual pathways during three-dimensional object vision. Cortex 98, 218–227. [DOI] [PubMed] [Google Scholar]
- 95.Pospisil DA, Pasupathy A, and Bair W (2018). ‘Artiphysiology’ reveals V4-like shape tuning in a deep network trained for image classification. Elife 7, e38242. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets/code supporting the current study have been deposited in a public Github repository https://github.com/ramanujansrinath/V4_solid_flat_data_code. This repository contains Matlab code to generate each figure in this publication and corresponding data. Further requests for data and analysis software can be sent to the corresponding author.


