Abstract
locStra is an R-package for the analysis of regional and global population stratification in whole-genome sequencing (WGS) studies, where regional stratification refers to the substructure defined by the loci in a particular region on the genome. Population substructure can be assessed based on the genetic covariance matrix, the genomic relationship matrix, and the unweighted/ weighted genetic Jaccard similarity matrix. Using a sliding window approach, the regional similarity matrices are compared with the global ones, based on user-defined window sizes and metrics, for example, the correlation between regional and global eigenvectors. An algorithm for the specification of the window size is provided. As the implementation fully exploits sparse matrix algebra and is written in C++, the analysis is highly efficient. Even on single cores, for realistic study sizes (several thousand subjects, several million rare variants per subject), the runtime for the genome-wide computation of all regional similarity matrices does typically not exceed one hour, enabling an unprecedented investigation of regional stratification across the entire genome. The package is applied to three WGS studies, illustrating the varying patterns of regional substructure across the genome and its beneficial effects on association testing.
Keywords: regional analysis, population stratification, population substructure, similarity matrix, whole-genome sequencing
1. ∣. INTRODUCTION
Genetic association studies are a popular mapping tool; however, they can be vulnerable to confounding due to population substructure (Laird & Lange, 2010). Numerous methods have been proposed to address this issue (Devlin & Roeder, 1999; Pritchard, Stephens, Rosenberg, & Donnelly, 2000). Popular approaches rely on the genetic covariance matrix of the genotype data: EIGENSTRAT, STRATSCORE, multidimensional scaling (Lee, Epstein, Duncan, & Lin, 2012; Patterson, Price, & Reich, 2006; Price et al., 2006), or on the genomic relationship matrix (Yang, Lee, Goddard, & Visscher, 2011). For populations with recent admixture where each subject contains different proportions of the ancestral genomes, local ancestry-approaches have been suggested, for example, RFMix (Maples, Gravel, Kenny, & Bustamante, 2013), LAMP (Sankararaman, Sridhar, Kimmel, & Halperin, 2008), HAPMIX (Price et al., 2009), SABER (Tang, Coram, Wang, Zhu, & Risch, 2006), or ADMIXMAP (McKeigue, Carpenter, Parra, & Shriver, 2000). While such software packages are able to estimate local ancestry, they require the availability of the reference populations. Approaches as the ones developed by X. Wang et al. (2011) can incorporate the local ancestry information into the association testing framework.
While there is strong evidence for regional stratification (Martin et al., 2018; Zhong, Perera, & Gamazon, 2019), the aforementioned matrix-based approaches are typically computed only globally. For the validity of the matrix-based approaches, it is only required that the selected loci are not in linkage disequilibrium (LD) (Laird & Lange, 2010). There are no theoretical constraints as to whether the loci are selected genome-wide or from a specific region. However, the computational burden has generally been prohibitive to use existing implementations for genome-wide analysis of regional stratification. As most matrix-based approaches are designed for common, uncorrelated variant data, that is, loci that are not in LD, many genomic regions do not contain a sufficient number of such loci for a regional computation of matrix-based approaches.
With the arrival of whole-genome sequencing (WGS) data, an abundance of data on densely spaced rare variants (RVs) that are mostly not in LD became generally available. As RVs are often population specific, they can be highly informative about population substructure and recent admixture (Bodmer & Bonilla, 2008; Keinan & Clark, 2012; Kryukov, Shpunt, Stamatoyannopoulos, & Sunyaev, 2009). Consequently, approaches based on Jaccard similarity matrices that utilize RV/WGS data have been developed (Prokopenko et al., 2016; Schlauch, Fier, & Lange, 2017). However, the computational bottleneck has persisted for these approaches as well.
We developed locStra, an R-package implementing four approaches to assess population stratification in RVs at the regional and global level using (1) the genetic covariance matrix, (2) the genomic relationship matrix, (3) the unweighted, and (4) weighted Jaccard similarity matrices (the weighted Jaccard matrix is also sometimes called s-matrix). The package is entirely written in C++, and all similarity matrices are algebraically transformed so that the computations are executed on sparse data structures. The sparse matrix structure is maintained throughout all computations to maximize computational efficiency. As a result, the runtimes for computing genetic similarity matrices are substantially shorter for locStra than for existing packages. Using sliding windows (Morrison et al., 2013; Panoutsopoulou, Tachmazidou, & Zeggini, 2013; Yazdani, Yazdani, & Boerwinkle, 2015) of user-specified length, locStra enables the fast analysis of regional stratification at the genome-wide level, even on desktop computers.
The article is structured as follows. Section 2 briefly introduces the methodology we employ in this study, in particular, we describe the functionality of our software. Results are presented in Section 3, investigating amongst others the regional stratification in data from the 1000 Genome Project (Section 3.1), a comparison with PLINK2 (Section 3.1.3), and the selection of suitable window sizes (Section 3.1.4). Moreover, we visualize regional substructures using a population isolate (Section 3.2) and demonstrate the beneficial effects of regional stratification on association testing by correcting a linear regression using global and regional principal components (Section 3.3). The article concludes with a discussion in Section 4. The appendix highlights certain details of our optimized implementations including theoretical runtimes (Section A).
2 ∣. METHODS
2.1 ∣. Software description
The core implementation of locStra is based on fully sparse matrix algebra in C++, using RcppEigen of Bates and Eddelbuettel (2013). Our package is available on The Comprehensive R Archive Network, see Hahn, Lutz, and Lange (2020).
The locStra package makes a total of seven functions available which are described in the following subsections.
2.1.1 ∣. Dense and sparse matrix implementations
Four functions provide C++ implementations of standard approaches to population stratification, both for dense and sparse matrix algebra. The code handles dense and sparse input matrices separately since either version can be inefficient if used for matrices of the wrong type. Each of the functions listed below takes at least two arguments: the input matrix (which can be in dense or sparse format) on which to compute the similarity measure, and a boolean argument dense to switch between C++ implementations for dense and sparse matrix algebra. The default is dense=False. The input matrix always contains the genotype/dosage data oriented as number of variants/rows by number of people/columns.
The function covMatrix computes the genetic covariance matrix (Price et al., 2006). The entries of the input are allowed to be any real-valued numbers.
The function grMatrix computes the genomic relationship matrix (GRM) as defined in Yang et al. (2011). The input must be a binary matrix. Both the classic and robust versions (B. Wang, Sverdlov, & Thompson, 2017) of the GRM are supported and can be switched using the boolean flag robust. The default is robust=True.
The function jaccardMatrix computes the Jaccard similarity matrix (Prokopenko et al., 2016). The input must be a binary matrix, where one indicates the presence of a variant.
The function sMatrix implements the weighted Jaccard matrix (Schlauch, 2016; Schlauch et al., 2017). In addition to the boolean dense argument, the function sMatrix also has a boolean argument phased to indicate if the input data are phased (default is phased=False). The input can be any real-valued matrix. The last argument is the integer minVariants which is a cutoff value for the minimal number of variants to consider (default is minVariants=5). If no variants remain after applying the minVariants cutoff, the output will be a matrix with NA.
The unweighted and weighted Jaccard indices, traditionally a similarity index for sets, are two recently proposed approaches for the analysis of rare variant data which were shown to provide a higher resolution than the other approaches (Prokopenko et al., 2016). The entries of the Jaccard matrix measure the set-theoretic similarity of the genomic data of all pairs of subjects, and can be computed efficiently using only binary operations.
2.1.2 ∣. Main function
The main function of the package is fullscan. It has five arguments and allows for a flexible specification of the regional population stratification scan of the data through its generic structure.
The first input is the (sparse) matrix containing the sequencing data. The input matrix is assumed to be oriented to contain the data for each individual per column, thus the dimension of the input is the number of variants by the number of people.
The second argument is a two-column matrix (called windows) that contains the window specification of the scan. The window matrix has as many rows as there are windows to iterate over and two columns. The two columns are the start and end positions of each window. The matrix of sliding windows can easily be generated with the auxiliary function makeWindows described in the next subsection.
The third argument, matrixFunction, handles the processing of each sliding window. The function takes one input argument (often a matrix). Any function can in principle be used. Typical choices are covMatrix, grMatrix, jaccardMatrix, or sMatrix.
Next, the modular structure of fullscan requires the specification of a summaryFunction for the processed data before comparison. This can be any function of one input argument that is compatible with the output of matrixFunction. As an example, one might want to set the matrixFunction to covMatrix, which returns a square similarity matrix, and accordingly define the summaryFunction to compute the largest eigenvector on its square matrix input. This can easily be done with the function powerMethod described in the next subsection.
fullscan uses its fifth input argument, the function comparisonFunction, to compare summaries (e.g., first eigenvectors) on a regional and a global level. The comparisonFunction must have two arguments as input, both of which need to be compatible with the output of the function summaryFunction. For instance, given the summaryFunction computes the first eigenvector, we might want to compare the first eigenvectors on a global and regional level by means of the native R correlation function cor for two vectors.
The output of fullscan is a two column matrix with global and regional comparison values per row, where each row corresponds to a row (and thus a window) in matrix windows in the same order.
2.1.3 ∣. Auxiliary functions
Two functions provide additional functionality:
The function makeWindows generates a two-column matrix of nonoverlapping or overlapping windows for the main function fullscan. The function takes as its arguments the length of the data, the window size and an offset. If the offset is set equal to the window size, nonoverlapping windows are obtained. If the offset is less than the window size, sliding windows of given window size and offset are obtained.
The function powerMethod provides a C++ implementation of the power method for fast iterative computation of the largest eigenvector (von Mises & Pollaczek-Geiringer, 1929). The function can be used as summaryFunction in the main function fullscan.
2.1.4 ∣. Other comparison measures
The modular structure of locStra allows one to specify (1) the similarity measure on the genome (the matrixFunction; for instance, the Jaccard matrix); (2) the summary statistic for the similarity matrix as function summaryFunction; and (3) a comparison measure on either the similarity matrices or the summary statistic (function comparisonFunction). In this study, we always summarize the four similarity matrices with the first eigenvector (as summaryFunction) and compare the correlation between eigenvectors (as comparisonFunction). However, many more sensible choices exist which include:
The similarity matrices can be compared directly using, for instance, the Lp,q, Frobenius, maximum or Schatten matrix norms as comparisonFunction. In this case, the summaryFunction is the identity function.
Apart from eigenvectors, two similarity matrices can be summarized using other traditional tools such as their eigenvalues, or the condition number of the difference between both which, if large, indicates that the matrices are close in this specific sense.
Apart from the first eigenvector, the similarity matrices can be summarized with a linear combination of higher order eigenvectors to capture more principal components. Moreover, the eigenvectors can be weighted with their corresponding eigenvalues.
Apart from using vector correlation, eigenvectors and other vector-valued measures can be compared using vector norms, the angle between them, and so forth.
However, some measures might be more meaningful than others depending on the context of the comparison and application. We did experiment with different measures and found the correlation between the first eigenvectors to capture best the variability within each chromosome.
3 ∣. RESULTS
3.1 ∣. Regional stratification analysis of the 1000 Genome Project
To illustrate the practical relevance of regional substructure analysis and its feasibility at the genome-wide level, we apply locStra to all chromosomes of the 1000 Genome Project (The 1000 Genomes Project Consortium, 2015) and take a closer look at the results for four chromosomes, precisely chromosomes 5, 7, 12, and 16. Importantly, we investigate runtimes across all chromosomes, and present an approach to select suitable window sizes for population stratification.
Before applying locStra, the raw data from the 1000 Genome Project is prepared using PLINK2 (Purcell & Chang, 2019) with cutoff value 0.01 for option --max-maf to select rare variants. We applied LD pruning with parameters --indep-pairwise 2000 10 0.01. Analysis results are shown for the European super population alone (503 subjects, ca. 5 million RVs) of the 1000 Genome Project. All timings presented in this and the following sections were measured on one Intel QuadCore i5-7200 CPU with 2.5 GHz and 8 GiB of RAM.
Using a sliding window approach of 128,000 RVs (as suggested by our window selection algorithm), we used locStra to compute the correlations between the first eigenvector of all regional similarity matrices with the corresponding first eigenvector of the global similarity matrix.
3.1.1. ∣. Data analysis results for certain chromosomes of the 1000 Genome Project
The regional substructure analysis in Figure 1 reveals several notable features. Regardless of the type of similarity matrix used for the regional substructure analysis, there are only a few genomic regions for which the regional and global substructures are similar in terms of the first eigenvectors. Overall, there is substantial variability of the regional substructure across the genome, when measured via the similarity matrices. This observation also has implications for association mapping, as the association analysis is typically adjusted for the global eigenvectors to minimize potential genetic confounding. It will be subject of future research to investigate the best ways to incorporate regional substructure adjustments based on RVs in genetic association testing.
FIGURE 1.
Rare variants (RVs) for the super population EUR of the 1000 Genomes Project. Correlation of regional to global eigenvectors for chromosomes 5 (top left), 7 (top right), 12 (bottom left), and 16 (bottom right). Covariance matrix, GRM matrix, s-matrix, and Jaccard matrix. Window size 128,000 RVs
In the areas where the correlation between the regional and global first eigenvector is not high, the standard Jaccard approach is able to maintain the highest correlation values compared to the other similarity matrices. In the areas where the regional first eigenvectors of Cov, GRM, and s-matrix/weighted Jaccard are highly correlated with the corresponding global first eigenvectors, the first eigenvector of the standard Jaccard approach is often almost uncorrelated with the global one. Further methodological and substantive research is required to understand the reasons for these performance differences. This is part of our ongoing research and beyond the scope of this manuscript.
To contrast rare and common variants, Figure 2 shows similar plots for the same four chromosomes on common variants. We observe that, as expected, there are little to no variation across the genome.
FIGURE 2.
Common variants for the super population EUR of the 1000 Genomes Project. Correlation of regional to global eigenvectors for chromosomes 5 (top left), 7 (top right), 12 (bottom left), and 16 (bottom right). Covariance matrix, GRM matrix, s-matrix, and Jaccard matrix. Window size 100 RVs
3.1.2 ∣. Runtime of locStra for the 1000 Genome Project Analysis
Figure 3 shows the runtime in seconds for the R function fullscan (see Section 2.1.2) as a function of the window sizes. Each plot depicts the minimal and maximal runtime observed among any of the chromosomes per window size, as well as the mean runtime for a particular window size when averaged across all chromosomes.
FIGURE 3.
Super population EUR of the 1000 Genomes Project. Runtime in seconds as a function of the window sizes across all chromosomes for the computation of the covariance matrix (top left), GRM matrix (top right), s-matrix (bottom left), and Jaccard matrix (bottom right). All plots show the minimal and maximal runtimes for any of the chromosomes, as well as the mean runtime averaged across all chromosomes. Logarithmic scale on the x- and y-axes
One can see that the mean runtime never exceeds 500 s for a complete scan of any chromosome. As expected, the runtime decreases for larger window sizes. For a realistic window size of, for example, 104 or 105 (see Section 3.1.4), the runtime for any method is in the neighborhood of 1 min for a full scan. Repeating the runtime analysis for the AFR super population group of the 1000 Genome Project shows qualitative similar results.
3.1.3 ∣. Comparison of locStra to PLINK2 on chromosome 1 of the 1000 Genome Project
Performing a similar scan of the genome with PLINK2 (Purcell & Chang, 2019), which is one of the most frequently used tools to compute genetic variance/covariance matrices, is possible but has a considerably higher computational runtime. This is due to the fact that, although PLINK2 can both extract genomic regions specified by rs numbers and compute eigenvectors, it does so via file operations which are very slow, especially if called multiple times as it is needed for a genomewide scan.
To compare locStra to PLINK2, we first prepare the data of chromosome 1 using the same parameters as in the previous subsections. Since locStra and PLINK2 require different input files, we write the curated data for chromosome 1 once in the. bed format for PLINK2 to read, and once convert it into a sparse matrix of class Matrix in R (saved as. Rdata file).
In PLINK2, the first eigenvector can be computed on the .bed file input with the option --pca 1, and to do a regional scan, a variant range on the data can be specified with the parameters --from and --to followed by the rs numbers. After computing the first global eigenvector or one regional eigenvector, PLINK2 writes the vector data into a file .eigenvec, from which the eigenvectors are read to compute correlations between them. In this way, a complete scan of correlations between global and regional eigenvectors can be carried out in PLINK2.
For locStra, we load the sparse matrix input data into R and employ the function fullscan from the R package to carry out a complete scan (Table 1).
TABLE 1.
Comparison of locStra and PLINK2
| locStra | PLINK2 | |||
|---|---|---|---|---|
| Window size | Global EV | Full scan | Global EV | Full scan |
| 1000 | 1.4 | 332.1 | 65.3 | 6343.6 |
| 10,000 | 1.5 | 31.3 | 61.2 | 731.7 |
| 100,000 | 1.5 | 4.9 | 66.7 | 189.1 |
Note: Runtimes in seconds for the computation of the global eigenvector (global EV) and for a full stratification scan of chromosome 1 of the 1000 Genome Project as a function of the window size.
Results for three different window sizes are given in Table 1, showing both the runtimes (in seconds) for the computation of the single global eigenvector on the full data, as well as for a complete scan (which includes the computation of the global eigenvector before starting the scan). Since the times for PLINK2 necessarily include the read/write operations for file in- and outputs, we likewise report times for locStra that include the reading time of the input data for a fair comparison. As visible from Table 1, locStra is at least one order of magnitude faster than PLINK2 on the data of the 1000 Genome Project. Moreover, the speed-up seems to be more pronounced for larger window sizes. Based on further experiments (not reported here), we expect those results to generalize for larger datasets.
Figure 4 shows how the results of PLINK2 and locStra compare. For this, we compute the GRM similarity matrix on the EUR super population of the 1000 Genome Project with both programs. We then plot the first two principle components against each other using the same x-axis and y-axis scaling. We observe that throughout our experiments (results for other chromosomes not shown), the stratification is similar, in particular, the point clouds are located in roughly the same spots. However, the projection of locStra is often more spread out, making it easier to differentiate between the population subgroups contained in the data set.
FIGURE 4.
Super population EUR of the 1000 Genomes Project with British (GBR), Finnish (FIN), Iberian (IBS), Utah resident (CEU), and Toscani (TSI) subgroups. First two principal components for the GRM similarity matrix computed with PLINK2 (left) and locStra (right) for chromosome 1 (top) and chromosome 6 (bottom)
3.1.4 ∣. Selecting suitable window sizes for population stratification
An interesting question pertains to the selection of an appropriate window size for population stratification. Two quantities work against each other in the process of selecting a suitable window size: As the window size becomes larger, fewer windows are used in the scan of the data, and thus the correlation between regional and global eigenvectors increases as seen in Figure 5 (left). On the other hand, larger window sizes imply the usage of fewer windows in the scan, thus causing fewer data points to be calculated.
FIGURE 5.
Super population EUR of the 1000 Genomes Project. Left: Mean correlation across all windows as a function of the window size. Right: Mean correlation across all windows multiplied by the logarithm of the number of windows, again as a function of the window size. Input data are the correlations between global and regional eigenvectors of the Jaccard matrices for different window sizes
This gives rise to a variety of heuristics which can be used to trade off the two quantities (correlation and number of data points), with the aim to arrive at a sensible (though not theoretically proven) measure indicating good selections for the window size. As an example, we multiply the mean correlation among all windows (for a particular window size) with the logarithm of the number of windows generated using that size (alternatively, any monotonic transformation of the number of windows can be used).
The resulting measure is displayed in Figure 5 (right) for the EUR super population, and in Figure 6 (right) for the AFR super population of the 1000 Genome Project. It can be seen that for very small and large window sizes, the heuristic measure is lower than in-between the two extremes. For both the EUR and AFR super populations of the 1000 Genomes Project, we observe a peak at roughly a window size of 105 RVs. Interestingly, the shape of the curves is almost identical across all chromosomes. This is attributed to the fact that the slopes in Figure 5 (left) and Figure 6 (left) is very similar for all chromosomes.
FIGURE 6.
Super population AFR of the 1000 Genomes Project. Setting as in Figure 5. Left: Mean correlation across all windows as a function of the window size. Right: Mean correlation across all windows multiplied by the logarithm of the number of windows, again as a function of the window size
For the analysis of EUR and AFR super population data from the 1000 Genomes Project, we will use a window size of around 105 RVs. This idea of trading off the mean correlation with the number of data points generalizes to other datasets and can be seen as an heuristic guideline.
3.2 ∣. Data analysis of a Childhood Asthma Study from Costa Rica (population isolate)
We now analyze the global and the regional population substructure and the differences they exhibit on a cluster level in a data set of a Costa Rica population isolate, as one expects stronger degrees of stratification in such a sample. The data set includes children aged 6 to 14 and their parents (2736 subjects, 1824 of which are parents) from GACRS (Genetics of Asthma in Costa Rica Study) family-based trios recruited from a genetically homogeneous Hispanic population isolate living in the Central Valley of Costa Rica. This population has one of the highest prevalences of asthma in the world. Please see Hunninghake et al. (2007) for a detailed description of the recruitment process. The study has been sequenced as part of the TOPMED Project. The data are available through dbGaP (NHLBI TOPMed, 2019).
To avoid genetic correlations among study subjects due to family structure, we only select the parents for the analysis, and prepare their genetic data using PLINK2 with cutoff value 0.01 for option --max-maf to select rare variants. We applied LD pruning with parameters --indep-pairwise 2000 10 0.01.
To evaluate the population substructure in the data, we compute the Jaccard similarity matrix globally and regionally for one window (the middle window) on each chromosome. We selected here the Jaccard approach for ease of presentation. None of the qualitative conclusions that we reach below would have been different had we selected a different similarity matrix.
Figure 7 shows the first two “global” principal components of the Jaccard matrix, meaning the first two principal components of the Jaccard matrix which was computed globally based on subsampled loci from the entire genome. To be precise, to generate Figure 7, we randomly sampled 105 RVs from each chromosome and combined them into one matrix on which the Jaccard similarity measure was computed. The plot shows that most samples get mapped into a consistent point cloud. However, we observe that this cloud stretches out to the above and below, with three clear outliers marked in red.
FIGURE 7.
Costa Rica population isolate. First two principal components for the Jaccard similarity matrix. All chromosomes combined. Three outliers are marked with red crosses
For each of the 22 autosomal chromosomes, Figure 8 shows the plots of the first two “regional” principal components of the Jaccard matrix computed on the middle region (of size 105 loci) on the chromosome. To generate each of the subplots in Figure 8, we selected a window size of 105 for each chromosome (resulting in around 20 windows per chromosome depending on the size of the chromosome data) and computed the similarity matrix on the middle window.
FIGURE 8.
All 22 chromosomes of the Costa Rica population isolate. First two principal components for the Jaccard similarity matrix computed for the middle window of a stratification scan with window size 105. Separate plot for each chromosome (starting with chromosome 1 in the top left corner and continuing in a row-wise fashion). The three outliers of Figure 7 are marked again in each subplot in red
Interestingly, Figure 8 shows that on a regional level, the substructure can vary substantially. While it can be very similar to the global substructure for some of the regions, often it is more extreme or fundamentally different, showing sub-clusters that are not detectable in the global components. Moreover, we observe that on a regional level, the structure is often more extreme, exhibiting large branches that are substantial proportion of samples fall into. By exemplarily marking the three outliers of Figure 7 in each of the 22 subplots (in red), we observe that each subplot exhibits are much finer structure than the global one, with outliers which are not detectable in a global analysis.
Analyzing the relationship of regional outliers among each other and with respect to the global PCA plot, and inferring possible conclusions from it, remains for further research. A first impression is given in Figure 9, which shows where the outliers from the branches observed in Figure 8 are located in the global PCA plot (all outliers from the 22 regional plots are displayed in Figure 9 with their chromosome number). We observe that there is indeed a structure: for instance, samples from the outliers of chromosomes 1, 8, and 15 seem to be located exclusively in the upper part of Figure 9.
FIGURE 9.
Costa Rica population isolate. First two principal components for the Jaccard similarity matrix. All chromosomes combined. The samples contained in the branches of the 22 regional plots of Figure 8 are both colored by chromosome and labeled with their chromosome number
The corresponding results for the other similarity matrix approaches support the same conclusion (data not shown). The findings of the Costa Rica data analysis clearly demonstrate the importance of regional substructure analysis and the utility of the proposed locStra package.
3.3 ∣. Correcting a linear regression with global and regional principal components
To assess the effects of regional substructure on association testing, we consider an example in the COPDGene study, a case-control study of Chronic Obstructive Pulmonary Disease (COPD) in current and former smokers (Regan et al., 2010). The study has been sequenced as part of the TOPMED Project. The data are available through dbGaP (NHLBI TOPMed, 2018).
We examine the effect of the particular SNP rs16969968 (chromosome 15) on FEV1 which is a well-established risk locus for COPD and cigarette smoking (Lutz et al., 2015; Pillai et al., 2009). It is unclear whether the regional substructure or the global substructure is more relevant for a particular locus that is tested for association. It is important to note that the inclusion of additional principal components will not have a major impact on the power of the association analysis, given the current sample size of such studies. As a consequence, the analysis plan is to evaluate three regression models:
Model 1: Regress FEV1 on rs16969968 adjusting for age, height, sex, and the first five global principal components.
Model 2: Regress FEV1 on rs16969968 adjusting for age, height, sex, and the first five regional principal components that are computed for the region that harbors rs16969968.
Model 3: Regress FEV1 on rs16969968 adjusting for age, height, sex, and the first 5 regional principal components and on the first 5 global principal components.
We will assess the association p values for rs16969968 on FEV1 to evaluate whether the analysis benefits from the inclusion of the regional principal components (X. Wang et al., 2011).
We conducted the analysis in the following way. We first prepared the genetic data from the COPDGene study for chromosome 15 with PLINK2. We employed a maximal allele frequency cutoff of --max-maf 0.01, LD pruning with parameters --indep-pairwise 2000 10 0.01, and filtered out the snp of interest using the command --snp rs16969968. To specify regional windows around rs16969968, we employed --window W, where we chose the window size W ∈ {1600, 3200, 6400}. We made sure that due to its high allele frequency (maf = 0.597), the snp rs16969968 was indeed not included in any window. Since we compute our similarity matrices on rare variants having very different allele frequencies than the common ones, they are virtually uncorrelated with the common loci that are typically tested for association in single-locus analyses. After preparing the data with PLINK2, we are left with 5765 subjects and 94,497 RVs.
Using the genetic data above and, additionally, the covariates age, sex, an indicator of current smoking status (smoker=1 for current smokers and 0 for former smokers), as well as the subject's height (in centimeters), we fit the regression models
| (1) |
where SNP is the allele count data for rs16969968, and PCAi for i ∈ {1, …, 5} are the first five principal components for either the global or regional similarity matrices. We test the hypothesis that βS = 0 against the alternative that βS ≠ 0. The global principal components are computed by applying any similarity matrix approach to the full genomic data, and computing the first eigenvectors. The regional principal components are computed by extracting a region around rs16969968 (of window size given in Table 2), computing the similarity matrix on that region, and then calculating the first eigenvectors of that similarity matrix.
TABLE 2.
Regression (1) on the FEV1 for the COPDGene study
| Similarity matrix |
Window size |
Global | Regional | Global and regional |
% reduction over global |
|---|---|---|---|---|---|
| Cov | 1600 | 1.81e–9 | 3.58e–9 | 1.44e–9 | 20 |
| 3200 | 1.81e–9 | 2.92e–9 | 1.08e–9 | 40 | |
| 6400 | 1.81e–9 | 2.92e–9 | 1.08e–9 | 40 | |
| Jaccard | 1600 | 1.82e–9 | 1.40e–9 | 9.90e–10 | 46 |
| 3200 | 1.82e–9 | 1.53e–9 | 1.06e–9 | 42 | |
| 6400 | 1.82e–9 | 1.53e–9 | 1.06e–9 | 42 | |
| s-matrix | 1600 | 1.29e–9 | 3.51e–9 | 8.61e–10 | 33 |
| 3200 | 1.29e–9 | 3.76e–9 | 1.18e–9 | 9 | |
| 6400 | 1.29e–9 | 3.76e–9 | 1.18e–9 | 9 | |
| GRM | 1600 | 8.61e–10 | 2.90e–09 | 5.33e–10 | 38 |
| 3200 | 8.61e–10 | 2.82e–9 | 4.82e–10 | 44 | |
| 6400 | 8.61e–10 | 2.82e–9 | 4.82e–10 | 44 |
Note: Columns show p values for different similarity matrices and window sizes. Five principal components each for both global and regional adjustments. Last column shows the reduction in % for the regression p value of the combined global and regional adjustment compared with the global adjustment only.
In this way, we regress FEV1 on the above covariates, where for global and regional adjustments we each use the first five principal components. For the combined global and regional adjustment, we add both the five global and the five regional eigenvectors to the model (1).
Results are given in Table 2. The table shows that for any of the four similarity matrices under investigation, and for any of the reported window sizes, the combined global and regional adjustment yields a p value for the hypothesis βS = 0 that is more significant (up to 46% smaller) than the global (or regional) adjustment alone. Though further investigations are necessary, these results hint at the fact that adjusting for both “global” and “regional” principal components can be beneficial in genetic association testing.
As we discussed above, to run the regional scans, we propose here to compute the similarity matrices based on rare variants (RVs) which have very different allele frequencies than the common variants and are therefore virtually uncorrelated with the common loci that are typically tested for association in single-locus analyses. We believe therefore that the “proximal contamination” effects (Baran et al., 2012; Gazal et al., 2017, 2018; Listgarten, 2012; Salter-Townshend & Myers, 2019; Thornton & Bermejo, 2014) can largely be avoided here. If RVs are to be tested for association, they should be excluded from the computation of the regional similarity matrices. Given the computational efficiency of locStra, this does not create a bottleneck in terms of computation time.
To assess the aforementioned proximal contamination effects (due to potential collinearity between test SNP and the estimate), we repeat the analysis above using all common snps on chromosome 1 of the EUR super population of the 1000 Genome Project. For each common snp, we again fit the model in Equation (1). As before, this is done in three cases: for a global adjustment only (i.e., only the five global PCs), for a regional adjustment only (using 10 windows across the chromosome), and for a combined global and regional adjustment (with five global and five regional PCs). The global and regional eigenvectors were computed on the covariance matrix.
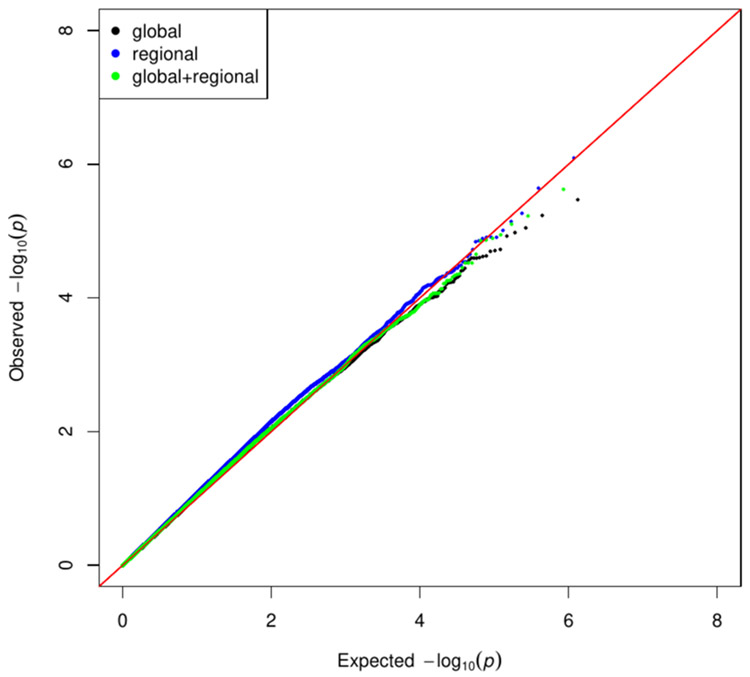
The resulting Q-Q plot is given in Figure 10. We see that the distribution of unadjusted p values is consistent across the three cases of a global, regional, or global and regional analysis, and that the type 1 error is well controlled.
FIGURE 10.
Q-Q plot for a chromosome-wide regression of all common SNPs using a global, regional, and global and regional adjustment according to the model of Equation (1). Chromosome 1 of the 1000 Genome Project. Global and regional eigenvectors were computed on the covariance matrix
Subsequent research is needed to evaluate the effects of other confounding variables, for example, sequencing depth, batch effects, and so forth, on the globally and regionally computed similarity matrices. Approaches similar to the one developed for association testing (Sankararaman et al., 2008) could be utilized here.
4 ∣. DISCUSSION
Our R-package locStra is the first software package that enables a comprehensive genome-wide analysis of regional stratification based on similarity matrices in WGS studies. Given a runtime of around 500 s for the genomewide analysis of all sliding windows in the European super population of the 1000 Genome Project (one Intel QuadCore i5-7200 CPU with 2.5 GHz and 8 GiB of RAM), locStra enables the community to conduct substantive research into regional stratification patterns at a genomewide level in their WGS studies. At the same time, it will foster methodological work in many fields of statistical genetics, including approaches on how to incorporate regional stratification information into association studies.
ACKNOWLEDGMENTS
Molecular data for the Trans-Omics in Precision Medicine (TOPMed) program was supported by theNational Heart, Lung and Blood Institute (NHLBI). See the TOPMed Omics Support Table (Table 3) for study-specific omics support information. Core support including centralized genomic read mapping and genotype calling, along with variant quality metrics and filtering were provided by the TOPMed Informatics Research Center (3R01HL-117626-02S1; contract HHSN268201800002I). Core support including phenotype harmonization, data management, sample-identity QC, and general program coordination were provided by the TOPMed Data Coordinating Center (R01HL-120393; U01HL-120393; contract HHSN268201800001I). We gratefully acknowledge the studies and participants who provided biological samples and data for TOPMed.
TABLE 3.
TOPMed omics support table
| TOPMed accession no. |
TOPMed project |
Parent study short name |
TOPMed phase |
Omics center | Omics support | Omics type |
|---|---|---|---|---|---|---|
| phs001726 | CRA_CAMP | CAMP | 3 | NWGC | HHSN268201600032I | WGS |
| phs001726 | CRA_CAMP | CAMP | 5 | Broad Metabolomics | HHSN268201600034I | Metabolomics |
| phs001726 | CRA_CAMP | CAMP | 5 | Keck MGC | HHSN268201600038I | Methylomics |
| phs000951 | COPD | COPDGene | 1 | NWGC | 3R01HL089856-08S1 | WGS |
| phs000951 | COPD | COPDGene | 2 | Broad Genomics | HHSN268201500014C | WGS |
| phs000951 | COPD | COPDGene | 2.5 | Broad Genomics | HHSN268201500014C | WGS |
| phs000951 | COPD | COPDGene | 4 | NWGC | HHSN268201600032I | RNASeq |
| phs000951 | COPD | COPDGene | 5 | NWGC | HHSN268201600032I | Methylomics |
| phs000988 | CRA_CAMP | CRA | 1 | NWGC | 3R37HL066289-13S1 | WGS |
| phs000988 | CRA_CAMP | CRA | 3 | NWGC | HHSN268201600032I | WGS |
| phs000988 | CRA_CAMP | CRA | 5 | Broad Metabolomics | HHSN268201600034I | Metabolomics |
| phs000988 | CRA_CAMP | CRA | 5 | Keck MGC | HHSN268201600038I | Methylomics |
Abbreviations: Broad Genomics, Broad Institute Genomics Platform; Broad Metabolomics, Broad Institute and Beth Israel Metabolomics Platform; Keck MGC, Keck Molecular Genomics Core Facility; NWGC, Northwest Genomics Center.
Parent Study-specific Acknowledgments:
NHLBI TOPMed: Childhood Asthma Management Program (CAMP).
NHLBI TOPMed: Genetic Epidemiology of COPD Study (COPDGene). The COPDGene project described was supported by Award Number U01 HL089897 and Award Number U01 HL089856 from the National Heart, Lung, and Blood Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung, and Blood Institute or the National Institutes of Health. The COPDGene project is also supported by the COPD Foundation through contributions made to an Industry Advisory Board comprised of AstraZeneca, Boehringer Ingelheim, GlaxoSmithKline, Novartis, Pfizer, Siemens and Sunovion. A full listing of COPDGene investigators can be found at: http://www.copdgene.org/directory.
NHLBI TOPMed: The Genetic Epidemiology of Asthma in Costa Rica—Asthma in Costa Rica cohort (CRA).
Funding information
National Heart, Lung and Blood Institute (NHLBI)
Appendix
APPENDIX A: DETAILS ON THE IMPLEMENTATION
This section briefly describes two important implementation details (for computing the covariance and Jaccard matrices) employed to enable fully sparse matrix algebra. The GRM matrix (Yang et al., 2011) and the s-matrix (Schlauch, 2016) were computed as described in their respective publications. Throughout the section, the input data is assumed to contain (genomic) data of length m in each of the n columns, one column per individual. The parameter m therefore represents the number of loci included in the computation of the similarity matrix and n is the number of study subjects. At the end of this section, theoretical runtimes of our implementations are given.
A.1 ∣. Covariance matrix
To compute the covariance matrix in dense algebra, let be the column means and let be the matrix consisting of the rows of X with their mean subtracted. Then
TABLE A1.
Theoretical runtimes of the four matrix approaches to compute similarity measures for both dense and sparse implementations
| Method | Dense | Sparse |
|---|---|---|
| Covariance matrix | O(mn2) | O(smn2) |
| Unweighted Jaccard | O(mn2) | O(smn2) |
| Weighted Jaccard | O(mn2) | O(smn2) |
| GRM matrix | O(mn2) | O(smn2) |
Note: The runtimes are given in the parameters and of the input data as well as the matrix sparsity parameter s ∈ [0,1].
In sparse algebra, the matrix X cannot be normalized as in the dense case by simply subtracting the column means, since this would result in a dense matrix which easily exceeds available memory. To always stay within sparse algebra, the computation is split up suitably. To be precise, let v denote the column means as above, and be the column sums, then
This formula has the advantage that the computation of X⊺X can be carried out using only one sparse matrix multiplication involving the sparse input matrix, and the remaining three outer vector products result in n × n matrices, thus never exceeding the size of the output covariance matrix.
A.2 ∣. Jaccard similarity matrix
The entry (i, j) of the Jaccard matrix jac(X) is given as
where the matrix X is binary.
A naïve approach to compute the entries of the Jaccard matrix loops over all entries of the Jaccard matrix and calculates the binary and as well as binary or operations on all combinations of two columns of X. Though having the same theoretical runtime, this naïve approach turned out to be slower in practice than the following technique which uses only one (sparse) matrix–matrix multiplication which is typically highly optimized in sparse matrix algebra packages.
Let be the column sums of X as before. Compute Y = X⊺X via sparse matrix multiplication. The resulting matrix is dense. Compute a second matrix by adding w to all rows and all columns of −Y. Then, jac(X) = Y/Z, where the division operation is performed componentwise. This approach is computationally very fast since it relies solely on one sparse matrix multiplication and a few more operations on the matrices Y and Z which are already of the same size as the dense Jaccard output matrix.
A.3 ∣. Theoretical runtimes of dense and sparse implementations
Table A1 shows theoretical runtimes for both the dense and sparse matrix versions of the four similarity matrix approaches. It turns out that the runtimes for the dense and sparse computations of all similarity matrices coincide. The following highlights the effort of the main computation steps in each case as a function of the parameters and of the input data , as well as the matrix sparsity parameter s ∈ [0,1] (the proportion of non-zero matrix entries).
In the dense case, computing the covariance matrix involves subtracting the column means in O(mn) and multiplying Y⊺Y in O(mn2). In the sparse case, the computation of X⊺X requires O(smn2), and the computation of the three additional outer products requires another O(n2).
The Jaccard matrix involves computing Y = X⊺X in O(mn2) in the dense case and O(smn2) in the sparse case. Adding the column sums to the rows and columns of the resulting n × n matrix takes effort O(n2) in both the dense and sparse case.
The effort for computing the weighted Jaccard matrix (or s-matrix) stems from the computation of weights through row sums (O(mn) in dense algebra and O(smn) in sparse algebra), multiplying the input matrix with the weights (likewise O(mn) in dense algebra and O(smn) in sparse algebra), and one matrix-matrix multiplication (O(mn2) in dense algebra and O(smn2) in sparse algebra).
Computing the GRM matrix involves the calculation of population frequencies across rows (O(mn) in dense algebra and O(smn) in sparse algebra), one matrix–matrix multiplication (O(mn2) in dense algebra and O(smn2) in sparse algebra), multiplying the input matrix with the population frequencies (O(mn) in dense algebra and O(smn) in sparse algebra), and one outer product of the population frequencies in O(n2).
Footnotes
CONFLICT OF INTERESTS
The authors declare that there are no conflict of interests.
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in “NHLBI TOPMed: The Genetic Epidemiology of Asthma in Costa Rica” at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000988.v3.p1 as well as “NHLBI TOPMed: Boston Early-Onset COPD Study in the National Heart, Lung, and Blood Institute (NHLBI) Trans-Omics for Precision Medicine (TOPMed) Program” at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000946.v3.p1.
REFERENCES
- Baran Y, Pasaniuc B, Sankararaman S, Torgerson DG, Gignoux C, Eng C, … Halperin E (2012). Fast and accurate inference of local ancestry in Latino populations. Bioinformatics, 28(10), 1359–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, & Eddelbuettel D (2013). Fast and elegant numerical linear algebra using the RcppEigen package. Journal of Statistical Software, 52(5), 1–24.23761062 [Google Scholar]
- Bodmer W, & Bonilla C (2008). Common and rare variants in multifactorial susceptibility to common diseases. Nature Genetics, 40, 695–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin B, & Roeder K (1999). Genomic control for association studies. Biometrics, 55(4), 997–1004. [DOI] [PubMed] [Google Scholar]
- Gazal S, Finucane H, Furlotte N, Loh P, Palamara P, Liu X, . Price A (2017). Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nature Genetics, 49(10), 1421–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazal S , Loh P , Finucane H , Ganna A , Schoech A , Sunyaev S , & Price A (2018). Functional architecture of low-frequency variants highlights strength of negative selection across coding and noncoding annotations. Nat Genet, 50(11), 1600–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn G, Lutz SM, and Lange C (2020). locStra: Fast implementation of (Local) population stratification methods (Version 1.3) [Software]. https://cran.r-project.org/web/packages/locStra/index.html
- Hunninghake GM, Soto-Quiros ME, Avila L, Ly NP, Liang C, Sylvia JS, … Celedón JC (2007). Sensitization to Ascaris lumbricoides and severity of childhood asthma in Costa Rica. Journal of Allergy and Clinical Immunology, 119(3), 654–661. [DOI] [PubMed] [Google Scholar]
- Keinan A, & Clark A (2012). Recent explosive human population growth has resulted in an excess of rare genetic variants. Science, 336(6082), 470–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kryukov GV, Shpunt A, Stamatoyannopoulos JA, & Sunyaev SR (2009). Power of deep, all-exon resequencing for discovery of human trait genes. Proceedings of the National Academy of Sciences of the United States of America, 106(10), 3871–3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird NM and Lange C (2010). The fundamentals of modern statistical genetics. New York: Springer Science & Business Media. [Google Scholar]
- Lee S, Epstein M, Duncan R, & Lin X (2012). Sparse principal component analysis for identifying ancestry-informative markers in genome-wide association studies. Genetic Epidemiology, 36(4), 293–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J, Lippert C, Kadie CM, Davidson RI, Eskin E, & Heckerman D (2012). Improved linear mixed models for genome-wide association studies. Nature Methods, 9(6), 525–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutz SM, Cho MH, Young K, Hersh CP, Castaldi PJ, McDonald M-L, … Silverman EK (2015). A genome-wide association study identifies risk loci for spirometric measures among smokers of European and African ancestry. BMC Genetics, 16(138), 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maples B, Gravel S, Kenny E, & Bustamante C (2013). RFMix: A discriminative modeling approach for rapid and robust local-ancestry inference. American Journal of Human Genetics, 93(2), 278–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin ER, Tunc I, Liu Z, Slifer SH, Beecham AH, & Beecham GW (2018). Properties of global and local ancestry adjustments in genetic association tests in admixed populations. Genetic Epidemiology, 42(2), 214–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeigue P, Carpenter J, Parra E, & Shriver M (2000). Estimation of admixture and detection of linkage in admixed populations by a Bayesian approach: Application to African-American populations. Annals of Human Genetics, 64(2), 171–86. [DOI] [PubMed] [Google Scholar]
- Morrison A, Voorman A, Johnson A, Liu X, Yu J, Li A, … Boerwinkle E (2013). Whole genome sequence-based analysis of a model complex trait, high density lipoprotein cholesterol. Nature Genetics, 45(8), 899–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NHLBI TOPMed. (2018). Boston early-onset COPD study in the national heart, Lung, and Blood Institute (NHLBI) Trans-Omics for Precision Medicine (TOPMed) program.
- NHLBI TOPMed. (2019). The Genetic Epidemiology of Asthma in Costa Rica.
- Panoutsopoulou K, Tachmazidou I, & Zeggini E (2013). In search of low-frequency and rare variants affecting complex traits. Human Molecular Genetics, 22(R1), R16R21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price A, & Reich D (2006). Population structure and Eigenanalysis. PLoS Genetics, 2(12):e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillai SG, Ge D, Zhu G, Kong X, Shianna KV, Need AC, … Goldstein DB (2009). A genome-wide association study in Chronic Obstructive Pulmonary Disease (COPD): Identification of two major susceptibility loci. PLoS Genetics, 5(3):e1000421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, & Reich D (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics, 38, 904–909. [DOI] [PubMed] [Google Scholar]
- Price AL, Tandon A, Patterson N, Barnes KC, Rafaels N, Ruczinski I, … Myers S (2009). Sensitive Detection of Chromosomal Segments of Distinct Ancestry in Admixed Populations. PLOS Genetics, 5(6):e1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard J, Stephens M, Rosenberg N, & Donnelly P (2000). Association mapping in structured populations. American Journal of Human Genetics, 67(1), 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prokopenko D, Hecker J, Silverman EK, Pagano M, Nothen MM, Dina C, … Fier HL (2016). Utilizing the Jaccard index to reveal population stratification in sequencing data: a simulation study and an application to the 1000 Genomes Project. Bioinformatics, 32(9), 1366–1372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S and Chang C (2019). PLINK2 (Version 2.0) [Software]. www.cog-genomics.org/plink/2.0/
- Regan EA, Hokanson JE, Murphy JR, Make B, Lynch DA, Beaty TH,… Crapo JD (2010). Genetic epidemiology of COPD (COPDGene) study design. COPD, 7(7), 32–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salter-Townshend M, & Myers S (2019). Fine-scale inference of ancestry segments without prior knowledge of admixing groups. Genetics, 212(3), 869–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankararaman S, Sridhar S, Kimmel G, & Halperin E (2008). Estimating local ancestry in admixed populations. American Journal of Human Genetics, 82(2), 290–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlauch D (2016). Implementation of the stego algorithm—Similarity test for estimating genetic outliers (Version 1.0) [Software]. https://github.com/dschlauch/stego
- Schlauch D, Fier H, & Lange C (2017). Identification of genetic outliers due to sub-structure and cryptic relationships. Bioinformatics, 33(13), 1972–1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Coram M, Wang P, Zhu X, & Risch N (2006). Reconstructing genetic ancestry blocks in admixed individuals. American Journal of Human Genetics, 79, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium. (2015). A global reference for human genetic variation. Nature, 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton TA, & Bermejo JL (2014). Local and global ancestry inference, and applications to genetic association analysis for admixed populations. Genetic Epidemiology, 38(01), S5S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- vonMises R, & Pollaczek-Geiringer H (1929). Praktische Verfahren der Gleichungsaufloesung. ZAMM Zeitschrift fr Angewandte Mathematik und Mechanik, 9, 152–164. [Google Scholar]
- Wang B, Sverdlov S, & Thompson E (2017). Efficient estimation of realized kinship from single nucleotide polymorphism genotypes. Genetics, 205(3), 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Zhu X, Qin H, Cooper RS, Ewens WJ, Li C, & Li M (2011). Adjustment for local ancestry in genetic association analysis of admixed populations. Bioinformatics, 27, 670–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee S, Goddard M, & Visscher P (2011). GCTA: a tool for genome-wide complex trait analysis. American Journal of Human Genetics, 88(1), 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yazdani A, Yazdani A, & Boerwinkle E (2015). Rare variants analysis using penalization methods for whole genome sequence data. BMC Bioinformatics, 16(1), 405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong Y, Perera MA, & Gamazon ER (2019). On using local ancestry to characterize the genetic architecture of human traits: Genetic regulation of gene expression in multiethnic or admixed populations. American Journal of Human Genetics, 104(6), 1097–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are openly available in “NHLBI TOPMed: The Genetic Epidemiology of Asthma in Costa Rica” at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000988.v3.p1 as well as “NHLBI TOPMed: Boston Early-Onset COPD Study in the National Heart, Lung, and Blood Institute (NHLBI) Trans-Omics for Precision Medicine (TOPMed) Program” at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000946.v3.p1.