Abstract
Few-shot learning is an almost unexplored area in the field of medical image analysis. We propose a method for few-shot diagnosis of diseases and conditions from chest x-rays using discriminative ensemble learning. Our design involves a CNN-based coarse-learner in the first step to learn the general characteristics of chest x-rays. In the second step, we introduce a saliency-based classifier to extract disease-specific salient features from the output of the coarse-learner and classify based on the salient features. We propose a novel discriminative autoencoder ensemble to design the saliency-based classifier. The classification of the diseases is performed based on the salient features. Our algorithm proceeds through meta-training and meta-testing. During the training phase of meta-training, we train the coarse-learner. However, during the training phase of meta-testing, we train only the saliency-based classifier. Thus, our method is first-of-its-kind where the training phase of meta-training and the training phase of meta-testing are architecturally disjoint, making the method modular and easily adaptable to new tasks requiring the training of only the saliency-based classifier. Experiments show as high as ~ 19% improvement in terms of F1 score compared to the baseline in the diagnosis of chest x-rays from publicly available datasets.
Keywords: Few-shot, x-ray, autoencoder, ensemble, discriminative
1. Introduction
Recent advancements in machine learning, in particular deep convolutional neural networks (CNN) (LeCun et al., 2015), have enabled computer-aided diagnosis algorithms to match or exceed human performance in different clinical tasks. These include skin cancer classification (Esteva et al., 2017), diabetic retinopathy detection (Ting et al., 2017), wrist fracture detection (Lindsey et al., 2018), and age-related macular degeneration detection (Peng et al., 2019). Although very promising, these algorithms generally rely on large volumes of training data with carefully curated annotations by experts. While medical image datasets consisting of hundreds of thousands of images with various diseases were recently made publicly available to researchers (Wang et al., 2017; Irvin et al., 2019; Johnson et al., 2019), only major diseases (or pathologies, clinical findings and conditions) were extracted and labeled using natural language processing (NLP) techniques (Peng et al., 2018). In practice, it can be difficult to obtain and annotate a sufficient amount of examples for rare diseases that have low population prevalence for large-scale training. Dealing with this kind of long-tailed, imbalanced datasets that are prevalent in real-world settings is challenging in both computer vision (Ouyang et al., 2016; Johnson and Khoshgoftaar, 2019) and medical imaging (Li et al., 2019). In these datasets, overfitting can be a critical issue as deep neural networks may memorize specific patterns of the under-represented training data, resulting in poor generalization ability at inference time. To alleviate class imbalance, previous works often use data augmentation (Salehinejad et al., 2019), modification of the sampling weight per class in each batch (Taylor et al., 2018) or assigning different weights to different classes in the loss function (Wang et al., 2017) to balance the under-represented classes in the training data. Once trained, these neural network models can not be readily adapted to unseen classes – they need to be re-trained or fine-tuned with large annotated training sets of new classes.
A particularly appealing property of human vision and cognition is that human beings are able to learn new concepts from just a few examples. Few-shot learning (FSL) (Snell et al., 2017) is an exciting field of machine learning that offers an alternative solution to training robust and discriminative classifiers from a limited amount of training data. In few-shot classification, we learn a classification model from a large labeled training set of base classes and aim to generalize it to novel classes not seen in the training set, given only a small number (e.g., five) of examples per novel class. However, the extremely limited number of training examples per class can hardly represent the real distribution of the new data efficiently, making this task significantly challenging. In response to these challenges, FSL has attracted increasing attention in the computer vision community (see a survey paper in (Wang and Yao, 2019)).
Radiology trainees (residents) are often required to transfer knowledge from what they have learnt previously to perform few-shot diagnosis in their rotating training program (Thrall et al., 2018), where only a few samples of each new disease or modalities are given. Towards advanced computer-aided detection (CADe) and computer-aided diagnosis (CADx), FSL may therefore play a crucial role, especially for identification of rare or low prevalence diseases. However, applying FSL techniques for medical image diagnosis poses compelling challenges. A major difficulty is on how to learn disease-specific, discriminative image features for novel classes from only a few examples. The high appearance similarity due to the chest anatomy and inter-class disease similarity in chest x-rays may obstruct the learning of salient features for the target task.
In this paper, we design a method for few-shot diagnosis of chest radiographs. This work builds on our preliminary work published in (Paul et al., 2020). Our design philosophy is based on learning general characteristics of chest x-rays first and then extracting disease-specific characteristics to perform disease classification with only a few training examples. Our method is capable of learning disease-specific characteristics from as little as five training data. We design a two-step solution for few-shot learning from chest x-rays. The first step involves a CNN-based coarse-learner to learn the general characteristics of thoracic diseases in chest x-rays. In the second step, we introduce a saliency-based classifier to extract disease-specific salient features from the output of the coarse-learner and classify the disease. We propose a novel discriminative autoencoder ensemble to design the saliency-based classifier. Each autoencoder is assigned a novel weight based on its internal characteristics. Weighted voting is performed during inference to determine the class label for a query image. Our contributions in this paper are as follows:
We design a two-step solution consisting of a coarse-learner and a saliency-based classifier for few-shot diagnosis of chest radiographs.
The saliency-based classifier is designed using a novel discriminative autoencoder ensemble.
We introduce a novel intrinsic weight to be assigned to each autoencoder for weighted voting during inference.
The proposed method can be trained with one dataset and can still be effectively applied to similar datasets (datasets of the same modality that contain images of the same diseases and conditions) from different sources.
Rigorous experiments show as high as ~ 19% improvement in F1 score compared to the baseline.
The rest of the paper is organized as follows. We present the related works in Section 2 followed by the proposed method in Section 3. The details of the experiments and the results are presented in Section 4. Finally, we conclude the paper in Section 5.
2. Related Work
2.1. Deep CNN-based Chest X-ray Diagnosis
Chest radiography is the most common diagnostic imaging test worldwide. It is widely used for screening and monitoring various thoracic diseases (de Hoop et al., 2010; Team, 2011). Recent advances in deep learning and availability of hospital-scale chest x-ray datasets (Wang et al., 2017; Irvin et al., 2019; Johnson et al., 2019) provide scopes for improving automated interpretation and diagnosis of chest x-rays. In (Lakhani and Sundaram, 2017), the authors used an ensemble of deep CNN models to identify pulmonary tuberculosis on chest x-rays, achieving an accuracy of 96%. Nam et al. (Nam et al., 2018) developed a deep learning-based automated detection algorithm for malignant pulmonary nodules on chest x-rays. Fourteen thoracic disease labels were text-mined from the associated radiology reports using NLP techniques (Peng et al., 2018) on the NIH ChestX-ray14 dataset (Wang et al., 2017) containing 112,120 frontal-view chest x-ray images. The authors trained a weakly-supervised CNN model for multi-label thoracic disease classification and localization, using only image-level labels. In (Tang et al., 2018), the authors incorporated disease severity level information extracted from radiology reports to facilitate curriculum learning in an attention-guided model for a more accurate diagnosis. Rajpurkar et al. and Zhou et al. improved classification and localization performance by training with Densely Connected Convolutional Networks (Huang et al., 2017; Rajpurkar et al., 2017, 2018; Zhou et al., 2018) to make the optimization of such a deep network tractable. Li et al. (Li et al., 2018) presented a unified network that simultaneously improved classification and localization with the help of additional bounding boxes indicating disease location used in the training stage. See (Wang et al., 2018) for an end-to-end deep learning architecture that learns to embed visual images and text reports for disease classification and automated radiology report generation. Guan et al. (Guan et al., 2019) proposed to ensemble the global and local cues into a three-branch, attention-guided CNN to better identify diseases. In order to alleviate data scarcity, (Salehinejad et al., 2019; Tang et al., 2019) used variants of generative adversarial networks (GANs) (Goodfellow et al., 2014) to synthesize chest x-ray images to augment training data for disease classification and pathological lung segmentation. For anomaly detection in chest x-rays, (Tang et al., 2019) proposed a one-class classifier based on the GAN architecture using only normal chest x-rays. In the present work, we exploit the few-shot learning principle for chest x-ray diagnosis, requiring only a few examples from each novel class. To the best of our knowledge, none of these previous works have been able to deal with merely a few training examples, as they usually need a large amount of data to avoid overfitting.
2.2. Few-shot Learning
Recently, few-shot learning has become a hot topic (Wang and Yao, 2019; Zhang et al., 2018; Yoon et al., 2018; Ren et al., 2018) in the computer vision community. Major approaches include meta-learning and metric-learning. Meta-learning based algorithms (Finn et al., 2017; Zhang et al., 2018; Ren et al., 2018) generally rely on transfer learning techniques and have two learning stages. In the first stage, a model is often trained with a set of classes containing a large number of labeled samples, called base classes. The objective of this stage is to enable the model to learn some transferable visual representations that are also useful for recognizing a different set of classes, called the novel classes. In the second stage, the model learns to recognize novel classes that are unseen during the first stage, using only a few training examples, typically 1 to 5 per class. In the second stage, the model learns to recognize novel classes that are unseen during the first stage, using only a few training examples, typically 1 to 5 per class. Few-shot classification is an instantiation of meta-learning in the field of supervised learning.
Metric-learning based approaches (Hoffer and Ailon, 2015; Vinyals et al., 2016; Snell et al., 2017) have been proposed to learn the best distance metric by comparing target examples and few labeled examples in an embedding space. The objective of metric learning is to learn a projection function that can map images to an embedding space (e.g., feature space) in which images from the same class are projected close to each other while images from different classes are projected far apart. The fundamental hypothesis behind this technique is that the learned feature representations from the base classes can be generalized to the novel classes. Our proposed method is related to meta-learning where we learn a generic chest x-ray classifier for multi-class classification on base classes in the first stage. In the second stage, the learned model is generalized into the novel classes with only a few labeled samples.
Few-shot learning and self-supervised learning (Gidaris et al., 2018, 2019) tackle different aspects of the same problem: how to train a model with little or no labeled data. Self-supervised representation learning is a subset of unsupervised learning methods. Like few-shot meta-learning methods, self-supervised learning approaches also have two stages. In the first stage, the visual feature representations are learned through the process of training deep neural networks with one or a few multiple pre-defined pretext tasks. These pretext tasks should be designed to favor the second stage in such a way that: 1) visual features need to be extracted by deep learning models to solve them, 2) models can be explicitly trained with automatically generated pseudo labels from unlabeled data. Examples of these tasks include image colorization, prediction of image rotations, prediction of the relative position of image patches, etc. In the second stage, the learned deep neural networks (usually lower layers) can be further transferred to downstream tasks, especially when only relatively small data is available, as pre-trained models to overcome overfitting and improve performance.
There is a relatively small body of work on few-shot learning in the medical imaging domain. In (Mondal et al., 2018), the authors utilized a GAN-based method for few-shot 3D multi-modal brain MRI image segmentation. Puch et al. (Puch et al., 2019) proposed a few-shot learning model for brain imaging modality recognition based on Deep Triplet Networks (Hoffer and Ailon, 2015). They first meta-trained the model with several tasks containing small meta-training sets, and then trained the model to solve the particular task of interest. Lacking pre-trained models to start from, (Roy et al., 2020) designed ‘channel squeeze and spatial excitation’ blocks for aiding proper training of the volumetric medical image segmentation framework from scratch, with only a few annotated slices. However, it is difficult to find methods addressing the problem of few-shot medical image diagnosis. We introduce a first-of-its-kind discriminative autoencoder ensemble for few-shot diagnosis of chest radiographs. In the next section, we present the proposed method in detail.
3. Methods
Few-shot learning proceeds through meta-training and meta-testing phases (Ravi and Larochelle, 2016). Meta-training phase is composed of a training and a testing (and/or a validation) phase. Similarly, meta-testing also involves training and testing phases. Accordingly, a dataset for few-shot learning is divided into meta-train set and meta-test set. Both the meta-train set and the meta-test set contain training data and test data (may also contain validation data). The meta-test set contains only a few training data per class. Meta-training involves training and testing with the meta-train set while meta-testing involves training and testing with the meta-test set (Finn et al., 2017). The class labels in the meta-train set do not overlap with the class labels in the meta-test set.
Following this protocol, we prepare meta-train and meta-test sets from chest x-ray images such that the disease labels in the meta-train and the meta-test sets do not overlap. The meta-test set contains diseases with only a few training examples per class. We design a few-shot learning method to identify the diseases in the meta-test set.
In few-shot learning, the lack of data points is the main prohibiting factor in drawing a good classification boundary in the feature space. Nevertheless, if we can represent the small amount of training data in a feature space that is highly discriminative w.r.t. the classes, it is still possible to draw a good classification boundary (Wang and Yao, 2019). Based on this fact, we aim to design a few-shot learning technique that would perform classification using salient features which are class-discriminative.
However, finding disease-specific salient features from chest x-rays is a non-trivial problem due to the following reason. Different lung diseases affect different regions of the lungs. Hence, to find the salient characteristics of different diseases, it is important to localize the affected regions from the chest x-rays. Localizing the affected regions often becomes difficult due to poor contrast.
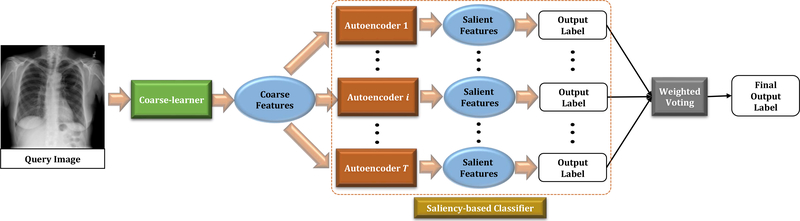
Hence, we take an indirect approach to find the disease-specific salient features from the chest x-rays. We first extract coarse-level features from the entire chest x-ray without requiring to localize the affected region. This task is performed by a coarse-learner implemented using a CNN. Subsequently, we design a novel saliency-based classifier that extracts salient features from the coarse-level features, extracted by the coarse-learner and performs classification based on the salient features. We propose a discriminative autoencoder ensemble with intrinsic weights to design the saliency-based classifier. Our design of the method adds several advantages that we discuss in Section 3.3.3. Note that during meta-training, we train only the coarse-learner whereas meta-testing involves training of the saliency-based classifier. In the next few paragraphs we describe our method in details. The proposed architecture is presented in Fig. 1.
Fig. 1:
Pipeline of the proposed method. The saliency-based classifier is composed of T autoencoders.
3.1. Coarse-learner
The coarse-learner is a module that extracts imaging modality-based features from the images of a specific body part. For example, in our application, the imaging modality is x-ray and the body part is chest. So, for this application, the coarse-learner is expected to extract the common features of chest x-rays across different diseases and conditions. However, the coarse-learner may not extract disease-specific features for all the diseases.
3.1.1. Network Architecture
To design a coarse-learner, we need a network capable of utilizing the information in medical images in the best possible way to generate a feature vector for an input image. Dense Convolutional Network (DenseNet) (Huang et al., 2017) is a network architecture that utilizes information in an effective manner through strengthening feature propagation and encouraging feature reuse. Furthermore, by allowing exhaustive connections from one layer to all of its subsequent layers, DenseNet can alleviate the vanishing gradient problem. Due to these qualities, DenseNet has been successfully used in the diagnosis of chest x-rays (Rajpurkar et al., 2017). Motivated from this success, the coarse-learner in our application is designed using 121-layer DenseNet (DenseNet-121) (Huang et al., 2017) architecture.
3.1.2. Training
We use the network design of (Rajpurkar et al., 2017) to implement the coarse-learner. The output from the penultimate layer of the network is used as the feature vector corresponding to an input x-ray image. The coarse-learner produces 1024 feature maps of dimension 7×7 in the penultimate layer. We flatten these feature maps to get the feature vector corresponding to an input image. Hence the dimension of the feature vector put out by the coarse-learner is 50176 (i.e. 7 × 7 × 1024).
To train the coarse-learner, we first initialize its weights with the weights of a DenseNet-121 model pre-trained on ImageNet (Deng et al., 2009). We further train this model to minimize the summation of weighted binary cross entropy losses (Wang et al., 2017) for multi-label and multi-class chest x-ray disease classification on the base classes. The Adam optimizer with the standard parameters (β1 = 0.9 and β2 = 0.999) (Kingma and Ba, 2014) is used for training. We use a mini-batch size of 16 and an initial learning rate of 0.001. Following the protocol of (Rajpurkar et al., 2017), the learning rate is decayed by a factor of 10 whenever the validation loss reaches a plateau after an epoch. At the end of the training, we pick the model with the lowest validation loss.
Unlike (Huang et al., 2017), we train the coarse-learner with the training data from only the meta-train set. So, training of the coarse-learner is actually the training phase of meta-training. Hence, the different class labels of the meta-test set remain unseen to the coarse-learner during training. At the time of meta-testing, we use the trained coarse-learner to extract feature vectors corresponding to the images of the meta-test set. As a result, the extracted features from the x-ray images of the meta-test set are likely to be noisy, redundant and not disease-specific. Hence, we look for a saliency-based classifier that can extract disease-specific salient features from the noisy feature vectors extracted by the coarse-learner and perform classification of the input data based on those features.
3.2. Saliency-based Classifier
Design of the saliency-based classifier is challenging due to several reasons. First, the output of the coarse-learner is high dimensional (50176 dimensions). Moreover, the coarse-learner is trained on the meta-train set. However, since at the time of meta-testing, we use the trained coarse-learner to extract feature vectors corresponding to the images of the meta-test set, the extracted features from the x-ray images of the meta-test set are likely to be noisy and redundant. Most importantly, since this is a few-shot learning problem (Wang and Yao, 2019), we have only a few training examples per class label in the meta-test set. So, the problem boils down to finding salient features from high dimensional, noisy and redundant feature vectors with a small number (typically five) of training data.
Autoencoders are generally helpful in finding salient features from input data (Hinton and Salakhutdinov, 2006) from which the input may be reconstructed. Usually, by minimization of a reconstruction loss, it is possible to force the autoencoder to generate salient features in the hidden space so that the input may be reconstructed well. However, the aforementioned simple autoencoder architecture can not effectively deal with noisy data. Hence, it is not a good solution for our problem. In order to get rid of the noise, the autoencoder training process requires certain modifications that call for a large training dataset (Lu et al., 2013) which we do not have in a few-shot learning problem like ours. Furthermore, typical autoencoders are not guaranteed to produce class-discriminative feature space in the hidden layer. We make novel modifications in the autoencoder architecture that allow the autoencoder to deal with noise and produce a discriminative feature space in the hidden layer through training with a small number of training data. Towards that goal, we consider the following facts.
Ensemble learning is a popular choice to deal with noisy features (Breiman, 2001). Each learner in the ensemble is termed as a ‘weak-learner’. We fuse the idea of ensemble learning and discriminative autoencoders (Paul et al., 2018) with novel modifications to introduce a first-of-its-kind discriminative autoencoder ensemble. Our model can produce salient and discriminative hidden feature space by training with small number of training data that may even be noisy. Nevertheless, in an ensemble learning scenario, each weak-learner (autoencoder, in our problem) in an ensemble may not be trained equally well (Paul and Mukherjee, 2019). These bad weak-learners may adversely affect the outcome of the ensemble learning. In order to handle the bad autoencoders in the proposed ensemble, we bring in the idea of assigning weights to each autoencoder based on the quality of training. We calculate the weights from an intrinsic property of each autoencoder. The weights of the autoencoders are used during inference to identify the class label of a query data through weighted voting. Before we discuss the proposed discriminative autoencoder ensemble, we first present the basics of autoencoders.
3.2.1. Autoencoders
An autoencoder (Hinton and Salakhutdinov, 2006) consists of an encoder that maps an input to a hidden feature space and a decoder that reconstructs the input from the hidden representation. The encoder may contain several linear layers of neurons. Each linear layer r may have an activation ϕr(·) following it.
Consider X to be the input to an autoencoder with linear layers of the encoder having weights W1, W2, … and so on. Then after the first linear layer and the first activation layer of the encoder, we have:
| (1) |
Similarly, after the second linear layer, we have Z2 = ϕ2(W2Z1) and so on. Eventually, at the end of the encoder, we have the hidden space representation Z corresponding to X. Considering an encoder of R layers, we have
| (2) |
The decoder operates in the opposite fashion and produces a reconstructed output corresponding to the input X. For the decoder layer r, let us assume the decoder weight to be and activation function to be . Then the reconstructed input is for a decoder with R layers is
| (3) |
The typical objective function of the autoencoder is designed to minimize the reconstruction error. The objective function of a vanilla autoencoder (Hinton and Salakhutdinov, 2006) is given by:
| (4) |
We modify the above objective function to design a discriminative autoencoder.
3.2.2. Discriminative Autoencoders
We want the hidden space representation Z to be class-discriminative. This requires modification of the objective function of (4). Let Zu and Zv be the hidden space representations of input data points Xu and Xv respectively. In order to be discriminative, Zu and Zv should be closely spaced if data points Xu and Xv belong to the same class. Otherwise, Zu and Zv should be well-separated. We use these facts to design the objective function of the discriminative autoencoder. Towards that end, we use an indicator function I(·). Let I(u, v) = 1 when data points Xu and Xv have the same class label and I(u, v) = −1, otherwise. Subsequently, we modify the objective function of (4) to design the objective function of the discriminative autoencoder
| (5) |
where λ is a pre-defined regularization constant. The term containing λ in (5) acts as a regularizer in the autoencoder objective function. Minimization of (5) forces the hidden space representations of the data from different classes to be away from each other. It also forces the representations of the data arising from the same classes to be close to each other.
The encoder in our model consists of an d′-dimensional input layer that maps the input to 1024 dimensions. Subsequent linear layers map the intermediate representations to 256, 128, 64 and 16 dimensions respectively. Each linear layer except the last layer is followed by a ReLU activation function (Krizhevsky et al., 2012). The decoder has the same number of linear layers mapping the 16 dimensional representation to 64, 128, 256, 1024 and d′ dimensions respectively. Each linear layer in the decoder except the last layer is followed by a ReLU activation as well. The last layer of the decoder is followed by a tanh activation. Next we show how to construct an ensemble of discriminative autoencoders and assign intrinsic weights to each of the autoencoders.
3.2.3. Ensemble of Weighted Discriminative Autoencoders
An ensemble consists of weak-learners which in our case are the discriminative autoencoders. According to (Breiman, 2001), when the weak-learners are trained with sufficient diversity, the probability of over-fitting reduces and the classification accuracy improves. This fact is even more important when dealing with a small training dataset like the one we have. Therefore, it is required that the individual discriminative autoencoders are trained with sufficient diversity.
There are two ways to create diversity among the weak-learners during training. One is based on the data and the other is based on the features. We exploit both of these forms to create diversity in our training of the discriminative autoencoder ensemble. Furthermore, we want to train each autoencoder in the ensemble with class-discriminative features. However, the feature vectors extracted by the coarse-learner are likely to be noisy (as described in Section 3.1.2). Our mechanism of creating diversity in terms of the features comes with an additional benefit of mining class-discriminative features from the noisy feature vectors for training the autoencoders.
Assume that X is composed of N number of feature vectors from the coarse-learner. X is the input to the discriminative autoencoder ensemble. Let the ensemble be composed of T autoencoders. The training data for the ith (i ∈ 1,2, …, T) discriminative autoencoder is created through the following steps:
I. Generation of Bootstrap Sample:
We want the training data for each autoencoder to be different from each other. To achieve this, we create bootstrap samples by randomly choosing N′ training feature vectors (with replacement) from the pool of the N number of training feature vectors. Let Bi be the bootstrap sample for the ith autoencoder. We prepare the training data for the ith autoencoder using Bi.
II. Feature Selection:
We employ a two-step quasi-random mechanism to bring in diversity in the features with which each autoencoder is trained. Assume that the dimension of each input feature vector in X is d. For the ith autoencoder, we first choose M number of random d′-dimensional feature subspaces. Then we select the best out of those subspaces. The best subspace is selected based on how well the data of different class labels are separated in the subspace. The details of the method for finding the best subspace are presented in Appendix A. Thus the mechanism for selecting the best subspace helps to train each autoencoder with class-discriminative features from the noisy feature vectors extracted by the coarse-learner. Since the subspace selection process involves some degree of randomness, the best subspaces chosen for different autoencoders are likely to be different. Let the best subspace for the ith autoencoder is found to be S*(i). We prepare the training data for the ith autoencoder using S*(i).
III. Preparation of the Training Data:
We project the bootstrap sample Bi into the best (out of M) subspace S*(i). Let this projection be . We use to train autoencoder i. The randomness involved in the process of generating bootstrap samples and choosing the best subspaces causes diversity in training. Due to the use of the best subspace, is expected to contain class-discriminative information. This separation is further enhanced by the discriminative autoencoder i in its hidden space representation. Thus, our method to create diversity in training the autoencoders also helps to create more class-discriminative hidden space representations.
3.2.4. Training the Ensemble
For each discriminative autoencoder in the ensemble, we create the training data following steps I, II and III. During feature selection for each discriminative autoencoder, we select the best subspace out of M = 20 random subspaces of dimension d′ = 40000 from the feature space of dimension d = 50176. We minimize the objective function of (5) through back-propagation to train each autoencoder in the ensemble. Autoencoders are trained using the Adam optimizer (Kingma and Ba, 2014) with a mini batch size of 16 and a learning rate of 0.001. The regularization constant λ is set to 0.001. An advantage of using the discriminative autoencoders is that the autoencoders are trained fast and can produce a salient discriminative hidden space representation in as few as fifteen epochs.
Due to the process of preparing the training data, each autoencoder (‘weak-learner’) is trained effectively with different training data leading to diversity among the trained autoencoders. It also makes each autoencoder explore feature subspaces that are likely to be different for different autoencoders. Furthermore, the use of the best subspace helps us to get rid of the noisy features to a great extent. All these factors lead to better classification by the ensemble. The training data for each autoencoder can be prepared independently. Therefore, each autoencoder can be trained independently as well. As a result, the time required to train the ensemble is the same as the time required to train one autoencoder. Furthermore, assume the time complexity of training one autoencoder to be O(f(N′)), where N′ is the number of data points in the bootstrap sample for training an autoencoder. Therefore, the time complexity of training an ensemble of T autoencoders is O(T f(N′)) = O(f(N′)), since T is a constant. Thus, the time complexity of training the ensemble is the same as the time complexity of training one autoencoder. Once the ensemble is trained, we assign weights to individual autoencoders based on the test data. Hence the weight is dynamic in nature w.r.t. the test data. Note that we do not need to know the ground truth class labels of the test data to assign the weights to the autoencoders.
3.2.5. Assigning Weights to the Autoencoders
Due to the random nature of the input to the autoencoders, all the autoencoders are not exposed to the same data points or same feature subspaces. For example, some of the autoencoders are trained with a balanced (w.r.t. class labels) dataset while some others may be trained with a skewed one. The subspace that an autoencoder explores might not be as discriminative as the subspaces explored by other autoencoders. Hence, each of the autoencoders is not expected to be trained equally well. We assign an importance weight to each of the autoencoders based on the quality of the training. The formulation of the weight is derived from an intrinsic property of the autoencoder.
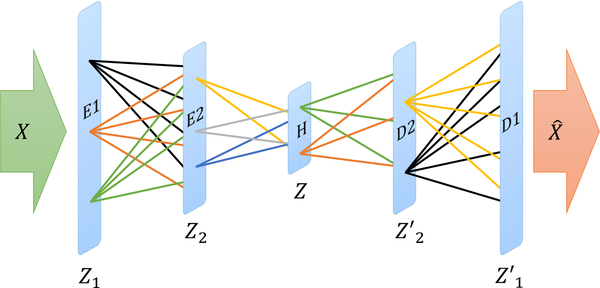
Consider an autoencoder with input X and output (reconstructed input) . As an example, let there be two encoder layers E1 and E2, hidden layer H and two decoder layers D1 and D2 as presented in Fig. 2. The outputs of layers E1, E2, H, D2, and D1 are Z1, Z2, Z, Z′2, and Z′1 respectively. Let there be C different class labels in the training data X. The projection of the training data X in the hidden layer H is Z. Assume Z(c) to be the projection corresponding to the training data of class label c. Let be the center of the projection. Similarly, we can find the center of the projections for all the other class labels. We can also find the center of the projections for different class labels at layers E1, E2, D2 and D1. Let the centers of the projections for class label c at layers E1, E2, D2 and D1 be , , , and respectively. For an autoencoder with R encoding layers and R decoding layers, the centers of the projections would be , , and respectively.
Fig. 2:
Different layers of a sample autoencoder and the outputs. The input to the autoencoder is X and the output (reconstructed input) is . Encoder layers E1 and E2 the corresponding outputs are Z1, Z2. The output of the hidden layer H is Z. There are two decoder layers D2 and D1 with corresponding outputs Z′2 and Z′1 and respectively.
Now consider a test data point Xtest at the input of the autoencoder i. Let the projections of Xtest at layers E2 and D2 be , and respectively. Also, let the projection of Xtest at the hidden layer H be Ztest. Now we analyze the center of the projections corresponding to different class labels. Let the center of the projection closest to Ztest correspond to class label ch. So, from the hidden space representation Ztest, we may infer that the test data belongs to class label ch. Similarly, let the center of the projections closest to correspond to class label c2 and the center of the projections closest to correspond to class label . Recall that and are the projections of the test data at the layer before and after the hidden layer respectively. If the autoencoder is well-trained, each layer of the autoencoder is expected to contain some class-discriminative information about the test data. Therefore, we can expect to obtain the same class label for a test data if the projections of the test data at different layers (especially at the hidden layer and the layers close to the hidden layer) are used for classification of the test data. Thus, the better the autoencoder is trained, the more identical the class labels (obtained from the projections of the test data at different layers) are. Hence, after a good training of autoencoder i, we should get . More generally, for an autoencoder with R number of encoder and decoder layers, if we consider k number of encoder layers and k number of decoder layers close to the hidden layer, a good training should yield
| (6) |
Based on this fact, we formulate the weight of each individual autoencoder. Let the number of test data be Ntest. Out of these, assume that N(i) number of test data satisfies (6). Then the weight of the ith (i ∈ 1,2, …, T) discriminative autoencoder is computed as
| (7) |
The weight of a discriminative autoencoder (β(i) ∈ [0, 1]) indicates the consistency of the different layers of a discriminative autoencoder in inferring the class labels of the test data points. Since the weights of the individual autoencoders are dependent on the test data, the weights are dynamic w.r.t. the test data. We use the weights of the individual autoencoders during the inference in few-shot learning as described next.
3.3. Few-shot Learning
Most of the existing few-shot learning techniques require training the entire process pipeline during training phases of meta-training and meta-testing. This incurs substantial overhead when one tries to include new class labels in the meta-test set. We propose a novel scheme where the training phases of neither meta-training nor meta-testing require training the entire pipeline. Instead, we need to train only a specific portion of the pipeline during the training phases of meta-training and meta-testing. In fact, the training phases of meta-training and meta-testing are architecturally disjoint in our method. This makes the training processes faster and adding new class labels in the meta-test set easier. Next we discuss how to perform meta-training and meta-testing in our model.
3.3.1. Meta-training
We train only the coarse-learner during meta-training. We use the meta-train set to train the coarse-learner in an end-to-end fashion. Hence, the training of the coarse-learner is not dependent on the saliency-based classifier by any means. We perform meta-training following the protocol of Section 3.1.2 and use the validation set of the meta-train set to find the best meta-training (coarse-learner) model.
3.3.2. Meta-testing
The training phase of meta-testing involves training the saliency-based classifier. For this, we first extract the feature vectors corresponding to the training images of the meta-test set. We train the saliency-based classifier with these features vectors as described in Section 3.2.4. Each discriminative autoencoder inside the saliency-based classifier is trained during the above training process. The training is performed with T = 15 autoencoders considering k = 1, i.e., one encoder layer before the hidden layer and one decoder layer after the hidden layer for computing the weights of the autoencoders. Consider the ith (i ∈ 1,2, …, T) discriminative autoencoder. At the end of the training, we obtain the centers of projections in the different layers of the autoencoder i for each class label in the meta-test set. Let the center of projection at the hidden layer for meta-test class label c be . Once the training phase of meta-testing is complete, we obtain the weights of individual autoencoders using (7).
To test the performance of the proposed method, we use the test images of the meta-test set. First, the feature vector corresponding to a test image Imtest is extracted by a coarse-learner. Let this feature vector be Xtest. When we apply Xtest to the autoencoder i of the saliency-based classifier, we get the projection Ztest at the hidden layer. The class label corresponding to the nearest center of projection is assigned to the test image Imtest by autoencoder i. Therefore, the class label assigned to Imtest by autoencoder i is:
| (8) |
In this way, each autoencoder in the ensemble assigns a class label to the input test image Imtest. Let β(i) be the weight of autoencoder i. Then the final output class label, determined by our method is obtained by taking weighted votes from individual autoencoders in the ensemble. The total weighted vote for class label c is:
| (9) |
Consequently, we compute the final output class label by the proposed method to be the class label with the highest vote. Therefore, the output class label for Imtest using the proposed method is :
| (10) |
A pictorial representation of the meta-training and the meta-testing phases are presented in Fig. 3.
Fig. 3:
Pictorial representation of meta-training and meta-testing in our model. The block with the red dotted line is the block that is trained in a particular phase. A block with a green dotted line indicates a block that is already trained.
3.3.3. Comments on Few-shot Learning
Training (or even fine-tuning) the coarse-learner adds substantial computational overhead due to the very deep architecture of the coarse-learner. Whereas, training the saliency-based classifier is relatively simple due to the shallower structures of the autoencoders and also since the ensemble can be trained in parallel fashion. Now, suppose we try to include new class labels in the meta-test set. Then we do not need to train the coarse-learner afresh (or do a fine-tuning) as long as the images of the new class labels are of same modality as that of the meta-train set. The coarse-learner extracts somewhat noisy features from the images of the new labels. We use these feature vectors to train only the saliency-based classifier. This makes the process of incorporating new meta-test labels faster.
Furthermore, the characteristics that depend on the imaging modality (such as x-ray) is taken care of by the coarse-learner. However, to design the saliency-based classifier, we do not make any assumptions, specific to the imaging modality. As a result, if we want to use our model for the images from a different modality, we need to change the architecture of just the coarse-learner. This potentially makes our model portable across different modalities without requiring to change the architecture of the saliency-based classifier. However, note that with the change of imaging modalities, both the coarse-learner and the saliency-based classifier needs to be retrained.
4. Experiments & Results
4.1. Dataset
In medical imaging applications, robustness of a method across different datasets is a major concern. Towards this end, we perform experiments on chest x-ray datasets from two different sources: the NIH chest x-ray dataset (Wang et al., 2017) and the Open-i dataset (Demner-Fushman et al., 2015) (frontal images). Note that we use only the NIH dataset (Wang et al., 2017) for training during meta-training and meta-testing phases. The test phase of meta-testing is performed on the test datasets from the above two sources (NIH and Open-i). Therefore, the results on the Open-i dataset also show the applicability of our training in the diagnosis of chest x-rays from a different source.
The disease labels corresponding to the above chest x-ray images are extracted using a rule-based natural language processing method from the x-ray reports (Wang et al., 2017). Any word or phrase that falls outside the scope of the rules may therefore lead to incorrect disease labels. Hence, our results indicate the usefulness of the proposed method in datasets with noisy labels.
Our datasets contain x-ray images corresponding to 14 thorax diseases/conditions. The diseases/conditions are atelectasis, consolidation, infiltration, pneumothorax, fibrosis, effusion, pneumonia, pleural thickening, nodule, mass, hernia, edema, emphysema, and cardiomegaly. If none of these diseases are present in an x-ray, we assign a label ‘no finding’ to that x-ray. Out of these 15 classes (14 disease classes+no finding), we randomly choose 12 classes without replacement to be the base classes and the remaining 3 classes to be the novel classes. We construct the meta-train set and the meta-test set for meta-training and meta-testing respectively.
The datasets that we use are multi-label datasets where each x-ray may have multiple disease labels. While constructing the meta-train set, we make sure that each data point in the meta-train set has all the labels from the base classes only. This ensures that the meta-train set does not contain any information of the novel classes. On the other hand, few-shot learning requires the meta-test set to be composed of data points from novel classes (Wang and Yao, 2019). Therefore, each x-ray image in the meta-test set must contain at least one of the novel classes as its label. That particular novel class is treated as the label for the corresponding x-ray image of the meta-test set. If there is more than one novel class associated with an x-ray image of the meta-test set, we randomly choose one of those classes as the label for the corresponding x-ray image. Thus, the meta-train set contains x-rays with only the base classes while the meta-test set consists of x-rays with only the novel classes.
The training during meta-testing is performed with five x-ray images corresponding to each of the novel classes in accordance with the requirements of few-shot learning (Wang and Yao, 2019). The training data for meta-testing is chosen randomly from (Wang et al., 2017) such that the training data and the test data for the novel classes in the NIH dataset never overlap. For our experiments on the Open-i dataset, the training phase of meta-training and the training phase of meta-testing are performed using the NIH dataset while the test phase of meta-testing is performed on the Open-i dataset. Recall that the training phase of meta-training involves training the coarse-learner and the training phase of meta-testing involves training the saliency-based classifier. Therefore, we can say that for our experiment on Open-i dataset, we train the coarse-learner and the saliency-based classifier with the NIH dataset while the Open-i dataset is used to perform the test phase of meta-testing.
We have 15 different classes in our dataset and we randomly select (without replacement) 3 disease classes as novel classes at a time for our experiments. Hence we try five different combinations of the base classes and the novel classes. The combinations are presented in Table 1. Since we choose the novel classes (and hence the base classes also) without replacement, the novel classes chosen at each of the five combinations do not overlap. Consequently, the union of all novel classes in Table 1 becomes the full set of labels. The number of test data points corresponding to different novel classes in the NIH and the Open-i datasets are also indicated in this table. We randomly select the training data from the NIH dataset for training the saliency-based classifier. To look into the effect of this randomness in training data selection, we repeat our experiments five times and calculate mean and standard deviation of different performance measures.
Table 1:
Combinations of the novel and the base classes (with the number of test data points for different novel classes in the NIH, the Open-i datasets)
| Novel Classes (#test data points in NIH, Open-i) | Base Classes |
|---|---|
| Fibrosis (308, 9), Hernia (61, 34), Pneumonia (85, 26) | Atelectasis, Consolidation, Infiltration, Pneumothorax, Effusion, Pleural Thickening, Nodule, Mass, Edema, Emphysema, Cardiomegaly, No Finding |
| Mass (723, 11), Nodule (575, 82), Pleural Thickening (344, 15) | Atelectasis, Consolidation, Infiltration, Pneumothorax, Fibrosis, Effusion, Pneumonia, Hernia, Edema, Emphysema, Cardiomegaly, No Finding |
| Cardiomegaly (884, 262), Edema (735, 5), Emphysema (760, 80) | Atelectasis, Consolidation, Infiltration, Pneumothorax, Fibrosis, Effusion, Pneumonia, Pleural Thickening, Nodule, Mass, Hernia, No Finding |
| Consolidation (1270, 3), Effusion (2674, 44), Pneumothorax (954, 7) | Atelectasis, Infiltration, Fibrosis, Pneumonia, Pleural Thickening, Nodule, Mass, Hernia, Edema, Emphysema, Cardiomegaly, No Finding |
| Atelectasis (3260, 257), Infiltration (3032, 22), No Finding (9856, 2858) | Consolidation, Pneumothorax, Fibrosis, Effusion, Pneumonia, Pleural Thickening, Nodule, Mass, Hernia, Edema, Emphysema, Cardiomegaly |
4.2. Performance Measures & Comparisons
4.2.1. Performance Measures
The performance of our method is evaluated through recall, precision and F1 score for different diseases in novel classes. As presented in Table 1, we have five different combinations of novel classes. We evaluate the performance of different methods on each combination separately.
4.2.2. Competing Methods
There is no existing baseline in the literature for few-shot chest x-ray diagnosis. So, we set the baseline method. Consider a combination of the base and the novel classes from Table 1. Towards setting the baseline, we extract feature vectors corresponding to the training data of the meta-test set (i.e. the training data from each of the novel classes) using our coarse-learner. Subsequently, we find the cluster centers from the above training feature vectors corresponding to each novel class. At test time, we extract the feature vectors for the test data from the novel classes with the help of the coarse-learner. The class label corresponding to the nearest cluster center is assigned to each test data. These class labels are considered for evaluating the baseline performance. Therefore, the baseline method is same as the proposed method excluding the saliency-based classifier. However, the baseline method uses all the features extracted by the coarse-learner whereas the proposed method uses the benefit of feature selection. Therefore, we set a stronger baseline, denoted as Baseline+ that uses the advantage of feature selection. The Baseline+ method is same as the proposed method except the fact that we use vanilla autoencoder (with the loss function of (4)) instead of the proposed discriminative autoencoder to design the saliency-based classifier. Hence, the performance of the Baseline+ method also helps to look into the roles of discriminative autoencoders.
Since we design an ensemble based few-shot learning technique, we compare the performance of the proposed method with other ensemble based approaches. In particular, we compare with random forest (Breiman, 2001) (RF), AdaBoost (Freund and Schapire, 1997) (Ada), and ExtraTree (Geurts et al., 2006) (ET). We also compare with support vector machine (Boser et al., 1992) (SVM). Finally, we perform comparisions with several state-of-the-art few-shot learning methods. These methods include recent techniques such as MetaOptNet (Lee et al., 2019) (with SVM base learner) and ANIL (Raghu et al., 2020), and well-known few-shot learning techniques such as MAML (Finn et al., 2017) and ProtoNet (Snell et al., 2017). For all of the aforementioned competing methods, the meta-training phase remains the same as that of the proposed method. The coarse-learner is trained during meta-training. At the time of meta-testing, each of the above models is trained with the training feature vectors corresponding to the different novel classes extracted by the coarse-learner. We train each of the competing methods with only five training examples from each of the novel classes. The performance of the competing methods are evaluated through recall, precision and F1 score on different novel classes.
4.2.3. Performance Analysis
The performances of different methods for different combinations of base and novel classes in the NIH dataset are presented through Table 2 to Table 6. The best value in each column is the one with the lowest standard deviation among the values with the highest mean. Notice that for most of the disease classes, the proposed method outperforms the competitors by a significant margin in terms of the F1 score. The superiority of the proposed method over state-of-the-art few-shot learning techniques such as MAML, ProtoNet, MetaOptNet, and ANIL shows the utility of our design for few-shot chest x-ray diagnosis. We also have noticeable improvement compared to the baseline and Baseline+ in most cases. This shows the efficacy of the proposed method in few-shot diagnosis of chest radiographs. The superiority of the proposed method compared to the Baseline+ method indicates the improvement due to the use of the discriminative autoencoders (used in the proposed method) instead of the vanilla autoencoders (used in Baseline+). However, it can be observed that for diseases like hernia and effusion, our method does not obtain the best results. In the following paragraphs we analyze the possible reasons.
Table 2:
Performances of different methods for fibrosis, hernia and pneumonia as novel classes in the NIH dataset.
| Method | Fibrosis | Hernia | Pneumonia | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | F1 Score | Recall | Precision | F1 Score | |
| Ada | 0.50±0.09 | 0.73±0.03 | 0.59±0.06 | 0.49±0.12 | 0.21±0.03 | 0.28±0.04 | 0.44±0.07 | 0.25±0.04 | 0.32±0.03 |
| ET | 0.08±0.02 | 0.91±0.07 | 0.14±0.03 | 0.18±0.04 | 0.52±0.11 | 0.26±0.03 | 0.11±0.02 | 0.72±0.20 | 0.19±0.03 |
| RF | 0.03±0.01 | 0.82±0.04 | 0.06±0.02 | 0.04±0.01 | 0.54±0.27 | 0.08± 0.02 | 0.10±0.07 | 0.54±0.14 | 0.16±0.09 |
| SVM | 0.16±0.17 | 0.73±0.07 | 0.22±0.18 | 0.07±0.05 | 0.18±0.07 | 0.09±0.05 | 0.07±0.06 | 0.19±0.10 | 0.09±0.07 |
| MAML | 0.48±0.06 | 0.72±0.06 | 0.57±0.05 | 0.74±0.11 | 0.18±0.0l | 0.29±0.01 | 0.59±0.08 | 0.36±0.04 | 0.45±0.02 |
| ProtoNet | 0.49±0.12 | 0.68±0.07 | 0.56±0.08 | 0.50±0.18 | 0.14±0.02 | 0.21±0.02 | 0.69±0.06 | 0.28±0.05 | 0.39±0.04 |
| MetaOptNet | 0.28±0.06 | 0.74±0.03 | 0.41±0.06 | 0.20±0.11 | 0.13±0.01 | 0.15±0.03 | 0.22±0.06 | 0.29±0.11 | 0.23±0.02 |
| ANIL | 0.47±0.09 | 0.71±0.06 | 0.56±0.07 | 0.63±0.09 | 0.17±0.02 | 0.27±0.03 | 0.65±0.12 | 0.28±0.07 | 0.38±0.06 |
| Baseline | 0.39±0.06 | 0.80±0.03 | 0.52±0.05 | 0.56±0.02 | 0.37± 0.05 | 0.45±0.04 | 0.42±0.05 | 0.43±0.06 | 0.42±0.04 |
| Baseline+ | 0.54±0.08 | 0.77±0.03 | 0.63±0.06 | 0.58±0.12 | 0.26±0.04 | 0.35±0.04 | 0.55±0.05 | 0.38±0.03 | 0.45±0.03 |
| Proposed | 0.55±0.08 | 0.76±0.03 | 0.63±0.04 | 0.47 ±0.11 | 0.35±0.07 | 0.38±0.02 | 0.55±0.03 | 0.44±0.03 | 0.49±0.02 |
Bold fonts indicate the best values in each column.
Table 6:
Performances of different methods for atelectasis, infiltration and no finding as novel classes in the NIH dataset.
| Method | Atelectasis | Infiltration | No Finding | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | F1 Score | Recall | Precision | F1 Score | |
| Ada | 0.44±0.08 | 0.21±0.01 | 0.28±0.02 | 0.39±0.05 | 0.21±0.03 | 0.27±0.01 | 0.48±0.07 | 0.64±0.01 | 0.54±0.05 |
| ET | 0.03±0.01 | 0.33±0.08 | 0.06±0.02 | 0.02±0.00 | 0.26±0.04 | 0.04±0.00 | 0.11±0.14 | 0.74±0.06 | 0.16±0.18 |
| RF | 0.02±0.01 | 0.28±0.05 | 0.03±0.02 | 0.02±0.01 | 0.31±0.07 | 0.03±0.02 | 0.04±0.03 | 0.74±0.08 | 0.08±0.05 |
| SVM | 0.15±0.11 | 0.21±0.01 | 0.16±0.07 | 0.07±0.05 | 0.19±0.03 | 0.09±0.04 | 0.02±0.02 | 0.63±0.03 | 0.05±0.03 |
| MAML | 0.52±0.04 | 0.22±0.02 | 0.31±0.03 | 0.52±0.13 | 0.21±0.04 | 0.30±0.06 | 0.50±0.04 | 0.66±0.07 | 0.57±0.05 |
| ProtoNet | 0.46±0.23 | 0.20±0.01 | 0.27±0.06 | 0.51±0.24 | 0.19±0.04 | 0.28±0.08 | 0.38±0.16 | 0.65±0.07 | 0.45±0.10 |
| MetaOptNet | 0.29±0.06 | 0.20±0.01 | 0.24±0.03 | 0.22±0.07 | 0.20±0.04 | 0.20±0.03 | 0.13±0.12 | 0.61±0.06 | 0.18±0.13 |
| ANIL | 0.50±0.03 | 0.19±0.02 | 0.27±0.02 | 0.50±0.13 | 0.21±0.06 | 0.29±0.07 | 0.41±0.08 | 0.64±0.08 | 0.50±0.08 |
| Baseline | 0.20±0.05 | 0.29±0.02 | 0.23±0.04 | 0.32±0.04 | 0.26±0.03 | 0.29±0.02 | 0.31±0.05 | 0.72±0.03 | 0.43±0.05 |
| Baseline+ | 0.39±0.07 | 0.25±0.01 | 0.30±0.02 | 0.53±0.05 | 0.26±0.01 | 0.35±0.02 | 0.52±0.04 | 0.71±0.02 | 0.60±0.02 |
| Proposed | 0.45±0.08 | 0.27±0.02 | 0.33±0.02 | 0.49±0.11 | 0.27±0.02 | 0.34±0.01 | 0.56±0.05 | 0.71±0.01 | 0.62±0.02 |
Bold fonts indicate the best values in each column.
There are a number of causes of pleural effusion that also cause lung consolidation. So, it is possible that one may have effusion and consolidation at the same time. Consequently, during the training at meta-testing phase, the saliency-based classifier may be trained with x-ray images that contains both effusion and consolidation. Since our method deals with only one label for an x-ray image, the saliency-based classifier either learns the characteristics of effusion or consolidation (but not both) from such x-ray images. This learning causes confusion at the test time of meta-testing phase resulting in poor classification performance. Similar values of F1 scores for consolidation and effusion (see Table 5) support the above claim.
Table 5:
Performances of different methods for consolidation, effusion and pneumothorax as novel classes in the NIH dataset.
| Method | Consolidation | Effusion | Pneumothorax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | F1 Score | Recall | Precision | F1 Score | |
| Ada | 0.44±0.06 | 0.27±0.01 | 0.33±0.02 | 0.46±0.05 | 0.55±0.02 | 0.50±0.03 | 0.34±0.06 | 0.25±0.04 | 0.28±0.01 |
| ET | 0.03±0.02 | 0.44±0.07 | 0.06±0.03 | 0.05±0.03 | 0.63±0.06 | 0.09±0.05 | 0.10±0.05 | 0.37±0.04 | 0.15±0.06 |
| RF | 0.05±0.03 | 0.41±0.06 | 0.09±0.05 | 0.01±0.01 | 0.61±0.07 | 0.03±0.02 | 0.06±0.04 | 0.45±0.24 | 0.10±0.05 |
| SVM | 0.06±0.03 | 0.26±0.06 | 0.09±0.05 | 0.06±0.08 | 0.54±0.07 | 0.09±0.12 | 0.11±0.07 | 0.20±0.03 | 0.12±0.06 |
| MAML | 0.64±0.11 | 0.33±0.01 | 0.44±0.02 | 0.37±0.06 | 0.57±0.01 | 0.44±0.04 | 0.56±0.08 | 0.29±0.01 | 0.38±0.00 |
| ProtoNet | 0.54±0.31 | 0.24±0.06 | 0.32±0.13 | 0.34±0.21 | 0.57±0.02 | 0.39±0.13 | 0.53±0.18 | 0.21±0.06 | 0.29±0.05 |
| MetaOptNet | 0.21±0.05 | 0.27±0.04 | 0.23±0.05 | 0.25±0.06 | 0.54±0.01 | 0.34±0.05 | 0.37±0.27 | 0.24±0.04 | 0.25±0.10 |
| ANIL | 0.63±0.09 | 0.34±0.00 | 0.44±0.02 | 0.43±0.04 | 0.54±0.01 | 0.48±0.03 | 0.61±0.10 | 0.28±0.02 | 0.38±0.01 |
| Baseline | 0.36±0.13 | 0.37±0.02 | 0.35±0.06 | 0.23±0.05 | 0.56±0.04 | 0.32±0.04 | 0.44±0.04 | 0.30±0.01 | 0.36±0.02 |
| Baseline+ | 0.62±0.03 | 0.34±0.01 | 0.44±0.01 | 0.36±0.10 | 0.55±0.01 | 0.43±0.07 | 0.56±0.06 | 0.30±0.01 | 0.39±0.01 |
| Proposed | 0.63±0.10 | 0.34±0.01 | 0.44±0.02 | 0.41±0.03 | 0.56±0.01 | 0.47±0.03 | 0.69±0.03 | 0.29±0.01 | 0.40±0.01 |
Bold fonts indicate the best values in each column.
In many occasions, a small hiatal hernia may appear as a gas-filled structure in the chest cavity. This often makes visual detection of hernias from chest x-rays a challenging task. Also, as evident from Table 1, hernia has the smallest number of test data points in the NIH dataset. As a result, only a few mis-classified data points may affect especially the precision. This is likely to be the cause of the inferior performance of the proposed method for hernia.
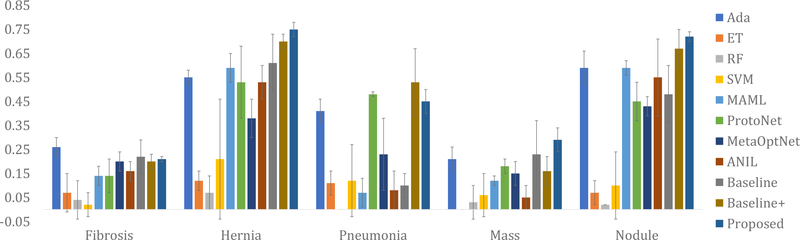
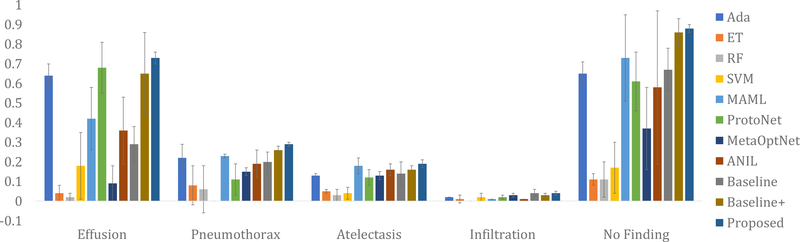
When it comes to datasets from different sources, our method is still found to be superior compared to its competitors. The results of different methods on the Open-i dataset are presented in Fig. 4, Fig. 5, and Fig. 6. For experiments on the Open-i dataset, we plot the mean and the standard deviation of F1 scores over five runs for different novel classes. Notice that for most of the diseases and conditions, our method outperforms the competing methods by a significant margin. The exception occurs in case of fibrosis where we have only 9 test data. Even a small number of mis-classifications significantly affects the performance when the number of test data is so small. This is the most probable cause behind our poor performance for fibrosis in case of the Open-i dataset. We have also evaluated the area under the ROC curve (AUROC) for different diseases and conditions in the NIH and the Open-i datasets using different methods. The AUROC using the proposed method ranges from 0.55 to 0.79 for different diseases and conditions (see the supplementary material for the details of AUROC values using different methods). The comparative standing of different methods in terms of AUROC almost identically follows that in terms of F1 Scores.
Fig. 4:
Comparative performances of different methods on the Open-i dataset in terms of the mean and standard deviation (presented through error bars) of F1 scores over five runs for fibrosis, hernia, pneumonia, mass, and nodule.
Fig. 5:
Comparative performances of different methods on the Open-i dataset in terms of the mean and standard deviation (presented through error bars) of F1 scores over five runs for pleural thickening, cardiomegaly, edema, emphysema, and consolidation.
Fig. 6:
Comparative performances of different methods on the Open-i dataset in terms of the mean and standard deviation (presented through error bars) of F1 scores over five runs for effusion, pneumothorax, atelectasis, infiltration, and no finding.
As discussed in Section 2, in recent years, several methods have been successfully applied for automated diagnosis of chest radiographs. However, only a few of them report the F1 scores. In (Rajpurkar et al., 2017), an F1 score of 0.435 has been reported for diagnosis of pneumonia in the NIH dataset. F1 scores for diagnosis of different diseases in the NIH dataset have been reported in (Rajpurkar et al., 2018) as well. The F1 scores for atelectasis, cardiomegaly, consolidation, edema, effusion, emphysema, fibrosis, hernia, infiltration, mass, nodule, pleural thickening, pneumonia, and pneumothorax are 0.512, 0.47, 0.656, 0.672, 0.728, 0.125, 0.243, 0.374, 0.33, 0.662, 0.632, 0.52, 0.477, and 0.635 respectively. Recall that none of the above methods are few-shot learning methods and all of them are trained with a large number of training images for each disease category. In contrast, our method is trained with only five images for each novel class. Furthermore, the experimental setups of the above methods are different from that of ours. Nevertheless, from Table 2 to Table 6, notice that our method, in spite of being a few-shot learning method, has values of F1 scores that are comparable with those of (Rajpurkar et al., 2017) and (Rajpurkar et al., 2018) for different diseases. In fact, for diseases like pneumonia, emphysema, fibrosis, hernia, and infiltration the values of F1 scores obtained by the proposed method are higher than those of (Rajpurkar et al., 2017) and (Rajpurkar et al., 2018). Although this is not a direct comparison of the performances, the values of the F1 scores obtained using the proposed method indicates the potential of our technique in few-shot chest x-ray diagnosis.
4.3. Ablation Studies
We perform ablation studies to evaluate the role of different components in the proposed architecture. First, we look into the importance of the ensemble in comparison with a single autoencoder. Then we evaluate the role of assigning weights to individual autoencoders.
4.3.1. Importance of the Ensemble
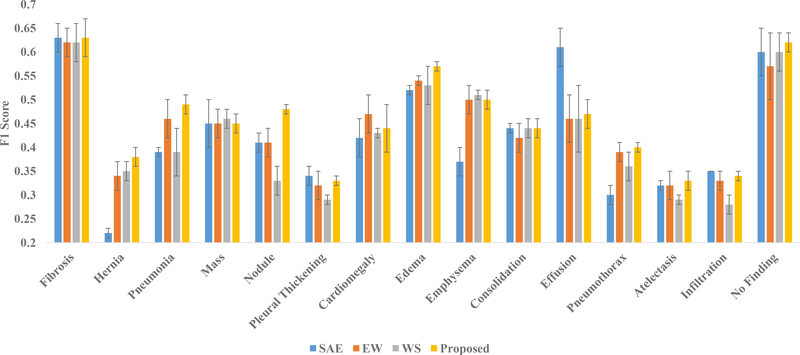
In order to evaluate the importance of the ensemble, we construct the saliency-based classifier with only a single discriminative autoencoder instead of T number of discriminative autoencoders. The autoencoder takes the 50176-dimensional feature vectors put out by the coarse-learner as input for few-shot classification. The training procedure of the saliency-based classifier remains exactly the same as that of the proposed method. This technique with a single autoencoder is abbreviated as SAE. The results of using SAE on the NIH and the Open-i datasets are presented in Fig. 7 and Fig. 8 respectively. Notice that for both of these datasets, our method outperforms SAE by a significant margin for most of the novel classes. This demonstrates the utility of the proposed ensemble for good classification.
Fig. 7:
Results of ablation studies with single autoencoder (SAE), autoencoders with equal weights (EW) and without feature selection (WS) alongside the proposed method for NIH dataset in terms of the mean and standard deviation (presented through error bars) of F1 scores over five runs.
Fig. 8:
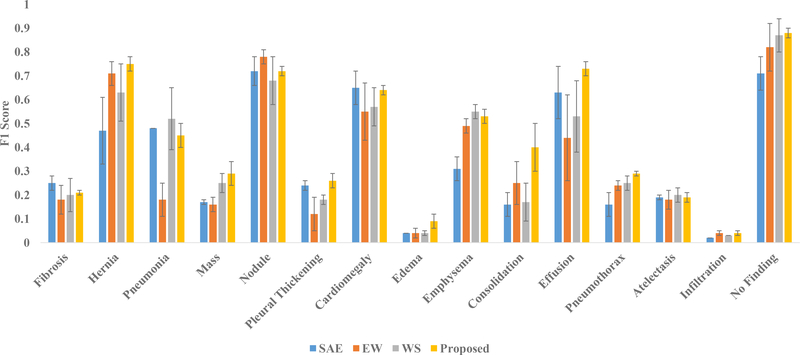
Results of ablation studies with single autoencoder (SAE), autoencoders with equal weights (EW) and without feature selection (WS) alongside the proposed method for the Open-i dataset in terms of the mean and standard deviation (presented through error bars) of F1 scores over five runs.
The results for the Open-i dataset are especially interesting. Recall that for testing on the Open-i dataset, we train our coarse-learner and saliency-based classifier using the NIH dataset. From Fig. 7, it can be observed that for effusion in the NIH dataset, SAE obtains a far better result compared to the proposed method. However, when it comes to the Open-i dataset where the test data is from a different source than that of the training data, our method outperforms SAE for effusion. In case of the Open-i dataset, the proposed method obtains better or comparable performances for all the novel classes. Therefore, we conclude that the proposed ensemble helps in generalization across datasets.
4.3.2. Role of Autoencoder Weights
We have introduced weights for the autoencoders in Section 3.2.5. The output class label of a query x-ray images is computed in the proposed method through weighted voting, as explained in (9) and (10). In order to look into the role of the autoencoder weights in finding the class label, we run our method assigning equal weights to each of the autoencoders. This technique is abbreviated as EW. We present the results with EW alongside the proposed method for the NIH and the Open-i dataset in Fig. 7 and Fig. 8 respectively.
Notice that the proposed method outperforms EW for most of the novel classes in both the datasets. From the results, especially on the Open-i dataset, it can be observed that for diseases like pneumonia and consolidation, our method performs significantly better compared to EW. Also in case of infiltration, we achieve results that are comparable with the results using EW. These facts are of significant importance because consolidation, infiltration and pneumonia often cause similar lung opacity in chest x-rays making it difficult to find visually distinguishable features. The use of the autoencoder weights in our method tend to assign more importance to the autoencoders that learns the visual discrimination among the different classes in a better way. As a result, our method successfully handles the problem of visual similarity among the above diseases/conditions through the use of autoencoder weights. However, in case of the EW method, each autoencoder is assigned equal weight that results in failure to distinguish between visually similar diseases/conditions. This fact is evident from the results on consolidation, infiltration and pneumonia from Fig. 7 and 8. Hence, we conclude that use of autoencoder weights helps the proposed ensemble in discriminating between the visually similar classes.
4.3.3. Role of Feature Selection
While training the autoencoder ensemble, we have performed feature selection as described in in Section 3.2.3. Each autoencoder has been trained with a feature subspace chosen in a quasi-random manner. We analyze the role of feature selection in the performance of the ensemble through the following ablation study. We train each autoencoder of the ensemble using the entire d-dimensional feature space instead of the d′-dimensional subspace. Therefore, each autoencoder is trained with the same set of features. This technique is abbreviated as WS (WS stands for Without Selection of feature subspace). The results of WS alongside the result of the proposed method for the NIH and the Open-i dataset are presented in Fig. 7 and Fig. 8 respectively.
From the figures, it can be observed that for most of the novel classes, the proposed method yields better performance compared to WS. This indicates that feature selection plays an important role in the performance of the ensemble. There are two main reasons behind the improved performance due to feature selection in the proposed method. First, the proposed feature selection method is quasi-random that increases diversity among the autoencoders in training. Performance of an ensemble improves with this diversity (Breiman, 2001). Second, the feature vectors extracted by the coarse-learner are likely to be noisy (see Section 3.1.2). The feature selection helps us to choose class-discriminative feature subspaces from the noisy features which eventually leads to better training. However, for the ablation study WS, since there is no feature selection, the autoencoders in the ensemble are trained with noisy features resulting in inferior training. Therefore, we conclude that feature selection helps to improve the performance of the proposed method.
4.3.4. The Number of Autoencoders in the Saliency-based Classifier
We analyze the effect of the number of autoencoders in the performance of the saliency-based classifier. For this, we run the proposed method with different number of autoencoders in the saliency-based classifier. In particular, we take 5, 10, 20, and 25 autoencoders to evaluate the results. Recall that, we have already reported the performance of our method with 15 autoencoders in the ensemble. Therefore, we now have the performance of the proposed method with 5, 10, 15, 20, and 25 autoencoders for the NIH and the Open-i dataset. F1 Scores for different disease and conditions in the NIH and the Open-i datasets with varying number of discriminative autoencoders (T) in the ensemble are presented in Table 7 and Table 8 respectively. The best value in each row is the one with the lowest standard deviation among the values with the highest mean. From both of these tables, notice that with T = 15 autoencoders in the ensemble, we obtain the best results for more diseases and conditions across the NIH and Open-i datasets than we obtain with any other value of T. This justifies our choice of the number of autoencoders in the ensemble. Nevertheless, in a more flexible setting, different values of T can be chosen using Table 7 and Table 8 for different combinations of base and novel classes in different datasets.
Table 7:
F1 Scores for different disease and conditions in the NIH dataset with varying number of discriminative autoencoders (T) in the saliency-based classifier.
| T | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|
| Fibrosis | 0.74±0.03 | 0.67±0.03 | 0.63±0.04 | 0.65±0.04 | 0.66±0.03 |
| Hernia | 0.32±0.03 | 0.32±0.04 | 0.38±0.02 | 0.38±0.04 | 0.37±0.04 |
| Pneumonia | 0.45±0.01 | 0.43±0.02 | 0.49±0.02 | 0.43±0.02 | 0.43±0.02 |
| Mass | 0.45±0.02 | 0.48±0.03 | 0.45±0.02 | 0.45±0.02 | 0.46±0.03 |
| Nodule | 0.42±0.02 | 0.42±0.03 | 0.48±0.01 | 0.44±0.02 | 0.40±0.03 |
| Pleural Thickening | 0.32±0.02 | 0.31±0.02 | 0.33±0.01 | 0.30±0.03 | 0.30±0.02 |
| Cardiomegaly | 0.48±0.05 | 0.44±0.03 | 0.44±0.05 | 0.45±0.04 | 0.46±0.02 |
| Edema | 0.55±0.01 | 0.54±0.02 | 0.57±0.01 | 0.54±0.02 | 0.54±0.01 |
| Emphysema | 0.48±0.03 | 0.51±0.02 | 0.50±0.02 | 0.50±0.02 | 0.51±0.03 |
| Consolidation | 0.44±0.02 | 0.46±0.01 | 0.44±0.02 | 0.44±0.02 | 0.43±0.05 |
| Effusion | 0.51±0.05 | 0.52±0.03 | 0.47±0.03 | 0.54±0.02 | 0.48±0.04 |
| Pneumothorax | 0.38±0.03 | 0.38±0.02 | 0.40±0.01 | 0.40±0.01 | 0.40±0.0 |
| Atelectasis | 0.31±0.04 | 0.35±0.01 | 0.33±0.02 | 0.34±0.03 | 0.32±0.04 |
| Infiltration | 0.30±0.02 | 0.31±0.02 | 0.34±0.01 | 0.31±0.03 | 0.32±0.02 |
| No Finding | 0.57±0.04 | 0.57±0.05 | 0.62±0.02 | 0.60±0.05 | 0.62±0.03 |
Bold fonts indicate the best values in each row.
Table 8:
F1 Scores for different disease and conditions in the Open-i dataset with varying number of discriminative autoencoders (T) in the saliency-based classifier.
| T | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|
| Fibrosis | 0.25±0.01 | 0.23±0.01 | 0.21±0.01 | 0.24±0.02 | 0.24±0.03 |
| Hernia | 0.65±0.02 | 0.71±0.07 | 0.75±0.03 | 0.70±0.08 | 0.76±0.02 |
| Pneumonia | 0.46±0.13 | 0.37±0.06 | 0.45±0.05 | 0.40±0.10 | 0.48±0.18 |
| Mass | 0.22±0.01 | 0.20±0.06 | 0.29±0.05 | 0.29±0.02 | 0.21±0.08 |
| Nodule | 0.64±0.09 | 0.72±0.06 | 0.72±0.02 | 0.70±0.06 | 0.70±0.08 |
| Pleural Thickening | 0.25±0.02 | 0.24±0.02 | 0.26±0.03 | 0.21±0.04 | 0.23±0.03 |
| Cardiomegaly | 0.69±0.12 | 0.78±0.02 | 0.64±0.02 | 0.77±0.02 | 0.74±0.07 |
| Edema | 0.01±0.02 | 0.00±0.00 | 0.09±0.03 | 0.02±0.02 | 0.03±0.01 |
| Emphysema | 0.45±0.03 | 0.45±0.02 | 0.53±0.03 | 0.44±0.02 | 0.42±0.01 |
| Consolidation | 0.14±0.07 | 0.13±0.04 | 0.40±0.1 | 0.11±0.07 | 0.05±0.06 |
| Effusion | 0.77±0.06 | 0.70±0.17 | 0.73±0.03 | 0.72±0.12 | 0.62±0.21 |
| Pneumothorax | 0.21±0.02 | 0.24±0.12 | 0.29±0.01 | 0.24±0.01 | 0.30±0.05 |
| Atelectasis | 0.22±0.01 | 0.21±0.02 | 0.19±0.02 | 0.23±0.02 | 0.23±0.01 |
| Infiltration | 0.02±0.00 | 0.02±0.01 | 0.04±0.01 | 0.02±0.00 | 0.02±0.00 |
| No Finding | 0.74±0.05 | 0.79±0.10 | 0.88±0.02 | 0.84±0.05 | 0.85±0.08 |
Bold fonts indicate the best values in each row.
As we start increasing the number of autoencoders in the ensemble, more feature subspaces are explored for disease-specific information. As complementary information is brought in with the addition of new autoencoders, the performance of the ensemble improves. However, after a certain number of autoencoders (when the feature space is sufficiently explored), further addition of new autoencoders only brings in redundant information. Hence, performance of the ensemble may not change (or may even degrade) with further addition of autoencoders. Nevertheless, for different diseases and conditions, the disease-specific information contained in the feature space varies. Therefore, we need different number of autoencoders in the ensemble to sufficiently explore the feature space in order to find disease-specific information for different diseases and conditions. That is why, for different diseases and conditions, the best performance is obtained for different number of autoencoders in the ensemble.
4.4. Notes on Clinical Applications
Few-shot diagnosis opens up the possibility of automated detection of rare diseases since the training requires only a few image examples. For the purposes of performing a proof-of-principle research study, we have chosen common diseases for both the base and novel classes. From Tables 2 to 6, it can be observed that for almost all the novel classes in the NIH dataset, our method yields a low value of standard deviation. More interestingly, even in case of the Open-i dataset, the values of standard deviations of F1 score (see Fig. 4, Fig. 5, and Fig. 6) for different novel classes is ≤ 0.05 (except for consolidation with only 3 test data points). These are important observations in terms of repeatability of the results when clinical applications are concerned. Low values of standard deviations in the NIH and the Open-i datasets indicate that the proposed method yields consistent results not only for the test data from same source (test data of NIH dataset) but also for the test data from a different source (Open-i dataset). This makes our model applicable with good repeatability across different datasets.
Through the ablation studies, we have seen that our method can effectively diagnose diseases with similar visual appearance in chest x-rays. Such diseases include consolidation, infiltration and pneumonia. Therefore, our method can be helpful in scenarios where disease with visual similarities are to be identified even with a small number of training examples.
Furthermore, our model has a modular architecture. In order to add more disease categories, one needs to train only the saliency-based classifier that too with as few as five chest x-ray images of each disease category. This makes adding more diseases in our model easier and less time consuming. We have also explained in Section 3.3.3 that application of our model for modalities other than chest x-rays requires the modification of only the coarse-learner with a modality-specific suitable network. Hence, our model can potentially serve as the basis for the development of a method for the few-shot diagnosis of different diseases including the rare ones from the images of different modalities in a clinical setup.
5. Conclusions
We propose a method for few-shot diagnosis of chest x-ray images using a novel ensemble of discriminative autoencoders. Each autoencoder in the ensemble is assigned a weight based on its layer-wise consistency in classification. Rigorous experiments show the utility of the ensemble in making our method applicable across different datasets. Assignment of weights to the discriminative autoencoders enables us to detect even the visually similar diseases and conditions from x-ray images. This opens up the possibility of few-shot fine-grained disease classification using the our technique. The proposed method has good repeatability even for a test dataset from a source which is different from the source of training data. These characteristics make our method potentially useful in a clinical setup. In the future, we would like to explore the possibility of end-to-end training and the use of attention models to improve the performance. We would also extend our method to multi-label few-shot diagnosis of images from different imaging modalities.
Supplementary Material
Table 3:
Performances of different methods for mass, nodule and pleural thickening as novel classes in the NIH dataset.
| Method | Mass | Nodule | Pleural Thickening | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | F1 Score | Recall | Precision | F1 Score | |
| Ada | 0.43±0.04 | 0.45±0.02 | 0.44±0.02 | 0.45±0.09 | 0.35±0.01 | 0.39±0.04 | 0.32±0.07 | 0.23±0.02 | 0.26±0.02 |
| ET | 0.02±0.00 | 0.44±0.06 | 0.04±0.01 | 0.05±0.04 | 0.44±0.08 | 0.09±0.05 | 0.07±0.10 | 0.29±0.10 | 0.09±0.09 |
| RF | 0.01±0.01 | 0.62±0.07 | 0.02±0.01 | 0.01±0.00 | 0.49±0.19 | 0.02±0.01 | 0.03±0.02 | 0.34–0.12 | 0.06±0.03 |
| SVM | 0.05±0.02 | 0.46±0.08 | 0.09±0.04 | 0.15±0.08 | 0.34±0.03 | 0.19±0.07 | 0.11±0.05 | 0.21±0.05 | 0.14±0.05 |
| MAML | 0.38±0.03 | 0.44±0.02 | 0.41±0.02 | 0.39±0.02 | 0.39±0.05 | 0.38±0.03 | 0.39±0.08 | 0.23±0.03 | 0.28±0.02 |
| ProtoNet | 0.35±0.17 | 0.45±0.01 | 0.37±0.11 | 0.41±0.08 | 0.37±0.03 | 0.38±0.02 | 0.51±0.25 | 0.20±0.04 | 0.28±0.08 |
| MetaOptNet | 0.20±0.01 | 0.42±0.01 | 0.28±0.01 | 0.27±0.05 | 0.38±0.03 | 0.31±0.03 | 0.22±0.05 | 0.23±0.01 | 0.22±0.03 |
| ANIL | 0.37±0.03 | 0.44±0.02 | 0.40±0.02 | 0.43±0.11 | 0.33±0.03 | 0.37±0.05 | 0.41±0.03 | 0.24±0.02 | 0.30±0.01 |
| Baseline | 0.22±0.03 | 0.49±0.03 | 0.30±0.04 | 0.27±0.10 | 0.38±0.03 | 0.31±0.08 | 0.19±0.10 | 0.30±0.03 | 0.22±0.07 |
| Baseline+ | 0.37±0.03 | 0.46±0.01 | 0.41±0.02 | 0.50±0.13 | 0.36±0.03 | 0.41±0.06 | 0.38±0.09 | 0.23±0.01 | 0.28±0.02 |
| Proposed | 0.44±0.05 | 0.46±0.01 | 0.45±0.02 | 0.63–0.05 | 0.39±0.01 | 0.48±0.01 | 0.40±0.04 | 0.28±0.01 | 0.33±0.01 |
Bold fonts indicate the best values in each column.
Table 4:
Performances of different methods for cardiomegaly, edema and emphysema as novel classes in the NIH dataset.
| Method | Cardiomegaly | Edema | Emphysema | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | Fi Score | Recall | Precision | F1 Score | |
| Ada | 0.39±0.07 | 0.42±0.05 | 0.40±0.06 | 0.49±0.09 | 0.40±0.05 | 0.44±0.04 | 0.35±0.02 | 0.38±0.07 | 0.36±0.03 |
| ET | 0.04±0.02 | 0.66±0.11 | 0.08±0.04 | 0.10±0.04 | 0.53±0.06 | 0.17±0.05 | 0.07±0.04 | 0.72±0.09 | 0.13±0.06 |
| RF | 0.01±0.00 | 0.70±0.18 | 0.01±0.00 | 0.02±0.01 | 0.61 ±0.06 | 0.04±0.01 | 0.08±0.02 | 0.60±0.09 | 0.13±0.03 |
| SVM | 0.02±0.02 | 0.37±0.08 | 0.04±0.03 | 0.05±0.02 | 0.36±0.04 | 0.08±0.04 | 0.07±0.06 | 0.35±0.04 | 0.10±0.08 |
| MAML | 0.43±0.05 | 0.37±0.01 | 0.39±0.02 | 0.71±0.04 | 0.46±0.02 | 0.56±0.01 | 0.47±0.05 | 0.43±0.07 | 0.44±0.04 |
| ProtoNet | 0.30±0.12 | 0.40±0.07 | 0.32±0.07 | 0.63±0.28 | 0.36±0.05 | 0.43±0.14 | 0.40±0.16 | 0.36±0.05 | 0.36±0.06 |
| MetaOptNet | 0.20±0.05 | 0.38±0.04 | 0.26±0.04 | 0.28±0.08 | 0.41±0.06 | 0.32±0.05 | 0.15±0.06 | 0.32±0.06 | 0.19±0.05 |
| ANIL | 0.44±0.07 | 0.38±0.02 | 0.40±0.02 | 0.59±0.09 | 0.43±0.02 | 0.49±0.03 | 0.53±0.13 | 0.42±0.07 | 0.46±0.05 |
| Baseline | 0.25±0.04 | 0.65±0.08 | 0.35±0.04 | 0.50±0.02 | 0.53±0.01 | 0.52±0.01 | 0.27±0.04 | 0.56±0.10 | 0.36±0.02 |
| Baseline+ | 0.32±0.07 | 0.56±0.06 | 0.40±0.05 | 0.70±0.05 | 0.47±0.01 | 0.56±0.01 | 0.49±0.04 | 0.48±0.02 | 0.49±0.02 |
| Proposed | 0.45±0.15 | 0.47±0.05 | 0.44±0.05 | 0.77±0.07 | 0.46±0.02 | 0.57±0.01 | 0.52±0.05 | 0.48±0.01 | 0.50±0.02 |
Bold fonts indicate the best values in each column.
Highlights.
We design a two-step solution for few-shot diagnosis of chest x-rays.
Our model is composed of a coarse-learner and a saliency-based classifier.
The saliency-based classifier is designed using a novel discriminative autoencoder ensemble.
We introduce a novel intrinsic weight to be assigned to each autoencoder for weighted voting during inference.
Our method can be trained with one dataset and can still be effectively applied to similar datasets from different sources.
Acknowledgment
This project was supported by the Intramural Research Program of the National Institutes of Health, Clinical Center, and by a Cooperative Research and Development Agreement with PingAn. We thank NVIDIA for GPU card donation.
Appendix A. On Feature Selection for Autoencoders
We find a d′-dimensional best subspace from the feature space of d dimensions for each discriminative autoencoder. We use the bootstrap sample Bi composed of N′ feature vectors to find the best subspace for autoencoder i. For this, we first choose M number of randomly selected d′-dimensional subspaces. The best out of these M subspaces is selected based on the discrimination index, defined as follows. Assume that we have C number of different class labels in Bi. Consider a d′-dimensional subspace S j. Let Xu and Xv be any two data points in subspace S j. Consider r(u, v) to be the distance between Xu and Xv in the above subspace. Let L(u, v) = 1 if the class labels of Xu and Xv are not same and L(u, v) = −1 otherwise. Then the discrimination index of subspace S j is defined as
| (A.1) |
where is the maximum possible distance between any two data points in the subspace S j. From our formulation of discrimination index, it is evident that the discrimination index is higher if data with same class labels are closely spaced and data with different class labels remains distant from each other in the subspace. Hence, a high value of the discrimination index indicates a better separability of data from different classes. We choose the subspace with the highest discrimination index out of the M subspaces to be the best subspace S*(i) for the ith (i ∈ 1,2, …, T) autoencoder. The dimensions corresponding to the best subspace are used for preparing the training data for the autoencoder.
Footnotes
Declaration of interests
☒The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Ronald M. Summers receives royalties from PingAn, iCAD, ScanMed and Philips, research support from PingAn, and GPU card donations from NVIDIA.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Boser BE, Guyon IM, Vapnik VN, 1992. A training algorithm for optimal margin classifiers, in: Proceedings of the fifth annual workshop on Computational learning theory, ACM; pp. 144–152. [Google Scholar]
- Breiman L, 2001. Random forests. Machine learning 45, 5–32. [Google Scholar]
- Demner-Fushman D, Kohli MD, Rosenman MB, Shooshan SE, Rodriguez L, Antani S, Thoma GR, McDonald CJ, 2015. Preparing a collection of radiology examinations for distribution and retrieval. Journal of the American Medical Informatics Association 23, 304–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L, 2009. Imagenet: A large-scale hierarchical image database, in: 2009 IEEE conference on computer vision and pattern recognition, Ieee pp. 248–255. [Google Scholar]
- Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S, 2017. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn C, Abbeel P, Levine S, 2017. Model-agnostic meta-learning for fast adaptation of deep networks, in: Proceedings of the 34th International Conference on Machine Learning-Volume 70, JMLR. Org. pp. 1126–1135. [Google Scholar]
- Freund Y, Schapire RE, 1997. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of computer and system sciences 55, 119–139. [Google Scholar]
- Geurts P, Ernst D, Wehenkel L, 2006. Extremely randomized trees. Machine learning 63, 3–42. [Google Scholar]
- Gidaris S, Bursuc A, Komodakis N, Pérez P, Cord M, 2019. Boosting few-shot visual learning with self-supervision, in: Proceedings of the IEEE International Conference on Computer Vision, pp. 8059–8068. [Google Scholar]
- Gidaris S, Singh P, Komodakis N, 2018. Unsupervised representation learning by predicting image rotations. arXiv preprint arXiv:1803.07728. [Google Scholar]
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y, 2014. Generative adversarial nets, in: Advances in Neural Information Processing Systems, pp. 2672–2680. [Google Scholar]
- Guan Q, Huang Y, Zhong Z, Zheng Z, Zheng L, Yang Y, 2019. Thorax disease classification with attention guided convolutional neural network. Pattern Recognition Letters. [Google Scholar]
- Hinton GE, Salakhutdinov RR, 2006. Reducing the dimensionality of data with neural networks. Science 313, 504–507. [DOI] [PubMed] [Google Scholar]
- Hoffer E, Ailon N, 2015. Deep metric learning using triplet network, in: International Workshop on Similarity-Based Pattern Recognition, Springer; pp. 84–92. [Google Scholar]
- de Hoop B, De Boo DW, Gietema HA, van Hoorn F, Mearadji B, Schijf L, van Ginneken B, Prokop M, Schaefer-Prokop C, 2010. Computer-aided detection of lung cancer on chest radiographs: effect on observer performance. Radiology 257, 532–540. [DOI] [PubMed] [Google Scholar]
- Huang G, Liu Z, Van Der Maaten L, Weinberger KQ, 2017. Densely connected convolutional networks, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 4700–4708. [Google Scholar]
- Irvin J, Rajpurkar P, Ko M, Yu Y, Ciurea-Ilcus S, Chute C, Marklund H, Haghgoo B, Ball R, Shpanskaya K, et al. , 2019. Chexpert: A large chest radiograph dataset with uncertainty labels and expert comparison. arXiv preprint arXiv:1901.07031 [Google Scholar]
- Johnson AE, Pollard TJ, Berkowitz S, Greenbaum NR, Lungren MP, Deng C.y., Mark RG, Horng S, 2019. Mimic-cxr: A large publicly available database of labeled chest radiographs. arXiv preprint arXiv:1901.07042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JM, Khoshgoftaar TM, 2019. Survey on deep learning with class imbalance. Journal of Big Data 6, 27. [Google Scholar]
- Kingma DP, Ba J, 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton GE, 2012. Imagenet classification with deep convolutional neural networks, in: Advances in neural information processing systems, pp. 1097–1105. [Google Scholar]
- Lakhani P, Sundaram B, 2017. Deep learning at chest radiography: automated classification of pulmonary tuberculosis by using convolutional neural networks. Radiology 284, 574–582. [DOI] [PubMed] [Google Scholar]
- LeCun Y, Bengio Y, Hinton G, 2015. Deep learning. Nature 521, 436–444. [DOI] [PubMed] [Google Scholar]
- Lee K, Maji S, Ravichandran A, Soatto S, 2019. Meta-learning with differentiable convex optimization, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 10657–10665. [Google Scholar]
- Li Z, Kamnitsas K, Glocker B, 2019. Overfitting of neural nets under class imbalance: Analysis and improvements for segmentation, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer; pp. 402–410. [Google Scholar]
- Li Z, Wang C, Han M, Xue Y, Wei W, Li LJ, Fei-Fei L, 2018. Thoracic disease identification and localization with limited supervision, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 8290–8299. [Google Scholar]
- Lindsey R, Daluiski A, Chopra S, Lachapelle A, Mozer M, Sicular S, Hanel D, Gardner M, Gupta A, Hotchkiss R, et al. , 2018. Deep neural network improves fracture detection by clinicians. Proceedings of the National Academy of Sciences 115, 11591–11596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X, Tsao Y, Matsuda S, Hori C, 2013. Speech enhancement based on deep denoising autoencoder., in: Interspeech, pp. 436–440. [Google Scholar]
- Mondal AK, Dolz J, Desrosiers C, 2018. Few-shot 3d multi-modal medical image segmentation using generative adversarial learning. arXiv preprint arXiv:1810.12241. [Google Scholar]
- Nam JG, Park S, Hwang EJ, Lee JH, Jin KN, Lim KY, Vu TH, Sohn JH, Hwang S, Goo JM, et al. , 2018. Development and validation of deep learning–based automatic detection algorithm for malignant pulmonary nodules on chest radiographs. Radiology 290, 218–228. [DOI] [PubMed] [Google Scholar]
- Ouyang W, Wang X, Zhang C, Yang X, 2016. Factors in finetuning deep model for object detection with long-tail distribution, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 864–873. [Google Scholar]
- Paul A, Majumdar A, Mukherjee DP, 2018. Discriminative autoencoder, in: 2018 25th IEEE International Conference on Image Processing (ICIP), IEEE; pp. 3049–3053. [Google Scholar]
- Paul A, Mukherjee DP, 2019. Reinforced quasi-random forest. Pattern Recognition 94, 13–24. [Google Scholar]
- Paul A, Tang YX, Summers RM, 2020. Fast few-shot transfer learning for disease identification from chest x-ray images using autoencoder ensemble, in: Medical Imaging 2020: Computer-Aided Diagnosis, International Society for Optics and Photonics; p. 1131407. [Google Scholar]
- Peng Y, Dharssi S, Chen Q, Keenan TD, Agrón E, Wong WT, Chew EY, Lu Z, 2019. Deepseenet: A deep learning model for automated classification of patient-based age-related macular degeneration severity from color fundus photographs. Ophthalmology 126, 565–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y, Wang X, Lu L, Bagheri M, Summers R, Lu Z, 2018. Negbio: a high-performance tool for negation and uncertainty detection in radiology reports. AMIA Summits on Translational Science Proceedings 2018, 188. [PMC free article] [PubMed] [Google Scholar]
- Puch S, Sánchez I, Rowe M, 2019. Few-shot learning with deep triplet networks for brain imaging modality recognition, in: Domain Adaptation and Representation Transfer and Medical Image Learning with Less Labels and Imperfect Data. Springer, pp. 181–189. [Google Scholar]
- Raghu A, Raghu M, Bengio S, Vinyals O, 2020. Rapid learning or feature reuse? towards understanding the effectiveness of maml, in: International Conference on Learning Representations. [Google Scholar]
- Rajpurkar P, Irvin J, Ball RL, Zhu K, Yang B, Mehta H, Duan T, Ding D, Bagul A, Langlotz CP, et al. , 2018. Deep learning for chest radiograph diagnosis: A retrospective comparison of the chexnext algorithm to practicing radiologists. PLoS medicine 15, e1002686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajpurkar P, Irvin J, Zhu K, Yang B, Mehta H, Duan T, Ding D, Bagul A, Langlotz C, Shpanskaya K, et al. , 2017. Chexnet: Radiologist-level pneumonia detection on chest x-rays with deep learning. arXiv preprint arXiv:1711.05225. [Google Scholar]
- Ravi S, Larochelle H, 2016. Optimization as a model for few-shot learning. [Google Scholar]
- Ren M, Triantafillou E, Ravi S, Snell J, Swersky K, Tenenbaum JB, Larochelle H, Zemel RS, 2018. Meta-learning for semi-supervised few-shot classification. arXiv preprint arXiv:1803.00676. [Google Scholar]
- Roy AG, Siddiqui S, Pölsterl S, Navab N, Wachinger C, 2020. ‘squeeze & excite’ guided few-shot segmentation of volumetric images. Medical image analysis 59, 101587. [DOI] [PubMed] [Google Scholar]
- Salehinejad H, Colak E, Dowdell T, Barfett J, Valaee S, 2019. Synthesizing chest x-ray pathology for training deep convolutional neural networks. IEEE Transactions on Medical Imaging 38, 1197–1206. [DOI] [PubMed] [Google Scholar]
- Snell J, Swersky K, Zemel R, 2017. Prototypical networks for few-shot learning, in: Advances in Neural Information Processing Systems, pp. 4077–4087. [Google Scholar]
- Tang Y, Tang Y, Han M, Xiao J, Summers RM, 2019. Abnormal chest x-ray identification with generative adversarial one-class classifier, in: IEEE 16th International Symposium on Biomedical Imaging, pp. 1358–1361. [Google Scholar]
- Tang Y, Wang X, Harrison AP, Lu L, Xiao J, Summers RM, 2018. Attention-guided curriculum learning for weakly supervised classification and localization of thoracic diseases on chest radiographs, in: Machine Learning in Medical Imaging, Springer; pp. 249–258. [Google Scholar]
- Tang YB, Tang YX, Xiao J, Summers RM, 2019. XLSor: A robust and accurate lung segmentor on chest x-rays using criss-cross attention and customized radiorealistic abnormalities generation, in: Proceedings of The 2nd International Conference on Medical Imaging with Deep Learning, PMLR; pp. 457–467. [Google Scholar]
- Taylor AG, Mielke C, Mongan J, 2018. Automated detection of moderate and large pneumothorax on frontal chest x-rays using deep convolutional neural networks: A retrospective study. PLoS medicine 15, e1002697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Team NLSTR, 2011. The national lung screening trial: overview and study design. Radiology 258, 243–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thrall JH, Li X, Li Q, Cruz C, Do S, Dreyer K, Brink J, 2018. Artificial intelligence and machine learning in radiology: opportunities, challenges, pitfalls, and criteria for success. Journal of the American College of Radiology 15, 504–508. [DOI] [PubMed] [Google Scholar]
- Ting DSW, Cheung CYL, Lim G, Tan GSW, Quang ND, Gan A, Hamzah H, Garcia-Franco R, San Yeo IY, Lee SY, et al. , 2017. Development and validation of a deep learning system for diabetic retinopathy and related eye diseases using retinal images from multiethnic populations with diabetes. JAMA 318, 2211–2223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinyals O, Blundell C, Lillicrap T, Wierstra D, et al. , 2016. Matching networks for one shot learning, in: Advances in neural information processing systems, pp. 3630–3638. [Google Scholar]
- Wang X, Peng Y, Lu L, Lu Z, Bagheri M, Summers RM, 2017. Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2097–2106. [Google Scholar]
- Wang X, Peng Y, Lu L, Lu Z, Summers RM, 2018. TieNet: Text-image embedding network for common thorax disease classification and reporting in chest x-rays, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 9049–9058. [Google Scholar]
- Wang Y, Yao Q, 2019. Few-shot learning: A survey. CoRR abs/1904.05046. URL: http://arxiv.org/abs/1904.05046, arXiv:1904.05046. [Google Scholar]
- Yoon J, Kim T, Dia O, Kim S, Bengio Y, Ahn S, 2018. Bayesian model-agnostic meta-learning, in: Advances in Neural Information Processing Systems, pp. 7332–7342. [Google Scholar]
- Zhang R, Che T, Ghahramani Z, Bengio Y, Song Y, 2018. Metagan: An adversarial approach to few-shot learning, in: Advances in Neural Information Processing Systems, pp. 2365–2374. [Google Scholar]
- Zhou B, Li Y, Wang J, 2018. A weakly supervised adaptive densenet for classifying thoracic diseases and identifying abnormalities. arXiv preprint arXiv:1807.01257. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.