Perceptual learning of tone patterns changes the effective connectivity between Heschl's gyrus and planum temporale

Abstract

Learning of complex auditory sequences such as music can be thought of as optimizing an internal model of regularities through unpredicted events (or “prediction errors”). We used dynamic causal modeling (DCM) and parametric empirical Bayes on functional magnetic resonance imaging (fMRI) data to identify modulation of effective brain connectivity that takes place during perceptual learning of complex tone patterns. Our approach differs from previous studies in two aspects. First, we used a complex oddball paradigm based on tone patterns as opposed to simple deviant tones. Second, the use of fMRI allowed us to identify cortical regions with high spatial accuracy. These regions served as empirical regions‐of‐interest for the analysis of effective connectivity. Deviant patterns induced an increased blood oxygenation level‐dependent response, compared to standards, in early auditory (Heschl's gyrus [HG]) and association auditory areas (planum temporale [PT]) bilaterally. Within this network, we found a left‐lateralized increase in feedforward connectivity from HG to PT during deviant responses and an increase in excitation within left HG. In contrast to previous findings, we did not find frontal activity, nor did we find modulations of backward connections in response to oddball sounds. Our results suggest that complex auditory prediction errors are encoded by changes in feedforward and intrinsic connections, confined to superior temporal gyrus.

Perception of complex auditory stimuli requires the brain to update a model of its environment. Using dynamic causal modeling for functional magnetic resonance imaging during a melodic oddball paradigm, we show increased intrinsic connectivity within Heschl's gyrus (HG) and a concomitant increase in forward connectivity from HG to planum temporale in the left cerebral hemisphere. We did not find evidence of frontal activity. Our results are consistent with a predictive coding account of perceptual learning within the superior temporal gyrus.

1. INTRODUCTION

Predictive coding (PC) is a unifying theory of brain function that formally links human learning and neuroplasticity (Friston, 2002). The key notion in PC is that the brain embodies an internal model of the environment, which constantly generates predictions of future sensory inputs and is updated by the discrepancy of predicted and actual input. When predictions fail, the brain generates “prediction error signals” that pass from lower to higher levels of the brain's hierarchy revising the model's predictions (Dietz, Friston, Mattingley, Roepstorff, & Garrido, 2014). Learning can thus be thought of as a process of recurrent model updating through prediction error signaling. Here, we focus on tone‐pattern learning, that is, the optimization of an internal model of regularities during the listening of short tone‐patterns.

Sound‐patterns are the building blocks of musical and language structure. In music, tone‐pattern learning reflects the update of internalized probabilities acquired through statistical learning and relates to melodic continuations (Hansen & Pearce, 2014) at two pitch‐processing levels: (a) “contour”—the rise and fall of pitch changes—and (b) pitch “interval”—the distance between adjacent tones (Quiroga‐Martinez et al., 2020; Schmuckler, 2016). The maintenance and updating of melodic predictive models have been studied using auditory oddball paradigms, whereby magnetoencephalographic and/or electrophysiological (M/EEG) brain activity is recorded while participants listen to streams of repeated short melodies typically based on tones from the 12‐tone‐equal‐tempered scale, omnipresent in Western tonal music (e.g., Hsu, le Bars, Hämäläinen, & Waszak, 2015; Lappe, Lappe, & Pantev, 2016; Tervaniemi, Maury, & Näätänen, 1994). The mismatch negativity (MMN) elicited by occasional pitch contour or interval deviations in these patterns is evidence that a melodic predictive model has been formed during the auditory stimulation and thought to represent the message passing of precision‐weighted prediction errors in the cortical auditory hierarchy (Auksztulewicz & Friston, 2015; Dietz et al., 2014; Vuust, Dietz, Witek, & Kringelbach, 2018; Vuust, Gebauer, & Witek, 2014; Vuust, Ostergaard, Pallesen, Bailey, & Roepstorff, 2009).

In the past two decades, studies have used dynamic causal modeling (DCM) of M/EEG data collected from simple oddball tasks to provide a mechanistic account for the emergence of the auditory MMN (e.g., Dietz et al., 2014; Garrido, Kilner, Kiebel, & Friston, 2009; Garrido, Kilner, Kiebel, Stephan, & Friston, 2007; Kiebel, Garrido, & Friston, 2007). These studies showed that occasional deviations in a stream of repeated tones evoke MMN responses that are best explained by changes in effective connectivity of a wide temporo‐frontal network. This network is typically defined a priori from previous fMRI oddball studies (e.g., Doeller et al., 2003; Liebenthal et al., 2003; Opitz, Rinne, Mecklinger, von Cramon, & Schröger, 2002) and includes HG, STG, and right inferior frontal gyrus (IFG). A comparison of DCMs with different network architectures shows that models including intrinsic connections in HG, and both backward and feedforward connections between STG and frontal regions, provide the best explanation of brain responses to deviant events. While simple oddball paradigms have proven useful for assessing expectations of individual pitches, they are not adequate in the context of the complex stimulation that occurs in natural sound environments, such as speech and musical patterns (McDermott, Schemitsch, & Simoncelli, 2013). Also, an accurate DCM relies on properly assigned cortical sources (Friston, 2003). In previous studies, the use of an a priori network, in combination with the relatively poor spatial resolution of M/EEG, adds uncertainty to the construct validity of the network models.

So far, a millimetric localization of the cortical generators that underpin melodic MMNs has been addressed in one functional magnetic resonance imaging (fMRI) study (Habermeyer et al., 2009). Habermeyer et al. (2009) used fMRI in combination with an event‐related melodic oddball paradigm (Tervaniemi, Rytkönen, Schröger, Ilmoniemi, & Näätänen, 2001) to test the effect of musical expertise on melodic pattern deviations. Based on previous observations (e.g., Opitz et al., 2002), they hypothesized that temporal and frontal cortices would be recruited during preattentive encoding of complex violations, with stronger effects in professional musicians compared to naive listeners. They found regions of the middle and superior temporal gyrus, in combination with frontal cortices, as the main cortical generators of melodic MMN. Their study was the first to show an involvement of temporo‐frontal regions in the processing of melodic contour changes. However, frontal activations were only reported in the group comparison (musicians vs. nonmusicians) by contrasting deviant responses with the silent baseline. The more traditional contrast between deviant and standard conditions yielded no significant activations within groups. This limits the interpretability of their findings in two regards: (a) the localization of the brain regions that selectively respond more strongly to melodic oddballs than to standard melodic stimuli and (b) the contribution of frontal cortices in deviance detection for musically naive individuals (Deouell, 2007).

To investigate the mechanisms of effective connectivity between these cortical regions during pattern learning, we used DCM of fMRI data acquired in human volunteers (nonmusicians; N = 52) presented with an unfamiliar musical tuning system, the Bohlen–Pierce (BP) scale (Mathews, Pierce, Reeves, & Roberts, 1988) (Figure 1a). This artificial scale has the advantage of preserving intervallic properties from the 12‐tone equal‐tempered scale without being contaminated by prior knowledge about pitch categories and intervals. This ensures a more controlled setting to test hypotheses about the generation and revision of an internal predictive model. First, we identified an MMN auditory network using a melodic oddball paradigm (Lumaca & Baggio, 2016). Participants listened to streams of five‐tone BP melodic patterns (Figure 1b). Occasionally, the fourth tone was pitch‐shifted to violate the contour (“contour” deviant; 10%) or the melodic interval structure (“interval” deviant; 10%) of the “standard” sequence. Brain imaging studies on preattentive pitch deviance detection have consistently found activity in the bilateral STG, with only few of them observing activations in frontal areas (Molholm, Martinez, Ritter, Javitt, & Foxe, 2005; Opitz et al., 2002; see Deouell, 2007 for a more comprehensive review). Thus, we expected to find activations in a bilateral temporal network including HG and PT. Based on the role of frontal cortices in melodic processing (Habermeyer et al., 2009; Zatorre, Evans, & Meyer, 1994), we further hypothesized to find activation in prefrontal areas. We then used a DCM to analyze changes in the effective connectivity within and between the cortical regions identified during deviant stimuli, relative to standard stimuli. Specifically, we used Bayesian model reduction and parametric empirical Bayes (PEB) (Friston et al., 2015) to compare, at the group level, different hypotheses about effective connectivity during auditory pattern learning that encode differences between deviant and standard conditions in those cortical areas, including changes in both feedforward and feedback connections, as well as their intrinsic (inhibitory) connections.

FIGURE 1.

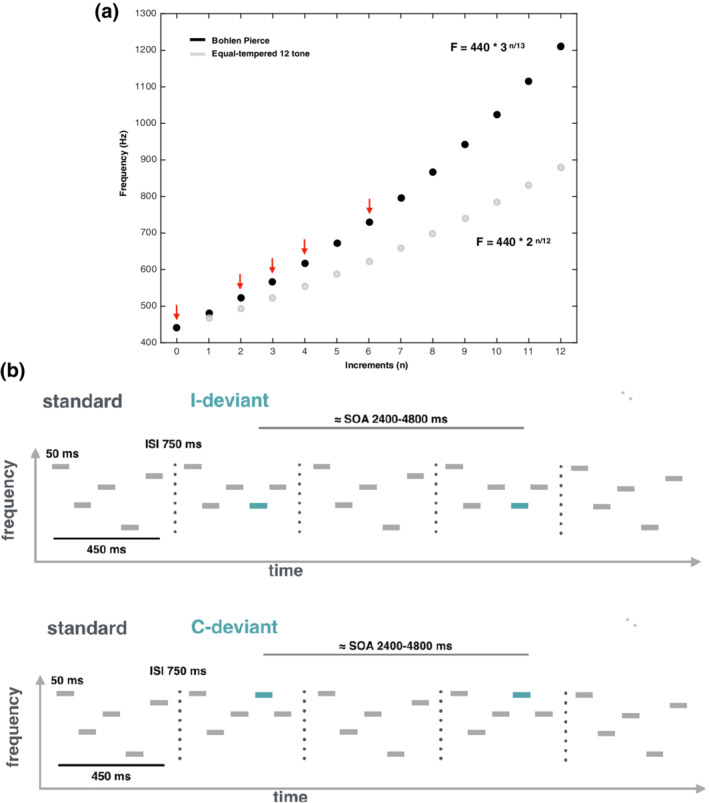
Musical scale and auditory patterns used in the current study. (a) Illustration of pitch frequencies along the Western equal‐tempered 12‐tone scale (in gray) and the BP scale (in black). Red arrows point to the BP frequencies used to build melodic material (k = 440 Hz; n = 0, 2, 3, 4, or 6). (b) Schematic illustration of the melodic patterns presented to participants during the auditory oddball paradigm (adapted from Lumaca, Kleber, Brattico, Vuust, and Baggio (2019)). Participants were scanned while listening to these melodic patterns. Each pattern was 450‐ms long, and consisted of five 50‐ms sinusoidal tones separated by 50‐ms silent intervals. Melodic patterns were presented with 750‐ms of interstimulus interval (ISI) randomly at three frequency levels (lowest frequency: 440, 478, 567 Hz) belonging to the BP musical scale. Standard patterns (80%) followed the abstract rule EBCAD. In deviant patterns, the fourth tone was changed in frequency compared to its standard position, either producing a change in the melodic interval (I‐deviants; 10%) or in the pitch contour (C‐deviant; 10%). Pairs of deviant stimuli occurred in close temporal succession (jittering stimulus‐onset asynchrony [SOA] range, 2,400–4,800 ms) and were randomly interleaved with standard stimuli

2. MATERIALS AND METHODS

2.1. Participants

A total of 52 participants (33 females, mean age 24.5 years, range 20–34, right‐handed) with normal hearing took part in the fMRI experiment. Participants were all nonmusicians (i.e., none of them had three or more years of formal musical training) and all gave informed consent before the experiment. The neuroimaging data used in this work were acquired as part of another project approved by the local ethics committee of the Central Denmark Region (nr. 1083).

2.2. MRI procedure

2.2.1. BP scale

The auditory stimulation used in our fMRI oddball paradigm was adopted from an EEG paradigm by Lumaca and Baggio (2016). Tone sequences were constructed using tones from the equal‐tempered version of the BP scale (Loui, Wu, Wessel, & Knight, 2009; Mathews et al., 1988), a microtonal tuning system with 13 logarithmic even divisions of a tritave (corresponding to a 3:1 frequency ratio). In the equal‐tempered version of the scale, frequencies (F) are defined by the following:

$$\mathsf{F}\mathsf{=}\mathsf{k}\mathsf{x}{\mathsf{3}}^{\left(\mathsf{n}/\mathsf{13}\right)}$$

where n is the number of steps along the scale, and k is a constant that corresponds to the fundamental frequency. Based on this equation, we defined n = 0, 2, 3, 4, or 6 and k = 440 Hz (Figure 1a).

2.2.2. Stimuli

The pattern deviance paradigm and stimuli were adapted from an EEG paradigm by Lumaca and Baggio (2016), and have been shown to produce an MMN evoked potential (Näätänen, Gaillard, & Mäntysalo, 1978). Stimuli were five‐tone melodic patterns presented in a single block, consisting of collections of five 50 ms sinusoidal tones (5 ms rise and fall; 50 ms intertone intervals) with the frequencies 440, 521, 567, 617, and 730.6 Hz (henceforth referred to as ABCDE in the context of the low register) (Figure 1b). During stimulation, sequences were randomly transposed to three different baseline frequencies (henceforth referred as “A”), corresponding to three different registers of the BP scale (baseline tones: 440, 478, 567 Hz). This design feature is critical to avoid that differences between activity evoked by standard and deviant tones were driven by acoustic differences between the standards and deviants, rather than by model‐based expectations (Lumaca & Baggio, 2016). The patterns were presented with an “inter‐stimulus interval” of 750 ms. Standard patterns (80%) were randomly interspersed with “contour” (10%) and “interval” (10%) deviant sequences for a total of 1,260 stimuli. In abstract terms, the standard pattern always followed the sequence EBCAD across the three different registers. In contour deviant stimuli, the fourth tone changed the surface structure (“ups” and “downs”) of the standard stimuli without changing the interval (i.e., EBCED); vice versa for the interval deviants (i.e., EBCBD). Deviant stimuli were pseudorandomized in order to present deviant tones of the same type in close temporal succession (jittering stimulus‐onset asynchrony [SOA] range 2,400–4,800 ms) and to induce an increase of the blood oxygenation level‐dependent (BOLD) response by superposition. The use of multiple deviants in close succession can be found in other fMRI oddball studies (Cacciaglia et al., 2015).

2.2.3. Image acquisition

The fMRI data were acquired on a 3 T MRI scanner (Siemens Prisma). The subjects' head was fixated with cushions to minimize movement during the experiment. The participants wore earplugs, MR‐compatible headphones, and ear bandages to attenuate the scanner noise. A sham scan with auditory stimulation was also used to assess their levels of hearing. All participants reported a perfect hearing of auditory stimulation and a drastic attenuation of scanner noise. Finally, participants were instructed to be still and to watch a subtitled silent movie projected on a MRI‐compatible screen located at the rear of the scanner. During MRI acquisition, auditory stimulation was delivered by MR‐compatible headphones using Presentation software (www.neurobs.com). A total of 1,535 volumes were acquired over 25 min using a fast T2*‐weighted echo‐planar imaging (EPI) multiband sequence (TR, 1,000 ms; TE, 29.6 ms; voxel size, 2.5 mm³). A T1‐high resolution image was also acquired using an MP2RAGE sequence (TR, 5,000 ms; TE = 2.87 ms; voxel size, 0.9 mm³).

2.2.4. Preprocessing and analyses

Image time‐series were preprocessed and analyzed using SPM12 (r7487), implemented in MATLAB R2016b (MathWorks). EPI images were first spatially realigned to the first EPI volume. Then, individual high‐resolution T1‐images were coregistered to the mean EPI image and segmented using the standard tissue probability maps of SPM12. The resulting deformation fields were used to normalize functional EPI images to a standard Montreal Neurological Institute (MNI) reference brain. Normalized functional images were then resliced to 2 × 2 × 2 mm³ and smoothed with an isotropic 6 mm Gaussian kernel. Low frequency noise was removed through the use of a high‐pass filter (cutoff 1/128 Hz), and time‐series were corrected for serial autocorrelations using a first‐order autoregressive (AR(1)) model.

First‐level analysis consisted of a general linear model (GLM) with standard (STD; implicitly modeled), deviant contour (C‐deviant), and deviant interval (I‐deviant) regressors convolved with a canonical HRF, plus realignment parameters to account for head motion. To assure a balanced contrast in the second‐level GLM, we used the same number of events (i.e., onsets of the fourth tone in a pattern) for the STD, C‐deviant, and I‐deviant conditions (n = 126). For the STD condition, we first produced a list of the standard events that were preceded and followed by at least 25 other standard events. Then, 126 events were bootstrapped from this list, with the further selection constraint that at least two consecutive of them were not further apart than 4,800 ms (SOA, range 1,200–4,800 ms). These standard events were implicitly modeled in the GLM design matrix. The remaining standard events (n = 882) (STD882), together with C‐deviant (n = 126) and I‐deviant events (n = 126) were explicitly modeled in the GLM design matrix. Finally, we used the contrast [0 1 0] (STD882 C‐deviant I‐deviant) in SPM. This GLM approach is equivalent to modeling the standard events (the ones far away from deviant events) explicitly as a regressor, and contrasting them to the contour deviant events. At the second level, we used a whole‐brain random‐effects analysis using t‐test for the main contrasts C‐deviant > STD and I‐deviant > STD at p < .001 familywise error (FWE) corrected at voxel level.

2.2.5. Volume‐of‐interest extraction

We summarized the BOLD signal in each participant using the first eigenvariate (principal component) of voxels within a sphere of 8 mm radius centered on each participant's local maximum within Heschl's gyrus (HG) and planum temporale (PT) in their left and right hemispheres. This subject‐specific local maximum was identified within a sphere of 20 mm radius centered on the group‐level peak within HG and PT at p < .001, FWE corrected at peak level using random field theory.

2.3. Dynamic causal modeling

DCM uses a biologically inspired generative model of neuronal dynamics to estimate the directed coupling between brain regions and how this coupling changes with stimulus or behavioral context. This context‐dependent coupling is referred to as effective connectivity (Friston, Harrison, & Penny, 2003). DCM models the hierarchical organization of the brain using forward and backward connections between regions, as well as intrinsic connections within a region. We used a two‐state DCM for fMRI (DCM12, revision 7487) to estimate the effective connectivity between HG and PT within the left and right hemispheres, as well as the intrinsic connectivity within each region, given observed hemodynamic measurements (Friston et al., 2003). In two‐state DCM, each region comprises one excitatory and one inhibitory population of neurons. This allows us to model the intrinsic connectivity within each cortical area as an increase or decrease in cortical inhibition (Marreiros, Kiebel, & Friston, 2008) (see Figure 5a for a schematic).

Although fMRI is an indirect measure of neuronal activity based on the observed BOLD signal, the biophysical model employed in DCM is equipped with a detailed hemodynamic forward model that describes how neuronal activity translates into changes in regional blood flow (Friston, Mechelli, Turner, & Price, 2000), blood volume and deoxyhemoglobin concentration (Buxton, Wong, & Frank, 1998) that combine nonlinearly to produce the BOLD signal (Stephan, Weiskopf, Drysdale, Robinson, & Friston, 2007). This means that the neuronal model comprised of excitatory and inhibitory populations can be used to make inferences about both long‐range excitatory connectivity between brain regions as well as local connectivity within a region that reflects changes in excitatory and inhibitory activity (Logothetis, 2008).

Hemodynamic responses to all auditory stimuli (standard stimuli and contour deviants) were mean‐centered and modeled as a driving input to HG in both hemispheres (C‐matrix). Using parametric modulation of the regressor encoding all stimuli, responses to contour deviants compared to standard stimuli were modeled as a change (increase or decrease) of the intrinsic and extrinsic connection strengths (B‐matrix) in relation to the average connectivity estimated from the mean‐centered responses to all auditory stimuli (A‐matrix). We analyzed the intrinsic and extrinsic connectivity between HG and STG in each hemisphere under four different hypotheses about how connection strengths change during auditory contour deviancy: The first DCM comprised a full network, where changes in both feedforward and feedback connections between HG and PT, as well as their intrinsic (inhibitory) connections, encode the differences between deviant and standard conditions. Within PC, this hypothesis states that both forward prediction errors and backward predictions mediate the statistical learning of melodic regularities and that the intrinsic connectivity may encode the precision with which prediction error is broadcasted during belief updating. The second DCM was formulated as a reduced model where only feedforward and feedback connections between HG and PT encode the differences between deviant and standard conditions. According to this hypothesis, both prediction errors and predictions mediate the statistical learning of melodic regularities, in the absence of notable changes in the intrinsic connectivity encoding the precision. The third hypothesis was formulated as another reduced model where only the forward connections from HG to PT encodes the differences between deviant and standard conditions. The hypothesis is here that only forward prediction errors mediate the statistical learning of melodic regularities, in the absence of notable changes in feedback and intrinsic connections. The fourth hypothesis was a null model, where no cortical connections are thought to change during statistical learning of melodic regularities (see Figure 3a for a schematic of different hypotheses). We then inverted the full model using variational Laplace (Friston, Mattout, Trujillo‐Barreto, Ashburner, & Penny, 2007). This provides the posterior probability of connection strengths and the free‐energy approximation to the Bayesian model evidence. The reduced models and the null model were then estimated using Bayesian model reduction (Friston et al., 2016).

2.3.1. PEB analysis of group effects

We then used PEB (Friston et al., 2016; Zeidman et al., 2019) to identify increases or decreases in extrinsic (excitatory) connections between HG and PT and intrinsic (inhibitory) connections within each region at the group level. PEB is a hierarchical Bayesian model in which empirical priors on the connection strengths at the first (single‐subject) level are estimated empirically from the data themselves using a Bayesian GLM at the group level. In this way, PEB provides both the posterior probability of connection strengths and the Bayesian model evidence for Bayesian inference and model comparison at the group level. The model evidence of the PEB model is given by the sum of DCM accuracies for all participants, minus the complexity of both the first‐level DCMs and the second‐level Bayesian GLM. During PEB estimation, we used the updated DCM parameters where the connection strengths had been reevaluated using the group means as priors to obtain the most robust estimates (Zeidman et al., 2019). An advantage of PEB, as opposed to classical random‐effects (RFX) analysis, is that PEB takes not only the mean, but also the uncertainty of individual connection strengths into account. This means that participants with more uncertain parameter estimates will be down‐weighted, while participants with more precise estimates receive greater influence (Zeidman et al., 2019).

3. RESULTS

3.1. Auditory‐cortex functional localizer

Contour deviant stimuli produced significantly greater activation than standard stimuli in bilateral STG (Table 1). Specifically, the contrast C‐deviant > STD revealed four clusters of activation (p _FWE < .001): two localized in the left and right HG (cytoarchitectonic areas Te 1 and Te 1.2) and two more posterior localized in the PT (cytoarchitectonic area Te 3) (Morosan, Schleicher, Amunts, & Zilles, 2005) (Figure 2). Conversely, the contrast between interval deviant stimuli and standard stimuli (I‐deviant > STD) did not produce any significant activation (p _FWE > .05).

TABLE 1.

MNI coordinates of brain regions activated in the C‐deviant > STD contrast (height threshold: T = 6.76, p _FWE < .001; extent threshold: k = 0 voxels)

T statistic	MNI coordinate	Anatomical region	Probabilistic atlas a
8.83	[54 2 ‐4]	Right superior Temporal gyrus	Area TE (1.2) 28% OP4 (PV) 17%
8.54	[66 ‐16 4]	Right superior Temporal gyrus	Area TE (3) 57%
7.93	[‐52 ‐14 4]	Left superior Temporal gyrus	Area TE (1) 46% Area TE (1.2) 13%
7.88	[‐66 ‐22 6]	Left superior Temporal gyrus	Area TE (3) 73%

Note: C‐deviant = contour deviant; STD = standard; r = right hemisphere; l = left hemisphere.

Abbreviation: MNI, Montreal Neurological Institute.

^a Anatomical classification using the SPM anatomy toolbox (Eickhoff et al., 2005).

FIGURE 2.

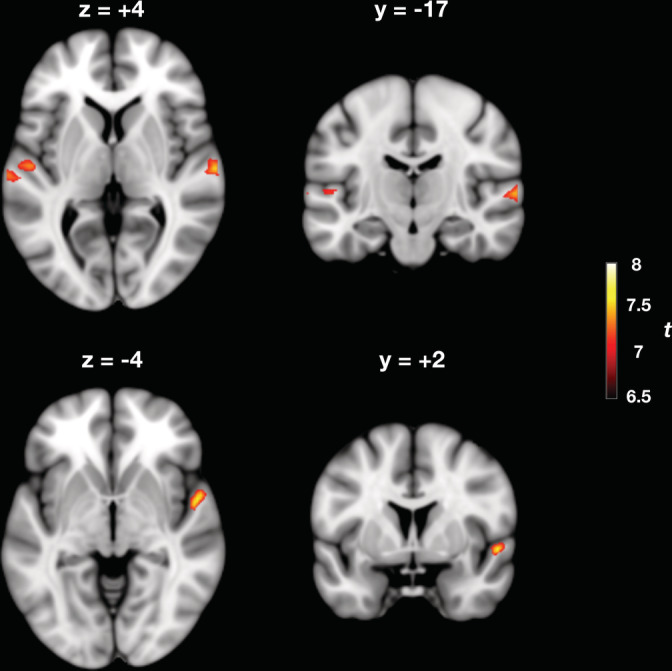
Cortical areas responding to contour deviants in melodic patterns (C‐deviant > STD). Shown in the figure are the cortical loci where event‐related activity was greater for contour deviant events (C‐deviants) compared to the standard events occurring in the same position of the pattern (i.e., the fourth tone) (p < .001, familywise error [FWE] corrected). Activated areas are shown projected onto a Montreal Neurological Institute (MNI) standard template, and include bilateral Heschl's gyrus (HG) and planum temporale (PT). Color map intensities indicate t‐values

3.2. DCM of effective connectivity in the auditory system

The coordinates of the four peak activations observed for the contrast C‐deviant > STD were used to define volumes of interest in the DCM analysis (Figure 3b). Bayesian model comparison (Figure 3a) showed high evidence for a full DCM, where the intrinsic (inhibitory) coupling within regions and the extrinsic (excitatory) coupling between regions were modulated during deviant stimuli, relative to frequent standard stimuli (model posterior probability >.99). Within this bilateral network, we observed a left‐hemispheric increase in (excitatory) feedforward connectivity from HG to PT (posterior probability >.99) and a concomitant decrease in the intrinsic (inhibitory) connectivity within left HG (posterior probability >.99) during deviant melodic stimuli (Figure 4). See Figure 5 for a schematic of the two‐state DCM used in this study.

FIGURE 3.

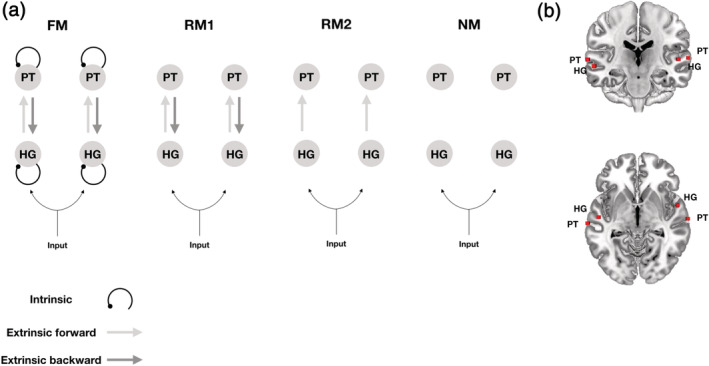
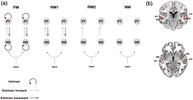
Different hypotheses about effective connectivity. (a) The dynamic causal models comprise a bilateral “input,” four “sources,” and ipsilateral “connections” among (extrinsic connections) and within (intrinsic connections) these sources. HG, Heschl's gyrus; PT, planum temporale. The four models tested had the same anatomical architecture but differed in terms of the embedding connections: intrinsic and extrinsic (forward and backward) in the full model (FM), only forward and backward in the reduced model 1 (RM1), only forward in the reduced model 2 (RM2), and no connections in the null model (NM). (b) Sources (red squares) were defined by using peak activations of the auditory oddball localizer, and are here projected onto an anatomical Montreal Neurological Institute (MNI) standard template

FIGURE 4.

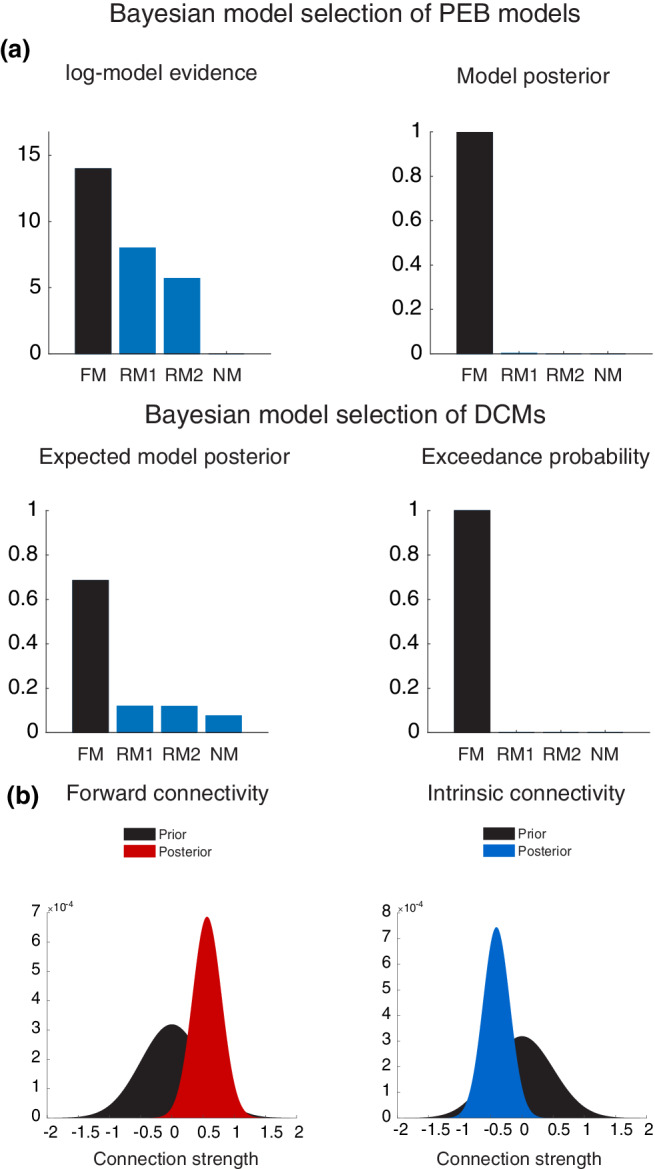
(a) Bayesian model selection of different hypotheses revealed that the full model with extrinsic and intrinsic connections outperforms the other models, both at the first‐ and the second levels of model inference. (b) Posterior probabilities of the excitatory feedforward connection strength from left Heschl's gyrus (HG) to planum temporale (PT) and the intrinsic inhibitory connection strength within left HG. This shows the posterior distribution of the increase in feedforward connection strength (red probability density) and the posterior distribution of the decrease in self‐inhibition (blue density) as they moved away from their prior distribution (black density) after model inversion

FIGURE 5.

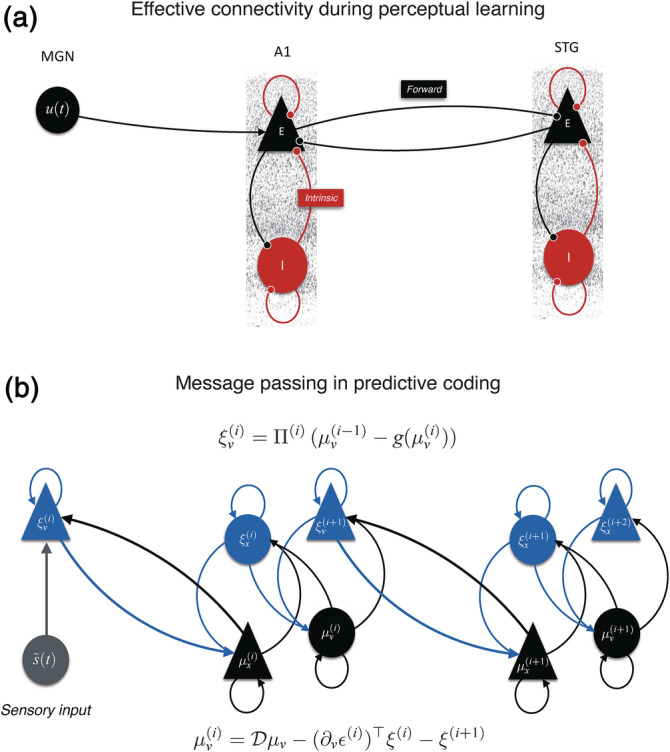
(a) Representation of the two‐state dynamic causal modeling (DCM) with one excitatory (E) and one inhibitory (I) population of neurons. In this cortical network, Heschl's gyrus (HG) receives input from the medial geniculate nucleus (MGN) of the thalamus and is connected to the planum temporale (PT) through (excitatory) forward and backward connections. (b) Message passing scheme proposed by predictive coding. Prediction units (in black) encode expectations (μ) about hidden causes (v) and hidden states (x). The gain of prediction error (ξ) units (in blue) is modulated by their expected precision (Π). Superindices indicate the level of processing in the hierarchy. Time‐dependent sensory input (s(t)) is indicated in gray

4. DISCUSSION

Using DCM on fMRI oddball data, we found BOLD responses for deviant sounds in complex tone patterns to be best explained by a fully connected bilateral auditory network. Within this network, hierarchical Bayesian inference revealed a decrease in inhibitory connectivity within left HG and an increase in feedforward connectivity from left HG to PT. Unlike previous studies, we did not find frontal activity, nor did we find modulations of backward connections in response to oddball sounds.

Our findings can be interpreted in the light of PC, which is a framework for understanding the computational mechanisms of perception and learning in the brain. The key notion in PC is that the brain creates a hierarchical generative model of its environment. Here, higher levels provide predictions or expectations about the hidden causes of sensory inputs. These causes are hidden in the sense that they are not directly observed, but can only be inferred from sensory data, given a generative model of how they were caused. When a sensory input does not conform to prior expectations, the ensuing prediction errors generated at lower levels serve to update beliefs at higher levels to optimize predictions (Friston & Kiebel, 2009).

Crucially, the relative influence of prior expectations and prediction errors on perceptual inference is controlled by their relative precision or confidence (i.e., inverse variance). This means the brain has a first‐order system for expectations and prediction errors that encodes hidden causes in terms of their first‐order statistics, and a second‐order system that encodes the precision of first‐order expectations and prediction errors in terms of their expected precision and ensuing prediction errors on the precision. Biologically, the hierarchical architecture of predictive processing is likely implemented in the brain via feedback and feedforward connections that mediate prediction and prediction errors (Bastos et al., 2012) (Figure 5).

Our DCM results can be mapped onto the above‐mentioned PC scheme (Koelsch, Vuust, & Friston, 2019). Bayesian model selection shows that melodic deviance processing occurs throughout a hierarchy of bilateral superior temporal regions, with a left‐hemispheric lateralization in the modulation of connection strengths during melodic deviance processing. Specifically, we provide strong evidence that mismatch responses were generated by a decrease in intrinsic (inhibitory) connectivity within left HG and an increase in feedforward (excitatory) connectivity from left HG to PT. From a PC perspective, an increase in feedforward connectivity corresponds to the passing of prediction error from lower to higher areas of the hierarchical processing network, so that it can effectively update the internal generative model (Lieder, Daunizeau, Garrido, Friston, & Stephan, 2013; Wacongne, Changeux, & Dehaene, 2012). Similarly, the decrease in intrinsic (inhibitory) connectivity in HG can be interpreted as a precision‐related increase in the gain of the superficial pyramidal cells encoding prediction error (Feldman & Friston, 2010; Kiebel et al., 2007) (Figure 5).

In two‐state DCM, this gain modulation arises from the excitation/inhibition balance of excitatory pyramidal cells and inhibitory interneurons. This interpretation entails that, besides generating prediction error signals, melodic deviants are afforded a higher precision than standards, which is consistent with the role of salient stimuli in the orientation of attention (Hannon & Trainor, 2007; Parr & Friston, 2017; Polich & Criado, 2006). Thus, unexpected sounds would point to the sources in the auditory scene that are most informative and relevant and need to be prioritized for processing through gain mechanisms. This interpretation is also in agreement with studies showing an attentional enhancement of auditory prediction error responses (Garrido, Rowe, Halász, & Mattingley, 2018), which has been associated with an intrinsic gain modulation in superficial pyramidal cells, mediated by a decrease in the input of inhibitory interneurons (Auksztulewicz & Friston, 2015).

Earlier DCM work on the auditory MMN using M/EEG data (e.g., Dietz et al., 2014; Garrido et al., 2007, 2009; Kiebel et al., 2007) found that temporal (A1 and STG) and frontal sources (IFG) in the DCM models, with forward, backward and intrinsic modulations, were the best to explain MMN evoked responses to frequency deviants. Unlike previous studies, we did not find a modulation of backward connections, which may be due to a number of reasons. First, we have taken advantage of the recently developed PEB approach (Friston et al., 2016; Zeidman et al., 2019), which allows more precise inferences at the single parameter level, informed by empirical priors taken from group‐level estimates, as compared to classical random‐fixed effect modeling. The lack of a modulation of feedback connectivity is consistent with the hypothesis proposed by Koelsch et al. (2019) according to which predictions in auditory oddball paradigms are so precise that prediction errors keep being elicited at lower hierarchical levels, without generating a major update of the predictive model at higher levels, something typically associated with feedback loops. Second, the stimulation used in past studies is inherently different from ours. In past DCM studies, participants were presented with “classical” oddball stimulation, whereby trains of standard tones were randomly interleaved with frequency deviants. The more complex stimulation of the present study might have affected the connectivity of the auditory temporal network differently. To our knowledge, our study is the first to look at the neural dynamics underlying the violation of complex regularities during listening to melodic patterns.

Another reason for the discrepancies might be that the neural “architecture” employed in past DCM models included approximate locations of the MMN generators, which may have reduced their construct validity (Friston, 2003). At present, there has been a lack of anatomical accuracy in the characterization of cortical networks recruited during deviance detection. In most DCM studies, cortical sources are defined a priori, based on previous fMRI studies using different experimental setups and stimuli (e.g., see Garrido et al., 2007, 2009; Kiebel et al., 2007). This may have led to the inclusion of sources, such as the right IFG, that fit the measured MMN waveform but that were not actual generators for the sample at hand. In some M/EEG studies, this issue was addressed with source reconstruction (Auksztulewicz & Friston, 2015; Fardo et al., 2017). However, the lower spatial resolution and inherent spatial inverse problem of M/EEG techniques, relative to fMRI, make it harder to resolve MMN cortical generators from neighboring neural populations, thus producing coarser maps at which these computational units operate. To our knowledge, this study is the first to use DCM on auditory networks functionally defined within the same fMRI sample in an event‐related design.

The fMRI oddball localizer in the present study indicates that melodic contour mismatch responses are encoded in two core regions of the bilateral superior temporal plane: HG and PT. No significant modulation of brain activity was observed for interval changes. Contour processing is more fundamental and basic than melodic interval processing. It is critical in the perception of music as well as speech (Patel, Peretz, Tramo, & Labreque, 1998), develops earlier in the ontogeny of individuals (Lamont, 2016), and changes in its content are more easily detected than interval changes (Edworthy, 1985). Conversely, encoding of interval information requires more intensive training and long retention intervals (Dowling & Bartlett, 1981). In the current experiment, the use of the BP scale ensures that there is no contamination of prior knowledge from earlier music life exposure (Ross & Hansen, 2016). The fact that a tonal hierarchy is not readily available to the participants may have hindered the detection of interval changes. It is thus not surprising that the modulation of responses to interval changes was not strong enough to produce detectable effects.

The auditory network identified in the current experiment is consistent with previous fMRI studies addressing the location of MMN generators for pitch deviants (e.g., Liebenthal et al., 2003; Molholm et al., 2005; Opitz et al., 2002; Schönwiesner et al., 2007). All of them reported a major activity at bilateral locations of the STG to pitch deviants, including primary and secondary auditory cortices, while only a minority reported activation of frontal areas (Alho, Rinne, Herron, & Woods, 2014; Deouell, 2007). In this work, we extend this finding to more complex auditory patterns. Habermeyer et al. (2009) were the first to address a high‐resolution spatial cortical origin of preattentive melodic deviance detection, using a paradigm where streams of five‐tone melodic patterns playing in the equal‐tempered scale were randomly interleaved by melodic contour deviations. When comparing groups on the deviant responses against the silent baseline, they observed activation of a fronto‐temporal auditory network in musicians that included auditory—middle and superior temporal gyri—and frontal cortices—left IFG and right ventromedial prefrontal cortex. This study was the first to show the effects of neuroplastic changes induced by long musical training on a preattentive deviance detection auditory network that included frontal generators. Their result supports previous studies showing an improved and more accurate preattentive processing of deviant stimuli in expert musicians (Kölsch, Schroger, & Tervaniemi, 1999; Pantev et al., 2003). In contrast to our study, the authors did not find any significant results for the comparison between deviant and standard conditions, neither in the two groups separately nor across all subjects. This discrepancy between results could be explained by a number of factors. The first is methodological and likely relates to the use of different stimulation paradigms and analyses. In our study, pairs of contour deviant events were closer in temporal succession (SOA <4.8 s vs. an SOA of 16.8–19.2 s in Habermeyer's study). This could allow for an additive effect on the measured deviant BOLD response and, thus, for a more robust activation produced by the deviant versus standard contrast. Furthermore, different strategies in the extraction of standard tones (pseudorandom sampling vs. random sampling), and the way standard events were modeled in GLM (partly implicit vs. fully explicit) may have affected the detection of activity in the traditional deviant vs. standard contrast. These hypotheses require further investigation. Another reason might relate to the power to detect the main contrast, with a significantly smaller sample size in Habermeyer's study (N = 16, including musicians and nonmusicians).

Unlike Habermeyer et al. (2009), we did not find modulation of frontal lobe activity. A first plausible account is the virtual absence in our paradigm of top‐down “schematic” expectations, which are thought to be related to frontal areas (Garza Villarreal, Brattico, Leino, Ostergaard, & Vuust, 2011; Koelsch, 2002). Frontal sources yield in general a lower signal‐to‐noise compared to temporal sources, and their activity is difficult to target with the low temporal resolution of fMRI techniques. For example, it is known that higher‐order cortical areas, including BA 44 and BA 45, exhibit larger intersubject anatomical variability than primary and secondary sensory areas (Fischl et al., 2008), resulting in a poorer alignment during normalization to standard space. This may account for a decrease in the SNR when traditional whole‐brain group‐level analyses are performed (see Fedorenko, Hsieh, Nieto‐Castañón, Whitfield‐Gabrieli, & Kanwisher, 2010 for a similar discussion). Also, EEG models suggest that frontal activity relies on a smaller number of neurons than activity in STG, and that an increase in the BOLD signal in frontal areas is smaller than in STG regions. Thus, it is more difficult to detect activity in frontal than in temporal regions, using the same threshold and contrast (Deouell, 2007). Evidence for a frontal contribution to MMN is also scarce for fast‐tracking techniques such as M/EEG (Deouell, 2007). For example, EEG frontal dipoles do not greatly improve the adequacy of inverse models with bilateral superior temporal dipoles, which alone often explained >90% variance in brain activity. A second account concerns the recruitment of attention brain networks. Frontal generators are thought to trigger for attention location (Näätänen, 1990). According to this view, contour deviants might not be salient (or large) enough to trigger an attention switch and thus to reclute the frontal generators (Opitz et al., 2002). Nevertheless, most participants of our study reported hearing of deviant sounds during fMRI recording. Also, the relation between deviant interval‐size and frontal activation is not straightforward, and small pitch deviants can recruit IFG more than larger pitch deviants (Doeller et al., 2003).

In conclusion, consistent with PC, our results show that learning of complex auditory patterns is associated with changes in excitatory feedforward connections for encoding prediction errors and changes in intrinsic connectivity for encoding the precision of prediction errors within the auditory cortex. Contrary to previous literature, our findings support an interpretation whereby intrinsic and extrinsic neuronal circuitry in the superior temporal gyrus “alone” may establish models of short‐term statistical regularities, generate predictions, and update the internal model when predictions are not fulfilled. Our findings highlight the need to account for the type of stimulus and the stimulation paradigm, the methods of spatial localization and the statistical inference procedures, as factors influencing the generalizability of DCM findings.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

AUTHOR CONTRIBUTIONS

Massimo Lumaca: Conceptualization, Investigation, Formal analysis, Visualization, Project administration, Writing – Original draft, Writing – Review and Editing. Martin J. Dietz: Conceptualization, Methodology, Formal analysis, Visualization, Writing – Original draft, Writing – Review and Editing. Niels Chr. Hansen: Writing – Review and Editing. David R. Quiroga‐Martinez: Writing – Review and Editing. Peter Vuust: Supervision, Funding acquisition.

Lumaca M, Dietz MJ, Hansen NC, Quiroga‐Martinez DR, Vuust P. Perceptual learning of tone patterns changes the effective connectivity between Heschl's gyrus and planum temporale. Hum Brain Mapp. 2021;42:941–952. 10.1002/hbm.25269

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.