External validation of prognostic models: what, why, how, when and where?

Abstract

Prognostic models that aim to improve the prediction of clinical events, individualized treatment and decision-making are increasingly being developed and published. However, relatively few models are externally validated and validation by independent researchers is rare. External validation is necessary to determine a prediction model’s reproducibility and generalizability to new and different patients. Various methodological considerations are important when assessing or designing an external validation study. In this article, an overview is provided of these considerations, starting with what external validation is, what types of external validation can be distinguished and why such studies are a crucial step towards the clinical implementation of accurate prediction models. Statistical analyses and interpretation of external validation results are reviewed in an intuitive manner and considerations for selecting an appropriate existing prediction model and external validation population are discussed. This study enables clinicians and researchers to gain a deeper understanding of how to interpret model validation results and how to translate these results to their own patient population.

INTRODUCTION

In recent years there has been a surge in the development of prognostic prediction models in the medical field. A prediction model is a mathematical equation that calculates an individual’s risk of an outcome based on his/her characteristics (predictors). Such models have been of interest due to their potential use in personalized medicine, individualized decision-making and risk stratification. This has spurred researchers to develop a myriad of prediction tools, risk scores, nomograms, decision trees and web applications. Although this development has improved patient care and outcomes in some fields, the quality and clinical impact of these prediction models lag behind their projected potential. One of the reasons is that although many models are developed, only a small number are externally validated, and the nephrology field is no exception [1–3]. As the performance of prediction models is generally poorer in new patients than in the development population, models should not be recommended for clinical use before external validity is established [4]. To combat research waste, it is imperative that models are properly externally validated and existing models are compared head-to-head in comprehensive external validation studies. In this article we aim to provide a framework for the external validation of prognostic prediction models by explaining what external validation is, why it is important, how to correctly perform such a study, when it is appropriate to validate an existing model and which factors should be taken into account when selecting a suitable validation population. Our aim is to provide readers with the tools to understand and critically review external validation studies. Furthermore, we hope that this study may stimulate researchers to externally validate prognostic prediction models and be used as a framework for designing an external validation study.

WHAT IS EXTERNAL VALIDATION?

To assess whether a prediction model is accurate, demonstrating that it predicts the outcome in patients on whom the model was developed is not sufficient. As the prediction formula is tailored to the development data, a model may show excellent performance in the development population but perform poorly in an external cohort [1]. External validation is the action of testing the original prediction model in a set of new patients to determine whether the model works to a satisfactory degree.

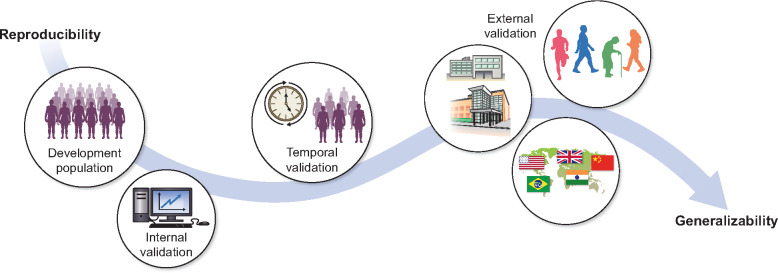
Different validation strategies, such as internal, temporal and external validation, can be distinguished, varying in levels of rigor. Internal validation makes use of the same data from which the model was derived [4–6]. The most used forms of internal validation, namely split-sample, cross-validation and bootstrapping, are explained in Box 1. Temporal validation means that the patients in the validation cohort were sampled at a later (or earlier) time point, for instance, by developing a model on patients treated from 2010 to 2015 and validating the model on patients treated in the same hospital from 2015 to 2020. Such splitting of a single cohort into development and validation sets by time is often regarded as an approach that lies midway between internal and external validation [4, 8]. External validation means that patients in the validation cohort structurally differ from the development cohort. These differences may vary: patients may be from a different region or country (sometimes termed geographic validation), from a different type of care setting or have a different underlying disease [5, 8]. Independent external validation generally means that the validation cohort was assembled in a completely separate manner from the development cohort [9]. The various types of validation are illustrated in Figure 1.

Box 1:

The basis of internal validation types explained

Split-sample validation

A cohort of patients is randomly divided into a development cohort and internal validation cohort. Often two-thirds of the patients are used to make a prognostic model, and this model is then tested on the remaining one-third.

Cross-validation

Cross-validation can be seen as an extension of the split-sample approach. In a 10-fold cross-validation, the model is developed on 90% of the population and tested in the remaining 10%. This is repeated 10 times, each time using another 10% of the population for testing so that all patients have been included in the test group once.

Bootstrapping

Bootstrapping is a resampling method. For example, in a development population in which a total of 1000 patients are included, we may perform a 200-fold bootstrap internal validation. This entails that from the 1000 included patients, a ‘new’ and slightly different cohort of 1000 patients is randomly selected by sampling with replacement (each patient may be sampled multiple times) [7]. This process is repeated numerous times; in our example, it is repeated 200 times to form 200 resampled cohorts (which each include 1000 patients). In each of these resampled cohorts, the model performance is tested and these results are pooled to determine internal validation performance.

FIGURE 1.

Illustration of different validation types. A developed prediction model can be validated in various ways and in populations that differ from the development cohort to varying degrees. Internal validation uses the patients from the development population and can therefore always be performed. As internal validation does not include new patients, it mainly provides information on the reproducibility of the prediction model. Temporal validation is often considered to lie midway between internal and external validation. It entails validating the model on new patients who were included in the same study as patients from the development cohort but sampled at an earlier or later time point. It provides some information on both the reproducibility and generalizability of a model. External validation mainly provides evidence on the generalizability to various different patient populations. Patients included in external validation studies may differ from the development population in various ways: they may be from different countries (geographic validation), from different types of care facilities or have different general characteristics (e.g. frail older patients versus fit young patients). Not every model needs to be validated in all the ways depicted. In certain cases, internal validation or only geographic external validation may be sufficient; this is dependent on the research question and size of the development cohort.

It is a misconception that randomly splitting a dataset into a development set and validation set is a form of external validation. This split-sample approach is generally an inefficient form of internal validation, specifically in small datasets. When datasets are sufficiently large to split into validation subgroups, a temporal or geographical split is preferable to a random split [4, 6, 10]. Ideally, external validation is performed in a separate study by different researchers to prevent the temptation of fine-tuning the model formula based on external validation results [1, 9, 11]. To avoid research becoming inbred and moving forward with the model that was ‘sold’ in the best manner, some advocate that external validation should not be included in the model development study [9, 11]. This conflicts with the increasing number of high-impact journals that require prediction model development papers to include an external validation. Although stimulating external validation in this manner may decrease the number of models that are developed but never validated, independent assessment and validation of study results remains crucial to the scientific process.

WHY IS EXTERNAL VALIDATION IMPORTANT?

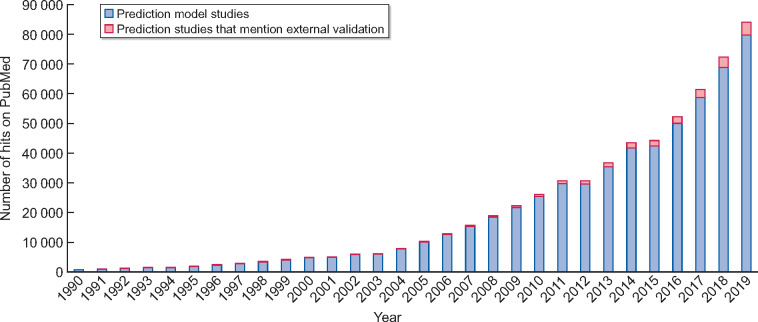
Prediction models, risk scores and decision tools are becoming a more integral part of medical practice. As we move towards a clinical practice in which we want to individualize treatment, care and monitoring as much as possible, it is imperative to collect information on an individual’s risk profile. Before implementation of any prediction model is merited, external validation is imperative, as prediction models generally perform more poorly in external validation than in development [1]. If we base clinical decisions on incorrect prediction models, this could have adverse effects on various patient outcomes. For instance, if clinicians were to base dialysis preparation on a prediction model that underpredicts risk, more patients would start dialysis without adequate vascular access, which in turn could lead to higher morbidity and mortality rates. Considering the number of prediction models that are developed, the percentage of external validation studies is small. A quick PubMed search retrieved 84 032 studies on prediction models, of which only 4309 (5%) mentioned external validation in the title or abstract (see Figure 2). Although the development of a new and potentially better model might be tempting for researchers, the overwhelming majority of developed models will never be utilized. External validation of existing models may combat this research waste and help bridge the gap between the development and implementation of prediction models.

FIGURE 2.

Cumulative histogram of the number of hits on PubMed when using a simple search strategy of prediction models and adding external validation to this search. Search strategies are given in Appendix A. PubMed was searched from 1961 to 2019. The total number of prediction model studies retrieved was 84 032, of which 4309 were found when adding an external validation search term. The percentage of studies with external validation increased over the years; in 1990, 0.5% of published prediction studies mentioned external validation, while in 2019 this was 7%.

In nephrology, some models are used in current practice, but the use of scores and prediction tools seems to lag behind compared with fields such as oncology or surgery. For instance, the Kidney Failure Risk Equation, which predicts the risk of kidney failure in patients with chronic kidney disease, has made a significant impact and has been proposed for use to help general practitioners determine when to refer patients to a nephrologist [12, 13]. A more recent prediction model by Grams et al. (the CKD G4+ risk calculator) predicts multiple clinical outcomes and has been recommended for use in patients with advanced CKD [14, 15]. Moreover, prediction models are implemented in the US kidney transplant allocation system to predict kidney graft quality and life expectancy of the recipient [16, 17].

External validation is necessary to assess a model’s reproducibility and generalizability [18]. Evaluating reproducibility, sometimes called validity, is a cornerstone of all scientific research. Prediction models may correspond too closely or accidentally be fitted to idiosyncrasies in the development dataset. This is called overfitting. If by chance half the patients that developed kidney failure were wearing red socks, an overfit model may include sock colour as a predictor of kidney failure. This will result in predicted risks that are too extreme when used in new patients [19]. Therefore it is important to test whether the prediction formula would be valid in new individuals that are similar to the development population (reproducibility). Testing of reproducibility can be done through internal and external validation. In a large enough dataset, internal validation can give an indication of the model’s external performance [20]. When assessing the reproducibility it is usually sufficient to perform a temporal or geographic validation, as this will determine if the model performs satisfactorily in new patients that are similar to the development cohort. Generalizability (also called transportability) involves exploring whether the prediction tool is transportable to a separate population with different patient characteristics. For instance, we might be interested in whether an existing prediction model developed for a primary care population might also be valid for patients treated in secondary care. Generalizability cannot be assessed once but should be examined through independent external validation for each population in which the use of the model is desirable if the population differs considerably in setting, baseline characteristics or outcome incidence.

In many prediction articles, a validation cohort that highly resembles the development cohort is presented as an advantage. This means that the validation can only assess reproducibility and, depending on the research question, it may be a greater strength to demonstrate that a prediction model is generalizable to different populations.

HOW DOES EXTERNAL VALIDATION OF A PREDICTION MODEL WORK?

Validating a prediction model essentially comes down to comparing the predicted risks to the actual observed outcomes in a patient population. There are various methods that can be used to compare these in order to assess predictive performance. For researchers planning an external validation study we highly recommend consulting the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis checklist and explanation and elaboration document [4]. Methods for validation of the two most used regression models in prediction, namely logistic and Cox proportional hazards, are discussed below.

Calculating the predicted risk

The first step to validating an existing prediction model is to calculate the predicted risk for each individual in the external validation cohort. To compute the predicted risk, we need the prediction formula from the existing model and the predictor values per individual. A key component of a prediction formula is the prognostic index (PI), also called the linear predictor. The PI is calculated by taking the sum of each of the model’s predictors multiplied by their regression coefficients (β). The PI is then transformed to a risk (between 0 and 1); the transformation formula differs by the type of statistical model (see Box 2). In the case of a logistic regression, the model intercept (a constant that is added to the PI) is needed to calculate an individual’s risk. For Cox proportional hazards prediction models the baseline hazard at a specified time point is needed. While the PI differs per individual, the intercept and baseline hazard remain constant. Unfortunately, many prediction papers do not publish the intercept or baseline hazard.

Box 2:

Probability equations for logistic and Cox proportional hazards prediction models. Prognostic index (sometimes termed linear predictor)

$$\mathrm{Prognostic}\mathrm{ }\mathrm{Index}\mathrm{ }\left(\mathrm{PI}\right)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{\beta }}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}$$

Logistic regression:

$$\begin{array}{c}\beta =\text{ln}\left(\text{odds} \text{ratio}\right)\\ \mathrm{P}\left(\text{probability}\right)=\frac{1}{{1+\mathrm{e}}^{{-(\beta }_0+\text{PI})}}\\ {\beta }_0=\text{the} \text{intercept}\end{array}$$

Cox proportional hazards regression:

$$\begin{array}{c}\beta =\text{ln}\left(\text{hazard} \text{ratio}\right)\\ \mathrm{P}\left(\text{probability}\right)=1-{\left(S_0(t)\right)}^{{\mathrm{e}}^{\text{PI}}}\end{array}$$

$S_0\left(t\right)=$the baseline hazard of the outcome for specified prediction-horizon t.

Assessing model performance

Two key elements of assessing the predictive performance are calibration and discrimination. Calibration assesses how well the absolute predicted risks correspond to the observed risks on a (sub)group level. Discrimination is a relative measure of how well a model can discriminate between patients with and without the event of interest. When models are developed it is important that the prediction horizon is explicitly specified, for example, a 2-year or 5-year risk. After all, if we were to predict mortality in a cohort with 150 years of follow-up without specifying the prediction horizon (how far ahead the model predicts the future), everyone’s risk would be 100%.

Calibration

Calibration determines whether the absolute predicted risks are similar to the observed risks [21]. There are different measures of calibration, including calibration-in-the-large, calibration plot and calibration slope.

Calibration-in-the-large is the average predicted risk in the entire validation population compared with the average observed risk [5]. For instance, if on average a model predicts 20% risk of mortality and we observe that 21% of patients died, the calibration-in-the-large is rather accurate. When validating a logistic prediction model, time to event is not considered and the average observed risk is the proportion of patients who experience the outcome within the prediction horizon. For a Cox proportional hazards prediction model in which censoring is assumed to be uninformative, the observed risk can be estimated by the Kaplan–Meier cumulative incidence.

A calibration plot compares predicted risks to observed risks within subgroups of patients, based on the predicted probabilities. An example of a calibration plot with interpretation is given in Figure 3. A calibration plot provides the most information on calibration accuracy and should always be included in an external validation. It allows us to recognize patterns of miscalibration, for instance, if a model only underestimates in low-risk patients.

FIGURE 3.

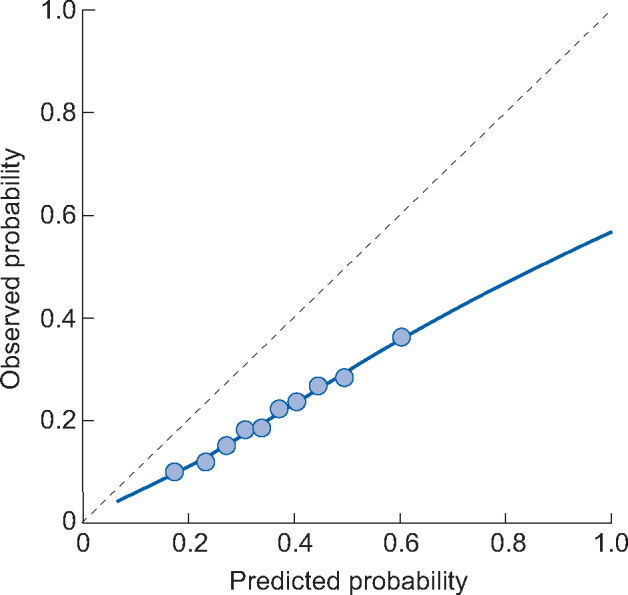
Example of a calibration plot. The dotted line at 45 degrees indicates perfect calibration, as predicted and observed probabilities are equal. The 10 dots represent tenths of the population divided based on predicted probability. The 10% of patients with the lowest predicted probability are grouped together. Within this group the average predicted risk and proportion of patients who experience the outcome (observed probability) are computed. This is repeated for subsequent tenths of the patient population. The blue line is a smoothed lowess line. For a logistic model this is computed by plotting each patient individually according to their predicted probability and outcome (0 or 1) and plotting a flexible averaged line based on these points. In this example calibration plot we can see that the model overpredicts risk; when the predicted risk is 60%, the observed risk is ∼35%. This overprediction is more extreme for the high-risk x-axis. If a prediction model has suggested cut-off points for risk groups, then we recommend plotting these various risk groups in the calibration plot (instead of tenths of the population).

The calibration slope can be computed by estimating a new logistic or Cox proportional hazards model with the PI as the only predictor in the validation dataset. The regression coefficient given to the PI is the calibration slope. A perfect calibration slope is 1, a calibration slope <1 is seen in overfit models that overestimate the risks [5, 21]. The often-used Hosmer–Lemeshow test is not recommended, as it only provides an overall measure of calibration and is highly dependent on sample size [22, 23].

Discrimination

To assess discrimination the concordance index (C-index) can be computed. This measure assesses whether patients who experience the outcome have a higher predicted risk than patients who do not. For discrimination, it does not matter if the absolute predicted risk is 8% or 80%, as long as the patient with the outcome has the higher risk. Therefore discrimination can also be assessed using the PI or risk score.

For logistic regression models, the C-index is equivalent to the area under the curve (AUC). To compute this, all possible pairs between a patient with and without the outcome are analysed. A pair is concordant if the patient with the outcome has a higher predicted risk than the patient without the outcome. A C-index of 1 is perfect and 0.5 is equivalent to chance. A C-index of 0.60 means 60% of all possible pairs were concordant, and this is generally considered rather poor discrimination, while a C-index of 0.8 is usually considered good and ≥0.9 is excellent [24].

For Cox proportional hazards prediction models a time-to-event C-index such as Harrel’s C-index or Uno’s C-index can be computed [21, 25]. In these measures, two patients who both experience the outcome can also be paired up; patients are then considered a concordant pair if the patient who gets the outcome sooner has the higher predicted risk.

Discrimination versus calibration

When assessing the overall performance of a prognostic model, it is important to take both discrimination and calibration into account, as well as the intended use of the model [4, 26, 27]. Good discrimination is important, as it enables the model to correctly classify patients into risk groups [26]. If the aim is to select a group of patients with the highest risk for a clinical trial, good discrimination is most important. Calibration is important, as the model should communicate an accurate absolute risk to patients and physicians. A predicted risk that is too high or too low may result in incorrect treatment decisions. Other performance measures of overall fit (e.g. R², Brier score), reclassification (e.g. net reclassification index, integrated discrimination index) or clinical usefulness (e.g. net benefit, decision analysis) may also be assessed but are generally complementary to the discrimination and calibration results [22].

Model formulas versus risk scores

Many prediction articles do not present the full model formula but instead simplify this to a risk score with a corresponding absolute risk table. For instance, this table may indicate that a score of 5 points corresponds to an absolute risk of 20%. If the risk score is intended for clinical use, the score itself should be externally validated rather than the underlying model. Unfortunately, development studies often only present relative risks per predictor, making it impossible to determine an individual’s absolute predicted risk.

Model updating

Model updating aims to improve upon existing prediction models by adding more predictors or changing part of the formula to better suit the external population; the latter is also called recalibration. Opinions on whether model updating is appropriate in external validation differ among researchers. Some say that even with very slight updates the researchers are in fact developing a new prediction model, which in turn requires internal and external validation to assess validity [19, 28]. Others encourage adjusting the model to better fit the external validation cohort [18, 29, 30]. In a validation study in which the model is poorly calibrated or the full model formula is not provided, we would only recommend conservative model recalibration by adjusting the model intercept or baseline hazard.

WHEN IS A PREDICTION MODEL SUITABLE FOR EXTERNAL VALIDATION?

Whether prediction models are suitable for external validation mainly depends on clinical context. A model that is proposed for implementation in clinical practice or risk stratification in research should be externally validated for these populations. By carefully exploring the potential use, it should be determined whether the included predictors and outcome definitions are appropriate. If multiple developed prediction models are considered appropriate, the availability of model information, potential risk of bias and reported predictive performance may help guide model selection. These considerations are discussed below.

In general for external validation, prediction models that provide the entire model formula and specify the prediction horizon are preferable to models that do not allow for absolute risk calculations. If the full model formula is not available, then calibration cannot be assessed without updating the prediction model.

Furthermore, a model that was developed with a low risk of bias is favoured for external validation. A high risk of bias in prognostic model development studies may lead to systematically distorted estimates of predicted risk. Bias in prognostic models can be assessed using the Prediction model Risk Of Bias ASsessment Tool tool [31]. Some methodological flaws from the development study can be corrected in external validation. For instance, the sample size can be increased or the patient inclusion criteria may be adapted. However, some methodological issues that potentially induce bias cannot be refuted through external validation. This may be the case if the predictors are measured later than the relevant moment of prediction, continuous predictors are modelled inappropriately or the prediction horizon is unsuitable. For instance, if a model is intended for use in kidney transplant allocation, the predictors should be measured prior to transplantation and not during or after.

Finally, predictive performance reported in model development or previous validation may be considered when deciding whether an existing model should be externally validated. The predictive performance should be placed in the context of the intended use and existing literature, as some outcomes are more difficult to predict than others. For instance, long-term outcomes after kidney transplantation are difficult to predict accurately. On the other hand, correctly discriminating between primary care CKD patients who will need renal replacement therapy and those who will not is easier.

It is often the case that researchers who develop a new prediction model also externally validate a well-known existing prediction model in their development cohort and conclude that their new model shows superior performance. This is an inappropriate comparison, as the researchers then compare performance in development or internal validation to another model’s performance in external validation. The newly developed model will almost always seem superior, as it is optimally designed to fit the data. The direct comparison of performance between two existing prediction models should be done in an external validation dataset that is independent of both model development cohorts. When various prediction models for the same outcome and population are available, a comprehensive external validation of multiple prediction models on the same cohort can provide a head-to-head comparison of predictive performance between models [32]. Direct comparison provides evidence regarding which model performs best and can provide model recommendations for future research and clinical practice.

WHERE SHOULD A PREDICTION MODEL BE EXTERNALLY VALIDATED? CHOOSING THE VALIDATION COHORT

Ideally, external validation studies are performed in large observational cohorts (retrospective or prospective) that have been carefully designed to accurately represent a specific real-world patient population that is seen in the clinic. Randomized controlled trial populations are usually less suitable; these patients are often healthier than most patients seen in the clinic and predictors may be measured differently than is standard practice. There should be clear inclusion and exclusion criteria and efforts to minimize missing data as well as loss to follow-up. The sample size should be adequate, particularly the number of events. Some simulation studies have shown that in validation a minimum of 100 events (and 100 non-events) are needed and ≥200 events are preferred [33, 34]. Preferably, all predictors are included in the validation dataset. Changing the measurement procedure of a predictor may influence model performance and has been shown to induce miscalibration [35].

The optimal degree of resemblance between a validation and development cohort depends on whether researchers want to assess reproducibility or transportability. Most importantly, a validation population should include patients on whom clinicians would want to use the prognostic model. The moment of prediction should be when clinical decisions will be made or when informing patients on their prognosis is beneficial. For instance, this may be at the first referral to a nephrologist or shortly after kidney biopsy.

Heterogeneity in predictor effects will influence a model’s performance across different settings and populations [36]. Heterogeneity of predictor effects means that the same predictor may have different prognostic value in varying populations. For instance, socio-economic status may be an important prognostic factor in countries with privatized healthcare systems, while it is less predictive of outcomes in countries with universal healthcare. Such heterogeneity will most likely lead to poorer discrimination and calibration in validation.

Additionally, differences in outcome incidence can also affect a model’s performance and will mainly induce miscalibration. Miscalibration due to differences in outcome incidence is likely to occur when testing the transportability across various care settings. The model can then be updated in a conservative manner by adjusting the baseline hazard or model intercept to better suit the average outcome risk in an external population.

Finally, differences in case mix between the development and validation cohorts can significantly influence predictive performance, even if the predictor effects are the same [36]. In prediction studies, case mix refers to the distribution of predictor values. For instance, a mortality prediction model that includes age as a predictor, will have better discrimination in a population with ages ranging from 18 to 100 years than in a population with ages ranging from 40 to 60 years: a large variation in predictor values will make it easier for the model to discriminate between patients who do and do not have the outcome. Differences in case mix may influence model performance positively or negatively. In a comprehensive external validation study from our research group, we validated mortality prediction models that were developed on haemodialysis (HD) patients [3]. Table 1 shows the discrimination results from this study, in which we stratified our dialysis population into HD and peritoneal dialysis (PD) patients. Despite all validated models being developed on HD patients, the models had a considerably better discrimination in our PD subgroup. This is due to the fact that the PD group was more heterogeneous in predictor levels: the age range was broader and the group included both relatively healthy and extremely frail patients.

Table 1.

Difference in discriminatory performance of mortality prediction models when validated on a population of HD versus PD patients

Prediction model	Original	Discrimination: C-statistic
	Population	HD	PD
Floege 1	HD	0.70	0.78
Floege 2	HD	0.71	0.78
Holme	HD	0.71	0.77
Mauri	HD	0.67	0.80
Hutchinson	HD	0.67	0.77

All prediction models listed were exclusively developed on an HD population. This table was adapted from Table 4 published in a study by Ramspek et al., with permission [3].

As exemplified above, the degree of relatedness between development and external validation can greatly influence model performance. In order to interpret to what extent external validation is testing reproducibility versus generalizability, case mix should be compared between the development and validation cohort. This can be done by comparing baseline characteristics between both cohorts. If individual participant data from development and validation cohorts are available, more advanced statistical approaches have been developed to calculate an overall measure of similarity between cohorts [18].

Although it is preferable to have one prediction model that is valid in all settings and individuals, researchers should strive to validate models in clinically relevant subgroups as well. When validating a model predicting mortality in a research cohort that includes patients with CKD Stages 1–5, paediatric kidney patients, dialysis patients and transplant recipients, it will be easier to discriminate between patients who will and will not die. However, mortality prediction is probably not relevant for clinical decisions in many of these patients and it would be preferable to assess mortality risk in more homogeneous patient groups. It is difficult to determine when a model has been sufficiently externally validated. This is dependent on the research question and if the aim was to determine reproducibility or generalizability. For instance, if a developed model is only meant for local use and the development dataset is large, internal validation may be sufficient. If the research question is whether a prediction model developed in the USA is transportable to a European population, geographic external validation should be performed. The model may then be recalibrated to different countries. This has been done with the Framingham model, which has been recalibrated to patient populations in various countries including the UK [37]. As standard practice changes over time, models are ideally validated every few years to ensure that the prediction tool is still valid. This is probably only feasible for models that are internationally integrated in clinical practice and have a wide reach.

BEYOND EXTERNAL VALIDATION OF REGRESSION MODELS

In recent years, prediction models based on artificial intelligence and machine learning have become a hot topic [38]. In principle, all methodologic considerations surrounding external validation are also valid in machine-learning algorithms. However, the inherent complexity of these models complicates risk calculation and external validation of such ‘black-box’ models is still highly infrequent [39]. Successful external validation of any prediction tool is ideally followed by research that assesses the clinical impact of the model. This can be done by randomizing use of a prediction model between physicians and assessing whether use improves patient outcomes such as morbidity or quality of life. While external validation studies are rare, clinical impact studies are hardly ever performed. Decision-analytic studies may provide evidence of clinical impact, but a prospective randomized comparative impact study is the ideal method to assess clinical effectivity [22, 40–42].

CONCLUSION

In this article we have provided a framework for interpreting and conducting external validation studies of prognostic models. A summary of the key points, including dos and don’ts is given in Table 2. This article may enable clinicians to critically assess external validation studies of prognostic models. Furthermore, it may serve as the starting point for conducting an external validation study.

Table 2.

Key points, dos and don’ts concerning the external validation of prognostic models

Key points	Dos	Don’ts
What is external validation?
External validation is testing a prediction model in new individuals External validation cohorts may differ from the development cohort in geographic location, care-setting or patient characteristics	Do externally validate prediction models in separate studies and by independent researchers	Do not perform a random split-sample validation; this is an inefficient type of internal validation
Why is external validation important?
External validation is needed to determine a model’s reproducibility and transportability Most developed models are never validated or used, which leads to significant research waste.	Do assess a prediction model’s transportability for each population in which clinical usage is desired	Do not implement a prediction model in clinical practice before external validity has been established
How does external validation of a prediction model work?
Validating a prediction model essentially means comparing predicted risks to observed outcomes Discrimination and calibration are the most important elements of model performance	Do externally validate the model in the form which is intended for use; this may be a simplified risk score	Do not extensively update a prediction model without subsequently determining its external validity in new individuals
When is a prediction model suitable for external validation?
Prediction models which are appropriate for the intended clinical use, regarding predictors and outcome, are suitable for external validation Models which allow an individual’s absolute risk calculation, were developed with a low risk of bias and show relatively good predictive performance in previous validation are preferred	Do assess whether design flaws in model development cause biased predictions by correcting these flaws in the external validation	Do not externally validate an existing model in the development cohort of a new model; the new model will almost always seem superior
Where should a prediction model be externally validated? Choosing the validation cohort
The ideal validation population is a large observational cohort which is designed to accurately represent a specific clinical patient population Differences in predictive performance between validation cohorts may be caused by heterogeneity in predictor effects, varying outcome incidence and differences in case-mix	Do report the degree of relatedness between development and external validation cohorts	Do not combine heterogeneous subgroups to assess whether a prediction model works for everybody, as model discrimination will be deceptively good

FUNDING

The work on this study by M.v.D. was supported by a grant from the Dutch Kidney Foundation (16OKG12).

CONFLICT OF INTEREST STATEMENT

All authors declare no conflicts of interest.

APPENDIX A

Pubmed search strategies

N prediction model studies : (‘predictive model’[tw] OR ‘predictive models’[tw] OR predictive model*[tw] OR ‘prediction model’[tw] OR ‘prediction models’[tw] OR prediction model*[tw] OR ‘prediction rule’[tw] OR ‘prediction rules’[tw] OR ‘predictive rule’[tw] OR ‘predictive rules’[tw] OR ‘prognostic model’[tw] OR ‘prognostic models’[tw] OR prognostic model*[tw] OR ‘risk score’[tw] OR ‘risk scores’[tw]) OR ((‘Algorithms’[Majr] OR ‘algorithm’[ti] OR ‘algorithms’[ti] OR ‘Risk Assessment’[Majr] OR ‘risk assessment’[ti] OR ‘risk assessments’[ti]) AND (‘predict’[tw] OR ‘prediction’[tw] OR ‘predicting’[tw] OR ‘prognostic’[tw] OR ‘prognosis’[tw] OR ‘predictive’[tw])).

N prediction model studies that mention external validation: (‘predictive model’[tw] OR ‘predictive models’[tw] OR predictive model*[tw] OR ‘prediction model’[tw] OR ‘prediction models’[tw] OR prediction model*[tw] OR ‘prediction rule’[tw] OR ‘prediction rules’[tw] OR ‘predictive rule’[tw] OR ‘predictive rules’[tw] OR ‘prognostic model’[tw] OR ‘prognostic models’[tw] OR prognostic model*[tw] OR ‘risk score’[tw] OR ‘risk scores’[tw]) OR ((‘Algorithms’[Majr] OR ‘algorithm’[ti] OR ‘algorithms’[ti] OR ‘Risk Assessment’[Majr] OR ‘risk assessment’[ti] OR ‘risk assessments’[ti]) AND (‘predict’[tw] OR ‘prediction’[tw] OR ‘predicting’[tw] OR ‘prognostic’[tw] OR ‘prognosis’[tw] OR ‘predictive’[tw])) AND ((‘validation’ [tw] OR ‘validated’ [tw] OR ‘validating’ [tw] OR ‘validity’ [tw] OR ‘validate’ [tw]) AND (‘external’[tw] OR ‘temporal’[tw] OR ‘externally’[tw] OR ‘temporally’[tw] OR ‘geographic’[tw] OR ‘independent validation’[tw])).