Analysis of COVID-19 epidemic and clinical risk factors of patients under epidemiological Markov model

Abstract

Objective

It aimed to analyze the epidemic situation of new coronary pneumonia (COVID-19) based on the epidemiological Markov model, and to study the clinical risk factors of the patients based on the patient’s cardinal data and clinical symptoms.

Methods

A total of 500 patients with COVID-19 diagnosed by nucleic acid testing in the X hospital from January 2020 to May 2020 were collected. According to the severity of the disease, they were classified into general group (200 cases) and acute critical group (300 cases). Markov model to predict the number of COVID-19 infections was constructed. Patient’s general information, clinical characteristics, and prevention methods were analyzed.

Results

According to Markov model statistics, the developmental expected stay time of patients infected with COVID-19 was 14 days. 2. The two groups of patients had statistically considerable differences in complications such as gender, age, hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia (P < 0.05). 3. Logistic multivariate regression analysis showed that the clinical risk factors for patients with COVID-19 mainly included the patient’s gender, age, whether they were associated with hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia.

Conclusion

Markov model can be utilized to judge the time course of the COVID-19 in various development states. In addition, the COVID-19 spread rapidly and is extremely harmful. Clinically, through active prevention, the treatment effect can be improved, the patient’s respiratory function, and the quality of life can also be improved.

Introduction

At the end of 2019, a severe epidemic broke out in Wuhan, Hubei. In early 2020, the pathogen was confirmed as COVID-19, and the pneumonia caused by the infection was named COVID-19. The disease is a respiratory disease with extremely high contagiousness and great harm. After being discovered, it quickly spread to all parts of the country, leading to a rapid increase in suspected and confirmed cases everywhere [1]. With continuous in-depth research, it is found that it belongs to a new type of acute respiratory infectious disease, and the diseased body often has symptoms of lung infection. In the initial stage, it may manifest as uncomfortable reactions such as fever, fatigue, and dry cough. Some patients may have symptoms such as nasal congestion, runny nose, sore throat, and diarrhea. In severe cases, dyspnea or hypoxemia may occur one week after the onset of symptoms. When the disease progresses rapidly, it can develop into acute respiratory distress syndrome, shock, metabolic acidosis, coagulation dysfunction, and multiple organ failure. Failure to treat in time can lead to death [2].

Since the outbreak was sudden and rapid, and happened on the eve of the Spring Festival, the mass gathering of floating population became the booster, which brought severe test to the epidemic prevention and control in China. It was not until the end of January 2020 that the data released by national Health commissions became increasingly accurate [3]. In view of the spreading epidemic, it is imperative to predict it with appropriate big data analysis means, so as to make timely and appropriate control means. Novel software for analyzing data is not available and requires the epidemiological models. Markov model is a statistical model, which is widely adopted in various natural language processing applications such as speech recognition, automatic part-of-speech tagging, phonetic character conversion, and probabilistic grammar. After long-term development, especially its successful application in speech recognition, it has become a general statistical tool. It assumes that the future state of a given process depends only on the current state. According to whether the system state is fully observable and whether the system is automatic or controlled, the common Markov models are classified into four types: Markov chain, hidden Markov model, Markov decision process, and partially observable Markov decision process. In epidemiology, the Markov model has attracted attention for a process that has two transient states and two or more absorbed states. This model has been widely utilized to quantitatively predict the personnel distribution at the time interval point and the reliability theory of biological analysis, etc., all of which have achieved satisfactory results [4]. After the outbreak of the epidemic, local governments successively launched emergency plans. They adopted a series of strict prevention and control measures, such as restricting travel, banning gatherings, and controlling public places, so as to actively mobilize the enthusiasm of people from all walks of life to fight against the epidemic, and finally effectively controlled the epidemic [5]. However, a series of prevention and control measures have caused serious images to the national economy and brought a lot of inconvenience to people’s daily life. At present, the epidemic situation in China has been effectively controlled. The application of appropriate models to analyze the current and future epidemic trends is conducive to an objective and reasonable evaluation of the epidemic prevention achievements so far achieved. The prediction of the future epidemic trend is obtained, and then timely and effective deployment is made accordingly [6].

In this research, the development trend of the epidemic was studied by analyzing the official data of the epidemic released by the National Health Commission, and the epidemiological Markov model was employed to explore the COVID-19 epidemic and the clinical risk factors of patients. The following report was made.

Materials and methods

Research subjects

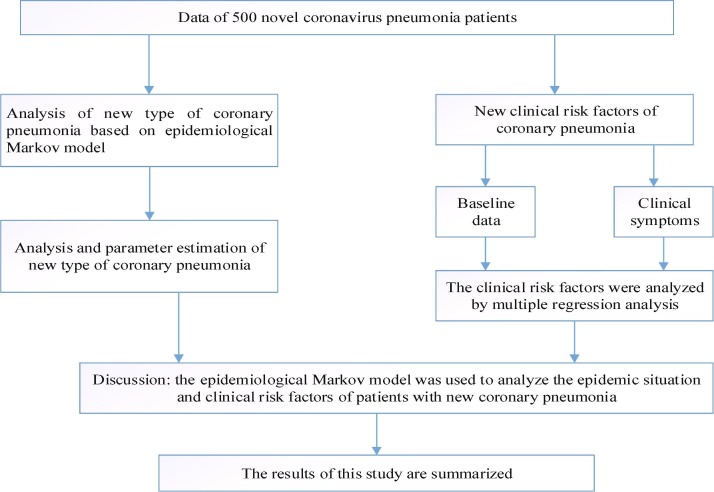
500 COVID-19 patients confirmed by nucleic acid testing in hospital from January 2020 to May 2020 were selected. According to the severity of the disease, the patients were divided into the general group (200 cases) and the acute critical group (300 cases). There were 82 males and 118 females in the general group whose average age was (22.59 ± 2.61) years, and 186 males and 114 females in the acute critical disease group whose average age was (52.66 ± 14.42) years old. No evident difference between the two groups was found in terms of gender, age, and other general information (P > 0.05), indicating comparability between the two groups. The medical ethics committee of the hospital reviewed and approved the study. Diagnostic criteria: the diagnostic criteria of COVID-19 in the Diagnosis and Treatment Protocol for COVID-19 (Trial version 7) released by the National Health Commission was referred. Inclusion criteria: those who met the above diagnostic criteria; those who with history of contact with an infected person two weeks prior to onset of illness; those who had fever or respiratory symptoms; those who were confirmed by nucleic acid testing. Patients and their family members knew the situation and signed informed consents. Exclusion criteria: patients with other malignant tumors; patients with hypertension, heart disease, diabetes, and other diseases; patients had poor compliance. The research scheme of this study was shown in Fig. 1 .

Fig. 1.

Process of research plan.

Analysis of COVID-19 epidemic based on epidemiological Markov model

Part I: principle

It is assumed that the state space of the random process {X(a), a ∈ A} is W. If for any value of time a, a₁ < a₂ < … < a_n, n ≥ 3, and a₁ ∈ A are satisfied, then, when X(a_W) = x_W, x_W ∈ W, W = 1, 2, …, n − 1, the conditional distribution function of x(a_n) is exactly equal to the conditional probability distribution function of x(a_n) under the condition X(a_n−1) = x_n−1, namely, P{(X(a_n)) ≤ xn| X(a₁) = x₁, X(a₂) = x₂, …, X(a_n−1) = x_n−1} = P{X(an) ≤ xn|X(a_n−2) = x_n−1}, xn ∈ R. It is said that {X(a),a ∈ A} has Markov property, and its future value has no correlation with the past value, and is only related to the present. This process is the Markov process.

Part II: structure

A Markov process {X(a),a ∈ A} with a state space of {1, 2, …, k} can be determined by the k-order transition probability matrix P(s, s + a) = {P_Wj(s, s + a)}(a ≥ 0). P_Wj(s, s + a) is the transition probability, 0 ≤ P_Wj(s, s + a) ≤ 1, and it represents the probability from state w to state j from time s to time s + a. When the transition probability P_Wj(s, s + a) is only related to the state wj and the time interval a, the transition probability is stationary, and the process is time-aligned. In this study, a continuous-time homogeneous Markov process was utilized to establish the model. It satisfies the Chapman-Kolmgorov equation. For vu ≥ a ≥ s, P(s, u) = P(s, a)P(a, u), and its component form is $\mathrm{p}\mathrm{W}\mathrm{j}(\mathrm{s},\mathrm{u})={\sum }_k^{n}Pik\left(s,t\right)xPik(t,u)$.

It is supposed there are N research objects, and each object goes through k states (the k-th state is an absorbing state, that is, the object stays in state k forever after reaching state k), and the state transition occurs in adjacent states W and W + 1 (or state W and absorption state k). Q_Wj represents each element in the transition intensity matrix, and yW represents the transition intensity from state W to state W + 1. Assume that all the transfer intensities are different, that is, if W ≠ j then YW ≠ Yj, the transition probability between different states is calculated as follows.

$$\mathit{PWj}(s,s+a)=(-1)j-WYWYW+1\cdots Yj-1{\sum }_{m=i}^{j}e-Ymt|{\prod }_{\begin{array}{c}f=i\\ f=m\end{array}}^j\left(ym-yf\right)i=1,2\cdots k-1;j\ge i,i<k$$ (1)

The transition probability from state W to absorption state k is as follows.

$${\mathrm{P}}_{\mathrm{W}\mathrm{k}}(\mathrm{s},\mathrm{s}+\mathrm{a})={\left(-1\right)}^{\mathrm{k}-1-\mathrm{j}}{\mathrm{Y}}_{\mathrm{W}}{\mathrm{Y}}_{\mathrm{W}+1}\cdots {\mathrm{Y}}_{\mathrm{k}-1}{\sum }_{m=i}^{k-1}(1-e-\mathrm{Y}\mathrm{m}\mathrm{a})|{\prod }_{\begin{array}{c}f=i\\ f=m\end{array}}^{k-1}\left(ym-yf\right)i=1,2\cdots k-1$$ (2)

The research object’s staying duration in state W is u_w. The continuous time Markov process has the following property, that is, the staying duration of the object in state W obeys an exponential distribution. Then, E(u_W) = 1/Y_W, Var(u_W) = 1/Y_W ², and the median time u_Wo = u_Wln2.

Part III: Parameter estimation

The relevant parameters are estimated by establishing the likelihood function equation. j = 1, 2, …, n, represents n research objects, while y_jo, y_j1, …, y_jm, represents the different states of the j-th research object. If aj0 = 0, then a_j1, a_j2, …, a_jm, represents the time corresponding to different states of the j-th research object. According to the properties of the continuous-time homogeneous Markov process, the following likelihood function can be constructed.

$$\mathrm{L}(\mathrm{y})={\prod }_j^n{\prod }_{y=o}^{m=2}{P}_{\mathrm{y}\mathrm{j}\mathrm{k}\mathrm{y}\mathrm{k}-1}\left({\mathrm{a}}_{\mathrm{j}\mathrm{k}+2}-{\mathrm{a}}_{\mathrm{j}\mathrm{k}}\right)$$ (3)

The estimated value of related parameters can be obtained by using the maximum likelihood function. Each parameter has practical meaning to guide actual work [7].

Part IV: Multi-state Markov model of the development process of COVID-19 epidemic

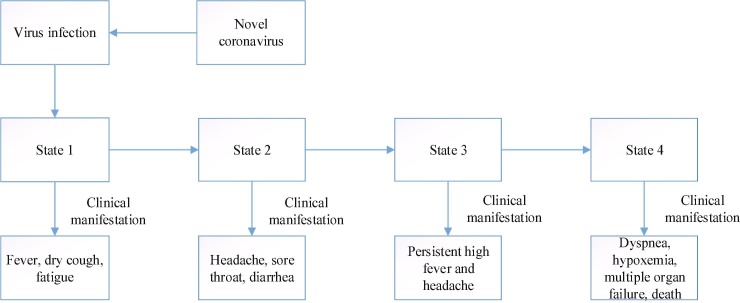
Fig. 2 showed that the development process of COVID-19 pneumonia is classified into the pre-infection period, the acute infection period, the pre-new coronary pneumonia period, and the acute critically ill period, which are designated as state 1, state 2, state 3, and state 4, respectively.

Fig. 2.

The development process of COVID-19 pneumonia.

From the above equations, the likelihood function of the transition probability between the above 4 different states is as follows.

$$\mathrm{L}\left(\mathrm{Y}\right)={\prod }_{k=1}^{\infty }{\prod }_j^{n}pj22\left(tj2-tj1\right)pj23\left(tj3-tj2\right)pj24(tj4-tj3)$$ (4)

Observation indicators

The clinical data of the two groups of patients were collected, the clinical symptoms of the patients were closely observed and recorded, and the severity was accurately recorded according to the status of the patients. The previous history of the patients was collected, including alcohol consumption, smoking, arrhythmia, hypertension, and gastrointestinal diseases. The clinical data of the two groups were analyzed by single factor analysis, and the clinical risk factors of COVID-19 patients were analyzed by multivariate Logistic regression analysis.

Statistical methods

SPSS 22.0 statistical software was utilized for data analysis. The count data was expressed as [case (%)], and the comparison between groups was performed by χ² test. The risk factor was analyzed by multivariate unconditional Logistic regression analysis. The parameter estimates were solved by Matlab statistical software. P < 0.05 was considered statistically significant.

Results

Analysis of COVID-19 epidemic via epidemiological Markov model

• I: case distribution of COVID-19 patients from state 1 to state 4, as shown in Table 1 .

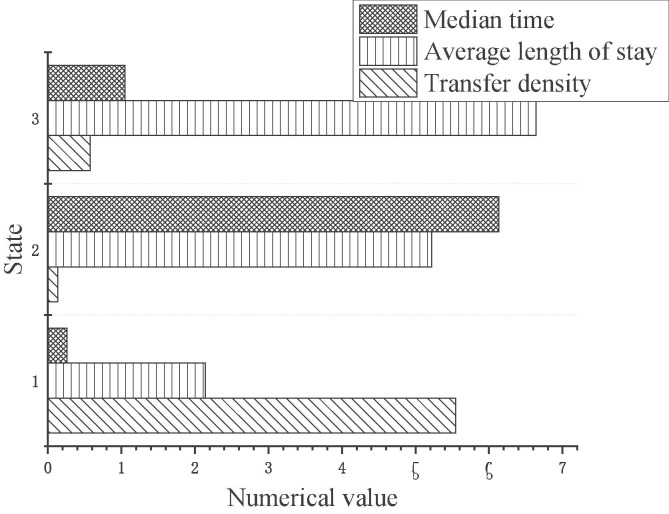
• II: parameter estimation results. Calculated by Matlab statistical software, the data were obtained, as shown in Table 2 and Fig. 3 . The developmental expected stay time of people infected with COVID-19 was 14 days, of which the average stay in state 1 was 2.14 days, that in state 2 was 5.22 days, and that in state 3 was 6.64 days. In clinical practice, the statistical results of the Markov model can be combined to predict the speed and distribution of COVID-19 infections, which was of great significance to the prevention and treatment of it.

Table 1.

Case distribution of COVID-19 patients from state N to state M.

State 1	State 4				Total
	1	2	3	4
1	78	67	5	9	159
2		132	27	17	176
3			39	63	102
4					63
Total					500

Table 2.

Parameter estimation results.

State	Transfer density	Average length of stay (days)	Median time (days)
1	5.5461	2.14	0.26
2	0.1372	5.22	6.13
3	0.5764	6.64	1.05

Fig. 3.

Parameter estimation results. (State 1: early stage of infection; State 2: acute stage of infection; State 3: early stage of COVID-19.)

Contrast of basic information of patients

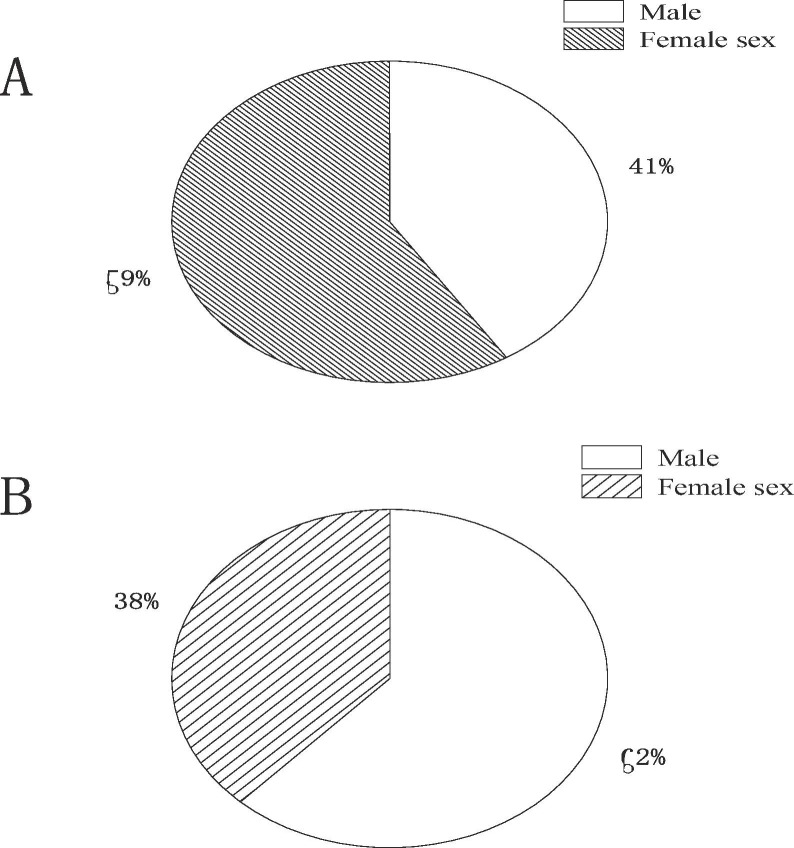
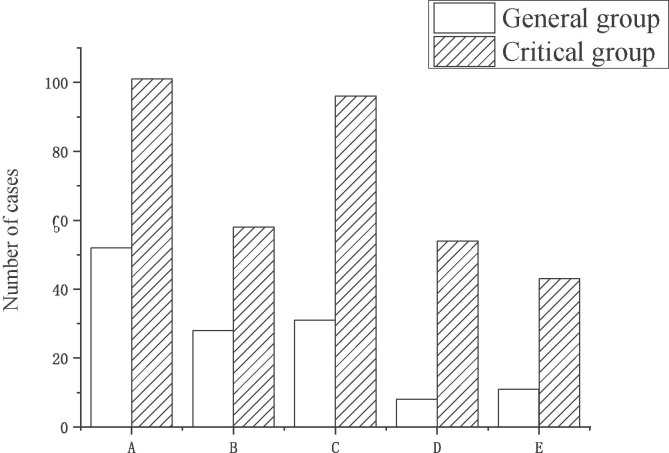
After the baseline data of the two groups of patients were compared, the differences in gender, age, hypertension, and coronary heart disease between the two groups were substantial (P < 0.05), while other related factors were not (P > 0.05). The corresponding data descriptions were shown in Table 3 and Fig. 4, Fig. 5 .

Table 3.

Comparison of baseline data between the two groups of patients.

Symptoms/Group	General group (n = 200)	Acute critical group (n = 300)	P
Gender (n (%))
Male	82 (41%)	186 (62%)	P < 0.05
Female	118 (59%)	114 (38%)	P < 0.05
Age/years old	22.59 ± 2.61	52.66 ± 14.42	P < 0.05
Personal history/n (%)
Smoking	7 (3.5%)	5 (2.5%)	P > 0.05
Drinking	5 (1.7%)	3 (1%)	P > 0.05
Disease history/n (%)
Tuberculosis	2 (1%)	1 (0.3%)	P > 0.05
Chronic obstructive tuberculosis	10 (5%)	6 (2%)	P > 0.05
Hypertension	52 (26%)	101 (33.7%)	P < 0.05
Coronary heart disease	28 (14%)	58 (19.3%)	P < 0.05
Arrhythmia	13 (6.5%)	9 (3%)	P > 0.05
Gallbladder disease	8 (4%)	2 (0.7%)	P > 0.05
Gastrointestinal disease	22 (11%)	18 (6%)	P > 0.05
Liver disease	11 (5.5%)	5 (1.7%)	P > 0.05
Cancer	14 (7%)	8 (2.7%)	P > 0.05
Diabetes	62 (31%)	81 (27%)	P > 0.05
Thyroid disease	15 (7.5%)	18 (6%)	P > 0.05

Fig. 4.

Male to female ratio. (A: general group; B acute critical group.)

Fig. 5.

Summary of single factors of patient clinical outcomes. (Note: A: hypertension B: coronary heart disease C: shortness of breath D: myocardial damage E: thrombocytopenia.)

Comparison of clinical symptoms

After comparison, the two groups of patients had considerable differences in shortness of breath, myocardial damage, and thrombocytopenia complications (P < 0.05), while other clinical symptom factors were not evidently different (P > 0.05), as illustrated in Table 4 .

Table 4.

Comparison of clinical symptoms between the two groups of patients (n (%)).

Symptoms/Group	General group (n = 200)	Acute critical group (n = 300)	P
Systemic symptoms
Fever	83 (91.5%)	256 (85.3%)	P > 0.05
Cold fear	53 (26.5%)	77 (25.7%)	P > 0.05
Headache	17 (8.5%)	15 (5%)	P > 0.05
Myalgia	33 (16.5%)	46 (15.3%)	P > 0.05
Respiratory symptoms
Sore throat	17 (8.5%)	39 (13%)	P > 0.05
Dry cough	15 (7.5%)	18 (6%)	P > 0.05
Expectoration	43 (21.5%)	59 (19.7%)	P > 0.05
Chest uncomfortable	89 (44.5%)	97 (32.3%)	P > 0.05
Circulatory system symptoms
Shortness of breath	31 (15.5%)	96 (32%)	P < 0.05
Chest pain	9 (4.5%)	13 (4.3%)	P > 0.05
Digestive system symptoms
Stomach ache	1 (0.5%)	1 (0.3%)	P > 0.05
Diarrhea	53 (26.5%)	74 (24.7%)	P > 0.05
Complications	8 (4%)	54 (18%)	P < 0.05
Myocardial damage	11 (5.5%)	43 (14.3%)	P < 0.05
Thrombocytopenia	13 (6.5%)	16 (5.3%)	P > 0.05
Liver insufficiency	9 (4.5%)	10 (3.3%)	P > 0.05
Renal insufficiency

Multivariate analysis of clinical risk factors in COVID-19 patients

After Logistic multivariate regression analysis on the general group and the acute and severe group, the results showed that the clinical risk factors of COVID-19 patients mainly included gender, age, and whether the patient was complicated with hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia. The results were shown in Table 5 .

Table 5.

Multivariate analysis of clinical risk for COVID-19 patients.

Factors	β	S.E.	Wald χ2	P	OR	95% CI
Gender	1.341	0.431	5.024	0.002	3.823	1.643–8.897
Age	0.618	0.278	4.048	0.026	1.855	1.076–3.199
Hypertension	1.627	0.621	7.055	0.009	5.089	1.507–17.187
Coronary heart disease	1.171	0.451	5.135	0.009	3.225	1.332–7.807
Shortness of breath	1.124	0.321	4.353	0.000	3.077	1.640–5.773
Myocardial damage	1.625	0.652	6.312	0.013	5.078	1.415–18.227
Thrombocytopenia	2.156	0.323	7.421	0.002	3.9973.997	1.363–34.4271.363–34.427

Platelet count

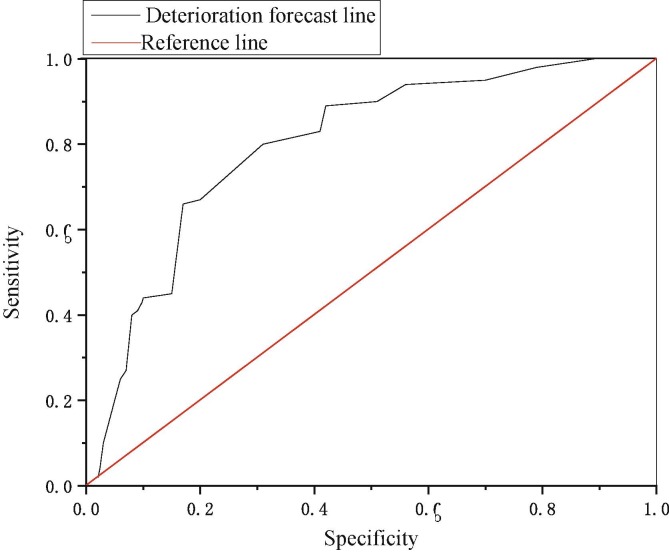
Receiver operating characteristic curve (ROC curve) analysis of platelets showed that the area under the curve was 75%, which had certain diagnostic accuracy, as shown in Fig. 6 .

Fig. 6.

ROC curve for predicting the deterioration of clinical patients.

Discussion

The Markov model is considered to be the most successful and effective method to achieve accurate and fast speech recognition systems [8]. No matter how complicated the speech recognition problem is, it can be expressed and solved simply by implying the model. It has also been highly recognized in the medical field. In response to the sudden outbreak of the epidemic at the end of 2019, the Markov model statistical method played an imperative role [9]. Due to the rapid spread of the COVID-19 and its uncontrollable nature, after infection, the development of the body’s disease course is multi-state and complex. Traditional statistical methods have a single research direction and can’t consider the continuity of the disease course. Therefore, scientific and reasonable predictions can’t be made. Calculated by Markov model, the development expectation of people infected with COVID-19 was 14 days. Moreover, the average stay in state 1 was 2.14 days, the average stay in state 2 was 5.22 days, and the average stay in state 3 was 6.64 days. In clinical practice, the statistical results of Markov model are combined to predict the speed and distribution of patients infected with COVID-19. It reflected the strong practicality of the Markov model in the research of COVID-19 related fields [10]. Constructing a Markov model that included covariates can further study the relevant influencing factors of the asymptomatic infection period of COVID-19, and finally control the COVID-19 [11].

In view of the current uncertainty of the spread of the COVID-19, its clinical stages can be classified according to the patient’s clinical manifestations or immunology, which contain multiple stages. The multi-state Markov model can be classified into four kinds of modes: time and state continuous; time and state discrete; time discrete and state continuous; and time continuous and state discrete. The choice of a specific model depends on specific circumstances and professional judgment [12].

After in-depth research on COVID-19 in the medical community, new progress has been made. In August 2020, according to the latest research results, the transmission characteristics of the new coronavirus were highly infectious and highly concealed [13]. In September, the research group of Academician Lanjuan Li of the State Key Laboratory of Infectious Diseases Diagnosis and Treatment of Zhejiang University First Hospital and the research group of Researcher Sai Li of the School of Life Sciences of Tsinghua University analyzed the three-dimensional fine structure of the real COVID-19 virus for the first time in the world. In October, a new study in Australia showed that the new coronavirus can survive on banknotes, glass, and other surfaces for nearly a month [14]. According to cytological studies, it is a coronavirus of the genus β, which is enveloped in a round or oval shape, and is often pleomorphic. Its genetic characteristics are significantly different from those of Middle East Respiratory Syndrome Coronavirus. Since it is good at “camouflage”, it is not easy to be detected by lymphocytes, and it can’t be cleared out of the body in time and effectively. It has strong fertility, rapid spread, and can invade the human body in a short time to cause disease. The first symptoms of patients are fever, headache, and cough. In acute critically ill cases, patients may suffer from respiratory syndrome, renal failure, and even death [15].

Comparative test analysis on the baseline data and clinical symptoms of COVID-19 patients were implemented. After the clinical characteristics and risk factors of respiratory were compared in patients in the general disease group and the acute critical ill group, it was concluded that there were considerable differences in gender, age, hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia of patients. Logistic multiple factor regression analysis was adopted, and the results showed that gender, age, hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia were all independent risk factors for the clinical symptoms of COVID-19 patients. Studies have shown that the incidence of acute and critical new coronary pneumonia in male patients was about 60%, and the majority of deaths were male patients. Investigations have shown that COVID-19 was closely related to bat coronaviruses. The way for the virus to enter host cells was via the S protein, and it had a high affinity for human angiotensin-converting enzyme 2 receptors. The tensin-converting enzyme was highly expressed in the male body, so it was likely to be the cause of the majority of male patients with new coronary pneumonia [16]. Most of the acute and acute critical patients of COVID-19 were people over 50 years old, indicating that the elderly had low body resistance and often had chronic diseases, and the prognosis was poor. In this work, the number of patients with acute and severe diseases combined with hypertension and coronary heart disease was evidently higher than that of the general disease group. Multivariate analysis results showed that hypertension and coronary heart disease were independent risk factors for the clinical deterioration of COVID-19 patients. Moreover, it may be related to the human angiotensin-converting enzyme 2 receptor. Due to myocardial injury and insufficient blood and oxygen supply in the body, CHD patients were vulnerable to virus attack due to reduced resistance of various organs. Once infected, it was very easy to cause hypoxemia and acute respiratory distress syndrome, and accelerate the deterioration of the disease [17]. In addition, the results of multi-factor analysis showed that the number of cases of shortness of breath in the clinical manifestations of critically ill patients was substantially higher than that of the common patients, which may be related to severe respiratory system damage of the patients [18]. Platelets have the function of hemostasis and are inflammatory factors. When activated, they can release inflammatory factors and thus trigger an inflammatory response. In this work, multi-factor analysis showed that thrombocytopenia was an independent risk factor for the disease, which was related to the non-immune platelet destruction caused by the virus, and once the infection was controlled, the platelet count would return to normal level [19].

It is crucial to pay attention to the patient’s gender and age during treatment. If the patient is elderly and male, it needs to pay close attention to the patient’s vital signs and mental status during treatment and care. For patients with coronary heart disease and hypertension, it needs to strengthen observation, install ECG monitoring if necessary, and follow the doctor’s advice to collect blood for the patients. The platelet count should be checked in time to prevent the blood platelets from being too low and the immune function dropping sharply, which will cause bleeding. At present, there is still no specific treatment for diseases caused by COVID-19, and only symptomatic treatment can be adopted. In daily life, precautions should be taken first, such as wearing masks when going out and avoid going to crowded public places. People should wash hands frequently when they are contaminated with respiratory secretions, after touching public facilities, and after taking care of patients with fever, respiratory infection, or vomiting and diarrhea. Exercise should be strengthened daily, and contacts with poultry, wild animals, and their excreta and secretions should be avoided. If one has symptoms of respiratory tract infections such as fever and cough, he shall stay at home and reduce going out and traveling. When the weather is good, the air in the room should be refreshed. People should take regular work and rest to strengthen the immunity of body.

Conclusion

In summary, the Markov model can be adopted to determine the time course of the COVID-19 in various development states. In addition, COVID-19 spreads rapidly and is extremely harmful. The first symptoms of patients were fever, headache, and cough. Acute critical cases were often accompanied by symptoms such as respiratory failure in the late stage. Gender, age, hypertension, coronary heart disease, shortness of breath, myocardial damage, and thrombocytopenia were all independent risk factors for clinical deterioration in patients with COVID-19, which seriously affected the quality of life of patients. Clinically, through active prevention, the treatment effect can be improved, the patient’s respiratory function, and the quality of life can also be improved.

The results provide some clinical reference information, but there are still many shortcomings. For example, the sample size of this research is small and limited to patients admitted to this hospital, while there is a statistical deviation for patients who are still under treatment. Therefore, it is necessary to continue to collect and analyze large sample sizes for severe patients in the future.

CRediT authorship contribution statement

Wei Zhang: Writing - original draft, Conceptualization. Caiping Zhang: Methodology, Supervision. Yifang Bi: Data curation, Software. Lirong Yuan: Formal analysis. Yi Jiang: Validation. Chaolu Hasi: Visualization. Xinri Zhang: Resources. Xiaomei Kong: Methodology, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.