Computational evaluation of rebreathing and effective dead space on a helmet-like interface during the COVID-19 pandemic

Abstract

The coronavirus disease 2019 (COVID-19) is a potentially severe acute respiratory infection caused by severe acute respiratory syndrome coronavirus 2. The potential for transmission of this disease has led to an important scarcity of health-care resources. Consequently, alternative solutions have been explored by many physicians and researchers. Non-invasive Ventilation has been revealed as one alternative for patients with associated acute respiratory distress syndrome. This technique is being used in combination with helmet-like interfaces because of their versatility and affordability. However, these interfaces could experience important problems of ${\mathrm{C}\mathrm{O}}_2$ rebreathing, especially under low flow rate conditions. This work proposes a Computational Fluid Dynamics method to accurately characterize the fluid flow in a pre-design environment of helmet-like interfaces. Parameters as effective dead space, rebreathing, pressure, or temperature field distribution are quantified and analysed in detail in order to study the performance and feasibility of such devices to relieve the effects of respiratory infections.

1. Introduction

The coronavirus disease 2019 (COVID-19) is a potentially severe acute respiratory infection caused by coronavirus 2 (SARS-CoV-2) (Gorbalenya et al., 2020). COVID-19 infection requires intensive care in, approximately, 5% of proven infections (Wu & McGoogan, 2020). An important number of patients in intensive care, develop criteria of acute respiratory distress syndrome (ARDS) (Wang et al., 2020), requiring respiratory support.

As the pandemic has advanced, public health systems have experienced an overload of their resources, leading to an important lack of ventilators for invasive ventilation (Wu & McGoogan, 2020). Non-invasive ventilation (NIV) is effective in terms of alveolar recruitment in ARDS (Lazzeri et al., 2020). However, there exists no consensus about its use with COVID-19 patients, mainly due to the possible virus spread among Intensive Care Unit (ICU) staff via aerosol generation (Murthy et al., 2020, Yang et al., 2020). Nevertheless, the use of non-vented interfaces, with a virus filter in the exhalation port, could be an effective way of treating contagious patients, ensuring staff safety (Vaughan et al., 2020). Moreover, NIV avoids intubation for a wide number of critical patients (Nava et al., 2006, Nava and Hill, 2009).

Continuous positive airway pressure (CPAP) allows the insufflation of air at over-atmospheric pressure in the interface, decreasing respiratory work. During CPAP, air is introduced through an inhalation port in the interface. A correct choice of the interface is crucial for the successful treatment of the patient. For ARDS patients due to COVID-19, the use of the helmet interface is becoming especially relevant, as deduced from the work of Radovanovic et al., 2020, who concluded a better tolerability for the helmet and reduced room contamination compared with oronasal masks. Moreover, choice of an adequate interface for each patient should be carried out considering fluid dynamic features of each device. Only a few numbers of studies have addressed the problem in this way. Therefore, some questions about the use of NIV interfaces remain unanswered. One such question is ${\mathrm{C}\mathrm{O}}_2$ rebreathing, which takes place when air scavenge process is not correctly performed (Yañez et al., 2008). Schettino et al., 2003 addressed this problem using experimental measurements in mannequins. Their work concluded that gas exchange in the interior of the interface is determined by the position of inhalation and exhalation ports. However, they did not perform an exhaustive fluid dynamic analysis and, therefore, they could not propose an optimization strategy for NIV interfaces. In this sense, Computational Fluid Dynamics (CFD) could play a major role for evaluating performance of NIV interfaces.

A wide number of CFD applications have been carried out in the context of the COVID-19 pandemic. However, they are mostly related to the study of droplet dispersion from coughs or speaking, as it could be inferred from the works of Dbouk & Drikakis, 2020 or Yan et al., 2020. CFD has only marginally been applied to NIV. Fodil et al., 2011 performed a computational study for analysing the fluid flow in different interfaces. However, they did not perform the evaluation of the mass flow through the inhalation circuit and, therefore, they were not able to compute the model in conditions of CPAP ventilation.

Additionally, some researchers showed how CFD is a reliable tool for modelling phenomena related with the respiratory system. Nof et al., 2020 proposed a computational model for reconstructing the fluid flow in an upper airway model of an intubated neonate undergoing mechanical ventilation, spanning conventional to high-frequency ventilation modes. Also, Ahookhosh et al., 2020 computed the fluid flow inside the tracheobronchial airways in order to study aerosol deposition.

Current work proposes a computational method for the study of a helmet interface, as it has been shown to be one of the most useful during the COVID-19 pandemic (Radovanovic et al., 2020). The main aim of this paper is characterizing the fluid dynamic phenomena in the interface, as well as obtaining the minimum required ventilation flow rate for respiratory support, contributing to an efficient use of medical resources. The method could be extrapolated for the evaluation of any kind of NIV interface. A mesh independent grid setup and representative boundary conditions will be presented.

2. Methodology

2.1. Geometry, computational domain and mesh

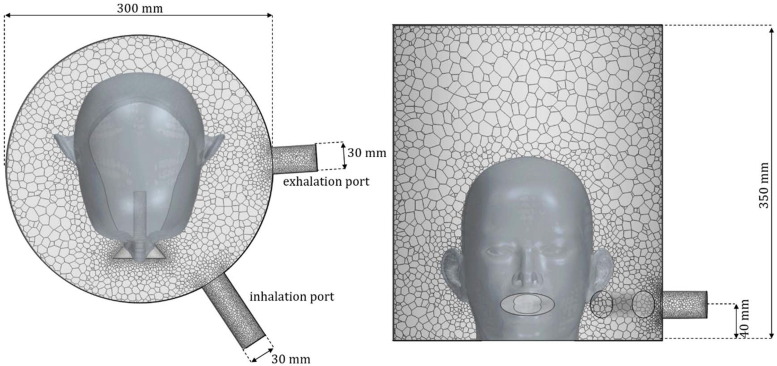
During this study, a given design of a helmet-like interface was evaluated in terms of its fluid dynamic features. The geometry of the interface was chosen to represent a prototype which is being tested on healthy volunteers. A generic patient’s head with a volume of $V_{\mathit{head}}=3.62\mathrm{L}$ was placed in the interior of the interface. The mouth was modeled by a simplified duct connecting lungs (represented by imposing the flow-rate) and the fluid domain, consisting on a cylindrical duct of diameter $D_{\mathit{duct}}=20\mathrm{m}\mathrm{m}$, being in the order of the upper airways diameter for an average adult (Ajmani, 1990, Zrunek et al., 1988). The length of the duct was $L_{\mathit{duct}}=100\mathrm{m}\mathrm{m}$, which is enough to ensure that fully developed flow was obtained at this region both during inhalation and exhalation. Mouth was modeled by a maximum ellipsoidal section whose axes were taken in order to represent an adult’s open mouth, being $a_{\mathit{mouth}}=25\mathrm{m}\mathrm{m}$ and $b_{\mathit{mouth}}=50\mathrm{m}\mathrm{m}$. The length of this region was $25\mathrm{m}\mathrm{m}$, which ensures that flow is not detached in this zone under the studied working conditions.

As it can be observed at Fig. 1 , the helmet consists of a cylindrical geometry of diameter $D_{\mathit{helmet}}=300\mathrm{m}\mathrm{m}$ and height $L_{\mathit{helmet}}=350\mathrm{m}\mathrm{m}$, leading to an inner volume of $V_{\mathit{helmet}}=24.74\mathrm{L}$. Fresh air enters into the domain through the inhalation port, with diameter $D_{\mathit{ins}}=30\mathrm{m}\mathrm{m}$ and leaves through the exhalation port, with diameter $D_{\mathit{exp}}=30\mathrm{m}\mathrm{m}$. They are both located at $40\mathrm{m}\mathrm{m}$ from the base. In order to ensure that flow is not unphysically affected by boundary conditions, the length of the ports was 10 times its diameter.

Fig. 1.

Sketch (not scale) of the geometry and mesh of helmet interface.

The geometry was discretized using a polyhedral mesh whose maximum size was set to be $\mathrm{\Delta }x=11\mathrm{m}\mathrm{m}$. Polyhedral mesh was chosen as it normally ensures grid independence with fewer elements than tetrahedral meshes (Spiegel et al., 2011). A surface size of $\mathrm{\Delta }x=6\mathrm{m}\mathrm{m}$ was used to represent domain’s walls, while the ports and the simplified mouth were refined with a size of $\mathrm{\Delta }x=1\mathrm{m}\mathrm{m}$. With this configuration, a mesh with approximately $N=1·{10}^6$ elements was generated, which is shown at Fig. 1. Time was discretized using a second order approach, with a time step of $\mathrm{\Delta }t=0.0100\mathrm{s}$. A grid independence study was performed with meshes up to $N=6·{10}^6$ and time steps of $\mathrm{\Delta }t=0.0010\mathrm{s}$, without finding significant discrepancies between computed results (EDS and rebreathing).

2.2. Boundary conditions

Constant volume flow $Q_{\mathit{in}}$ at temperature $T_{\mathit{in}}=27{}^{°}\mathrm{C}$ is imposed at the inhalation port, using a low turbulence intensity of $0.01\%$ and turbulent length scale of $2\mathrm{m}\mathrm{m}$. Inlet volume flow was varied between $Q_{\mathit{in}}=10\mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}$ and $Q_{\mathit{in}}=90\mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}$. The inflow fluid is supposed to be fresh air, whose concentration is given by a scalar value, ${\varphi }_{\mathit{fresh}}$, similarly to Fodil et al., 2011 or Trescher & Trescher, 2008.

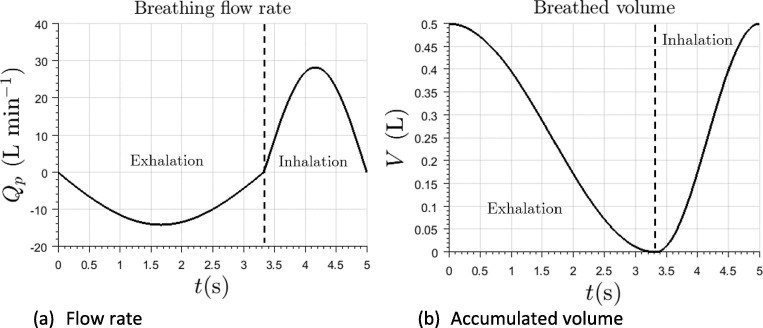
Patient is supposed to inhale the gas in the interface, exhaling rebreathed air, rich in ${\mathrm{C}\mathrm{O}}_2$, at temperature $T_p=39{}^{°}\mathrm{C}$, simulating febrile condition. Walls of the helmet and patient’s skin were modeled as adiabatic boundary conditions. Given the nature and characteristics of the flow inside the helmet, this hypothesis does not significantly affect main features of the analysis. Concentration of exhaled gas is given by the scalar variable ${\varphi }_{\mathit{exhaled}}$. Thermodynamic properties of both inlet and exhaled gas are assumed to be the same. Breathing of the patient was be modeled by imposing the volume flow through the simplified upper airways. Two characteristic breathing laws will be supposed, with tidal volumes of $V_t=500\mathrm{m}\mathrm{L}$ and $V_t=250\mathrm{m}\mathrm{L}$. Respiratory frequency was set to $f_{\mathit{respiratory}}=12\mathrm{b}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{h}\mathrm{s}/\mathrm{m}\mathrm{i}\mathrm{n}$. The duration of the exhalation and inhalation phases was $T_{\mathit{expiratory}}=3.33\mathrm{s}$ and $T_{\mathit{inspiratory}}=1.67\mathrm{s}$, respectively. Tidal volumes were selected in order to represent a wide adult population (L’her et al., 2016, Hallett and Ashurst, 2018), while the respiratory frequency was taken for an average adult (Barret et al., 2019). The breathing law is modeled using sinusoidal functions and is shown at Fig. 2 . Peak inhalation flow rate can be estimated as stated by Equation (1).

$$Q_{\mathit{peak}}=\frac{\pi }{2}\frac{f_{\mathit{respiratory}}}{r_{\mathit{respiratory}}}{V}_t$$ (1)

Where $r_{\mathit{inspiratory}}=\frac{T_{\mathit{inspiratory}}}{T_{\mathit{inspiratory}}+T_{\mathit{expiratory}}}$ is the ratio of the active inhalation over the total time of the respiratory cycle, which is 0.33 for the current case.

Fig. 2.

Imposed breathing law in terms of volume flow rate (left) and accumulated air volume in patient’s lungs (right).

Gas leaves the domain through the exhalation port. It will be supposed that there exists a resistance circuit which allows to set pressure at this boundary to be $p_{\mathit{outlet}}=10{\mathrm{c}\mathrm{m}\mathrm{H}}_2\mathrm{O}$. This could be achieved using a PEEP valve. The atmosphere temperature is $T_{\mathit{out}}=20{}^{°}\mathrm{C}$. Note that, due to the low velocities of the flow, air can be considered to be incompressible (Anderson Jr, 2010). Therefore, following results can be applied for different values of the outlet pressure. Neck was supposed to be perfectly sealed, so no leaks were considered, representing the system under ideal conditions.

The helmet is supposed to be initially filled with fresh air. This initial condition did not affect the final gas distribution when a cyclic state was obtained.

2.3. CFD simulation

Simulations were performed by means of the Finite Volume Method, using the commercial software Simcenter STAR-CCM+ for the resolution of the Unsteady Reynolds Averaged Navier-Stokes (URANS) equations (Pope, 2012). $k-\omega$ with shear stress transport turbulence model (Menter, 1993) is chosen. This model varies from the $k-\omega$ turbulence model proposed by Wilcox, 1988 to the $k-\epsilon$ model away from them, solving the main inconveniences of both models. This was successfully used for a similar case by Fodil et al., 2011. Other turbulence models were used in previous simulations, resulting on differences below 5% on the investigated variables. Spatial derivatives were discretized using a second order upwind approach, while time discretization was second order.

3. Results and discussion

3.1. Exhaled gas distribution

There are two main variables which establish mixture of fresh and exhaled air inside the interface: the incoming fresh flow through inhalation port and the unsteady patient’s breathing flow rate. Therefore, both rebreathed flow rate and the mass of exhaled gases in the interface interior are not constant during the breathing cycle. After a few respiration cycles are simulated, a cyclic state is reached. For the current simulations, this circumstance was achieved after 8–25 breathing cycles, depending on the incoming flow rate. Calculations were performed on a multiuser cluster, using 15 Intel Xeon Gold 6154 CPUs, and took approximately $3.25\mathrm{h}$ per breathing cycle. Note how the initial conditions should not affect the final results but could influence the computational cost for reaching a cyclic state, as it could be checked at the animations attached in the Electronic Supplementary Materials (ESM).

In this study, the composition of the mixture during a cycle was analyzed for different values of the incoming flow rate. This could be quantified in terms of mass fraction of fresh air $\left({\mathit{MF}}_{\mathit{fresh}}=\frac{{\varphi }_{\mathit{fresh}}}{{\varphi }_{\mathit{fresh}}+{\varphi }_{\mathit{exhaled}}}\right)$ and mass fraction of exhaled air $\left({\mathit{MF}}_{\mathit{exhaled}}=\frac{{\varphi }_{\mathit{exhaled}}}{{\varphi }_{\mathit{fresh}}+{\varphi }_{\mathit{exhaled}}}\right)$.

Fig. 3 represents distribution of $M{F}_{\mathit{exhaled}}$ in the interface at the end of inhalation time for different flow rates at a given value of tidal volume, as well as the flow patterns at this instant, represented by white lines. $M{F}_{\mathit{exhaled}}$ over 10% is represented by yellow while $M{F}_{\mathit{exhaled}}$ of 0% is represented by blue. A predominant vortex at the right of the patient’s head can be observed for any value of the incoming flow rate. Transient phenomena are better illustrated by observing animations available in the ESM. Also, is observed from Fig. 3, that exhaled gas tends to accumulate at the right of the patient’s head, far from the exhausting port. Observe that setting patient’s head between exhalation and inhalation ports, scavenge of exhaled gases should be benefited

Fig. 3.

Distribution of exhaled gas at the end of the inhalation time by means of its percentage concentration at different fresh inflow air rates for a tidal volume $V_t=500\mathrm{m}\mathrm{L}.$

3.2. Effective dead space (EDS) and rebreathing

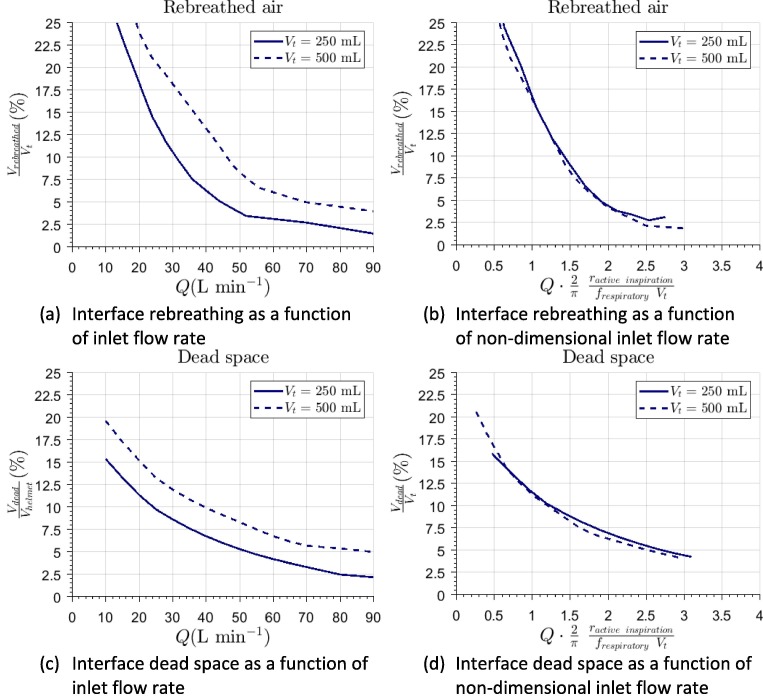
In accordance with Fletcher et al., 1981, physiological dead space is defined as “the extent to which expired gas contains alveolar gas”. In the case of NIV we will refer to EDS which, in accordance with Fodil et al., 2011, is defined as the volume of exhaled gas inside the helmet. This parameter can be established by means of Equation (2). Additionally, it is of interest computing the amount of rebreathed gas through mouth during inhalation. These are shown in percentage at Fig. 4 . Additionally, Fig. 4 shows these results using a non-dimensional volume flow as the independent variable, defined as $Q^{\ast }=Q\frac{2}{\pi }\frac{r_{\mathit{active}respiration}}{f_{\mathit{respiratory}}{V}_t}$. Note how the curves collapse, indicating how this figure permits a prediction for any combination of breathing frequency and tidal volumes.

$$V_{\mathit{dead}}=\iiint {\varphi }_{\mathit{exhaled}}dV$$ (2)

Fig. 4.

Evaluation of interface performance in terms of rebreathed gas and dead space in the interior of the helmet interface for different values of the incoming fresh flow rate in dimensional form (a and c) and non-dimensionalized (b and d).

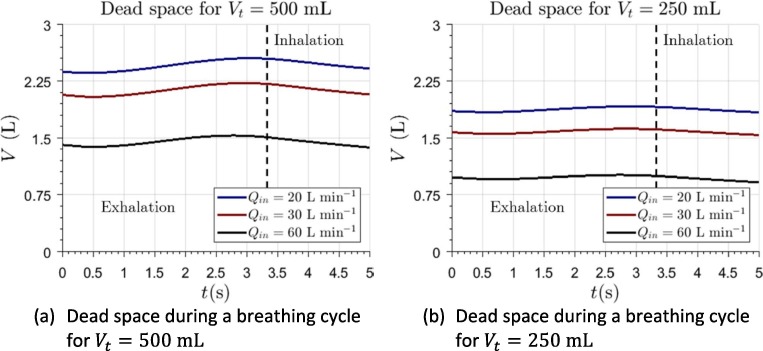
The results of the simulations for $V_t=500\mathrm{m}\mathrm{L}$ show how, for any value above $25\mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}$, EDS in the interior of the helmet was below 13.3% (3.29L). EDS reaches values lower than 7.4% (2.05L) for inlet flow rates above 55 L/min. For higher values of the parameter, EDS becomes approximately constant. Similar results can be observed from the non-dimensional representation given in Fig. 4 which, additionally, allows establishing that EDS percentage should be decreased with the decrease of patient’s tidal volume. EDS of the helmet interface is much lower than its actual volume. This is in agreement with previous studies, which allows to establish reliability of current calculations. Fodil et al., 2011 obtained comparable results for a similar interface of smaller volume. From their results, it can also be suggested that, in interfaces of lower volume, EDS can be up to 15%. Therefore, helmet interface seems to be more effective in terms of this parameter. EDS varies slightly during a breathing cycle (Fig. 5 ), although its temporal variation is bounded.

Fig. 5.

Computation of dead space in the interior of the interface during a breathing cycle.

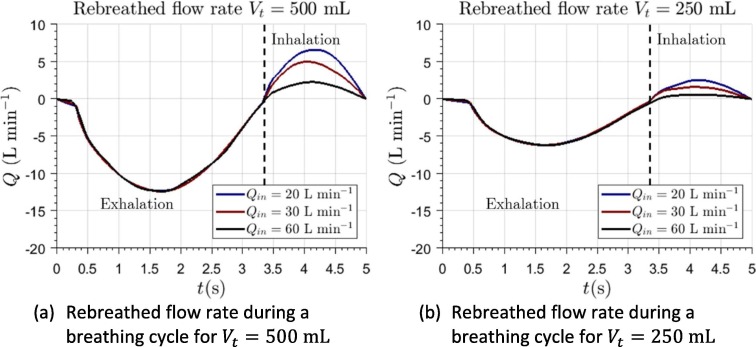
In terms of effectiveness, the most important variable is the quantity of gas which is rebreathed by the patient. Fig. 6 represents the flow rate of rebreathed air during a whole breathing cycle.

Fig. 6.

Computation of the rebreathed flow rate through patient’s mouth during a whole breathing cycle.

Although there exists a relationship between EDS and rebreathed gases, they are not interchangeable. Observation of the flow field and comparison with literature data allows one to infer that the higher volume should be beneficial in terms of rebreathing. In an interface of low volume, the amount of not scavenged gas is significantly lower in absolute values. However, this is not the case when the percentage EDS is evaluated. In fact, in these interfaces, exhaled gases remain close to patient’s mouth, being easily rebreathed. Therefore, for a low volume interface, even for high values of flow rate, a remarkable amount of rebreathing could be expected. On the other hand, for high flow rates, the evaluation of rebreathed gas in the helmet interface is below 5%. These results can be intuitively explained observing the distribution of exhaled air in Fig. 3. At the end of the exhalation process, the exhaled gas has mixed with the remaining gas in the helmet. Therefore, the global mass concentration of exhaled air is relatively low inside the interface. This is in agreement with the previous findings of Taccone et al., 2004.

EDS and rebreathed air tend to decrease when increasing flow rate. On the other hand, the lower tidal volume leads to lower EDS and rebreathed gases. This can be explained as follows: a patient with low tidal volume exhales a lower amount of gases and, therefore, they can be easily scavenged from the helmet. Therefore, it could be deduced that, in terms of fluid dynamic behavior, helmet interface should be the optimum one for patients with low tidal volume, such as pediatric patients, as it was suggested by Milési et al., 2010.

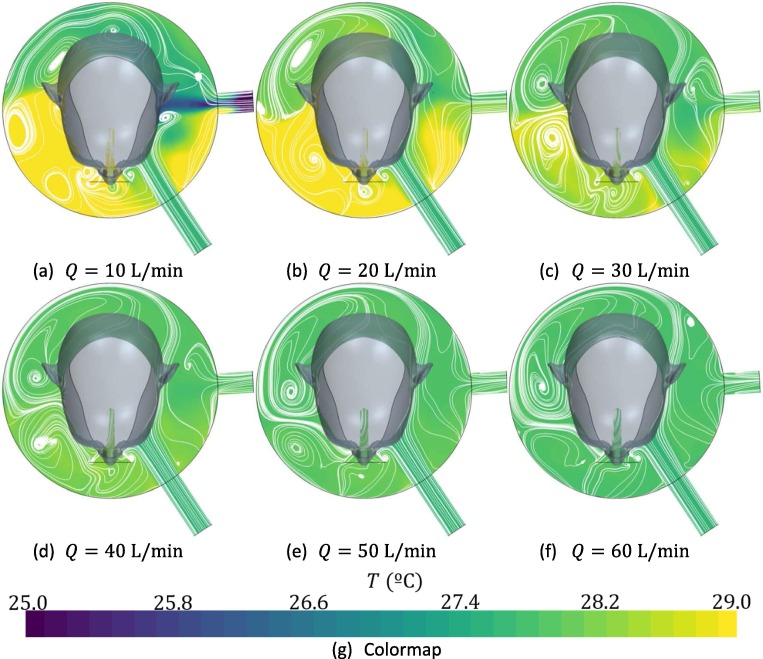
3.3. Temperature distribution

Temperature inside the interface is uniform, with variability below 1 °C (Fig. 7 ). For incoming flow rates below 20 L/min, a zone of low temperature is found near the exhalation port. This can be attributed to the fact that, when flow rates are below this value, patient is not capable to obtain his peak inhalation flow rate from the incoming flow or the reservoirs in the helmet and, therefore, air begins to be reversed from the atmosphere.

Fig. 7.

Distribution of temperature at the end of the inhalation time as a function of the incoming fresh flow rate for a tidal volume $V_t=500\mathrm{m}\mathrm{L}.$

3.4. Pressure distribution

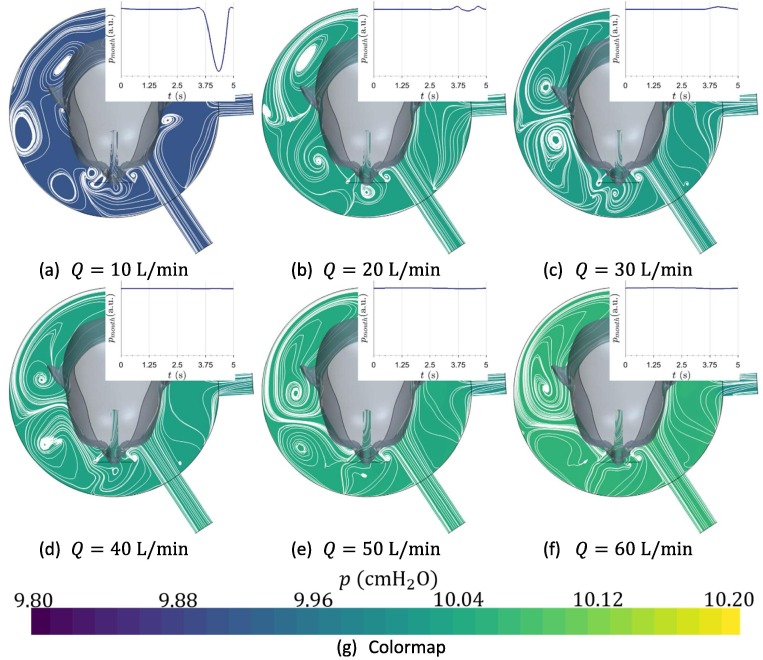
Pressure was found to be uniform in the interface, as can be observed at Fig. 8 , where time evolution of static pressure at the patient’s mouth is qualitatively shown, with arbitrary units. Pressure is fixed mainly by the resistive components located at the exhalation port. These results are in fair agreement with those suggested by Chiumello et al., 2003.

Fig. 8.

Distribution of pressure at the end of the inhalation time as function of the incoming fresh flow rate for a tidal volume $V_t=500\mathrm{m}\mathrm{L}$. Temporal evolution of pressure in the interface during a breathing cycle is qualitatively shown.

This study allows to deduce that for flow rates below 20 L/min, support pressure cannot be achieved, as there is not enough fluid for satisfying patient’s peak inhalation demands. Under these circumstances, pressure experiences an abrupt drop. Current results suggest that the helmet interface can be used even for an incoming flow rate as low as 20 L/min, assuming that rebreathing level is acceptable. Lower values of flow rate would not be capable of satisfying the peak flow demand. However, it has been found how these values are significantly lower than those which are traditionally expected, as can be inferred from Bello et al., 2013, who recommends flows higher than 45 L/min. The computational results allow providing an accurate explanation for this phenomenon: the air inside the interface acts as a reservoir. Therefore, when patient’s peak inhalation flow rate is higher than the supplied flow rate, he is able of breathing this accumulated air. This would not be the case if using low volume interfaces, where volume is not enough for satisfying the respiratory demand, as can be concluded from the works of Patroniti et al., 2003.

3.5. Minimum required flow rate into the interface

It is possible to propose a tool for estimating the minimum required incoming flow rate for the current helmet interface, $Q_{\mathit{min}}$, as stated by Equation (3). This is a correction of Equation (1), considering the effects of tidal and reservoir volume. The equation was constructed by finding the minimum value of non-dimensional flow rate at which air was recirculated from the exhalation port.

$$Q_{\mathit{min}}=0.70\frac{\pi }{2}\frac{f_{\mathit{respiratory}}}{r_{\mathit{respiratoru}}}{V}_t=0.70Q_{\mathit{peak}}$$ (3)

3.6. Limitations

During the current study, non-intentional leaks were not considered. Under some circumstances, these leaks could lead to a malfunctioning of the interface for NIV, as suggested by Louis et al., 2010. Nevertheless, the current study could be directly applied when leaking flow rate is much lower than inlet flow rate. Future studies are proposed to establish the actual effect of leaks around the neck. Additionally, it was assumed that the wall of the interface is infinitely rigid. In fact, once the helmet interface is pressurized, its geometry can be supposed to be unchanged with time and pressure, as can be observed when using the device. Therefore, although it could be interesting to consider the flexibility of the wall in future works, it is expected to be of second order. No heat transfer between the fluid and walls was modeled. Future research should be dedicated to establishing a proper heat transfer model for quantifying temperature distribution in the interior of the helmet. Finally, the study did only consider one generic patient’s head and position. Future studies should be performed to establish the sensibility of the computed variables for different patients and positions.

4. Conclusions

This work has presented a method for estimating the fluid flow features in the interior of a helmet-like interface under conditions of NIV. Comparison of the results with the known behavior of these interfaces extracted from the literature allows to ensure reliability, at least during pre-design stages, of the presented computations. The work has been focused on the evaluation of a helmet interface, as it is one of the most used devices when using NIV during the COVID-19 health crisis.

The distribution of exhaled air concentration, temperature and pressure has been evaluated. This knowledge can be used for better design or usability improvements. For instance, it has been observed how, placing the patient’s head between the exhalation and inhalation ports, the scavenging of the interface should improve. Moreover, it has been shown that rebreathing and EDS are functions of the non-dimensional flow rate. This could be used by physicians in order to ensure the most efficient treatment for each patient, in terms of their tidal volume and range of respiratory frequency.

It was possible to propose an equation for obtaining the minimum fresh air supply needed for a correct ventilation of the patient. It should be noted that the corrective factor (0.70) of such derived equation is dependent on the kind of interface. Therefore, this should be carefully used for similar helmet interfaces. It should never be used for estimating flow requirements with low volume interfaces. Additional research effort should be dedicated for its estimation in other interfaces.

Current results show that the helmet interface is an excellent choice for providing NIV, both in terms of rebreathing (4.0–15%), EDS (5.0–10%) and uniformity of pressure and temperature fields. Due to the low cost associated with its manufacturing and its ease of use, it can be an adequate option for NIV during the current COVID-19 pandemic. Moreover, the low minimum flow predicted with the current method indicates that its use would lead to a better use of resources during a health crisis or in developing countries.

Finally, this article shows the potential of the proposed method for understanding, designing, and improving the use of NIV. An important lack of knowledge in this field has been detected, and future efforts should be dedicated to the study fluid dynamics phenomena in NIV. Although the method was applied for a helmet interface, it could be used for exploring suitability of new designs or other kind of interfaces.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

The following are the Supplementary data to this article: