Stability analysis of fractional nabla difference COVID-19 model

Abstract

Microorganisms lives with us in our environment, touching infectious material on the surfaces by hand-mouth which causes infectious diseases and some of these diseases are rapidly spreading from person to person. These days the world facing COVID-19 pandemic disease. This article concerned with existence of results and stability analysis for a nabla discrete ABC-fractional order COVID-19. The nabla discrete ABC-fractional operator as more general and applicable in modeling of dynamical problems due to its non-singular kernel. For the existence and uniqueness theorems and Hyers-Ulam stability, we need to suppose some conditions which will play important role in the proof of our main results. At the end, an expressive example is given to provide an application for the nabla discrete ABC-fractional order COVID-19 model.

Introduction

Humans born on the earth with some active viruses and inactive bacteria. Infectious diseases caused by viruses, bacteria, fungi and arthropods. Due to these infectious diseases humans worldwide facing pandemic diseases such as HIV, COVID-19, Malaria, Influenza, Tuberculosis, Zika virus infection, Smallpox, measles, yellow fever, Cholera and Leprosy. In 2018, according to WHO 37.9 million infected and 770,000 peoples died from HIV/AIDS, three to five million peoples dying from Influenza yearly, 20,000 peoples dying from dengue yearly, 405,000 peoples died from malaria. In Dec 2019 a new virous disease COVID-19 identified in Wuhan city capital of Hubei provence China. COVID-19 pandemic shocked the whole world because of economic disruption and rapidly spreading from person to person. According to WHO main source of COVID-19 viruses spreading between the peoples by close contact, sneezing, coughing and talking. Common symptoms appears in the infected person fever, fatigue, shortness of breath, cough, sense of smell lass, respiratory syndrome and pneumonia. COVID-19 spread in 188 countries on going 5.69 million peoples infected and resulting 355,000 peoples died, further details [1], [2], [3]. To understand the dynamics of these pandemic diseases, mathematical tools play a vital role in the field of biological sciences and numbers of diseases have been modeled such as HIV, ebola virus diseases, dengue fever, measles epidemic [35], [36], [37], [38], [39], [40]. In the last two decades biological models have been extensively studied. Chetterjee et al. [41] developed SEIR model for COVID-19 and studied different aspects of the model. Wen et al. [42] provided positive periodic results for the stochastic SIV model. Ivorra et al. [4] modeled special cases of diseases, infectious conditions and sanitary condition of hospitalized people and numerical results were obtained to express obtained results.

In recent years, a lot of researchers paid their attentions to the study of fractional differences, which is the generalization or extension of classical calculus. Gray and Zhang [41] introduced some basic properties of fractional difference. Miller and Ross [4] provided research studies on fractional sums and differences with the use of nabla and delta operator in the frame of Riemann–Liouville. After that, by combine efforts numbers of mathematicians have provided qualitative theories such as, existence and uniqueness of solutions (EUS), stability analysis, oscillations, asymptotic, periodicity and multiple solutions. The usability of fractional differences are encountered in various area of applied sciences, such as, engineering, physics, computer science, chemistry, biology, signal processing, electrochemistry, viscoelasticity, fluid dynamics and image processing [5], [6], [7], [8], [9], [12], [13], [14], [15], [16], [17].

Due to non-singular, non-local properties and historical dependence of variable state researchers investigate numerous aspects fractional differences, for example, Khan et al. [20] provided fractional order HIV-TB model and analyzed existence solutions, stability results and numerical solutions. Zhang et al. [21], [22] developed fractional order turbulent flow model and studied EUS by using fixed point theorem and illustrated the results. Khan et al. [21], [22] studied HIV/AIDS model in sense of Atangana-Baleanu operator and provided existence results, stability criteria and numerical results for the generalized model. Abdeljawad and Al-Mdallal [23] used the Banach contraction principle theorem to get existence results for the discrete fractional differences in sense of discrete Mittage Leffler kernel and numerical results were provided for the results illustration. Khan et al. [24] studied existence of solutions, stability for the fractional order advection diffusion model in sense of Mittage Leffler kernel and exemplified the results numerically. Abdeljawad et al. [25] studied existence solution of q-fractional difference equations with help of Krasnoselskii’s theorem and demonstrate the results by Lotka-Volterra model. For more explanation and details about discrete Mittage-Leffler and exponential kernels we suggest to readers the recent manuscripts [26], [27], [28], [29], [30], [31], [32], [33], [34].

The predominant goal of this article, to obtain existence results and stability analysis of the nabla ABC-fractional COVID-19 model. Fixed point theorem use for the existence results and Hyres-Ullam technique utilize to obtain stability analysis for the nabla ABC-fractional COVID-19 model. The whole study work has been arranged as follows: Section ‘Basic definitions of nabla fractional calculus’, the basic definitions. Section ‘Model description’, model description. Section ‘Existence of solutions’, existence results. Section ‘Hyers-Ulam stability’, stability analysis. Section ‘Numerical data fitting’, numerical illustration. Section ‘Conclusion’, Conclusion.

Basic definitions of nabla fractional calculus

.

Definition 0.1

(See [6], [9], [10], [11], [12]) Suppose $\rho \left(r\right)=r-1$, which is known as backward jump. Then for a function $Ϝ:{\mathbf{N}}_a=\{a,a+1,a+2,..\}\to \mathbf{R}$, the left type nabla fractional sum of order $\theta >0$ is defined by

$${}^a{\nabla }^{-\theta }Ϝ\left(r\right)=\frac{1}{\mathrm{\Gamma }\left(\theta \right)}{\displaystyle \sum _{z=a+1}^r}{(r-\rho (z\left)\right)}^{\overline{1-\theta }}Ϝ\left(z\right),r\in {\mathbf{N}}_{a+1}\text{.}$$ (1)

Similarly, for a function $Ϝ:{}_b\mathbf{N}=\{b,b-1,b+2,..\}\to \mathbf{R}$, the right type nabla fractional sum of order $\theta >0$ is defined by

$${\displaystyle \underset{b}{\overset{\theta }{\nabla }}}Ϝ\left(r\right)=\frac{1}{\mathrm{\Gamma }\left(\theta \right)}{\displaystyle \sum _{z=r}^{b-1}}{(z-\rho (z\left)\right)}^{\overline{1-\theta }}Ϝ\left(z\right),$$ (2)

$$=\frac{1}{\mathrm{\Gamma }\left(\theta \right)}{\displaystyle \sum _{z=r}^{b-1}}{\left(\sigma \right(r)-z)}^{\overline{1-\theta }}Ϝ\left(z\right),r\in {}_{b-1}\mathbf{N}\text{.}$$ (3)

Definition 0.2

(See [6], [9], [10], [11], [12]) Let $a<b$ in $\mathfrak{R}$, for a function $Ϝ$ defined on ${\mathbf{N}}_a$, the left discrete nabla AB fractional difference is given in sense of Caputo by

$$\left({}^{\mathit{ABC}}{}_a{\nabla }^{\theta }Ϝ\right)\left(r\right)=\frac{\mathcal{W}\left(\theta \right)}{\mathrm{\Gamma }(1-\theta )}{\displaystyle \sum _{z=a+1}^r}{\nabla }_zϜ\left(z\right){\mathbb{E}}_{\bar{\theta }}\left[\frac{-\theta }{1-\theta },r-\rho \left(z\right)\right],\theta \in (0,1/2),$$ (4)

in Riemann–Liouville sense by

$$\left({}^{\mathit{ABR}}{}_a{\nabla }^{\theta }Ϝ\right)\left(r\right)=\frac{\mathcal{W}\left(\theta \right)}{\mathrm{\Gamma }(1-\theta )}{\nabla }_r{\displaystyle \sum _{z=a+1}^r}Ϝ\left(z\right){\mathbb{E}}_{\bar{\theta }}\left[\frac{-\theta }{1-\theta },r-\rho \left(z\right)\right],\theta \in (0,1/2)\text{.}$$ (5)

Similarly, for a function $Ϝ$ defined on ${}_b\mathbf{N}$, the right discrete nabla AB fractional difference is given in sense of Caputo by

$$\left({}^{\mathit{ABC}}{\nabla }_b^{\theta }Ϝ\right)\left(r\right)=\frac{\mathcal{W}\left(\theta \right)}{\mathrm{\Gamma }(1-\theta )}{\displaystyle \sum _{z=r}^{b-1}}(-{\mathrm{\Delta }}_zϜ)\left(z\right){\mathbb{E}}_{\bar{\theta }}\left[\frac{-\theta }{1-\theta },r-\rho \left(z\right)\right],\theta \in (0,1/2),$$ (6)

in Riemann–Liouville sense by

$$\left({}^{\mathit{ABR}}{\nabla }_b^{\theta }Ϝ\right)\left(r\right)=\frac{\mathcal{W}\left(\theta \right)}{\mathrm{\Gamma }(1-\theta )}(-{\mathrm{\Delta }}_r){\displaystyle \sum _{z=r}^{b-1}}Ϝ\left(z\right){\mathbb{E}}_{\bar{\theta }}\left[\frac{-\theta }{1-\theta },r-\rho \left(z\right)\right],\theta \in (0,1/2)\text{.}$$ (7)

where $\mathcal{W}\left(\theta \right)$ with $\mathcal{W}\left(\theta \right){|}_{\theta =0,1}=1$ denotes of normalization function and ${\mathbb{E}}_{\bar{\theta }}$ is ML function. The notions ${}^{\mathit{ABC}}{}_a{\nabla }^{\theta },{}^{\mathit{ABR}}{}_a{\nabla }^{\theta },{}^{\mathit{ABC}}{\nabla }_b^{\theta }$ and ${}^{\mathit{ABR}}{\nabla }_b^{\theta }$ denotes the right and left nabla AB fractional differences in Caputo sense, right and left nabla AB fractional differences in the frame of Riemann–Liouville.

Definition 0.3

(See [6], [9], [10], [11], [12]) For $\theta \in (0,1)$ and a function $Ϝ$defined on ${}^a\mathbf{N}$, the left nebla AB fractional sum is given by

$$\left({}^{\mathit{ABC}}{}_a{\nabla }^{-\theta }Ϝ\right)\left(r\right)=\frac{1-\theta }{\mathcal{W}\left(\theta \right)}Ϝ\left(r\right)+\frac{\theta }{\mathcal{W}\left(\theta \right)}\left({}^a{\nabla }^{-\theta }Ϝ\right)\left(r\right),\theta \in (0,1/2)\text{.}$$ (8)

Similarly, right nabla Ab fractional for a function $Ϝ$ defined on ${\mathbf{N}}_b$ given by

$$\left({}^{\mathit{ABC}}{\nabla }_b^{-\theta }Ϝ\right)\left(r\right)=\frac{1-\theta }{\mathcal{W}\left(\theta \right)}Ϝ\left(r\right)+\frac{\theta }{\mathcal{W}\left(\theta \right)}\left({\nabla }_b^{-\theta }Ϝ\right)\left(r\right),\theta \in (0,1/2)\text{.}$$ (9)

where $\mathcal{W}\left(\theta \right)$ with $\mathcal{W}\left(\theta \right){|}_{\theta =0,1}=1$, represent the normalization function.

Model description

In this section, we present Khan et al. [19] formulated the integer order COVID-19 model, in which $\mathbf{S}$ rate of susceptible, $\mathbf{E}$ exposed people, $\mathbf{I}$ infected people, $\mathbf{A}$ asymptomatic infected people and $\mathbf{R}$ recovered from disease, infected place or market $\mathbf{Q}$. The integer order COVID-19 model is given

$$\begin{array}{cc}\hfill \mathcal{D}\left\{\mathbf{S}\right(t\left)\right\}=& \mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right),\hfill \\ \hfill \mathcal{D}\left\{\mathbf{E}\right(t\left)\right\}=& \frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}+\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)-(1-\varphi )\delta \mathbf{E}\left(t\right)-\varphi \mu \mathbf{E}\left(t\right)-\lambda \mathbf{E}\left(t\right),\hfill \\ \hfill \mathcal{D}\left\{\mathbf{I}\right(t\left)\right\}=& (1-\varphi )\delta \mathbf{E}\left(t\right)-(\sigma +\lambda )\mathbf{I}\left(t\right),\hfill \\ \hfill \mathcal{D}\left\{\mathbf{A}\right(t\left)\right\}=& \varphi \mu \mathbf{E}\left(t\right)-(\rho +\lambda )\mathbf{A}\left(t\right),\hfill \\ \hfill \mathcal{D}\left\{\mathbf{R}\right(t\left)\right\}=& \sigma \mathbf{I}\left(t\right)+\rho \mathbf{A}\left(t\right)-\lambda \mathbf{R}\left(t\right),\hfill \\ \hfill \mathcal{D}\left\{\mathbf{Q}\right(t\left)\right\}=& \kappa \mathbf{I}\left(t\right)+\tau \mathbf{A}\left(t\right)-\eta \mathbf{Q}\left(t\right),\hfill \end{array}$$ (10)

with initial conditions

$$\mathbf{S}\left(t\right)⩾0,\mathbf{E}\left(t\right)⩾0,\mathbf{I}⩾0,\mathbf{A}\left(t\right)⩾0,\mathbf{R}\left(t\right)⩾0,\mathbf{Q}\left(t\right)⩾0\text{.}$$

Where $\mathbf{N}$ denotes total population of people $\mathbf{N}=\mathbf{S}\left(t\right)+\mathbf{E}\left(t\right)+\mathbf{I}\left(t\right)+\mathbf{A}\left(t\right)+\mathbf{R}\left(t\right)+\mathbf{Q}\left(t\right)$, Birth rate $\mathrm{\Delta }$, rate of contact $\alpha$, rate of natural mortality $\lambda$, rate of transmission $\beta$, period of incubation $\delta$, period of incubation $\mu$, asymptomatic infection proportion $\varphi$, transmission of disease coefficient $\gamma$, Recovery of $\mathbf{I}$ $\sigma$, Recovery of $\mathbf{A}$ $\rho$, virus contribution to $\mathbf{Q}$ by $\mathbf{I}$ is denoted by $\kappa$, virus contribution to $\mathbf{Q}$ by $\mathbf{A}$ is denoted by $\tau$ and removing rate of virus from $\mathbf{Q}$ is denoted by $\eta$. Here, we study existence results and HUS for a nabla discrete AB-fractional COVID-19 model.

Existence of solutions

In this section, we study the existence results for (10) by replacing the time derivative by nabla discrete ABC-fractional difference

$$\begin{array}{cc}\hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{S}\right)\left(t\right)=& \mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right),\hfill \\ \hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{E}\right)\left(t\right)=& \frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}+\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)-(1-\varphi )\delta \mathbf{E}\left(t\right)-\varphi \mu \mathbf{E}\left(t\right)-\lambda \mathbf{E}\left(t\right),\hfill \\ \hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{I}\right)\left(t\right)=& (1-\varphi )\delta \mathbf{E}\left(t\right)-(\sigma +\lambda )\mathbf{I}\left(t\right),\hfill \\ \hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{A}\right)\left(t\right)=& \varphi \mu \mathbf{E}\left(t\right)-(\rho +\lambda )\mathbf{A}\left(t\right),\hfill \\ \hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{R}\right)\left(t\right)=& \sigma \mathbf{I}\left(t\right)+\rho \mathbf{A}\left(t\right)-\lambda \mathbf{R}\left(t\right),\hfill \\ \hfill \left({}^{\mathit{ABC}}{}_a{\nabla }^{∊}\mathbf{Q}\right)\left(t\right)=& \kappa \mathbf{I}\left(t\right)+\tau \mathbf{A}\left(t\right)-\eta \mathbf{Q}\left(t\right),\hfill \end{array}$$ (11)

with initial conditions

$$\mathbf{S}\left(t\right)⩾0,\mathbf{E}\left(t\right)⩾0,\mathbf{I}\left(t\right)⩾0,\mathbf{A}\left(t\right)⩾0,\mathbf{R}\left(t\right)⩾0,\mathbf{Q}\left(t\right)⩾0\text{.}$$

By applying AB-fractional sums on two sides of each equation in (11), the system can be converted to the Volterra-type integral as below:

$$\begin{array}{cc}\hfill \mathbf{S}\left(t\right)-\mathbf{S}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[\mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[\mathrm{\Delta }-\lambda \mathbf{S}\left(z\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(z)+\beta \mathbf{A}(z\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(z\right)\mathbf{Q}\left(z\right)\right],\hfill \\ \hfill \mathbf{E}\left(t\right)-\mathbf{E}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}+\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)-(1-\varphi )\delta \mathbf{E}\left(t\right)-\varphi \mu \mathbf{E}\left(t\right)-\lambda \mathbf{E}\left(t\right),\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(z)+\beta \mathbf{A}(z\left)\right)}{\mathbf{N}}+\gamma \mathbf{S}\left(z\right)\mathbf{Q}\left(z\right)\right)\hfill \\ \hfill -& \left((1-\varphi )\delta \mathbf{E}\left(z\right)-\varphi \mu \mathbf{E}\left(z\right)-\lambda \mathbf{E}\left(z\right)\right],\hfill \\ \hfill \mathbf{I}\left(t\right)-\mathbf{I}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[(1-\varphi )\delta \mathbf{E}\left(t\right)-(\delta +\lambda )\mathbf{I}\left(t\right)\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[(1-\varphi )\delta \mathbf{E}\left(z\right)-(\delta +\lambda )\mathbf{I}\left(z\right)\right],\hfill \\ \hfill \mathbf{A}\left(t\right)-\mathbf{A}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[(1-\varphi )\delta \mathbf{E}\left(t\right)-(\sigma +\lambda )\mathbf{I}\left(t\right)\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[(1-\varphi )\delta \mathbf{E}\left(z\right)-(\sigma +\lambda )\mathbf{I}\left(z\right)\right],\hfill \\ \hfill \mathbf{R}\left(t\right)-\mathbf{R}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[\sigma \mathbf{I}\left(t\right)+\rho \mathbf{A}\left(t\right)-\lambda \mathbf{R}\left(t\right)\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[\sigma \mathbf{I}\left(z\right)+\rho \mathbf{A}\left(z\right)-\lambda \mathbf{R}\left(z\right)\right],\hfill \\ \hfill \mathbf{Q}\left(t\right)-\mathbf{Q}\left(0\right)=& \frac{1-∊}{\mathcal{W}\left(∊\right)}\left[\kappa \mathbf{I}\left(t\right)+\tau \mathbf{A}\left(t\right)-\eta \mathbf{Q}\left(t\right)\right]\hfill \\ \hfill +& \frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\left[\kappa \mathbf{I}\left(z\right)+\tau \mathbf{A}\left(z\right)-\eta \mathbf{Q}\left(z\right)\right]\text{.}\hfill \end{array}$$ (12)

For simplicity, we define $F_i,i\in {\mathbb{N}}_1^6$ as follows:

$$\begin{array}{cc}\hfill F_1(t,\mathbf{S})=& \mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right),\hfill \\ \hfill F_2(t,\mathbf{E})=& \frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}+\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)-(1-\varphi )\delta \mathbf{E}\left(t\right)-\varphi \mu \mathbf{E}\left(t\right)-\lambda \mathbf{E}\left(t\right),\hfill \end{array}$$ (13)

$$\begin{array}{cc}\hfill F_3(t,\mathbf{I})=& (1-\varphi )\delta \mathbf{E}\left(t\right)-(\sigma +\lambda )\mathbf{I}\left(t\right),\hfill \\ \hfill F_4(t,\mathbf{A})=& \varphi \mu \mathbf{E}\left(t\right)-(\rho +\lambda )\mathbf{A}\left(t\right),\hfill \\ \hfill F_5(t,\mathbf{R})=& \sigma \mathbf{I}\left(t\right)+\rho \mathbf{A}\left(t\right)-\lambda \mathbf{R}\left(t\right),\hfill \\ \hfill F_6(t,\mathbf{Q})=& \kappa \mathbf{I}\left(t\right)+\tau \mathbf{A}\left(t\right)-\eta \mathbf{Q}\left(t\right)\text{.}\hfill \end{array}$$

Theorem 0.4

The kernels $F_i,i=1,2,3,4,5,6$ hold the Lipschitz condition and contractions, If the subsequent respective conditions $0⩽{\mathrm{\Omega }}_j<1,j\in {\mathbb{N}}_1^6$ are satisfied.

Proof

Consider the kernel $F_1(t,\mathbf{S})=\mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)$. Let ${\mathbf{S}}_1,{\mathbf{S}}_2$ are two functions, then we have

$$\begin{array}{cc}\hfill \Vert F_1(t,{\mathbf{S}}_1)-F_1(t,{\mathbf{S}}_2)\Vert =& \Vert \mathrm{\Delta }-\lambda \mathbf{S}\left(t\right)-\frac{\alpha \mathbf{S}\left(t\right)\left(\mathbf{I}\right(t)+\beta \mathbf{A}(t\left)\right)}{\mathbf{N}}-\gamma \mathbf{S}\left(t\right)\mathbf{Q}\left(t\right)\Vert \hfill \\ \hfill ⩽& \left(-\lambda -\frac{\alpha (\Vert \mathbf{I}(t)\Vert +\beta \Vert \mathbf{A}(t)\Vert )}{\mathbf{N}}-\gamma \Vert \mathbf{Q}\left(t\right)\Vert \right)\Vert {\mathbf{S}}_1-{\mathbf{S}}_2\Vert \hfill \\ \hfill ⩽& \left(-\lambda -\frac{\alpha ({\pi }_3+\beta {\pi }_4)}{\mathbf{N}}-\gamma {\pi }_6\right)\Vert {\mathbf{S}}_1-{\mathbf{S}}_2\Vert \text{.}\hfill \end{array}$$

Taking ${\mathrm{\Omega }}_1=\left(-\lambda -\frac{\alpha ({\pi }_3+\beta {\pi }_4)}{\mathbf{N}}-\gamma {\pi }_6\right)$, where ${\pi }_1={\max }_{t\in P}\Vert \mathbf{S}\left(t\right)\Vert ,{\pi }_2={\max }_{t\in p}\Vert \mathbf{E}\left(t\right)\Vert ,{\pi }_3={\max }_{t\in p}\Vert \mathbf{I}\left(t\right)\Vert ,{\pi }_4={\max }_{t\in p}\Vert \mathbf{A}\left(t\right)\Vert ,{\pi }_5={\max }_{t\in p}\Vert \mathbf{R}\left(t\right)\Vert ,{\pi }_6={\max }_{t\in p}\Vert \mathbf{Q}\left(t\right)\Vert$, we obtain

$$\Vert F_1(t,{\mathbf{S}}_1)-F_1(t,{\mathbf{S}}_2)\Vert ⩽{\mathrm{\Omega }}_1\Vert {\mathbf{S}}_1-{\mathbf{S}}_2\Vert \text{.}$$ (14)

From (14), we find that the kernel $F_1$ is satisfying the Lipschitz condition, moreover if $0⩽{\mathrm{\Omega }}_1<1$, then the kernel $F_1$ is contraction. Similarly, we can get for $F_2,F_3,F_4,F_5$ and $F_6$ as follow

$$\begin{array}{cc}\hfill & \Vert F_2(t,{\mathbf{E}}_1)-F_2(t,{\mathbf{E}}_2)\Vert ⩽{\mathrm{\Omega }}_2\Vert {\mathbf{E}}_1-{\mathbf{E}}_2\Vert ,\hfill \\ \hfill & \Vert F_3(t,{\mathbf{I}}_1)-F_3(t,{\mathbf{I}}_2)\Vert ⩽{\mathrm{\Omega }}_3\Vert {\mathbf{I}}_1-{\mathbf{I}}_2\Vert ,\hfill \\ \hfill & \Vert F_4(t,{\mathbf{A}}_1)-F_4(t,{\mathbf{A}}_2)\Vert ⩽{\mathrm{\Omega }}_4\Vert {\mathbf{A}}_1-{\mathbf{A}}_2\Vert ,\hfill \\ \hfill & \Vert F_5(t,{\mathbf{R}}_1)-F_5(t,{\mathbf{R}}_2)\Vert ⩽{\mathrm{\Omega }}_5\Vert {\mathbf{R}}_1-{\mathbf{R}}_2\Vert ,\hfill \\ \hfill & \Vert F_6(t,{\mathbf{Q}}_1)-F_6(t,{\mathbf{Q}}_2)\Vert ⩽{\mathrm{\Omega }}_6\Vert {\mathbf{Q}}_1-{\mathbf{Q}}_2\Vert \text{.}\hfill \end{array}$$ (15)

From (15), we find that the kernels $F_2,F_3,F_4,F_5$ and $F_6$ is satisfying the Lipschitz condition, moreover if $0⩽{\mathrm{\Omega }}_i<1$, for $i=1,2,3,4,5,6$ then the kernel $F_i$ for $i=1,2,3,4,5,6$ is contraction.

By using the above kernels, one can rewrite the system (12) in the following simple form:

$$\begin{array}{cc}\hfill \mathbf{S}\left(t\right)=& S\left(0\right)+\frac{(1-∊)F_1(t,\mathbf{S})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_1(z,\mathbf{S}(z\left)\right),\hfill \\ \hfill \mathbf{E}\left(t\right)=& E\left(0\right)+\frac{(1-∊)F_2(t,\mathbf{E})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_2(z,\mathbf{E}(z\left)\right),\hfill \\ \hfill \mathbf{I}\left(t\right)=& I\left(0\right)+\frac{(1-∊)F_3(t,\mathbf{I})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_3(z,\mathbf{I}(z\left)\right),\hfill \\ \hfill \mathbf{A}\left(t\right)=& A\left(0\right)+\frac{(1-∊)F_4(t,\mathbf{A})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_4(z,\mathbf{A}(z\left)\right),\hfill \\ \hfill \mathbf{R}\left(t\right)=& R\left(0\right)+\frac{(1-∊)F_5(t,\mathbf{R})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_5(z,\mathbf{R}(z\left)\right),\hfill \\ \hfill \mathbf{Q}\left(t\right)=& Q\left(0\right)+\frac{(1-∊)F_6(t,\mathbf{Q})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_6(z,\mathbf{Q}(z\left)\right)\text{.}\hfill \end{array}$$ (16)

Now, we construct the subsequent recursive formula as follows:

$$\begin{array}{cc}\hfill {\mathbf{S}}_n\left(t\right)=& S_n\left(0\right)+\frac{(1-∊)F_1(t,{\mathbf{S}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_1(z,{\mathbf{S}}_{n-1}(z\left)\right),\hfill \\ \hfill {\mathbf{E}}_n\left(t\right)=& E_n\left(0\right)+\frac{(1-∊)F_2(t,{\mathbf{E}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_2(z,{\mathbf{E}}_{n-1}(z\left)\right),\hfill \\ \hfill {\mathbf{I}}_n\left(t\right)=& I_n\left(0\right)+\frac{(1-∊)F_3(t,{\mathbf{I}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_3(z,{\mathbf{I}}_{n-1}(z\left)\right),\hfill \\ \hfill {\mathbf{A}}_n\left(t\right)=& A_n\left(0\right)+\frac{(1-∊)F_4(t,{\mathbf{A}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_4(z,{\mathbf{A}}_{n-1}(z\left)\right),\hfill \\ \hfill {\mathbf{R}}_n\left(t\right)=& R_n\left(0\right)+\frac{(1-∊)F_5(t,{\mathbf{R}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_5(z,{\mathbf{R}}_{n-1}(z\left)\right),\hfill \\ \hfill {\mathbf{Q}}_n\left(t\right)=& Q_n\left(0\right)+\frac{(1-∊)F_6(t,{\mathbf{Q}}_{n-1})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_6(z,{\mathbf{Q}}_{n-1}(z\left)\right)\text{.}\hfill \end{array}$$ (17)

Let us define a new expressions for the difference between the successive term as follows:

$$\begin{array}{cc}\hfill {}_{\mathbf{S}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{S}}_n\left(t\right)-{\mathbf{S}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_1(t,{\mathbf{S}}_{n-1})-F_1(t,{\mathbf{S}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_1(z,{\mathbf{S}}_{n-1}(z\left)\right)-F_1(z,{\mathbf{S}}_{n-2}(z\left)\right)\right),\hfill \\ \hfill {}_{\mathbf{E}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{E}}_n\left(t\right)-{\mathbf{E}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_2(t,{\mathbf{E}}_{n-1})-F_2(t,{\mathbf{S}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_2(z,{\mathbf{E}}_{n-1}(z\left)\right)-F_2(z,{\mathbf{E}}_{n-2}(z\left)\right)\right),\hfill \\ \hfill {}_{\mathbf{I}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{I}}_n\left(t\right)-{\mathbf{I}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_3(t,{\mathbf{I}}_{n-1})-F_3(t,{\mathbf{I}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_3(z,{\mathbf{I}}_{n-1}(z\left)\right)-F_3(z,{\mathbf{I}}_{n-2}(z\left)\right)\right),\hfill \\ \hfill {}_{\mathbf{A}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{A}}_n\left(t\right)-{\mathbf{A}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_4(t,{\mathbf{S}}_{n-1})-F_4(t,{\mathbf{A}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_4(z,{\mathbf{A}}_{n-1}(z\left)\right)-F_4(z,{\mathbf{A}}_{n-2}(z\left)\right)\right),\hfill \\ \hfill {}_{\mathbf{R}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{R}}_n\left(t\right)-{\mathbf{R}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_5(t,{\mathbf{E}}_{n-1})-F_5(t,{\mathbf{R}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_5(z,{\mathbf{R}}_{n-1}(z\left)\right)-F_5(z,{\mathbf{R}}_{n-2}(z\left)\right)\right),\hfill \\ \hfill {}_{\mathbf{Q}}{\mathbb{D}}_n\left(t\right)=& {\mathbf{Q}}_n\left(t\right)-{\mathbf{Q}}_{n-1}\left(t\right)\hfill \\ \hfill =& \frac{(1-∊)\left(F_6(t,{\mathbf{Q}}_{n-1})-F_6(t,{\mathbf{Q}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_6(z,{\mathbf{Q}}_{n-1}(z\left)\right)-F_6(z,{\mathbf{Q}}_{n-2}(z\left)\right)\right)\text{.}\hfill \end{array}$$ (18)

It is interesting to note that

$${\mathbf{S}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{S}}{\mathbb{D}}_i\left(t\right),{\mathbf{E}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{E}}{\mathbb{D}}_i\left(t\right),{\mathbf{I}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{I}}{\mathbb{D}}_i\left(t\right),$$ (19)

$${\mathbf{A}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{A}}{\mathbb{D}}_i\left(t\right),{\mathbf{R}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{R}}{\mathbb{D}}_i\left(t\right),{\mathbf{Q}}_n\left(t\right)={{\displaystyle \sum _{i=0}^n}}_{\mathbf{Q}}{\mathbb{D}}_i\left(t\right)\text{.}$$

Taking the norm for both sides of(18)

$$\begin{array}{cc}\hfill \Vert {}_{\mathbf{S}}{\mathbb{D}}_n\Vert ⩽& \frac{1-∊}{\mathcal{W}\left(∊\right)}\Vert F_1(t,{\mathbf{S}}_{n-1})-F_1(t,{\mathbf{S}}_{n-2})\Vert +\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill & \times \Vert F_1(z,{\mathbf{S}}_{n-1})-F_1(z,{\mathbf{S}}_{n-2})\Vert ,\hfill \\ \hfill ⩽& \frac{(1-∊){\mathrm{\Omega }}_1}{\mathcal{W}\left(∊\right)}\Vert {\mathbf{S}}_{n-1}-{\mathbf{S}}_{n-2}\Vert +\frac{∊{\mathrm{\Omega }}_1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\Vert {\mathbf{S}}_{n-1}-{\mathbf{S}}_{n-2}\Vert \text{.}\hfill \end{array}$$

This implies

$$\Vert {}_{\mathbf{S}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_1}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{S}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{S}}{\mathbb{D}}_{n-1}\Vert \text{.}$$

Similarly, we get the following results:

$$\begin{array}{cc}\hfill & \Vert {}_{\mathbf{E}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_2}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{E}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_2}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{E}}{\mathbb{D}}_{n-1}\Vert ,\hfill \\ \hfill & \Vert {}_{\mathbf{I}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_3}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{I}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_3}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{I}}{\mathbb{D}}_{n-1}\Vert ,\hfill \\ \hfill & \Vert {}_{\mathbf{A}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_4}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{A}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_4}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{A}}{\mathbb{D}}_{n-1}\Vert ,\hfill \\ \hfill & \Vert {}_{\mathbf{R}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_5}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{R}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_5}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{R}}{\mathbb{D}}_{n-1}\Vert ,\hfill \\ \hfill & \Vert {}_{\mathbf{Q}}{\mathbb{D}}_n\Vert ⩽\frac{(1-∊){\mathrm{\Omega }}_6}{\mathcal{W}\left(∊\right)}{\Vert }_{\mathbf{Q}}{\mathbb{D}}_{n-1}\Vert +\frac{∊{\mathrm{\Omega }}_6}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{\Vert }_{\mathbf{Q}}{\mathbb{D}}_{n-1}\Vert ,\hfill \end{array}$$ (20)

By using recursive method with Eq.(20) Eq.(21), we get

$$\begin{array}{cc}\hfill \Vert {}_{\mathbf{S}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{S}}_n\left(0\right)\Vert {\mathrm{\Omega }}_1^n,\hfill \\ \hfill \Vert {}_{\mathbf{E}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{E}}_n\left(0\right)\Vert {\mathrm{\Omega }}_2^n,\hfill \\ \hfill \Vert {}_{\mathbf{I}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{I}}_n\left(0\right)\Vert {\mathrm{\Omega }}_3^n\text{.}\hfill \\ \hfill \Vert {}_{\mathbf{A}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{A}}_n\left(0\right)\Vert {\mathrm{\Omega }}_4^n,\hfill \\ \hfill \Vert {}_{\mathbf{R}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{R}}_n\left(0\right)\Vert {\mathrm{\Omega }}_5^n,\hfill \\ \hfill \Vert {}_{\mathbf{Q}}{\mathbb{D}}_n\Vert ⩽& {\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^n\Vert {\mathbf{Q}}_n\left(0\right)\Vert {\mathrm{\Omega }}_6^n\text{.}\hfill \end{array}$$ (21)

Theorem 0.5

The nabla discrete ABC fractional order system (11) has a system of solutions if the following restrictions are hold:

$$\left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_i<1,i=1,2,3,4,5,6\text{.}$$ (22)

Proof

From (16), (17), we assume

$$\begin{array}{cc}\hfill \mathbf{S}\left(t\right)=& {\mathbf{S}}_n\left(t\right),\mathbf{E}\left(t\right)={\mathbf{E}}_n\left(t\right),\mathbf{I}\left(t\right)={\mathbf{I}}_n\left(t\right)\text{.}\hfill \\ \hfill \mathbf{A}\left(t\right)=& {\mathbf{A}}_n\left(t\right),\mathbf{R}\left(t\right)={\mathbf{R}}_n\left(t\right),\mathbf{Q}\left(t\right)={\mathbf{Q}}_n\left(t\right)\text{.}\hfill \end{array}$$

Let us define ${}_1{\mathrm{\Lambda }}_n,{}_2{\mathrm{\Lambda }}_n,{}_3{\mathrm{\Lambda }}_n,{}_4{\mathrm{\Lambda }}_n,{}_5{\mathrm{\Lambda }}_n$ ${}_6{\mathrm{\Lambda }}_n$ as follows

$${}_1{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{S}\left(t\right)-{\mathbf{S}}_n\left(t\right),{}_2{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{E}\left(t\right)-{\mathbf{E}}_n\left(t\right),{}_3{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{I}\left(t\right)-{\mathbf{I}}_n\left(t\right),$$ (23)

$${}_4{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{A}\left(t\right)-{\mathbf{A}}_n\left(t\right),{}_5{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{R}\left(t\right)-{\mathbf{R}}_n\left(t\right),{}_6{\mathrm{\Lambda }}_n\left(t\right)=\mathbf{Q}\left(t\right)-{\mathbf{Q}}_n\left(t\right)\text{.}$$ (24)

Now, we show that ${\Vert }_i{\mathrm{\Lambda }}_n\Vert \to 0$for $i=1,2,3,4,5,6$ as $n\to \infty$.

$$\begin{array}{cc}\hfill \Vert {}_1{\mathrm{\Lambda }}_n\Vert =& \Vert \frac{(1-∊)\left(F_1(t,{\mathbf{S}}_{n-1})-F_1(t,{\mathbf{S}}_{n-2})\right)}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \left(F_1(z,{\mathbf{S}}_{n-1})-F_1(z,{\mathbf{S}}_{n-2})\right)\Vert ,\hfill \\ \hfill ⩽& \frac{1-∊}{\mathcal{W}\left(∊\right)}\Vert F_1(t,{\mathbf{S}}_{n-1})-F_1(t,{\mathbf{S}}_{n-2})\Vert +\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\hfill \\ \hfill \times & \Vert F_1(z,{\mathbf{S}}_{n-1})-F_1(z,{\mathbf{S}}_{n-2})\Vert ,\hfill \\ \hfill ⩽& \frac{1-∊}{\mathcal{W}\left(∊\right)}{\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}_{n-1}\Vert +\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}_{n-1}\Vert \text{.}\hfill \end{array}$$ (25)

This implies

$$\Vert {}_1{\mathrm{\Lambda }}_n\Vert ⩽\left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}_{n-1}\Vert \text{.}$$ (26)

With help of (21), we obtain

$$\Vert {}_1{\mathrm{\Lambda }}_n\Vert ⩽{\mathrm{\Omega }}_1^{n+1}{\left[\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right]}^{n+1}\text{.}$$ (27)

From Eq. (27), we see that ${\Vert }_1{\mathrm{\Lambda }}_n\Vert \to 0$ as $n\to \infty$. In the same way and the previous steps, we find that ${\Vert }_i{\mathrm{\Lambda }}_n\Vert \to 0$ for $i=2,3,4,5,6$ as $n\to \infty$.

Theorem 0.6

The system (11) has a unique system of solutions if the following conditions are hold:

$$\left(\frac{(1-∊)}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_i-1<0,i=1,2,3,4,5,6\text{.}$$ (28)

Proof

We consider that there is another system of solutions ${\mathbf{S}}^{\ast }\left(t\right),{\mathbf{E}}^{\ast }\left(t\right),{\mathbf{I}}^{\ast }\left(t\right),{\mathbf{A}}^{\ast }\left(t\right),{\mathbf{R}}^{\ast }\left(t\right)$ and ${\mathbf{Q}}^{\ast }\left(t\right)$ for the system (11), then we have

$$\begin{array}{cc}\hfill \Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert ⩽& \frac{(1-∊)}{\mathcal{W}\left(∊\right)}\Vert F_1(t,\mathbf{S})-F_1(t,{\mathbf{S}}^{\ast })\Vert +\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\Vert F_1(z,\mathcal{S})-F_1(z,{\mathcal{S}}^{\ast })\Vert \hfill \\ \hfill ⩽& \frac{1-∊}{\mathcal{W}\left(∊\right)}{\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert +\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert \text{.}\hfill \end{array}$$ (29)

Making use of (29), we get

$$\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert \left(\left(\frac{(1-∊)}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1-1\right)⩾0\text{.}$$ (30)

Eq.(30) is valid if and only if

$$\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert =0\text{.}$$

This implies

$$\mathbf{S}\left(t\right)={\mathbf{S}}^{\ast }\left(t\right)\text{.}$$

Repeating the same procedure with $\mathbf{E}\left(t\right),\mathbf{I}\left(t\right),\mathbf{A}\left(t\right),\mathbf{R}\left(t\right)$ and $\mathbf{Q}\left(t\right)$ we obtain

$$\mathbf{E}\left(t\right)={\mathbf{E}}^{\ast }\left(t\right),\mathbf{I}\left(t\right)={\mathbf{I}}^{\ast }\left(t\right),\mathbf{A}\left(t\right)={\mathbf{A}}^{\ast }\left(t\right),\mathbf{R}\left(t\right)={\mathbf{R}}^{\ast }\left(t\right),\mathbf{Q}\left(t\right)={\mathbf{Q}}^{\ast }\left(t\right)\text{.}$$

This proves that the system (11) has a unique system of solutions.

Hyers-Ulam stability

.

Definition 0.7

The integral Eqs. (16) is Hyers-Ulam stability if there exists non-negative constants ${\mathrm{\Delta }}_i,i\in {\mathbb{N}}_1^6$ satisfying:

For every ${\alpha }_i>0,i\in {\mathbb{N}}_1^6$, if

$$\begin{array}{cc}\hfill & \left|\mathbf{S}\right(t)-\frac{(1-∊)F_1(t,\mathbf{S})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_1(z,\mathbf{S}\left(z\right)\left)\right|⩽{\alpha }_1,\hfill \\ \hfill & \left|\mathbf{E}\right(t)-\frac{(1-∊)F_2(t,\mathbf{E})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_2(z,\mathbf{E}\left(z\right)\left)\right|⩽{\alpha }_2,\hfill \end{array}$$ (31)

$$\begin{array}{cc}\hfill & \left|\mathbf{I}\right(t)-\frac{(1-∊)F_3(t,\mathbf{I})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_3(z,\mathbf{I}\left(z\right)\left)\right|⩽{\alpha }_3,\hfill \\ \hfill & \left|\mathbf{A}\right(t)-\frac{(1-∊)F_4(t,\mathbf{A})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_4(z,\mathbf{A}\left(z\right)\left)\right|⩽{\alpha }_4,\hfill \\ \hfill & \left|\mathbf{R}\right(t)-\frac{(1-∊)F_5(t,\mathbf{R})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_5(z,\mathbf{R}\left(z\right)\left)\right|⩽{\alpha }_5,\hfill \\ \hfill & \left|\mathbf{Q}\right(t)-\frac{(1-∊)F_6(t,\mathbf{Q})}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_6(z,\mathbf{Q}\left(z\right)\left)\right|⩽{\alpha }_6,\hfill \end{array}$$

there exist ${\mathbf{S}}^{\ast }\left(t\right),{\mathbf{E}}^{\ast }\left(t\right),{\mathbf{I}}^{\ast }\left(t\right),{\mathbf{A}}^{\ast }\left(t\right),{\mathbf{R}}^{\ast }\left(t\right)$ and ${\mathbf{Q}}^{\ast }\left(t\right)$ are satisfying

$$\begin{array}{cc}\hfill {\mathbf{S}}^{\ast }\left(t\right)=& \frac{(1-∊)F_1(t,{\mathbf{S}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_1(z,{\mathbf{S}}^{\ast }(z\left)\right),\hfill \\ \hfill {\mathbf{E}}^{\ast }\left(t\right)=& \frac{(1-∊)F_2(t,{\mathbf{E}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_2(z,{\mathbf{E}}^{\ast }(z\left)\right),\hfill \end{array}$$ (32)

$$\begin{array}{cc}\hfill {\mathbf{I}}^{\ast }\left(t\right)=& \frac{(1-∊)F_3(t,{\mathbf{I}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_3(z,{\mathbf{I}}^{\ast }(z\left)\right),\hfill \\ \hfill {\mathbf{A}}^{\ast }\left(t\right)=& \frac{(1-∊)F_4(t,{\mathbf{A}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_4(z,{\mathbf{A}}^{\ast }(z\left)\right),\hfill \\ \hfill {\mathbf{R}}^{\ast }\left(t\right)=& \frac{(1-∊)F_5(t,{\mathbf{R}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_5(z,{\mathbf{R}}^{\ast }(z\left)\right),\hfill \\ \hfill {\mathbf{Q}}^{\ast }\left(t\right)=& \frac{(1-∊)F_6(t,{\mathbf{Q}}^{\ast })}{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}{F}_6(z,{\mathbf{Q}}^{\ast }(z\left)\right),\hfill \end{array}$$

such that

$$\begin{array}{cc}\hfill \Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert ⩽& {\alpha }_1{\mathrm{\Delta }}_1,\Vert \mathbf{E}-{\mathbf{E}}^{\ast }\Vert ⩽{\alpha }_2{\mathrm{\Delta }}_2\mathrm{and}\Vert \mathbf{I}-{\mathbf{I}}^{\ast }\Vert ⩽{\alpha }_3{\mathrm{\Delta }}_3,\hfill \\ \hfill \Vert \mathbf{A}-{\mathbf{A}}^{\ast }\Vert ⩽& {\alpha }_4{\mathrm{\Delta }}_4,\Vert \mathbf{R}-{\mathbf{R}}^{\ast }\Vert ⩽{\alpha }_5{\mathrm{\Delta }}_5\mathrm{and}\Vert \mathbf{Q}-{\mathbf{Q}}^{\ast }\Vert ⩽{\alpha }_6{\mathrm{\Delta }}_6\text{.}\hfill \end{array}$$ (33)

Theorem 0.8

The nabla discrete ABC fractional order COVID-19 model (11) is Hyers-Ulam stable.

Proof

By Def. 0.7 and Eq.(16), consider $\left(\mathbf{S}\right(t),\mathbf{E}(t),\mathbf{I}(t),\mathbf{A}(t),\mathbf{R}(t),\mathbf{Q}(t\left)\right)$ be the fact solution of (16) and $\left({\mathbf{S}}^{\ast }\right(t),{\mathbf{E}}^{\ast }(t),{\mathbf{I}}^{\ast }(t),{\mathbf{A}}^{\ast }(t),{\mathbf{R}}^{\ast }(t),{\mathbf{Q}}^{\ast }(t\left)\right)$ be an approximate solution satisfying (33). Then, we have

$$\begin{array}{cc}\hfill \Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert ⩽& \frac{(1-∊)\Vert F_1(t,\mathbf{S})-F_1(t,{\mathbf{S}}^{\ast })\Vert }{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\displaystyle \sum _{z=a+1}^t}{(t-\rho (z\left)\right)}^{\overline{∊-1}}\Vert F_1(z,\mathbf{S})-F_1(z,{\mathbf{S}}^{\ast })\Vert \hfill \\ \hfill ⩽& \frac{(1-∊){\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert }{\mathcal{W}\left(∊\right)}+\frac{∊}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}{\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert \hfill \\ \hfill =& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{S}-{\mathbf{S}}^{\ast }\Vert \text{.}\hfill \end{array}$$ (34)

Similarly, we get

$$\begin{array}{cc}\hfill \Vert \mathbf{E}-{\mathbf{E}}^{\ast }\Vert ⩽& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{E}-{\mathbf{E}}^{\ast }\Vert ,\hfill \\ \hfill \Vert \mathbf{I}-{\mathbf{I}}^{\ast }\Vert ⩽& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{I}-{\mathbf{I}}^{\ast }\Vert ,\hfill \\ \hfill \Vert \mathbf{A}-{\mathbf{A}}^{\ast }\Vert ⩽& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{A}-{\mathbf{A}}^{\ast }\Vert ,\hfill \\ \hfill \Vert \mathbf{R}-{\mathbf{R}}^{\ast }\Vert ⩽& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{R}-{\mathbf{R}}^{\ast }\Vert ,\hfill \\ \hfill \Vert \mathbf{Q}-{\mathbf{Q}}^{\ast }\Vert ⩽& \left(\frac{1-∊}{\mathcal{W}\left(∊\right)}+\frac{1}{\mathcal{W}\left(∊\right)\mathrm{\Gamma }\left(∊\right)}\right){\mathrm{\Omega }}_1\Vert \mathbf{Q}-{\mathbf{Q}}^{\ast }\Vert \text{.}\hfill \end{array}$$ (35)

Hence, by (34), (35) the integral Eqs. (16) are Hyers-Ulam stable. Thus, the nabla discrete AB-fractional version of COVID-19 model (11) is Hyers-Ulam stable.

Numerical data fitting

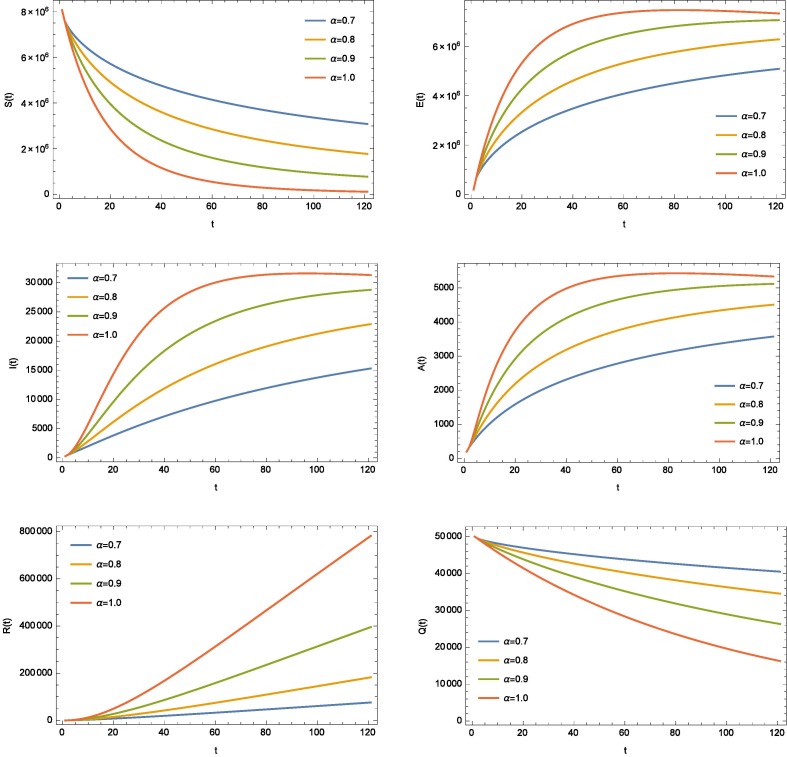
In this section, we study the dynamical activates of the model (11), in sense of nabla discrete AB-fractional derivative. We consider the initial values for the proposed model, total papulation of the Wuhan city $\mathbf{N}\left(0\right)=8,266,000$, infected people $\mathbf{I}\left(0\right)=282$, we suppose there is no recovery rate $\mathbf{R}=0,\mathbf{E}\left(0\right)=200000,\mathbf{A}\left(0\right)=200,\mathbf{S}\left(0\right)=8065518,\mathbf{Q}\left(0\right)=50000$. The remaining parameters values are given in the Table 1 , which are use in the model (11). In this situation, the small value of $∊$ , the corresponding states has a lower equilibrium level. It should be noted that the system (16) is solved using the Gauss–Seidel method. In addition, figures shows the phase portraits for the commensurate nabla discrete model involving the Atangana-Baleanu-Caputo derivative. see Fig. 1 .

Table 1.

Shows the values of parameters given in Eq. (11). The time units is taken in years [18], [19].

Parameter	Description	Value	Reference
$\mathrm{\Delta }$	Birth rate	$\lambda N$	[19]
$\lambda$	Natural mortality rate	$\frac{1}{76.79\times 365}$	[18], [19]
$\alpha$	Contact rate	0.05	[19]
$\beta$	Transmissibility multiple	0.02	[19]
$\gamma$	Disease Transmission coefficient	0.000001231	[19]
$\varphi$	The proportion of asymptomatic infection	0.1243	[19]
$\delta$	Incubation period	0.00047876	[19]
$\mu$	Incubation period	0.005	[19]
$\sigma$	Removal or recovery rate of $\mathbf{I}$	0.09871	[19]
$\rho$	Removal or recovery rate of $\mathbf{A}$	0.854302	[19]
$\kappa$	Contribution of the virus to $\mathbf{Q}$ by $\mathbf{I}$	0.000398	[19]
$\tau$	Contribution of the virus to $\mathbf{Q}$ by $\mathbf{A}$	0.001	[19]
$\eta$	Contribution of the virus to $\mathbf{Q}$	0.01	[19]

Fig. 1.

The dynamics of corona virus model with different fractional order $\alpha$.

Conclusion

In this paper, we investigated the nabla discrete AB-fractional order COVID-19 model. We study existence results of fractional order COVID-19 model by employing fixed point theorem and HUS approach is used for the stability analysis. For further study about the model (11), we suggest the readers to consider its no-solution and multiplicity results using different mathematical techniques including the upper lower solution methods and topological degree theory. One may also study the numerical solution of the proposed model by several numerical methods.

Authors’ contributions

All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.

CRediT authorship contribution statement

Aziz Khan: Conceptualization, Methodology, Resources, Investigation, Project administration, Visualization, Writing - original draft, Writing - review & editing. Hashim M. Alshehri: Conceptualization, Methodology, Investigation, Visualization, Writing - original draft, Supervision, Writing - review & editing. Thabet Abdeljawad: Conceptualization, Methodology, Investigation, Visualization, Writing - original draft, Supervision, Writing - review & editing, Funding acquisition. Qasem M. Al-Madlal: Conceptualization, Methodology, Investigation, Visualization, Writing - original draft, Supervision, Writing - review & editing, Data curation, Formal analysis. Hasib Khan: Conceptualization, Methodology, Investigation, Visualization, Writing - original draft, Supervision, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.