Reconstructing Undersampled Photoacoustic Microscopy Images using Deep Learning

Abstract

One primary technical challenge in photoacoustic microscopy (PAM) is the necessary compromise between spatial resolution and imaging speed. In this study, we propose a novel application of deep learning principles to reconstruct undersampled PAM images and transcend the trade-off between spatial resolution and imaging speed. We compared various convolutional neural network (CNN) architectures, and selected a Fully Dense U-net (FD U-net) model that produced the best results. To mimic various undersampling conditions in practice, we artificially downsampled fully-sampled PAM images of mouse brain vasculature at different ratios. This allowed us to not only definitively establish the ground truth, but also train and test our deep learning model at various imaging conditions. Our results and numerical analysis have collectively demonstrated the robust performance of our model to reconstruct PAM images with as few as 2% of the original pixels, which can effectively shorten the imaging time without substantially sacrificing the image quality.

I. INTRODUCTION

Photoacoustic microscopy (PAM) is a hybrid imaging modality that combines optical excitation and ultrasonic detection [1, 2, 3]. In PAM, a pulsed laser provides excitation light that is absorbed by biological tissues. The photothermal effect induces a temperature rise that generates a pressure rise via thermo-elastic expansion that is proportional to the original optical absorption [2]. This pressure rise propagates as ultrasound waves, which are detected by an ultrasonic transducer to form an image of the original optical energy deposition inside the tissue. PAM utilizes either tightly or weakly focused optical excitation and focused ultrasound detection, combined with point-by-point scanning, to form high-resolution three-dimensional (3D) images [4].

In PAM, there is usually a trade-off between the imaging speed and the spatial resolution. To ensure the high spatial resolution, the scanning step size in PAM needs to be no larger than half of the expected spatial resolution, according to the Nyquist sampling theorem, similar to other pure optical microscopy technologies. However, pure optical microscopy can use air-based optical scanners (e.g., MEMS mirror and galvo scanner) and easily achieve a high imaging speed over a large field of view. PAM, conversely, requires simultaneous scanning of both the optical excitation beam and the resultant ultrasound waves in an aqueous environment [4]. This restriction results in the low imaging speed of traditional PAM systems that mostly use slow mechanical scanning methods, especially when a large field of view is imaged without sacrificing the spatial resolution. If undersampling is performed with a large scanning step size, the imaging speed can be improved, but at the cost of the spatial resolution and thus image quality.

There have been great efforts toward improving PAM imaging speed via advanced scanning mechanisms, such as water-immersible MEMS and polygon scanners [2, 4]. In addition, compressive sensing methods like single pixel and digital micromirror devices have been explored in PAM as an avenue to speed up imaging [5, 6, 7, 8]. However, unlike traditional PAM systems relying on slow mechanical scanning, the imaging speed of state-of-the-art high-speed PAM systems is often limited by the laser’s pulse repetition rate, rather than the motor’s scanning speed. For example, for our recently published polygon-scanner based PAM system [4], the laser’s maximum pulse repetition rate is 800 kHz and the B-scan (i.e., the fast-scanning axis) rate can reach as high as 2000 Hz over a 10 mm scanning range. However, in order to satisfy the Nyquist sampling theorem, the B-scan rate is limited to 200 Hz in practice, which is much lower than the maximum achievable speed. One way to increase the scanning speed is to increase the scanning step size. Sparse sampling has thus become a necessary compromise when the imaging speed needs to be increased. In other words, in modern high-speed PAM, reducing the number of image pixels by sparse sampling would lead to the same percentage increase in the imaging speed.

There have been a number of deep learning applications in photoacoustic computed tomography (PACT) to remove artifacts [9, 10, 11, 12, 13, 14, 15, 16, 17] and improve contrast [18, 19, 20] from undersampled data. However, unlike PACT, PAM uses direct image formation without inverse image reconstruction [21, 22, 23, 24]. This absence of inverse image reconstruction has led the application of deep learning in PAM to be scarce so far, with one example using the technique for PAM motion-correction [25]. It is worth noting that the task of upsampling PAM images differs significantly from that in PACT due to different image formation methods. In the undersampled PAM application, the deep learning method is approximating missing pixels, whereas undersampled PACT applications use deep learning to remove artifacts introduced by ill-posed reconstruction. Outside of deep learning, dictionary learning has recently been reported to reconstruct undersampled PAM images [26]. However, dictionary learning often learns far fewer parameters than deep neural networks and lacks the benefit of layered operations. Thus, there is still a strong need for novel methods that can improve the imaging speed of PAM systems without deteriorating the image quality or increasing the system complexity.

In this paper, we propose a deep learning approach to improve undersampled PAM images, using as few as 2% of the original pixels. Our deep learning technique offers an improved ability to approximate the nonlinear mapping of the undersampled images to their fully-sampled counterparts. Our method differs from previous efforts in high-speed scanners because it offers a software-only solution to the resolution-speed tradeoff. Moreover, our deep learning model was trained on a large number of fully-sampled PAM images as the ground truth, and thus we were able to circumvent the obstacle phantom studies often have of validating the in vivo testing results.

II. METHODS

A. Deep Learning Framework

We first assume in (1) that there exists an approximate function F that maps the undersampled PAM image, X ∈ ℝ^m×n, to the fully-sampled PAM image, Y ∈ ℝ^u×v. We then train our deep learning model to learn a mapping G(θ,X), with both a parameter matrix θ and the downsampled image X as input, such that our specified loss function is minimized via supervised learning so G(θ,X) ≈ F(X) = Y.

$$F:X\to Y$$ (1)

B. Loss Function

For the primary loss function, representing the pixel-wise error, we use the mean squared error (MSE) between the ground truth image Y_true and the upsampled image Y_pred:

$$L_{MSE}=\frac{1}{N}{\sum }_{i=1}^N{\left(Y_{\mathit{\text{true}}}-Y_{\mathit{\text{pred}}}\right)}^2$$ (2)

Similar to [27], we also use Fourier loss (FMSE) where the mean squared error is calculated from the magnitude of the 2D Fourier transform of Y_true and Y_pred:

$$L_{\mathit{\text{FMSE}}}=\frac{1}{N}{\sum }_{i=1}^N{\left(|\mathcal{F}\left(Y_{\mathit{\text{true}}}\right)|-|\mathcal{F}\left(Y_{\mathit{\text{pred}}}\right)|\right)}^2$$ (3)

The MSE and FMSE are combined via a weighted sum with a quality loss term that derives from SSIM and PSNR:

$$L_{\mathit{\text{Total}}}= {\lambda }_1{L}_{MSE}+ {\lambda }_2{L}_{\mathit{\text{FMSE}}}+ {\lambda }_3{L}_{\mathit{\text{Quality}}}$$ (4)

$$L_{\mathit{\text{Quality}}}=\left(1-\mathit{\text{SSIM}}\right)+\frac{40-\mathit{\text{PSNR}}}{275}$$ (5)

We use the weights of λ₁ = 1.0, λ₂ = 7.5×10⁻⁵, and λ₃ = 1.0×10⁻³ respectively, which were found via heuristic and fine-tuning to be optimal for all of the tested models. The general strategy is that the pixel-wise loss serves as the primary loss function, with the two other loss terms contributing frequency features and reconstruction quality. These weights provide balanced pixel-wise approximation, removal of undersampling frequency-space artifacts, and upsampling quality. When designing the loss function, we tested both MSE and MAE as pixel-wise loss terms, and both had similar performance with properly tuned hyperparameter weights. The one benefit of MSE over MAE in our method was that MSE fluctuated less during training and thus was more stable for the optimization of FMSE and the image quality term. This gives fewer spikes in the loss function, allowing the optimizer to better stabilize to a minimum. We chose to incorporate pixel-wise loss in the Fourier domain as it provides the optimizer with the vessel orientations and may highlight remnants of uniform downsampling as frequency corruptions. However, because the FMSE loss can contribute to the training instability (especially during the early iterations) [27], we have decided to use a small weighting factor to limit its overall impact on the loss function. The weighting factors between SSIM and PSNR in (5) derive from observations. During training, the PSNR between the ground truth and the model output never exceeded ~35.0 dB, so 40.0 dB was used in (5) as an empirical PNSR limit. SSIM is unitless and has a theoretical limit of one. Subtraction by these limits creates an SSIM and PNSR loss to be minimized. To combine SSIM and PSNR, we divided the latter by 275 to ensure both loss terms were on the same scale and that SSIM was weighted more than PSNR.

C. Deep Learning Architectures

Each of the tested deep learning models serves as a modification of the general U-net structure, which has been shown to work well when removing downsampling aberrations like those that arise in the upsampling of undersampled PAM images. The models tested are as follows: modified U-net, Res U-net, Res ICL U-net, and Fully Dense U-net (FD U-net) (see Fig. 1 for a depiction of FD U-net and the Supplemental Materials for figures of the other model architectures).

Fig. 1.

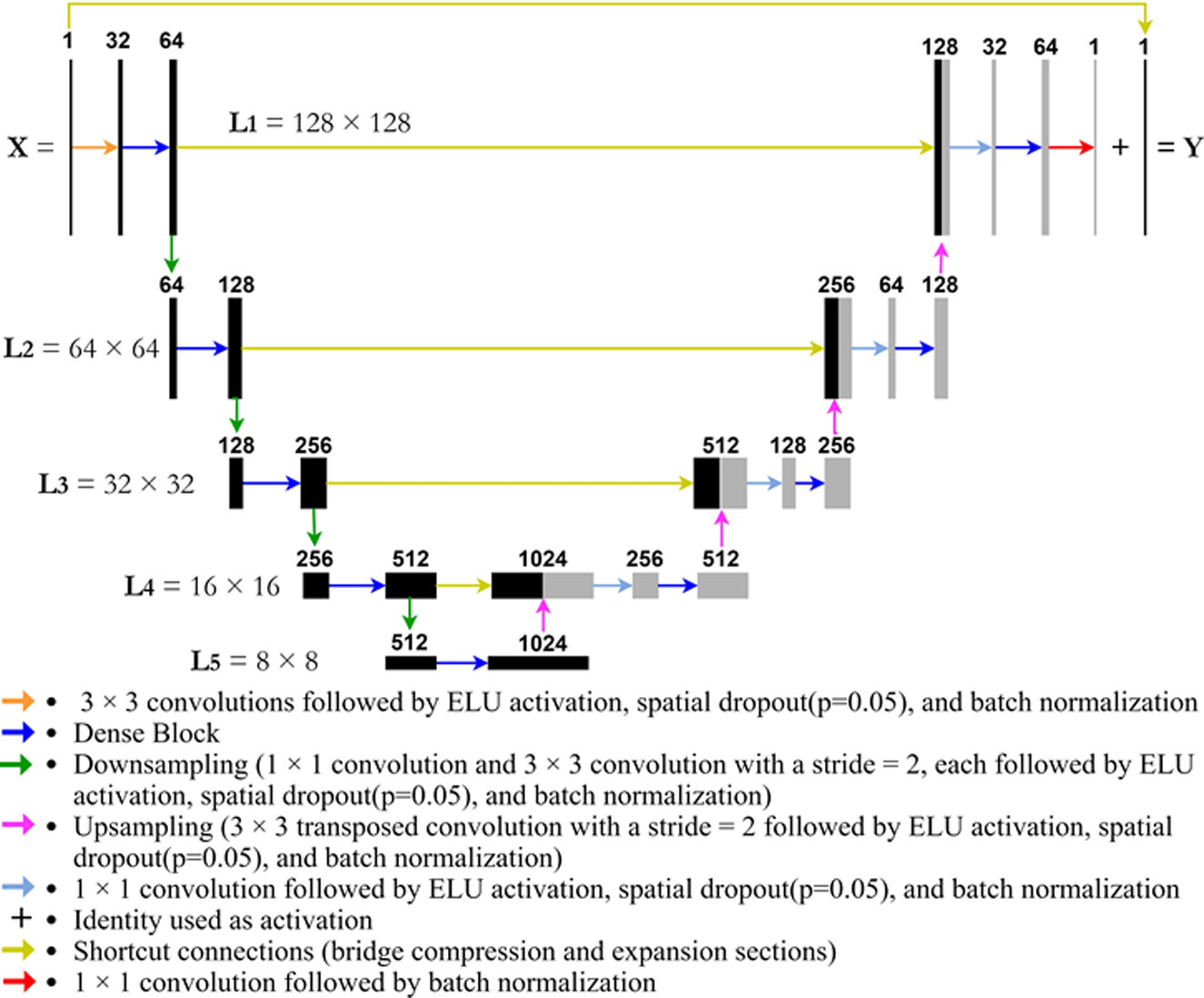
Visual representation of FD U-net architecture used as the basis for our model. The variables L₁, L₂, L₃…Li refer to the level of compression depth (i) within the model and the image size (n × n) at that compression depth.

D. U-net

Our network is a direct modification of the classic U-net architecture [28], which is known for its ability to remove imaging artifacts through a process of spatial compression and subsequent spatial decompression using information from the skip connections. For our modified U-net, we exchanged the max pooling layers of the classic U-net architecture with a convolutional downsampling layer, added an identity activation [10] and batch normalization [29], and exchanged RELU activation for ELU. By substituting max pooling for a 1 × 1 convolution followed by a 3 × 3 convolution with a stride of 2, our architecture gained greater flexibility in the downsampling procedure. With a moderate increase in parameters, this convolutional downsampling modification should [30] and has in our testing been found to have equal or greater performance than the classic U-net architecture. The addition of an identity activation has been proven effective in applications that seek to remove image aberrations in undersampled PACT [10], such that the whole network becomes reminiscent of a residual block. The inclusion of batch normalization allows the network to more aptly avoid internal covariate shift and has improved model generalizability [29]. We switched to ELU activation because it can mitigate an exploding gradient and improve learning speed in deeper residual networks [31, 32].

E. Res U-net

Res U-net is built upon our previously mentioned modified U-net by including residual connections [33] that span every two main convolutional blocks. These residual connections are composed of a 1 × 1 convolution block to change the channel depth, followed by an addition layer to combine the residual connection with the output of the residual block. These residual connections can allow the model to more efficiently learn from the work of previous layers within the network, reducing the vanishing gradient and improving the performance of deeper networks [33].

F. Res ICL U-net

The Res ICL U-net is built upon our Res U-net by incorporating modified independent component layer (ICL) blocks [34]. These blocks reorganize the order of layers in a typical convolutional block. Our modification incorporates spatial dropout as opposed to regular dropout, similar to [35]. The spatial dropout provides a comparable regularizing effect while not dropping individual pixels, as our task of upsampling is especially dependent on utilizing the effective pixels. The ICL residual block is composed of two ICL convolutional blocks, which include a 3 × 3 convolution that is preceded by ELU activation, batch normalization, and a spatial dropout operation (with p = 0.05).

G. Fully Dense U-net

Then lastly we modified a promising new U-net architecture that incorporates dense blocks, called Fully Dense U-net (FD U-net). FD U-net (see Fig. 1), first proposed by Guan et al. [11] and later used by Nguyen et al. [27] and Vu et al. [16], implements dense blocks (see Fig. 2) in both the expanding and contracting paths of U-net. These dense blocks allow each layer to learn additional feature maps based on the knowledge gained by all previous layers. Doing so, FD U-net effectively allows each layer within the dense block to build on each other, as the input of each dense block layer is the outputs of the previous dense block layers concatenated with the original input to the dense block [11]. This ensures that each layer only needs to learn refinements that either augment the previous layers or diversify the collective feature set [11]. In addition, these dense blocks also allow for deeper networks without the issue of a vanishing gradient [11].

Fig. 2.

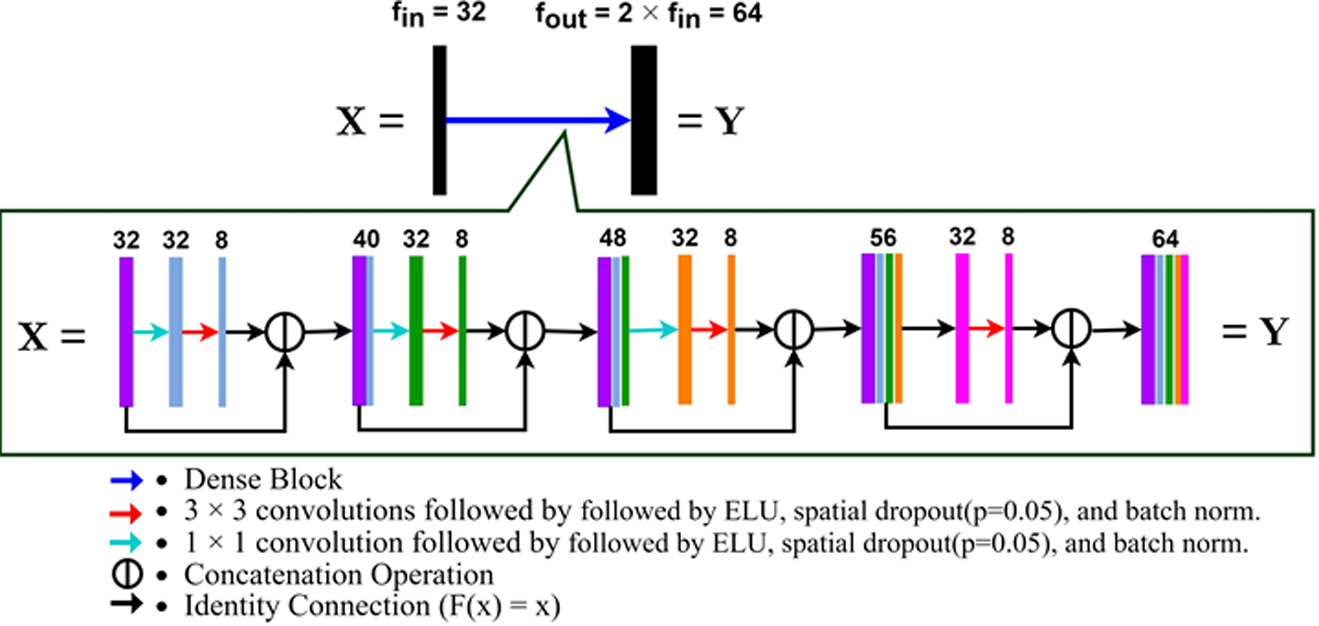
A detailed view of an FD U-net Dense Block. X is the input to the Dense Block and Y is the output. f is the number of filters. f_out= 2 × f_in; for f_in = 32, f_out = 64. k = 8 as k = f_in/4.

Our implementation of FD U-net has three modifications from the original model: (1) RELU activation is replaced with ELU activation, (2) the max pooling layers are replaced with a 1 × 1 convolution block and a 3 × 3 convolution block with a stride of 2, and (3) spatial dropout is added with a probability of 0.05 within each convolution block (see Fig. 1). The first modification benefits from batch normalization in mitigating an exploding gradient, and has been shown to improve learning speed in deeper residual networks [31, 32]. The second modification allows for a learned downsampling operation rather than the rigid max pooling procedure [30], as stated previously. The third modification can help with model generalization, especially in dense networks [35]. In our testing, this addition allows FD U-net to achieve the same validation performance in ~25–30% of the total iterations when compared to the model without spatial dropout.

III. Experimental Procedures

A. Data Preparation

Our dataset is composed primarily of in vivo mouse brain microvasculature data acquired by the Photoacoustic Imaging Lab at Duke University, using the PAM system previously published in [36]. This PAM system has a lateral resolution of 5 μm and an axial resolution of 15 μm. We are particularly interested with in vivo mouse brain imaging, because (1) PAM has been playing an increasingly important role in neuroscience, (2) functional brain imaging needs a high imaging speed, and (3) mouse brain vasculature has clear organization and patterns to be learned [37, 38, 39, 40, 41, 42, 43, 44]. Our dataset contains 381 images of mouse brain vasculature, all acquired at a wavelength of 532 nm. Most mouse brain vessels visible to PAM have a minimum diameter of ~10 μm [41], so a scanning step size of 5 μm was used for the fully sampled brain images. For pre-processing, we applied a slight thresholding, a 3 × 1 median filter along both axes, and a 2D Gaussian filter with a standard deviation of 0.01. The data was then randomly divided into approximately 80 percent training (304 images), 10 percent validation (39 images), and 10 percent testing (38 images). The training dataset was used in the optimization of the stochastic gradient descent algorithm, the validation dataset was used during training to save the best model according to the validation metrics, and the testing dataset was reserved to compare model inference performance.

B. Downsampling Procedure

We artificially downsampled our fully-sampled PAM images in order to mimic the undersampling performed in practice. For example, if the artificial scanning step size in the x-direction is five times as large as the fully-sampled step size, we downsample the x-axis by a ratio of 5:1 (sampling the first image column out of each group of 5). This method can be used to synthetically recreate different downsampling ratios. The downsampling ratio follows the format of [Sx, Sy], where Sx and Sy are the downsampling ratios along the x-axis and y-axis, respectively. Note the x and y directions are with respect to the images. For example, if an image is undersampled by a factor of 5 in the x-direction and 7 in the y-direction, the downsampling ratio is [5, 7].

To restore the true size of the downsampled images, we tested two different approaches to add back in these missing pixels. The first approach used zero-filling, in which missing pixels were replaced with zero, as shown in Fig. 3. This approach has the same effect as applying a binary mask to the fully-sampled images. The second approach resized the downsampled images using bicubic interpolation. After testing both approaches as the input to our deep learning models, we found that the zero-fill input method outperformed the bicubic resizing input method according to both peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) [45]. As such, we chose to proceed with the zero-fill method for resizing the inputted downsampled images in all of our experiments. After this downsampling procedure, each image was normalized between 0–1.

Fig. 3.

Depiction of how a fully-sampled image (a) can be downsampled in practice or artificially into image (b), which has missing pixels represented by zero-fill.

In some super-resolution or upsampling techniques, like SR-GAN [46], the image size is actually changed within the network using deconvolutions or bilinear interpolation. However, these techniques are often implemented with the upsampling ratios being equal for both axes. In practice, PAM images are often downsampled differently along the slow-scanning and fast-scanning axes. By initially upsampling our images using the zero-fill method, we allow for greater flexibility in the downsampling ratio, as it does not modify the underlying model architecture.

C. Data Augmentation

Our dataset is composed of images that are greater than 128-by-128 pixels, but our model expects an input image size of 128-by-128. First, all images were zero padded so that the pixel sizes of the images were evenly divisible by 128 in both the x and y directions. Our model during the inference phase worked with 128-by-128-pixel patches cropped from padded images (see Model Patchwork Algorithm). In order to augment and standardize the images we used random crop, which created a standard sub-image with 128-by-128 pixels at a random location within the image. This data augmentation step was performed every time the deep learning algorithm loaded a batch of fully-sampled images and downsampled input images for training and metric evaluation. To stabilize training, as the random crop may land in a sub-image with too few blood vessels, we performed 10 random crops per training iteration.

We also performed random rotation (up to 20 degrees), random lateral shift (up to 10% of the image width), random vertical shift (up to 10% of the image height), and random shear (up to shear factor of 0.2) [47]. Each of the augmentation methods used a fill value of 0. Each image had a 25% chance of a random brightness shift and a random contrast adjustment. There was then a 12.5% chance of random additive Gaussian noise, with a zero mean and a standard deviation between 0.003–0.015, and a random jpeg quality adjustment of 10–30 to simulate various image qualities. All of the random augmentation techniques used a random seed of 7 for reproducible results. The validation dataset used 10 random 128-by-128 pixels crops. Other than random crops being used on the validation dataset to stabilize the performance of our saving metrics (see Network Training), none of the data augmentation techniques were used on the validation and testing datasets.

D. Network Training

All of the networks were optimized using the Adam algorithm [48] with a mini-batch size of 16 and initial learning rate of 0.005, that was found to be balanced for all the models. As an optimization technique, Adam is generally considered quite robust to one’s choice of hyperparameter values, so we kept many of the balanced default values provided by Tensorflow [49]. The models were trained for 200 epochs (~8 hours for each of the models), with 10 random crops per training image and 10 random crops per validation image. The performance gain after ~100 epochs (~4 hours) was insignificant (~1–2%) in some cases, and may not be necessary if the training time is constrained. For the batch normalization, the momentum parameter was set to 0.99 and ε was set to 0.001. For each of the models trained, two metrics were used to determine when to set model checkpoints. One metric was the full model loss on the validation set, and the other metric was specifically the L_Quality loss term on the validation set, which combines SSIM and PSNR in (5).

The networks were implemented using Python 3.7.6 in Keras with a Tensorflow backend. The workstation setup included an AMD Ryzen 7 1700x CPU, 32 GB RAM, and a NVIDIA GTX 1080Ti.

E. Model Patchwork Algorithm

In ideal conditions, our deep learning model should take 128 × 128 pixel downsampled PAM images – with missing pixels represented by zero-fill – as the input, and output 128 × 128 pixel images that approximate the fully-sampled ground truth. However, a full murine brain image might have at least 1500 × 1500 pixels, which cannot be directly fed into our model. To overcome the image size limitation of our model, we developed an algorithm to transform larger images into 128 × 128 pixel patches that could be processed by our model and stitched back into the original image size. Our patchwork algorithm pads both image axes with zeros such that the dimensions of the image are evenly divisible by 128. Next, the algorithm loops through the image to form non-overlapping patches of 128 × 128 pixels.

In the first pass, each patch is fed into our model as X and the output Y (Fig. 1) is placed at the patch’s original location within the full-size image. However, refinement is needed as each patch may contain artifacts on its edges (Fig. 4 (c)). These artifacts are removed by two subsequent cleaning passes. The second pass reprocesses the original downsampled image, but with patches offset such that the patch center falls on the edges of the first pass patches (the red dotted lines in Fig. 4 (a)). The output of the second pass replaces the edge pixels of the first pass with a vertical or horizontal 20-pixel buffer zone (red regions in Fig. 2 (b)) at the center of the second pass patches. The third pass then refines the horizontal-vertical intersection areas of the first and second pass results, to eliminate the edge artifacts left from the first pass or introduced in the second pass (blue regions in Fig. 2 (b)). The three passes cover all possible edge aberrations. After extensive optimization, this model patchwork algorithm can process a full image from the test set (n = 38) in an average time of 4.3 ± 1.7 seconds. When considering image loading and saving, image padding, and the calculation of various metrics, the average total processing time was 11.1 ± 3.9 seconds per test image. The model patchwork time was similar for all the tested model architectures.

Fig. 4.

Illustration of the patchwork algorithm for the first pass and subsequent cleaning passes. Due to edge aberrations that can occur in the first pass patches (numbered in (a) and colored black in (b)), we perform a second pass (shown in red in (b)) and a third pass (shown in blue in (b)) to remove the edge distortions visible in (c) as horizontal and vertical dark lines (see red arrows).

IV. Results

A. Model Architecture comparison

As seen in Table I, for each of the downsampling ratios tested, the deep learning models outperformed both interpolation methods and clearly improved the zero-fill input images. Among the deep learning architectures, FD U-net consistently had the best performance for each of the downsampling ratios tested. Therefore, our analysis focused on FD U-net. Because bicubic interpolation outperformed Lanczos, we used bicubic interpolation as the primary point of comparison.

TABLE I.

STATISTICAL METRICS (MEAN ± SD) TO COMPARE DOWNSAMPLING RATIOS

Ratios	Metrics	Zero-Fill	Lanczos Interpolation	Bicubic Interpolation	U-net	Res U-net	ICL Res U-net	FD U-net
[5, 1]	SSIM	0.510 ± 0.110	0.893 ± 0.028	0.903 ± 0.264	0.950 ± 0.012	0.954 ± 0.013	0.953 ± 0.012	0.961 ± 0.011
	MS-SSIM	0.585 ± 0.098	0.961 ± 0.013	0.962 ± 0.013	0.986 ± 0.003	0.987 ± 0.003	0.986 ± 0.003	0.990 ± 0.002
	PSNR (dB)	16.94 ± 3.23	29.04 ± 2.21	29.16 ± 2.22	32.36 ± 2.58	32.96 ± 2.84	32.06 ± 3.06	34.04 ± 2.16
	MAE	0.0701 ± 0.0378	0.0160 ± 0.0052	0.0152 ± 0.0051	0.0115 ± 0.0043	0.0109 ± 0.0047	0.0119 ± 0.0052	0.00849 ± 0.00285
	MSE	0.027 ± 0.021	0.0014 ± 0.0071	0.0014 ± 0.0007	0.00069 ± 0.00039	0.00061 ± 0.0004	0.00078 ± 0.00051	0.00044 ± 0.00020
[7, 3]	SSIM	0.436 ± 0.111	0.834 ± 0.048	0.848 ± 0.048	0.859 ± 0.035	0.876 ± 0.036	0.868 ± 0.025	0.898 ± 0.026
	MS-SSIM	0.433 ± 0.135	0.932 ± 0.022	0.935 ± 0.021	0.961 ± 0.008	0.955 ± 0.012	0.954 ± 0.010	0.964 ± 0.008
	PSNR (dB)	16.19 ± 3.23	26.69 ± 2.44	26.84 ± 2.45	28.60 ± 2.13	27.86 ± 2.44	28.67 ± 1.79	29.05 ± 1.80
	MAE	0.0834 ± 0.0450	0.0220 ± 0.0093	0.0209 ± 0.0091	0.0193 ± 0.0064	0.0201 ± 0.0084	0.0191 ± 0.0053	0.0173 ± 0.0057
	MSE	0.032 ± 0.024	0.0025 ± 0.0016	0.0024 ± 0.0016	0.0016 ± 0.0008	0.0019 ± 0.0011	0.0015 ± 0.0006	0.0014 ± 0.0006
[10, 5]	SSIM	0.422 ± 0.112	0.681 ± 0.072	0.701 ± 0.070	0.785 ± 0.055	0.805 ± 0.054	0.803 ± 0.049	0.819 ± 0.054
	MS-SSIM	0.404 ± 0.143	0.813 ± 0.046	0.819 ± 0.045	0.906 ± 0.021	0.912 ± 0.020	0.908 ± 0.021	0.915 ± 0.021
	PSNR (dB)	16.06 ± 3.23	22.43 ± 2.25	22.69 ± 2.27	25.49 ± 2.46	25.36 ± 2.00	25.48 ± 2.53	25.79 ± 2.42
	MAE	0.0858 ± 0.0463	0.0385 ± 0.0132	0.0363 ± 0.0129	0.0270 ± 0.0099	0.0278 ± 0.0097	0.0259 ± 0.0103	0.0247 ± 0.0098
	MSE	0.033 ± 0.025	0.0065 ± 0.0031	0.0060 ± 0.0030	0.0033 ± 0.0018	0.0032 ± 0.0015	0.0033 ± 0.0019	0.0030 ± 0.0017

PSNR, peak signal-to-noise; SSIM, structural similarity index; MS-SSIM, multiscale structural similarity index; MAE, mean absolute error; MSE, mean squared error

B. Downsampling Ratio: [5, 1] – 20% effective pixels

We first examined a downsampling ratio of [5, 1], in which only 20% of the original pixels were used for the image upsampling. A sub-region of the fully-sampled image is shown in Fig. 5 (a2), while the downsampled image is depicted in Fig. 6 (a-I). The results from FD U-net and bicubic interpolation are shown in Fig. 6 (a-II) and (a-III) respectively. It is clear from the statistical results (Table I) that the deep learning model vastly outperformed both interpolation methods. However, the differences in the image results can be subtle. A clear distinction that can be made between the two methods is in the quality of “vesselness” (i.e., smoothness and roundness). As visible in the profiles of vessels, especially in the small vessels (Fig. 7), bicubic interpolation suffers from jagged and disjointed features (i.e., spatial aliasing) that do not exist in the learned FD U-net reconstruction.

Fig. 5.

The performance of FD U-net compared to bicubic interpolation with a downsampling ratio of [7, 3]. (a) Fully-sampled whole-brain vascular image as the ground truth. Close-up images of the dashed box regions (1–4) are shown to the right as (a1)-(a4). (b) FD U-net results from the downsampled data. (c) Bicubic interpolation results from the downsampled data.

Fig. 6.

Comparison of FD U-net performance with different downsampling ratios of the full-sampled image in Fig. 5 (a2). At downsampling ratios of [5, 1], [7, 3], and [10, 5] (as rows (a), (b), (c) respectively), we have depicted (I) the downsampled images, (II) the FD U-net predictions, and (III) the bicubic interpolation results.

Fig. 7.

Comparison of upsampling performance on two small vessels (~50 μm in diameter) labeled by the red lines in Fig. 6 (b-I) as vessel 1 (a) and vessel 2 (b). The downsampling ratio used was [7, 3]. As shown bicubic interpolation smooths a vessel in (a) and introduces a vessel discontinuity in (b) which does not exist in the ground truth and in the deep learning results.

C. Downsampling Ratio: [7, 3] – 4.76% effective pixels

The comparative metrics continue to show the superior performance of the FD U-net model in the [7, 3] downsampled data (Table I), with FD U-net’s performance at this downsampling ratio being similar to the performance of interpolation methods at [5, 1]. In addition, the image quality differences between the two methods have become more significant at this sparsity. At the [7, 3] downsampling ratio, FD U-net’s upsampling result in Fig. 5 (b) greatly outperforms bicubic interpolation in Fig. 5 (c) in terms of vesselness. Using less than 5% of the pixels, bicubic interpolation creates reconstructions with jagged and biologically improbable vessel profiles (see Fig. 7), while the deep learning model is able to reconstruct smoother vessels. This quality of vesselness is difficult to replicate with phantoms, which highlights the importance of our training strategy using fully-sampled in vivo data as the ground truth. The image quality of FD U-net at [7, 3] downsampling is still acceptable.

D. Downsampling Ratio: [10, 5] – 2% effective pixels

The third downsampling ratio we tested was [10, 5], which constituted upsampling from ~2% of the original pixels. We tested this downsampling ratio to explore the limits of the deep learning model. At [10, 5], as shown in Table I, the FD U-net still outperformed the bicubic interpolation in all the listed metrics. As shown in Fig. 6 (c-II), the FD U-net model begins to blur vessels that are close together or overlapping. Although the performance of our model decreased at this very high level of downsampling, the bulk physiology of the vasculature would still be acceptable, given that in modern PAM systems the imaging speed could be potentially improved by 50 times.

V. Discussion

Our work builds on the many recent innovations in deep learning, and applies these advances to the rapidly growing field of PAM. By collecting and training on an expanding set of in vivo mouse brain microvascular data, our FD U-net model was able to learn how to reconstruct images at downsampling ratios of up to 50 times. Using between 2% and 20% of the original pixels, our FD U-net model can potentially accelerate the imaging speed of modern high-speed PAM systems by 5 to 50 times, assuming the imaging speed is mainly limited by the laser’s pulse repetition rate. This approach circumvents the expensive hardware advances that are currently researched and, as our dataset expands, builds an avenue to even greater performance with continuous retraining and refinement. The three representative downsampling ratios enabled us to demonstrate the relative performance of the deep learning models, and highlight the superior capability of the learned FD U-net model to improve the vesselness of downsampled PAM images. Our results show a deterioration in performance as sparsity increases (Fig. 6), but this deterioration should always be put into the context of the desired resolution and imaging speed of the experiment. For example, at high downsampling ratios like [10, 5], it will likely be difficult to fully reconstruct small vessel features less than approximately 50 microns in the x-direction and 25 microns in the y-direction (given an original scanning step size of 5 μm). As such, these higher downsampling ratios are likely better suited for low-resolution functional imaging than high-resolution structural imaging. However, even for structural imaging, the model is still able to reconstruct small vessels with less aliasing and better overall vessel quality than interpolation methods (like bicubic interpolation). Moreover, such high downsampling ratios may still be able to capture segments of small vessels, which are typically nonlinear, and thus allow the model to improve the overall vessel continuity. Downsampling ratios can thus be appropriately tuned to best fit specific applications with balanced imaging quality and imaging speed. Our deep learning model expands the range of acceptable downsampling ratios into those that were previously considered forbidden in PAM.

By training and testing on various downsampling ratios, we were also able to demonstrate the limitations of the current deep learning architectures and forge paths toward new innovations. Moving forward, a key improvement will be the refinement and application of new model architectures such as generative adversarial networks (GANs) [16, 49, 50], which may yield modest performance gains. In addition, we will develop tailored deep learning models for specific PAM system implementations. This may be done in conjunction with technical advances in compressed sensing or fast-scanning mechanisms [2, 4, 5, 6, 7, 8]. Our method differs from the traditional super-resolution imaging approaches, as we do not exceed the baseline resolution achievable by our system, but rather improve image quality after pixel-wise subsampling [51].

One of the most prominent challenges in implementing deep learning models in PAM has been the need to acquire a large amount of fully-sampled in vivo PAM data. Our lab hopes to be the first of many to take steps toward openly sharing PAM data for the benefit of the community [52]. At the end of the paper, researchers can find a link to the entire dataset used in our work as well as our source code. We aim to create and share a large database of PAM vascular images to which many researchers can contribute and use for their own machine learning applications. This database will grow continuously as our lab generates new data, allowing for continuous retraining and refinement. In addition, because of the high quality of PAM vessel data, it should be possible for researchers in other imaging fields such as two-photon microscopy and optical coherence tomography to train models using this PAM dataset.

VI. Conclusion

Here, we have demonstrated a novel application of deep learning principles in order to address the trade-off of imaging speed and spatial resolution in undersampled PAM. We tested different model architectures and found that FD U-net has the best performance (Table I). Our modified FD U-net model architecture outperformed bicubic interpolation (Figs. 5–7) at all of the representative downsampling ratios. By making our mouse brain microvasculature dataset and deep learning model source code freely available to the research community, we hope to maximize the impact of our deep-learning enhanced PAM.