Abstract
Background
Schistosomiasis is a neglected tropical disease endemic in 54 countries. A major Schistosoma species, Schistosoma mansoni, is sustained via a life cycle that includes both human and snail hosts. Mathematical models of S. mansoni transmission, used to elucidate the complexities of the transmission cycle and estimate the impact of intervention efforts, often focus primarily on the human host. However, S. mansoni incurs physiological costs in snails that vary with the age of the snail when first infected. Snail demography and the age of snail infection could thus affect the force of infection experienced by humans, which is frequently used to predict the impact of various control strategies.
Methods
To address how these snail host and parasite interactions influence model predictions, we developed deterministic models of schistosomiasis transmission that include varying complexity in the snail population age structure. Specifically, we examined how model outputs, such as schistosome prevalence in human and snail populations, respond to the inclusion of snail age structure.
Results
Our models suggest that snail population age structure modifies the force of infection experienced by humans and the relationship between snail infection prevalence and corresponding human infection prevalence. There are significant differences in estimated snail infection, cercarial density and mean worm burden between models without snail population dynamics and those with snail populations, and between models with a homogeneous snail population and those with age stratification. The variation between finely age-stratified snail populations and those grouped into only juvenile and adult life stages is, however, minimal.
Conclusions
These results indicate that including snails and snail age structure in a schistosomiasis transmission model alters the relationship between snail and human infection prevalence. This highlights the importance of accounting for a heterogeneous intermediate host population in models of schistosomiasis transmission where the impact of proposed control measures is being considered.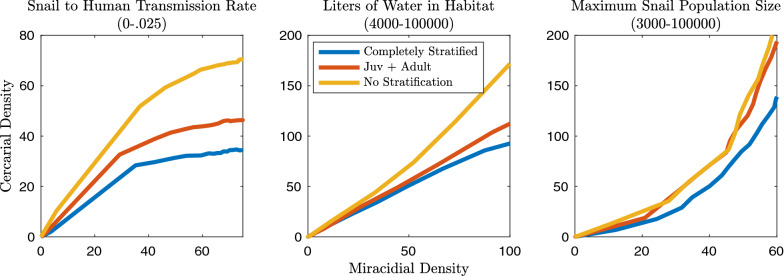
Keywords: Schistosomiasis, Mathematical modeling
Background
Schistosomiasis is a neglected parasitic disease caused by various trematode species of the genus Schistosoma, for which 218 million people needed treatment in 2015 [1]. Chronic schistosomiasis infections can lead to serious complications such as kidney damage and enlargement of the liver and spleen [2]. One of the most common Schistosoma species, Schistosoma mansoni, is dependent on both humans and specific species of planorbid snails within the genus Biomphalaria for sustained transmission and survival. However, modeling efforts are frequently focused solely on the human host and typically neglect the non-linear dynamics that may be occurring within the snail segment of the transmission cycle. Because this parasitic life cycle has proved robust to elimination, a re-examination of the key assumptions of mathematical models and their consequences for informing control interventions is warranted.
There is a long tradition of the application of mathematical modeling to problems of schistosomiasis control. Numerous mathematical models of schistosomiasis transmission have addressed heterogeneity in infection risk in humans due to spatial factors, socioeconomic status, immune competency and behavior [3–10]. There have been fewer studies that address the role of heterogeneity in the intermediate host population for S. mansoni transmission. These studies have incorporated spatial distribution of snails, the prepatent infection period, differential mortality, logistic population growth and parasite-induced castration [3–10]. However, models often classify the snail population as relatively homogeneous, discounting the role that age structure of intermediate hosts could play in disease dynamics.
Age structure within definitive hosts has been shown to impact transmission, and for some diseases, to change the basic reproductive number (R0) and estimates of the impact of proposed control measures [11–14]. For instance, age population structure has been found to alter R0 estimates for rubella, influenza and other diseases [15, 16]. Broadly, host age effects are due to age-specific differences in contact patterns, host immune competency, susceptibility and transmission capability, and fitness costs [12, 17–24]. Overall, significantly less work has centered on the consequences of age structure in intermediate host populations. However, population age structure has been shown to be important in models of Echinococcus transmission. In that system, age structure is relevant because the parasite maturation is fast relative to the intermediate host lifespan and there is differential infection load and output between intermediate host age classes [25]. There are distinct parallels between that system and the Biomphalaria and S. mansoni interaction with respect to infection persistence in the intermediate host and the relationship between intermediate host age and parasite output.
Schistosoma infection in the intermediate host incurs an array of fitness costs. These costs include: reduced fecundity and the eventual castration of the snail, increased rates of mortality, and in certain life stages a reduction in growth rate [26–28]. The consequences of infection may then play a role in the structuring of the snail population and its growth rate. Conversely, the age of the snail at the time of infection can also impact the relative success of the parasite. The quantity of cercariae produced by the infection of a single snail is dependent on the snail surviving the prepatent period, its subsequent lifespan and the size of snail [29, 30]. In general, the greater the snail size the greater the gonadal tissue volume available for cercarial production within the snail host [31]. As schistosomiasis infection can decrease the lifespan and growth rate of the intermediate host, the timing of infection may impact the lifetime cercarial output of the snail. There are several competing fitness costs associated with S. mansoni infection, which may lead to interactions between snail and human host infection levels that are not immediately obvious or intuitive.
In the present work, we assess the effect of age structure within the intermediate host population on the potential force of infection (FOI) to humans. The FOI is an integral component of mathematical models and is used to estimate the impact of treatment interventions on overall schistosomiasis prevalence [32–38]. Estimates of the FOI are usually extrapolated from human or snail prevalence data [27, 37]. In models without the inclusion of snails, the FOI is assumed to be directly (and linearly) related to the human infection prevalence or overall population egg output [33]. Herein we show that FOI estimates may vary widely depending on the inclusion of snails in the model and the age structure profile of the snail host population.
Methods
Mathematical model
We developed a deterministic model framework, formally described by a system of ordinary differential equations, which allows us to study the impact of snail population structure on schistosomiasis transmission. Compartments within the mechanistic model include schistosome, cercarial and miracidial life stages and definitive human hosts, and allow us to consider intermediate hosts of several age groups. The human population is kept constant in size as schistosomiasis results in morbidity but not in significant mortality in humans; it is also kept constant in size to isolate the effects of snail dynamics. Humans can have a worm burden of zero, a prepatent infection or a worm burden corresponding to a light, moderate or heavy infection. We also explore an alternative model that utilizes mean worm burden instead of infection intensity, the results of which are presented in the Additional file 1. These infection intensity designations are based on the World Health Organization’s classification system and relate directly to the number of schistosome eggs found per gram of stool in infected individuals [1]. The snail hosts can be susceptible to schistosome infection, exposed and in a pre-patent stage of infection, or infectious. Infection in humans lasts on average 3 years, after which they are again susceptible to reinfection without any additional immune protection [39]. Acquired immunity to schistosomiasis following infection has been extensively debated: reinfection is common, and any acquired immunity may only be partially protective and take a long period of intense exposure to develop; therefore, human immunity is not included within this model [40–42]. Within the snail population, S. mansoni infection is assumed to be lifelong.
We consider seven different model structures, six of which represent varying complexity in snail age structure and one model without the inclusion of any snails in the S. mansoni transmission model (Fig. 1). This level of detail is included to determine if non-linear feedback between human and snail infection predicted to occur with fine-scale snail age stratification, due to the age-specific fitness costs, is significantly different enough between population structure options to warrant the added complexity of the inclusion of all age groups. This is of particular interest as parameterizing detailed snail age structure from field studies may be time intensive and logistically difficult.
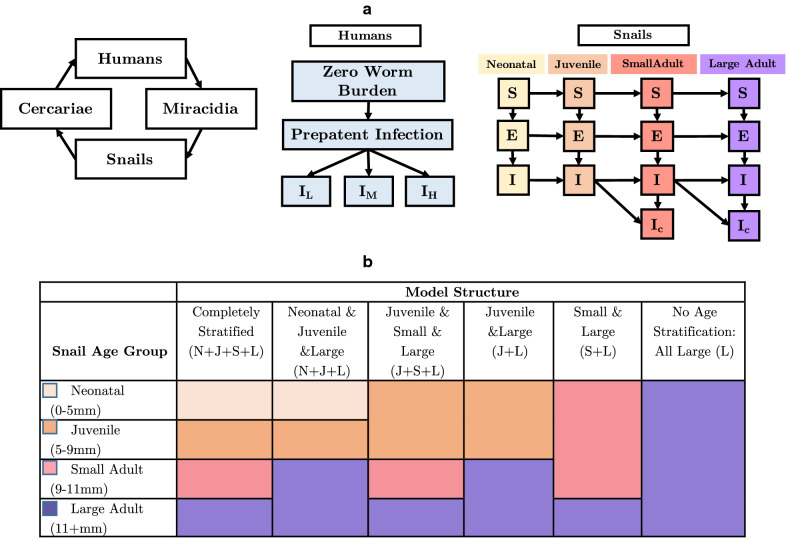
Fig. 1a, b.
Model structure diagrams. a Diagrams of the model framework illustrating the complete transmission cycle, the human infection status with variable Schistosoma mansoni worm burden, and the age-stratified snail population. S Susceptible class, E exposed class, I infected class, IC infected and castrated snails; IL infected humans with a low S. mansoni burden, IM infected humans with a moderate S. mansoni burden, IH infected humans with a heavy S. mansoni burden. b The completely stratified model for the snail population includes neonatal (N), juvenile (J), small (S) and large (L) adult age classes; this is simplified in various combinations in later model structures. The colors represent the way in which the age classes are combined in each model structure. The missing age groups in all models, excluding the completely stratified model, are subsumed into the larger age class. For example, in the neonatal and juvenile and large (N+J+L) model, small adults are subsumed into the large adult age class. In the small and large (S+L) model, neonatal and juvenile snails are subsumed into the small adult snail class. In every version of the model the snails can still be assigned to any of the infection statuses
Within the completely stratified model, snail age groups include neonatal, juvenile, small adult and large adult life stages. These correspond to specific Biomphalaria glabrata shell size classes of 0–5 mm, 5–9 mm, 9–11 mm and 11+ mm, respectively. The size classes have been shown in laboratory studies to have varying fitness responses to infection and differential schistosome cercarial shedding after infection [5, 29, 30, 43–45]. All model versions include fitness costs of infection. These fitness costs include: reduced growth rate, reduced or arrested fecundity, and increased mortality with infection. Snails infected in either the neonatal or juvenile class have slowed growth rates and therefore slowed progression into the adult classes [5, 24]. Snails that are infected in either adult class do not display diminished growth. Increased mortality after infection is consistent across all age classes. If infection with S. mansoni occurs prior to reproductive maturity then reproduction does not occur; after reproductive age is reached castration of the snail occurs after approximately 6 weeks [46]. These age categories and their corresponding snail shell size represent differing cercarial output post-S. mansoni infection [5, 27, 29, 30, 47].
Conceptual diagrams of the completely stratified and alternative model structures are portrayed in Fig. 1. In general, the merged groups are considered to have the averages of the characteristics and parameters associated with the component groups and weighted by the time spent in each age group. For instance, the juvenile and small and large (J+S+L) model has effectively three age classes: juvenile, small adult and large adult, as the neonatal age group is subsumed into the juvenile age group. The merged neonatal and juvenile group will have a parameter that is a weighted average of the neonatal and the juvenile values. The model without snail age groups assumes all snails are large adults; this is a common assumption in other models, as large snails are more likely to be collected in field surveys. A full description of the model parameters is found in Table 1, and a full description of all model subset equations can be found in the supplementary materials.
Table 1.
Description of model parameters and ranges used in the Latin hypercube parameter sets. All parameter values correspond to Schistosoma mansoni and Biomphalaria glabrata
| Parameter name | Parameter description | Parameter range | References |
|---|---|---|---|
| m | Maximum number of snails in the environment | 5000–20,000 | Estimated |
| c | Liters of water in the environment | 1000–100,000 | Estimated |
| l2 | Reduced rate of maturation in infected neonates/juveniles | 0.714 of maturation rate in uninfected neonates/juveniles | [35, 38] |
| l3 | Averaged reduced rate of maturation in infected snails in the combined neonate/juvenile/small adult class | 0.75 of maturation rate in uninfected snails | [35, 38] |
| w1 | Average time to mature from neonate to juvenile | 7 weeks | [35, 38, 51] |
| w2 | Average time to mature from juvenile to small adult | 5 weeks | [35, 38, 51] |
| w3 | Average time to mature from small adult to large adult | 2 weeks | [35, 38, 51] |
| 1/dm | Lifespan of miracidia | 4–16 h | [10] |
| 1/dc | Lifespan of cercariae | 8–20 h | [10] |
| u1 | Mortality rate of uninfected neonatal snails | 0.007–0.152/week | [35, 36] |
| u2 | Mortality rate of infected neonatal snails | 0.062–0.607/week | [35, 36] |
| u3 | Mortality rate of uninfected juvenile snails | 0.007–0.152/week | [35, 36] |
| u4 | Mortality rate of infected juvenile snails | 0.062–0.607/week | [35, 36] |
| u5 | Mortality rate of uninfected small adult snails | 0.007–0.152/week | [35, 36] |
| u6 | Mortality rate of infected small adult snails | 0.062–0.607/week | [35, 36] |
| u7 | Mortality rate of uninfected large adult snails | 0.007–0.152/week | [35, 36] |
| u8 | Mortality rate of infected large adult snails | 0.062–0.607/week | [35, 36] |
| 1/u9 | Lifespan of humans | 60 years | [48] |
| f1 | Fecundity of susceptible small adult snails | 40/week | [26, 29, 30, 46, 49] |
| f2 | Fecundity of exposed small adult snails | 4.77/week | [5, 29, 46, 49, 50] |
| f3 | Fecundity of infected but not castrated snails | 4.77/week | [5, 29, 30, 46, 49, 50] |
| f4 | Fecundity of susceptible large adult snails | 40/week | [5, 29, 30, 46, 49, 50] |
| f5 | Fecundity of exposed large adult snails | 4.77/week | [5, 29, 30, 46, 49, 50] |
| f6 | Fecundity of infected but not castrated adult snails | 4.77/week | [5, 29, 30, 46, 49, 50] |
| f7 | Weighted average fecundity of susceptible snails in the combined neonatal/juvenile/small adult class | 13.33/week | [5, 29, 30, 46, 49, 50] |
| f8 | Weighted average fecundity of exposed or infected but not castrated snails in the combined neonatal/juvenile/small adult class | 1.59/week | [5, 29, 30, 46, 49, 50] |
| g | Castration rate of snails | 0.1667/week | [46] |
| 1/y | Prepatent period in snails | 18–45 days | [39] |
| e1 | Exposure rate of neonatal snails to miracidia | 50–150/week | Estimated |
| e2 | Exposure rate of juvenile snails to miracidia | 50–150/week | Estimated |
| e3 | Exposure rate of small adult snails to miracidia | 50–150/week | Estimated |
| e4 | Exposure rate of large adult snails to miracidia | 50–150/week | Estimated |
| p1 | Per parasite susceptibility for neonatal snails | 0–1 | [5, 51, 52] |
| p2 | Per parasite susceptibility for juvenile snails | 0–1 | [5, 51, 52] |
| p3 | Per parasite susceptibility for small adult snails | 0–1 | [5, 51, 52] |
| p4 | Per parasite susceptibility for large adult snails | 0–1 | [5, 51, 52] |
| s1 | Shedding rate of neonatal snails | 2800/week | [29, 43] |
| s2 | Shedding rate of juvenile snails | 5500/week | [29, 43] |
| s3 | Shedding rate of small adult snails | 6000/week | [29, 43] |
| s4 | Shedding rate of large adult snails | 6800/week | [29, 43] |
| s5 | Averaged shedding rate in combined neonatal/juvenile snail class | 3925/week | [29, 43] |
| s6 | Averaged shedding rate in combined small/large adult snail class | 6774/week | [29, 43] |
| s7 | Averaged shedding rate in combined neonatal/juvenile/small adult snail class | 4925/week | [29, 43] |
| b | Snail-to-human transmission rate | 0.00001–0.001/week | Estimated |
| hw | Probability of eggs reaching water and hatching | 0–1 | [27, 39, 51] |
| q1 | Recovery rate among lightly infected humans | 0.2–0.333/year | [39] |
| q2 | Recovery rate among moderately infected humans | 0.2–0.333/year | [39] |
| q3 | Recovery rate among heavily infected humans | 0.2–0.333/year | [39] |
| 1/lh | Latent period in humans | 25–30 days | [39] |
| v1 | Proportion of infected humans who are lightly infected | 0–1 | Estimated |
| v2 | Proportion of infected humans who are moderately infected | 0–1 | Estimated |
| v3 | Proportion of infected humans who are heavily infected | 0–1 | Estimated |
| g1 | Eggs produced by a lightly infected human | 7000/week | [39, 53] |
| g2 | Eggs produced by a moderately infected human | 28000/week | [39, 53] |
| g3 | Eggs produced by a heavily infected human | 70000/week | [39, 53] |
| g4 | Eggs produced per mated female schistosome | 350 /day | [54] |
| i | Grams of feces produced per human | 200/day | [55] |
| Nh | Total human population size | 200 | Estimated |
| z | Scaling parameter | 1–10 | Estimated |
| k | Worm aggregation constant | 0.24 | [51] |
Model simulations and output
The seven model structures (detailed in Fig. 2) were explored to discover the impact of varying levels of complexity in age structure. The metrics calculated to evaluate the effect of age structure include: snail and human infection prevalence, the relationship between these infection levels at equilibrium, cercarial density, mean worm burden, the ratio of cercarial and miracidial density at equilibrium, and the R0 of the transmission system. The snail-to-human transmission rate was estimated and represents a compound rate of weekly exposure given cercarial density and the probability of infection given exposure. Multiplied by the density of cercariae in the environment, this represents the FOI experienced by humans. In models without snails, the FOI is the product of the transmission rate and the miracidial density. Mean worm burden was calculated by using estimates of eggs produced per mated pair of worms per day, eggs produced per gram of feces in each human infection class, grams of feces produced per human per day and the set number of humans in our system [1, 54, 55]. The classic Anderson and May mean worm burden model was also used for comparison and is presented in Additional file 1: Figures S18 and S19 [39]. The system R0 values for age class combinations were obtained through next generation matrix methods [18, 56]. The R0 sensitivity analyses, simulation results, and next generation matrix equations are fully described in the Additional file 1. All model simulations were performed in (MATLAB r2019; The MathWorks, Natick, MA).
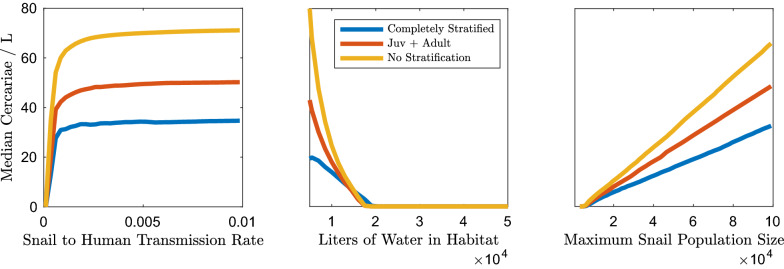
Fig. 2.
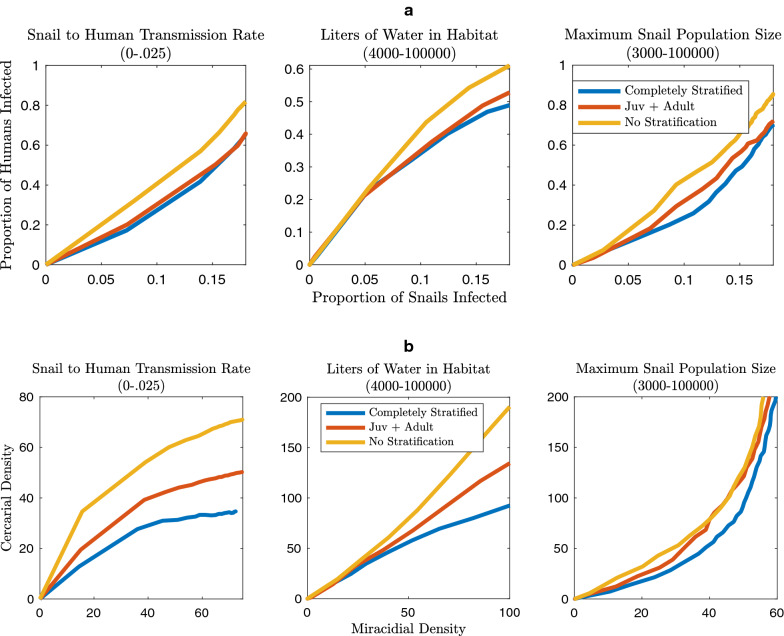
Global sensitivity analyses using Latin hypercube sampling (LHS) parameter sets and isolating the impact of changes in median cercarial density to force of infection (FOI) and snail density. The median cercarial density is primarily sensitive to the density of snails with high levels of infection possible only with high snail density, irrespective of the snail-to-human transmission rate. There are greater levels of cercarial density for the model without snail age stratification than for models with snail age stratification at comparable snail density and snail-to-human transmission rate values. Juv Juvenile
Sensitivity analyses
In order to account for the potential variability in parameter values, two types of sensitivity analyses were performed. First, we performed local sensitivity, varying each parameter value while keeping all others constant. These sensitivity analyses determined the model parameters with the most impact on the key model outcomes of interest: human infection prevalence, mean worm burden, snail infection prevalence, cercarial density, and R0 of the entire system. The resulting line plots for those parameters found to alter our model outcomes are presented in the supplementary information (Additional file 1: Figures S1–S5). The interaction of parameters that were found to impact the outcomes of interest was further explored by the generation of heat maps. The interaction of the snail-to-human transmission rate and the snail density, both estimated parameters, and their impact on cercarial density, snail and human infection levels and mean worm burden are shown in Additional file 1: Figures S6–S9. The remaining heat maps are presented in the supplementary materials (Additional file 1: Figures S10–S12).
Second, we performed global multivariate sensitivity analyses using Latin hypercube sampling (LHS) for the 44 parameters presented in Table 1. Those parameters that represented probabilities were uniformly sampled within the range 0–1. In the specific case of the proportion of infected humans the total proportion was set to 1. Parameters not restricted to values between 0 and 1 were sampled from uniform distributions within the empirically determined ranges presented in Table 1. Parameters with only a single estimate from the literature or a minuscule range were sampled from a range 0.5–2 times that presented in Table 1. The sensitivity of the transmission system to any estimated parameters is explored over an extensive range. Due to the large number of parameters and the paucity of data, LHS was used to compile 10,000 possible parameter sets to gain confidence in the relationships between these variables and snail and human infection prevalence over a spectrum of parameter values. These 10,000 possible parameter sets were used for each of the seven model options: completely age stratified; neonatal and juvenile and large adult snails; juvenile and small and large adult snails; juvenile and large adult snails; small and large adult snails; no age stratification—all large adults; snail-less model.
Results
Sensitivity analyses
Sensitivity analysis allowed us to identify the parameters that are most influential for the outcomes of interest. The outcomes of interest (R0, mean worm burden, human and snail prevalence, and cercarial density—which is directly related to the FOI experienced by humans), are impacted by snail density and the snail-to-human transmission rate. The impact of snail density and snail-to-human transmission rate on cercarial density and human infection prevalence are presented in Figs. 2 and 3. The impacts on snail infection prevalence, mean worm burden and R0 are shown in Additional file 1: Figures S13, S14 and S17. Snail density can be altered in one of two ways, either by modifying the maximum number of snails in the environment or the size of the habitat. These may change through different mechanisms. For instance, maximum snail population size may be impacted by competition, resource availability (which may not be exclusively correlated with habitat size), and snail control measures. Habitat size may fluctuate due to seasonal variation in rainfall or human-mediated habitat alteration.
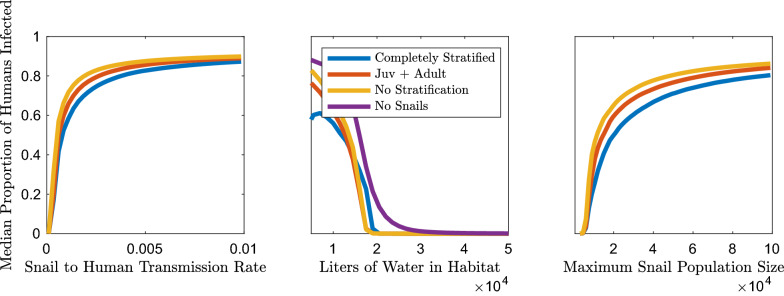
Fig. 3.
Global sensitivity analyses using LHS parameter sets and isolating the impact of changes in median proportion of humans infected to FOI and snail density. The median proportion of humans infected at equilibrium is sensitive to both the snail-to-human transmission rate, and the density of snails. There are greater proportions of humans infected for the model without snail age stratification than for models with snail age stratification at comparable snail density and snail-to-human transmission rate values. For abbreviations, see Fig. 2
The relative ranking of unstratified, partially age stratified and completely age stratified for the highest median cercarial densities, holds over a range of snail-to-human transmission rates, habitat sizes and maximum snail populations sizes (Fig. 2). The sensitivity analyses indicate that snail density, as modified by habitat size or maximum snail population size, has an appreciable impact on cercarial density and snail infection prevalence (Fig. 2; Additional file 1: Figure S13). The snail-to-human transmission rate impacts the median cercarial density only in that there is a threshold it needs to exceed for sustained S. mansoni transmission, after which there is no appreciable impact on median cercarial density (Fig. 2). Increases in the maximum snail population size lead to linear increases in cercarial density because, with a constant habitat size, the cercarial population is directly related to the absolute quantity of snails in the environment (Fig. 2). The unstratified model displays higher median cercarial density because the cercarial production for an infected snail is related to snail age and size and the unstratified model is comprised of only large adult snails. These large adult snails produce more per capita cercariae when infected than any other snail age class.
The median proportion of snails infected saturates over a range of snail-to-human transmission rate values (Additional file 1: Figure S13). The impact of the snail-to-human transmission rate is directly applied to human infection; however, the effect on snail infection is diluted by the processes occurring in the human to snail portion of the transmission cycle. Similarly, maximum snail population size did not have an appreciable effect on the median proportion of snails infected after a certain snail population size was reached (Additional file 1: Figure S13). Conversely, the habitat size had a substantial impact on snail infection; as the habitat size increased the snail infection levels decreased (Additional file 1: Figure S13). This reduction is due to the decrease in the miracidial and cercarial density with larger water body volume. Common to all of these simulations is the negligible differences in median snail infection levels for unstratified snail age models versus age-stratified models.
In contrast to cercarial density and snail infection prevalence, human infection prevalence and mean worm burden are not only heavily impacted by snail density but show a more nuanced relationship with the snail-to-human transmission rate (Fig. 3; Additional file 1: Figure S14). This disparity is due to the composition of the FOI experienced by humans. The FOI is the product of the snail-to-human transmission rate and cercarial density, which is correlated with snail density, whereas snail infection prevalence is indirectly related to the snail-to-human FOI through the link between human infection prevalence and snail infection prevalence. Similar to snail infection and cercarial density, all model types display decreasing human infection as the habitat size increases (Fig. 3). The increase in habitat size decreases miracidial density, and therefore the human-to-snail FOI, snail density, cercarial density and subsequently the snail-to-human FOI. The maximum snail population size only marginally increases the median proportion of infected humans after a snail population size sufficient for sustaining transmission has been reached. The impact of the snail-to-human transmission rate does saturate as human infection prevalence nears 100%; however, at more moderate levels of human infection prevalence (40–80%) there are disparities between model types. In particular, as with cercarial density, unstratified models predicted higher values than age-stratified model types (Fig. 3).
Snail infection
Estimates of the proportion of snails infected do not vary considerably between models with snail age stratification (Fig. 4a; Additional file 1: Figure S7). Kruskal-Wallis tests indicated that there were not significant differences in the median snail infection prevalence between the model without stratification and all age-stratified models.
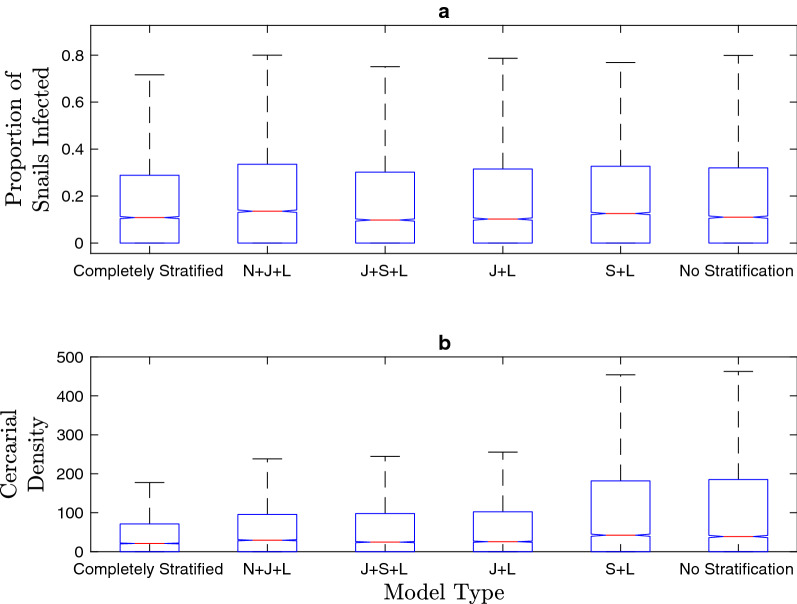
Fig. 4.
Estimates of a snail infection prevalence, and b cercarial density for each model subset with constructed possible parameter sets from LHS. a All models display comparable median snail infection prevalence. b The models with juvenile and adult snail age stratification display a lower median and a narrower range of probable cercarial densities than the models with only adult snails. For abbreviations, see Figs. 1 and 2
The overall cercarial population size, and cercarial density, which is an integral component of the FOI experienced by the human population, varied between the age-stratified and unstratified models (Fig. 4b). The Kruskal-Wallis tests indicate that the median cercarial densities for the unstratified model and the small and large (S+L) model are significantly different from those of the more age-stratified models. The greater cercarial density for the unstratified model, comprised entirely of large adult snails, and for the S+L model is partially due to the greater cercarial output of small and large adult snails and the compounding effect that this has on the levels of human infection and snail infection levels. However, as in the case of snail infection prevalence, the difference between the completely stratified model and the other models with juvenile and adult age classes is negligible. Specific p-values for the Kruskal-Wallis tests for cercarial density, snail infection prevalence, human infection prevalence, mean worm burden and R0 are presented in Additional file 1: Tables S3–S6.
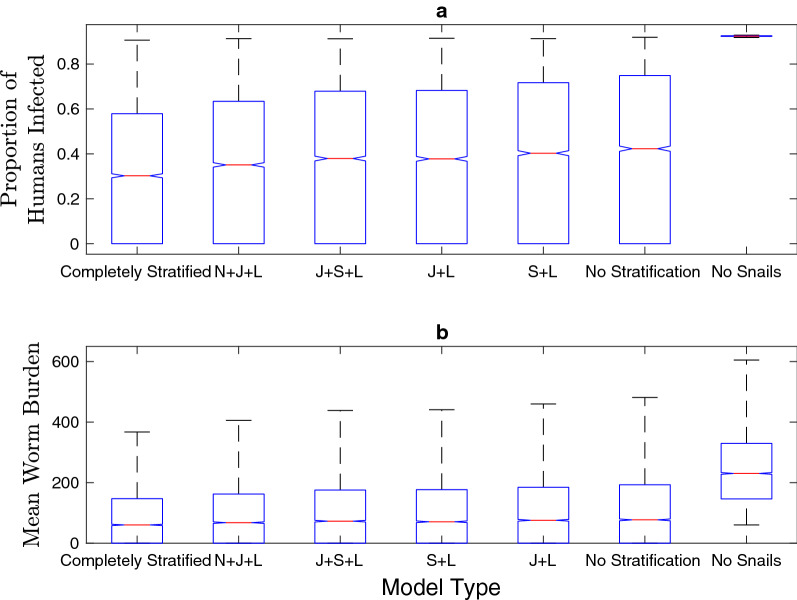
Human infection
Similar to predicted cercarial densities, the models without snail age stratification resulted in altered human infection prevalence estimates over a wide range of possible parameter sets, habitat sizes and snail-to-human transmission rate values (Figs. 3, 5a). A model that does not explicitly include the snail population, which assumes a linear feedback between parasite egg output and snail-to-human FOI, also results in human infection levels that differ substantially from models with snail age stratification (Fig. 5a). In the models with a snail population, the snail-to-human FOI is the product of the snail-to-human transmission rate, the rate of infection given exposure, and the density of cercariae in the water, which is assumed to be directly related to exposure risk. Kruskal-Wallis tests indicate that the distribution of the human infection prevalence differed between: models with age stratification including sub-adult classes and the models without sub-adult snail classes (unstratified and S+L), the model without snails and all models including snails. The completely stratified model was different from only the unstratified and model without snails. Within the age-stratified models which include neonatal or juvenile stages none are significantly different from each other.
Fig. 5a, b.
Estimates of median human infection prevalence and mean worm burden for each model subset with constructed possible parameter sets from LHS. The models without any snails or with only adult snails display an expanded range and higher estimates of probable human infection prevalence and mean worm burden than models with any snail age stratification over these ranges. For abbreviations, see Figs. 1 and 2
Mean worm burden mirrors the human infection prevalence trends and Kruskal-Wallis test results because the differences in mean worm burden between the various age-stratified models were minimal (Fig. 5b). We found that mean worm burden as calculated in the method of the Anderson and May model [39] followed the same trends but showed greater differences between the age-stratified models (Additional file 1: Figures S18, S19). It is important to note that the differences in cercarial density, human infection and mean worm burden are quite small between models with snails, and that the overall trends show that any stratification of the snail population that includes juvenile and adult stages appears to be sufficient to capture the variation between unstratified and stratified models.
Relationship between human and snail infection prevalence
The relationship between human infection prevalence and snail infection prevalence over a range of snail-to-human transmission rate values, and maximum snail population sizes is shown in Fig. 6a. There exists a consistent positive correlation between increasing human infection prevalence and snail infection prevalence. This relationship is consistent with the low levels of snail infection and corresponding high levels of human infection found in field studies in endemic areas [57–65]. Over a large range of habitat sizes, increasing snail infection is associated with increasing human prevalence (Fig. 6a). However, low snail infection can be associated with the majority of the range of possible human infection prevalence. There is also minimal disparity between age-stratified and unstratified models over a range of maximum snail population sizes.
Fig. 6.
a The relationship between snail infection prevalence and human infection prevalence over a large range of snail-to-human transmission rate values, snail populations and habitat sizes. All other parameters are obtained from LHS. The model without snail age stratification estimates higher snail infection prevalence necessary to reach low (0–10%), medium (10–50%) and high (50+%) levels of human infection over a range of FOI and snail densities. b The relationship between the total miracidia and cercariae populations over a large range of snail-to-human transmission rate values and snail densities demonstrates a consistent positive relationship between miracidial and cercarial density. For abbreviations, see Fig. 2
Relationship between cercariae and miracidia
The relationship between miracidial and cercarial density is not consistent over snail-to-human transmission rate values, maximum snail population sizes and habitat volumes. Over a large range of snail-to-human transmission rates, cercarial density saturates with increasing miracidial density, and unstratified models saturate at a higher cercarial density. Equivalent miracidial densities result in higher cercarial density in unstratified models than in age-stratified models. Cercarial density also increases with miracidial density over a range of habitat sizes and unstratified models have higher cercarial densities than stratified models with similar miracidial density values. Over a large range of snail population sizes miracidial density and cercarial density are positively correlated. While there is a difference between the unstratified models and those incorporating snail age, there is a smaller disparity between models including various levels of snail age structure. Overall, the consistency of human infection prevalence, snail infection prevalence, mean worm burden, and of R0, between all models with snail age stratification indicates that any stratification that includes both adult and sub-adult groups is sufficient to capture the non-linear dynamics that occur with the inclusion of snails and snail age stratification.
Discussion
While schistosomiasis-transmission models without explicit snail populations are common in the literature, they may not accurately reflect the range of human infection prevalence or the relationship between snail and human infection prevalence seen in endemic areas [57–61, 63–66]. Accurate estimates of probable changes in snail and human prevalence after reductions in one or both populations are essential to predicting the impact of schistosomiasis control. The changes in predicted FOI and infection prevalence with the inclusion of a snail population indicate that outcomes of major control interest will differ in models which include more detailed snail dynamics. Due to the differences in the feedback between human egg output, FOI, and estimated R0 values, the inclusion of snail age structure in models could alter the projected impact of proposed control measures.
Sensitivity analyses
The sensitivity analyses indicate that snail density is a major driver of the outcomes of interest, though the snail-to-human transmission rate is influential in determining the level of human infection. The importance of the snail-to-human transmission rate in this portion of the transmission cycle is due to the fact that the FOI experienced by the human population in this model is a product of cercarial density, which is highly correlated with snail density, and the snail-to-human transmission rate. The effect of the snail-to-human transmission rate may be diluted by the processes occurring between human exposure and snail exposure; the level of human infection and the probability of eggs reaching water sources and successfully hatching.
Impact of snail age structure
The exclusion of the snail population from the model structure assumes that there is a linear relationship between human egg excretion and the FOI to humans. The differential shedding rates among snails of different ages, and the physiological repercussions of S. mansoni infection are predicted to affect the feedback between snail and human infection levels. The results in Figs. 3, 4, 5 support the prediction that the inclusion of snail dynamics in the model influences these outcomes of interest. All of these patterns are consistent for the suite of model simulations run with potential parameter sets produced with LHS.
In our model framework there are two ways to change snail density: alteration of habitat size or maximum snail population size. Changing the habitat size has a direct effect on not only cercarial density but miracidial density as well. Alteration of the maximum snail population size has direct impacts on cercarial density (Fig. 2) but indirect effects on miracidial density. The relationship between cercarial output and miracidial output in this system appears to be linear, with different snail age structure assumptions altering the slope of the linear dependence. However, this linear relationship only holds for lower snail-to-human transmission rates. Over a range of snail-to-human transmission rates, cercariae and miracidia display a saturating relationship as the increased mortality and reduced fecundity associated with S. mansoni limits the proportion of snails infected in the population. The greater proportion of large snails in unstratified and S+L model types in comparison to a fully stratified model and their capacity for greater cercarial production is evident in the spread of the median cercarial densities in Fig. 6b. As this cercarial density is directly related to the FOI to humans in these models, human egg output may be robust to fluctuations in the FOI but not changes in habitat size, which may fluctuate seasonally. This is due to the disparity in infection levels between snails and humans; only a small percentage of snails need to be infected and shedding for high levels of human infection to occur. More precise model outcomes could be obtained with additional information on parameter ranges. For instance, the probability of Schistosoma eggs reaching water and hatching could be refined with improved estimates on egg viability and hatching rates in the field.
Implications for control programs
The model output was most sensitive to snail density; however, only relative density of intermediate host species is routinely collected [5]. In order to gain a more precise understanding of this system, it would be prudent to collect information on the absolute density of the intermediate host species. In Echinococcus transmission, another intermediate host and parasite system, it is hypothesized that the impacts on definitive host infection level of the intermediate host population age profile could obscure the effects of seasonality on the system as this may be the primary mechanism through which seasonal fluctuations manifest [25]. As snail population size and habitat size may change seasonally it is crucial to understand how the relationship between snail and human prevalence and resulting cercarial and miracidial populations may be altered as these fluctuate. There is evidence that Biomphalaria population size varies seasonally, and it is possible that the population age structure shifts seasonally as well [67–69]. Seasonal fluctuations could alter the impact of control measures. Snail density is a crucial measure for the estimation of the FOI for S. mansoni transmission models that include snails. However, the underlying forces driving changes in snail density, habitat size and snail population size may result in differing impacts on the transmission cycle.
Further work is needed to quantify the effects of reduction in prevalence in either snail or human infection, as would occur after chemoprophylaxis or molluscicide events, on infection in the other host. It is clear from Fig. 6 that inclusion of snail age structure results in a different relationship between snail and human infection levels than in models without age. However, only minimal age structure needs to be included to capture these differences. With varying snail-to-human transmission rate values, which are often estimated from data, there are disparate estimates of the proportion of snails needed to sustain levels of human infection and vice versa. This may be problematic if those values are used to estimate the impact that a decrease in prevalence for either species would have on the other. For instance, a reduction in snail prevalence from 10 to 5% in a model without snail age stratification would assume a decrease in equilibrium human infection from 75 to 25%, whereas in a model with a fully age-stratified snail population the change would be from 45 to 15%; the same levels of snail infection are assumed to be able to support completely different human infection regimes. Overall, in order to accurately estimate the FOI to humans and the impact of various control strategies, snail demographics should be considered in future modeling efforts.
Supplementary Information
Acknowledgements
We thank the anonymous reviewers for their careful comments which helped to improve our paper.
Authors’ contributions
LCA and HW conceived of the original idea and study design. LCA created the model and carried out the implementation of the analyses. LCA wrote the manuscript with support and input from HW and ESL. All authors read and approved the final manuscript.
Funding
No funding supported the development of this study.
Availability of data and materials
All relevant parameters and model equations are available in the manuscript or in the supplementary material.
Ethics approval and consent to participate
This study required no institutional review board approval.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing financial or intellectual interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Larissa C. Anderson, Email: larissaa@unm.edu
Eric S. Loker, Email: esloker@unm.edu
Helen J. Wearing, Email: hwearing@unm.edu
Supplementary Information
The online version contains supplementary material available at 10.1186/s13071-021-04587-8.
References
- 1.World Health Organization Schistosomiasis and soil-transmitted helminthiases: number of people treated in 2016. Wkly Epidemiol Rec. 2017;92:749–760. [PubMed] [Google Scholar]
- 2.Gryseels B, Polman K, Clerinx J, Kestens L. Human schistosomiasis. Lancet. 2006;368:1106–1118. doi: 10.1016/S0140-6736(06)69440-3. [DOI] [PubMed] [Google Scholar]
- 3.Woolhouse MEJ. On the application of mathematical models of schistosome transmission dynamics. I. Natural transmission. Acta Trop. 1991;49:241–270. doi: 10.1016/0001-706X(91)90077-W. [DOI] [PubMed] [Google Scholar]
- 4.Woolhouse ME. The epidemiology of schistosome infections of snails: taking the theory into the field. Parasitol Today. 1990;6:65–70. doi: 10.1016/0169-4758(90)90211-L. [DOI] [PubMed] [Google Scholar]
- 5.Theron A, Rognon A, Pages J-R. Host choice by larval parasites: a study of Biomphalaria glabrata snails and Schistosoma mansoni miracidia related to host size. Parasitol Res. 1998;84:727–732. doi: 10.1007/s004360050477. [DOI] [PubMed] [Google Scholar]
- 6.Feng Z, Li CC, Milner FA. Schistosomiasis models with density dependence and age of infection in snail dynamics. Math Biosci. 2002;177–178:271–286. doi: 10.1016/S0025-5564(01)00115-8. [DOI] [PubMed] [Google Scholar]
- 7.Allen EJ, Victory HD. Modelling and simulation of a schistosomiasis infection with biological control. Acta Trop. 2003;87:251–267. doi: 10.1016/S0001-706X(03)00065-2. [DOI] [PubMed] [Google Scholar]
- 8.Gurarie D, King CH. Heterogeneous model of schistosomiasis transmission and long-term control: the combined influence of spatial variation and age-dependent factors on optimal allocation of drug therapy. Parasitology. 2005;130:49–65. doi: 10.1017/S0031182004006341. [DOI] [PubMed] [Google Scholar]
- 9.Zhao R, Milner FA. A mathematical model of Schistosoma mansoni in Biomphalaria glabrata with control strategies. Bull Math Biol. 2008;70:1886–1905. doi: 10.1007/s11538-008-9330-5. [DOI] [PubMed] [Google Scholar]
- 10.Chiyaka ET, Garira W. Mathematical analysis of the transmission dynamics of schistosomiasis in the human-snail hosts. J Biol Syst. 2009;17:397–423. doi: 10.1142/S0218339009002910. [DOI] [Google Scholar]
- 11.Diekmann O, Heesterbeek JAP, Metz JA. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J Math Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 12.Brooks-Pollock E, Cohen T, Murray M. The impact of realistic age structure in simple models of tuberculosis transmission. PLoS ONE. 2010;5:e8479. doi: 10.1371/journal.pone.0008479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Novoseltsev VN, Michalski AI, Novoseltseva JA, Yashin AI, Carey JR, Ellis AM. An age-structured extension to the vectorial capacity model. PLoS ONE. 2012;7:e39479. doi: 10.1371/journal.pone.0039479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bolker B, Grenfell B. Chaos and biological complexity in measles dynamics. Proc R Soc B Biol Sci. 1993;251:75–81. doi: 10.1098/rspb.1993.0011. [DOI] [PubMed] [Google Scholar]
- 15.Clamer V, Dorigatti I, Fumanelli L, Rizzo C, Pugliese A. Estimating transmission probability in schools for the 2009 H1N1 influenza pandemic in Italy. Theor Biol Med Model. 2016;13:19. doi: 10.1186/s12976-016-0045-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Metcalf CJ, Lessler J, Klepac P, Cutts F, Grenfell BT. Impact of birth rate, seasonality and transmission rate on minimum levels of coverage needed for rubella vaccination. Epidemiol Infect. 2012;140:2290–2301. doi: 10.1017/S0950268812000131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Edmunds WJ, Kafatos G, Wallinga J, Mossong JR. Mixing patterns and the spread of close-contact infectious diseases. Emerg Themes Epidemiol. 2006;3:10. doi: 10.1186/1742-7622-3-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Diekmann O, Heesterbeek JAP, Roberts MG. The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface. 2010;7:873–885. doi: 10.1098/rsif.2009.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vogt-Geisse K, Lorenzo C, Feng Z. Impact of age-dependent relapse and immunity on malaria dynamics. J Biol Syst. 2014;21:1–50. [Google Scholar]
- 20.Pitzer VE, Lipsitch M. Exploring the relationship between incidence and the average age of infection during seasonal epidemics. J Theor Biol. 2009;260:175–185. doi: 10.1016/j.jtbi.2009.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Apolloni A, Poletto C, Colizza V. Age-specific contacts and travel patterns in the spatial spread of 2009 H1N1 influenza pandemic. BMC Infect Dis. 2013;13:176. doi: 10.1186/1471-2334-13-176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gambhir M, Basáñez MG, Burton MJ, Solomon AW, Bailey RL, Holland MJ, et al. The development of an age-structured model for trachoma transmission dynamics, pathogenesis and control. PLoS Negl Trop Dis. 2009;3:e462. doi: 10.1371/journal.pntd.0000462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kwok KO, Davoudi B, Riley S, Pourbohloul B. Early real-time estimation of the basic reproduction number of emerging or reemerging infectious diseases in a community with heterogeneous contact pattern: using data from Hong Kong 2009 H1N1 Pandemic Influenza as an illustrative example. PLoS ONE. 2015;10:e0137959. doi: 10.1371/journal.pone.0137959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thornhill JA. Increased oviposition and growth in immature Biomphalaria glabrata after exposure to Schistosoma mansoni. Parasitology. 1986;93:443–450. doi: 10.1017/S0031182000081166. [DOI] [PubMed] [Google Scholar]
- 25.Atkinson JAM, Williams GM, Yakob L, Clements ACA, Barnes TS, McManus DP, et al. Synthesising 30 years of mathematical modelling of Echinococcus transmission. PLoS Negl Trop Dis. 2013;7:e2386. doi: 10.1371/journal.pntd.0002386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Costa MDL, Rocha RS, Filho PC, Katz N. A 13-year follow-up of treatment and snail control in an area endemic for Schistosoma mansoni in Brazil: incidence of infection and reinfection. Bull World Health Organ. 1993;71:197–205. [PMC free article] [PubMed] [Google Scholar]
- 27.Anderson RM, Crombie J. Experimental studies of age-prevalence curves for Schistosoma mansoni infections in populations of Biomphalaria glabrata. Parasitology. 1984;89:79–104. doi: 10.1017/S0031182000001153. [DOI] [PubMed] [Google Scholar]
- 28.Toledo R, Fried B. Biomphalaria snails and larval trematodes. New York: Springer; 2011. [Google Scholar]
- 29.Niemann GM, Lewis FA. Schistosoma mansoni: influence of Biomphalaria glabrata size on susceptibility to infection and resultant cercarial production. Exp Parasitol. 1990;70:286–292. doi: 10.1016/0014-4894(90)90110-X. [DOI] [PubMed] [Google Scholar]
- 30.Gerard C, Theron A. Age/size and time specific effects of Schistosoma mansoni on energy allocation patterns of its snail host Biomphalaria glabrata. Oecologia. 1997;112:447–452. doi: 10.1007/s004420050331. [DOI] [PubMed] [Google Scholar]
- 31.Theron A, Mone H, Gerard C. Spatial and energy compromise between host and parasite: the Biomphalaria glabrata-Schistosoma mansoni system. Int J Parasitol. 1992;22:91–94. doi: 10.1016/0020-7519(92)90084-X. [DOI] [PubMed] [Google Scholar]
- 32.Chan M-S, Montresor A, Savioli L, Bundy DAP. Planning chemotherapy based schistosomiasis control: validation of a mathematical model using data on Schistosoma haematobium from Pemba. Tanzania. Epidemiol Infect. 1999;123:487–497. doi: 10.1017/S0950268899003167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Barbour AD. Modeling the transmission of schistosomiasis: an introductory view. Am J Trop Med Hyg. 1996;55:135–143. doi: 10.4269/ajtmh.1996.55.135. [DOI] [PubMed] [Google Scholar]
- 34.Yang HM, Bezerra Coutinho FA. Acquired immunity of a schistosomiasis transmission model—analysis of the stabilizing effects. J Theor Biol. 1999;196:473–482. doi: 10.1006/jtbi.1998.0837. [DOI] [PubMed] [Google Scholar]
- 35.Mushayabasa S, Bhunu CP. Modeling schistosomiasis and HIV/AIDS codynamics. Comput Math Methods Med. 2011 doi: 10.1155/2011/846174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Brooker S, Whawell S, Kabatereine NB, Fenwick A, Anderson RM. Evaluating the epidemiological impact of national control programmes for helminths. Trends Parasitol. 2004;20:537–545. doi: 10.1016/j.pt.2004.08.012. [DOI] [PubMed] [Google Scholar]
- 37.French MD, Churcher TS, Gambhir M, Fenwick A, Webster JP. Observed reductions in Schistosoma mansoni transmission from large-scale administration of praziquantel in Uganda: a mathematical modelling study. PLoS Negl Trop Dis. 2010;4:e897. doi: 10.1371/journal.pntd.0000897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gurarie D, King CH. Population biology of Schistosoma mating, aggregation, and transmission breakpoints: more reliable model analysis for the end-game in communities at risk. PLoS ONE. 2014;9:e115875. doi: 10.1371/journal.pone.0115875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Anderson R, May RM. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press; 1991. [Google Scholar]
- 40.Bourke CD, Maizels RM, Mutapi F. Acquired immune heterogeneity and its sources in human helminth infection. Parasitology. 2011;138:139–159. doi: 10.1017/S0031182010001216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Colley DG, Secor WE. Immunology of human schistosomiasis. Parasite Immunol. 2014;36:347–357. doi: 10.1111/pim.12087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tchuenté LT, Momo SC, Stothard JR, Rollinson D. Efficacy of praziquantel and reinfection patterns in single and mixed infection foci for intestinal and urogenital schistosomiasis in Cameroon. Acta Trop. 2013;128:275–283. doi: 10.1016/j.actatropica.2013.06.007. [DOI] [PubMed] [Google Scholar]
- 43.Gerard C, Mone H, Theron A. Schistosoma mansoni–Biomphalaria glabrata: dynamics of the sporocyst population in relation to the miracidial dose and the host size. Can J Zool. 1993;9:1880–1885. doi: 10.1139/z93-268. [DOI] [Google Scholar]
- 44.Cooper LA, Ramani SK, Martin AE, Richards CS, Fred A, Cooper LA, et al. Schistosoma mansoni infections in neonatal Biomphalaria glabrata snails. J Parasitol. 1992;78:441–446. doi: 10.2307/3283641. [DOI] [PubMed] [Google Scholar]
- 45.Theron A. Dynamics of larval populations of Schistosoma mansoni in Biomphalaria glabrata. II. Chronobiology of the intramolluscal larval development during the shedding period. Ann Trop Med Parasitol. 1981;75:547–554. doi: 10.1080/00034983.1981.11687479. [DOI] [PubMed] [Google Scholar]
- 46.Faro JM, Perazzini M, dos Reis CL, Mello-Silva CC, Pinheiro J, Mota EM, et al. Biological, biochemical and histopathological features related to parasitic castration of Biomphalaria glabrata infected by Schistosoma mansoni. Exp Parasitol. 2013;134:228–234. doi: 10.1016/j.exppara.2013.03.020. [DOI] [PubMed] [Google Scholar]
- 47.Schneck JL, Fried B. Growth of Biomphalaria glabrata (NMRI strain) and Helisoma trivolvis (Colorado strain) under laboratory conditions. Am Malacol Bull. 2005;20:71–73. [Google Scholar]
- 48.World Bank. World DataBank—World Development Indicators—Kenya.
- 49.Crews AE, Yoshino TP. Schistosoma mansoni: effect of infection on reproduction and gonadal growth in Biomphalaria glabrata. Exp Parasitol. 1989;68:326–334. doi: 10.1016/0014-4894(89)90114-8. [DOI] [PubMed] [Google Scholar]
- 50.Costa MJFS, Grault CE, Confalonieri UEC. Comparative study of the fecundity and fertility of Biomphalaria glabrata (Say, 1818) and Biomphalaria straminea (Dunker, 1848) in a laboratory through self-fertilization and cross-fertilization. Rev Inst Med Trop Sao Paulo. 2004;46:157–163. doi: 10.1590/S0036-46652004000300007. [DOI] [PubMed] [Google Scholar]
- 51.Feng Z, Eppert A, Milner FA, Minchella DJ. Estimation of parameters governing the transmission dynamics of schistosomes. Appl Math Lett. 2004;17:1105–1112. doi: 10.1016/j.aml.2004.02.002. [DOI] [Google Scholar]
- 52.Theron A, Rognon A, Gourbal B, Mitta G. Multi-parasite host susceptibility and multi-host parasite infectivity: a new approach of the Biomphalaria glabrata/Schistosoma mansoni compatibility polymorphism. Infect Genet Evol. 2014;26:80–88. doi: 10.1016/j.meegid.2014.04.025. [DOI] [PubMed] [Google Scholar]
- 53.Cheever AW. A quantitative post-mortem study of Schistosomiasis mansoni in man. Am J Trop Med Hyg. 1968;17:38–64. doi: 10.4269/ajtmh.1968.17.38. [DOI] [PubMed] [Google Scholar]
- 54.Cheever AW, Macedonia JG, Mosimann JE, Cheever EA. Kinetics of egg production and egg excretion by Schistosoma mansoni and S. japonicum in mice infected with a single pair of worms. Am J Trop Med Hyg. 1994;50:281–295. doi: 10.4269/ajtmh.1994.50.281. [DOI] [PubMed] [Google Scholar]
- 55.Cummings JH, Bingham SA, Eastwood MA, Heaton KW. Fecal weight, colon cancer risk, and dietary intake of nonstarch polysaccharides (dietary fiber) Gastroenterology. 1992;103:1783–1789. doi: 10.1016/0016-5085(92)91435-7. [DOI] [PubMed] [Google Scholar]
- 56.Hartemink NA, Randolph SE, Davis SA, Heesterbeek JAP. The basic reproduction number for complex disease systems: defining R0 for tick-borne infections. Am Nat. 2008;171:743–754. doi: 10.1086/587530. [DOI] [PubMed] [Google Scholar]
- 57.Opisa S, Odiere MR, Jura WGZO, Karanja DMS, Mwinzi PNM. Malacological survey and geographical distribution of vector snails for schistosomiasis within informal settlements of Kisumu City, western Kenya. Parasites Vectors. 2011;4:226. doi: 10.1186/1756-3305-4-226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Poole H, Terlouw DJ, Naunje A, Mzembe K, Stanton M, Betson M, et al. Schistosomiasis in pre-school-age children and their mothers in Chikhwawa district, Malawi with notes on characterization of schistosomes and snails. Parasites Vectors. 2014;7:153. doi: 10.1186/1756-3305-7-153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Standley CJ, Vounatsou P, Gosoniu L. The distribution of Biomphalaria (Gastropoda: Planorbidae) in Lake Victoria with ecological and spatial predictions using Bayesian modelling. Hydrobiologia. 2012;683:249–264. doi: 10.1007/s10750-011-0962-3. [DOI] [Google Scholar]
- 60.Mutuku FM, King CH, Bustinduy AL, Mungai PL, Muchiri EM, Kitron U. Impact of drought on the spatial pattern of transmission of Schistosoma haematobium in Coastal Kenya. Am J Trop Med Hyg. 2011;85:1065–1070. doi: 10.4269/ajtmh.2011.11-0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gashaw F, Aemero M, Legesse M, Petros B, Teklehaimanot T, Medhin G, et al. Prevalence of intestinal helminth infection among school children in Maksegnit and Enfranz towns, northwestern Ethiopia, with emphasis on Schistosoma mansoni infection. Parasites Vectors. 2015;8:567. doi: 10.1186/s13071-015-1178-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Standley CJ, Adriko M, Arinaitwe M, Atuhaire A, Kazibwe F, Fenwick A, et al. Epidemiology and control of intestinal schistosomiasis on the Sesse Islands, Uganda: integrating malacology and parasitology to tailor local treatment recommendations. Parasites Vectors. 2010;3:64. doi: 10.1186/1756-3305-3-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Landouré A, Dembélé R, Goita S, Kané M, Tuinsma M, Sacko M, et al. Significantly reduced intensity of infection but persistent prevalence of schistosomiasis in a highly endemic region in Mali after repeated treatment. PLoS Negl Trop Dis. 2012;6:e1774. doi: 10.1371/journal.pntd.0001774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Stanton MC, Adriko M, Arinaitwe M, Howell A, Davies J, Allison G, et al. Intestinal schistosomiasis in Uganda at high altitude (> 1400 m): malacological and epidemiological surveys on Mount Elgon and in Fort Portal crater lakes reveal extra preventive chemotherapy needs. Infect Dis Poverty. 2017;6:34. doi: 10.1186/s40249-017-0248-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Alemayehu B, Tomass Z, Wadilo F, Leja D, Liang S, Erko B. Epidemiology of intestinal helminthiasis among school children with emphasis on Schistosoma mansoni infection in Wolaita. BMC Public Health. 2017;17:587. doi: 10.1186/s12889-017-4499-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Standley CJ, Adriko M, Arinaitwe M, Atuhaire A, Kazibwe F, Fenwick A, et al. Epidemiology and control of intestinal schistosomiasis on the Sesse Islands, Uganda: integrating malacology and parasitology to tailor local treatment recommendations. Parasites Vectors. 2010;3:64. doi: 10.1186/1756-3305-3-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Scott JT, Vereecken K, Fall A, Diop M, Ly A, De CD, et al. Human water contacts patterns in Schistosoma mansoni epidemic foci in northern Senegal change according to age, sex and place of residence, but are not related to intensity of infection. Trop Med Int Heal. 2003;8:100–108. doi: 10.1046/j.1365-3156.2003.00993.x. [DOI] [PubMed] [Google Scholar]
- 68.Coulibaly G, Madsen H. Seasonal density fluctuations of intermediate hosts of schistosomes in two streams in Bamako Mali. J Afr Zool. 1990;104:201–212. [Google Scholar]
- 69.Perez-saez J, Mande T, Ceperley N, Bertuzzo E, Mari L, Gatto M. Hydrology and density feedbacks control the ecology of intermediate hosts of schistosomiasis across habitats in seasonal climates. Proc Natl Acad Sci. 2016;113:6427–6432. doi: 10.1073/pnas.1602251113. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant parameters and model equations are available in the manuscript or in the supplementary material.